| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.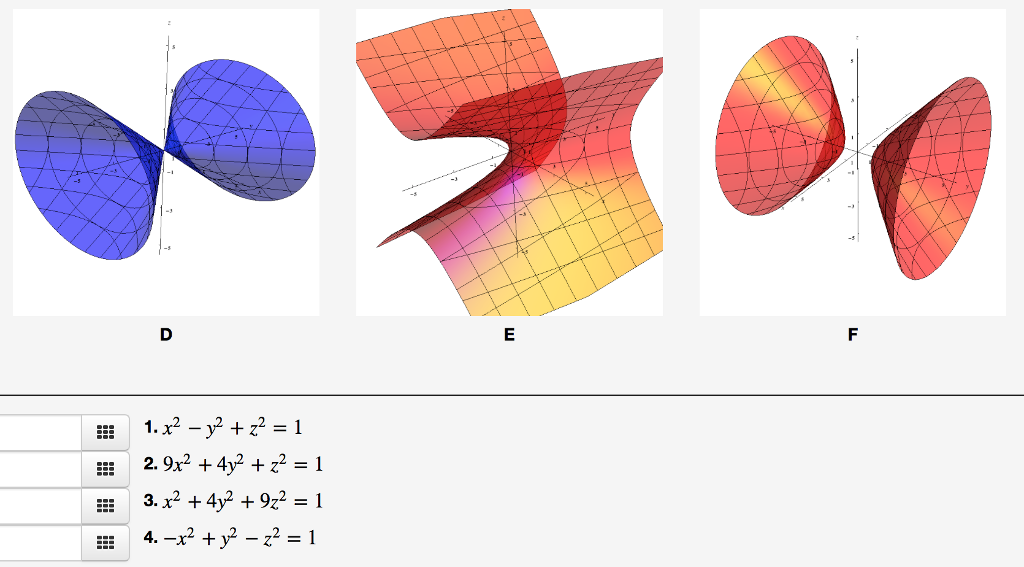 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.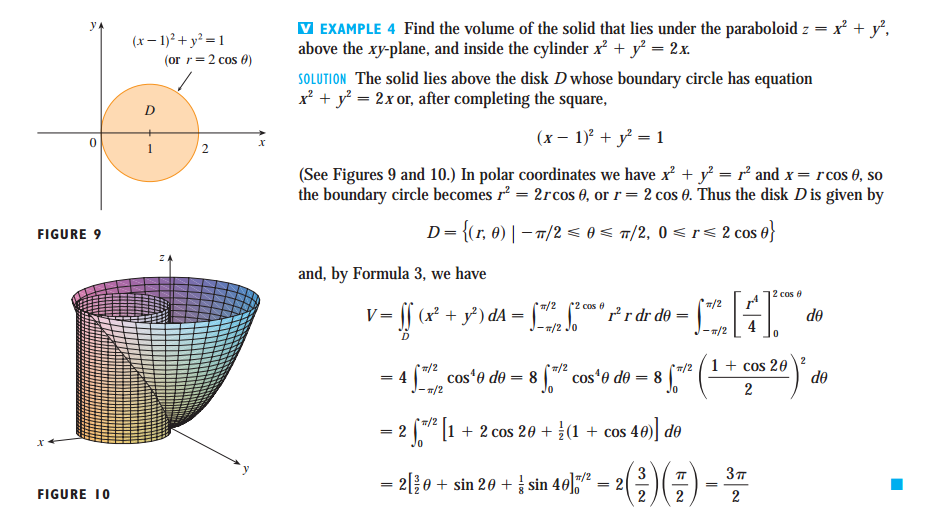 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
 Для целочисленных решений с пифагорейскими тройками происходит сведение к случаю примитивных троек, но при $a \neq 0$ существует ограничение на общие множители $(x,y,z)$, а при $a = \pm 1$ все целочисленные решения примитивны. Организация пифагорейских троек с использованием нескольких целочисленных матриц 3×3 в качестве преобразований, соединяющих разные решения, действительно использует структуру $O(2,1)$, и множество решений для уравнения с $a \neq 0$ может быть представлено таким же образом ( возможно, с более чем одним компонентом связности, когда $|a| > 1$). 92}$
Для целочисленных решений с пифагорейскими тройками происходит сведение к случаю примитивных троек, но при $a \neq 0$ существует ограничение на общие множители $(x,y,z)$, а при $a = \pm 1$ все целочисленные решения примитивны. Организация пифагорейских троек с использованием нескольких целочисленных матриц 3×3 в качестве преобразований, соединяющих разные решения, действительно использует структуру $O(2,1)$, и множество решений для уравнения с $a \neq 0$ может быть представлено таким же образом ( возможно, с более чем одним компонентом связности, когда $|a| > 1$). 92}$Правда, я использую эту формулу в обратном порядке. Найти решения уравнения Пелла гораздо сложнее, чем простых уравнений типа пифагорейских троек. Так что найдите их, а затем получите решения уравнения Пелла. Самое интересное, что решение Пелла связано с пифагорейскими тройками.
$\endgroup$
Поверхности, часть 2
Поверхности, часть 2Поверхности и контурные графики
Часть 2: квадратные поверхности
Квадратные поверхности — это графики квадратных уравнений с тремя декартовыми переменными.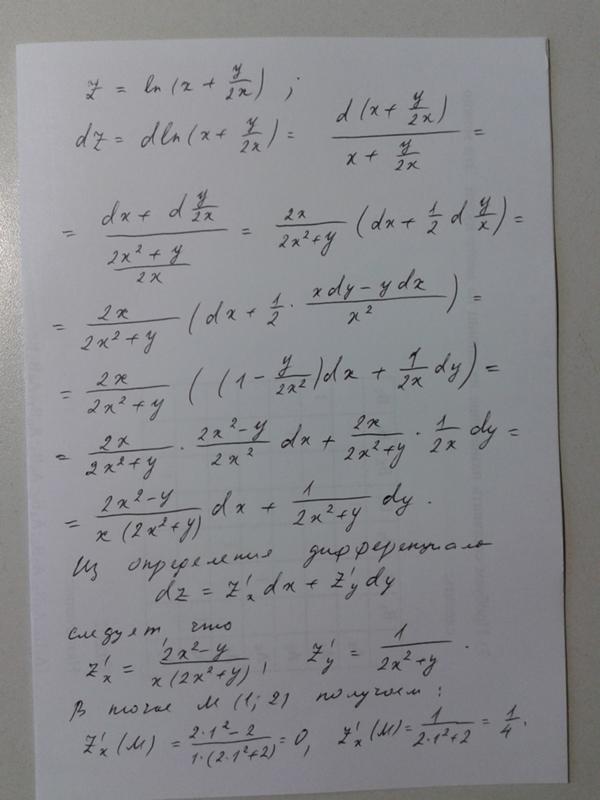 в космосе. Подобно графикам квадратичных уравнений на плоскости, их формы зависят от
знаки различных коэффициентов в их квадратных уравнениях.
в космосе. Подобно графикам квадратичных уравнений на плоскости, их формы зависят от
знаки различных коэффициентов в их квадратных уравнениях.
Сферы и эллипсоиды
сфера — это граф уравнение вида x 2 + y 2 + z 2 = p 2 для некоторого действительного числа p . Радиус сферы равен p (см. рисунок ниже). Эллипсоиды представляют собой графики уравнений вида x 2 + на 2 + c z 2 = p 2 , где a , b и c все положительные. В частности, сфера — это особый эллипсоид, для которого a , b и c все равны.
- Постройте график x 2 + y 2 + z 2 = 4
на вашем листе в декартовых координатах.
 Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид.
Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид. - Какие кривые вы найдете, когда вы пересекают сферу плоскостью, перпендикулярной одной из осей координат? Что вы нашли для эллипсоида?
Параболоиды
Поверхности, пересечения которых с плоскости, перпендикулярные любым двум координатным осям, являются параболами в тех самолеты называются параболоиды . Пример показан на рисунке ниже — это график z = x 2 + y 2 .
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения
эта поверхность с плоскостями, перпендикулярными х- и у- оси
являются параболами.
 [Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .]
[Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .] - Измените уравнение на z = 3 x 2 + y 2 , и снова сюжет. Как изменится поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.
поверхность на следующем рисунке представляет собой график z = x 2 — y 2 . В этом случае пересечения с плоскостями, перпендикулярными x и и оси по-прежнему являются параболами, но два набора парабол отличаются направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его также называют «седловидная поверхность».
- Сделайте свой собственный сюжет этой гиперболы
параболоида на листе и поворачивайте график, чтобы увидеть его с разных точек зрения.
 Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Гиперболоиды
Гиперболоиды — это поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определение характерно то, что их пересечения с плоскостями, перпендикулярными какому-либо две оси координат являются гиперболами. Есть два типа гиперболоидов — первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1, что показано на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на форму, обычно используемую для атомных электростанций градирни. (Источник: Агентство по охране окружающей среды Ответ на инцидент в Три-Майл-Айленде.)
Эта поверхность называется гиперболоидом .
одного листа , потому что это все «связано» в одно целое. (Мы будем
перейти к другому делу в настоящее время.)
(Мы будем
перейти к другому делу в настоящее время.)
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами. [Подсказка: установите либо y = c или x = c для некоторой константы c .]
Другой тип — гиперболоид . из двух листов , что иллюстрируется графиком x 2 — y 2 — z 2 = 1, показано ниже.
- Сделайте свой собственный участок этой поверхности
на листе и поверните график, чтобы увидеть его с разных точек зрения.


 Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид.
Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид. [Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .]
[Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .]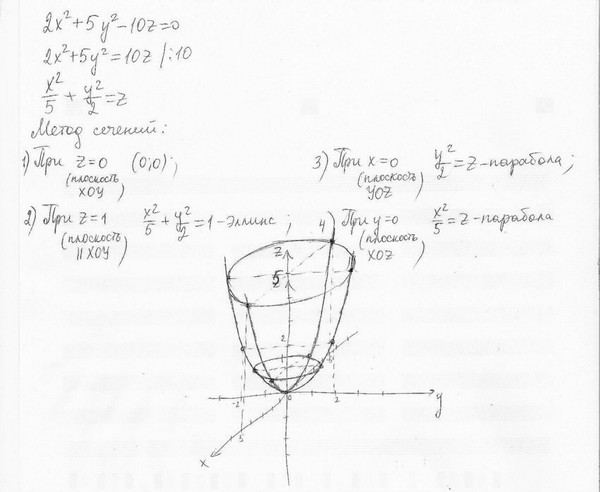 Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.