Круг окружность это: Окружность и круг — что это, определение и ответ

Содержание

Окружность и круг — что это, определение и ответ

Окружность – это множество всех точек плоскости, равноудаленных от данной точки на плоскости.

Круг – это часть плоскости, ограниченная окружностью.

Окружность – это замкнутая линия, а круг – это площадь, находящаяся внутри окружности:

Длина окружности равна:

$l = 2\pi R = \text{dπ}$

где $R$ – это радиус, а $D$ – диаметр окружности

ЭЛЕМЕНТЫ ОКРУЖНОСТИ:

Центр окружности – точка O.

Радиус окружности – отрезок R, соединяющий точку окружности с центром. Все радиусы одной окружности равны.

Хорда – это отрезок АВ, соединяющий любые две точки окружности.

Диаметр – это хорда d, проходящая через центр окружности. Диаметр равен двум радиусам.

ДУГА И СЕКТОР:

Дуга – это часть окружности, заключенная между точками на ней. \circ}}\) показывает, какую часть от всей окружности занимает дуга

КАСАТЕЛЬНАЯ:

Касательная к окружности – это прямая, которая пересекается с окружностью в одной точке.

Свойства касательной:

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания:

$a\bot OA,\ A \in a,\ OA = R$

2. Отрезки касательных, проведенных из одной точки, равны до точек касания.

$CA = CB,\ a,\ b\ –\ касательные$

ЦЕНТРАЛЬНЫЕ И ВПИСАНЫЕ УГЛЫ:

С окружностью связано два вида углов – вписанные и центральные. Рассмотрим такую окружность:

На данном чертеже угол АОС является центральным, а угол АВС – вписанным.

Вписанный угол – угол, вершина которого лежит на окружности, а стороны являются ее хордами.

Свойства вписанного угла:

1. Измеряется половиной дуги, на которую он опирается.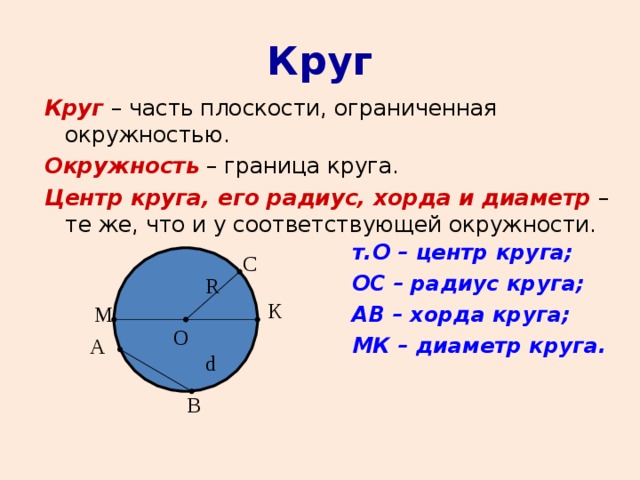

2. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

3. Вписанный угол, опирающийся на диаметр — прямой.

Центральный угол – угол, образованный двумя радиусами. Его вершина лежит на центре окружности.

Свойства центрального угла:

1. Измеряется дугой, на которую опирается;

2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.

КОМБИНАЦИИ ХОРД, КАСАТЕЛЬНЫХ И СЕКУЩИХ:

Секущая – это прямая, которая пересекает окружность в двух точках.

ПЕРЕСЕЧЕНИЕ ХОРД

Хорды AB и CD пересекаются в точке M

1. Произведение длин отрезков пересекающихся хорд равны:

$AM \bullet MB = CM \bullet MD$

2. Угол между двумя пересекающихся хорд равен полусумме высекаемых ими дуг:

$\angle AMD = \angle CMD = \frac{дуга\ AD + дуга\ \text{CB}\ }{2}$

ХОРДА И КАСАТЕЛЬНАЯ

Прямая AB касается окружности в точке B, BC – хорда. {2}\)

2. Угол между секущей и касательной равен полуразности высекаемых ими дуг:

$\angle DAC = \frac{дуга\ DC\ –\ дуга\ \text{CB}}{2}$

УГОЛ МЕЖДУ СЕКУЩИМИ

AD и AE – секущие, выходящие из одной точки, пересекающие окружность в точках В и С соответственно.

Угол между секущими равен полуразности большей и меньшей высекаемых ими дуг:

$\angle BAC = \frac{дуга\ \text{DE}\ –\ дуга\ \text{BC}}{2}$

Окружность и круг — Умскул Учебник

На этой странице вы узнаете
Где в ловце снов спрятана хорда?
В чем отличие окружности от пиццы?
Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360?
Оглянитесь вокруг: геометрические фигуры окружают нас повсюду, а в математике и вовсе встречаются почти в каждом задании. Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.
Обруч и окружность
Давайте вспомним один из предметов инвентаря художественной гимнастики – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца. Именно с помощью обруча мы приближаемся к термину “окружность”.
Окружность – это замкнутая кривая, все точки которой равноудалены от центра.
Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой.
То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра.
Элементы окружности
Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.
Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности.
Диаметр обозначается буквой D и равняется двум радиусам.
D = 2R
Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности.
Где в ловце снов спрятана хорда?
Представим ловец снов. Когда его изготавливают, натягивают нитку от точки на ободе до точки на другом конце обода. Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр.
Получается, каждая ниточка внутри ловца слов будет хордой.
Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности.
Рассмотрим свойства хорды.
1 свойство. При пересечении двух хорд произведения их отрезков равны.
Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.
2 свойство. Равные хорды стягивают равные дуги.
3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам.
Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ.
Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный.
Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию.
Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ.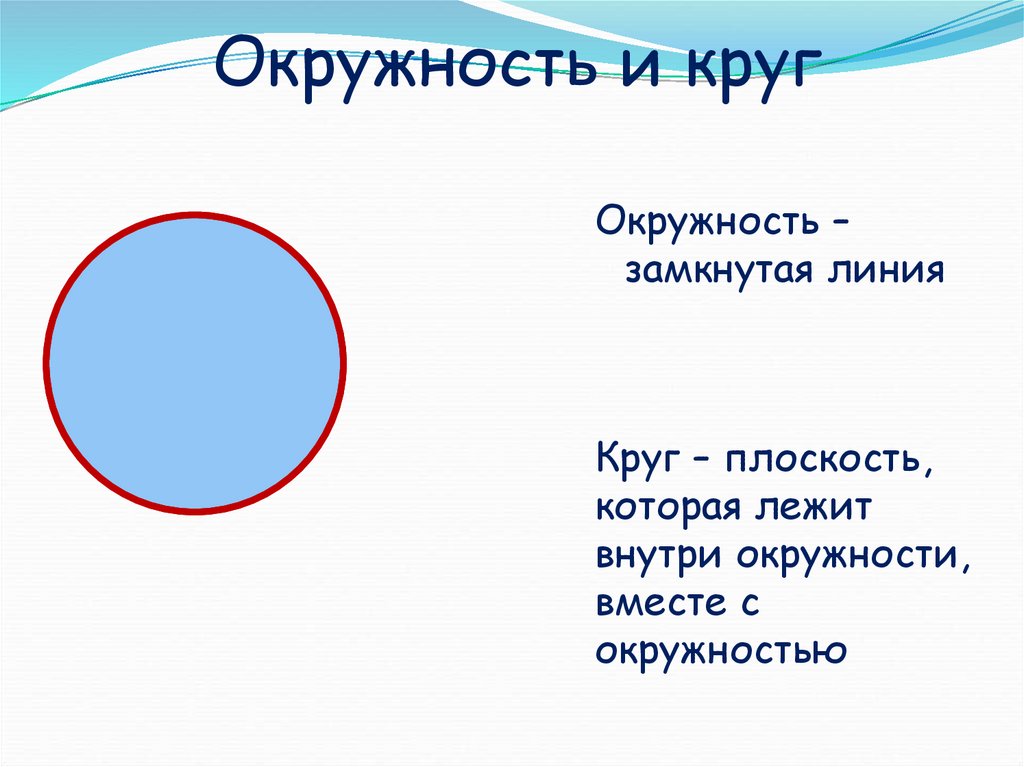
Дуга – это часть окружности, началом и концом которой являются две произвольные точки.
Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.
Пицца и круг
Мы рассмотрели окружность. Тут уже может возникнуть вопрос: чем круг отличается от окружности?
В чем отличие окружности от пиццы?
Представим пиццу. Она круглой формы? Да. Похожа она на обруч? Нет. И пицца, и обруч имеют форму круга. Разница в том, что обруч внутри полый, а пицца полностью состоит из теста и начинки. Иными словами, в пицце есть не только контур в виде корочки, но и все, что лежит внутри него.
Когда окружность внутри заполнена “начинкой” – это уже круг.
Круг – это геометрическая фигура, которая ограничена окружностью.
Элементы круга
Рассмотрим элементы круга.
Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы.
Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков.
Форма кусочков пиццы очень напоминает сектор круга.
Сектор – это часть круга, которую ограничивают радиусы и дуга.
При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым.
Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга.
Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину:
Таким образом, мы отрежем уже не сектор, а сегмент от пиццы.
Сегмент – это часть круга, которая ограничена хордой и дугой.
Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым.
Подведем итог:
И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент.
Формулы для окружности и круга
Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их.
Однако перед этим необходимо ввести еще несколько терминов.
Длина окружности – это длина кривой, которая образует окружности.
Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности.
Длина дуги – это длина части кривой, которая образует окружность.
Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть.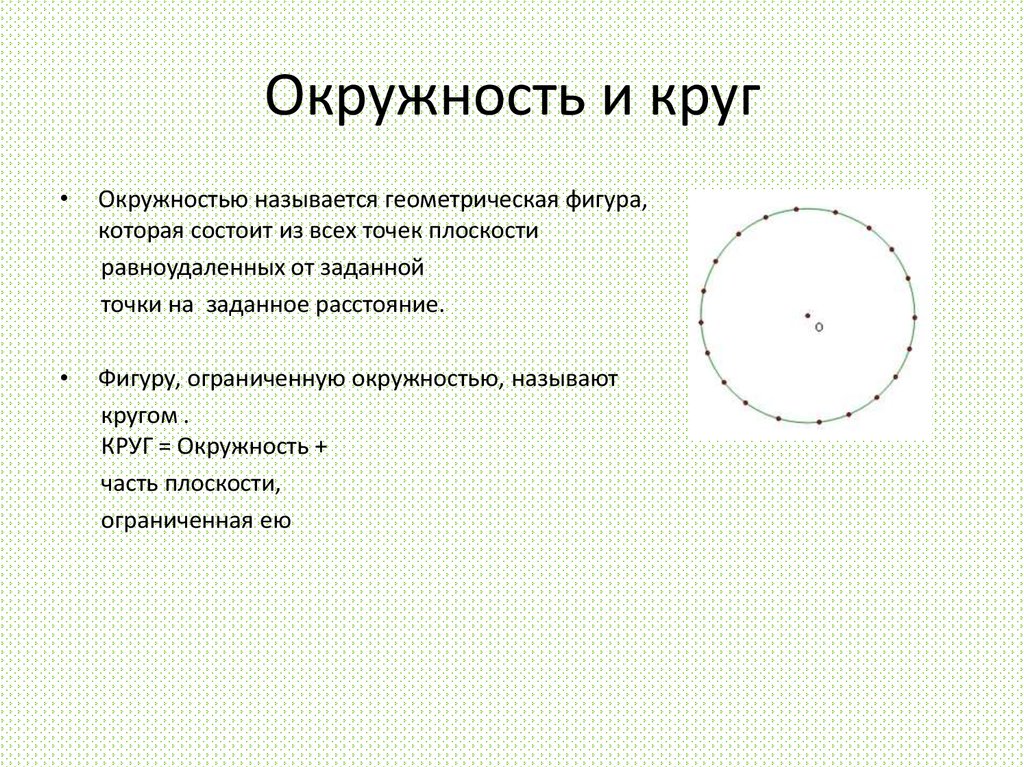
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач.
Дуга окружности
Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360^$\circ$. Тогда половина дуги окружности будет равняться 180.
При этом дуга, равная 180^$\circ$, называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.
Думаем, хоть раз в жизни вы слышали фразу “повернуться на 180^$\circ$ градусов” или “поменять свое мнение на 180^$\circ$ градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180^$\circ$.
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности.
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А.
Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360?
При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.
Углы в окружности
Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности.
На рисунке угол АОВ будет центральным.
Свойство центрального угла:
Центральный угол равен градусной мере дуги, на которую он опирается.
Например, дуга АВ равна 36^$\circ$, тогда угол АОВ также равен 36^$\circ$.
Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.
На рисунке угол АСВ – вписанный.
Свойства вписанного угла окружности:
Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Например, дуга АВ равна 50^$\circ$, тогда угол АСВ равен 25^$\circ$.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой.
Вписанный угол, опирающийся на диаметр, равен 90^$\circ$.
Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180^$\circ$. Тогда вписанный угол будет равняться 180^$\circ$ : 2 = 90^$\circ$.
Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу.
Это легко доказать, если вспомнить, что:
центральный угол равен градусной мере дуги, на которую он опирается,
вписанный угол равен половине градусной меры дуги, на которую он опирается.
Следовательно, $∠ACB = \frac{1}{2}∠AOB$.
Фактчек
Окружность – это замкнутая кривая, все точки которой равноудалены от центра. Элементами окружности являются радиус, диаметр, хорда, дуга.
Круг – это геометрическая фигура, которая ограничена окружностью. Помимо радиуса, диаметра и хорды, в круге может встретиться сегмент и сектор.
Вся дуга окружности имеет величину 360 градусов. Тогда половина дуги будет равняться 180 градусам.
В окружности встречаются центральные и вписанные углы. При этом вписанный угол равен половине дуги, на которую он опирается, а центральный угол равен градусной мере дуги, на которую он опирается. Как следствие, если центральный и вписанный углы опираются на одну дугу, то центральный угол равен двум вписанным углам.
Проверь себя
Задание 1.
Что такое окружность?
Замкнутая кривая, все точки которой равноудалены от центра;
Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
Геометрическая фигура, которая имеет круглую форму;
Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра.
Задание 2.
Что такое диаметр окружности?
Это отрезок, соединяющий центр окружности и любую точку на окружности;
Это отрезок, соединяющий две произвольные точки на окружности;
Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
Это половина дуги окружности.
Задание 3.
По какой формуле можно найти длину окружности?
$l = \frac{R}{180} * n$
$C=2 \pi R$
C=2R
$l = \pi R$
Задание 4.
На окружности выделили дугу в 60 градусов. Какую часть от всей окружности занимает эта дуга?
$\frac{1}{2}$
$\frac{1}{3}$
$\frac{1}{6}$
$\frac{1}{4}$
Задание 5.
Вписанный угол равен 50 градусов. Чему равен центральный угол, опирающийся на ту же дугу?
200
50
100
150
Ответы: 1. – 1 2. – 3 3. – 2 4. – 3 5. – 3
Окружность — Формула, Примеры | Окружность круга
Окружность окружности — это периметр окружности. Это общая длина границы круга. Длина окружности есть произведение постоянной π на диаметр окружности. Человеку, идущему по круглому парку или окаймленному круглому столу, требуется эта метрика окружности круга. Длина окружности является линейной величиной, и ее единицы измерения такие же, как единицы длины.
Окружность — это круглая замкнутая фигура , все ее граничные точки равноудалены от фиксированной точки, называемой центром. Двумя важными показателями круга являются площадь круга и длина окружности. Здесь мы будем стремиться к пониманию формулы и вычислению длины окружности.

1. Что такое длина окружности?
2. Длина окружности Формула
3. Как найти длину окружности?
4. Окружность к диаметру
5. Часто задаваемые вопросы Окружность круга?
Что такое длина окружности?
Окружность окружности – это ее граница или длина полной дуги окружности. Давайте разберемся с этой концепцией на примере. Рассмотрим круговой парк, показанный ниже.
Если мальчик начинает бежать из точки «А» и достигает той же точки, пройдя один полный круг по парку, он преодолевает расстояние. Это расстояние или граница называется окружностью парка, который имеет форму круга. Окружность — это длина границы.
Окружность круга Определение
Окружность круга относится к размеру его границы. Если мы откроем круг и измерим границу точно так же, как измеряем прямую линию, мы получим длину окружности в единицах длины, таких как сантиметры, метры или километры.

Теперь давайте узнаем об элементах, из которых состоит окружность. Это три самых важных элемента круга.
Центр: Центром окружности называется точка, находящаяся на фиксированном расстоянии от любой другой точки окружности.
Диаметр: Диаметр — это расстояние по окружности через центр, это линия, которая пересекает окружность с обоих концов и должна проходить через центр.
Радиус: Радиус круга — это расстояние от центра круга до любой точки на окружности круга.
Длина окружности Формула
Формула длины окружности выражается с использованием радиуса окружности r и значения числа пи. Это выражается как: Длина окружности по формуле = 2πr. При использовании этой формулы окружности, если у нас нет значения радиуса, мы можем найти его, используя диаметр. То есть, если диаметр известен, его можно разделить на 2, чтобы получить значение радиуса, потому что диаметр круга = 2 × радиус. Другой способ рассчитать длину окружности — использовать формулу: длина окружности = π × диаметр. Если нам нужно вычислить радиус или диаметр, когда дана длина окружности, мы используем формулу: Радиус = Длина окружности/2π

Как найти длину окружности?
Хотя длина окружности равна длине ее границы, ее нельзя вычислить с помощью линейки (шкалы), как это обычно делают для других многоугольников. Это потому, что круг — это изогнутая фигура. Следовательно, чтобы вычислить длину окружности, мы применяем формулу, которая использует радиуса или диаметра круга и значение Пи (π).

Пи — это специальная математическая константа, значение которой приблизительно равно 3,14159 или π = 22/7. Значение π = 22/7 используется в различных формулах. Это отношение длины окружности к диаметру, где C = πD. Рассмотрим практическую иллюстрацию, чтобы понять, как вычислить длину окружности с помощью формулы длины окружности.
Пример: Если радиус окружности равен 25 единицам, найдите длину окружности. (Возьмем π = 3,14)
Решение: Дано, радиус = 25 единиц
Напишем формулу окружности, а затем подставим в нее значение r (радиуса).
Формула длины окружности = 2πr
С = 2 × π × 25
С = 2 × 3,14 × 25 = 157 единиц
Следовательно, длина окружности равна 157 единицам.
Окружность к диаметру
Отношение длины окружности к диаметру круга используется для определения стандартного определения числа Пи (π). Если вы знаете диаметр ‘d’ круга, то вы можете легко найти длину окружности C, используя соотношение: C = πd. Итак, если окружность C поставить в отношении к диаметру d, мы получим ответ π.

Важные замечания по длине окружности
π(Pi) — математическая константа, представляющая собой отношение длины окружности к ее диаметру. Оно приближается к π = 22/7 или 3,14
.
Если радиус круга увеличивается дальше и касается границы круга, он становится диаметром круга. Следовательно, Диаметр = 2 × Радиус
Окружность — это расстояние по окружности или длина окружности.
Мы можем найти длину окружности, используя радиус или диаметр.
Формула длины окружности = π× Диаметр; Окружность = 2πr.
☛ Статьи по теме
Окружность Земли
Окружность кругов Рабочие листы
Калькулятор отношения диаметра к окружности
Калькулятор окружности

Длина окружности Примеры
Пример 1: Если радиус круга равен 28 см, найдите длину окружности.
Решение:
Дано, Радиус круга = 28 см. Чтобы найти длину окружности, воспользуемся формулой длины окружности: 2πr = 2×22/7×28 = 176 см.
Следовательно, длина окружности равна 176 см.
Пример 2: Длина окружности колеса 440 см. Найдите его радиус и диаметр.
Решение:
Дано, Окружность колеса = 440 см
Длина окружности формула = 2πr
Подставим известные значения, чтобы сначала найти радиус.
440 = 2πr
440 = 2 × (22/7) × г
радиус = 70 см
Диаметр = 2 × радиус 90 113 Диаметр = 2 × 70
Следовательно, радиус равен 70 см, а диаметр 140 см.
Пример 3: Периметр прямоугольного провода равен 264 м. Та же проволока сгибается в форме круга. Найдите радиус окружности, образованной по формуле длины окружности.

Решение:
Мы знаем, что периметр прямоугольника = Общая длина используемой проволоки = Длина окружности образовавшегося круга.
Следовательно, длина окружности образовавшегося круга = 264 м
Длина окружности формула = 2πr
Длина окружности = 264
Подставим известные значения, чтобы найти радиус.
264 = 2πr
264 = 2 × (22/7) × г
Следовательно, радиус окружности равен 42 м.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок

Практические вопросы по длине окружности

перейти к слайдуперейти к слайду
Часто задаваемые вопросы об окружности окружности
Что такое длина окружности в геометрии?
Длина окружности — это мера границы или длина полной дуги окружности. Длина окружности равна произведению π (пи) на диаметр окружности. Длина окружности — это линейная величина, имеющая одинаковые единицы длины.
Как найти длину окружности?
Длина окружности рассчитывается с помощью формулы длины окружности, для которой требуется значение радиуса окружности и значение π (пи). Окружность круга = 2πr, где «r» — радиус круга, а π (пи) — специальная математическая константа со значением, приблизительно равным 3,14159 или π = 22/7.
Как найти диаметр по длине окружности?
Если нам нужно вычислить диаметр, когда дана длина окружности, мы используем формулу: Длина окружности = π × диаметр или Диаметр = длина окружности/π
Как найти длину окружности по площади?
Длину окружности можно рассчитать, если известна площадь круга. По формуле площади круга можно вычислить радиус. Зная радиус, можно вычислить длину окружности. Площадь круга = πr ² , $радиус = \sqrt{\frac{A}{\pi}}$, и C = 2πr = 2$\pi\sqrt{\frac{A}{\pi }}$.
Какова единица длины окружности?
Окружность круга представляет собой одномерную линейную величину, а единица измерения длины окружности выражается в метрах, дюймах, сантиметрах, футах и т. д. Длина окружности связана с другими линейными величинами, такими как радиус и диаметр окружности.
Что такое периметр круга?
Периметр круга равен длине окружности. Это общая длина внешней границы круга. Периметр или длина окружности — это произведение константы «пи» и диаметра окружности. Он выражается в линейных единицах, таких как м, дюйм, см, фут.
Каково число Пи?
Пи — постоянная величина, используемая для измерения площади и длины окружности круга или других круглых фигур. Символом числа пи является π, а его числовое значение равно 22/7 или 3,14. Кроме того, эти числовые значения используются в зависимости от контекста уравнения.
В чем разница между диаметром и длиной окружности?
Диаметр окружности — это самая длинная хорда, проходящая через центр окружности. Длина окружности – это длина внешней границы окружности. И диаметр, и длина окружности являются длинами и выражаются в линейных единицах. Длина окружности равна произведению диаметра на константу π (пи).
Как найти длину окружности по диаметру?
Длина окружности может быть вычислена, если диаметр известен, поскольку отношение между длиной окружности и диаметром окружности выражается как Окружность = π × Диаметр, или диаметр = Окружность/π.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по кругам
Математика, счет и статистика — Комплект академических навыков
Геометрия круга
Примеры работы 4 Рабочая тетрадь 5 См. также 6 Внешние ресурсы 7 Проверьте себя
Определение
Расстояние вокруг границы круга называется окружностью .
Расстояние по окружности через центр называется диаметром .
Расстояние от центра круга до любой точки на границе называется радиусом . Радиус равен половине диаметра; $2r=d$.
Отрезок, соединяющий две точки окружности, равен хорда . Каждый диаметр является хордой, но не каждая хорда является диаметром.
Область, которую отсекает хорда, называется сегментом .
Область внутри круга, ограниченная двумя радиусами, представляет собой сектор .
Длина между двумя точками по окружности равна
дуге .
Окружность
Определение
Формула для вычисления длины окружности: \[C = \pi d \qquad\text{или } \qquad C = 2\pi r\], где $d$ — диаметр, а $r$ — радиус.
Примеры работы
Пример 1
Радиус данной окружности равен $r=4$см. Вычислите окружность.
Решение
\begin{align} C &= 2\pi r\\ &= 2 \times \pi \times 4\\ &= 8 \pi \\ &\ приблизительно 25,1 \text{см (до 1 десятичного знака) place)} \end{align}
Пример 2
Найдите диаметр круга с длиной окружности $18$см. 92 &= \frac{50}{\pi}\\ r &= \sqrt{\frac{50}{\pi} }\\ r &\приблизительно 4,0 \text{см (до 1 знака после запятой)} \end {align}
Рабочая тетрадь
Эта рабочая тетрадь, созданная HELM, является хорошим пособием по пересмотру, содержащим ключевые моменты для исправления и множество рабочих примеров.
No related posts.