Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не \(12\) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3.
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. {o}}=\frac{a\sqrt{3}}{2}\)
Радиус вписанной окружности равностороннего треугольника
\(r=\frac{a\sqrt{3}}{6}\)
Это уже теперь должно быть совсем ясно:
Бонус 2: Вебинары о треугольниках, чтобы набить руку в решении задач
А в этих видео из нашего курса подготовки к ЕГЭ по математике вы можете потренироваться, решая задачи вместе с нашим репетитором Алексеем Шевчуком.
Это не просто вебинары, «бла-бла-бла» о теории математики. Это разбор задач в режиме реального времени.
Вы точно научитесь решать любые задачи на эти темы, если их прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.

Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но в этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
На этом уроке мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Также мы научимся решать и «обычные» треугольники. Убедимся в утверждении из прошлого урока — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Итак, задача 16 профильного ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
высота, медиана, углы и др.
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
- Определение равностороннего треугольника
- Свойства равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Пример задачи
Определение равностороннего треугольника
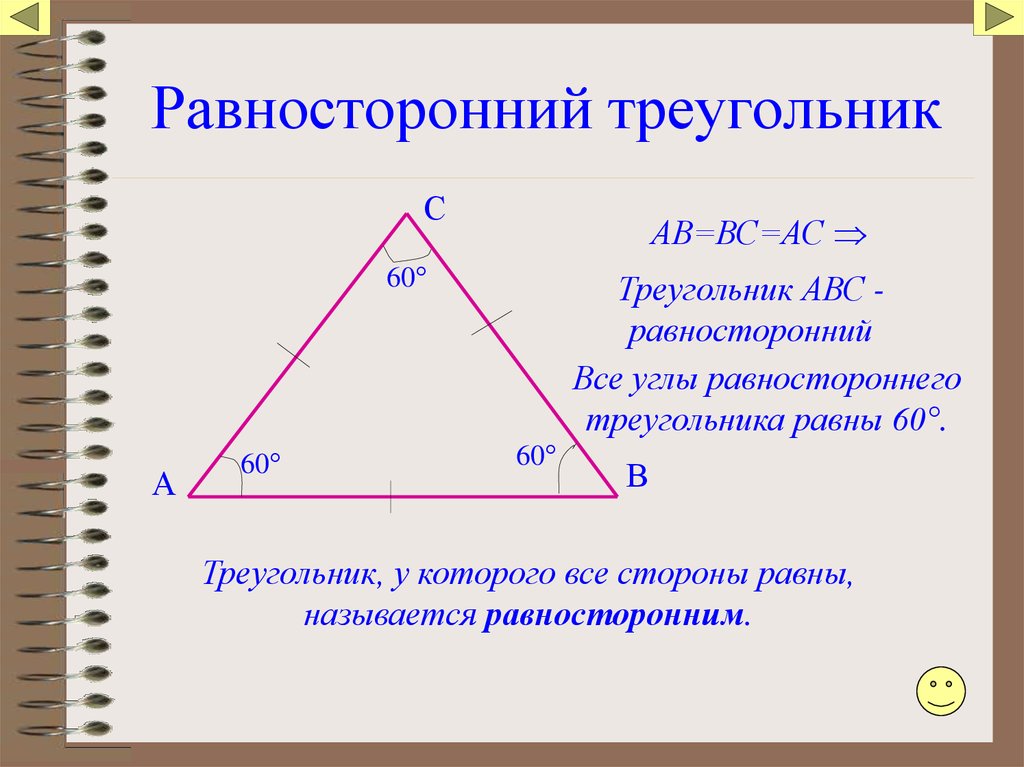
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину.
Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
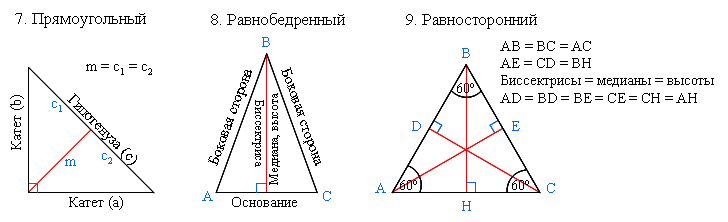
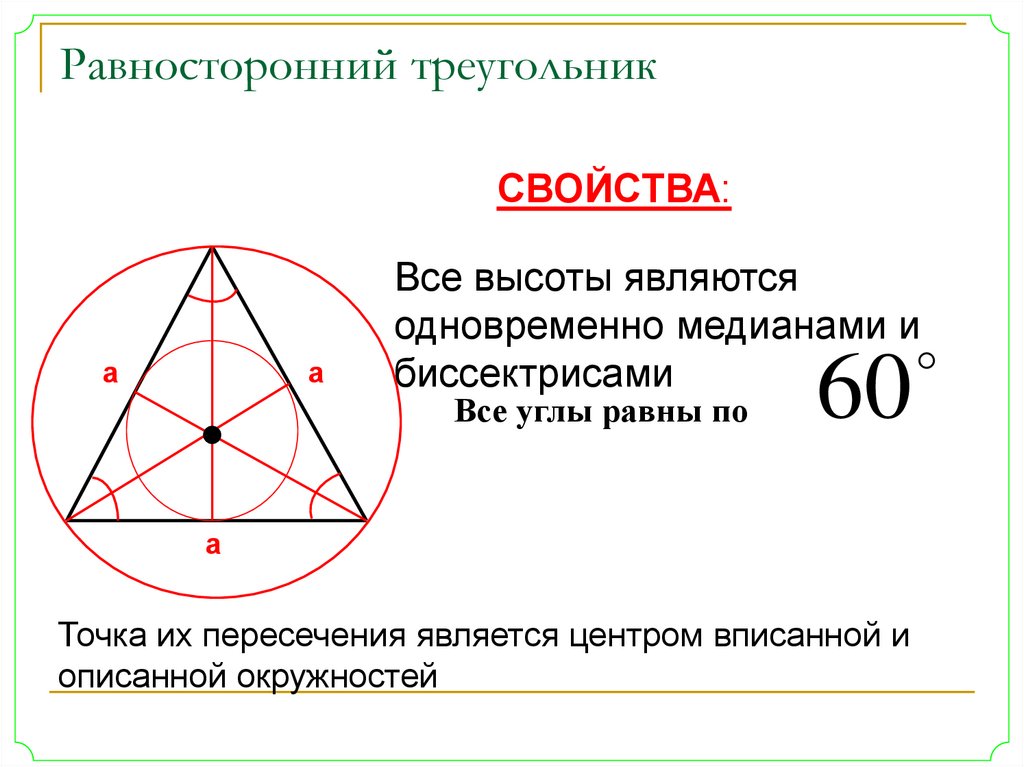
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
- CD перпендикулярна AB => ∠ADC = ∠BDC = 90°
- AD = DB
- ∠ACD = ∠DCB = 30°
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Равносторонний треугольник — определение, свойства, пример, факт
Определение равностороннего треугольника
В геометрии равносторонний треугольник — это треугольник, все три стороны которого имеют одинаковую длину.
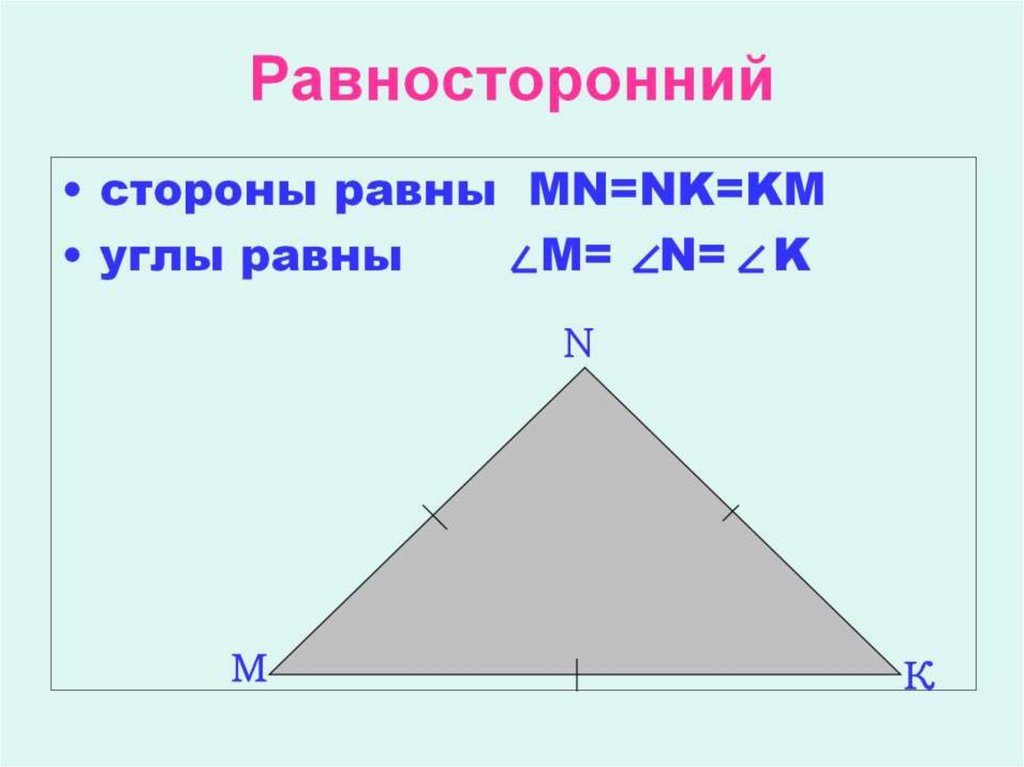
Стороны равностороннего треугольника равны, что означает, что все стороны имеют одинаковую длину. Все внутренние углы равны (60 градусов).
Термин «равносторонний» состоит из слов «экви», что означает «равный», и «латеральный», что означает «сторона». Итак, треугольник с равными сторонами называется равносторонним треугольником.
Родственные игры
История равносторонних треугольников
Следы треугольников можно найти во всем мире, особенно в строительстве. Их любили древние египтяне. Лица знаменитых египетских пирамид треугольные. Пирамиды Гизы – самые известные пирамиды, построенные египтянами во втором веке до нашей эры. Египтяне думали, что треугольная форма пирамиды символизирует местопребывание их бога Солнца Ра на земле.
Связанные рабочие листы
Равносторонние треугольники, используемые в реальной жизни
- Дорожные знаки, которые мы видим на дороге, имеют форму равносторонних треугольников. В следующий раз, когда вы отправитесь кататься на машине, обратите внимание, что все три стороны вывески кажутся одинаковой длины.
- Стойки, используемые для установки бильярдного стола с шарами, представляют собой равносторонние треугольники. Всего в них помещается 15 шаров, образуя идеальный равносторонний треугольник.
- Начос, обычная закуска, также имеют треугольную форму. Некоторые из них действительно равносторонние.
Что НЕ является равносторонним треугольником?
- Поверхность дорожного конуса не является равносторонним треугольником, потому что все три стороны не равны. Дорожный конус имеет удлиненные стороны с меньшим основанием.
- Паруса на парусной лодке не являются равносторонними треугольниками, так как стороны не равны по длине. Две стороны длиннее, чем оставшаяся сторона.
Свойства равносторонних треугольников
- Все стороны имеют одинаковую длину «а»
- Все внутренние углы равны 60 градусам.
- Равносторонний треугольник симметричен, а это означает, что если вы сложите его, чтобы соединить его вершины, он сложится так, что две половины будут полностью перекрывать друг друга.
Периметр и площадь равностороннего треугольника
- Вы можете рассчитать периметр (длину всей границы) равностороннего треугольника, сложив длины всех трех сторон. В равностороннем треугольнике со стороной «а» длины сторон равны. Таким образом, периметр равностороннего треугольника = a + a + a = 3.a 92$; где а — сторона равностороннего треугольника.
Забавные факты о равностороннем треугольнике
- Грани пирамид Гизы в Египте — один из старейших и крупнейших в мире примеров равносторонних треугольников. Они были построены в 26 веке до н.э. и являются совершенно равносторонними.
- Равносторонний треугольник — это особый равнобедренный треугольник, у которого все три стороны равны.
Решенные примеры
Q1. Чему будет равен периметр равностороннего треугольника, если предположить, что все его стороны имеют длину 30 дюймов?
Решение :
Вы знаете, что периметр равностороннего треугольника в 3 раза больше длины стороны.
В вопросе указано, что длина стороны = 30 дюймов.
Следовательно, периметр равностороннего треугольника будет 3 × 30 = 90 дюймов.
Q2. Чему будут равны периметр и полупериметр равностороннего треугольника, сторона которого равна 10 единицам?
Решение :
Вы знаете, что периметр равностороннего треугольника в 3 раза больше длины стороны, а полупериметр равен половине периметра. 9{2}$ = $100\sqrt{3}$ квадратных дюймов
Часто задаваемые вопросы
Что мы подразумеваем под равносторонним?
Термин «равносторонний» состоит из слов «экви», что означает «равный», и «латеральный», что означает «сторона». Итак, если фигура имеет все стороны одинаковой длины, она называется равносторонней.
Каковы свойства равностороннего треугольника?
Три свойства равностороннего треугольника:
- Все три стороны равны.
- Все три угла равны.
- Фигура имеет три оси симметрии.
Как узнать, является ли треугольник равносторонним?
Вы можете узнать, что треугольник равносторонний, измерив его стороны. Если они одинаковой длины, то треугольник равносторонний.
Может ли прямоугольный треугольник быть равносторонним?
Равносторонний треугольник никогда не может быть прямоугольным, так как в прямоугольном треугольнике один из углов равен 90°, тогда как в равностороннем треугольнике все углы равны 60°
Является ли равносторонний треугольник равнобедренным?
Равносторонний треугольник — это частный случай равнобедренного треугольника, у которого равны не две, а все три стороны и углы.
Равносторонний треугольник – формула, свойства, определение, примеры
В геометрии треугольник, все стороны которого равны, называется равносторонним треугольником. Если мы разберем слово «равносторонний», здесь «экви» означает эквивалент, а «боковой» — стороны.
Равносторонний треугольник также называют правильным многоугольником, у которого три равные стороны. В этой статье мы узнаем о равностороннем треугольнике, свойствах равностороннего треугольника и формулах равностороннего треугольника.
1. Что такое равносторонний треугольник 2. Свойства равностороннего треугольника 3. Формулы равностороннего треугольника 4. Часто задаваемые вопросы о равностороннем треугольнике Что такое равносторонний треугольник?
Равносторонний треугольник — это треугольник, у которого все три стороны равны и углы также равны. Значение каждого угла равностороннего треугольника составляет 60 градусов, поэтому он также известен как равносторонний треугольник. Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы равны и стороны также равны.
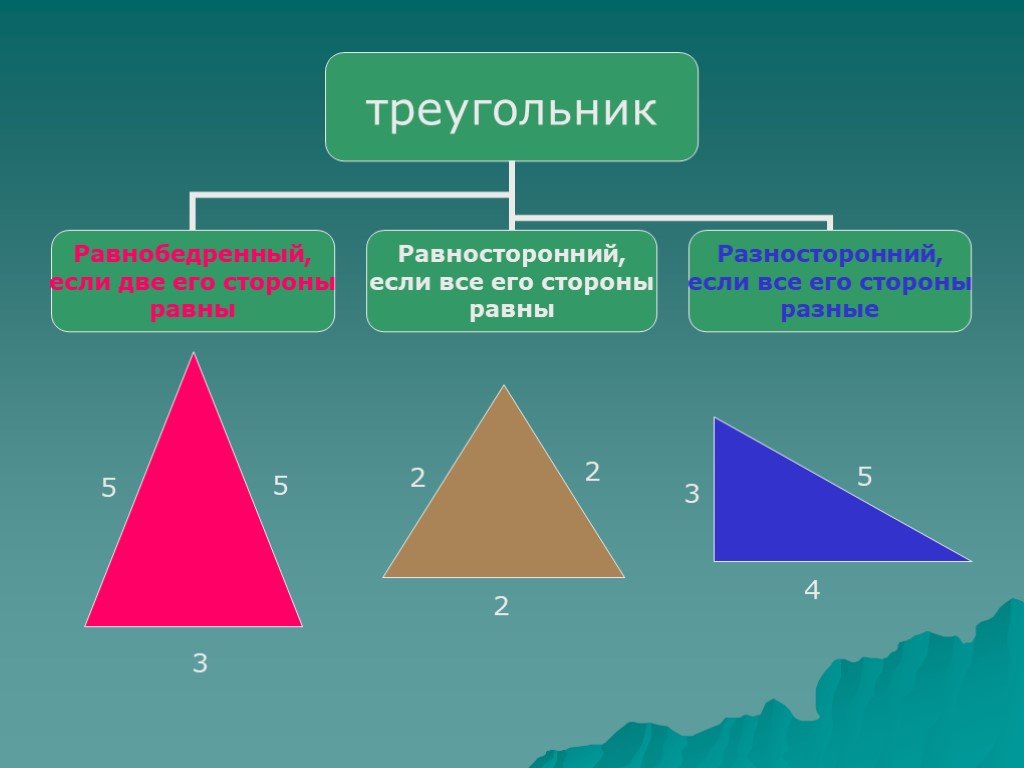
Треугольники делятся на три разных типа в зависимости от их сторон. Это равнобедренный треугольник, разносторонний треугольник и равносторонний треугольник. Равносторонний треугольник отличается от равнобедренного и разностороннего треугольника.
- В разностороннем треугольнике все стороны треугольника не равны и углы тоже не равны.
- В равнобедренном треугольнике две стороны равны и противоположные углы равных сторон равны.
- В равностороннем треугольнике все стороны равны и углы тоже равны.
Посмотрите на данный рисунок
На данном рисунке стороны треугольника ABC равны, т.е.
AB=BC=CA = единицы.Кроме того, ∠A, ∠B и ∠C = 60°
Следовательно, по определению равностороннего треугольника треугольник АВС является равносторонним треугольником.Свойства равностороннего треугольника
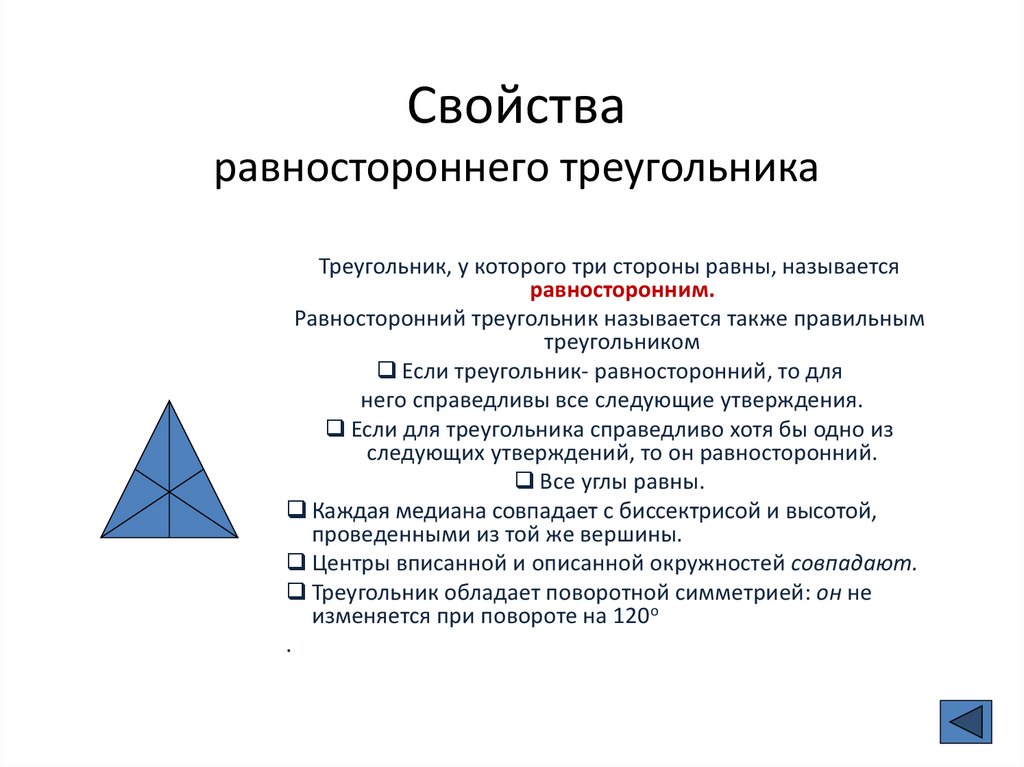
Равносторонний треугольник обладает некоторыми свойствами, которые определяют его как равносторонний треугольник.
Следуйте приведенным ниже свойствам для идентификации равностороннего треугольника.
- Стороны равностороннего треугольника равны по размерам.
У равностороннего треугольника- углов равны 60 градусам.
- правильный многоугольник, потому что у него три стороны.
- перпендикуляр, проведенный из любой вершины к противоположной стороне равностороннего треугольника, делит сторону пополам на равные длины. Он также делит пополам угол вершины на равные половины, т.е. по 30 градусов каждая от того места, где проведен перпендикуляр.
- Ортоцентр и центроид находятся в одной точке.
- медиана, биссектриса угла и высота равностороннего треугольника для всех сторон одинаковы.
- площадь равностороннего треугольника = √3a 2 / 4, здесь a = сторона равностороннего треугольника
- периметр равностороннего треугольника = 3а, здесь а = сторона равностороннего треугольника
- Сумма всех углов равностороннего треугольника равна 180 градусам.
Формулы равностороннего треугольника
Формулы для нахождения площади равностороннего треугольника и периметра равностороннего треугольника приведены ниже.
Площадь равностороннего треугольника
Площадь равностороннего треугольника — это пространство, покрываемое треугольником в двумерной плоскости. Вот формула для нахождения площади равностороннего треугольника:
. Площадь равностороннего треугольника = √3a 2 /4, где a — сторона равностороннего треугольника.Периметр равностороннего треугольника
Сумма всех сторон равностороннего треугольника равна периметру равностороннего треугольника или умножению стороны на три, поскольку в равностороннем треугольнике все стороны равны.
Периметр равностороннего треугольника = 3a, где a — сторонаТакже обратите внимание,
- Полупериметр равностороннего треугольника = 3a/2
- Высота равностороннего треугольника = √3a/ 2
☛Похожие статьи о равностороннем треугольнике
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о равностороннем треугольнике и связанных с ним темах.
- Площадь равностороннего треугольника
- Формулы равностороннего треугольника
- Периметр равностороннего треугольника
Примеры равностороннего треугольника
Пример 1: Вычислите площадь равностороннего треугольника со стороной 20 дюймов.
Решение: Площадь равностороннего треугольника = √3a 2 / 4, где a — сторона
Дано, а = 20 дюймов
Следовательно, площадь = √3×20×20/4
Площадь равностороннего треугольника = 100√3 квадратных дюймаПример 2: Каков периметр равностороннего треугольника со сторонами 40 дюймов. Также найдите высоту равностороннего треугольника
Решение: Периметр равностороннего треугольника = 3а, где а — сторона
Учитывая a = 40 дюймов
Периметр равностороннего треугольника = 3 × 40 = 120 дюймов 90 107 Высота равностороннего треугольника = √3a/ 2 = √3 × 40 / 2 = 20 √3Пример 3: Каковы периметр и полупериметр равностороннего треугольника со стороной, равной 12 единицам.
Решение:
Периметр равностороннего треугольника = 3а, а полупериметр равностороннего треугольника = 3а/2, где а — сторона. Дано а = 12 единиц. Следовательно, периметр равностороннего треугольника = 3 × 12 = 36 единиц, а полупериметр равностороннего треугольника = 36/2 = 18 единиц.
перейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по равностороннему треугольнику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о равностороннем треугольнике
Что такое равносторонний треугольник в геометрии?
Равносторонний треугольник – это треугольник, у которого все стороны равны и углы также равны. Значение каждого угла равностороннего треугольника составляет 60 градусов, поэтому он также известен как равносторонний треугольник.
Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы равны и стороны также равны.
Является ли равносторонний треугольник правильным многоугольником Почему?
Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как его углы и стороны равны.
Какова сумма всех углов равностороннего треугольника?
Сумма всех углов равностороннего треугольника равна 180 градусам. Поскольку все углы равны 60 градусам, сумма равна 60°+ 60°+ 60° =180 градусов
Какие формулы равностороннего треугольника в геометрии?
В геометрии все фигуры, как двухмерные, так и трехмерные, имеют определенные специальные формулы, которые используются для вычисления площади, высоты, периметра и полупериметра. Точно так же равносторонний треугольник имеет приведенные ниже формулы:
- Площадь равностороннего треугольника, A = (√3/4)a 2
- Периметр равностороннего треугольника, P = 3a
- Полупериметр равностороннего треугольника = 3a/2
- Высота равностороннего треугольника, h = (√3a/2)
Как найти площадь равностороннего треугольника?
Площадь равностороннего треугольника можно найти по формуле площади равностороннего треугольника.

 {o}}=\frac{a\sqrt{3}}{2}\)
{o}}=\frac{a\sqrt{3}}{2}\)
 Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ. ru Математика Геометрия Свойства равностороннего треугольника: теория и пример задачи
ru Математика Геометрия Свойства равностороннего треугольника: теория и пример задачи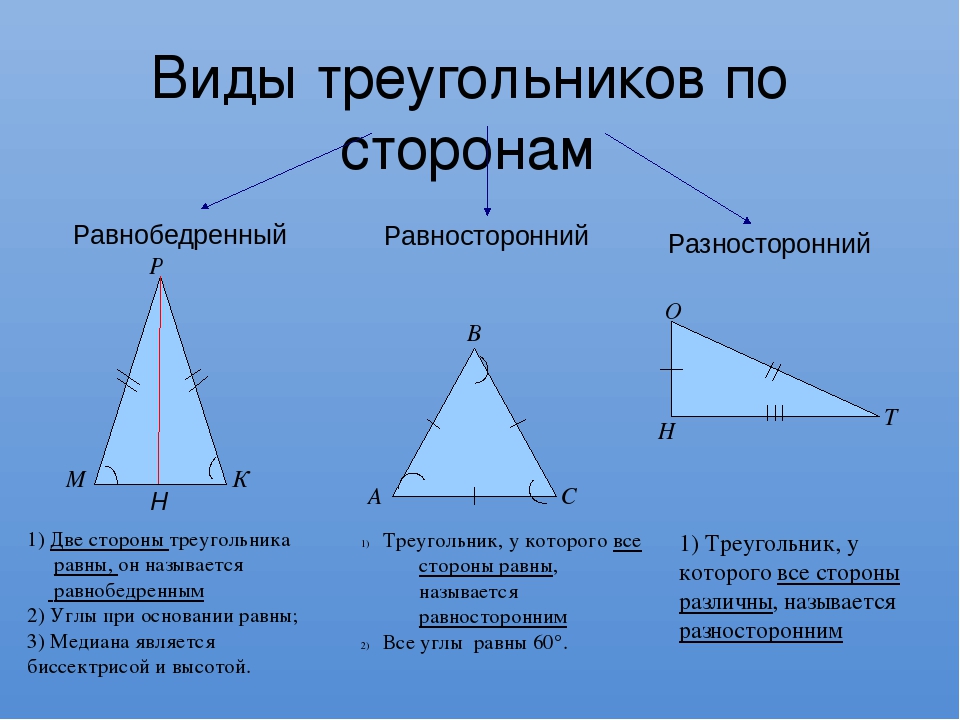 Т.е. AB = BC = AC.
Т.е. AB = BC = AC.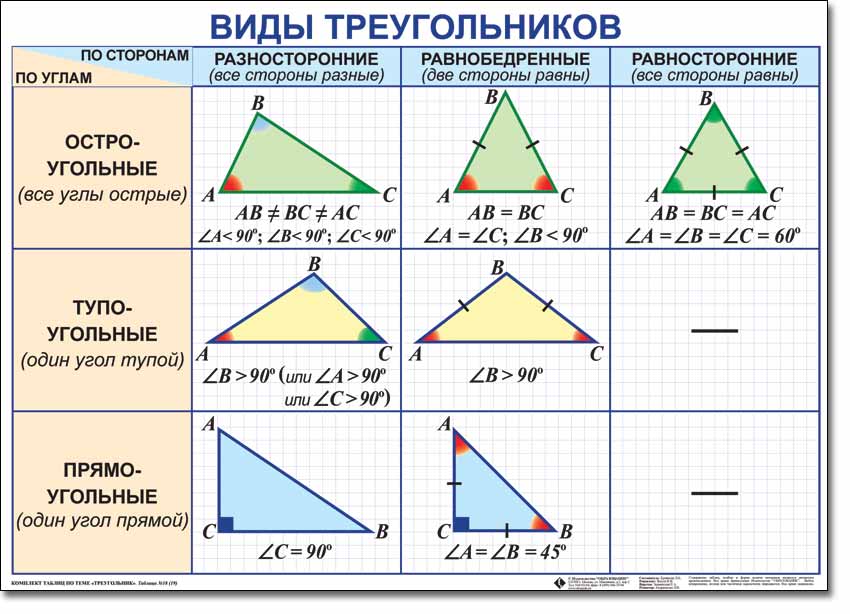
 Стороны равностороннего треугольника равны, что означает, что все стороны имеют одинаковую длину. Все внутренние углы равны (60 градусов).
Стороны равностороннего треугольника равны, что означает, что все стороны имеют одинаковую длину. Все внутренние углы равны (60 градусов).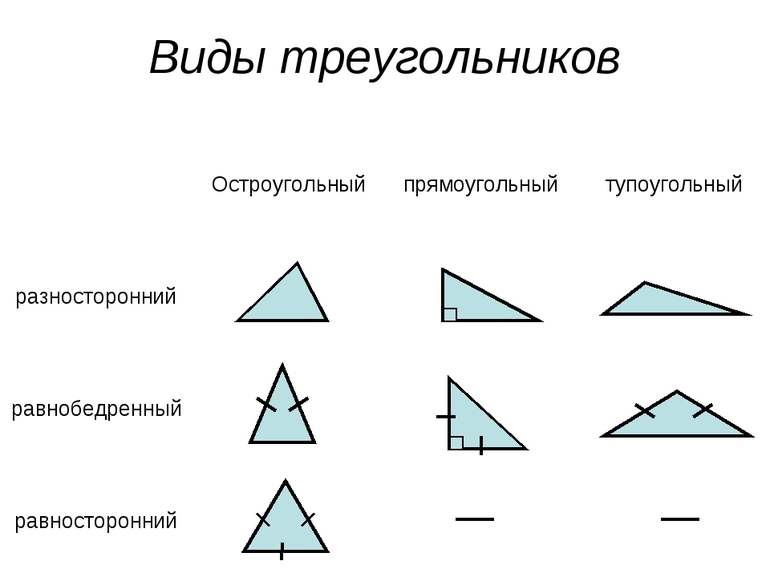
 В вопросе указано, что длина стороны = 30 дюймов.
В вопросе указано, что длина стороны = 30 дюймов.
 Равносторонний треугольник также называют правильным многоугольником, у которого три равные стороны. В этой статье мы узнаем о равностороннем треугольнике, свойствах равностороннего треугольника и формулах равностороннего треугольника.
Равносторонний треугольник также называют правильным многоугольником, у которого три равные стороны. В этой статье мы узнаем о равностороннем треугольнике, свойствах равностороннего треугольника и формулах равностороннего треугольника.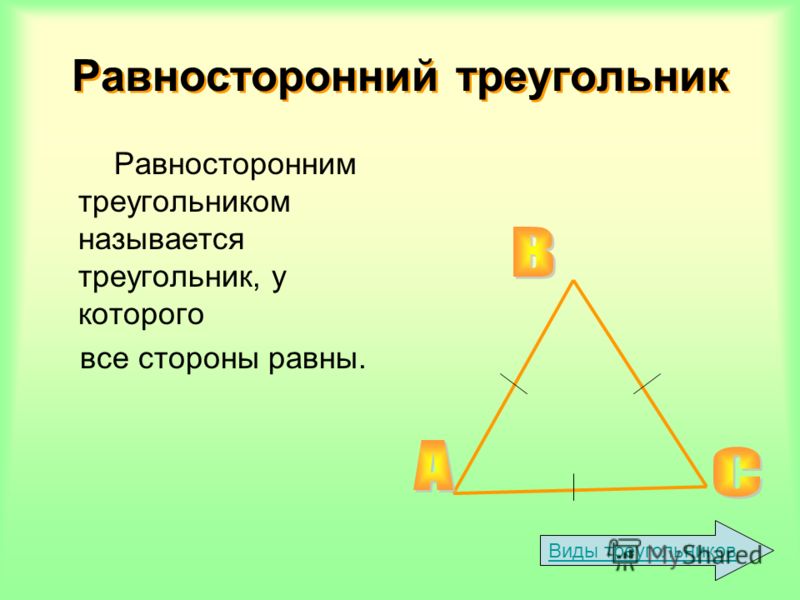
 Следуйте приведенным ниже свойствам для идентификации равностороннего треугольника.
Следуйте приведенным ниже свойствам для идентификации равностороннего треугольника.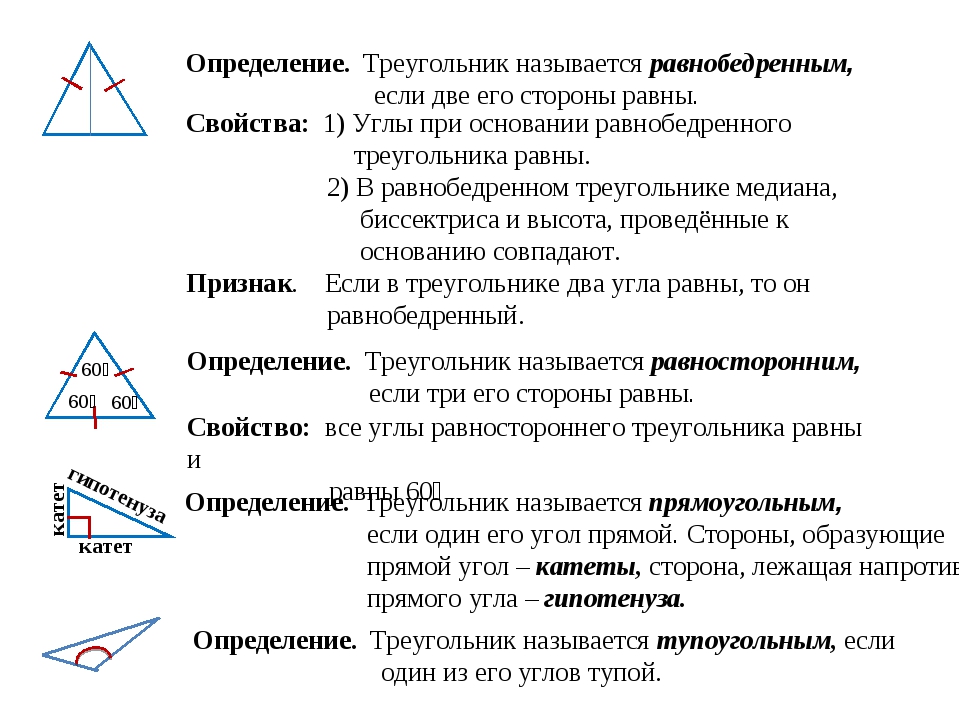

 Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы равны и стороны также равны.
Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы равны и стороны также равны.