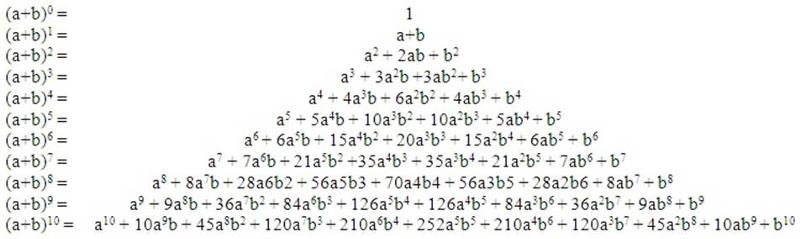Разложение бинома: Бином Ньютона

alexxlab / / Разное

Оценить калькулятор:

Формула Бинома Ньютона

Для натурального n формула принимает такой вид:

(a + b)n = C0n · an + C1n · an-1 · b + C2n · an-2 · b2 + … + Cn-1n · a · bn-1 + Cnn · bn,

где Ckn – биномиальные коэффициенты.

Примеры:

  • (x + y)2 = x2 + 2 · x · y + y2,
  • (x + y)3 = x3 + 3 · x2 · y + 3 · x · y2 + y3,
  • (x + y)4 = x4 + 4 · x3 · y + 6 · x2 · y2 + 4 · x · y3 + y4,
  • (x + y)5 = x5 + 5 · x4 · y + 10 · x3 · y2 + 10 · x2 · y
    3     + 5 · x · y4 + y5,

Треугольник Паскаля

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, которые для удобства восприятия записаны в форме треугольника. На его вершинах и по боковым сторонам стоят единицы, а каждое число равно сумме двух чисел над ним.

1    
1    1    
1    2    1    
1    3    3    1    
1    4    6    4    1    
1    5    10    10    5    1    
1    6    15    20    15    6    1    
–    –    –    –    –    –    –    –    –    

Комментарии к калькулятору

Количество комментариев: 4

Похожие калькуляторы

Математика

Число перестановок

Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.

Перейти к расчету

Математика

Число сочетаний

Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.

Перейти к расчету

Математика

Число размещений

Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.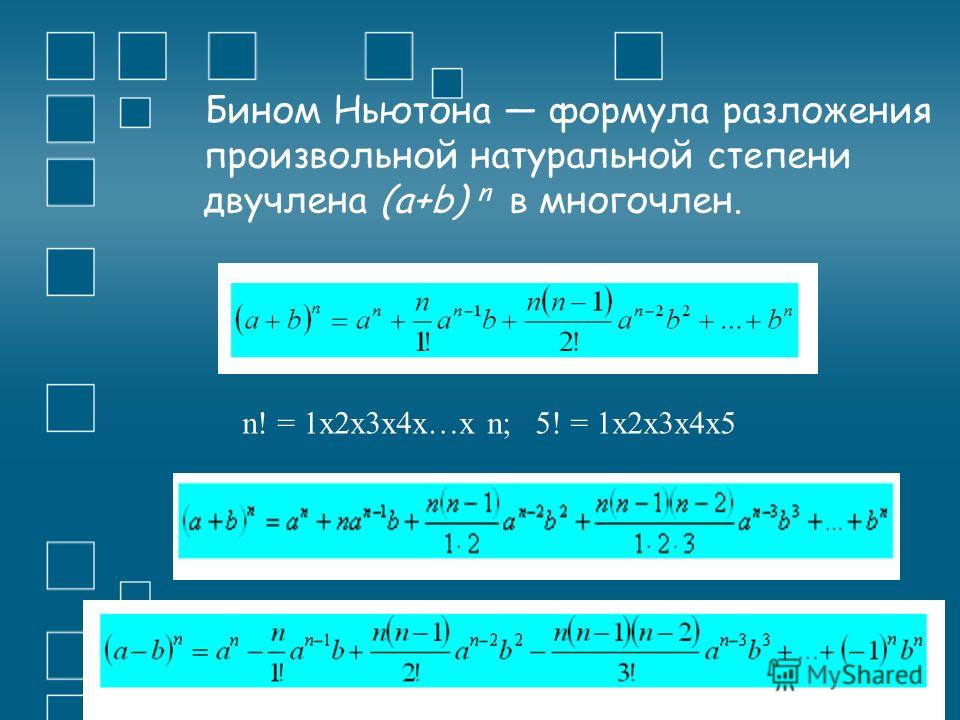

Перейти к расчету

Мы используем cookies для улучшения взаимодействия с сайтом, подробнее в Cookie Policy.

О биномиальном разложении функций OWA, 3-аддитивный случай в n измерениях

Автор

Перечислено:

  • Сильвия Борто

    (Университет Тренто, Италия)

  • Рикардо Альберто Маркес Перейра

    (Университет Тренто, Италия)

  • Thuy Nguyen

    (Университет Тренто, Италия)

Зарегистрирован:

    Abstract

    В контексте биномиальной декомпозиции функций OWA мы исследуем параметрические ограничения, связанные с 3-аддитивным случаем в n измерениях. Полученная допустимая область с двумя коэффициентами представляет собой выпуклый многоугольник с n вершинами и n ребрами и строго возрастает по размерности n. Оральность функций OWA в допустимой области является линейной по двум коэффициентам, и идентифицируются вершины, связанные с максимальной и минимальной орностью.

    Предлагаемое цитирование

  • Сильвия Борто и Рикардо Альберто Маркес Перейра и Туи Нгуен, 2015. »
    О биномиальном разложении функций OWA, 3-аддитивный случай в n измерениях     ,» Рабочие бумаги 360, ECINEQ, Общество изучения экономического неравенства.

    • Обработчик: RePEc:inq:inqwps:ecineq2015-360

    как

    HTMLHTML с абстрактным простым текстом обычный текст с абстрактнымBibTeXRIS (EndNote, RefMan, ProCite)ReDIFJSON

    Скачать полный текст от издателя

    URL-адрес файла: http://www.ecineq.org/milano/WP/ECINEQ2015-360.pdf
    Ограничение на загрузку: нет
    —>

    Ссылки перечислены в IDEAS

    как

    HTMLHTML с абстрактным простым текстомпростой текст с абстрактнымBibTeXRIS (EndNote, RefMan, ProCite)ReDIFJSON

    1. Грабиш, Мишель и Кожадинович, Иван и Мейер, Патрик, 2008 г. Обзор методов определения пропускной способности в теории многоатрибутной полезности на основе интеграла Шоке: приложения пакета Kappalab R ,» Европейский журнал операционных исследований, Elsevier, vol.
      186(2), страницы 766-785, апрель.
      • Мишель Грабиш, Иван Кожадинович и Патрик Мейер, 2008 г. » Обзор методов определения пропускной способности в теории многоатрибутной полезности на основе интеграла Шоке: приложения пакета Kappalab R ,» Université Paris1 Panthéon-Sorbonne (послепечатные и рабочие документы) halshs-00187175, HAL.
      • Мишель Грабиш, Иван Кожадинович и Патрик Мейер, 2008 г. Обзор методов определения пропускной способности в теории многоатрибутной полезности на основе интеграла Шоке: приложения пакета Kappalab R , » Пост-печать halshs-00187175, HAL.
    2. Порат Эльханан Бен и Гилбоа Ицхак, 1994 г. « Линейные показатели, индекс Джини и компромисс между доходом и равенством », Журнал экономической теории, Elsevier, vol. 64(2), страницы 443-467, декабрь.
      • Эльханан Бен Порат и Ицхак Гильбоа, 1991 год. Линейные показатели, индекс Джини и компромисс между доходом и равенством
        ,» Документы для обсуждения 944, Северо-Западный университет, Центр математических исследований в области экономики и управления.
      • Ицхак Гильбоа и Эльханан Бен Порат, 1994 г. « Линейные показатели, индекс Джини и компромисс между доходом и равенством », Пост-печать hal-00481365, HAL.
    3. Тибо Гайдос, 2002 г. « Измерение неравенства без линейности в зависти с помощью интеграла Шоке с симметричными емкостями », Université Paris1 Panthéon-Sorbonne (послепечатные и рабочие документы) halshs-00085888, HAL.
    4. Эберт, Удо, 1987 г. « Размер и распределение доходов как определяющие факторы общественного благосостояния «, Журнал экономической теории, Elsevier, vol. 41(1), страницы 23-33, февраль.
    5. Чарльз Блэкорби, Дэвид Дональдсон и Мария Ауэрсперг, 1981 год. « Новая процедура измерения неравенства внутри и между подгруппами населения
      », Канадский журнал экономики, Канадская экономическая ассоциация, том. 14(4), страницы 665-685, ноябрь.
    6. Ицхак Гильбоа и Дэвид Шмайдлер, 19 лет95. « Каноническое представление множества функций «, Математика исследования операций, ИНФОРМ, вып. 20(1), страницы 197-212, февраль.
      • Ицхак Гильбоа и Дэвид Шмайдлер, 1992 г. « Каноническое представление множества функций «, Документы для обсуждения 986, Северо-Западный университет, Центр математических исследований в области экономики и управления.
      • Ицхак Гильбоа и Дэвид Шмайдлер, 1995 г. « Каноническое представление множества функций «, Пост-печать hal-00481346, HAL.
    7. Аткинсон, Энтони Б., 1970 г. « Об измерении неравенства «, Журнал экономической теории, Elsevier, vol. 2(3), страницы 244-263, сентябрь.
    8. Дональдсон, Дэвид и Веймарк, Джон А., 1983 г. « Этически гибкие индексы Джини для распределения доходов в континууме «, Журнал экономической теории, Elsevier, vol. 29(2), страницы 353-358, апрель.
      • ДОНАЛЬДСОН, Дэвид и ВЕЙМАРК, Джон А., 1983. Этически гибкие индексы Джини для распределения доходов в континууме ,» LIDAM перепечатывает CORE 520, Католический университет Лувена, Центр исследования операций и эконометрики (CORE).
    9. Гайдос, Тибо, 2002 г. « Измерение неравенств без линейности в Envy: интегралы Шоке для симметричных емкостей », Журнал экономической теории, Elsevier, vol. 106(1), страницы 190-200, сентябрь.
    10. Чарльз Блэкорби и Дэвид Дональдсон, 1984 год. » Этические социальные индексы и измерение эффективной прогрессивности налогов и пособий ,» Канадский журнал экономики, Канадская экономическая ассоциация, том. 17(4), страницы 683-694, ноябрь.
    11. Дональдсон, Дэвид и Веймарк, Джон А., 1980 г. » Однопараметрическое обобщение индексов Джини неравенства ,» Журнал экономической теории, Elsevier, vol. 22(1), страницы 67-86, февраль.
    12. Блэкорби, Чарльз и Дональдсон, Дэвид, 1980 г. « Теоретическая обработка индексов абсолютного неравенства », International Economic Review, Департамент экономики, Университет Пенсильвании и Институт ассоциации социальных и экономических исследований Университета Осаки, vol. 21(1), страницы 107-136, февраль.
    13. Блэкорби, Чарльз и Дональдсон, Дэвид, 1978 г. « Показатели относительного равенства и их значение с точки зрения социального обеспечения «, Журнал экономической теории, Elsevier, vol. 18(1), страницы 59-80, июнь.
    14. Блакорби, Чарльз и Дональдсон, Дэвид, 1980 г. «
      Этические показатели для измерения бедности       », Эконометрика, Эконометрическое общество, том. 48(4), страницы 1053-1060, май.
    15. Грабиш, Мишель, 1996 г. Применение нечетких интегралов при многокритериальном принятии решений ,» Европейский журнал операционных исследований, Elsevier, vol. 89(3), страницы 445-456, март.

    Полные ссылки (включая те, которые не соответствуют элементам в IDEAS)

    Наиболее связанные элементы

    Это элементы, которые чаще всего цитируют те же работы, что и этот, и цитируются теми же работами, что и этот.

    1. Сильвия Борто и Рикардо Альберто Маркес Перейра и Туи Х. Нгуен, 2015 г. Функции благосостояния и индексы неравенства в биномиальном разложении функций OWA ,» Документы для обсуждения DEM 2015/08, кафедра экономики и управления.
    2. Сильвия Борто и Рикардо Альберто Маркес Перейра, 2013 г. » Биномиальные индексы неравенства Джини и биномиальное разложение функций благосостояния ,» Рабочие бумаги 305, ECINEQ, Общество изучения экономического неравенства.
    3. Сатья Р. Чакраварти и Пьетро Мульере, 2003 г. » Показатели благосостояния: обзор и новые перспективы. 1. Измерение неравенства ,» Metron — Международный статистический журнал, Dipartimento di Statistica, Probabilità e Statistiche Applicate — University of Rome, vol. 0(3), страницы 457-497.
    4. Йорам Амиэль и Фрэнк Коуэлл, 1997 г. « Неравенство, благосостояние и монотонность », STICERD — Документы программы исследований в области дистрибутивного анализа 29, Международные центры экономики и смежных дисциплин Suntory и Toyota, LSE.
      • Амиэль, Йорам и Коуэлл, Фрэнк, 1997 г.
        « Неравенство, благосостояние и монотонность «, Онлайн-документы LSE Research по экономике 2222, Лондонская школа экономики и политических наук, библиотека LSE.
    5. Эберт У., 1996 г. « Неравенство доходов и различия в размере домохозяйства «, Математические социальные науки, Elsevier, vol. 31(1), страницы 57-58, февраль.
      • Эберт, Удо, 1995 г. « Неравенство доходов и различия в размере домохозяйства «, Математические социальные науки, Elsevier, vol. 30(1), страницы 37-55, август.
    6. Дюкло, Жан-Ив и Жальбер, Винсент и Араар, Абделькрим, 2000 г. » Классическое горизонтальное неравенство и реранжировка: комплексный подход ,» Cahiers de recherche 0002, Университет Лаваля — Экономический факультет.
      • Жан-Ив Дюкло, Винсент Жальбер и Абделькрим Араар, 2001 г. « Классическое горизонтальное неравенство и переоценка: комплексный подход », Рабочие документы UFAE и IAE 478.01, Unitat de Fonaments de l’Analisi Econòmica (UAB) и Institut d’Analisi Econòmica (CSIC).
      • Дюкло, Дж.Ю. и Джалберт, В. и Араар, А., 2000. » Классическое горизонтальное неравенство и реранжировка: комплексный подход ,» Документы 0002, Laval — Recherche en Politique Economique.
    7. Сатья Р. Чакраварти, 2009 г. « Справедливость и эффективность как компоненты функции социального обеспечения », Международный журнал экономической теории, Международное общество экономической теории, том. 5(2), страницы 181-199, июнь.
    8. Ааберж, Рольф, 2001 г. « Аксиоматическая характеристика коэффициента Джини и порядка кривой Лоренца «, Журнал экономической теории, Elsevier, vol. 101(1), страницы 115-132, ноябрь.
    9. Оихана Аристондо и Хосе Луис Гарка-Лапреста и Касильда Лассо де ла Вега и Рикардо Альберто Маркес Перейра, 2012 г. » Классические индексы неравенства, функции благосостояния и двойное разложение ,» Рабочие документы DISA 2012/06, Департамент компьютерных наук и управления, Университет Тренто, Италия, пересмотрено в июне 2012 г.
      • Оихана Аристондо, Хосе Луис Гарсия-Лапрес, Касильда Лассо де ла Вега и Рикардо Альберто Маркес Перейра, 2012 г. » Классические индексы неравенства, функции благосостояния и двойное разложение ,» Рабочие бумаги 253, ECINEQ, Общество изучения экономического неравенства.
    10. Дюкло, Жан-Ив и Жальбер, Винсент и Араар, Абделькрим, 2003 г. « Классическое горизонтальное неравенство и переоценка: комплексный подход », Cahiers de recherche 0306, ЦИРПИ.
    11. Ааберже, Рольф и Могстад, Магне и Перагин, Вито, 2011 г. « Измерение долгосрочного неравенства возможностей «, Журнал общественной экономики, Elsevier, vol. 95(3-4), стр. 193-204, апрель.
      • Ааберж, Рольф и Могстад, Магне и Перагин, Вито, 2011 г. « Измерение долгосрочного неравенства возможностей «, Журнал общественной экономики, Elsevier, vol. 95(3), страницы 193-204.
      • Рольф Оберж, Магне Могстад ​​и Вито Перагине, 2010 г. « Измерение долгосрочного неравенства возможностей «, Документы для обсуждения 620, Статистическое управление Норвегии, Исследовательский отдел.
      • Ааберж, Рольф и Могстад, Магне и Перагин, Вито, 2010 г. Измерение долгосрочного неравенства возможностей ,» Документы для обсуждения IZA 4714, Институт экономики труда (ИЗА).
      • Рольф Оберж, Магне Могстад ​​и Вито Перагине, 2010 г. « Измерение долгосрочного неравенства возможностей «, Рабочие бумаги 158, ECINEQ, Общество изучения экономического неравенства.
    12. Чакраварти, Сатья Р. и Саркар, Палаш, 2022 г. « Синтез местного и эффективного измерения прогрессивности налогообложения ,» Бумага МПРА 115180, Университетская библиотека Мюнхена, Германия.
    13. repec:ebl:ecbull:v:3:y:2003:i:19:p:1-16 не указан в IDEAS
    14. Зоргер, Герхард и Старк, Одед, 2013 г. » Перераспределение доходов идет наперекосяк: обратная сила заботы об относительной депривации ,» Журнал экономического поведения и организации, Elsevier, vol. 86(С), страницы 1-9.
      • Старк, Одед и Зоргер, Герхард, 2012 г. » Перераспределение доходов идет наперекосяк: обратная сила заботы об относительной депривации ,» Рабочие документы Тюбингенского университета по бизнесу и экономике 47, Тюбингенский университет, факультет экономики и социальных наук, Школа бизнеса и экономики.
      • Зоргер, Герхард и Старк, Одед, 2012 г. » Перераспределение доходов идет наперекосяк: обратная сила заботы об относительной депривации ,» Документы для обсуждения 142407, Боннский университет, Центр исследований в области развития (ZEF).
    15. Фостер, Джеймс Э. и Шнееров, Артем А., 2000. « Независимые от пути меры неравенства «, Журнал экономической теории, Elsevier, vol. 91(2), страницы 199-222, апрель.
    16. Рольф Оберж и Уго Коломбино, 2012 г. Учет семейного происхождения при расчете оптимального подоходного налога: анализ микроэконометрического моделирования ,» Журнал экономики народонаселения, Springer; Европейское общество экономики народонаселения, том. 25(2), страницы 741-761, январь.
      • Ааберж, Рольф и Коломбино, Уго, 2009 г. « Учет семейного фона при разработке оптимальных подоходных налогов: анализ микроэконометрического моделирования », Документы для обсуждения IZA 4598, Институт экономики труда (ИЗА).
      • Рольф Оберж и Уго Коломбино, 2010 г. « Учет семейного опыта при разработке оптимального подоходного налога. Анализ микроэконометрического моделирования », Документы для обсуждения 619, Статистическое управление Норвегии, Исследовательский отдел.
      • Рольф Оберж и Уго Коломбино, 2010 г. » Учет семейного происхождения при расчете оптимального подоходного налога: анализ микроэконометрического моделирования ,» Рабочие бумаги 157, ECINEQ, Общество изучения экономического неравенства.
    17. Родригес, Хуан Габриэль и Салас, Рафаэль, 2014 г. » Коэффициент Джини: голосование большинства и социальное обеспечение ,» Журнал экономической теории, Elsevier, vol. 152(С), страницы 214-223.
    18. Жан-Ив Дюкло и Абделькрим Араар, 2003 г. « Семейство функций социальной оценки Аткинсона-Джини «, Бюллетень экономики, AccessEcon, vol. 3(19), страницы 1-16.
      • Араар, Абделькрим и Дюкло, Жан-Ив, 1998 г. Семейство функций социальной оценки Аткинсона-Джини ,» Cahiers de recherche 9826, Университет Лаваля — Экономический факультет.
      • Абделькрим Араар и Жан-Ив Дюкло, 2001 г. « Семейство функций социальной оценки Аткинсона-Джини «, Рабочие документы UFAE и IAE 476.01, Unitat de Fonaments de l’Analisi Econòmica (UAB) и Institut d’Analisi Econòmica (CSIC).
    19. Рольф Оберж, 2003 г. » Преобразования с сохранением среднего значения ,» Документы для обсуждения 360, Статистическое управление Норвегии, Исследовательский отдел.
    20. Барт Капео, 2013 г. » Компромиссы размера и распределения для заказа лексимина ,» Журнал экономического неравенства, Springer; Общество изучения экономического неравенства, том. 11(2), страницы 237-248, июнь.
    21. Рольф Оберж и Магне Могстад, 2009 г. « Об измерении долгосрочного неравенства доходов и мобильности доходов », Рабочие документы ICER 09-2009, ICER — Международный центр экономических исследований.
      • Рольф Оберж и Магне Могстад, 2010 г. Об измерении долгосрочного неравенства доходов и мобильности доходов ,» Рабочие бумаги 156, ECINEQ, Общество изучения экономического неравенства.
      • Рольф Оберж и Магне Могстад, 2010 г. « Об измерении долгосрочного неравенства доходов и мобильности доходов «, Документы для обсуждения 622, Статистическое управление Норвегии, Исследовательский отдел.
      • Ааберж, Рольф и Могстад, Магне, 2010 г. » Об измерении долгосрочного неравенства доходов и мобильности доходов ,» Документы для обсуждения IZA 4699, Институт экономики труда (ИЗА).

    Подробнее об этом изделии

    Ключевые слова

    Обобщенные функции благосостояния Джини и индексы неравенства; симметричные емкости и интегралы Шоке; OWA функции и удобство; биномиальное разложение и k-аддитивность;
    Все эти ключевые слова.

    Классификация JEL:

    • D31 — Микроэкономика — — Распределение — — — Распределение личного дохода и богатства
    • D63 – Микроэкономика – – Экономика благосостояния – – – Справедливость, справедливость, неравенство и другие нормативные критерии и измерения
    • I31 – здравоохранение, образование и социальное обеспечение – – социальное обеспечение, благополучие и бедность – – – общее благосостояние, благополучие

    Статистика

    Статистика доступа и загрузки

    Исправления

    Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения. При запросе исправления, пожалуйста, укажите дескриптор этого элемента: RePEc:inq:inqwps:ecineq2015-360 . См. общую информацию о том, как исправить материал в RePEc.

    По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, реферата, библиографической информации или информации для загрузки, обращайтесь: . Общие контактные данные провайдера: https://edirc.repec.org/data/ecineea.html .

    Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь. Это позволяет связать ваш профиль с этим элементом. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.

    Если CitEc распознал библиографическую ссылку, но не связал с ней элемент в RePEc, вы можете помочь с помощью этой формы .

    Если вы знаете об отсутствующих элементах, ссылающихся на этот, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылающегося элемента. {N}$. Биномиальные коэффициенты обозначаются 9{п} $ как количество различимых неупорядоченных комбинаций (ср. Комбинация) из $N$ разные объекты с $n$ предметы в каждой комбинации. Биномиальные коэффициенты удобнее всего записывать в виде чисел в арифметическом треугольнике, или треугольнике Паскаля, построение которого основано на следующем свойстве биномиальных коэффициентов:

    $$ \тег{2} \влево ( \начать{массив}{с} Н\ н \конец{массив} \справа) + \слева (\начать{массив}{с} Н\ п+1 \конец{массив} \ справа ) = \ \влево ( \начать{массив}{с} N+1 \\ п+1 \конец{массив} \верно ) . $$

    Биномиальные коэффициенты, как и арифметический треугольник, были известными математикам древности понятиями в более или менее развитых формах. Б. Паскаль (1665) провел подробное исследование биномиальных коэффициентов. Биномиальные коэффициенты также связаны многими полезными соотношениями, отличными от (2), например:

    $$ \tag{3a} \влево ( \начать{массив}{с} Н\ н \конец{массив} \справа) = \слева (\начало{массив}{с} Н\ Н-н \конец{массив} \верно ) ; $$

    $$ \тег{3b} \влево ( \начать{массив}{с} Н\ н \конец{массив} \справа) = \сумма _ {к = 0} ^ {п} \влево ( \начать{массив}{с} м\\ к \конец{массив} \справа) \слева (\начать{массив}{с} Н-м\ н-к \конец{массив} \верно ) ,\ \ n \leq m \leq N — n; $$ 9{н} {н! } . $$

    В случае комплексного числа $\alpha$, биномиальные коэффициенты обобщаются по формуле

    $$ \левый ( \начать{массив}{с} \альфа\\ н \конец{массив} \ \ справа ) = \ \ frac{\ alpha ( \ alpha — 1) \ dots ( \ alpha — n + 1) }{n! } ,\\ п > 0; \\ \левый ( \начать{массив}{с} \альфа\\ 0 \конец{массив} \ \справа ) = 1. $$

    При этом обобщении часть соотношений (2)–(4) сохраняется, но обычно в модифицированном виде. Например, 9{k} \left ( \begin{массив}{c} \альфа\\ к \конец{массив} \right ) = 0,\ \mathop{\rm Re} \alpha > 0. $$

    Таблицы биномиальных коэффициентов см. в [2], [3].

    Ссылки
    [1] Г.А. Корн, Т.М. Корн, «Математический справочник для ученых и инженеров», McGraw-Hill (1968) Zbl 0177.29301
    [2] Л.Н. Большев, Н. В. Смирнов, «Таблицы математической статистики», пер., , Libr. математика. столы , 46 , Наука (1983) (на русском языке) (обработка Л.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта