Разложение в ряд маклорена онлайн с решением: Ряд Маклорена онлайн

Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.

		Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0. Поделиться:    Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0. Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0: При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование. Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид: 1) , где f(x) — функция, имеющая при а=0 производные всех порядков. Rn — остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением 2) k-тый коэффициент (при хk) ряда определяется формулой Ряды Маклорена являются частным случаем рядов Тейлора. Условия применния рядов Маклорена (=Макларена). 1) Для того, чтобы функция f(x) могла быть разложена в ряд Маклорена (=Макларена) на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Маклорена (=Макларена) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R). 2) Необходимо чтобы существовали производные для данной функции в точке а=0, в окрестности которой мы собираемся строить ряд Маклорена (=Макларена). Численное интегрирование с использованием рядов Маклорена (=Макларена). Значения многих интегралов нельзя найти с помощью каких-либо аналитических методов. Мы уже рассказывали о вычислении таких интегралов с помощью формулы трапеций, формулы Симпсона. Другой метод нахождения числового значения определенного интеграла — выражение функции в виде ряда Маклорена (=Макларена) с последующим поочередным интегрированием каждого члена. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA. ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Ряд Маклорена с примером решения

Содержание:

1. Разложение в ряд Маклорена некоторых функций
2. Рассмотрим геометрический ряд
3. Пример с решением

Предположим, что функция , определенная и раз дифференцируемая в окрестности точки может быть представлена в виде суммы степенного ряда или, другими словами, может быть разложена в степенной ряд

Выразим коэффициенты ряда через Найдем производные функции почленно дифференцируя ряд раз:

Полагая в полученных равенствах х=0. получим

Подставляя значения коэффициентов получим ряд

называемый рядом Маклорена.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Следует отметить, что не все функции могут быть разложены в рад Маклорена- Может оказаться, что ряд Маклорена, составленный формально для функции , является расходящимся либо сходящимся не к функции .

Так же как и для числовых рядов, сумму ряда Маклорена можно представить в виде (13.9)

где частичная сумма ряда; остаток ряда.

Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.

Теорема. Для того чтобы ряд Маклорена сходился к функции необходимо и достаточно, чтобы при остаток рядо стремился к нулю, т.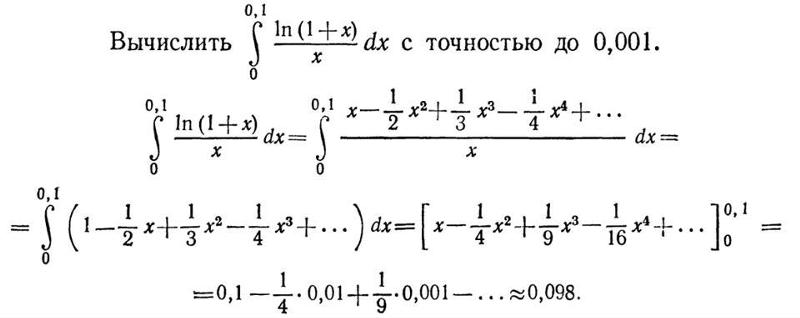 е. для всех значений х из интервала сходимости рядо.

Возможно вам будут полезны данные страницы:

Метод вариации постоянных произвольных

Правило Крамера

Разложение в ряд маклорена

Исследовать функцию на непрерывность: пример решения

Можно доказать, что если функция разложима в ряд Макларена, то зто разложение единственное.

Замечание. Ряд Маклорена является частным случаем рядо Тейлора

Ряд Тейлора тесно связан с формулой Тейлора:

где — остаточный член формулы Тейлора:

записанный в форме Лагранжа.

Очевидно, что при выполнении условия (14.7) остаток ряда Тейлора равен остаточному члену формулы Тейлора.

Разложение в ряд Маклорена некоторых функций

1.

Имеем

По формуле (13.6)

Область сходимости ряда (см. пример 14.3а).

2.

Имеем откуда и т.д.

Очевидно, что производные четного порядка а нечетного порядка По формуле (14.6) Область сходимости ряда

3. Рассматривая аналогично, получим Область сходимости ряда

4. , где — любое действительное число. Имеем

Интервал сходимости ряда (-1; 1) (на концах интервала при сходимость ряда зависит от конкретных значений ).

Рад (14.11) называется биномиальным. Если — целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при член рада и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.

5.

Получить разложение для этой функции можно проще, ие вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.

Рассмотрим геометрический ряд

со знаменателем , который сходится при т.е. при к функции

Интегрируя почленно равенство (14.12) в интервале (0; х), где

с учетом того, что получим

Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть (—1; 1].

Можно доказать, что рады, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.

При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) — (14.13).

Пример с решением

Разложить в ряд функции:

Решение:

а) Так как по (14.8)

то, заменяя , получим

и, наконец,

Область сходимости рада б) В разложении заменим получим

Теперь

Область сходимости ряда (—1; 1).

Калькулятор серии Маклорена

Калькулятор серии Маклорена

Калькулятор серии Маклорена — это онлайн-инструмент, используемый для расширения функции вокруг фиксированной точки. Центральная точка в ряду Маклорена зафиксирована как a = 0. Он вычисляет ряд, взяв производные функции до порядка n .

Как работает калькулятор полиномов Маклорена?

Чтобы найти серию функций Маклорена, выполните следующие действия.

• Запишите функцию с одной переменной в поле ввода.
• Напишите n-й порядок ряда.
• Центральная точка по умолчанию фиксирована. Значение по умолчанию: a = 0.
• Нажмите кнопку , вычислить , чтобы получить результат.
• Чтобы войти в новую функцию, нажмите кнопку сброса .

Что такое серия Маклорена?

Ряд Маклорена — это форма ряда Тейлора, в которой центральная точка всегда фиксируется как а = 0. В ряду Тейлора мы можем выбрать любое значение а, но в ряду Маклорена точка всегда равна а = 0. 9n\left(0\right)\) — n-я производная функции.

0 — фиксированная точка.

«n» — общее количество.

Как рассчитать ряд Маклорена?

Ниже приведен пример серии Маклорена.

Пример 

Вычислите ряд Маклорена cos(x) до порядка 7.

Решение 

Шаг 1: Запишите заданные члены.

\(f\влево(x\вправо)=cos\влево(x\вправо)\) 95+\ldots \:\)

Ссылки

• Определение ряда Маклорена | Криста Кинг Математика | Онлайн-помощь по математике.
• Формула серии Маклорена | Study.com (без даты).
• Примеры серии Маклорена | Исчисление II — ряд Тейлора. (н.д.).

Калькулятор серии Маклорена

---

Калькулятор серии Маклорена

Калькулятор серии Маклюрена используется для расширения функции для создания серии вокруг фиксированной центральной точки. Точка a = 0 является неподвижной точкой ряда Маклорена. Этот решатель серии Маклорена расширяет заданную функцию, дифференцируя ее до n-го порядка.

Как работает калькулятор серии Маклорена?

Калькулятор расширения серии Maclaurin представляет собой простой в использовании инструмент. Чтобы расширить любую функцию, выполните следующие шаги.

• Введите функцию в поле ввода.
• Нажмите кнопку загрузить пример , чтобы использовать образцы примеров.
• Запишите порядок функции.
• Центральная точка (a=0) фиксирована по умолчанию.
• Нажмите кнопку вычислить , чтобы получить ряд Маклорена для данной функции.
• Нажмите кнопку очистки , чтобы выполнить перерасчет.

Что такое серия Маклорена?

Степенной ряд, который позволяет оценить аппроксимацию функции f(x) для входных значений, близких к нулю, при условии, что известны значения последовательных дифференциалов функции при a=0, известен как ряд Маклорена. Это тип серии Тейлора.

Формула ряда Маклорена

Общее уравнение или формула ряда Маклорена приведены ниже. 9n\left(0\right)\) — n-я производная данной функции.

Ноль — фиксированная центральная точка.

Общее количество терминов в ряду равно «n».

Как рассчитать ряд Маклорена?

Вот пример, решенный нашим калькулятором ряда Маклорена для получения ряда Маклорена.

Пример

Какой ряд Маклорена для sin(x) имеет n=6?

Решение

Шаг 1: Возьмите заданные данные из задачи.