Разложить по синусам: Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье периодических функций с периодом 2π. Четные и нечетные функции. Разложение в ряд Фурье по синусам. Ряд Фурье для произвольного интервала.

Ряд Фурье непериодических функций с периодом 2π. Разложение в ряд Фурье по косинусам. Ряд Фурье на полупериоде. Ряд Фурье на полупериоде для функций, заданных на интервале L≠2π.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂cos2x+a₃cos3x+…+b₁sinx+b₂sin2x+b₃sin3x+…,

где a_o, a₁,a₂,…,b₁,b₂,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x).

Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=a_o+c₁sin(x+α₁)+c₂sin(2x+α₂)+…+c_nsin(nx+α_n)

Где a_o — константа, с ₁=(a₁²+b₁²)^1/2 , с _n=(a_n²+b_n²)^1/2— амплитуды различных компонент, а фазовый угол равен a_n=arctg a_n/b_n.

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой, (a₂cos2x+b₂sin2x) или c₂sin(2x+α₂) называется

второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций в ряд Фурье.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис.

ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.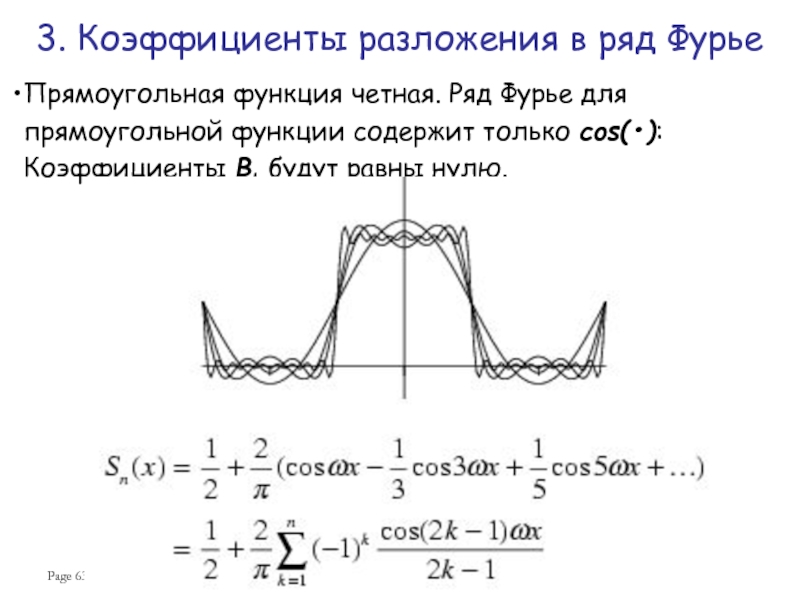 е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис.

Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

Где коэффициенты ряда Фурье, 

Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

Помогите решить / разобраться (М)

Сообщения без ответов | Активные темы | Избранное

Правила форума

Посмотреть правила форума

artempalkin	Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 14:16
14/02/20 777	Дорогие друзья, подскажите, что может значить такое задание? Разложить в ряд Фурье следующую функцию по синусам четных дуг: . Что-то задание не совсем мне понятно. Во-первых, не дана область, на которой нужно разложить, а во-вторых, непонятно, что значит «по синусам четных дуг». Я уж было подумал, что это значит разложить на , тогда будут синусы типа . Но в соседнем задании: Разложить по синусам НЕЧЕТНЫХ дуг на . Короче, чего-то я не понимаю в этой терминологии, и гугл не помог. Что такое разложение по синусам либо косинусам КРАТНЫХ дуг, понятно, хотя глубокую суть этих терминов я не понимаю (почему не просто «по синусам» или «косинусам»? причем тут дуги?). А четные или нечетные дуги — вообще загадка.

Aritaborian	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07.05.2021, 14:21
11/06/12 10361 стихия.вздох.мюсли	А что за книга?

artempalkin	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 14:25
14/02/20 777	Aritaborian в сообщении #1517340 писал(а): А что за книга? Не книга, д/з 4-го семестра ВМК МГУ. В книгах пока не смог найти, как и в гугле.

alisa-lebovski	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 14:48
Заслуженный участник 05/12/09 1685 Москва	По-моему, это значит по , где четные или нечетные соответственно.

artempalkin	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 15:26
14/02/20 777	alisa-lebovski в сообщении #1517349 писал(а): По-моему, это значит по , где четные или нечетные соответственно. Ну допустим, но как этого добиться? Особенно в случае заданного сегмента типа .

alisa-lebovski	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 15:31
Заслуженный участник 05/12/09 1685 Москва	Уточните, в чем проблема. Функция нечетная, синусы тоже. Косинусов не будет.

artempalkin	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 15:44
14/02/20 777	alisa-lebovski в сообщении #1517352 писал(а): Уточните, в чем проблема. Функция нечетная, синусы тоже. Косинусов не будет. Непонятно, что означает разложить «по синусам четных дуг» и по «синусам нечетных дуг».

alisa-lebovski	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 15:57
Заслуженный участник 05/12/09 1685 Москва	Представить в виде

artempalkin	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07. 05.2021, 16:03
14/02/20 777	alisa-lebovski в сообщении #1517356 писал(а): Представить в виде Но, по моим представлениям, это невозможно 🙂 Если раскладывать на , то ни один из этих рядов ни с какими коэффициентами не сойдется к функции. Если раскладывать на , то первый ряд подойдет, но тогда непонятно вот это задание artempalkin в сообщении #1517337 писал(а): Разложить по синусам НЕЧЕТНЫХ дуг на . Подскажите, а где будет сходиться к функции такое разложение alisa-lebovski в сообщении #1517356 писал(а): Я что-то не очень понимаю.

alisa-lebovski	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07.05.2021, 16:16
Заслуженный участник 05/12/09 1685 Москва	Имеется в виду, первое на , второе на . Это определяется первым синусом в ряду. Возможно, имеется в виду формальное разложение Фурье, сходимость не гарантируется.

svv	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07.05.2021, 18:51
Заслуженный участник 23/07/08 10037 Crna Gora	Вот статья, где это выражение употребляется. Стр. 25 и 26. https://izv.etu.ru/assets/files/izv-etu … -25-30.pdf

arseniiv	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 07.05.2021, 19:00
Заслуженный участник 27/04/09 28128	Да, не было бы проблем, если бы сразу давали функцию, определённую на окружности, и спрашивали разложить в обычный и единственно естественный для таких функций ряд Фурье по экспонентам, путают людей без повода. А преобразовывать функции на отрезке — это химера, ни тебе с преобразованием Фурье, ни с рядом, непонятно какие естественные требования к разложению. На практике всегда должно будет оказаться ясно, что применять, и по идее можно будет сформулировать интересующее преобразование как одно из таких естественных, где условия «лишь коэффициенты с номерами могут быть ненулевыми» автоматически испарятся выбором правильной области определения.

RIP	Re: Разложить по синусам (косинусам) ЧЁТНЫХ дуг 09.05.2021, 07:47
Заслуженный участник 11/01/06 3778	Определения термина не встречал, но в методе Фурье при определённых краевых условиях приходится раскладывать по нечётным синусам/косинусам, правда, на промежутке . Если функцию продолжить на промежуток  по правилам: 1) , 2) , то её р.Ф. на промежутке  будет иметь вид Для косинусов похоже.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 13 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Калькулятор тригонометрического расширения — Solumaths

Expand trigo, онлайн-исчисление

Резюме:

Калькулятор позволяет получить тригонометрическое разложение выражения.

expand_trigo онлайн

---

Описание :

Калькулятор позволяет вычислить онлайн тригонометрическое разложение выражения, которое включает в себя синусы или косинусы, для этого он использует формулы дублирования, связанные с этими функциями. Калькулятор позволяет производить символьные вычисления, поэтому можно комбинировать цифры и буквы.

Вычисление выражения формы cos(a+b)

Калькулятор может составить тригонометрических разложений выражения вида cos(a+b), предоставив результаты в точной форме: таким образом, чтобы расширить `cos(pi/6+pi/3)` введите expand_trigo(`cos(pi/6+pi/3)`), после расчета возвращается результат.

Вычисление выражения формы cos(a-b)

Калькулятор может расширить тригонометрических формул формы cos(a-b), предоставив результаты в точной форме: таким образом, чтобы расширить `cos(pi/6-pi/3)` введите expand_trigo(`cos(pi/6-pi/3)`), после расчета возвращается результат.

Вычисление выражения формы sin(a+b)

Калькулятор также может составить тригонометрических разложений формулы вида `sin(a+b)`, предоставив результаты в точной форме: таким образом, чтобы расширить `sin(pi/6+pi/3)` введите expand_trigo(`sin(pi/6+pi/3)`), после расчета возвращается результат.

Вычисление выражения формы sin(a-b)

Калькулятор может расширить до тригонометрических выражений вида `sin(a-b)`, предоставив результаты в точной форме: таким образом, чтобы расширить `sin(pi/6-pi/3)` введите expand_trigo(`sin(pi/6-pi/3)`), после расчета возвращается результат.

Синтаксис:

expand_trigo(выражение), где выражение является тригонометрическим выражением

---

Примеры:

• expand_trigo(`cos(a+b)`) возвращает `cos(a)*cos(b)+sin(a)*sin(b)`
• expand_trigo(`cos(a-b)`) возвращает `cos(a)*cos(b)-sin(a)*sin(b)`
• expand_trigo(`sin(a-b)`) возвращает `cos(a)*sin(b)-sin(a)*cos(b)`
• expand_trigo(`sin(a+b)`) возвращает `cos(a)*sin(b)+sin(a)*cos(b)`

Расчет онлайн с помощью expand_trigo (тригонометрическое расширение)

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
• Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
• Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
• Расчет ежемесячных платежей по страхованию кредита: кредит_страхование. Калькулятор ежемесячных платежей по кредитному страхованию: кредит под залог недвижимости, потребительский кредит и другие виды кредита.
• Калькулятор алгебры: калькулятор. Калькулятор, позволяющий производить алгебраические вычисления, комбинируя операции с буквами и цифрами, а также указывать этапы вычислений.
• Калькулятор упрощения surds :simple_surd. Онлайн-калькулятор, который позволяет производить расчеты в точной форме с квадратными корнями: сумма, произведение, разность, отношение.
• Список вычислений, применимых к алгебраическому выражению: см._возможные_вычисления. Возвращает список вычислений, которые можно выполнить над алгебраическим выражением.
• Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
• Калькулятор разложения на частичные дроби: partial_fraction_decomposition. Калькулятор позволяет разбить рациональную дробь на простые элементы.
• Калькулятор производных: производная. Калькулятор производной позволяет пошагово вычислить производную функции по переменной.
• Калькулятор расширения Тейлора: taylor_series_expansion. Калькулятор ряда Тейлора позволяет вычислить разложение Тейлора функции.
• Логарифмическое расширение: expand_log. Калькулятор позволяет получить логарифмическое расширение выражения.
• Расширить калькулятор : развернуть. Калькулятор умеет расширять алгебраическое выражение онлайн и удалять ненужные скобки.
• Расширьте и упростите алгебраическое выражение онлайн: expand_and_simplify. Онлайн-калькулятор, позволяющий расширить и сократить алгебраическое выражение.
• Калькулятор факторинга: коэффициент. Калькулятор факторинга позволяет факторизовать алгебраическое выражение онлайн с шагом.
• Генератор решенных математических упражнений : Exercise_generator. Возвращает список утверждений математических упражнений и их решений, которые могут использоваться учителями для подготовки тестов и викторин.
• Интегральный калькулятор: интегральный. Калькулятор интегралов вычисляет онлайн интеграл функции между двумя значениями, результат выдается в точном или приближенном виде.
• Калькулятор неопределенных интегралов: первообразная. Калькулятор первообразной позволяет рассчитать первообразную онлайн с подробностями и шагами расчета.

  No related posts.