Разница косинусов: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

Метрики сходства и расстояния для науки о данных и машинного обучения

  Перевод   Ссылка на автора

В предыдущая статья о системах рекомендаций мы несколько раз упоминали концепцию «мер сходства». Зачем? Потому что в Рекомендационных системах как алгоритмы контентной фильтрации, так и алгоритмы совместной фильтрации используют определенную меру сходства, чтобы найти, насколько равны два вектора пользователей или элементов между ними. Таким образом, в конце, мера сходства не больше, чем расстояние между векторами.

Примечание: помните, что вся моя работа, включая специальный репозиторий с применением всего этого контента и больше о Системах Рекомендаций, доступна в моем Профиль GitHub ,

В любом типе алгоритма наиболее распространенной мерой подобия является нахождение косинуса угла между векторами, то есть сходства косинусов. Предположим, что A — это список фильмов с рейтингом пользователя, а B — список фильмов с рейтингом пользователя B, тогда сходство между ними можно рассчитать как:

Математически косинусное сходство измеряет косинус угла между двумя векторами, спроецированными в многомерном пространстве. При построении в многомерном пространстве косинусное сходство фиксирует ориентацию (угол) каждого вектора, а не величину. Если вы хотите получить величину, вместо этого вычислите евклидово расстояние.

Сходство по косинусу выгодно, потому что даже если два одинаковых документа находятся далеко друг от друга на евклидовом расстоянии из-за размера (например, одно слово, появляющееся много раз в документе, или пользователь, часто видящий один фильм), они все равно могут иметь меньший угол между ними. Чем меньше угол, тем выше сходство.

Возьмите следующий пример из www.machinelearningplus.com:

На изображении выше показано количество появлений слов «sachin», «dhoni» и «cricket» в трех показанных документах.

Теперь, регулярное косинусное сходство по определению отражает различия в направлении, но не в местоположении. Следовательно, использование метрики косинусного сходства не учитывает, например, разницу в рейтингах пользователей. Скорректированное косинусное сходство компенсирует этот недостаток путем вычитания среднего рейтинга соответствующего пользователя из каждой пары с равным рейтингом и определяется следующим образом:

Давайте возьмем следующий пример из Stackoverflow, чтобы лучше объяснить разницу между косинусом и скорректированным сходством косинусов:

Предположим, пользователь дает оценки в 0 ~ 5 для двух фильмов.

Интуитивно мы бы сказали, что у пользователей b и c одинаковые вкусы, и a довольно сильно отличается от них. Но регулярное косинусное сходство говорит нам неверную историю. В подобных случаях вычисление скорректированного косинусного сходства даст нам лучшее понимание сходства между пользователями.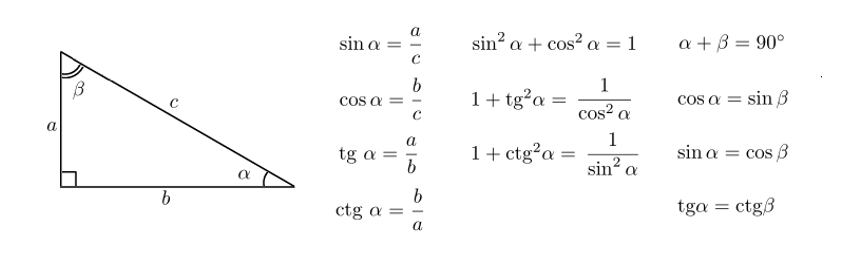

Кстати, в нашем предыдущая статья о Системах Рекомендаций мы представили следующую функцию, чтобы найти скорректированное косинусное сходство:

from scipy import spatialdef adjusted_cos_distance_matrix(size, matrix, row_column):
distances = np.zeros((size,size))
if row_column == 0:
M_u = matrix.mean(axis=1)
m_sub = matrix - M_u[:,None]
if row_column == 1:
M_u = matrix.T.mean(axis=1)
m_sub = matrix.T - M_u[:,None]
 for first in range(0,size):
for sec in range(0,size):
distance = spatial.distance.cosine(m_sub[first],m_sub[sec])
distances[first,sec] = distance
return distances

И вы можете использовать эту функцию очень просто, просто кормя:

1. «Матрица»: это просто исходная матрица рейтингов, просмотров или того, что вы измеряете между пользователями и элементами вашего бизнеса
2. «Row_columns»: указывает 1, если вы будете измерять расстояния между столбцами, и 0 для расстояний между рядами
3. «Размер»: для желаемого размера результирующей матрицы. То есть при поиске сходства пользователей или элементов это будет просто количество пользователей или элементов. Таким образом, если у вас есть 500 уникальных пользователей, вы получите матрицу расстояний 500×500

Возьмите следующий пример в качестве ссылки:

user_similarity = adjusted_cos_distance_matrix(n_users,data_matrix,0)
item_similarity = adjusted_cos_distance_matrix(n_items,data_matrix,1)

Наконец, давайте кратко рассмотрим некоторые другие методы, которые можно использовать для вычисления подобия для систем рекомендаций, но также и для любого другого алгоритма на основе расстояния в машинном обучении:

• Евклидово расстояние: похожие элементы будут лежать в непосредственной близости друг от друга, если они нанесены в n-мерном пространстве.

• Корреляция Пирсона или корреляционное сходство: он говорит нам, насколько тесно связаны два элемента. Чем выше корреляция, тем выше сходство.

• Средняя квадратическая разница: о нахождении среднего квадрата расхождения между рейтингами пользователей.
  MSE уделяет больше внимания наказанию за большие ошибки.

А потом:

Где | 𝐼𝑢𝑣 | это просто количество предметов, оцененных как пользователями 𝑢, так и 𝑣.

Давайте кратко вспомним, как работает совместная фильтрация на примере нашего предыдущая вступительная статья о системах рекомендаций: предположим, мне нравятся следующие книги: «Слепой убийца» и «Джентльмен в Москве». И моему другу Матиасу нравятся «Слепой убийца» и «Джентльмен в Москве», а также «Там, где поют кроады». Похоже, у нас с Матиасом одинаковые интересы Таким образом, вы, вероятно, могли бы подтвердить, что я хотел бы «Где поют кроады», хотя я этого не читал. И это именно логика, лежащая в основе совместной фильтрации, за исключением того, чтоВы можете сравнивать пользователей между ними, а также сравнивать предметы,

Давайте наглядно представим разницу между вычислительным использованием пользователей и подобий элементов в системе рекомендаций:

Сходство пользователя и пользователя

Схожесть предметов

Теперь, понимая это, давайте проиллюстрируем некоторые из мер, которые мы представили, на следующих примерах от нашего друга из Аналитика Видхья, что я нашел особенно очевидным для сходства пользователя и пользователя и элемента:

• Сходство пользователя и пользователя

Изображение и пример взяты из аналитики Vidhya

Здесь у нас есть матрица рейтинга фильмов пользователя. Чтобы понять это на практике, давайте найдем сходство между пользователями (A, C) и (B, C) в приведенной выше таблице. Обычные фильмы с рейтингом A и C — это фильмы x2 и x4, а под B и C — фильмы x2, x4 и x5. Зная это, давайте найдем корреляцию Пирсона или подобие корреляции:

Корреляция между пользователем A и C больше, чем корреляция между B и C. Следовательно, пользователи A и C имеют большее сходство, и фильмы, которые нравятся пользователю A, будут рекомендованы пользователю C, и наоборот.

• Схожесть предметов

Здесь средний рейтинг элемента — это среднее значение всех оценок, присвоенных конкретному элементу (сравните его с таблицей, которую мы видели при фильтрации пользователей). Вместо того, чтобы находить сходство пользователя и пользователя, мы находим сходство элемент-элемент. Для этого сначала нужно найти таких пользователей, которые оценили эти элементы и на основе оценок вычисляется сходство между элементами. Давайте найдем сходство между фильмами (x1, x4) и (x1, x5). Обычные пользователи, которые оценили фильмы x1 и x4, являются A и B, в то время как пользователи, которые оценили фильмы x1 и x5, также являются A и B.

Сходство между фильмами x1 и x4 больше, чем сходство между фильмами x1 и x5. Поэтому, исходя из этих значений подобия, если какой-либо пользователь ищет фильм x1, ему будет рекомендован фильм x4 и наоборот.

Ну, это пока все о Рекомендационных системах. Тем не менее, помните, что показатели сходства и метрики расстояния появляются в машинном обучении как очень фундаментальная концепция. Поэтому я надеюсь, что вы нашли этот контент полезным не только для повышения производительности вашего Рекомендатора;)

Если вам понравился этот пост, не забудьте проверить некоторые из моих последних статей, например 10 советов, как улучшить свои навыки прорисовки, 6 любительских ошибок, которые я допустил, работая с разделением поезда-теста или Соскоб в сети за 5 минут, Все они и многое другое доступно в мой средний профиль,

Связаться также . ..

• LinkedIn: https://www.linkedin.com/in/gferreirovolpi/
• GitHub: https://github.com/gonzaferreiro (где весь мой код доступен)

Увидимся в следующем посте!

Приветствия.

1. Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.

φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах

Δλ — разница координат по долготе

Δδ — угловая разница

Δδ = arccos {sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ}

Для перевода углового расстояния (Δδ) в метрическое (L), нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае – метры).

Используется, чтобы избежать проблем с небольшими расстояниями.

Формулу для расчета расстояний студенты выбирают самостоятельно. Однако, предпочтительнее расчеты выполнить по формуле №2.

Расчет направления дрейфа судна

Осуществляется по формуле:

ctgα = cosϕ1 + tgϕ2·cosec(λ2 – λ1) – sinϕ1·ctg(λ2 – λ1),

α – ортодромический путевой угол

Если α получается отрицательным, то необходимо увеличить значение угла на 360.

2. На основании данных о пройденном расстоянии и времени снятия координат в начальной (t_нач.) и конечной (t_кон.) точке надо определить скорость дрейфа судна (V _дрейф.) и еe проекции на меридиан (V _мер.) и широту (V _шир.).

V _дрейф. = L/( t_кон. — t_нач.)(сек)

V1=V _мер.=V_дрейф.*SIN(α)

V2=V _шир.=V_дрейф.*COS(α)

Метры переводить в сантиметры.

3. На основании имеющихся данных выполнить осреднение данных полученных прибором «Вектор-2»

Первичная обработка данных измерителя течении «Вектор-2» заключается в расчете средних значений гидрологических характеристик на горизонте наблюдения. Все операции производятся путем математического осреднения.

4. На основании осредненных данных о проекциях скорости определить направление течения по данным прибора и суммарную скорость

Расчет направления течения

Сначала определяется квадрант, в котором находится вектор скорости течения. При этом направление на север принимается за 0°, направление на восток за 90°. Квадрант определяется по соотношению знаков проекции скорости V мер. и V шир. Согласно таблице.

Угол направления течения в диапазоне от 0° до 360° с округлением до 1° рассчитывается по формулам:

1 квадрант

2 и 3 квадрант

4 квадрант

V сумарная=

Полученные по прибору значения скорости и направления течения содержат в себе данные как о дрейфе судна так и об истинной скорости течения.

5. На основании показаний прибора и данных о дрейфе судна требуется определить истинную скорость и направление течений.

После того как определены характеристики дрейфа судна за период измерения и средние характеристики течений на горизонте производится расчет истинных скоростей и направлений течения. Долготные и широтные компоненты скорости по показаниям прибора и по результатам дрейфа судна складываются. По полученным компонентам определяется истинная скорость и направления течения на горизонте наблюдения. По уже известным формулам.

Косинусное сходство и косинусное расстояние | Анджани Кумар

Введение:

Косинусное сходство используется для определения сходства между документами или векторами. Математически он измеряет косинус угла между двумя векторами, спроецированными в многомерном пространстве. Существуют и другие методы измерения подобия, такие как евклидово расстояние или манхэттенское расстояние, но мы сосредоточимся здесь на косинусном сходстве и косинусном расстоянии.

Связь между косинусным сходством и косинусным расстоянием может быть определена следующим образом.

1. Сходство уменьшается, когда расстояние между двумя векторами увеличивается

2. Сходство увеличивается, когда расстояние между двумя векторами уменьшается.

Косинусное сходство говорит о том, что для нахождения сходства между двумя точками или векторами нам нужно найти угол между ними .

Формула для нахождения сходства косинуса и расстояния выглядит следующим образом:

Здесь A=точка P1, B=точка P2 (в нашем примере)

Давайте посмотрим на различные значения Cos Θ, чтобы понять косинусное сходство и косинусное расстояние между двумя точками данных (векторами) P1 и P2 с учетом двух осей X и Y.

Ниже на рисунке показаны случаи.

Случай 1: Когда угол между точками P1 и P2 равен 45 градусам, тогда

cosine_similarity= Cos 45 = 0,525 90 градусов, затем

cosine_similarity= Cos 90 = 0

Случай 3: Когда две точки P1 и P2 очень близки и лежат на одной оси друг к другу, а угол между точками равен 0 градусов, тогда

cosine_similarity= Cos 0 = 1

Ниже на картинке показаны следующие три ящика.

Случай 4: Когда точки P1 и P2 лежат друг напротив друга и угол между точками равен 180 градусов, тогда

cosine_similarity= Cos 180 = -1

Случай 5: Когда угол между точками P1 и P2 равен 270 градусам, тогда

cosine_similarity= Cos 270 = 0

Случай 6: Когда угол между точками P1 и P2 равен 360 градусам, тогда

cosine_similarity = Cos1

Давайте передадим эти значения каждого угла, рассмотренного выше, и посмотрим Косинусное расстояние между двумя точками.

1 — Cosine_Similarity=Cosine_Distance

Случай 1 : Когда Cos 45 градусов

Заменим значения в приведенной выше формуле.

1–0,525 = cosine_distance

0,475 = Cosine_distance

Случай 2 : когда COS 90 градусов

1–0 = Cosine_distance

1 = Cosine_distance

Case 3 9000: Cosine_distance

: 38: Cosine_distance

: Cosicine_distance

. 1= Cosine_Distance

0 =Cosine_Distance

Случай 4 : Когда Cos 180 градусов

1–(-1)= Cosine_Distance

2 =Cosine_Distance

Case 5 : When Cos 270 Degree

1–0= Cosine_Distance

1 =Cosine_Distance

Case 6 : When Cos 360 Degree

1–1= Cosine_Distance

0 =Cosine_Distance

We can clearly видеть, что, когда расстояние меньше, сходство больше (точки расположены близко друг к другу) и расстояние больше, две точки не похожи (далеко друг от друга)

Косинусное сходство и косинусное расстояние широко используются в рекомендательных системах продукты пользователям на основе их симпатий и антипатий.

Несколько примеров, где это используется, — это веб-сайты, такие как Amazon, Flipkart, чтобы рекомендовать товары клиентам для персонализированного опыта, оценки и рекомендации фильмов и т. д. косинусное сходство и косинусное расстояние и их использование.

Надеюсь, вам понравилась моя статья. Пожалуйста, нажмите 👏 (50 раз), чтобы мотивировать меня писать дальше.

Хотите подключиться:

Ссылка: https://www.linkedin.com/in/anjani-kumar-9b969a39/

Если вам нравятся мои посты здесь, на Medium, и вы хотели бы, чтобы я продолжил эту работу, поддержите меня на patreon

Косинусное сходство — Понимание математики и того, как она работает? (с python)

Косинусное сходство — это метрика, используемая для измерения того, насколько похожи документы независимо от их размера. Математически он измеряет косинус угла между двумя векторами, спроецированными в многомерном пространстве.

Косинусное подобие выгодно, потому что даже если два похожих документа находятся далеко друг от друга на евклидово расстояние (из-за размера документа), есть вероятность, что они все же могут быть ориентированы ближе друг к другу. Чем меньше угол, тем выше подобие косинуса.

К концу этого урока вы будете знать:

1. Что такое косинусное сходство и как оно работает?
2. Как вычислить косинусное сходство документов в python?
3. Что такое мягкое косинусное сходство и чем оно отличается от косинусного сходства?
4. Когда использовать подобия мягкого косинуса и как его вычислить в python?

Подобие косинуса – Понимание математики и того, как она работает. Фото Мэтта Ламерса

1. Введение
2. Что такое косинусное сходство и почему оно полезно?
3. Пример подобия косинуса
4. Как вычислить сходство косинуса в Python?
5. Мягкое косинусное сходство 6. Заключение

1. Введение

Обычно используемый подход к сопоставлению похожих документов основан на подсчете максимального количества общих слов между документами.

Но у этого подхода есть существенный недостаток.

То есть по мере увеличения размера документа количество общих слов имеет тенденцию к увеличению, даже если в документах говорится о разных темах. Косинусное подобие помогает преодолеть этот фундаментальный недостаток подхода «подсчет общих слов» или евклидова расстояния.

2. Что такое косинусное сходство и почему оно полезно?

Косинусное сходство — это метрика, используемая для определения того, насколько похожи документы независимо от их размера.

Математически, Подобие косинуса измеряет косинус угла между двумя векторами, спроецированными в многомерном пространстве.

В этом контексте два вектора, о которых я говорю, представляют собой массивы, содержащие количество слов в двух документах.

В качестве показателя подобия, как косинусное сходство отличается от количества общих слов?

При построении в многомерном пространстве, где каждое измерение соответствует слову в документе, косинусное сходство фиксирует ориентацию (угол) документов, а не величину. Если вам нужна величина, вместо этого вычислите евклидово расстояние.

Косинусное сходство выгодно, потому что даже если два похожих документа находятся далеко друг от друга на евклидовом расстоянии из-за размера (например, слово «сверчок» появляется 50 раз в одном документе и 10 раз в другом), они все равно могут иметь меньший угол между ними. Чем меньше угол, тем выше сходство.

3. Косинус подобия Пример

Предположим, у вас есть 3 документа, основанные на паре звездных игроков в крикет – Сачин Тендулкар и Дхони.

Бесплатный шаблон проекта временных рядов

Хотите узнать, как подходить к проектам в разных областях с помощью временных рядов?

Начните свой первый отраслевой проект временных рядов и узнайте, как использовать и реализовывать такие алгоритмы, как ARIMA, SARIMA, SARIMAX, простое экспоненциальное сглаживание и алгоритм Холта-Винтерса.

Загрузить шаблон проекта временных рядов

Хотите узнать, как подходить к проектам в разных областях с помощью временных рядов?

Начните свой первый отраслевой проект временных рядов и узнайте, как использовать и внедрять такие алгоритмы, как ARIMA, SARIMA, SARIMAX, простое экспоненциальное сглаживание и алгоритм Холта-Винтерса.

Шаблон проекта Free Time Series

Два документа (A) и (B) взяты со страниц википедии соответствующих игроков, а третий документ (C) представляет собой меньший фрагмент страницы википедии Дхони. Три документа

Как видите, все три документа объединяет общая тема – игра в крикет.

Наша цель — количественно оценить сходство между документами.

Для простоты понимания давайте рассмотрим только 3 наиболее часто встречающихся слова в документах: «Дхони», «Сачин» и «Крикет».

Можно ожидать, что Doc B и Doc C , то есть два документа на Дхони будут иметь большее сходство, чем Doc A и Doc B , потому что Doc C по сути является фрагментом самого Doc B .

Однако, если мы будем исходить из числа общих слов, два больших документа будут содержать самые распространенные слова и, следовательно, будут рассматриваться как наиболее похожие, чего мы и хотим избежать.

Результаты будут более конгруэнтными, если для оценки сходства мы будем использовать показатель косинусного сходства.

Поясню.

Давайте спроецируем документы в трехмерное пространство, где каждое измерение представляет собой частотный подсчет: «Сачин», «Дхони» или «Крикет». При построении в этом пространстве 3 документа будут выглядеть примерно так. отдельно по величине.

Оказывается, чем ближе документы по углу, тем выше Косинусное сходство (Cos theta). Формула косинусного сходства

Чем больше слов вы включаете в документ, тем сложнее визуализировать многомерное пространство. Но вы можете напрямую вычислить косинусное сходство, используя эту математическую формулу. Хватит теории. Давайте вычислим косинусное сходство с Python’ом scikitlearn.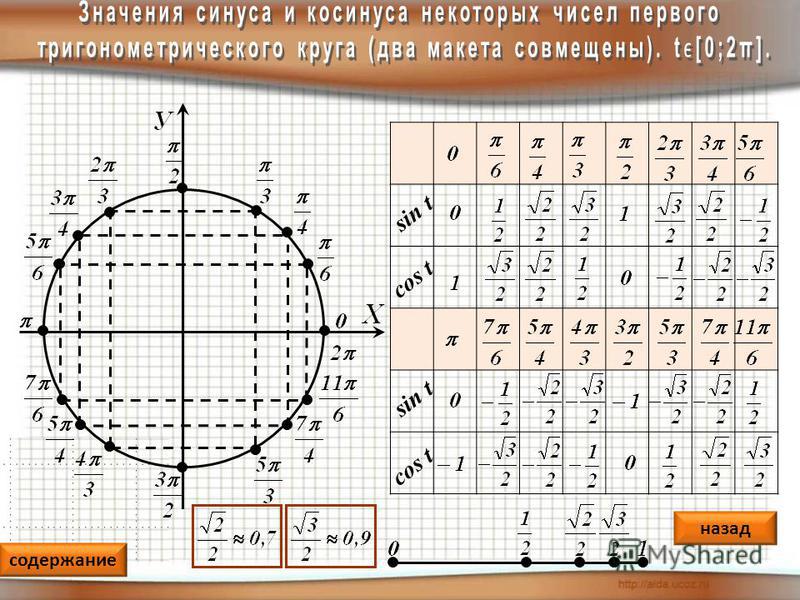

4. Как вычислить сходство косинусов в Python?

У нас есть следующие 3 сообщения:
1. Док Трамп (A): Г-н Трамп стал президентом после победы на политических выборах. Хотя он потерял поддержку некоторых друзей-республиканцев, Трамп дружит с президентом Путиным.

2. Doc Trump Election (B) : Президент Трамп говорит, что Путин не имел никакого политического вмешательства, таковы результаты выборов. Он говорит, что это была охота на ведьм со стороны политических партий. Он заявил, что президент Путин — его друг, который не имеет никакого отношения к выборам.

3. Док Путин (C): После выборов Владимир Путин стал Президентом России.

Президент Путин в начале своей политической карьеры занимал пост премьер-министра.

Поскольку документ B имеет больше общего с документом A, чем с документом C, я ожидаю, что косинус между A и B будет больше, чем (C и B).

 # Определить документы
doc_trump = "Г-н Трамп стал президентом после победы на политических выборах.  Хотя он потерял поддержку некоторых друзей-республиканцев, Трамп дружит с президентом Путиным"
doc_election = "Президент Трамп говорит, что Путин не имел политического вмешательства в исход выборов. Он говорит, что это была охота на ведьм со стороны политических партий. Он утверждал, что президент Путин - друг, который не имеет никакого отношения к выборам"
doc_putin = "После выборов Владимир Путин стал президентом России. Ранее в своей политической карьере президент Путин занимал пост премьер-министра"
документы = [doc_trump, doc_election, doc_putin]
 

Чтобы вычислить косинусное сходство, вам нужно количество слов в каждом документе.

CountVectorizer или TfidfVectorizer из scikit Learn позволяет нам вычислить это.

На выходе получается sparse_matrix .

При этом я дополнительно преобразовываю его в кадр данных pandas, чтобы увидеть частоты слов в табличном формате.

 # Scikit Learn
из sklearn.feature_extraction. text импортировать CountVectorizer
импортировать панд как pd
# Создайте матрицу терминов документа
count_vectorizer = CountVectorizer (stop_words = 'английский')
count_vectorizer = Счетчик векторизаторов()
sparse_matrix = count_vectorizer.fit_transform (документы)
# НЕОБЯЗАТЕЛЬНО: конвертируйте разреженную матрицу в Pandas Dataframe, если вы хотите увидеть частоты слов.
doc_term_matrix = разреженная_матрица.todense()
df = pd.DataFrame(doc_term_matrix,
                  столбцы = count_vectorizer.get_feature_names(),
                  index=['doc_trump', 'doc_election', 'doc_putin'])
дф
 

 # Вычисление подобия косинуса
из sklearn.metrics.pairwise импортировать cosine_similarity
печать (косинусное_подобие (df, df))
#> [[ 1. 0,48927489 0,37139068]
#> [ 0,48927489 1. 0,38829014]
#> [ 0,37139068 0,38829014 1. ]]
 

 # Определить документы
doc_soup = "Суп — это преимущественно жидкая пища, обычно подаваемая теплой или горячей (но может быть прохладной или холодной), приготовленная путем смешивания мясных или овощных ингредиентов с бульоном, соком, водой или другой жидкостью."
doc_noodles = "Лапша является основным продуктом питания во многих культурах. Ее готовят из пресного теста, которое растягивают, экструдируют или раскатывают и нарезают одной из множества форм."
doc_dosa = "Доса — это разновидность блинов с Индийского субконтинента, приготовленных из ферментированного жидкого теста. По внешнему виду они чем-то похожи на блины. Его основными ингредиентами являются рис и черный грамм."
документы = [doc_trump, doc_election, doc_putin, doc_soup, doc_noodles, doc_dosa]
 

 импортный генсим
# обновите gensim, если не можете импортировать softcossim
из gensim. matutils импортировать softcossim
из корпусов импорта gensim
импортировать gensim.downloader как API
из gensim.utils импортировать simple_preprocess
печать (gensim.__version__)
#> '3.6.0'
# Загрузите модель FastText
fasttext_model300 = api.load('fasttext-wiki-news-subwords-300')
 

 # Подготовить словарь и корпус.
словарь = corpora.Dictionary([simple_preprocess(doc) для документа в документах])
# Подготовить матрицу подобия
матрица сходства = fasttext_model300.similarity_matrix (словарь, tfidf = нет, порог = 0,0, показатель степени = 2,0, nonzero_limit = 100)
# Преобразование предложений в набор векторов слов.
sent_1 = Dictionary.doc2bow (simple_preprocess (doc_trump))
sent_2 = Dictionary.doc2bow (простой_предварительный процесс (doc_election))
sent_3 = Dictionary.doc2bow(simple_preprocess(doc_putin))
sent_4 = Dictionary. doc2bow (simple_preprocess (doc_soup))
sent_5 = Dictionary.doc2bow(simple_preprocess(doc_noodles))
sent_6 = Dictionary.doc2bow (simple_preprocess (doc_dosa))
предложения = [отправлено_1, отправлено_2, отправлено_3, отправлено_4, отправлено_5, отправлено_6]
 

 # Вычислить мягкое косинусное сходство
печать (softcossim (отправлено_1, отправлено_2, матрица_сходства))
#> 0,567228632589
 

 импортировать numpy как np
импортировать панд как pd
def create_soft_cossim_matrix (предложения):
    len_array = np.arange (len (предложения))
    хх, уу = np.meshgrid(len_array, len_array)
    cossim_mat = pd.DataFrame([[round(softcossim(предложения[i],предложения[j], матрица сходства) ,2) для i, j в zip(x,y)] для y, x в zip(xx, yy) ])
    вернуть cossim_mat
soft_cosine_similarity_matrix (предложения)