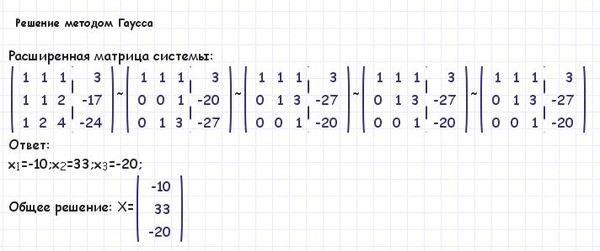
Пошаговое решение системы линейных уравнений методом Гаусса
На рис.2.3.3. приведены результаты пошагового решения методом Гаусса следующей системы линейных уравнений:
Рис.2.3.3. Решение СЛУ методом Гаусса
Введите на рабочем листе исходные данные. Для этого:
1. В ячейки диапазона А2:С4 введите коэффициенты системы, стоящие при неизвестных.
2. В ячейках диапазона D2:D4 задайте свободные члены.
Прямая прогонка метода Гаусса:
1. Через буфер обмена скопируйте диапазон A2:D2 на A6:D6.
2. Выберите диапазон A7:D7.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
=A3:D3-$A$2:$D$2*A3/$A$2
4. Выберите диапазон A7:D7, расположите указатель мыши на маркере заполнения для этого диапазона и пробуксируйте его вниз на одну строку.
5. Выделите диапазон
A6:D7
и скопируйте его содержимое в буфер
обмена.
7. Выберите команду Специальная вставка (Вкладка ленты Главная, группа команд Буфер обмена – Вставить – Специальная вставка). На экране отобразится диалоговое окно Специальная вставка (рис.2.3.4.). выберите переключатель значения в группе Вставить и нажмите кнопку ОК. В результате в диапазон А10:D10 из диапазона A6:D7 будут скопированы только значения, а не формулы.
Рис.2.3.4. Диалоговое окно «Специальная вставка»
8. Выделите диапазон А12:D12.
9. Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>:
=А8:D8-
Обратная прогонка:
1. выберите диапазон F8:I8.
2. Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
=А12:D12/С12
3. Выделите диапазон F7:I7.
4. Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>:
=(А11:D11-F8:I8*С11)/В11
5.
Выберите диапазон
F6:I6.
6. Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>:
=(А10:D10-F7:I7*B10-F8:I8*C10)/A10
Итак, решением системы уравнений является следующий вектор
. (диапазон ячеек I6:I8).
Математические модели
Основные понятия
Математическая модель — это модель, созданная с помощью математических понятий.
Математическое моделирование — процесс построения и изучения математических моделей.
Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю.
Математической моделью задачи называется совокупность математических соотношений, описывающих рассматриваемый процесс.
Для составления математической модели необходимо:
выбрать переменные задачи;
составить систему ограничений;
задать целевую функцию.
Переменными задачи называются величины , которые полностью характеризуют рассматриваемый процесс. Их обычно записывают в виде набора значений .
Системой ограничений задачи называют совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других условий, например, условия положительности переменных.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум (то есть наибольшее или наименьшее значение) которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти переменные задачи , которые обеспечивают наибольшее или наименьшее значение целевой функции
и удовлетворяют системе ограничений
.
Если целевая функция и система ограничений линейны, то задача математического
программирования называется задачей
линейного программирования.
Допустимым решением задачи линейного программирования называется любой набор из n значений , удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений задачи образует область допустимых решений.
Оптимальным решением задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума (наибольшего или наименьшего значения).
Метод исключения — определение, шаги, примеры, решение системы уравнений
Метод исключения решения системы линейных уравнений алгебраическим путем является наиболее широко используемым методом из всех методов решения линейных уравнений. В методе исключения мы исключаем любую из переменных, используя основные арифметические операции, а затем упрощаем уравнение, чтобы найти значение другой переменной. Затем мы можем подставить это значение в любое из уравнений, чтобы найти значение исключаемой переменной.
Метод исключения прост в использовании, потому что здесь мы исключаем одно из условий, упрощающих наши расчеты.
В этой статье мы научимся решать системы уравнений методом исключения. Мы будем решать различные примеры, основанные на концепции для лучшего понимания.
| 1. | Что такое метод исключения? |
| 2. | Решение систем уравнений методом исключения |
| 3. | шагов по использованию метода исключения |
| 4. | Система решения 3 уравнений с использованием метода исключения |
| 5. | Часто задаваемые вопросы о методе исключения |
Что такое метод исключения?
Согласно определению метода исключения, речь идет об исключении одного из терминов, содержащих любую из переменных, для упрощения вычислений. Это делается путем умножения или деления числа на уравнение (я) таким образом, чтобы коэффициенты любого из переменных членов стали одинаковыми. Затем мы добавляем или вычитаем оба уравнения, чтобы исключить или удалить этот член из результата.
Поэтому метод исключения также называют методом сложения. Например, давайте решим два линейных уравнения, содержащих две переменные, методом исключения.
Решение систем уравнений методом исключения
Метод исключения используется для решения систем уравнений путем исключения переменной и определения значения переменной для поиска решения. Ниже приведено изображение, показывающее применение метода исключения для решения системы уравнений с двумя переменными. Рассмотрим два уравнения x — 2y = 8 и 2x + y = 5.
Шаги по использованию метода исключения
Метод исключения полезен для решения линейных уравнений, содержащих две или три переменные. Мы также можем решить три уравнения, используя этот метод. Но его можно применить только к двум уравнениям одновременно. Рассмотрим этапы решения системы уравнений методом исключения.
- Шаг-1: Первый шаг — умножить или разделить оба линейных уравнения на ненулевое число, чтобы получить общий коэффициент любой из переменных в обоих уравнениях.
- Шаг 2: Сложите или вычтите оба уравнения так, чтобы исключить одни и те же члены.
- Шаг 3: Упростите результат, чтобы получить окончательный ответ от пропущенной переменной (скажем, y), так что мы получим ответ только в форме y=c, где c — любая константа.
- Шаг-4: Наконец, подставьте это значение в любое из данных уравнений, чтобы найти значение другой заданной переменной.
Это шаги метода исключения для решения одновременных линейных уравнений. Давайте возьмем пример двух линейных уравнений x + y = 8 и 2x-3y = 4, чтобы лучше понять его.
Пусть x + y = 8 → (1) и 2x — 3y = 4 → (2)
Шаг 1: Чтобы сделать коэффициенты при x равными, умножьте уравнение (1) на 2 и уравнение (2) на 1. , Мы получаем,
(x+y=8) × 2 → (1)
(2x-3y=4) × 1 → (2)
Итак, теперь у нас есть два уравнения: 2x + 2y = 16 → (1) и 2x — 3y = 4 → (2).
Шаг 2: Вычтем уравнение 2 из 1, получим y=12/5.
Шаг 3: Подставляем значение y в уравнение 1, получаем x + 12/5 = 8
x = 8 — 12/5
x = 28/5
Следовательно, x = 28/5 и y=12/5.
Но что, если при умножении ненулевой константы мы получим равные коэффициенты обеих переменных? Что, если оба члена были исключены при добавлении или вычитании? Такие случаи мы получаем при решении уравнений параллельных и совпадающих прямых. Уравнения двух пересекающихся прямых будут иметь только два непротиворечивых решения, а уравнения двух параллельных прямых не имеют решений, так как эти прямые никогда не пересекаются друг с другом. И уравнения совпадающих прямых имеют бесконечно много решений, поскольку они лежат друг на друге, поэтому каждая точка является пересечением или общей точкой этих прямых. Рассмотрим подробно каждый из этих двух случаев.
Метод исключения: Нет решений
Как известно, уравнения двух параллельных прямых не имеют решений. Итак, если мы решим любые такие уравнения методом исключения, мы получим ответ в виде двух неравных чисел по обе стороны от знака неравно. Например, 0≠8, -2≠0 и т. д. В таких случаях мы не можем исключить только одну переменную.
Обе переменные удаляются. Например, решим два уравнения 2x — y = 4 → (1) и 4x — 2y = 7 → (2) методом исключения. Чтобы сделать коэффициенты x равными в обоих уравнениях, мы умножаем уравнение (1) на 2 и уравнение (2) на 1. Таким образом, мы получаем, 4x — 2y = 8 → (3) и 4x — 2y = 7 → (4). Теперь, если мы попытаемся вычесть уравнение 4 из уравнения 3, мы получим 0=1, так как обе переменные исключаются. Другого способа решить эти уравнения нет, так как решения противоречивы. Итак, в методе исключения, когда решения нет, мы получаем результат в таком виде.
Метод исключения: бесконечно много решений
Два уравнения совпадающих прямых имеют бесконечно много возможных решений. Итак, если методом исключения решить систему уравнений совпадающих прямых, то получится непротиворечивая система с бесконечными решениями. В таких случаях мы получаем ответ в виде 0=0, если применяем метод исключения. Например, попробуйте решить уравнения x+y=2 и 2x+2y-4=0. Если вы умножите любую ненулевую константу на оба уравнения, вы обнаружите, что каждый раз, когда члены переменной x и члены переменной y отменяются или исключаются.
Итак, в методе исключения, когда возможных решений бесконечно много, мы получаем результат в виде 0=0. Рекомендуется проверить, являются ли заданные линейные уравнения пересекающимися, параллельными или совпадающими прямыми, прежде чем пытаться их решить. Прочтите эту статью, чтобы узнать о решениях линейных уравнений.Система решения 3 уравнений с использованием метода исключения
Давайте решим три уравнения 3x-y+2z=5, 4x+2y-z=6 и 5x-3y+z=1 для лучшего понимания.
Итак, мы нашли, что x=1. Подставляем это значение в уравнение P, получаем 9×(1)-y=7.
9-y=7
y=2
Теперь подставим значения x и y в третье уравнение 5x-3y+z=1, и мы получим z=2. Следовательно, x=1, y=2 и z=2.
Важные замечания по методу исключения
- Метод исключения используется для решения системы уравнений.
- Этот метод прост и упрощает расчеты, поскольку исключает одну переменную и, следовательно, сокращает объем вычислений.
- Мы делаем коэффициент переменной одинаковым, чтобы исключить соответствующую переменную.
Похожие статьи
- Калькулятор метода исключения
- Метод замены
- Решатель системы уравнений
- Метод перекрестного умножения
- Графическое решение пары линейных уравнений
- Решение линейных уравнений
Часто задаваемые вопросы о методе исключения
Что такое метод исключения в математике?
В математике метод исключения используется для решения системы линейных уравнений.
Это наиболее широко используемый и простой метод, так как он требует меньше вычислений и шагов. В этом методе мы исключаем одну из двух переменных и пытаемся решить уравнения с одной переменной. Найденное здесь значение можно подставить в любое из приведенных уравнений, чтобы найти также значение другой переменной.
Как решать линейные уравнения методом исключения?
Одновременные линейные уравнения могут быть решены методом исключения. Прежде всего убедитесь, что уравнения записаны в стандартной форме либо Ax+By=C, либо Ax+By+C=0. В этом методе мы умножаем оба уравнения на ненулевое число, чтобы сделать коэффициенты любой одной переменной равными. Затем мы добавляем или вычитаем уравнения, чтобы исключить одну из переменных и найти значение другой переменной. Вот как мы решаем линейные уравнения методом исключения.
Какие этапы метода ликвидации?
Шаги метода исключения приведены ниже:
- Выберите любую переменную для исключения. Умножьте или разделите оба уравнения с ненулевой константой, чтобы сделать коэффициенты этой переменной равными.
- Сложите или вычтите полученные уравнения так, чтобы выбранная переменная была исключена.
- Упростите и найдите значение другой переменной.
- Подставьте это значение в любое из приведенных уравнений, чтобы найти значение исключаемой переменной.
Можно ли использовать метод исключения для решения системы уравнений с тремя переменными?
Да, метод исключения можно использовать для решения линейных уравнений с тремя переменными. С тремя уравнениями мы берем любые два уравнения и выбираем переменную, которую нужно исключить. Затем мы повторяем тот же процесс, беря другую пару уравнений и исключая ту же переменную. Таким образом, у нас останутся два уравнения только с двумя переменными, которые можно решить методом исключения. Наконец, мы помещаем значения этих двух переменных в любое из данных уравнений, чтобы найти значение третьей переменной.
Когда следует использовать метод исключения?
Метод исключения лучше использовать, когда коэффициенты какой-либо одной переменной в уравнениях одинаковы.
Например, 3x+7y+2=0 и 3x-4y+5=0. Другими методами решения линейных уравнений являются метод подстановки, метод перекрестного умножения, графический метод и матричный метод.
В чем разница между методом исключения и методом замены?
Разница между методом замены и методом исключения заключается в том, что в методе замены мы находим значение одной переменной через другую переменную. Затем мы подставляем это значение во второе уравнение, чтобы найти значение другой переменной. Но в методе исключения мы исключаем любую переменную, а затем находим значение другой переменной.
Как решать системы уравнений методом исключения?
Чтобы решить систему уравнений методом исключения, мы делаем коэффициент одной из участвующих переменных одинаковыми, а затем складываем/вычитаем уравнения, чтобы исключить эту переменную и найти значение другой переменной.
Почему метод исключения лучше?
Метод исключения считается лучшим, чем другие методы решения системы уравнений, поскольку он упрощает вычисления за счет исключения переменной.
Как только переменная исключена, становится проще определить значение другой переменной, а затем использовать это значение, чтобы найти значение исключенной переменной.
решение набора линейных методом исключения Гуаса, a+2b+3c=5,3a-b+2c=8,4a-6b-4c=-2 найти a,b и c
Вы можете разместить это решение на ВАШЕМ сайте!
ваше решение:
а = -1
б = -3
с = 4
замените a на -1, b на -3 и c на 4 во всех трех ваших уравнениях, и все они должны быть верны.
, когда вы делаете это:
a + 2b + 3c = 5 становится -1 — 6 + 12 = 5, что становится -7 + 12 = 5, что становится 5 = 5.
3a — b + 2c = 8 становится -3 + 3 + 8 = 8, что становится 8 = 8.
4a — 6b — 4c = -2 становится -4 + 18 — 16 = -2, что становится -20 + 18 = -2, что становится -2 = -2.
решение хорошее.
в Интернете есть небольшой удобный инструмент, который можно использовать для проверки своей работы.
этот инструмент можно найти здесь:
http://www.
gregthatcher.com/Mathematics/GaussJordan.aspx
инструмент может не решить его точно так же, как вы решили бы его вручную, но вы должны получить тот же ответ, что и инструмент.
Я рекомендую вам использовать этот инструмент только для проверки вашей работы, потому что вам нужно сделать это вручную, чтобы по-настоящему оценить процесс и подготовиться к сдаче теста.
метод Гаусса работает с табло.
Каждая таблица представляет собой матрицу, сделанную на один шаг дальше к решению с использованием методов манипулирования строками.
инструмент использует метод Гаусса-Джордана, который представляет собой метод Гаусса, усовершенствованный на один шаг вперед.
мои ручные расчеты показаны ниже:
в моих ручных расчетах метод Гаусса приведет вас к шагу 3.
с этой таблицей легко решить сначала для с, затем решить для b, затем решить для а.
третья строка позволяет решить c.
вторая строка позволяет найти b.
первая строка позволяет решить для a.
в моих ручных расчетах метод Гаусса-Джордана приведет вас к шагу 6.
метод Гаусса-Жордана ведет вас до тех пор, пока вы не останетесь с таблицей, показанной на шаге 6.
в этой таблице вы можете автоматически увидеть, что:
с = 4
б = -3
а = -1
, поскольку вас интересовал гаусс, а не гаусс-джордан, то на шаге 3 вы хотели бы остановиться.
из вывода шага 3, вы должны решить для c из строки 3 следующим образом:
-2c = -8
разделите обе части уравнения на -2, чтобы получить:
c = 4
как только у вас будет c = 4, вы должны найти b из строки 2 следующим образом:
7b + 7c = 7
замените c на 4, чтобы получить:
7b + 28 = 7
вычтите 28 с обеих сторон, чтобы получить:
7b = -21
разделите обе стороны на 7, чтобы получить:
b = -3
если у вас есть b = -3 и c = 4, вы должны найти a из строки 1 следующим образом:
a + 2b + 3c = 5
замените c на 4 и b на -3, чтобы получить:
a + 2*-3 + 3*4 = 5, что станет:
a — 6 + 12 = 5, что станет:
а + 6 = 5, что становится:
а = -1
вы получаете a = -1, b = -3, c = 4
это то же самое решение, которое gauss-jordan дал вам на шаге 6.