Упражнение на самопознание “4 квадрата”
Главная / Студентам / Психолого-педагогическая поддержка / Педагог — психолог студентам / Упражнение на самопознание “4 квадрата”
Наверняка ты задумываешься о том, какой ты – какие у тебя качества, достоинства, что в тебе притягивает или раздражает окружающих. Чтобы лучше понять себя и проанализировать свои особенности, выполни психологическое упражнение «Четыре квадрата».
Возьми лист бумаги и раздели его на четыре квадрата. В углу каждого из них поставь цифры 1, 2, 3, 4 – как на рисунке справа.
1) В квадрате №1 напиши пять своих положительных черт. Можешь назвать их одним словом, например, «дружелюбный», или описать подробнее – «я умею готовить».
2) Перейди к квадрату №3. Заполни его, указав такие личные качества, которые тебе в себе не нравятся. Не стесняйся и будь искренним, выполняя это задание, – никто ведь не увидит таблицу с квадратами, если только ты сам не покажешь.
3) Следующий этап: посмотри еще раз на характеристики в квадрате №3 и переформулируй их таким образом, чтобы вместо негативных они выглядели позитивными.
Скажем, у тебя написано, что ты «жадный». Подумай, что в этом хорошего? Возможно, то, что ты бережно относишься к деньгам, не переплачиваешь и не тратишь попусту, ценишь вещи. Чтобы тебе легче выполнить задание, представь, что список с твоими недостатками видит человек, который тебя любит и не согласен с тем, что у тебя есть негативные особенности. Вспомни – когда мы влюблены, недостатки возлюбленных кажутся нам достоинствами. Посмотри на себя глазами влюбленного в тебя человека или мамы, которая тебя обожает.
4) Возвратись к квадрату №1 с пятью положительными качествами и переделай их на отрицательные, записав в квадрате №4. Снова может помочь воображаемый человек, который тебя настолько не “переваривает”, что в штыки воспринимает любые твои слова и действия, и все его в тебе категорически не устраивает. Даже то, что ты «белый и пушистый», дико раздражает. К примеру, ты считаешь себя «добрым». Что же плохого в доброте? Иногда под ее видом удобно совершать манипуляции и вынуждать людей делать то, что нужно «добренькому»: «Я тебе помог – теперь верни-ка мне должок».
Заполнил четыре квадрата? Молодец. Закрой ладонью квадраты 3 и 4, и посмотри на квадраты 1 и 2. Приятно? Еще бы – столько положительных характеристик! Многие мечтают о таком сыне/дочери, друге/подруге, внуке/внучке, брате/сестре и т.д.
Теперь, наоборот, прикрой квадраты 1 и 2, и взгляни на квадраты 3 и 4. Неприятно? Не хочется общаться с такой личностью.
Затем убери ладонь и посмотри на лист бумаги с квадратами в целом. Все эти качества – твои. Одни и те же характеристики описаны с разных сторон – глазами друга и врага. Нарисуй круг на пересечении квадратов и напиши в центре «Я». Недостатки – продолжение наших достоинств, равно как и достоинства найдутся в недостатках. В одних ситуациях определенное качество окажется уместным и полезным, а в других – нет.
Ты сам выбираешь, как относиться к себе. Если видишь только квадраты 3 и 4 – негатив, то будешь себя презирать, ругать, ненавидеть.
Если ты стараешься увидеть квадраты 1 и 2 – позитив, ты будешь уважать, ценить и принимать себя.
От того, как ты к себе относишься, зависит, как тебя воспринимают окружающие, и какими ты видишь их.
Упражнение «4 квадрата» полезно проделывать, если у тебя с кем-то конфликт. Попробуй пересмотреть то, что тебе не нравится в «противнике», переформулировать его качества с отрицательных на положительные. Это поможет наладить контакт, разрешить сложную ситуацию. Также постарайся увидеть себя глазами «противника» – иногда это позволяет понять, где и из-за чего произошло недопонимание. Тогда легче восстановить доверие и доброжелательные отношения.
Вариант 1. С-39. № 1. ГДЗ Алгебра 7 класс Звавич. Представьте многочлен в виде квадрата двучлена – Рамблер/класс
Вариант 1. С-39. № 1. ГДЗ Алгебра 7 класс Звавич. Представьте многочлен в виде квадрата двучлена – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Представьте многочлен в виде квадрата двучлена:
1) а) 4а2 + 4аb + b2; б) 4а2 — 4аb + b2;
3) a) a2b2 + 2ab + 1; б) b2 — 2а2b +а4.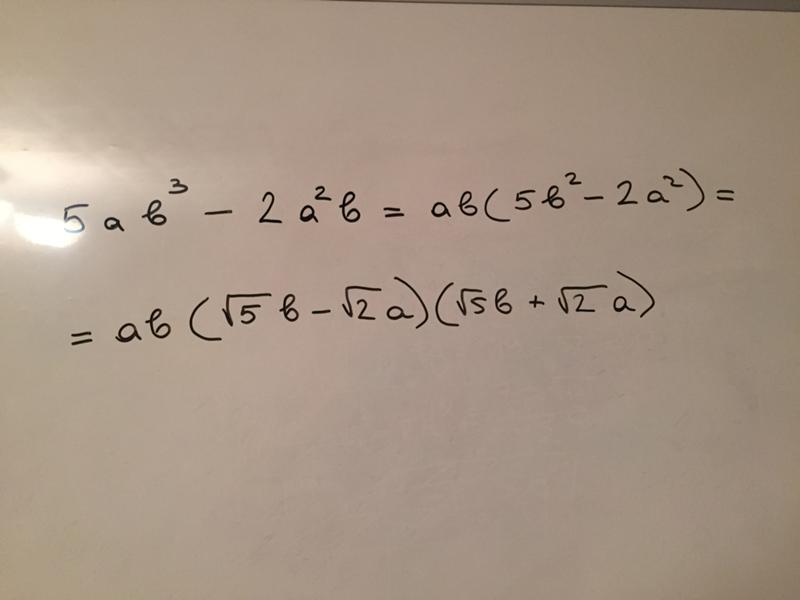
ответы
1. а) 4а2 + 4ab + b2 = (2а + b)2;
б) 4а2 — 4аb + b2 = (2а — b)2;
2. a) (3/4a — 4/3b)2;
б) (1/2а + b)2;
3. а) a2b2 + 2аb + 1 = (аb + 1)2;
б) b2 — 2а2b + а4 = (b — а2)2.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
9 класс
11 класс
похожие вопросы 5
Помогите ответить на вопросы
1)Назовите основные формы международного сотрудничества в области охраны окружающей среды. Приведите примеры участия России в таком (Подробнее.
..)
ГДЗ
физика….помогите
в одном из ядерных экспериментов протон с энергией в 1МэВ движется в однородном магнитном поле по круговой траектории. какой энергией (Подробнее…)
ЕГЭЭкзаменыГДЗУчебники
Вариант 1. С-21. № 6. ГДЗ Алгебра 7 класс Звавич. Замените значок * таким выражением, чтобы выполнялось равенство
Замените значок * таким выражением, чтобы выполнялось равенство:
1) (*)5 = a25; 2) (*)2 = а10; 3) (*)3 = а3n; 4) (*)n = (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Вариант 1. С-32. № 1. ГДЗ Алгебра 7 класс Звавич. Помогите вынести общий множитель за скобки
Вынесите общий множитель за скобки (проверьте свои действия умножением):
1) а) 2x + 3ху; б) 3ху — 5у; в) -7ху + (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Вариант 1. С-36. № 1. ГДЗ Алгебра 7 класс Звавич.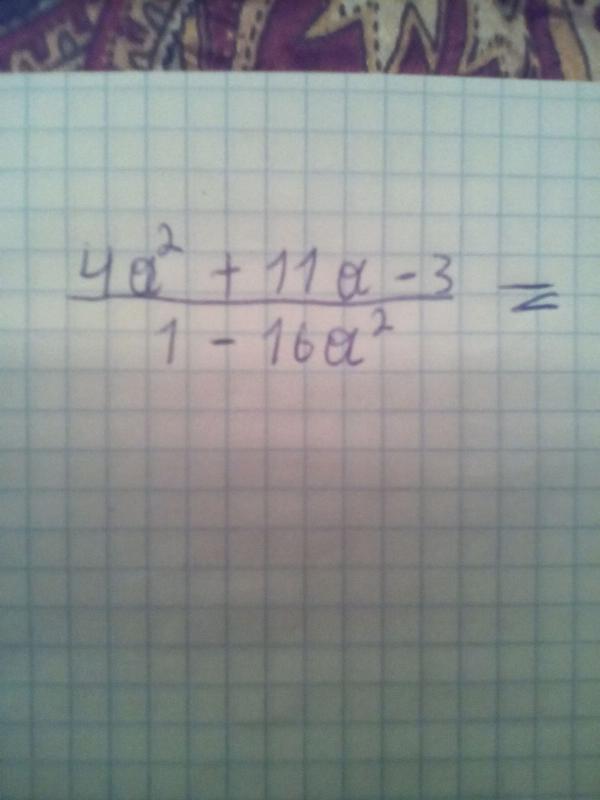
Помогите записать в виде выражения.
Запишите в виде выражения:
1) сумму квадратов чисел а и b;
2) квадрат разности чисел а и b; (Подробнее…)
ГДЗАлгебра7 классЗвавич Л.И.
Теорема Пифагора — ChiliMath
Если у нас есть прямоугольный треугольник (треугольник с прямым углом), и мы строим квадраты, используя только ребра или стороны прямоугольного треугольника (серый треугольник в середине), площадь наибольшего квадрата равно сумме площадей меньших квадратов. Это в двух словах теорема Пифагора.
Обратите внимание, что мы возводим в квадрат каждую переменную a, b и c для обозначения площади. Сумма меньших квадратов (оранжевого и желтого) равна большему квадрату (синему). 92}.
Теорема Пифагора гарантирует нам, что если мы знаем две стороны прямоугольного треугольника, мы можем ВСЕГДА получить меру третьей стороны.
Давайте посмотрим несколько примеров!
Пример 1: Найдите длину гипотенузы.
Наша цель найти длину гипотенузы. Нам даны длины двух ног. Мы знаем две стороны из трех! Этой информации достаточно, чтобы формула работала.
Для ног не имеет значения, какую из них мы назначаем для a или b. Результат будет таким же. Итак, если мы допустим a=5, то b=7. Подставляя эти значения в уравнение Формулы Пифагора, мы получаем
Чтобы выделить переменную c, мы возьмем квадратные корни из обеих частей уравнения. Это устраняет квадрат (степень числа 2) с правой стороны. А слева у нас просто квадратный корень из числа, что не имеет большого значения.
Однако здесь нужно быть внимательным, когда мы извлекаем квадратный корень из числа. Мы хотим рассматривать только главный квадратный корень или положительный квадратный корень, поскольку мы имеем дело с длиной. Не имеет смысла иметь отрицательную длину, поэтому мы игнорируем отрицательную длину!
Следовательно, длина гипотенузы равна \sqrt {74} дюйма. Если мы хотим приблизить его к ближайшей десятой, у нас есть 8,6 дюйма.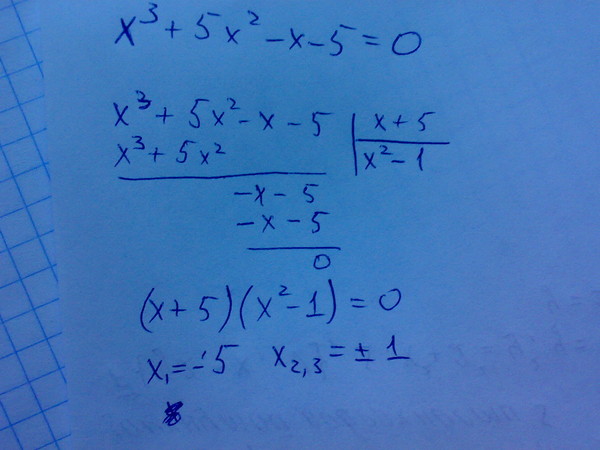
Пример 2: Найдите длину отрезка.
Просто взглянув на рисунок выше, мы знаем, что у нас достаточно информации, чтобы найти отсутствующую сторону. Причина в том, что измерены две стороны, а другая сторона оставлена неизвестной. Даны две стороны из трех возможных.
Здесь мы можем положить a или b равным 7. На самом деле это не имеет значения. Итак, для этого мы допустим a=7. Это означает, что мы решаем для ноги b. Но для гипотенузы нет права на ошибку. Мы должны быть уверены, что присваиваем с длину, то есть самую длинную сторону. В этом случае самая длинная сторона имеет меру 9см, и это значение, которое мы присвоим для с, поэтому с = 9.
Рассчитаем длину ноги b. У нас есть a=7 и c=9.
Следовательно, длина отсутствующей ноги равна 4\sqrt 2 см. Округлив до двух знаков после запятой, получим 5,66 см.
Пример 3: Стороны 17, 15 и 8 образуют прямоугольный треугольник? Если да, то какими сторонами являются катет и гипотенуза?
Если это стороны прямоугольного треугольника, то он должен удовлетворять теореме Пифагора.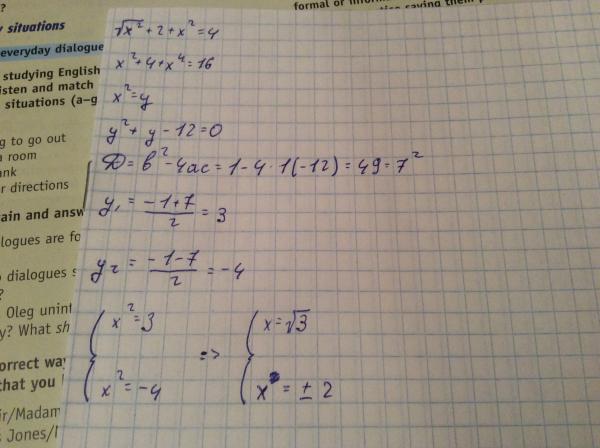
Сумма квадратов меньших сторон должна быть равна квадрату большей стороны. Очевидно, что стороны 8 и 15 короче 17, поэтому будем предполагают, что это катеты, а 17 это гипотенуза. Итак, пусть a=8, b=15 и c=17.
Подставим эти значения в уравнение Пифагора и проверим, верно ли оно.
Так как у нас есть истинное утверждение, то у нас есть случай прямоугольного треугольника! Теперь мы можем точно сказать, что более короткие стороны 8 и 15 — это катеты прямоугольного треугольника, а самая длинная сторона 17 — гипотенуза.
Пример 4: Прямоугольник имеет длину 8 метров и ширину 6 метров. Какова длина диагонали прямоугольника?
Диагональ прямоугольника — это просто отрезок, соединяющий две несмежные вершины. На рисунке ниже очевидно, что диагональ — это гипотенуза прямоугольного треугольника, а две другие стороны — катеты, равные 8 и 6.
Если мы допустим a=6 и b=8, мы можем найти c в уравнении Пифагора это просто диагональ.
Следовательно, диагональ равна 10 метрам.
Пример 5: Лестница прислонена к стене. Расстояние от вершины лестницы до земли составляет 20 футов. Если основание лестницы находится на расстоянии 4 м от стены, какой длины будет лестница?
Если вы изучите иллюстрацию, длина лестницы равна гипотенузе прямоугольного треугольника с катетами 20 футов и 4 фута.
Опять же, нам просто нужно выполнить прямую подстановку в формулу теоремы Пифагора, используя известные значения, а затем найти с или гипотенузу.
Таким образом, длина лестницы составляет 4\sqrt {26} футов или примерно 20,4 фута.
Пример 6: В прямоугольном равнобедренном треугольнике гипотенуза равна 12 футам. Какова длина каждой ноги?
Помните, что прямоугольный равнобедренный треугольник — это треугольник, в котором есть угол 90 градусов и две его стороны конгруэнтны.
На рисунке ниже гипотенуза равна 12 футам. Обе стороны помечены как x, так как они конгруэнтны.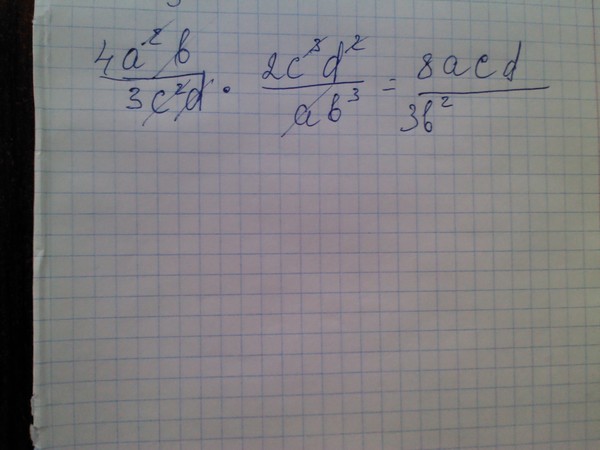
Давайте подставим эти значения в формулу, а затем найдем значение x. Мы знаем, что x — это просто катет прямоугольного равнобедренного треугольника, который является неизвестным, для которого мы пытаемся найти.
Следовательно, катет прямоугольного равнобедренного треугольника равен 6\sqrt 2 фута. Если нам нужно приблизительное значение, это 8,49.2, где s — сторона квадрата. Это означает, что нам нужно найти сторону квадрата по диагонали. Если мы посмотрим внимательно, диагональ — это просто гипотенуза прямоугольного треугольника. Что еще более важно, стороны прямоугольного треугольника также конгруэнтны.
Поскольку катеты конгруэнтны, мы можем положить его равным x.
Подставьте эти значения в формулу теоремы Пифагора, затем найдите x.
Мы рассчитали длину ноги в 2 единицы. Это также сторона квадрата. Итак, чтобы найти площадь квадрата, воспользуемся формулой 9.2} = 4
Следовательно, площадь квадрата равна 4 квадратным единицам.
Вы также можете быть заинтересованы в:
Проблемы с теоремами Пифагореей с ответами
Pythagorean Triples
Генерирующие пифагорские тройки
Как найти длину гипотенузы правого трава: Pythagorean
111111111111111111111111111111111888888888888888888888888888888888888888888888 8.
1111111111111111111111111111111111111111111111111111111111111111111111111111111111888 Математические ресурсы16 диагностических тестов 660 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 5 6 Следующая →
SAT Math Help » Геометрия » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти длину гипотенузы прямоугольного треугольника : Теорема Пифагора
Если и , то какова длина стороны?
Возможные ответы:
Недостаточно информации для решения
Правильный ответ:
Объяснение:
Эта задача решается с помощью теоремы Пифагора . В этой формуле и являются катетами прямоугольного треугольника, а является гипотенузой.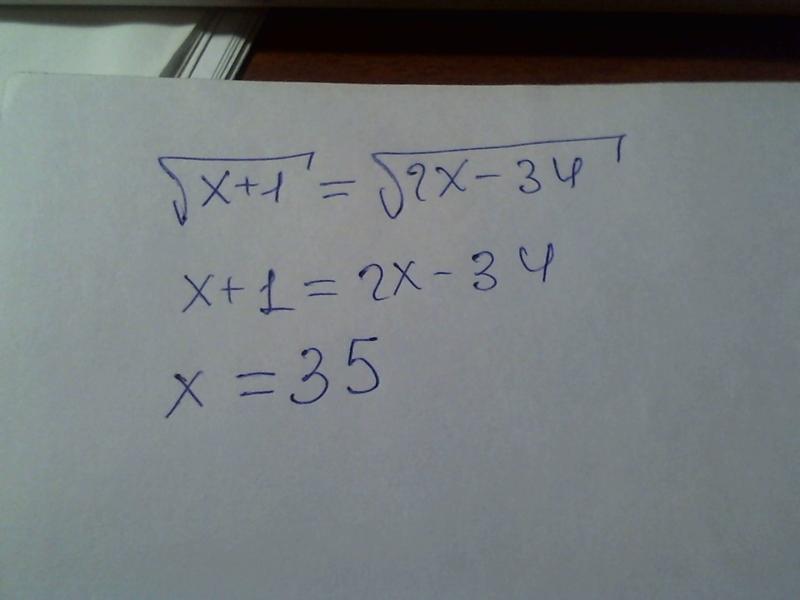
Использование меток нашего треугольника. длина гипотенузы?
Возможные ответы:
√10
√15
5√2
π
5
Правильный ответ:
5√2
. Объяснение:
Используя теорему Пифагора, x 2 + y 2 = ч 2 . А поскольку это треугольник 45-45-90, две короткие стороны равны. Следовательно, 5 2 + 5 2 = ч 2 . Умножить 25 + 25 = ч 2 .
Следовательно, ч 2 = 50, поэтому ч = √50 = √2 * √25 или 5√2.
Сообщить об ошибке
Высота правильного круглого цилиндра составляет 10 дюймов, а диаметр его основания — 6 дюймов. Каково расстояние от точки на краю основания до центра всего цилиндра?
Возможные ответы:
√(43)/2
Ни один из других ответов
√(34)
3π/4
4π/5
Правильный ответ:
√(34)
Объяснение:
Здесь лучше всего нарисовать диаграмму и начертить треугольник, соответствующий заданному вопросу.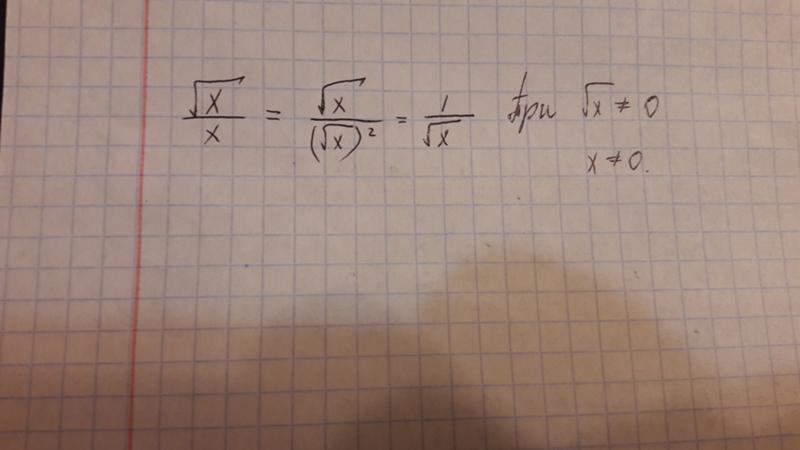
Неважно, где вы поместите свою точку на основании, потому что любая точка даст тот же результат. Мы знаем, что центр основания цилиндра находится на расстоянии 3 дюймов от основания (6/2). Мы также знаем, что центр цилиндра находится на расстоянии 5 дюймов от основания цилиндра (10/2). Итак, у нас есть прямоугольный треугольник с высотой 5 дм и основанием 3 дм. Таким образом, используя теорему Пифагора 3
Сообщить об ошибке
Прямоугольный треугольник со сторонами A, B, C и соответствующими углами a, b, c имеет следующие размеры.
Сторона A = 3 дюйма. Сторона В = 4 дюйма. Какова длина стороны С?
Возможные ответы:
5
7
25
6
Правильный ответ:
5
Объяснение:
Правильный ответ: 5.
Теорема Пифагора утверждает, что a 2 + b 2 = c 2 . Так что в этом случае 3 2 + 4 2 = C 2 . Таким образом, C 2 = 25 и C = 5. Это также пример обычного треугольника 3-4-5.
Сообщить об ошибке
Длины трех сторон прямоугольного треугольника образуют набор последовательных четных целых чисел, если они расположены от наименьшего к наибольшему. Если вторая по величине сторона имеет длину x, то какое из следующих уравнений можно использовать для решения x?
Возможные ответы:
x 2 + (x + 2) 2 = (x + 4) 2
(x – 9 2) + x 0 + 2) 2 + (x — 2) 2 = x 2
(x — 1) 2 + x 2 = (x+ 1) 2
= (x+ 1) 2(x – 2 (x+ 1) 2
. ) 2 + х 2 = (х + 2) 2Правильный ответ:
(х – 2) 2 + х 2 (2 0213 2
Объяснение:
Нам говорят, что длины образуют ряд последовательных четных целых чисел.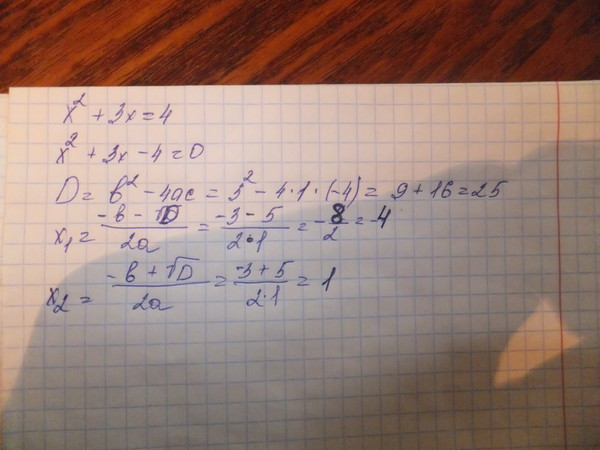
Поскольку четные целые числа разделены двумя единицами, длины сторон должны отличаться на два. Другими словами, длина наибольшей стороны в два раза больше второй по величине, а вторая по величине длина на два больше наименьшей длины.
Вторая по величине длина равна x. Таким образом, вторая по величине длина должна быть на два меньше наибольшей длины. Мы могли бы представить наибольшую длину как x + 2,
Точно так же вторая по величине длина на два больше наименьшей длины, которую мы могли бы таким образом представить как x – 2.
Подводя итог, длины треугольника (в единицах x) равны x – 2, x и x + 2.
Чтобы найти x, мы можем использовать тот факт, что треугольник прямоугольный. Если мы применим теорему Пифагора, мы можем составить уравнение, которое можно использовать для решения x. Теорема Пифагора утверждает, что если a и b — длины катетов треугольника, а c — длина гипотенузы, то верно следующее:
a 2 + b 2 = c 2
В данном конкретном случае две стороны нашего треугольника равны x – 2 и x, так как катеты являются двумя наименьшими сторонами; следовательно, мы можем сказать, что a = x – 2 и b = x.
Наконец, мы можем сказать, что с = х + 2, так как х + 2 — это длина гипотенузы. Подстановка этих значений для a, b и c в теорему Пифагора дает следующее: 2) 2 + х 2 = (х + 2) 2 .
Сообщить об ошибке
Чему равна гипотенуза прямоугольного треугольника со сторонами 5 и 8?
Возможные ответы:
8√13
15
12
5√4
√89
Правильный ответ:
√89
Объяснение:
Так как это прямоугольный треугольник, мы можем использовать теорему Пифагора, которая говорит a 2 + b 2 = c 2 , или квадраты двух сторон прямоугольного треугольника должны быть равны квадрату гипотенузы. Here we have a = 5 and b = 8.
a 2 + b 2 = c 2
5 2 + 8 2 = с 2
25 + 64 = с 2
89 = с 2
c = √89
Сообщить об ошибке
Стороны прямоугольного треугольника равны 21 и 72.
Какова длина гипотенузы?
Возможные ответы:
84
70
80
75
67
Правильный ответ:
Объяснение:
По теореме Пифагора 21 2 + 72 2 = hyp 2 . Тогда гип 2 = 5625, а гипотенуза = 75. Если вы не знали, как вычислить, что 75 2 = 5625, ничего страшного. Посмотрите на варианты ответов. Мы могли бы легко возвести их в квадрат и выбрать такой вариант ответа, который при возведении в квадрат будет равен 5625.
Сообщить об ошибке
Сэм и Джон начинают с одной и той же точки. Сэм проходит 30 футов на север, а Джон — 40 футов на запад. Как далеко они друг от друга в своих новых местах?
Возможные ответы:
Правильный ответ:
Пояснение:
Сэм и Джон шли под прямым углом друг к другу, поэтому расстояние между ними равно гипотенузе треугольника.
Расстояние можно найти по теореме Пифагора.
Сообщить об ошибке
Дарья и Эшли начинают с одного и того же места и ведут своих двух собак в парк разными маршрутами. Дарья проходит 1 милю на север, а затем 1 милю на восток. Эшли выгуливает свою собаку по тропе, идущей на северо-восток, которая ведет прямо в парк. Насколько дальше Дарья идет, чем Эшли?
Возможные ответы:
2 +√2 миль
2 — √2 миль
1 миля
Нельзя определить
√2 миль
Правильный ответ:
2 a a
Пояснение:
Сначала посчитаем, какое расстояние проходит Дарья. Это просто 1 миля на север + 1 миля на восток = 2 мили. Теперь давайте посчитаем, какое расстояние проходит Эшли. Мы можем думать об этой задаче, используя прямоугольный треугольник. Две стороны треугольника — это 1 миля к северу и 1 миля к востоку, а расстояние Эшли — это диагональ.
Используя теорему Пифагора, мы вычисляем диагональ как √(1 2 + 1 2 ) = √2. Итак, Дарья прошла 2 мили, а Эшли прошла √2 мили. Таким образом, разница составляет всего 2– √2 мили.
Сообщить об ошибке
Какой из следующих наборов сторон не может принадлежать прямоугольному треугольнику?
Возможные ответы:
2, 2√3, 4
3, 4, 5
2, 2, 2√2
6, 7, 8
5, 12, 13
Правильно ответ:
6, 7, 8
Объяснение:
Чтобы ответить на этот вопрос, не подставляя все пять вариантов ответа в теорему Пифагора (что занимает слишком много времени на GRE), мы можем использовать специальные формулы треугольника. Помните, что треугольники 45-45-90 имеют длины x, x, x√2. Точно так же треугольники 30-60-90 имеют длину x, x√3, 2x. Также следует помнить, что 3,4,5 и 5,12,13 — особые прямоугольные треугольники.