Высшая математика Т2
Высшая математика Т2
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.1. Предмет математики. Переменные и постоянные величины, множества § 1.2. Операции над множествами § 1.3. Символика математической логики § 1.4. Действительные числа § 1.5. Определение равенства и неравенства § 1.6. Определение арифметических действий 1.6.1. Общие соображения 1.6.2. Стабилизирующиеся последовательности 1.6.3. Определение арифметических действий § 1.7. Основные свойства действительных чисел § 1.8. Аксиоматический подход к понятию действительного числа § 1.9. Неравенства для абсолютных величин § 1.10. Отрезок, интервал, ограниченное множество § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 2. Предел последовательности § 2.1. Понятие предела последовательности § 2.  2. Арифметические действия с переменными, имеющими предел 2. Арифметические действия с переменными, имеющими предел§ 2.3. Бесконечно малая и бесконечно большая величины § 2.4. Неопределенные выражения § 2.5. Монотонные последовательности § 2.6. Число e § 2.7. Принцип вложенных отрезков § 2.8. Точные верхняя и нижняя грани множества § 2.9. Теорема Больцано-Вейерштрасса § 2.10. Верхний и нижний пределы § 2.11. Условие Коши сходимости последовательности § 2.12. Полнота и непрерывность множества действительных чисел Глава 3. Функция. Предел функции § 3.1. Функция 3.1.1. Функция от одной переменной. 3.1.2. Функции многих переменных. 3.1.3. Полярная система координат § 3.2. Предел функции § 3.3. Непрерывность функции § 3.4. Разрывы первого и второго рода § 3.5. Функции, непрерывные на отрезке § 3.7. Равномерная непрерывность функции § 3.8. Элементарные функции § 3.9. Замечательные пределы § 3.10. Порядок переменной. Эквивалентность Глава 4.  Дифференциальное исчисление функций одной переменной Дифференциальное исчисление функций одной переменной§ 4.1. Производная § 4.2. Геометрический смысл производной § 4.3. Производные элементарных функций § 4.4. Производная сложной функции § 4.5. Производная обратной функции § 4.6. Производные элементарных функций (продолжение) § 4.7. Дифференциал функции 4.7.1. Дифференцируемые функции 4.7.2. Дифференциал функции 4.7.3. Приближенное выражение приращения функции § 4.8. Другое определение касательной § 4.9. Производная высшего порядка § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка § 4.11 Дифференцирование параметрически заданных функций § 4.12. Теоремы о среднем значении § 4.13. Раскрытие неопределенностей § 4.14. Формула Тейлора § 4.15. Ряд Тейлора § 4.16. Формулы и ряды Тейлора элементарных функций § 4.17. Локальный экстремум функции § 4.18. Экстремальные значения функции на отрезке § 4.19. Выпуклость кривой.  Точка перегиба Точка перегиба§ 4.20. Асимптота графика функции § 4.21. Непрерывная и гладкая кривая § 4.22. Схема построения графика функции § 4.23. Вектор-функция. Векторы касательной и нормали Глава 5. неопределенные интегралы § 5.1. Неопределенный интеграл. Таблица интегралов § 5.2. Методы интегрирования § 5.3. Комплексные числа § 5.4. Теория многочлена n-й степени § 5.5. Действительный многочлен n-й степени § 5.6. Интегрирование рациональных выражений § 5.7. Интегрирование иррациональных функций Глава 6. Определенный Интеграл § 6.2. Свойства определенных интегралов § 6.3. Интеграл как функция верхнего предела § 6.4. Формула Ньютона – Лейбница § 6.5. Остаток формулы Тейлора в интегральной форме § 6.6. Суммы Дарбу. Условия существования интеграла § 6.7. Интегрируемость непрерывных и монотонных функций § 6.8. Несобственные интегралы § 6. 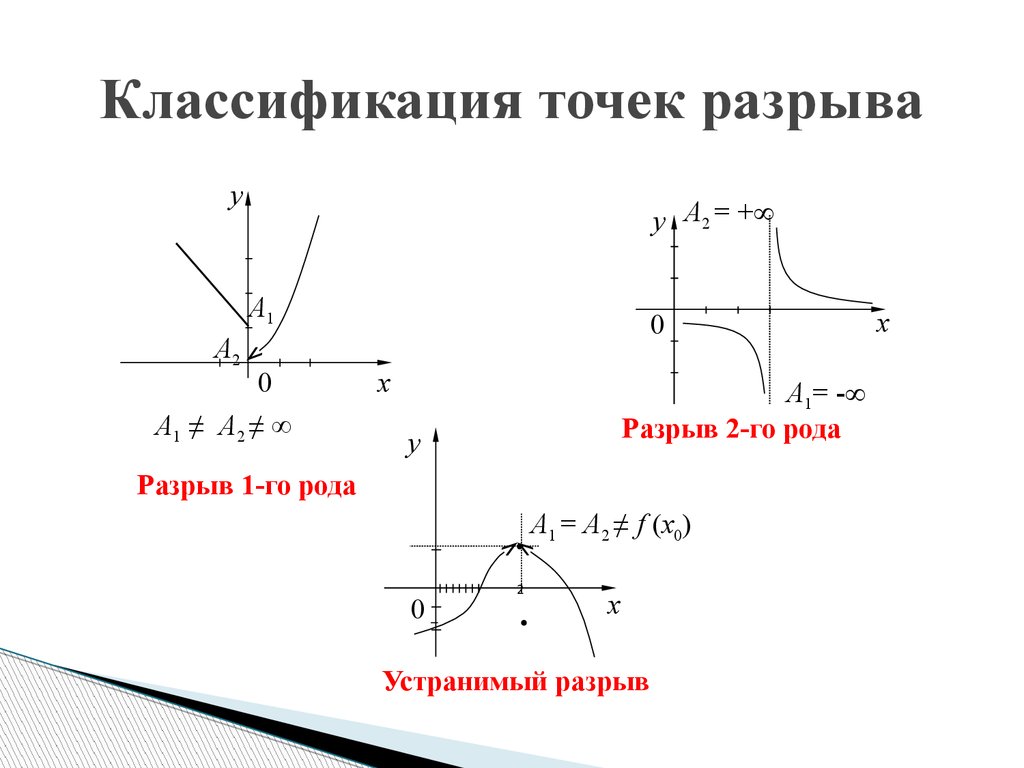 9. Несобственные интегралы от неотрицательных функций 9. Несобственные интегралы от неотрицательных функций§ 6.10. Интегрирование по частям несобственных интегралов § 6.11. Несобственный интеграл с особенностями в нескольких точках Глава 7. Приложения интегралов. Приближенные методы § 7.1. Площадь в полярных координатах § 7.2. Объем тела вращения § 7.3. Гладкая кривая в пространстве. Длина дуги § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента § 7.5. Площадь поверхности вращения § 7.6. Интерполяционная формула Лагранжа § 7.7. Квадратурные формулы прямоугольников и трапеций § 7.8. Формула Симпсона Глава 8. Дифференциальное исчисление функций многих переменных § 8.1. Предварительные сведения § 8.2. Предел функции § 8.3. Непрерывная функция § 8.4. Частные производные и производная по направлению § 8.5. Дифференцируемые функции § 8.6. Применение дифференциала в приближенных вычислениях § 8.7. Касательная плоскость. Геометрический смысл дифференциала § 8. 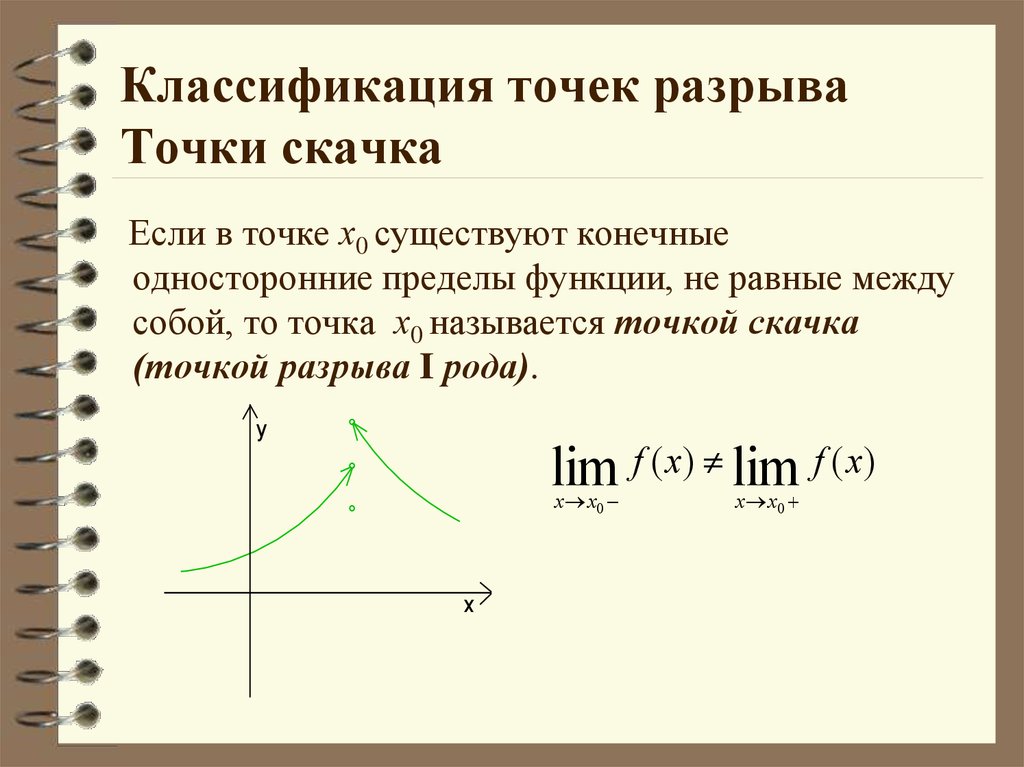 8. Производная сложной функции. Производная по направлению. Градиент 8. Производная сложной функции. Производная по направлению. Градиент8.8.1. Производная сложной функции 8.8.2. Производная по направлению 8.8.3. Градиент функции 8.8.4. Однородные функции § 8.9. Дифференциал функции. Дифференциал высшего порядка § 8.10. Формула Тейлора § 8.12. Непрерывная функция на замкнутом ограниченном множестве § 8.13. Экстремумы § 8.14. Нахождение наибольших и наименьших значений функции § 8.15. Теорема существования неявной функции § 8.16. Касательная плоскость и нормаль § 8.17. Системы функций, заданных неявно § 8.18. Отображения § 8.19. Условный (относительный) экстремум Глава 9. Ряды § 9.1. Понятие ряда § 9.2. Несобственный интеграл и ряд § 9.3. Действия с рядами § 9.4. Ряды с неотрицательными членами § 9.5. Ряд Лейбница § 9.6. Абсолютно сходящиеся ряды § 9.7. Условно сходящиеся ряды с действительными членами § 9.8. Последовательности и ряды функций.  Равномерная сходимость Равномерная сходимость§ 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов § 9.10. Перемножение абсолютно сходящихся рядов § 9.11. Степенные ряды § 9.12. Дифференцирование и интегрирование степенных рядов § 9.13. Функции exp(z), sinz, cosz от комплексного переменного § 9.14. Ряды в приближенных вычислениях § 9.15. Понятие кратного ряда § 9.16. Суммирование рядов и последовательностей |
Разрыв первого рода | это… Что такое Разрыв первого рода?
ТолкованиеПеревод
- Разрыв первого рода
Непреры́вное отображе́ние или непрерывная функция — это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения.
Это понятие определятся немного по-разному в различных разделах математики; наиболее общее определение используется в общей топологии.

Содержание
- 1 Определения
- 1.1 Непрерывная числовая функция
- 1.2 Непрерывное отображение из Rm в Rn
- 1.3 Непрерывное отображение метрических пространств
- 1.4 Непрерывное отображение топологических пространств
- 2 Связанные определения
- 3 Свойства
- 3.1 Вещественнозначаные функции
- 4 Примеры
- 5 Вариации и бобщения
- 5.1 Односторнняя непрерывность
- 5.1.1 Замечания
- 5.1.2 Примеры
- 5.1 Односторнняя непрерывность
- 6 См. также
Определения
Непрерывная числовая функция
- Пусть дана функция и Тогда говорят, что f непрерывна в точке a и пишут если
- Пусть дано подмножество Тогда говорят, что f непрерывна на N и пишут если
Непрерывное отображение из R
m в RnОбобщая одномерный случай, функция называется непрерывной в точке если
где
- — евклидова норма в
Непрерывное отображение метрических пространств
В предыдущем определении наличие операции вычитания, точнее линейной структуры, в евклидовых пространствах не играет принципиальной роли.
 Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если
Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, еслиНепрерывное отображение топологических пространств
В предыдущих определениях важно не наличие точной меры расстояния, а лишь понятия близости. Непрерывное отображение переводит близкие точки в близкие. Множество, в котором указан некоторый набор подмножеств , позволяющий говорить о близких точках, называется топологическим пространством. Отображение топологического пространства в топологическое пространство называется непрерывным, если прообраз любого открытого множества открыт:
Связанные определения
Если функция не является непрерывной в точке a, то говорят, что она в ней разры́вна и пишут Согласно замечанию выше функция может быть разрывной только в предельной точке области определения, и справедливо одно из двух:
- Либо предел не существует;
- Либо он существует, но
Пусть существует но или Тогда a называется то́чкой устрани́мого разры́ва. Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
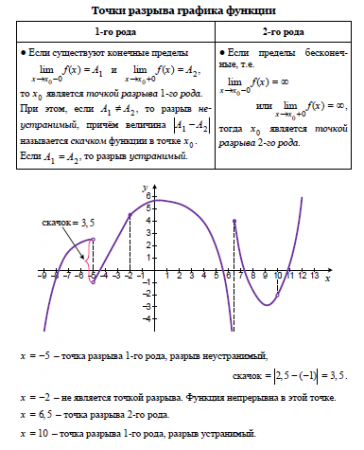
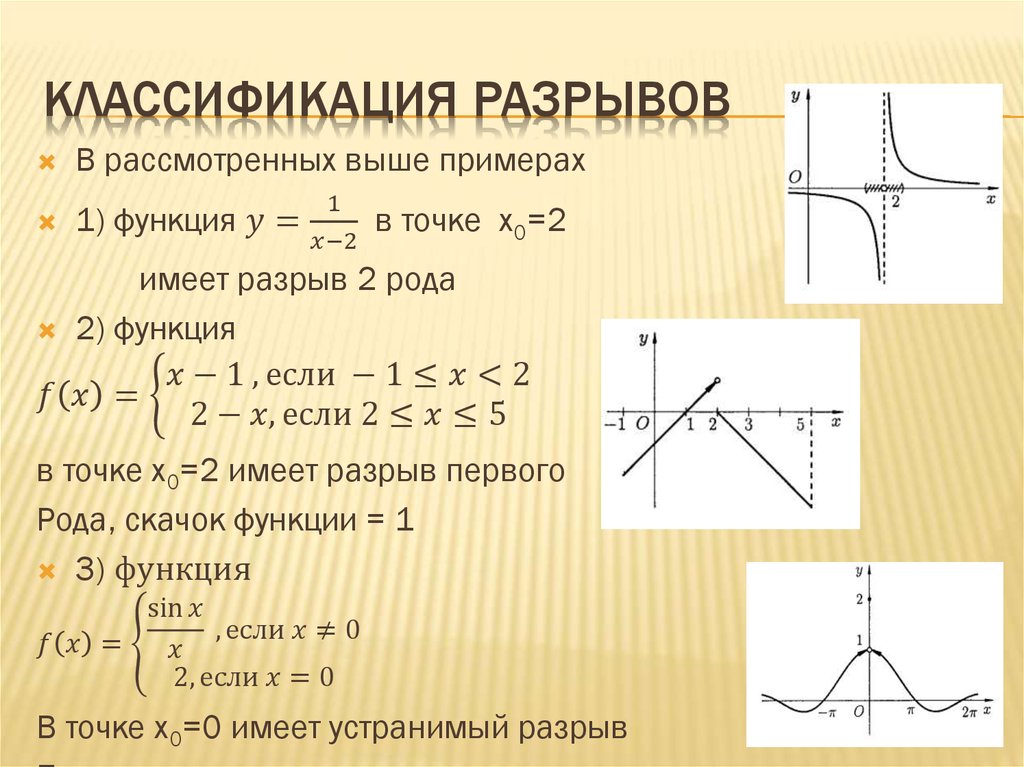
Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.Пусть не сущестует двусторонний предел но существуют конечные (и различные) односторонние пределы и Тогда и a называется то́чкой разры́ва пе́рвого ро́да.
Если и a не является точкой устранимого разрыва или разрыва первого рода, то есть хотя бы один односторонний предел не существует или бесконечен, то она называется то́чкой разры́ва второ́го ро́да.
Свойства
- Функция всегда непрерывна в изолированной точке области определения, то есть
- В предельной точке области определения непрерывность функции эквивалентна существованию предела, равного значению функции в точке:
Вещественнозначаные функции
- Функция сохраняет знак в окрестности точки непрерывности.
 Пусть Тогда существует окрестность U(a) такая, что
Пусть Тогда существует окрестность U(a) такая, что
- Сумма непрерывных функций также является непрерывной. Пусть . Тогда
- Непрерывная функция умноженная на константу также является непрерывной. Пусть и — произвольная константа. Тогда
- Произведение непрерывных функций также является непрерывным. Пусть . Тогда
- Частное непрерывных функций также является непрерывным. Пусть и Тогда существует окрестность U(a), в которой функция определена, и
- Композиция двух непрерывных функций так же является непрерывной. Пусть Тогда
- Дифференцируемая функция всегда непрерывна. Обратное, вообще говоря, неверно. Например, функция Ван-дер-Вардена непрерывна, но не дифференцируема на всей прямой.
- Теорема Больцано — Коши;
- Теорема Вейерштрасса о функции, непрерывной на компакте.
Примеры
- Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические прямые и обратные функции непрерывны везде в своей области определения.

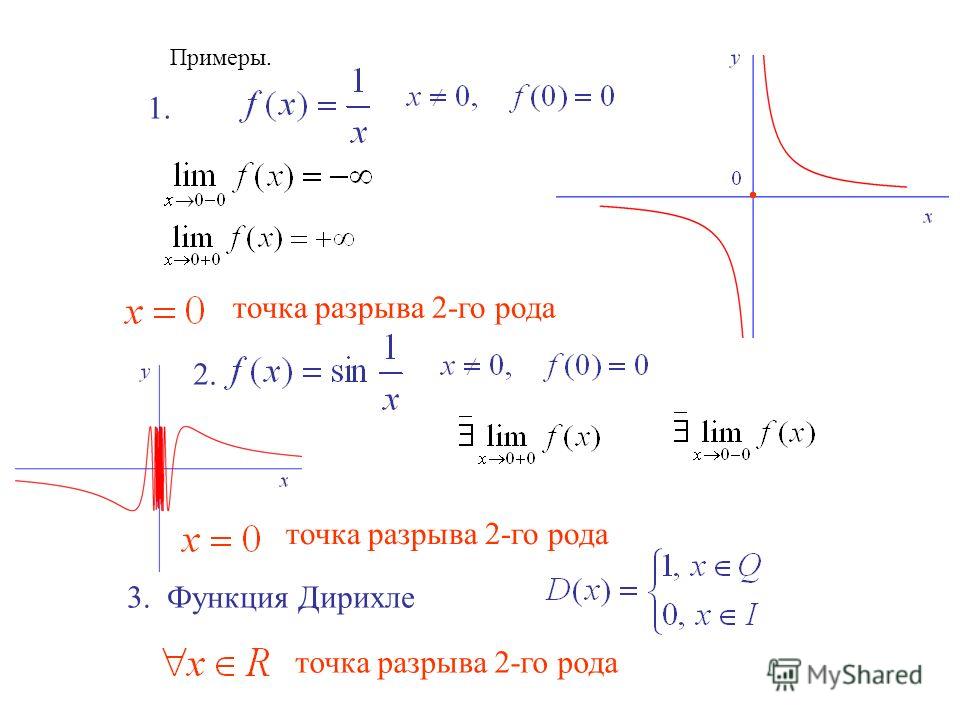
- Функция задаваемая формулой
непрерывна в любой точке Точка x = 0 является точкой устранимого разрыва, ибо
- Функция знака
непрерывна в любом Точка x = 0 является точкой разрыва первого рода, ибо
непрерывна в любом
Вариации и бобщения
Односторнняя непрерывность
- Пусть дана функция и Тогда говорят, что f непреры́вна спра́ва в точке a, если
- Говорят, что f непреры́вна сле́ва в точке a, если
Замечания
- Функция непрерывна тогда и только тогда, когда она непрерывна одновременно справа и слева.
- Функция непрерывна справа в предельной точке области определения тогда и только тогда, когда существует правосторонний предел
- Функция непрерывна слева в предельной точке области определения тогда и только тогда, когда существует левосторонний предел
- Все базовые свойства непрерывных функций переносятся на односторонне непрерывные функции.

Примеры
- Функция
непрерывна справа (но не слева) в точке x = 0. Во всех других точках она непрерывна.
- Кумулятивная функция распределения дискретной случайной величины в теории вероятностей непрерывна справа в любой точке.
См. также
- Пространство непрерывных функций
- Общая топология
- Топологическое пространство
- Открытое отображение
- 1 Определения
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- Разрушители мифов (6 сезон)
- Разрушители мифов (2 сезон)
Полезное
Каковы степени разрывов промежности? Что они означают и как с ними обращаются
Авторы: Редакторы WebMD
В этой статье
- Что вызывает разрыв промежности?
- 4 степени разрыва промежности: что каждая из них означает
- Каковы факторы риска разрыва промежности?
- Каковы возможные осложнения разрыва промежности?
- Как лечат разрывы промежности?
Разрыв промежности — это повреждение влагалища, которое может произойти во время родов. Различают четыре степени разрывов промежности. Они оцениваются по степени тяжести разрыва, причем разрыв четвертой степени является худшим. Эпизиотомия может быть сделана, чтобы помочь контролировать слезотечение.
Различают четыре степени разрывов промежности. Они оцениваются по степени тяжести разрыва, причем разрыв четвертой степени является худшим. Эпизиотомия может быть сделана, чтобы помочь контролировать слезотечение.
Разрывы промежности очень распространены во время вагинальных родов. Они могут поражать влагалище, половые губы, шейку матки и область между влагалищем и прямой кишкой. Многие разрывы заживают без лечения, но сильные разрывы могут вызвать длительную боль, проблемы с сексом и смущение.
Ваше тело готовится к рождению ребенка, истончая кожу вокруг влагалища, чтобы вы могли вытолкнуть ребенка наружу. Ваше влагалище растягивается и пропускает головку ребенка. Иногда кожа может не успеть стать достаточно тонкой, чтобы растянуться. Если это произойдет, ткани вокруг влагалища могут порваться.
У вас больше шансов получить разрыв промежности, если у вас крупный ребенок, быстрые роды или вашему врачу приходится использовать щипцы, чтобы родить ребенка. Ваш врач может сделать эпизиотомию, то есть хирургический разрез, чтобы расширить вход во влагалище. Это может быть сделано, чтобы уменьшить количество крови, которую вы теряете из-за сильного разрыва, или если вашему ребенку нужно быстро родить.
Это может быть сделано, чтобы уменьшить количество крови, которую вы теряете из-за сильного разрыва, или если вашему ребенку нужно быстро родить.
Как уже говорилось, существует четыре степени разрывов промежности, и они классифицируются в зависимости от того, насколько серьезными являются разрывы.
Разрыв первой степени. Этот тип разрыва промежности затрагивает только кожу и ткани непосредственно под кожей промежности, то есть в области между влагалищем и прямой кишкой. Если у вас слеза первой степени, у вас может быть небольшая боль или жжение при мочеиспускании. Эти разрывы могут не требовать наложения швов, хотя некоторые из них требуют. Обычно они заживают в течение нескольких недель.
Разрыв второй степени. Этот тип разрыва промежности является наиболее распространенным типом, который возникает во время родов и является более глубоким, чем разрыв первой степени. Он затрагивает кожу и мышцы промежности и может распространяться глубоко во влагалище. Разрыв второй степени обычно требует наложения швов и обычно заживает в течение нескольких недель.
Разрыв второй степени обычно требует наложения швов и обычно заживает в течение нескольких недель.
Разрыв третьей степени. Этот тип разрыва промежности распространяется на мышцы вокруг заднего прохода. Возможно, вам понадобится анестезия, и вам сделают ремонт в операционной. На заживление разрыва третьей степени может уйти больше нескольких недель. У вас могут быть осложнения, такие как подтекание стула и болезненный половой акт.
Разрыв четвертой степени. Этот тип разрыва промежности является наиболее тяжелым. Он проходит через мышцы вокруг заднего прохода и проникает в слизистую оболочку прямой кишки. Разрыв четвертой степени обычно необходимо зашивать в операционной с применением анестезии. Вам также может понадобиться более специализированный вид ремонта. Заживление может занять больше нескольких недель. Как и при разрыве третьей степени, у вас могут быть осложнения, такие как недержание стула и болезненный половой акт.
Несколько факторов повышают вероятность разрыва промежности, в том числе:
- Рождение первого ребенка
- Необходимость щипцов или вакуума при родах
- Наличие крупного ребенка
- Быть азиатом
- Быть пожилая мать
- Ягодичное предлежание, при котором ваш ребенок находится лицом вверх, а не лицом вниз, когда вы начинаете рожать0008
Возможные осложнения, связанные с разрывами промежности:
Лечение разрыва промежности зависит от того, насколько он серьезен.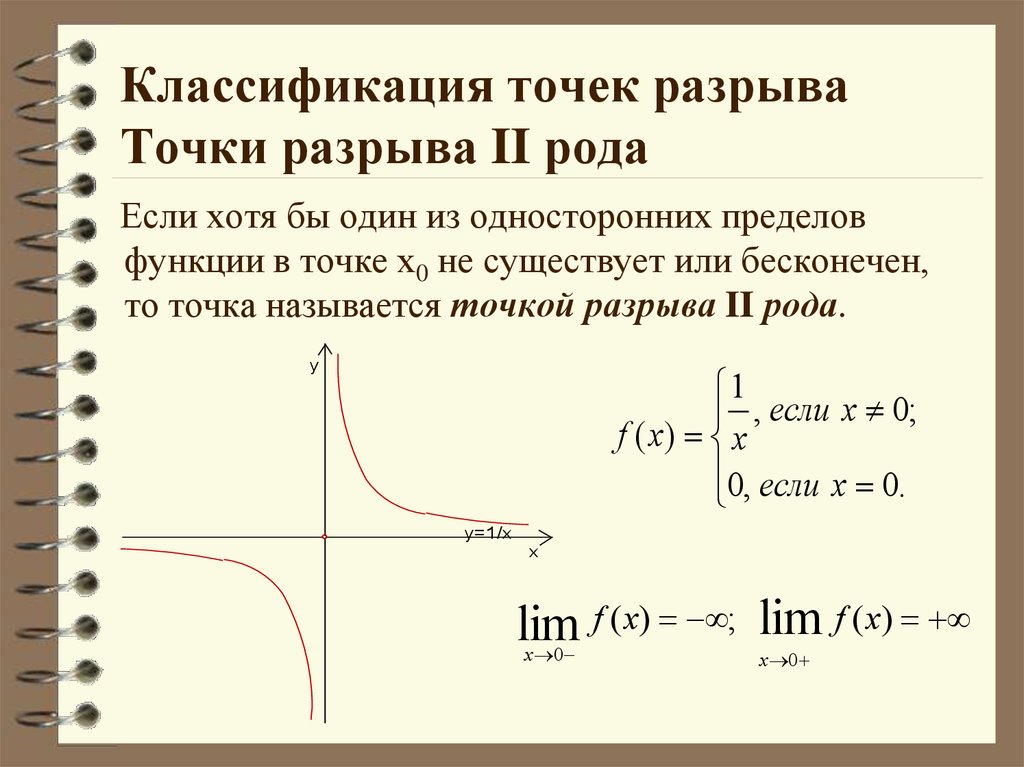 Разрыв первой степени может не потребовать наложения швов, но более серьезные разрывы промежности потребуют. Если вам нужно наложить швы для устранения разрыва промежности, эти швы рассосутся сами по себе в течение шести недель.
Разрыв первой степени может не потребовать наложения швов, но более серьезные разрывы промежности потребуют. Если вам нужно наложить швы для устранения разрыва промежности, эти швы рассосутся сами по себе в течение шести недель.
Анальный сфинктер представляет собой группу мышц, окружающих задний проход и контролирующих выделение стула. Если он поврежден разрывом промежности, вашему врачу, возможно, придется восстановить его. Эти швы также рассасываются сами по себе.
Боль, связанная с разрывом промежности, должна пройти примерно через две недели после родов. Вы можете испытывать боль при сексе после разрыва промежности. Поговорите со своим врачом, если вы испытываете боль во время секса или у вас есть какие-либо признаки инфекции после разрыва. Признаки инфекции могут включать лихорадку, зловонные выделения и боль, которая не проходит при приеме обезболивающих препаратов.
Top Picks
Преждевременный разрыв плодных оболочек: Med Медицинская энциклопедия linePlus
Слои ткани, называемые амниотическим мешком, содержат жидкость, окружающую ребенка в утробе матери. В большинстве случаев эти оболочки разрываются во время родов или в течение 24 часов до начала родов. Говорят, что преждевременный разрыв плодных оболочек (PROM) происходит, когда плодные оболочки разрываются до 37-й недели беременности.
В большинстве случаев эти оболочки разрываются во время родов или в течение 24 часов до начала родов. Говорят, что преждевременный разрыв плодных оболочек (PROM) происходит, когда плодные оболочки разрываются до 37-й недели беременности.
Амниотическая жидкость — это вода, которая окружает вашего ребенка в утробе матери. Мембраны или слои ткани удерживают эту жидкость. Эта оболочка называется амниотическим мешком.
Часто во время родов происходит разрыв плодных оболочек. Это часто называют «когда отойдут воды».
Иногда плодные оболочки рвутся перед родами. Когда воды отходят рано, это называется преждевременным разрывом плодных оболочек (ПРОП). У большинства женщин роды начинаются самостоятельно в течение 24 часов.
Если воды отходят до 37-й недели беременности, это называется преждевременным преждевременным излитием плодных оболочек (ПРПО). Чем раньше отойдут воды, тем серьезнее это будет для вас и вашего ребенка.
В большинстве случаев причина PROM неизвестна. Некоторыми причинами или факторами риска могут быть:
Некоторыми причинами или факторами риска могут быть:
- Инфекции матки, шейки матки или влагалища
- Слишком сильное растяжение амниотического мешка (это может произойти, если слишком много жидкости или более одного ребенка давит на плодные оболочки )
- Курение
- Если вы перенесли операцию или биопсию шейки матки
- Если вы были беременны ранее и у вас был PROM или PPROM
Большинство женщин, у которых отходят воды перед родами, не имеют фактора риска.
Самым важным признаком, на который следует обратить внимание, является выделение жидкости из влагалища. Она может медленно течь, а может выливаться наружу. Часть жидкости теряется при разрыве мембран. Мембраны могут продолжать протекать.
Иногда, когда жидкость вытекает медленно, женщины принимают ее за мочу. Если вы заметили утечку жидкости, используйте салфетку, чтобы впитать ее часть. Посмотрите на него и понюхайте. Амниотическая жидкость обычно не имеет цвета и не пахнет мочой (она имеет гораздо более сладкий запах).
Если вы считаете, что у вас произошел разрыв плодных оболочек, немедленно позвоните своему лечащему врачу. Вам нужно будет провериться как можно скорее.
В больнице простые анализы могут подтвердить разрыв плодных оболочек. Ваш врач проверит вашу шейку матки, чтобы увидеть, не размягчилась ли она и не начинает ли она расширяться (раскрываться).
Если ваш врач обнаружит у вас ПРОПО, вам придется находиться в больнице до рождения ребенка.
ПОСЛЕ 37 НЕДЕЛЬ
Если срок вашей беременности превышает 37 недель, ваш ребенок готов к рождению. Вам скоро нужно будет рожать. Чем больше времени требуется для начала родов, тем выше вероятность заражения.
Вы можете либо немного подождать, пока у вас не начнутся роды сами по себе, либо вас можно вызвать (получить лекарство для начала родов). Женщины, которые рожают в течение 24 часов после отхождения вод, менее подвержены инфекции. Таким образом, если роды не начинаются сами по себе, безопаснее их стимулировать.
В МЕЖДУ 34 ДО 37 НЕДЕЛЬ
Если у вас отходят воды в сроке от 34 до 37 недель, врач, скорее всего, предложит вам провести стимуляцию. Для ребенка безопаснее родиться на несколько недель раньше, чем для вас риск заражения.
ДО 34 НЕДЕЛЬ
Если у вас отошли воды до 34 недель, это более серьезно. Если признаков инфекции нет, врач может попытаться отсрочить роды, положив вам постельный режим. Стероидные препараты могут быть назначены для быстрого роста легких ребенка. Ребенок будет чувствовать себя лучше, если его легкие будут иметь больше времени для роста до рождения.
Вы также получите антибиотики для предотвращения инфекций. В больнице за вами и вашим ребенком будут наблюдать очень внимательно. Ваш врач может провести тесты, чтобы проверить легкие вашего ребенка. Когда легкие достаточно вырастут, ваш врач вызовет роды.
Если у вас рано отошли воды, ваш врач скажет вам, что будет самым безопасным способом. Есть некоторые риски преждевременных родов, но больница, в которой вы рожаете, направит вашего ребенка в отделение для недоношенных (специальное отделение для детей, рожденных раньше срока). Если в месте, где вы рожаете, нет отделения для недоношенных, вас и вашего ребенка переведут в больницу, где оно есть.
Если в месте, где вы рожаете, нет отделения для недоношенных, вас и вашего ребенка переведут в больницу, где оно есть.
ПРОМ; ПРОМ; Осложнения беременности — преждевременный разрыв
Mercer BM, Chien EKS. Преждевременный разрыв плодных оболочек. В: Резник Р., Локвуд С.Дж., Мур Т.Р., Грин М.Ф., Копел Дж.А., Сильвер Р.М., ред. Медицина матери и плода Кризи и Резника: принципы и практика . 8-е изд. Филадельфия, Пенсильвания: Elsevier; 2019: глава 42.
Mercer BM, Chien EKS. Преждевременный разрыв плодных оболочек. В: Landon MB, Galan HL, Jauniaux ERM и др., ред. Акушерство Габбе: нормальная и проблемная беременность . 8-е изд. Филадельфия, Пенсильвания: Elsevier; 2021: глава 37.
Обновлено: Джон Д. Джейкобсон, доктор медицинских наук, отделение акушерства и гинекологии, Медицинский факультет Университета Лома Линда, Лома Линда, Калифорния. Также рецензировали Дэвид С. Дагдейл, доктор медицинских наук, медицинский директор, Бренда Конауэй, главный редактор, и A.


 Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если
Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.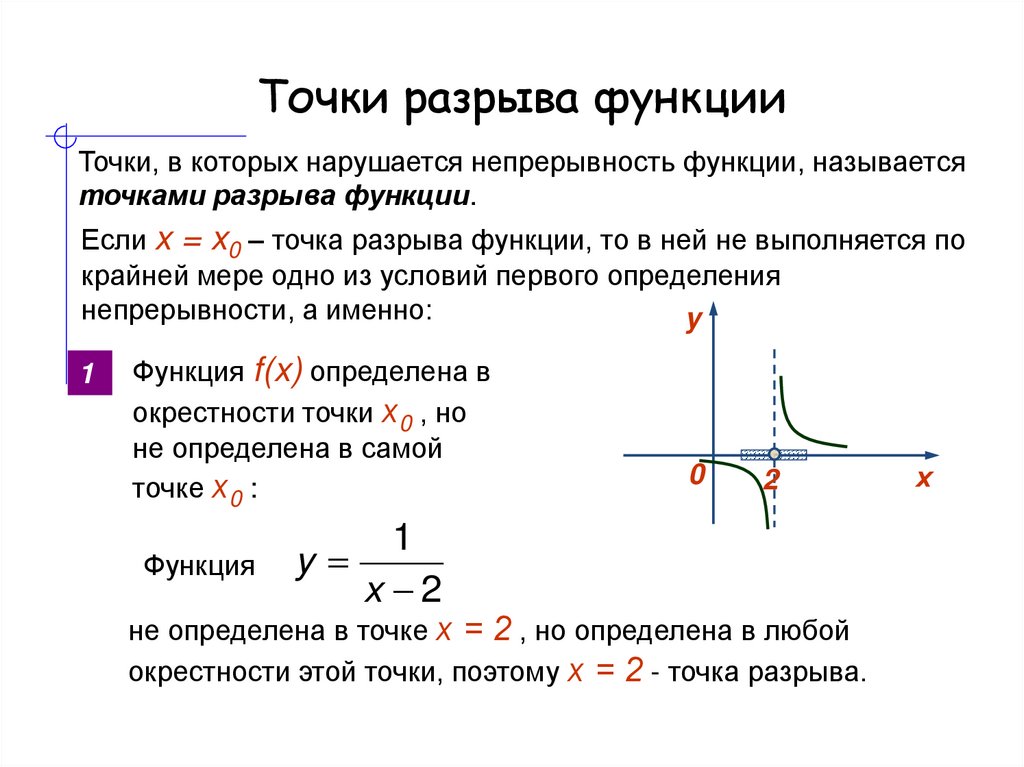 Пусть Тогда существует окрестность U(a) такая, что
Пусть Тогда существует окрестность U(a) такая, что