ГДЗ по Алгебре 8 класс
Начать самоподготовку с помощью гдз по алгебре за 8 класс желательно с составления эффективного индивидуального плана. В нем желательно учесть такие ключевые моменты успешной и результативной работы:
- Количество времени, которое планируется потратить на занятия с решебником. Многое будет зависеть от целей такой подготовки. Если они перспективные, например, заблаговременная, начатая за полтора-два года, подготовка к ОГЭ по математике, эксперты рекомендуют ежедневные часовые занятия. Если планируется готовиться к участию в математических олимпиадах и предметных конкурсах по алгебре, актуальны двух-трехчасовые занятия каждый день. Или интенсивные, по 4-5 академических часов несколько раз в неделю, например, во время выходных, каникул и т. п.
- Регулярность занятий. Наиболее высокие результаты будут получены в том случае, если заниматься с онлайн помощниками по алгебре в 8 классе на постоянной основе, не допуская пропусков и длительных перерывов.

- Систематический качественный контроль. Преимущество работы с решебниками заключается, в том числе, в возможности самостоятельно контролировать ход и результат проведенной работы, без привлечения сторонней помощи. Это, с одной стороны, позволит сэкономить семейный бюджет, отказавшись или существенно сократив дорогостоящую помощь репетиторов и посещение специализированных кружков и курсов. С другой – научит восьмиклассников грамотно работать с информацией:
- находить нужные данные, проводить их оценку и отбор;
- анализировать и использовать необходимые в работе сведения;
- запоминать технологию и принцип записи верного решения.
Последнее крайне актуально, поскольку нередки ситуации, когда задание решено верно, но ответ записан неграмотно. Это приводит к потере баллов и призовых мест, проигрышу в конкурсах, занижению оценок на контрольных, диагностических и ВПР по дисциплине.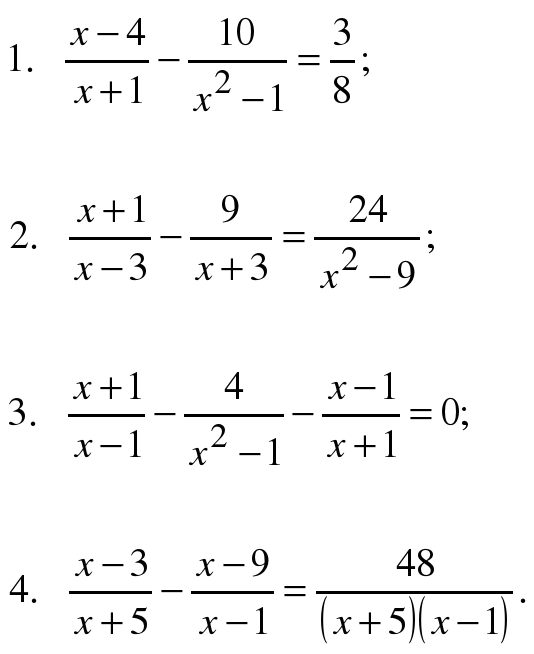
Помимо запоминания технологии отображения ответов, сборники готовых решений позволяют отследить:
- логику получения верного ответа в заданиях различных типов — графических, текстовых задач, примеров, уравнений и неравенств и т.д.;
- алгоритм поиска ответа, сравнение различных методов, сопоставление вариантов, выбор оптимального из них, математическую запись и пояснение к выбору того или иного решения;
- отражение условия заданий – дано, вопроса, непосредственно решения, чертежей если это необходимо, ответов.
Некоторые школьные учителя выступают против применения готовых ответов по алгебре в 8 классе, считая что таким образом восьмиклассники просто переписывают готовые решения, не думая самостоятельно над их получением. Их оппоненты, среди которых немало педагогов-предметников и экспертов ОГЭ и ЕГЭ, напротив, считают такую работу интересной и полезной для школьников. Последние не всегда просто переписывают ответ и сдают домашнюю или классную работу учителю на проверку. Многие применяют решебники как раз для того, чтобы дома, в условиях достаточного количества времени, задуматься и разобраться с решением. В школе, когда материал просто переписывается у одноклассников перед уроками, такой возможности нет. Кроме того, переписывание – далеко не единственный и даже не самый популярный способ применения сборников ответов.
Последние не всегда просто переписывают ответ и сдают домашнюю или классную работу учителю на проверку. Многие применяют решебники как раз для того, чтобы дома, в условиях достаточного количества времени, задуматься и разобраться с решением. В школе, когда материал просто переписывается у одноклассников перед уроками, такой возможности нет. Кроме того, переписывание – далеко не единственный и даже не самый популярный способ применения сборников ответов.
Распространенная технология работы с онлайн сборниками по алгебре для школьников
Хотя бы единожды сборниками с решениями по алгебре пользовался практически каждый восьмиклассник. Например, когда было необходимо дать быстрый и правильный ответ, который повлияет на важную оценку (четвертную, по диагностической и пр.), а самостоятельное решение вызывает затруднения, школьники прибегают к использованию готовых домашних заданий по алгебре. Другой часто встречающийся случай – отсутствие ученика на уроке по болезни или иной аналогичной причине.
Для тех же, кто применяет готовые ответы на постоянной основе, может быть предложена такая схема эффективной работы:
- Прочтение теоретического материала параграфа, темы, повторение материала, изучаемого в рамках школьного урока.
- Самостоятельное выполнение заданий, предлагаемых после параграфа или заданных учителем.
- Сверка полученных собственных ответов с представленными в еуроки ГДЗ эталонными.
- При наличии расхождений – их оценка: существенность, причины, по которым они появились, факторы, так или иначе оказавшие влияние на выявленные расхождения и ошибки.

- Самостоятельное решение аналогичных заданий, представленных в другом варианте. Для отработки материала можно использовать варианты из того же учебного пособия или взять предлагаемые в комплекте к учебнику практикумы. Возможно использование учебных пособий из других УМК и программ по предмету и решебников к ним.
- Пункт 5 схемы следует повторять до тех пор, пока свои ответы и эталонные не будут полностью совпадать, а сами задания и принцип их выполнения не будет абсолютно понятен. Только в этом случае можно считать, что тема усвоена полностью и получены глубокие знания по ней.
Если восьмиклассник не может применить пункт 2, так как у него нет идей по самостоятельному выполнению задания, следует сразу же переходить к пункту 3 представленной схемы. То есть решебник станет наглядной базой для изучения правил и порядка применения теоретических знаний на практике. Но следующие пункты и в этом случае обязательны для применения. После того как материал будет проработан, можно считать результат успешно достигнутым.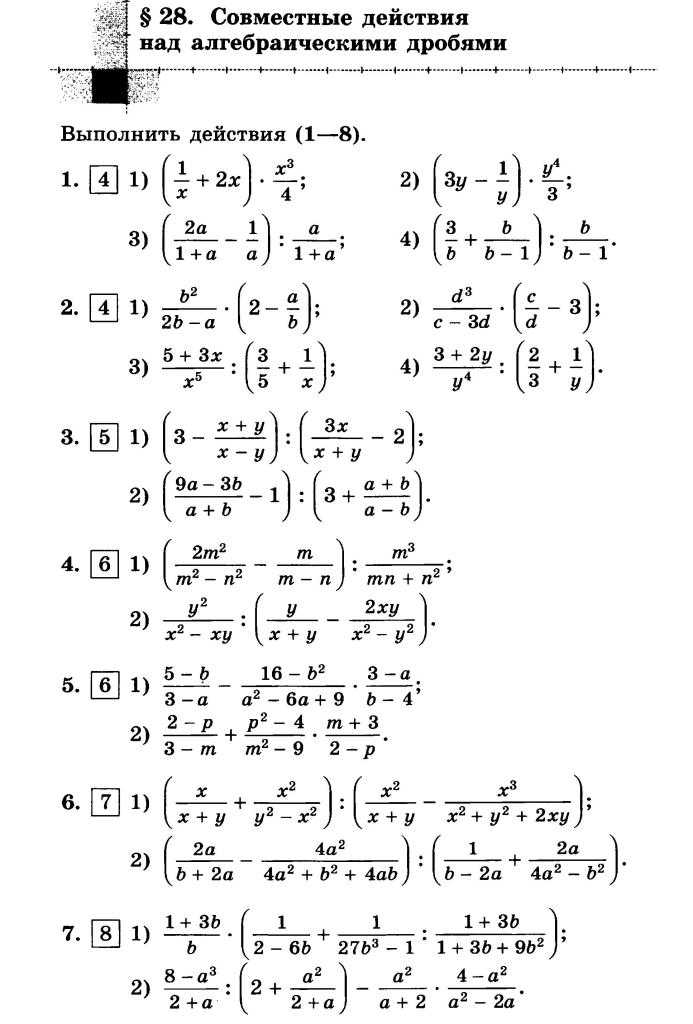
Группы активных пользователей готовых домашних заданий по алгебре за 8 класс к школьным учебникам
На постоянной основе такими ресурсами пользуются:
Репетиторы, не являющиеся школьными учителями и экспертами ОГЭ и ЕГЭ. Так как справочники по алгебре 8 класс полностью отвечает действующим образовательным ФГОСам, их требованиям, для них такие пособия – идеальная и готовая методическая разработка, по которой можно понять и как следует:
- объяснять материал;
- записывать основные пункты задания с учетом последних нормативов и их изменений;
- выбирать и анализировать решения;
- отображать готовые ответы.
Восьмиклассники, находящиеся на домашней или семейной форме обучения. Они могут получить всего несколько консультаций по предмету, то есть, регулярные объяснения учителя-предметника в полном объеме им недоступны. А требования к качеству знаний одинаковы для всех. Поэтому школьники, выбравшие эти форматы обучения, успешно применяют решебники в качестве основы для понимания практической части алгебраического материала за восьмой класс.

Введение повсеместной дистанционной формы обучения во время проведения карантинных мероприятий существенно увеличило количество пользователей ресурсов с готовыми заданиями по алгебре среди старшеклассников. Многие оценили безусловную полезность и удобство такого формата подачи материала. А полученные навыки этой работы пригодятся учащимся и впоследствии, в том числе – после окончания школы, в профессиональной и трудовой деятельности и в бизнесе.
Решение примеров по алгебре 8 класс: Алгебра (математика) 8 класс
Популярные запросы- Обстоятельство Дополнение Определение Деление дробей Русский язык 6 класс Алгебра 8 класс Русский язык 7 класс Математика 6 класс Алгебра 7 класс Русский язык 5 класс Математика 5 класс Наименьшее общее кратное Буквы о и а в корнях — кос — / — кас-; — гор — / — гар-; — клан — / — клон-; — зар — / — зор- Наибольший общий делитель. Взаимно простые числа Квадратный корень из неотрицательного числа Доли. Обыкновенные дроби Деление и дроби Буквы о и а в корнях — кос — / — кас-; — гор — / — гар-; — клан — / — клон-; — зар — / — зор- Окружность и круг Антонимы.

Урок 29. решение задач с помощью квадратных уравнений — Алгебра — 8 класс
Тема: Решение задач с помощью квадратных уравнений.
Содержание модуля (краткое изложение модуля):
Задача №1.
Иван Иванович приехал в магазин покупать изгородь для своего дачного участка, имеющего прямоугольную форму, но забыл его размеры. Какой длины изгородь надо купить Ивану Ивановичу, если единственное, что он помнит, это площадь участка – 750 м 2 , и то, что длина участка на 5 метров больше ширины?
Пусть ширина участка будет Х. Чаще всего удобнее брать за Х меньшую из неизвестных величин. Тогда длина участка составит Х + 5.
Площадь прямоугольника S = Х • (X + 5)
X • (X + 5) = 750,
X 2 + 5X — 750 = 0.
Найдем дискриминант этого уравнения и его корни.
A = 1, B = 5, C = -750
D = B 2 — 4Ac
D = 5 2 — 4 • 1 • (-750) = 25 + 3000 = 3025 = 55 2
X1,2 = (-5 ± √3025)/(2 • 1), X1 = (-5 — 55)/2 или X2 = (-5 + 55)/2.
X1 = -30 или X2 = 25
Первый из найденных корней является посторонним по смыслу задачи, значит, ширина участка будет равна 25 м. Следовательно, длина окажется равной 25 + 5 = 30 м.
Теперь Иван Иванович может рассчитать периметр своего участка.
P = 2 • (25 + 30) = 110 м
Необходимо купить 110 м изгороди.
Задача №2.
Известно, что в прямоугольном треугольнике один из катетов на 4 сантиметра меньше гипотенузы, а другой – на 2 сантиметра меньше гипотенузы. Найдем длину гипотенузы.
Пусть гипотенуза треугольника будет равна Х см. Тогда бОльший катет будет равен Х – 2 см, а меньший Х – 4 см.
По теореме Пифагора
X 2 = (X — 2) 2 + (X — 4) 2
Упростим полученное уравнение, используя формулу квадрат разности.
X 2 = X 2 — 4X + 4 + X 2 — 8X + 16
X 2 = 2X 2 — 12X + 20
X 2 — 12X + 20 = 0
Решив полученное квадратное уравнение, найдем два корня.
X1
= 2, X2 = 10
2 является посторонним корнем по смыслу задачи, т. к. в этом случае один из катетов получится равным 0, а второй будет отрицательным. Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Алгебра 8 класс — Math
Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.
Подробности Автор: Math Категория: Алгебра 8 класс.
Квадратные уравнения. Теорема Виета. Решение квадратных уравнений по теореме Виета. Решение квадратных уравнений методом подбора. Какое квадратное уравнение называется приведенным? Как решить квадратное уравнение без дискриминанта. Как решить квадратное уравнение методом подбора. Как записать теорему Виета. Как решить квадратное уравнение по теореме Виета. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Решение квадратных уравнений методом подбора. Какое квадратное уравнение называется приведенным? Как решить квадратное уравнение без дискриминанта. Как решить квадратное уравнение методом подбора. Как записать теорему Виета. Как решить квадратное уравнение по теореме Виета. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Подробности Автор: Math Категория: Алгебра 8 класс.
Квадратные уравнения. Какое квадратное уравнение называется полным? Формула дискриминанта и корней полного квадратного уравнения. Уравнения с дробями. Как избавиться от всех знаменателей сразу. Алгебра 8 класс. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Подробности Автор: Math Категория: Алгебра 8 класс.
Материал доступен только для зарегистрированных пользователей.
Здравствуйте:-). Искренне надеюсь, что видео уроки просмотрены, теория записана, задания сделаны и пришло время сверять ответы:-).
- #91 Урок 1. Арифметический квадратный корень. Понятие и основные свойства корня. Алгебра 8 класс. #92 Урок 2. Уравнения, содержащие знак корня. Иррациональные уравнения. Алгебра 8 класс. #93 Урок 3. Неполные квадратные уравнения. х2=а. Алгебра 8 класс. #94 Урок 4. Преобразование выражений с квадратным корнем. Корень из а в квадрате. Алгебра 8 класс. #95 Урок 5. Квадратный корень. Решение уравнений и построение графиков с преобразованием квадратного корня. Алгебра 8 класс. #96 Урок 6. Вынесение множителя из под знака корня. Алгебра 8 класс. Подробности Автор: Math Категория: Алгебра 8 класс.
Преобразование выражений с корнем. Приведение дробей с квадратным корнем к общему знаменателю. Иррациональные дроби. Арифметический квадратный корень. Упростить выражение с квадратным корнем. Деление дробей с корнем. Сокращение дробей с корнем. Умножение выражений с квадратным корнем. Разложение на множители выражений с корнем. Разложение на множители выражений с иррациональностью. Алгебра 8 класс. Примеры с решением. Задания с объяснением. Иррациональные выражения. Выражения с иррациональностью. Математика. Образование.
Умножение выражений с квадратным корнем. Разложение на множители выражений с корнем. Разложение на множители выражений с иррациональностью. Алгебра 8 класс. Примеры с решением. Задания с объяснением. Иррациональные выражения. Выражения с иррациональностью. Математика. Образование.
Подробности Автор: Math Категория: Алгебра 8 класс.
Арифметический квадратный корень. Упростить выражение, вынеся множитель из-под знака корня и преобразовав подкоренное выражение. Алгебра 8 класс. Математика, образование. Вынести множитель. Вынести множитель в выражении с переменными. Примеры с решением.
Подробности Автор: Math Категория: Алгебра 8 класс.
Урок 1. Арифметический квадратный корень. Определение арифметического квадратного корня. Основные понятия. Базовые свойства. Как извлечь арифметический квадратный корень. Свойства корня. Математика. Алгебра 8 класс. Образование. Примеры с решением.
- Пример 1: Найдите значение арифметического квадратного корня.
 Пример 2: Имеет ли смысл выражение. Пример 3-4: Найдите значение выражения. Пример 5: Найдите значение корня. Подробности Автор: Math Категория: Алгебра 8 класс.
Пример 2: Имеет ли смысл выражение. Пример 3-4: Найдите значение выражения. Пример 5: Найдите значение корня. Подробности Автор: Math Категория: Алгебра 8 класс.Материал доступен только для зарегистрированных пользователей.
Тест сделан и можно сверять ответы:-). Искренне надеюсь, что у Вас все правильно. Если это так, то Вы молодцы и можете смело приступать к изучению программы 9 класса. Но если вдруг случилось ток, что % правильных ответов меньше 80, то пробелы в знаниях есть, причем существенные. И, возможно, есть смысл обратится к профессиональному преподавателю или репетитору для их устранения. Если такой возможности, по каким-либо причинам нет, то предлагаем пройти курс дистанционный курс «Алгебра 8 класс».
Подробности Автор: Math Категория: Алгебра 8 класс.
Прежде, чем проходить тест АЛГЕБРА 8 КЛАСС, очень рекомендуем пройти тесты на знание базовых тем по программам математики 5, 6 классов и алгебры 7 класса.
Математика 5 класс. Тест.
Тест.
Математика 6 класс. Тест.
Алгебра 7 класс. Тест.
Почему это важно? Дело в том, что если есть «пробелы» в знаниях по программе 5, 6 или 7 классов, то с освоением программы алгебры 8 класса могут возникнуть определенные трудности.
Дело в том, что математика ( алгебра, геометрия ), в отличие от, например, географии, преподается «линейно-прогрессивно». Географию можно представить в виде огромной игры — сложение паззлов, в которой вы должны подобрать друг к другу все кусочки. Если вдруг вы не можете найти соответствующего кусочка (то есть не понимаете чего-то), это не так уж страшно — вы можете отложить это занятие и подобрать нужный элемент после.
Подробности Автор: Math Категория: Алгебра 8 класс.
Конспект открытого урока по алгебре 8 класс по теме «Решение квадратных уравнений»
Конспект открытого урока по алгебре в 8 классе по теме «Решение квадратных уравнений»
Учебник: Алгебра. 8 класс: учеб. для общеобразоват. организаций / Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова, М. И., М. И.Шабунин –4-е изд. – М. : Просвещение, 2016. – 336 с.
8 класс: учеб. для общеобразоват. организаций / Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова, М. И., М. И.Шабунин –4-е изд. – М. : Просвещение, 2016. – 336 с.
Цель: закрепить знание формулы корней квадратного уравнения, знание количества корней в зависимости от значения дискриминанта, умение находить корни квадратного уравнения с помощью формулы корней квадратного уравнения,
1) Предметные: закрепить знание формулы корней квадратного уравнения, знание количества корней в зависимости от значения дискриминанта, умение находить корни квадратного уравнения по формуле корней.
2) личностные: выступать перед публикой (классом), умение представлять задачу, коммуникабельность, умение работать в коллективе, умение оценивать свою деятельность и деятельность коллектива, умение правильно вести себя на уроке.
2) метапредметные: развивать умения самостоятельно определять цели обучения, оценивать правильность выполнения задачи, умение осуществлять контроль и оценку результатов своей деятельности, умения владеть основами самоконтроля, самооценки,
Принятия решений.
Используемые материалы: раздаточный материал, презентация.
1. Определение темы урока(2 мин).
Учитель: Здравствуйте дети и гости. Садитесь, пожалуйста. Хотелось бы начать урок с такого стихотворения:
Чтобы «х» нам узнать, надо дробь написать.
«b» в числителе поставить, знак при этом изменить.
И советуем плюс, минус перед корнем не забыть.
А под корнем «b» квадрат, минус, только не спешить,
«a» на «с» умножить нужно, а потом учетверить.
Вот числитель весь, друзья. В знаменателе «2а».
Как выдумаете, о чем это стихотворение? (Ответ: формула корней квадратного уравнения)
Совершенно верно и тема сегодняшнего занятия «Решение квадратных уравнений»
(Учащиеся записывают число, классная работа, «Решение квадратных уравнений», так же на доске записаны номера(№436(1,3), 437(1,3)), которые нужно выполнить в классе (на левой доске) и домашнее задание(на правой доске))
2. Актуализация изученной на предыдущем занятии темы (1 мин).
Учитель вызывает одного из учащихся, который на доске записывает вид квадратного уравнения, формулу корней, и зависимость количества корней от значения дискриминанта)
3. Устная работа по теме урока(5-6 мин).
Учитель: Решим следующие задания. (Презентация «Решение квадратных корней», слайд 2,3)
1. Ученики устно исправляют ошибки и называют количество корней в зависимости от дискриминанта.
2. Ученики называют пропущенные числа.
(После ответа ученика, учитель просит поднять руки всем кто согласен с ответом)
3. Закрепление изученного материала (работа с учебником)(12-15мин).
Решение у доски №435(1), № 436(1), 437(3).
Учитель вызывает к доске 3 учеников (центральная доска пополам), один работает вслух с пояснениями, остальные молча. Когда садится первый, вызывает еще одного. Затем оставшиеся ученики также объясняют решение примеров. Суть задания в том чтобы посмотреть различные результаты при решении квадратных уравнений и сделать выводы о трех возможных результатах в зависимости от D.
Если остается время решить еще № 435(5,7), №440(1).
4. Физминутка (минутка расслабления и отдыха). (1 мин)
Учитель предлагает детям расслабиться, закрыть глаза и представить себе берег моря, представить, как они отдыхают на берегу моря. Учитель включает музыку «Шум моря». (слайд 4)
5. Обучающая самостоятельная работа.
На столах учащихся раздаточный материал. Ученики решают самостоятельно уравнения. Затем на слайде 5 учитель выводит верные ответы, ученики меняются работами и проводят рефлексию.
Учитель: проверьте работу соседа по слайду 5, если выполнены все примеры верно – оценка «5», если 2 — «4», если один – «3».
6. Выступление ученика (учеников) с докладом по применению квадратных уравнений к решению задач из других наук.
Учитель: Давайте теперь посмотрим, как применяется решение квадратных уравнений для решения задач в других наук. Ученик вашего класса (ИФ называет) представит вам решение физической задачи.
Ученик выходит к доске и представляет на слайде 6 решение задачи №5 стр. 221 учебника. (Подготовить выступление заранее)
Если останется время представить химическую задачу №491 стр. 198, тоже заранее подготовленную (слайд 7).
Ученики делают вывод, что квадратные уравнения используются при решении задач из других наук и учебных курсов.
7. Домашнее задание.
Записать д/з с доски № 435(6,8), 436(2,4), 437(2,4).
8. Рефлексия учебной деятельности.
Какой основной термин сегодняшнего занятия вы можете назвать?
Как вы думаете, что нужно сделать, чтобы научиться решать квадратные уравнения и хорошо усвоить тему урока?
Оцените свою работу на уроке по пятибалльной шкале.
Оцените урок по пятибалльной шкале.
Учитель: Какой основной термин сегодняшнего занятия вы можете назвать?
Ученики: Квадратное уравнение.
Учитель: Как вы думаете, что нужно сделать, чтобы решать квадратные уравнения и хорошо усвоить тему урока?
Ученики: Выучить формулу корней квадратного уравнения и уметь подставлять а, в и с в формулу.
Учитель: Оцените себя и урок по пятибалльной шкале.
Учитель выставляет оценки и благодарит учеников за урок.
Учебники по алгебре за 8 класс в электронном виде
Показано 1 — 13 из 13
Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики, примеры решений типовых задач. В конце книги помещен …
Пособие содержит контрольные работы для 8-11 классов, задания выпускных экзаменов по математике в 9 и 11 классах с углубленным и профильным изучением математики, а также практикум для поступающих в вузы. Ко всем заданиям даны ответы. Книга может испо
Данное пособие предусматривает занятия с учащимися, проявляющими интерес и способности к математике. Целью работы в соответствующих классах является формирование у школьников устойчивого интереса к предмету, дальнейшее развитие их математических спос …
Задачник полностью соответствует учебнику. В каждом параграфе содержится система упражнений, тщательно выстроенная по степени нарастания трудности и достаточная для занятий в классе, выполнения домашних заданий и самостоятельных работ. ОГЛАВЛЕНИЕ …
В каждом параграфе содержится система упражнений, тщательно выстроенная по степени нарастания трудности и достаточная для занятий в классе, выполнения домашних заданий и самостоятельных работ. ОГЛАВЛЕНИЕ …
Учебник для 8 класса с углубленным изучением математики под редакцией Н. Я. Виленкина: — Полностью соответствует современным образовательным стандартам; — Содержит весь необходимый текстовый и иллюстрированный материал для изучения курса по основным и
. ..
Учебник по алгебре для 8 классов общеобразовательных учреждений. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. ОГЛАВЛЕНИЕ Глава I. Неравенства § 1. Положительные и отрицательные числа 3 § 2. Числовые неравенства 10 § 3. Основные свойства ч …
Учебник соответствует федеральным компонентам Государственного стандарта общего образования. Учебно-методический комплект по алгебре для 8 класса под редакцией Г. В. Дорофеева включает учебник, рабочую тетрадь, тематические тесты, дидактические матер …
Алгебра. 8 класс. Учебник. Макарычев Ю. Н. и др. ОГЛАВЛЕНИЕ ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ § 1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА 3 1. Рациональные выражения — 2. Основное свойство дроби. Сокращение дробей 7 § 2. СУММА И РАЗНОСТЬ ДРОБЕЙ 15 3. Сл …
8 класс. Учебник. Макарычев Ю. Н. и др. ОГЛАВЛЕНИЕ ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ § 1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА 3 1. Рациональные выражения — 2. Основное свойство дроби. Сокращение дробей 7 § 2. СУММА И РАЗНОСТЬ ДРОБЕЙ 15 3. Сл …
Данный учебник предназначен для углубленного изучения алгебры в 8 классе и входит в комплект из трех книг: «Алгебра-7», «Алгебра-8» и «Алгебра-9». Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются …
Учебник написан в соответствии с действующими программами для общеобразовательной школы. Материалы учебника изложены подробно и обстоятельно, что позволяет использовать их для самостоятельного изучения. Приоритетной содержательно-методической основой …
Это — учебник для классов с повышенным уровнем математической подготовки в общеобразовательных школах. Он написан в русле той концепции, которая использована в соответствующем учебнике А. Г. Мордковича для 8-го класса общеобразовательных учреждений,
Учебник представляет собой новый тип учебника, который содержит материал, как для общеобразовательных классов, так и для классов с углубленным изучением Математики. Учащиеся могут переходить с одной Программы обучения на другую, не меняя книги. Глав …
Учащиеся могут переходить с одной Программы обучения на другую, не меняя книги. Глав …
Книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики. В пособии содержатся задачи, способствующие систематическому углублению изучаемого материала и развитию навыков реше …
. ..
- Популярные запросы
- Обстоятельство Дополнение Определение Деление дробей Русский язык 6 класс Алгебра 8 класс Русский язык 7 класс Математика 6 класс Алгебра 7 класс Русский язык 5 класс Математика 5 класс Наименьшее общее кратное Буквы о и а в корнях — кос — / — кас-; — гор — / — гар-; — клан — / — клон-; — зар — / — зор- Наибольший общий делитель. Взаимно простые числа Квадратный корень из неотрицательного числа Доли. Обыкновенные дроби Деление и дроби Буквы о и а в корнях — кос — / — кас-; — гор — / — гар-; — клан — / — клон-; — зар — / — зор- Окружность и круг Антонимы. Синонимы Десятичная запись дробных чисел Буквы о – а в корнях — лаг — / — лож-, — рос — / — раст — (-ращ-)
Тема: Решение задач с помощью квадратных уравнений.
Содержание модуля (краткое изложение модуля):
Задача №1.
Иван Иванович приехал в магазин покупать изгородь для своего дачного участка, имеющего прямоугольную форму, но забыл его размеры. Какой длины изгородь надо купить Ивану Ивановичу, если единственное, что он помнит, это площадь участка – 750 м 2 , и то, что длина участка на 5 метров больше ширины?
Пусть ширина участка будет Х. Чаще всего удобнее брать за Х меньшую из неизвестных величин. Тогда длина участка составит Х + 5.
Площадь прямоугольника S = Х • (X + 5)
X • (X + 5) = 750,
X 2 + 5X — 750 = 0.
Найдем дискриминант этого уравнения и его корни.
A = 1, B = 5, C = -750
D = B 2 — 4Ac
D = 5 2 — 4 • 1 • (-750) = 25 + 3000 = 3025 = 55 2
X1,2 = (-5 ± √3025)/(2 • 1), X1 = (-5 — 55)/2 или X2 = (-5 + 55)/2.
X1 = -30 или X2 = 25
Первый из найденных корней является посторонним по смыслу задачи, значит, ширина участка будет равна 25 м. Следовательно, длина окажется равной 25 + 5 = 30 м.
Следовательно, длина окажется равной 25 + 5 = 30 м.
Теперь Иван Иванович может рассчитать периметр своего участка.
P = 2 • (25 + 30) = 110 м
Необходимо купить 110 м изгороди.
Задача №2.
Известно, что в прямоугольном треугольнике один из катетов на 4 сантиметра меньше гипотенузы, а другой – на 2 сантиметра меньше гипотенузы. Найдем длину гипотенузы.
Пусть гипотенуза треугольника будет равна Х см. Тогда бОльший катет будет равен Х – 2 см, а меньший Х – 4 см.
По теореме Пифагора
X 2 = (X — 2) 2 + (X — 4) 2
Упростим полученное уравнение, используя формулу квадрат разности.
X 2 = X 2 — 4X + 4 + X 2 — 8X + 16
X 2 = 2X 2 — 12X + 20
X 2 — 12X + 20 = 0
Решив полученное квадратное уравнение, найдем два корня.
X1
= 2, X2 = 10
2 является посторонним корнем по смыслу задачи, т. к. в этом случае один из катетов получится равным 0, а второй будет отрицательным. Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.
Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Оцените свою работу на уроке по пятибалльной шкале.
В знаменателе 2а.
Xn—96-5cd3cgu2f. xn--p1ai
14.06.2019 2:10:52
2019-06-14 02:10:52
Источники:
Https://xn—96-5cd3cgu2f. xn--p1ai/8-klass/reshenie-primerov-po-algebre-8-klass-algebra-matematika-8-klass. html
Урок алгебры в 8 классе. Тема урока: «Решение задач с помощью рациональных уравнений» » /> » /> .keyword { color: red; }
Математика 8 класс решение задачОписание работы: Урок — практикум с использованием компьютерных технологий.
Этот материал будет полезен для учителей математики, работающих в 8 классах, для учащихся 14-15 лет.
Вид урока: Урок — практикум с использованием компьютерных технологий.
Тип урока: урок практического применения знаний.
Цель урока: формировать умения и навыки применения полученных знаний в ходе изучения алгебры по теме «Решение задач с помощью уравнений».
Образовательные задачи:
1. Обучение способам решения задач на вычисление концентрации растворов.
2. Практическое применение знаний при Решении задач.
3. Создание условий для развития творческих способностей и познавательной активности учащихся.
Воспитательные задачи:
1. Развитие навыков коммуникативного общения.
2. Воспитание чувства ответственности, трудолюбия.
3. Формирование мотивации к изучению химии и математики.
4. Формирование чувства бережного отношения к своему здоровью. На примерах показать, чем вреден алкоголь и каковы последствия его применения.
Развивающие задачи:
Развитие практических способностей обучающихся.
Профориентационная задача:
Развитие интереса к профессиям, основанным на знаниях математики.
Оборудование: мультимедиапроектор, интерактивная доска, компьютер.
Словарь: пропорция, концентрация, процентное содержание, алкоголь. Учитель: «Тема нашего сегодняшнего урока – «Решение задач с помощью рациональных уравнений». В ходе урока мы с вами должны научиться составлять уравнения по условию задачи, а для решения уравнений вы будете применять известные вам способы и приемы. На этом уроке мы рассмотрим задачи на вычисление процентного содержания веществ: так называемые в математике задачи на «смеси и сплавы». Именно такие задачи вам часто приходится решать на уроках химии».
С целью повторения обратимся к таким простым задачам. Условие задач приведено на экране.
Учитель Тема нашего сегодняшнего урока Решение задач с помощью рациональных уравнений.
Ped-kopilka. ru
16.02.2017 13:46:27
2017-02-16 13:46:27
Источники:
Https://ped-kopilka. ru/uchiteljam-predmetnikam/matematika/urok-algebry-v-8-klase-tema-uroka-reshenie-zadach-s-pomoschyu-racionalnyh-uravnenii. html
html
Презентация на тему: Алгебра.8 класс Решение задач с помощью квадратных уравнений. Проверь себя. Задания для закрепления учебного материала. flash-карточки (. Скачать бесплатно и без регистрации. » /> » /> .keyword { color: red; }
Математика 8 класс решение задачПрезентация 8 класса по предмету «Математика» на тему: «Алгебра.8 класс Решение задач с помощью квадратных уравнений. Проверь себя. Задания для закрепления учебного материала. flash-карточки («. Скачать бесплатно и без регистрации. — Транскрипт:
1 Алгебра.8 класс Решение задач с помощью квадратных уравнений. Проверь себя. Задания для закрепления учебного материала. flash-карточки ( Учитель математики Муниципального общеобразовательного учреждения «Средняя общеобразовательная школа 19» г. Кандалакша Чернявская Татьяна Борисовна
Flash-карточки — презентация.
Www. myshared. ru
25.11.2017 0:43:40
2017-11-25 00:43:40
Источники:
Http://www. myshared. ru/slide/101417/
ГДЗ Алгебра 8 класс Макарычев, Миндюк, Нешков, Суворова на Решалка
ГДЗ Алгебра 8 класс Макарычев, Миндюк, Нешков, Суворова
авторы: Макарычев, Миндюк, Нешков, Суворова.
издательство: «Просвещение» 2013 г
Задачи
- ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ
- §1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА
- 1. Рациональные выражения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 2.
 Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 5
- 1. Рациональные выражения
- §2. СУММА И РАЗНОСТЬ ДРОБЕЙ
- 3. Сложение и вычитание дробей с одинаковыми знаменателями
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 4.
 Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- Контрольные вопросы и задания
- 1
- 2
- 3
- 3. Сложение и вычитание дробей с одинаковыми знаменателями
- §3. ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ
- 5.
 Умножение дробей. Возведение дроби в степень
Умножение дробей. Возведение дроби в степень- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 6. Деление дробей
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 7.
 Преобразование рациональных выражений
Преобразование рациональных выражений- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 8. Функция y = k/x и ее график
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 9.
 Представление дроби в виде суммы дробей
Представление дроби в виде суммы дробей- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 5.
- Дополнительные упражнения к главе I
- К параграфу 1
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- К параграфу 2
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- К параграфу 3
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- К параграфу 1
- §1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА
- ГЛАВА II.
 КВАДРАТНЫЕ КОРНИ
КВАДРАТНЫЕ КОРНИ- §4. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
- 10. Рациональные числа
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 11. Иррациональные числа
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 10. Рациональные числа
- §5.
 2 = a
2 = a- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
- 335
- 14. Нахождение приближенных значений квадратного корня
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- 350
- 351
- 15. Функция y = √x и ее график
- 352
- 353
- 354
- 355
- 356
- 357
- 358
- 359
- 360
- 361
- 362
- 363
- 364
- 365
- 366
- 367
- 368
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 5
- §4. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
- §6.
 СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ
СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ- 16. Квадратный корень из произведения и дроби
- 369
- 370
- 371
- 372
- 373
- 374
- 375
- 376
- 377
- 378
- 379
- 380
- 381
- 382
- 383
- 384
- 385
- 386
- 387
- 388
- 389
- 390
- 391
- 392
- 17. Квадратный корень из степени
- 393
- 394
- 395
- 396
- 397
- 398
- 399
- 400
- 401
- 402
- 403
- 404
- 405
- 406
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 16. Квадратный корень из произведения и дроби
- §7.
 ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ
ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ- 18. Вынесение множителя за знак корня. Внесение множителя под знак корня
- 407
- 408
- 409
- 410
- 411
- 412
- 413
- 414
- 415
- 416
- 417
- 418
- 419
- 420
- 19. Преобразование выражений, содержащих квадратные корни
- 421
- 422
- 423
- 424
- 425
- 426
- 427
- 428
- 429
- 430
- 431
- 432
- 433
- 434
- 435
- 436
- 437
- 438
- 439
- 440
- 441
- 442
- 443
- Контрольные вопросы и задания
- 1
- 2
- 3
- 20.
 Преобразование двойных радикалов
Преобразование двойных радикалов- 444
- 445
- 446
- 447
- 448
- 449
- 450
- 451
- 452
- 453
- 18. Вынесение множителя за знак корня. Внесение множителя под знак корня
- Дополнительные упражнение к главе II
- К параграфу 4
- 454
- 455
- 456
- 457
- 458
- 459
- 460
- 461
- 462
- К параграфу 5
- 463
- 464
- 465
- 466
- 467
- 468
- 469
- 470
- 471
- 472
- 473
- 474
- 475
- К параграфу 6
- 476
- 477
- 478
- 479
- 480
- 481
- 482
- 483
- 484
- 485
- 486
- 487
- 488
- 489
- К параграфу 7
- 490
- 491
- 492
- 493
- 494
- 495
- 496
- 497
- 498
- 499
- 500
- 501
- 502
- 503
- 504
- 505
- 506
- 507
- 508
- 509
- 510
- 511
- К параграфу 4
 КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ- §8. КВАДРАТНОЕ УРАВНЕНИЕ И ЕГО КОРНИ
- 21. Неполные квадратные уравнения
- 512
- 513
- 514
- 515
- 516
- 517
- 518
- 519
- 520
- 521
- 522
- 523
- 524
- 525
- 526
- 527
- 528
- 529
- 530
- 531
- 532
- 22. Формула корней квадратного уравнения
- 533
- 534
- 535
- 536
- 537
- 538
- 539
- 540
- 541
- 542
- 543
- 544
- 545
- 546
- 547
- 548
- 549
- 550
- 551
- 552
- 553
- 554
- 555
- 556
- 557
- 558
- 23.
 Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений- 559
- 560
- 561
- 562
- 563
- 564
- 565
- 566
- 567
- 568
- 569
- 570
- 571
- 572
- 573
- 574
- 575
- 576
- 577
- 578
- 579
- 24. Теорема Виета
- 580
- 581
- 582
- 583
- 584
- 585
- 586
- 587
- 588
- 589
- 590
- 591
- 592
- 593
- 594
- 595
- 596
- 597
- 598
- 599
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 5
- 21. Неполные квадратные уравнения
- §9.
 ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ- 25. Решение дробных рациональных уравнений
- 600
- 601
- 602
- 603
- 604
- 605
- 606
- 607
- 608
- 609
- 610
- 611
- 612
- 613
- 614
- 615
- 616
- 26. Решение задач с помощью рациональных уравнений
- 617
- 618
- 619
- 620
- 621
- 622
- 623
- 624
- 625
- 626
- 627
- 628
- 629
- 630
- 631
- 632
- 633
- 634
- 635
- 636
- 637
- 638
- 639
- Контрольные вопросы и задания
- 1
- 2
- 27.
 Уравнения с параметром
Уравнения с параметром- 640
- 641
- 642
- 643
- 644
- 645
- 646
- 647
- 648
- 649
- Дополнительные упражнения к главе III
- К параграфу 8
- 650
- 651
- 652
- 653
- 654
- 655
- 656
- 657
- 658
- 659
- 660
- 661
- 662
- 663
- 664
- 665
- 666
- 667
- 668
- 669
- 670
- 671
- 672
- 673
- 674
- 675
- 676
- 677
- 678
- 679
- 680
- 681
- 682
- 683
- 684
- 685
- 686
- 687
- 688
- 689
- К параграфу 9
- 690
- 691
- 692
- 693
- 694
- 695
- 696
- 697
- 698
- 699
- 700
- 701
- 702
- 703
- 704
- 705
- 706
- 707
- 708
- 709
- 710
- 711
- 712
- 713
- 714
- 715
- 716
- 717
- 718
- 719
- 720
- 721
- 722
- 723
- К параграфу 8
- 25. Решение дробных рациональных уравнений
 НЕРАВЕНСТВА
НЕРАВЕНСТВА- §10. ЧИСЛОВЫЕ НЕРАВЕНСТВА И ИХ СВОЙСТВА
- 28. Числовые неравенства
- 724
- 725
- 726
- 727
- 728
- 729
- 730
- 731
- 732
- 733
- 734
- 735
- 736
- 737
- 738
- 739
- 740
- 741
- 742
- 743
- 744
- 745
- 29. Свойства числовых неравенств
- 746
- 747
- 748
- 749
- 750
- 751
- 752
- 753
- 754
- 755
- 756
- 757
- 758
- 759
- 760
- 761
- 762
- 763
- 764
- 30.
 Сложение и умножение числовых неравенств
Сложение и умножение числовых неравенств- 765
- 766
- 767
- 768
- 769
- 770
- 771
- 772
- 773
- 774
- 775
- 776
- 777
- 778
- 779
- 780
- 781
- 31. Погрешность и точность приближения
- 782
- 783
- 784
- 785
- 786
- 787
- 788
- 789
- 790
- 791
- 792
- 793
- 794
- 795
- 796
- 797
- 798
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 5
- 28. Числовые неравенства
- §11.
 НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ
НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ- 32. Пересечение и объединение множеств
- 799
- 800
- 801
- 802
- 803
- 804
- 805
- 806
- 807
- 808
- 809
- 810
- 811
- 33. Числовые промежутки
- 812
- 813
- 814
- 815
- 816
- 817
- 818
- 819
- 820
- 821
- 822
- 823
- 824
- 825
- 826
- 827
- 828
- 829
- 830
- 831
- 832
- 34.
 Решение неравенств с одной переменной
Решение неравенств с одной переменной- 833
- 834
- 835
- 836
- 837
- 838
- 839
- 840
- 841
- 842
- 843
- 844
- 845
- 846
- 847
- 848
- 849
- 850
- 851
- 852
- 853
- 854
- 855
- 856
- 857
- 858
- 859
- 860
- 861
- 862
- 863
- 864
- 865
- 866
- 867
- 868
- 869
- 870
- 871
- 872
- 873
- 35.
 Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной- 874
- 875
- 876
- 877
- 878
- 879
- 880
- 881
- 882
- 883
- 884
- 885
- 886
- 887
- 888
- 889
- 890
- 891
- 892
- 893
- 894
- 895
- 896
- 897
- 898
- 899
- 900
- 901
- 902
- 903
- 904
- Контрольные вопросы и задания
- 1
- 2
- 3
- 4
- 36. Доказательство неравенств
- 905
- 906
- 907
- 908
- 909
- 910
- 911
- 912
- 913
- 914
- 32. Пересечение и объединение множеств
- Дополнительные упражнения к главе IV
- К параграфу 10
- 915
- 916
- 917
- 918
- 919
- 920
- 921
- 922
- 923
- 924
- 925
- 926
- 927
- 928
- 929
- 930
- 931
- 932
- К параграфу 11
- 933
- 934
- 935
- 936
- 937
- 938
- 939
- 940
- 941
- 942
- 943
- 944
- 945
- 946
- 947
- 948
- 949
- 950
- 951
- 952
- 953
- 954
- 955
- 956
- 957
- 958
- 959
- 960
- 961
- 962
- 963
- К параграфу 10
 -2 и их свойства
-2 и их свойстваИнтересуют готовые домашние задания по алгебре за 8 класс Макарычева, Миндюк, Суворова? На нашем сайте предложены ответы к этому учебнику и большому перечню других, которые используются в школах. Мы призываем школьников и их родителей грамотно пользоваться ГДЗ с пользой для успеваемости ребенка. Как это возможно? Все достаточно легко, если прибегать к готовым домашним заданиям за 8 класс в случае:
- Сложной темы, с которой не удалось полностью разобраться на уроке. Рассмотрев примеры решения заданий, ученик сможет понять алгоритм, восполнить пробелы и решить аналогичные упражнения уже самостоятельно;
- Пропуска уроков и необходимости наверстать упущенное. На примере готовых решений это делать намного проще;
- Трудностей с заданием и потребности в подсказке – подсмотреть порядок решения будет только на пользу;
- Слишком большой нагрузки на ребенка и насыщенного дня, когда нет ни времени, ни сил на домашку.
 В виде исключение можно просто переписать задание и дать школьнику возможность восстановить силы.
В виде исключение можно просто переписать задание и дать школьнику возможность восстановить силы.
Готовые ответы к учебникам могут быть полезными
Отлично, что сейчас нет необходимости покупать печатные издания по каждому предмету, а ГДЗ по алгебре за 8 класс доступны онлайн совершенно бесплатно. Но старайтесь внимательно выбирать ресурс. Например, мы вручную проверяем все ответы и не публикуем чужие наработки, в которых не уверены, также заботимся об удобстве сайта и интерфейса для быстрого поиска информации. У нас есть ГДЗ по алгебре за 8 класс Макарычева, Миндюк, Нешкова и Суворова, а также ко многим другим учебникам. Приятного пользования и успешного обучения.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Математические задачи 8-го класса с ответами
Вопрос 1 :
На какое наименьшее число можно разделить 256 так, чтобы частное было полным кубом?
(A) 2 (B) 3 (C) 4
Решение:
= ∛256 = ∛(2⋅2⋅2⋅2⋅2⋅2⋅2⋅2) Когда мы группируем простые множители внутри кубического корня в виде троек, у нас остается 2⋅ 2. То есть 4. Следовательно, 4 — наименьшее число, необходимое для деления 256 так, чтобы частное было полным кубом. |
Вопрос 2:
Сколько цифр в квадратном корне из 4456321?
(A) 2 цифры (B) 4 цифры (C) 3 цифры
Решение:
Квадратный корень из 1 цифры и 2-значного числа содержит 1 цифру.
Квадратный корень из 3-х и 4-значного числа содержит 2 цифры.
Квадратный корень из 5- и 6-значного числа содержит 3 цифры.
Квадратный корень из 7 и 8-значного числа содержит 4 цифры.
Итак, квадратный корень из данного числа состоит из 4 цифр.
Вопрос 3:
Найдите значение 3x 3 -4x 2 + x -5 Когда x = -3
(a) -54 (b) -71 (c) -32
Решение:
Пусть f(x) = 3x 3 — 4x 2 + x — 5
x = — 3
f(-3) = 3(-3) 3 — 4(-3) 2 + (-3) — 3 9000 = 3(9) — 4(9) — 3 — 5
= 27 — 36 — 3 — 5
= 27 — 44
= -17
Периметр прямоугольника равен
3 52 см. Найдите размеры прямоугольника, если его ширина на 2 см больше трети длины.
(A) 12 см x 4 см (B) 18 см x 8 см (C) 15 см x 9см
Решение:
Периметр прямоугольника = 52 см
2(длина + ширина) = 52 ==> l + w = 26
Пусть x длина
2 ширина) = ( + 2
x + (x/3) + 2 = 26
[(3x + x)/3] + 2 = 26
4x / 3 = 24
4x = 24 (3)
x 6 6 6 (3) ==> 18 см
Ширина = (18/3) + 2
= 6 + 2 = 8 см
Итак, требуемый размер 18 см х 8 см.
Вопрос 5 :
Что нужно прибавить к каждому из числителя и знаменателя дроби 7/11, чтобы она стала равной 3/4
(A) 9
Решение:
Пусть x будет числом, которое нужно прибавить к числителю и знаменателю дроби.
(7 + х) / (11 + х) = 3/4
4(7 + х) = 3(11 + х)
28 + 4х = 33 + 3х
4х — 3х = 33 — 28
x = 5
Итак, 5 – это необходимое число, которое нужно добавить, чтобы дробь 7/11 превратилась в 3/4.
Вопрос 6 :
Прямая, которая пересекает две или более прямых в разных точках, называется ____________
(A) параллельной (B) Пересекающейся пересекает две или более прямых в разных точках, называется параллельным.
Вопрос 7 :
Противоположные углы вписанного четырехугольника _______________
(A) Дополнительный (B) Дополнительный (C) Ни один из этих
Решение:
Сумма противоположных углов вписанного четырехугольника равна 180 градусам.
Итак, ответ дополнительный.
Вопрос 8 :
В треугольник ABC вписана окружность с центром O и BC диаметр, если угол BAC равен 50°, найти угол ABC.
(A) 50° (B) 40° (C) 48°
Решение:
В прямоугольном треугольнике ABC,




 Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Умножение дробей. Возведение дроби в степень
Умножение дробей. Возведение дроби в степень Преобразование рациональных выражений
Преобразование рациональных выражений Представление дроби в виде суммы дробей
Представление дроби в виде суммы дробей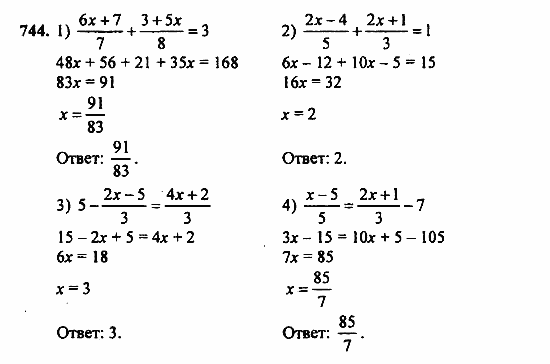 КВАДРАТНЫЕ КОРНИ
КВАДРАТНЫЕ КОРНИ 2 = a
2 = a СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ
СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ
ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ Преобразование двойных радикалов
Преобразование двойных радикалов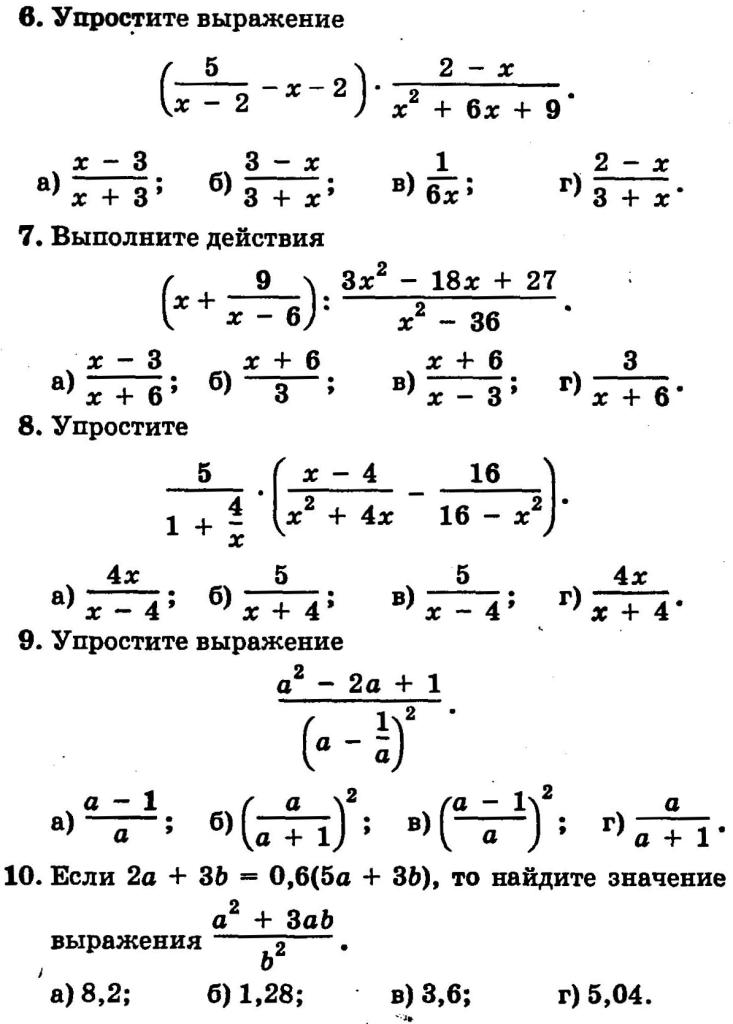 Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ Уравнения с параметром
Уравнения с параметром Сложение и умножение числовых неравенств
Сложение и умножение числовых неравенств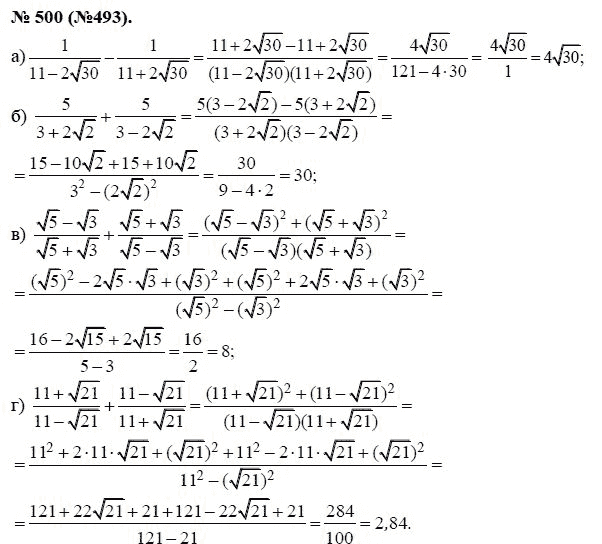 НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ
НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ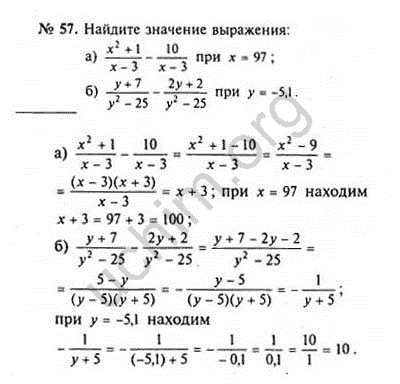 Решение неравенств с одной переменной
Решение неравенств с одной переменной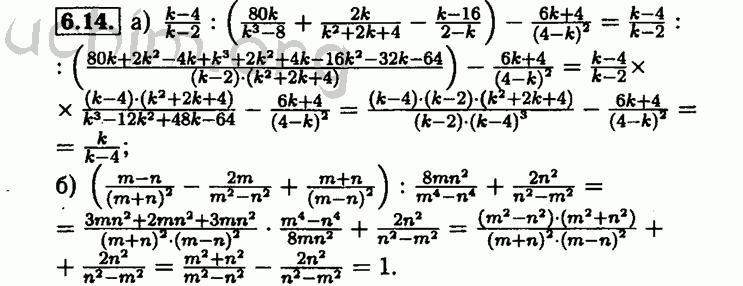 Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной В виде исключение можно просто переписать задание и дать школьнику возможность восстановить силы.
В виде исключение можно просто переписать задание и дать школьнику возможность восстановить силы. см. Вычислите площадь его криволинейной поверхности.
см. Вычислите площадь его криволинейной поверхности.  com
com Вместе они могут завершить проект за 10 часов. Сколько времени потребуется каждому из них, чтобы завершить проект в одиночку?
Вместе они могут завершить проект за 10 часов. Сколько времени потребуется каждому из них, чтобы завершить проект в одиночку? Кларк занимает 2 часа.
Кларк занимает 2 часа. Двое работающих вместе могут выполнить работу за 1,2 часа. Сколько времени потребовалось бы каждому, если бы они работали в одиночку?
Двое работающих вместе могут выполнить работу за 1,2 часа. Сколько времени потребовалось бы каждому, если бы они работали в одиночку?
 Выходная труба опорожняет резервуар в два раза дольше. За какое время наполнится бак, если обе трубы будут открыты?
Выходная труба опорожняет резервуар в два раза дольше. За какое время наполнится бак, если обе трубы будут открыты?