Четыре замечательные точки треугольника 8 класс онлайн-подготовка на Ростелеком Лицей
Четыре замечательные точки треугольника.
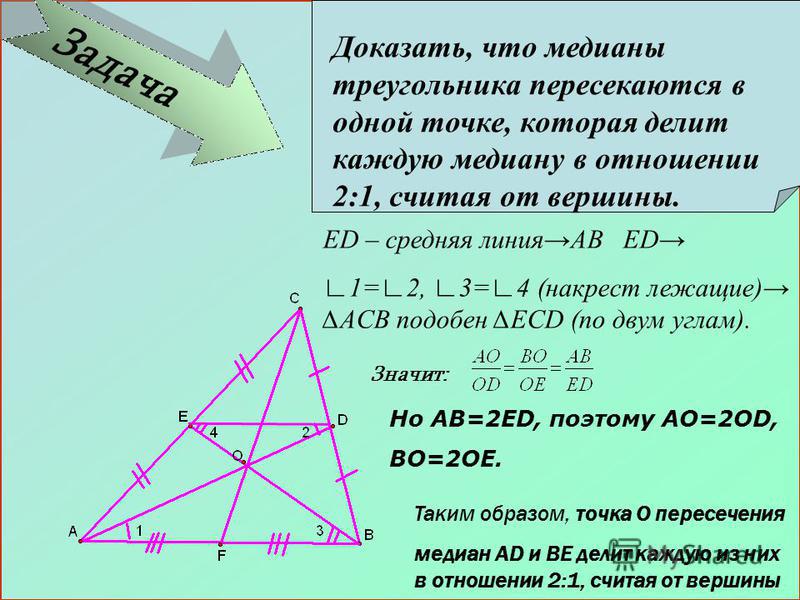
С каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.
Задан отрезок АВ. У любого отрезка есть середина, и через нее можно провести перпендикуляр – обозначим его за р. Таким образом, р – серединный перпендикуляр.
Теорема (основное свойство серединного перпендикуляра): любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
Доказать, что АМ = МВ
Доказательство:
Рассмотрим треугольники ⊿МОА и ⊿МОВ. Они прямоугольные и равные, т.к. имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, то есть АМ = МВ, что и требовалось доказать.
Отсюда следует, что гипотенузы треугольников тоже равны, то есть АМ = МВ, что и требовалось доказать.
Справедлива обратная теорема.
Теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Задан отрезок АВ, серединный перпендикуляр к нему р, точка М, равноудаленная от концов отрезка.
Доказать, что точка М лежит на серединном перпендикуляре к отрезку.
Доказательство:
Рассмотрим треугольник АВМ. Он равнобедренный, так как АМ = МВ по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана. Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что ОМ⟂АВ. Но прямая р также перпендикулярна АВ. Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит, прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.
Если необходимо описать окружность около одного отрезка, это можно сделать, и таких окружностей бесконечно много, но центр каждой из них будет лежать на серединном перпендикуляре к отрезку.
Говорят, что серединный перпендикуляр есть геометрическое место точек, равноудаленных от концов отрезка.
Треугольник состоит из трех отрезков. Проведем к двум из них серединные перпендикуляры и получим точку О их пересечения.
Точка О принадлежит серединному перпендикуляру к стороне ВС треугольника, значит, она равноудалена от его вершин В и С, обозначим это расстояние за R, то есть ОВ = ОС = R.
Кроме того, точка О находится на серединном перпендикуляре к отрезку АВ, т.е. OA = OB, вместе с тем OB = R, отсюда OA = R.
Таким образом, точка О пересечения двух серединных перпендикуляров треугольника равноудалена от его вершин, а значит, она лежит и на третьем серединном перпендикуляре.
Три серединных перпендикуляра треугольника пересекаются в одной точке – центре описанной окружности.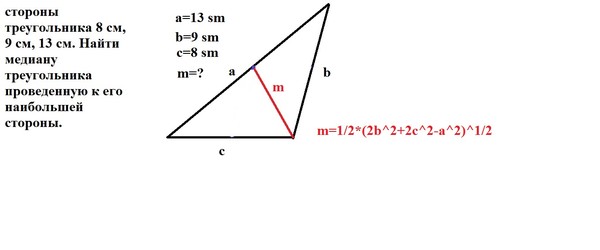
Для доказательства этого утверждения рассмотрим серединные перпендикуляры m и n к сторонам АВ и ВС треугольника АВС. Эти прямые пересекаются в некоторой точке О. В самом деле, если предположить противное, т.е. то, что m||n, то прямая ВА, будучи перпендикулярной к прямой m, была бы перпендикулярна и к параллельной ей прямой n, а тогда через точку В проходили бы две прямые ВА и ВС, перпендикулярные к прямой n, что невозможно.
По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА = ОС, то есть точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре р к этому отрезку. Следовательно, все три серединных перпендикуляра m, n, p к сторонам треугольника АВС пересекаются в точке О.
Итак, мы рассмотрели первую замечательную точку треугольника – точку пересечения его серединных перпендикуляров.
Перейдем к свойству произвольного угла.
Задан угол ∠ВАС , его биссектриса AL, точка М лежит на биссектрисе.
Свойство биссектрисы угла:
Если точка М лежит на биссектрисе угла, то она равноудалена от сторон угла, то есть расстояния от точки М до АС и до ВС сторон угла равны.
Доказательство:
Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.
Рассмотрим треугольники ⊿АМК и ⊿АМР . Это прямоугольные треугольники, и они равны, т.к. имеют общую гипотенузу АМ, а углы ∠КАМ и ∠РАМ равны, так как AL – биссектриса угла ∠ВАС. Таким образом, прямоугольные треугольники равны по гипотенузе и острому углу, отсюда следует, что МК = МР = d, что и требовалось доказать. Таким образом, точка на биссектрисе угла равноудалена от сторон этого угла.
Справедлива обратная теорема.
Теорема. Если точка равноудалена от сторон неразвернутого угла, то она лежит на его биссектрисе.
Задан неразвернутый угол ∠ВАС, точка М, такая, что расстояние от нее до сторон угла одинаковое. Доказать, что точка М лежит на биссектрисе угла.
Доказать, что точка М лежит на биссектрисе угла.
Доказательство:
Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.
Рассмотрим треугольники ⊿АМК и ⊿АМР . Это прямоугольные треугольники, и они равны, т.к. имеют общую гипотенузу АМ, катеты МК и МР равны по условию. Таким образом, прямоугольные треугольники равны по гипотенузе и катету. Из равенства треугольников следует равенство соответствующих элементов, против равных катетов лежат равные углы, таким образом,∠КАМ и ∠РАМ равны , следовательно, точка М лежит на биссектрисе данного угла.
Если необходимо вписать в угол окружность, это можно сделать, и таких окружностей бесконечно много, но центры вписанных окружностей лежат на биссектрисе данного угла.
Говорят, что биссектриса есть геометрическое место точек, равноудаленных от сторон угла.
Треугольник состоит из трех углов. Построим биссектрисы двух из них, получим точку О их пересечения.
Построим биссектрисы двух из них, получим точку О их пересечения.
Точка О лежит на биссектрисе угла ∠В, значит, она равноудалена от его сторон АВ и ВС, обозначим расстояние за r: ρ(О,АВ) = ρ(О,ВС) = r. Также точка О лежит на биссектрисе угла ∠C, значит, она равноудалена от его сторон АС и ВС, то есть ρ(О,АC) = ρ(О,ВС), ρ(О,ВС) = r, отсюда ρ(О,АC) = r.
Несложно заметить, что точка пересечения биссектрис равноудалена от сторон третьего угла, а значит, она лежит на биссектрисе угла ∠A. Таким образом, все три биссектрисы треугольника пересекаются в одной точке.
Биссектрисы углов треугольника пересекаются в одной точке – центре вписанной окружности.
Итак, мы рассмотрели вторую замечательную точку треугольника – точку пересечения биссектрис.
Аналогичным свойством обладают высоты и медианы.
Высоты треугольника (или их продолжение) пересекаются в одной точке.
Медианы треугольника пересекаются в одной точке.
Как найти стороны равнобедренного треугольника зная площадь. Как находить площадь треугольника (формулы)
Для того чтобы помочь своему ребенку с уроками, родители должны сами знать множество вещей. Как найти площадь равнобедренного треугольника, чем причастный оборот отличается от деепричастного, что такое ускорение свободного падения?
С любым из этих вопросов у ваших сына или дочери могут возникнуть проблемы, и они именно к вам обратятся за разъяснениями. Чтобы не упасть лицом в грязь и поддержать свой авторитет в детских глазах, стоит освежить в памяти некоторые элементы школьной программы.
Возьмем для примера вопрос о равнобедренном треугольнике. Геометрия в школе многим тяжело дается, а после школы быстрее всех забывается.
Но когда ваши дети пойдут в 8 класс, придется вспомнить формулы, касающиеся геометрических фигур. Равнобедренный треугольник — одна из самых простых фигур в плане нахождения ее параметров.
Если все, что вы когда-то учили о треугольниках, забыто, давайте вспоминать.
Существует такой вариант, при котором равны между собой все 3 стороны. Он носит название равностороннего треугольника. На него распространяются все формулы, применяемые к равнобедренному, и в случае необходимости любую из его сторон можно назвать основанием.
Для нахождения площади нам понадобится разделить основание пополам. Прямая, опущенная к полученной точке из вершины, соединяющей боковые стороны, пересечет основание под прямым углом.
Таково уж свойство подобных треугольников: медиана, то есть прямая от вершины к середине противоположной стороны, в равнобедренном треугольнике является его биссектрисой (прямой, делящей угол пополам) и его высотой (перпендикуляром к противоположной стороне).
Чтобы найти площадь равнобедренного треугольника, надо умножить его высоту на основание, а затем поделить это произведение пополам
.
Для нахождения площади треугольника формула проста: S=ah/2, где а — длина основания, h — высота.
Наглядно это можно объяснить следующим образом. Вырежьте из бумаги аналогичную фигуру, найдите середину основания, проведите к этой точке высоту и аккуратно разрежьте по этой высоте. Получатся два прямоугольных треугольника.
Если приставить их друг к другу гипотенузами (длинными сторонами), то составится прямоугольник, одна сторона которого будет равна высоте нашей фигуры, а другая — половине ее основания. То есть подтвердится формула.
Наглядная демонстрация очень важна. Если ваш ребенок научится не бездумно запоминать формулы, а понимать их смысл, геометрия уже не покажется ему сложным предметом.
Лучшим учеником в классе становится не зазубривающий, а думающий и, главное, понимающий школьник.
Как найти площадь фигуры, если один угол прямой?
Может так оказаться, что угол между боковыми сторонами заданной треугольной фигуры составляет 90°. Тогда этот треугольник будет называться прямоугольным, его боковые стороны — катетами, а основание — гипотенузой.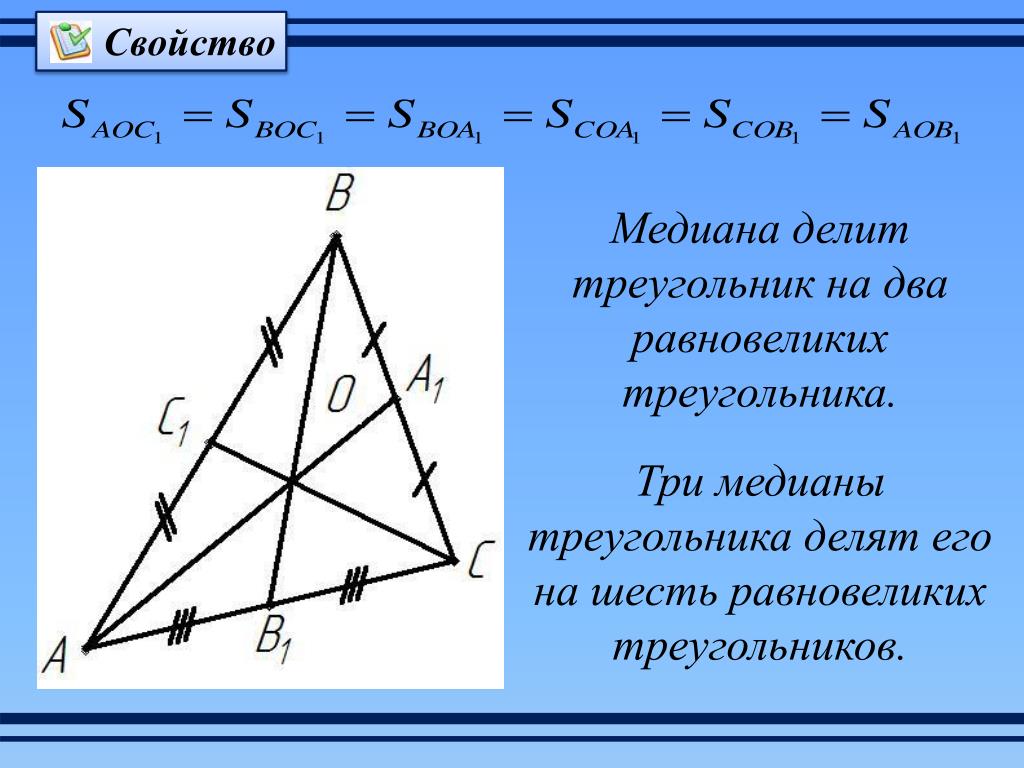
Площадь такой фигуры можно вычислить вышеизложенным способом (находим середину гипотенузы, проводим к ней высоту, умножаем ее на гипотенузу, делим пополам). Но можно решить проблему гораздо проще.
Начнем с наглядности. Прямоугольный равнобедренный треугольник представляет собой ровно половину квадрата, если разрезать тот по диагонали. И если площадь квадрата находится простым возведением во вторую степень его стороны, то площадь нужной нам фигуры будет вдвое меньше.
S=a 2 /2, где а — длина катета.
Площадь равнобедренного прямоугольного треугольника равна половине квадрата его боковой стороны. Проблема оказалась не такой уж серьезной, какой была на первый взгляд.
Решение геометрических задач не требует сверхчеловеческих усилий и вполне может пригодиться не только детям, но и вам при нахождении ответов на какие-либо практические вопросы.
Геометрия — точная наука. Если вникнуть в ее основы, то трудностей с ней будет немного, а логичность доказательств может очень увлечь вашего ребенка. Нужно просто немного ему помочь. Какой бы хороший учитель ему ни достался, родительская помощь лишней не будет.
Нужно просто немного ему помочь. Какой бы хороший учитель ему ни достался, родительская помощь лишней не будет.
А в случае с изучением геометрии очень полезным станет метод, о котором говорилось выше, — наглядности и простоты объяснения.
При этом нельзя забывать о точности формулировок, иначе можно сделать эту науку гораздо сложней, чем она есть на самом деле.
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь, нужно решать задачи и примеры, чертить схемы и рисунки, доказывать теоремы.
Путь к пониманию геометрии лежит через решение задач. Отличным примером могут служить задания, в которых нужно найти площадь равнобедренного треугольника.
Что такое равнобедренный треугольник, и в чем его отличие от других?
Чтобы не пугаться терминов «высота», «площадь», «основания», «равнобедренного треугольника» и прочих, потребуется начать с теоретических основ.
Сначала о треугольнике. Это плоская фигура, которая образована из трех точек — вершин, в свою очередь, соединенных отрезками. Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.
Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.
Существует частный случай равнобедренного треугольника — равносторонний, когда и третья сторона равна двум боковым.
Свойства фигуры
Они оказываются верными помощниками в решении задач, которые требуют найти площадь равнобедренного треугольника. Поэтому знать и помнить о них необходимо.
- Первое из них: углы равнобедренного треугольника, одна сторона которых — основание, всегда равны друг другу.
- Важным является и свойство о дополнительных построениях. Проведенные к непарной стороне высота, медиана и биссектриса совпадают.
- Эти же отрезки, проведенные из углов при основании треугольника, попарно равны. Это тоже часто облегчает поиск решения.
- Два равных угла в нем всегда имеют значение меньше чем 90º.
- И последнее: вписанная и описанная окружности строятся так, что их центры лежат на высоте к основанию треугольника, а значит медиане и биссектрисе.

Как в задаче распознать равнобедренный треугольник?
Если при решении задания встает вопрос о том, как найти площадь равнобедренного треугольника, то сначала нужно понять, что он относится к этой группе. А в этом помогут определенные признаки.
- Равны два угла или две стороны треугольника.
- Биссектриса является еще и медианой.
- Высота треугольника оказывается медианой или биссектрисой.
- Равны две высоты, медианы или биссектрисы фигуры.
Обозначения величин, принятые в рассматриваемых формулах
Для упрощения того, как находить площадь равнобедренного треугольника по формулам, введена замена его элементов на буквы.
Внимание! Важно не путать «а» с «А» и «в» с «В». Это разные величины.
Формулы, которыми можно воспользоваться в разных задачах
Известны длины сторон, и требуется найти площадь равнобедренного треугольника.
В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Пусть она будет записана под №1.
Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.
Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:
Это формула №2.
Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.
Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:
Номер этой формулы — 3.
В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.
Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Порядковый номер формулы — 4.
В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.
Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:
Ее номер — 5.
Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.
Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение.
Номер последней формулы — 6.
Примеры задач
Первая задача: известно, что основание равнобедренного треугольника равно 10 см, а его высота — 5 см. Нужно определить его площадь.
Для ее решения логично выбрать формулу под номером 3. В ней все известно. Подставить числа и сосчитать. Получится, что площадь равна 10 * 5 / 2. То есть 25 см 2 .
Вторая задача: в равнобедренном треугольнике даны боковая сторона и основание, которые равны соответственно 5 и 8 см. Найти его площадь.
Первый способ. По формуле №1. При возведении в квадрат основания получается число 64, а учетверенный квадрат боковой стороны — 100. После вычитания из второго первого получится 36. Из него прекрасно извлекается корень, который равен 6. Основание, поделенное на 4, равно 2. Итоговое значение определится как произведение 2 и 6, то есть 12. Это ответ: искомая площадь равна 12 см 2 .
Второй способ. По формуле №2.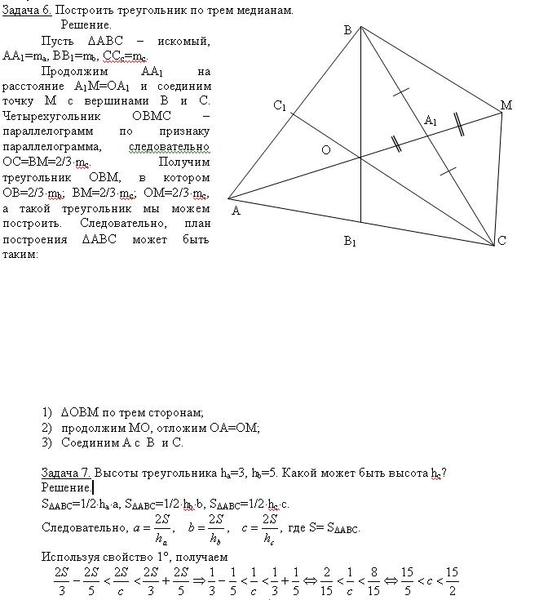 Половина основания равна 4. Сумма боковой стороны и найденного числа дает 9, их же разность — 1. После умножения получается 9. Извлечение квадратного корня дает 3. И последнее действие, умножение 3 на 4, что дает те же 12 см 2 .
Половина основания равна 4. Сумма боковой стороны и найденного числа дает 9, их же разность — 1. После умножения получается 9. Извлечение квадратного корня дает 3. И последнее действие, умножение 3 на 4, что дает те же 12 см 2 .
Решая задачи по геометрии и определяя, как найти площадь равнобедренного треугольника, можно получить неоценимый опыт. Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.
Встаёт не только перед школьниками или студентами, но и в реальной, практической жизни. Например, во время строительства возникает необходимость отделки фасадной части, находящейся под крышей. Как вычислить количество нужного материала?
Часто с подобными задачами сталкиваются мастера, которые работают с тканью или кожей. Ведь многие детали, которые предстоит выкроить мастеру, имеют как раз форму равнобедренного треугольника.
Итак, существует несколько способов, помогающих найти площадь равнобедренного треугольника. Первый — вычисление её по основанию и высоте.
Первый — вычисление её по основанию и высоте.
Для решения нам необходимо построить для наглядности треугольник MNP с основанием MN и высотой PO. Теперь кое-что достроим в чертеже: из точки P провести линию, параллельную основанию, а из точки M — линию, параллельную высоте. Точку пересечения назовём Q. Чтобы узнать, как найти площадь равнобедренного треугольника, нужно рассмотреть полученный четырёхугольник MOPQ, в котором боковая сторона данного нам треугольника MP является уже его диагональю.
Докажем сначала, что это прямоугольник. Так как мы строили его сами, то знаем, что стороны MO и OQ параллельны. И стороны QM и OP тоже параллельны. Угол POM прямой, значит и угол OPQ тоже прямой. Следовательно, получившийся чётырёхугольник является прямоугольником. Найти его площадь не составит труда, она равна произведению PO на OM. OM — это половина основания данного треугольника MPN. Отсюда вытекает, что площадь построенного нами прямоугольника равна полупроизведению высоты прямоугольного треугольника на его основание.
Вторым этапом поставленной перед нами задачи, как определить площадь треугольника, является доказательство того факта, что полученный нами прямоугольник по площади соответствует данному равнобедренному треугольнику, то есть, что площадь треугольника также равна полупроизведению основания и высоты.
Сравним для начала треугольник PON и PMQ. Они оба прямоугольны, так как прямой угол в одном из них образован высотой, а прямой угол в другом является углом прямоугольника. Гипотенузы в них являются сторонами равнобедренного треугольника, следовательно, также равны. Катеты PO и QM также равны как параллельные стороны прямоугольника. Значит, и площадь треугольника PON , и треугольника PMQ равны между собой.
Площадь прямоугольника QPOM равна площадям треугольников PQM и MOP в сумме. Заменив надстроенный треугольник QPM треугольником PON, получаем в сумме данный нам для вывода теоремы треугольник. Теперь мы знаем, как найти площадь равнобедренного треугольника по основанию и высоте — вычислить их полупроизведение.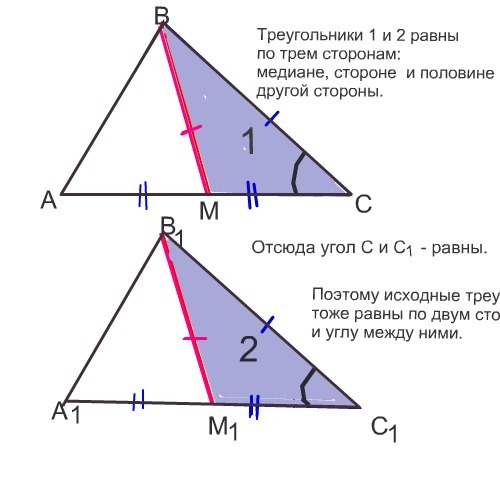
Но можно узнать, как найти площадь равнобедренного треугольника по основанию и боковой стороне. Здесь также существует два варианта: теорема Герона и Пифагора. Рассмотрим решение с применением теоремы Пифагора. Для примера возьмём тот же PMN с высотой PO.
В прямоугольном треугольнике POM MP — гипотенуза. Её квадрат равен сумме квадратов PO и OM. А так как OM — половина основания, которое нам известно, то мы легко может найти OM и возвести число в квадрат. Произведя вычитание из квадрата гипотенузы полученное число, узнаем, чему равен квадрат другого катета, который в равнобедренном треугольнике является высотой. Найдя из разности и узнав высоту прямоугольного треугольника, можно дать ответ на поставленное перед нами задание.
Нужно просто перемножить высоту на основание и полученный результат разделить напополам. Почему именно так следует поступать, мы объяснили в первом варианте доказательства.
Бывает, что нужно произвести вычисления по боковой стороне и углу. Тогда находим высоту и основание, используя формулу с синусами и косинусами, и, опять же, перемножаем их и делим результат пополам.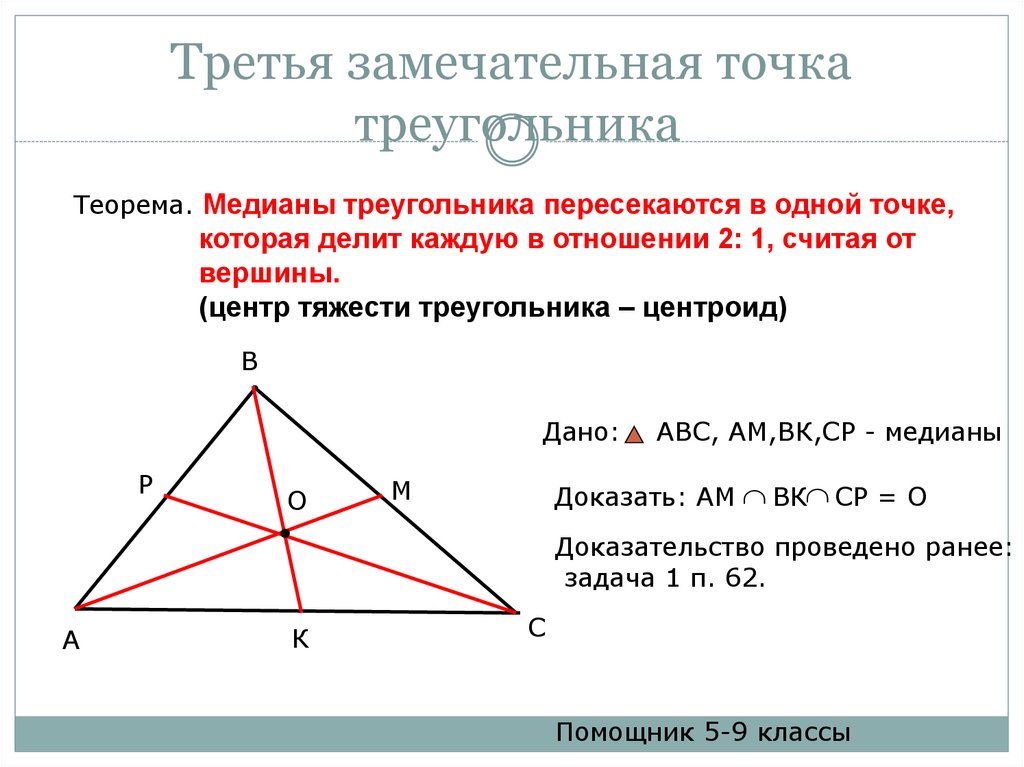 2)*tg(B)/2 d случае, если вам задан только один из катетов (a), но также известен и прилежащий этому катету угол (B).
2)*tg(B)/2 d случае, если вам задан только один из катетов (a), но также известен и прилежащий этому катету угол (B).
Видео по теме
Источники:
- «Пособие по математике для поступающих в вузы», под ред. Г.Н. Яковлева, 1982.
Равнобедренным считается такой треугольник, у которого две стороны равны. Площадь этого треугольника можно рассчитать несколькими методами.
Инструкция
Видео по теме
Обратите внимание
Существуют признаки равнобедренного треугольника:
1) У равнобедренного треугольника есть 2 равных угла;
2) Высота треугольника совпадает с его медианой;
3) Высота треугольника совпадает с его биссектрисой;
4) Биссектриса треугольника совпадает с его медианой;
5) У равнобедренного треугольника 2 медианы равны;
6) У равнобедренного треугольника 2 высоты равны;
7) У равнобедренного треугольник 2 биссектрисы равны.
Источники:
- площадь треугольника равнобедренного
Одной из фигур, рассматриваемых на уроках математики и геометрии, является треугольник. Треугольник — многоугольник, у которого есть 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, попарно соединенные тремя отрезками. Существует множество задач, связанных с нахождением различных величин этой фигуры. Одна из них – площадь . В зависимости от исходных данных задачи имеется несколько формул для определения площади треугольника .
Треугольник — многоугольник, у которого есть 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, попарно соединенные тремя отрезками. Существует множество задач, связанных с нахождением различных величин этой фигуры. Одна из них – площадь . В зависимости от исходных данных задачи имеется несколько формул для определения площади треугольника .
Инструкция
Если вам известны длина стороны а и проведенная на нее высота h треугольника , используйте формулу S= ?h*a.
Если известны длина одной из сторон треугольника и его высота, опущенная на эту сторону, перемножьте длину стороны на высоту, а полученный результат разделите на два.
Если перед вами прямоугольный треугольник, измерьте при помощи линейки длины егo катетoв, то есть сторон, которые прилегают к прямому углу. Перемножьте длины катетов, а полученный результат разделите на два.
Если вы располагаете данными о величине угла между двумя треугольника, и вам известны длины этих сторон, то площадь треугольника найдите по формуле:
St = ½ * A * B * sinα, где St – площадь треугольника; A и B – длины сторон треугольника; α — угла, расположенного между этими сторонами.
S = 1/2 (АВ + ВС + AC) = р r.
Вычислите полупериметр:
р = (5 + 7 + 10) = 11.
Рассчитайте искомую величину:
S = √(11 (11-5) (11-7) (11-10)) ≈ 16,2.
Три точки, однозначно определяющие треугольник в Декартовой системе координат — это его вершины. Зная их положение относительно каждой из координатных осей можно вычислить любые параметры этой плоской фигуры, включая и ограничиваемую ее периметром площадь . Это можно сделать несколькими способами.
Инструкция
Используйте формулу Герона для расчета площади треугольника . В ней задействованы размеры трех сторон фигуры, поэтому вычисления начините с . Длина каждой стороны должна быть равна корню из суммы квадратов длин ее проекций на координатные оси. Если обозначить координаты A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃), длины их сторон можно выразить так: AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Для упрощения расчетов введите вспомогательную переменную — полупериметр (Р). Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Рассчитайте площадь (S) по формуле Герона — извлеките корень из произведения полупериметра на разность между ним и длиной каждой из сторон. В общем виде ее можно записать так: S = √(P*(P-AB)*(P-BC)*(P-AC)) = √(P*(P-√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²))*(P-√((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²))*(P-√((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²)).
Для практических расчетов удобно пользоваться специализированными -калькуляторами. Это скрипты, размещенные на серверах некоторых сайтов, которые проделают все необходимые расчеты на основе координат, введенных вами в соответствующую форму. Единственный такого сервиса — он не дает объяснений и обоснований для каждого шага вычислений. Поэтому, если вас интересует только конечный результат, а не вычисления в общем виде, перейдите, например, на страницу http://planetcalc.ru/218/.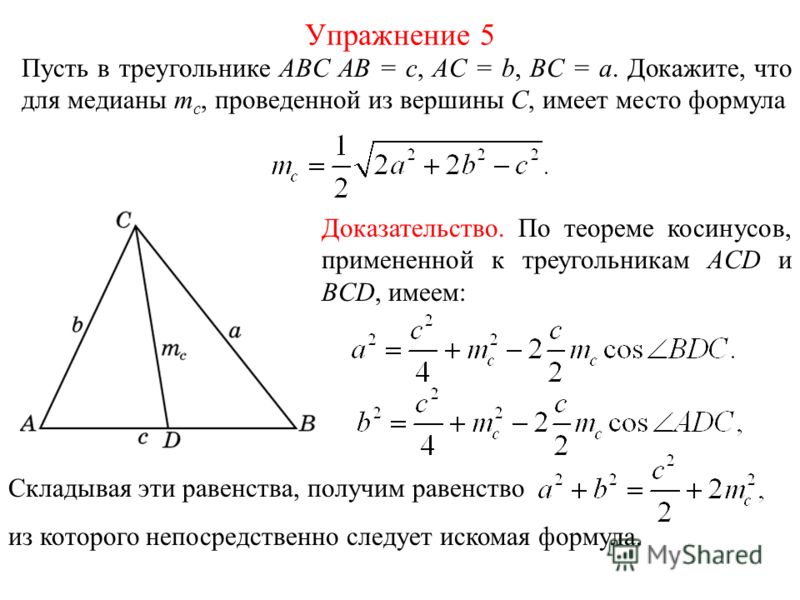
В поля формы введите каждую координату каждой из вершин треугольника — они здесь как Ax, Ay, Az и т.д. Если треугольник задан двухмерными координатами, в поля — Az, Bz и Cz — пишите ноль. В поле «Точность вычисления» установите нужное число знаков после запятой, кликая мышкой
В данной статье речь пойдет о том как найти площадь равнобедренного треугольника и формулы для решения.
Равнобедренный треугольник это такой треугольник у которого две параллельные основанию стороны равны . Он изображен на рисунке.
Стоит заметить что буквы которыми обозначены стороны и углы, используются в формулах, для вашего удобства.
Заметка: Если вам нужна качественно выполненная курсовая или контрольная работа, без посредников. Тогда Вам на сайт tvoi5.ru. Так же Вы можете перейти по ссылке курсовая на заказ (http://tvoi5.ru/zakazat-kursovuyu-rabotu.html) и все подробности.
Площадь равнобедренного треугольника формула.
Первая формула говорит о том что площадь находится, если нам известна только одна сторона и основа треугольника . Получили эту формула с помощью использования общей формулы. Когда основным является формула Герона и стороны фигуры равны, она сама по себе будет выглядеть проще.
Получили эту формула с помощью использования общей формулы. Когда основным является формула Герона и стороны фигуры равны, она сама по себе будет выглядеть проще.
Во второй формуле говориться о том что площадь находится через боковые стороны и угол находящийся между ними . Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту.
В третьей формуле площадь находится с помощью одной параллельной стороны, основания и угла находящегося на вершине . Другими словами можно сказать так: когда известен хоть один угол в равнобедренном треугольнике, с его помощью можно узнать и два других. Данная формула схожа со второй формулой, можно использовать и запомнить любую из них. Но из этой формулы выйдет пятая, которую опишу чуть ниже.
Другими словами можно сказать так: когда известен хоть один угол в равнобедренном треугольнике, с его помощью можно узнать и два других. Данная формула схожа со второй формулой, можно использовать и запомнить любую из них. Но из этой формулы выйдет пятая, которую опишу чуть ниже.
Четвертая формула показывает что найти площадь можно зная величину основания и угла при нем . Все углы у основания одинаковы и квадрат стороны основания разделенный на 4 tg пол угла, появившиеся от его боковых сторон. Когда внимательно разглядеть, можно понять, пол стороны основания b/2, при умножении tg (? /2) дает высоту. Которая в свою очередь играет роль медианы и биссектрисы, а значит tg (? /2)= (b/2)/h, из чего h=b/(2tg (? /2)) и сводиться к упрощенной формуле №5.
Итак пятая формула она гласит о том, что найти площадь можно с помощью высоты которая берет начало в вершине треугольника и заканчивается в его основании, при этом разделяя его на прямоугольные треугольники. А дальше как в третьей и четвертой формулах. Пол величины высоты умноженное на величину основания.
А дальше как в третьей и четвертой формулах. Пол величины высоты умноженное на величину основания.
Шестая и заключительная формула. Она появляется в ходе решения площади треугольника через теорему Пифагора . Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу — основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного, найдем высоту.
Как найти неизвестный катет. Решение прямоугольного треугольника
Инструкция
Углы, противолежащие катетам a и b обозначим соответственно через A и B. Гипотенуза, по определению, это сторона прямоугольного треугольника, которая противоположна прямому углу (при этом с другими сторонами треугольника гипотенуза образует острые углы). Длину гипотенузы обозначим через с. 2″ означает возведение во вторую степень.
2″ означает возведение во вторую степень.
Используйте формулу a=c*sinA, если вам известна гипотенуза (c) и угол, противолежащий искомому катету (этот угол мы обозначили, как A).
Выражение a=c*cosB используйте для нахождения катета, если вам известна гипотенуза (c) и угол, прилежащий искомому катету (этот угол мы обозначили как B).
Вычислите катет по формуле a=b*tgA в случае, когда задан катет b и угол, противолежащий искомому катету (этот угол мы условились обозначать A).
Обратите внимание:
Если же в вашей задаче катет не находится ни одним из описанных способов, скорее всего, её можно свести к какому-то из них.
Полезные советы:
Все эти выражения получаются из общеизвестных определений тригонометрических функций, поэтому, даже если вы забыли какое-то из них, вы всегда сможете путём несложных операций его быстро вывести. Также, полезно знать значения тригонометрических функций для наиболее типичных углов 30, 45, 60, 90, 180 градусов.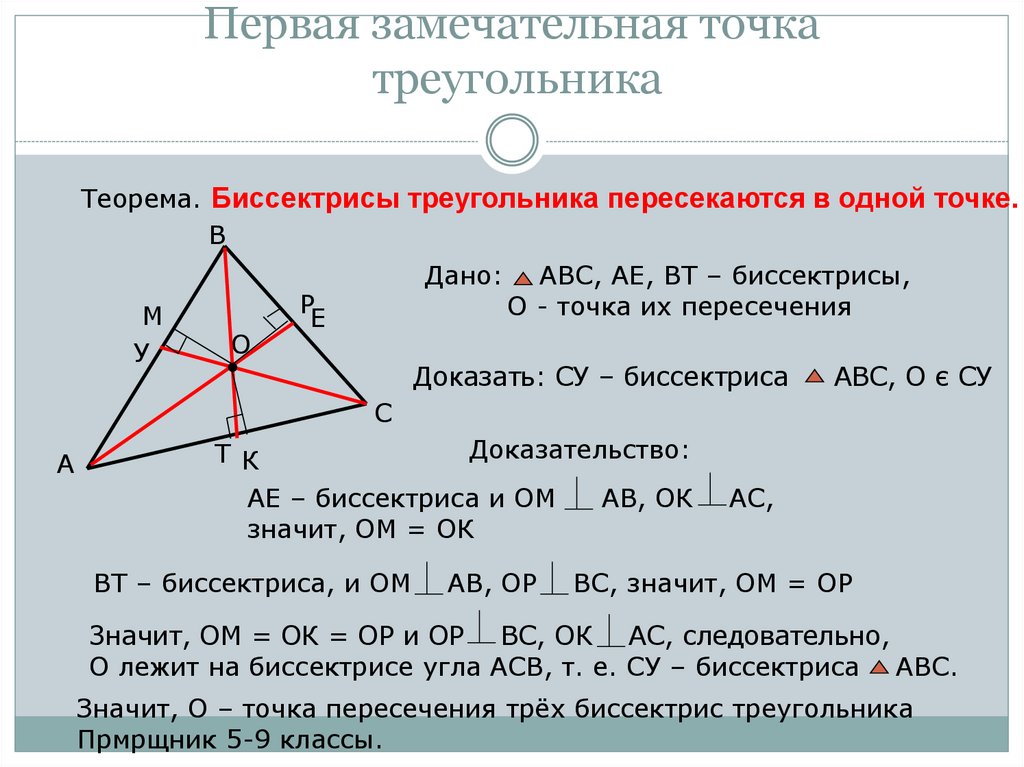
Перед тем, как найти гипотенузу треугольника, необходимо разобраться, какие особенности имеет данная фигура. Рассмотрим главные из них:
- В прямоугольном треугольнике оба острых угла в сумме будут равны 90º.
- Катет, лежащий против угла в 30º, будет равен ½ от величины гипотенузы.
- Если катет равен ½ от значения гипотенузы, тогда второй угол будет иметь такую же величину – 30º.
Найти гипотенузу в прямоугольном треугольнике можно несколькими способами. Самым простым решением является вычисление через катеты. Допустим, вам известны значения катетов сторон А и В. Тогда на выручку приходит теорема Пифагора, повествующая нам, что если поставить каждую величину катета в квадрат и просуммировать полученные данные, мы узнаем чему равна гипотенуза. Таким образом, нам необходимо просто извлечь значение квадратного корня:
Например, если катет А = 3 см, а катет В = 4 см, тогда вычисление будет иметь следующий вид:
Как найти гипотенузу через угол?
Еще одним способом, который поможет узнать, чему равна гипотенуза в прямоугольном треугольнике, является вычисление через заданный угол. Для этого нам потребуется вывести величину через формулу синуса. Допустим, нам известна величина катета (А) и значение противолежащего угла (α). Тогда все решение заключается в одной формуле: С=А/sin(α).
Для этого нам потребуется вывести величину через формулу синуса. Допустим, нам известна величина катета (А) и значение противолежащего угла (α). Тогда все решение заключается в одной формуле: С=А/sin(α).
Например, если длина катета 40 см, а угол составляет 45°, тогда длину гипотенузы можно вывести следующим образом:
Определить искомую величину можно также через косинус заданного угла. Допустим, нам известно значение одного катета (В) и острого прилежащего угла (α). Тогда для решения задачи понадобится одна формула: С=В/ cos(α).
К примеру, если длина катета имеет значение 50 см, а угол составляет 45°, тогда гипотенузу можно вычислить следующим образом:
Таким образом, мы рассмотрели основные способы как узнать гипотенузу в треугольнике. В ходе решения задания важно сконцентрировать внимание на имеющихся данных, тогда найти неизвестную величину будет достаточно просто. Необходимо знать всего пару формул и процесс решения задач станет простым и приятным.
Зная один из катетов в прямоугольном треугольнике, можно найти второй катет и гипотенузу используя тригонометрические отношения – синус и тангенс известного угла. 2+2bc))/(b+c)=(b√(2c(b+c)))/(b+c)=(a/tanα √(2c(a/tanα +c)))/(a/tanα +c)=(a√(2c(a/tanα +c)))/(a+c tanα)
l_b=√(ac(a+b+c)(a+c-b))/(a+c)=(a√(2c(a+c)))/(a+c)=(a√(2c(a+a/sinα)))/(a+a/sinα)=(a sinα √(2c(a+a/sinα)))/(a sinα+a)
2+2bc))/(b+c)=(b√(2c(b+c)))/(b+c)=(a/tanα √(2c(a/tanα +c)))/(a/tanα +c)=(a√(2c(a/tanα +c)))/(a+c tanα)
l_b=√(ac(a+b+c)(a+c-b))/(a+c)=(a√(2c(a+c)))/(a+c)=(a√(2c(a+a/sinα)))/(a+a/sinα)=(a sinα √(2c(a+a/sinα)))/(a sinα+a)
Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tanα) M_c=c/2=a/(2 sinα)
Радиус вписанной окружности равен разности катетов и гипотенузы, деленной на два, а чтобы найти радиус описанной окружности, нужно разделить на два гипотенузу. Заменяем второй катет и гипотенузу на отношения катета a к синусу и тангенсу соответственно. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+a/tanα -a/sinα)/2=(a tanα sinα+a sinα-a tanα)/(2 tanα sinα) R=c/2=a/2sinα
Первые — это отрезки, которые прилегают к прямому углу, а гипотенуза является самой длинной частью фигуры и находится напротив угла в 90 о.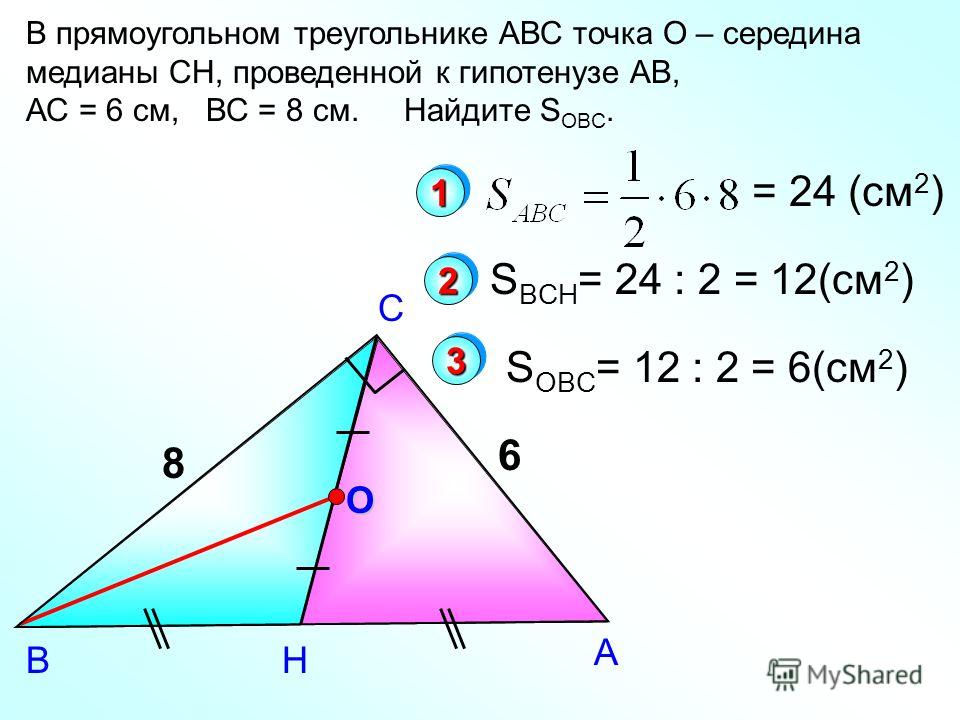 Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».
Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».
Египетский треугольник
Для того чтобы нынешнее поколение узнало геометрию в том виде, в котором ее преподают в школе сейчас, она развивалась несколько веков. Основополагающим моментом считается теорема Пифагора. Стороны прямоугольного известна на весь мир) составляют 3, 4, 5.
Мало кто не знаком с фразой «Пифагоровы штаны во все стороны равны». Однако на самом деле теорема звучит так: c 2 (квадрат гипотенузы) = a 2 +b 2 (сумма квадратов катетов).
Среди математиков треугольник со сторонами 3, 4, 5 (см, м и т. д.) называется «египетским». Интересно то, что которая вписана в фигуру, равняется единице. Название возникло примерно в V столетии до н.э., когда философы Греции ездили в Египет.
При построении пирамид архитекторы и землемеры пользовались соотношением 3:4:5. Такие сооружения получались пропорциональными, приятными на вид и просторными, а также редко рушились.
Для того чтобы построить прямой угол, строители использовали веревку, на которой было завязано 12 узлов. В таком случае вероятность построения именно прямоугольного треугольника повышалась до 95%.
Признаки равенства фигур
- Острый угол в прямоугольном треугольнике и большая сторона, которые равны тем же элементам во втором треугольнике, — бесспорный признак равенства фигур. Беря во внимание сумму углов, легко доказать, что вторые острые углы также равны. Таким образом, треугольники одинаковы по второму признаку.
- При наложении двух фигур друг на друга повернем их таким образом, чтобы они, совместившись, стали одним равнобедренным треугольником. По его свойству стороны, а точнее, гипотенузы, равны, так же как и углы при основании, а значит, эти фигуры одинаковые.
По первому признаку очень просто доказать то, что треугольники действительно равны, главное, чтобы две меньшие стороны (т. е. катеты) были равными между собой.
Треугольники будут одинаковыми по II признаку, суть которого заключается в равенстве катета и острого угла.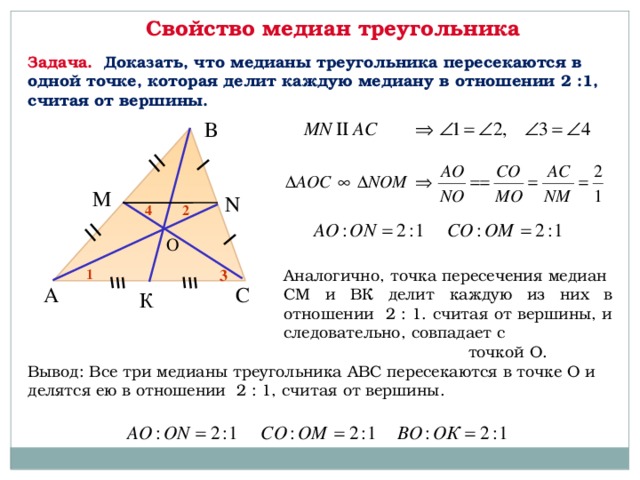
Свойства треугольника с прямым углом
Высота, которую опустили из прямого угла, разбивает фигуру на две равные части.
Стороны прямоугольного треугольника и его медианы легко узнать по правилу: медиана, которая опущена на гипотенузу, равна ее половине. можно найти как по формуле Герона, так и по утверждению, что она равна половине произведению катетов.
В прямоугольном треугольнике действуют свойства углов в 30 о, 45 о и 60 о.
- При угле, который равен 30 о, следует помнить, что противолежащий катет будет равен 1/2 самой большой стороны.
- Если угол 45 о, значит, второй острый угол также 45 о. Это говорит о том, что треугольник равнобедренный, и его катеты одинаковы.
- Свойство угла в 60 о заключается в том, что третий угол имеет градусную меру в 30 о.
Площадь легко узнать по одной из трех формул:
- через высоту и сторону, на которую она опускается;
- по формуле Герона;
- по сторонам и углу между ними.
Стороны прямоугольного треугольника, а точнее катеты, сходятся с двумя высотами.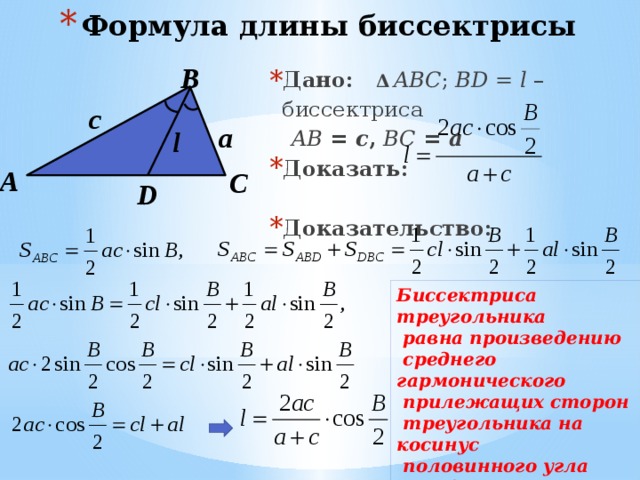 Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.
Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.
Теоремы, применяемые к прямоугольному треугольнику
Геометрия прямоугольного треугольника включает в себя использование таких теорем, как:
Прямоугольный треугольник содержит в себе огромное множество зависимостей. Это делает его привлекательным объектом для разного рода геометрических задач. Одной из наиболее часто встречающихся задач считается нахождение гипотенузы.
Прямоугольный треугольник
Прямоугольный треугольник – это треугольник, который содержит в себе прямой угол, т.е. угол в 90 градусов. Только в прямоугольном треугольнике можно выразить тригонометрические функции через величины сторон. В произвольном треугольнике придется производить дополнительные построения.
В прямоугольном треугольнике две из трех высот совпадают со сторонами зовутся катетами. Третья сторона зовется гипотенузой. Высота, проведенная к гипотенузе единственная в этом виде треугольника, требующая дополнительных построений.
Рис. 1. Виды треугольников.
В прямоугольном треугольнике не может быть тупых углов. Так же, как невозможно и существование второго прямого угла. В этом случае нарушается тождество суммы углов треугольника, которая всегда равна 180 градусам.
Гипотенуза
Перейдем непосредственно к гипотенузе треугольника. Гипотенуза – это наибольшая сторона треугольника. Гипотенуза всегда больше любого из катетов, но при этом всегда меньше суммы катетов. Это следствие из теоремы неравенства треугольника.
Теорема гласит: в треугольнике ни одна из сторон не может больше суммы двух других. Существует и вторая формулировка или вторая часть теоремы: в треугольнике напротив большей стороны лежит больший угол и наоборот.
Рис. 2. Прямоугольный треугольник.
Прямоугольный треугольник.
В прямоугольном треугольнике большим углом является прямой угол, так как второго прямого угла или тупого угла быть не может по уже названным причинам. Значит напротив прямого угла всегда лежит большая сторона.
Кажется непонятным, почему именно прямоугольный треугольник заслужил отдельное наименование каждой из сторон. На самом деле, в равнобедренном треугольнике стороны так же носят свои названия: боковые стороны и основание. Но именно за катеты и гипотенузы учителя особенно любят ставить двойки. Почему? С одной стороны это дань памяти древним грекам, изобретателям математики. Именно они изучали прямоугольные треугольники и наряду с этими знаниями оставили целый пласт информации, на котором строится современная наука. С другой же стороны существование этих названий значительно упрощает формулировки теорем и тригонометрических тождеств.
Теорема Пифагора
Если учитель спрашивает о формуле гипотенузы прямоугольного треугольника, значит, с вероятностью 90 %, он имеет в виду теорему Пифагора.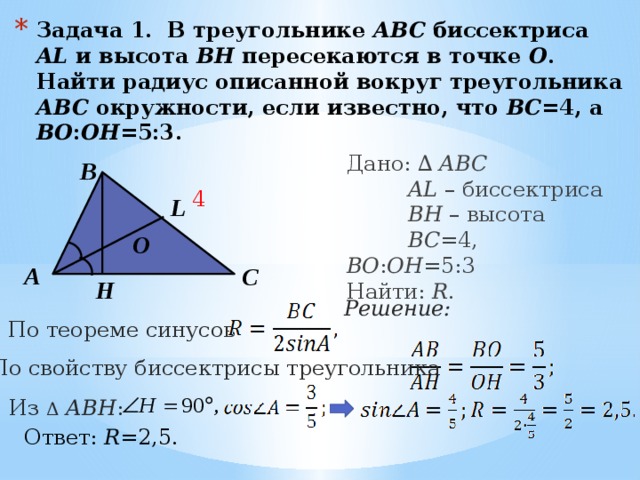 2$ – где с — гипотенуза, a и b — катеты прямоугольного треугольника.
2$ – где с — гипотенуза, a и b — катеты прямоугольного треугольника.
Что мы узнали?
Мы поговорили о том, что такое прямоугольный треугольник. Узнали, зачем вообще придумали названия катетов и гипотенузы. Выяснили некоторые свойства гипотенузы и привели формулу длины гипотенузы треугольника через теорему Пифагора.
Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 213.
Медиана средней стороны разностороннего треугольника с учетом трех сторон Калькулятор
✖Более длинная сторона разностороннего треугольника равна длине большей стороны из трех сторон. Другими словами, более длинная сторона неравностороннего треугольника — это сторона, противоположная большему углу.ⓘ Более длинная сторона несимметричного треугольника [S Longer ] | )Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman) Миля (исследование США) МиллиметрМиллион светового годаГвоздь (ткань)НанометрМорская лига (внутренняя)Морская лига ВеликобританииМорская миля (международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланковая длинаТочкаПолюсКварталТростник (L ong)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Меньшая сторона несимметричного треугольника – это длина меньшей стороны из трех сторон. | (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile ( US Survey) МиллиметрМиллион светового годаГвоздь (ткань)НанометрМорская лига (внутренняя)Морская лига ВеликобританииМорская миля (международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (длинный) RodRoman ActusВеревкаРусский АрчинПролет (Ткань)Радиус СолнцаТераметрTwipVara CastellanaVara ConuqueraVara De TareaЯрдYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Средняя сторона несимметричного треугольника — это длина второй более длинной стороны из трех сторон. | +10% -10% |
✖ Медиана средней стороны разностороннего треугольника представляет собой отрезок, соединяющий среднюю точку средней стороны с противоположной ему вершиной. | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Медиана средней стороны разностороннего треугольника по трем сторонам Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Длинная сторона разностороннего треугольника: 11 метров —> 11 метров Преобразование не требуется
Более короткая сторона разностороннего треугольника: 10 метров — -> 10 метров Преобразование не требуется
Средняя сторона разностороннего треугольника: 10 метров —> 10 метров Преобразование не требуется
ШАГ 2: Вычислите формулу
ШАГ 3: Преобразуйте результат в единицу измерения
9. 24662100445346 Нет Метр Требуется преобразование 92))/2
24662100445346 Нет Метр Требуется преобразование 92))/2
Медиана лестничного треугольника и ее значение
В разностороннем треугольнике расстояние от определенного угла до середины стороны, которая прямо противоположна этому углу, называется медианой разностороннего треугольника с этой стороны. Любой треугольник, даже если он не является разносторонним, имеет три медианы, а для разносторонних треугольников все эти медианы имеют разную длину. Все медианы треугольника сходятся в одной точке, которая называется центром треугольника.
Что такое Разносторонний треугольник?
Треугольник, у которого все стороны различны по длине, называется разносторонним треугольником. В основном треугольники делятся на три на основе длин сторон. Если все стороны равны по длине, то такой треугольник называется равносторонним. Если только две стороны равны по длине, то такой треугольник называется равнобедренным.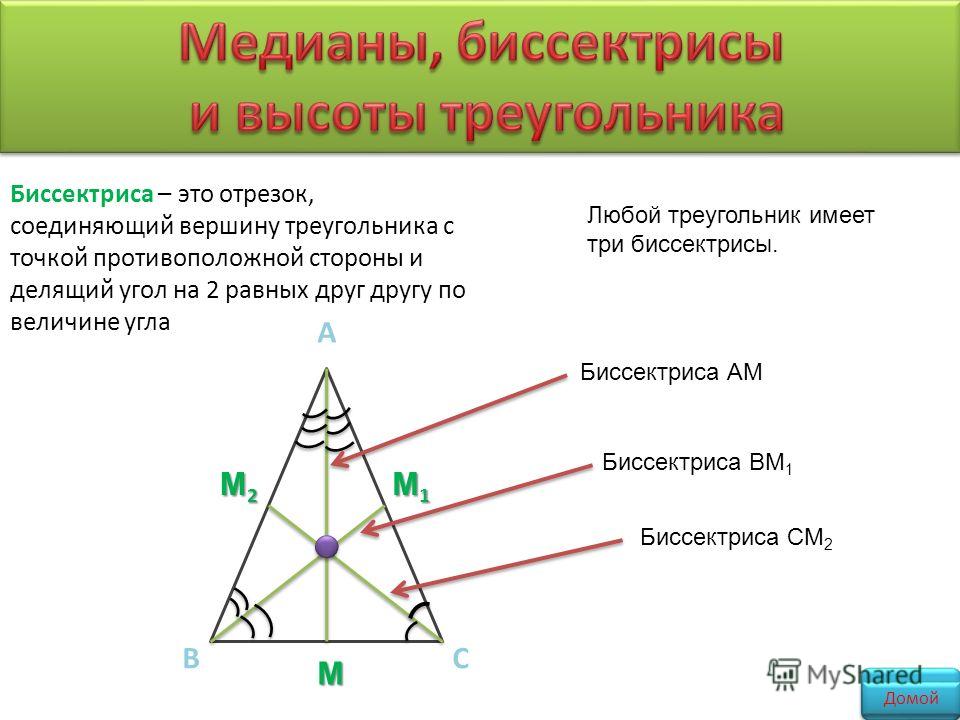 Если нет равных сторон или все стороны различны по длине, то такой треугольник называется разносторонним. Случаи аналогичны и с точки зрения углов. То есть в равносторонних треугольниках все три угла равны. В равнобедренных треугольниках хотя бы два угла равны. И потом, у разносторонних треугольников все три угла различны.
92))/2 для расчета медианы на средней стороне разностороннего треугольника, медианы на средней стороне разностороннего треугольника с учетом формулы трех сторон определяется как расстояние между средним углом угла и серединой средней стороны разностороннего треугольника, найденное по формуле используя все длины сторон. Медиана средней стороны разностороннего треугольника обозначена символом M Medium .
Если нет равных сторон или все стороны различны по длине, то такой треугольник называется разносторонним. Случаи аналогичны и с точки зрения углов. То есть в равносторонних треугольниках все три угла равны. В равнобедренных треугольниках хотя бы два угла равны. И потом, у разносторонних треугольников все три угла различны.
92))/2 для расчета медианы на средней стороне разностороннего треугольника, медианы на средней стороне разностороннего треугольника с учетом формулы трех сторон определяется как расстояние между средним углом угла и серединой средней стороны разностороннего треугольника, найденное по формуле используя все длины сторон. Медиана средней стороны разностороннего треугольника обозначена символом M Medium .
Как рассчитать медиану средней стороны разностороннего треугольника по трем сторонам с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для расчета медианы средней стороны разностороннего треугольника с учетом трех сторон, введите Длинная сторона разностороннего треугольника 92))/2 . Более длинная сторона несимметричного треугольника равна длине большей стороны из трех сторон. Другими словами, более длинная сторона несимметричного треугольника — это сторона, противоположная большему углу. Более короткая сторона несимметричного треугольника — это длина более короткой стороны из трех сторон. Другими словами, более короткая сторона разностороннего треугольника — это сторона, противоположная меньшему углу, а средняя сторона разностороннего треугольника — это длина второй более длинной стороны из трех сторон. Другими словами, средняя сторона разностороннего треугольника — это сторона, противоположная второму большему углу. 92))/2 . Чтобы вычислить медиану на средней стороне разностороннего треугольника с учетом трех сторон, вам потребуется длинная сторона разностороннего треугольника (S более длинная ) , более короткая сторона разностороннего треугольника (S более короткая ) и средняя сторона разностороннего треугольника ( S Средний ) .
Более длинная сторона несимметричного треугольника равна длине большей стороны из трех сторон. Другими словами, более длинная сторона несимметричного треугольника — это сторона, противоположная большему углу. Более короткая сторона несимметричного треугольника — это длина более короткой стороны из трех сторон. Другими словами, более короткая сторона разностороннего треугольника — это сторона, противоположная меньшему углу, а средняя сторона разностороннего треугольника — это длина второй более длинной стороны из трех сторон. Другими словами, средняя сторона разностороннего треугольника — это сторона, противоположная второму большему углу. 92))/2 . Чтобы вычислить медиану на средней стороне разностороннего треугольника с учетом трех сторон, вам потребуется длинная сторона разностороннего треугольника (S более длинная ) , более короткая сторона разностороннего треугольника (S более короткая ) и средняя сторона разностороннего треугольника ( S Средний ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для более длинной стороны разностороннего треугольника, более короткой стороны разностороннего треугольника и средней стороны разностороннего треугольника и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода. 92)+(2*Более длинная сторона разностороннего треугольника*Короткая сторона разностороннего треугольника*cos(Средний угол разностороннего треугольника)))/2
С помощью нашего инструмента вам нужно ввести соответствующее значение для более длинной стороны разностороннего треугольника, более короткой стороны разностороннего треугольника и средней стороны разностороннего треугольника и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода. 92)+(2*Более длинная сторона разностороннего треугольника*Короткая сторона разностороннего треугольника*cos(Средний угол разностороннего треугольника)))/2
Share
Скопировано!
Математическая задача: Центроид треугольника — вопрос № 43261, алгебра
В треугольнике ABC заданы длины его медиан tc = 9, ta = 6. Пусть T пересечение медиан (центроид треугольника), а точка S — центр стороны BC. Величина угла CTS составляет 60°.
Рассчитайте длину стороны ВС с точностью до 2 знаков после запятой.
Правильный ответ:
a = 10,58 смПошаговое объяснение:
tc=9 см ta=6 см CTS=60°→ рад=60°⋅ 180π=60°⋅ 1803,14159272= =π/3 CT=1+22⋅ tc=1+22⋅ 9=6 см ST=1+21⋅ ta=1+21⋅ 6=2 см x2=CT2+ST2−2⋅ CT⋅ ST⋅ cosCTS x=CT2+ST2−2⋅ CT⋅ ST⋅ cos(CTS)
=62+22−2⋅ 6⋅ 2⋅ cos1,0472
=2 7
см≐5,2915 см≐5,2915 =2⋅ x=2⋅ 5,2915=4 7
=10,58 см
Нашли ошибку или неточность? Не стесняйтесь
напишите нам . Благодарю вас!
Благодарю вас!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Правило косинуса использует тригонометрический калькулятор треугольников SAS.
См. также наш калькулятор тригонометрического треугольника.
Для решения данной словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- планиметрика
- right triangle
- triangle
- The Law of Cosines
- The Law of Sines
- goniometry and trigonometry
- sine
- cosine
Grade of the word problem:
- high school
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1
- Координаты центроида
Пусть A = [3, 2, 0], B = [1, -2, 4] и C = [1, 1, 1] — 3 точки в пространстве. Вычислите координаты центроида △ABC (пересечение медиан).
Вычислите координаты центроида △ABC (пересечение медиан). - Вычислить 4425
В треугольнике ABC с центром тяжести T, b = 7см, медиана к c: tc = 9см, угол АТС равен 112 градусов. Рассчитайте длину линии ta. - Периметр 6002
В треугольнике ABC сторона c = 5 см и медианы ta = 6 см (медиана стороны a), tb = 4,5 см (медиана стороны b). Найдите периметр треугольника АВТ (Т = центр тяжести). - Медиана
В треугольнике ABC даны сторона a=10 см и медиана стороны a: ta=13 см, а угол gamma 90°. Вычислите длину медианы до стороны b (tb). - Треугольник в квадрате
В квадрате ABCD со стороной a = 6 см точка E — центр стороны AB, а точка F — центр стороны BC. Вычислить величину всех углов треугольника DEF и длины его сторон. - Треугольники
Даны два подобных треугольника, KLM и ABC. Вычислите длины остальных сторон треугольника KLM. Если длины сторон равны a = 7 b = 5,6 c = 4,9 k = 5 - Треугольник KLB
Дан равносторонний треугольник ABC. Из точки L, середины стороны ВС треугольника, проведен перпендикуляр к стороне АВ. Точкой пересечения перпендикуляра и стороны AB является точка K. Сколько процентов площади треугольника ABC
Из точки L, середины стороны ВС треугольника, проведен перпендикуляр к стороне АВ. Точкой пересечения перпендикуляра и стороны AB является точка K. Сколько процентов площади треугольника ABC - Отношение площадей треугольников
В равностороннем треугольнике ABC точка T является его центром тяжести, точка R является изображение точки T в осевой симметрии вдоль линии AB, а точка N — изображение точки T в осевой симметрии вдоль линии BC. Найдите отношение площадей - MO Z7–I–6 2021
В треугольнике ABC точка D лежит на стороне AC, а точка E на стороне BC. Размеры углов ABD, BAE, CAE и CBD равны 30°, 60°, 20° и 30° соответственно. Найдите величину угла AED. - Прямоугольный треугольник
В прямоугольном треугольнике ABC с прямым углом C известны длины сторон AC = 9 см и BC = 7 см. Вычислите длину оставшейся стороны треугольника и величину всех углов. - Окружность вписанная
Имеется треугольник ABC и вписанная в него окружность радиусом 15. Точка T является точкой касания вписанной окружности со стороной BC. Чему равна площадь треугольника ABC, если | БТ | = 25 а | ТК | = 26?
Точка T является точкой касания вписанной окружности со стороной BC. Чему равна площадь треугольника ABC, если | БТ | = 25 а | ТК | = 26? - Треугольник ABC
В треугольнике ABC со стороной BC длиной 2 см. Точка К является средней точкой АВ. Точки L и M делят сторону АС на три равные линии. KLM – равнобедренный треугольник с прямым углом в точке K. Определить длины сторон AB, AC треугольника A - Диагонали трапеции
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Биссектрисы
Как показано, в △ ABC, ∠C = 90°, AD делит пополам ∠BAC, DE⊥AB и E, BE = 2, BC = 6. Найдите периметр треугольника △ BDE. - Внутренние углы
Внутренние углы треугольника равны 30°, 45° и 105°, а его самая длинная сторона равна 10 см. Вычислите длину наименьшей стороны и запишите результат в см с точностью до двух знаков после запятой. - Внутренние углы
ABCD — это равнобедренная трапеция, на которой выполняются: |AB| = 2 |ВС| = 2 |CD| = 2 |DA|: На стороне BC есть точка K такая, что |BK| = 2 |KC|, на его стороне CD есть точка L такая, что |CL| = 2 |LD|, а на его стороне DA точка M такова, что | ДМ | = 2 |МА|. Дет
Дет - Параллелограмм 65334
В параллелограмме сумма длин сторон a+b = 234. Угол между сторонами a и b равен 60°. Размер диагонали относительно заданного угла 60° равен u=162. Вычислите стороны параллелограмма, его периметр и площадь.
Формула Герона для площади треугольника с 3 сторонами
Как вычислить площадь треугольника с 3 известными сторонами
Чтобы вычислить площадь треугольника с тремя известными сторонами, используйте формулу Герона. Формула Герона: Площадь = √(s(s-a)(s-b)(s-c)), где a , b и c являются длинами трех сторон треугольника, а s = ( a + b + c ) 1 1 390 3 ÷ 2. Просто найдите значения 4,3 ÷ 2. a , b и c и подставьте их в формулу площади.
Шаги, чтобы найти площадь треугольника с 3 сторонами (a, b и c):
- Выработка s = (a + b + c) ÷ 2.
- Подставьте значения s, a, b и c в формулу Площадь = √( s(s-a)(s-b)(s-c) ).

Например, найдите площадь треугольника со сторонами 8 м, 3 м и 9 м.
Неважно, какие стороны а, b или с.
Положим a = 8, b = 3 и c = 9.
Первым делом необходимо отработать полупериметр, с. Полупериметр — это просто половина периметра. Найдем полупериметр, сложив длины сторон и разделив на 2.
8 + 3 + 9 = 20 и 20 ÷ 2 = 10. Следовательно, полупериметр равен 10.
с = 10.
Второй шаг — подставить значения s = 10, a = 8, b = 3 и c = 9 в формулу Герона.
Площадь = √(s(s-a)(s-b)(s-c)) становится площадью = √(10(10-8)(10-3)(10-9)).
Это становится площадью = √(10 × 2 × 7 × 1), что упрощается до площади = √140.
Наконец, квадратный корень из 140 вычисляется с помощью калькулятора. Площадь = 11,8 м 2 .
Что такое формула Герона
Формула Герона: Площадь = √(s(s-a)(s-b)(s-c)), где a, b и c — три длины сторон треугольника, а s = (a + b + c) ÷ 2. Это может быть используется для вычисления площади любого треугольника, если известны длины всех трех сторон. Формула названа в честь Герона Александрийского (10-70 гг. н.э.), открывшего ее.
Формула названа в честь Герона Александрийского (10-70 гг. н.э.), открывшего ее.
Зачем использовать Формулу Герона
Формула Герона позволяет вычислить площадь треугольника, если известны все три его стороны. Преимущество формулы Герона в том, что не нужно знать другие длины или углы треугольника. Пока известны длины трех сторон, формула Герона работает для всех треугольников.
Формула Герона для равнобедренного треугольника
Формула Герона для любого треугольника: Площадь = √( s(s-a)(s-b)(s-c) ). Для равнобедренного треугольника две стороны имеют одинаковую длину, и мы можем сказать, что сторона с = стороне а. Тогда формула Герона для равнобедренного треугольника принимает вид Area = √( s(s-a) 2 (s-b) ), где a — длина двух равных сторон, b — длина другой стороны и s = (2a + b) ÷ 2,
Например, вот формула Герона для равнобедренного треугольника со сторонами 2 см, 6 см и 6 см.
Мы можем использовать обычную форму формулы Герона, чтобы найти площадь. Полупериметр — это сумма сторон деленная на 2.
Полупериметр — это сумма сторон деленная на 2.
2 + 6 + 6 = 14 и 14 ÷ 2 = 7. Следовательно, s = 7.
Мы можем использовать Площадь = √s(s-a)(s-b)(s-c), которая становится Площадью = √7(7-2)(7-6)(7-6). Это становится площадью = √35, что равно 5,9.2 см 2 .
Вот пример использования равнобедренной версии формулы Герона: Площадь = √s(s-a) 2 (s-b). Здесь a = 6 и b = 2. Полупериметр по-прежнему равен 7.
Площадь = √s(s-a) 2 (s-b) становится площадью = √7(7-6) 2 (7-2).
Получается Площадь = √35, что равно 5,92 см 2 . Это тот же ответ, что и раньше, и можно использовать любой метод.
Как вычислить площадь треугольника с 3 равными сторонами
Площадь треугольника с 3 равными сторонами можно рассчитать по формуле Площадь = √3 / 4 a 2 , где а — длина одной из сторон. Альтернативно, формула Герона для равностороннего треугольника: Площадь = √(s(s-a) 3 ), где a — длина стороны, а s = 3a / 2 .
Равносторонний треугольник – это треугольник с 3 сторонами одинаковой длины. Сначала рассмотрим нахождение площади равностороннего треугольника по формуле Герона.
Формула Герона для площади равностороннего треугольника: Площадь = √(s(s-a) 3 ), где a — длина стороны.
В приведенном ниже примере a = 8 метров.
Для треугольника с 3 равными сторонами полупериметр равен просто s = 3a / 2 . Здесь при a = 8, s = 12.
Площадь = √(s(s-a) 3 ) становится Площадью = √(12(12-8) 3 ), что становится Площадью = √768.
Площадь 27,7 м 2 .
Вот еще один способ вычисления площади равностороннего треугольника.
Формула площади равностороннего треугольника: Площадь = √3 / 4 a 2 , где а — длина одной из сторон.
В этом примере а = 8 метров.
Площадь = √3 / 4 a 2 становится Площадь = √3 / 4 × 8 2 .


 Другими словами, более короткая сторона разностороннего треугольника — это сторона, противоположная меньшему углу.ⓘ Более короткая сторона разностороннего треугольника [S Shorter ]
Другими словами, более короткая сторона разностороннего треугольника — это сторона, противоположная меньшему углу.ⓘ Более короткая сторона разностороннего треугольника [S Shorter ]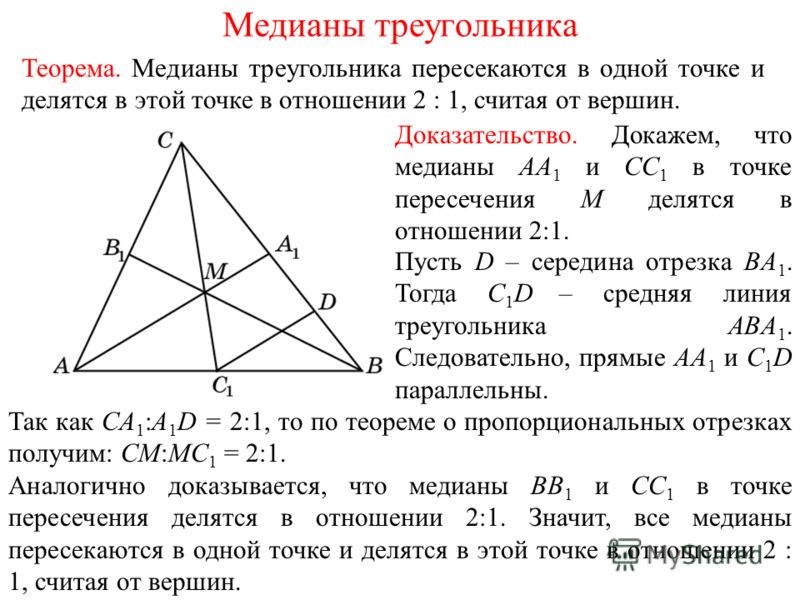 Другими словами, средняя сторона неравностороннего треугольника — это сторона, противоположная второму большему углу. )Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman) Миля (исследование США) МиллиметрМиллион светового годаГвоздь (ткань)НанометрМорская лига (внутренняя)Морская лига ВеликобританииМорская миля (международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter
Другими словами, средняя сторона неравностороннего треугольника — это сторона, противоположная второму большему углу. )Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman) Миля (исследование США) МиллиметрМиллион светового годаГвоздь (ткань)НанометрМорская лига (внутренняя)Морская лига ВеликобританииМорская миля (международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter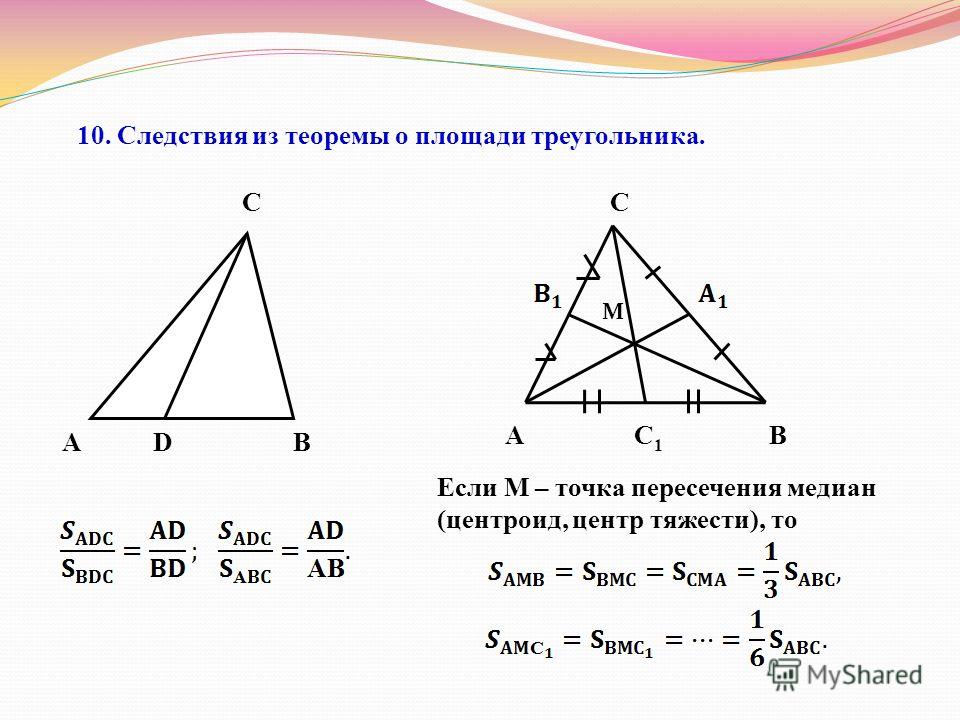 ⓘ Медиана средней стороны разностороннего треугольника с учетом трех сторон [M Medium ]
ⓘ Медиана средней стороны разностороннего треугольника с учетом трех сторон [M Medium ]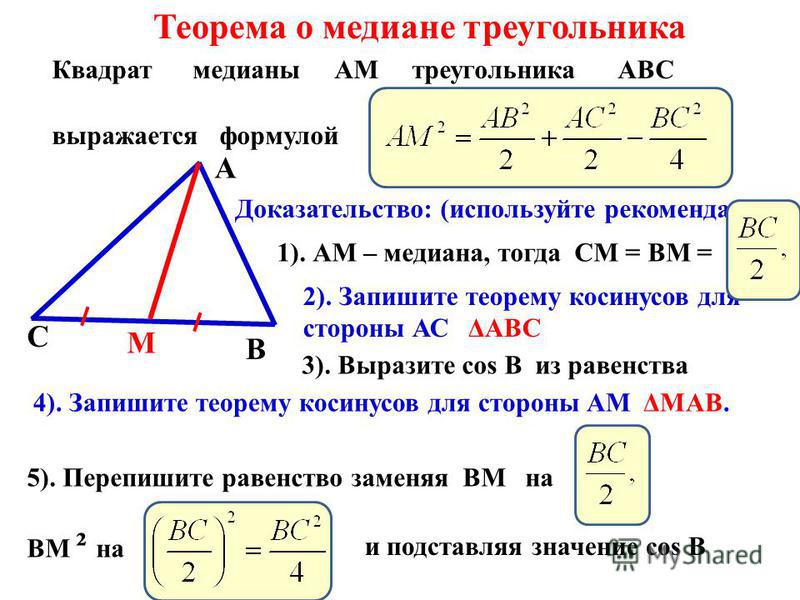 Вычислите координаты центроида △ABC (пересечение медиан).
Вычислите координаты центроида △ABC (пересечение медиан). Из точки L, середины стороны ВС треугольника, проведен перпендикуляр к стороне АВ. Точкой пересечения перпендикуляра и стороны AB является точка K. Сколько процентов площади треугольника ABC
Из точки L, середины стороны ВС треугольника, проведен перпендикуляр к стороне АВ. Точкой пересечения перпендикуляра и стороны AB является точка K. Сколько процентов площади треугольника ABC Точка T является точкой касания вписанной окружности со стороной BC. Чему равна площадь треугольника ABC, если | БТ | = 25 а | ТК | = 26?
Точка T является точкой касания вписанной окружности со стороной BC. Чему равна площадь треугольника ABC, если | БТ | = 25 а | ТК | = 26? Дет
Дет