Непрерывность
Рассмотрим функцию f(x)=x2+3x+1. Чему равен её предел при x→x0? С помощью арифметики пределов легко показать, что он равен x20+3×0+1, то есть значению функции f в точке x0. Мы обсуждали (см. пример 12 из лекции 10), что это не всегда так работает. Однако, случай, когда работает, очень важен, и имеет специальное название.
13.1Непрерывность функции в точке
13.1.1Определение непрерывности
Определение 1. Пусть функция f определена в некоторой окрестности точки x0 (включая саму точку x0). Говорят, что f непрерывна в точке x0, если предел f(x) при x→x0 равен значению функции в этой точке:
limx→x0f(x)=f(x0).(13.1)
Как видно из этого определения, чтобы функция была непрерывной в некоторой
точке, она должна как минимум быть определена в этой точке и иметь в ней предел.
Если какое-то из этих условий нарушается, функция не является непрерывной
автоматически. Наконец, может статься, что и значение функции в точке x0
есть, и предел есть, но они не равны друг другу.
Условие (13.1) можно переписать в кванторах:
∀ε>0 ∃δ>0 ∀x:0<|x−x0|<δ⇒|f(x)−f(x0)|<ε.
∀ε>0 ∃δ>0 ∀x:0<|x−x0|<δ⇒|f(x)−f(x0)|<ε.
В условии на x как обычно в определении предела записана проколотая окрестность. Но что будет, если x=x0? В этом случае условие после знака импликации превращается в |f(x0)−f(x0)|<ε. В левой части стоит ноль, поэтому это условие всегда выполнено. Таким образом, условие непрерывности можно записать таким образом:
∀ε>0 ∃δ>0 ∀x:|x−x0|<δ⇒|f(x)−f(x0)|<ε.(13.2)
∀ε>0 ∃δ>0 ∀x:|x−x0|<δ⇒⇒|f(x)−f(x0)|<ε.(13.2)
Упражнение 1. Докажите, что функция f непрерывна в точке x0 тогда и только тогда,
когда выполняется следующее утверждение: для всякой последовательности
{xn}, стремящейся к x0, f(xn) стремится к f(x0). Иными
словами, в определении предела по Гейне в этом случае можно убрать
требование xn≠x0 для всех n.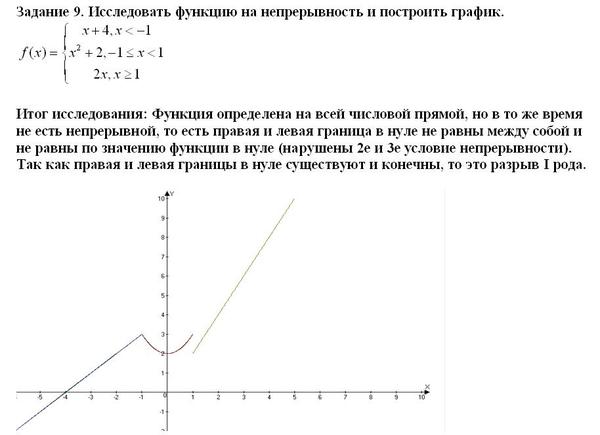
13.1.2Односторонняя непрерывность
Чтобы говорить о непрерывности функции в точке, нам нужно, чтобы функция была определена в окрестности этой точки. Но часто бывает, что функции определены на каких-то отрезках или лучах (например, x≥0). В этом случае определение 1 неприменимо для граничных точек области определения функции. Если мы всё-таки хотим сказать, что функция непрерывна в такой точке (а мы скоро захотим), нам нужно будет использовать определение односторонней непрерывности.
Определение 2. Пусть функция f определена в некоторой правой полуокрестности точки x0, включая саму точку x0 (то есть на некотором полуинтервале [x0,x0+δ)), δ>0. Говорят, что f непрерывна справа в точке x0, если предел f(x) при x→x+0 равен значению функции в этой точке:
limx→x+0f(x)=f(x0).
Аналогично определяется непрерывность слева.
Определение 3. Пусть A⊂D(f) — некоторое подмножество области определения функции. Если функция f непрерывна для всякого x∈A, мы будем говорить, что f непрерывна на A. Если A — отрезок или луч, мы как правило будем
требовать лишь соответствующую одностороннюю непрерывность на его концах.
Если функция f непрерывна для всякого x∈A, мы будем говорить, что f непрерывна на A. Если A — отрезок или луч, мы как правило будем
требовать лишь соответствующую одностороннюю непрерывность на его концах.
13.1.3Какие функции непрерывны
Неформально говоря, условие непрерывности означает, что если x не сильно
отличается от x0, значение функции f(x) не сильно отличается от f(x0).
Это очень важное условие с практической точки зрения: как правило, мы не знаем
точных значений никаких величин. Если бы интересующие нас функции не были
непрерывными, мы бы мало что могли сказать о их значениях. Пусть мы хотим
вычислить f(x0), но знаем величину x0 лишь с какой-то точностью. Иными
словами, мы знаем на самом деле величину x1, и знаем, что расстояние от неё
до x0 маленькое. Если f не является непрерывной в точке x0, посчитав
её значение в точке x1, мы бы не получили никакой информации о значениях этой
же функции в точке x0, сколь бы близким x1 ни было к x0.
Например, все вычисления на компьютере с вещественными числами происходят с некоторыми погрешностями: компьютер не может запомнить бесконечное число цифр после запятой, и постоянно прибегает к округлениям. Если бы не непрерывность, компьютерные вычисления были бы в основном бессмысленными.
Поэтому очень важно понимать, какие функции являются непрерывными, и в каких случаях непрерывность может нарушаться. К счастью, те функции, которые нас интересуют, часто являются непрерывными на своей области определения.
Утверждение 1. Пусть функции f и g непрерывны в точке x0. Тогда
- функция h(x)=f(x)+g(x) непрерывна в x0;
- функция u(x)=f(x)g(x) непрерывна в x0;
- функция v(x)=f(x)g(x) непрерывна в x0 если g(x0)≠0.
Доказательство. Это утверждение является мгновенным следствием из арифметики пределов. Например, пусть h(x)=f(x)+g(x). Докажем, что h непрерывна в x0.
limx→x0h(x)=limx→x0(f(x)+g(x))=limx→x0f(x)+limx→x0g(x)=f(x0)+g(x0)=h(x0).
limx→x0h(x)=limx→x0(f(x)+g(x))==limx→x0f(x)+limx→x0g(x)==f(x0)+g(x0)=h(x0).
Мы применили арифметику пределов (третье равенство) и условие непрерывности f и g (предпоследнее равенство).
Остальные утверждения доказываются аналогично.∎
Следствие. Из утверждения 1 мгновенно следует, что
- Многочлены, то есть функции вида
P(x)=a0+a1x+a2x2+…+anxn
непрерывны на всём множестве вещественных чисел. - Рациональные функции, то есть функции вида
R(x)=P(x)Q(x),
где P(x) и Q(x) — многочлены, являются непрерывными на всей области определения (то есть при таких x, при которых знаменатель не обнуляется).
На семинарах мы также докажем непрерывность синуса, косинуса, тангенса,
экспоненты, логарифма, квадратного корня на всей области определения. Ниже мы
докажем ещё одну важную теорему — о непрерывности композиции — но пока давайте
поговорим, что бывает, когда непрерывность нарушается.
Определение 4. Пусть функция f определена в некоторой проколотой окрестности точки x0, но не является непрерывной в x0. Тогда мы скажем, что она терпит разрыв в этой точке.
Какими бывают разрывы? Тут принята такая немножко условия классификация.
13.2.1Разрывы первого рода
Определение 5. Пусть функция f не является непрерывной в точке x0, но существуют
односторонние пределы limx→x+0f(x) и limx→x−0f(x).
Тогда разрыв в точке x0 называется
Если односторонние пределы существуют, они могут совпадать, а могут не
совпадать. Если они совпадают (и равны какому-то числу b), существует предел
limx→x0f(x) и тоже равен числу b. (См.
упражнение 3 из лекции 10.)
Поскольку функция не является непрерывной в x0, либо f(x0) не определено,
либо f(x0)≠b. Такой тип разрывов называется устранимым: достаточно
«отредактировать» (доопределить или переопределить) значение функции f в
единственной точке x0, чтобы она стала непрерывной, то есть разрыв был бы
устранён.
Если односторонние пределы существуют, но различны, такой разрыв называется скачком.
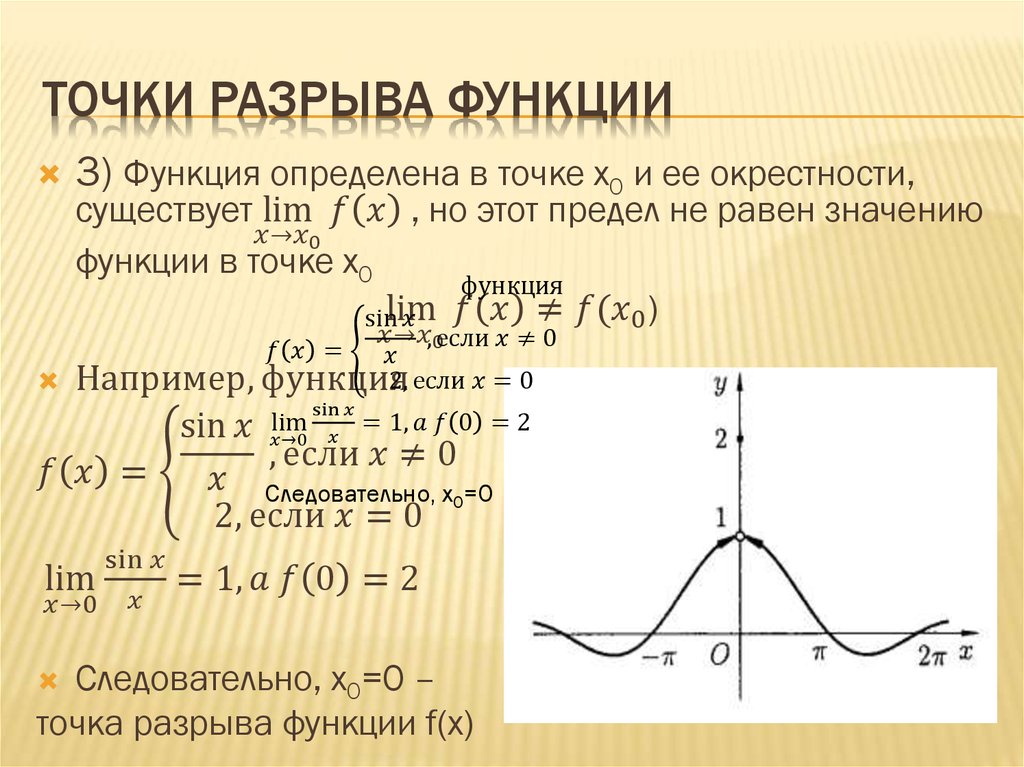
Пример 1. Рассмотрим функцию
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x,x<−1;−x,−1≤x<2;5,x=2;x2−6,x>2.
Она является непрерывной во всех точках, кроме −1 и 2, в точке −1 у неё разрыв типа «скачок», а в точке 2 — устранимый разрыв.
13.2.2Разрывы второго рода
Любые разрывы, не являющиеся разрывами первого рода, называются разрывами второго рода (неожиданно, правда?)
Какими они бывают?
Может статься, что предел f(x) при x→x0 не существует, но при этом равен бесконечности (вы ведь помните, что когда предел равен бесконечности, он не существует?). Такие разрывы мы будем называть полюсами.
Всё остальное будем называть существенными разрывами. (Тут терминология
может быть не очень однозначной и разные источники могут вкладывать несколько
разный смысл. Например, можно считать полюсом любой разрыв с
вертикальной асимптотой. Но мы будем придерживаться этих определений.)
Например, можно считать полюсом любой разрыв с
вертикальной асимптотой. Но мы будем придерживаться этих определений.)
Рис. 13.1: Функция y=e1/x имеет существенный разрыв в точке x=0.
Пример 3. Рассмотрим функцию f(x)=sin(π/x). Как обсуждалось в примере 14 из лекции 10, у неё нет предела при x→0, поскольку в любой окрестности нуля она может принимать различные значения (например, 0, 1 и −1). Это означает, что в нуле она терпит разрыв. Поскольку функция является ограниченной, она не может стремиться к бесконечности, и значит это существенный разрыв (хотя, пожалуй, он и не похож на то, что хочется себе представить, когда слышишь слово «разрыв»).
Рис. 13.2: Функция f(x)=sinπ/x имеет существенный разрыв в точке x=0.
13.3Непрерывность композиции
13.3.1Сложные функции
Мы часто сталкиваемся функциями, заданными выражениями вида h(x)=√x2+1.
Определение 6. Функция h(x)=g(f(x)) называется композицией или суперпозицией функций f и g, или сложной функцией. Часто пишут так: h(x)=(g∘f)(x). Функции в композиции применяются «справа налево»: сначала x подставляется в f, потом результат подставляется в g.
13.3.2Предел сложной функции
Мы бы хотели доказать утвердение, кратко формулируемое как «композиция
непрерывных функций непрерывна». Это позволит нам доказывать непрерывность
разнообразных функций, заданных формулами. Чтобы это сделать, нам сперва
придётся доказать теорему о пределе сложной функции.
Вопрос 1. Пусть
limx→x0f(x)=y0(13.3)
и
limy→y0g(y)=b.(13.4)
Верно ли, что
limx→x0g(f(x))=b?(13.5)
Хочется ответить утвердительно. Действительно, если x→x0, согласно первому пределу (13.3), f(x) становится близок к y0. В третьем пределе (13.5) мы подставляем g именно f(x), а из второго предела следует, что если аргумент функции g близок к y0, то значение g близко к b. Казалось бы, что может пойти не так?
Пример 4. Пусть
g(x)={1x=0,3x≠0
и f(x)=0 для всех x. Тогда
limx→2f(x)=0
и
limy→0g(y)=3.
Рассмотрим предел
limx→2g(f(x)).
Поскольку g(f(x))=g(0)=1 при всех x, этот предел равен 1 и не равен
3. Таким образом, утверждение (13. 5) в этом случае неверно.
5) в этом случае неверно.
Вопрос 2. В чём проблема? Где мы ошиблись в неформальном рассуждении?
Узнать ответ.
Верный ответ. Утверждение (13.4) говорит, что g(y) становится близок к b, если y близок к y0, но не равен y0. В нашем случае f(y) равен y0=0 во всех точках. Вместе с нарушением непрерывности функции g(y), это приводит к проблеме.
Теперь сформулируем правильное утверждение.
Теорема 1. Пусть
limx→x0f(x)=y0(13.6)
и
limy→y0g(y)=g(y0),(13.7)
то есть функция g(y) непрерывна в точке y0.
Тогда
limx→x0g(f(x))=g(limx→x0f(x))=g(y0).(13.8)
limx→x0g(f(x))=g(limx→x0f(x))==g(y0).(13.8)
Доказательство. Запишем всё в кванторах.
Нам дано. Первый предел:
∀ε1>0 ∃δ1=δ1(ε1)>0 ∀x:0<|x−x0|<δ1⇒|f(x)−y0|<ε1. (13.9)
(13.9)
∀ε1>0 ∃δ1=δ1(ε1)>0 ∀x:0<|x−x0|<δ1⇒⇒|f(x)−y0|<ε1.(13.9)
Второй предел:
∀ε2>0 ∃δ2=δ2(ε2)>0 ∀y:|y−y0|<δ2⇒|g(y)−g(y0)|<ε2.(13.10)
∀ε2>0 ∃δ2=δ2(ε2)>0 ∀y:|y−y0|<δ2⇒⇒|g(y)−g(y0)|<ε2.(13.10)
Здесь в определении предела мы убрали требование проколотости окрестности в силу непрерывности функции g в точке y0 (см. (13.2)).
Надо доказать.
∀ε>0 ∃δ=δ(ε)>0 ∀x:0<|x−x0|<δ⇒|g(f(x))−g(y0)|<ε.
∀ε>0 ∃δ=δ(ε)>0 ∀x:0<|x−x0|<δ⇒|g(f(x))−g(y0)|<ε.
Выбор δ(ε). Согласно (13.10), мы можем добиться, чтобы g(y) был ε-близок к g(y0), если потребуем, чтобы y был δ2(ε)-близок к y0. Чтобы значение f(x) было δ2(ε)-близким к y0, достаточно в (13.9) положить ε1=δ2(ε) и потребовать, чтобы x лежал в соответствующей δ2-окрестности точки x0. В этом случае |f(x)−y0|<ε1=δ2(ε) и мы победили.
Итак, искомая δ задаётся следующим образом:
δ(ε):=δ1(δ2(ε)).
Как показано выше, эта δ сработает, и теорема доказана.∎
Следствие 1. Пусть функция f непрерывна в точке x0, а функция g непрерывна в точке f(x0). Тогда функция h(x)=g(f(x)) непрерывна в точке x0.
Доказательство. Предел
limx→x0h(x)=limx→x0g(f(x))
удовлетворяет условию теоремы. Значит,
limx→x0g(f(x))=g(limx→x0f(x))=g(f(x0))=h(x0),(13.11)
limx→x0g(f(x))=g(limx→x0f(x))==g(f(x0))=h(x0),(13.11)
то есть h(x) непрерывна в точке x0.∎
Пример 5. Докажем, что функция f(x)=sin(ex2+cosx) непрерывна на всём R. Действительно, cosx и x2 непрерывны, а значит их сумма непрерывна. Экспонента непрерывна и её аргумент непрерывен, значит, аргумент синуса непрерывен. И синус непрерывен. Значит, и вся функция непрерывна.
Вопрос 3. В скольких точках функция f(x)=1sinπ/x терпит разрывы?
Ни в одной — это композиция непрерывных функций!
Неверный ответ. Разве π/x всюду непрерывна?
Разве π/x всюду непрерывна?
В одной точке.
Неверный ответ. Думаете, только в нуле? В этом выражении больше, чем один знаменатель.
В бесконечном количестве точек.
Верный ответ. Верно! Во-первых, в точке x=0. Во-вторых, во всех точках, где обнуляется sinπ/x, то есть во всех x=1/k, k∈Z.
Упражнение 2. Докажите следующее утверждение. Пусть в теореме 1 условие непрерывности функции g в точке y0 не выполняется, но зато выполняется другое условие: существует такая проколотая окрестность точки x0, что в этой окрестности f(x)≠y0. Тогда (13.8) всё равно выполняется.
13.4Заключение
Непрерывность — первое важное «хорошее» свойство функций на нашем пути. К
счастью, обычно функции, задаваемые формулами, непрерывны на своей области
определения. Нарушения непрерывности как правило связаны либо с обнулением
знаменателей, либо с разрывами кусочно заданных функций (как в
примере 1). Для аккуратного анализа функции на непрерывность
нужно использовать теоремы о непрерывности суммы, произведения, частного и
композиции функций. На следующей лекции мы обсудим, чем так хороши непрерывные
функции.
Для аккуратного анализа функции на непрерывность
нужно использовать теоремы о непрерывности суммы, произведения, частного и
композиции функций. На следующей лекции мы обсудим, чем так хороши непрерывные
функции.
← Предыдущая глава Следующая глава →
Непрерывность функций (теоремы и свойства)
Определение непрерывности функции
Определение
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности этой точки, если существует предел при x стремящемся к x0, и если этот предел равен значению функции в x0:
.
Используя определения предела функции по Коши и по Гейне, можно дать развернутые определения непрерывности функции в точке.
Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Тогда функция непрерывна в точке , если
.
Введем новую функцию:
.
Ее называют приращением функции в точке . Тогда функция непрерывна в точке , если
.
Определение непрерывности справа (слева)
Функция f(x) называется непрерывной справа (слева) в точке x0, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x0 равен значению функции в x0:
.
Более подробно, см. «Определение непрерывности функции в точке».
Свойства непрерывных в точке функций
Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Теорема о сохранении знака непрерывной функции
Пусть функция непрерывна в точке . И пусть она имеет положительное (отрицательное) значение в этой точке:
.
Тогда существует такая окрестность точки , на которой функция имеет положительное (отрицательное) значение:
при .
Арифметические свойства непрерывных функций
Пусть функции и непрерывны в точке .
Тогда функции , и непрерывны в .
Если , то и функция непрерывна в точке .
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Теорема о непрерывности сложной функции
Пусть функция t = g(x) непрерывна в точке x0. И пусть функция f(t) непрерывна в точке t0 = g(x0).
Тогда сложная функция f(g(x)) непрерывна в точке x0.
Доказательство
Предел сложной функции
Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.
Доказательство
Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство
Точки разрыва
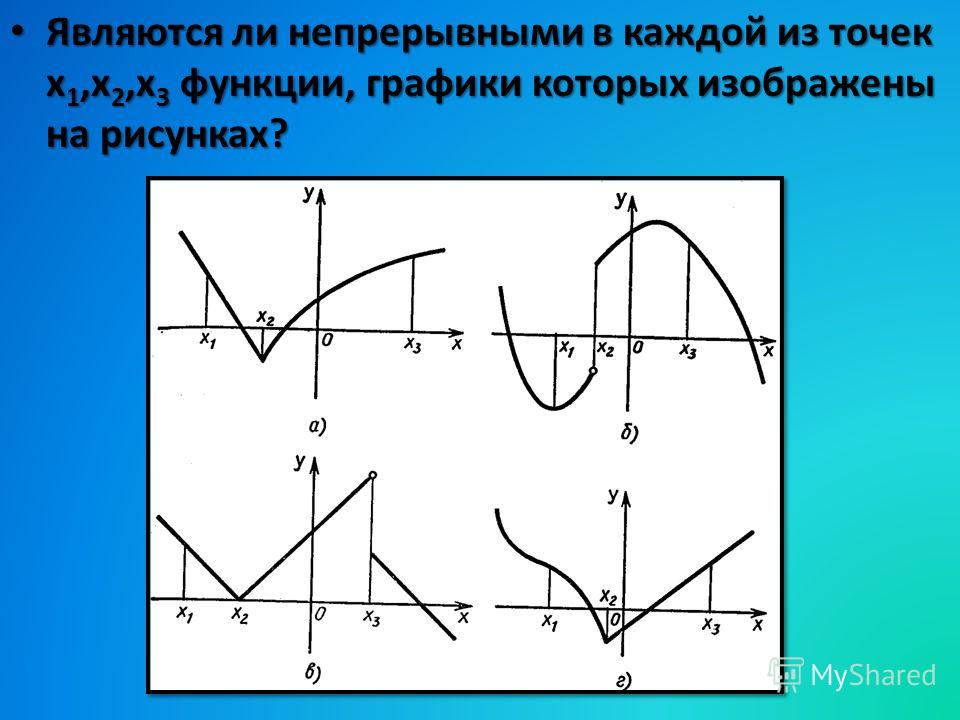
Определение точки разрыва
Пусть функция определена на некоторой проколотой окрестности точки . Точка называется точкой разрыва функции , если выполняется одно из двух условий:
1) не определена в ;
2) определена в , но не является непрерывной ⇑ в этой точке.
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Подробнее, см. «Точки разрыва функции – определения, классификация и примеры».
Свойства функций, непрерывных на отрезке
Определение функции, непрерывной на отрезке
Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и непрерывна справа и слева ⇑ в точках a и b, соответственно.
Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке , то она ограничена на этом отрезке.
Определение достижимости максимума (минимума)
Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех .
Определение достижимости верхней (нижней) грани
Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
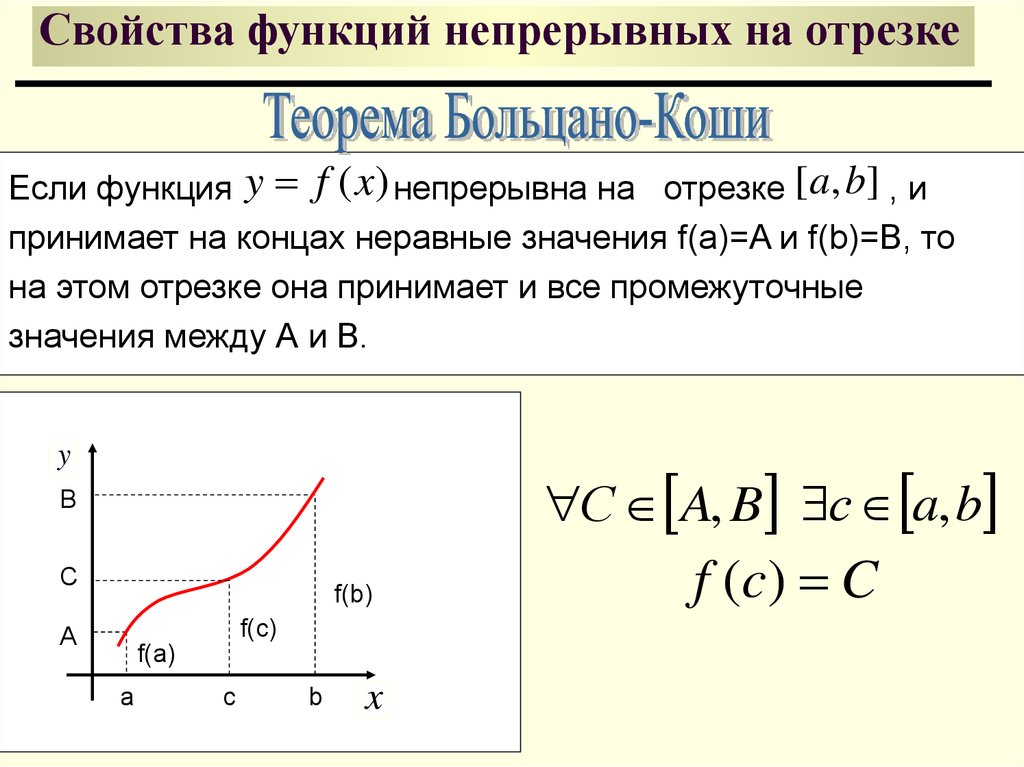
Теорема Больцано – Коши о промежуточном значении
Пусть функция непрерывна на отрезке . И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой
.
Следствие 1
Пусть функция непрерывна на отрезке .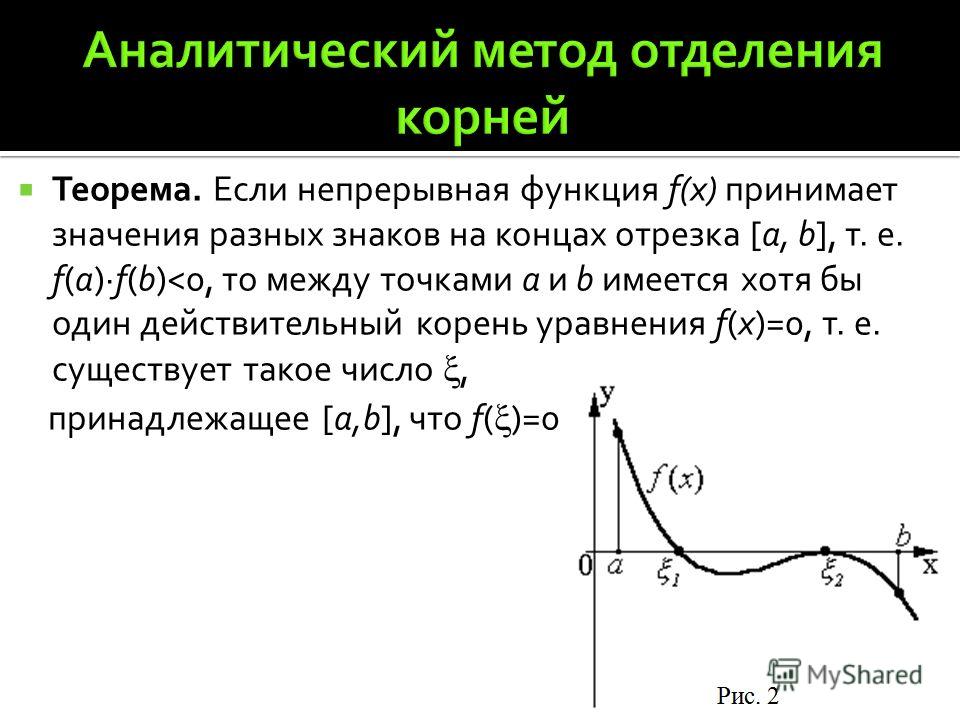 И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
.
Следствие 2
Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:
при .
Подробнее, см. «Свойства функций, непрерывных на отрезке».
Обратные функции
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (строго убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (строго убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Подробнее, см. «Обратные функции – определение и свойства».
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Теорема. Свойства показательной функции
Показательная функция имеет следующие свойства:
(П.0) определена, при , для всех ;
(П.1) при a ≠ 1 имеет множество значений ;
(П.2) строго возрастает при , строго убывает при , является постоянной при ;
(П.3) ;
(П.3*) ;
(П.4) ;
(П.5) ;
(П.6) ;
(П.7) ;
(П.8) непрерывна для всех ;
(П.9) при ;
при .
Подробнее, см. «Определение и доказательство свойств показательной функции».
Логарифм
Логарифмическая функция, или логарифм, y = loga x, с основанием a – это функция, обратная к показательной функции с основанием a.
Теорема. Свойства логарифма
Функция, y = loga x, имеет следующие свойства:
(Л.1) определена и непрерывна, при и , для положительных значений аргумента,;
(Л.2) имеет множество значений ;
(Л.3) строго возрастает при , строго убывает при ;
(Л.4) при ;
при ;
(Л.5) ;
(Л.6) при ;
(Л.7) при ;
(Л.8) при ;
(Л.9) при .
Подробнее, см. «Определение и доказательство свойств логарифма».
Экспонента и натуральный логарифм
В определениях показательной функции и логарифма фигурирует постоянная a, которая называется основанием степени или основанием логарифма. В математическом анализе, в подавляющем большинстве случаев, получаются более простые вычисления, если в качестве основания использовать число e:
.
Показательную функцию с основанием e называют экспонентой: , а логарифм по основанию e – натуральным логарифмом: .
Свойства экспоненты и натурального логарифма изложены на страницах
«Число e – его смысл и доказательство сходимости последовательности»;
«Экспонента, е в степени х»;
«Натуральный логарифм, функция ln x».
Степенная функция
Степенная функция с показателем степени p – это функция f(x) = x p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого, f(0) = 0 p = 0 при p > 0.
Здесь мы рассмотрим свойства степенной функции y = x p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».
Теорема. Свойства степенной функции (x ≥ 0)
Степенная функция, y = x p, с показателем p имеет следующие свойства:
(С. 1) определена и непрерывна на множестве
1) определена и непрерывна на множестве
при ,
при ;
(С.2) имеет множество значений
при ,
при ;
(С.3) строго возрастает при ,
строго убывает при ;
(С.4) при ;
при ;
(С.5) ;
(С.5*) ;
(С.6) ;
(С.7) ;
(С.8) ;
(С.9) .
Подробнее, см. «Непрерывность и свойства степенной функции».
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус (sin x), косинус (cos x), тангенс (tg x) и котангенс (ctg x), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x) и арккотангенс (arcctg x), непрерывны на своих областях определения.
Подробнее, см. «Доказательство непрерывности тригонометрических функций». {2}-2 x+11
\) непрерывна при \(\
x=a
\). Так как точка \(\
x=a
\) — произвольная точка, то доказано, что функция непрерывна при всех значениях \(\
x
\).
{2}-2 x+11
\) непрерывна при \(\
x=a
\). Так как точка \(\
x=a
\) — произвольная точка, то доказано, что функция непрерывна при всех значениях \(\
x
\).
Пусть \(\ \Delta x=x \) и \(\ \Delta y=\Delta f(x)=f(x)-f(a) \) — приращение функции, соответствующей этому приращению аргумента.
(Необходимое и достаточное условие непрерывности функции в точке). Функция \(\ y=f(x) \) непрерывна в точке \(\ x=a \) тогда и только тогда, когда
\(\ \lim _{\Delta x \rightarrow 0} \Delta f(x)=0 \)
То есть функция \(\ y=f(x) \) называется непрерывной в точке \(\ x=a \), если она определена в точке \(\ x=a \), а ее окрестность и равенство \(\ \lim _{\Delta x \rightarrow 0} \Delta f(x)=0 \) выполняется (инфинитезимальное приращение аргумента соответствует инфинитезимальному приращению функции).
ПРИМЕР
Чтобы исследовать функцию непрерывности \(\ y=\sin x \)
Указанная функция определена для всех \(\
x \in R
\) . Возьмем произвольную точку \(\
x
\) и найдем приращение функции \(\
\Delta y
\) :
Возьмем произвольную точку \(\
x
\) и найдем приращение функции \(\
\Delta y
\) :
\(\ \Delta y=\Delta f(x)=f(x+\Delta x)-f(x)=\sin (x+\Delta x)-\sin x \)
Примените формулу «разница синусов»:
\(\ \sin x-\sin y=2 \sin \frac{x-y}{2} \cos \frac{x+y}{2} \)
Буду иметь:
\(\ \Delta y=2 \sin \frac{\Delta x}{2} \cos \left(x+\frac{\Delta x}{2}\right) \)
Найдите предел приращения функции при условии, что приращение аргумента стремится к нулю:
\(\ \lim _{\Delta x \rightarrow 0} \Delta y=\lim _{\Delta x \rightarrow 0} 2 \sin \frac{\Delta x}{2} \cos \left(x+\frac{\Delta x}{2}\right)=2 \lim _{\Delta x \rightarrow 0} \sin \frac{\Delta x}{2} \cos \left(x+\frac{\Delta x}{2}\right) \)
Поскольку аргумент синуса стремится к нулю, его можно заменить его аргументом (так как эти функции эквивалентны бесконечно малым функциям):
\(\ \lim _{\Delta x \rightarrow 0} \Delta y=\lim _{\Delta x \rightarrow 0} 2 \sin \frac{\Delta x}{2} \cos \left(x+\frac{\Delta x}{2}\right)=2 \lim _{\Delta x \rightarrow 0} \frac{\Delta x}{2} \cos \left(x+\frac{\Delta x}{2}\right)=2 \cdot \frac{0}{2} \cdot \cos x=0 \)
Тогда по определению функция \(\
y=\sin x
\) непрерывна в произвольной точке \(\
x
\).
Функция непрерывна для любого \(\ x \in R \)
Непрерывность функции справа и слева в точке
Рассмотрим функцию \(\ y=f(x) \), которая определена в полуинтервале \(\ [a ; a+\delta) \)
ОПРЕДЕЛЕНИЕ
Функция \(\ y=f(x) \) называется непрерывной справа при \(\ x=a \), если существует односторонний предел
\(\ f(a+0)=\lim _{x \rightarrow a+0} f(x)=f(a) \)
Пусть функция \(\ y=f(x) \) определена в полуинтервале \(\ (a-\delta ; a] \)
ОПРЕДЕЛЕНИЕ
Функция \(\ y=f(x) \) называется левой непрерывной в точке \(\ x=a \), если в этой точке есть левый предел
\(\ f(a-0)=\lim _{x \rightarrow a-0} f(x)=f(a) \)
Если функции \(\ f(x) ; \quad g(x) \) непрерывны при \(\ x=a \), то функции в этой точке также будут непрерывными
\(\ f(x) \pm g(x), f(x) \cdot g(x), \frac{f(x)}{g(x)}, g(a) \neq 0 \)
Если функция \(\
t(x)
\) непрерывна при \(\
x=a
\), а функция \(\
f(t)
\) непрерывна в соответствующей точке \(\
t_{0}=f(a)
\) , то комплекс \(\
f(t(x))
\) непрерывен при \(\
x=a
\).
Все элементарные функции непрерывны в каждой точке их областей.
(Ограниченность непрерывной функции). Если функция \(\ y=f(x) \) непрерывна в точке \(\ x=a \), то существует окрестность этой точки, где данная функция ограничена.
(Об устойчивости знака непрерывной функции). Если функция \(\ y=f(x) \) непрерывна в точке \(\ x=a ; \quad f(a) \neq 0 \) , то существует окрестность этой точки, в которой \(\ f(a) \neq 0 \) , а знак функции в этой окрестности совпадает со знаком \(\ f(a) \) .
Функция непрерывности на зазоре
ОПРЕДЕЛЕНИЕ
Функция \(\ y=f(x) \) называется непрерывной на отрезке \(\ (a ; b) \) , если она непрерывна в каждой точке этого интервала.
Функция \(\ y=f(x) \) называется непрерывной на отрезке \(\ [a ; b] \) , если она непрерывна на отрезке \(\ (a ; b) \), непрерывном справа в точке а и непрерывном слева в точке \(\ b \).
Комментарий. Функция, непрерывная на отрезке \(\
[a ; b]
\) , может быть разрывной в точках \(\
a
\) и \(\
\mathrm{b}
\).
(Об ограниченности непрерывной функции на отрезке). Если функция \(\ y=f(x) \) непрерывна на отрезке \(\ [a ; b] \) , то она ограничена на этом отрезке, т. е. Существует такое число \(\ M>0 \), что для любого \(\ x \in[a ; b] \) неравенства \(\ |f(x)| \leq M \)
(Теорема Вейерштрасса). Если функция \(\ y=f(x) \) непрерывна на отрезке \(\ [a ; b] \) , то она достигает на этом отрезке своих наибольших \(\ \mathrm{M} \) и наименьших значений \(\ \mathrm{m} \).
(О существовании нуля на отрезке непрерывности). Если функция \(\ y=f(x) \) непрерывна на отрезке \(\ y=f(x) \) , а на концах отрезка принимает ненулевые значения разных знаков, то на интервале \(\ [a ; b] \) имеется по крайней мере одна точка \(\ \mathrm{C} \), в которой \(\ f(c)=0 \)
(Теорема Больцано-Коши). Если функция \(\ y=f(x) \) непрерывна на отрезке \(\ [a ; b] \) , то она принимает на интервале \(\ (a ; b) \) все промежуточные значения между \(\ f(a) \) и \(\ f(b) \)
(О существовании непрерывной обратной функции). {-1}(y)
\) строго монотонна и непрерывна на отрезке \(\
[\alpha ; \beta]
\)
{-1}(y)
\) строго монотонна и непрерывна на отрезке \(\
[\alpha ; \beta]
\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Ограниченные последовательности Числовая последовательность и ее предел Основные теоремы о пределах функции Таблица эквивалентности пределов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Реальный анализ: 6.
 2. Непрерывные функции
2. Непрерывные функции6.2. Непрерывные функции
Если поискать непрерывность в тезаурусе, можно найти синонимы как вечность или отсутствие прерывания . Декарт говорят, что функция непрерывна, если ее график можно построить без отрывая карандаш от бумаги.
| Пример 6.2.1: | |
| |
Однако, если мы хотим иметь дело с более сложными функциями, мы
нужны математические понятия, которыми мы можем манипулировать.
| Определение 6.2.2: Непрерывность | |
| Функция непрерывна в точке c в своей области определения D если: при наличии > 0 существует > 0 такое, что: если х Г а также | х — с | < тогда | f(x) — f(c) | < Функция непрерывна в своей области определения D , если она непрерывна в каждой точке своей области. | |
Это, как и многие определения и аргументы эпсилон-дельта , не легко понять. Нажмите на значок
Java, чтобы увидеть апплет, который пытается проиллюстрировать определение.
Непрерывные функции — это именно те группы функций, которые сохранять пределы, как показывает следующее предложение:
Предложение 6. 2.3: Непрерывность сохраняет пределы 2.3: Непрерывность сохраняет пределы | |
| Если f непрерывен в точке c в домене D и { x n } — последовательность точек в D сходится к c , тогда f(x) = f(c) . Если f(x) = f(c) для каждой последовательности { x n } точек в D сходящаяся к c , то f непрерывна в точке c . | |
Опять же, как и в случае пределов, это предложение дает нам два эквивалентных математические условия непрерывности функции, и либо можно использовать в конкретной ситуации.
| Пример 6.2.4: | |
| |
Непрерывные функции могут быть добавлены, умножены, разделены и составлены друг с другом и снова дают непрерывные функции.
| Предложение 6.2.5: Алгебра с непрерывными функциями | |
| |
Хотя это предложение кажется не очень важным, его можно использовать чтобы быстро доказать следующее:
| Примеры 6.2.6: | |
| |
Непрерывность определяется в одной точке, а эпсилон и дельта фигурирующие в определении, могут отличаться от одной точки преемственность к другому. Однако существует и другой вид непрерывность, которая работает для всех точек домена одновременно.
| Определение 6.2.7: Равномерная непрерывность | |
| Функция f с доменом D называется единообразно. непрерывный на домене D если для любого > 0 существует > 0 такое, что: если с , т Д и | с — т | < тогда | f(s) — f(t) | < . Нажмите здесь для графического объяснение. | |
Взгляните на этот апплет Java, иллюстрирующий единую непрерывность.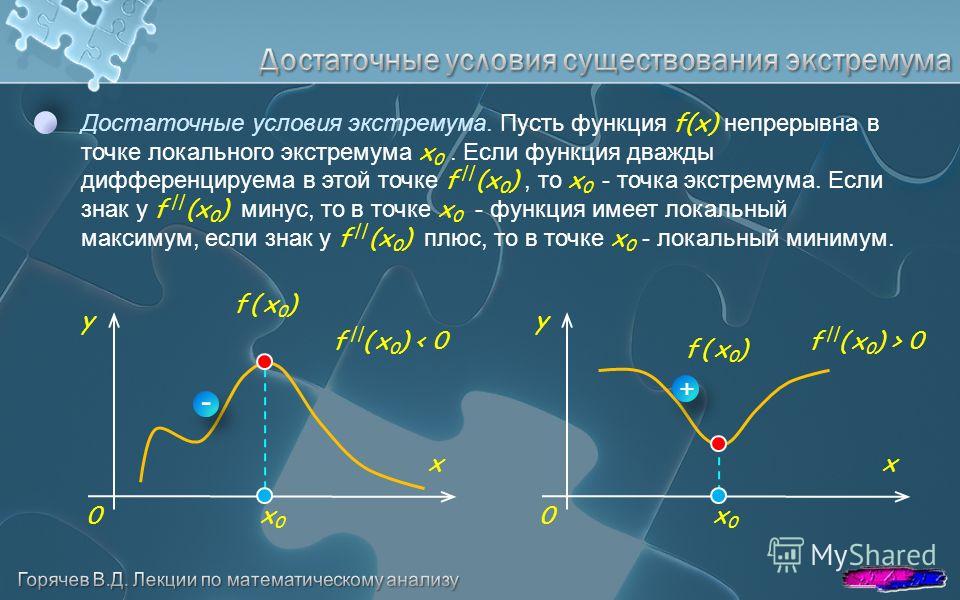
Хотя это определение очень похоже на исходное определение непрерывности, на самом деле это не одно и то же: функция может быть непрерывной, но не равномерно непрерывно. Отличие в том, что дельта в определении равномерной непрерывности зависит только от эпсилон, тогда как в определении просто непрерывности дельта зависит от эпсилон, а также в конкретной точке c под вопросом.
| Пример 6.2.8: | |
| |
Следующая теорема иллюстрирует связь между непрерывностью
равномерная непрерывность и дает простое условие непрерывности
функция должна быть равномерно непрерывной.
| Теорема 6.2.9: Непрерывность и равномерная непрерывность | |
| Если f равномерно непрерывно в области D , то f является продолжением D . Если f непрерывно на компактной области D , то f равномерно непрерывен в D . | |
Далее мы рассмотрим функции, которые не являются непрерывными.
Следующий | предыдущий | Глоссарий | карта
Формализация свойств непрерывных функций на отрезках
Реферат
Формальная математика получает все большее внимание в математике и информатике. В частности, формализация исчисления имеет важные приложения в инженерном проектировании и анализе. В этой статье мы представляем формальное доказательство некоторых фундаментальных теорем о непрерывных функциях на отрезках, основанное на помощнике по доказательству Кока. В этой формализации мы строим действительную систему счисления, ссылаясь на «Основы анализа» Ландау. Затем мы завершаем формализацию основных определений интервала, функции и предела и формально доказываем теоремы, включая теорему о полноте, теорему о промежуточном значении, теорему о равномерной непрерывности и другие в Coq. Процесс доказательства нормализован, строг и надежен.
В этой формализации мы строим действительную систему счисления, ссылаясь на «Основы анализа» Ландау. Затем мы завершаем формализацию основных определений интервала, функции и предела и формально доказываем теоремы, включая теорему о полноте, теорему о промежуточном значении, теорему о равномерной непрерывности и другие в Coq. Процесс доказательства нормализован, строг и надежен.
Ключевые слова
- COQ
- Формализация
- Ограничения
- Непрерывные функции
- Закрытые интервалы
Это исследование поддерживается Национальным фондом естественных наук (NNSF) Китая под грантом 61936818, 6111111111111111111111111111111. Фонд естественных наук (NNSF)
. Скачать документ конференции в формате PDF
1 Введение
Анализ — одно из величайших достижений в истории математики. Достижение открывает новую эру математического прогресса и играет важную роль в развитии физики, астрономии, обработки сигналов и других дисциплин.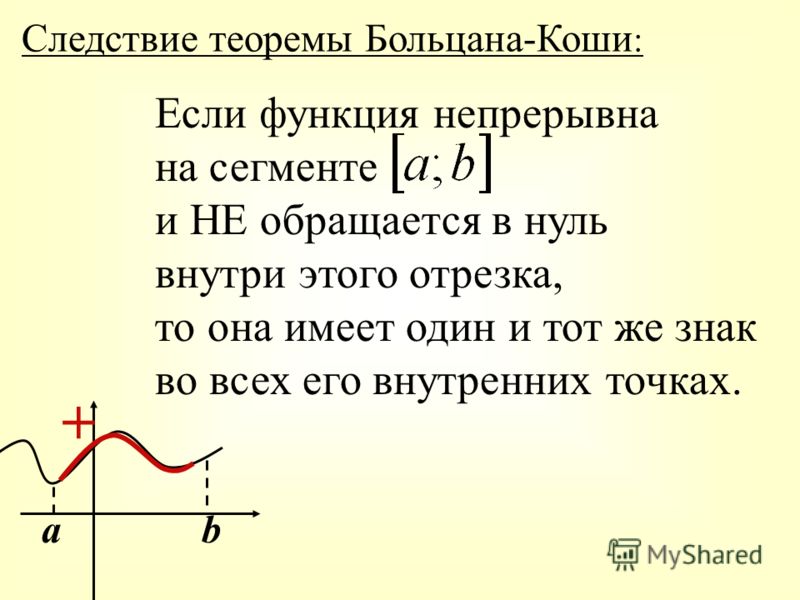 Анализ, возникший из исчисления, представляет собой раздел математики, изучающий пределы и связанные с ним теории [12].
Анализ, возникший из исчисления, представляет собой раздел математики, изучающий пределы и связанные с ним теории [12].
В конце XIX века математики вывели многие свойства непрерывных функций на отрезках, что, несомненно, способствовало развитию аналитической теории. Есть некоторые важные свойства непрерывных функций на замкнутых интервалах, включая вторую теорему Вейерштрасса: теорему об ограниченности, первую теорему Вейерштрасса: теорему об экстремальном значении, вторую теорему Больцано-Коши: теорему о промежуточном значении, теорему Кантора: теорему о равномерной непрерывности.
Теория функций Больцано дает самые ранние доказательства теоремы об ограниченности и теоремы об экстремальном значении (но опубликованные примерно 100 лет спустя) [15], а Вейерштрасс доказал теорему об экстремальном значении в берлинской лекции. Теорема о промежуточном значении впервые была доказана в 1817 г. Больцано, а затем Коши [7] дал доказательство в 1821 г. Определение равномерной непрерывности предложено Гейне, и он опубликовал доказательство теоремы о равномерной непрерывности.
С дальнейшим исследованием пределов математиками создание строгой и полной системы теории действительных чисел стало ключевым вопросом. В 1872 году в Германии появились три основные теории действительных чисел: теория разреза Дедекинда, теория «основной последовательности» Кантора-Хени-Мерея и теория «ограниченной монотонной последовательности» Вейерштрасса. Среди них особо признается разрез Дедекинда, и его называют созданием человеческого интеллекта, не опирающегося на интуитивность пространства и времени. Затем Пеано создал теорию натуральных чисел с помощью набора аксиом, тем самым решив основные проблемы теории рациональных чисел, а также основные проблемы теории действительных чисел.
В последние годы, с быстрым развитием компьютерных наук, особенно с появлением помощника по доказательству Coq, Isabelle и HOL Light и т. д. [2, 4, 8, 10, 14, 17], формальное доказательство математических теорем сделал большой прогресс. В 2005 г. международные компьютерные эксперты Гонтье и Вернер успешно представили формальное доказательство знаменитой «теоремы о четырех красках» на языке Coq [5]. После многих лет напряженной работы Гонтье снова добился машинного доказательства «теоремы нечетного порядка» в Coq в 2012 году [6]. Этот прогресс делает Coq все более и более популярным в академических кругах. Видийк указал, что соответствующие исследовательские группы по всему миру завершили или планируют формализовать доказательство таких теорем, как первая теорема Гёделя о неполноте, теорема Жордана о кривой, простая теорема и последняя теорема Ферма из сотен известных математических теорем [17].
После многих лет напряженной работы Гонтье снова добился машинного доказательства «теоремы нечетного порядка» в Coq в 2012 году [6]. Этот прогресс делает Coq все более и более популярным в академических кругах. Видийк указал, что соответствующие исследовательские группы по всему миру завершили или планируют формализовать доказательство таких теорем, как первая теорема Гёделя о неполноте, теорема Жордана о кривой, простая теорема и последняя теорема Ферма из сотен известных математических теорем [17].
На основе формальной системы «Теория действительных чисел» мы формализуем свойства непрерывных функций на отрезках. Кроме того, мы приводим формальные доказательства этих теорем, к которым относятся теорема об ограниченности, теорема об экстремальном значении, теорема о промежуточном значении, теорема о равномерной непрерывности. Следует отметить, что свойство непрерывных функций на отрезках является важной теоремой анализа.
Структура этой статьи выглядит следующим образом: В разд. 2 мы вводим систему машинного доказательства «теория действительных чисел». В разд. В разделе 3 мы приводим формальное определение предела функции и связанных с ним свойств. В разд. В разделе 4 мы подробно обсуждаем машинное доказательство свойств непрерывных функций на отрезках, которые выводятся с помощью теоремы о супремуме. В разд. 5, мы делаем выводы и обсуждаем возможные дальнейшие работы.
2 мы вводим систему машинного доказательства «теория действительных чисел». В разд. В разделе 3 мы приводим формальное определение предела функции и связанных с ним свойств. В разд. В разделе 4 мы подробно обсуждаем машинное доказательство свойств непрерывных функций на отрезках, которые выводятся с помощью теоремы о супремуме. В разд. 5, мы делаем выводы и обсуждаем возможные дальнейшие работы.
2 Система теории действительных чисел
Прежде чем формально доказать свойства непрерывных функций на замкнутых интервалах, нам сначала нужно построить формальную систему теории действительных чисел. ван Бентем Юттинг [1] завершил формализацию в Automath «Основы анализа» Ландау, что явилось значительным ранним прогрессом в формальной математике. Харрисон [9] представляет формализованные действительные числа и дифференциальное исчисление в своей системе HOL Light. Определение действительных чисел в стандартной библиотеке Coq использует аксиоматический способ, и на его основе была создана превосходная библиотека анализа вещественных чисел Coquelicot [3].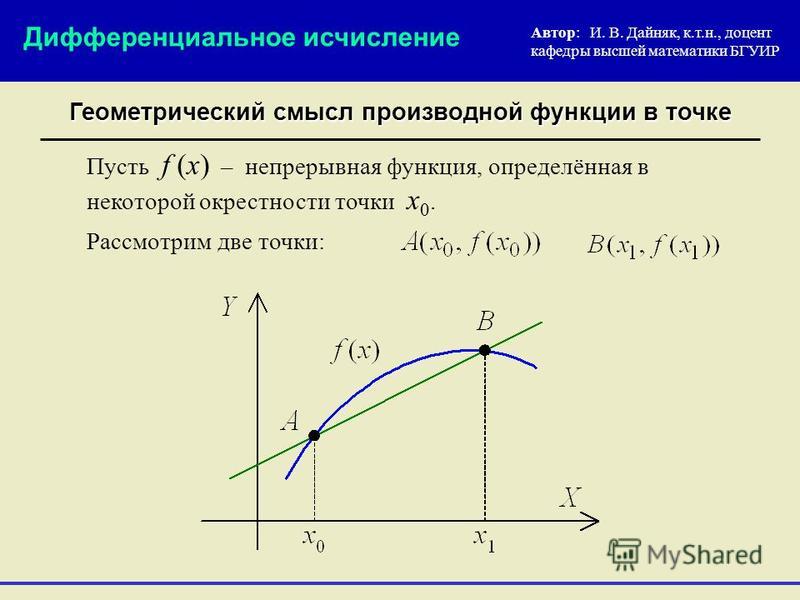 Эта библиотека добилась многих успехов, но ее определение действительного числа неконструктивно. Хорнунг [11] завершил первые четыре главы «Основ анализа» на языке Coq, который тесно связан с нашей работой, однако наша система ближе к выражению Ландау и более читабельна. Мы также завершили часть, посвященную комплексным числам, и доказали эквивалентность восьми теорем о полноте вещественных чисел.
Эта библиотека добилась многих успехов, но ее определение действительного числа неконструктивно. Хорнунг [11] завершил первые четыре главы «Основ анализа» на языке Coq, который тесно связан с нашей работой, однако наша система ближе к выражению Ландау и более читабельна. Мы также завершили часть, посвященную комплексным числам, и доказали эквивалентность восьми теорем о полноте вещественных чисел.
Существует несколько способов определения натуральных чисел в Coq. Основанная на аксиоматической теории множеств Морса-Келли, она предназначена для быстрого и естественного обоснования математики, а также для вывода аксиом Пеано в виде теорем [16, 18]. Если мы начнем с более высокого типа, а не с теории множеств, мы можем формализовать прямые аксиомы Пеано следующим образом:
Основываясь на этом, мы можем использовать «Параметр» и «Аксиому» для определения функций, связанных с натуральными числами, таких как сложение и умножение. Этот способ интуитивно понятен, но не элегантен. Натуральные числа, определенные «индукцией», могут рекурсивно определять функции, связанные с натуральными числами.
Натуральные числа, определенные «индукцией», могут рекурсивно определять функции, связанные с натуральными числами.
«Основы анализа» Ландау [13] основаны на наивной теории множеств и некоторой базовой логике. Начиная с аксиом Пеано, натуральные числа (целые положительные числа), дроби (положительные), рациональные числа/целые числа (положительные) определяются по порядку. Вещественное число, определяемое разрезом Дедекинда, определяет комплексные числа через действительные числа для систематического построения всей теории системы счисления. Мы завершили формализацию системы Coq, и полный исходный код доступен онлайн:
https://github.com/coderfys/analysis/
В этой системе мы можем доказать фундаментальную теорему Дедекинда и вывести теорему о супремуме. Детали доказательства не описываются, а формализация такова.
2.1 Основная теорема Дедекинда
Разделите все действительные числа на два класса так, чтобы первый класс и второй класс не были пустыми, и каждое число в первом классе было меньше каждого числа во втором классе. Тогда существует единственное действительное число E , так что любое число меньше E относится к первому классу, а любое число больше E относится ко второму классу.
Тогда существует единственное действительное число E , так что любое число меньше E относится к первому классу, а любое число больше E относится ко второму классу.
2.2 Теорема о супремуме
Если непустое множество действительных чисел имеет верхнюю границу, то должна быть и наименьшая граница (например, супремум).
3 Основные определения и свойства
Формальное определение функций в этой системе выглядит следующим образом:
Связанные определения непрерывности функции:
Функция f ( x ) непрерывна в одной точке, что означает, что
Функция f ( x ) непрерывна (слева, справа) в точке, тогда функция f (6 x
) локально ограничена в этой точке (например, взять непрерывную правую):
В этой действительной системе счисления функция деления требует трех параметров, третий из которых является доказательством того, что второй не равен 0. Следовательно, “ NoO_N» выше означает «\(2 \ne 0\)».
Функция f ( x ) непрерывна на [ a , b ], тогда \(-f (x)\) непрерывна на [ a , b ]. Функция f ( x ) непрерывна на [ a , b ] и не везде равна 0, тогда \(\frac{1}{f(x)}\) непрерывна на (взять \ (f(x)>0\) в качестве примера).
4 Свойства непрерывных функций на замкнутых интервалах
Непрерывные функции обладают четырьмя фундаментальными свойствами на замкнутых интервалах: теорема об ограниченности (вторая теорема Вейерштрасса), теорема об экстремальном значении (первая теорема Вейерштрасса), теорема о промежуточном значении (вторая теорема Больцано-Коши), Теорема о равномерной непрерывности (теорема Кантора). Эти теоремы являются основой математического анализа и прямым выражением теории действительных чисел в функциях. Наши формализации опираются на закон логической аксиомы исключенного третьего.
Теорема 1
Теорема об ограниченности: непрерывная функция на отрезке должна быть ограничена на этом отрезке.
Сначала докажем лемму L1: если f ( x ) непрерывно на [ a , b ], то некоторая окрестность z ограничена для любого \(z \in (a ,б)\). Обозначение «\([x0|-\delta ]\)» ниже представляет \(U_{x_0}(\delta )\) в математике.
Верхняя граница: построить набор действительных чисел \(\{t: f(x)\) имеет верхнюю границу на \([a, t] \}\). Формальное определение следующее:
Поскольку f ( x ) непрерывно справа в точке a , существует \(\delta > 0\), и f ( x ) имеет верхнюю границу на \((a , a + \delta )\), когда \(b \le a + \delta \) доказывает предложение. Когда \(a + \delta
Случай 1(\(\xi  Предложение доказано, когда \(b <\xi + \delta _1\). Когда \(\xi + \delta _1 \le b\), существует \(\xi + \delta _1 \in R\), что противоречит \(\xi \) является супремумом R .
Предложение доказано, когда \(b <\xi + \delta _1\). Когда \(\xi + \delta _1 \le b\), существует \(\xi + \delta _1 \in R\), что противоречит \(\xi \) является супремумом R .
Случай 2(\(\xi = b\)): Предложение доказано, так как \(b <\xi + \delta _1\).
Нижняя оценка: Согласно лемме Pr_fun1 можно вывести, что \(-f(x)\) непрерывна на [ a , b ]. Из теоремы T1 мы знаем, что \(-f(x)\) имеет верхнюю границу «вверх», тогда «-вверх» является нижней границей f ( x ) на [ a , b ].
Теорема 2
Теорема об экстремальном значении: непрерывная функция на отрезке должна достигать максимального и минимального значений на этом отрезке.
Максимальное значение: построить набор действительных чисел \(\{f(x): x \in [a, b] \}\). Формальное определение таково:
Очевидно, R не пусто, и мы можем сделать вывод, что R имеет верхнюю границу по T1, следовательно, R имеет верхнюю грань M . Если существует \(x \in (a, b)\) и \(f(x) = M\), то предложение доказано. В противном случае \(f(x) < M\) для любого \(x \in [a, b]\). Постройте новую функцию \(g(x) = \frac{1}{M-f (x)}\). Поскольку \(g(x) > 0\) для любого \(x \in \) [a, b], поэтому g ( x ) непрерывно на [ a , b ] по Pr_fun2. Начиная с Т1, г ( x ) имеет супремум K на [ a , b ] и \(K > 0\). После вывода \(M- \frac{1}{K}\) является верхней границей f ( x ) на [ a , b ], что противоречит M является супремумом р .
Если существует \(x \in (a, b)\) и \(f(x) = M\), то предложение доказано. В противном случае \(f(x) < M\) для любого \(x \in [a, b]\). Постройте новую функцию \(g(x) = \frac{1}{M-f (x)}\). Поскольку \(g(x) > 0\) для любого \(x \in \) [a, b], поэтому g ( x ) непрерывно на [ a , b ] по Pr_fun2. Начиная с Т1, г ( x ) имеет супремум K на [ a , b ] и \(K > 0\). После вывода \(M- \frac{1}{K}\) является верхней границей f ( x ) на [ a , b ], что противоречит M является супремумом р .
Минимальное значение: Согласно лемме Pr_fun1 можно сделать вывод, что \(-f(x)\) непрерывно на [ a , b ]. Из теоремы T2 мы знаем, что \(-f(x)\) имеет максимальное значение «max», тогда «-max» является минимальным значением f ( x ) на [ a , b ].
Теорема 3
Теорема о промежуточном значении: Если \(f(a) \ne f(b)\), то для любого действительного числа C между f ( a ), f ( b ), хотя бы одна точка c на ( a , b ) удовлетворяет условию f (c) = C.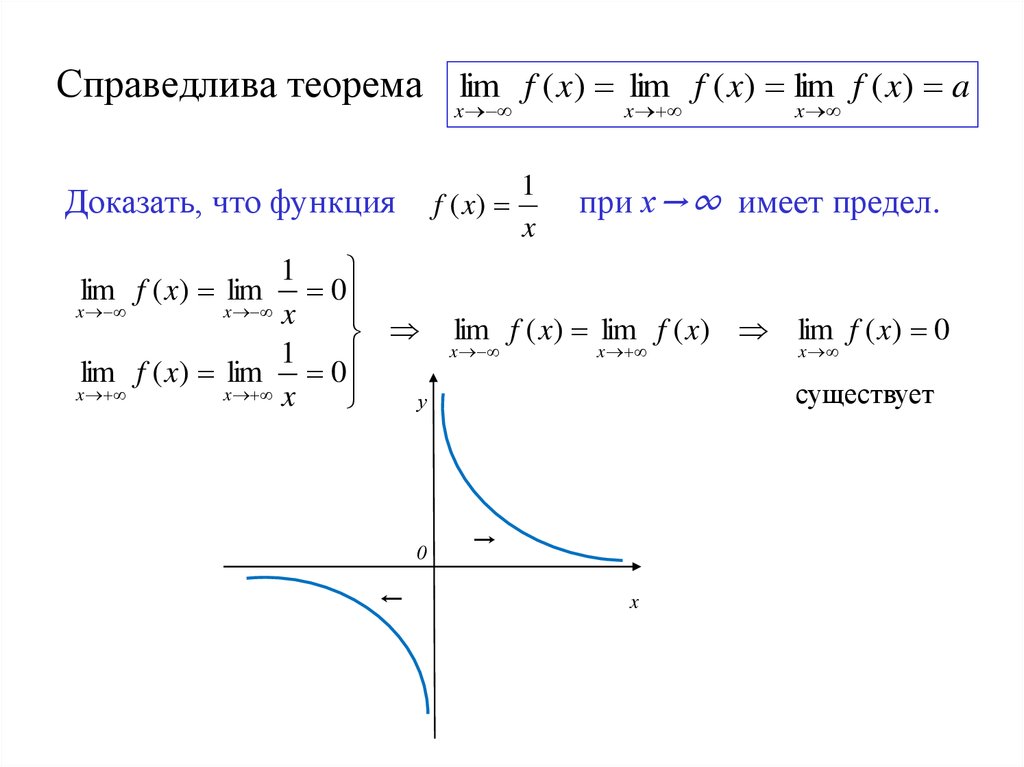
Сначала докажем лемму L3: b , \(a
\(f(a)< f(b)\): построить набор действительных чисел \(\{t: f(x) \(f(a)> f(b)\): f ( x ) непрерывно справа в точке a , тогда существует \(\delta _1> 0 \) и \(|f(x) — f(a)|< C - f(a)\) в \((a, a + \delta _1)\), которые можно вывести \(f(x ) < С\). \((a+\frac{\delta _1}{2}) \in R\), когда \(\delta _1 <(b - a)\) и \(\frac{a + b}{2} \in R \) когда \((b - a) \le \delta _1\). В общем, R не пусто, а b является верхней границей R , поэтому R имеет верхнюю грань \(\xi \) и \(\xi \le b\). Когда \(\xi = b\), он может вывести противоречие согласно Pr_supremum и L3. Поэтому \(\xi \in (a, b)\). Случай 1(\(f(\xi ) Случай 2(\(f(\xi )> C\)): f ( x ) непрерывно в точке \(\xi \), следовательно, f ( x ) непрерывно слева в точке точка \(\xi \). По L3 должны существовать \(z \in (a, \xi )\) и \(f (z)>C\), поэтому z является верхней границей R , что противоречит \(\xi \ ) является супремумом R . \(f(a)> f(b)\): см. доказательство T1’, T2’. Теорема о равномерной непрерывности: функция непрерывна на отрезке, тогда функция равномерно непрерывна на этом отрезке. Пусть f ( x ) непрерывно на [ a , b ], зафиксируйте любое \(\epsilon> 0\). мы строим множество действительных чисел \(\{t: \exists \delta > 0\) и \(| f(x_1)-f(x_2) | <\epsilon \), когда \(x_1, x_2 \in [a, t]\) и \(| x_1-x_2 | \le \delta \}\). Формальное определение выглядит следующим образом: Поскольку f ( x ) непрерывно справа в точке a , должны существовать \(\delta _1> 0\) и \(| f(x)-f (a) | <\frac{\epsilon}{2}\) для любого \(x \in [a, a + \delta _1)\). Случай 1(\(\xi Случай 2(\(\xi = b\)): \(b <\xi + \delta \), предложение доказывается произволом \(\epsilon \). В этой статье формализуются пределы, непрерывные функции и родственные теоремы. Эти теоремы включают теорему об ограниченности, теорему об экстремальном значении, теорему о промежуточном значении и теорему о равномерной непрерывности. Мы завершили их формальные доказательства на основе разработанной нами системы теории действительных чисел. В будущем мы формализуем больше теорем о непрерывных функциях и предпримем значимые попытки формальной работы в области реального анализа и комплексного анализа. Мы благодарны анонимным рецензентам, чьи комментарии помогли улучшить представление исследования в этой статье. van Benthem Jutting, L.S.: Проверка «Grundlagen» Ландау в системе AUTOMATH. Северная Голландия, Амстердам (1994) МАТЕМАТИКА
Google ученый Берто, Ю., Кастеран, П.: Интерактивное доказательство теорем и разработка программ: Coq’Art: Исчисление индуктивных построений. Перекрестная ссылка
МАТЕМАТИКА
Google ученый Boldo, S., Lelay, C., Melquiond, G.: Coquelicot: удобная библиотека реального анализа для Coq. Мат. вычисл. науч. 9 (1), 41–62 (2015). https://doi.org/10.1007/s11786-014-0181-1 MathSciNet
перекрестная ссылка
МАТЕМАТИКА
Google ученый Члипала, А.: Сертифицированное программирование с зависимыми типами: практическое введение в Coq Proof Assistant. MIT Press, Кембридж (2013) Перекрёстная ссылка
Google ученый Гонтье Г.: Формальное доказательство теоремы о четырех красках. Уведомления AMS 55 (11), 1382–1393 (2008) MathSciNet
МАТЕМАТИКА
Google ученый Гонтье Г. и др.: Машинно проверенное доказательство теоремы о нечетном порядке. В: Блейзи, С., Паулин-Моринг, К., Пичарди, Д. (ред.) ITP 2013. LNCS, vol. 7998, стр. 163–179. Спрингер, Гейдельберг (2013). https://doi.org/10.1007/978-3-642-39634-2_14 Перекрестная ссылка
Google ученый Грабинер, Дж. В.: Кто дал вам эпсилон? Коши и истоки строгого исчисления. Являюсь. Мат. Пн. 90 (3), 185–194 (1983) MathSciNet
перекрестная ссылка
Google ученый Хейлз, Т.К.: Формальное доказательство. Уведомления AMS 55 (11), 1370–1380 (2008) MathSciNet
МАТЕМАТИКА
Google ученый Харрисон Дж.: Доказательство теорем с использованием действительных чисел. Спрингер, Гейдельберг (1994) МАТЕМАТИКА
Google ученый Харрисон, Дж.: Формальное доказательство — теория и практика. Уведомления AMS 55 (11), 1395–1406 (2008) MathSciNet
МАТЕМАТИКА
Google ученый Hornung, C.: Построение систем счисления в Coq. Саарский университет, Саарбрюккен (2011) Google ученый Кац, В. Дж.: История математики. Пирсон/Аддисон-Уэсли, Бостон (2004) МАТЕМАТИКА
Google ученый Ландау, Э.: Основы анализа: арифметика целых, рациональных, иррациональных и комплексных чисел. Издательская компания Челси, Нью-Йорк (1966) Google ученый Нипков Т., Венцель М., Полсон Л.К. (ред.): Изабель / HOL. LNCS, том. 2283. Спрингер, Гейдельберг (2002). https://doi.org/10.1007/3-540-45949-9 CrossRef
МАТЕМАТИКА
Google ученый Раснок, П., Керр-Лоусон, А.: Больцано и равномерная непрерывность. Historia Mathematica 32 (3), 303–311 (2005) MathSciNet
перекрестная ссылка
Google ученый Сунь Т., Ю. В.: Формальная система аксиоматической теории множеств в Coq. IEEE Access 8 , 21510–21523 (2020) CrossRef
Google ученый Wiedijk, F.: Начало формального подтверждения. Уведомления AMS 55 (11), 1408–1414 (2008) MathSciNet
МАТЕМАТИКА
Google ученый Ю. В., Сун Т., Фу Ю.: Система машинных доказательств аксиоматической теории множеств. Science Press, Пекин (2020) Google ученый Ссылки на скачивание Пекинская ключевая лаборатория космонавтики и конвергенции Школа электронной инженерии, Пекинский университет почты и телекоммуникаций, Пекин, 100811 Фухун Теорема 4
 Пусть \(\delta _2 = min (a + \frac{\delta _1}{2}) (b-a)\), докажем, что \(a + \delta _2 \in R\). Очевидно, b является верхней границей R , поэтому R имеет верхнюю грань \(\xi \) и \(\xi \le b\). Поскольку f ( x ) непрерывно в точке \(\xi \), существует \(\delta > 0\) и \(| f(x) -f (\xi ) | <\frac{ \epsilon}{2}\) для любого \(x \in [\xi - \delta , \xi + \delta ]\). Далее, мы можем вывести \(| f (x_1)-f (x_2) | <\epsilon \) для любого \(x_1, x_2 \in [\xi - \delta , \xi + \delta ]\). Следовательно, \(| f(x_1)-f(x_2) | <\epsilon \) для любых \(x_1, x_2 \in [a, \xi + \delta ]\) и \(| x_1-x_2 | \le \дельта\).
Пусть \(\delta _2 = min (a + \frac{\delta _1}{2}) (b-a)\), докажем, что \(a + \delta _2 \in R\). Очевидно, b является верхней границей R , поэтому R имеет верхнюю грань \(\xi \) и \(\xi \le b\). Поскольку f ( x ) непрерывно в точке \(\xi \), существует \(\delta > 0\) и \(| f(x) -f (\xi ) | <\frac{ \epsilon}{2}\) для любого \(x \in [\xi - \delta , \xi + \delta ]\). Далее, мы можем вывести \(| f (x_1)-f (x_2) | <\epsilon \) для любого \(x_1, x_2 \in [\xi - \delta , \xi + \delta ]\). Следовательно, \(| f(x_1)-f(x_2) | <\epsilon \) для любых \(x_1, x_2 \in [a, \xi + \delta ]\) и \(| x_1-x_2 | \le \дельта\).
5 Заключение
Ссылки
 Тексты по теоретической информатике. Серия EATCS. Spring-Verlag, Гейдельберг (2004). https://doi.org/10.1007/978-3-662-07964-5
Тексты по теоретической информатике. Серия EATCS. Spring-Verlag, Гейдельберг (2004). https://doi.org/10.1007/978-3-662-07964-5 Информация об авторе
Авторы и организации
Авторы
- Yaoshun Fu
Посмотреть публикации авторов
Вы также можете искать этого автора в PubMed Google Scholar
- Wensheng Yu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Авторы, переписывающиеся по номеру
Яошун Фу или Вэньшэн Юй.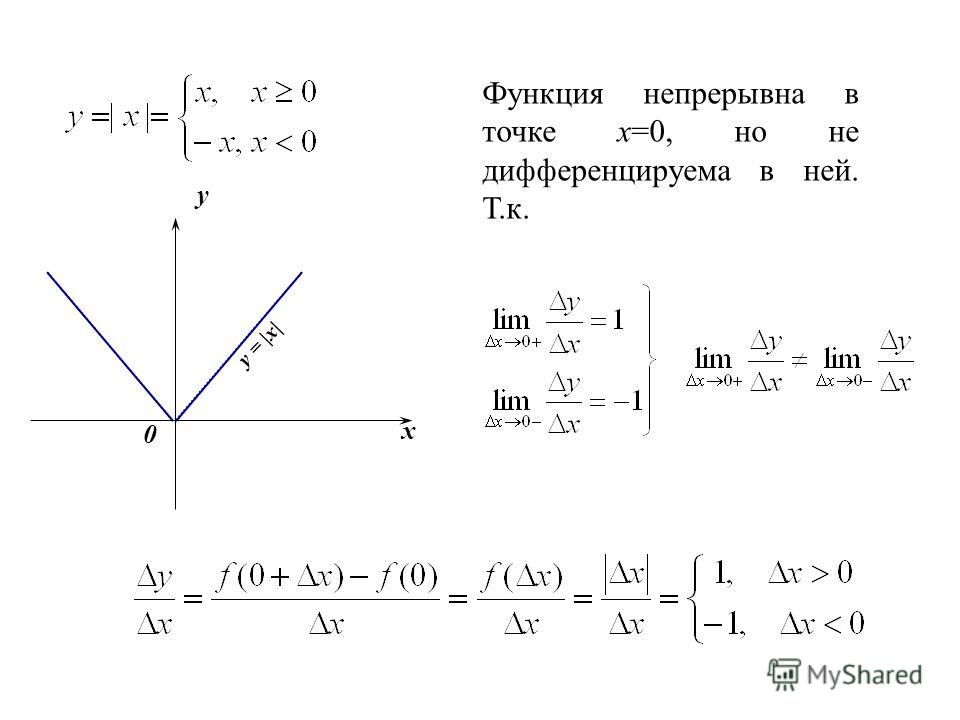
Информация для редактора
Редакторы и сотрудники
Математический отдел, Università degli Studi di Genova, Генуя, Генуя, Италия
Анна Мария Бигатти
Компьютеры и программное обеспечение, Университет Макмастера, Гамильтон, Онтарио, Канада
Жак Каретт
Факультет компьютерных наук, Университет Бата, Батпорт, Великобритания
619Джеймс Х. Дэвен
Institut für Mathematik, MA 6-2, TU Berlin, Berlin, Germany
Prof. Michael Joswig
Технический университет Брауншвейга, Брауншвейг, Германия
Timo de Wolff
Права и разрешения
Перепечатки и разрешения
. section):- Что такое непрерывная функция?
- Порядок непрерывности: функции C0, C1, C2
- Различные типы непрерывности
- Абсолютно непрерывный
- Левый непрерывный
- Правая непрерывная
- Равномерно непрерывный
- Список общих непрерывных функций.

- Как проверить непрерывность функции.
- Непрерывные переменные и данные
Посмотрите видео с обзором и примерами или прочитайте ниже:
Непрерывные функции
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Эта функция непрерывна.
Говоря простым языком, непрерывная функция — это функция, которую можно нарисовать, не отрывая карандаша от бумаги. Если у вас есть отверстия, скачки или вертикальные асимптоты, вам придется поднять карандаш вверх, и поэтому у вас не будет непрерывной функции.
Если ваша функция скачет таким образом, она не является непрерывной.
Формально функция (f) непрерывна, если для каждой точки x = a :
- Функция определена в и . Другими словами, точка a находится в области f, .
- Предел функции существует в этой точке и равен x, приближающемуся к a с обеих сторон,
- Предел функции, когда x приближается к a , совпадает с выходом функции (т.
 е. значением y) при a .
е. значением y) при a .
Порядок непрерывности, или «гладкость» функции, определяется тем, как эта функция ведет себя на интервале, а также поведением производных.
Функция C0
A Функция C 0 является непрерывной функцией. Более конкретно, это функция с действительным знаком, которая непрерывна на определенном замкнутом интервале.
Это простое определение образует строительный блок для более высоких порядков непрерывности.
Функция C1
A C 1 Функция непрерывна и имеет непрерывную первую производную.
Функция C2
A Функция C 2 имеет как непрерывную первую производную, так и непрерывную вторую производную.
Обратите внимание, что верхний индекс равен количеству производных, которые являются непрерывными , поэтому порядок непрерывности иногда описывается как « количество производных, которые должны соответствовать ». Это простой способ взглянуть на порядок непрерывности, но следует соблюдать осторожность, если вы используете это определение, поскольку производные также должны совпадать по порядку (первый, второй, третий…) без пропусков. Например, предположим, что у вас есть непрерывная первая производная и третья производная с прерывистой второй производной. Есть две «совпадающие» непрерывные производные (первая и третья), но это не будет C 2 — это будет функция C 1 из-за отсутствия непрерывности второй производной.
Это простой способ взглянуть на порядок непрерывности, но следует соблюдать осторожность, если вы используете это определение, поскольку производные также должны совпадать по порядку (первый, второй, третий…) без пропусков. Например, предположим, что у вас есть непрерывная первая производная и третья производная с прерывистой второй производной. Есть две «совпадающие» непрерывные производные (первая и третья), но это не будет C 2 — это будет функция C 1 из-за отсутствия непрерывности второй производной.
Моделирование с порядком непрерывности
Непрерывность в технике и физике также определяется более конкретно, чем просто «непрерывность». Например, этот отчет ЕС о методах геометрического моделирования на основе PDE описывает математические модели, в которых поверхности C 0 являются позиционными, C 1 позиционными и тангенциальными, а C 3 — позиционный, тангенциальный и кривизнальный. Требуемая непрерывность зависит от приложения. Например, моделирование высокоскоростного транспортного средства (например, самолета) требует более высокого порядка непрерывности по сравнению с медленным транспортным средством.
Например, моделирование высокоскоростного транспортного средства (например, самолета) требует более высокого порядка непрерывности по сравнению с медленным транспортным средством.
Если функция просто «непрерывна» без какой-либо дополнительной информации, то вы, как правило, предполагаете, что функция непрерывна везде (т. е. множество всех действительных чисел от -∞ до + ∞). Однако иногда конкретная часть функции может быть непрерывной, а остальные — нет.
- Непрерывность на интервале: Функция f является непрерывной на интервале, если она непрерывна в каждой точке интервала. Например, вы можете определить интервал от -1 до +1. Пока функция непрерывна в этой небольшой области, вы можете сказать, что она непрерывна на этом конкретном интервале.
- Непрерывность в конечной точке: У функции есть две возможные конечные точки: полностью влево (в крайнем отрицательном направлении) и полностью вправо (в крайне положительном направлении).
 Предполагая, что предел существует, «непрерывность в конечной точке» означает, что функция непрерывна справа (для левого конца) или непрерывна слева (для правого конца).
Предполагая, что предел существует, «непрерывность в конечной точке» означает, что функция непрерывна справа (для левого конца) или непрерывна слева (для правого конца).
Абсолютно непрерывные функции с действительными числами — это функции, для которых справедлива Основная теорема исчисления (FTC) [1]. Другими словами, абсолютная непрерывность определяет , какие функции могут быть первообразными : функция на замкнутом ограниченном интервале абсолютно непрерывна на этом интервале, если она также является первообразной на том же интервале [2].
Эти функции имеют самый «гладкий» тип непрерывности, за которым следует равномерная непрерывность, а затем — обычная непрерывность. Все абсолютно непрерывные функции непрерывны, но обратное неверно.
Абсолютно непрерывные функции и случайные величины связаны друг с другом следующим образом: Действительнозначная случайная величина X абсолютно непрерывна, если ее функция распределения F X абсолютно непрерывна [3]
Формальное определение
Формальное определение часто используется в реальном анализе, в частности, для доказательства основной теоремы исчисления для интеграла Лебега [4].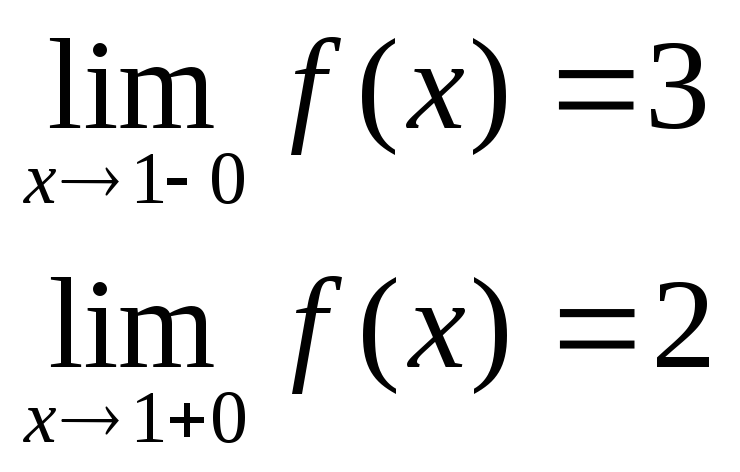
Абсолютно непрерывная функция, заданная на отрезке, обладает следующим свойством. Это свойство основано на положительном числе ε и его эквиваленте, другом положительном числе δ.
- Возьмите интервал, для которого мы хотим определить абсолютную непрерывность, затем разбейте его на набор конечных непересекающихся интервалов. Длины этих интервалов имеют сумму меньше, чем δ,
- Далее рассмотрим абсолютные значения разностей значений функций на концах интервалов; Сумма по этим интервалам меньше ε [5].
В суммирующей записи мы можем сформулировать вышеизложенное как: когда конечная последовательность непересекающихся интервалов удовлетворяет:
, затем
Где (x k , y k ) — непересекающиеся подинтервалы.
Примеры и свойства абсолютно непрерывных функций
Каждая выпуклая функция и каждая непрерывно дифференцируемая функция абсолютно непрерывна [3].
Для вещественнозначной абсолютно непрерывной функции выполняются следующие свойства [6]:
- cf, где c ∈ ℝ
- ж + г
- фг
- 1/f, если f(x) ≠ 0 для каждого x ∈ [a, b]
- |ф|.

Несколько конкретных примеров: функция Липшица абсолютно непрерывна; Функция Кантора не является (хотя она всюду непрерывна) [7]. Функция tan(x) не является ни равномерно непрерывной, ни абсолютно непрерывной на отрезке [0, π/2].
Абсолютно непрерывный: Ссылки
[1] Heil, C. Конспект лекций по реальному анализу. 3.5. Абс. продолжение и сингулярные функции. Получено 4 мая 2021 г. с: https://people.math.gatech.edu/~heil/handouts/ac.pdf 9.1057 [2] 7.4 Абс. продолжение & Сингулярные функции. Получено 4 мая 2021 г. с: https://www.math.lsu.edu/~rich/Absolute_Continuity
[3] Hill, T. & Berger, A. (2015). Введение в закон Бенфорда. Издательство Принстонского университета.
[4] Поусо, Р. (2012). Простое доказательство основной теоремы исчисления для интеграла Лебега. Получено 5 мая 2021 г. с: https://arxiv.org/pdf/1203.1462.pdf
[5] Математический словарь McGraw-Hill, 2/E. (2002). Макгроу-Хилл.
[6] Всемирный научный. (2014). Задачи и доказательства в реальном анализе. стр. 314-352. Получено 5 мая 2021 г. с: https://www.worldscientific.com/doi/10.1142/9.789814578516_0013
стр. 314-352. Получено 5 мая 2021 г. с: https://www.worldscientific.com/doi/10.1142/9.789814578516_0013
[7] Реальный анализ 9 января 2016 г. Глава 6. Дифференциация и интегрирование. Получено 4 мая 2021 г. с: https://faculty.etsu.edu/gardnerr/5210/Beamer-Proofs/Proofs-6-5.pdf
Непрерывная слева функция непрерывна для всех точек только в одном направлении. (при подходе слева).
Это функция, определенная до определенной точки, c , где:
- Функция определена на замкнутом интервале [ d, c ], лежащий слева от c ,
- Предел в этой точке, с, равен значению функции в этой точке.
На следующем рисунке показана непрерывная влево функция до точки x = 4:
Обратите внимание, что значение функции при x = 4 равно пределу функции, когда функция приближается к точке слева.
Формальное определение непрерывной слева функции
Формально непрерывная слева функция f является непрерывной слева в точке c if
lim x → c — f(x) = f(c) .
Другими словами, f(x) приближается к c снизу или слева, или для x < c (Morris, 1992). Точно так же определяется непрерывная справа функция (заменяя левый предел с- на правый предел с+ в нижнем индексе).
A правая непрерывная функция определена до определенной точки . На следующем рисунке показана непрерывная справа функция до точки x = 4:
Эта функция непрерывна справа в точке x = 4. Предел при x = 4 равен значению функции в этой точке (y = 6) . Это равно пределу функции по мере приближения к x = 4.
Обратите внимание, что точка на изображении выше заполнена. На графике это говорит о том, что точка входит в область определения функция. Если точка была представлена полым кругом, то точка равна , а не включены в домен (только каждая точка справа от него на этом графике), и функция , а не будет непрерывной справа.
Точка не существует при x = 4, поэтому функция не является непрерывной справа в этой точке.
Обратите внимание, что этот тип непрерывности определен для точки, а не для всей функции.
Более формальное определение непрерывной справа функции
Причина, по которой функция не считается непрерывной справа, заключается в формальном определении этих функций. Должны выполняться два условия о поведении функции по мере ее продвижения к точке:
- существует: предел функций должен существовать в точке. Знак + над «а» означает, что к точке приближаются с положительного конца числовой прямой; Другими словами, он приближается справа.
- Правый предел, ведущий к точке a, должен равняться пределу функции в этой точке.
Во втором примере выше круг был выдолблен, указывает на то, что точка не входит в область определения функции. Поскольку точки не существует, предела в этой точке тоже не существует.
На самом деле это не непрерывные функции!
Ярлык «непрерывная правая функция» немного неверен, потому что это не непрерывные функции. Чтобы функция была непрерывной, правый предел должен быть равен f(a), а левый предел также должен быть равен f(a). В определении функции, непрерывной справа, ничего не говорится о том, что происходит слева от точки. Функция может быть там непрерывной, а может и не быть. Единственный способ узнать наверняка — рассмотреть также определение функции, непрерывной слева.
Равномерно непрерывная функция на заданном множестве A непрерывна в каждой точке на A. Это проверяется путем проверки окрестностей вокруг каждой точки, определяя небольшую область, в которой функция должна оставаться внутри.
Более формально это формулируется как:
Функция f : A → ℝ равномерно непрерывна на A, если для каждого числа ε > 0 существует δ > 0; всякий раз, когда x, y ∈ A и |x − y| < δ следует, что |f(x) − f(y)| < ε.
Это формальное определение в основном говорит о том, что нужно выбрать несколько значений для ε, а затем найти δ, которое работает для всех значений x в наборе. Если работают одни и те же значения, функция соответствует определению.
График равномерно непрерывной функции
Графически найдите точки, где функция резко увеличивает или уменьшает кривизну . Определение не допускает таких больших изменений; Очень маловероятно, что вы сможете создать «коробку» одинакового размера, содержащую график. Функция может быть непрерывной, но она не является равномерно непрерывной.
Равномерно непрерывная функция g(x) = √(x) не выходит за края красного прямоугольника. Функция f(x) = 1/x проходит через верх и низ, поэтому , а не равномерно непрерывны. Изображение: Эскил Саймон Канне Вадшолт | Викисклад.
Игра здесь состоит в том, чтобы попытаться найти однородный ящик высотой x шириной = 2ε x 2 δ, который при перемещении сохранит граф, содержащийся внутри краев ящика. Таким образом, «однородная» часть определения относится к «коробке одинакового размера».
Таким образом, «однородная» часть определения относится к «коробке одинакового размера».
Свойства равномерно непрерывной функции
Эти функции имеют некоторые общих свойств .
- Все эти функции ограничивает на отрезке [a, b] и достигает максимума на множестве (a, b).
- Каждая равномерно непрерывная функция также является непрерывной функцией. Однако не все непрерывные функции равномерно непрерывны. Таким образом, вы можете думать об этих функциях как о «более» непрерывных.
- Они могут быть или не быть дифференцируемыми. Равномерная непрерывность не обязательно подразумевает дифференцируемость.
Все следующие функции, как правило, непрерывны:
- Функция абсолютного значения,
- Экспоненциальная функция,
- Логарифмическая функция,
- Все полиномиальные функции,
- Все силовые функции,
- Все тригонометрические функции.

- Естественная показательная функция e x (где e — число Эйлера)
Существует несколько общих правил , на которые можно ссылаться при попытке определить, является ли ваша функция непрерывной. Для некоторых функций вам нужно проделать небольшую детективную работу. (Более строгий подход см. в разделе «Проверка непрерывности»).
Sin(x) — пример непрерывной функции.
Шаг 1: Нарисуйте график карандашом , чтобы проверить непрерывность функции. Если ваш карандаш остается на бумаге слева направо на всем графике, не отрывая карандаша, ваша функция непрерывна. Другими словами, если ваш график имеет пробелы, дыры или является разделенным графиком, ваш график не является непрерывным.
Шаг 2: Выясните, есть ли ваша функция в списке непрерывных функций. Если да, то дальше идти не надо; ваша функция непрерывна.
Шаг 3: Проверьте, является ли ваша функция суммой (сложением), разностью (вычитанием) или произведением (умножением) одной из непрерывных функций, перечисленных в шаге 2. Если да, то ваша функция непрерывна. Например, sin(x) * cos(x) является произведением двух непрерывных функций и поэтому является непрерывным.
Если да, то ваша функция непрерывна. Например, sin(x) * cos(x) является произведением двух непрерывных функций и поэтому является непрерывным.
Шаг 4: Проверьте свою функцию на возможность наличия нуля в знаменателе . Отношение f(x)/g(x) непрерывно во всех точках x, где знаменатель не равен нулю. Другими словами, в точке x = 0 будет разрыв, что означает, что ваша функция не является непрерывной .
Вот и все!
Содержание (щелкните, чтобы перейти к этому разделу):
- Непрерывная переменная
- Интервальная переменная и масштаб
- Переменная соотношения и шкала
- Дискретная переменная
непрерывная переменная имеет бесконечное число потенциальных значений .
Это противоположность дискретной переменной, которая может принимать только конечное (фиксированное) число значений.
Посмотрите видео или прочитайте ниже:
Дискретные и непрерывные переменные
Посмотрите это видео на YouTube.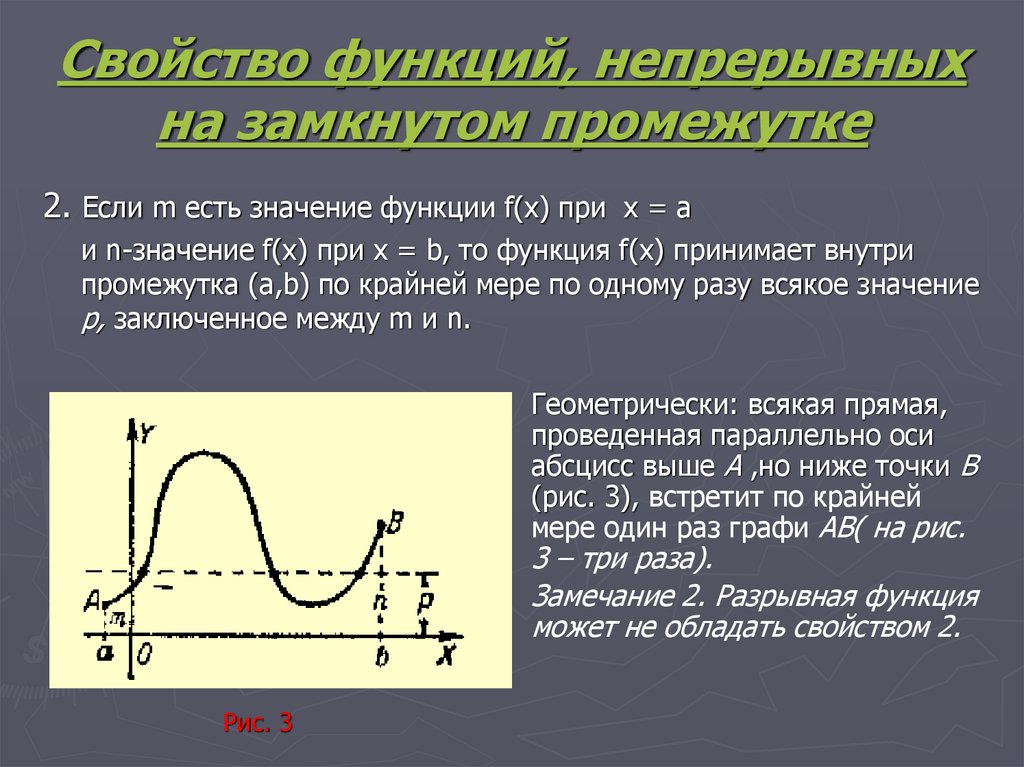
Непрерывная переменная Диапазон
Непрерывная переменная не обязательно должна включать каждое возможное число от отрицательной бесконечности до положительной бесконечности. В большинстве случаев он определяется в диапазоне. Например, диапазон может быть между 9и 10 или от 0 до 100. Несмотря на то, что эти диапазоны отличаются в 100 раз, они имеют бесконечное число возможных значений.
В качестве примера возьмем диапазон от 9 до 10 . Возможные непрерывные переменные включают:
- 9, 9,01, 9,001, 9,051, 9,000301, 9,000000801
.
Примеры непрерывных данных
Несколько примеров:
- Время, необходимое для бега на 100 м . Посмотрите любое спортивное мероприятие, рассчитанное на время, и вы увидите время, указанное с точностью до мельчайшей ширины волоса. На момент написания этой статьи мировой рекорд принадлежит Усэйну Болту в возрасте 9 лет.0,572 секунды.
- Ваш вес.
 Ваши весы в ванной, вероятно, округляют до одной десятой фунта, поэтому вы можете весить 151,1 фунта. Но вы действительно? Вы можете весить 151,14 или 151,143. Возможности для веса безграничны.
Ваши весы в ванной, вероятно, округляют до одной десятой фунта, поэтому вы можете весить 151,1 фунта. Но вы действительно? Вы можете весить 151,14 или 151,143. Возможности для веса безграничны. - Деньги. В далеком прошлом было время, когда деньги были конечными (это было количество банкнот и монет в обращении). С появлением банковской системы и криптовалюты «деньги» теперь неисчислимы.
- Цены на автомобили. Конечно, этот Форд может стоить вам 30 тысяч долларов прямо сейчас. Но что будет через 100 лет? 1000 лет? Цена автомобиля будет расти и расти. Вы можете возразить, что автомобили устареют в будущем, и, следовательно, есть момент, когда цены на автомобили достигнут максимума. Но у кого-то где-то будет древний автомобиль стоимостью в миллионы или миллиарды).
Рост и вес являются примерами величин, которые являются непрерывными переменными.
Дискретная переменная может принимать только значение определенное количество значений . Другими словами, у них нет бесконечного числа значений. Если вы можете сосчитать набор элементов, то переменные в этом наборе являются дискретными переменными.
Другими словами, у них нет бесконечного числа значений. Если вы можете сосчитать набор элементов, то переменные в этом наборе являются дискретными переменными.
Противоположностью дискретной переменной является непрерывная переменная. Непрерывные переменные могут принимать бесконечное количество возможностей.
Что такое дискретная переменная? Примеры
Некоторые примеры дискретных переменных:
- Количество монет в кошельке, банке или банке. Дискретно, потому что может быть только определенное количество монет (1, 2, 3, 4, 5…). Монеты не бывают в количестве 2,3 монеты или 10 ½ монет, поэтому невозможно бесконечное количество возможностей. Кроме того, кошелек или даже банк ограничены по размеру, поэтому монет может быть только определенное количество.
- Количество автомобилей на стоянке. Парковка может вместить только определенное количество автомобилей.
- Баллы по 10-балльной шкале. Если вы оцениваетесь по 10-балльной шкале, единственными возможными значениями являются 1, 2, 3, 4, 5, 6, 7, 8, 9и 10.

- Возраст на поздравительных открытках. Поздравительные открытки бывают только годами, а не дробями. Таким образом, существует конечное количество возможностей (предположительно, около сотни).
Дискретные случайные величины
Дискретные случайные переменные — это переменные, являющиеся результатом случайного события. Например, бросок игральной кости. Дискретные случайные величины обозначаются буквой X и имеют распределение вероятностей P(X). Если вы подбросили монету два раза и подсчитали количество решек, это дискретная случайная величина. Он представлен буквой X. X в этом случае может принимать только одну из трех возможных переменных: 0, 1 или 2 [решка].
Интервальная переменная — это просто любая переменная на шкале интервалов. Шкала интервалов имеет значимые интервалы между значениями. Интервалы между точками на шкале интервалов одинаковы. Например, разница между 10°C и 20°C такая же, как разница между 40°F и 50°F.
Интервальная переменная — это разновидность непрерывной переменной. Технически (и это действительно мудрено), шкала является интервальной переменной, а не самой переменной. Например, переменная 102°F находится на шкале интервалов; на самом деле вы бы не определили «102 градуса» как интервальную переменную. Это потому, что само по себе это довольно бессмысленно.
Проблемы с нулем
Даты являются переменными интервальной шкалы. Например, столетие длится 100 лет независимо от того, какой период времени вы измеряете: 100 лет между 29-м и 20-м веками — это то же самое, что 100 лет между 5-м и 6-м веками. Хотя это кажется интуитивно понятным, даты подчеркивают серьезную проблему с интервальными шкалами: ноль является произвольным. Это означает, что вы должны быть очень осторожны при интерпретации интервалов. Например, в системе AD года 0 не существует (AD начинается с года 1). Однако некоторые календари включают ноль, например, буддийские и индуистские календари.
Произвольные нули означают, что нельзя сказать, что «первое тысячелетие имеет ту же длину, что и второе тысячелетие».
Это приводит к другой проблеме с нулями на шкале интервалов: ноль не означает, что чего-то не существует. Например, тот факт, что в календаре нашей эры нет нулевого года, не означает, что времени в тот момент не существовало. Наоборот, должно быть, потому что есть годы до 1 года нашей эры (до н.э.!). Точно так же нулевая температура не означает, что температуры в этой точке не существует (она должна существовать, потому что температура опускается ниже точки замерзания).
Произвольные нули также означают, что вы не можете вычислять коэффициенты. Шкалы отношений (которые имеют значащие нули) не имеют этих проблем, поэтому иногда предпочтение отдается именно этой шкале.
Вес измеряется по шкале соотношений (без каламбура!).
Шкала отношений обладает всеми свойствами шкалы интервалов, а также фиксированным натуральным нулем.
Данные соотношения по этой шкале имеют измеримые интервалы. Например, разница между ростом в шесть футов и пять футов такая же, как интервал между двумя и тремя футами. Чем шкала отношений отличается от шкалы интервалов, так это тем, что она также имеет значимый ноль . Ноль означает, что что-то не существует или не имеет измеряемого свойства. Например, ноль на шкале температур Кельвина означает, что свойство температуры не существует при нуле.
Другие примеры шкалы отношений:
- Возраст . Часы начинают тикать, когда вы рождаетесь, но возраст «0» технически означает, что вы не существуете.
- Вес . При 0 фунтах вы бы ничего не весили и, следовательно, не существовали бы.
- Высота . Если бы вы были 0″, у вас не было бы роста.
- Данные о продажах. Продажи, равные нулю, означают, что вы ничего не продали, поэтому продаж не было.
- Приобретенное количество .
 Если вы купили 0 товаров, то не было куплено ни одного количества.
Если вы купили 0 товаров, то не было куплено ни одного количества. - Время отсчитывается от «Большого взрыва».
Шкала отношений и отрицательные числа
Поскольку «0» на шкале отношений означает полное отсутствие чего-либо, на этой шкале нет отрицательных чисел.
Инвариантность при преобразовании подобия
Данные на шкале отношений инвариантны при преобразовании подобия, y=ax, a >0. Например, вы можете преобразовать фунты в килограммы с помощью преобразования подобия K = 2,2 P. Отношение остается неизменным, используете ли вы фунты или килограммы. Хотя шкала отношений описывается как имеющая «значимый» ноль, было бы точнее сказать, что она имеет значимое отсутствие свойства; Ноль на самом деле не является измерением чего-либо — это указание на то, что что-то не обладает измеряемым свойством. Например, 0 фунтов означает, что измеряемый предмет не имеет свойства «вес в фунтах».
Шкала отношений и отношения
Как следует из названия, мы можем создавать осмысленные отношения между числами на шкале отношений.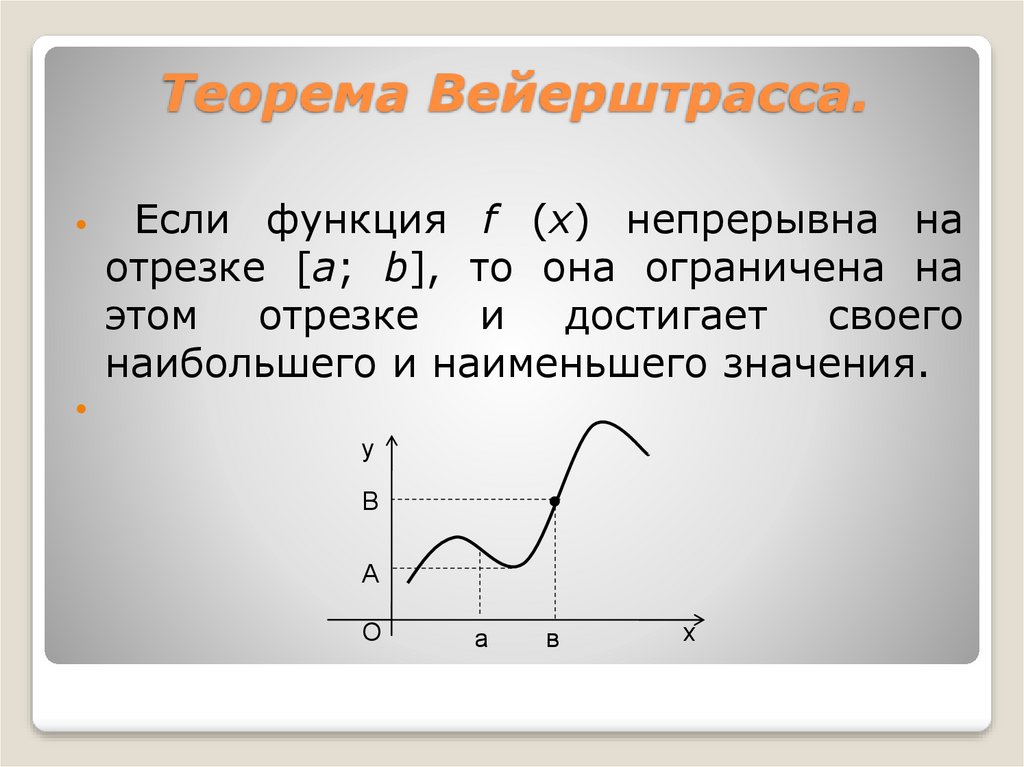
Например, количество тестов, которые вы сдали в прошлом семестре, может быть равно нулю, если вы не сдавали ни одного теста. Однако, если вы сдали два экзамена в этом семестре и четыре в прошлом семестре, вы можете сказать, что частота ваших тестов в этом семестре была вдвое меньше, чем в прошлом семестре.
Использование в математическом анализе
Шкалы измерения, такие как шкала отношений, редко упоминаются на занятиях по математическому анализу. Но в прикладном исчислении (т. е. в реальном мире) вы, вероятно, часто их используете. Например, экономические исследования с использованием векторного исчисления часто ограничены шкалой измерения; только те значения, которые образуют шкалу отношений, могут формировать поле (Nermend, 2009).).
Следующий :
Прерывистые функции
Ссылки
Изображение: Эскил Саймон Канне Вадшолт — собственная работа, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=50614728
Богачев, В.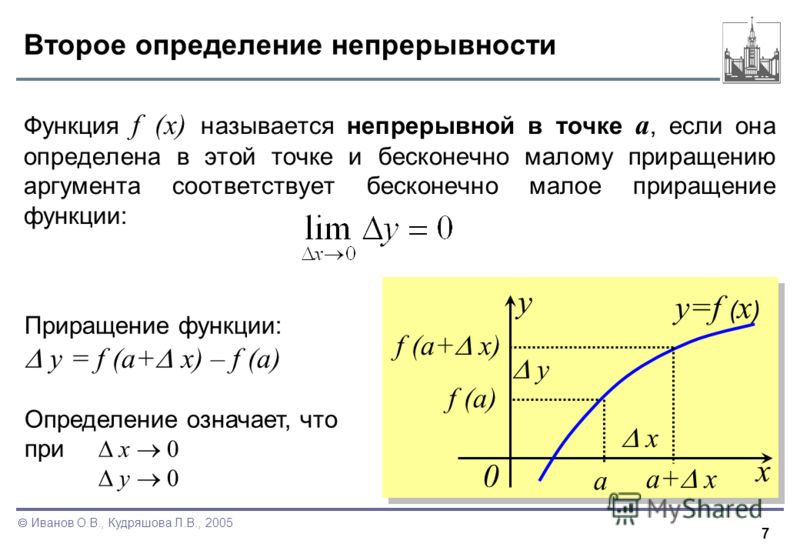 (2006). Теория меры, том 1 . Спрингер.
(2006). Теория меры, том 1 . Спрингер.
Карозерс, Н. Л. Реальный анализ. Нью-Йорк: Издательство Кембриджского университета, 2000.
Дартмутский университет (2005). Непрерывность. Получено 14 декабря 2018 г. с: https://math.dartmouth.edu//archive/m3f05/public_html/ionescuslides/Lecture8.pdf
Гуха, С. (2018). Компьютерная графика через OpenGL®: от теории к экспериментам. КПР Пресс.
Каплан, В. «Пределы и непрерывность». §2.4 в Advanced Calculus, 4-е изд. Чтение, Массачусетс: Аддисон-Уэсли, стр. 82-86, 1992.
Ларсен, Р. Краткий расчет: прикладной подход.
Моррис, К. (1992). Академический пресс-словарь науки и техники. Эльзевир Наука.
Нерменд, К. (2009). Векторное исчисление в анализе регионального развития. Сравнительный региональный анализ на примере Польши.
Росс, К. (2013). Элементарный анализ: теория исчисления (тексты для студентов по математике), 2-е изд. Спрингер.
Титчмарш, Э. (1964). Теория функций, 2-е издание. Издательство Оксфордского университета.


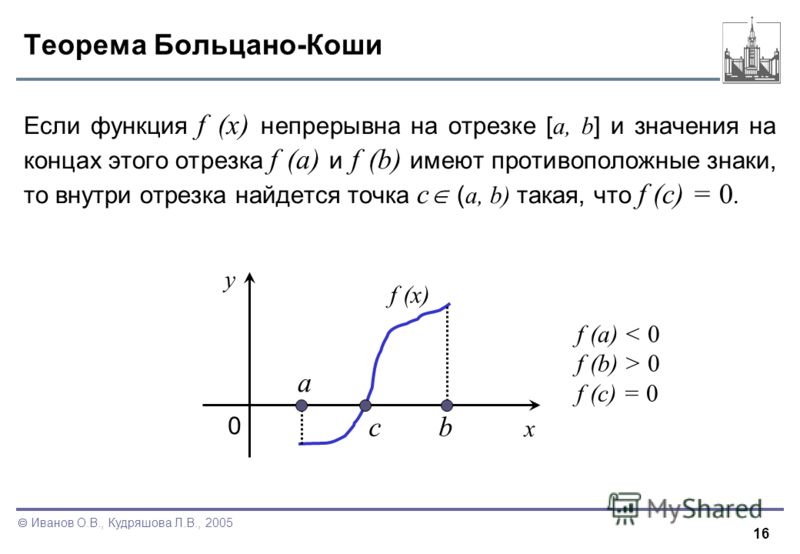
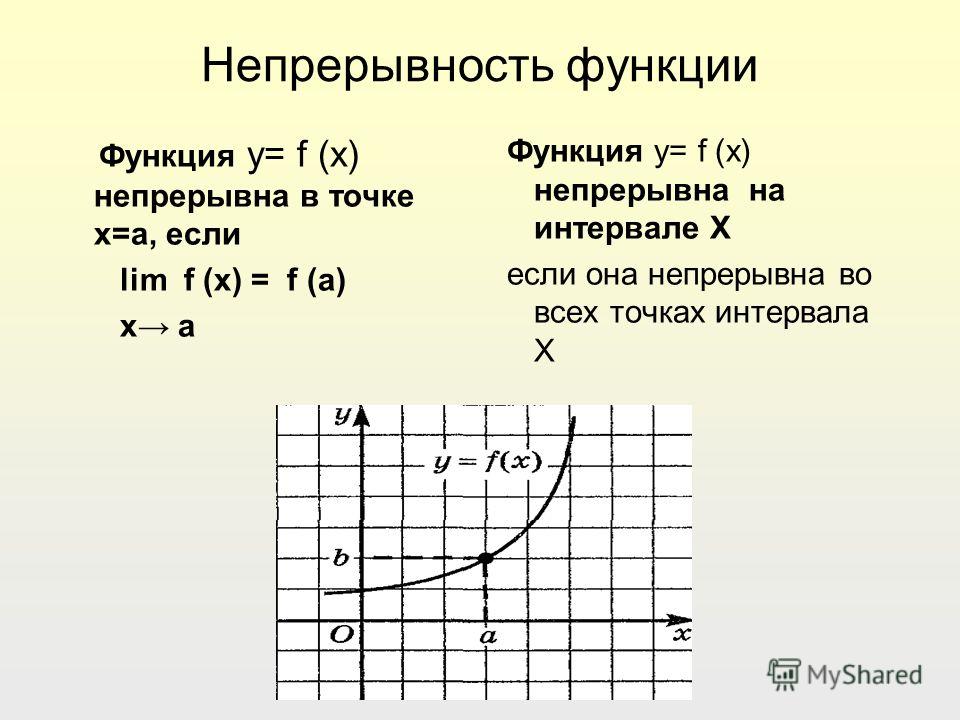

 е. значением y) при a .
е. значением y) при a . Предполагая, что предел существует, «непрерывность в конечной точке» означает, что функция непрерывна справа (для левого конца) или непрерывна слева (для правого конца).
Предполагая, что предел существует, «непрерывность в конечной точке» означает, что функция непрерывна справа (для левого конца) или непрерывна слева (для правого конца).


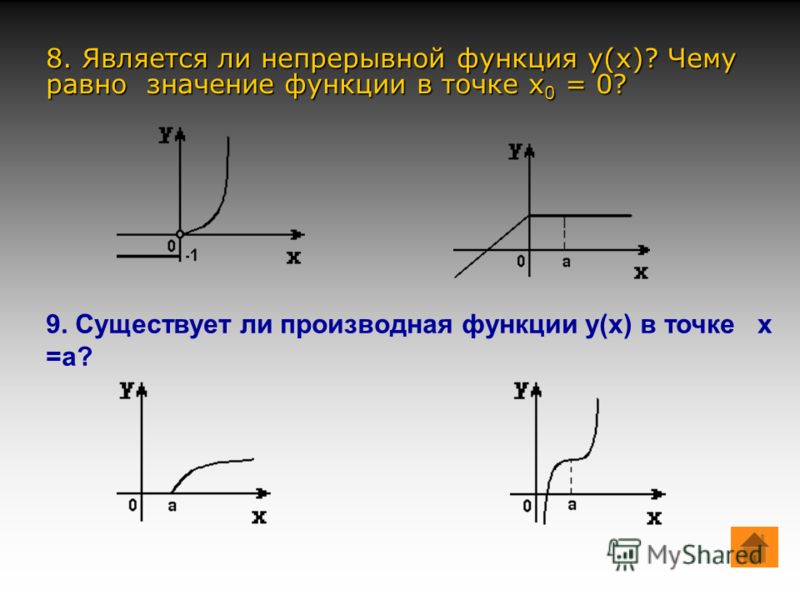 Ваши весы в ванной, вероятно, округляют до одной десятой фунта, поэтому вы можете весить 151,1 фунта. Но вы действительно? Вы можете весить 151,14 или 151,143. Возможности для веса безграничны.
Ваши весы в ванной, вероятно, округляют до одной десятой фунта, поэтому вы можете весить 151,1 фунта. Но вы действительно? Вы можете весить 151,14 или 151,143. Возможности для веса безграничны.
 Если вы купили 0 товаров, то не было куплено ни одного количества.
Если вы купили 0 товаров, то не было куплено ни одного количества.