Сложение и вычитание смешанных чисел, дробная часть с одинаковыми знаменателями
Тему «Сложение и вычитание смешанных чисел» рассмотрим в два этапа для более лучшего восприятия. В данной статье рассмотрим как складываются и вычитаются смешанные числа с дробной частью, которая имеет дроби с одинаковыми знаменателями (как правило, данная тема изучается в 5 классе). Как складываются смешанные числа с дробной частью, имеющей дроби с разными знаменателями, рассмотрим отдельно, в другой статье (изучается в 6 классе). Все правила наизусть!!! Тема не сложная, но напрячься чуть надо… Ну что, набираемся терпенья и поехали…
Для сложения данных смешанных чисел действует следующее правило.
Правило. При сложении (вычитании) смешанных чисел целые части складываем (вычитаем) отдельно, а дробные отдельно. (Т.е. «целые с целыми», «дробные с дробными»).
Как применяется правило?
Рассмотрим пример на сложение.
Выполнить действие.
Решение.
Определяем, где целые и где дробные части. Целые части — это 5 и 3, дробные части — это . А дальше начинаем складывать по правилу: целые с целыми, дробные с дробными. Как сложить целые числа, думаю, проблем не возникнет. Сложение дробных частей представляет собой сложение дробей с одинаковыми знаменателями, для тех, кто не знает как выполнить такое сложение можно посмотреть здесь. Т.е.
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число число пойдет в ответ.
На первых этапах решения таких примеров лучше все расписывать, после, когда уже «рука набьется», можно записывать короче:
Рассмотрим примеры на вычитание.
Случай I. Дробная часть уменьшаемого больше дробной части вычитаемогоРассмотрим следующий пример.
Выполнить действие.
Решение.
Начинаем решение примера с определения целых и дробных частей. Целые части — это 6 и 3, дробные части это . А дальше начинаем вычитать по правилу. Как вычитать целые числа, думаю, проблем не возникнет. Вычитание дробных частей представляет собой вычитание дробей с одинаковыми знаменателями, для тех, кто не знает как выполнить такое сложение можно посмотреть здесь. Т.е.
Не забываем про рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
На первых этапах решения таких примеров лучше все расписывать, после, когда уже «рука набьется», можно записывать короче:
Случай II. Дробная часть уменьшаемого меньше дробной части вычитаемого.
При решении примеров на вычитание смешанных чисел может встретиться случай, когда дробная часть уменьшаемого меньше дробной части вычитаемого. Как поступать в этом случае?
Как поступать в этом случае?
Рассмотрим на примере.
Выполните действие.
Решение.
Смотрим на пример и видим, что перед нами вычитание смешанных чисел. Как обычно поступаем со сложением (вычитанием) смешанных чисел: «складываем (вычитаем) целое с целым, дробное с дробным». Но не тут — то было: (7-3) – сможем вычесть, а вот из — не сможем. Как поступить с вычитанием дробных частей? Рассуждаем. Когда мы сможем вычесть? Когда первая дробь будет больше второй, поэтому наша задача состоит в том, чтобы увеличить первую дробь. Каким же образом будем увеличивать? Очень просто, будем у 7 «забирать» единицу и добавлять ее к дроби и затем «превратим» ее в неправильную… Ну что, поехали…
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Что же делаем в данном случае, когда будем вычитать дробь из натурального числа, и если будем вычитать смешанное число из натурального числа.
Рассмотрим примеры.
Выполнить действие.
Решение.
В данном примере надо выполнить действие на вычитание дроби из целого числа. Что же делаем? У 3 «забираем» единицу, почему же единицу, чем она хороша в данном случае? Да потому, что ее можно представить в виде дроби с одинаковым числителем и знаменателем, т.е. и т.д.
В нашем случае будем ориентироваться на дробь , точнее на ее знаменатель. У нее знаменатель равен 8, тогда и нашу 1 будем представлять в виде дроби . А далее выполняем нужное нам действие: вычитание смешанных чисел.
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Таким же образом поступаем и в следующем примере на вычитание смешанного числа из целого.
Выполнить действие.
Решение.
Не забываем про рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Что осталось сделать по данной теме, так это отработать навыки решения.
Большую проблему вызывает вычитание смешанных чисел. Поэтому, у кого есть вопросы, смотрим внимательно видео и пытаемся разобраться. Рекомендую посмотреть разбор всех примеров, каждый из которых хорош по — своему.
P.S. Есть второй способ вычитания (сложения), который, по моему мнению хорош, когда мы работаем с маленькими числами. Если его применять для сложения и вычитания любых смешанных чисел, то можно в результате получить «работу» с большими числами, что может привести к арифметическим ошибкам. Поэтому в видео его не рассматриваю. Применять можно, если ориентироваться, где и когда он будет рационален.
Поэтому в видео его не рассматриваю. Применять можно, если ориентироваться, где и когда он будет рационален.
Просто и доступно о сложении смешанных чисел. Рассматриваем примеры на применение правила сложения смешанных чисел, при этом обращаем внимание на то, каким должен быть ответ, т.е. пример должен быть до конца решенным.
P.S. Есть второй способ вычитания (сложения), который, по моему мнению, хорош, когда мы работаем с маленькими числами. Если его применять для сложения и вычитания любых смешанных чисел, то можно в результате получить «работу» с большими числами, что может привести к арифметическим ошибкам. Поэтому в видео его не рассматриваю.
)» src=»https://www.youtube.com/embed/vOtjanJX2G0?feature=oembed&wmode=opaque» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Технологическая карта урока алгебры на тему «Решение рациональных уравнений»
Технологическая карта урока №8:
Педагог: Самуткин Элезарь Валериянович
Предмет: Алгебра. Класс: 8
Учебник (УМК): С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. Алгебра. 8 класс. – М.: Просвещение, 2018. – 303 с.
Тема урока: Решение рациональных уравнений.
Тип урока: Комбинированный.
Оборудование: компьютер, мультипроектор.
Цель темы как достигаемые образовательные результаты:
создать условия для формирования представлений о решении произвольных рациональных уравнений, левые и правые части которых – целые или дробно-рациональные выражения.
Предметные: сформировать у обучающихся умение решать рациональные уравнения с произвольной левой и правой частью.
Метапредметные:
Регулятивные – уметь ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку, осуществлять оценку результата действия, различать способ и результат действия; корректировать процесс (решения рациональных уравнений с произвольной правой частью), оценивать правильность выполнения действий;
Коммуникативные – планировать учебное сотрудничество, уметь вести диалог, аргументированно высказывать свои суждения, договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов; умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи; выстраивать аргументацию, приводить примеры и контрпримеры;
Познавательные – уметь читать математический текст и находить информацию в учебнике по заданной теме, на наглядно-интуитивном уровне проводить наблюдение, анализ и делать выводы; подведение под понятие (рационального уравнения, равносильности уравнений), логически мыслить, рассуждать; работать по правилу, алгоритму и образцу, владеть общим приемом решения уравнений; рефлексия и оценка способов и условий действия;
Личностные: смыслообразование (обучающийся задается вопросом, какое значение имеет изучение данного понятия), формирование ответственного отношения к успешной учебной деятельности.
Цели урока как планируемые результаты обучения, планируемый уровень достижения целей: обучающийся выделяет равносильные уравнения и неравносильные, применяет равносильные преобразования для приведения произвольного рационального уравнения к уравнению, одна часть которого алгебраическая дробь, а другая – нуль, применяет алгоритм решения таких уравнений, исследует число корней уравнения.
Уровень/планируемый результат | Способ оценивания результата |
Знание: способность воспроизвести правило решения рационального уравнения с произвольной левой и правой частью | Опрос, взаимопроверка и взаимооценка |
Понимание: способность различить равносильные уравнения от неравносильных, применять равносильные преобразования для приведения рационального уравнения к требуемому виду. | Групповая и самостоятельная работа над учебными примерами с итоговой проверкой |
Применение: способность привести примеры равносильных преобразований рациональных уравнений до уравнения, одна часть которого алгебраическая дробь, а другая – нуль. | Опрос, презентация |
Анализ: способность анализировать уравнения в зависимости от состава левой и правой части, возможности его приведения к уравнению с нулевой правой частью, сделать вывод о равносильности проводимых преобразований, о числе корней | В ходе модерации |
Синтез: умение преобразовать разные типы уравнений и устанавливать их равносильность, обобщать методы равносильных преобразований, обосновывать отсутствие посторонних корней, потери корней. | В ходе фасилитации, опроса и самопрезентации |
Оценка: способность формулировать правило решения произвольных рациональных уравнений и аргументировать вывод о числе их корней. | Тест. Взаимооценка по ходу решения примеров. |
Технологическая карта урока №8 (продолжение)
Этап урока | Время, мин | Деятельность учителя | Деятельность учеников (УЧЕБНОЕ ЗАДАНИЕ) |
1.Мотивационно- организационный | 5 мин | Слайд №1 Представляется набор примеров рациональных уравнений, среди которых имеются и нерешаемые на данном уровне. «Группируйте данные уравнения по их способам решения: а) x+2=10 б) 3x=24 в) г) x(x – 5)=0 д) =0 е) » | Ученики просматривают слайд в ходе подготовки к занятию, обсуждают между собой, делают пометки в тетради, размышляют о теме урока. |
2. Создание проблемной ситуации | 3 мин | Понимание: Модерация «По каким группам вы их могли разделить?» Знание, анализ: Какие виды уравнений, содержащих алгебраические дроби, вы знаете и умеете решать? | Выскажите своё мнение, к какому виду относится каждая группа уравнений? Перечислите виды уравнений, содержащих алгебраические дроби, которые вы знаете? |
3. Постановка проблемы | 3 мин | Анализ, применение: Управление дискуссией: «Какой тип уравнений вы не умеете решать?» | Сделайте вывод о возможности решения этих уравнений известными вам способами. Предложите способ, как их привести к известному вам виду. |
4. Выдвижение предположений и гипотез | 3 мин | Применение, понимание: Модерация. «Как можно назвать уравнения данного вида?» «Как по вашему мнению можно решить данные уравнения?» «Какие действия мы можем выполнить, чтобы получить равносильные уравнения?» | Определите, что из себя представляет левая и правая часть уравнения? Предложите, как можно решить данные уравнения? Докажите, что их можно привести к известному вам виду и решать дальше по известному алгоритму. |
5. Доказательство гипотезы и решение проблемы | 10 мин | Анализ: Подведение под понятие «Равносильные рациональные уравнения». (№317) (Слайд №2) | Работая в парах, выясните, какие из перечисленных уравнений являются равносильными? Отделите равносильные уравнения от не равносильных. |
6. Проверка решения | 16 мин | Применение, оценивание: Фасилитация. Оценка работы товарищей. (№318 а,б). («Можете ли решить следующие уравнения по сформулированному алгоритму?») | Примените алгоритм решения рационального уравнения приведением к уравнению, одна часть которого алгебраическая дробь, а другая – нуль. Оцените работу товарищей, обоснуйте правильность решения. |
7. Домашнее задание | 3 мин | Анализ и синтез: Проанализируйте алгоритм решения уравнения с произвольными левыми и правыми частями (п. 5.5), решите №319. | |
дробей — что такое дробь?
Дробь определяется как часть целого. Дробь часто используется не только в математике, но и в реальной жизни. Древние египтяне были первыми людьми, которые начали использовать дроби. Они использовали его в своих повседневных жизненных проблемах, таких как раздача еды и припасов. Слово «фракция» происходит от латинского слова «fractus», что в переводе с английского означает «сломанный», и соответствует значению дроби. Давайте подробнее узнаем о дробях и их типах.
Древние египтяне были первыми людьми, которые начали использовать дроби. Они использовали его в своих повседневных жизненных проблемах, таких как раздача еды и припасов. Слово «фракция» происходит от латинского слова «fractus», что в переводе с английского означает «сломанный», и соответствует значению дроби. Давайте подробнее узнаем о дробях и их типах.
Что такое дробь?
Фракции определяются как часть целого. Дроби — это числовое значение, которое может быть частью или частью любого количества, где количество может быть любым. Итак, дроби – это часть или часть величины. Ниже приведен пример дробей, пицца делится на 8 равных частей, и каждая часть является долей всей пиццы, поэтому части — это доли пиццы, то есть количество (целое). Если вынуть одну часть, она представляется как 1/8 в форме дроби. Дробь может быть записана разными способами,
- Одна восьмая
- 1/8
- 1 на 8
Остальные части вместе составляют 7/8 пиццы на данный момент; осталось всего 7 шт. Точно так же, если вынуть 2 куска, они составят 2/8 всей пиццы. Его можно упростить и записать как 1/4.
Точно так же, если вынуть 2 куска, они составят 2/8 всей пиццы. Его можно упростить и записать как 1/4.
Части дроби
Дробь состоит из двух частей, т. е. числителя и знаменателя. Число, указанное сверху, называется числителем, а число, расположенное внизу, называется знаменателем. Часть числителя определяет количество частей целого, тогда как знаменатель определяет общее количество равных частей в целом. Числитель и знаменатель разделены дробной чертой.
- Числитель : Числитель представляет часть дроби. Это верхняя часть дроби.
- Знаменатель : Знаменатель представляет собой целое, на которое делится дробь. Это нижняя часть дроби.
Операции с дробями
Операции с дробями — это простые арифметические операции, такие как сложение, умножение, деление и т. д. Давайте посмотрим на операции, которые мы можем выполнять с дробями:
Сокращение дробей
Сокращение дробей — это упрощение дробей путем деления числителя и знаменателя на одно и то же значение. Важно отметить, что деление их на 1 не изменит дробь.
Важно отметить, что деление их на 1 не изменит дробь.
Пример: Сократите дробь ⇢ 88/42
Решение:
88/42 — неправильная дробь, и числитель, и знаменатель делятся на 2. Деление их на 2 = 8:
3 3 44/21
Таким образом, сокращенная дробь становится 44/21.
Умножение дробей
Умножение дробей не требует общего знаменателя. Здесь просто числитель умножается на числитель другой дроби, а знаменатель умножается на знаменатель. Его также можно упростить впоследствии, если дробь можно уменьшить. Дроби также могут быть упрощены при умножении друг на друга.
Пример: Как умножать дроби, дроби 21/5 и 35/12.
Решение:
Умножение дробей:
Сложение дробей
Сложение дробей возможно только при совпадении знаменателей, знаменателей у дробей не совпадают важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель.
Найдите НОК дробей, чтобы найти общий знаменатель.
Пример: Как сложить дроби 4/5 и 7/3.
Решение:
Здесь знаменатели обеих дробей не совпадают, НОК 3 и 5 равен 15,
Деление дробей
Деление дробей не требует каких-либо общих знаменателей. Самый простой способ делить дроби — перевернуть дробь после знака деления, то есть сделать дробь обратным образом и изменить знак с деления на умножение. Теперь просто примените правила умножения дробей и решите.
Пример: Как разделить дроби 35/20 и 5/10.
Решение:
Деление дробей: 35/20 ÷ 7/10
Переворот дроби после знака деления и замена знака на знак умножения:
35/20 × 10/7
Сокращение дробей :
7/4 × 10/7 = 70/28 = 10/4 = 5/2
Следовательно, ответ 5/2.
Вычитание дробей
Вычитание дробей возможно только при условии, что знаменатели совпадают. В случае, если знаменатели дробей не совпадают, важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель.
В случае, если знаменатели дробей не совпадают, важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель.
Пример: Вычтите дроби 1/2 из 3/5.
Решение:
Наименьший общий знаменатель 2 и 5 равен 10. Решение:
Свойства дробей
Существуют некоторые важные свойства дробей, аналогичные целым числам и т. д. Давайте посмотрим на эти свойства:
- Для сложения дробей и умножения дробей верны коммутативные и ассоциативные свойства.
- Дробное умножение дает 1, а элемент идентичности равен 0.
- Мультипликативное обратное свойство возвращает дробь. То есть a/b — это b/a, где a и b — ненулевые числа.
- Распределительное свойство умножения над сложением верно для дробей.
В основном существует четыре типа дробей. Это единичные дроби, правильные дроби, неправильные дроби и смешанные дроби. Они классифицируются на основе их числителя и знаменателя. Давайте узнаем обо всех четырех типах подробно:
Они классифицируются на основе их числителя и знаменателя. Давайте узнаем обо всех четырех типах подробно:
Дробная единица
Дробная единица определяется как дробь с 1 в качестве числителя и известна как дробная единица, например – 1/8, 1/10, 1/4, 1/6, 1/11, и т. д. Можно сказать, что все единичные дроби являются правильными дробями, поскольку все единичные дроби имеют 1 в числителе, что меньше знаменателя. Приведенный ниже пример очень хорошо объясняет дробь единицы. Здесь торт делится на 4 равные части. Если весь торт равен 1, то каждая четверть торта — это дробь 1/4.
Правильная дробь
Правильная дробь определяется как дробь, в которой значение числителя меньше значения знаменателя. Она известна как правильная дробь, например, 4/9, 1/10, 2/5, 3/7, 5/9 и т. д.
Неправильная дробь дробь, у которой значение числителя больше значения знаменателя, то она называется неправильной дробью, например, 6/5, 11/10, 11/5, 5/3, 2/1 и т.
 д.
д.Смешанная дробь
Смешанная дробь состоит из целого числа с соответствующей дробью и называется смешанной дробью. Например, если 2 — целое число, а 1/4 — дробь, то 2¼ — смешанная дробь.
Другие типы дробей
Другие типы дробей основаны на группах. Они включают в себя подобные и неодинаковые дроби и эквивалентные дроби. Ниже подробно описаны все три типа дробей.
Подобные дробиДве или более двух дробей с одинаковыми знаменателями называются подобными дробями. Примеры подобных дробей:
- 2/9, 3/9, 5/9, 9/9, 4/9 (Здесь знаменатели всех дробей одинаковы, то есть 9).
- 3/10, 7/10, 1/10, 9/10, 6/10 (Здесь знаменатели у всех дробей одинаковые, то есть 10).
- 1/7, 2/7, 4/7, 5/7, 7/7, 8/7.
- 1/2, 7/2, 6/2, 5/2, 9/2.
- 7/5, 1/5, 4/5, 3/5.
Дроби с разными знаменателями называются разнородными дробями. Пример, в отличие от дробей,
Пример, в отличие от дробей,
- 9/2, 1/6, 5/4, 7/3 (Здесь знаменатель у всех дробей разный).
- 1/2, 1/4, 2/3, 5/6, 8/9 (здесь знаменатель у всех дробей разный).
- 3/8, 2/3, 3/5, 2/7.
- 1/9, 2/7, 3/4, 2/5, 3/2.
- 4/2, 1/6, 2/3, 7/5.
Эквивалентные дроби определяются как те дроби, которые после упрощения дают одно и то же значение, и тогда они эквивалентны друг другу. Равнозначные дроби можно решить, умножив числитель и знаменатель на одно и то же число или разделив числитель и знаменатель на одно и то же число. Ниже приведены некоторые примеры эквивалентных дробей:
Пример. Найдите две эквивалентные дроби числа 4/12.
Решение:
Эквивалентная дробь путем умножения на то же число, умножим на 2:
(4 × 2)/(12 × 2)
= 8/24
Деление эквивалентной дроби на 2 одно и то же число, здесь и числитель, и знаменатель делятся на 4, делящиеся на 4:
(4 ÷ 4)/(12 ÷ 4)
= 1/3
Дробь в числовой строке
Дроби в числовая линия представлена между интервалом двух целых чисел. Дробь – это часть целого. Следовательно, целое делится на равные части, количество частей между целыми числами определяется значением знаменателя, а значением числителя является точка, в которой лежит дробь. Например, если нам требуется представить 1/8 на числовой прямой, деление будет между 0 и 1, а так как 8 в знаменателе, то целое делится на 8 равных частей, где первая представляет 1/8 . Точно так же вторая часть представляет 2/8 и так далее.
Дробь – это часть целого. Следовательно, целое делится на равные части, количество частей между целыми числами определяется значением знаменателя, а значением числителя является точка, в которой лежит дробь. Например, если нам требуется представить 1/8 на числовой прямой, деление будет между 0 и 1, а так как 8 в знаменателе, то целое делится на 8 равных частей, где первая представляет 1/8 . Точно так же вторая часть представляет 2/8 и так далее.
Как преобразовать дроби в десятичные?
Десятичные числа — это числа, представляющие дроби, но в десятичной форме. Например, 1/4 дроби можно записать как 0,25 в десятичной форме. Десятичные числа в основном предпочтительнее, так как их можно использовать для нескольких математических операций, где решение дробей кажется сложным, например, сложение, вычитание и т. д. Например: чтобы сложить 1/2 и 1/4, проще решать десятичные дроби. . Преобразование дробей в десятичные ⇢ 0,5 + 0,25 = 0,75.
Как преобразовать десятичную дробь в дробь?
Десятичные числа преобразуются в десятичные, так как иногда математические операции легко решаются в дробной форме. Математические операции, такие как умножение и деление, иногда проще выполнять с дробями. Ниже приведены шаги, которые можно выполнить, чтобы преобразовать десятичную дробь в дробь:
Математические операции, такие как умножение и деление, иногда проще выполнять с дробями. Ниже приведены шаги, которые можно выполнить, чтобы преобразовать десятичную дробь в дробь:
- Преобразовать десятичную дробь в форму p/q, где q = 1.
- Теперь умножьте числитель и знаменатель на 10, пока числитель не станет целым числом из десятичные дроби. Например, если после запятой два числа, умножьте 100/100.
- Теперь упростите полученную дробь.
Значение числа Пи в дробях
Пи (π) — это математическая константа, определяемая как отношение длины окружности к ее диаметру. Значение числа пи в десятичном виде примерно равно 3,14. Значение числа пи (π) в дробях равно 22/7. Значение числа пи используется как в десятичной, так и в дробной форме в зависимости от типа заданного вопроса.
Например: преобразовать 0,8 в дробь.
- Преобразовать в форму p/q ⇢ 0,8/1
- Умножить 10/10 ⇢ 0,8/1 × 10/10
- Упрощающая дробь ⇢ 8/10 = 4/5.
Решенные примеры на дроби
Вопрос 1: Запишите две эквивалентные дроби 3/39.
Решение:
Эквивалентная дробь путем умножения на то же число, давайте умножим на 2:
(3 × 2)/(39 × 2)
= 6/78
с эквивалентной дробью делением одно и то же число, здесь и числитель, и знаменатель делятся на 3, деление на 3:
(3 ÷ 3)/(39 ÷ 3)
= 1/13
Вопрос 2: В классе из 90 учеников 1/3 учеников не любит крикет. Сколько студентов любят крикет?
Решение:
Доля учеников, которые не любят крикет = 1/3
Доля учеников, которые любят крикет = 1 – 1/3
= (3 – 1)/3
2 /3 ученики любят крикет.
Количество учащихся, которым нравится крикет = 2/3 × 90
= (2 × 30)
= 60
Следовательно, 60 учащихся любят крикет.
Вопрос 3: Что это за дробь – 1/2, 1/5, 1/7, 1/10, 1/3?
Ответ:
Это а Единичная дробь, потому что все дроби имеют 1 в качестве числителя.
Вопрос 4: Определите вид дроби 7¼.
Ответ:
Смешанная дробь, потому что это комбинация целого числа и правильной дроби, в которой 7 — это целое число, а 1/4 — правильная дробь.
Вопрос 5: Чему равна дробь 7/5?
Ответ:
Чтобы найти эквивалент дроби 7/5, нам нужно умножить числитель и знаменатель на одно и то же число.
Следовательно, (7/5) × (2/2) = 14/10
Следовательно, эквивалентная дробь 7/5 равна 14/10.
Часто задаваемые вопросы о дробях
Вопрос 1: Что такое сравнение дробей?
Ответ:
Сравнение дробей делается для того, чтобы понять, какая из данных дробей больше, а какая меньше. Если знаменатели данных дробей одинаковы, сравнивают только числители, если дроби имеют разные знаменатели, то сначала берут НОК дробей, а затем сравнивают числители.
Например, при сравнении 3/19 и 7/19 можно заметить, что знаменатели одинаковы, следовательно, сравниваются числители, 3 > 7, следовательно, 7/19 > 3/19..
Вопрос 2: Как умножать дроби?
Ответы:
Умножение дробей не требует общего знаменателя. Здесь просто числитель умножается на числитель другой дроби, а знаменатель умножается на знаменатель. Его также можно упростить впоследствии, если дробь можно уменьшить. Дроби также могут быть упрощены при умножении друг на друга. Например: 3/7 × 1/2 = 3/14.
Вопрос 3: Как делить дроби?
Ответ:
Для деления дробей не требуется никаких общих знаменателей, самый простой способ разделить дроби — перевернуть дробь после знака деления, то есть произвести обратную дробь и изменить знак с деления на умножение. . Теперь просто примените правила умножения дробей и решите. Например: 4/9 ÷ 2/3 = 4/9 × 3/2 = 2/3.
Вопрос 4: Как складывать дроби?
Ответ:
Сложение дробей возможно только при одинаковых знаменателях, если знаменатели дробей не совпадают, важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель. Например: 3/4 + 1/2 = 3/4 + 2/4 = 5/4.
Вопрос 5: Что такое неправильная дробь?
Ответ:
Неправильная дробь определяется как дробь, в которой значение числителя больше значения знаменателя, тогда она известна как неправильная дробь, например, 7/5, 13/10, 9/5, 17/3, 5/1 и т. д.
Вопрос 6: Какую часть дня составляют 8 часов?
Ответ:
Мы знаем, что в 1 дне 24 часа.
1 час = 1/24 дня
8 часов = 1/24 × 8 дней
8 часов = 8/24 = 1/3 дня
Следовательно, в 8 часах 1/3 дня.
Похожие статьи
- Целые числа
- Натуральные числа
- Вещественные числа
Функция дробной части | Brilliant Math & Science Wiki
Патрик Корн, Кристофер Уильямс, Хамза А, и
способствовал
Содержимое
- Свойства дробной части
- Решение проблем
- Дробные части и интегральное исчисление
Ниже приведены некоторые свойства дробной части:
- \( 0 \le \{ x \} < 1 \) и \( 0 = \{ x \} \) тогда и только тогда, когда \( x \) является целым числом.
- \( \{x \} + \{-x\} = \begin{cases} 0 & \text{если } x \text{ является целым числом} \\ 1 & \text{иначе.} \end{cases } \)
- Если \( a \) и \( b \) являются целыми числами и \( b > 0 \), то \( \big\{ \frac{a}{b} \big\} = \frac{r}{b } \), где \( r \) — остаток от деления \( a \) на \( b \).
\( \{ 9 \} + \{-9\} = 0+0 = 0 \), но \( \{9,01\} + \{-9,01\} = 0,01+0,99 = 1 \). Дробная часть всегда неотрицательна.
Так как \( 47 = 13 \cdot 3 + 8 \), то \( \left\{\frac{47}{13} \right\} = \frac{8}{13}\).
Для задач, связанных с функцией пола и функцией дробной части, часто помогает (для простоты записи) запись \( x = n+r ,\) где \( n = \lfloor x \rfloor \) и \ ( г = \{х\} \). Тогда \( n \) является целым числом и \( 0 \le r < 1 \). 92+10r-2 &= 0, \end{выравнивание} \]
, поэтому \( r = \frac{-5+\sqrt{29}}2\) по квадратичной формуле.
Следовательно, \( x = 5 + r = \frac{5+\sqrt{29}}2\).
\[ \left \{\frac 1x \right \} = \{ x \} \]
Найдите число решений \(x\) в диапазоне \([1,6] \) такое, что приведенное выше уравнение выполняется.
Обратите внимание, что \( \{ x \} \) обозначает дробную часть \(x\).
Найдите наименьшее действительное число \( m \) такое, что для всех положительных действительных чисел \( x \),
\[ \{ x \} + \left\{ \frac1{x} \right\} < m. \]
Если \( x < 1 \), мы можем написать \( x = \frac1y, y \ge 1, \) и \( \{ x \} + \big\{ \frac1{x} \big\} = \{ y \} + \big\{ \frac1{y} \big\}. \) Таким образом, мы можем считать \( x \ge 1 \). Тогда \( \big\{ \frac1{x} \big\} = \frac1{x}\). При записи \( x = n+r \), где \(n \) является положительным целым числом, левая часть становится равной
.\[ г + \frac1{n+r}. \]
Для фиксированного \( r \) это максимизируется при минимизации знаменателя, т.е. \(n = 1 \). 9- \), сумма переходит в \( 1+\frac1{1+1} = \frac{3}{2} \).

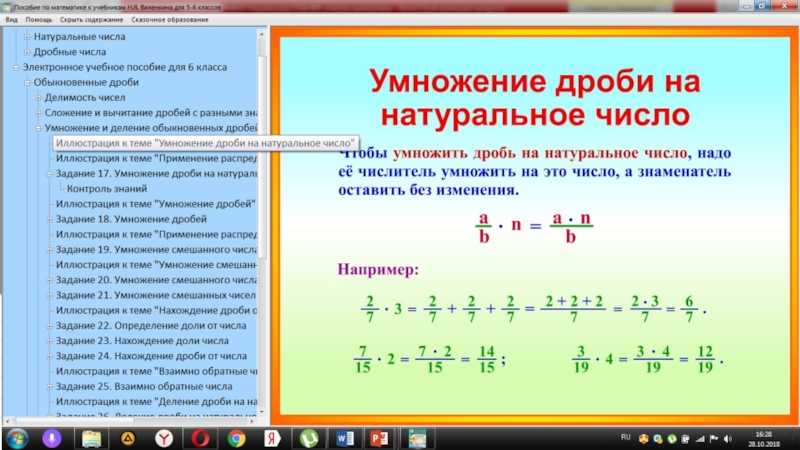



 Сделайте вывод, какие способы решения можно использовать дальше?
Сделайте вывод, какие способы решения можно использовать дальше?

 Например, при сравнении 3/19 и 7/19 можно заметить, что знаменатели одинаковы, следовательно, сравниваются числители, 3 > 7, следовательно, 7/19 > 3/19..
Например, при сравнении 3/19 и 7/19 можно заметить, что знаменатели одинаковы, следовательно, сравниваются числители, 3 > 7, следовательно, 7/19 > 3/19..

