Решение дробных уравнений 7 класс: Уравнения с дробями 7 класса онлайн

способы и алгоритм решения, примеры задач

Определение основных понятий по теме

Рациональным выражением является такое выражение в алгебре, в состав которого включены числа и переменная х, а также операции сложения, вычитания, умножения, деления, возведения в степень с натуральным показателем. Если пара рациональных выражений объединены знаком равенства, то перед нами рациональное уравнение.

Определение 

Дробно-рациональное уравнение представляет собой не имеющее знак корня рациональное уравнение, в котором обе части записаны в виде дробных выражений.

В дробно-рациональном уравнении имеется как минимум одна дробь, содержащая в знаменателе переменную.

Пример 

Например, дробно-рациональными уравнениями являются:

9×2-13x=0

12x+xx+1=12

6x+1=x2-5xx+1

Уравнения, которые нельзя отнести к дробно-рациональным:

9×2-13=0

x2+8×2=6

Алгоритм решения дробно-рациональных уравнений

В процессе решения дробно-рациональных уравнений требуется правильно определить область допустимых значений (ОДЗ). Когда корни уравнения найдены, следует проверить их на соответствие ОДЗ и выяснить, какие являются допустимыми. В противном случае образуются посторонние решения, что автоматически делает ответ неверным.

Предусмотрен стандартный алгоритм действий для поиска корней дробно-рациональных уравнений:

1. Выписать и определить ОДЗ.
2. Вычислить общий знаменатель дробей.
3. Найти произведение каждого члена уравнения и общего знаменателя. После чего следует сократить полученные дроби, чтобы избавиться от знаменателей.
4. Записать уравнение со скобками.
5. Раскрыть скобки и привести подобные слагаемые.
6. Найти корни уравнения, которое получилось после раскрытия скобок.
7. Сверить найденные корни с ОДЗ.
8. Решения, которые успешно прошли проверку, записать в ответ.

Примеры решения задач

Задача 1

Требуется найти корни дробно-рационального уравнения:

xx-2-7x+2=8×2-4

Решение

Рассмотрим уравнение из условия задания:

xx-2-7x+2=8×2-4

Определим область допустимых значений:

x-2≠0⇔x≠2

x+2≠0⇔x≠-2

x2-4≠0⇔x≠±2

Воспользуемся формулой сокращенного умножения:

xx-2-7x+2=8×2-4

x2-4=(x-2)(x+2)

В таком случае, общим знаменателем является следующее выражение:

 (x-2)(x+2)

Согласно стандартной последовательности действий, найдем произведение каждого члена уравнения и (x-2)(x+2):x(x-2)(x+2)x-2-7(x-2)(x+2)x+2=8(x-2)(x+2)(x-2)(x+2)

Выполним сокращение:

x(x+2)-7(x-2)=8

Раскроем скобки:

x2+2x-7x+14=8

Затем следует привести подобные слагаемые:

x2-5x+6=0

Решениями получившегося квадратного уравнения являются следующие корни:

x1=2

x2=3

Сравним результат вычислений с ОДЗ.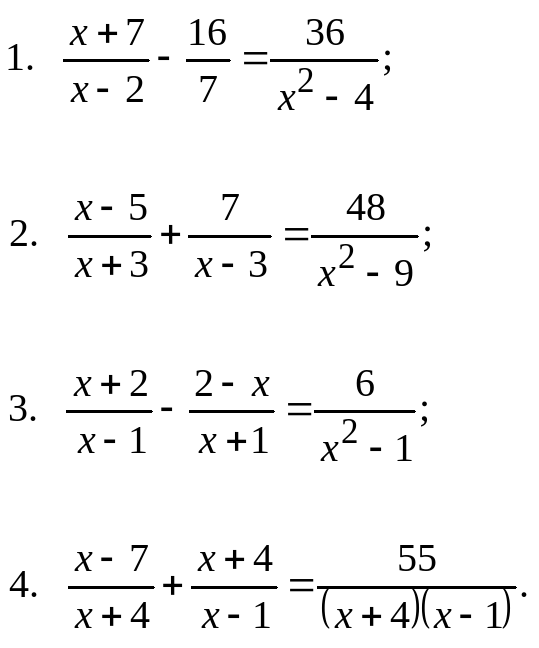 Зная, что x≠2, исключим первый корень, как посторонний. Запишем в ответ второй корень.

Ответ: 3.

Для закрепления материала и знаний метода решения дробно-рациональных уравнений попробуем решить еще одно задание с объяснением действий. Подобные задачи нередко приходится решать на уроках алгебры в восьмом классе.

Задача 2

Решить дробно-рациональное уравнение:

xx+2+x+1x+5-7-xx2+7x+10=0

Решение

Рассмотрим уравнение из условия задания:

xx+2+x+1x+5-7-xx2+7x+10=0

Определим область допустимых значений:

x+2≠0⇔x≠-2

x+5≠0⇔x≠-5

x2+7x+10≠0

D=49-4·10=9

x1≠-7+32=-2

x2≠-7-32=-5

Воспользуемся способом разложения квадратного трехчлена на множители:

ax2+bx+c=a(x-x1)(x-x2)

Преобразуем квадратный трехчлен x2+7x+10 с учетом найденных x1 и x2:

xx+2+x+1x+5-7-x(x+2)(x+5)=0

В результате общий знаменатель равен:

 (x+2)(x+5)

Умножим все части уравнения на общий знаменатель:

x(x+2)(x+5)x+2+(x+1)(x+2)(x+5)x+5—(7-x)(x+2)(x+5)(x+2)(x+5)=0

Выполним сокращение дробей:

x(x+5)+(x+1)(x+2)-7+x=0

Избавимся от скобок:

x2+5x+x2+3x+2-7+x=0

Приведем подобные слагаемые:

2×2+9x-5=0

Тогда получим корни уравнения:

x1=-5

x2=12

Соотнесем решения с областью допустимых значений, которую определили ранее. Первый корень является посторонним, что выявлено с помощью контрольной проверки. По этой причине в ответ следует записать только второй корень.

Ответ: 12.

Задания для самостоятельной работы

Задача 3

Найти корни уравнения:

x-12+2×3=5×6

Решение

x-12+2×3=5×6

3x-3+4×6=5×6

7x-3=5x

x=1,5

Ответ: 1,5

Задача 4

Требуется решить дробно-рациональное уравнение:

x-3x-5+1x=x+5x(x-5)

Решение

x-3x-5+1x=x+5x(x-5)

ОДЗ:

x≠5

x≠0

Получим:

x2-3x+x-5=x+5

x2-3x-10=0

x=5

x=-2

Согласно ОДЗ:

x=-2

Ответ: -2

Задача 5

Вычислить корни уравнения:

33+x29-x2+7+xx-3=-2+4-xx+3

Решение

33+x29-x2+7+xx-3=-2+4-xx+3

ОДЗ:

x≠3

x≠-3

-33-x2+(7+x)·(x+3)=-2(x2-9)+(4-x)·(x-3)

x2+x-6=0

x=-3

x=2

Согласно ОДЗ, первый вариант решения не подходит:

x=2

Ответ: 2

Уравнения. 5 класс — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Уравнения

Выполнила: Арзамас
Анастасия

2. 5 класс

Задачи на уравнение – 1 час
Уметь: анализировать условие задачи; иллюстрировать
схематически рисунками условие задачи; решать задачи на
уравнивание различными способами.

3. 6 класс. Выражения, формулы, уравнения

Решение уравнений – 1 час
Знать понятие: уравнение, решение уравнения, корень
уравнения. Уметь решать уравнения.
Решение задач уравнением – 1 час
Знать понятие: уравнение, решение уравнения, корень
уравнения. Уметь решать задачи уравнением.

4. 7 класс. Уравнения

Алгебраический способ решения задач. Составление
уравнений – 1 час
Знать понятие: уравнение. Уметь составлять уравнения.
Корни уравнения. Определение корня уравнения – 1 час
Знать понятие: корня уравнения. Уметь определять корни
уравнения.
Корни уравнения. Проверка корней – 1 час
Знать понятие: корня уравнения. Уметь определять корни
уравнения, делать проверку корней.
Решение уравнения. Правила преобразования уравнений –
1 час
Знать: простейшие правила преобразования уравнений.
Уметь решать простейшие уравнения.
Решение уравнений. Перенос слагаемых – 1 час
Знать: правило переноса слагаемых в уравнении. Уметь
решать уравнения.
Решение уравнений. Умножение на число – 1 час
Знать: правило умножения на число в уравнении. Уметь
решать уравнения.
Решение уравнений с дробной чертой – 1 час
Уметь: решать уравнения, содержащих дробную черту.
Решение уравнений. Отработка навыков – 1 час
Уметь: решать различные уравнения.
Решение задач с помощью уравнений. Анализ текста
задачи – 1 час
Уметь: анализировать текст задачи, решать простейшие
задачи с помощью уравнений.
Решение задач с помощью уравнений. Практические
правила составления уравнений к задаче – 1 час
Знать: практические правила составления уравнений к
задаче.Уметь решать задачи с помощью уравнений
Решение задач с помощью уравнений. Задачи на части,
соотношения – 1 час
Уметь: решать задачи на части и на соотношения с
помощью уравнений
Решение задач с помощью уравнений. Задачи на движение
– 1 час
Уметь: решать задачи на движение с помощью уравнени
Решение задач с помощью уравнений. Различные типы
задач – 1 час
Уметь: решать различные типы задач с помощью
уравнений
Какие уравнения называют квадратными – 2 часа
Формула корней квадратного уравнения – 4 часа
Знать: определение квадратного уравнения; что первый
коэффициент не может быть равен нулю.
Уметь: записать квадратное уравнение в общем виде;
неприведенное квадратное уравнение преобразовать в
приведенное; свободно владеть терминологией
Вторая формула корней квадратного уравнения – 2 часа
Знать: формулу корней квадратного уравнения.
Уметь: решать квадратные уравнения по формуле; решать
уравнения высших степеней заменой переменной
Решение задач – 3 часа
Уметь: составить уравнение по условию задачи; соотнести
найденные корни с условием задачи
Неполные квадратные уравнения – 3 часа
Знать: термин «неполное квадратное уравнение»; приемы
решения неполных квадратных уравнений.
Уметь: распознавать и решать неполные квадратные
уравнения
Теорема Виета – 2 часа
Знать: формулы Виета. Уметь применять теорему Виета
для решения упражнений
Разложение квадратного трехчлена на множители – 3 часа
Знать: что если квадратный трехчлен имеет корни, то его
можно разложить на множители; что если квадратный
трехчлен не имеет корней, то разложить его на множители
нельзя

12. 8 класс. Системы уравнений

Линейное уравнение с двумя переменными и его график – 3 часа
Уметь: выражать из линейного уравнения одну переменную через
другую; находить пары чисел, являющиеся решением уравнения;
строить график заданного линейного уравнения
Уравнение прямой вида у = кх +l – 3 часа
Системы уравнений. Решение систем способом сложения – 3 часа
Знать/понимать: уравнение прямой; алгоритм построения прямой.
Уметь: перейти от уравнения вида ах + by = с к уравнению вида y =
kx + l, указать коэффициенты к,1; схематически показать
положение прямой, заданной уравнением указанного вида; решать
системы способом сложения
Решение систем способом подстановки – 3 часа
Знать/понимать: если графики имеют общие точки, то
система имеет решения; если у графиков нет общих точек,
то система решений не имеет; алгоритм решения систем
уравнений.
Уметь: решать системы способом подстановки
Решение задач с помощью систем уравнений – 4 часа
Знать/понимать: значимость и полезность математического
аппарата.
Уметь: ввести переменные; перевести условие на
математический язык; решить систему или уравнение;
соотнести полученный результат с условием задачи
Задачи на координатной плоскости – 2 часа
Знать: геометрический смысл коэффициентов; условие
параллельности прямых.
Уметь: свободно решать системы линейных уравнений

15. 9 класс. Уравнения и системы уравнений

Рациональные выражения – 4 часа
Целые уравнения – 2 часа
Знать/понимать: смысл понятия «целые выражения» и
«целые уравнения»
Уметь: решать целые уравнения; применять полученные
знания при выполнении действий с целыми выражениями
и уравнениями
Дробные уравнения – 4 часа
Знать/понимать: смысл понятия «дробные уравнения»,
способы преобразования и решения дробных уравнений,
нахождения их корней
Уметь: выделять из ряда уравнений дробные,
преобразовывать их; решать дробные уравнения;
применять полученные знания при выполнении действий с
дробными выражениями и уравнениями
Знать/понимать: как составлять математическую модель
текстовой задачи и решать её
Уметь: составлять и решать текстовые задачи
Решение задач – 4 часа
Системы уравнений с двумя переменными – 4 часа
Знать/понимать: смысл понятия «системы уравнений с
двумя переменными», способы решения этих систем
Уметь: решать системы уравнений с двумя переменными
разными способами
Решение задач – 2 часа
Графическое исследование уравнений – 4 часа
Знать: способы исследования уравнения с помощью
графиков
Уметь: находить точки пересечения графиков различных
функций и исследовать уравнения с помощью графиков
Знать: основные способы решения задач и систем
уравнений
Уметь: применять полученные знания при решении задач и
систем уравнений

English     Русский Правила

Решение уравнений путем очистки дробей | Преалгебра |

Модуль 9: Многошаговые линейные уравнения

Результаты обучения

• Используйте наименьший общий знаменатель, чтобы исключить дроби из линейного уравнения перед его решением
• Решение уравнений с дробями, требующее нескольких шагов

Вы можете чувствовать себя ошеломленными, когда видите дроби в уравнении, поэтому мы собираемся показать метод решения уравнений с дробями, в котором вы используете общий знаменатель, чтобы исключить дроби из уравнения. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей.

Обратите внимание, что каждый член уравнения умножается на наименьший общий знаменатель. Вот что делает его равным оригиналу!

ПРИМЕР

Решите:

18x+12=14\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}81​x+21​=41​

.

Решение:

	18x+12=14LCD=8\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\quad{LCD=8}81​x+21​=41 ЖК-дисплей=8
Умножьте обе части уравнения на этот ЖК-дисплей, 888 . Это очищает дроби.	8(18x+12)=8(14)\color{red}{8(}\frac{1}{8}x+\frac{1}{2}\color{red}{)}=\color {red}{8(}\frac{1}{4}\color{red}{)}8(81​x+21​)=8(41​)
Использовать Распределительное свойство.	8⋅18x+8⋅12=8⋅148\cdot\frac{1}{8}x+8\cdot\frac{1}{2}=8\cdot\frac{1}{4}8⋅ 81​x+8⋅21​=8⋅41​
Упростите — и заметьте, больше никаких дробей!	х+4=2х+4=2х+4=2
Решите, используя общую стратегию решения линейных уравнений.	x+4−4=2−4x+4\цвет{красный}{-4}=2\цвет{красный}{-4}x+4−4=2−4
Упрощение.	х=-2х=-2х=-2
Проверить: Пусть x=−2x=-2x=−2 18x+12=14\frac{1}{8}x+\frac{1}{2}=\frac{1}{4} 81​x+21​=41​ 18(−2)+12=?14\frac{1}{8}(\color{red}{-2})+\frac{1}{2}\ stackrel{\text{?}}{=}\frac{1}{4}81​(−2)+21​=?41​ −28+12=?14\frac{-2}{8} +\frac{1}{2}\stackrel{\text{?}}{=}\frac{1}{4}8−2​+21​=?41​ −28+48=?14\frac{-2}{8}+\frac{4}{8}\stackrel{\text{?}}{=}\frac{1}{4}8−2 ​+84​=?41​ 28=?14\frac{2}{8}\stackrel{\text{?}}{=}\frac{1}{4}82​=?41​ 14=14✓\frac{1}{4}=\frac{1}{4}\quad\checkmark41​=41​✓

В последнем примере наименьший общий знаменатель был

888

. Теперь ваша очередь найти ЖК-дисплей и очистить дроби, прежде чем решать эти линейные уравнения.

Обратите внимание, что после того, как мы очистили уравнение дробей, оно стало таким же, как те, которые мы решали ранее в этой главе. Мы изменили задачу на ту, которую уже знали, как решить!

Решите уравнения, очистив знаменатели

1. Найдите наименьший общий знаменатель всех дробей в уравнении.
2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
3. Изолируйте переменные члены с одной стороны и постоянные члены с другой стороны.
4. Упростить обе стороны.
5. Используйте свойство умножения или деления, чтобы сделать коэффициент переменной равным

   111

   .

Вот пример с тремя переменными терминами. После того, как вы очистите дроби с помощью ЖК-дисплея, вы упростите три члена переменных, а затем изолируете переменную.

Пример

Решите:

7=12x+34x−23×7=\frac{1}{2}x+\frac{3}{4}x-\frac{2}{3}x7=21​x+43​x-32 х

.

Показать решение

Решение:

Мы хотим очистить дроби, умножив обе части уравнения на LCD всех дробей в уравнении.

Найдите наименьший общий знаменатель всех дробей в уравнении.	7=12x+34x−23xLCD=127=\frac{1}{2}x+\frac{3}{4}x-\frac{2}{3}x\quad{LCD=12}7=21 ​x+43​x−32​xLCD=12
Умножьте обе части уравнения на 121212 .	12(7)=12⋅(12x+34x−23x)\color{red}{12}(7)=\color{red}{12}\cdot(\frac{1}{2}x+\frac {3}{4}x-\frac{2}{3}x)12(7)=12⋅(21​x+43​x−32​x)
Распределить.	12(7)=12⋅12x+12⋅34x−12⋅23×12(7)=12\cdot\frac{1}{2}x+12\cdot\frac{3}{4}x-12\ cdot\frac{2}{3}x12(7)=12⋅21​x+12⋅43​x−12⋅32​x
Упростите — и заметьте, больше никаких дробей!	84=6х+9х-8х84=6х+9х-8х84=6х+9х-8х
Объедините похожие термины.	84=7×84=7×84=7x
Разделить на 777 .	847=7×7\frac{84}{\color{red}{7}}=\frac{7x}{\color{red}{7}}784​=77x​
Упрощение.	12=х12=х12=х
Проверка: Пусть x=12x=12x=12 .
7=12x+34x−23×7=\frac{1}{2}x+\frac{3}{4}x-\frac{2}{3}x7=21​x+43​x−32 ​x 7=?12(12)+34(12)−23(12)7\stackrel{\text{?}}{=}\frac{1}{2}(\color{red}{12 })+\frac{3}{4}(\color{red}{12})-\frac{2}{3}(\color{red}{12})7=?21​(12)+43 ​(12)−32​(12) 7=?6+9−87\stackrel{\text{?}}{=}6+9-87=?6+9−8 7=7✓7=7\quad\checkmark7=7✓

А теперь попробуйте решить похожую задачу. Очистите дроби, упростите, затем решите.

Внимание!

Одна из самых распространенных ошибок при очистке дробей — это забывание умножить ОБЕ части уравнения на ЖК-дисплей. Если ваш ответ не проходит проверку, убедитесь, что вы умножили обе части уравнения на LCD.

В следующем примере у нас будут переменные и дроби с обеих сторон уравнения. После того, как вы очистите дроби с помощью ЖК-дисплея, вы увидите, что это уравнение похоже на уравнения с переменными с обеих сторон, которые мы решали ранее. Не забудьте выбрать переменную сторону и постоянную сторону, чтобы помочь вам организовать свою работу.

Пример

Решите:

x+13=16x−12x+\frac{1}{3}=\frac{1}{6}x-\frac{1}{2}x+31​=61​x−21​

.

Показать решение

Решение:

Найдите ЖК всех дробей в уравнении.	x+13=16x−12,LCD=6x+\frac{1}{3}=\frac{1}{6}x-\frac{1}{2},\quad{LCD=6}x+ 31​=61​x−21​,ЖК=6
Умножьте обе стороны на LCD.	6(x+13)=6(16x−12)\color{red}{6}(x+\frac{1}{3})=\color{red}{6}(\frac{1}{ 6}x-\frac{1}{2})6(x+31​)=6(61​x−21​)
Распределить.	6⋅x+6⋅13=6⋅16x−6⋅126\cdot{x}+6\cdot\frac{1}{3}=6\cdot\frac{1}{6}x-6\ cdot\frac{1}{2}6⋅x+6⋅31​=6⋅61​x−6⋅21​
Упрости — больше никаких дробей!	6x+2=x−36x+2=x-36x+2=x−3
Вычесть xxx с обеих сторон.	6x−x+2=x−x−36x-\color{red}{x}+2=x-\color{red}{x}-36x−x+2=x−x−3
Упрощение.	5x+2=-35x+2=-35x+2=-3
Вычтите 2 с обеих сторон.	5x+2−2=−3−25x+2\цвет{красный}{-2}=-3\цвет{красный}{-2}5x+2−2=−3−2
Упрощение.	5х=-55х=-55х=-5
Разделить на 555 .	5×5=−55\frac{5x}{\color{red}{5}}=\frac{-5}{\color{red}{5}}55x​=5−5​
Упрощение.	х=-1х=-1х=-1
Проверить: Подставить x=−1x=-1x=−1 .
x+13=16x−12x+\frac{1}{3}=\frac{1}{6}x-\frac{1}{2}x+31​=61​x−21​ (−1) + 13 = ?16 (−1) −12 (\ color {red} {-1}) + \ frac {1} {3} \ stackrel {\ text {?}} {=} \ frac {1}{6}(\color{red}{-1})-\frac{1}{2}(−1)+31​=?61​(−1)−21​ (−1) +13=?−16−12(-1)+\frac{1}{3}\stackrel{\text{?}}{=}-\frac{1}{6}-\frac{1}{2 }(−1)+31​=?−61​−21​ −33+13=?−16−36-\frac{3}{3}+\frac{1}{3}\stackrel{\ text{?}}{=}-\frac{1}{6}-\frac{3}{6}−33​+31​=?−61​−63​ −23=?−46-\frac{2}{3}\stackrel{\text{?}}{=}-\frac{4}{6}−32​=?−64​ −23 =−23✓-\frac{2}{3}=-\frac{2}{3}\quad\checkmark−32​=−32​✓

Теперь вы можете попробовать решить уравнение с дробями, в котором переменные стоят по обе стороны от знака равенства. Ответ может быть дробным.

В следующем видео мы покажем еще один пример того, как решить уравнение, которое содержит дроби и переменные по обе стороны от знака равенства.

В следующем примере мы начнем с уравнения, в котором переменный член заключен в скобки и умножен на дробь. Вы можете очистить дробь, или, если вы используете распределительное свойство, дробь будет удалена. Вы видите, почему?

ПРИМЕР

Решите:

1=12(4x+2)1=\frac{1}{2}\left(4x+2\right)1=21​(4x+2)

.

Показать решение

Решение:

	1=12(4x+2)1=\frac{1}{2}(4x+2)1=21​(4x+2)
Распределить.	1=12⋅4x+12⋅21=\frac{1}{2}\cdot4x+\frac{1}{2}\cdot21=21​⋅4x+21​⋅2
Упрощение. Теперь не нужно очищать дроби!	1=2x+11=2x+11=2x+1
Вычтите 1 с обеих сторон.	1−1=2x+1−11\цвет{красный}{-1}=2x+1\цвет{красный}{-1}1−1=2x+1−1
Упрощение.	0=2×0=2×0=2x
Разделить на 222 .	02=2×2\frac{0}{\color{red}{2}}=\frac{2x}{\color{red}{2}}20​=22x​
Упрощение.	0=х0=х0=х
Проверка: Пусть x=0x=0x=0 .
1=12(4x+2)1=\frac{1}{2}(4x+2)1=21​(4x+2) 1=?12(4(0)+2) 1\stackrel{\text{?}}{=}\frac{1}{2}(4(\color{red}{0})+2)1=?21​(4(0)+2) 1=?12(2)1\stackrel{\text{?}}{=}\frac{1}{2}(2)1=?21​(2) 1=?221\stackrel{\ text{?}}{=}\frac{2}{2}1=?22​ 1=1✓1=1\quad\checkmark1=1✓

Теперь вы можете попробовать решить уравнение, в котором переменный член в скобках умножается на дробь.

Лицензии и атрибуты

Содержимое по лицензии CC, совместное использование ранее

• Пример 1. Решите уравнение с дробями с переменными членами с обеих сторон. Автор : Джеймс Соуза (Mathispower4u.com). Лицензия : CC BY: Атрибуция
• Идентификатор вопроса 71948. Автор : Элисон Дэй. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия сообщества IMathAS, CC-BY + GPL

Контент под лицензией CC, конкретное указание авторства

• Преалгебра. Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии : Загрузите бесплатно с http://cnx.org/contents/[email protected]

Предыдущая

Следующая

К концу этого раздела вы сможете:

• Решать уравнения с дробными коэффициентами
• Решение уравнений с десятичными коэффициентами

Давайте воспользуемся общей стратегией решения линейных уравнений, представленной ранее, для решения уравнения .

Чтобы изолировать термин, вычтите его с обеих сторон.
Упростите левую сторону.
Измените константы на эквивалентные дроби с помощью ЖК-дисплея.
Вычесть.
Умножьте обе части на обратную величину .
Упрощение.

Этот метод работал нормально, но многие студенты не чувствуют себя очень уверенно, когда видят все эти дроби. Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.

Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется очистка уравнения дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.

Решить: .

Решение

Below that is negative 2 over 8 plus 4 over 8, equal sign with a question mark, one-fourth. Below that is 2 over 8, equal sign with a question mark, one-fourth. The last line says one-fourth equals one-fourth.» data-label=»»>

Найдите наименьший общий знаменатель всех дробей в уравнении.
Умножьте обе части уравнения на ЖК-дисплей, 8. Это очищает дроби.
Использовать Распределительное свойство.
Упростите — и заметьте, больше никаких дробей!
Решите, используя общую стратегию решения линейных уравнений.
Упрощение.
Проверить: Пусть

Решить: .

Показать ответ

Решить: .

Показать ответ

y = 3

Обратите внимание на (рисунок), что после того, как мы очистили уравнение дробей, оно стало таким же, как те, которые мы решали ранее в этой главе. Мы изменили задачу на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.

1. Найдите наименьший общий знаменатель всех дробей в уравнении.
2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
3. Решите, используя общую стратегию решения линейных уравнений.

Решить: .

Решение

Мы хотим очистить дроби, умножив обе части уравнения на LCD всех дробей в уравнении.

The next line says, “Combine like terms,” and shows 84 equals 7x. The next line says, “Divide by 7,” and shows 84 over a red 7 equals 7x over a red 7. The next line says, “Simplify,” and shows 12 equals x. The last step says, “Check: Let x equal 12.” Beside that is the original equation. Below that is 7 followed by an equal sign with a question mark, then one-half times a red 12 plus three-fourths times a red 12 minus two-thirds times a red 12. Bellow that is 7 followed by an equal sign with a question mark, then 6 plus 9 minus 8. The last line says 7 equals 7, followed by a check mark.» data-label=»»>

Найдите наименьший общий знаменатель всех дробей в уравнении.
Умножьте обе части уравнения на 12.
Распределить.
Упростите — и заметьте, больше никаких дробей!
Объедините похожие термины.
Разделить на 7.
Упрощение.
Проверить: Пусть .

Решить: .

Показать ответ

v = 40

Решить: .

Показать ответ

u = −12

В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.

Решить: .

Решение

The next line says, “Simplify,” and shows 5x plus 2 equals negative 3. The next line says, “Subtract 2 from both sides,” and shows 5x plus 2 minus a red 2 equals negative 3 minus a red 2. The next line says, “Simplify,” and shows 5x equals negative 5. The next line says, “Divide by 5,” and shows 5x over a red 5 equals negative 5 over a red 5. The next line says, “Simplify,” and shows x equals negative 1. The next line says, “Check,” and shows the original equation. The following line says, “Substitute x equals negative 1.” Beside that is a red negative 1 plus one-third followed by an equal sign with a question mark, then one-sixth times a red negative 1 minus one-half. Below that is negative 1 plus one-third followed by an equal sign with a question mark, then negative one-sixth minus one-half. Below that is negative 3 over 3 plus 1 over 3 followed by an equal sign with a question mark, then negative 1 over 6 minus 3 over 6. Below that is negative 2 over 3 followed by an equal sign with a question mark, then negative 4 over 6. The last line says negative 2 over 3 equals negative 2 over 3.» data-label=»»>

Найдите ЖК всех дробей в уравнении.
Умножьте обе стороны на LCD.
Распределить.
Упрости — больше никаких дробей!
Вычесть с обеих сторон.
Упрощение.
Вычтите 2 с обеих сторон.
Упрощение.
Разделить на 5.
Упрощение.
Проверить: заменить .

Решить: .

Показать ответ

a = −2

Решить: .

Показать ответ

c = −2

На (рис.) мы начнем с использования свойства Distribution. Этот шаг сразу очистит дроби!

Решить: .

Раствор

» data-label=»»>

Распределить.
Упрощение. Теперь не нужно очищать дроби!
Вычтите 1 с обеих сторон.
Упрощение.
Разделить на 2.
Упрощение.
Проверить: Пусть .

Решить: .

Показать ответ

p = −4

Решить: .

Показать ответ

q = 2

Во многих случаях даже после распределения будут дроби.

Решить: .

Решение

The next step says, “Multiply by the LCD, 4,” and shows a red 4 times each side. The next step says, “Distribute,” and shows 4 times one-half y minus 4 times 5 over 2 equals 4 times one-fourth y minus 4 times one-fourth. The next line says, “Simplify,” and shows 2y minus 10 equals y minus 1. The next line says, “Collect the y terms to the left,” and shows 2y minus 10 minus a red y equals y minus 1 minus a red y. The next line says, “Simplify,” and shows y minus 10 equals negative 1. The next line says, “Collect the constants to the right,” and shows y minus 10 plus a red 10 equals negative 1 plus a red 10. The next line says, “Simplify,” and shows y equals 9. The last step says, “Check. Substitute: 9 for y,” and shows the original equation. Below that is one-half times parentheses red 9 minus 5, equal sign with a question mark, one-fourth times parentheses red 9 minus 1. Below that is one-half times 4, equal sign with a question mark, one-fourth times 8, then 2 equals 2 followed by a check mark. » data-label=»»>

Распределить.
Упрощение.
Умножение на LCD, 4.
Распределить.
Упрощение.
Соберите термины слева.
Упрощение.
Соберите константы справа.
Упрощение.
Проверить: заменить .

Решить: .

Показать ответ

n = 2

Решить: .

Показать ответ

м = −1

В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем задачи, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей. Например, и . Итак, когда у нас есть уравнение с десятичными дробями, мы можем использовать тот же процесс, который мы использовали для очистки дробей — умножить обе части уравнения на наименьший общий знаменатель.

Решить: .

Решение

Единственным десятичным знаком в уравнении является . Так как , LCD есть . Мы можем умножить обе части на, чтобы очистить десятичную дробь.

» data-label=»»>

Умножьте обе стороны на LCD.
Распределить.
Умножьте и заметьте, больше нет десятичных знаков!
Добавьте 50, чтобы получить все константы справа.
Упрощение.
Разделите обе части на 8.
Упрощение.
Проверить: Пусть .

Решить: .

Показать ответ

x = 20

Решить: .

Показать ответ

x = 10

Решить: .

Решение

Посмотрите на десятичные дроби и придумайте эквивалентные дроби.

Обратите внимание, ЖК-дисплей.

Путем умножения на ЖК-дисплее мы очистим десятичные дроби.

The last line says, “Check: Let x equal 8,” and shows 0.06 times a red 8 plus 0.02 equals 0.25 times a red 8 minus 1.5. Below that is 0.48 plus 0.02 equals 2.00 minus 1.5. The last line says 0.50 equals 0.50.» data-label=»»>

Умножьте обе стороны на 100.
Распределить.
Умножить, и больше никаких десятичных знаков.
Соберите переменные справа.
Упрощение.
Соберите константы слева.
Упрощение.
Разделить на 19.
Упрощение.
Проверить: Пусть .

Решить: .

Показать ответ

ч = 12

Решить: .

Показать ответ

k = −1

В следующем примере используется уравнение, типичное для тех, которые мы увидим в приложении к деньгам в следующей главе. Обратите внимание, что мы сначала распределим десятичную дробь, прежде чем очистим все десятичные дроби в уравнении.

Решить: .

Решение

Below that is “Let x equal 9” and 0.25 times a red 9 plus 0.05 times parentheses red 9 plus 3, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.05 times 12, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.60 followed by an equal sign with a question mark, then 2.85. The last line shows 2.85 equals 2.85.» data-label=»»>

Сначала раздайте.
Объедините похожие термины.
Чтобы убрать десятичные дроби, умножьте на 100.
Распределить.
Вычтите 15 с обеих сторон.
Упрощение.
Разделить на 30.
Упрощение.
Проверить: Пусть .

Решить: .

Показать ответ

n = 9

Решить: .

Показать ответ

d = 16

• Решайте уравнения с дробными коэффициентами, очищая дроби.
  1. Найдите наименьший общий знаменатель всех дробей в уравнении.
  2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
  3. Решите, используя общую стратегию решения линейных уравнений.

Решите уравнения с дробными коэффициентами

В следующих упражнениях решите уравнение, очистив дроби.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.

Решение уравнений с десятичными коэффициентами

В следующих упражнениях решите уравнение, удалив десятичные дроби.

25.	26.
27.	28.
29.	30.
31.	32.
33.	34.
35.	36.
37.	38.
39.	40.

Математика на каждый день

Монеты 41 . У Тейлора есть десять центов. Количество копеек больше, чем количество десятицентовиков. Решите уравнение для , количество десятицентовиков.

Марки 42. Трэвис накупил марок и марок. Количество марок было меньше количества марок. Решите уравнение для , чтобы найти количество марок, купленных Трэвисом.

Письменные упражнения

43. Объясните, как найти наименьший общий знаменатель .	44. Если в уравнении несколько дробей, как умножение обеих частей на ЖК облегчает решение?
45. Если в уравнении дроби есть только с одной стороны, зачем обе части уравнения умножать на LCD?	46. Что такое LCD в уравнении? Откуда вы знаете?

1.	3.	5.
7.	9.	11.
13.	15.	17.
19.	21.	23.
25.	27.	29.
31.	33.	35.
37.	39.	41.
43. Ответы будут разными. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт