Решить {l}{x+y=60}{x-y=40} | Microsoft Math Solver
\left\{ \begin{array} { l } { x + y = 60 } \\ { x — y = 40 } \end{array} \right.
x=50
y=10
Викторина
Simultaneous Equation
5 задач, подобных этой:
\left\{ \begin{array} { l } { x + y = 60 } \\ { x — y = 40 } \end{array} \right.
Подобные задачи из результатов поиска в Интернете
Поделиться
Скопировано в буфер обмена
x+y=60,x-y=40
Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных. Затем подставьте результат для этой переменной в другое уравнение.
x+y=60
Выберите один из уравнений и решите его для x, изолируя x в левой части знака равенства.
x=-y+60
Вычтите y из обеих частей уравнения.
-y+60-y=40
Подставьте -y+60 вместо x в другом уравнении x-y=40.
-2y+60=40
Прибавьте -y к -y.
-2y=-20
Вычтите 60 из обеих частей уравнения.
y=10
Разделите обе части на -2.
x=-10+60
Подставьте 10 вместо y в x=-y+60. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.
x=50
Прибавьте 60 к -10.
x=50,y=10
Система решена.
x+y=60,x-y=40
Приведите уравнения к стандартному виду, а затем решите систему уравнений с помощью матриц.
\left(\begin{matrix}1&1\\1&-1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}60\\40\end{matrix}\right)
Запишите уравнения в матричном виде.
inverse(\left(\begin{matrix}1&1\\1&-1\end{matrix}\right))\left(\begin{matrix}1&1\\1&-1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&1\\1&-1\end{matrix}\right))\left(\begin{matrix}60\\40\end{matrix}\right)
Левое произведение с матрицей, обратной \left(\begin{matrix}1&1\\1&-1\end{matrix}\right).
\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&1\\1&-1\end{matrix}\right))\left(\begin{matrix}60\\40\end{matrix}\right)
Произведение матрицы на обратную ей является единичной матрицей.
\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&1\\1&-1\end{matrix}\right))\left(\begin{matrix}60\\40\end{matrix}\right)
Перемножение матриц слева от знака равенства.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{-1}{-1-1}&-\frac{1}{-1-1}\\-\frac{1}{-1-1}&\frac{1}{-1-1}\end{matrix}\right)\left(\begin{matrix}60\\40\end{matrix}\right)
Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) с размерностью 2\times 2 обратная матрица имеет вид \left(\begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матричное уравнение можно переписать в виде задачи умножения матриц.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{2}&\frac{1}{2}\\\frac{1}{2}&-\frac{1}{2}\end{matrix}\right)\left(\begin{matrix}60\\40\end{matrix}\right)
Выполните арифметические операции.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{2}\times 60+\frac{1}{2}\times 40\\\frac{1}{2}\times 60-\frac{1}{2}\times 40\end{matrix}\right)
Перемножьте матрицы.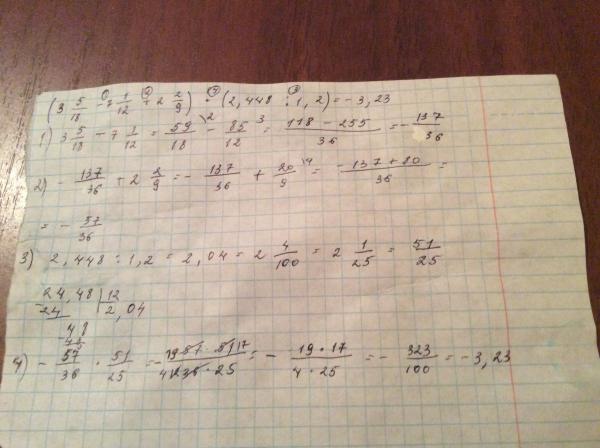
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}50\\10\end{matrix}\right)
Выполните арифметические операции.
x=50,y=10
Извлеките элементы матрицы x и y.
x+y=60,x-y=40
Для решения методом исключения коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сократилась при вычитании одного уравнения из другого.
x-x+y+y=60-40
Вычтите x-y=40 из x+y=60 путем вычитания подобных членов в обеих частях уравнения.
y+y=60-40
Прибавьте x к -x. Члены x и -x сокращаются, после чего в уравнении остается только одна переменная, и его можно решить.
2y=60-40
Прибавьте y к y.
2y=20
Прибавьте 60 к -40.
y=10
Разделите обе части на 2.
x-10=40
Подставьте 10 вместо y в x-y=40. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.
x=50
Прибавьте 10 к обеим частям уравнения.
x=50,y=10
Система решена.
помогите решить систему уравнений {x-y=40,корень x-корень y=10} — Знания.site
Ответы 1
x-y=40 это уравнение представим так (√х)² -(√у)²= 40, т.е (√х-√у)(√х+√у)=40 т.к √x — √y=10то √х+√у=4
имеем новую систему
√x — √y=10√х+√у=4 сложим1 уравнение со 2
имеем
2√х=14
√х=7
х=49
подставим значение х в 1 уравнение получаем у= 9
Знаешь ответ? Добавь его сюда!
Последние вопросы
Французский язык
4 часа назад
Помогите пожалуйста с французским упр 4🙏🙏🙏
Математика
8 часов назад
24.02.2022?
Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг?10 часов назад
32) найдите область определение функции z = (1/x) + (1/y)Математика
10 часов назад
33) найдите область определение функции z = (y — 1) / (x² + y²)Математика
10 часов назад
31) найдите область определение функции z = 1 / (x-y)Геометрия
12 часов назад
100 баллов таму кто поможетАнглийский язык
12 часов назад
Subjunctive Mood
Test
I.
Choose the right form:1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today. If it (were/ had been) a little warmer, we would (go/ have gone) for a walk. 6.
II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Английский язык
12 часов назад
Subjunctive Mood
Test
I. Choose the right form:
1. Jack doesn’t speak English.
II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Литература
18 часов назад
А где почему это напряжоный момент
Биология
1 день назад
У голонасінних рослин уперше з’являєтся:
Математика
1 день назад
Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140
Алгебра
1 день назад
Решите графически системы уравнений (выражая у через х) 1 система {х+2у=6 х-4у=0} 2 система{3у-х=3 х-4у=1}
Физика
1 день назад
Електричний нагрівник за 7 хв доводить до кипіння 10 кг води, початкова температура якої дорівнює 20 °С.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.Физика
2 дня назад
Тело движется вдоль оси Ох. График зависимости проекции его скорости Vх от времени t изображён на рисунке. Найди путь S, пройденный телом за рассмотренный промежуток времени. Результат вырази в метрах, округлив до целого числа.
Українська мова
2 дня назад
Допоможіть будь ласка! Написати твір — роздум за алгоритмом.
Choose the right form:
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he ( had/ had had) more money, he would (buy/ have bought) new toys for his children.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.Решить {l}{x+y=40}{x-y=10} | Microsoft Math Solver. \begin{array} { l } { x + y = 40 } \\ { x — y = 10 } \end{array} \right.
Аналогичные задачи из веб-поиска
Поделиться
Скопировано в буфер обмена
x+y=40,x-y=10
Чтобы решить пару уравнений с помощью подстановки, сначала решите одно из уравнений для одной из переменных.
Затем подставьте результат этой переменной в другое уравнение.
x+y=40
Выберите одно из уравнений и решите его относительно x, выделив x слева от знака равенства.
x=-y+40
Вычтите y из обеих частей уравнения.
-y+40-y=10
Подставьте -y+40 вместо x в другое уравнение, x-y=10.
-2y+40=10
Добавить -y к -y.
-2y=-30
Вычтите 40 из обеих частей уравнения.
y=15
Разделите обе части на -2.
х=-15+40
Подставьте 15 вместо y в x=-y+40. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую.
x=25
Добавьте 40 к -15.
x=25,y=15
Теперь система решена.
x+y=40,x-y=10
Приведите уравнения к стандартной форме и затем используйте матрицы для решения системы уравнений.
\left(\begin{matrix}1&1\\1&-1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin {матрица}40\\10\конец{матрица}\справа)
Запишите уравнения в матричной форме.
обратная(\левая(\начало{матрица}1&1\\1&-1\конец{матрица}\правая))\левая(\начало{матрица}1&1\\1&-1\конец{матрица}\правая)\ влево (\ начало {матрица} х \\ у \ конец {матрица} \ вправо) = обратное (\ влево (\ начало {матрица} 1 & 1 \\ 1 & -1 \ конец {матрица} \ вправо)) \ влево (\ начало {matrix}40\\10\end{matrix}\right)
Слева умножьте уравнение на обратную матрицу \left(\begin{matrix}1&1\\1&-1\end{matrix}\right).
\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin {матрица}1&1\\1&-1\конец{матрица}\справа))\слева(\начало{матрица}40\\10\конец{матрица}\справа)
Произведение матрицы и ее обратной является единичной матрицей.
\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&1\\1&-1\end{matrix}\right))\left (\begin{matrix}40\\10\end{matrix}\right)
Умножьте матрицы слева от знака равенства.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{-1}{-1-1}&-\frac{1} {-1-1}\\-\frac{1}{-1-1}&\frac{1}{-1-1}\end{matrix}\right)\left(\begin{matrix}40\ \10\конец{матрица}\справа)
Для матрицы 2\x 2 \left(\begin{matrix}a&b\\c&d\end{matrix}\right) обратная матрица равна \left(\begin{matrix}\frac{d}{ad- bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матрица уравнение можно переписать как задачу умножения матриц.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&-\frac{1}{2}\end{matrix}\right)\left(\begin{matrix}40\\10\end{matrix}\right)
Выполните арифметические действия.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{2}\times 40+\frac{1}{2 }\times 10\\\frac{1}{2}\times 40-\frac{1}{2}\times 10\end{matrix}\right)
Умножьте матрицы.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}25\\15\end{matrix}\right)
Выполните арифметические действия.
x=25,y=15
Извлечь элементы матрицы x и y.
x+y=40,x-y=10
Чтобы решить методом исключения, коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сокращалась при вычитании одного уравнения из другого.
x-x+y+y=40-10
Вычтите x-y=10 из x+y=40, вычитая одинаковые члены по обе стороны от знака равенства.
y+y=40-10
Добавить x к -x.
Члены x и -x сокращаются, оставляя уравнение только с одной переменной, которую можно решить.
2y=40-10
Добавить y к y.
2y=30
Добавьте 40 к -10.
y=15
Разделите обе части на 2.
x-15=10
Подставьте 15 вместо y в x-y=10. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую. 93
