Решение графическим методом задач онлайн: Графический метод решения задач линейного программирования. Решение задач и контрольных работ по линейному программированию онлайн

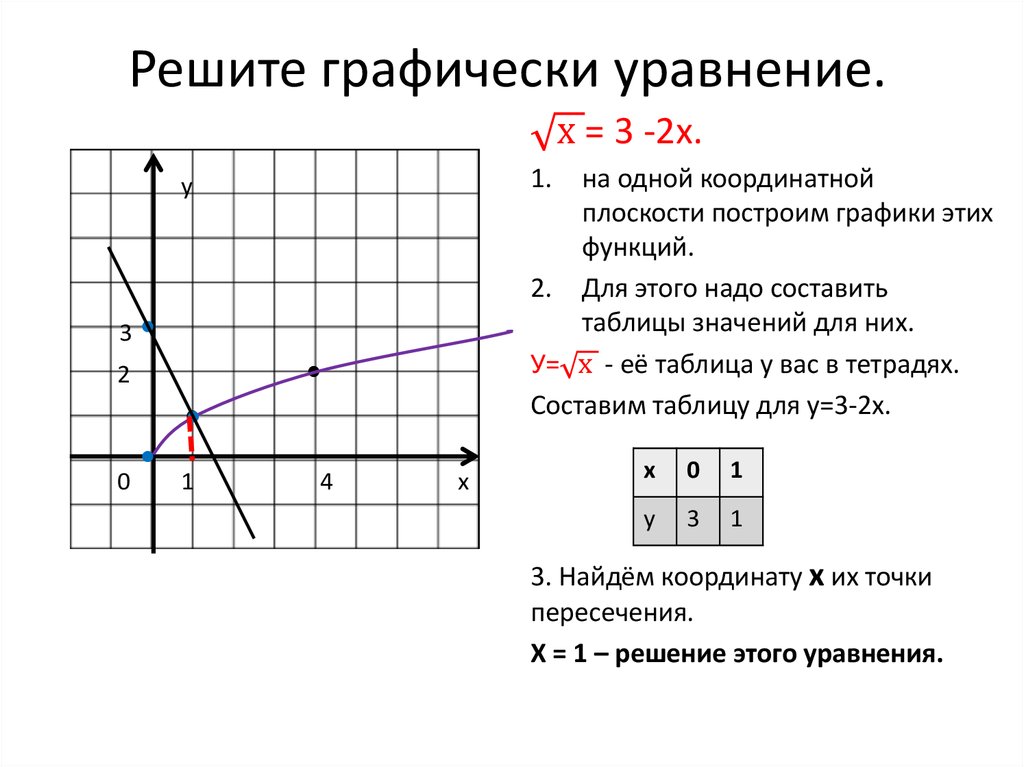
Пример 6.2. Решить задачу линейного про- граммирования геометрическим методом:

Решение:

Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функцииF (X).

5 этап: построение прямой целевой функ-ции.

Построение прямой целевой функции F(X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 4).

Рис. 4. Построение целевой функции F(x) и вектора-градиента С

6 этап: определение оптимума целевой функ-ции.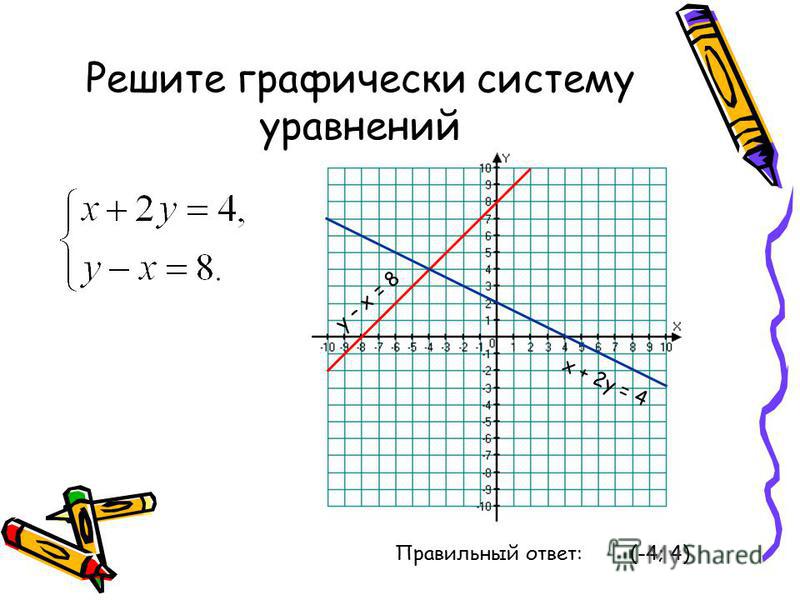

Перемещая прямую F(x) параллельно са-мой себе в направлении, обратном вектору-градиенту, опреде-ляем крайнюю точку (точки) ОДР. Согласно графику (рис. 5), та- кой точкой является точка О с координатами (0; 0).

Рис. 5. Определение точки минимума целевой функции

Подставляя координаты точки минимума в целевую функ-цию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ: при заданных ограничениях минимальное значение целевой функции F(Х)=0, которое достигается в точке О (0; 0).

Пример 6.3. Решить следующую задачу ли-нейного программирования геометрическим методом:

Решение:

Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x 1 и x2.

Составим расширенную матрицу и выделим с помощью метода Жордана- Гаусса базисные переменныеx1 и x 2.

Умножим (поэлементно) первую строку на –3 и сложим со вто-рой:
.

Умножим вторую строку на :

.

Сложим вторую с первой строкой:

.

В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные перемен-ные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

Запишем полученную задачу линейного программирования:

Так как переменные x1 и x2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:

Тогда исходную задачу можно записать в виде следующей эк- вивалентной ей стандартной задаче линейного программирования:

Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим мето-дом.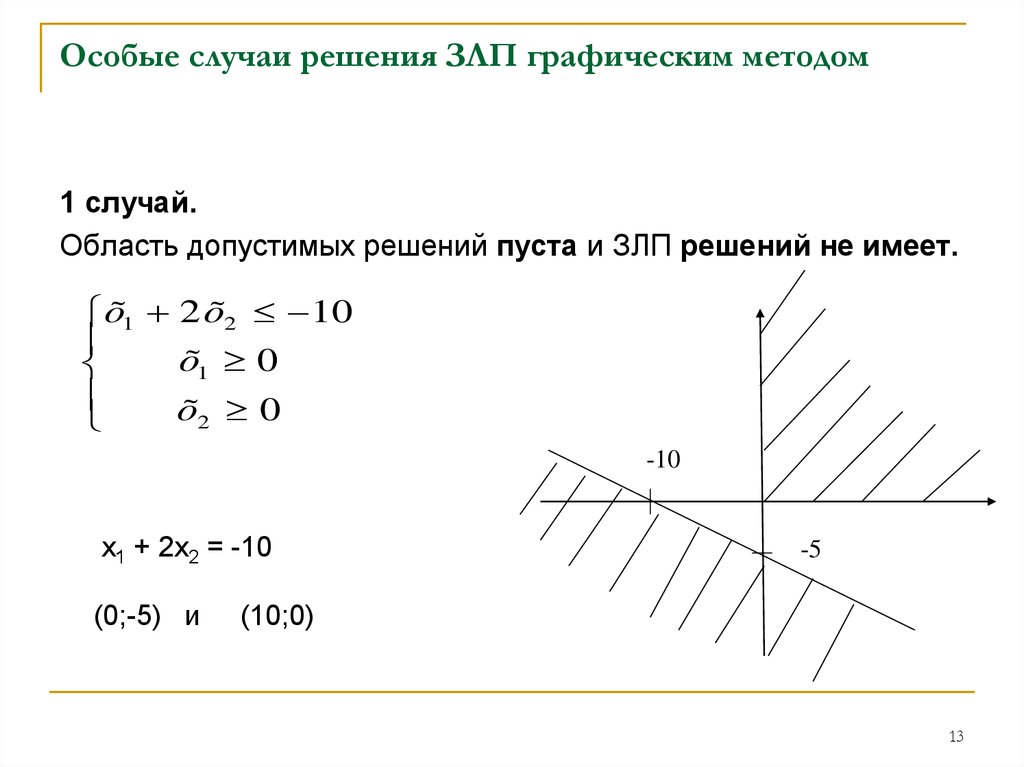

1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).

Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):

Построим прямые, соответствующие каждому неравенству (рис. 6). Прямые пронумеруем согласно принятой ранее схе-ме.

2 этап: определение решения каждого из нера-венств системы ограничений.

С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 6) с помощью стрелок.

3 этап: определение ОДР задачи линейного про- граммирования.

Найденные полуплоскости (т.е. решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.

Рис. 6. Фрагмент MathCAD-документа:

построение области допустимых решений задачи

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.

Если после подстановки координат контрольной точки в неравенство его смысл нарушается, то решением данного неравенства является полуплоскость не содержащая данную точку (т.е. расположенная по другую сторону прямой).

Направление, обратное вектору-градиенту, соответствует направлению минимизации целевой функции.

Урок математики во 2 классе «Решение задач графическим способом» | План-конспект урока по математике (2 класс) по теме:

Решение задач графическим способом.

Цели. 1.Развивать умение решать текстовые задачи графическим способом.

              2. Развивать математическую речь, логическое мышление.

 3. Воспитывать интерес к точным наукам, аккуратность,  чувство товарищества, взаимопомощи.

Ход урока.

Организационный момент.

Перемену отдыхали,

Набирались сил, играли,

Но сейчас пора опять

Складывать и вычитать.

Сели ровно, рот закрыт,

Носик дышит, рот молчит.

Минутка чистописания.

Я тетрадь свою открою,

Под наклоном положу.

А за партой на уроке

Правильно всегда сижу.

Запишите число, классная работа. Подчеркните все орфограммы.

Пропишите число, которое у вас написано. Цифры пишите правильно, аккуратно

49        49

    49        49

        49        49

Дайте полную характеристику числа.

Устный счёт.

А сейчас, ребятки,

«Математическая зарядка»

Прочитайте задачу на доске. «В мультфильме про динозавров 9 серий. Коля уже посмотрел 2 серии. Сколько серий ему осталось посмотреть?»

  1)                 9                                   3)                       ?

                           ?                                          9                 2

         2                                                        

 2)                    9                                 4)                     9

          ?                2                                               9

                                                                      ?              2

      Какая схема подходит к задаче? Объясните свой выбор.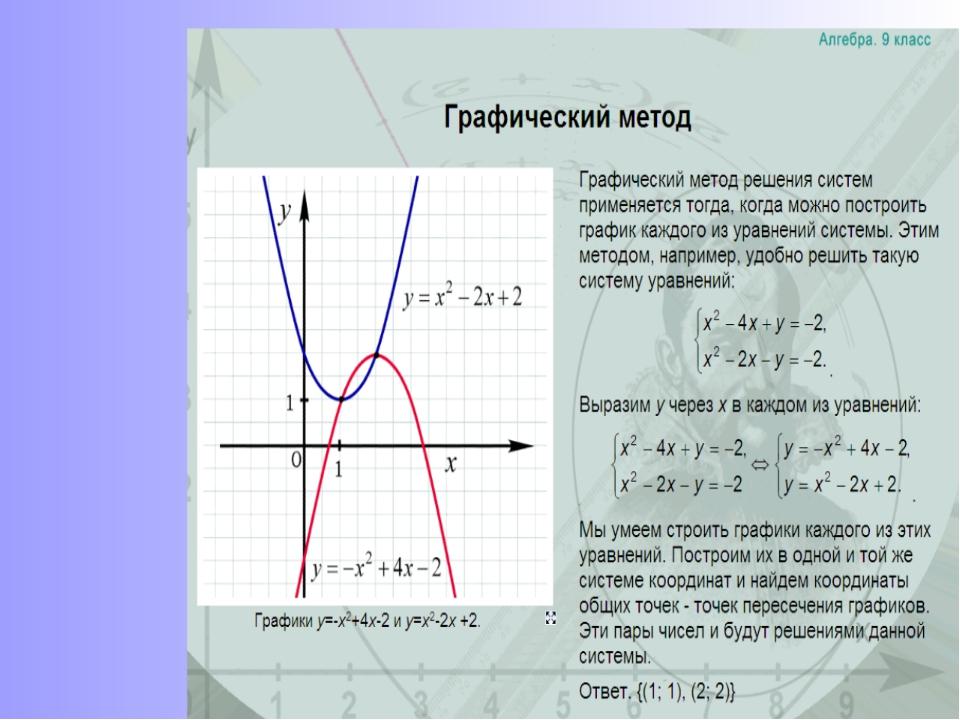

Сделайте вывод, опираясь на чертёж, как найти неизвестную часть?

Целеполагание.

Чему мы учимся на уроках математики? (Работать с величинами).

Как вы думаете, чему будем учиться сегодня на уроке? (На доске появляется вопрос и тема урока «Решение задач»)

А зачем нужно учиться решать задачи?

Коллективная работа.

Тогда я предлагаю вам познакомиться со следующей задачей. Прочитайте её (текст задачи на доске). «К Васе  пришёл друг Миша. Вася решил поделиться с ним  конфетами. Вася взял себе 12 конфет, а Мише дал 8 конфет. На сколько конфет больше у Васи, чем у Миши?»

(Работа идёт у доски и на местах).

Сколько действующих лиц в задаче?

Сколько отрезков будем чертить?

Что сказано про Васю? Как изобразим?

Что сказано про Мишу? Как изобразим?

На какой вопрос нужно ответить? Как изобразим? Почему?

К.                          12

                   8                     ?

М.

Посмотрите на чертёж. Какая величина целое?

Что будет часть? Что нам неизвестно?

Как найти неизвестную часть?

Запишите решение.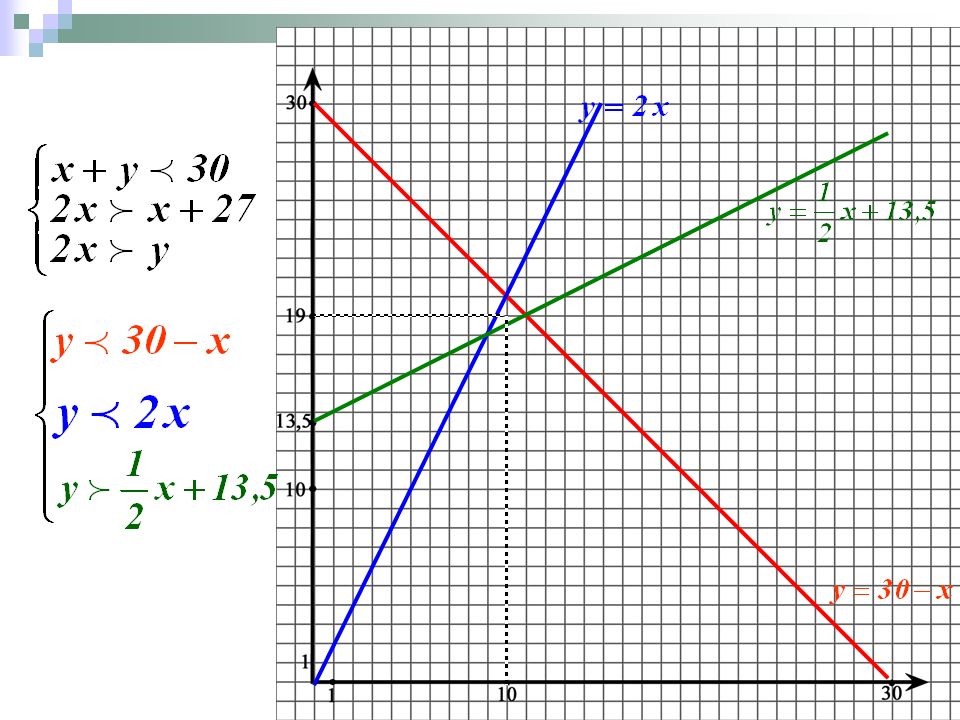

12 – 8 = 4 (к)

Ответили на вопрос? Как звучал вопрос? Как запишем ответ?

Скажите, а правильно ли поступил Вася? Как нужно было ему поступить? Почему? По сколько конфет должен был получить каждый?

Сделаем вывод. Что учились делать? (Учились сравнивать величины. Находить разницу величин – часть).

Для чего решали эту задачу?

Физминутка.

Самостоятельная работа.

(Задачи на карточках по вариантам).

1 в. «Дима нашёл 7 белых грибов, а лисичек на 4 больше. Сколько лисичек нашёл Дима?»

2 в. «Оля высадила на клумбу 12 васильков, а ромашек на 5 меньше. Сколько ромашек высадила Оля?»

Взаимопроверка в парах. (Чья пара будет готова первой – записывает решение у доски).

      Итог урока.

Чему учились на уроке?

Для чего мы это делали?

Резерв. 

Составьте задачу по краткой записи.

Было – ? кг.

Продали — 10 кг.

Осталось – 8 кг.

Как будем решать? Почему?

Д/з: записать решение задачи.

Математико-графический метод решения задач линейного программирования

Задачи линейного программирования являются жизненно важным классом задач оптимизации, помогающим найти надежные решения для получения наименьшего или наибольшего значения функции. В основном существует четыре типа задач линейного программирования. За прошедшие годы несколько методов решения линейного программирования приобрели огромную популярность и широко используются; однако они не универсальны. Графический метод является одним из методов, который является универсальным.

С помощью графического метода можно решить любую задачу оптимизации линейного программирования, состоящую из двух переменных. Еще одно существенное преимущество использования графических методов перед другими заключается в том, что они наглядны и дают более четкую картину. Сегодня мы подробно обсудим графический метод решения задач линейного программирования. Здесь начинается!

Объяснение линейного программирования 

Линейное программирование, также известное как линейная оптимизация или ЛП, может быть описано как оптимизация повседневных операций с определенными ограничениями.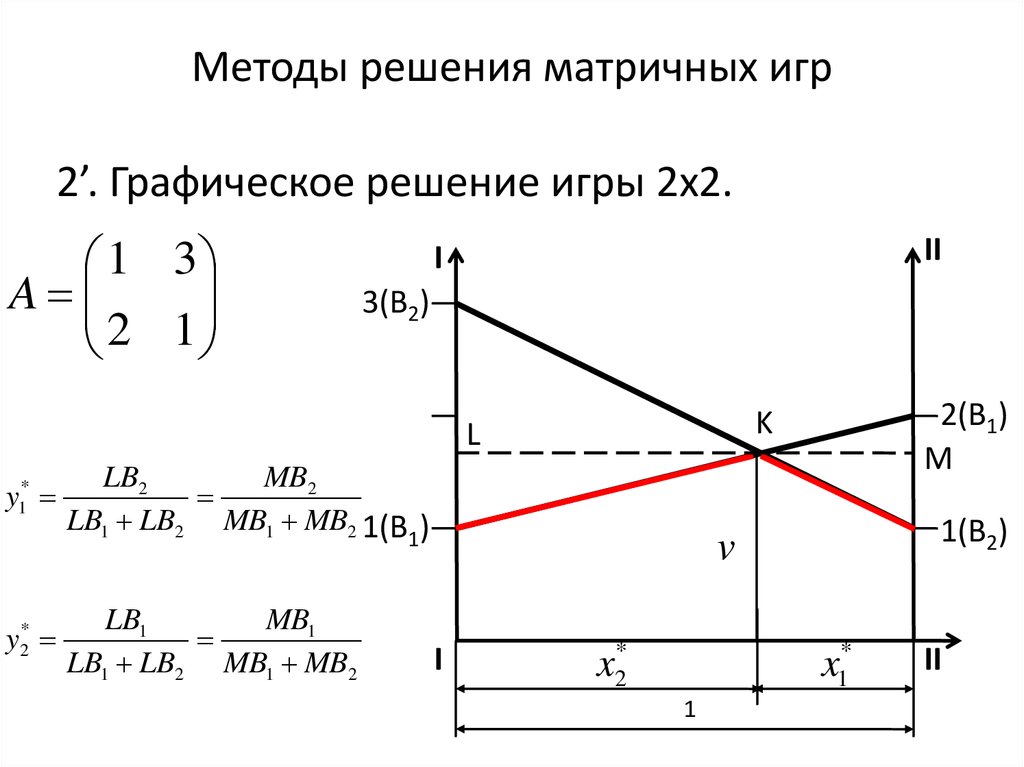 Основная цель линейного программирования — максимизировать или минимизировать общее числовое значение. Он считается одним из наиболее важных методов поиска оптимального использования ресурсов.

Линейное программирование состоит из четырех основных компонентов. К ним относятся переменные решения, данные, ограничения и целевые функции. При работе с линейным программированием необходимо учитывать некоторые допущения для получения лучших результатов:

• Связь между целевой функцией и ограничениями должна быть линейной.
• Ограничения могут быть записаны только в количественном выражении.
• Необходимо оптимизировать линейные функции.

Задачи линейного программирования

Существует четыре различных типа задач линейного программирования. Это следующие:

• Задачи оптимального распределения
• Задачи транспорта
• Задачи производства
• Задачи диеты

Графический метод — задача линейного программирования

две переменные в младших классах. В линейном программировании ясно, что существует более одного уравнения, зависящего от заданного условия. Здесь мы найдем решения задач линейного программирования графическим методом.

Поясним это на примере –

Z = 40x + 15y,

Имеем,

X+2y ≤ 100

X≥0,y

X+2y ≤ 20003

Шаг 0 30 90 90 90 90 данные уравнения, x≥0 и y≥0; поэтому мы сосредоточимся только на первом квадранте.

Шаг 2: Линейные уравнения будут нанесены на график x + 2y = 100 путем построения (100,0) и (0,50) и x + y = 70 путем построения (0,70) и (70,0) ).

После построения графика важно определить наиболее подходящую область. Именно область определяется уже заданными ограничениями.

Каждая точка допустимой области называется выбором и удовлетворяет всем указанным условиям. Если есть какая-либо точка за пределами допустимой области, называется недопустимым решением и не удовлетворяет условиям.

Согласно приведенному выше примеру мы уже знаем, что x и y, скорее всего, удовлетворят условиям.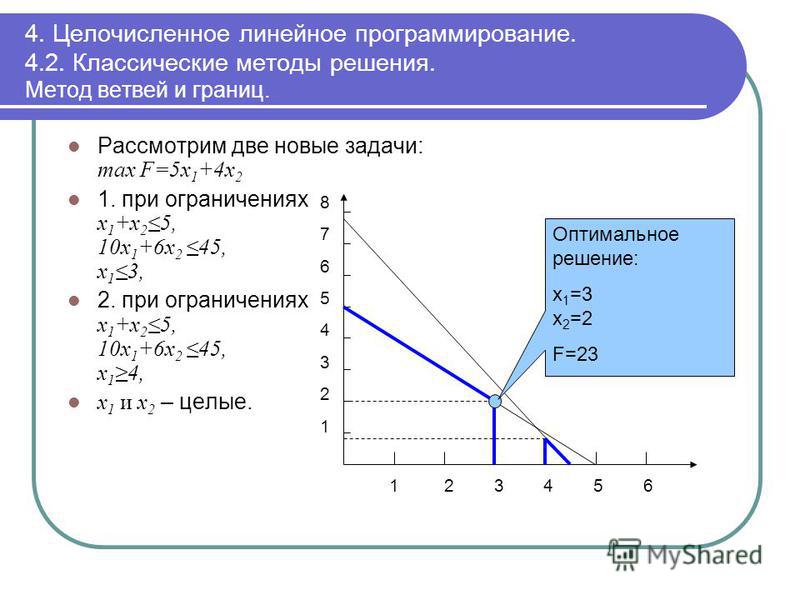 Этот метод можно рассматривать для получения оптимального решения, которое может быть определено как любая точка, предлагающая минимальное или максимальное значение целевой функции. Здесь видно, что несколько точек удовлетворяют заданным ограничениям.

Вот как можно получить минимальное и максимальное значение целевой функции, которое равно Z = 40x + 15y?

Мы можем следовать данной теореме для нахождения оптимального решения –

R здесь допустимая область для задачи программирования, тогда как Z = Ax + By является целевой функцией. Здесь минимальное и максимальное оптимальное значение Z будет иметь место в вершине, если оптимальное значение Z существует.

Если R неограничен, больше шансов, что максимальное и минимальное значение Z не существует. Однако если он и существует, то, скорее всего, в угловой точке области R. 

Вот угловые точки (70,0), (40,30), (0,0) и (0,50). Если мы подставим эти значения Z= 40x + 15y в целевую функцию, мы получим

Z= 2050 для (40,30)

Z= 2800 для (70,0)

Z= 750 для (0,50) )

Z= 0 для (0,0)

В этом случае минимальное значение, встречающееся в Z, равно (0,0), тогда как максимальное значение, которое возникает, равно (70,0).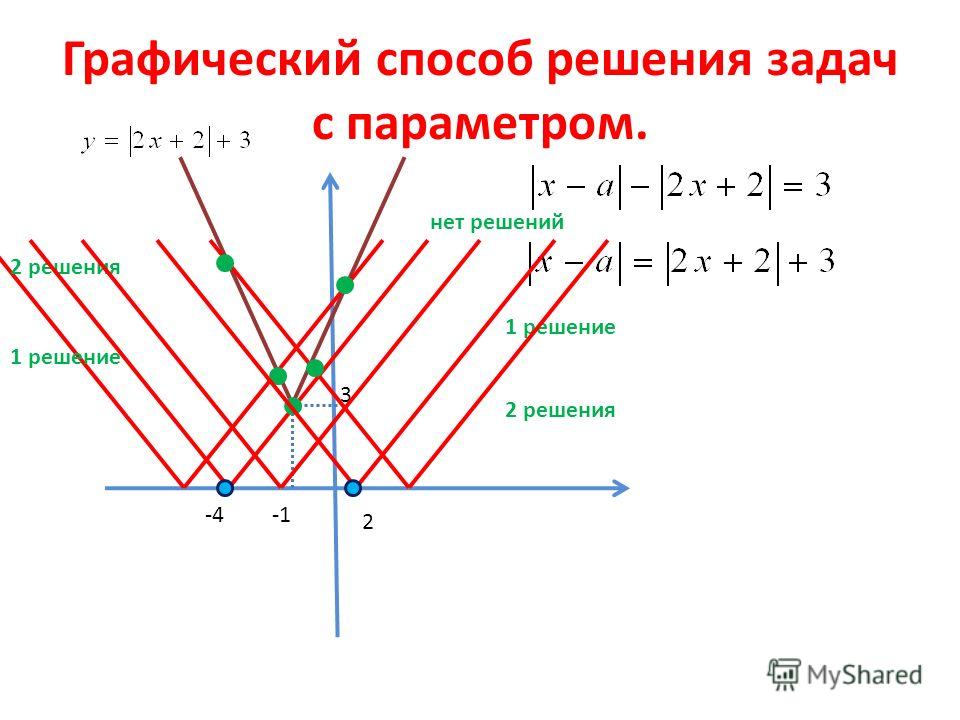

Заключение 

Линейное программирование, широко известное как линейная оптимизация, часто называют задачей максимизации или минимизации линейной функции, на которую наложены линейные ограничения. Это могут быть как равенства, так и неравенства. Задачи линейного программирования — жизненно важный класс задач оптимизации, который помогает найти надежные решения для получения наименьшего или наибольшего значения функции. В основном существует четыре типа задач линейного программирования.

Лучший способ решить задачи линейного программирования — использовать метод графического представления, который мы обсуждали здесь. Графический метод является одним из методов, который является универсальным. С помощью графического метода можно решить любую задачу оптимизации линейного программирования, состоящую из двух переменных. Еще одно существенное преимущество использования графических методов перед другими заключается в том, что они наглядны и дают более четкую картину. В конце мы объяснили графический метод для пошагового решения задач линейного программирования для лучшего понимания.

Блок-схема решения проблем: визуальный метод поиска идеальных решений

Время чтения: около 7 минут

Автор: Lucid Content Team

«Люди задают мне вопросы
Потерялся в замешательстве
Ну, я говорю им, что нет проблем
Только решения»

— Джон Леннон, «Watching the Wheels»

Несмотря на лирику Джона Леннона, никто не свободен от проблем, особенно в бизнесе. Скорее всего, вы сталкиваетесь с какой-то проблемой на работе почти каждый день, и, возможно, вам приходилось «тушить пожар» до обеда один или два раза в вашей карьере.

Но, возможно, Леннон говорит, что независимо от того, что встречается на нашем пути, мы можем найти решение. Как вы подходите к проблемам? Есть ли у вас процесс, гарантирующий, что вы и ваши коллеги придете к правильному решению?

В этой статье мы дадим вам несколько советов о том, как визуально находить решения с помощью блок-схем решения проблем и других методов.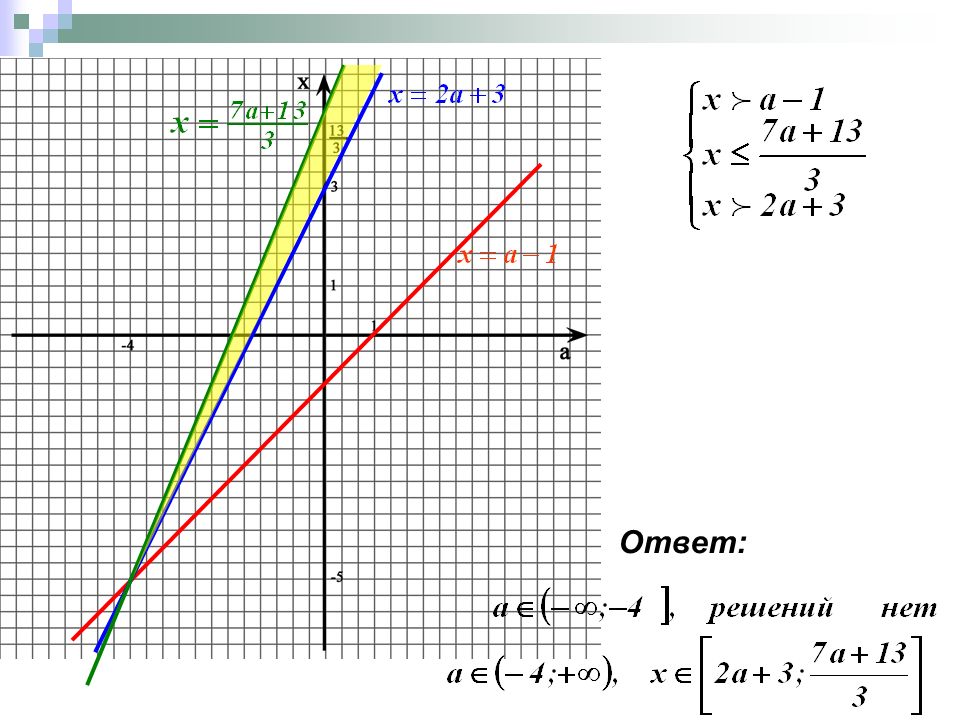

Что такое визуальное решение проблем?

Если вы мыслите буквально, вы можете подумать, что решение проблем со зрением — это то, что делает ваш офтальмолог, когда ваше зрение нечеткое. Для остальных из нас визуальное решение задач включает в себя выполнение следующих шагов визуальным способом:

1. Определите проблему.
2. Решения мозгового штурма.
3. Выберите решение.
4. Реализовать решения.
5. Просмотрите результаты.

Узнайте больше об этапах решения проблем.

Как сделать процесс решения проблем более наглядным

Слова обладают огромной силой и очень важны для нашего повседневного общения. Используя только слова, вы можете провести мозговой штурм, упорядочить данные, выявить проблемы и найти возможные решения. То, как вы пишете свои идеи, может иметь смысл для вас, но другим членам команды может быть не так легко следовать этому.

Когда вы используете блок-схемы, диаграммы, интеллект-карты и другие наглядные материалы, информацию легче усваивать.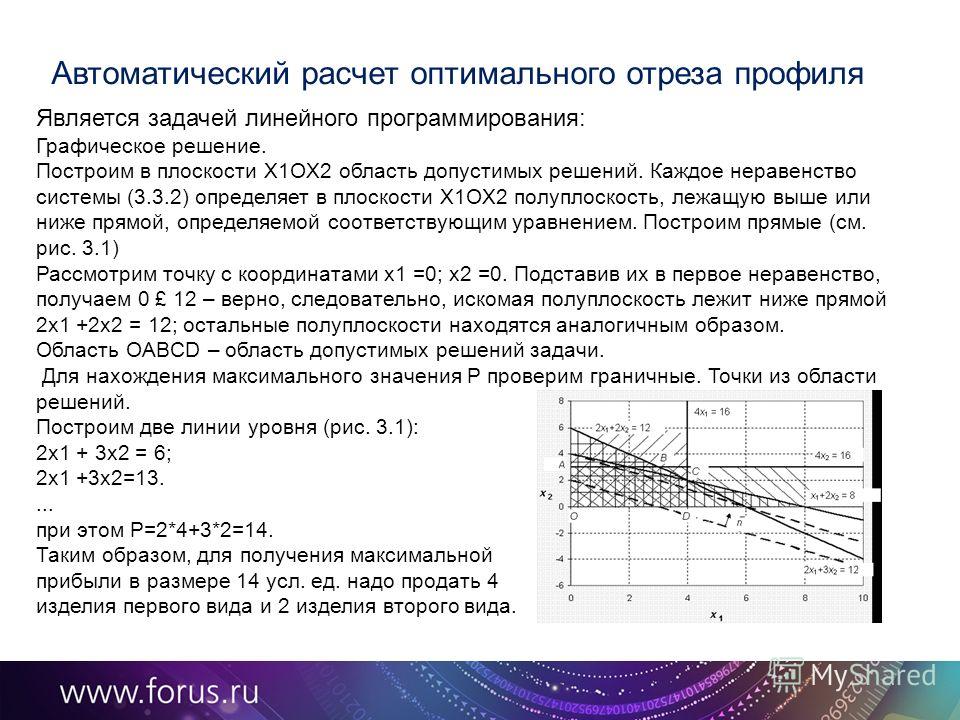 Ваши глаза бегают по странице, быстро собирая информацию, более полно задействуя свой мозг, чтобы найти закономерности и осмыслить данные.

Определите проблему с помощью ментальных карт

Итак, вы знаете, что есть проблема, которую необходимо решить. Вы знаете, что это за проблема? Есть только одна проблема? Является ли проблема суммой множества более мелких проблем?

Такие вопросы необходимо задавать, чтобы убедиться, что вы работаете над корнем проблемы. Вы не хотите тратить слишком много времени и энергии на решение неправильной проблемы.

Чтобы определить проблему, используйте интеллект-карту. Интеллект-карты могут помочь вам визуально провести мозговой штурм и собрать идеи без строгой организации или структуры. Интеллект-карта более тесно связана с тем, как работает большая часть нашего мозга: участники могут прыгать от одной мысли к другой, определяя отношения по мере их развития.

Базовая интеллект-карта (Нажмите на изображение, чтобы изменить его онлайн)

Интеллект-карта для решения проблемы включает, помимо прочего, следующие относительно простые шаги:

1. В центре страницы добавьте свою основную идею или концепцию (в в данном случае проблема).
2. Ответвление от центра с возможными основными причинами проблемы. Соедините каждую причину с центральной идеей.
3. Ответвление от каждой подтемы с примерами или дополнительными сведениями о возможной причине. Добавляя дополнительную информацию, убедитесь, что самые важные идеи находятся ближе к основной идее в центре.
4. Используйте разные цвета, диаграммы и формы для организации различных уровней мышления.

В качестве альтернативы вы можете использовать интеллект-карты для мозгового штурма решений, как только вы обнаружите основную причину. Выполните поиск в библиотеке шаблонов Lucidchart или добавьте библиотеку форм карты разума, чтобы быстро создать собственную карту разума.

Создайте блок-схему решения проблем

Интеллект-карта обычно является хорошим инструментом для нелинейных мыслителей. Однако, если вы мыслите линейно, человек, который мыслит в терминах пошагового прогресса, создавая блок-схему, может лучше подойти для вашей стратегии решения проблем. Блок-схема — это графическое представление рабочего процесса или процесса с различными фигурами, соединенными стрелками, представляющими каждый шаг.

Независимо от того, пытаетесь ли вы решить простую или сложную проблему, шаги, которые вы предпринимаете для решения этой проблемы с помощью блок-схемы, просты и понятны. Используя прямоугольники и другие фигуры для обозначения шагов, вы соединяете фигуры стрелками, которые ведут вас по разным путям, пока в конце вы не найдете логическое решение.

Дерево решений по разработке проекта (Щелкните изображение, чтобы изменить его онлайн)

Блок-схемы или деревья решений лучше всего использовать для решения проблем или ответов на вопросы, которые могут возникать несколько раз. Например, Yoder Lumber, семейный производитель древесины лиственных пород, построил в Lucidchart деревья решений, чтобы продемонстрировать, что сотрудники должны делать в случае травмы.

Чтобы начать блок-схему решения проблем, выполните следующие действия:

1. Нарисуйте исходную форму, чтобы сформулировать свою проблему.
2. Нарисуйте фигуру решения, в которой вы можете задавать вопросы, на которые можно ответить «да» или «нет».
3. На основе ответов «да» или «нет» нарисуйте стрелки, соединяющие возможные пути, по которым вы можете пройти через этапы и отдельные процессы.
4. Продолжайте следовать путям и задавать вопросы, пока не найдете логическое решение указанной проблемы.
5. Попробуйте решение. Если это работает, все готово. Если это не работает, просмотрите блок-схему, чтобы проанализировать, что могло пойти не так, и переделайте блок-схему, пока не найдете работающее решение.

Если ваша проблема связана с процессом или рабочим процессом, вы также можете использовать блок-схемы для визуализации текущего состояния вашего процесса, чтобы найти узкое место или проблему, которая стоит вашей компании времени и денег.

Пример производственного процесса (Нажмите на изображение, чтобы изменить его онлайн)

Lucidchart имеет большую библиотеку шаблонов блок-схем, которые помогут вам анализировать, проектировать и документировать процессы решения проблем или любые другие типы процедур, которые вы можете себе представить.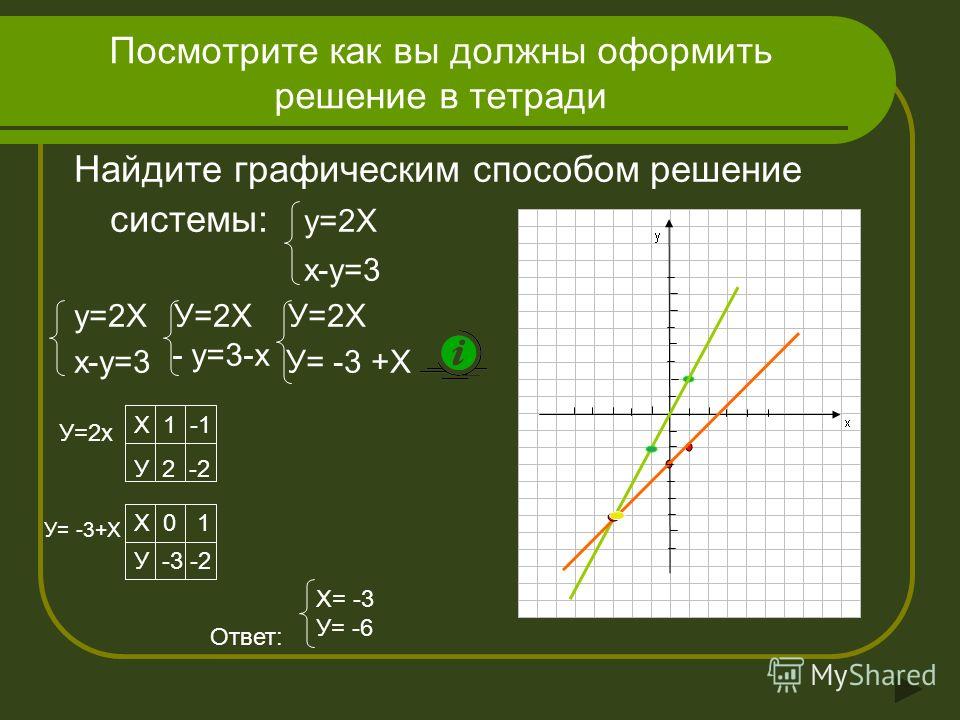

Начертить причинно-следственную диаграмму

Причинно-следственная диаграмма используется для анализа взаимосвязи между событием или проблемой и причиной, по которой они произошли. Не всегда существует только одна основная причина проблемы, поэтому этот визуальный метод может помочь вам обдумать различные потенциальные причины и точно определить фактическую причину заявленной проблемы.

Причинно-следственные диаграммы, созданные Каору Исикавой, также известны как диаграммы Исикавы, диаграммы «рыбья кость» или «елочка» (поскольку в завершенном виде они напоминают рыбью кость). Сгруппировав причины и следствия в более мелкие категории, эти диаграммы можно использовать для изучения того, почему что-то пошло не так или может пойти не так.

Пример причинно-следственной диаграммы (Щелкните изображение, чтобы изменить его онлайн)

Чтобы выполнить причинно-следственный анализ, выполните следующие действия.

1.

Начните с постановки задачи.

Формулировка проблемы обычно помещается в рамку или другую фигуру в крайнем правом углу страницы. Нарисуйте горизонтальную линию, называемую «корешок» или «позвоночник», вдоль центра страницы, указывающую на формулировку вашей проблемы.

2. Добавьте категории, представляющие возможные причины.

Например, категория «Материалы» может содержать такие причины, как «низкое качество», «слишком дорого» и «мало запасов». Нарисуйте угловые линии (или «кости»), которые ответвляются от позвоночника к этим категориям.

3. Добавьте причины в каждую категорию.

Нарисуйте столько ветвей, сколько вам нужно, чтобы провести мозговой штурм о причинах, принадлежащих к каждой категории.

Как и все изображения и диаграммы, причинно-следственная диаграмма может быть простой или сложной в зависимости от того, что вам нужно, чтобы помочь вам проанализировать операции и другие факторы для выявления причин, связанных с нежелательными эффектами.

Сотрудничайте с Lucidchart

У вас могут быть превосходные навыки решения проблем, но это не означает, что вам нужно решать проблемы в одиночку. Приведенные выше визуальные стратегии могут помочь вам привлечь остальную часть вашей команды. Чем больше команда вовлечена в создание вашего визуального повествования о решении проблем, тем охотнее они будут брать на себя ответственность за процесс и тем больше они будут вкладываться в его результат.

В Lucidchart вы можете просто поделиться документами с членами команды, которых вы хотите привлечь к процессу решения проблем. Неважно, где находятся эти люди, потому что к документам Lucidchart можно получить доступ в любое время из любой точки мира.

Какой бы метод вы ни выбрали для решения проблем, работайте с Lucidchart над созданием необходимых вам документов. Зарегистрируйте бесплатную учетную запись сегодня и начните строить диаграммы за считанные минуты.

Начните строить диаграммы с Lucidchart сегодня — попробуйте бесплатно!

Зарегистрируйтесь бесплатно

Популярно сейчас

Что такое интеллектуальное построение диаграмм? 4 фазы жизненного цикла управления проектамиИнструментарий для удобного документирования

Подпишитесь, чтобы получать последние обновления и советы Lucidchart по электронной почте один раз в месяц.

No related posts.