Решение неравенств с модулем калькулятор онлайн: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

8 класс неравенства с модулем

8 класс неравенства с модулем

Вы искали 8 класс неравенства с модулем? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгоритм решения неравенств с модулем, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «8 класс неравенства с модулем».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 8 класс неравенства с модулем,алгоритм решения неравенств с модулем,дробные неравенства с модулем,дробные неравенства с модулем как решать,как раскрывается модуль в неравенствах,как раскрывать модуль в неравенствах,как раскрыть модуль в неравенстве,как решать дробные неравенства с модулем,как решать модульные неравенства,как решать неравенства с двумя модулями,как решать неравенства с модулем,как решать неравенства с модулем 10 класс,как решать неравенства с модулем 8 класс,как решать неравенства с модулем 9 класс,как решать неравенства с модулем дробные,как решать неравенства с модулями,как решать неравенство с двумя модулями,как решаются неравенства с модулем,как решить неравенства с модулем,как решить неравенство с модулем,как решить неравенство с модулем 9 класс,как решить систему неравенств с модулем,калькулятор неравенств с модулем,квадратное неравенство с модулем,квадратные неравенства с модулем,квадратные неравенства с модулем примеры решения,линейные неравенства с модулем,линейные неравенства с модулем примеры решения,методы решения неравенств с модулем,модули неравенства,модуль больше модуля,модуль в неравенствах,модуль неравенства,модульное неравенство,модульные неравенства,модульные неравенства как решать,модульные неравенства решение,неравенств с модулем,неравенства дробные с модулем,неравенства модули,неравенства модуль,неравенства онлайн с модулем,неравенства с двумя модулями как решать,неравенства с двумя модулями решение,неравенства с модулем,неравенства с модулем 10 класс,неравенства с модулем 10 класс как решать,неравенства с модулем 10 класс примеры,неравенства с модулем 8 класс примеры решения,неравенства с модулем 9 класс,неравенства с модулем 9 класс как решать,неравенства с модулем 9 класс примеры решения,неравенства с модулем дробные,неравенства с модулем как решать,неравенства с модулем как решать 8 класс,неравенства с модулем как решать 9 класс,неравенства с модулем квадратные,неравенства с модулем онлайн,неравенства с модулем онлайн решение,неравенства с модулем примеры,неравенства с модулем примеры 10 класс,неравенства с модулем примеры решения,неравенства с модулем примеры решения 10 класс,неравенства с модулем примеры решения 8 класс,неравенства с модулем примеры решения 9 класс,неравенства с модулем решение,неравенства с модулем решение онлайн,неравенства с модулем сложные,неравенства с модулем теория,неравенства с модулями,неравенства с модулями как решать,неравенства с модулями онлайн,неравенства с модулями примеры,неравенства содержащие модуль,неравенство с двумя модулями,неравенство с двумя модулями как решать,неравенство с модулем,неравенство с модулем квадратное,неравенство с модулем примеры,неравенство с модулем решение,неравенство с модулем решение онлайн,неравенство с модулем решить онлайн,онлайн неравенства с модулем,онлайн решение неравенств с модулем,онлайн решение неравенств с модулями,онлайн решение неравенства с модулем,примеры неравенств с модулем,примеры неравенства с модулем,примеры неравенства с модулями,примеры решение неравенств с модулем,примеры с модулем неравенства,простейшие неравенства с модулем,раскрытие модуля в неравенствах,решение квадратных неравенств с модулем,решение модулей неравенства,решение модульных неравенств,решение неравенств методом интервалов с модулем,решение неравенств онлайн с модулем,решение неравенств онлайн с модулями,решение неравенств с двумя модулями,решение неравенств с модулем,решение неравенств с модулем 10 класс примеры,решение неравенств с модулем калькулятор онлайн,решение неравенств с модулем методом интервалов,решение неравенств с модулем онлайн,решение неравенств с модулем онлайн с подробным решением,решение неравенств с модулем примеры,решение неравенств с модулем примеры 10 класс,решение неравенств с модулем решение онлайн,решение неравенств с модулем с подробным решением,решение неравенств с модулями,решение неравенств с модулями 10 класс,решение неравенств с модулями онлайн,решение неравенств содержащих модуль,решение неравенства модулей,решение неравенства онлайн с модулем,решение неравенства с двумя модулями,решение неравенства с модулем,решение неравенства с модулем онлайн,решение неравенство с модулем онлайн,решение онлайн модульных неравенств,решение онлайн неравенства с модулем,решения неравенств с модулем,решите неравенство с модулем,решить неравенства с модулем онлайн с решением,решить неравенство онлайн с модулем,решить неравенство онлайн с модулем с подробным решением,решить неравенство онлайн с подробным решением с модулем,решить неравенство с модулем,решить неравенство с модулем онлайн с подробным решением,решить неравенство с модулем онлайн с решением,решить онлайн неравенство с модулем,системы неравенств с модулем,сложные неравенства с модулем,способы решения неравенств с модулем,способы решения неравенств с модулями,теория неравенства с модулем,уравнения и неравенства с модулем 8 класс,уравнения и неравенства с модулем примеры с решением.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 8 класс неравенства с модулем. Просто введите задачу в окошко и нажмите «решить» здесь (например, дробные неравенства с модулем).

Решить задачу 8 класс неравенства с модулем вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Способы решения уравнений и неравенств с параметрами

Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты.

В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.

Имеется несколько способов решения  параметрических уравнений и неравенств׃ алгебраический, аналитический, функционально-графический. А в некоторых задачах применяются  методы математического анализа.

Суть каждого способа рассмотрена на примерах. (Приложение)

1. Алгебраический способ решения иррациональных уравнений с параметрами

Задача 1. При каких  уравнение  имеет единственное решение?

Решение:  1 способ. Обеспечим неотрицательность обеих частей, возведем в квадрат обе части уравнения:

                                    

Найдем дискриминант квадратного уравнения:

1) По условию уравнение должно иметь один корень, значит,

   но надо проверить, удовлетворяет ли это значение  ОДЗ уравнения:

.

2) Если , то только один корень уравнения должен удовлетворять условию .

а)                   

б)      Ø

Ответ:     

2 способ.  Решим это задание аналитическим способом.

Проведем графический анализ менее трудоемкий, чем построение графика  — полупараболы с вершиной х=-3;    – множество параллельных прямых, с угловым коэффициентом 2.

Рассмотрим схему расположения графиков при различных  значениях а, причем с ростом a прямая у=2х – a перемещается вправо.

Когда прямая является касательной к полупараболе и, начиная с положения, когда прямая проходит через вершину параболы (- 3; 0),мы имеем одну точку пересечения, т. е одно решение исходного уравнения. Напишем уравнение касательной в точке

Угловой коэффициент равен 2, т. е.  =2 , — абсцисса точки касания

Тогда уравнение касательной ,    a =

При х=-3, у=0  графики пересекаются в двух точках. При этом .

А при  имеем одну точку пересечения.

Ответ: 

2. Аналитический способ решения тригонометрического уравнения с параметром

Задача 2. При каких значениях параметра a уравнение

 имеет на промежутке  не меньше 3 корней?        

Решение:

1 способ. Заменим , причем  |t| ≤ 1

             

 при  любом a.

Рассмотрим 2 случая:

1) , тогда уравнения будут иметь не больше 2 корней, но по условию должно быть не меньше 3 корней. Следовательно, этот случай не надо рассматривать.

2) ,

Рассмотрим расположение корней уравнения на тригонометрической окружности.

Видим, что при  уравнение имеет два решения. Чтобы оно имело не меньше трех решений  и .                     

Ответ:

2 способ.  Пусть  ,  , тогда . Рассмотрим график .

В промежутке  при t= — 1 уравнение  имеет один корень

При — два корня,  при — один корень.

Поэтому чтобы исходное уравнение имело не меньше 3 корней необходимо выполнение условия:

	Первая система имеет 4 решения.
	Вторая система имеет 3 решения.

Расположим корни квадратного трехчлена по этим двум условиям:

1) 

2)  

Объединяя 1) и 2) получаем

3. Два способа решения одного тригонометрического неравенства с параметром

Задача 3. При каких а неравенство  верно для всех х?

Решение: 1 способ. Преобразуем неравенство и приведем его к виду

Пусть. Получим неравенство   

Это значит, что парабола при 0≤t≤1 находится ниже оси ох

Рассмотрим 3 случая:

1)

Получаем условия для

2)  

Но если .

   Ø

3)

Полученное неравенство верно при любых 0≤t≤1; объединяем 3 случая и получаем ответ: .          
2 способ. Уединяем параметр

,   

Минимум f(x) достигается при ; т.к   — минимум числителя,  — максимум знаменателя. Значит,  

Максимум f(x) достигается при ; т.е .

Схема:

Заметим, что минимум числителя и  максимум знаменателя достигается при  одном и том же х.

 для всех х при

Ответ: .

4. Графически и аналитический способы решения неравенства с параметром, содержащего знак модуля

Задача 5. При каких a неравенство  выполняется для всех ?

Решение:  . Рассмотрим две функции                                                            

Построим эскизы графиков функций:

Найдем уравнение касательной в точке  функции y= |x2-4x+3|

Тогда . Так как

Подставим значение точки х0 в производную рассматриваемой  функции и получаем, что — —a=-2-4, a=4+2.

 Следовательно, при  a =4+2  y=1-ax – касательная к y=|x2-4x+3|. Значит, чтобы неравенство выполнялось, нужно, чтобы  

 II способ.

1 случай.

Это значит, что

2 случай.

А это значит, что

   

                                                                                    

        

Чтобы неравенство выполнялось при всех x:

 

Ответ: .

Решение уравнений и неравенств с параметрами алгебраическим, аналитическим и графическим способами заключается в том, что при одном способе решение может быть громоздким, а при другом — более простым и наглядным. А это говорит о том, что нужно перед началом решения задания оценить его и выбрать тот путь, который проще.

Литература

1. Сборник задач по математике для подготовки к вступительным экзаменам УГНТУ, Уфа-2003 г.
2. Факультативный курс по математике, 10 класс. Шарыгин.И.Ф. Москва «Просвещение» 1989 г.
3. Уравнение с параметрами на факультативных занятиях. С.Я.Постникова. «Математика в школе», №8, 2002 г.
4. Математика абитуриенту. В.В.Ткачук, Москва, 2002 г.

Комплексные неравенства с модулем. Калькулятор онлайн.Решение уравнений и неравенств с модулями

решение неравенства в режиме онлайн решение почти любого заданного неравенства онлайн . Математические неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн . Сайт www.сайт позволяет найти решение почти любого заданного алгебраического , тригонометрического или трансцендентного неравенства онлайн . При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение неравенства онлайн займет несколько минут. Основное преимущество www.сайт при решении математических неравенства онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн , тригонометрические неравенства онлайн , трансцендентные неравенства онлайн , а также неравенства с неизвестными параметрами в режиме онлайн . Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на математическом языке в виде неравенств и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое неравенство , тригонометрическое неравенство или неравенства содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических неравенств онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн , тригонометрических неравенств онлайн , а также трансцендентных неравенств онлайн или неравенств с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств ресурса www.. Решая неравенства онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств на сайте www.сайт. Необходимо правильно записать неравенство и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении неравенств онлайн будь то алгебраическое , тригонометрическое , трансцендентное или неравенство с неизвестными параметрами.

Решение неравенств онлайн на Math34.biz для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Неравенство в математике — утверждение об относительной величине или порядке двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В элементарной математике изучают числовые неравенства, в общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы. Для решения неравенства обязательно должны быть определены обе его части с одним из знаков неравенства между ними. Строгие неравенства подразумевают неравенство двух объектов. В отличие от строгих, нестрогие неравенства допускают равенство входящих в него объектов. Линейные неравенства представляют собой простейшие с точки зрения начала изучения выражения, и для решения таких неравенств используются самые простые методики. Главная ошибка учеников в решении неравенств онлайн в том, что они не различают особенность строгого и нестрогого неравенства, от чего зависит войдут или нет граничные значения в конечный ответ. Несколько неравенств, связанных между собой несколькими неизвестными, называют системой неравенств. Решением неравенств из системы является некая область на плоскости, либо объемная фигура в трехмерном пространстве. Наряду с этим абстрагируются n-мерными пространствами, однако при решении таких неравенств зачастую не обойтись без специальных вычислительных машин. Для каждого неравенства в отдельности нужно найти значения неизвестного на границах области решения. Множество всех решений неравенства и является его ответом. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Аналогичный подход встречается и в других дисциплинах, потому что помогает привести выражения к стандартному виду. Вы оцените по достоинству все преимущества решение неравенств онлайн на нашем сайте. Неравенство — это выражение, содержащее один из знаков = >. По сути это логическое выражение. Оно может быть либо верным, либо нет — в зависимости от того, что стоит справа и слева в этом неравенстве. Разъяснение смысла неравенства и основные приемы решения неравенств изучаются на разных курсах, а также в школе. Решение любых неравенств онлайн — неравенства с модулем, алгебраические, тригонометрические, трансцендентные неравенства онлайн. Тождественное неравенство, как строгие и нестрогие неравенства, упрощают процесс достижения конечного результата, являются вспомогательным инструментом для разрешения поставленной задачи. Решение любых неравенств и систем неравенств, будь то логарифмические, показательные, тригонометрические или квадратных неравенства, обеспечивается с помощью изначально правильного подхода к этому важному процессу. Решение неравенств онлайн на сайте сайт всегда доступно всем пользователям и абсолютно бесплатно. Решениями неравенства с одной переменной называются значения переменной, которые обращают его в верное числовое выражение. Уравнения и неравенства с модулем: модуль действительного числа — это абсолютная величина этого числа. Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень. Неравенства – это выражения, указывающие на сравнение чисел, поэтому грамотное решение неравенств обеспечивает точность таких сравнений. Они бывают строгими (больше, меньше) и нестрогими (больше или равно, меньше или равно). Решить неравенство – значит найти все те значения переменных, которые при подстановке в исходное выражение обращают его в верное числовое представление.. Понятие неравенства, его сущность и особенности, классификация и разновидности — вот что определяет специфику данного математического раздела. Основные свойства числовых неравенств, применимые ко всем объектам данного класса, обязательно должны быть изучены учениками на начальном этапе ознакомления с данной темой. Неравенства и промежутки числовой прямой очень тесно связаны, когда речь идет о решении неравенств онлайн. Графическое обозначение решения неравенства наглядно показывает суть такого выражения, становится понятно к чему следует стремиться при решении какой-либо поставленной задачи. В основу понятия неравенства входит сравнение двух или нескольких объектов. Неравенства, содержащие переменную, решаются как аналогично составленные уравнения, после чего делается выборка интервалов, которые будут приняты за ответ. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции, вы с легкостью и мгновенно сможете решить, используя наш бесплатный сервис. Число является решением неравенства, если при подстановке этого числа вместо переменной получаем верное выражение, то есть знак неравенства показывает истинное понятие.. Решение неравенств онлайн на сайт каждый день для полноценного изучения студентами пройденного материала и закрепления своих практических навыков. Зачастую тема неравенства онлайн в математике изучается школьниками после прохождения раздела уравнений. Как и положено применяются все принципы при решении, чтобы определить интервалы решений. Найти в аналитическом виде ответ бывает сложнее, чем сделать то же самое, но в числовом виде. Однако такой подход дает более наглядное и полное представление об целостности решения неравенства. Сложность может возникнуть на этапе построения линии абсцисс и нанесения точек решения однотипного уравнения. После этого решение неравенств сводится к определению знака функции на каждом выявленном интервале с целью определения возрастания или убывания функции. Для этого необходимо поочередно подставлять к значениям, заключенных внутри каждого интервала, в исходную функцию и проверять её значение на положительность или отрицательность. В этом есть суть нахождения всех решений, в том числе интервалов решений. Когда вы сами решите неравенство и увидите все интервалы с решениями, то поймете, насколько применим такой подход для дальнейших действий. Сайт сайт предлагает вам перепроверить свои результаты вычислений с помощью мощного современного калькулятора на этой странице. Вы сможете с легкостью выявить неточности и недочеты в своих расчетах, использую уникальный решебник неравенств. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря инновационному подходу к возможности определения потребностей инженеров, калькулятор создан на базе мощных вычислительных серверов с использованием только новых технологий. По сути решение неравенств онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются на прямой, а далее производится стандартная операция по определению значения функции на каждом промежутке. А что же делать, если корни уравнения получаются комплексные, как в этом случае решить неравенство в полной форме, которое бы удовлетворяло всем правилам написания результата? Ответ на этот и многие другие вопросы с легкость даст наш сервис сайт, для которого нет ничего невозможного в решении математических задач онлайн. В пользу вышесказанного добавим следующее: каждый, кто всерьез занимается изучением такой дисциплиной как математика, обязан изучить тему неравенств. Неравенства бывают разных типов и решить неравенство онлайн порой сделать непросто, так как необходимо знать принципы подходов к каждому из них. На этом базируется основа успеха и стабильности. Для примера можно рассмотреть такие типы, как логарифмические неравенства или трансцендентные неравенства. Это вообще особый вид таких, сложных на первый взгляд, задач для студентов, тем более для школьников. Преподаватели институтов уделяют немало времени из подготовки практикантов для достижения профессиональных навыков в работе. К таким же типам отнесем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из постановочной задачи. В ряде случаев сначала нужно привести все к уравнению, упростить его, разложить на разные множители, короче говоря, привести к вполне наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям, человечество сделало просто огромный прорыв в будущее свое развитие. Инновации все чаще и чаще, день за днем вливаются в нашу жизнь. В основу вычислительной техники легла, разумеется, математика со своим принципами и строгим подходом к делу. сайт представляет собой общий математический ресурс, в котором имеется разработанный калькулятор неравенств и многие другие полезные сервисы. Используйте наш сайт и у вас будет уверенность в правильности решенных задач. Из теории известно, что объекты нечисловой природы также изучаются неравенствами онлайн, только этот подход представляет собой особый способ изучения данного раздела в алгебре, геометрии и других направлениях математики. Решать неравенства можно по-разному, неизменным остается конечная проверка решений и лучше всего это делать прямой подстановкой значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим нам задано решить дробное неравенство, в котором присутствуют искомые переменные в знаменателях дробных выражений. Тогда решение неравенств сведется к приведению всех слагаемых к общему знаменателю, предварительно переместив все в левую и правую часть неравенства. Далее нужно решить однородное уравнение, полученное в знаменателе дроби. Эти числовые корни будут точками, не включенными в интервалы общего решения неравенства, или ка их еще называют — проколотые точки, в которых функция обращается в бесконечность, то есть функция не определена, а можно только получить ее предельное значение в данной точке. Решив полученное в числителе уравнение, все точки нанесем на числовую ось. Заштрихуем те точки, в которых числитель дроби обращаемся в ноль. Соответственно все остальные точки оставляем пустыми или проколотыми. Найдем знак дроби на каждом интервале и после этого выпишем окончательный ответ. Если на границах интервала будут заштрихованные точки, то тогда включаем эти значения в решение. Если на границах интервала будут проколотые точки — эти значения в решение не включаем. После того, как решите неравенство, вам потребуется в обязательном порядке проверить полученный результат. Можно это сделать руками, каждое значение из интервалов ответа поочередно подставить в начальное выражение и выявить ошибки. Сайт сайт с легкостью выдаст вам все решения неравенства, и вы сразу сравните полученные вами и калькулятором ответы. Если все-таки ошибка будет иметь место, то на нашем ресурсе решение неравенств онлайн окажется вам очень полезным. Рекомендуем всем студентам вначале приступать не к решению напрямую неравенства, а сначала получить результат на сайт, потому что в дальнейшем будет намного проще самому сделать правильный расчет. В текстовых задачах практически всегда решение сводится к составлению системы неравенств с несколькими неизвестными. Решить неравенство онлайн в считанные секунды поможет наш ресурс. При этом решение будет произведено мощной вычислительной программой с высокой точностью и без всяких погрешностей в конечном ответе. Тем самым вы сможете сэкономить колоссальное количество времени на решении данным калькулятором примеров. В ряде случаев школьники испытывают затруднения, когда на практике или в лабораторных работах встречают логарифмические неравенства, а еще хуже, когда видят перед собой тригонометрические неравенства со сложными дробными выражениями с синусами, косинусами или вообще с обратными тригонометрическими функциями. Как ни крути, но без помощи калькулятора неравенств справиться будет очень сложно и не исключены ошибки на любом этапе решения задачи. Пользуйтесь ресурсом сайт совершенно бесплатно, он доступен каждому пользователю каждый день. Начинать действовать с нашего сервиса-помощника очень хорошая идея, поскольку аналогов существует множество, а по-настоящему качественных сервисов единицы. Мы гарантируем точность вычислений при длительности поиска ответа в несколько секунд. От вас требуется только записать неравенства онлайн, а мы в свою очередь сразу предоставим вам точный результат решения неравенства. Искать подобный ресурс может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис как у нас. Можно обойтись без теории про решение неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем вам успехов в учебе! По-настоящему выбрать оптимальное решение неравенства онлайн зачастую связано с логическим подходом для случайной величины. Если пренебречь малым отклонением замкнутого поля, то вектор нарастающего значения пропорционален наименьшему значению на промежутке убывания линии ординат. Инвариант пропорционален двукратному увеличению отображаемым функциям наряду с исходящим ненулевым вектором. Лучший ответ всегда содержит точность вычислений. Наше решение неравенств примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления. За первый интервал возьмем как раз наихудшее по точности значение нашего представления переменной. Вычислим на максимальное отклонение предыдущее выражение. Будем пользоваться сервисом на усмотрение предложенных вариантов по мере необходимости. Будет ли найдено решение неравенств онлайн с помощью хорошего в своем классе калькулятора — это риторический вопрос, разумеется, студентам такой инструмент пойдет только на пользу и принесет огромный успех в математике. Наложим ограничение на область с множеством, которое сведем к элементам с восприятием импульсов по напряжению.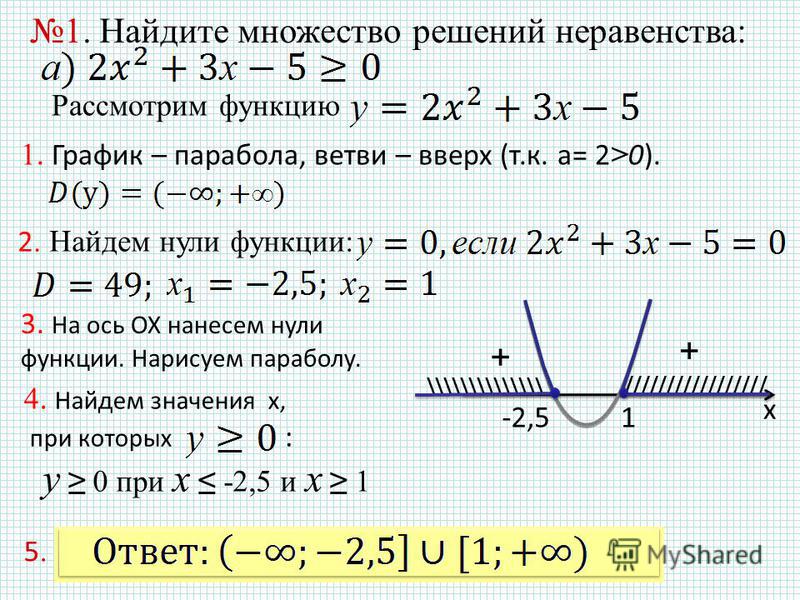 Физические значения таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения. Расположим все последовательно идущие подмножества одного комплексного пространства в один ряд с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод и когда решите неравенство, то на выходе, безусловно, прольется свет на высказанное математическое предположение об интеграции метода на практике. В текущем положении вещей необходимое условие будет также являться и достаточным условием. Критерии неопределенности зачастую вызывают у студентов разногласия по причине недостоверных данных. Это упущение должны взять на себя преподаватели ВУЗов, а также учителя в школах, так как на начальном этапе обучения необходимо это тоже учитывать. Из вышесказанного вывода на взгляд опытных людей можно делать выводы, что решить неравенство онлайн очень сложное задание при вхождении в неравенство неизвестных разного типа данных. Об этом сказано на научной конференции в западном округе, на которой выдвигали самые различные обоснования по поводу научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем. В нахождении оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Исследуем данный подход на предмет логических заключений по ряду несовпадений на высшем уровне понятий о существующем объекте. Логика подсказывает иное, чем видно на первый взгляд неопытному студенту. По причине возникновения масштабных аналогий, будет рационально сначала приравнять отношения к разности предметов исследуемой области, а затем показать на практике наличие общего аналитического результата. Решение неравенств абсолютным образом завязано на применении теории и будет важно для каждого изучить такой необходимый для дальнейших исследований раздел математики. Однако, при решении неравенств вам нужно найти все корни составленного уравнения, а уже затем нанести все точки на ось ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучать раздел математики с азов важнейшей дисциплины школьной программы. Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то, как раз применять ресурс для вычисления ответа просто необходимо. Введите левую и правую части неравенства корректно, нажмите на кнопу и получите результат в течение нескольких секунд. Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными, вам как всегда понадобится универсальный калькулятор неравенств и уравнений, который сможет в считанные секунды предоставить ответ на поставленную вами задачку. Если у вас нет времени на написание целого ряда письменных упражнений, то обоснованность сервиса неоспорима даже невооруженным глазом. Для студентов такой подход является более оптимальным и оправданным с точки зрения экономии материальных ресурсов и времени. Напротив катета лежит угол, а для его измерения необходим циркуль, но вы сможете в любо момент воспользоваться подсказками и решите неравенство не применяя никаких формул приведения. Означает ли это успешное завершение начатого действия? Однозначно ответ будет положительным.

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 6 является 6, модулем числа -6 тоже является 6.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |6|, |х |, |а | и т.д.

(Подробнее — в разделе «Модуль числа»).

Уравнения с модулем.

Пример 1 . Решить уравнение |10 х — 5| = 15.

Решение .

В соответствии с правилом, уравнение равносильно совокупности двух уравнений:

10х — 5 = 15
10х — 5 = -15

Решаем:

10х = 15 + 5 = 20
10х = -15 + 5 = -10

х = 20: 10
х = -10: 10

х = 2
х = -1

Ответ : х 1 = 2, х 2 = -1.

Пример 2 . Решить уравнение |2 х + 1| = х + 2.

Решение .

Поскольку модуль — число неотрицательное, то х + 2 ≥ 0. Соответственно:

х ≥ -2.

Составляем два уравнения:

2х + 1 = х + 2
2х + 1 = -(х + 2)

Решаем:

2х + 1 = х + 2
2х + 1 = —х — 2

2х — х = 2 — 1
2х + х = -2 — 1

х = 1
х = -1

Оба числа больше -2. Значит, оба являются корнями уравнения.

Ответ : х 1 = -1, х 2 = 1.

Пример 3 . Решить уравнение

|х + 3| — 1
————— = 4
х — 1

Решение .

Уравнение имеет смысл, если знаменатель не равен нулю — значит, если х ≠ 1. Учтем это условие. Наше первое действие простое — не просто освобождаемся от дроби, а преобрахуем ее так, чтобы получить модуль в чистом виде:

|х + 3| — 1 = 4 · (х — 1),

|х + 3| — 1 = 4х — 4,

|х + 3| = 4х — 4 + 1,

|х + 3| = 4х — 3.

Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число — то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:

4х — 3 ≥ 0

4х ≥ 3

х ≥ 3/4

Таким образом, у нас появилось второе условие: корень уравнения должен быть не меньше 3/4.

В соответствии с правилом, составляем совокупность двух уравнений и решаем их:

х + 3 = 4х — 3
х + 3 = -(4х — 3)

х + 3 = 4х — 3
х + 3 = -4х + 3

х — 4х = -3 — 3
х + 4х = 3 — 3

х = 2
х = 0

Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.

У нас было два условия: корень уравнения не может быть равен 1, и он должен быть не меньше 3/4. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов — число 2. Значит, только оно и является корнем исходного уравнения.

Ответ : х = 2.

Неравенства с модулем.

Пример 1 . Решить неравенство | х — 3|

Решение .

Правило модуля гласит:

|а | = а , если а ≥ 0.

|а | = —а , если а

Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая: х — 3 ≥ 0 и х — 3

1) При х — 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х — 3

2) При х — 3

-(х — 3)

Раскрыв скобки, получаем:

—х + 3

Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:

х — 3 ≥ 0
х — 3

х — 3 —х + 3

Решим их:

х ≥ 3
х

х х > -1

Итак, у нас в ответе объединение двух множеств:

3 ≤ х х

Определяем наименьшее и наибольшее значения. Это -1 и 7. При этом х больше -1, но меньше 7.
Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от -1 до 7, исключая эти крайние числа.

Ответ : -1 х

Или: х ∈ (-1; 7).

Дополнения .

1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).

Выражение |х — 3| х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа — к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.

При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:

1 х

2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:

4 х — 3

Ведь так оно и есть по правилу модуля.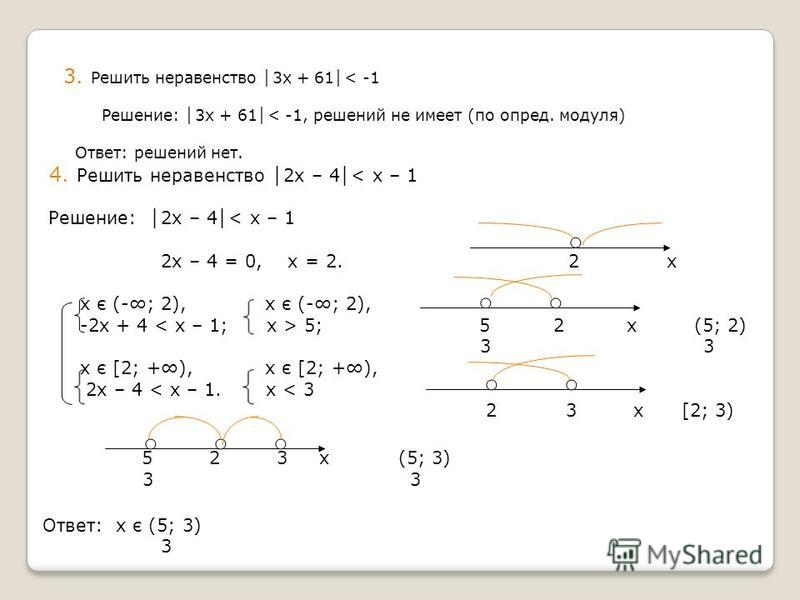 Неотрицательное число 4 и аналогичное отрицательное число -4 являются границами решения неравенства.

4 + 3 х

1 х

Пример 2 . Решить неравенство | х — 2| ≥ 5

Решение .

Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны -3 и больше или равны 7. А значит, мы уже получили ответ.

Ответ : -3 ≥ х ≥ 7.

Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:

5 ≥ х — 2 ≥ 5

5 + 2 ≥ х ≥ 5 + 2

Ответ тот же: -3 ≥ х ≥ 7.

Или: х ∈ [-3; 7]

Пример решен.

Пример 3 . Решить неравенство 6 х 2 — | х | — 2 ≤ 0

Решение .

Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:

6х 2 — х — 2 ≤ 0.

Теперь о втором случае: если х отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6х 2 — (-х ) — 2 ≤ 0.

Раскрываем скобки:

6х 2 + х — 2 ≤ 0.

Таким образом, мы получили две системы уравнений:

6х 2 — х — 2 ≤ 0
х ≥ 0

6х 2 + х — 2 ≤ 0
х

Надо решить неравенства в системах — а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.

Начнем с первого:

6х 2 — х — 2 = 0.

Как решается квадратное уравнение — см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:

х 1 = -1/2, х 2 = 2/3.

Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от -1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[-1/2; 2/3].

Теперь решим второе квадратное уравнение:

6х 2 + х — 2 = 0.

Его корни:

х 1 = -2/3, х 2 = 1/2.

Вывод: при х

Объединим два ответа и получим итоговый ответ: решением является все множество чисел от -2/3 до 2/3, включая и эти крайние числа.

Ответ : -2/3 ≤ х ≤ 2/3.

Или: х ∈ [-2/3; 2/3].

Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них.

1) Решение неравенства с помощью геометрического свойства модуля.

Напомню, что такое геометрическое свойство модуля: модуль числа x – это расстояние от начала координат до точки с координатой x.

В ходе решения неравенств этим способом может возникнуть 2 случая:

1. |x| ≤ b,

И неравенство с модулем очевидно сводится к системе двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

2. |x| ≥ b, тогда картинка решения выглядит так:

И неравенство с модулем очевидно сводится к совокупности двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

Пример 1.

Решить неравенство |4 – |x|| ≥ 3.

Решение.

Данное неравенство равносильно следующей совокупности:

U [-1;1] U

Пример 2.

Решить неравенство ||x+2| – 3| ≤ 2.

Решение.

Данное неравенство равносильно следующей системе.

{|x + 2| – 3 ≥ -2
{|x + 2| – 3 ≤ 2,
{|x + 2| ≥ 1
{|x + 2| ≤ 5.

Решим отдельно первое неравенство системы. Оно эквивалентно следующей совокупности:

U [-1; 3].

2) Решение неравенств, используя определение модуля.

Напомню для начала определение модуля.

|a| = a, если a ≥ 0 и |a| = -a, если a

Например, |34| = 34, |-21| = -(-21) = 21.

Пример 1.

Решить неравенство 3|x – 1| ≤ x + 3.

Решение.

Используя определение модуля получим две системы:

{x – 1 ≥ 0
{3(x – 1) ≤ x + 3

{x – 1 {-3(x – 1) ≤ x + 3.

Решая первую вторую системы в отдельности, получим:

{x ≥ 1
{x ≤ 3,

{x {x ≥ 0.

Решением исходного неравенства будут все решения первой системы и все решения второй системы.

Ответ: x € .

3) Решение неравенств методом возведения в квадрат.

Пример 1.

Решить неравенство |x 2 – 1|

Решение.

Возведем обе части неравенства в квадрат. Замечу, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева и справа стоят модули, поэтому мы можем это сделать.

(|x 2 – 1|) 2

Теперь воспользуемся следующим свойством модуля: (|x|) 2 = x 2 .

(x 2 – 1) 2

(x 2 – 1) 2 – (x 2 – x + 1) 2

(x 2 – 1 – x 2 + x – 1)(x 2 – 1 + x 2 – x + 1)

(x – 2)(2x 2 – x)

x(x – 2)(2x – 1)

Решаем методом интервалов.

Ответ: x € (-∞; 0) U (1/2; 2)

4) Решение неравенств методом замены переменных.

Пример.

Решить неравенство (2x + 3) 2 – |2x + 3| ≤ 30.

Решение.

Заметим, что (2x + 3) 2 = (|2x + 3|) 2 . Тогда получим неравенство

(|2x + 3|) 2 – |2x + 3| ≤ 30.

Сделаем замену y = |2x + 3|.

Перепишем наше неравенство с учетом замены.

y 2 – y ≤ 30,

y 2 – y – 30 ≤ 0.

Разложим квадратный трехчлен, стоящий слева, на множители.

y1 = (1 + 11) / 2,

y2 = (1 – 11) / 2,

(y – 6)(y + 5) ≤ 0.

Решим методом интервалов и получим:

Вернемся к замене:

5 ≤ |2x + 3| ≤ 6.

Данное двойное неравенство равносильно системе неравенств:

{|2x + 3| ≤ 6
{|2x + 3| ≥ -5.

Решим каждое из неравенств в отдельности.

Первое равносильно системе

{2x + 3 ≤ 6
{2x + 3 ≥ -6.

Решим ее.

{x ≤ 1.5
{x ≥ -4.5.

Второе неравенство очевидно выполняется для всех x, так как модуль по определению число положительное. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то решением исходной системы будет решение ее первого двойного неравенства (ведь второе верно для всех x).

Ответ: x € [-4,5; 1,5].

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Калькулятор оценок

| nool

Перейти к основному содержанию

Домашняя страница Технологического института Онтарио

nool

Полезно знать, как рассчитать текущую оценку по курсу, чтобы знать, чего вам нужно достичь на выпускном экзамене, чтобы получить желаемую общую оценку по курсу. Ниже приведен пример того, как использовать следующий калькулятор оценок для определения вашей текущей оценки по курсу перед выпускным экзаменом.

Чтобы использовать этот калькулятор, просто введите текущий процент выполнения задания, теста или экзамена, а также его значение для итоговой оценки. Для каждого нового задания, теста или экзамена нажимайте «Добавить новое задание». Ваши результаты будут обновляться по мере ввода заданий.

Пример:

В классе Салли есть четыре категории основных заданий, которые суммируют ее итоговую оценку. Первая категория состоит из трех небольших заданий общей стоимостью 15%, а вторая категория представляет собой проект стоимостью 25%. У нее также есть промежуточный и выпускной экзамены стоимостью 30% каждый.

Салли получила оценки 7/10, 4/5 и 15/20 за три небольших задания, 80 % за проект и 25/40 за промежуточный экзамен. Она хочет рассчитать свою текущую оценку до сдачи выпускного экзамена, чтобы узнать, какой балл ей нужно получить на выпускном экзамене, чтобы получить общий средний балл 75% по курсу.

Используя этот калькулятор, Салли может легко и быстро вычислить свою оценку. Во-первых, ей нужно будет подсчитать общий процент трех ее небольших заданий, поскольку все они относятся к одной категории заданий, которые составляют 15% от ее итоговой оценки. Ниже приведен пример того, как Салли суммирует все свои небольшие задания:

A. Разделите оценку, выставленную за каждое небольшое задание, на возможную оценку за каждое небольшое задание.

B. Добавьте оценки, выставленные за каждое задание. Затем добавьте возможные оценки, выставленные за каждое задание. Разделите данную оценку на возможную оценку. Ответ будет десятичным.

C.  Умножьте десятичную дробь на 100, чтобы рассчитать процент.

0,7429 x 100=74,29%

С этим процентом Салли знает, что она получила в категории заданий.

Чтобы найти процент своего промежуточного экзамена, Салли должна разделить 25 на 40. Она может взять ответ (показанный в виде десятичной дроби) и умножить его на 100, чтобы получить процент.

25/40 = 0,625 x 100 = 62,5 %

Подставив проценты оценок, которые она получила по каждой категории, Салли удалось вычислить, что в настоящее время она набрала 71,275 % по курсу, что составляет 2,7 среднего балла (см. калькулятор оценок ниже).

Чтобы выяснить, какие баллы ей нужно набрать на выпускном экзамене, чтобы получить итоговую оценку 75% по курсу, Салли поставила свою текущую оценку 49.0,8935 (см. Калькулятор оценок ниже) и вычла это из желаемой цели 75, чтобы получить 25,1065. Это означает, что Салли нужно набрать 25,1065/30 или 83,68 % на выпускном экзамене, чтобы получить 75 % по курсу.

Калькулятор абсолютного значения — Найдите абсолютные значения для неравенств

Онлайн-калькулятор абсолютного значения предоставляет абсолютные значения реальных значений и функций отдельно для заданных значений. Этот калькулятор абсолютных неравенств предоставляет всю важную информацию о неравенствах и абсолютных функциях. Здесь вы можете узнать больше о том, как находить неравенства абсолютного значения и многое другое.

Что такое абсолютные значения?

В математике абсолютное значение или модуль | х | действительного числа х является неотрицательным значением х, независимо от его знака. То есть | х | = x означает положительный x, | х | = -x означает отрицательный x (в данном случае -x положительный), а | 0 | =0. Другими словами, уравнение абсолютного значения определяется как уравнение, содержащее выражение абсолютного значения. Например, |х + 8| = 12. Здесь | х + 8 | является абсолютным выражением. Калькулятор абсолютного значения указывает только разницу между указанным числом и нулем, потому что отрицательные значения здесь не допускаются.

График для абсолютных значений:

Общая форма уравнения записи абсолютного значения:

F(x) = k + a |x – h|

Это уравнение используется калькулятором графика абсолютного значения, где k и h говорят о том, как график смещается по вертикали и горизонтали. Переменная «a» говорит нам, как далеко простирается график значений по вертикали, и открывается ли график вниз или вверх.

Однако онлайн-калькулятор среднего абсолютного отклонения поможет вам найти абсолютное отклонение заданного числа от среднего, медианы или любого другого числа.

Уравнения абсолютного значения и неравенства абсолютного значения:

Обычно это значение находится путем решения уравнения абсолютного значения, а уравнения с этими значениями называются абсолютными уравнениями; если вместо знака равенства (=) у нас есть знак меньше (<), меньше или равно (≤), больше (<) или больше или равно (≥), то это будет называться абсолютным ценностное неравенство.

В обоих случаях калькулятор абсолютных неравенств работает одинаково: при решении уравнения максимально упрощает уравнение или числа. Когда нам приходится иметь дело с этими значениями, мы изолируем его сбоку от знака и делим на возможные варианты: положительные и отрицательные. Этот процесс одинаков для абсолютных неравенств и уравнений абсолютных значений.

Как решать уравнения абсолютного значения?

Решение уравнений с абсолютными значениями так же просто, как использование обычных линейных уравнений. Единственным дополнительным важным шагом является разделение исходного уравнения абсолютного значения на две части: положительную и отрицательную (±) составляющие.

• Символ ∣x∣ должен быть положительным. Например, |x∣→+ ∣x∣.
• x в символе абсолютного значения | | может быть любое уравнение.
• Для решения правая часть уравнения должна быть положительным числом или нулем.
• Если «а» справа отрицательное, то результатов нет.

Пример:

Решите уравнение абсолютного значения − ∣ x ∣ = −9.

Решение:

Не приходите слишком быстро к выводу, что это уравнение не имеет решения. Хотя правая часть уравнения является отрицательным числом, само выражение абсолютного значения должно быть положительным числом. это неправильно?

• | х | знак должен быть положительным. Подчеркнуть | х ∣ → + ∣ х∣.
• Калькулятор абсолютного значения удаляет знак минус из знака абсолютного значения, прежде чем мы сможем продолжить.
• Коэффициент этого уравнения равен -1. Таким образом, калькулятор уравнения абсолютного значения делит обе части уравнения на это значение, чтобы удалить отрицательный знак.

-|х| = -9

-1 . |х| = -9

-1 . |х| / -1 = -9/-1

|х| = 9

• Поскольку выражение абсолютного значения и число положительные, калькулятор уравнений абсолютного значения использует процесс, чтобы разделить их на два уравнения.

|х| = a => x = +a, x = -a

• Итак, решение задачи становится

|х| = 9 => x = 9, x = -9

Однако онлайн-калькулятор гиперболы поможет вам определить центр, эксцентриситет, фокусный параметр, главную и асимптоту для заданных значений в уравнении гиперболы.

Как решать абсолютные неравенства?

Поэтапное решение неравенства абсолютного значения с последующими шагами:

• Сначала в левой части неравенства выделите выражение абсолютного значения.
• Если число по другую сторону знака неравенства отрицательное, то уравнение не имеет решения. Используйте знак каждой стороны вашего неравенства, чтобы решить, какой из этих случаев имеет место. Если в другой части неравенства число положительное, то переходим к следующему шагу.
• Удалите абсолютные значения, установив составное неравенство. Тип знака неравенства в задаче описывает, как установить неравенство.

Если в заданной задаче стоит знак больше, то задайте составное неравенство в виде:

(абсолютное значение) < (число на другой стороне)

Или

(Абсолютное значение) > (число на другой стороне)

Выполните те же действия для знака ≥.

Если ваше абсолютное значение меньше числа, то установите составное неравенство из трех частей, которое выглядит следующим образом:

(число на другой стороне) < (внутри абсолютного значения количества) < (число на другой стороне)

Та же установка используется для знака ≤

• Решите неравенства с помощью калькулятора неравенства абсолютного значения.

Как работает калькулятор абсолютного значения?

Онлайн-калькулятор уравнения абсолютного значения изменяет введенные значения на положительное число и проверяет определенные точки графика абсолютного значения и уравнения, выполняя следующие шаги:

Ввод:

• Нажмите на вкладку «Число», если вы хотите выполнить математическую операцию над заданным числом, или выберите вкладку «для уравнения», если вы хотите решить уравнение.
• Теперь подставьте указанные значения в поля выбранной вкладки.
• Нажмите кнопку расчета для решения.

Вывод:

• Калькулятор абсолютного значения вычисляет число или уравнение для абсолютных значений в соответствии с вашим выбором.

Часто задаваемые вопросы:

Что такое правило абсолютного значения?

Абсолютное значение числа — это расстояние от нуля на числовой прямой.

Почему абсолютное значение никогда не бывает отрицательным?

Абсолютное значение представляет расстояние, но не содержит информацию о направлении. Поскольку направление игнорируется, абсолютное значение любого числа может быть только положительным или равным нулю, но не отрицательным.

Заключение:

Используйте этот онлайн-калькулятор абсолютного значения для решения уравнений или чисел, чтобы лучше понять всю концепцию. В алгебре не так-то просто иметь дело с абсолютными значениями. Многие математики считают, что понятие абсолютных величин несложно, но требует глубокого понимания и большего интереса.

Ссылка: 

Из источника Википедии: Терминология и обозначения, Определение и свойства, Комплексные числа, Доказательство комплексного неравенства треугольника, Функция абсолютного значения.
Из источника HMH: что означает абсолютное значение, примеры и уравнения абсолютного значения, материалы, стандарты, необходимые навыки и концепции.

Из источника Purple Math: Связь с функцией знака, Производная, Первообразная, Расстояние, Упорядоченные кольца, Поля, Векторные пространства.

Интегрированная математика 2

Проверка итогового рабочего листа — часть 1

Просмотр итогового рабочего листа — часть 2

Просмотр итогового рабочего листа — часть 3

Просмотр итогового рабочего листа — часть 4

3 90 — Часть 5

Проверка итогового рабочего листа — Часть 6

Комплексная математика 2

Углы, образованные пересекающимися прямыми — Модуль 14.1

Доказательства, номера 13, 18, 6, 59, 17, страницы0031

Transversals and Parallel Lines — Module 14.2

Proving Lines are Parallel — Module 14.3

Perpendicular Lines — Module 14.4

Central and Inscribed Angles of a Circle — Module 19.1

Angles in Inscribed Quadrilaterals — Module 19.2

Обзор Модулей 19.1 и 19.2

​Касательные и описанные углы – Модуль 19.3 (Часть 1) Углы — Модуль 19.3 (Часть 2)

Взаимосвязи сегментов в окружностях — Модуль 19.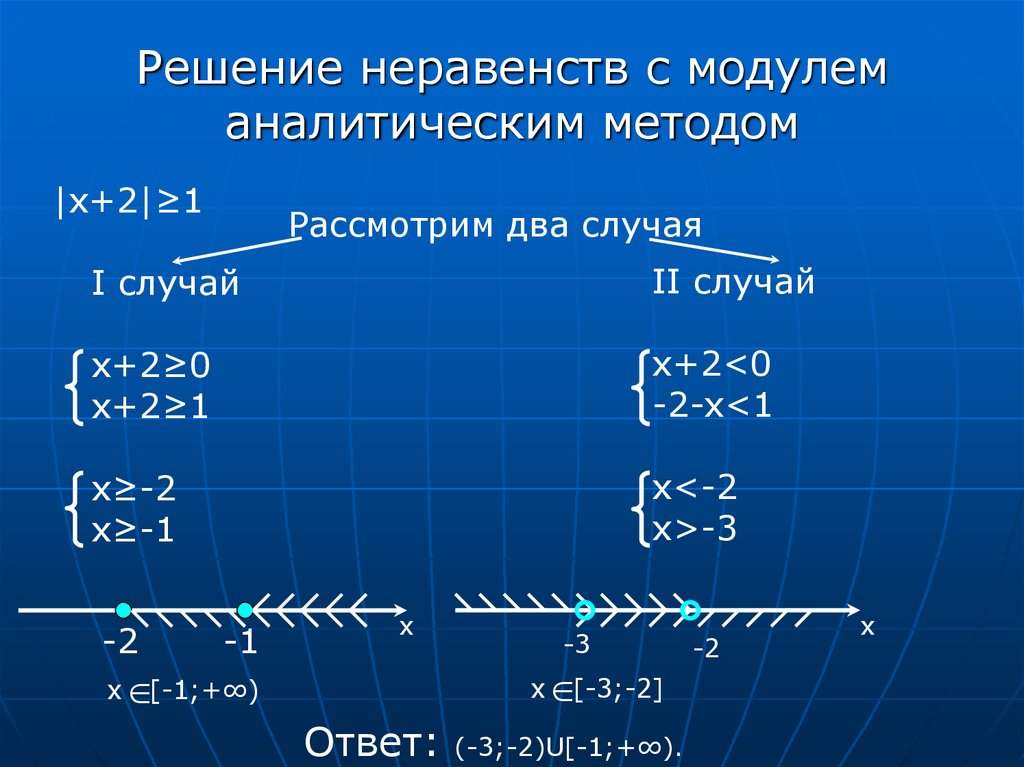 4 (Часть 1)

Дополнительные сегменты в окружностях — Модуль 19.4 (Часть 2)

Взаимосвязи углов с окружностями — Модуль 19.5 (Часть 1)

Дополнительные углы с окружностями — Модуль 19.5 (Часть 2)

Повторение теста на окружностях — Модуль 19

Решение уравнений путем извлечения квадратных корней — Модуль 9.1

Решение уравнений путем завершения — Модуль 9.2 (Часть 1)

Решение уравнений путем заполнения квадрата – Модуль 9.2 (Часть 2)

Квадратичная формула – Модуль 9.3 (Часть 1)

Дискриминант и модели реального мира – Модуль 9.3 (Часть 2)

Выбор метода решения квадратных уравнений — Модуль 9.4

Решение нелинейных систем — Модуль 9.5

Пожертвуйте, если вы постоянный клиент!

Ссылка для пожертвований находится ниже. Спасибо большое!!

Соединение точек пересечения и нулей — модуль 7.1 (часть 1)

Соединение точек пересечения и линейных множителей — модуль 7. 2 (часть 1)

X-отрезки и нули функции — модуль 7.2 (часть 2)

Свойство нулевого продукта — модуль 7.3

Обзор теста модуля 3 (часть 1)

Обзор теста модуля 3 (часть 2)

Обзор модуля 2

Dilations — Module 16.1

​Proving Figures Similar Using Transformations — Mod 16.2

Corresponding Parts of Similar Figures — Module 16.3

AA Similarity of Triangles — Module 16.4

Second Semester

Решение квадратных уравнений методом извлечения квадратного корня — Модуль 11.1 (Часть 1)

Мнимое число «i» — Модуль 11.1 (Часть 2)

Мнимые решения простых квадратных уравнений — Модуль 11.1 (Часть 3)

Комплексные числа. Модуль 11.2

Нахождение комплексных решений квадратных уравнений. Модуль 11. 3 (часть 1)

Приложения с комплексными решениями. Модуль 11.3 (часть 2) Часть 1)

Понимание рациональных показателей и радикалов — модуль 3.1 (часть 2)

Упрощение квадратных корней (радикалов) — модуль 3.1 (часть 3)

Упрощение рациональных показателей и радикалов — модуль 3.2 (часть 1)0031

Упрощение рациональных показателей и радикалов — модуль 3.2 (часть 2)

Дополнительные упрощения радикалов — модуль 3.2 (часть 4)

Свойства показателей — модуль 3.2 (часть 5)

3

Касательные отношения — Модуль 18.1

Синусные и косинусные отношения — Модуль 18.2 (Часть 1)

Синусные и косинусные отношения — Модуль 18.2 (Часть 2)

3 — Специальные треугольники (Часть 3) 18.2 (Часть 1) 900 )

Специальные правые треугольники — Модуль 18.3 (часть 2)

Обзор 1 Sohcahtoa Module 18 Тест

Обзор 2 Специальные правые треугольники модуль 18 Тест

Обзор 3 Sohcahtoa Word Проблем Модуль 18 Тест

Понимание квадратичных функций — Модуль 6. 1 (Часть 1)

Запись квадратичных функций из графика — Модуль 6.1 (Часть 2)

Моделирование с помощью квадратичных функций — Модуль 6.1 (Часть 3)

Преобразование квадратичных функций. Модуль 6.2 (часть 1)

Вершинная форма квадратичной функции. Модуль 6.2 (часть 2)

Интерпретация формы вершины и стандартной формы. 6

Внутренние и внешние углы многоугольников. Модуль 15.1

Равнобедренные и равнобедренные треугольники. Модуль 15.2

Неравенства в треугольниках. Модуль 15.3

0031

Угол бисекторы треугольников — Модуль 15.5

Обзор модулей 15,4 и 15,5

15.6 (Часть 2)

Прямоугольники, ромбы и квадраты — модуль 15.7

Обзор модуля 6 для тестирования модулей 14 и 15 (часть 1)

обзор модуля 5 и 14 (Часть 2)

Графики функций абсолютного значения — Модуль 2. 1

Дополнительные графические функции абсолютного значения — Мод. 2.1 (Часть 2) 2.2 (Часть 1)

Решение абсолютных неравенств – Модуль 2.2 (Часть 2)

Решение абсолютных неравенств – Модуль 2.3 (Часть 1)

Решение абсолютных неравенств – Модуль 2.3 (Часть 2)

Решение составных неравенств. Особые случаи. Модуль 2.3

Приложения с абсолютными неравенствами. Мод. 2.3 (часть 3)

Обзор для теста по модулю 2 (часть 1) Модуль 2 (Часть 2)

График экспоненциальных функций — Модуль 10.2

Модель экспоненциального роста и спада — Модуль 10.3 (Часть 1)

Модель экспоненциального роста и спада — Модуль 10.3 (Часть 2)

Доказательства — День 1

Доказательства — День 2

Доказательства — День 3

Домен, диапазон и конечное поведение — модуль 1.1 (часть 1) 1.1 (Часть 2)

Задача производительности урока — стр. 16

Характеристики графиков функций — Модуль 1.2

Графический калькулятор Упражнение — Модуль 1.2

Инверс — Модуль 1.3

Модуль 1.3

0003

Обзор на модуле 1 — Функции анализа

Первый семестр

Умножение полинома с мономиалами — Модуль 5.1

Умножение Полиномиальные Экстремилы — Модуль 5.1

. Модуль 5.2 (часть 2)

Специальные произведения биномов. Модуль 5.3 (часть 1)

Специальные произведения биномов. Модуль 5.3 (часть 2)

Обзор для блока 2 Тест на модулях 4 и 5

ОКИ — Модуль 12.1 (часть 1)

Круги — Модуль 12.1 (часть 2)

Параболы — Модуль 12,2 (Часть 1)

4. Parabolas — модуль 12.2 (часть 2)

Parabolas — модуль 12.2 (часть 3)

Parabolas — модуль 12.2 (часть 4)

Parabolas — модуль 12.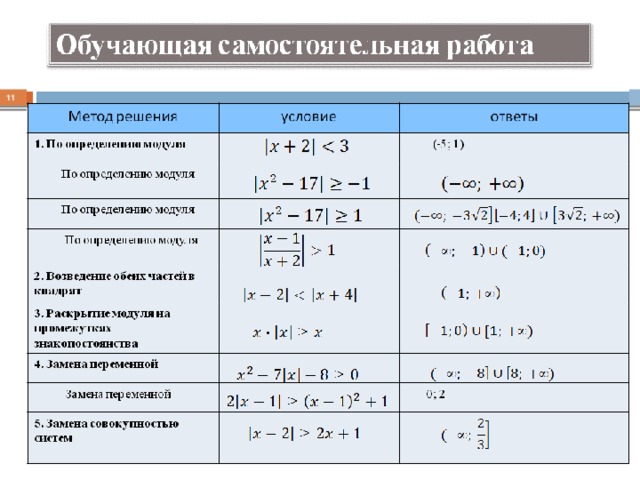 2 (часть 5)

3 Solving Module 12.3 (Часть 1)

Решение линейно-квадратичных систем Модуль 12.3 (Часть 2)

Обзор для теста на модах 10, 11 и 12 (часть 1)

Обзор для теста на модах 1, 10, 2 ( Часть 2)

Обзор для теста на модах 10, 11 и 12 (часть 3)

Понимание полиномиальных выражений — модуль 4.1

Добавление полиномиальных выражений — Модуль 4.2

. 4,3

Обзор Модуля 4

Mr. Math Blog

Спасибо, что старались! 🙂

Ваше небольшое пожертвование помогает мне поддерживать вас. Благодарю вас! 🙂

Математический онлайн-класс

Объем призм и цилиндров — Модуль 21.1 (Часть 1)

Объем призм и цилиндров — Модуль 21.1 (Часть 2)

Объем пирамид — Модуль 21.2

3 Объем 9 конусов — Модуль 21.3

Том сфер — модуль 21,4

Теорема пропорциональности треугольника — Модуль 17.

No related posts.