Дискретные распределения: 4.3.6. Дискретные распределения вероятностей

Дискретные распределения вероятностей и их параметры: определение, свойства, таблица, примеры

1. Общие свойства дискретного распределения
2. Функция распределения дискретной случайной величины
3. Числовые характеристики дискретного распределения
4. Таблица дискретных распределений, их параметров и числовых характеристик
5. Примеры

п.1. Общие свойства дискретного распределения

Величина, которая в результате испытания может принимать то или иное числовое значение, называется случайной величиной.
Случайная величина называется дискретной, если она принимает не более чем счетное количество значений.
Дискретная случайная величина называется конечной, если она принимает конечное число значений.

Согласно данному определению дискретная величина может быть определена либо на бесконечном счетном множестве, либо на конечном множестве (которое всегда счетное).
Напомним, что счетным называется множество, которое эквивалентно множеству натуральных чисел, т. е. элементы которого можно пронумеровать (см. §11 справочника для 8 класса).

Например:
1) При подбрасывании игрального кубика мы получаем всего 6 исходов. Случайная величина X – выпавшее число очков – принимает конечное число значений \(\Omega=\left\{1;2;3;4;5;6\right\}\), т.е. является дискретной конечной случайной величиной.
2) Случайная величина X – количество поступивших вызовов на сервер за сутки – не ограничена сверху и может принимать значения \(\Omega=\left\{1;2;3;…\right\}\)

Правило, устанавливающее связь между значениями случайной величины и вероятностью получения каждого из этих значений в испытании, называется законом распределения.

Случайная величина полностью описывается своим законом распределения.
Закон распределения может быть задан аналитически (формулой), таблично или графически.

Закон распределения конечной дискретной случайной величины, заданный в виде таблицы, называют рядом распределения.

Например:
В результате измерения температуры учеников школы получен следующий ряд распределения:

t, °C	36,3	36,4	36,5	36,6	36,7	36,8	36,9	37,0	37,1
p(t)	0,05	0,07	0,15	0,33	0,31	0,11	0,04	0,01	0,01

Значения \(\left\{x_1,x_2,…,x_k\right\}\), которые может принимать конечная случайная величина X, являются несовместными и образуют полную группу событий. 3 P(k)=\frac{27+54+36+8}{125}=1 $$

п.2. Функция распределения дискретной случайной величины

Функцией распределения дискретной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины X не превышает граничное значение x: $$ F(x)=P(X\leq x) $$

Для дискретной случайной величины функция распределения будет ступенчатой кусочно-непрерывной функцией, область значений которой: \(F(x)\in[0;1]\).

Слева на графике функции распределения будет нулевая «ступенька», а справа – единичная «ступенька».

Например:
Найдем из закона распределения случайной величины k, полученного в предыдущем примере для урны с шарами, функцию распределения.

k	0	1	2	3
\(P_3(k)\)	\(\frac{27}{125}\)	\(\frac{54}{125}\)	\(\frac{36}{125}\)	\(\frac{8}{125}\)
\(F(k)\)	\(\frac{27}{125}\)	\(\frac{27+54}{125}=\frac{81}{125}\)	\(\frac{81+36}{125}=\frac{117}{125}\)	\(\frac{117+8}{125}=1\)

Изобразим графически закон распределения в виде гистограммы:

Построим график для функции распределения: \begin{gather*} F(k)= \begin{cases} 0,\ k\leq 0\\ \frac{27}{125},\ 0\lt k\leq 1\\ \frac{81}{125},\ 1\lt k\lt 2\\ \frac{117}{125},\ 2\lt k\leq 3\\ 1,\ k\gt 3 \end{cases} \end{gather*}

п.

2=p(1-p)=pq \end{gather*}
Типичным примером является бросание монеты, где \(M(X)=p=0,5\) и \(D(X)=0,5\cdot 0,5=0,25\). Дисперсия максимальна для нефальшивой монеты.

Рассмотрим другой пример – бросание фальшивой монеты, для которой вероятность выпадения орла (k=1) равна p=0,7. Тогда \(M(k)=p=0,7\), дисперсия \(D(k)=0,7\cdot 0,3=0,21\). Как и ожидалось, для фальшивой монеты средняя величина возрастает (70% бросков заканчивается выпадением орла). При этом дисперсия уменьшается.

Ответ: \(M(X)=p,\ D(X)=pq\)

Пример 3. Выведите формулы для мат.ожидания и дисперсии биномиального распределения.

Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».
При этом вероятность успеха в каждом испытании постоянна и равна \(p\in(0;1)\).
Вероятность неудачи в каждом испытании \(q=1-p\).
Вероятность того, что событие A появится в n испытаниях Бернулли ровно k раз, выражается биномиальным распределением: $$ P_n(k)=C_n^k p^k q^{n-k} $$

Математическое ожидание и дисперсию для одного опыта Бернулли мы получили в примере 2: \(M(X)=p,\ D(X)=pq\).

Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. \(X=X_1+X_2+…+X_n\). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий (см. §41 справочника для 9 класса): \begin{gather*} M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)=\\ =\underbrace{p+p+…+p}_{n\ раз}=np \end{gather*} По свойству дисперсии суммы независимых событий (см. §41 справочника для 9 класса): \begin{gather*} D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)=\\ =\underbrace{pq+pq+…+pq}_{n\ раз}=npq \end{gather*} Например, пусть событие A=«уронить молоток на ногу» имеет вероятность p=0,1.
Тогда для n=100 забиваний гвоздей вы в среднем уроните молоток на ногу
\(M(X)=np=100\cdot 0,1=10\) раз
Дисперсия этого события \(D(X)=npq=100\cdot 0,1\cdot 0,9=9\)
СКО \(\sigma(X)=\sqrt{D(X)}=3\)
По правилу «трех сигм» интервал оценки: \begin{gather*} 10-3\cdot 3\lt X\lt 10+3\cdot 3\\ -17\lt X\lt 37\\ 0\leq X\leq 36 \end{gather*} Скорее всего (вероятность 99,72%), вы уроните молоток от 0 до 36 раз. {-0,001}=0,000999\approx 0,001 $$ Вероятность всех остальных случаев пренебрежимо мала.
Таким образом, при малых \(\lambda\) вероятности \(p_0\approx 1-\lambda,\ p_1\approx\lambda\), т.е. фактически мы получаем распределение Бернулли.
Ответ: \(M(X)=\lambda ,\ D(X)=\lambda\)

Дискретные распределения — Энциклопедия по экономике

В предыдущих разделах мы познакомились с дискретным распределением вероятностей, когда рассматриваемая переменная могла принимать только определенные (дискретные) значения. Например такие переменные, как количество брака, количество поступающих пациентов и количество несчастных случаев, могут быть выражены только целыми числовыми значениями. В этом разделе мы рассмотрим непрерывное распределение, когда теоретически переменная может иметь любое значение в пределах заданного диапазона.  [c.76]
Дисперсия характеризует степень разброса возможных результатов от наиболее вероятного значения по проекту. Дисперсия (а2 ) дискретного распределения рассчитывается по формуле  [c. 352]

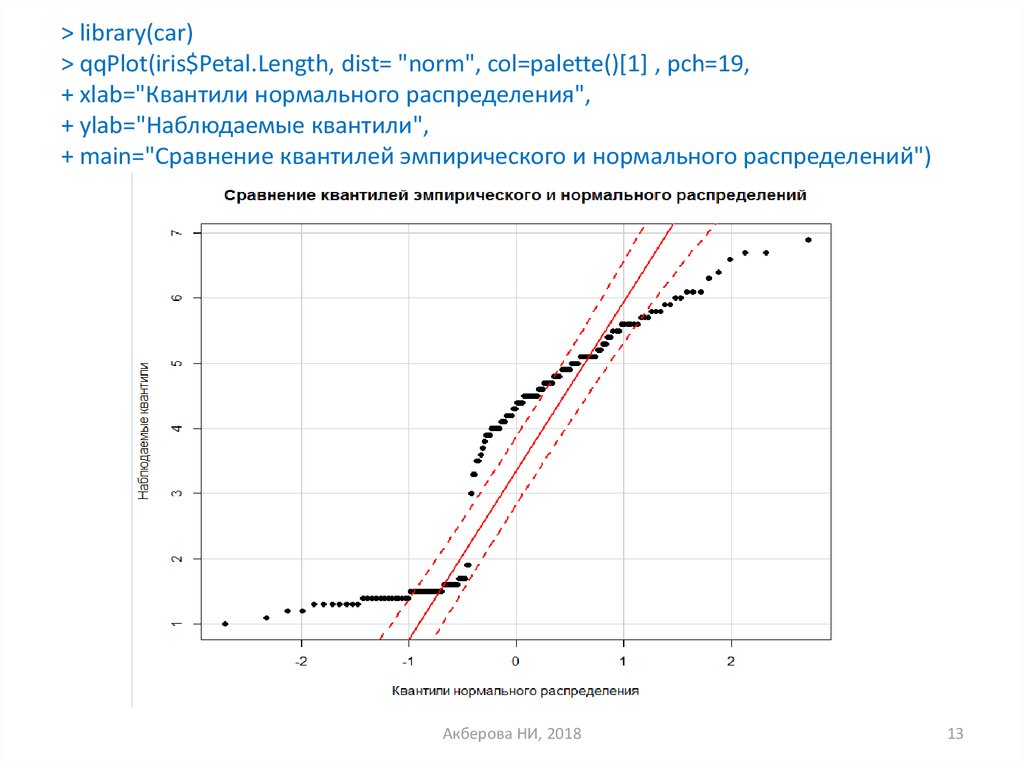
Если бы мы записали точное время финиша, а не округленное до секунд, то могли бы построить непрерывное распределение. При непрерывном распределении нет ячеек. Представьте непрерывное распределение как серию бесконечно малых ячеек (см. рисунок 3-1). Непрерывное распределение отличается от дискретного, которое является ячеистым распределением. Хотя создание ячеек уменьшает информационное содержание распределения, в реальной жизни это единственно возможный подход для обработки ячеистых данных, поэтому на практике приходится жертвовать частью информации, сохраняя при этом профиль распределения. И наконец, вы должны понимать, что можно взять непрерывное распределение и сделать его дискретным путем создания ячеек, но невозможно дискретное распределение переделать в непрерывное.  [c.83]

Сценарные спектры можно представлять себе как дискретные распределения. Такой же подход можно использовать и для определения вероятностей для непрерывного распределения, если рассматривать его как дискретное распределение с бесконечно малым шагом квантования (т. е. с бесконечным множеством сценариев).  [c.164]

Используя непрерывные распределения вероятностей, аналитик может отказаться от точной оценки каждого результата в отдельности. Вместо этого аналитик должен прочертить кривую, которая отразит ситуацию так, как он ее видит. Относительная вероятность каждого отдельного результата (скажем, доходов в расчете на акцию 1,035) равна нулю. Однако относительная вероятность любого диапазона доходов определяется путем простого измерения площади между кривой и горизонтальной осью. Так, вероятность того, что доходы окажутся в пределах от 1,03 до 1,04, может быть установлена при измерении площади под кривой между 1,03 и 1,04, что в данном случае составит приблизительно 0,07 (т.е. 7 шансов из 100, что в следующем году доходы будут в пределах 1,03 — 1,04). Для дискретных распределений вероятностей наподобие тех, что показаны на рис. 6.4 и 6.5, ранее отмечалось, что сумма вероятностей должна равняться 1,0. И тогда при непрерывном распределении вероятностей общая площадь под кривой должна составить 1,0.

 [c.153]

Укажите, в чем различие между непрерывными и дискретными распределениями вероятностей.  [c.165]

Напомним, что если число таких исходов конечно, то имеет место дискретное распределение вероятностей. В этом случае ожидаемую величину доходности можно представить в следующем виде  [c.58]

Дисперсия и среднее квадратическое отклонение. Дисперсией, напомним, называется мера разброса возможных исходов относительно ожидаемого значения, причем чем выше дисперсия, тем больше разброс. Дисперсия дискретного распределения (а2) рассчитывается следующим образом  [c.59]

При использовании сценарного подхода получают дискретное распределение вероятностей прогнозируемого показателя.  [c.121]

Затем рассчитывается дисперсия дискретного распределения следующим образом  [c.122]

При использовании сценарного подхода получают дискретное распределение вероятностей прогнозируемого показателя. Напомним, в этом случае ожидаемое значение показателя представляют в следующем виде  [c.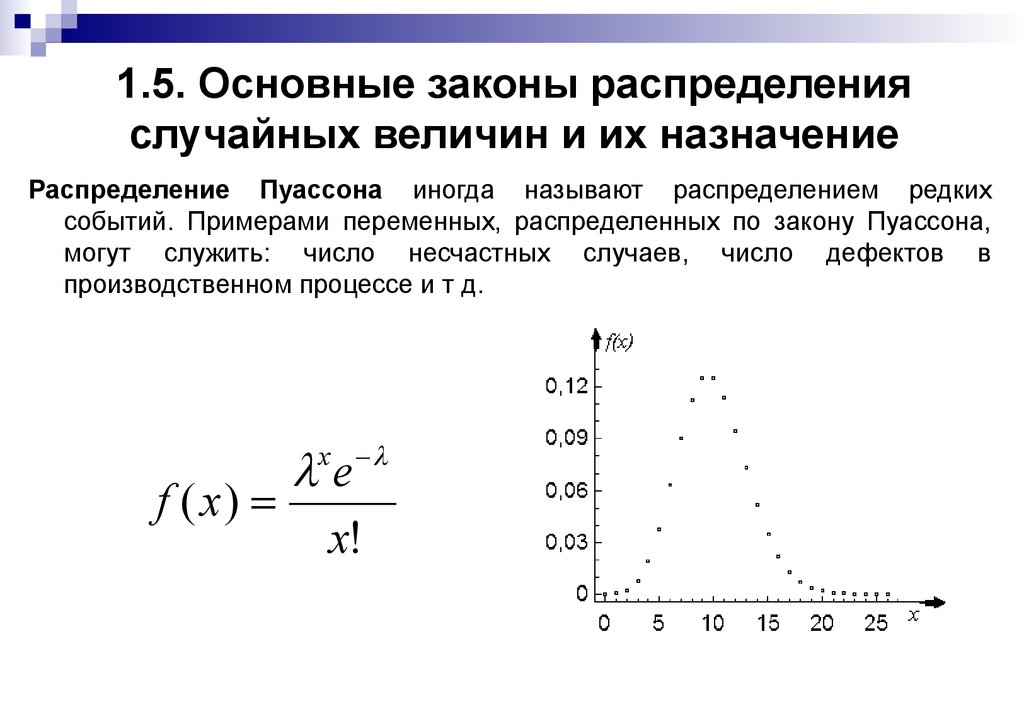 54]

Вы всегда принимаете решения на основе функции ожидаемой полезности. Для дискретных распределений доходов верно  [c.57]

Современные автоматизированные производства являются примером сложных комплексов дискретных распределенных объектов управления, включающих основное обрабатывающее и вспомогательное технологическое  [c.178]

Задачи контроля. Имеется система мониторинга, собирающая данные о состоянии комплекса дискретных распределенных объектов. Задана целе-  [c.180]

Внутренняя организация системы и технология создания в ее среде конкретных прикладных систем основана на использовании методологии и моделей искусственного интеллекта. Базовой моделью является продукционная система с прямым выводом, которая была развита, расширена и переработана для описания и реализации процессов управления комплексами дискретных распределенных объектов в реальном времени. Настраиваемая база продукционной системы реального времени предназначена для хранения данных о динамике изменения состояний объектов и имеет прямой асинхронный информационный вход от внешних объектов и подсистем.

Алгоритмы принятия решения и управления описываются на языке правил — продукций высокого уровня, допускающем квантификацию по объектам. Результатом продукционного логического вывода являются заключения о состоянии и ходе контролируемого процесса либо управляющие воздействия (команды) и сообщения, выдаваемые системой объектам по соответствующим каналам связи. Методы и внутренние формальные модели, положенные в основу реализации продукционной управляющей системы реального времени, демонстрируют следующие ключевые характеристики и особенности.  [c.185]

Рассматривая теорию статистических оценок с позиций применения в массовых автоматизированных производствах, можно выявить две причины, существенно ограничивающие ее применение. Во-первых, точные результаты могут быть получены по результатам контроля большого числа партий, следовательно, информация о состоянии ТП поступит со значительными задержками во времени и не может быть использована для оперативного вмешательства в ход процесса. Во-вторых, статистический анализ состояния ТП базируется на исследовании погрешностей изготовления, подчиняющихся непрерывным распределениям (законам Гаусса, Максвелла, модуля разности и т. п.), а в основу теории несмещенных оценок положены дискретные распределения. Исходя из этого, можно сделать вывод о необходимости создания таких методов оценки результатов контроля, которые позволят избежать указанных недостатков.  [c.12]

МЕТОД ДИСКРЕТНОГО РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (ДЕРЕВА ВЕРОЯТНЫХ ИСХОДОВ)  [c.235]

Таким образом, детерминированный эквивалент стохастической транспортной задачи с дискретно распределенным спросом может быть представлен следующей моделью линейного программирования  [c.37]

По аналогии с приведенными моделями могут быть исследованы постановки стохастических транспортных задач, в которых случайными являются объемы производства аг = аг((о), и более общие модели, в которых не могут быть заранее предсказаны как объемы производства, так и спрос в пунктах потребления.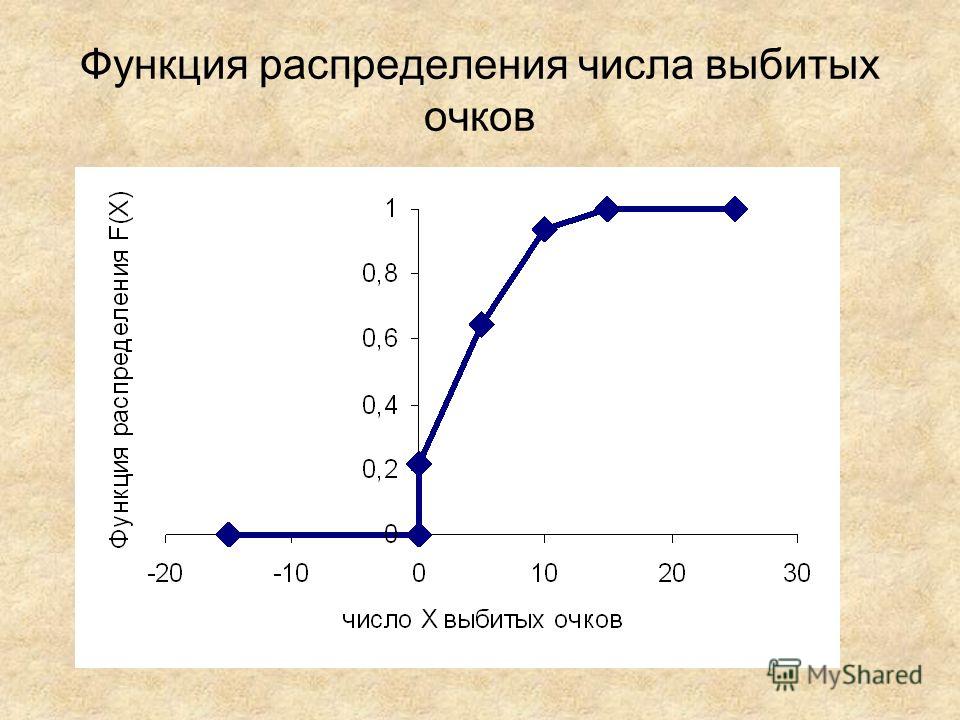 Известны только статистические характеристики соответствующих случайных величин. Анализ всех этих. моделей сводится к решению задач выпуклого или линейного программирования в зависимости от того, имеем ли мы дело с непрерывно или дискретно распределенными случайными параметрами условий задачи.  [c.38]

В [289] исследуются оптимальные смешанные стратегии детерминированной условной экстремальной задачи. Основной результат этой работы в том, что среди оптимальных решающих распределений задачи обязательно содержится дискретное распределение с не более чем т + 1 значениями составляющих решения (т — число ограничений). Как мы увидим далее, подобное утверждение справедливо для более широкого круга задач.  [c.134]

Из формулы (ЗЛ9) видно, что в случае дискретного распределения случайного вектора Ь(ш) функции г(Хг), определяющие показатель качества двухэтапной задачи (3.15) — (3.18), являются кусочно-линейными функциями переменных v.i. Ввод дополнительных переменных и ограничений позволяет свести выпуклую кусочно-линейную задачу к задаче линейного программирования.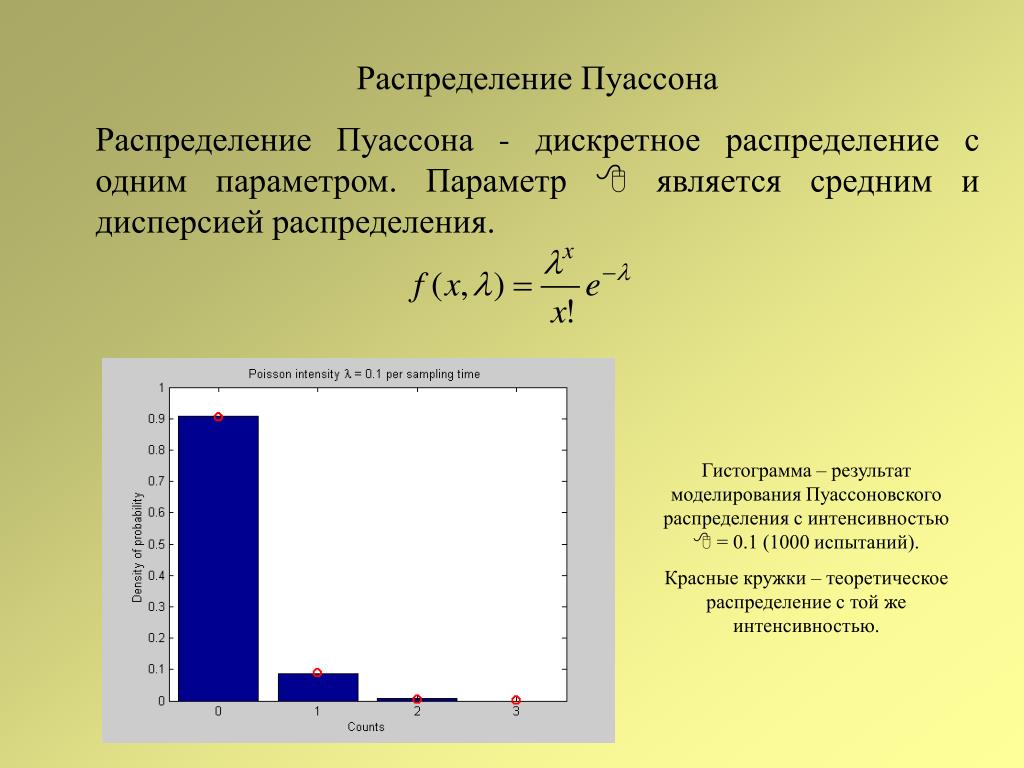  [c.178]

В книге концентрируется внимание только на дискретных распределениях, по скольку они лучше иллюстрируют основные концепции риска и доходности. Однако непрерывные распределения также нашли широкое применение в финансовом анализе, поэтому они рассмотрены в Приложении 2А  [c.39]

Рис 2 1 Графическое представление дискретного распределения вероятностей  [c.40]

Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения чем выше дисперсия, тем больше разброс Для расчета дисперсии дискретного распределения используется следующая формула  [c.42]

Рис. 2.5. Дискретное распределение (графики разброса).

Примерами дискретного распределения являются биномиальное и триномиальное распределения. Подбрасывание монеты приводит к биномиальному распределению результатов, поскольку результат может быть либо «орлом», либо «решкой». Цены активов могут падать, расти или оставаться неизменными, что приводит к триномиальному распределению, поскольку могут быть три вида результатов — рост, падение и отсутствие изменений.  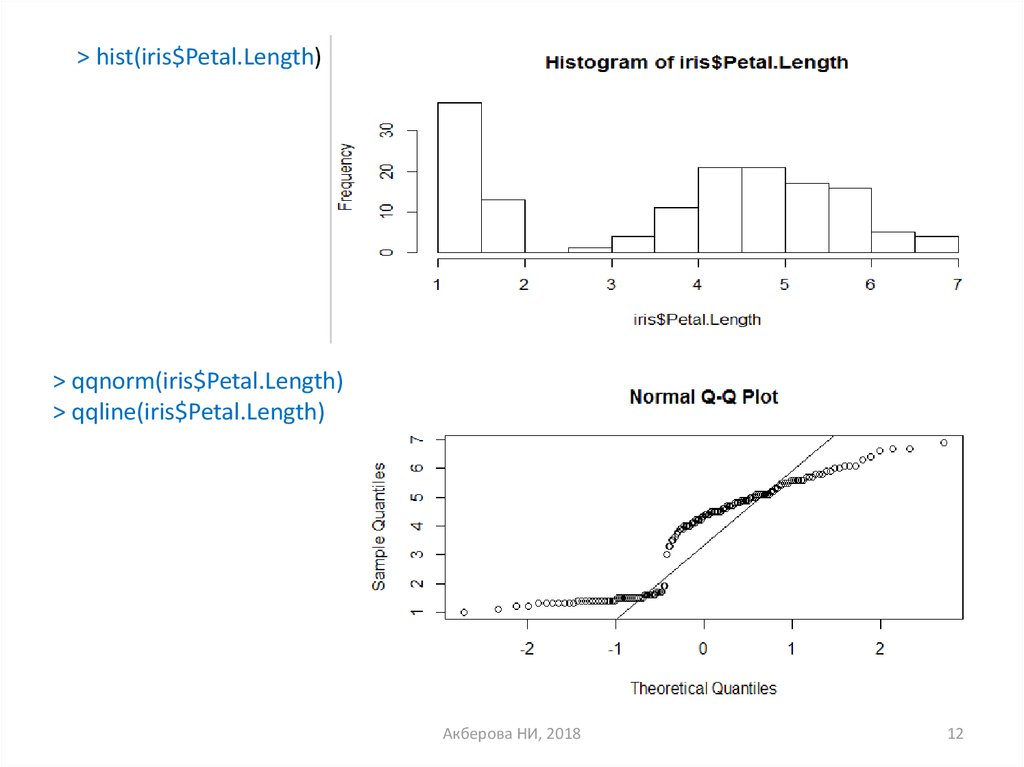[c.180]

Оставшаяся часть этой главы посвящена анализу различных распределений вероятностей, применимых при оценке поведения рентабельности активов при условии соответствующих допущений. Начнем с двух непрерывных распределений — нормального и логнормального. Затем рассмотрим два дискретных распределения — биномиальное и Пуассона. Закончим рассмотрение группой других непрерывных распределений, в том числе и распределением Парето—Леви. Объясним наиболее желательные характеристики распределений с точки зрения финансового аналитика.  [c.189]

Одним их наиболее важных дискретных распределений в финансах является биномиальное распределение. Для формирования биномиального распределения случайная переменная должна отвечать следующим четырем условиям.  [c.200]

Определение издержек при эксплуатации объекта. Издержки при эксплуатации объекта направляются на выполнение технологических процессов, обеспечение действия инженерного оборудования зданий, поддержания в них нормативных санитарно-гигиенических условий и на содержание строительных конструкций в технически исправном состоянии. По периодичности выполнения их разделяют на две группы — дискретно распределенные по времени и непрерывно распределенные (текущие). К издержкам первой группы относятся годовые отчисления на полное восстановление и выполнение работ по капитальному ремонту (частичному восстановлению) основных фондов объекта (эти равномерно производимые начисления реализуются по времени неравномерно). Вторая группа — основные текущие годовые издержки Сэ при экплуатации промышленных зданий  [c.183]

Для каждой реализации матрицы потоков = л /-/- в случае дискретно распределенной функции /(А) среднее количество частиц в f -м интервале вычислится по формуле  [c.107]

Сейчас мы разработаем метод поиска оптимального f по нормально распределенным данным. Как и формула Келли, это способ относится к параметрическим методам. Однако он намного мощнее, так как формула Келли отражает только два возможных результата события, а этот метод позволяет получить полный спектр результатов (при условии, что результаты нормально распределены). Удобство нормально распределенных результатов (кроме того факта, что в реальности они часто являются пределом многих других распределений) состоит в том, что их можно описать двумя параметрами. Формулы Келли дадут вам оптимальное f для бернуллиевых результатов, если известны два параметра отношение выигрыша к проигрышу и вероятность выигрыша. Метод расчета оптимального f, о котором мы сейчас расскажем, также требует только два параметра — среднее значение и стандартное отклонение результатов. Вспомним, что нормальное распределение является непрерывным распределением. Для того, чтобы использовать этот метод, необходимо дискретное распределение. Далее вспомним, что нормальное распределение является неограниченным распределением. Первые два шага, которые мы должны сделать для нахождения оптимального f по нормально распределенным данным, — это определить, (1) на сколько сигма от среднего значения мы усекаем распределение и (2) на сколько равноотстоящих точек данных мы разделим интервал между двумя крайними точками, найденными в (1). Например, мы знаем, что 99,73% всех точек данных находятся между плюс и  [c.107]

В третьей главе мы ознакомились с понятием изгиба цены опциона. Используя упрощенно-дискретное распределение, мы смогли увидеть, что этот изгиб возник благодаря тому, что к сроку истечения линия цены искривляется. Понятно, что, каковы бы ни были предположения о распределении цены акции, ценовой профиль всегда будет изогнут. А также каким бы ни было распределение, если волатильность высокая, то цена опциона должна направляться вдоль той кривой, что находится выше, и все утверждения, сделанные в четвертой главе по поводу влияния вола-тильности на дельту, гамму и тэту, остаются в силе. Модель Блэка-Шоул-за предполагает, что распределение основного инструмента логнормаль-ное. Вопрос о том, верно ли это предположение или нет, все еще является спорным. Эмпирические исследования показывают, что если изучаемый период не слишком длительный, то логнормальное распределение очень близко действительному процессу основного инструмента. Модель также предполагает, что ценовая волатильность акции постоянна, но чаще всего это совсем не так. Цены акции проходят как через волатильные, так и спокойные периоды. Некоторые исследования предполагают, что волатильность следует усредненно-оборотному процессу. То есть волатильность колеблется вокруг некоторой долгосрочной средней волатиль-ности. Итак, можно ли пользоваться моделью для торговли волатильностью или для оценки основного риска опционного портфеля Ответ поло-  [c.193]

ДИСПЕРСИЯ [varian e] — характеристика рассеивания значений случайной величины, измеряемая квадратом их отклонений от среднего значения (обозначается 82). Различается Д. теоретического (непрерывного или дискретного) и эмпирического (также непрерывного и дискретного) распределений. Для наиболее часто применяемого в экономике эмпирического (дискретного) распределения Д. определяется по формуле  [c.89]

Задачи управления комплексами дискретных распределенных объектов в реальном времени. Эти задачи являются наиболее функционально емкими и включают в себя задачи мониторинга, контроля и принятия решений. Наиболее простым развитием рассмотренных выше систем контроля, в том числе интеллектуальных, является управление компенсацией выявленных нежелательных отклонений от заданной идеальной целевой траектории системы в пространстве состояний. Необходимым дополнительным элементом здесь становится модель, описывающая структуру комплекса объектов, их свойства и среду функционирования, а также динамику их поведения. Такие модели должны содержать сложноструктурированный декларированный компонент, а описания процессов будут иметь вид логико-динамических моделей. В связи с этим процедуры обработки целесообразно строить как решающие процедуры определенных интеллектуальных систем.  [c.181]

Коэффициент смещения (k- 1)/2л, полученный Г.П. Башариным для дискретных распределений, улучшает оценку энтропии непрерывного распределения. Предел точности измерений Ах (интервал группирования выборочных данных) позволяет свести дискретную величину к непрерывной, причем, чем меньше Ах, тем точнее выборочная энтропия описывает соответствующее теоретическое значение.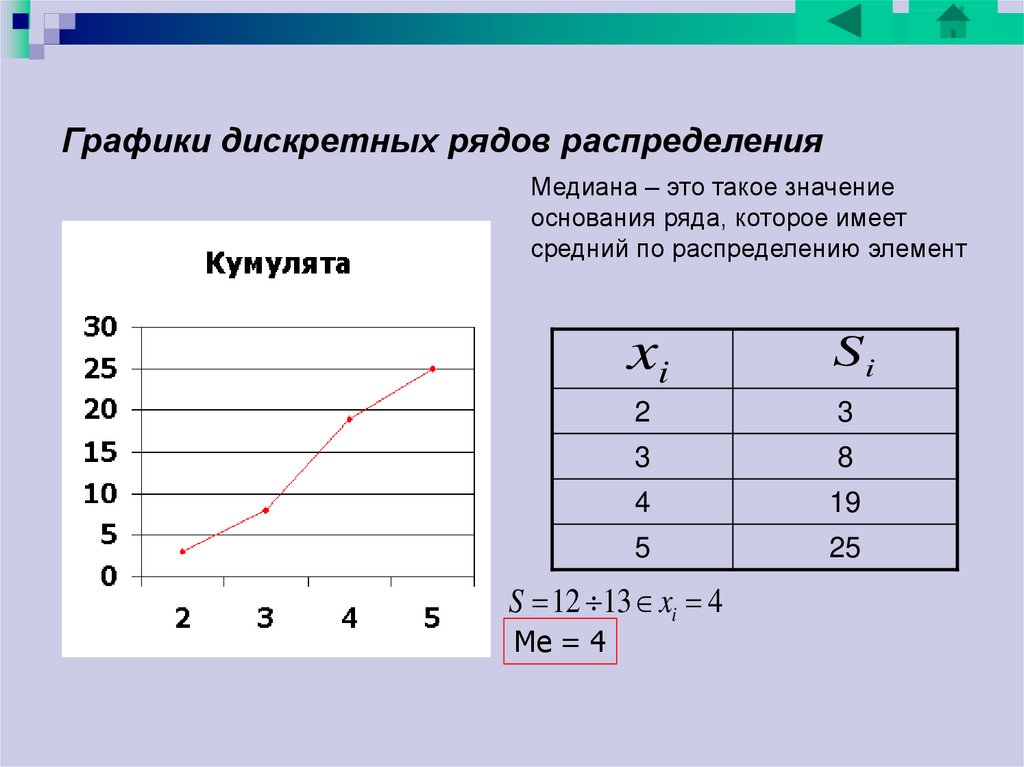  [c.26]

Распределения вероятностей бывают дискретными или непрерывными 2 Дискретное распределение вероятностей имеет конечное число исходов так, в табл 2.1 приведены дискретные распределения вероятностей Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов Ка ждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облига ций составит 9%, ранна 0 50  [c.39]

Дискретные распределения вероятностей могут быть представлены графи чески или в табличной форме На рис 2 1 приведены столбиковые диаграммы (или гистограммы) проектов 1 и 2 Возможные значения доходности проекта 1 принадлежат промежутку от —3.0 до +19.0%, а проекта 2 от —2.0 до +26.0% Отметим, что высота каждого столбца представляет собой вероятность появле ния соответствующего исхода, а сумма этих вероятностей по каждому вари анту равна 1. 00. Отметим также, что распределение значений доходности про екта 2 симметрично, тогда как соответствующее распределение для проекта 1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначей ских векселей представлена единственным столбцом, а доходность корпорацион ных облигаций представлена диаграммой, имеющей правостороннюю асиммет рию  [c.40]

15. Основные дискретные распределения случайных величин.

1. Биноминальное распределение. Рассмотрим схему Бернулли. Производится последовательность n независимых испытаний в каждом из которых возможно только 2 исхода: событие А появилось с вероятностью p и событие А не появилось с вероятностью q, т.е.

P(A)=p P( )=q p+q=1

возможное распределение этой величины. Вероятность этих значений вычисляется по формуле Бернулли. . (1)

Закон распределения случайной величины, определяется по формуле (1), называется биноминальным.

, где -число появлений события в i-ом (одном) испытании.

Закон распределения

	0	1
P	q	p

Мат. ожид.: М=0*q+1*p=p ; M =np

Чтобы найти дисперсию M ₂=0²*q+1²*p=p, D = M _2- (M )²=p-p²=p(1-p)=pq

Так как дисперсии независимы D =npq с корня кв.

2. Распределением Пуассона называется распределение вероятностей дискретной сл. величины, определяемое формулой

.

— параметр распределения Пуассона.

Характерным свойством распределения Пуассона является равенство матожидания и дисперсии:

.

3. Геометрическое распределение. Производится последовательность независимых испытаний, в каждом из которых только 2 исхода:

P(A)=p P( )=q p+q=1

Испытание производится до появления события А.

Возможные значения сл.величины =0,1,…,m,…,

вероятности этих значений определяются по формуле

(1)

Геометрическим распределением называется распределение дискретной случайной величины , определяемое формулой (1).

Геом. распред. имеет один параметр p.

Мат. ожид. и дисперсия этой случайной величины:

D

Название геометрическое распределение связано с тем, что вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем .

16. Равномерное и показательное распределение.

Равномерное распределение.

Плотность распределения:

Функция распределения:

Равномерное распределение имеет два параметра а и b

Матожидание и дисперсия:

, .

Показательным, называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Функция распределения:

, ,

Характерное свойство показательного распределения: матожидание равно среднеквадратическому отклонению: .

Показательный закон распределения вероятностей встречается в задачах, где в качестве случайной величины рассматривается интервал времени между последовательно появляющимися событиями. Например, интервал времени между появлением автомобилей на дороге.

17. Нормальное распределение.

Нормальным (распределением Гаусса) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью.

.

Нормальное распределение определятся 2 параметрами а и σ. а – мат ожидание, – мат ожидание, — квадратическое отклонение нормального распределения.

При получим стандартное нормальное распределение. От произвольного перейти к стандартному можно с помощью преобразования .

От произвольного нормального распределения можно перейти к стандартному с помощью преобразования z=(x—a)/σ

Функция стандартного нормального распределения имеет вид.

Часто вместо приводится функция Лапласа

Вероятность попадания случайной величины в заданный интервал:

.

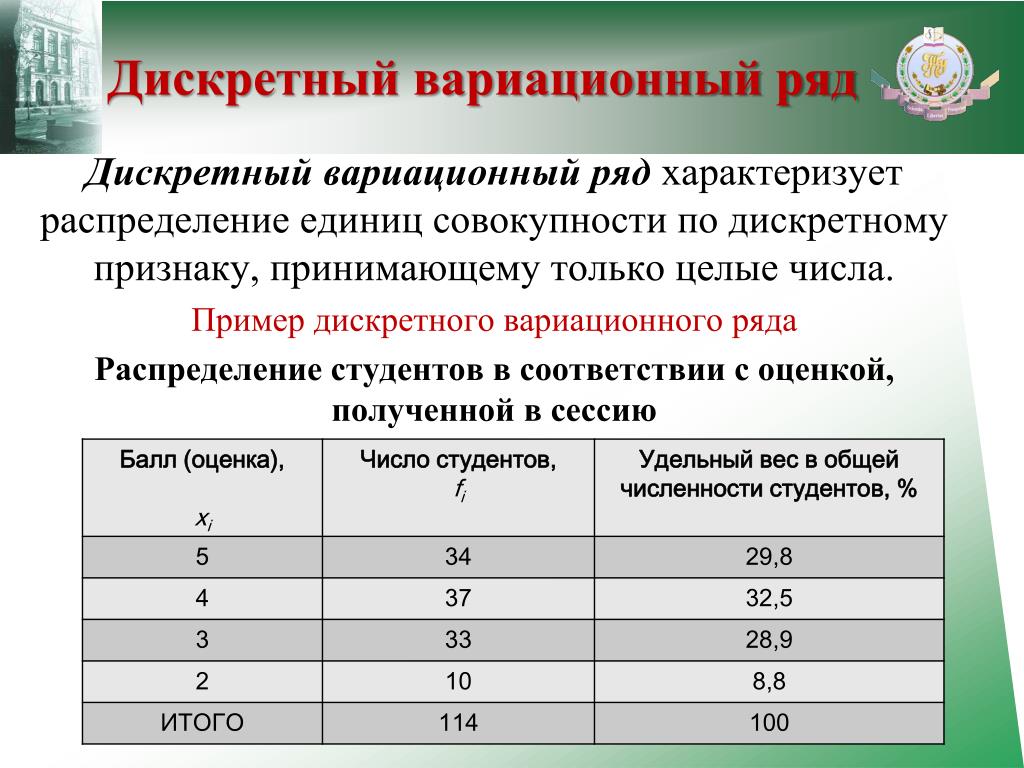
Вычисление вероятности заданного отклонения от матожидания для нормальной случайной величины

Преобразуем данную формулу положив , получим

.

Если t=3, то

.

Правило трех сигм:

Если случайная величина распределена нормально, то с вероятностью, близкой к единице, абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Дискретные распределения вероятностей|Типы распределений вероятностей

Приянка Мадираджу — Опубликовано 25 января 2021 г. и изменено 27 января 2021 г.

Новичок Статистика

Эта статья была опубликована в рамках блога по науке о данных.

Введение

Сегодня давайте поговорим об одном из основополагающих понятий статистики: распределении вероятностей. Они помогают лучше понять данные и служат основой для понимания дополнительных статистических концепций, таких как доверительные интервалы и проверка гипотез.

 

Неофициальное определение

Пусть X — случайная величина, имеющая более одного возможного результата. Постройте вероятность на оси y и результат на оси x. Если мы повторим эксперимент много раз и нанесем на график вероятность каждого возможного исхода, мы получим график, представляющий вероятности. Этот график называется распределением вероятностей (PD). Высота графика для X дает вероятность этого исхода.

 

Типы вероятностных распределений

Существует два типа распределений в зависимости от типа данных, полученных в ходе экспериментов.

1. Дискретные распределения вероятностей

Эти распределения моделируют вероятности случайных величин, которые могут иметь дискретные значения в качестве результатов. Например, возможные значения для случайной величины X, представляющей количество решек, которые могут выпасть при двойном подбрасывании монеты, представляют собой набор {0, 1, 2}, а не любое значение от 0 до 2, например 0,1 или 1,6.

Примеры: Бернулли, биномиальный, отрицательный биномиальный, гипергеометрический и т. д.,

 

2. Непрерывные распределения вероятностей

Эти распределения моделируют вероятности случайных величин, которые могут иметь любой возможный результат. Например, возможные значения случайной величины X, представляющей вес жителей города, могут принимать любые значения, такие как 34,5, 47,7 и т. д.,

.

Примеры: нормальный, Т Стьюдента, хи-квадрат, экспоненциальный и т. д.,

 

Терминология

Каждый PD предоставляет нам дополнительную информацию о поведении задействованных данных. Каждая PD задается функцией вероятности, которая обобщает вероятности исходов.

Используя это, мы можем оценить вероятность конкретного исхода (дискретную) или вероятность того, что он находится в определенном диапазоне значений для любого заданного исхода (непрерывного). Эта функция называется функцией массы вероятности (PMF) для дискретных распределений и функцией плотности вероятности (PDF) для непрерывных распределений. Суммарное значение PMF и PDF по всему домену всегда равно единице.

 

Суммарная функция распределения

PDF дает вероятность определенного результата, тогда как кумулятивная функция распределения дает вероятность увидеть результат, меньший или равный определенному значению случайной величины. CDF используются для проверки того, как сложилась вероятность до определенной точки. Например, если P(X = 5) — это вероятность того, что количество орлов при подбрасывании монеты равно 5, то P(X <= 5) обозначает кумулятивную вероятность выпадения орла от 1 до 5.

Кумулятивные функции распределения также используются для расчета p-значений в рамках проверки гипотез.

 

Дискретные распределения вероятностей

Существует множество дискретных вероятностных распределений, которые можно использовать в различных сценариях. В этом посте мы обсудим дискретные дистрибутивы. Биномиальное распределение и распределение Пуассона являются наиболее обсуждаемыми в следующем списке.

1.

Распределение Бернулли

Это распределение генерируется, когда мы проводим эксперимент один раз, и у него есть только два возможных результата — успех и неудача. Испытания этого типа называются испытаниями Бернулли, которые составляют основу многих распределений, обсуждаемых ниже. Пусть p — вероятность успеха, а 1 — p — вероятность неудачи.

PMF задается как

Одним из примеров этого может быть подбрасывание монеты один раз. p — вероятность вырваться вперед, а 1 — p — вероятность выпадения хвоста. Обратите внимание, что успех и неудача субъективны и определяются нами в зависимости от контекста.

 

2.

Биномиальное распределение

Генерируется для случайных величин только с двумя возможными исходами. Пусть p обозначает вероятность того, что событие является успешным, из чего следует, что 1 — p — это вероятность того, что событие является неудачным. Повторное выполнение эксперимента и каждый раз построение графика вероятности дает нам биномиальное распределение.

Самый распространенный пример биномиального распределения — подбрасывание монеты n раз и вычисление вероятности выпадения определенного количества орлов. Более реальные примеры включают количество успешных продаж для компании или то, работает ли лекарство от болезни или нет.

PMF задается как

, где p — вероятность успеха, n — количество попыток, а x — количество удачных попыток.

 

3.

Гипергеометрическое распределение

Рассмотрим событие извлечения красного шарика из коробки с разноцветными шариками. Событие вытягивания красного шара считается успешным, а невытягивание — неудачей. Но каждый раз, когда вынимается шарик, он не возвращается в коробку, и, следовательно, это влияет на вероятность извлечения шарика в следующем испытании. Гипергеометрическое распределение моделирует вероятность k успехов в n испытаниях, где каждое испытание проводится без замены. Это отличается от биномиального распределения, где вероятность остается постоянной на протяжении испытаний.

PMF задается как

, где k — количество возможных успехов, x — желаемое количество успехов, N — размер популяции, а n — количество испытаний.

 

4. 

Отрицательное биномиальное распределение

Иногда мы хотим проверить, сколько испытаний Бернулли нам нужно провести, чтобы получить определенный результат. Желаемый результат оговаривается заранее, и мы продолжаем эксперимент, пока он не будет достигнут. Рассмотрим пример броска игральной кости. Наш желаемый результат, определяемый как успех, выбрасывает 4. Мы хотим знать вероятность получения этого результата трижды. Это интерпретируется как количество неудач (другие числа, кроме 4), которые произойдут до того, как мы увидим третий успех.

PMF задается как

, где p — вероятность успеха, k — количество наблюдаемых неудач, r — желаемое количество успехов, пока эксперимент не будет остановлен.

Как и в биномиальном распределении, вероятность в испытаниях остается постоянной, и каждое испытание не зависит от другого.

 

5.

Геометрическое распределение

Это частный случай отрицательного биномиального распределения, когда желаемое количество успехов равно 1. Он измеряет количество неудач, которые мы получаем до одного успеха. Используя тот же пример, что и в предыдущем разделе, мы хотели бы знать количество неудач, которые мы видим, прежде чем мы получим первые 4 при броске костей.

, где p — вероятность успеха, а k — количество неудач. Здесь г = 1,

 

6.

Распределение Пуассона

Это распределение описывает события, происходящие в фиксированный интервал времени или пространства. Пример может прояснить это. Рассмотрим случай количества звонков, полученных центром обслуживания клиентов в час. Мы можем оценить среднее количество звонков в час, но мы не можем определить точное количество и точное время, когда был звонок. Каждое вхождение события не зависит от других вхождений.

PMF задается как

, где λ – среднее количество раз, когда событие произошло за определенный период времени, x – желаемый результат, а – число Эйлера.

 

7.

Полиномиальное распределение

В приведенных выше раздачах возможны только два исхода — успех и неудача. Однако полиномиальное распределение описывает случайные величины со многими возможными исходами. Это также иногда называют категориальным распределением, поскольку каждый возможный результат рассматривается как отдельная категория. Рассмотрим сценарий прохождения игры n раз. Полиномиальное распределение помогает нам определить общую вероятность того, что игрок 1 выиграет, умноженную на 9.0152 1  раза, игрок 2 выиграет x ₂  раза, а игрок k выиграет x _k  раз.

PMF задается как

, где n — количество испытаний, p _1, ……p _k обозначают вероятности исходов x ₁ ……x _k соответственно.

В этом посте мы определили распределения вероятностей и кратко обсудили различные дискретные распределения вероятностей. Дайте мне знать ваши мысли о статье в разделе комментариев ниже.

 

Каталожные номера

1. https://www.statisticshowto.com/

2. https://stattrek.com/

3. Википедия

 

Обо мне

Я бывший инженер-программист, работаю над переходом на науку о данных. Я студент магистратуры в области Data Science. Пожалуйста, не стесняйтесь связаться со мной на https://www.linkedin.com/in/priyanka-madiraju/

Медиафайлы, показанные в этой статье, не принадлежат Analytics Vidhya и используются по усмотрению Автора.

blogathonДискретные распределения вероятностей

Содержание

Лучшие ресурсы

Скачать приложение

Мы используем файлы cookie на веб-сайтах Analytics Vidhya для предоставления наших услуг, анализа веб-трафика и улучшения вашего опыта на сайте. Используя Analytics Vidhya, вы соглашаетесь с нашей Политикой конфиденциальности и Условиями использования. Принять

Политика конфиденциальности и использования файлов cookie

Узнать | Написать | Заработайте

гарантированных 2000 индийских рупий (26 долларов США) за каждую опубликованную статью! Зарегистрируйтесь сейчас

7 Типы дискретных вероятностных распределений и их применение в R

Photo by Lucas Santos on Unsplash

Вероятностные распределения — это статистические функции, которые описывают вероятность получения возможных значений, которые может принимать случайная величина. В этой статье будут рассмотрены различные типы дискретных вероятностных распределений вместе с их кодом в R. Каждое распределение дополнено реальным примером.

В целом распределения вероятностей можно разделить на две категории:

A. Дискретное распределение вероятностей

Он моделирует вероятности случайных величин, которые могут иметь дискретные значения в качестве результатов. Дискретная случайная величина — это случайная величина, имеющая исчисляемые значения, например список неотрицательных целых чисел. Дискретные функции вероятности также известны как функций массы вероятности.

Пример : Если вы подсчитываете количество книг, которые библиотека выдает в час, вы можете насчитать 15 или 16 книг, но ничего между ними.

Дискретные распределения вероятностей можно дополнительно разделено на

1. Биномиальное распределение

2. Многономиальное распределение

3. Бернулли распределение

4. Отрицательный Бин.

6. Геометрическое распределение

7. Гипергеометрическое распределение

B. Непрерывное распределение вероятностей

Он моделирует вероятности возможных значений непрерывной случайной величины. Непрерывная случайная величина — это случайная величина с набором возможных значений, которые бесконечны и несчетны. Непрерывные переменные часто представляют собой измерения на шкале, такие как вес и температура. Непрерывные функции вероятности также известны как функций плотности вероятности .

Давайте посмотрим на типы дискретных вероятностных распределений:

1. Биномиальное распределение

Биномиальное распределение часто используется для моделирования количества успешных результатов в выборке размером n , взятой с заменой из совокупности размером N . Каждый эксперимент имеет логический результат, такой как успех/да/истина/один (с вероятностью p ) или неудача/нет/ложь/ноль (с вероятностью q=1-p ). Чтобы эксперимент можно было назвать биномиальным экспериментом, должны быть выполнены следующие условия :

и. Фиксированное количество n испытаний.

ii. Каждое испытание является независимым.

iii. Возможны только два исхода (Успех или Неудача).

iv. Вероятность успеха ( p ) для каждого испытания постоянна.

v. Случайная величина Y = количество успехов.

Пример : Для монеты, подброшенной n раз, можно использовать биномиальное распределение для моделирования вероятности количества успехов (скажем, орла).

Код : чтобы найти вероятность выпадения 6 орлов при 10 подбрасываниях монеты, мы используем dbinom(x, size, prob) .

• x = вектор длины k целых чисел в 0:размер
• размер = общее количество испытаний.
• prob = вероятность успеха в каждом испытании. Недопустимы бесконечные и отсутствующие значения.

 dbinom(6,size=10,prob=0,5) 

Чтобы построить функцию массы вероятности для биномиальной функции в R:

  dbinom(x, size, prob)  используется для создания функции массы вероятности  plot(0:x, dbinom(0:x, size, prob), type = 'h')  для построения графика массы вероятности функция, задающая график в виде гистограммы (type='h') 

Предположим, что для монеты, подброшенной 10 раз, можно использовать биномиальное распределение для моделирования вероятности выпадения орла (от 1 до 10). Вот функция массы вероятности для биномиального распределения, созданного с размером = 10 и p=0,5

 успех <- 0:10plot(успех,dbinom(успех,размер=10,вероятность=0,5),тип='h',main='Биномиальное распределение (размер=10, p=0,5)' ,ylab='Вероятность',xlab ='# Успехов (орел)',lwd=3) 

Функция массы вероятности для биномиального распределения | Изображение автора

Примечание:

• dbinom = Биномиальная функция массы вероятности (pmf).
• pbinom = биномиальное распределение (кумулятивная функция распределения).
• qbinom = Биномиальная квантильная функция.
• rbinom = Генерация биномиальных псевдослучайных чисел.

Поскольку в этой статье сообщается о функциях массы вероятностей, мы будем использовать только pmf (здесь dbinom ), связанный с типом дискретного распределения вероятностей.

2. Полиномиальное Распределение

Это обобщение биномиального распределения на k категорий, а не просто бинарное (успех/неудача). Для n независимых испытаний, каждое из которых приводит к успеху ровно в одном из k категорий полиномиальное распределение дает вероятность любой конкретной комбинации чисел успехов для различных категорий.

Пример : Многономинальное распределение моделирует вероятность подсчета каждой стороны при броске k -гранного кубика n раз.

• Когда k = 2 и n = 1 , полиномиальное распределение является распределением Бернулли.
• Когда k = 2 и n > 1 , это биномиальное распределение.
• Когда k > 2 и n = 1 , это категориальное распределение.
• Когда k > 2 и n > 1 , это называется полиномиальным распределением.

Код: Мы используем Dmultinom (x, размер, Prob, log = false)

• x = вектор длины K из Integers In 0: Размер K из интуитивных общее количество испытаний. Для dmultinom() , по умолчанию sum(x)
• prob = вероятность успеха в каждом испытании. Недопустимы бесконечные и отсутствующие значения.
• журнал = логический. Если TRUE , то сообщается логарифмическая вероятность.

Предположим, что два шахматиста А и В имеют вероятность выиграть партию, равную 0,40 и 0,35 соответственно. Вероятность того, что игра закончится вничью, равна 0,25.

Мы можем использовать полиномиальное распределение, чтобы ответить: если эти два шахматиста сыграли 12 партий, какова вероятность того, что игрок A выиграет 7 партий, игрок B выиграет 2 партии, а в оставшихся 3 партиях будет ничья?

 dmultinom(x=c(7,2,3), prob = c(0.4,0.35,0.25)) 

3. Распределение Бернулли

Это частный случай биномиального распределения, где только проводится однократное испытание. Для 90 285 n = 1 90 286 (один эксперимент) биномиальное распределение можно назвать распределением Бернулли. Отдельный эксперимент с успехом/неудачей также называется испытанием Бернулли или экспериментом Бернулли, а последовательность результатов называется процессом Бернулли.

Пример : Рассмотрим подбрасывание монеты, при котором вероятность выпадения орла равна 0,5, а выпадения решки равна 0,5.

Код : Мы используем dbern(x, prob)

• x = вектор длины 1
• prob = вероятность успеха для каждого испытания. Недопустимы бесконечные и отсутствующие значения.

Чтобы найти вероятность выпадения 1 орла при 1 подбрасывании правильной монеты:

 dbern(1, prob = 0,5) 

Чтобы построить функцию массы вероятности для функции Бернулли в R, мы можем использовать следующие функции :

  dbern(x, prob)  используется для создания функции массы вероятности  plot(0:x, dbern(0:x, prob), type = 'h')  для построения функции массы вероятности с указанием график в виде гистограммы (тип='h') 

Для подброшенной один раз честной монеты функция массы вероятности для распределения Бернулли имеет вид: , type='h', main='Распределение Бернулли (размер=1, p=0,5)', ylab='Вероятность', xlab ='# Успехов (орел)', lwd=3,ylim=c(0,1 )) Функция массы вероятности для распределения Бернулли | Изображение автора

4. Отрицательное биномиальное распределение

Это тип биномиального распределения, в котором количество испытаний n не является фиксированным, а случайная величина Y равна количеству испытаний, необходимых для выполнения р успехов. Отрицательное биномиальное распределение известно как распределение Паскаля .

Пример : Вы опрашиваете людей, выходящих из кабины для голосования, и спрашиваете их, голосовали ли они независимо. Вероятность ( р ) что человек проголосовал за независимого составляет 20%. Какова вероятность того, что нужно опросить 70 человек, прежде чем вы найдете 5 человек, проголосовавших за независимость?

Код : Мы используем dnbinom(x, size, prob)

• x = количество отказов, которые должны произойти, прежде чем будет достигнуто необходимое количество успехов.
• размер = количество успехов.
• prob = вероятность успеха в каждом испытании. Недопустимы бесконечные и отсутствующие значения.

Чтобы ответить на поставленный выше вопрос:

 dnbinom(65,5,0.2) 

Чтобы построить функцию массы вероятности для отрицательной биномиальной функции в R, мы можем использовать следующие функции:

  dnbinom(x, size , prob)  используется для создания функции массы вероятности  plot(0:x, dnbinom(0:x, size, prob)   , type = 'h')  для построения функции массы вероятности, определяющей быть гистограммой (type='h') 

График функции массы вероятности для вышеупомянутого вопроса:

 success<-0:65plot(success,dnbinom(success,5, prob = 0.2) , type='h', main='Отрицательное биномиальное распределение', ylab='Вероятность', xlab ='# успехов (людей, которые проголосовали за независимость)', lwd=3) 

Функция массы вероятности для отрицательного биномиального распределения | Изображение автора

5. Распределение Пуассона

Он используется для моделирования количества независимых событий, происходящих в течение заданного интервала времени. Он показывает, сколько раз событие может произойти в течение фиксированного интервала времени, если эти события происходят с известной средней скоростью и независимо от времени, прошедшего с момента последнего события.

Пример : Рассмотрим центр поддержки клиентов. В среднем в час звонит, скажем, 10 клиентов. Таким образом, распределение Пуассона можно использовать для моделирования вероятности того, что в течение часа позвонит разное количество клиентов (скажем, 5, 6 или 7 и т. д.).

Код : Мы используем dpois(x, lambda, log=FALSE)

• x = вектор длины K
• 2 означает вектор лямбда = 6.
• журнал = логический; если TRUE , вероятности p задаются как log(p) .

Найдем вероятность того, что 20 клиентов позвонят в течение часа.

 dpois(20, lambda=10) 

Чтобы построить функцию массы вероятности для функции Пуассона в R, мы можем использовать следующие функции:

  dpois(x, лямбда)  используется для создания функции массы вероятности  plot(0:x, dpois(0:x, lambda)   , type = 'h')  для построения функции массы вероятности, указав, что график является гистограммой (type='h') 

Построение графика функции массы вероятности для вышеупомянутого вопроса:

 success<-0:20plot(success,dpois(success, lambda=10) , type='h', main='Распределение Пуассона (лямбда=10)', ylab='Вероятность', xlab ='# Успехов (количество позвонивших клиентов)', lwd=3) 

Функция массы вероятности для распределения Пуассона | Изображение автора

6. Геометрическое распределение

Это распределение вероятностей количества испытаний, необходимых для получения первого успеха в повторных независимых испытаниях Бернулли. Геометрическое распределение также может быть определено как количество неудач до того, как произойдет первый успех.

Геометрическое распределение является подходящей моделью, если верны следующие предположения:

i. Моделируемое явление представляет собой последовательность независимых испытаний.

ii. У каждого испытания есть только два возможных результата, часто обозначаемых как успех или неудача.

iii. Вероятность успеха p одинакова для каждого испытания.

Пример : Исследователь ждет возле библиотеки, чтобы спросить людей, поддерживают ли они определенный закон. Вероятность того, что данное лицо поддерживает закон, равна 9.0285 р = 0,2 . Какова вероятность того, что четвертый человек, с которым разговаривает исследователь, первым поддержит закон?

Код : Мы используем dgeom(x, prob, log = FALSE)

• x = количество неудач, которые должны произойти, прежде чем будет достигнуто n успехов.
• prob = вероятность успеха в каждом испытании. Недопустимы бесконечные и отсутствующие значения.
• журнал = логический. Если ИСТИНА , затем сообщается логарифмическая вероятность.

Чтобы ответить на вышеупомянутый вопрос:

 dgeom(x=3, prob=0,2) 

Чтобы построить функцию массы вероятности для геометрической функции в R, мы можем использовать следующие функции:

  dgeom(x, prob)  используется для создания функции массы вероятности  plot(0:x, dgeom(0:x, prob), type = 'h')  для построения функции массы вероятности, определяя график как гистограмму (тип ='h') 

График функции массы вероятности:

 success<-0:3plot(success,dgeom(success, prob = 0.2) , type='h', main='Geometric Distribution', ylab='Probability', xlab ='# Successs (человек поддерживает закон) ', lwd=3) 

Функция массы вероятности для геометрического распределения | Изображение автора

7. Гипергеометрическое распределение

Оно описывает количество успехов в последовательности из k розыгрышей из конечной популяции без замены , так же как биномиальное распределение описывает количество успехов в розыгрышах с заменой .

Пример : Колода карт содержит 20 карт: 6 красных карт и 14 черных карт. Случайным образом вытягиваются 5 карт без замены . Какова вероятность того, что вытянуто ровно 4 красные карточки?

Код : Мы используем dhyper(x, m, n, k, log = FALSE)

• x = вектор целых чисел в 0:n
элементов в популяции, которые классифицируются как успехи.
• n = количество элементов в совокупности, которые не классифицируются как успехи.
• k = количество элементов в выборке, классифицированных как успешные.
• журнал = логический. Если TRUE , то сообщается логарифмическая вероятность.

Чтобы ответить на вышеупомянутый вопрос:

 dhyper(4,6,14,5) 

Чтобы построить функцию массы вероятности для гипергеометрической функции в R, мы можем использовать следующие функции:

  dhyper(x, m, n, k)  используется для создания функции массы вероятности  plot(0:x, dhyper(0:x, m, n, k), type = 'h')  to построить функцию массы вероятности, указав, что график должен быть гистограммой (type='h') 

Построить график функции массы вероятности:

 success<-0:4plot(success,dhyper(0:4,6,14,5 ), type='h', main='Гипергеометрическое распределение', ylab='Вероятность', xlab ='# Успехов', lwd=3) 

Функция массы вероятности для гипергеометрического распределения | Изображение автора

Надеюсь, теперь вы знакомы с техническими и теоретическими возможностями дискретных вероятностных распределений!

Ссылки:

[1]: https://www.math.ucla.edu/~anderson/rw1001/library/base/html/Geometric.html

[2]: https://www. statisticshowto. com/negative-binomial-experiment/

[3]: https://www.r-bloggers.com/2011/02/using-r-for-introductory-statistics-chapter-5-hypergeometric-distribution/

[4]: https://www.statisticshowto.com/hypergeometric-distribution-examples/

5 дискретных распределений, которые должен знать каждый специалист по данным | Рауль Агарвал

Фото Алекса Чемберса на Unsplash

История, доказательства и интуиция

Распределения играют важную роль в жизни каждого специалиста по данным.

Теперь, исходя из нестатистического фона, распределения всегда кажутся мне чем-то мистическим.

А дело в том, что их очень много.

Итак, какие из них я должен знать? И откуда я их знаю и понимаю?

Этот пост посвящен некоторым из наиболее часто используемых дискретных дистрибутивов, которые вам нужно знать, а также интуиции и доказательствам.

Это, пожалуй, самый простой дискретный дистрибутив из всех и, возможно, самый полезный.

История: Монета подбрасывается с вероятностью p выпадения орла.

Где использовать?: Мы можем представить цель бинарной классификации как RV Бернулли.

PMF Распределения Бернулли определяется:

CDF распределения Бернулли определяется как:

Ожидаемое значение:

Дисперсия:

Распределение Бернулли тесно связано со многими распределениями, как мы увидим ниже.

Одно из самых основных распределений в инструментарии Statistician. Параметрами этого распределения являются n (количество испытаний) и p (вероятность успеха).

История: Вероятность получить ровно k успехов в n испытаниях

Где использовать?: Предположим, у нас есть n яиц в шкатулке. Вероятность того, что яйцо будет разбито, равна p. Затем количество разбитых яиц в шкатулке распределяется биномиально.

PMF биномиального распределения определяется как:

Согласно нашей истории, это вероятность того, что k лампочек разбиты.

CDF биномиального распределения определяется как:

Ожидаемое значение:

Первое решение:

Лучший способ решить это:

X — это сумма n индикаторных случайных величин, где каждая I — это случайная величина Бернулли.

Дисперсия:

Мы также можем использовать случайную переменную индикатора с использованием дисперсии, так как каждая случайная переменная индикатора независима.

Параметром этого распределения является p(вероятность успеха).

История: Количество неудач до первого успеха (орел) при подбрасывании монеты с вероятностью p.

Где использовать: Предположим, вы сдаете экзамен, и вероятность того, что вы его сдадите, определяется p. Количество неудач, которые у вас будут до сдачи экзамена, распределяется геометрически.

PMF геометрического распределения определяется как:

CDF геометрического распределения определяется как:

Ожидаемое значение:

Дисперсия:

Таким образом,

Пример:

2 Доктор ищет антидепрессант 9 вновь диагностированный пациент. Предположим, что среди доступных антидепрессантов вероятность того, что какое-либо конкретное лекарство будет эффективным для конкретного пациента, составляет p=0,6. Какова вероятность того, что первое лекарство, которое оказалось эффективным для этого пациента, является первым испробованным лекарством, вторым испробованным лекарством и так далее? Каково ожидаемое количество лекарств, которые будут испробованы, чтобы найти эффективное?

Ожидаемое количество лекарств, которые будут испробованы, чтобы найти одно эффективное =

q/p = 0,4/0,6 = 0,67

Параметрами этого распределения являются p (вероятность успеха) и r (число успехов).

История: количество неудач независимых испытаний Бернулли(р) до r-го успеха.

Где использовать: Вам нужно продать r шоколадных батончиков в разные дома. Вероятность того, что вы продадите шоколадный батончик, равна p. Количество неудач, которые вам придется пережить, прежде чем вы получите r успехов, распределяется как отрицательное биномиальное число.

PMF отрицательного биномиального распределения определяется как:

r успехов, k неудач, последняя попытка должна быть успешной:

Ожидаемое значение:

Отрицательное биномиальное RV может быть выражено как сумма r геометрических RV, поскольку Геометрическое распределение — это просто количество неудач до первого успеха.

Таким образом,

Дисперсия:

Так как r геометрических СВ независимы.

Пример:

Пэт должна продавать шоколадные батончики, чтобы собрать деньги на экскурсию для шестиклассников. По соседству тридцать домов, и Пэт не должна возвращаться домой, пока не будет продано пять шоколадных батончиков. Итак, ребенок ходит от двери к двери, продавая шоколадные батончики. В каждом доме существует вероятность 0,4 продать один шоколадный батончик и 0,6 вероятность не продать ничего. Какова вероятность продажи последнего батончика в n-м доме?

Здесь r = 5 ; k = n — r

Вероятность продажи последнего батончика в n-м доме =

Параметром этого распределения является λ, параметр скорости.

Мотивация: В этом дистрибутиве нет истории, но есть мотивация для использования этого дистрибутива. Распределение Пуассона часто используется для приложений, в которых мы подсчитываем успехи большого количества испытаний, когда процент успешных испытаний низок.

Например, распределение Пуассона является хорошей отправной точкой для подсчета количества людей, которые отправят вам электронное письмо в течение часа. В вашей адресной книге много людей, и вероятность того, что кто-то из них отправит вам письмо, очень мала.

PMF распределения Пуассона определяется как:

Ожидаемое значение:

Отклонение:

Пример:

вероятность того, что в течение конкретной недели произойдет не более одного отказа?

Вероятность = P(X=0)+P(X=1) =

И здесь я сгенерирую PMF дискретных распределений, которые мы только что обсуждали выше, используя встроенные функции Python. Дополнительные сведения о верхней функции см. в моем предыдущем посте «Создание базовых графических визуализаций с помощью SeaBorn». Кроме того, взгляните на руководство по документации для следующих функций:

 # Binomial: 
 из scipy.stats import binom 
 n = 30 
 p = 0,5 
 k = range(0,n) 
 pmf = binom.pmf(k , н, р) 
 chart_creator(k,pmf,"Binomial PMF") 

 # Геометрический: 
 из scipy.stats import geom 
 n=30 
 p=0.5 
 k = range(0,n) 
 # -1 здесь параметр местоположения для создания PMF, который мы хотим. 
 pmf = geom. pmf(k, p,-1) 
 chart_creator(k,pmf,"Geometric PMF") 

 # Отрицательный бином : 
 from scipy.stats import nbinom 
 r=5 # количество успехов 
 p= 0.5 # вероятность успеха 
 k = range(0,25) # количество неудач 
 # -1 здесь параметр местоположения для создания нужного PMF. 
 pmf = nbinom.pmf(k, r, p) 
 chart_creator(k,pmf,"Nbinom PMF") 

 #Poisson 
 from scipy.stats import poisson 
 lamb = .3 # Rate 
 k = range(0, 5) 
 pmf = poisson.pmf(k, lamb) 
 chart_creator(k,pmf,"Poisson PMF") 

Вы также можете попробовать визуализировать распределения с другими параметрами, чем я использовал.

Понимание распределений жизненно важно для любого специалиста по данным.

Они очень часто встречаются в жизни, и их понимание облегчает вам жизнь, так как вы можете довольно быстро найти решение, просто используя простое уравнение.

В этой статье я рассказал о некоторых важных дискретных дистрибутивах, а также рассказал об их поддержке.

No related posts.