Решить уравнение с х онлайн калькулятор
Для обозначения неизвестного числа используются буквенные обозначения. Именно значение этих букв и приходится искать с помощью решений уравнения.
Так же читайте нашу статью «Решить уравнение Эйлера онлайн»
Работая над решением уравнения, мы стараемся на первых этапах привести его к более простому виду, позволяющему получить результат с помощью простых математических манипуляций. Для этого мы выполняем перенос слагаемых с левой стороны на правую, изменяем знаки, умножаем/делим части предложения на какое-то число, раскрываем скобки. Но выполняем все эти действия мы только с одной целью — получения простого уравнения.
Уравнения \[rx+c=0\] — является уравнением с одной неизвестной линейного вида, в котором r и c — обозначение для числовых значений. Чтобы решить уравнение данного вида необходимо произвести перенос его членов:
\[x=-b\div a.
Например, нам необходимо решить такое уравнение:
\[3-2х=5-3х\]
Начинаем решение данного уравнения с переноса его членов: с \[х\] — в левую часть, остальные — в правую. При переносе помним о том, что меняется \[+\] на \[-.\] Получим:
\[-2х+3х=5-3\]
Выполнив простые арифметические действия, получим следующий результат:
\[x=2\]
Где можно решить уравнение с х онлайн?
Решить уравнение с иксом онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн
решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher.
Решение уравнений с дробями — как решать дробные уравнения
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
- Алгебраические — состоят из переменных.
 Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
| Основные свойства дробей |
|---|
|
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
| Универсальный алгоритм решения |
|---|
|
А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
| Что еще важно учитывать при решении |
|---|
|
А вот и полезные видео для закрепления материала:
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя.
 Умножим каждый член уравнения на х.
Умножим каждый член уравнения на х.
- Переведем новый множитель в числитель..
- Сократим левую часть на (х+2), а правую на 2.
4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3(x-3)(x+3)
- Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
- Выполним возможные преобразования. Получилось квадратное уравнение:
x2-9=0
- Решим полученное квадратное уравнение:
x2=9
- Получили два возможных корня:
x1=−3, x2=3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равен нулю:
3(x-3)(x+3)=0
Если x = 3 — знаменатель тоже равен нулю.
- Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Ответ: нет решения.
Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Электронный справочник по математике для школьников тригонометрия решение простейших тригонометрических уравнений
Содержание
Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1
Рис. 1
Частные случаи решения уравнений sin x = a
Уравнение: sin x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 1 Решение: |
Решение уравнения cos
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2
Рис. 2
Частные случаи решения уравнений cos x = a
Уравнение: cos x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 1 Решение: |
Решение уравнения tg
x = a| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Решение уравнения ctg
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
Уравнения и задачи на подбор параметра в Excel
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
2x+1=7
- y=7 является функцией x;
- нам известно значение y, следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
- Заполните ячейки листа, так как показано на рисунке:
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
На этот раз формула выглядит следующим образом:
x2=4
Решение:
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
x=(7-1)/2
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.
Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид Ax4+B=0.
Определение 1Для решения этого типа уравнений применяются формулы сокращенного умножения:
Ax4+B=0x4+BA=0x4+2BAx2+BA-2BAx2=0x2+BA2-2BAx2=0x2-2BA4x+BAx2+2BA4x+BA=0
Остается лишь найти корни квадратных трехчленов.
Пример 1Решить уравнение четвертой степени 4×4+1=0.
Решение
Для начала проведем разложение многочлена 4×4+1 на множители:
4×4+1=4×4+4×2+1=(2×2+1)2-4×2=2×2-2x+1(2×2+2x+1)
Теперь найдем корни квадратных трехчленов.
Первого:
2×2-2x+1=0D=(-2)2-4·2·1=-4×1=2+D2·2=12+ix2=2-D2·2=12-i
Второго:
2×2+2x+1=0D=22-4·2·1=-4×3=-2+D2·2=-12+ix4=-2-D2·2=-12-i
Мы получили четыре комплексных корня.
Ответ: x=12±i и x=-12±i.
Решение возвратного уравнения четвертой степени
Определение 2Возвратные уравнения четвертого порядка имеют вид Ax4+Bx3+Cx2+Bx+A=0
х=0 не является корнем этого уравнения: A·04+B·03+C·02+B·0+A=A≠0. Поэтому на x2 можно смело разделить обе части этого уравнения:
Ax4+Bx3+Cx2+Bx+A=0Ax2+Bx+C+Bx+Ax2=0Ax2+Ax2+Bx+Bx+C=0Ax2+1×2+Bx+1x+C=0
Проведем замену переменных x+1x=y⇒x+1×2=y2⇒x2+1×2=y2-2:
Ax2+1×2+Bx+1x+C=0A(y2-2)+By+C=0Ay2+By+C-2A=0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Пример 2Найти все комплексные корни уравнения 2×4+23+2×3+4+6×2+23+2x+2=0.
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x2:
Проведем деление обеих частей на x2:
2×2+23+2x+4+6+23+2x+2×2=0
Проведем группировку:
2×2+2×2+23+2x+23+2x+4+6+=02×2+1×2+23+2x+1x+4+6=0
Проведем замену переменной x+1x=y⇒x+1×2=y2⇒x2+1×2=y2-2
2×2+1×2+23+2x+1x+4+6=02y2-2+23+2y+4+6=02y2+23+2y+6=0
Решим полученное квадратное уравнение:
D=23+22-4·2·6=12+46+2-86==12-46+2=23-22y1=-23-2+D2·2=-23-2+23-24=-22y2=-23-2-D2·2=-23-2-23+24=-3
Вернемся к замене: x+1x=-22, x+1x=-3.
Решим первое уравнение:
x+1x=-22⇒2×2+2x+2=0D=22-4·2·2=-14×1=-2-D2·2=-24+i·144×2=-2-D2·2=-24-i·144
Решим второе уравнение:
x+1x=-3⇒x2+3x+1=0D=32-4·1·1=-1×3=-3+D2=-32+i·12×4=-3-D2=-32-i·12
Ответ: x=-24±i·144 и x=-32±i·12.
Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид Ax4+Bx2+C=0. Мы можем свести такое уравнение к квадратному Ay2+By+C=0 путем замены y=x2. Это стандартный прием.
Пример 3Решить биквадратное уравнение 2×4+5×2-3=0.
Решение
Выполним замену переменной y=x2, что позволит нам свести исходное уравнение к квадратному:
2y2+5y-3=0D=52-4·2·(-3)=49y1=-5+D2·2=-5+74=12y2=-5-D2·2=-5-74=-3
Следовательно, x2=12 или x2=-3.
Первое равенство позволяет нам получить корень x=±12. Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x=±i·3.
Ответ: x=±12 и x=±i·3.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 4Найти все комплексные корни биквадратного уравнения 16×4+145×2+9=0.
Решение
Используем метод замены y=x2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16y2+145y+9=0D=1452-4·16·9=20449y1=-145+D2·16=-145+14332=-116y2=-145-D2·16=-145-14332=-9
Поэтому, в силу замены переменной, x2=-116 или x2=-9.
Ответ: x1, 2=±14·i, x3, 4=±3·i.
Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x4+Ax3+Bx2+Cx+D=0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y0. Это любой из корней кубического уравнения y3-By2+AC-4Dy-A2D+4BD-C2=0. После этого необходимо решить два квадратных уравнения x2+A2x+y02+A24-B+y0x2+A2y0-Cx+y024-D=0, у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Пример 5Найти корни уравнения x4+3×3+3×2-x-6=0.
Решение
Имеем А=3, В=3, С=-1, D=-6. Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y3-By2+AC-4Dy-A2D+4BD-C2=0y3-3y2+21y-19=0
Одним из корней кубического уравнения будет y0=1, так как 13-3·12+21·1-19=0.
Запишем два квадратных уравнения:
x2+A2x+y02±A24-B+y0x2+A2y0-Cx+y024-D=0x2+32x+12±14×2+52x+254=0x2+32x+12±12x+522=0
x2+32x+12+12x+52=0 или x2+32x+12-12x-52=0
x2+2x+3=0 или x2+x-2=0
Корнями первого уравнения будут x=-1±i·2, корнями второго х=1 и х=-2.
Ответ: x1,2=-1±i2, x3=1, x4=-2.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из
слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением
является уравнение .
Например, дробным уравнением
является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
При решении квадратного уравнения получаем его корни:
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
.
Решенив квадратное уравнение, получаем его корни:
.
Если x = -3, то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3.
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
Решенив квадратное уравнение, получаем его корни:
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y:
.
Корни этого уравнения:
Значит
или .
Из уравнения находим, что
.
Из уравнения находим, что
.
Итак, данное уравнение имеет четыре корня:
, .
Другие темы в блоке «Школьная математика»
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Предварительные навыкиЧто такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5.
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x, значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
8 + 2
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
8 + 2 = 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
2 = 10 − 8
Мы выразили число 2 из равенства 8 + 2 = 10. Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8. Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
или
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
8 + 2 = 10
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
8 = 10 − 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
8 + 2 = 10
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
10 = 8 + 2
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
8 = 6 + 2
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
8 − 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
2 = 8 − 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство в первоначальное состояние:
3 × 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
15 = 3 × 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
2 = 10 − 8
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
8 + x = 10
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10, а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10. Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10. Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
2 = 10 − 8
А сейчас, чтобы найти неизвестное слагаемое x, мы должны из суммы 10 вычесть известное слагаемое 8:
x = 10 − 8
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
x = 2
Мы решили уравнение. Значение переменной x равно 2. Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
x + 2 = 10
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2
x = 10 − 2
x = 8
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
8 = 6 + 2
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
x − 2 = 6
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6. Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x, мы должны к разности 6 прибавить вычитаемое 2
x = 6 + 2
Если вычислить правую часть, то можно узнать чему равна переменная x
x = 8
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
8 − x = 6
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
x = 8 − 6
Вычисляем правую часть и находим значение x
x = 2
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
x × 2 = 6
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6. Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x, нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
x = 3
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6. Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства позволяет узнать чему равно x
x = 2
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда .
Решим уравнение x × 3 = 27. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда .
Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.
Чтобы выразить число 15 мы поступили следующим образом:
15 = 3 × 5
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве вместо числа 15 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.
А сейчас, чтобы найти неизвестное делимое x, нужно частное 3 умножить на делитель 5
x = 3 × 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x.
x = 15
Теперь представим, что в равенстве вместо числа 5 располагается переменная x.
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
А сейчас, чтобы найти неизвестный делитель x, нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x.
x = 5
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
x = 60 − 45
Вычислим правую часть, получим значение x равное 15
x = 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x. После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение и подставим вместо x
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56, мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56. Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2. Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56, а затем в уравнение 28x = 56, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56, которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
и аналогично:
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 10 разделить на известный сомножитель 5.
Отсюда .
Вернемся к исходному уравнению и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы вычли из обеих частей уравнения число 10. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x, а в правой части число 4
Получили уравнение 4x = 4. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12. В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x, а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения .
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x. Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2. Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12. В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15. Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x. Корень этого уравнения, как и уравнения равен 5. Значит эти уравнения равносильны.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x, сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x. Для этого разделим произведение 28 на известный сомножитель 7
Отсюда x = 4.
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно . Теперь найдем значение переменной B. То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно
Видим, что значение переменной B, как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42. Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2. Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14, нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1.
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение . Чему равен корень этого уравнения?
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . Это есть произведение минус единицы и переменной x
То есть минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом:
Имеем дело с компонентами умножения. Чтобы найти х, нужно произведение −5 разделить на известный сомножитель −1.
или разделить обе части уравнения на −1, что еще проще
Итак, корень уравнения равен 5. Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения на минус единицу:
После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10
Корень этого уравнения, как и уравнения равен 5
Значит уравнения и равносильны.
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1.
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения на −1 можно записать подробно следующим образом:
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения на −1, мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1. Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77, и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2
Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5
Уравнения вида мы решали выражая неизвестное слагаемое:
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9.
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9), которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
x = 0 или x + 9 = 0
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0. Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0. Несложно догадаться, что корень этого уравнения равен −9. Проверка показывает, что корень верный:
−9 + 9 = 0
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2). А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2)).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю:
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14. Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x, левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y. Например, пусть y = 3.
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s.
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения определить время. Для этого нужно выразить переменную t.
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
v = 50 км/ч
А расстояние равно 100 км
s = 100 км
Тогда буквенное уравнение примет следующий вид
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t. Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c, то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10. Оно похоже на буквенное уравнение a + bx = c. Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0), поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x, сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b. Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d), то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4). Оно похоже на уравнение a(x − c) = b(x + d). Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d. Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0). Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d). В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2(x + 3) = 16. Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x, разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2(x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10, для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x. Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0, то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0. При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0, то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5. Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0, и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3, и b равно какому-нибудь числу, скажем числу 6, то уравнение примет вид .
Отсюда .
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0. Это то же самое уравнение, что и ax = b, но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0. Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
Задания для самостоятельного решения
Задание 1. Используя метод переноса слагаемого, решите следующее уравнение:
Задание 2. Используя метод прибавления (или вычитания) числа к обеим частям, решите следующее уравнение:
Задание 3. Решите уравнение:
Задание 4. Решите уравнение:
Задание 5. Решите уравнение:
Задание 6. Решите уравнение:
Задание 7. Решите уравнение:
Задание 8. Решите уравнение:
Задание 9. Решите уравнение:
Задание 10. Решите уравнение:
Задание 11. Решите уравнение:
Задание 12. Решите уравнение:
Задание 13. Решите уравнение:
Задание 14. Решите уравнение:
Задание 15. Решите уравнение:
Задание 16. Решите уравнение:
Задание 17. Решите уравнение:
Задание 18. Решите уравнение:
Задание 19. Решите уравнение:
Задание 20. Решите уравнение:
Задание 21. Решите уравнение:
Задание 22. Решите уравнение:
Задание 23. Решите уравнение:
Задание 24. Решите уравнение:
Задание 25. Решите уравнение:
Задание 26. Решите уравнение:
Задание 27. Решите уравнение:
Задание 28. Решите уравнение:
Задание 29. Решите уравнение:
Задание 30. Решите уравнение:
Задание 31. Решите уравнение:
Задание 32. В следующем буквенном уравнении выразите переменную x:
Задание 33. В следующем буквенном уравнении выразите переменную x:
Задание 34. В следующем буквенном уравнении выразите переменную x:
Задание 35. В следующем буквенном уравнении выразите переменную x:
Задание 36. В следующем буквенном уравнении выразите переменную y:
Задание 37. В следующем буквенном уравнении выразите переменную z:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Решение линейных уравнений: с пареном; «All x», «No x» Soln’s
Purplemath
В этом уроке мы сначала попрактикуемся в решении линейных уравнений, содержащих скобки. Их решение потребует умножения и упрощения, прежде чем приступить к фактическому процессу решения. Если вам не нравятся скобки, сначала займитесь изучением. Тогда вернись сюда.
Затем мы рассмотрим два странных типа решений: «нет решения» и решение «все x ». В первом случае процесс решения заканчивается бессмыслицей, а во втором — тривиально верным утверждением. Поскольку учащиеся не часто сталкиваются с такими решениями, их легко забыть, а значит, и запутать. Но я бы поставил хорошие деньги на то, что в следующем тесте будет хотя бы одно из этих уравнений, а в финале, вероятно, будет еще одно.Так что изучите и сделайте заметку, чтобы просмотреть уравнения «без решения» и «все уравнения — x » перед следующим экзаменом.
MathHelp.com
После того, как вы изучите основы решения линейных уравнений, ваш учебник и инструктор начнут предлагать вам упражнения, которые включают в себя скобки, которые обычно необходимо сначала упростить (или «расширить», что означает, что вы умножили, а затем упростил результат).
Во-первых, мне нужно умножить скобки в правой части. Затем я могу продолжить как обычно:
Тогда мое решение:
Решить 6
x — (3 x + 8) = 16
Сначала я упрощу левую часть; тогда решу обычным способом.Я хочу быть осторожным, когда пишу негатив в скобках. Если у меня возникают проблемы с отслеживанием знаков «минус», я ставлю «1» перед круглыми скобками.
Тогда мое решение:
Решите 7 (5
x — 2) = 6 (6 x — 1)
Это уравнение заключено в скобки с обеих сторон уравнения.Я должен обязательно взять 7 и 6 до их соответствующих скобок.
После того, как я упростил любую сторону, я переместил меньший из двух членов переменной («35 x » с левой стороны), чтобы убедиться, что у полученного в результате члена переменной не было знака «минус». Это не «правило», но, безусловно, облегчает мою жизнь. И мой окончательный ответ:
Для уравнений с скобками, не торопитесь и выпишите всех ваших шагов, как я сделал выше.Не пытайтесь делать все в своей голове.
Во-первых, мне нужно умножить в левой части, взяв 3 через —
Подождите … В этом уравнении я действительно могу избавиться от 3, разделив его на части, потому что 6 в правой части делится на 3. На самом деле мне не нужно распределять для этого конкретного уравнения. Вместо:
3 (х — 2) = 6
——— —
3 3
х — 2 = 2
+2 +2
———-
х = 4
Тогда мое решение:
Если бы я не заметил, что могу начать с разделения, я бы все равно получил правильный ответ.Но если есть возможность разделить, предоставив себе меньшие числа для работы, я бы хотел этим воспользоваться. Это упрощение случается нечасто, но постарайтесь не закрывать глаза на то, что несколько раз оно появляется.
Решить 13 — (2
x + 2) = 2 ( x + 2) + 3 x
Я начну с умножения на каждую скобку (знак «минус» слева и 2 справа).Затем я объединю похожие термины, упрощу и решу:
Тогда мой ответ:
Не забывайте: никогда нет причин быть неуверенным в своем решении линейного уравнения, потому что вы всегда можете проверить свой ответ. Значение решения состоит в том, что именно значение x делает уравнение истинным. Итак, чтобы проверить свой ответ, вы вставляете значение решения обратно в исходное уравнение и убедитесь, что уравнение «работает» с этим значением.Например, в последнем упражнении выше мое решение было x = 1. Чтобы проверить свое решение, я подставлю свое значение в левую (LHS) и правую (RHS) части исходного уравнения. , и убедитесь, что обе стороны оценивают одно и то же число.
13 — (2 x + 2) = 2 ( x + 2) + 3 x
слева: 13 — (2 [1] + 2)
= 13 — (2 + 2) = 13-4 = 9
ПРА: 2 ([1] + 2) + 3 [1]
Две стороны уравнения оценивают одно и то же значение, поэтому решение «проверяет», и теперь я знаю , что мой ответ правильный
Кстати, если есть возможность, попробуйте проверить свои ответы при сдаче тестов.После того, как вы ответили на все вопросы (при условии, что у вас осталось немного времени), вернитесь и вставьте свои решения обратно в исходный вопрос. Если ваше решение вопроса «проверяет», значит, вы знаете, что ответили правильно. Если он не проверит, то у вас есть шанс исправить свою ошибку до того, как вы сдадите свой тест.
Вам также может потребоваться решить линейные уравнения с вложенными скобками .
Решите 2 [3
x + 4 (3 — x )] = 3 (5 — 4 x ) — 11
Прежде чем я смогу решить, мне нужно упростить.Сначала я упрощу левую часть:
2 [3 x + 4 (3 — x )]
2 [3 x + 4 (3) + 4 (- x )]
2 [3 x + 12–4 x ]
2 [12 — x ]
24-2 х
Тогда я упрощу правую часть:
3 (5 — 4 x ) — 11
3 (5) + 3 (–4 x ) — 11
15 — 12 x — 11
4–12 x
Теперь, когда я упростил обе стороны уравнения, я могу перейти к решению.
24 — 2x = 4 — 12x
+ 12x + 12x
——————-
24 + 10x = 4
-24-24
—————
10x = -20
— —
10 10
х = -2
Итак, мой окончательный ответ:
Решение 3 [
x — 2 (3 x — 4)] + 15 = 5 — [2 x — (3 + x )] — 11
Моим первым шагом будет упростить каждую часть этого уравнения, работая изнутри.Начну с левой стороны:
3 [ x — 2 (3 x — 4)] + 15
3 [ x — 6 x + 8] + 15
3 [–5 x + 8] + 15
–15 x + 24 + 15
–15 x + 39
Тогда я упрощу правую часть:
5 — [2 x — (3 + x )] — 11
5 — [2 x — 3 — x ] — 11
5 — [ x — 3] — 11
5 — х + 3 — 11
— х — 3
После упрощения каждой стороны я могу приступить к решению.Мое упрощенное уравнение:
Я перемещаю меньший член переменной (равный –15 x слева), а затем перемещаю числа, чтобы закончить решение.
-15x + 39 = -x — 3
+ 15x + 15x
——————-
39 = 14x — 3
+3 +3
————
42 = 14x
— —
14 14
3 = х
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейных уравнений с вложенными круглыми скобками.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить для x», чтобы сравнить свой ответ с ответом Матвея. (Или пропустите виджет и перейдите к следующей странице.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https: //www.purplemath.com / modules / solvelin4.htm
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения
Введение
Учебник
Нужна дополнительная помощь по этим темам? |
Узнайте, как решить для X в алгебраических уравнениях
В этом видео мы узнаем, как найти x (или другую переменную) в сложных алгебраических уравнениях, используя обратные операции. После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и алгебры и попрактикуйтесь.
Пример решения многоступенчатого алгебраического уравнения
Вычтем 2 с обеих сторон
Разделить на 5 с обеих сторон
Вычесть 4 с обеих сторон
Пример 1
Во-первых, распределите термины внутри скобок
Затем вычтите с обеих сторон
разделить с двух сторон
Теперь у нас:
Пример 2
Во-первых, распределите термины внутри скобок
Затем прибавляем с обеих сторон
разделить с двух сторон
Теперь у нас:
Другой способ решения этой проблемы:
Распределить 5 по x и 4
Упростить с помощью сложения
Вычтем 22 с обеих сторон
Разделить на 5 с каждой стороны
Стенограмма видеоурока
Давайте займемся решением сложных алгебраических уравнений.Это предполагает более чем одну операцию.
Для просмотра, порядок работы или PEMDAS, у нас есть.
PEMDAS — это аббревиатура, обозначающая
Круглая скобка
Экспоненты
Умножение
Деление
Сложение
Вычитание
Давайте оценим.
Итак, у нас есть.
Решая алгебраические уравнения, мы используем не все целые числа. Вместо этого у нас есть переменные.
Итак, возможно.
Из нашего примера мы это уже знаем.
Но давайте попробуем решить это алгебраически.
Нам просто нужно сделать несколько шагов, чтобы решить эту проблему.
1. По возможности упростите обе части уравнений.
2. Если есть условия с обеих сторон, мы должны получить все условия с одной стороны. Вы можете разместить его слева или справа, в зависимости от того, что вам больше нравится.
3. Обратный PEMDAS. Мы собираемся выполнить порядок операций в обратном порядке, используя обратные операции.
4. Наша цель — изолировать переменную.
Возвращаясь к, давайте проделаем вышеописанные действия.
1. Упростите — это самое простое из возможных.
2. Весь термин на одной стороне — всего один, и он слева.
3. Теперь давайте сделаем обратный PEMDAS, используя обратные операции.
Давайте вычтем обе части уравнения.
Будет.
4. Изолятор
Здесь мы должны разделить обе стороны на.
И у нас будет.
Приведем еще один пример.
У нас
Итак, давайте начнем с сложения обеих частей уравнения.
Получим
Затем умножаем на обе стороны.
Ответ
Приведем еще один пример. Я покажу вам, как решить эту проблему двумя разными способами.
У нас
Первый метод решения:
Давайте вычтем обе части уравнения.
У нас будет
Затем мы должны разделить обе стороны на
.Получим
Затем, чтобы изолировать, мы должны вычесть с обеих сторон
Наш окончательный ответ —
Итак, теперь перейдем ко второму методу решения того же уравнения.
Второй метод — максимально упростить уравнение.
Давайте начнем с распределения в уравнение в скобках —
Итак, приступим!
и
У нас будет
Теперь мы можем комбинировать похожие термины, чтобы еще больше упростить
Затем мы должны сделать обратный PEMDAS.
Вычтем с обеих сторон
Получим
Теперь давайте сделаем обратное умножению — деление.
Разделите обе стороны на
Наш окончательный ответ —
Оба метода дали нам одинаковый ответ.
Подводя итог, независимо от того, насколько сложным является наше алгебраическое уравнение, мы можем выполнить обратный PEMDAS или обратный порядок операций, чтобы изолировать.
Решайте уравнения с переменными и константами с обеих сторон — предалгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите уравнение с константами с обеих сторон
- Решите уравнение с переменными с обеих сторон
- Решите уравнение с переменными и константами с обеих сторон
- Решите уравнения, используя общую стратегию
Перед тем, как начать, пройдите тест на готовность.
- Упростить:
Если вы пропустили эту проблему, просмотрите (рисунок). - Решение:
Если вы пропустили эту проблему, просмотрите (рисунок). - Решение:
Если вы пропустили эту проблему, просмотрите (рисунок).
Решите уравнение с константами с обеих сторон
Возможно, вы заметили, что во всех уравнениях, которые мы решили до сих пор, все переменные члены находились только на одной стороне уравнения, а константы — на другой стороне. Это не происходит постоянно, поэтому теперь мы увидим, как решать уравнения, в которых переменные и / или постоянные члены находятся по обе стороны уравнения.
Наша стратегия будет включать выбор одной стороны уравнения в качестве переменной, а другой стороны уравнения в качестве постоянной. Затем мы будем использовать свойства равенства вычитания и сложения, шаг за шагом, чтобы собрать все переменные члены вместе на одной стороне уравнения и постоянные члены вместе на другой стороне.
Сделав это, мы преобразуем уравнение, которое начиналось с переменных и констант с обеих сторон, в форму. Мы уже знаем, как решать уравнения этой формы с помощью свойств равенства или деления или умножения.
Решить:
Решение
В этом уравнении переменная находится только в левой части. Левую часть имеет смысл называть стороной переменных. Следовательно, правая сторона будет постоянной стороной. Мы напишем метки над уравнением, чтобы помочь нам запомнить, что куда идет.
Решить:
Решить:
Решить:
Решение
Обратите внимание, что переменная находится только в левой части уравнения, поэтому это будет сторона переменной, а правая сторона будет стороной константы.Так как левая сторона — переменная сторона, это неуместно. Он вычитается из так для «отмены» вычитания, прибавляется к обеим сторонам.
Решить:
Решить:
Решите уравнение с переменными с обеих сторон
Что, если есть переменные с обеих сторон уравнения? Мы начнем так же, как и выше, — выберем сторону переменной и сторону константы, а затем воспользуемся свойствами равенства вычитания и сложения, чтобы собрать все переменные с одной стороны и все константы с другой стороны.Помните, что то, что вы делаете с левой частью уравнения, вы должны делать и с правой.
Решить:
Решение
Здесь переменная находится с обеих сторон, но константы появляются только с правой стороны, поэтому давайте сделаем правую сторону «постоянной». Тогда левая сторона будет «переменной» стороной.
Решить:
Решить:
Решить:
Решение
Единственная постоянная находится в левой части уравнения, а переменная — в обеих сторонах.Оставим константу слева и соберем переменные справа.
Решить:
Решить:
Решить:
Решение
Единственная константа находится справа, поэтому пусть левая сторона будет стороной переменной.
Решить:
Решить:
Решение уравнений с переменными и константами с обеих сторон
Следующий пример будет первым, в котором переменные и константы будут по обе стороны уравнения.Как и раньше, мы соберем члены переменных в одну сторону, а константы — в другую.
Решить:
Решить:
Мы кратко опишем предпринятые шаги, чтобы вы могли легко к ним обратиться.
Решите уравнение с переменными и константами с обеих сторон.
- Выберите одну сторону, чтобы она была переменной стороной, тогда другая будет постоянной стороной.
- Соберите переменные члены в сторону переменной, используя свойство равенства сложения или вычитания.
- Соберите константы с другой стороны, используя свойство равенства сложения или вычитания.
- Сделайте коэффициент переменной, используя свойство равенства умножения или деления.
- Проверьте решение, подставив его в исходное уравнение.
Хорошей идеей будет сделать сторону переменной той, в которой переменная имеет больший коэффициент. Обычно это упрощает арифметику.
Решить:
Решение
У нас слева и справа.Так как левую часть сделайте стороной «переменной».
Решить:
Решить:
Решить:
Решение
Это уравнение имеет слева и справа. Так как правую сторону сделайте переменной стороной, а левую — постоянной стороной.
Обратите внимание, что мы могли бы сделать левую часть переменной стороной вместо правой, но это привело бы к отрицательному коэффициенту при переменной составляющей. Хотя мы можем работать с негативом, вероятность ошибки при работе с позитивом меньше.Описанная выше стратегия помогает избежать негатива!
Решить:
Решить:
Чтобы решить уравнение с дробями, мы по-прежнему выполняем те же шаги, чтобы получить решение.
Решить:
Решение
Т.к. левую сторону сделайте переменной стороной, а правую — постоянной стороной.
Решить:
Решить:
Мы проделываем те же шаги, когда в уравнении есть десятичные дроби.
Решить:
Решение
Т.к. левую сторону сделайте переменной стороной, а правую — постоянной стороной.
Решить:
Решить:
Решение уравнений с использованием общей стратегии
Каждый из первых нескольких разделов этой главы имел дело с решением одной конкретной формы линейного уравнения. Пришло время разработать общую стратегию, которую можно использовать для решения любого линейного уравнения . Мы называем это общей стратегией .Для решения некоторых уравнений не потребуется выполнять все шаги, но для многих потребуется. Если сначала максимально упростить каждую часть уравнения, остальные шаги будут проще.
Используйте общую стратегию для решения линейных уравнений.
- Максимально упростите каждую часть уравнения. Используйте свойство Distributive, чтобы удалить скобки. Комбинируйте похожие термины.
- Соберите все переменные члены в одну сторону уравнения. Используйте свойство равенства сложения или вычитания.
- Соберите все постоянные члены другой стороны уравнения. Используйте свойство равенства сложения или вычитания.
- Сделайте коэффициент при переменной составляющей равным Использовать свойство равенства умножения или деления. Сформулируйте решение уравнения.
- Проверить решение. Подставьте решение в исходное уравнение, чтобы убедиться, что результат верный.
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решение
Будьте осторожны при распространении негатива.
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Решить:
Во многих приложениях нам придется решать уравнения с десятичными знаками. Та же самая общая стратегия будет работать для этих уравнений.
Решить:
Решить:
Решить:
Ключевые понятия
- Решите уравнение с переменными и константами с обеих сторон
- Выберите одну сторону, чтобы она была переменной стороной, тогда другая будет постоянной стороной.
- Соберите переменные члены в сторону переменной, используя свойство равенства сложения или вычитания.
- Соберите константы с другой стороны, используя свойство равенства сложения или вычитания.
- Сделайте коэффициент переменной равным 1, используя свойство равенства умножения или деления.
- Проверьте решение, подставив его в исходное уравнение.
- Общая стратегия решения линейных уравнений
- Максимально упростите каждую часть уравнения.Используйте свойство Distributive, чтобы удалить скобки. Комбинируйте похожие термины.
- Соберите все переменные члены в одну сторону уравнения. Используйте свойство равенства сложения или вычитания.
- Соберите все постоянные члены другой стороны уравнения. Используйте свойство равенства сложения или вычитания.
- Сделайте коэффициент при переменной составляющей равным 1. Используйте свойство равенства умножения или деления. Сформулируйте решение уравнения.
- Проверить решение. Подставьте решение в исходное уравнение, чтобы убедиться, что результат верный.
Практика ведет к совершенству
Решите уравнение с константами с обеих сторон
В следующих упражнениях решите уравнение для переменной.
Решите уравнение с переменными с обеих сторон
В следующих упражнениях решите уравнение для переменной.
Решите уравнение с переменными и константами с обеих сторон
В следующих упражнениях решите уравнения для переменной.
Решите уравнение с помощью общей стратегии
В следующих упражнениях решите линейное уравнение, используя общую стратегию.
Письменные упражнения
Почему при решении уравнения с переменными с обеих сторон обычно лучше выбирать сторону с большим коэффициентом в качестве стороны переменной?
Решите уравнение, объясняющее все этапы вашего решения.
Какой первый шаг вы делаете при решении уравнения Объясните, почему это ваш первый шаг.
Решите уравнение, объясняющее все этапы вашего решения, как в примерах в этом разделе.
Своими словами перечислите шаги в Общей стратегии решения линейных уравнений.
Объясните, почему вам следует максимально упростить обе стороны уравнения, прежде чем собирать переменные члены в одну сторону и постоянные члены — в другую.x} = 9 \) Показать решение
Итак, мы сказали выше, что если бы у нас был логарифм перед левой частью, мы могли бы получить \ (x \) из экспоненты. Сделать это достаточно просто. Мы просто поставим логарифм перед левой частью. Однако, если мы поместим туда логарифм, мы также должны поставить логарифм перед правой частью. Это обычно обозначается как , логарифмируя обе стороны .
Мы можем использовать любой логарифм, который захотим, поэтому давайте попробуем натуральный логарифм.x} & = \ ln 9 \\ x \ ln 7 & = \ ln 9 \ end {align *} \]
Теперь нам нужно найти \ (x \). Это проще, чем кажется. Если бы у нас было \ (7x = 9 \), то мы все могли бы решить для \ (x \), просто разделив обе части на 7. Здесь это работает точно так же. И ln7, и ln9 — просто числа. По общему признанию, потребуется калькулятор, чтобы определить, что это за числа, но это числа, и поэтому мы можем сделать то же самое здесь.
\ [\ begin {align *} \ frac {{x \ ln 7}} {{\ ln 7}} & = \ frac {{\ ln 9}} {{\ ln 7}} \\ x & = \ frac {{\ ln 9}} {{\ ln 7}} \ end {align *} \]Это технически точный ответ.Однако в этом случае обычно лучше получить десятичный ответ, так что давайте сделаем еще один шаг.
\ [x = \ frac {{\ ln 9}} {{\ ln 7}} = \ frac {{2.19722458}} {{1.945}} = 1.127 \]
Обратите внимание, что ответы на эти вопросы чаще всего являются десятичными.
Также будьте осторожны, чтобы не допустить следующей ошибки.
\ [1.127 = \ frac {{\ ln 9}} {{\ ln 7}} \ ne \ ln \ left ({\ frac {9} {7}} \ right) = 0.y} = 0 \) Показать решение
В этом случае мы не можем просто поставить логарифм перед обеими сторонами. На это есть две причины. Сначала в правой части у нас есть ноль, и мы знаем из предыдущего раздела, что не можем логарифмировать ноль. Затем, чтобы сместить показатель вниз, он должен быть на всем члене внутри логарифма, и этого не будет с этим уравнением в его нынешнем виде.
Итак, первым делом переместим члены на другую сторону от знака равенства, затем мы возьмем логарифм обеих сторон, используя натуральный логарифм.y} \\ \ left ({4y + 1} \ right) \ ln 2 & = y \ ln 3 \ end {align *} \]
Хорошо, это выглядит неаккуратно, но опять же, это действительно не так уж и плохо. Давайте сначала посмотрим на следующее уравнение.
\ [\ begin {align *} 2 \ left ({4y + 1} \ right) & = 3y \\ 8y + 2 & = 3y \\ 5y & = — 2 \\ y & = — \ frac {2} { 5} \ end {align *} \]Мы все можем решить это уравнение, а это значит, что мы можем решить то, что у нас есть. Опять же, ln2 и ln3 — это просто числа, поэтому процесс точно такой же.Ответ будет сложнее, чем это уравнение, но процесс идентичен. Вот работа для этого.
\ [\ begin {align *} \ left ({4y + 1} \ right) \ ln 2 & = y \ ln 3 \\ 4y \ ln 2 + \ ln 2 & = y \ ln 3 \\ 4y \ ln 2 — y \ ln 3 & = — \ ln 2 \\ y \ left ({4 \ ln 2 — \ ln 3} \ right) & = — \ ln 2 \\ y & = — \ frac {{\ ln 2} } {{4 \ ln 2 — \ ln 3}} \ end {align *} \]Итак, мы получили все члены с \ (y \) в них с одной стороны и всеми другими членами с другой стороны.{е \ влево (х \ вправо)}} = е \ влево (х \ вправо) \]
Мы видели это в предыдущем разделе (в более общем виде), и, используя это здесь, мы значительно упростим нашу жизнь. Использование этого свойства дает
\ [\ begin {align *} t + 6 & = \ ln 2 \\ t & = \ ln \ left (2 \ right) — 6 = 0,69314718 — 6 = — 5,30685202 \ end {align *} \]Обратите внимание на скобки вокруг 2 в логарифме на этот раз. Они нужны для того, чтобы мы не допустили следующей ошибки.{2z + 4}} & = \ ln \ left ({\ frac {8} {5}} \ right) \\ 2z + 4 & = \ ln \ left ({\ frac {8} {5}} \ right ) \\ 2z & = \ ln \ left ({\ frac {8} {5}} \ right) — 4 \\ z & = \ frac {1} {2} \ left ({\ ln \ left ({\ frac {8} {5}} \ right) — 4} \ right) = \ frac {1} {2} \ left ({0,470003629 — 4} \ right) = — 1,76499819 \ end {align *} \]
Решение линейных уравнений | Уравнения и неравенства
Упражнение 4.1\ begin {align *} 2г — 3 & = 7 \\ 2л & = 10 \\ y & = 5 \ end {выровнять *}
\ begin {align *} 2c & = c — 8 \\ c & = -8 \ end {выровнять *}
\ begin {align *} 3 & = 1 — 2c \\ 2c & = 1 — (3) \\ 2c & = -2 \\ c & = \ frac {-2} {2} \\ & = -1 \ end {align *}
\ begin {align *} 4b +5 & = -7 \\ 4b & = -7 — (5) \\ 4b & = -12 \\ b & = \ frac {-12} {4} \\ & = -3 \ end {align *}
\ begin {align *} -3y & = 0 \\ у & = 0 \ end {выровнять *}
\ begin {align *} 16л + 4 & = -10 \\ 16лет & = -14 \\ y & = — \ frac {14} {16} \\ & = — \ frac {7} {8} \ end {выровнять *}
\ begin {align *} 12лет + 0 & = 144 \\ 12лет & = 144 \\ y & = 12 \ end {выровнять *}
\ begin {align *} 7 + 5л & = 62 \\ 5лет & = 55 \\ y & = 11 \ end {выровнять *}
\ (55 = 5x + \ frac {3} {4} \)
\ begin {align *} 55 & = 5x + \ frac {3} {4} \\ 220 & = 20х + 3 \\ 20x & = 217 \\ х & = \ frac {217} {20} \ end {выровнять *}
\ begin {align *} 5х & = 2х + 45 \\ 3x & = 45 \\ х & = 15 \ end {выровнять *}
\ begin {align *} 23х — 12 & = 6 + 3х \\ 20x & = 18 \\ x & = \ frac {18} {20} \\ & = \ frac {9} {10} \ end {выровнять *}
\ (12 — 6x + 34x = 2x — 24 — 64 \)
\ begin {align *} 12 — 6x + 34x & = 2x — 24 — 64 \\ 12 + 28x & = 2x — 88 \\ 26x & = -100 \\ x & = — \ frac {100} {26} \\ & = — \ frac {50} {13} \ end {выровнять *}
\ (6x + 3x = 4-5 (2x — 3) \)
\ begin {align *} 6x + 3x & = 4-5 (2x — 3) \\ 9x & = 4 — 10x + 15 \\ 19x & = 19 \\ х & = 1 \ end {выровнять *}
\ begin {align *} 18 — 2р & = р + 9 \\ 9 & = 3п \\ p & = 3 \ end {выровнять *}
\ (\ dfrac {4} {p} = \ dfrac {16} {24} \)
\ begin {align *} \ frac {4} {p} & = \ frac {16} {24} \\ (4) (24) & = (16) (p) \\ 16p & = 96 \\ p & = 6 \ end {выровнять *}
\ begin {align *} — (- 16 — п) & = 13п — 1 \\ 16 + п & = 13п — 1 \\ 17 & = 12п \\ p & = \ frac {17} {12} \ end {выровнять *}
\ begin {align *} 3f — 10 & = 10 \\ 3f & = 20 \\ f & = \ frac {20} {3} \ end {выровнять *}
\ begin {align *} 3f + 16 & = 4f — 10 \\ f & = 26 \ end {выровнять *}
\ (10f + 5 = -2f -3f + 80 \)
\ begin {align *} 10f + 5 & = -2f — 3f + 80 \\ 10f + 5 & = -5f + 80 \\ 15f & = 75 \\ f & = 5 \ end {выровнять *}
\ begin {align *} 8 (ф — 4) & = 5 (ф — 4) \\ 8f — 32 & = 5f — 20 \\ 3f & = 12 \\ f & = 4 \ end {выровнять *}
\ begin {align *} 6 & = 6 (f + 7) + 5f \\ 6 & = 6f + 42 + 5f \\ -36 & = 11f \\ f & = — \ frac {36} {11} \ end {выровнять *}
\ begin {align *} -7x & = 8 (1 — х) \\ -7x & = 8 — 8x \\ х & = 8 \ end {выровнять *}
\ (5 — \ dfrac {7} {b} = \ dfrac {2 (b + 4)} {b} \)
\ begin {align *} 5 — \ frac {7} {b} & = \ frac {2 (b + 4)} {b} \\ \ frac {5b — 7} {b} & = \ frac {2b + 8} {b} \\ 5b — 7 & = 2b + 8 \\ 3b & = 15 \\ b & = 5 \ end {выровнять *}
\ (\ dfrac {x + 2} {4} — \ dfrac {x — 6} {3} = \ dfrac {1} {2} \)
\ begin {align *} \ frac {x + 2} {4} — \ frac {x — 6} {3} & = \ frac {1} {2} \\ \ frac {3 (x + 2) — 4 (x — 6)} {12} & = \ frac {1} {2} \\ \ frac {3x + 6 — 4x + 24} {12} & = \ frac {1} {2} \\ (-x + 30) (2) & = 12 \\ -2x + 60 & = 12 \\ -2x & = -48 \\ х & = 24 \ end {выровнять *}
\ (1 = \ dfrac {3a — 4} {2a + 6} \)
Обратите внимание, что \ (a \ neq — -3 \)
\ begin {align *} 1 & = \ frac {3a — 4} {2a + 6} \\ 2а + 6 & = 3а — 4 \\ а & = 10 \ end {выровнять *}\ (\ dfrac {2-5a} {3} — 6 = \ dfrac {4a} {3} +2 — a \)
\ begin {align *} \ frac {2-5a} {3} — 6 & = \ frac {4a} {3} +2 — a \\ \ frac {2-5a} {3} — \ frac {4a} {3} + a & = 8 \\ \ frac {2-5a — 4 a + 3a} {3} & = 8 \\ 2 — 6а & = 24 \\ 6а & = -22 \\ a & = — \ frac {22} {6} \ end {выровнять *}
\ (2 — \ dfrac {4} {b + 5} = \ dfrac {3b} {b + 5} \)
Примечание \ (b \ neq -5 \)
\ begin {align *} 2 — \ frac {4} {b + 5} & = \ frac {3b} {b + 5} \\ 2 & = \ frac {3b + 4} {b + 5} \\ 2b + 10 & = 3b + 4 \\ b & = 6 \ end {выровнять *}\ (3 — \ dfrac {y — 2} {4} = 4 \)
\ begin {align *} 3 — \ frac {y — 2} {4} & = 4 \\ — \ frac {y — 2} {4} & = 1 \\ -у + 2 & = 4 \\ y & = -2 \ end {выровнять *}
\ (\ text {1,5} x + \ text {3,125} = \ text {1,25} x \)
\ begin {align *} \ text {1,5} x + \ text {3,125} & = \ text {1,25} x \\ \ text {1,5} x — \ text {1,25} x & = — \ text {3,125} \\ \ text {0,25} x & = — \ text {3,125} \\ х & = — \ текст {12,5} \ end {выровнять *}
\ (\ текст {1,3} (\ текст {2,7} х + 1) = \ текст {4,1} — х \)
\ begin {align *} \ text {1,3} (\ text {2,7} x + 1) & = \ text {4,1} — x \\ \ text {3,51} x + \ text {1,3} & = \ text {4,1} — x \\ \ text {4,51} x & = \ text {2,8} \\ x & = \ frac {\ text {2,8}} {\ text {4,51}} \\ & = \ frac {280} {451} \ end {выровнять *}
\ (\ текст {6,5} х — \ текст {4,15} = 7 + \ текст {4,25} х \)
\ begin {align *} \ text {6,5} x — \ text {4,15} & = 7 + \ text {4,25} x \\ \ text {2,25} x & = \ text {11,15} \\ x & = \ frac {\ text {11,15}} {\ text {2,25}} \\ & = \ frac {\ text {1 115}} {225} \\ & = \ frac {223} {45} \ end {выровнять *}
\ (\ frac {1} {3} P + \ frac {1} {2} P — 10 = 0 \)
\ begin {align *} \ frac {1} {3} P + \ frac {1} {2} P — 10 & = 0 \\ \ frac {2 + 3} {6} P & = 10 \\ 5П & = 60 \\ P & = 12 \ end {выровнять *}
\ (1 \ frac {1} {4} (x — 1) — 1 \ frac {1} {2} (3x + 2) = 0 \)
\ begin {align *} 1 \ frac {1} {4} (x — 1) — 1 \ frac {1} {2} (3x + 2) & = 0 \\ \ frac {5} {4} x — \ frac {5} {4} — \ frac {3} {2} (3x) — \ frac {3} {2} (2) & = 0 \\ \ frac {5} {4} x — \ frac {5} {4} — \ frac {9} {2} x — \ frac {6} {2} & = 0 \\ \ frac {5 — 18} {4} x + \ frac {-5 — 12} {4} & = 0 \\ \ frac {-13} {4} x & = \ frac {17} {4} \\ -13x & = 17 \\ х & = — \ frac {17} {13} \ end {выровнять *}
\ (\ frac {1} {5} (x- 1) = \ frac {1} {3} (x-2) + 3 \)
\ begin {align *} \ frac {1} {5} (x- 1) & = \ frac {1} {3} (x-2) + 3 \\ \ frac {1} {5} x- \ frac {1} {5} & = \ frac {1} {3} x- \ frac {2} {3} + 3 \\ — \ frac {1} {5} + \ frac {2} {3} — 3 & = \ frac {2} {15} x \\ — \ frac {38} {15} & = \ frac {2} {15} x \\ х & = — \ frac {38} {2} \\ х & = -19 \ end {выровнять *}
\ (\ dfrac {5} {2a} + \ dfrac {1} {6a} — \ dfrac {3} {a} = 2 \)
\ begin {align *} \ frac {5} {2a} + \ frac {1} {6a} — \ frac {3} {a} & = 2 \\ \ frac {5 (3) + 1-3 (6)} {6a} & = 2 \\ \ frac {15 + 1 — 18} {6a} & = 2 \\ \ frac {-2} {6a} & = 2 \\ -2 & = 12а \\ а & = — \ frac {1} {6} \ end {выровнять *}
2.6: Решение уравнений — математика LibreTexts
Напомним (см. Раздел 1.6), что переменная — это символ (обычно буква), обозначающий изменяющееся значение. Если переменная в уравнении заменяется числом и получается истинное утверждение, то это число называется решением уравнения.
Пример 1
Является ли −6 решением уравнения 2x + 5 = −7?
Решение
Замените −6 на x в уравнении.
\ [\ begin {align} 2x + 5 = 7 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ 2 (-6) +5 = -7 ~ & \ textcolor {red} {\ text {Substitute} -6 \ text {for} x.} \\ -12 + 5 = -7 ~ & \ textcolor {red} {\ text {Слева сначала умножьте.}} \\ -7 = -7 ~ & \ textcolor {red} {\ text {Слева, добавьте.}} \ end {align} \ nonumber \ ]
Поскольку последнее утверждение истинно, −6 является решением уравнения.
Упражнение
Является ли −4 решением 8-2 x = 5?
- Ответ
№
Сложение или вычитание одной и той же суммы
Два уравнения с одинаковым набором решений равны эквиваленту .Например, 2 x +5 = −7 и x = −6 имеют одинаковые решения. Следовательно, они эквивалентны уравнениям. Некоторые алгебраические операции приводят к эквивалентным уравнениям.
Получение эквивалентных уравнений
Добавление одного и того же количества к обеим сторонам уравнения. Если мы начнем с уравнения
\ [a = b, \ nonumber \]
, затем прибавляя c к обеим сторонам уравнения, получаем эквивалентное уравнение
\ [а + с = Ь + с.\ nonumber \]
Вычитание одинаковой величины с обеих сторон уравнения . Если мы начнем с уравнения
\ [a = b, \ nonumber \]
, затем вычитание c из обеих частей уравнения дает эквивалентное уравнение
\ [a — c = b — c. \ Nonumber \]
То есть добавление или вычитание одной и той же суммы из обеих частей уравнения не изменит решения уравнения.
Пример 2
Решите относительно x : x + 3 = −7.
Решение
Чтобы отменить эффект добавления 3, вычтите 3 из обеих частей уравнения.
\ [\ begin {align} x + 3 = -7 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ x + 3 — 3 = -7-3 ~ & \ textcolor {red} { \ text {Вычтите 3 с обеих сторон.}} \\ x = -7 + (-3) ~ & \ begin {array} {l} \ textcolor {red} {\ text {Упростите левую часть. Справа:}} \\ \ textcolor {red} {\ text {выражает вычитание как добавление противоположного.}} \ End {array} \\ x = -10 \ end {выравнивается} \ nonumber \]
Чтобы проверить решение, замените -10 на x в исходном уравнении и упростите.
\ [\ begin {align} x + 3 = -7 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -10 + 3 = -7 ~ & \ textcolor {red} {\ text { Заменить} -10 \ text {for} x.} \\ = 7 = -7 ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \ End {align} \ nonumber \]
Поскольку последняя строка проверки является истинным утверждением, это подтверждает, что -10 является решением.
Упражнение
Решите относительно x : x + 9 = -11.
- Ответ
х = -20
Пример 3
Решите относительно x : x — 8 = −11.
Решение
Чтобы отменить эффект вычитания 8, прибавьте 8 к обеим частям уравнения.
\ [\ begin {align} x — 8 = -11 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ x — 8 + 8 = -11+ 8 ~ & \ textcolor {red} { \ text {Добавьте 8 с обеих сторон.}} \\ x = -3 ~ & \ textcolor {red} {\ text {Упростите оба уравнения.}} \ end {align} \ nonumber \]
Чтобы проверить решение, замените −3 на x в исходном уравнении и упростите.
\ [\ begin {align} x — 8 = -11 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -3 — 8 = -11 ~ & \ textcolor {red} {\ text { Заменить} -3 \ text {вместо} x.} \\ -11 = -11 ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \ End {align} \ nonumber \]
Поскольку последняя строка проверки является истинным утверждением, это подтверждает, что −3 является решением.
Упражнение
Решите относительно x : x — 2 = −7
- Ответ
х = −5
Иногда необходимо немного упростить задачу, прежде чем начинать процесс решения.
Пример 4
Решите относительно y : −8 + 2 = y -11 (−4).
Решение
Во-первых, упростим обе части уравнения.
\ [\ begin {align} -8 + 2 = y -11 (-4) ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -6 = y — (- 44) ~ & \ begin {array} {l} \ textcolor {red} {\ text {Упростить. Слева} -8 + 2 = -6.} \\ \ textcolor {red} {\ text {Справа} 11 (-4) = -44.} \ End {array} \\ -6 = y + 44 — 44 ~ & \ textcolor {red} {\ text {Вычтите 44 из обеих частей уравнения.}} \\ -6 + (-44) = y ~ & \ textcolor {red} {\ text {Выражение вычитания как сложения. Упростите справа.}} \\ -50 = y \ end {align} \ nonumber \]
Чтобы проверить решение, замените -50 на y в исходном уравнении и упростите.
\ [\ begin {align} -8 + 2 = y -11 (-4) ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -8 + 2 = -50 -11 (-4 ) ~ & \ textcolor {red} {\ text {Substitute} -50 \ text {for} y.} \\ -6 = -50 — (- 44) ~ & \ textcolor {red} {\ text {Быстрое вычитание при право как дополнение.}} \\ -6 = -6 ~ & \ textcolor {red} {\ text {Справа добавьте:} -50 + 44 = -6.} \ End {align} \ nonumber \]
Поскольку последняя строка проверки является истинным утверждением, это подтверждает, что -50 является решением.
Упражнение
Решить относительно y : y + 2 (−4) = −8 + 6
- Ответ
y = 6
Умножение или деление на одинаковую сумму
Сложение и вычитание — не единственный способ составить эквивалентное уравнение.
Получение эквивалентных уравнений
Умножение обеих сторон уравнения на одинаковую величину. Если мы начнем с уравнения
\ [a = b, \ nonumber \]
, затем умножение обеих частей уравнения на c дает эквивалентное уравнение
\ [a \ cdot c = b \ cdot c, \ text {или эквивалентно} ac = bc, \ nonumber \]
при условии c 0.
Разделение обеих сторон уравнения на одно и то же количество. Если мы начнем с уравнения
\ [a = b, \ nonumber \]
, затем разделив обе части уравнения на c, получим эквивалентное уравнение
\ [\ frac {a} {c} = \ frac {b} {c}, \ nonumber \]
при условии c 0.
То есть умножение или деление обеих частей уравнения на одинаковую величину не изменит решения уравнения.
Пример 5
Решите относительно x : −3 x = 30.
Решение
Чтобы отменить эффект умножения на −3, разделите обе части уравнения на −3.
\ [\ begin {align} -3x = 30 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ \ frac {-3x} {- 3} = \ frac {30} {- 3} ~ & \ textcolor {red} {\ text {Разделите обе стороны на} -3.} \\ x = -10 ~ & \ begin {array} {l} \ textcolor {red} {\ text {Слева,} -3 \ text {times} x, \ text {разделить на} -3 \ text {is} x.} \\ \ textcolor {red} {\ text {Справа} 30 / (- 3) = — 10 .} \ конец {массив} \ конец {выровненный} \ nonumber \]
Чтобы проверить решение, подставьте −10 вместо x в исходном уравнении и упростите.
\ [\ begin {align} -3x = 30 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -3 (-10) = 30 ~ & \ textcolor {red} {\ text {Заменить } -10 \ text {for} x.} \\ 30 — 30 ~ & \ textcolor {red} {\ text {Simplify.}} \ End {align} \ nonumber \]
Поскольку последняя строка проверки является истинным утверждением, это подтверждает, что -10 является решением.
Упражнение
Решить относительно z : −4z = −28
- Ответ
z = 7
Пример 6
Решите относительно x : \ (\ frac {x} {- 2} = -20 \).
Решение
Чтобы отменить эффект деления на −2, умножьте обе части уравнения на −2.
\ [\ begin {align} \ frac {x} {- 2} = -20 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -2 \ left (\ frac {x} {- 2} \ right) — -2 (-20) ~ & \ textcolor {red} {\ text {Умножьте обе стороны на} -2.} \\ x = 40 ~ & \ begin {array} {l} \ textcolor { red} {\ text {Слева} x \ text {делится на} -2, \ text {умножается на} -2,} \\ \ textcolor {red} {\ text {результат} x.\ text {Справа} -2 (-20) = 40.} \ end {array} \ end {align} \ nonumber \]
Чтобы проверить решение, замените 40 на x в исходном уравнении и упростите.
\ [\ begin {align} \ frac {x} {- 2} = -20 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ \ frac {40} {- 2} = -20 ~ & \ textcolor {red} {\ text {Заменить 40 на} x.} \\ -20 = -20 ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \ end {align} \ nonumber \ ]
Поскольку последняя строка проверки является истинным утверждением, это подтверждает, что 40 является решением.
Объединение операций
Вспомните обсуждение «Заворачивать» и «Распаковывать» из Раздела 1.6. Чтобы обернуть подарок, мы: (1) надеваем подарочную бумагу, (2) наклеиваем ленту и (3) надеваем декоративный бант. Чтобы развернуть подарок, мы должны «отменить» каждый из этих шагов в обратном порядке. Следовательно, чтобы развернуть подарок, мы: (1) снимаем декоративный бант, (2) снимаем ленту и (3) снимаем подарочную бумагу.
Теперь представьте машину, которая принимает входные данные, а затем: (1) умножает входные данные на 2 и (2) добавляет 3 к результату.Эта машина изображена слева на Рисунке 2.16.
Рисунок 2.16: Вторая машина «разворачивает» первую.Чтобы «развернуть» эффект машины слева, нам понадобится машина, которая «отменяет» каждый из шагов первой машины, но в обратном порядке. Машина для «разворачивания» изображена справа на рис. 2.16. Сначала он вычитает три из своих входных данных, а затем делит результат на 2. Обратите внимание, что каждая из этих операций «отменяет» соответствующую операцию первой машины, но в обратном порядке.
Например, поместите целое число 7 в первую машину слева на рис. 2.16. Сначала мы удваиваем 7, затем прибавляем к результату 3. Результат: 2 (7) + 3 = 17.
Теперь, чтобы «развернуть» этот результат, мы помещаем 17 во вторую машину. Сначала вычитаем 3, затем делим на 2. Результатом будет (17 — 3) / 2 = 7, исходное целое число, введенное в первую машину.
Теперь рассмотрим уравнение
\ [2x + 3 = 7. \ Nonumber \]
Слева порядок операций требует, чтобы мы сначала умножили x на 2, а затем прибавили 3.Чтобы решить это уравнение относительно x, мы должны «отменить» каждую из этих операций в обратном порядке. Таким образом, мы (1) вычтем три из обеих частей уравнения, затем (2) разделим обе части полученного уравнения на 2.
\ [\ begin {align} 2x + 3 — 3 = 7 — 3 ~ & \ textcolor {red} {\ text {Вычтите 3 с обеих сторон.}} \\ 2x = 4 ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \\ \ frac {2x} {2} = \ frac {4} {2} ~ & \ textcolor {red} {\ text {Разделите обе стороны на 2.}} \\ x = 2 ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \ конец {выровнено} \ nonumber \]
Читатели должны проверить это решение в исходном уравнении.
Пример 7
Решите относительно x : \ (\ frac {x} {4} — 3 = -7 \).
Решение
Слева порядок операций требует, чтобы мы сначала разделили x на 4, а затем вычли 3. Чтобы решить это уравнение для x , мы должны «отменить» каждую из этих операций в обратном порядке. Таким образом, мы (1) прибавим 3 к обеим сторонам уравнения, затем (2) умножим обе части полученного уравнения на 4.
\ [\ begin {align} \ frac {x} {4} — 3 = -7 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ \ frac {x} {4} — 3 + 3 = -7 + 3 ~ & \ textcolor {red} {\ text {Добавить 3 с обеих сторон.}} \\ \ frac {x} {4} = -4 ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \\ 4 \ left (\ frac {x} {4} \ right) = 4 (-4) ~ & \ textcolor {red} {\ text {Умножаем обе стороны на 4.}} \\ x = -16 ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \ End {align} \ nonumber \]
Чек
Замените −16 вместо x в исходном уравнении.
\ [\ begin {align} \ frac {x} {4} — 3 = 7 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ \ frac {-16} {4} — 3 = -7 ~ & \ textcolor {red} {\ text {Substitute} -16 \ text {for} x.} \\ -4 -3 = -7 ~ & \ textcolor {red} {\ text {Сначала разделить:} — 16/4 = -4.} \\ -7 = — 7 ~ & \ textcolor {красный} {\ text {Subtract:} -4 -3 = -7.} \ End {align} \ nonumber \]
Поскольку последняя строка проверки является истинным утверждением, −16 является решением исходного уравнения.
Упражнение
Решить относительно x :
\ [\ frac {x} {2} + 6 = 4 \ nonumber \]
- Ответ
х = -4
Пример 8
Решить относительно t : 0 = 8-2 t .
Решение
Справа порядок операций требует, чтобы мы сначала умножили t на −2, а затем прибавили 8. Чтобы решить это уравнение относительно t, мы должны «отменить» каждую из этих операций в обратном порядке. Таким образом, мы (1) вычтем 8 из обеих частей уравнения, затем (2) разделим обе части полученного уравнения на −2.
\ [\ begin {align} 0 = 8 -2t ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ 0-8 = 8 — 2t — 8 ~ & \ textcolor {red} {\ text {Вычтите 8 с обеих сторон.}} \\ -8 = -2t ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \\ \ frac {-8} {- 2} = \ frac {-2t} {- 2} ~ & \ textcolor {red} {\ text {Разделите обе стороны на 2.}} \\ 4 = t ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \ end {align} \ nonumber \]
Чек
Замените t на 4 в исходном уравнении.
\ [\ begin {align} 0 = 8 — 2t ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ 0 = 8 — 2 (4) ~ & \ textcolor {red} {\ text { Заменить 4 на} t.} \\ 0 = 8-8 ~ & \ textcolor {red} {\ text {Сначала умножить: 2 (4) = 8.}} \\ 0 = 0 ~ & \ textcolor {red} {\ text {Вычесть:} 8-8 = 0.} \ End {выровнено} \ nonumber \]
Поскольку последняя строка в проверке является истинным утверждением, 4 является решением исходного уравнения.
Упражнение
Решить относительно r : 0 = 9 + 3 r
- Ответ
r = -3
Пример 9
Решите относительно p : \ (- 12 + 3 = -8 + 4 + \ frac {p} {- 3}.\)
Решение
Всегда упрощайте, когда это возможно.
\ [\ begin {align} -12 + 3 = -8 + 4 + \ frac {p} {- 3} ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ -9 = -4 + \ frac {p} {- 3} ~ & \ textcolor {red} {\ text {Упростить обе стороны.}} \ end {align} \ nonumber \]
Справа порядок операций требует, чтобы мы сначала разделили p на −3, а затем прибавили −4. Чтобы решить это уравнение для p , мы должны «отменить» каждую из этих операций в обратном порядке.Таким образом, мы (1) добавим положительное число 4 к обеим сторонам уравнения, затем (2) умножим обе части полученного уравнения на −3.
\ [\ begin {align} -9 + -4 = -4+ \ frac {p} {- 3} + 4 ~ & \ textcolor {red} {\ text {Добавьте 4 с обеих сторон.}} \\ — 5 = \ frac {p} {- 3} ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \\ -3 (-5) = -3 \ left (\ frac {p} {- 3 } \ right) ~ & \ textcolor {red} {\ text {Умножьте обе стороны на} -3.} \\ 15 = p ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \ end {выровнено } \ nonumber \]
Чек
Замените 15 на p в исходном уравнении.
\ [\ begin {align} -12 + 3 = = 8 + 4 + \ frac {p} {- 3} ~ & \ textcolor {red} {\ text {Исходное уравнение}} \\ -12 + 3 = -8 + 4 + \ frac {15} {- 3} ~ & \ textcolor {red} {\ text {Заменить 15 на} p.} \\ -9 = -8 + 4 + (-5) ~ & \ begin {выравнивается} \ textcolor {red} {\ text {Слева добавьте:} -12 + 3 = -9. \ text {На полосе}} \\ \ textcolor {red} {\ text {right, DivX:} 15 / (- 3) = -5.} \ end {align} \\ -9 = -4 + (-5 ) ~ & \ textcolor {red} {\ text {Справа} -8 + 4 = -4.} \\ -9 = -9 ~ & \ textcolor {red} {\ text {Справа добавьте: } -4 + (-5) = -9.} \ конец {выровнено} \ nonumber \]
Поскольку последняя строка в проверке является истинным утверждением, 15 является решением исходного уравнения.
Упражнение
Решить относительно q :
\ [\ frac {q} {- 2} -9 = -8 + 3 \ nonumber \]
- Ответ
q = −8
Приложения
Давайте посмотрим на некоторые приложения уравнений с целыми числами. Во-первых, мы напоминаем читателям, что решение проблемы со словом должно включать в себя каждый из следующих шагов.
Требования к решению проблем Word
- Настройте словарь переменных. Вы должны сообщить своим читателям, что представляет каждая переменная в вашей проблеме. Это можно сделать несколькими способами:
- Такие утверждения, как «Пусть P представляет периметр прямоугольника».
- Обозначение неизвестных значений переменными в таблице.
- Обозначение неизвестных величин на эскизе или диаграмме.
- Задайте уравнение. Каждое решение проблемы со словом должно включать тщательно составленное уравнение, которое точно описывает ограничения в постановке задачи.
- Решите уравнение. Вы всегда должны решать уравнение, заданное на предыдущем шаге.
- Ответьте на вопрос. Этот шаг легко упустить из виду. Например, в задаче может задаваться вопрос о возрасте Джейн, но решение вашего уравнения дает возраст сестры Джейн, Лиз. Убедитесь, что вы ответили на исходный вопрос, заданный в задаче.Ваше решение должно быть записано в предложении с соответствующими единицами.
- Оглянитесь назад. Важно отметить, что этот шаг не означает, что вы должны просто проверить решение в своем уравнении. В конце концов, возможно, что ваше уравнение неверно моделирует ситуацию проблемы, поэтому у вас может быть действительное решение неправильного уравнения. Важный вопрос: «Имеет ли ваш ответ смысл на основе слов в исходной постановке проблемы».
Пример 10
Банковский счет студента превышен.Сделав свой счет, Аллен обнаруживает, что у него перерасход на 15 долларов. Каков был баланс его счета до его вывода? депозит в размере 120 долларов, он обнаруживает, что на его счету по-прежнему превышена сумма в 75 долларов. Каков был его баланс до внесения депозита?
Решение
В нашем решении мы обращаемся к каждому этапу Требования к решению проблем Word .
1. Настройка словаря переменных . В этом случае неизвестным является исходный баланс на счете студента.Пусть B представляет этот исходный баланс.
2. Установите уравнение. Положительное целое число представляет собой здоровый баланс, а отрицательное число представляет собой избыток средств на счете. После внесения студентом депозита на счету по-прежнему остается более 75 долларов США. Скажем, этот баланс — 75 долларов. Таким образом,
\ [\ begin {array} {ccccc} \ colorbox {cyan} {Исходный баланс} & \ text {plus} & \ colorbox {cyan} {Student Deposit} & \ text {equals} & \ colorbox {cyan} {Текущий Баланс} \\ B & + & $ 120 & = & — $ 75 \ end {array} \ nonumber \]
3. Решите уравнение. Чтобы «отменить» сложение, вычтите 120 из обеих частей уравнения.
\ [\ begin {align} B + 120 = -75 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ B + 120 — 120 = -75 — 120 ~ & \ textcolor {red} { \ text {Вычтите 120 с обеих сторон.}} \\ B = -195 ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \ end {align} \ nonumber \]
4. Ответьте на вопрос. Первоначальный баланс был переоценен до 195 долларов.
5. Оглянись назад. Если исходный баланс был превышен на 195 долларов, то мы позволяем — 195 долларов представлять этот баланс. Студент вносит залог в размере 120 долларов. Добавьте это к исходному балансу, чтобы получить — 195 долларов США + 120 долларов США = — 75 долларов США, правильный текущий баланс.
Упражнение
После снятия 125 долларов со своего счета, Аллен обнаруживает, что у него перерасход на 15 долларов. Каков был баланс его счета до его вывода?
- Ответ
$ 110
Пример 11
Три раза больше, чем определенное число равно −11.Найдите неизвестный номер.
Решение
В нашем решении мы обращаемся к каждому этапу Требования к решению проблем Word .
1. Настройка словаря переменных. Пусть x представляет неизвестное число. 2. Установите уравнение. «Три более чем в два раза больше определенного числа» становится:
\ [\ begin {array} {ccccc} \ colorbox {cyan} {Three} & \ text {more than} & \ colorbox {cyan} {Дважды определенное число} & \ text {is} & \ colorbox {cyan} {-11} \\ 3 & + & 2x & = & 11 \ end {array} \ nonumber \]
3. Решите уравнение. Слева порядок операций требует, чтобы мы сначала умножили x на 2, а затем прибавили 3. Чтобы решить это уравнение относительно x, мы должны «отменить» каждую из этих операций в обратном порядке. Таким образом, мы (1) вычтем 3 из обеих частей уравнения, затем (2) разделим обе части полученного уравнения на 2.
\ [\ begin {align} 3 + 2x = -11 ~ & \ textcolor {red} {\ text {Исходное уравнение.}} \\ 3 + 2x — 3 = -11 — 3 ~ & \ textcolor {red} { \ text {Вычтите 3 с обеих сторон.}} \\ 2x = -14 ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} ~ \\ \ frac {2x} {2} = \ frac {-14} {2} ~ & \ textcolor {red} {\ text {Разделите обе стороны на 2.}} \\ x = -7 ~ & \ textcolor {red} {\ text {Упростите обе стороны.}} \ end {align} \ nonumber \]
4. Ответьте на вопрос. Неизвестное число -7.
5. Оглянитесь назад. Удовлетворяет ли ответ ограничениям задачи? Три больше, чем дважды −7 — это три больше, чем −14 или −11. Значит, решение правильное.
Упражнение \ (\ PageIndex {1} \)
Пять меньше, чем удвоенное определенное число равно −7. Найдите неизвестный номер.
- Ответ
-1
Упражнения
1. Является ли −11 решением 2x + 3 = −19?
2. Является ли −8 решением 2x + 7 = −9?
3. Является ли 6 решением 3x + 1 = 19?
4. Является ли −6 решением 2x + 7 = −5?
5. Является ли 12 решением уравнения 4x + 5 = −8?
6.Является ли −8 решением −3x + 8 = 18?
7. Является ли 15 решением 2x + 6 = −9?
8. Является ли 3 решением −4x + 1 = −20?
9. Является ли −15 решением −3x + 6 = −17?
10. Является ли −18 решением −3x + 9 = −9?
11. Является ли −6 решением −2x + 3 = 15?
12. Является ли 7 решением −3x + 5 = −16?
В упражнениях 13-28 решите заданное уравнение относительно x.
13. х — 13 = 11
14. х — 6 = 12
15. х — 3 = 6
16.х — 3 = −19
17. х + 10 = 17
18. х + 3 = 9
19. х — 6 = 1
20. х — 10 = 12
21. х — 15 = −12
22. х — 2 = 13
23. х + 11 = −19
24. х + 3 = 17
25. х + 2 = 1
26. х + 2 = −20
27. х + 5 = −5
28. х + 14 = −15
В упражнениях 29–44 решите заданное уравнение относительно x.
29. −x = −20
30. 5x = −35
31.\ (\ frac {x} {- 7} \) = 10
32. \ (\ frac {x} {- 6} \) = −20
33. \ (\ frac {x} {- 10} \) = 12
34. \ (\ frac {x} {2} \) = 11
35. \ (\ frac {x} {9} \) = −16
36. \ (\ frac {x} {- 3} \) = −7
37. −10x = 20
38. −17x = −85
39. 14x = 84
40. −10x = −40
41. −2x = 28
42. −14x = 42
43. \ (\ frac {x} {- 10} \) = 15
44. \ (\ frac {x} {- 8} \) = −1
В упражнениях 45-68 решите заданное уравнение относительно x.
45. −4x — 4 = 16
46. −6x — 14 = 4
47. 4x — 4 = 76
48. −5x — 15 = 45
49. 5x — 14 = −79
50,15x — 2 = 43
51. −10x — 16 = 24
52. 2x — 7 = −11
53. 9x + 5 = -85
54. 8x + 8 = −16
55. 7x + 15 = −55
56. 2x + 2 = −38
57. −x + 8 = 13
58. −5x + 20 = −50
59. 12x — 15 = −3
60. −19x — 17 = −36
61.4х — 12 = −56
62. 7x — 16 = 40
63. 19x + 18 = 113
64. −6x + 20 = −64
65. −14x + 12 = −2
66. −9x + 5 = 104
67. 14x + 16 = 44
68. −14x + 10 = −60
69. Двойное меньшее восьмикратного неизвестного числа равно −74. Найдите неизвестный номер.
70. Шесть меньше, чем втрое неизвестное число равно 21. Найдите неизвестное число.
71. Неизвестное число больше восьми раз, если оно равно 0.Найдите неизвестный номер.
72. Неизвестное число в пять раз больше, чем восемь раз, равно −35. Найдите неизвестный номер.
73. Число −6 на 2 больше, чем неизвестное число. Найдите неизвестный номер.
74. Число −4 на 7 больше, чем неизвестное число. Найдите неизвестный номер.
75. Неизвестное число в три раза больше, чем восемь, равное −29. Найдите неизвестный номер.
76. Неизвестное число в четыре раза больше, чем девять раз — 85. Найдите неизвестное число.
77.На первых трех экзаменах Алан набрал 79, 61 и 54 балла. Какой результат Алан должен набрать на следующем экзамене, чтобы он составил 71 балл на всех четырех экзаменах?
78. Бенни набрал 54, 68 и 54 баллов на своих первых трех экзаменах. Какой результат Бенни должен набрать на следующем экзамене, чтобы он составил 61 балл на всех четырех экзаменах?
79. Частное двух целых чисел равно 5. Одно из целых чисел равно −2. Найдите другое целое число.
80. Частное двух целых чисел равно 3. Одно из целых чисел равно −7. Найдите другое целое число.
81.Частное двух целых чисел равно 9. Одно из целых чисел равно −8. Найдите другое целое число.
82. Частное двух целых чисел равно 9. Одно из целых чисел равно −2. Найдите другое целое число.
83. Число −5 на 8 больше, чем неизвестное число. Найдите неизвестный номер.
84. Число −6 на 8 больше, чем неизвестное число. Найдите неизвестный номер.
85. Банковский счет студента превышен. После внесения депозита в размере 260 долларов он обнаруживает, что на его счету по-прежнему превышена сумма в 70 долларов.Каков был его баланс до внесения депозита?
86. Банковский счет студента превышен. После внесения депозита в размере 300 долларов он обнаруживает, что на его счету по-прежнему превышена сумма в 70 долларов. Каков был его баланс до внесения депозита?
87. Банковский счет студента превышен. После внесения депозита в размере 360 долларов он обнаруживает, что на его счету по-прежнему превышена сумма в 90 долларов. Каков был его баланс до внесения депозита?
88. Банковский счет студента превышен.После внесения депозита в размере 260 долларов он обнаруживает, что на его счету по-прежнему превышена сумма в 50 долларов. Каков был его баланс до внесения депозита?
89. Число −10 в −5 раз больше неизвестного числа. Найдите неизвестный номер.
90. Число −3 в −3 раза больше неизвестного числа. Найдите неизвестный номер. 91. Число −15 в −5 раз больше неизвестного числа. Найдите неизвестный номер.
92. Число −16 в 4 раза больше неизвестного.Найдите неизвестный номер.
93. Неизвестное число в два раза меньше девяти и равно 7. Найдите неизвестное число.
94. Неизвестное число в четыре раза меньше, чем в два раза больше, чем 8. Найдите неизвестное число.
95. Марк набрал 79, 84 и 71 балл на своих первых трех экзаменах. Какой должен Марк набрать на следующем экзамене, чтобы он набрал в среднем 74 балла за все четыре экзамена?
96. Алан набрал 85, 90 и 61 баллов на своих первых трех экзаменах. Какой результат Алан должен набрать на следующем экзамене, чтобы в среднем 77 баллов за все четыре экзамена?
Ответы
1.Да
3. Есть
5. №
7. №
9. №
11. Есть
13. 24
15. 9
17. 7
19. 7
21. 3
23. −30
25 -1
27. −10
29. 20
31. −70
33. -120
35. −144
37. −2
39. 6
41. −14
43. -150
45. −5
47.20
49. −13
51,4
53. −10
55. −10
57. −5
59,1
61. −11
63,5
65. 1
67. 2
69. −9
71,4
73. −8
75,4
77. 90
79. −10
81. −72
83,13
85. — 330 долл. США
87. — 450 долларов США
89. 2
91,3
93.1
95.

 Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.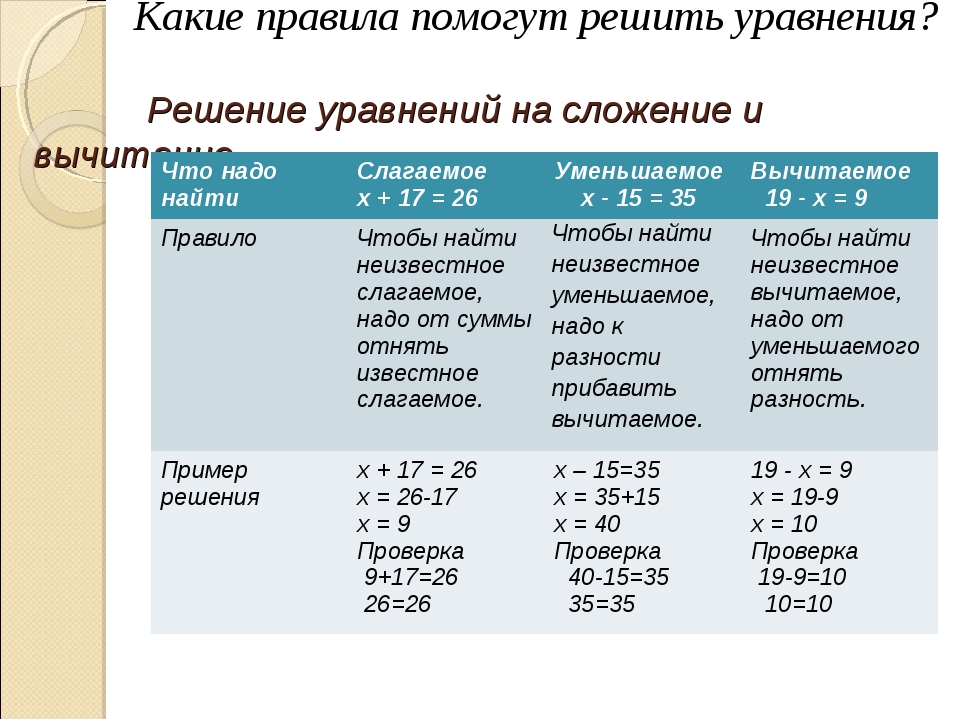

 Умножим каждый член уравнения на х.
Умножим каждый член уравнения на х.
