Решение задач с помощью графов
Прежде чем приступить к решению задач, стоит сказать, что графы, о которых пойдёт речь, к аристократам былых времён никакого отношения не имеют. У наших графов в корне есть греческое слово «графо», что значит «пишу». Этот же корень («граф») встречается, например, в словах «график, «биография», «орфография» и некоторых других.
Давайте выясним понятие графа на примере решения задачи.
В первенстве класса по настольному теннису шесть участников: Андрей, Саша, Вова, Оля, Дима и Лена. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Сашей, Олей и Леной; Саша, как уже говорилось, с Андреем и ещё с Олей; Вова – с Олей, Димой и Леной. Сколько игр уже проведено и сколько ещё осталось?
Итак,
изобразим данные этой задачи в виде схемы. Участников первенства обозначим
точками, расположив их по окружности: Андрей – А, Саша – ЭС, Вова – ВЭ, Оля –
О, Дима – ДЭ, Лена – ЭЛЬ.
Если двое участников уже сыграли между собой, то будем соединять, обозначающие их точки отрезками. В условии задачи сказано, что Андрей сыграл с Сашей, Олей и Леной.
Мы уже видим, что Саша сыграл с Андреем, а ещё он сыграл с Олей.
Вова сыграл с Олей, Димой и Леной.
Получившаяся схема называется графом. Точки А, С, В, О, ДЭ, Л называются вершинами графа. Отрезки, которые соединяют вершины графа, называются рёбрами графа. Каждое ребро соединяет две вершины графа.
При этом обратите внимание, что точки, в которых пересекаются рёбра графа, не являются его вершинами.
У графа 7 рёбер. Это означает, что к настоящему моменту было проведено 7 игр.
Чтобы
найти количество игр, которые осталось провести, продолжим построение этого
графа так, чтобы из каждой точки были проведены рёбра ко всем остальным точкам.
Но для того, чтобы потом легче было подсчитать количество добавленных рёбер,
рисовать их будем другим цветом.
Итак, известно, что Андрей сыграл с Сашей, Олей и Леной. А значит, он не играл с Вовой и Димой.
Также известно, что Саша сыграл с Андреем и с Олей, а значит, он не сыграл с Вовой, Димой и Леной.
Вова сыграл с Олей, Димой и Леной. Получается, что он не сыграл с Андреем и Сашей. Но соответствующие отрезки уже проведены.
Оля сыграла с Андреем и Сашей, а также с Вовой. Это значит, что она ещё не сыграла с Димой и Леной.
Дима сыграл только с Вовой. Ему предстоит сыграть с Олей, Сашей и Андреем, но эти отрезки мы уже провели. Осталось провести отрезок от Димы к Лене.
Лена сыграла с Андреем и Вовой. Ей предстоит сыграть с Димой, Олей и Сашей, но эти отрезки мы уже провели. Больше ничего добавлять не надо.
Мы добавили 8 рёбер. Это значит, что осталось провести ещё 8 игр. Получается, что ответ на вопрос задачи будет таким: проведено 7 игр, осталось провести 8 игр.
Отметим,
что граф для одной и той же задачи можно нарисовать разными способами. И
наоборот, для разных задач можно нарисовать одинаковые по виду графы.
И
наоборот, для разных задач можно нарисовать одинаковые по виду графы.
Также отметим, что иногда рёбра удобнее изображать не отрезками, а «дугами».
Граф можно представить как набор пуговиц, некоторые из которых соединены нитями. Пуговицы – это вершины графа, нити – его рёбра.
При этом, где именно расположены пуговицы, и как проходят нити не важно, ведь граф от этого не меняется. Важно то, какие пары пуговиц (то есть вершин графа) соединены нитями.
Но при решении задач, подобных приведённой, удобнее всё-таки располагать вершины по окружности. Тогда при проведении рёбер рисунок получается не таким запутанным.
Если из вершины графа выходит чётное количество рёбер, то её называют чётной. А если из вершины графа выходит нечётное количество рёбер, то её называют нечётной.
Посмотрите на такой граф.
У него вершины 1 и 4 являются нечётными, так как из них выходят по 3 ребра.
А
вот вершины 2, 3 и 5 являются чётными, так как из вершины под номером 2
выходят 4 ребра, из вершины под номером 3 тоже выходят 4 ребра, а из вершины
под номером 5 выходят 2 ребра.
Решим следующую задачу. Встретились три подруги: Белова, Чернова и Краснова. На одной из них было чёрное платье, на другой – красное, на третьей – белое. Девочка в белом платье говорит Черновой: «Нам надо поменяться платьями, а то у всех троих цвет платьев не соответствует фамилиям». Кто в какое платье был одет?
На одном из наших занятий было предложено решить эту задачу с помощью таблицы. Давайте решим её с помощью рисунка.
Обозначим фамилии девочек буквами. Пусть напротив буквы Б будет белое платье, напротив буквы Ч – чёрное, напротив буквы К – красное.
Соединим пунктирной линией букву Б и белое платье. Это означает, что Белова не в белом платье. Также соединим пунктирными линиями букву Ч и чёрное платье, букву К и красное платье. Это означает, что Чернова не в чёрном платье, а Краснова не в красном платье.
В условии задачи говорится, что девочка в
белом платье говорит Черновой: «Нам надо поменяться
платьями, а то у всех троих цвет платьев не соответствует фамилиям».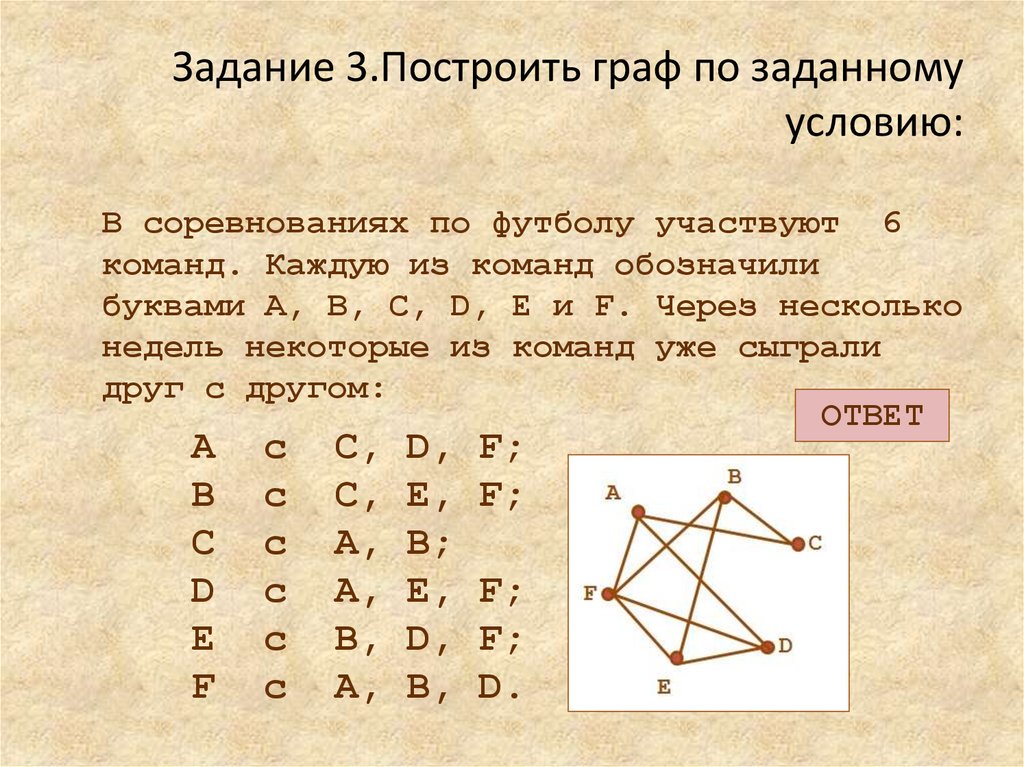 Получается, что Чернова одета не в
белое платье. Поэтому
соединим букву Ч с белым платьем пунктирной линией.
Получается, что Чернова одета не в
белое платье. Поэтому
соединим букву Ч с белым платьем пунктирной линией.
Теперь, внимательно посмотрев на рисунок, становится понятно, что ни Белова, ни Чернова не одеты в белое платье. Значит, в белое платье одета Краснова. Поэтому соединим букву К и белое платье сплошной линией.
Так как на Чернова была одета не в белое платье, а также на ней не могло быть чёрного платья, то, следовательно, она была в красном платье. Соединим сплошной линией букву Ч и красное платье.
Мы выяснили, что Краснова была в белом платье, а Чернова была в красном. А значит, Белова была в чёрном платье. Соединим букву Б и чёрное платье сплошной линией.
Ответ на вопрос задачи будет таким: Белова была одета в чёрное платье, Чернова – в красное платье, Краснова – в белое платье.
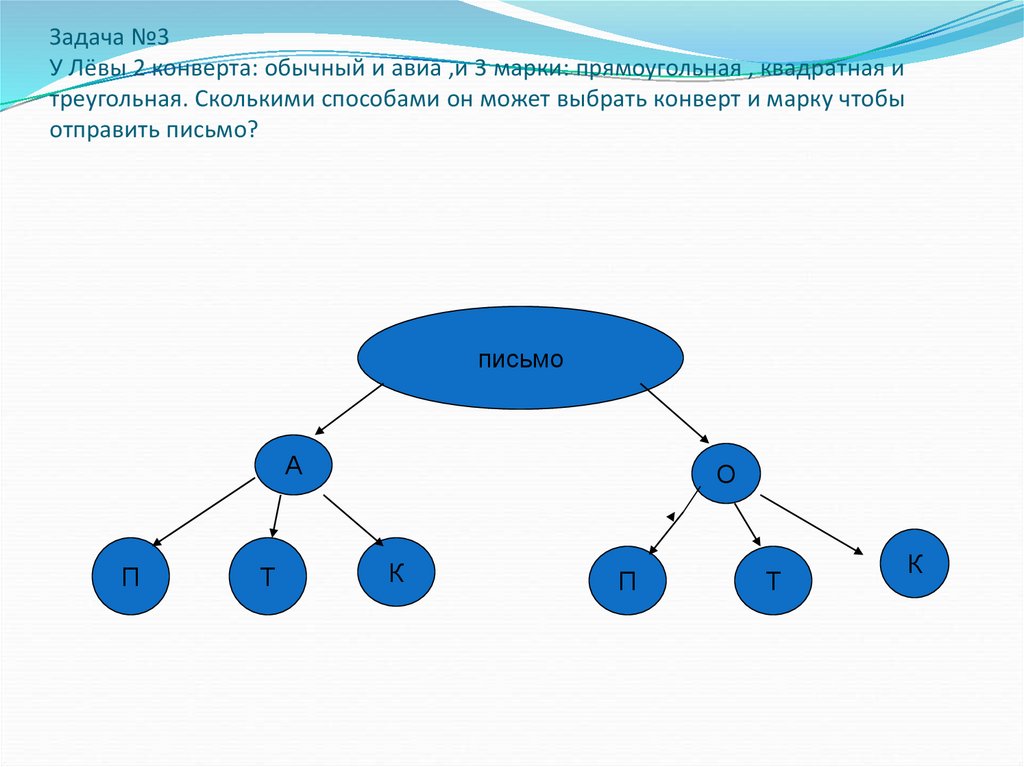
И решим ещё одну задачу. Из города А в город Б ведут 3 дороги, а из города Б в город Б – 4 дороги. Сколькими способами можно проехать из города А в город В, если по пути надо обязательно заехать в город Б?
Решение.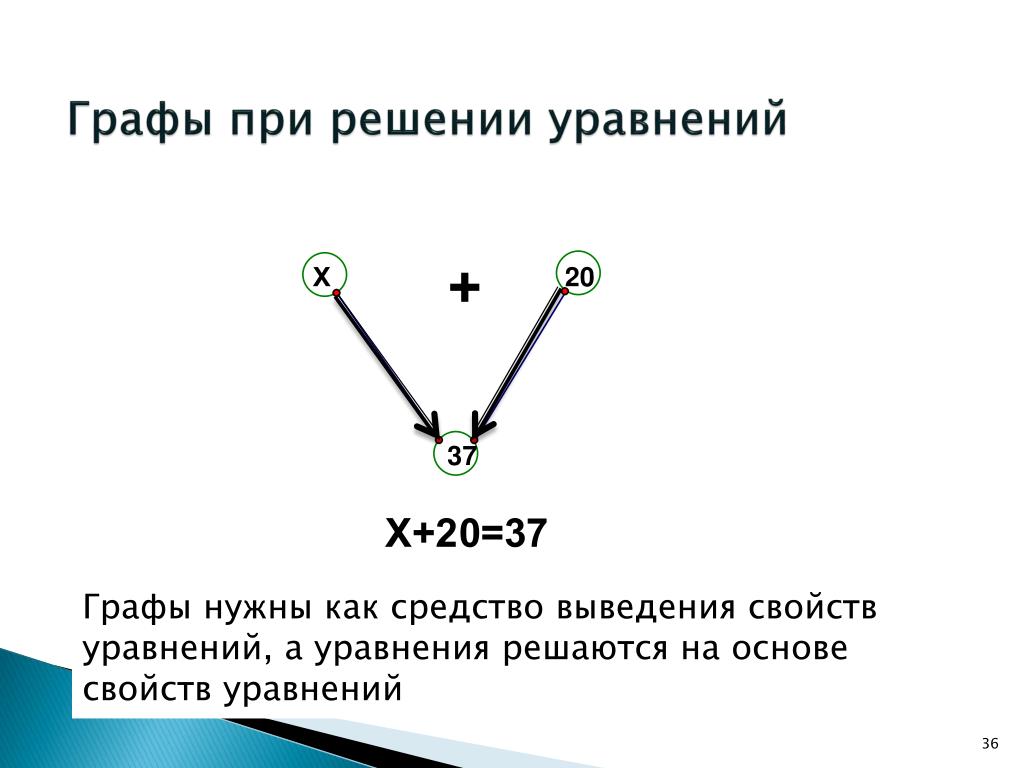 Отметим точками города А, Б и В. В условии задачи сказано, что из города А в
город Б ведут 3 дороги. Также сказано, что из города Б в город В ведут 4 дороги.
Отметим точками города А, Б и В. В условии задачи сказано, что из города А в
город Б ведут 3 дороги. Также сказано, что из города Б в город В ведут 4 дороги.
Возьмём одну дорогу, которая ведёт из города А в город Б. Её можно продолжить до города В четырьмя различными способами.
Если взять вторую дорогу, которая ведёт из города А в город Б, то и её можно продолжить до города В четырьмя различными способами.
То же самое можно сказать и про третью дорогу, ведущую из города А в город Б, то есть её также можно продолжить до города В четырьмя способами.
Получается, что по какой бы из трёх дорог из города А в город Б мы не поехали, продолжить дорогу в город В можно четырьмя способами.
Таким образом, из города А в город В через город Б можно проехать 3 умножить на 4, то есть 12 способами.
Ответ: 12 способов.
Решение задач по теории вероятностей с помощью графов
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Сандый С. А. 1
А. 1
1Муниципальное бюджетное общеобразовательное учреждение Чербинская средняя общеобразовательная школа муниципального района «Кызылский кожуун» республики Тыва
Сандый А.К. 1
1Муниципальное бюджетное общеобразовательное учреждение Чербинская средняя общеобразовательная школа муниципального района «Кызылский кожуун» республики Тыва
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Актуальность исследования заключается в том, что данная тема недостаточно еще изучена, использование метода решения задач с помощью графов не входит в школьную программу.
При использовании графов, решение задач упрощается. Задачи в виде графа дают возможность наглядно и достаточно просто представить данные.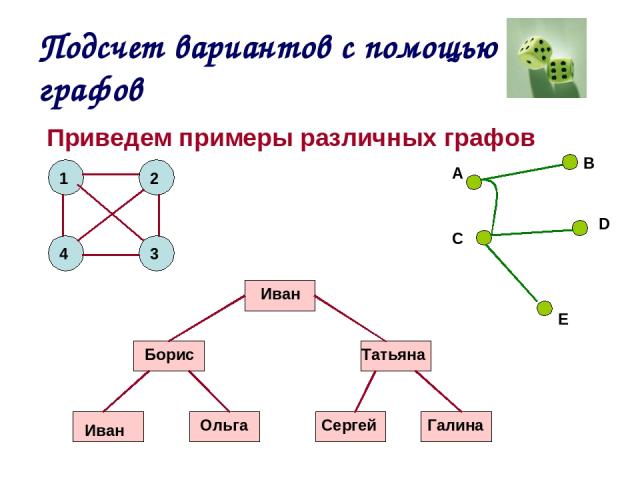
Примерами графов служат схемы метрополитена, железных или шоссейных дорог, структурные формулы молекул, планы выставок и т. д., то есть схемы и планы (или карты) без указанных масштабов, показывающие связь между принадлежащими им объектами.
Целью исследования является ознакомление с понятием графа, с теорией вероятностей, решение задач по теории вероятностей с помощью графов, изучение литературы по данной теме и расширение математического кругозора.
Чтобы достичь цели, были поставлены следующие задачи:
Дать определение графов и его составляющих;
Рассмотреть некоторые виды графов и их свойства;
Рассмотреть основные положения теории графов, а также теоремы, лежащие в основе данной теории с доказательством;
Изучить подробно теорию вероятностей;
Решить задачи по теории вероятностей с помощью графов;
Определить области применения теории графов и теории вероятностей в окружающей действительности.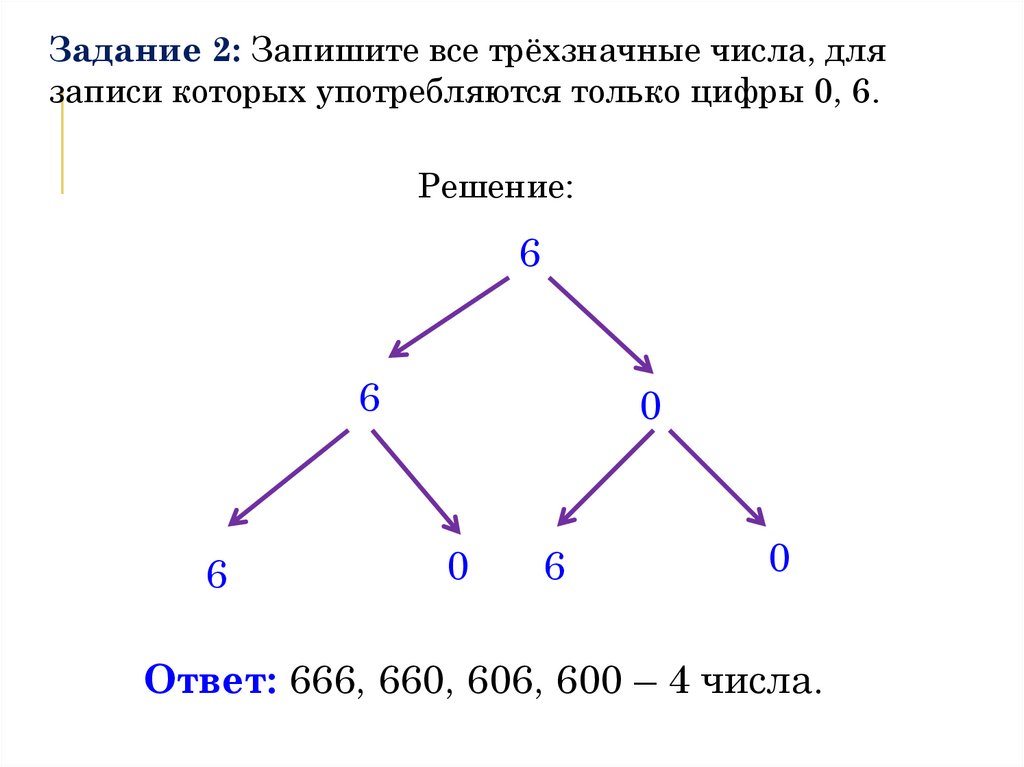
Объект исследования: теория вероятностей и графы.
Предмет исследования: задачи по теории вероятностей.
Гипотеза: с помощью графов можно решить задачи по теории вероятностей.
Для решения поставленных задач были использованы следующие методы исследования: сбор информации, анализ, решение задач.
В первой и второй главе представлены определение, основные понятия и формулы теории вероятностей и графов, а также историю возникновения теории вероятностей и графов.
Глава 1. Теория вероятностей
История
История теории вероятностей начинается с давних времен. Известно, что в древнейших государствах Египте, Греции, Китае и Индии уже использовались некоторые элементы рассуждений вероятности, которые использовались для переписи населения и для того, чтобы определить численность войска неприятеля.
Первые работы по теории вероятности, принадлежащие французским учёным Б. Паскалю и П. Ферма, голландскому учёному X. Гюйгенсу, появились в связи с подсчётом различных вероятностей в азартных играх. Успех теории вероятностей связан с именем швейцарского математика Я. Бернулли (1654-1705 гг.). Он открыл знаменитый закон больших чисел: дал возможность установить связь между вероятностью какого-либо случайного события и частотой его появления, наблюдаемой непосредственно из опыта. Следующий период истории теории вероятностей (XVIII в. и начало ХIХ в.) связан с именами А. Муавра, П. Лапласа, К. Гаусса и С. Пуассона. В этот период теория вероятностей находит ряд применений в естествознании и технике. Третий период истории теории вероятностей (вторая половина XIX в.) связан в основном с именами русских математиков П. Л. Чебышева, А. М. Ляпунова. Наиболее распространённая в настоящее время логическая схема построения основ теории вероятностей разработана в 1933 году математиком А. Н. Колмогоровым.
Н. Колмогоровым.
Определение и основные формулы
Основным понятием теории вероятностей является вероятность. Это слово часто применяется в повседневной жизни. Каждому знакомы фразы: «Завтра, вероятно, подует ветер», или «вероятнее всего завтра утром мы поедем на озеро». В словаре С.И.Ожегова дано толкование слова вероятность как «возможности осуществления чего-нибудь». И здесь же представлено определение понятию теории вероятностей как «разделу математики, изучающей закономерности, основанные на взаимодействии большого числа случайных явлений».
Теория вероятностей — раздел математики, который изучает закономерности в случайных явлениях.
Случайное явление – это явление с неопределенным исходом, происходящее при неоднократном воспроизведении определенного комплекса событий [4:7].
Событие называется достоверным, если в в результате испытания оно обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости.
Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости.
Случайным называют событие, которое при осуществлении некоторых испытаний может произойти или не произойти. Например, при однократном бросании игральной кости может выпасть число 1 или не выпасть, то есть событие является случайным, потому что оно может произойти, а может и не произойти.
Невозможным называют событие, которое в результате испытания произойти не может. Например, невозможным является выпадение числа 7 при бросании игрального кубика.
Равновозможные события – это события, которые при данных условиях имеют одинаковые шансы для наступления. Например, при подбрасывании монеты событие А (появление цифры) и событие В (появление герба) равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную форму и наличие чеканки не влияет на то, какая сторона монеты (герб или цифра) окажется верхней.
Каждое событие, которое может наступить в итоге испытания, называется элементарным исходом. Элементарные исходы, при котором данное событие наступает, называется благоприятным этому событию [2:5]
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов испытания, в котором может появиться это событие.Вероятность события А обозначают Р(А) (здесь Р –первая буква французского слова probabilite — вероятность). В соответствии с определением
Р(А) = ,
где m – число элементарных исходов, благоприятствующих данному событию А; n — число всех равновозможных исходов испытания, образующих полную группу событий.
Это определение вероятности называют классическим определением вероятности. Оно применяется, когда теоретически удается выявить все равновозможные исходы испытания и определить благоприятствующие исследуемому испытанию исходы.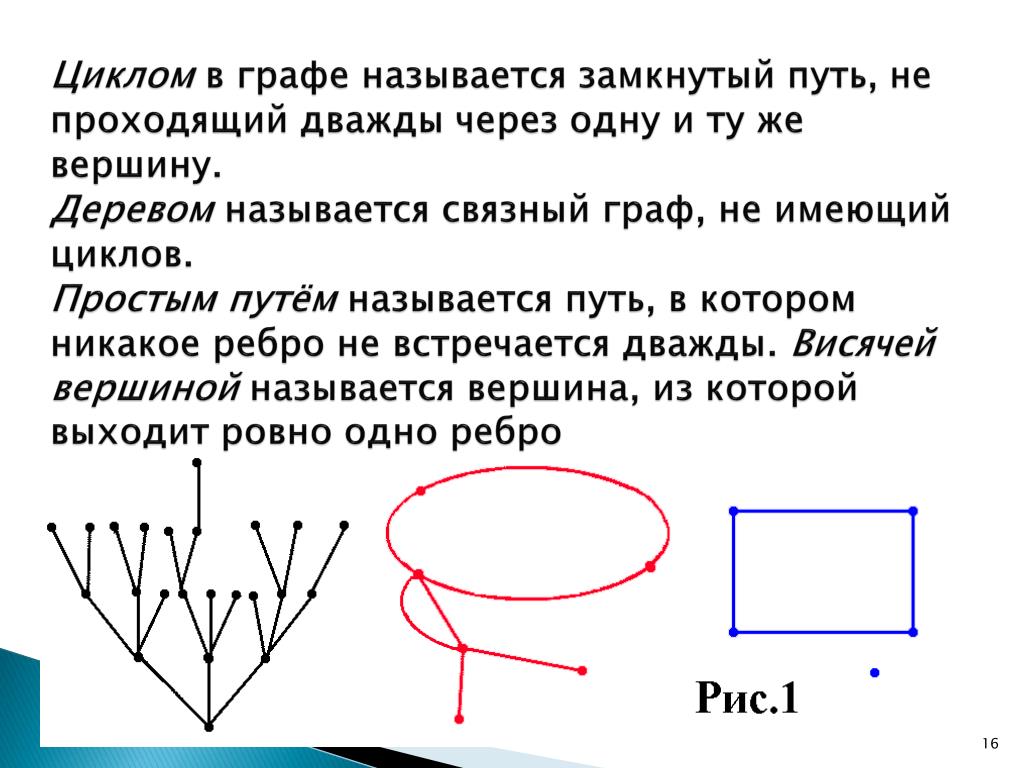
Вероятность события имеет следующие свойства:
Вероятность достоверного события равна единице. Обозначим досиоверное событие буквой В. Для достоверного события m = n, поэтому Р(В) = 1.
Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой V. Для невозможного события m = 0, поэтому Р (V) = 0.
Вероятность случайного события выражается положительным числом, меньшим единицы. Поскольку для случайного события А выполняется неравенство 0<m<n, или , то 0 < P(A) < 1.
Вероятность любого события В удовлетворяет неравенствам [2:9].
Классическое определение вероятности предполагает, что все элементарные исходы равновозможны. Однако, на практике часто встречаются испытания, число равновозможных исходов которых очень велико. Например, без многократного подбрасывания кнопки трудно определить, равновозможны ли ее падения «на плоскость» или на «острие». Поэтому используется и статистическое определение вероятности. Статистической вероятностью называют число, около которого группируются значения частоты события W(A) в различных сериях большого числа испытаний. Частотой события называется отношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов.
Поэтому используется и статистическое определение вероятности. Статистической вероятностью называют число, около которого группируются значения частоты события W(A) в различных сериях большого числа испытаний. Частотой события называется отношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов.
Статистическое определение обладает следующими свойствами:
Вероятность достоверного события равна 1.
Вероятность невозможного события равно нулю.
Вероятность случайного события заключена между нулем и единицей.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий [2:21].
Вероятность того, что в серии из n независимых испытаний событие А появилось ровно k раз (и не появлялось n-k раз), обозначим через
P(k)= , где .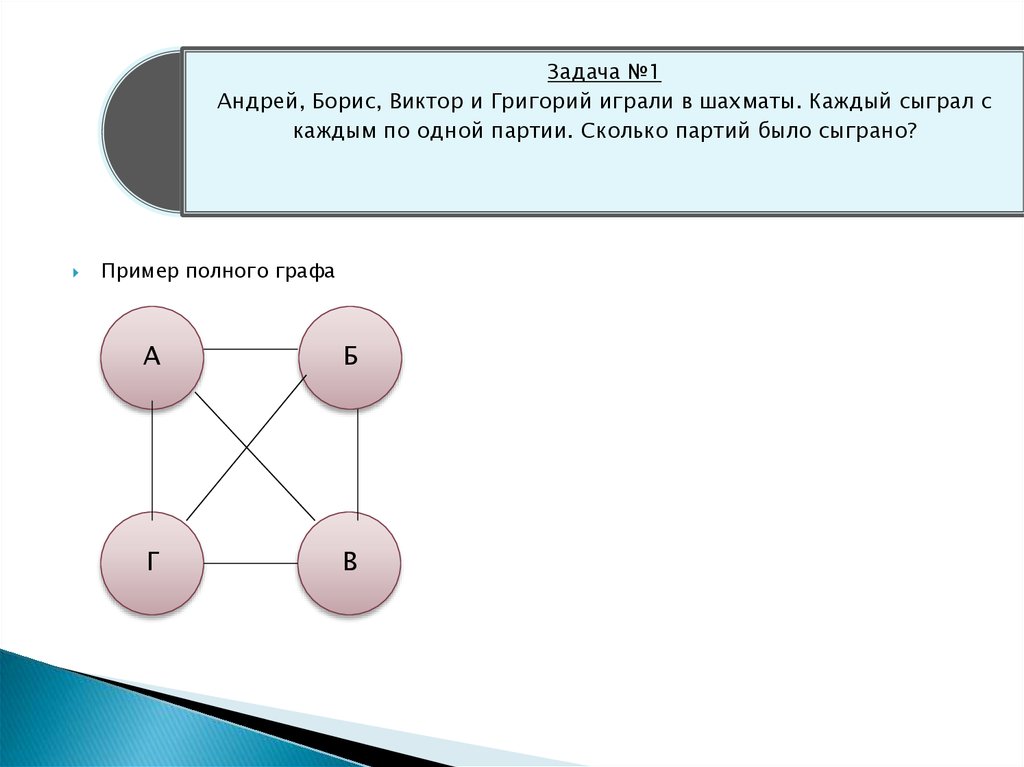
Данная формула называется формулой Бернулли [2:173] — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Названа в честь выдающегося швейцарского математика Якоба Бернулли, который и вывел формулу.
Глава 2. Графы
История возникновения графов
Огромный вклад в развитие математики внес российский, немецкий и швейцарский ученый Леонард Эйлер. История появления графов связана с его именем. Задачу о Кенигсбергских мостах составил именно он.
В городе Кенигсберге (ныне Калининград) протекает река Прегель, через которую построены мосты, связывающие все районы города. Во время прогулки по городу Эйлер захотел пройти по всем мостам, причем по каждому только один раз. Однако ему это не удалось. Вернувшись домой, ученый составил схему, изобразил участки суши точками, а мосты отрезками, это и был первый граф.
2.2. Понятие графа
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел математики, в котором системно изучают свойства графов.
Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – ребрами. Примерами графов могут служить любая карта дорог, схема метро, как было упомянуто выше, электросхема, чертеж многоугольника и т.д. Графы строят для того, чтобы визуально представить сложные взаимодействия.
Два ребра называются смежными, если у них есть общая вершина.
Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
Ребро называется петлей, если его концы совпадают.
Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра.
Вершина называется висячей, если из неё выходит ровно одно ребро.
Граф без кратных ребер и петель называется обыкновенным. [1]
Графы бывают полными и неполными. Полный граф — это простой граф, каждая пара различных вершин которого смежна. Неполный граф – это граф, в котором хотя бы 2 вершины не смежны.
Г раф, являющийся неполным, можно преобразовать в полный с теми же вершинами, добавив недостающие рёбра. Проведя недостающие рёбра, получим полный граф. Вершины графа Г и рёбра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа Г и обозначают его Г.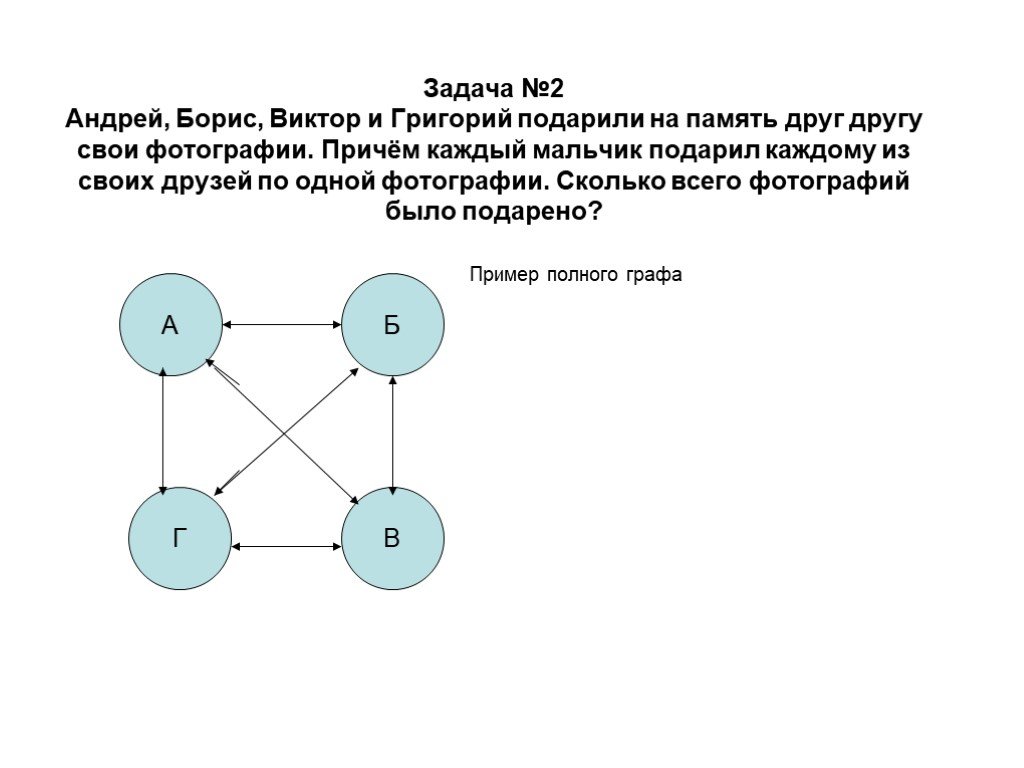
Г : Г:
Д ополнением графа Г называется граф Г с теми же вершинами, что и граф Г, и с теми и только с теми рёбрами, которые необходимо добавить графу Г, чтобы получился полный граф. Вершина называется нечётной, если её степень – число нечётное. Вершина называется четной, если её степень – четное число [5:63].
2.3.Виды графов:
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
Ориентированный (ребрам присвоено направление)
Неориентированный (у ребер нет направлений)
Смешанный (встречаются как ориентированные, так и неориентированные рёбра)
Связный (между любой парой вершин этого графа существует как минимум одно ребро)
— несвязный граф
Дерево (между любой парой вершин имеется только по одному пути)
Двудольный (множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.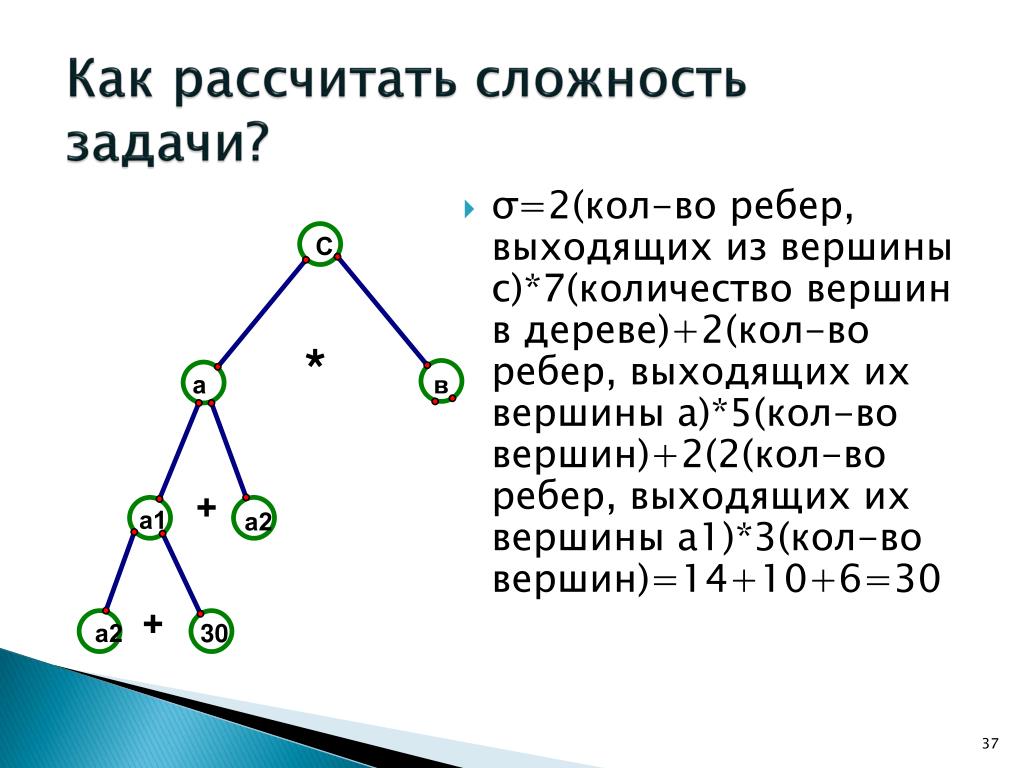 )
)
Эйлеров граф (в нём каждая вершина должна иметь только чётное число рёбер)
Взвешенный (каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра)
Глава 3. Решение задач по теории вероятностей
с помощью графов
В этой работе при решении задач по теории вероятности мы будем пользоваться только ориентированными графами
Правило вычисления вероятности по вероятностному графу
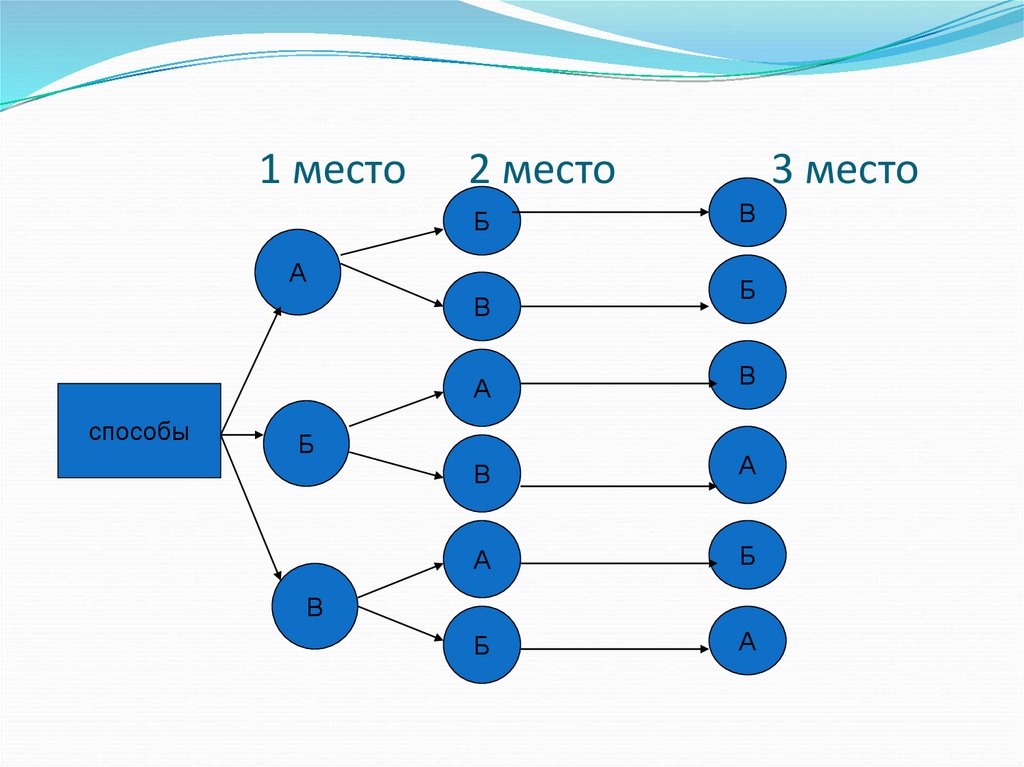
вероятность попадания в конечную вершину (вероятность исхода) можно вычислить, перемножая вероятности, встречаемые на ребрах соответствующего маршрута (рис. 1, жирный маршрут) [3:3];
2) если же нас интересует вероятность события, которому благоприятствуют несколько исходов, то вероятности соответствующих конечных вершин складываются (рис. 2, жирные маршруты) [3:3].
2, жирные маршруты) [3:3].
Задача 1: Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие в поле F или в болото М. Найдите вероятность того, что Павел Иванович забредет в болото?
Решение:
Построим вероятностный граф:
Пусть событие М — Павел Иванович забредет в болото. Этому событию на графе благоприятствуют три маршрута. Воспользуемся формулой , получим
Ответ: 0,42
Задача 2: Ковбой Джон попал в муху на стене с вероятностью 0,9, если стрелял их пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 2 пристрелянных. Ковбой видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху.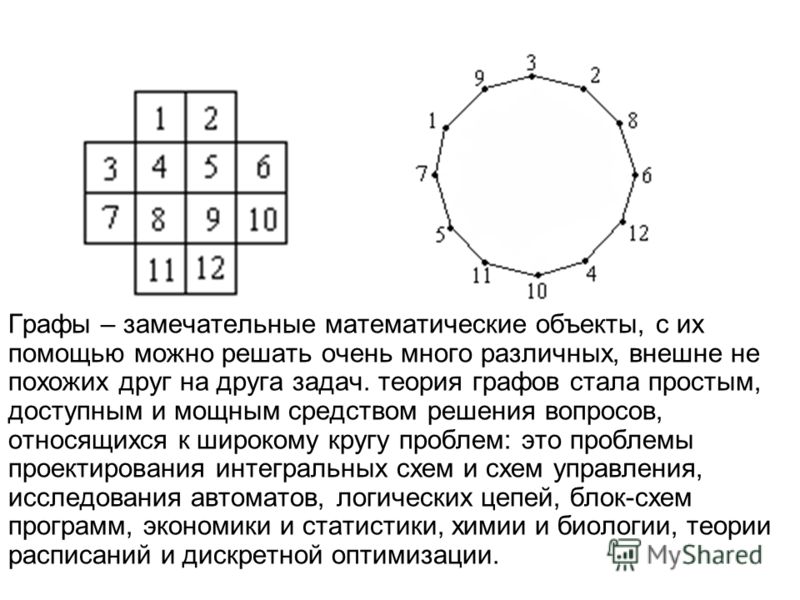 Найдите вероятность того, что Джон промахнется.
Найдите вероятность того, что Джон промахнется.
Решение:
Пусть событие А – Джон промахнулся
Построит вероятностный граф, где П – пристрелянный пистолет, Н – непристрелянный пистолет, «+» — попал, «-» — не попал.
То, что Джон взял пристрелянный револьвер, равен 0,2, а непристрелянный – 1-0,2=0,8. Из условия задачи следует, что с пристрелянным револьвером Джон попадает с вероятность. 0,9, а непристрелянным 1-0,9=0,1. Также из условия задачи мы знаем, что Джон из непристрелянного револьвера Джон попадает в муху с вероятностью 0,4, следовательно, промахнется 1-0,4=0,6 вероятностью.
Воспользуемся формулой правила 2, получим Р(А) = 0,2*0,1+0,8*0,6 = 0,02+0,48 = 0,5
Ответ: 0,5
Задача 3: В волшебной стране бывает 2 типа погоды: хорошая и замечательная, причем погода держится неизменно весь день. Известно , что с вероятностью 0,8 погода завтра будет такая же, как и сегодня. Сегодня 1 марта, и погода в волшебной стране замечательная. Найдите вероятность того, что 3 марта погода в волшебной стране также будет замечательной.
Известно , что с вероятностью 0,8 погода завтра будет такая же, как и сегодня. Сегодня 1 марта, и погода в волшебной стране замечательная. Найдите вероятность того, что 3 марта погода в волшебной стране также будет замечательной.
Решение: Пусть событие А – погода 3 марта замечательная.
Построим вероятностный граф:
Р(А) = 0,8*0,8+0,2*0,2 = 0,68
Ответ: 0,68
Задача 4: Из урны, где находятся 3 белых и 4 черных шаров, наугад без возвращения один за другим извлекают два шара. Какова вероятность того, что извлекут разноцветные шары?
Решение:
Построим вероятностный граф
Где Ш –шар, Ч – черный шар, Б – белый шар.
Пусть событие A – извлекли разноцветные шары. Этому событию на графе благоприятствуют 2 маршрута. Пользуемся вторым правилом, поэтому
Ответ: 0,57
Задача 5: В первой урне находятся 7 белых и 9 черных шаров, во второй — 6 белых и 4 черных шаров. Из первой урны во вторую переложили два шара, а затем из второй урны извлекли один шар. Найти вероятность того, что этот шар белый
Из первой урны во вторую переложили два шара, а затем из второй урны извлекли один шар. Найти вероятность того, что этот шар белый
Решение:
Построим вероятностный граф:
Пусть событие A — извлеченный из второй урны шар оказался белым. Этому событию на графе благоприятствуют четыре маршрута. Поэтому
Ответ: 0,57
Заключение
В результате проделанной работы сделаны следующие выводы:
теория вероятностей и теория графов — это огромный раздел науки математики, требующий дальнейшего подробного изучения;
изучив теорию, действительно возможно решить задачи по теории вероятностей с помощью графов;
практическое применение необычного способа решения задачи с помощью графов можно использовать на школьных математических олимпиадах, конкурсах, а также при подготовке к государственной итоговой аттестации.
Теория графов имеет свои преимущества в наглядности, доступности конкретности.
При этом нужно отметить, что имеются и некоторые недостатки применения этого способа. Не каждую задачу можно решить с помощью графов.
Таким образом, задачи исследовательской работы решены, поставленная цель достигнута, выдвинутая гипотеза подтверждена.
Список использованной литературы
https://skysmart.ru.Теория графов. Основные понятия и виды графов
Гусак, А.А. Теория вероятностей. Справочное пособие к решению задач/ А.А. Гусач, Е.А. Бричикова. – Изд-е 4-е, стереотип. — Минск.: ТетарСистемс, 2003. – 288 с. ISBN 985-470-138-7
Корниенко В.С. Теория вероятностей. Решение задач с помощью графов. Методическая разработка/ В.С. Корниенко. – Волгоград.: ИПК «Нива», 2010г. – 12 с.
Трофимова Е.А. Теория вероятностей и математическая статистика. Учебное пособие / Е.А.Трофимова, Н.В.Киселев, Д.В. Гиле; под ред. Е.А.Трофимовой; Екатеринбург: Изд-во Уральского университета, 2018. – 160 с. – ISBN 978-5-7996-2317-3
Березина Л. Ю. Графы и их применение. Пособие для учителей / Л. Ю. Березина. – Москва: Просвещение, 1979. – 143 с.
Ожегов С.И. Толковый словарь русского языка: 72500 слов и 7500 фразеологических выражений / С. И. Ожегов, Н. Ю. Шведова; Российская АН, Ин-т рус. яз., Российский фонд культуры. — 2-е изд., испр. и доп. — Москва : Азъ, 1994. — 907с. – ISBN 5-85632-007-7.
И.В.Ященко. Математика. Базовый уровень. 30 вариантов. Типовые варианты экзаменационных заданий. – Волгоград: Экзамен, 2021. – 188 с.
И.В.Ященко. Математика. Профильный уровень. 36 вариантов. Типовые варианты экзаменационных заданий.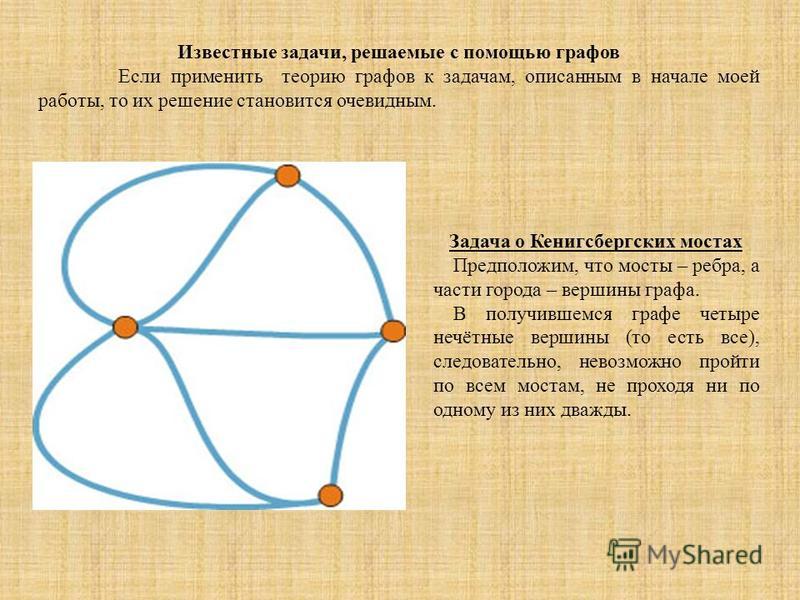 – Волгоград: Экзамен, 2021. – 230 с.
– Волгоград: Экзамен, 2021. – 230 с.
https://oge.sdamgia.ru. Банк заданий.
Просмотров работы: 1093
Решение бизнес-задач с помощью графиков
Всем организациям трудно полностью описать свою организацию с помощью данных. Предприятия потратили миллиарды, пытаясь создать взвешенное представление данных о своих организациях. Одной из наиболее распространенных ошибок является недооценка количества рукотворных связей между данными, которые никогда не были записаны в цифровом виде. Например, менеджер производственного предприятия знает финансового контролера, и они одинаково понимают, как два разных набора данных соотносятся друг с другом и где пролегают связи. Их рабочий процесс никогда не требовал формализации этих соединений и даже не обязательно выигрывал от этого. Тем не менее, попытка организации создать взвешенное представление обычно включает в себя внедрение нового программного обеспечения для изменения рабочих процессов с целью раскрытия связей. Такой подход требует одобрения на нескольких уровнях внутри организации, длительного периода внедрения и, как следствие, снижения производительности. С помощью графовых подходов эти скрытые соединения могут быть закодированы как представление вне хранилищ данных системы записи, не подвергаясь полной повторной интеграции.
Такой подход требует одобрения на нескольких уровнях внутри организации, длительного периода внедрения и, как следствие, снижения производительности. С помощью графовых подходов эти скрытые соединения могут быть закодированы как представление вне хранилищ данных системы записи, не подвергаясь полной повторной интеграции.
Рассматриваемые представления для бизнеса
Базы данных графов и абстракции графов позволяют курировать представления из нескольких и разнообразных источников данных. Редко существует единая графическая «картина мира», и поэтому целью упражнения является не создание монолитной основной базы данных, а курирование и разметка связей между хранилищами бизнес-данных в виде метаданных.
Затем эти метаданные могут использоваться графическим программным обеспечением для представления представления с помощью API, интерфейсов запросов и многофункциональных интерактивных визуализаций. Этот подход принципиально согласуется с современными архитектурами платформ данных децентрализованных микросервисов, которые взаимодействуют с помощью REST API, дизайн, который был разработан, чтобы избежать создания сильно связанных монолитных сервисов.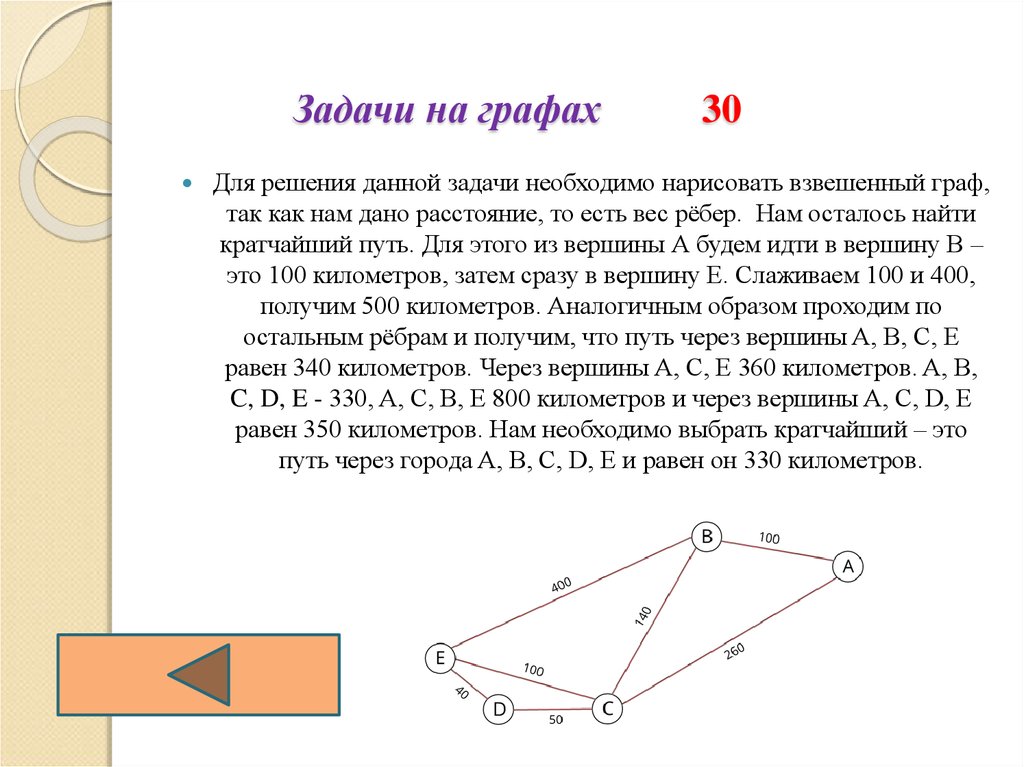 Таким образом, его также можно доставить с использованием современных гибких методов и поддерживать с помощью командных методологий DevOps и DataOps.
Таким образом, его также можно доставить с использованием современных гибких методов и поддерживать с помощью командных методологий DevOps и DataOps.
Типы задач, которые решают графы
Смелое заявление о том, что каждая бизнес-задача — это проблема с графами, имеет под собой реальную основу. Большинство бизнес-проблем связаны с объединением нужных ресурсов для решения проблемы. Граф может объединять различные наборы данных в структуру, позволяющую выявить связи.
- Обнаружение мошенничества: Бизнес-события и данные клиентов, такие как новые учетные записи, заявки на получение кредита и транзакции по кредитным картам, могут быть смоделированы в виде графика для обнаружения мошенничества. Выявляя подозрительные закономерности в метаданных о действиях клиентов и сопоставляя их с ранее выявленным мошенничеством, мы можем выявить потенциальное мошенничество, которое может продолжаться.
- 360-градусное представление клиента. Преимущество использования графических баз данных заключается в интеграции данных из разных хранилищ бизнес-данных для создания взвешенного представления об общем ландшафте.
 Одним из самых непосредственных применений такого представления является так называемое «360-градусное представление о клиенте», позволяющее интегрировать все данные, известные о клиенте, из хранилищ данных по всей организации.
Одним из самых непосредственных применений такого представления является так называемое «360-градусное представление о клиенте», позволяющее интегрировать все данные, известные о клиенте, из хранилищ данных по всей организации. - Network Mapping: картирование и инвентаризация инфраструктуры естественным образом подходят для представления в виде графика. В частности, при отображении взаимосвязей между подключенным физическим/виртуальным оборудованием и службами, которые они поддерживают. График взаимосвязей между компонентами инфраструктуры позволяет не только интерактивную визуализацию состояния сети, но и алгоритмы трассировки сети для обхода графа, выявления узких мест, оценки задержки и выполнения управления зависимостями.
Выбор графовой базы данных
При разработке графического решения необходимо учитывать, какую технологию использовать для моделирования данных. В частности, существует два хорошо поддерживаемых режима работы базы данных графов:
- Графики помеченных свойств (LPG)
- Графики структуры описания ресурсов (RDF)
Они похожи тем, что представляют данные с использованием узлов и ребер для формирования графов, но имеют разные подходы к использованию, сложности и функциям. Наиболее важные различия заключаются в форматах, используемых для описания данных, и в языках, используемых для запросов к графику:
Наиболее важные различия заключаются в форматах, используемых для описания данных, и в языках, используемых для запросов к графику:
Представление данных графа
При использовании графов RDF модель данных объявляется с помощью OWL, языка веб-онтологий, где классы данных и свойства идентифицируются с помощью URI. В диаграмме свойств с метками нет формальной спецификации таксономии/схемы данных, и вместо этого обычно используются короткие строки. Важным отличием является то, что ссылки на онтологии OWL доступны глобально и, следовательно, совместно используются публикаторами данных. Например, FIBO, бизнес-онтология финансовой отрасли, используется издателями в финансовой отрасли, такими как Bloomberg и Thomson Reuters. Когда данные от каждого издателя указывают объект как «Студенческий заем FIBO» (в частности, с использованием следующего URL), существует общее и задокументированное понимание того, что это означает (т. е. студенческий заем в данном случае). Это также означает, что график, загруженный данными из Bloomberg и Thomson Reuters, может быть запрошен для студенческого кредита FIBO, и данные от обоих издателей будут возвращены и учтены в запросе. Таким образом, данные из нескольких источников органично интегрируются в единый график.
Таким образом, данные из нескольких источников органично интегрируются в единый график.
Достижение масштаба
Существует несколько моделей, используемых графовыми базами данных для достижения масштаба с точки зрения количества загружаемых данных, скорости загрузки, времени запроса, числа операций чтения в секунду, записи в секунду и так далее. Модель масштабирования также влияет на то, масштабируется ли база данных вертикально (т. е. за счет увеличения размера сервера) или горизонтально (т. е. за счет увеличения количества серверов). Обычно вертикальное масштабирование достигает физических ограничений раньше и становится дороже по мере приближения к ограничениям, тогда как горизонтальное масштабирование, как правило, имеет гораздо большие ограничения и использует более дешевые серверы. Это различие является основным фактором при выборе программного обеспечения графовой базы данных для архитекторов больших данных. Двумя наиболее часто используемыми графовыми базами данных в настоящее время являются Amazon Neptune и Datastax Graph. Amazon Neptune масштабируется вертикально с использованием одного главного узла и до 15 реплик чтения, в то время как Datastax Graph масштабируется горизонтально с использованием базовой технологии базы данных Cassandra и, следовательно, может линейно масштабироваться до очень большого количества узлов (утверждается, что Apple использует более 75 000 узлов, достигая миллионов). чтения и записи в секунду).
Amazon Neptune масштабируется вертикально с использованием одного главного узла и до 15 реплик чтения, в то время как Datastax Graph масштабируется горизонтально с использованием базовой технологии базы данных Cassandra и, следовательно, может линейно масштабироваться до очень большого количества узлов (утверждается, что Apple использует более 75 000 узлов, достигая миллионов). чтения и записи в секунду).
СОВЕТЫ ПО РЕАЛИЗАЦИИ
Знайте варианты использования
Оцените размер графа на основе выбранной модели данных графа. Определите текущие схемы чтения и записи корпоративных данных и экстраполируйте будущее увеличение использования. Используйте эти измерения, чтобы убедиться, что выбранная вами графическая база данных масштабируется в соответствии с вашими потребностями, путем оценки ограничений каждой графической базы данных.
Проект для масштабирования
После того, как вы начнете работать с графиками, вам захочется поэкспериментировать с подключением большего количества источников данных и выполнением запросов к ним — спроектируйте свои конвейеры данных для обработки больших потоков данных, чтобы предотвратить препятствия в будущем.
Формализуйте модель данных
В будущем может возникнуть соблазн заняться формальностями, но наш опыт показывает, что вы получите максимальную отдачу от графового процесса, используя богатые выразительные модели данных на раннем этапе.
Убедитесь, что вы записываете происхождение данных
Происхождение данных по мере их перемещения через системы данных, обработки и объединения может быть записано как метаданные происхождения и включено в график. Обеспечение полного происхождения данных имеет важное значение для регулирования данных сейчас и в будущем.
Изучение RBAC в графе
Использование управления доступом на основе ролей с использованием онтологий в графе — это проторенный путь к элегантной интеграции безопасности данных на уровне графа; выяснить, работает ли это в вашей архитектуре безопасности.
Исследование бизнес-онтологий
В свободном доступе опубликовано множество онтологий, подробно охватывающих различные области бизнеса. Исследуйте области, охватываемые вашими данными, чтобы найти готовые онтологии для моделирования вашего бизнеса в виде графа.
Исследуйте области, охватываемые вашими данными, чтобы найти готовые онтологии для моделирования вашего бизнеса в виде графа.
В 6point6 мы обладаем обширным опытом предоставления решений графовых баз данных для наших клиентов и их поддержки с использованием нашей методологии DataOps.
Для получения дополнительной информации свяжитесь с нами.
Написано доктором Дэниелом Александром Смитом, ведущим архитектором больших данных
Иерархическая сеть Graph-to-Tree с расширенными возможностями для решения математических задач Word
Qinzhuo Wu, Ци Чжан, Zhongyu Wei
Abstract
Решение математических задач в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.
В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.- Anthology ID:
- 2021.findings-emnlp.127
- Volume:
- Findings of the Association for Computational Linguistics: EMNLP 2021
- Month:
- November
- Year:
- 2021
- Address:
- Пунта-Кана, Доминиканская Республика
- Место проведения:
- Findings
- SIG:
- SIGDAT
- Издатель:
- Association for Computational Linguistics
- Note0134
- Страницы:
- 1473–1482
- Язык:
- URL:
- https://aclanthology.
 org/2021.findings-ermslp.127
org/2021.findings-ermslp.127 - 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111. .127
- Bibkey:
- Cite (ACL):
- Qinzhuo Wu, Qi Zhang и Zhongyu Wei. 2021. Иерархическая сеть Graph-to-Tree с расширенными возможностями Edge для решения задач Math Word. В Выводах Ассоциации компьютерной лингвистики: EMNLP 2021 , страницы 1473–1482, Пунта-Кана, Доминиканская Республика. Ассоциация компьютерной лингвистики.
- Процитируйте (неофициально):
- Иерархическая сеть Graph-to-Tree с расширенными границами для решения математических задач Word (Wu et al., Findings 2021)
- Копия цитирования:
- PDF:
- https://aclanthology.org/2021.findings-emnlp.127.pdf
- Видео:
- https://aclanthology.org/2021.findings-emnlp.127.mp4
- 3 Код
- qinzhuowu/eeh_g2t
- Данные
- MAWPS, Math33K
- BibTeX
- MODS XML
- Endnote
- Предварительно отформатированный
@inproceedings{wu-etal-2021-edge-enhanced,
title = "Иерархическая сеть Graph-to-Tree с расширенными возможностями Edge для решения задач Math Word",
автор = "Ву, Циньчжуо и
Чжан, Ци и
Вэй, Чжунъюй»,
booktitle = "Выводы Ассоциации компьютерной лингвистики: EMNLP 2021",
месяц = ноябрь,
год = "2021",
address = "Пунта-Кана, Доминиканская Республика",
издатель = "Ассоциация вычислительной лингвистики",
url = "https://aclanthology. org/2021.findings-emnlp.127",
doi = "10.18653/v1/2021.findings-emnlp.127",
страницы = "1473--1482",
abstract = "Решение математических задач со словами в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. -диапазон отношений слов между предложениями. Кроме того, во время генерации они сосредотачиваются на наиболее важных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новый иерархический граф с расширенными границами. модель дерева (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, для включения информации о метках ребер используется кодировщик иерархического графа с расширенными ребрами. Этот кодировщик обновляет узлы графа иерархически в двух шаги: агрегация на уровне предложения и агрегация на уровне проблемы. Модель, чтобы обратить внимание на различные части входной задачи.
org/2021.findings-emnlp.127",
doi = "10.18653/v1/2021.findings-emnlp.127",
страницы = "1473--1482",
abstract = "Решение математических задач со словами в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. -диапазон отношений слов между предложениями. Кроме того, во время генерации они сосредотачиваются на наиболее важных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новый иерархический граф с расширенными границами. модель дерева (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, для включения информации о метках ребер используется кодировщик иерархического графа с расширенными ребрами. Этот кодировщик обновляет узлы графа иерархически в двух шаги: агрегация на уровне предложения и агрегация на уровне проблемы. Модель, чтобы обратить внимание на различные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.",
}
Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.",
}
<моды> <информация о заголовке> Усовершенствованная иерархическая сеть Graph-to-Tree для решения математических задач <название типа="личное">Циньчжуо Ву <роль>автор <название типа="личное">Ци Чжан <роль>автор <название типа="личное">Чжунъюй Вэй <роль>автор <информация о происхождении>2021-11 текст <информация о заголовке> Выводы Ассоциации компьютерной лингвистики: EMNLP 2021 <информация о происхождении>Ассоциация компьютерной лингвистики <место>Пунта-Кана, Доминиканская Республика публикация конференции Решение математических словесных задач в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.

wu-etal-2021-edge-enhanced 10.18653/v1/2021.findings-emnlp.127 <местоположение>https://aclanthology.org/2021.findings-emnlp.127 <часть> <дата>2021-11 <единица экстента="страница">1473 1482
%0 Материалы конференции %T Иерархическая сеть Graph-to-Tree с расширенными возможностями Edge для решения математических задач Word %A Ву, Циньчжуо %А Чжан, Ци %А Вэй, Чжунъюй %S Выводы Ассоциации компьютерной лингвистики: EMNLP 2021 %D 2021 %8 ноябрь %I Ассоциация компьютерной лингвистики %C Пунта-Кана, Доминиканская Республика %F wu-etal-2021-улучшенный край %X Решение математических задач в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче.Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.

 Одним из самых непосредственных применений такого представления является так называемое «360-градусное представление о клиенте», позволяющее интегрировать все данные, известные о клиенте, из хранилищ данных по всей организации.
Одним из самых непосредственных применений такого представления является так называемое «360-градусное представление о клиенте», позволяющее интегрировать все данные, известные о клиенте, из хранилищ данных по всей организации.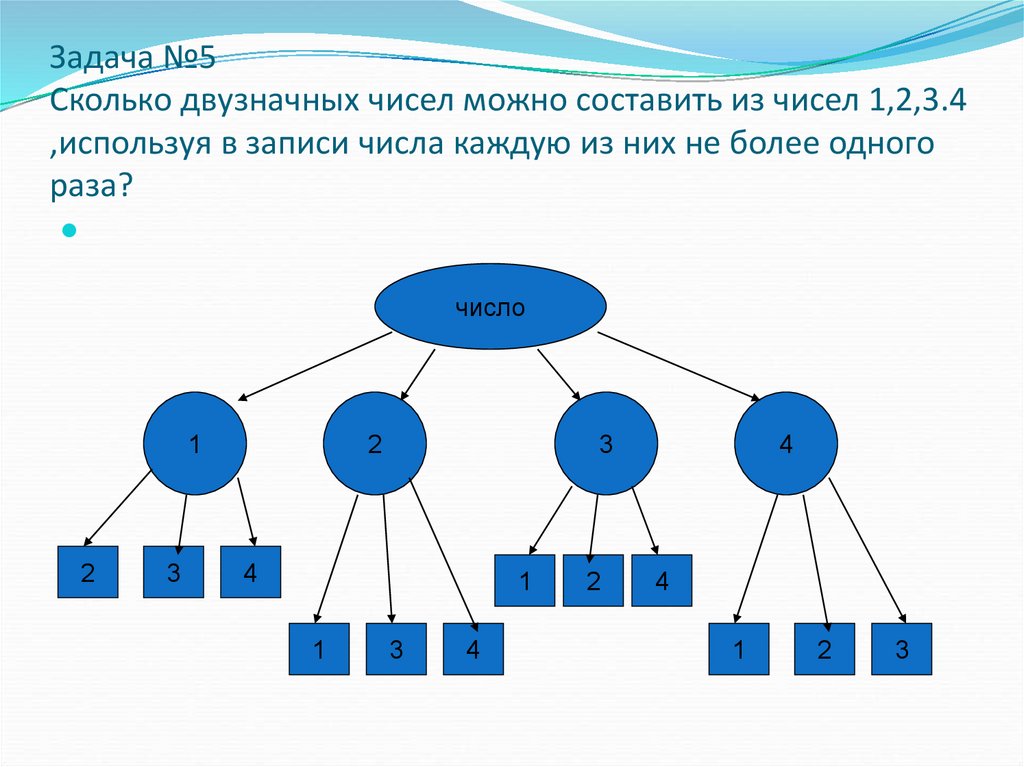 org/2021.findings-ermslp.127
org/2021.findings-ermslp.127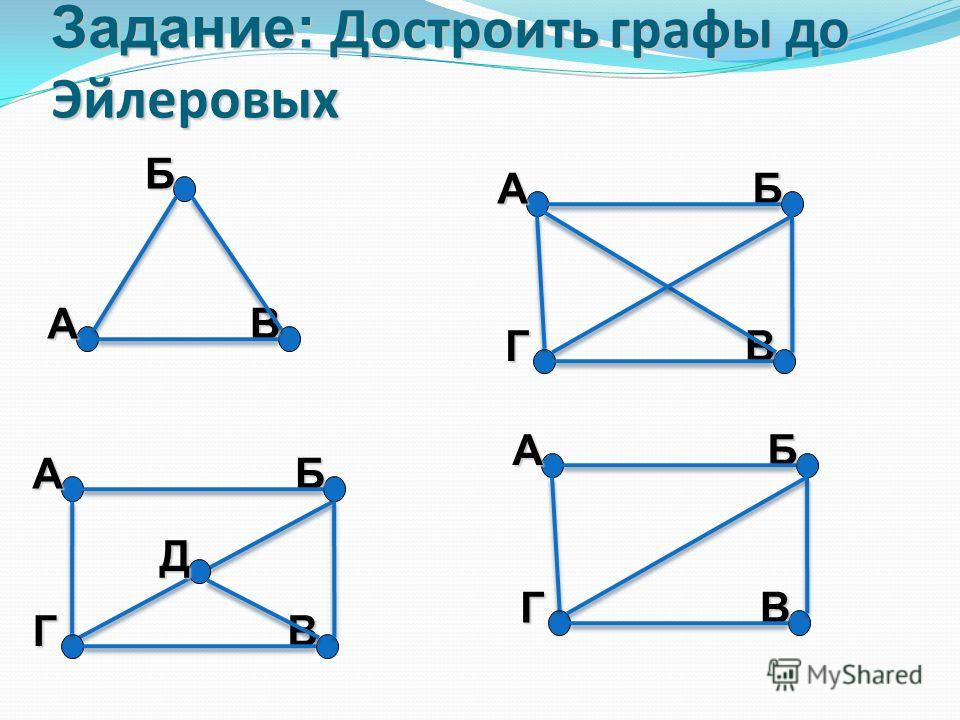 org/2021.findings-emnlp.127",
doi = "10.18653/v1/2021.findings-emnlp.127",
страницы = "1473--1482",
abstract = "Решение математических задач со словами в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. -диапазон отношений слов между предложениями. Кроме того, во время генерации они сосредотачиваются на наиболее важных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новый иерархический граф с расширенными границами. модель дерева (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, для включения информации о метках ребер используется кодировщик иерархического графа с расширенными ребрами. Этот кодировщик обновляет узлы графа иерархически в двух шаги: агрегация на уровне предложения и агрегация на уровне проблемы. Модель, чтобы обратить внимание на различные части входной задачи.
org/2021.findings-emnlp.127",
doi = "10.18653/v1/2021.findings-emnlp.127",
страницы = "1473--1482",
abstract = "Решение математических задач со словами в последние годы привлекло значительный исследовательский интерес. Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. -диапазон отношений слов между предложениями. Кроме того, во время генерации они сосредотачиваются на наиболее важных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новый иерархический граф с расширенными границами. модель дерева (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, для включения информации о метках ребер используется кодировщик иерархического графа с расширенными ребрами. Этот кодировщик обновляет узлы графа иерархически в двух шаги: агрегация на уровне предложения и агрегация на уровне проблемы. Модель, чтобы обратить внимание на различные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.",
}
Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.",
}
 Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.
Предыдущие работы показали эффективность использования графовых нейронных сетей для захвата взаимосвязей в задаче. Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.
 Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.
Однако в этих работах не учитывалась информация о краевых метках и дальние отношения слов в предложениях. Кроме того, при генерации они сосредотачиваются на наиболее актуальных областях генерируемого в данный момент слова, игнорируя при этом остальную часть проблемы. В этой статье мы предлагаем новую модель иерархического преобразования графа в дерево с расширенными границами (EEH-G2T), в которой задачи математических слов представлены в виде графов с метками ребер. В частности, кодировщик иерархического графа с расширенными границами используется для включения информации о метках границ. Этот кодировщик иерархически обновляет узлы графа в два этапа: агрегация на уровне предложения и агрегация на уровне проблемы. Кроме того, применяется декодер с древовидной структурой и механизмом разделения внимания, чтобы модель обращала внимание на разные части входной задачи. Экспериментальные результаты с набором данных MAWPS и Math33K показали, что наш EEH-G2T может эффективно повысить производительность по сравнению с современными методами.