Найдите наименьшее общее кратное чисел 9 и 12: НОД и НОК для 9 и 12 (с решением)

Как находить ноз дробей примеры. Как найти наименьшее общее кратное чисел

Общее кратное для двух целых чисел — это такое целое число, которое делится нацело без остатка на оба заданных числа.

Наименьшее общее кратное для двух целых чисел — это наименьшее из всех целых чисел, которое делится нацело и без остатка на оба заданных числа.

Способ 1 . Найти НОК можно, по очереди, для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются путем их умножения на 1, 2, 3, 4 и так далее.

Пример для чисел 6 и 9.
Умножаем число 6, последовательно, на 1, 2, 3, 4, 5.
Получаем: 6, 12, 18 , 24, 30
Умножаем число 9, последовательно, на 1, 2, 3, 4, 5.
Получаем: 9, 18 , 27, 36, 45
Как видно, НОК для чисел 6 и 9 будет равно 18.

Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.

Способ 2 . Найти НОК можно, разложив исходные числа на простые множители.
После разложения необходимо вычеркнуть из получившихся рядов простых множителей одинаковые числа. Оставшиеся числа первого числа будут множителем для второго, а оставшиеся числа второго — множителем для первого.

Пример для числе 75 и 60.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители:
75 = 3 * 5 * 5, а
60 = 2 * 2 * 3 * 5 .
Как видно, множители 3 и 5 встречаются в обоих строках. Мысленно их «зачеркиваем».
Выпишем оставшиеся множители, входящие в разложение каждого из этих чисел. При разложении числа 75 у нас осталось число 5, а при разложении числа 60 — остались 2 * 2
Значит, чтобы определить НОК для чисел 75 и 60, нам нужно оставшиеся числа от разложения 75 (это 5) умножить на 60, а числа, оставшиеся от разложения числа 60 (это 2 * 2) умножить на 75.

То есть, для простоты понимания, мы говорим, что умножаем «накрест».
75 * 2 * 2 = 300
60 * 5 = 300
Таким образом мы и нашли НОК для чисел 60 и 75. Это — число 300.

Пример . Определить НОК для чисел 12, 16, 24
В данном случае, наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим по его множителям, вычеркивая их, если хотя бы в одном из других рядов чисел встретился такой же, еще не зачеркнутый множитель.

Шаг 1 . Мы видим, что 2 * 2 встречаются во всех рядах чисел. Зачеркиваем их.
12 = 2 * 2 * 3

16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3

Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3

Как видим, при разложении числа 12 мы «вычеркнули» все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение.
Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию)
12 * 2 * 2 = 48
Это и есть НОК

Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.

Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.

Шаги

Ряд кратных чисел

Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.

• Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.

Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..

• Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.

Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.

• Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.

Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.

• Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.

Разложение на простые множители

1. Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.

   • Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.

2. Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.

   • Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20} и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10} . Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .

3. Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.

   • Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84} , 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42} и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6} . Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .

4. Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).

   • Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times } и зачеркните 2 в обоих выражениях.
   • Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.

5. К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.

   • Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
   • В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} также зачеркнуты обе двойки (2). Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} .

6. Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.

   • Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.

Нахождение общих делителей

1. Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.

   • Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.

2. Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.

   • Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.

3. Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.

   • Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
   • 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.

4. Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.

   • Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.

5. Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.

   • Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
   • 15 ÷ 3 = 5 {\displaystyle 15\div 3=5} , поэтому запишите 5 под 15.

6. Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.

7. Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.

   • Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .

8. Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.

   • Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} . Таким образом, наименьшее общее кратное 18 и 30 равно 90.

Алгоритм Евклида

1. Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.

   • Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2} ост. 3:
     15 – это делимое
     6 – это делитель
     2 – это частное
     3 – это остаток.

В реальной жизни нам необходимо оперировать обыкновенными дробями. Однако чтобы сложить или вычесть дроби с разными знаменателями, например, 2/3 и 5/7, нам потребуется найти общий знаменатель. Приведя дроби к общему знаменателю, мы сможем легко осуществить операции сложения или вычитания.

Определение

Дроби — одна из самых сложных тем в начальной арифметике, и рациональные числа пугают школьников, которые встречаются с ними впервые. Мы привыкли оперировать с числами, записанными в десятичном формате. Куда проще сходу сложить 0,71 и 0,44, чем суммировать 5/7 и 4/9. Ведь для суммирования дробей их необходимо привести к общему знаменателю. Однако дроби куда точнее представляют значение величин, чем их десятичные эквиваленты, а в математике представление рядов или иррациональных чисел в виде дроби становится приоритетной задачей. Такая задача носит название «приведение выражения к замкнутому виду».

Если и числитель, и знаменатель дроби умножить или разделить на один и тот же коэффициент, то значение дроби не изменится. Это одно из самых важных свойств дробных чисел. К примеру, дробь 3/4 в десятичной форме записывается как 0,75. Если умножить числитель и знаменатель на 3, то получим дробь 9/12, что точно также равняется 0,75. Благодаря этому свойству мы можем умножать разные дроби таким образом, чтобы они все имели одинаковые знаменатели. Как это сделать?

Поиск общего знаменателя

Наименьший общий знаменатель (НОЗ) — это наименьшее общее кратное для всех знаменателей выражения. Найти такое число мы можем тремя способами.

Использование максимального знаменателя

Это один из самых простых, но трудоемких методов поиска НОЗ. Вначале из знаменателей всех дробей выписываем самое большое число и проверяем его делимость на меньшие числа. Если делится, то наибольший знаменатель и есть НОЗ.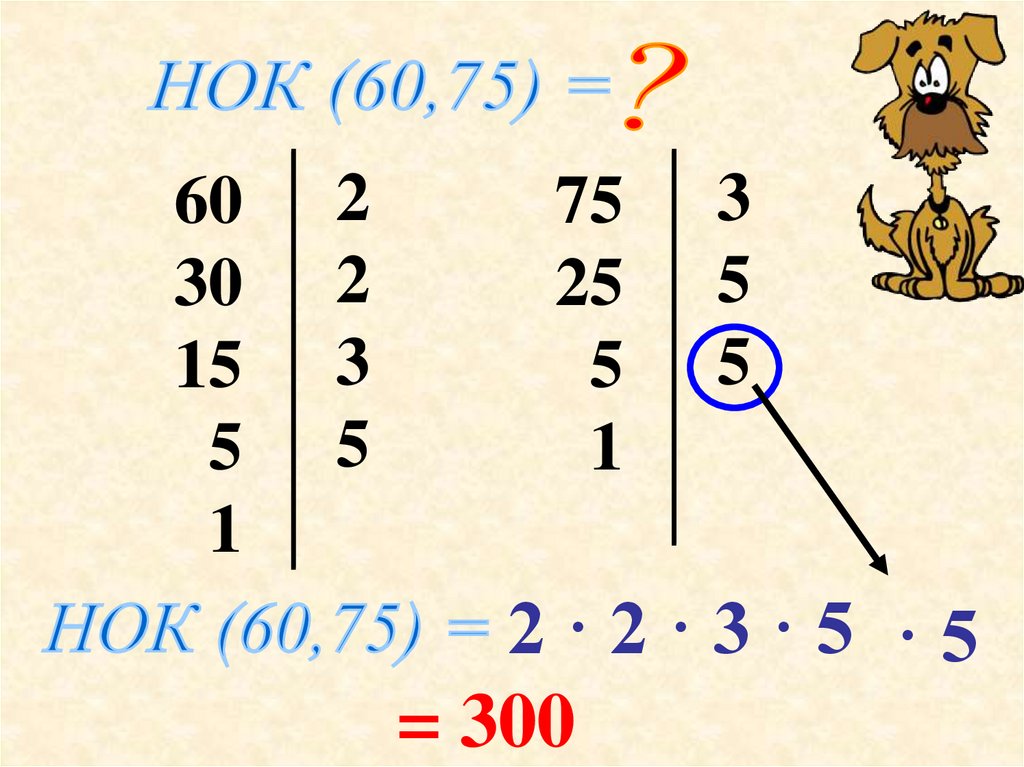

Если в предыдущей операции числа делятся с остатком, то необходимо самое большое из них умножить на 2 и повторить проверку на делимость. Если оно делится без остатка, то новый коэффициент становится НОЗ.

Если нет, то самый большой знаменатель умножается на 3, 4 , 5 и так далее, пока не будет найдено наименьшее общее кратное для нижних частей всех дробей. На практике это выглядит так.

Пусть у нас есть дроби 1/5, 1/8 и 1/20. Проверяем 20 на делимость 5 и 8. 20 не делится на 8. Умножаем 20 на 2. Проверяем 40 на делимость 5 и 8. Числа делятся без остатка, следовательно, НОЗ (1/5, 1/8 и 1/20) = 40, а дроби превращаются в 8/40, 5/40 и 2/40.

Последовательный перебор кратных

Второй способ — это простой перебор кратных и выбор из них наименьшего. Для поиска кратных мы умножаем число на 2, 3, 4 и так далее, поэтому количество кратных устремляется в бесконечность. Ограничить эту последовательность можно пределом, которое представляет собой произведение заданных чисел. К примеру, для чисел 12 и 20 НОК находится следующим образом:

• выписываем числа, кратные 12 — 24, 48, 60, 72, 84, 96, 108, 120;
• выписываем числа, кратные 20 — 40, 60, 80, 100, 120;
• определяем общие кратные — 60, 120;
• выбираем наименьшее из них — 60.

Таким образом, для 1/12 и 1/20 общим знаменателем будет 60, а дроби преобразуются в 5/60 и 3/60.

Разложение на простые множители

Этот способ нахождения НОК наиболее актуален. Данный метод подразумевает разложение всех чисел из нижних частей дробей на неделимые множители. После этого составляется число, которое содержит множители всех знаменателей. На практике это работает так. Найдем НОК для той же пары 12 и 20:

• раскладываем на множители 12 — 2 × 2 × 3;
• раскладываем 20 — 2 × 2 × 5;
• объединяем множители таким образом, чтобы они содержали в себе числа и 12, и 20 — 2 × 2 × 3 × 5;
• перемножаем неделимые и получаем результат — 60.

В третьем пункте мы объединяем множители без повторов, то есть двух двоек достаточно для формирования 12 в комбинации с тройкой и 20 — с пятеркой.

Наш калькулятор позволяет определить НОЗ для произвольного количества дробей, записанных как в обыкновенной, так и в десятичной форме. Для поиска НОЗ вам достаточно ввести значения через табуляцию или запятую, после чего программа вычислит общий знаменатель и выведет на экран преобразованные дроби.

Пример из реальной жизни

Сложение дробей

Пусть в задаче по арифметике нам необходимо сложить пять дробей:

0,75 + 1/5 + 0,875 + 1/4 + 1/20

Решение вручную производилось бы следующим способом. Для начала нам необходимо представить числа в одной форме записи:

• 0,75 = 75/100 = 3/4;
• 0,875 = 875/1000 = 35/40 = 7/8.

Теперь у нас есть ряд обыкновенных дробей, которые необходимо привести к одинаковому знаменателю:

3/4 + 1/5 + 7/8 + 1/4 + 1/20

Так как у нас 5 слагаемых, проще всего использовать способ поиска НОЗ по наибольшему числу. Проверяем 20 на делимость остальными числами. 20 не делится на 8 без остатка. Умножаем 20 на 2, проверим 40 на делимость — все числа делят 40 нацело. Это и есть наш общий знаменатель. Теперь для суммирования рациональных чисел нам необходимо определить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Дополнительные множители буду выглядеть так:

• 40/4 = 10;
• 40/5 = 8;
• 40/8 = 5;
• 40/4 = 10;
• 40/20 = 2.

Теперь умножим числитель и знаменатель дробей на соответствующие дополнительные множители:

30/40 + 8/40 + 35/40 + 10/40 + 2/40

Для такого выражения мы можем легко определить сумму, равную 85/40 или 2 целых и 1/8. Это громоздкие вычисления, поэтому вы можете просто ввести данные задачи в форму калькулятора и сразу получить ответ.

Заключение

Арифметические операции с дробями — не слишком удобная вещь, ведь для поиска ответа приходится осуществлять множество промежуточных вычислений. Используйте наш онлайн-калькулятор для приведения дробей к общему знаменателю и быстрого решения школьных задач.

Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.

Как найти наименьший общий знаменатель – понятие

Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.

Как найти наименьший общий знаменатель – примеры

Рассмотрим примеры нахождения НОЗ.

Вычислить: 3/5 + 2/15.

Решение (Последовательность действий):

• Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
• Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
• Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
• Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.

Ответ: 3/5 + 2/15 = 11/15.

Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.

Вычислить: 1/2 – 5/12 + 3/6

Решение (последовательность действий):

• Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
• Получим: 1/2 – 5/12 + 3/6 = ?/12.
• Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
• Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.

Ответ: 1/2 – 5/12 + 3/6 = 7/12.

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Yandex.RTB R-A-339285-1

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Определение 1

Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .

Пример 1

Необходимо найти НОК чисел 126 и 70 .

Решение

Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .

Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .

Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .

Ответ: НОК (126 , 70) = 630 .

Пример 2

Найдите нок чисел 68 и 34 .

Решение

НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .

Ответ: НОК (68 , 34) = 68 .

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Определение 2

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

• составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
• исключаем их полученных произведений все простые множители;
• полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Пример 3

У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .

Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .

Пример 4

Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .

Ответ: НОК (441 , 700) = 44 100 .

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Определение 3

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

• разложим оба числа на простые множители:
• добавим к произведению простых множителей первого числа недостающие множители второго числа;
• получим произведение, которое и будет искомым НОК двух чисел.

Пример 5

Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .

Пример 6

Необходимо вычислить НОК чисел 84 и 648 .

Решение

Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 ​​​​​​ ​.

Ответ: НОК (84 , 648) = 4 536 .

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теорема 1

Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Пример 7

Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .

Решение

Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .

Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .

Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .

Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .

НОК четырех чисел из условия примера равно 94500 .

Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Определение 4

Предлагаем вам следующий алгоритм действий:

• раскладываем все числа на простые множители;
• к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
• к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
• полученное произведение будет наименьшим общим кратным всех чисел из условия.

Пример 8

Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .

Решение

Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Пример 9

НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .

Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .

Пример 10

Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .

Решение

Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел − 145 и − 45 равно 1 305 .

Ответ: НОК (− 145 , − 45) = 1 305 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

12, 24, 36, 48, 60, 72, … 18, 36, 54, 72, 90, … НОК (12, 18) = 36.

а) числа 15 и 20; НОК (15, 20) = …; б) числа 25 и 30; НОК (25, 30) = …; в) числа 14 и 21; НОК (14, 21) = …; г) числа 12 и 20; НОК (12, 20) = …; д) числа 12 и 15; НОК (12, 15) = …; е) числа 12 и 30; НОК (12, 30) = …; ж) числа 15 и 25; НОК (15, 25) = …; з) числа 48 и 6; НОК (48, 6) = …; и) числа 9 и 12; НОК (9, 12) = …; к) числа 175 и 25; НОК (175, 25) = …; л) числа 400 и 100; НОК (400, 100) = …; м) числа 45 и 18; НОД (45, 18) = …. — Знания.site

Последние вопросы

• Математика

  19 секунд назад

  Катя и Миша поделили 428р. Катя получила на 82р. больше Мишы. Сколько получил каждый?​

• Математика

  19 секунд назад

  2+2= пожайлуста ришите как можно бистрее

• Математика

  34 минут назад

  Запиши слова в порядке схема

• Математика

  35 минут назад

  Знайти значення виразу — 2,5 — 3,7

• Математика

  35 минут назад

  ahhhhahответ нужно что такое ахахаха​

• Математика

  35 минут назад

  позначте на кординатній прямій точки А(2) В(-3) С(2,5) D(-2,5) Е(-4). Які з позначених точок мають протилежні координати ПЖЖЖЖЖЖ ДО КОНЦА 10 МИН ​

• Математика

  40 минут назад

  Допоможіть будь ласка. даю 50б.​

• Математика

  45 минут назад

  Аян выучила 6 считалок, а загадок-в 2 раза больше. Сколько загадок выучила Аян? Помогите пожалуйста

• Математика

  45 минут назад

  250. Велосипедист зі швидкістю велосипедиста їхав 2 год зі швидкістю 18 км/год і 3 год 16 км/год. Знайдіть середню швидкість протягом усього шляху.​

• Математика

  45 минут назад

  ДОПОМОЖІТЬ БУДЬ ЛАСКАА Розв’язати лінійне диференціальне рівняння першого порядку

• Математика

  45 минут назад

  Дано: ∆АВС ∠С=90⁰. Знайти АС і ВС, якщо АВ=13 см, tgA=5⁄12.​

• Математика

  47 минут назад

  Можете помочь? Если да то спасибо.

  Задача:

  Угол 1 составляет 2/3 угла 8.

  Я не понимаю решения😢

• Математика

  58 минут назад

  помогите найти производные номеров 2,8,11,12 с решение прошу

• Математика

  1 час назад

  Напишите термины, о которых идет речь. В скобках укажите к какой сфере жизни общества он относится. П — политической, Э — экономической. 1. Грамота монгольских ханов, позволявшая занять княжеский престол. 2. Сборщик налогов. 3. Часть единой Монгольской империи. 4. Налог в пользу монголов. 5. Натуральный налог в виде пушнины. Пример ответа: 1. Президент (п), 2. Деньги (э)

• Математика

  1 час назад

  Помогите пожалуйста, фото прикреплено

Все предметы

English

United States

Polski

Polska

Bahasa Indonesia

Indonesia

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Português

Brasil

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

LCM Калькулятор для вычисления наименьшего общего кратного 9, 12

Бесплатный калькулятор LCM определяет наименьшее общее кратное (НОК) между 9 и 12 — наименьшее целое число, равное 36, которое делится на оба числа.

Наименьшее общее кратное (НОК) чисел 9 и 12 равно 36 .

LCM(9,12) = 36

Наименьшее общее кратное или наименьший общий знаменатель (LCD) можно вычислить тремя способами;

• Наименьшее общее кратное 9 и 12 методом простых чисел
• Наименьшее общее кратное 9 и 12 по формуле GCF

Имя пользователя

НОК

и

Наименьшее общее кратное можно найти, умножив наибольшие простые множители степени 9 и 12. Сначала мы вычислим простых множителей 9 и 12 .

Простые множители 9

Простые множители 9 равны 3. Простые множители 9 в экспоненциальной форме:

9 = 3 ²

Prime Factorization of 12

2	12
2	6
3	3
	1

Prime factors of 12 2,3. Разложение числа 12 на простые множители в экспоненциальной форме:

12 = 2 ² × 3 ¹

Теперь, умножив самые высокие простые множители показателя степени, мы вычислим число 9.0005 LCM 9 и 12 .

НОК(9,12) = 2 ² ×3 ²
НОК(9,12) = 36

Делители 9

1, 3, 9

Делители числа 12

Список натуральных делителей числа 12, на которое 12 делится без остатка.

1, 2, 3, 4, 6, 12

Формула LCM : LCM(a,b) = (a × b) / GCF(a,b).
Нам нужно вычислить наибольший общий делитель 9и 12, чем применяются в уравнении LCM.

GCF(9,12) = 3
LCM(9,12) = ( 9 × 12) / 3
LCM(9,12) = 108 / 3
LCM(9,12) = 36

(i)

LCM 9 и 12 = LCM 12 и 9

• LCM 9 и 13
• LCM 9 и 14
• LCM 9 и 15
• LCM 9 и 15
• LCM 9 и 17

• LCM 12 и 16
• LCM 12 и 17
• LCM 12 и 18
• LCM 12 и 19
• LCM 12 и 20

1. Что такое LCM 9 и 12?

Ответ: НОК 9 и 12 равно 36.

2. Каковы множители числа 9?

Ответ: Делителями 9 являются 1, 3, 9. Есть 3 целых числа, которые являются делителями 9. Наибольший делитель 9 равен 9.

3. Каковы множители числа 12?

Ответ: Делители 12 равны 1, 2, 3, 4, 6, 12. Есть 6 целых чисел, которые являются делителями 12. Наибольший делитель 12 равен 12.

4. Как найти LCM 9 и 12?

Ответ:

Наименьшее общее кратное 9 и 12 = 36

Шаг 1: Найдите разложение числа 9 на простые множители

9 = 3 x 3

Шаг 2: Найдите разложение числа 12 на простые множители 2 x 3

Шаг 3: Умножьте каждый коэффициент на большее количество раз, которое он встречается в шагах i) или ii), чтобы найти lcm:

LCM = 36 = 2 x 2 x 3 x 3

Шаг 4: Следовательно , наименьшее общее кратное 9а 12 равно 36.

Как найти LCM 9 и 12, используя метод перечисления, деления, простой факторизации?

НОК 9 и 12 равно 36. НОК 9 и 12, также известный как наименьшее общее кратное или наименьшее общее кратное 9 и 12, является наименьшим общим числом, которое делится на 9 и 12.

Теперь посмотрим как найти LCM 9 и 12. Число, кратное 9, равно 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108,…, а число, кратное 12, равно 12, 24, 36, 48, 60, 72, 84, 96, 108,… Здесь и 36, и 72 — обычные числа, кратные 9.и 12 соответственно, или которые делятся на 9 и 12. Но когда вам нужно найти НОК, вы должны сосредоточиться на наименьшем общем числе. Таким образом, 36 является наименьшим общим числом среди всех кратных, которые делятся на 9 и 12, и, следовательно, НОК 9 и 12 равен 36.

Получите индивидуальные уроки математики от лучших преподавателей!
Изучите онлайн-сервисы Wiingy по обучению математике, чтобы изучить арифметику, алгебру, исчисление и многое другое

Методы нахождения НОК для 9 и 12

Существует три разных метода нахождения МОК для 9и 12. Это:

• Метод простой факторизации
• Метод перечисления
• Метод деления        

НОК 9 и 12 с использованием метода простой факторизации

Метод простой факторизации является одним из методов нахождения НОК. Чтобы найти НОК чисел 9 и 12 с помощью метода разложения на простые множители, выполните следующие действия:

• Шаг 1: Найдите простые делители чисел 9 и 12 с помощью метода повторного деления.
• Шаг 2: Запишите все простые множители в их экспоненциальных формах. Затем перемножьте простые множители, имеющие наибольшую мощность.
• Шаг 3: Конечным результатом после умножения будет НОК 9 и 12.

НОК 9 и 12 можно получить с помощью метода простой факторизации как:

• Простую факторизацию 9 можно выразить как 3 * 3 = 3 ¹ * 3 ¹ = 3 ²
• Разложение числа 12 на простые множители можно выразить как 2 * 2 * 3 = 2 ¹ * 2 ¹ * 3 ¹ = 2 ² * 3 ¹
• Итак, LCM 9 и 12 = 2 ² * 3 ² = 2 * 2 * 3 * 3 = 36

LCM 9 и 12 с использованием метода листинга

Метод листинга является одним из методов определения LCM. Чтобы найти НОК чисел 9 и 12 методом перечисления, выполните следующие действия:

• Шаг 1: Запишите первые несколько чисел, кратных 9 и 12, отдельно.
• Шаг 2: Из всех кратных 9 и 12 сосредоточьтесь на кратных, которые являются общими для обоих чисел, то есть 9 и 12.
• Шаг 3: Теперь, из всех общих кратных, вынесите наименьшее общее кратное. Это будет LCM 9 и 12.

LCM 9 и 12 можно получить, используя метод перечисления:

• Число, кратное 9, равно 9, 18, 27, 36, 45, 54, 63, 72, 81. , 90, 99, 108,…
• Число, кратное 12, равно 12, 24, 36, 48, 60, 72, 84, 9.6, 108,…
• Здесь ясно, что наименьшее общее кратное равно 36. Итак, НОК 9 и 12 равно 36.

НОК 9 и 12 Использование метода деления

Метод деления один из методов нахождения LCM. Чтобы найти НОК 9 и 12 методом деления, разделите 9 и 12 на наименьшее простое число, которое делится на любое из них. Затем полученные простые множители будут использоваться для расчета окончательного НОК для 9 и 12.

Выполните следующие шаги, чтобы найти НОК для 9.и 12, используя метод деления:

• Шаг 1: Запишите числа, для которых вам нужно найти НОК, то есть 9 и 12 в данном случае, через запятую.
• Шаг 2: Теперь найдите наименьшее простое число, которое делится либо на 9, либо на 12.
• Шаг 3: Если какое-либо из чисел из числа 9 и 12 не делится на соответствующее простое число, напишите, что номер в следующем ряду сразу под ним и продолжайте.
• Шаг 4: Продолжайте делить числа, полученные после каждого шага, на простые числа, пока не получите результат 1 во всей строке.
• Шаг 5: Теперь перемножьте все простые числа, и конечным результатом будет НОК 9 и 12.

МОК 9 и 12 можно получить, используя метод деления: Факторы Первый номер Второй номер 2 9 12 2 9 6 3               9 3 3 3 1   1 1

Итак, НОК чисел 9 и 12 = 2 * 2 * 3 * 3 = 36

Какая формула для нахождения НОК чисел 9 и 12?

LCM из 9 и 12 можно рассчитать по формуле:

LCM (9, 12) = (9 * 12) / HCF (9, 12),
, где HCF — наибольший общий множитель или наибольший общий делитель чисел 9 и 12.

Другая формула, с помощью которой НОК чисел 9 и 12 может быть найдено:
9 * 12 = НОК (9, 12) * ДКФ (9, 12), то есть

Произведение 9 и 12 равно произведению его НОК и ДКФ.

Проблемы, основанные на LCM 9 и 12

Вопрос 1: Что такое LCM 4, 9 и 12?
Решение:
Найдем НОК 4, 9, и 12, используя метод деления:
Чтобы найти НОК 4, 9 и 12, используя метод деления, сначала мы найдем наименьшее простое число, которое делится либо на 4, либо на 9, либо на 12. Если какое-либо из чисел среди 4, 9 и 12 не делится на соответствующее простое число, мы запишем это число в следующей строке сразу под ним и продолжим дальше. Мы будем продолжать делить числа, полученные после каждого шага, на простые числа, пока не получим результат как 1 во всей строке. Мы умножим все простые числа, и конечным результатом будет НОК 4, 9., and 12.

Prime Factors	First Number	Second Number	Third Number
2	4	9	12
2	2	9	6
3	1	9	3
3	1	3	1
	1	1	1

SO, LCM 4, 9 и 12 = 2 * 2 * 3 * 3 = 36

Вопрос 2: Если LCM из двух номеров. равно 36, HCF равно 3, а одно из чисел равно 12, найдите другое число.
Решение:
Как мы знаем,
произведение двух чисел = LCM * HCF
Дано, что
одно из чисел = 12, LCM = 36 и HCF = 3
Пусть другое число равно x .
Итак, 12 * х = 36 * 3
x = (36 * 3) / 12
x = 108 / 12
x = 9
Следовательно, второе число равно 9.

 

Вопрос 3. Найдите НОК 9 и 12, используя метод простой факторизации.
Решение:
Чтобы найти НОК чисел 9 и 12, используя метод разложения на простые множители, сначала мы найдем простые делители чисел 9 и 12, используя метод повторного деления. Затем мы запишем все простые множители в их экспоненциальных формах и перемножим простые множители, имеющие наибольшую степень. Окончательный результат после умножения будет LCM 9и 12.

• Разложение числа 9 на простые множители можно выразить как 3 * 3 = 3 ¹ * 3 ¹ = 3 ²
• Разложение числа 12 на простые множители можно выразить как 2 * 2 * 3 = 1 2 9004 1 * 2 ¹ * 3 ¹ = 2 ² * 3 ¹
• Итак, НОК 9 и 12 = 2 ² * 3 3 * 3 * ^{. = 36}

 

Вопрос 4: Найдите НОК чисел 9 и 12, используя метод деления.

Решение:

Чтобы найти НОК чисел 9 и 12, используя метод деления, сначала мы найдем наименьшее простое число, которое делится либо на 9, либо на 12. Если любое из чисел между 9 и 12 равно не делится на соответствующее простое число, мы запишем это число в следующей строке сразу под ним и продолжим дальше. Мы будем продолжать делить числа, полученные после каждого шага, на простые числа, пока не получим результат как 1 во всей строке. Мы умножим все простые числа, и конечным результатом будет НОК 9.and 12.

Prime Factors	First Number	Second Number
2	9	12
2	9	6
3		3
3	3	1
	1	1

9000 2

5

9002

9005

и 12 = 2 * 2 * 3 * 3 = 36

 

Вопрос 5: Какое наименьшее возможное число делится на 9 и 12?
Решение:
Есть три метода, с помощью которых можно найти наименьшее возможное число, которое делится на 9 и 12.
Мы найдем его методом листинга. Во-первых, мы запишем несколько первых чисел, кратных 9 и 12, отдельно. Из всех кратных 9 и 12 мы сосредоточимся на кратных, которые являются общими для обоих чисел.
Затем из всех общих кратных выберем наименьшее общее кратное. Это будет НОК 9 и 12.

• Кратные 9 равны 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108,…
• Кратные 12 равны 12, 24, 36, 48, 60, 72, 84, 96, 108,…
• Здесь ясно, что наименьшее общее кратное равно 36.

Таким образом, НОК чисел 9 и 12 равно 36.

Получите 1 Индивидуальные уроки математики от лучших преподавателей!
Изучите онлайн-услуги Wiingy по обучению математике, чтобы изучить арифметику, алгебру, исчисление и многое другое

Часто задаваемые вопросы (FAQ)

Считается ли число 72 LCM 9 и 12?
72 не считается НОК 9 и 12. 72 является общим кратным 9 и 12. Но это не наименьшее распространенное число, которое делится на 9 и 12, и при нахождении НОК вы должны сосредоточиться на наименьшем общем числе.