Решить линейное уравнение методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Как решить линейное уравнение: пошаговая инструкция

1. Что такое линейное уравнение?
2. Как решать линейные уравнения?
3. Какие операции можно выполнять с линейными уравнениями?
4. Решение системы линейных уравнение методом Крамера
5. Решение систем уравнений методом Гаусса

Линейные уравнения школьники решают, начиная с седьмого класса. С каждым годом примеры усложняются и для их успешного решения необходимо хорошо знать материал предыдущих годов. 

 

Старшеклассники и студенты технических специальностей оперируют целыми системами линейных уравнений и решают их разными методами. С понятием линейных уравнений и несколькими способами решения систем уравнений вы познакомитесь в этой статье.

Что такое линейное уравнение?

Уравнение вида а*х=b, где а и b – это какие-то числа, называется линейным. Если ученика 7 класса попросят решить уравнение Х*2=6, он сразу же ответит, что Х=3. Это и есть линейное уравнение. Записывается в рабочей тетради оно следующим образом.

 

Х*2=6
Х=3

 

Число, при котором уравнение превращается в верное равенство, называется корнем уравнения.

 

3х=7 – это линейное уравнение, потому что в нем на месте а и b стоят определенные числа и присутствует переменная х. А уравнение х2+х=9 нельзя назвать линейным, потому что в общем виде линейного уравнения переменная находится в первой степени, а в данном примере х во второй степени.

 

Рассмотрим еще одно уравнение.

В нем присутствует деление на переменную, которое отсутствует в общем виде линейного уравнение, поэтому данное уравнение не является линейным. 

 

Подытожим: в линейном уравнении переменная должна быть в первой степени и на нее нельзя делить.

Как решать линейные уравнения?

Рассмотрим решение на примере следующего линейного уравнения.

11 * х = -132

Все линейные уравнения такого вида решаются по аналогии с примерами 5 и 6 класса, в которых присутствовали два множителя и произведение.

Чтобы найти второй множитель, нужно произведение разделить на первый множитель.

х = -132 / 11

х = -12

Такое уравнение имеет один корень. Но бывают и другие ситуации. Например, у уравнения 0*Х=13 нет корней, потому что на ноль делить нельзя. А в уравнении 0*Х=0 бесконечно много корней, потому что любое число при умножении на ноль будет равно нулю. Поэтому линейное уравнение может иметь:

• Один корень;
• Ни одного корня;
• Бесконечно много корней (только в варианте 0*Х=0).

 

Читайте также: Логарифмы: свойства и формулы

Какие операции можно выполнять с линейными уравнениями?

Для успешного решения линейных уравнений, необходимо уметь выполнять с ними базовые действия.

Перенос слагаемых между частями

Для решения некоторых линейных уравнений необходимо перенести слагаемые из одной части в другую и при этом сменить знак на противоположный.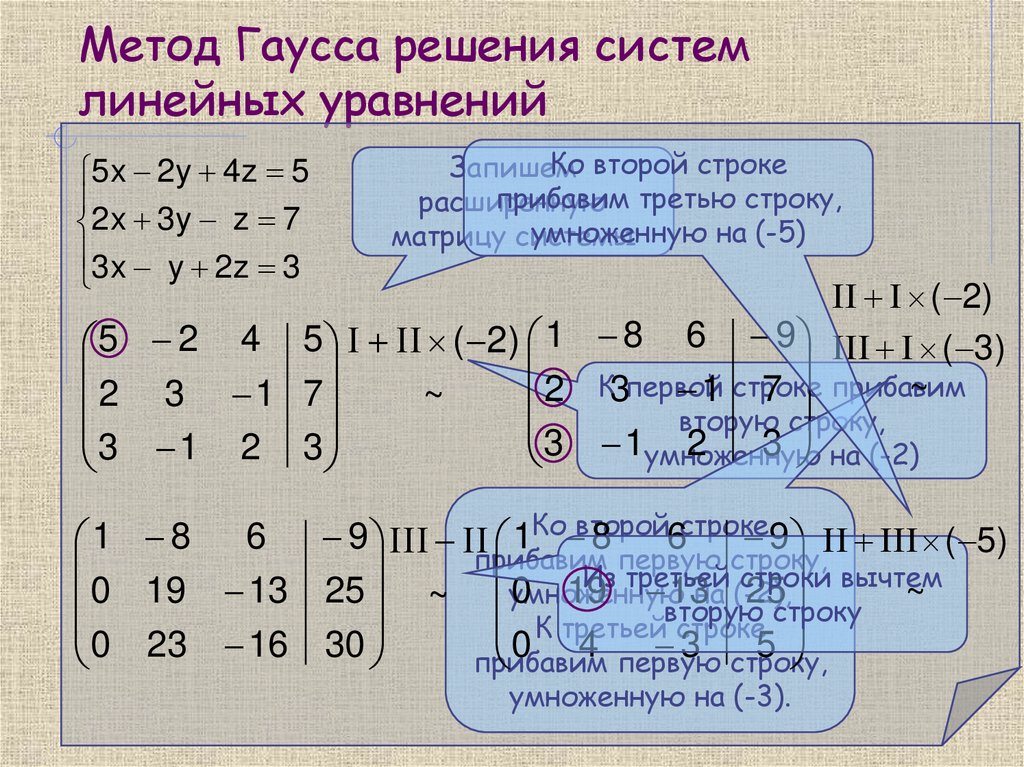 Рассмотрим на примере:

2х + 7 = -3х + 7

Все, что содержит переменную х, переносится влево, остальные числа – вправо. –3х перемещается в левую часть вместе со знаком, минус превращается в плюс.

2х + Зх

Число 7 из левой части переносится в правую, но уже со знаком минус.

2х + Зх = 7 — 7

Далее необходимо к 2х добавить 3х, а от 7 отнять 7.

5х = 0

Для нахождения второго множителя, необходимо произведение поделить на первый множитель.

х = 0

Умножение/деление частей уравнения на определенное число

В следующем линейном уравнении присутствуют дроби. 

Но не пугайтесь, от них можно легко избавиться. Для этого нужно воспользоваться одной доступной опцией: обе части линейного уравнения можно умножать или делить на одно и то же число.

 

Чтобы избавиться от дробей в линейном уравнении, нужно две части умножить на знаменатель, в данном случае – на 5.

х — 4 = 5

х = 5 + 4

х = 9

Читайте также: Как научиться собирать кубик Рубика

Решение системы линейных уравнение методом Крамера

Ученики 9 класса знакомятся с более сложными примерами и решают системы уравнений. Часто для этого используют формулу Крамера. 

 

Чтобы воспользоваться методом Крамера для решения системы уравнений, понадобится:

• Условие задачи;
• Четыре матрицы.

 

В верхнем ряду, возле условия, расположена основная матрица решения с условным обозначением . Она получена из коэффициентов при х, у, z. Коэффициент при х в первом уравнении 1, во втором 3, в третьем -2. Эти числа расположены в первом столбце матрицы. 2, -1 и 2 являются коэффициентами у и образуют второй столбец основной матрицы. Коэффициенты z 1, -1 и 3 расположены в третьем столбце.

 

Вторая матрица с условным обозначением х, которая расположена на изображении ниже условия, образована из основной матрицы, с заменой первого столбца на числа из условия, которые стоит после знака равенства. То есть коэффициент х в первом уравнении 1 нужно заменить на -1, в двух остальных уравнениях происходит аналогичная замена.

 

Третья матрица с условным обозначением у, которая расположена справа от второй, образована из основной матрицы с заменой второго столбца на числа из условия, которые стоит после знака равенства.

Если во второй матрице мы первый столбец 1, 3, -2 меняли на -1,-1 и 5, то во теперь первый столбец остается без изменений, а числа -1,-1 и 5 заменяют 2, -1 и 2.

 

В третьей матрице необходимо заменить третий столбец числами из условия, которые стоят после знака равенства. 

 

Четвертая матрица с условным обозначением z расположена справа от третьей матрицы. Она образована из основной матрицы с заменой третьего столбца на числа из условия, которые стоит после знака равенства.

 

Принцип образования матриц отобразить графически.

 

Теперь нужно выполнить самую сложную часть решения и найти детерминанты этих матриц. Для матрицы 3х3 детерминант можно найти двумя способами. В данной статье подробнее разберем правило треугольника. 

 

Необходимо перемножить элементы матрицы, соединенные красной линией, а затем сложить их, после этого перемножить элементы, соединенные синей линией и вычесть их из сумы красных.

 

Разберем на примере основной матрицы.

Det = 1 * (-1) * 3 + 3 * 2 * 1 + 2 * (-1) * (-2) — (-2) * (-1) * 1 — 2 * 3 * 3 — 1 * 2 * (-1) =
= -3 + 6 + 4 — 2 -18 + 2 = -11

 

Детерминант основной матрицы = -11, второй = 0, третьей = 22, четвертой =-33.

 

Третья вещь, которая нужна для решения системы уравнений методом Крамера – это простые формулы, которые называются формулы Крамера.

Далее подставляем значения и находим ответ.

х = 0

у = -2

z = 3

 

Важно научиться решать системы линейных уравнений самостоятельно, потому что подобные задания часто включают в экзамен по математике. Если ученик воспользуется одним из общедоступных сайтов и решит систему уравнений онлайн, он получит верный ответ, но не получит знаний, необходимых для успешного написания контрольной, выпускного или вступительного экзамена. Если у вас возникают проблемы с решением систем уравнений, нужно обратиться за помощью к репетитору по математике.

 

Педагог поможет разобраться с линейными уравнениями и подтянуть другие темы по математике. Учитель проведет комплексную оценку знаний и исходя из результатов, составит план работы. Репетитор во время уроков ориентируется только на одного ученика, объясняет материал в комфортном для него темпе, при необходимости останавливается на сложных или важных для подопечного темах. Индивидуальные занятия с педагогом помогут подготовиться к следующему уроку, выпускному экзамену и поступлению в вуз.

 

Найти репетитора по математике или другому предмету вы можете на сайте BUKI.

Решение систем уравнений методом Гаусса

Метод Гаусса – один из универсальных методов решения линейных систем уравнений. Состоит он из двух этапов:

1. Прямой ход – исключение переменной из уравнения так, чтобы в уравнении осталась всего одна переменная.
2. Подставление найденных переменных для нахождения оставшихся неизвестных.

 

Для наглядности разберем ту же систему уравнений, что и в методе Крамера.

Для решения этого примера достаточно знаний девятого класса: нужно уметь умножать уравнение на число и складывать два уравнения вместе.  

 

В начале нужно к первому уравнению прибавить второе. Второе и третье уравнение пока остаются без изменений.

 

Далее необходимо прибавить к третьему уравнению первое уравнение и утроенное второе уравнение, то есть нужно все второе уравнение умножить на три и результат прибавить к первому и третьему.

 

Первое и второе уравнения переписывается без изменений, а в третьем нужно проделать вышеизложенные действия и сократить переменные.

Далее для удобства и наглядности второе уравнение выносится на первое место, первое смещается на место второго, третье остается без изменений.

Теперь снизу вверх находим переменные из уравнений.

Метод Гаусса универсален, потому что он позволяет найти решение системы уравнений, когда она имеет множество решений и когда не имеет решений вовсе.

 

Существует немало онлайн-калькуляторов, которые позволяют решать уравнения методом Гаусса онлайн. Их удобно использовать для контроля своей работы после самостоятельного решения системы уравнений. Но не стоит пользоваться ими как основным способом, иначе есть риск плохо усвоить тему и получить неудовлетворительную оценку на контрольной или экзамене.

 

Читайте также: Развиваем логическое мышление у ребенка: список лучших игр, задач и мультфильмов

3.2 Метод Гаусса для решения систем линейных уравнений (метод последовательного исключения)

Метод Гаусса заключается в следующем. Допустим, что в системе (5) коэффициент при первом неизвестном a₁₁ 0.

Исключим сначала неизвестное х₁ из всех уравнений системы (5), кроме первого. Для этого, прежде всего, разделим обе части первого уравнения на коэффициент a₁₁0; тогда получим новую систему, равносильную данной:

(6)

Умножим теперь первое уравнение системы (6) на a₂₁ и вычтем из второго уравнения. Затем умножим первое уравнение на a₃₁ и вычтем из третьего уравнения и т.д. В результате получим новую систему, также равносильную данной:

(7)

Здесь введены обозначения:

(8)

Разделим теперь второе уравнение системы (7) на коэффициент а’₂₂, предполагая, что он отличен от нуля; затем умножим второе уравнение полученной системы последовательно на а’₃₂, …, а’_i2…,…, а’_m2 и вычтем поочередно из соответствующих уравнений системы, кроме первого и второго.

Если, продолжая этот процесс, мы придем к системе, содержащей уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, то эта система несовместна. В том случае, когда система совместна, приходим либо к системе

(9)

(причем р < n), либо к системе

(10)

Система вида (9) называется

ступенчатой, а система вида (10) — треугольной.

В случае треугольной системы из последнего уравнения находим x_п=β_n, затем, подставляя значение x_п в предыдущее уравнение, находим x_п-т, и т.д.

Таким образом, если данная система уравнений (5) после выполнения ряда элементарных преобразований приводится к треугольной системе (10), то это означает, что система (5) является совместной и определенной.

Если же данная система (5) после элементарных преобразований приводится к ступенчатой системе (9), то система (5) совместна и неопределенна.

Перенося в каждом из уравнений системы (10) члены с неизвестными

x_p+1,…, x_n в правую часть, получим систему вида

(11)

Придавая неизвестным x_p+1,. .., x_n ,которые называются свободными, произвольные значения , получим треугольную систему, из которой последовательно найдем все остальные неизвестные x_p, x_p-1,…, x₁. Так как числа могут иметь различные значения, то исходная система (3.1) имеет бесчисленное множество решений.

Процесс нахождения коэффициентов треугольной системы (10) называется прямым ходом, а процесс получения ее решения – обратным ходом метода Гаусса.

Пример 3.1. Решить систему уравнений:

Решение.

Разделив все члены первого уравнения на коэффициент а₁₁=2 получаем систему

Сначала умножим все члены первого уравнения полученной системы на 3 и вычтем из второго уравнения; затем из третьего уравнения вычтем первое:

Разделим все члены второго уравнения на а’₂₂=0,5:

Умножим второе уравнение на –1,5 и вычтем из третьего. Тогда получим систему

из которой последовательно находим x₁=1; x₂=2; x₃=3.

Решение треугольной системы, а, следовательно, и равносильной ей первоначальной –– x₁=1; x₂=2; x₃=3. Данная система является совместной и определенной.

Ответ: x₁=1; x₂=2; x₃=3.

При решении примеров методом Гаусса необходимости выписывать системы (3.1), (3.2), (3.3), (3.5) и (3.6) нет. Все преобразования можно проводить над матрицами, составленными из коэффициентов этих систем.

Системе (3.1) соответствуют две матрицы А и В:

(12)

Матрица А называется матрицей системы и состоит из коэффициентов системы, матрица В называется расширенной матрицей и отличается от матрицы системы столбцом, состоящим из свободных членов уравнений системы. При решении системы (5) методом Гаусса элементарные преобразования системы заменяются соответствующими элементарными преобразованиями, выполняемыми над ее расширенной матрицей В.

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями¹ над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

Последний, (n + 1) столбец этой матрицы содержит решение системы.

Пример 3.2. Решить систему уравнений:

Решение.

Таблица 3.1

Шаг	a(k)i1	a(k)i2	a(k)i3	a(k)i4	a(k)i5	a(k)i6
	1	0,17	0,25	0,54	0,3	-1,76
I	0,47	1	0,67	-0,32	0,5	-2,32
	-0,11	0,35	1	-0,74	0,7	-1,20
	0,55	0,43	0,36	1	0,9	-3,24
	1	0,17	0,25	0,54	0,3	-1,76
II		0,9201	0,7875	-0,5738	0,3590	-1,4928
		0,3687	0,9725	0,6806	0,7330	-1,3936
		0,3365	0,4975	0,7030	0,7350	-2,2720
		1	0,8559	-0,6236	0,3902	-1,6224
III			0,6569	-0,4507	0,5891	-0,7954
			0,2095	0,9128	0,6037	-1,7261
IV			1	-0,6861	0,8968	-1,2108
				1,0565	0,4158	-1,4724
				1	0,3936	-1,3937
V			1		1,1668	-2,1670
		1			-0,3630	-0,6368
	1				0,4409	-1,4409

Порядок заполнения таблицы.

Прямой ход.

1. Записываем коэффицненты данной системы в четырех строках и пяти столбцах шага I.

2. Суммируем все коэффициенты по строке и записываем сумму с обратным знаком в последний столбец, т.е. . Тогда сумма всех элементов каждой из четырех начальных строк будет равна нулю.

3. Выбираем из первого столбца главный элемент и меняем местами строку, содержащую этот элемент, с первой. Пусть главным элементом будет a⁽⁰⁾₁₁. Делим все числа, стоящие в первой строке, на a⁽⁰⁾₁₁ и записываем в первую строку шага II.

4. По формулам

a^(k)_kj= a^(k-1)_kj/ a^(k-1)_kk, a^(k)_ij= a^(k-1)_ij — a^(k-1)_ik a^(k)_kj (13)

где k+1jn+1, k+1in, k=1. .n (^a(0)_ij=a_ij, i,j=1..n+1).

Вычисляем коэффициенты a⁽¹⁾_ij, i=2..4, j=2..6. Результаты записываем в соответствующие строки шага II. С элементами последнего столбца поступаем так же, как с элементами предыдущих столбцов.

5. Для проверки правильности вычислений находим сумму элементов каждой строки. Величина суммы должна отличаться от нуля в пределах ошибок округления. Большое отклоненне от нуля свидетельствует о наличии грубой ошибки в вычислениях.

6. Среди элементов a⁽¹⁾₂₂, a⁽¹⁾_32, a⁽¹⁾₄₂ выбираем главный элемент и поступаем, как в п. 3. Пусть a⁽¹⁾₂₂^— главный элемент. Делим на него вторую строку шага II и результаты записываем в первую строку шага III .

7. По формулам (13) вычисляем коэффицциенты a⁽²⁾_ij, i=3..4, j=3..6. Результаты записываем во вторую и третью строки шага III.

8. Проверяем правильность произведенных вычислений (см. п. 5).

9. Пусть a⁽²⁾₃₃ главный элемент. Делим на него вторую строку шага III и результаты записываем в первую строку шага IV.

10. По формулам (3.9) вычисляем a⁽³⁾_4j, j=4..6. Результаты записываем во вторую строку шага IV.

11. Проверяем правильность вычислений (см. п. 5).

Обратный ход.

1. В шаге V записываем единицы, как указано в табл. 4.

2. Вычисляем x₄= a⁽³⁾₄₅/a⁽³⁾₄₄, = a⁽³⁾₄₆/a⁽³⁾₄₄.