Свойства операций над векторами: Свойства линейных операций над векторами.

Свойства линейных операций над векторами.

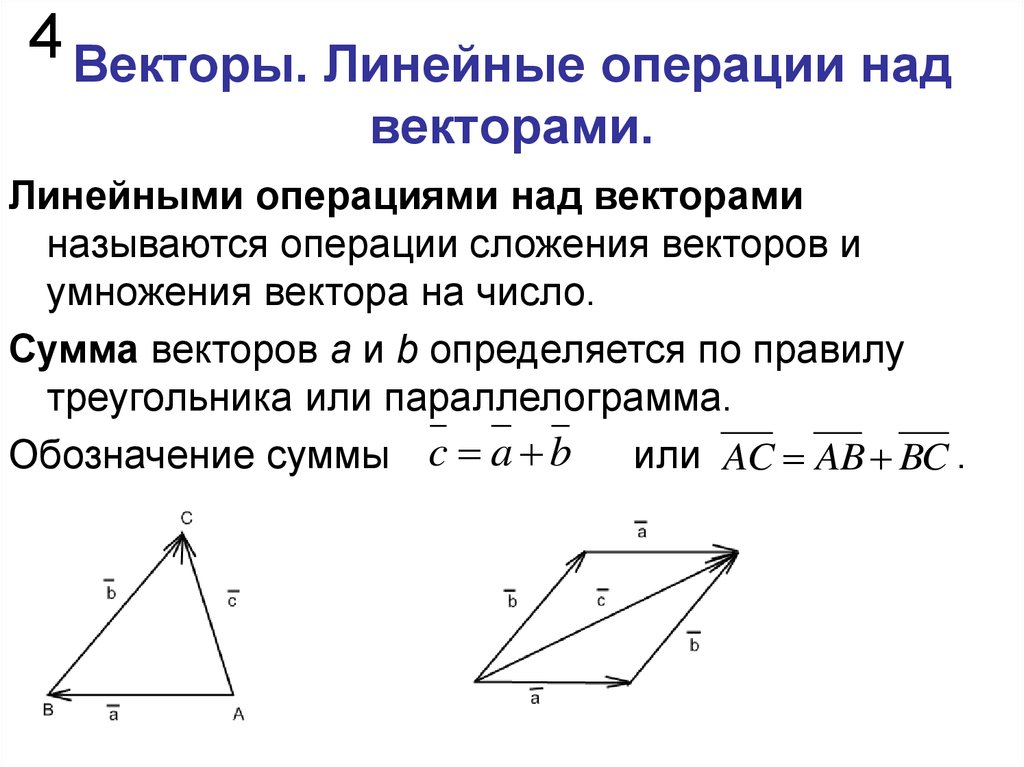
1. Сложение векторов коммутативно, т.е. для любых векторов и выполнено .

2. Сложение векторов ассоциативно, т.е. для любых векторов , и выполнено.

3. Прибавление нулевого вектора к любому вектору, не меняет последнего:.

4. Для любого вектора векторявляется противоположным, т.е..

5. Умножение вектора на число ассоциативно, т.е. для любых чисел ии любого вектора, выполнено.

6. Умножение вектора на число дистрибутивно по отношению к сложению чисел: .

7. Умножение вектора на число дистрибутивно по отношению к сложению векторов: .

8. Умножение вектора на единицу не меняет вектора: .

3. Понятие линейной зависимости векторов.

Определение 9. Пусть дана система векторов

1, ₂, …,_n и совокупность вещественных чисел . Тогда выражение виданазываетсялинейной комбинацией векторов, а числа называются коэффициентами линейной комбинации. Если некоторый вектор представлен как линейная комбинация векторов, т.е. в виде:, то говорят, что векторразложен по этим векторам.

Определение 10. Векторы ,, …,называютсялинейно зависимыми, если существует набор коэффициентов , одновременно не равных нулюи таких, что

.

Определение 11. Векторы называютсялинейно независимыми, если равенство нулю линейной комбинации этих векторов возможно лишь при всех коэффициентах одновременно равных нулю.

Определение 12. Базисом на прямой называется любой ненулевой вектор на этой прямой.

Определение 13. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Определение 14. Базисом в пространстве называются три линейно независимые вектора в этом пространстве, взятые в определенном порядке.

Теорема 1 (о разложении вектора по базису в пространстве R³)

Пусть даны три некомпланарные вектора: . Любой векторраскладывается по ним. Такое разложение единственно. Существует набор чиселтакой, что:

_.

Свойства линейно зависимой и линейно независимой системы векторов:

1. Если хотя бы один из векторов есть нуль вектор, то всевекторов линейно зависимы.

2. Если среди векторов какие-либовекторов линейно зависимы, то всевекторов линейно зависимы.

3. Для того чтобы два ненулевых вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарными.

4. Пусть — два неколлинеарных вектора плоскости. Любой компланарный с ними векторраскладывается по ним:. Такое разложение единственно.

5. Три компланарных вектора линейно зависимы. Три некомпланарных вектора пространства линейно независимы.

6. Любые четыре вектора пространства линейно зависимы.

7. Система векторов ₁, ₂, …,_n линейно зависима тогда и только тогда, когда один из них раскладывается в линейную комбинацию остальных.

4. Понятие о проекциях.

Пусть дан вектори ось,- угол между вектороми положительным направлением оси.и — основания перпендикуляров, опущенных из точек исоответственно (см. рис. 6).

Определение 15. Проекцией вектора на ось называется длина отрезка оси , взятая со знаком плюс, если векторобразует острый угол с направлением оси, и со знаком минус в противоположном случае.

Теорема 2. Проекция вектора на осьравна произведению длины вектора на косинус угла между вектором и осью: .

Следствие. При умножении вектора на некоторое числоего проекция умножается на это же число:.

Теорема 3 (о проекции суммы). Проекция суммы некоторого числа векторов на ось равна сумме проекций слагаемых векторов:,.

Операции над векторами, формулы и онлайн калькуляторы

Содержание:

• Сложение и вычитание векторов
• Умножение вектора на число

Определение

Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.

Сложение и вычитание векторов

Определение

Сложение векторов $\overline{a}$ и $\overline{b}$ осуществляется по правилу треугольника.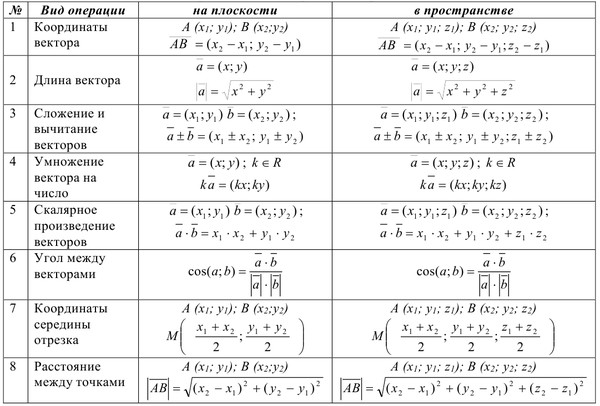

Суммой $\overline{a}+\overline{b}$ двух векторов $\overline{a}$ и $\overline{b}$ называют такой третий вектор $\overline{c}$, начало которого совпадает с началом $\overline{a}$, а конец — с концом $\overline{b}$ при условии, что конец вектора $\overline{a}$ и начало вектора $\overline{b}$ совпадают (рис. 1).

Для сложения векторов применяется также правило параллелограмма.

Определение

Правило параллелограмма — если два неколлинеарных вектора $\overline{a}$ и $\overline{b}$ привести к общему началу, то вектор $\overline{c}=\overline{a}+\overline{b}$ совпадает с диагональю параллелограмма, построенного на векторах $\overline{a}$ и $\overline{b}$ (рис. 2). Причем начало вектора $\overline{c}$ совпадает с началом заданных векторов.

Определение

Вектор $-\overline{a}$ называется противоположным вектором к вектору $\overline{a}$, если он коллинеарен вектору $\overline{a}$, равен ему по длине, но направлен в противоположную сторону вектору $\overline{a}$.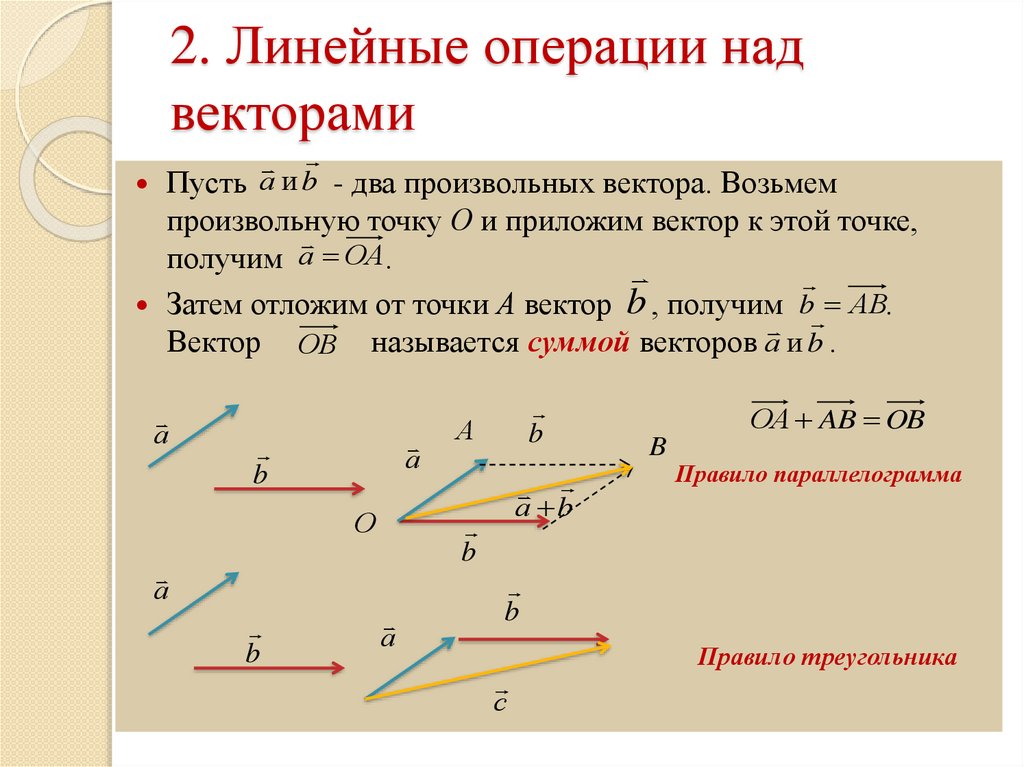

Операция сложения векторов обладает следующими свойствами:

1. $\overline{a}+\overline{b}=\overline{b}+\overline{a}$ — коммутативность
2. $(\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c})$ — ассоциативность
3. $\overline{a}+\overline{0}=\overline{a}$
4. $\overline{a}+(-\overline{a})=\overline{0}$

Определение

Разностью $\overline{a}-\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$ такой, что выполняется условие: $\overline{b}+\overline{c}=\overline{a}$ (рис. 3).

Умножение вектора на число

Определение

Произведением $\alpha \overline{a}$ вектора $\overline{a}$ на число $\alpha$ называется вектор $\overline{b}$, удовлетворяющий условиям:

1. $\overline{b}\|\overline{a}$
2. $|\overline{b}|=|\alpha||\vec{a}|$
3. $\overline{a} \uparrow \uparrow \overline{b}$, если $\alpha>0$, $\overline{a} \uparrow \downarrow \overline{b}$, если $\alpha \lt 0$.

Свойства умножения вектора на число:

1. $(\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a}$
2. $\alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b}$
3. $\alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a})$
4. $1 \cdot \overline{a}=\overline{a}$
5. $-1 \cdot \overline{a}=-\overline{a}$
6. $0 \cdot \overline{a}=\overline{0}$

Здесь $\overline{a}$ и $\overline{b}$ — произвольные векторы, $\alpha$, $\beta$ — произвольные числа.

Читать дальше: разложение вектора на составляющие.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Видео-урок: Свойства операций над векторами

Стенограмма видео

В этом видео мы научимся использовать свойства сложения и умножения векторов. Начнем с того, что вспомним, что вектор есть величина, имеющая как величину, так и направление. И мы можем представить вектор в виде подходящее пространство направленным отрезком линии определенной длины. В этом видео мы будем только рассматривать векторы в двух измерениях.

В двух измерениях мы можем представить величина и направление вектора с точки зрения горизонтального и вертикального изменения как показано. Если вектор 𝐯 имеет горизонталь компонент 𝑎 и вертикальный компонент 𝑏, мы можем думать об этом как о смещении 𝑎 единиц по горизонтали и смещение на 𝑏 единиц по вертикали. Мы можем использовать эту идею, чтобы добавить два векторы вместе, рассматривая их компоненты.

Графически сумма двух векторов 𝐮 и 𝐯 — их суммарное перемещение. Таким образом, мы можем сделать набросок конечная точка первого вектора как начальная точка второго вектора. Тогда сумма векторов имеет начальная точка первого вектора и конечная точка второго вектора как показано. Поскольку вектор 𝐮 плюс 𝐯 представляет смещение как вектора 𝐮, так и вектора 𝐯, оно будет иметь горизонтальная компонента равна сумме горизонтальных компонент вектора 𝐮 и вектор 𝐯 и вертикальная составляющая, равная сумме вертикальных составляющих вектор 𝐮 и вектор 𝐯.

Это можно записать более формально следующее. Для любых двух векторов из двух размеры 𝐮 с компонентами 𝑢 под один и 𝑢 под два и 𝐯 с компонентами 𝑣 sub one и 𝑣 sub two, то 𝐮 плюс 𝐯 имеет компоненты 𝑢 sub one плюс 𝑣 sub one и 𝑢 меньше двух плюс 𝑣 меньше двух. Так как сумма любых двух векторов в два измерения также являются двумерным вектором, мы можем сказать, что сложение векторов в два измерения закрыты. Это иногда называют свойство замыкания сложения векторов.

Хотя эта идея распространяется на более высокие измерения, в этом видео мы будем работать только в двух измерениях. Мы также можем определить скаляр умножение на вектор как скалярное умножение его компонентов.

Для любого вектора 𝐮 с компонентами 𝑢 меньше единицы и 𝑢 меньше двух и скаляр 𝑘, то 𝑘, умноженное на вектор 𝐮, имеет компоненты 𝑘𝑢 sub one и 𝑘𝑢 sub two. Графически скалярное умножение вектора скаляром 𝑘 — это расширение или увеличение вектора в множитель 𝑘. Сейчас мы рассмотрим пример как использовать эти определения, чтобы ответить на вопрос, связанный со свойством вектора добавление.

Завершите следующее: вектор один, девять плюс вектор пять, два равно вектору пять, два плюс что.

Здесь мы начнем с упрощения левая часть нашего уравнения. Начнем с того, что напомним, что найти сумма пары векторов, мы просто добавляем их соответствующие компоненты. В этом вопросе, чтобы добавить вектора один, девять и пять, два, складываем один и пять и потом отдельно девять и два. Это означает, что левая сторона нашего уравнения равен вектору шесть, 11. Если мы позволим недостающему вектору на правая часть имеет компоненты 𝑥 и 𝑦, мы можем упростить правую часть как показано. Вектор пять, два плюс вектор 𝑥, 𝑦 дает нам вектор пять плюс 𝑥, два плюс 𝑦.

Теперь мы можем приравнять две стороны наше уравнение. Шесть, 11 равно пяти плюс 𝑥, два плюс 𝑦. Чтобы два вектора были равны, мы известно, что их соответствующие компоненты должны быть равны. Это дает нам два уравнения, которые нам нужны решить: шесть равно пяти плюс 𝑥 и 11 равно двум плюс 𝑦. Вычитание пяти с обеих сторон наше первое уравнение, мы видим, что 𝑥 равно единице. И вычитая два с обеих сторон из нашего второго уравнения мы видим, что 𝑦 равно девяти. Таким образом, недостающий вектор равно единице, девяти. Вектор один, девять плюс вектор пять, два равен вектору пять, два плюс вектор один, девять.

Этот вопрос демонстрирует коммутативность сложения векторов, которую мы сейчас подытожим.

Для любых двух векторов из двух размеры 𝐮 и 𝐯, вектор 𝐮 плюс вектор 𝐯 равен вектору 𝐯 плюс вектор 𝐮. Графическая интерпретация имущество показано на схеме. Если два вектора 𝐮 и 𝐯 равны отличны от нуля, то мы можем изобразить эти векторы как стороны параллелограмма. Это означает, что вектор диагональ параллелограмма может быть представлена ​​как 𝐮 плюс 𝐯, так и 𝐯 плюс 𝐮. Поэтому эти выражения должны быть равным. В случае, когда один из vectors — нулевой вектор, это приводит нас к свойству аддитивной идентичности. Это одно из многих свойств векторное сложение и скалярное умножение в двух измерениях. Пока мы не будем доказывать это свойства в этом видео, мы перечислим их сейчас.

Для любых векторов 𝐮, 𝐯, 𝐰 и скаляров 𝑚 и 𝑛 рассмотрим следующее: во-первых, пять свойств добавление вектора. Мы уже видели этот вектор 𝐮 плюс вектор 𝐯 равен вектору 𝐯 плюс вектор 𝐮. это коммутативный свойство. Во-вторых, у нас есть вектор 𝐮 плюс вектор 𝐯 плюс вектор 𝐰 равен вектору 𝐮 плюс вектор 𝐯 плюс вектор 𝐰. Это известно как ассоциативный свойство и означает, что когда мы складываем три вектора, не имеет значения, какие два векторы, которые мы добавляем первыми. Далее у нас есть вектор 𝐮 плюс нулевой вектор равен вектору 𝐮. Это известно как добавка свойство тождественности и означает, что если мы добавим нулевой вектор к любому вектору, вектор остается неизменной.

Далее у нас есть обратная добавка свойство, которое утверждает, что вектор 𝐮 плюс отрицательный вектор 𝐮 равен нулю вектор. Добавление любого вектора к его обратному всегда дает нам нулевой вектор. Наконец, у нас есть устранение свойство. Это утверждает, что если 𝐮 плюс 𝐯 равно 𝐮 плюс 𝐰, то 𝐯 равно 𝐰. Это пять свойств добавление вектора.

Нам также необходимо рассмотреть пять свойства скалярного умножения векторов. Существуют две формы распределительное свойство. есть мультипликатив свойство тождества, свойство ассоциативности и, еще раз, исключение свойство. Умножая скаляр 𝑛 на векторная сумма 𝐮 плюс 𝐯 дает нам 𝑛𝐮 плюс 𝑛𝐯. И умножение суммы двух скаляры 𝑛 и 𝑚 вектором 𝐮 дает нам 𝑛𝐮 плюс 𝑚𝐮. Умножение любого вектора 𝐮 на скалярный дает нам вектор 𝐮. Это называется мультипликативным свойство идентичности. Ассоциативное свойство состояний что 𝑛𝑚, умноженное на вектор 𝐮, равно 𝑛, умноженному на 𝑚𝐮. Наконец, свойство исключения утверждает, что если 𝑛𝐮 равно 𝑛𝐯, то вектор 𝐮 должен быть равен вектору 𝐯.

Все 10 из этих свойств верны для векторов размерностью выше двух и, как упоминалось ранее, допустимым алгебраически. В оставшейся части этого видео мы рассмотрим примеры того, как мы можем использовать эти свойства для вычисления выражений с участием векторов.

Учитывая, что вектор 𝐚 равен единице, пять и вектор 𝐛 равен шести, два, найти 𝐚 плюс 𝐛 плюс минус 𝐚.

Мы можем ответить на этот вопрос непосредственно используя свойства сложения векторов. Во-первых, с помощью коммутативного свойство, которое утверждает, что вектор 𝐮 плюс вектор 𝐯 равен вектору 𝐯 плюс вектор 𝐮, мы можем переписать наше выражение 𝐚 плюс 𝐛 плюс минус 𝐚 как 𝐚 плюс минус 𝐚 плюс 𝐛. Далее воспользуемся добавкой обратное свойство, которое утверждает, что вектор 𝐮 плюс отрицательный вектор 𝐮 равен нулевой вектор. Применив это к нашему выражению, вектор 𝐚 плюс отрицательный вектор 𝐚 равен нулевому вектору. Итак, у нас остался нулевой вектор плюс вектор 𝐛.

Наконец, мы будем использовать добавку свойство идентичности, которое утверждает, что вектор 𝐮 плюс нулевой вектор равен вектор 𝐮. Это означает, что в нашем вопросе нулевой вектор плюс вектор 𝐛 просто равен вектору 𝐛. Нам говорят в вопросе, что вектор 𝐛 равен шести, двум. Это означает, что 𝐚 плюс 𝐛 плюс отрицательное 𝐚 также равно шести, двум. Вторым методом здесь было бы просто работайте с компонентами вектора 𝐚 и вектора 𝐛. Нам нужно добавить векторы один, пять и шесть, два, а затем добавить минус вектора один, пять. Мы можем распределить негатив по вектор, умножив все его компоненты на отрицательную единицу. Таким образом, третий вектор становится минус один, минус пять.

Теперь мы можем просто добавить три векторов путем нахождения суммы их соответствующих компонент. Начнем с прибавления единиц, шести и отрицательный. Это равно шести. Затем мы добавляем 𝑦-компоненты пять, два и минус пять, что дает нам два. Это подтверждает полученный нами ответ используя свойства сложения векторов. Вектор 𝐚 плюс вектор 𝐛 плюс отрицательный вектор 𝐚 равен шести, двум.

Теперь мы рассмотрим один последний пример.

Выполните следующие действия: два умножить на вектор два, пять плюс вектор пять, один равно чему плюс вектор 10, два.

Начнем этот вопрос с упрощение левой части уравнения. Во-первых, воспользуемся тем, что скалярное умножение является дистрибутивным по сравнению с векторным сложением. Это означает, что левая сторона становится два, умноженные на вектор два, пять плюс два, умноженные на вектор пять, один. Затем мы можем оценить скаляр умножение. Два умножить на вектор два, пять равно вектору два, умноженному на два, два, умноженному на пять. Это равно четырем, 10. Точно так же, умножая вектор пять, один на скаляр два дает нам вектор 10, два. Тогда мы можем приравнять это к в правой части нашего уравнения, и пусть компоненты неизвестного вектора равны 𝑥 и 𝑦.

Далее мы можем рассмотреть свойство устранения сложения векторов, которое гласит, что если вектор 𝐮 плюс вектор 𝐯 равен вектору 𝐮 плюс вектор 𝐰, тогда вектор 𝐯 равен вектору 𝐰. Вектор 10, два появляется в сумма в обеих частях нашего уравнения. Это означает, что другие векторы с каждой стороны также должны быть равны. Вектор четыре, 10 равен вектор 𝑥, 𝑦. Таким образом, мы можем сделать вывод, что недостающий вектор равен четырем, 10.

Мы закончим это видео резюмируя ключевые моменты. В этом видео мы увидели, что можем использовать свойства векторного сложения и скалярного умножения для упрощения выражения с использованием векторов. Пять свойств вектора дополнение, как показано. Они известны как коммутативные свойство, ассоциативное свойство, аддитивное тождественное свойство, аддитивное обратное свойство и свойство ликвидации соответственно. Пять свойств скаляра умножение векторов, как показано. Первые два здесь являются примерами распределительное свойство. Третье — мультипликативное. свойство идентичности, за которым следует ассоциативное свойство и, еще раз, ликвидационное свойство.

Мы можем доказать, что все эти свойства сохраняются при рассмотрении компонентов векторов. Пока мы рассмотрели только свойства для векторов в двух измерениях в этом видео, все эти свойства распространяется на векторы в более высоких измерениях.

Объяснение урока: Свойства операций над векторами

В этом объяснении мы узнаем, как использовать свойства сложения и умножения над векторами.

Начнем с того, что вспомним, что вектор — это величина, имеющая как величину, так и направление. Вектор может быть представлен в подходящем пространстве направленным отрезком линии определенной длины. Это означает, что мы можем думать о векторах как о определяющих движениях, путешествующих в заданном направлении на заданное расстояние.

Эта идея позволяет нам сложить два вектора вместе; если оба вектора можно рассматривать как движение в заданном направлении на заданное расстояние, то их сумму можно рассматривать как комбинацию обоих объединенных движений.

В двух измерениях мы можем выбрать пространство, где мы можем представить величину и направление в терминах горизонтального и вертикального изменения. В этом пространстве вектор (𝑎,𝑏) имеет горизонтальную составляющую 𝑎 и вертикальную составляющую 𝑏. Мы можем думать об этом как о смещении на 𝑎 единиц по горизонтали и смещении на 𝑏 единиц по вертикали.

Это означает, что мы можем сложить два вектора вместе, учитывая их компоненты. Графически сумма двух векторов ⃑𝑢 и ⃑𝑣 представляет собой комбинированное перемещение. Следовательно, мы можем нарисовать конечную точку первого вектора как начальную точку второго вектора. Затем сумма векторов имеет начальную точку первого вектора и конечную точку второго вектора, как показано на следующей диаграмме.

Поскольку вектор ⃑𝑢+⃑𝑣 представляет смещение как ⃑𝑢, так и ⃑𝑣, он будет иметь горизонтальную составляющую, равную сумме горизонтальных составляющих ⃑𝑢 и ⃑𝑣, и вертикальную составляющую, равную сумме вертикальных составляющих ⃑𝑢 и ⃑𝑣 . Это дает нам следующее.

Теорема: сложение векторов в двух измерениях

Для любых двух векторов в двух измерениях ⃑𝑢=(𝑢,𝑢) и ⃑𝑣=(𝑣,𝑣), ⃑𝑢+⃑𝑣=(𝑢+𝑣,𝑢+𝑣).

Поскольку сумма любых двух векторов в двух измерениях также является двумерным вектором, мы можем сказать, что сложение векторов в двух измерениях замкнуто. Это иногда называют свойством замыкания сложения векторов.

Эта идея распространяется на более высокие измерения; однако в этом объяснении мы будем работать только в двух измерениях.

Мы также можем определить скалярное умножение вектора как скалярное умножение его компонентов. Графически скалярное умножение вектора на скаляр 𝑘 представляет собой расширение вектора на коэффициент 𝑘.

Теорема: скалярное умножение векторов в двух измерениях

Для любых векторов ⃑𝑢=(𝑢,𝑢) и скаляра 𝑘, 𝑘⃑𝑢=(𝑘𝑢,𝑘𝑢).

Давайте рассмотрим пример использования этих определений для ответа на вопрос, связанный со свойством сложения векторов.

Пример 1: Коммутативность сложения векторов

Выполните следующие действия: (1,9)+(5,2)=(5,2)+(,).

Ответ

Начнем с упрощения левой части уравнения. Чтобы найти сумму пары векторов, вспомним, что ⃑𝑢=(𝑢,𝑢) и ⃑𝑣=(𝑣,𝑣).

Тогда, ⃑𝑢+⃑𝑣=(𝑢+𝑣,𝑢+𝑣).

В нашем случае ⃑𝑢=(1,9) и ⃑𝑣=(5,2); поэтому, (1,9)+(5,2)=(1+5,9+2)=(6,11).

Это равно правой части данного уравнения, поэтому мы будем называть недостающий вектор ⃑𝑤=(𝑤,𝑤).

Тогда мы можем упростить правую часть данного уравнения: (5,2)+(𝑤,𝑤)=(5+𝑤,2+𝑤).

Приравнивая это к правой части уравнения, получаем (6,11)=(5+𝑤,2+𝑤).

Чтобы два вектора были равны, их соответствующие компоненты должны быть равны. Если соответствующие компоненты равны, мы получаем два уравнения: 6=5+𝑤,11=2+𝑤.

Мы можем решить их, чтобы увидеть 𝑤=1 и 𝑤=9, поэтому недостающий вектор равен ⃑𝑤=(1,9).

Есть второй способ показать это. Начнем со сложения векторов в левой части уравнения: (1,9)+(5,2)=(1+5,9+2).

Затем воспользуемся коммутативным свойством сложения: (1+5,9+2)=(5+1,2+9).

Наконец, мы можем использовать сложение векторов: (5+1,2+9)=(5,2)+(1,9).

Следовательно, пропущенный вектор равен (1,9).

Второй метод из приведенного выше вопроса можно обобщить на любые два вектора: (𝑢,𝑢)+(𝑣,𝑣)=(𝑢+𝑣,𝑢+𝑣)=(𝑣+𝑢,𝑣+𝑢)=(𝑣,𝑣)+(𝑢,𝑢).  

Другими словами, для любых векторов в двух измерениях ⃑𝑢 и ⃑𝑣, ⃑𝑢+⃑𝑣=⃑𝑣+⃑𝑢.

Это известно как коммутативность сложения векторов. Графическая интерпретация этого свойства показана на следующей диаграмме.

Если ⃑𝑢 и ⃑𝑣 отличны от нуля, то мы можем изобразить эти векторы как стороны параллелограмма. Тогда вектор диагонали этого параллелограмма может быть представлен как ⃑𝑢+⃑𝑣, так и ⃑𝑣+⃑𝑢, поэтому эти выражения должны быть равны.

Нам нужно иметь дело со случаем, когда один или оба из этих векторов являются нулевыми. Если ⃑𝑢=(𝑢,𝑢), то мы можем показать, что (𝑢,𝑢)+⃑0=(𝑢,𝑢)+(0,0)=(𝑢+0,𝑢+0)=(𝑢,𝑢).

Следовательно, ⃑𝑢+⃑0=⃑𝑢.

Это называется свойством аддитивной идентичности, поскольку добавление нулевого вектора не меняет вектор.

Мы также можем продемонстрировать свойства, связанные со скалярным умножением. Например, для любого вектора ⃑𝑢=(𝑢,𝑢), 1⃑𝑢=1(𝑢,𝑢)=(1𝑢,1𝑢)=(𝑢,𝑢)=⃑𝑢.

Следовательно, 1⃑𝑢=⃑𝑢.

Это называется свойством мультипликативной идентичности, поскольку умножение вектора на скаляр 1 не влияет на его величину или направление.

Существует множество свойств сложения векторов и скалярного умножения в двух измерениях. Мы не будем доказывать все это; однако все они могут быть получены путем рассмотрения компонентов векторов.

Теорема: свойства векторного сложения и скалярного умножения в двух измерениях

Для любых векторов скаляров 𝑛 и 𝑚 рассмотрим следующее.

• Свойства сложения векторов: ⃑𝑢+⃑𝑣=⃑𝑣+⃑𝑢⃑𝑢+⃑𝑣+⃑𝑤=⃑𝑢+⃑𝑣+⃑𝑤⃑𝑢+⃑0=⃑𝑢⃑𝑢0+−⃑ 𝑢+⃑𝑣=⃑𝑢+⃑𝑤,⃑𝑣=⃑𝑤.(коммутативное свойство)(ассоциативное свойство )(additiveidentityproperty)(additiveinverseproperty)Ifthen(eliminationproperty)
• Свойства скалярного умножения векторов: 𝑛⃑𝑢+⃑𝑣=𝑛⃑𝑢+𝑛⃑𝑣(𝑛+𝑚)⃑𝑢=𝑛⃑𝑢+𝑚⃑𝑢1⃑𝑢=⃑𝑢(𝑛𝑚)⃑𝑢=𝑛𝑚)⃑𝑢= 𝑛⃑𝑢=𝑛⃑𝑣,⃑𝑢=⃑𝑣.(дистрибутивное свойство)(дистрибутивное свойство)(мультипликативное тождественное свойство)(ассоциативное свойство )Ifthen(свойство устранения)

Все эти свойства верны для векторов размерностей выше двух и доказуемы алгебраически. Давайте теперь посмотрим на пример того, как мы можем использовать эти свойства для вычисления выражения, включающего векторы.

Пример 2. Упрощение векторного выражения с использованием свойств векторных операций

Учитывая, что ⃑𝑎=(1,5) и ⃑𝑏=(6,2), найти ⃑𝑎+⃑𝑏+−⃑𝑎.

Ответ

Мы можем ответить на этот вопрос напрямую, используя свойства сложения векторов. Во-первых, мы воспользуемся коммутативным свойством сложения векторов, чтобы переупорядочить выражение. Это говорит о том, что для любых векторов ⃑𝑢 и ⃑𝑣 ⃑𝑢+⃑𝑣=⃑𝑣+⃑𝑢.

Применение этого выражения к нашему выражению дает ⃑𝑎+⃑𝑏+−⃑𝑎=⃑𝑎+−⃑𝑎+⃑𝑏.

Далее мы воспользуемся аддитивным обратным свойством сложения векторов, чтобы упростить выражение. Это говорит нам о том, что для любого вектора ⃑𝑢 ⃑𝑢+−⃑𝑢=⃑0.

Применяя это к нашему выражению вместе с ассоциативным свойством сложения векторов, получаем ⃑𝑎+−⃑𝑎+⃑𝑏=⃑0+⃑𝑏.

Наконец, мы будем использовать свойство аддитивной идентичности, которое говорит, что для любого вектора ⃑𝑢, ⃑𝑢+⃑0=⃑𝑢.

Следовательно, ⃑0+⃑𝑏=⃑𝑏=(6,2).

Второй метод заключается в работе с компонентами ⃑𝑎 и ⃑𝑏: ⃑𝑎+⃑𝑏+−⃑𝑎=(1,5)+(6,2)+(−(1,5)).

Распределим минус по вектору, умножив все его компоненты на −1: (1,5)+(6,2)+(-(1,5))=(1,5)+(6,2)+(-1,-5).

Теперь найдем сумму векторов, сложив вместе их соответствующие компоненты: (1,5)+(6,2)+(-1,-5)=(1+6-1,5+2-5)=(6,2).

В нашем следующем примере мы увидим демонстрацию того, как применять ассоциативное свойство сложения векторов. Метод сложения этих векторов вместе путем нахождения суммы их соответствующих компонентов можно обобщить, чтобы показать, что свойство ассоциативности верно для произвольных векторов.

Пример 3. Проверка ассоциативности сложения векторов в двух измерениях

Учтите, что ⃑𝑎=(1,6), ⃑𝑏=(3,7) и ⃑𝑐=(6,3).

1. Найти ⃑𝑎+⃑𝑏+⃑𝑐.
2. Найти ⃑𝑎+⃑𝑏+⃑𝑐.
3. Равен ⃑𝑎+⃑𝑏+⃑𝑐 ⃑𝑎+⃑𝑏+⃑𝑐?

Ответ

Часть 1

Чтобы найти сумму этих векторов, складываем соответствующие компоненты: ⃑𝑎+⃑𝑏+⃑𝑐=(1,6)+((3,7)+(6,3)).

Вычисление выражения в круглых скобках дает (1,6)+((3,7)+(6,3))=(1,6)+(3+6,7+3)=(1,6)+(9,10).

Сложение соответствующих компонентов этих векторов дает (1,6)+(9,10)=(1+9,6+10)=(10,16).

Часть 2

Для начала, ⃑𝑎+⃑𝑏+⃑𝑐=((1,6)+(3,7))+(6,3).

Вычисление выражения в круглых скобках дает ((1,6)+(3,7))+(6,3)=(1+3,6+7)+(6,3)=(4,13)+(6,3).

Сложение соответствующих компонентов этих векторов дает (4,13)+(6,3)=(4+6,13+3)=(10,16).

Часть 3

Мы показали, что оба этих выражения упрощаются и дают один и тот же вектор: (10,16). Это пример ассоциативного свойства сложения векторов. Мы можем использовать этот пример, чтобы обобщить это свойство.

Пусть ⃑𝑢=(𝑢,𝑢), ⃑𝑣=(𝑣,𝑣), и ⃑𝑤=(𝑤,𝑤).

Тогда, ⃑𝑢+⃑𝑣+⃑𝑤=((𝑢,𝑢)+(𝑣,𝑣))+(𝑤,𝑤)=(𝑢+𝑣,𝑢+𝑣)+(𝑤,𝑤)=((𝑢+𝑣) +𝑤,(𝑢+𝑣)+𝑤).

Затем мы можем использовать ассоциативное свойство сложения, чтобы переписать этот вектор: ((𝑢+𝑣)+𝑤,(𝑢+𝑣)+𝑤)=(𝑢+(𝑣+𝑤),𝑢+(𝑣+𝑤))=⃑𝑢+⃑𝑣+⃑𝑤.  

Следовательно, для любых векторов в двух измерениях ⃑𝑢, ⃑𝑣 и ⃑𝑤 ⃑𝑢+⃑𝑣+⃑𝑤=⃑𝑢+⃑𝑣+⃑𝑤.

В нашем следующем примере мы опишем свойство скалярного умножения и докажем, что это свойство выполняется для произвольных векторов и произвольного скаляра.

Пример 4. Описание свойства скалярного умножения

Какое свойство показывает, что 𝑐⃑𝑎+⃑𝑏=𝑐⃑𝑎+𝑐⃑𝑏?

Ответ

Это свойство называется распределительным свойством скалярного умножения над векторным сложением. Он утверждает, что для любых векторов ⃑𝑎=(𝑎,𝑎) и ⃑𝑏=(𝑏,𝑏) и скаляр 𝑐, 𝑐⃑𝑎+⃑𝑏=𝑐⃑𝑎+𝑐⃑𝑏.

Мы можем доказать это, рассмотрев компоненты ⃑𝑎 и ⃑𝑏: 𝑐⃑𝑎+⃑𝑏=𝑐((𝑎,𝑎)+(𝑏,𝑏))=𝑐(𝑎+𝑏,𝑎+𝑏).

Затем, чтобы умножить вектор на скаляр 𝑐, мы умножаем каждый компонент на 𝑐, что дает нам 𝑐(𝑎+𝑏,𝑎+𝑏)=(𝑐(𝑎+𝑏),𝑐(𝑎+𝑏)).

Далее, мы знаем, что умножение является дистрибутивным по отношению к сложению: (𝑐(𝑎+𝑏),𝑐(𝑎+𝑏))=(𝑐𝑎+𝑐𝑏,𝑐𝑎+𝑐𝑏).

Наконец, мы можем переписать это как (𝑐𝑎+𝑐𝑏,𝑐𝑎+𝑐𝑏)=(𝑐𝑎,𝑐𝑎)+(𝑐𝑏,𝑐𝑏)=𝑐(𝑎,𝑎)+𝑐(𝑏,𝑏)=𝏐⃑𝑧裡+𝑑  

Это свойство известно как распределительное свойство скалярного умножения над скалярным сложением.

В следующем примере мы будем использовать свойства векторов, чтобы помочь нам определить недостающий вектор из векторного уравнения.

Пример 5. Проверка распределительного свойства скалярного умножения при сложении векторов

Выполните следующие действия: 2((2,5)+(5,1))=(,)+(10,2).

Ответ

Начнем с упрощения левой части уравнения. Во-первых, мы используем тот факт, что скалярное умножение является дистрибутивным по сравнению с векторным сложением: 2((2,5)+(5,1))=2(2,5)+2(5,1).

Затем мы можем вычислить скалярное умножение: 2(2,5)+2(5,1)=(2×2,2×5)+(2×5,2×1)=(4,10)+(10,2).

Приравнивая это к левой части уравнения, получаем (4,10)+(10,2)=(,)+(10,2).

Затем мы можем упростить это уравнение, используя свойство исключения сложения векторов, которое говорит нам, что если ⃑𝑢+⃑𝑣=⃑𝑢+⃑𝑤, то ⃑𝑣=⃑𝑤.

Чтобы было понятно, воспользуемся коммутативным свойством сложения векторов, чтобы переписать наше уравнение в виде (10,2)+(4,10)=(10,2)+(,).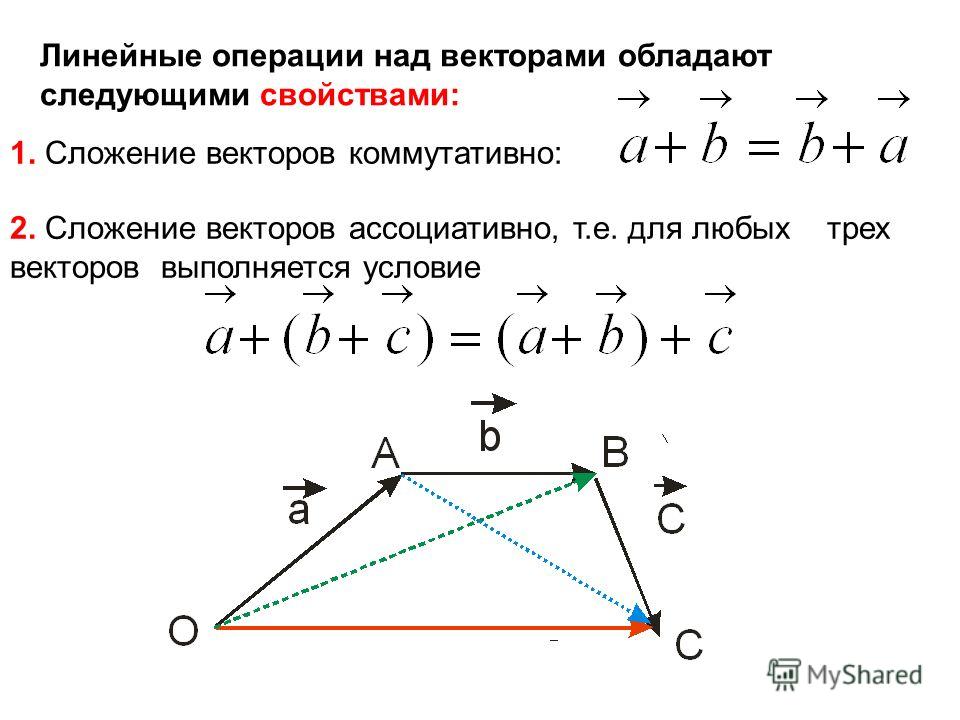

Затем мы исключаем вектор (10,2), что дает нам (4,10)=(,).

Следовательно, пропущенный вектор равен (4,10).

В нашем последнем примере мы докажем аддитивное свойство, обратное сложению векторов.

Пример 6. Описание свойства аддитивных инверсий для сложения векторов

Какое свойство сложения показывает, что ⃑𝑎+−⃑𝑎=⃑0?

Ответ

Это свойство называется аддитивным обратным свойством сложения векторов. Мы можем доказать это свойство, рассматривая компоненты вектора ⃑𝑎. Сначала пусть ⃑𝑎=(𝑎,𝑎).

Тогда, −⃑𝑎=(−1)(𝑎,𝑎)=(−𝑎,−𝑎).

Затем мы можем подставить это в наше выражение и вычислить: ⃑𝑎+−⃑𝑎=(𝑎,𝑎)+(−𝑎,−𝑎)=(𝑎−𝑎,𝑎−𝑎)=(0,0)=⃑0.

Это аддитивное обратное свойство состояний сложения векторов для любого вектора ⃑𝑎=(𝑎,𝑎), ⃑𝑎+−⃑𝑎=⃑0.

Давайте закончим повторением некоторых важных моментов этого объяснения.

Ключевые моменты

• Мы можем использовать свойства векторного сложения и скалярного умножения для упрощения выражений с участием векторов.

  No related posts.