Дифференциальные уравнения Бернулли в примерах решений
Дифференциальным уравнением Бернулли называется уравнение вида
,
где m ≠ 0 и m ≠ 1.
Таким образом, дифференциальное уравнение Бернулли обязательно содержит функцию y в степени, отличной от нуля и единицы.
В случае, если m = 0, уравнение является линейным, а в случае, если m = 1, уравнение является уравнением с разделяющимися переменными.
Дифференциальное уравнение Бернулли можно решить двумя методами.
- Переходом с помощью подстановки к линейному уравнению.
- Методом Бернулли.
Переход от уравнения Бернулли к линейному уравнению.
Уравнение делим на :
,
.
Обозначим . Тогда , откуда
. Переходя к новой
переменной, получим уравнение
Тогда , откуда
. Переходя к новой
переменной, получим уравнение
,
которое является линейным дифференциальным уравнение первого порядка. Его можно решить методом вариации константы Лагранжа или методом Бернулли.
Решение методом Бернулли.
Решение следует искать в виде произведения двух функций y = u ⋅ v. Подставив его в дифференциальное уравнение, получим уравнение
.
Из слагаемых, содержащих функцию u в первой степени, вынесем её за скобки:
.
Приравняв выражение в скобках нулю, то есть
,
получим дифференциальное уравнение с разделяющимися переменными для определения функции v.
Функцию u следует находить из дифференциального уравнения
,
которое также является уравнение с разделяющимися переменными.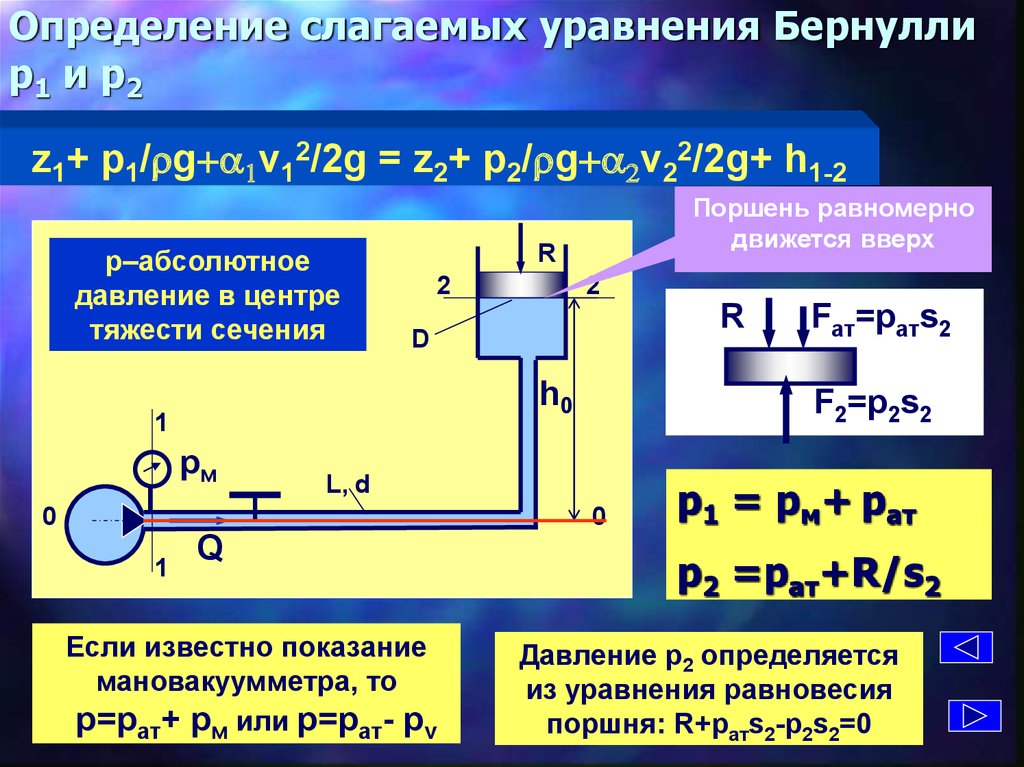
Пример 1. Решить дифференциальное уравнение Бернулли
.
Решение. Решим дифференциальное уравнение двумя методами.
1. Переход от уравнения Бернулли к линейному уравнению. Данное уравнение умножим на y³:
.
Введём обозначение , тогда , и приходим к уравнению
или
.
Решим его методом Бернулли. В последнее уравнение подставим z = u ⋅ v, z‘ = u‘v + uv‘:
,
.
Выражение в скобках приравняем нулю и решим полученное дифференциальное уравнение:
Полученную функцию v подставим в уравнение:
Тогда
2. Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v. Подставив
его и y‘ = u‘v + uv‘
в данное дифференциальное уравнение, получим
Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v. Подставив
его и y‘ = u‘v + uv‘
в данное дифференциальное уравнение, получим
Выражение в скобках приравняем нулю и определим функцию v:
Полученную функцию v подставим в уравнение и определим функцию u:
И, наконец, найдём решение данного дифференциального уравнения:
Пример 2. Решить дифференциальное уравнение Бернулли
.
Решение. Это уравнение, в котором m = −1. Применив подстановку y = u ⋅ v, получим
Выражение в скобках приравняем нулю и определим функцию v:
Полученную функцию v подставим в уравнение и определим функцию u:
Таким образом, получаем решение данного дифференциального уравнения:
.
Пример 3. Решить дифференциальное уравнение Бернулли
.
Решение. Это уравнение можно решить, используя подстановку y = u ⋅ v. Получаем
Подставляем v в данное уравнение и решаем полученное уравнение:
или
Разделим переменные:
и проинтегрируем обе части уравнения:
Далее используем подстановку
:
.
Введём обозначения:
Продолжаем:
Таким образом, получаем функцию u:
.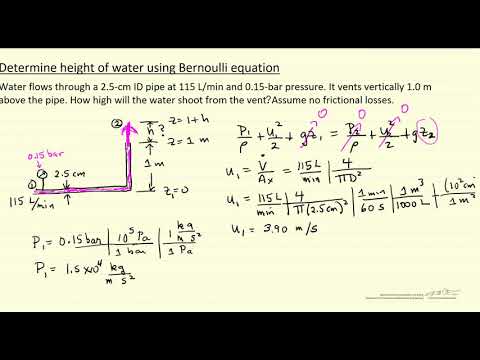
и решение данного дифференциального уравнения:
Нет времени вникать в решение? Можно заказать работу!
Пример 4. Решить задачу Коши для дифференциального уравненияпри условии .
Решение. Перепишем уравнение, перенося в левую сторону линейные слагаемые, а в правую — нелинейные:
.
Это уравнение Бернулли, которое можно решить, используя подстановку y = u ⋅ v, y‘ = u‘v + uv‘:
Выражение в скобках приравняем нулю и решим дифференциальное уравнение с разделяющимися переменными:
Подставим функцию v в данное уравнение и решим полученное дифференциальное уравнение:
Вычислим каждый интеграл отдельно. Первый:
Первый:
Второй интеграл интегрируем по частям. Введём обозначения:
Решаем:
Приравниваем друг другу найденные значения интегралов и находим функцию u:
Таким образом, общее решение данного дифференциального уравнения:
.
Используем начальное условие, чтобы определить значение константы:
Ищем частное решение, удовлетворяющее начальному условию:
В результате получаем следующее частное решение данного дифференциального уравнения:
.
И напоследок — пример с альтернативным обозначением производных — через дробь.
Пример 5. Решить дифференциальное уравнение Бернулли
.
Решение. Решим это уравнение первым из представленных в теоретической части методом — переходом к линейному уравнению. Разделив данное уравнение почленно на y³, получим
.
Введём новую функцию . Тогда
.
Подставляя эти значения в уравнение, полученное на первом шаге, получим линейное уравнение:
.
Найдём его общий интеграл:
,
.
Подставляя эти значение в полученное линейное уравнение, получаем
или
.
Приравниваем нулю выражение в скобках:
Для определения функции u получаем уравнение
.
Разделяем переменные:
Интегрируем по частям:
Таким образом, общий интеграл данного уравнения
или
.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Дифференциальные уравнения
Всё по теме «Дифференциальные уравнения»
Порядок дифференциального уравнения и его решения, задача Коши
Дифференциальные уравнения с разделяющимися переменными
Однородные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Дифференциальные уравнения второго порядка, допускающие понижение порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Поделиться с друзьями
Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли. (Семинар 34)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Презентация по Математическому Анализу Семинар 34
Линейные дифференциальные уравнения 1-го порядка.Уравнение Бернулли.
Дифференциальное уравнение вида
y’+P(x)y=Q(x) (1) относительно y,y’
Если функция
Q(x)=0 , то уравнение (1) принимает вид y’+P(x)y=0 (2)
называется однородным линейным дифференциальным уравнением. В этом случае
P ( x ) dx
переменные разделяются и общее решение уравнения (2) есть y Ce
(3)
Для решения неоднородного линейного уравнения (1) применяем так
называемый метод вариации произвольной постоянной.

Этот
метод
состоит
в
том,
что
сначала
находим
общее
решение
соответствующего однородного линейного уравнения, то есть соотношение (3).
Затем, полагая в этом соотношении величину С функцией от х, ищем решение
неоднородного уравнения (1) в виде (3).
Для этого подставляем в уравнение (1) y, y’, определяемые из (3), и из полученного
дифференциального уравнения определяем функцию С(х).
Таким образом, общее решение неоднородного уравнения (1) получаем в виде
y C ( x)e
P ( x ) dx
Для решения линейного уравнения (1) можно также применить подстановку y=uv (4) , где
u, v – функции от х.
Тогда уравнение (1) примет вид:
[u’+P(x)u]v+v’u=Q(x)
Если потребовать, чтобы
(5)
u’+P(x)u=0 (6), то из (6) найдем u, затем из (5) найдем v, а
следовательно, из (4) найдем y.
Уравнение Бернулли
Уравнение 1-го порядка вида
y’ P( x) y Q( x) y , где 0; 1 , называется
уравнением Бернулли. Оно приводится к линейному с помощью подстановки z y 1
Можно также непосредственно применять подстановку y=uv, или метод вариации
произвольной постоянной.

Примеры с решениями
1. Решить уравнение
Решение.
y ‘
2y
x3
x
Замена y=uv.
Далее решаем систему уравнений:
2
u
‘
u 0
x
v ‘ u x 3
u ‘ P ( x )u 0
v ‘ u Q ( x )
, то есть в нашем случае
Первое уравнение – уравнение с разделяющимися переменными:
du
2u
du
2dx
1
x6
1
3
5
ln u 2 ln x u 2 v’ 2 x v’ x v c
dx
x
u
x
6
x
x
Следовательно,
1
x6
y 2 (c )
6
x
2. Решить уравнение
y ‘ tgx y cos x
Решение. Соответствующее однородное уравнение есть y ‘ tgx y 0
Решая его, получим
y
C
cos x
.
.
Считая С функцией от х, дифференцируя, находим
y’
1 dC
sin x
C
2
cos x dx
cos x
Подставляя y и y’ в исходное уравнение, получим:
1 dC sin x
C
dC
1
1
2
2
C
tgx
cos
x
cos
x
C
(
x
)
cos
x
dx
x
sin 2 x C1
cos x dx cos 2 x
cos x
dx
2
4
Следовательно, общее решение исходного уравнения имеет вид
1
1
1
y
x
sin 2 x C1
4
2
cos x
.

3. Решить уравнение
Решение.
y’
4
y x
x
y
Это – уравнение Бернулли 2
1
Полагаем y=uv, получим:
u ‘ v uv’
4
4
uv x uv v u ‘ u v’ u x uv
x
x
(*)
4
Для определения функции u потребуем выполнения соотношения u ‘ u 0 u x 4
x
Подставляя это выражение в уравнение (*), получим:
1
v’ x x vx v ln | x | C
2
4
4
Следовательно, общее решение получим в виде:
1
y x ln | x | C
2
4
2
2
4. Решить уравнение
Решение.
y ‘
y
x2 y 4
x
Это – уравнение Бернулли.
Проинтегрируем его методом вариации произвольной постоянной.
Для этого интегрируем сначала соответствующее линейное однородное уравнение
,
y ‘
y
0 решение которого
x
y
C
x
.
Далее, ищем решение исходного уравнения Бернулли, полагая
y
C ( x)
C ‘ ( x) C ( x)
, y’
x
x
x2
Подстановка y, y’ в исходное уравнение дает
C ‘ ( x) C ( x) C ( x)
C ‘ ( x) C ( x)
2 C ( x)
x
x
x
x
x2
x2
x2
4
4
Интегрируем полученное уравнение:
dC ( x)
C ( x) 4
dx
1
1
3
ln
x
ln
C
C
(
x
)
3
x
3 ln( C / x)
3 C ( x)
Таким образом, общее решение исходного уравнения:
y
C ( x)
1
x
x3 3 ln( C / x)
Примеры для самостоятельного решения.
 {n}$, где $P\left(x\right)$ и $Q\left(x\right)$ — непрерывные функции, а $n$ — некоторое число, называется дифференциальным уравнением Якоба Бернулли.
{n}$, где $P\left(x\right)$ и $Q\left(x\right)$ — непрерывные функции, а $n$ — некоторое число, называется дифференциальным уравнением Якоба Бернулли.При этом на число $n$ накладываются ограничения:
- $n\ne 0$, так как при $n = 0$ дифференциальное уравнение представляет собой линейное неоднородное, и какой-то иной специальный метод решения в этом случае не нужен;
- $n\ne 1$, так как если мы имеем в качестве $n$ единицу, дифференциальное уравнение представляет собой линейное однородное, метод решения которого также известен.
Кроме того, не рассматривается специально тривиальное решение дифференциального уравнения Бернулли $y=0$.
Не следует путать дифференциальное уравнение математика Якоба Бернулли с законом Бернулли, названным в честь дяди его племянника, известного как Даниил Бернулли.
Замечание 1
Даниил Бернулли — физик, наиболее известная найденная им закономерность состоит в описании взаимосвязи скорости потока жидкости и давления. {3} }{2} -4\cdot x\cdot \ln \left|x\right|+C\cdot x$.
{3} }{2} -4\cdot x\cdot \ln \left|x\right|+C\cdot x$.
Давление в секции 1 из уравнения Бернулли Калькулятор
✖Удельный вес жидкости также известен как удельный вес, это вес на единицу объема жидкости. Например, удельный вес воды на Земле при 4 ° C составляет 9,807 кН / м3 или 62,43 фунта-силы / фут3.ⓘ Удельный вес жидкости [y] | Килоньютон на кубический метрНьютон на кубический сантиметрНьютон / кубический метрНьютон на кубический миллиметр | +10% -10% | |
✖Давление на участке 2 — это давление на участке трубы.ⓘ Давление на участке 2 [P2] | Атмосфера ТехническийАттопаскальБармикробарСантиметр Ртуть (0 ° С)Сантиметр воды (4 ° С)сантипаскальдекапаскальдесятипаскальДайн / кв.смэкса паскаль Фемто паскаль Foot морской воды (15 ° С)Нога воды (4 ° С)Нога воды (60 ° F)ГигапаскальГрамм-сила / кв. сантиметргектопаскальДюймовый Меркурий (32 ° F)Дюймовый Меркурий (60 ° F)КПа (4 ° С)КПа (60 ° F)кгс / кв. | +10% -10% | |
✖скорость в точке 2 – это скорость жидкости, проходящей через точку 2 в потоке.ⓘ Скорость в точке 2 [V2] | Сантиметр / часСантиметр / минутуСантиметр / секКосмическая скорость — ПервыйКосмическая скорость — ВторойКосмическая скорость — ТретьяСкорость ЗемлиЛапка / часЛапка / минутуНога / секКилометры / часКилометры / минутуКилометры / секМорской узелУзел (Великобритания)маакМаха (стандарт СИ)Метр / часМетр / минутуМетр / секмили / часмили / минутумили / секМиллиметр / часМиллиметр / минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% | |
✖Исходная высота на участке 2 — это высота потока на конкретном участке. | AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Исходная высота на участке 1 — это высота потока на конкретном участке. | AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Скорость в точке 1 — это скорость жидкости, проходящей через точку 1 в потоке. | Сантиметр / часСантиметр / минутуСантиметр / секКосмическая скорость — ПервыйКосмическая скорость — ВторойКосмическая скорость — ТретьяСкорость ЗемлиЛапка / часЛапка / минутуНога / секКилометры / часКилометры / минутуКилометры / секМорской узелУзел (Великобритания)маакМаха (стандарт СИ)Метр / часМетр / минутуМетр / секмили / часмили / минутумили / секМиллиметр / часМиллиметр / минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% |
|
✖Давление на участке 1 — это давление на участке трубы.ⓘ Давление в секции 1 из уравнения Бернулли [P1] |
Атмосфера ТехническийАттопаскальБармикробарСантиметр Ртуть (0 ° С)Сантиметр воды (4 ° С)сантипаскальдекапаскальдесятипаскальДайн / кв. |
⎘ копия |
👎
Формула
сбросить
👍
Давление в секции 1 из уравнения Бернулли Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Удельный вес жидкости: 9.81 Килоньютон на кубический метр —> 9810 Ньютон / кубический метр (Проверьте преобразование здесь)
Давление на участке 2: 10 Ньютон / квадратный миллиметр —> 10000000 паскаль (Проверьте преобразование здесь)
Скорость в точке 2: 57.91 Метр / сек —> 57.91 Метр / сек Конверсия не требуется
Базовая высота на сечении 2: 10 метр —> 10 метр Конверсия не требуется
Базовая высота на сечении 1: 10 метр —> 10 метр Конверсия не требуется
Скорость в точке 1: 3.05 Метр / сек —> 3.05 Метр / сек Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
11672704.0088103 паскаль —>11.6727040088103 Ньютон / квадратный миллиметр (Проверьте преобразование здесь)
< 10+ Уравнение движения Эйлера. Калькуляторы
Скорость на участке 1 из уравнения Бернулли
Скорость в точке 1 = sqrt(2*[g]*((Давление на участке 2/Удельный вес жидкости)+(0. 2)/[g])))
Идти
2)/[g])))
Идти
Приведенное давление пьезометрического напора для устойчивого невязкого потока
Давление = (Пьезометрический напор-Базовая высота на сечении 1)*Удельный вес жидкости Идти
Базовая высота с использованием пьезометрического напора для установившегося невязкого потока
Базовая высота на сечении 1 = Пьезометрический напор-Давление/Удельный вес жидкости Идти
Пьезометрический напор для установившегося невязкого потока
Пьезометрический напор = (Давление/Удельный вес жидкости)+Высота Идти
Скорость потока при заданном скоростном напоре для установившегося невязкого потока
Скорость = sqrt(Скоростной напор*2*[g]) Идти
Скоростной напор для устойчивого невязкого потока
Скоростной напор = (Скорость^2)/2*[g] Идти
Давление с использованием напора для устойчивого невязкого потока
Давление = Удельный вес жидкости*Напор Идти
Напор для устойчивого невязкого потока
Напор = Давление/Удельный вес жидкости Идти
Давление в секции 1 из уравнения Бернулли формула
Давление на участке 1 = Удельный вес жидкости*((Давление на участке 2/Удельный вес жидкости)+(0. 2)/[g])))
2)/[g])))
Что такое уравнение Бернулли жидкости?
Принцип Бернулли — это идея динамики жидкости. В нем говорится, что по мере увеличения скорости жидкости давление уменьшается. Более высокое давление подталкивает (ускоряет) жидкость к более низкому давлению. Таким образом, любое изменение скорости жидкости должно сопровождаться изменением давления (силы).
Share
Copied!
Решение методом вариации произвольных постоянных онлайн. Метод вариации произвольных постоянных
Метод вариации произвольной постоянной, или метод Лагранжа — еще один способ решения линейных дифференциальных уравнений первого порядка и уравнения Бернулли.
Линейные дифференциальные уравнения первого порядка — это уравнения вида y’+p(x)y=q(x). Если в правой части стоит нуль: y’+p(x)y=0, то это — линейное однородное уравнение 1го порядка. Соответственно, уравнение с ненулевой правой частью, y’+p(x)y=q(x), — неоднородное линейное уравнение 1го порядка.
Соответственно, уравнение с ненулевой правой частью, y’+p(x)y=q(x), — неоднородное линейное уравнение 1го порядка.
Метод вариации произвольной постоянной (метод Лагранжа) состоит в следующем:
1) Ищем общее решение однородного уравнения y’+p(x)y=0: y=y*.
2) В общем решении С считаем не константой, а функцией от икса: С=С(x). Находим производную общего решения (y*)’ и в первоначальное условие подставляем полученное выражение для y* и (y*)’. Из полученного уравнения находим функцию С(x).
3) В общее решение однородного уравнения вместо С подставляем найденное выражение С(x).
Рассмотрим примеры на метод вариации произвольной постоянной. Возьмем те же задания, что и в , сравним ход решения и убедимся, что полученные ответы совпадают.
1) y’=3x-y/x
Перепишем уравнение в стандартном виде (в отличие от метода Бернулли, где форма записи нам нужна была только для того, чтобы увидеть, что уравнение — линейное).
y’+y/x=3x (I). Теперь действуем по плану.
1) Решаем однородное уравнение y’+y/x=0. Это уравнение с разделяющимися переменными. Представляем y’=dy/dx, подставляем: dy/dx+y/x=0, dy/dx=-y/x. Обе части уравнения умножаем на dx и делим на xy≠0: dy/y=-dx/x. Интегрируем:
2) В полученном общем решении однородного уравнения будем считать С не константой, а функцией от x: С=С(x). Отсюда
Полученные выражения подставляем в условие (I):
Интегрируем обе части уравнения:
здесь С — уже некоторая новая константа.
3) В общее решение однородного уравнения y=C/x, где мы считали С=С(x), то есть y=C(x)/x, вместо С(x) подставляем найденное выражение x³+C: y=(x³+C)/x или y=x²+C/x. Получили такой же ответ, как и при решении методом Бернулли.
Ответ: y=x²+C/x.
2) y’+y=cosx.
Здесь уравнение уже записано в стандартном виде, преобразовывать не надо.
1) Решаем однородное линейное уравнение y’+y=0: dy/dx=-y; dy/y=-dx. Интегрируем:
Чтобы получить более удобную форму записи, экспоненту в степени С примем за новую С:
Это преобразование выполнили, чтобы удобнее было находить производную.
2) В полученном общем решении линейного однородного уравнения считаем С не константой, а функцией от x: С=С(x). При этом условии
Полученные выражения y и y’ подставляем в условие:
Умножим обе части уравнения на
Интегрируем обе части уравнения по формуле интегрирования по частям, получаем:
Здесь С уже не функция, а обычная константа.
3) В общее решение однородного уравнения
подставляем найденную функцию С(x):
Получили такой же ответ, как и при решении методом Бернулли.
Метод вариации произвольной постоянной применим и для решения .
y’x+y=-xy².
Приводим уравнение к стандартному виду: y’+y/x=-y² (II).
1) Решаем однородное уравнение y’+y/x=0. dy/dx=-y/x. Умножаем обе части уравнения на dx и делим на y: dy/y=-dx/x. Теперь интегрируем:
Подставляем полученные выражения в условие (II):
Упрощаем:
Получили уравнение с разделяющимися переменными относительно С и x:
Здесь С — уже обычная константа. В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.
В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.
3) В общее решение однородного уравнения y=C(x)/x подставляем найденную функцию С(x):
Получили такой же ответ, что и при решении способом Бернулли.
Примеры для самопроверки:
1. Перепишем уравнение в стандартном виде:y’-2y=x.
1) Решаем однородное уравнение y’-2y=0. y’=dy/dx, отсюда dy/dx=2y, умножаем обе части уравнения на dx, делим на y и интегрируем:
Отсюда находим y:
Выражения для y и y’ подставляем в условие (для краткости будем питать С вместо С(x) и С’ вместо C»(x)):
Для нахождения интеграла в правой части применяем формулу интегрирования по частям:
Теперь подставляем u, du и v в формулу:
Здесь С =const.
3) Теперь подставляем в решение однородного
Лекция 44. Линейные неоднородные уравнения второго порядка. Метод вариации произвольных постоянных. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. (специальная правая часть).
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. (специальная правая часть).
Социальные преобразования. Государство и церковь.
Социальная политика большевиков во многом диктовалась их классовым подходом. Декретом от 10 ноября 1917 г. уничтожена сословная система, отменены дореволюционные чины, титулы и награды. Установлена выборность судей; проведена секуляризация гражданских состояний. Установлено бесплатное образование и медицинское обслуживание (декрет от 31 октября 1918 г.). Женщины уравнивались в правах с мужчинами (декреты от 16 и 18 декабря 1917 г.). Декрет о браке вводил институт гражданского брака.
Декретом СНК от 20 января 1918 года церковь отделена от государства и от системы образования. Большая часть церковного имущества конфискована. Патриарх Московский и всея Руси Тихон (избран 5 ноября 1917 года) 19 января 1918 года предал анафеме Советскую власть и призвал к борьбе против большевиков.
Рассмотрим линейное неоднородное уравнение второго порядка
Структура общего решения такого уравнения определяется следующей теоремой:
Теорема 1. Общее решение неоднородного уравнения (1) представляется как сумма какого-нибудь частного решения этого уравнения и общего решения соответствующего однородного уравнения
Общее решение неоднородного уравнения (1) представляется как сумма какого-нибудь частного решения этого уравнения и общего решения соответствующего однородного уравнения
Доказательство . Нужно доказать, что сумма
есть общее решение уравнения (1). Докажем сначала, что функция (3) есть решение уравнения (1).
Подставляя сумму в уравнение (1) вместо у , будем иметь
Так как есть решение уравнение (2), то выражение, стоящее в первых скобках, тождественно равно нулю. Так как есть решение уравнения (1), то выражение, стоящее во вторых скобках, равно f(x) . Следовательно, равенство (4) является тождеством. Таким образом, первая часть теоремы доказана.
Докажем второе утверждение: выражение (3) есть общее решение уравнения (1). Мы должны доказать, что входящие в это выражение произвольные постоянные можно подобрать так, чтобы удовлетворялись начальные условия:
каковы бы ни были числа х 0 , y 0 и (лишь бы х 0 было взято из той области, где функции а 1 , а 2 и f(x) непрерывны).
Заметив, что можно представить в форме . Тогда на основании условий (5) будем иметь
Решим эту систему и определим С 1 и С 2 . Перепишем систему в виде:
Заметим, что определитель этой системы есть определитель Вронского для функций у 1 и у 2 в точке х=х 0 . Так как эти функции по условию линейно независимы, то определитель Вронского не равен нулю; следовательно система (6) имеет определенное решение С 1 и С 2 , т.е. существуют такие значения С 1 и С 2 , при которых формула (3) определяет решение уравнения (1), удовлетворяющее данным начальным условиям. Что и требовалось доказать.
Перейдем к общему методу нахождения частных решений неоднородного уравнения.
Напишем общее решение однородного уравнения (2)
Будем искать частное решение неоднородного уравнения (1) в форме (7), рассматривая С 1 и С 2 как некоторые пока неизвестные функции от х.
Продифференцируем равенство (7):
Подберем искомые функции С 1 и С 2 так, чтобы выполнялось равенство
Если учесть это дополнительное условие, то первая производная примет вид
Дифференцируя теперь это выражение, найдем :
Подставляя в уравнение (1), получим
Выражения, стоящие в первых двух скобках, обращаются в нуль, так как y 1 и y 2 – решения однородного уравнения. Следовательно, последнее равенство принимает вид
Следовательно, последнее равенство принимает вид
Таким образом, функция (7) будет решением неоднородного уравнения (1) в том случае, если функции С 1 и С 2 удовлетворяют уравнениям (8) и (9). Составим систему уравнений из уравнений (8) и (9).
Так как определителем этой системы является определитель Вронского для линейно независимых решений y 1 и y 2 уравнения (2), то он не равен нулю. Следовательно, решая систему, мы найдем как определенные функции от х :
Решая эту систему, найдем , откуда в результате интегрирования получаем . Далее подставим найденные функции в формулу , получаем общее решение неоднородного уравнения , где — произвольные постоянные.
Теоретический минимумВ теории дифференциальных уравнений существует метод, претендующий на достаточно высокую для этой теории степень универсальности.
Речь идёт о методе вариации произвольной постоянной, применимом к решению различных классов дифференциальных уравнений и их
систем.Это именно тот случай, когда теория — если вывести за скобки доказательства утверждений — минимальна, но позволяет добиваться
значительных результатов, поэтому основной акцент будет сделан на примерах.Общую идею метода сформулировать довольно просто. Пусть заданное уравнение (систему уравнений) решить сложно или вообще непонятно,
как его решать. Однако видно, что при исключении из уравнения некоторых слагаемых оно решается. Тогда решают именно такое упрощённое
уравнение (систему), получают решение, содержащее некоторое количество произвольных констант — в зависимости от порядка уравнения (количества
уравнений в системе). Затем полагают, что константы в найденном решении в действительности константами не являются, найденное решение
подставляется в исходное уравнение (систему), получается дифференциальное уравнение (или система уравнений) для определения «констант».
Существует определённая специфика в применении метода вариации произвольной постоянной к разным задачам, но это уже частности, которые будут
продемонстрированы на примерах.Отдельно рассмотрим решение линейных неоднородных уравнений высших порядков, т.е. уравнений вида
.
Общее решение линейного неоднородного уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения
данного уравнения. Предположим, что общее решение однородного уравнения уже найдено, а именно построена фундаментальная система решений (ФСР)
. Тогда общее решение однородного уравнения равно .
Нужно найти любое частное решение неоднородного уравнения. Для этого константы считаются зависящими от переменной .
Далее нужно решить систему уравнений
.
Теория гарантирует, что у этой системы алгебраических уравнений относительно производных от функций есть единственное решение.
При нахождении самих функций константы интегрирования не появляются: ищется ведь любое одно решение.В случае решения систем линейных неоднородных уравнений первого порядка вида
алгоритм почти не меняется. Сначала нужно найти ФСР соответствующей однородной системы уравнений, составить фундаментальную матрицу
системы , столбцы которой представляют собой элементы ФСР.Далее составляется уравнение
.
Решая систему, определяем функции , находя таким образом, частное решение исходной системы
(фундаментальная матрица умножается на столбец найденных функций ).
Прибавляем его к общему решению соответствующей системы однородных уравнений, которое строится на основе уже найденной ФСР.
Получается общее решение исходной системы.Примеры.
Пример 1. Линейные неоднородные уравнения первого порядка .
Рассмотрим соответствующее однородное уравнение (искомую функцию обозначим ):
.
Это уравнение легко решается методом разделения переменных:.
А теперь представим решение исходного уравнения в виде , где функцию ещё предстоит найти.
Подставляем такой вид решения в исходное уравнение:
.
Как видно, второе и третье слагаемое в левой части взаимно уничтожаются — это характерная черта метода вариации произвольной постоянной.Вот здесь уже — действительно, произвольная постоянная.
Таким образом,
.Пример 2. Уравнение Бернулли .
Действуем аналогично первому примеру — решаем уравнение
методом разделения переменных. Получится , поэтому решение исходного уравнения ищем в виде
.
Подставляем эту функцию в исходное уравнение:
.
И снова происходят сокращения:
.
Здесь нужно не забыть удостовериться, что при делении на не теряется решение. А случаю отвечает решение исходного
уравнения . Запомним его. Итак,
.
Запишем .
Это и есть решение. При записи ответа следует также указать найденное ранее решение , так как ему не соответствует никакое конечное значение
константы .Пример 3. Линейные неоднородные уравнения высших порядков .
Сразу заметим, что это уравнение можно решить и проще, но на нём удобно показать метод. Хотя некоторые преимущества
у метода вариации произвольной постоянной и в этом примере есть.
Итак, начинать нужно с ФСР соответствующего однородного уравнения.Напомним, что для нахождения ФСР составляется характеристическое
уравнение
.
Таким образом, общее решение однородного уравнения
.
Входящие сюда константы и предстоит варьировать. Составляем сист
Рассмотрим теперь линейное неоднородное уравнение
. (2)
Пусть y 1 ,y 2 ,.., y n — фундаментальная система решений, а — общее решение соответствующего однородного уравнения L(y)=0 . Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде
. (3)
Убедимся в том, что решение в таком виде существует. Для этого подставим функцию в уравнение. Для подстановки этой функции в уравнение найдём её производные. Первая производная равна
. (4)
При вычислении второй производной в правой части (4) появится четыре слагаемых, при вычислении третьей производной — восемь слагаемых и так далее. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (4) полагают равным нулю. С учётом этого, вторая производная равна
. (5)
(5)
По тем же, что и раньше, соображениям, в (5) также полагаем первое слагаемое равным нулю. Наконец, n-я производная равна
. (6)
Подставляя полученные значения производных в исходное уравнение, имеем
. (7)
Второе слагаемое в (7) равно нулю, так как функции y j , j=1,2,..,n, являются решениями соответствующего однородного уравнения L(y)=0. Объединяя с предыдущим, получаем систему алгебраических уравнений для нахождения функций C» j (x)
(8)
Определитель этой системы есть определитель Вронского фундаментальной системы решений y 1 ,y 2 ,..,y n соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C» j (x), j=1,2,…,n, а, следовательно, и C j (x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.
Изложенный метод называется методом вариации произвольной постоянной или методом Лагранжа.
Пример №1
. Найдём общее решение уравнения y»» + 4y» + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y»» + 4y» + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y 1 = e — x и y 2 = e -3 x . Решение неоднородного уравнения ищем в виде y = C 1 (x)e — x + C 2 (x)e -3 x . Для нахождения производных C» 1 , C» 2 составляем систему уравнений (8)
Рассмотрим соответствующее однородное уравнение y»» + 4y» + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y 1 = e — x и y 2 = e -3 x . Решение неоднородного уравнения ищем в виде y = C 1 (x)e — x + C 2 (x)e -3 x . Для нахождения производных C» 1 , C» 2 составляем систему уравнений (8)
C′ 1 ·e -x +C′ 2 ·e -3x =0
-C′ 1 ·e -x -3C′ 2 ·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
Окончательно получим
Пример №2
. Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
y(0) =1 + 3ln3
y’(0) = 10ln3
Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4
Корни характеристического уравнения: r 1 = 4, r 2 = 2
Следовательно, фундаментальную систему решений составляют функции: y 1 =e 4x , y 2 =e 2x
Общее решение однородного уравнения имеет вид: y
=C 1 ·e 4x +C 2 ·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C» i составляем систему уравнений:
C′ 1 ·e 4x +C′ 2 ·e 2x =0
C′ 1 (4e 4x) + C′ 2 (2e 2x) = 4/(2+e -2x)
Выразим C» 1 из первого уравнения:
C» 1 = -c 2 e -2x
и подставим во второе. В итоге получаем:
C» 1 = 2/(e 2x +2e 4x)
C» 2 = -2e 2x /(e 2x +2e 4x)
Интегрируем полученные функции C» i:
C 1 = 2ln(e -2x +2) — e -2x + C * 1
C 2 = ln(2e 2x +1) – 2x+ C * 2
Поскольку y
=C 1 ·e 4x +C 2 ·e 2x , то записываем полученные выражения в виде:
C 1 = (2ln(e -2x +2) — e -2x + C * 1) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x
C 2 = (ln(2e 2x +1) – 2x+ C * 2)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * 1 e 4x + C * 2 e 2x
Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3
Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * 1 + C * 2 = 3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C 1 e 2x + C 2 -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C 1 + C 2 +4 ln(3)+ ln(3)-2) = 4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
Получаем систему из двух уравнений:
3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
или
C * 1 + C * 2 = 2
4C 1 + 2C 2 = 4
или
C * 1 + C * 2 = 2
2C 1 + C 2 = 2
Откуда: C 1 = 0, C * 2 = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x
Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных Лагранжа. Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения.
Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения.
Содержание
См. также:
Метод Лагранжа (вариация постоянных)
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1) .
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка , также применим и для уравнений более высоких порядков.
Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.
Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений . Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.
Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.
Шаг 1. Решение однородного уравнения
Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2) .
Общее решение такого уравнения имеет вид:
(3) .
Здесь — произвольные постоянные; — n
линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.
Шаг 2. Вариация постоянных — замена постоянных функциями
На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x
:
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4) .
Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n
функций .
При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n
уравнений, из которых можно определить n
функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций .
Продемонстрируем это.
Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций .
Продемонстрируем это.
Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n
порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы и произведения :
.
Сгруппируем члены. Сначала выпишем члены с производными от ,
а затем — члены с производными от :
.
Наложим на функции первое условие:
(5.1) .
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1) .
Тем же способом находим вторую производную:
.
Наложим на функции второе условие:
(5.2) .
Тогда
(6.2) .
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций ,
к нулю.
Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k) ,
то первые производных по будут иметь наиболее простой вид:
(6.k) .
Здесь .
Находим n
-ю производную:
(6.n)
.
Подставляем в исходное уравнение (1):
(1) ;
.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7) .
В результате мы получили систему линейных уравнений для производных :
(5.1) ;
(5.2) ;
(5.3) ;
. . . . . . .
(5.n-1) ;
(7′) .
Решая эту систему, находим выражения для производных как функции от x
.
Интегрируя, получим:
.
Здесь — уже не зависящие от x
постоянные. Подставляя в (4), получаем общее решение исходного уравнения.
Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты a i
являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений , если известна фундаментальная система решений однородного уравнения (2).
Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений , если известна фундаментальная система решений однородного уравнения (2).
Примеры
Решить уравнения методом вариации постоянных (Лагранжа).
Решение примеров > > >
См. также:
Решение уравнений первого порядка методом вариации постоянной (Лагранжа)
Решение уравнений высших порядков методом Бернулли
Решение линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами линейной подстановкой
Понравилась статья? Поделись с друзьями:
Формула уравнения Бернулли в физике
Содержание:
- Определение и формула уравнения Бернулли
- Частные случаи уравнения Бернулли
- Следствие уравнения Бернулли
- Примеры решения задач
Определение и формула уравнения Бернулли
При рассмотрении движения жидкости очень часто считают, что перемещение одних частей жидкости относительно других не порождает сил трения. {2}}{2}=\rho g\left(h_{2}-h_{1}\right)=\rho g h \rightarrow v=\sqrt{2 g h}$$
{2}}{2}=\rho g\left(h_{2}-h_{1}\right)=\rho g h \rightarrow v=\sqrt{2 g h}$$
Ответ. $v=\sqrt{2 g h}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Используя уравнение Бернулли для идеальной несжимаемой жидкости, рассматривая истечение ее из маленького отверстия в широком открытом сосуде, получите формулу Торричелли: $v=\sqrt{2 g h}$, где h=h2-h1 — высота открытой поверхности жидкости над отверстием, v – скорость истечения жидкости из отверстия.
Решение. Сделаем рисунок.
Рассмотрим рис.2. Выделим в жидкости трубку тока с сечениями S1 – площадь открытой поверхности жидкости, S2 –
площадь сечения струи из отверстия. Будем считать, что для всех точек каждого из данных сечений скорость жидкости (v) и высота (h)
над избранным начальным уровнем одинаковы. {2}}{2}=g h_{2}-g h_{1} \rightarrow v=\sqrt{2 g h}(2.2)$$
{2}}{2}=g h_{2}-g h_{1} \rightarrow v=\sqrt{2 g h}(2.2)$$
здесь v – скорость, с которой вытекает жидкость из отверстия.
Что требовалось получить.
Читать дальше: Формула ЭДС.
Bernoulli’s principle calculator, online
Action
Calculation setup
Press what to calculate
Conditions at position one
pressure in position one (p1)
PakPaMPamm H₂Ocm H₂Om H₂Omm Hgbarmbaratatmkp/m²kp/cm²kp/mm²psilbf/ft²lbf/ yd²oz/in²in H₂Oft H₂Oin Hg
высота в первом положении (z1)
kmmcmmmmileydftin
скорость в первом положении (V1)
м/см/мин/часкм/скм/минкм/часфут/сфт/минид/смч
Размеры в одном
диаметр в первой позиции (D1)
сммммфуты
площадь поперечного сечения в первой позиции (A1)
мм²см²м²дюйм²фут²ярд²
Расход
объемный расход (qq/м3/м³с/с)
м ³ 9000 minl/hourft³/sft³/minft³/hourin³/sin³/minyd³/mingps UKgpm UKgph UKgps USgpm USgph US
Массовый расход (ṁ)
кг/skg/minkg/hourg/sg/ming/hourslug/sslug/minslug/hourlbm /slbm/minlbm/houroz/soz/minoz/час
Изменение давления (ΔP)
Pakpampamm h₂ocm h₂om h₂omm hgbarmbaratatmkp/m²kp/cm²kp/mm² pspilbf/ft²lbf/yd² восстанавливается/дюймовый h₂oft h₂oin hg
Условия в двухэтапных
h h₂oft h₂oin hg
. Hgbarmbaratatmkp/m²kp/cm²kp/mm²psilbf/ft²lbf/yd²oz/in²in H₂Oft H₂Oin Hg
Hgbarmbaratatmkp/m²kp/cm²kp/mm²psilbf/ft²lbf/yd²oz/in²in H₂Oft H₂Oin Hg
высота во втором положении (z2)
kmmcmmmmileydftin
скорость во втором положении (V2)
мкм/мин/мин/с/hourft/sft/minyd/smph
Размеры на двоих
диаметр во втором положении (D2)
сммммфуты
площадь поперечного сечения во втором положении (A2)
мм²см²м²дюйм²фут²ярд²
Свойства жидкости
плотность жидкости (ρ)
кг/м³кг/лг/лг/см³фунт/дюйм³фунт/фут³фунт/ярд³фунт/гал СШАфунт/галлон UKoz/дюйм³унция/фут³слаг/дюйм³слаг/фут³слаг/ярд³
На эксклюзивной странице калькулятора вы можете использовать онлайн-калькулятор без помех от рекламы,
дополнительный текст, ссылки и другой контент, который не требуется для самих расчетов. чистый
опыт использования калькулятора как с настольным приложением.
чистый
опыт использования калькулятора как с настольным приложением.
Зарегистрированным пользователям доступна эксклюзивная версия калькулятора. Выберите правильную продолжительность подписки и начните пользоваться эксклюзивным сервисом.
Эксклюзивный
Описание
- p 1 – давление в первой позиции
- Статическое давление жидкости в точке, в которой известны параметры потока – референтная позиция
- p 2 – давление во второй позиции
- Статическое давление жидкости в точке, в которой должны рассчитываться параметры потока
- Д 1 — диаметр в первой позиции
- Внутренний диаметр трубы или потока в точке, в которой известны параметры потока
- D 2 — диаметр во второй позиции
- Внутренний диаметр трубы или потока в точке, в которой должны рассчитываться параметры потока
- V 1 — скорость в первом положении
- Скорость потока при диаметре потока D1 и известных параметрах потока
- V 2 — скорость во втором положении
- Скорость потока, где диаметр потока равен D2 и где должны быть рассчитаны параметры потока
- z 1 – высота в первом положении
- Высота или отметка потока жидкости в точке, в которой известны параметры потока
- z 2 – высота во втором положении
- Высота или отметка потока жидкости в точке, в которой должны рассчитываться параметры потока
- q — объемный расход
- Расход жидкости в единицах объема в единицу времени.
 Считается константой
Считается константой - ṁ — массовый расход
- Расход жидкости в единицах массы в единицу времени. Считается константой
- ρ — плотность жидкости на входе
- Плотность жидкости по массе на единицу объема. Считается константой
- Δp — падение давления
- Разность давлений между двумя точками линии потока
Настройка расчета
- Выберите значение для расчета. Вы должны ввести не выбранный.
- р 2
- рассчитать давление во второй позиции
- z 2
- вычислить высоту во второй позиции
- v 2
- вычислить скорость во второй позиции
- Доступно, только если выбрано «использовать расход q в расчетах».
 Вы должны ввести значения для невыбранного.
Вы должны ввести значения для невыбранного. - v 1
- вычислить скорость в первой позиции
- D 1
- расчет диаметра в первой позиции
- q
- рассчитать расход
- Доступно, только если для вычисления v 2 выбрано значение , а не . Вы должны ввести значения для невыбранного.
- v 2
- вычислить скорость во второй позиции
- Д 2
- расчет диаметра во второй позиции
Почему вы должны использовать этот калькулятор?
Используйте этот калькулятор, чтобы легко рассчитать, как:
Свойства потока будут изменяться при изменении условий потока,
Статическое давление будет изменяться, когда жидкость течет по трубам с разными внутренними диаметрами,
Давление будет изменяться, когда текущая жидкость меняет высоту,
Описание калькулятора
Уравнение Бернулли является наиболее важным уравнением для инженерного анализа задач течения. Вы можете решить многие практические задачи путем непосредственной реализации уравнения Бернулли.
Вы можете решить многие практические задачи путем непосредственной реализации уравнения Бернулли.
Уравнение представляет собой баланс энергии жидкости, связанной с ее статической энергией. (давление), кинетическая энергия (скорость) и энергия высоты жидкости (гравитация).
уравнение Бернулли
Каждый член уравнения Бернулли в левой части приведенного выше уравнения представляет собой удельную энергию, содержащуюся в единице массы потока жидкости. Первый член — статическая энергия (давление), второй — кинетическая энергия (скорость), и третья — потенциальная энергия (гравитация). Константа в правой части приведенное выше уравнение означает, что сумма всех трех членов постоянна в любой точке поток жидкости.
Такое поведение соответствует принципу Бернулли, который гласит, что при увеличении скорости потока
статическое давление или потенциальная энергия будут уменьшаться.
Принцип Бернулли применяется в конструкции крыла, где форма крыла вызывает изменение скорости потока. В результате создается разность давлений на площадь верхней и нижней поверхности крыла, в результате чего сила направлена вверх, для самолетов (поднятие самолета) или вниз для гоночных автомобилей (добавление гравитации в дополнительной прижимной силе для лучшего сцепления).
Как выполняется расчет?
С помощью этого калькулятора вы можете рассчитать параметры потока, такие как давление, скорость, высота, и диаметр в любой точке потока, если вы знаете параметры в какой-то другой точке потока.
Точка линии тока, где известны параметры потока, отмечена как позиция один.
(левая часть калькулятора) и точка, в которой вы хотите рассчитать параметры потока
отмечен как два (правая сторона калькулятора). Параметры в пункте два, которые вы можете рассчитать
находятся:
Параметры в пункте два, которые вы можете рассчитать
находятся:
Давление
Скорость потока
Диаметр потока
Высота (геодезическое положение)
Если вы выбрали использование объемного расхода в расчетах, вы можете выбрать между:
Скорость потока в начале потока
Диаметр потока в начале потока
Объемный расход
Когда этот калькулятор не актуален?
Этот калькулятор действителен только для невязкого потока и потока непроводящей жидкости.
Выбор начала калькулятора
Читать все о доступных развертывания. При любом использовании калькулятора подключение к Интернету не требуется, но желательно иметь его хотя бы для аутентификации.
Если вам нужен быстрый расчет, но вы еще не знаете, как пользоваться калькулятором, вы
Вы можете заказать услугу расчета у разработчика калькулятора. 4}\ln x\end{align*}\]
4}\ln x\end{align*}\]
Обратите внимание, что мы опустили столбцы абсолютного значения для \(x\) в логарифме из-за предположения, что \(x > 0\).
Теперь нам нужно определить постоянную интегрирования. Это можно сделать одним из двух способов. Мы можем преобразовать приведенное выше решение в решение в терминах \(y\), а затем использовать исходное начальное условие, или мы можем преобразовать начальное условие в начальное условие в терминах \(v\) и использовать его. Поскольку в конце концов нам все равно придется преобразовать решение в \(y\), и это не добавит столько работы, мы сделаем это таким образом. 94}\left( {1 + 16\ln \frac{x}{2}} \right)}}\]
Обратите внимание, что мы немного упростили решение. Это поможет найти интервал действия.
Прежде чем найти интервал достоверности, мы упомянули выше, что можем преобразовать исходное начальное условие в начальное условие для \(v\). Кратко поговорим о том, как это сделать. Для этого все, что нам нужно сделать, это подставить \(x = 2\) в подстановку, а затем использовать исходное начальное условие. Это дает 9{- 1}} = — 1\]
Для этого все, что нам нужно сделать, это подставить \(x = 2\) в подстановку, а затем использовать исходное начальное условие. Это дает 9{- 1}} = — 1\]
Итак, в данном случае мы получили то же значение для \(v\), что и для \(y\). Не ожидайте, что это произойдет в целом, если вы решили решать задачи таким образом.
Хорошо, давайте теперь найдем интервал действия решения. Во-первых, мы уже знаем, что \(x > 0\), а это значит, что мы избежим проблем с логарифмированием отрицательных чисел и делением на ноль при \(x = 0\). Итак, все, о чем нам нужно беспокоиться, это деление на ноль во втором члене, и это произойдет там, где 9{ — \,\frac{1}{{16}}}} < x < \infty \).
Вот график решения.
Уравнение Бернулли
Утверждение сохранения энергии полезно при решении задач, связанных с жидкостями. Для невязкой несжимаемой жидкости в стационарном потоке сумма давления, потенциальной и кинетической энергии на единицу объема постоянна в любой точке.
Принцип Бернулли: В точках вдоль горизонтальной линии тока в областях с более высоким давлением скорость жидкости ниже, а в областях с более низким давлением скорость жидкости выше.
Специальная форма уравнения Эйлера, полученная вдоль линии тока жидкости, часто называется Уравнение Бернулли:
Форма энергии 1
/ ρ + v 1 2 / 2 + g h 1= p 2 / ρ + v 2 2 / 2 + g h 2 — E loss
= постоянная (1)
, где
E = энергия на единицу массы в потоке (J/кг, BTU/SLUG)
P = давление во флюд (PA, PSI)
ρ = плотность жидкости (кг/м 3 , порция/фут 3 )
v = скорость жидкости (м/с, фут/с)
8 потеря = потери энергии на единицу массы в потоке (Дж/кг, БТЕ/слаг)Форма головы
(1) можно изменить путем деления с гравитацией, как
h = p 1 / γ + v 1 2 h = 1 90 908 p 2 / γ + v 2 2 / (2 g) + h 2 — E loss / g = constant (2)
where
h = напор (м столба жидкости, футы столба жидкости)
γ = ρ г = удельный вес жидкости (Н/кг, фунт f /слаг)
Уравнение (2) часто называют «головкой », потому что все элементы имеют единицу измерения длины.
Внимание! — головка блока с привязкой к плотности протекающей жидкости. Для других единиц, таких как мм водяного столба , проверьте напор скорости.
Динамическое давление
(1) и (2) — две формы уравнения Бернулли для стационарного потока несжимаемой жидкости. Если предположить, что гравитационная сила тела пренебрежимо мала — возвышение мало — то уравнение Бернулли can be modified to
p = p 1 + ρ v 1 2 / 2
= p 2 + ρ v 2 2 / 2 — p loss
= p 1 + p d 1 = p 2 + p d2 — p loss ( 3)
, где
P = давление (PA, PSI)
P Потеря = Потеря давления (PA, PSI)
P D = 10363 P D = 103544. 2 = динамическое давление (Па, psi)
2 = динамическое давление (Па, psi)
Обычно компонент скорости потока называют динамическим давлением потока жидкости.
Внимание! — увеличение скорости потока снижает давление — уменьшение скорости потока увеличивает давление.
Это явление можно наблюдать в расходомере Вентури, где давление снижается в области сужения, а затем восстанавливается. Его также можно наблюдать в трубке Пито, где измеряется давление застоя. Давление застоя — это когда составляющая скорости равна нулю.
Уравнение Бернулли и поток из резервуара через маленькое отверстие
Жидкость вытекает из резервуара через отверстие близко к дну. Уравнение Бернулли можно адаптировать к линии тока с поверхности (1) к отверстию (2) :
P 1 / γ + V 1 2 / (2 G) + H 1 2 / (2 G) + H 1 2 / (2 G) + H 1 / (2 G) + H 1 / (2 G) + H 1 / (2 G) + H 1 / (2 G) + H 1 2 / (2 г).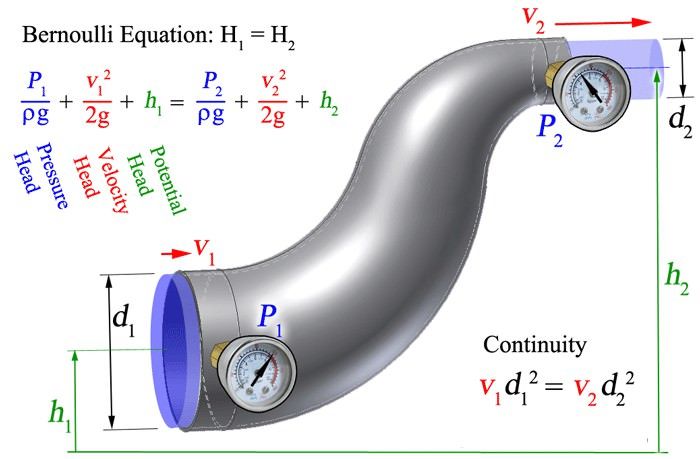 2 / γ + v 2 2 / (2 g) + h 2 — E потери / g -able — (4) можно преобразовать в
2 / γ + v 2 2 / (2 g) + h 2 — E потери / g -able — (4) можно преобразовать в
p 1 / ρ + v 1 2 /2 + G H 1
= P 2 / ρ + V 2 2 + G H 2 2 + G H 2 2 6 + G H 2 2 + G H 2 2 + V 2 2 + V 2 2 + V 2 2 . IF H = H 1 — H 2 (4C) и (в соответствии с уравнением непрерывности) V 1 = (A 2 / A 1 ). 2 (4d) , тогда скорость на выходе из отверстия можно выразить как v 2 = ([2 / (1 — A 2 2 / A 1 + 0) 90][3 P 1 — P 2 ) / 2]) 1/2 (5) для вентилируемого бака, где внутреннее давление равняется внешнему давлению P 1 = p. и площадь поверхности намного больше площади отверстия A 1 >> A 2 (5c) — тогда ур. 5 можно изменить на v 2 = (2g ч) 1/2 (6) «Скорость выхода из резервуара равна скорости свободного падения тела на расстояние 3 4 ч 4. » — также известная как Теорема Торричелли. Скорость на выходе из резервуара с уровнем 10 м можно рассчитать как v 2 = (2 (9,81 м/с 2 ) (10 м)) 1/2 0 = 14 м/с Ур. 6 – для идеального потока без потери давления в отверстии. В реальных условиях — с потерей давления — экв. 6 можно выразить через коэффициент расхода — коэффициент трения — как V 2 = C (2 г) 1/2 (6B) , где C = коэффициент выгрузки Коэффициент выгрузки может быть определен. Если резервуар закрыт, находится под давлением и уровень между поверхностью и выпускным отверстием минимальный (влияние разницы уровней очень мало по сравнению с влиянием давления в уравнении 5) — скорость нагнетания может быть выражена как V 2 = C (2 (стр. 1 — P 2 ) / ρ) 1/2 (7) Скорость розетки бака под давлением, где P 1 = 0,2 (MN/M 2 , 10 6 PA) Вентилируемый бак
 2 (5b)
2 (5b) Пример — скорость на выходе из резервуара с вентиляцией
Коэффициент расхода отверстия
 Для отверстий с острыми краями она может составлять всего 0,6 . Для гладких отверстий он может быть между 0,95 и 1 .
Для отверстий с острыми краями она может составлять всего 0,6 . Для гладких отверстий он может быть между 0,95 и 1 . Резервуар под давлением
9779. 70795 Draining Containcer или резервуары — объемный поток и расчета. Пример — скорость розетки из бака под давлением
 . 2 = 0.1 (MN/m 2 , 10 6 Pa)
. 2 = 0.1 (MN/m 2 , 10 6 Pa) A 2 / A 1 = 0.01
h = 10 (m)
can вычисляется как
В 2 = ( (2 / (1 — (0,01) 2 ) ((0,2 10 6 Н/м 2 ) — (0,1 10 6 2 )) / (1000 кг/м 3 ) + (9,81 м/с 2 ) (10 м))) 1/2
= 19,9 м/с
Потери энергии через редукционный клапан
При протекании жидкости через редукционный клапан и снижении давления происходит потеря энергии. Пренебрегая изменением высоты (h 1 = h 2 ) и изменением скорости жидкости (v 1 = v 2 ) , получаем энергию давления перед клапаном и энергию давления после клапана. клапана с учетом потерь энергии через клапан — постоянна. Уравнение Бернулли можно изменить до
P 1 / ρ = P 2 / ρ + E Потеря (8)
, где
E Потеря
63 = энергия vall Work 2 ( = EORCH 2VVE 9036 ( ( = энергия. (8) can be transformed to:
(8) can be transformed to:
E loss = ( p 1 — p 2 ) / ρ (8b)
Bernoulli’s Equation — AP Physics 2
Все ресурсы AP Physics 2
6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics 2 Help » Жидкости » Динамика жидкости » Уравнение Бернулли
Вода течет со скоростью по трубе диаметром 1 м. Если давление в этой точке равно 80 кПа, каково давление воды после того, как труба сузится до диаметра 0,5 м?
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно уравнение Бернулли, чтобы решить эту задачу:
Постановка задачи не говорит нам, что высота изменяется, поэтому мы можем удалить последний член с каждой стороны выражения, а затем договориться о решении для конечное давление:
Мы знаем начальное давление, поэтому нам все еще нужно вычислить начальную и конечную скорости.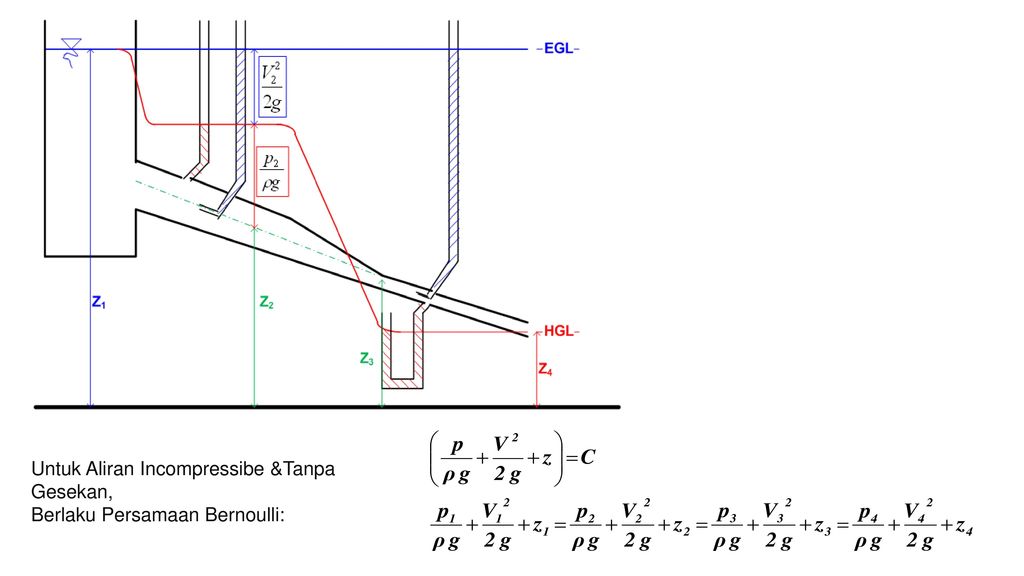 Мы будем использовать уравнение непрерывности:
Мы будем использовать уравнение непрерывности:
Переставить для скорости:
Где является площадью поперечного сечения. Мы можем рассчитать это для каждого диаметра трубы:
Теперь мы можем рассчитать скорость для каждого диаметра:
Теперь у нас есть все значения, необходимые для уравнения Бернулли, что позволяет нам решить:
Сообщить об ошибке
Предположим, что огромный резервуар высотой 50 м, наполненный водой, открыт для атмосферы и в него попала пуля, которая пробивает одну сторону резервуара, позволяя воде вытекать. Отверстие находится на высоте 2 м над землей. Если отверстие очень маленькое по сравнению с размером бака, как быстро вода будет вытекать из бака?
Возможные ответы:
Недостаточно информации
Правильный ответ: 3
Объяснение: Для начала необходимо будет воспользоваться уравнением Бернулли: Для ситуации, описанной в вопросе, мы обозначим вершину сосуда как точку 1, а отверстие, где вода вытекает как точка 2. Чтобы начать все упрощать, важно понять несколько вещей. Во-первых, обе точки открыты для атмосферы. Следовательно, член с каждой стороны приведенного выше уравнения равен 1 атм и, следовательно, может сокращаться. Во-вторых, поскольку размер отверстия сбоку резервуара настолько мал по сравнению с остальной частью резервуара, скорость воды в точке 1 почти равна 0. Следовательно, мы можем сократить член слева сторону уравнения. На данный момент имеем: Разделив все на , получим: И переставив: Сообщить об ошибке Ниже приведено изображение трубы с протекающей по ней жидкостью. Если начальная скорость жидкости , конечная скорость , а начальное давление (с неизменной потенциальной энергией), каково значение конечного давления? Возможные ответы: Ни один из других ответов не является правильным Правильный ответ: Объяснение: Уравнение, связывающее давление жидкости, кинетическую энергию и потенциальную энергию от состояния к состоянию, известное как уравнение Бернулли, выглядит следующим образом: Наша потенциальная энергия одинакова, поэтому мы можем удалить эту часть из уравнение. это плотность, которая в нашем случае равна 1, так что здесь это ничего не меняет. У нас есть значения начального давления, начальной скорости и конечной скорости, поэтому мы можем изменить наше уравнение так, чтобы оно равнялось конечному давлению. Теперь мы можем подставить наши значения. Следовательно, конечное давление равно . Сообщить об ошибке Дом должен быть спроектирован так, чтобы выдерживать ураганные ветры. Максимальная скорость ветра . Площадь поверхности крыши составляет . Если плотность воздуха равна , какую силу должны выдерживать опоры крыши? Возможные ответы: Правильный ответ: Пояснение: Это решается с помощью уравнения Бернулли и определения давления. Поскольку воздух все еще внутри, Поскольку наши точки находятся на одной высоте, условия сокращаются. Переставить: Так как нас интересует только разница давления внутри и снаружи. Подставьте известные значения и найдите разницу в давлении. Сила – это давление, умноженное на площадь: Сообщить об ошибке Кайтбордист использует воздушного змея для создания силы в ветреный день. Площадь воздушного змея . Скорость ветра . Плотность воздуха равна. Если воздушный змей сконструирован таким образом, что воздух неподвижен на внутренней поверхности, какую силу может ожидать кайтбордист от воздушного змея? Возможные ответы: Правильный ответ: Пояснение: Используйте уравнение Бернулли, чтобы найти разницу давлений с двух сторон воздушного змея. Поскольку точки находятся на одной высоте, условия отменяются. Поскольку воздух все еще находится в точке А, член равен нулю. Поскольку нас интересует только разница в давлении с двух сторон воздушного змея, найдите : Суммарная сила – это разность давлений, умноженная на площадь: Сообщить об ошибке В доке металлическая пластина полностью погружена в воду и прикреплена к подводной стене. Сторона металлической пластины подвергается воздействию океана и потокам воды, вызванным приливами. Пластина имеет размеры и . Если скорость течения равна максимальному приливному потоку, с какой силой вода будет воздействовать на металлическую пластину? Возможные ответы: Правильный ответ: Объяснение: Движущаяся вода с одной стороны металлической пластины имеет более низкое давление, чем неподвижная вода с другой стороны, что приводит к возникновению силы. Мы выбираем наши две «точки Бернулли», чтобы максимально упростить задачу. Возьмем точку А на той стороне, где вода неподвижна, а точку В — на той стороне, где вода движется. Если мы сделаем их на одной высоте, члены могут быть вычтены с обеих сторон. Поскольку вода все еще находится в точке А, член скорости в правой части уравнения равен нулю. Переставьте, чтобы найти разницу давлений со стороны А на сторону В: Это означает, что давление в точке B меньше, чем давление в точке A. Используя определение давления, найдите результирующую силу: Сообщить об ошибке фасонная трубка, в которой вертикальная трубка находится в воде. Через горизонтальную трубу нагнетается высокоскоростной поток воздуха. В результате вода поднимается по вертикальной трубе, как показано на данном рисунке. Если воздух нагнетается через горизонтальную трубу в точке , на какую высоту поднимется вода в вертикальной трубе? Возможные ответы: Вода в вертикальной трубе не изменит свою высоту Вода в вертикальной трубе будет выдвинута

 Сначала выберите «точки Бернулли», одну прямо внутри крыши, где воздух неподвижен (точка А), и одну сразу снаружи, где воздух движется (точка Б). Это позволит нам исключить многие члены:
Сначала выберите «точки Бернулли», одну прямо внутри крыши, где воздух неподвижен (точка А), и одну сразу снаружи, где воздух движется (точка Б). Это позволит нам исключить многие члены: Назовите точку А внутренней поверхностью (где воздух неподвижен) и точку В внешней поверхностью (где ветер дует на полной скорости).
Назовите точку А внутренней поверхностью (где воздух неподвижен) и точку В внешней поверхностью (где ветер дует на полной скорости). Мы начнем с написания уравнения Бернулли:
Мы начнем с написания уравнения Бернулли:
Правильный ответ:
Правильный ответ:
9 . Объяснение:
Объяснение:
Для решения этой задачи воспользуемся уравнением Бернулли. Мы должны сделать это дважды: один раз для воздуха и один раз для воды. Центральный принцип здесь заключается в том, что движущийся поток воздуха имеет более низкое давление, чем неподвижный воздух. В этой задаче мы пренебрежем атмосферным давлением, так как оно приложено к концам трубы и к поверхности воды вне вертикальной трубы. Для воздуха выберите две наши «точки Бернулли»: точка А находится сразу за пределами горизонтальной трубы, а точка В — сразу внутри. Напишите уравнение:
Высоты одинаковы, поэтому они исключаются из уравнения. Воздух все еще находится в точке А, поэтому член скорости равен нулю для левой стороны. Наконец, как уже упоминалось, нас интересует только разница в давлении:
Это говорит о том, что давление внутри трубы ниже давления снаружи.
Теперь решим для воды. Наши точки будут находиться на поверхности вне вертикальной трубы (точка А), где давление равно одной атмосфере, и внутри вертикальной трубы у поверхности поднявшейся колонны (точка В). Напишите уравнение:
Напишите уравнение:
Поскольку вода больше не движется, члены, содержащие равны нулю. Переставьте:
Вставьте числа и решите разницу в высоте:
Сообщить об ошибке
К какой из следующих текучих ситуаций применим принцип Бернулли?
Возможные ответы:
Сжимаемый, установившийся поток
Несжимаемый поток с внутренним трением
Несжимаемый, установившийся поток
Несжимаемый установившийся поток без внутреннего трения
Правильный ответ:
Несжимаемый установившийся поток без внутреннего трения
Пояснение:
Поскольку принцип Бернулли выводится из теоремы о работе и энергии, требуется, чтобы поток был несжимаемым, устойчивым и без внутреннего трения. В противном случае энергия будет теряться в этих выходах, и уравнение больше не будет применяться.
Сообщить об ошибке
Предположим, что жидкость с плотностью течет по горизонтальной трубе со скоростью и имеет давление 100000 Па. Если эта жидкость затем начнет течь по трубе со скоростью , какое новое давление будет оказывать эта жидкость?
Возможные ответы:
Правильный ответ:
Объяснение:
В основе вопроса нам сказано, что жидкость с плотностью движется по трубе со скоростью и имеет давление . Затем нам говорят, что та же самая жидкость начинает двигаться по трубе с новой скоростью , и нас просят определить, каким будет новое давление.
Чтобы ответить на этот вопрос, нам нужно использовать уравнение Бернулли. Это уравнение по существу говорит нам, что давление, кинетическая энергия и потенциальная энергия движущейся жидкости постоянны. Или, другими словами:
В качестве альтернативы, поскольку мы знаем, что сумма этих значений постоянна, мы можем связать сумму этих значений в один момент с суммой этих значений в другой момент.
Более того, поскольку нам сказали, что жидкость продолжает течь по горизонтальной трубе, высота жидкости не меняется. Следовательно, мы можем сократить члены потенциальной энергии с обеих сторон.
Далее, если мы определим начальные условия как момент 1, а конечные условия как момент 2, то термин, который мы пытаемся найти, равен .
Затем, подставив полученные значения, мы получим ответ:
Сообщить об ошибке
Вода течет через шланг. Он выходит из крана при давлении, скорости и высоте . Он выходит из сопла со скоростью и высотой . Каково давление воды на выходе из шланга?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, мы будем использовать уравнение Бернулли, упрощенную форму закона сохранения энергии. Это относится к несжимаемым (постоянной плотности) и невязким жидкостям.
Это относится к несжимаемым (постоянной плотности) и невязким жидкостям.
Уравнение Бернулли:
Где давление, плотность, гравитационная постоянная, скорость и высота.
В нашем вопросе состояние 1 соответствует крану, а состояние 2 — соплу. Введите переменные из вопроса в уравнение Бернулли:
Отчет о ошибке
← Предыдущий 1 2 Следующий →
Уведомление о соображении
All AP Physhics 2 Resourcics 2503
. Тесты 149 практических тестов Вопрос дня Карточки Учитесь по концепции
MAT 2680 Дифференциальные уравнения | «Чем он отличается от камней».
Опубликовано 26 мая 2015 г. Йонасом Райцем | Оставить комментарий
Привет всем,
Окончательные оценки за курс были отправлены в CUNYFirst, и можно найти подробную разбивку вашей оценки (включая итоговую оценку за экзамен, оценку за проект «Учебное пособие» и т. д.) на странице ОЦЕНКИ.
д.) на странице ОЦЕНКИ.
Желаю вам всего наилучшего в ваших будущих начинаниях – было очень приятно работать с вами в этом семестре. 9(4))….. = 0
Теперь примем равным 0
2a2 + 2a1 + a0 = 0
6a3 + 4a2 + a1 = 0
12a4 + 6a3 + a2 = 0
Помните, что y (0) =0 и y'(0)=2
Y(0) = 0 = a0
Y'(0)= 2 = a1
Теперь, зная, что мы подставим a0 и a1
2a2 + 2(2) + 0 =0
2a2 + 4 =0 2a2 =-4 a2 =-2
Опубликовано 20 мая 2015 г. автором Aayush | 1 комментарий
Преобразование Лапласа является важным методом в дифференциальных уравнениях, а также широко используется в электротехнике для решения линейного дифференциального уравнения. Преобразование Лапласа берет функцию, область определения которой находится во времени, и преобразует ее в функцию комплексного частота. 92 Y(s)-sy(0)-y'(0)
2) Как только мы применим правильное преобразование Лапласа к нашей функции, мы затем применим начальное условие
3) Затем, поскольку мы не можем найти y(t ) напрямую, мы находим Y(s), что является преобразованием Лапласа y(t)
4) Как только мы находим Y(s), нам может понадобиться разбить уравнение на частичную дробь в зависимости от знаменателя. (1/2t)-1 94)
(1/2t)-1 94)
Надеюсь, что ссылка на видео и изображения будет полезна.
https://www.khanacademy.org/math/дифференциальные-уравнения/laplace-transform/laplace-transform-to-solve- Differential-equation/v/laplace-transform-to-solve-an-equation
Опубликовано 18 мая 2015 г. Дэниелом Вонгом | 1 комментарий
Существует несколько улучшений метода Эйлера: обратный метод Эйлера и Метод Рунге-Кутты (о Улучшенный метод Эйлера см. в публикации BingJing Zheng Улучшенный метод Эйлера ).
Обратный метод Эйлера с примером
Вспоминая, что в методе Эйлера точка аппроксимируется по наклону предыдущей точки. Это дает уравнение , где функция f представляет наклон, или y'(t), а h представляет собой размер шага. Это оказывается довольно неточным, поскольку наклон в новой точке не будет таким же, как в предыдущей точке.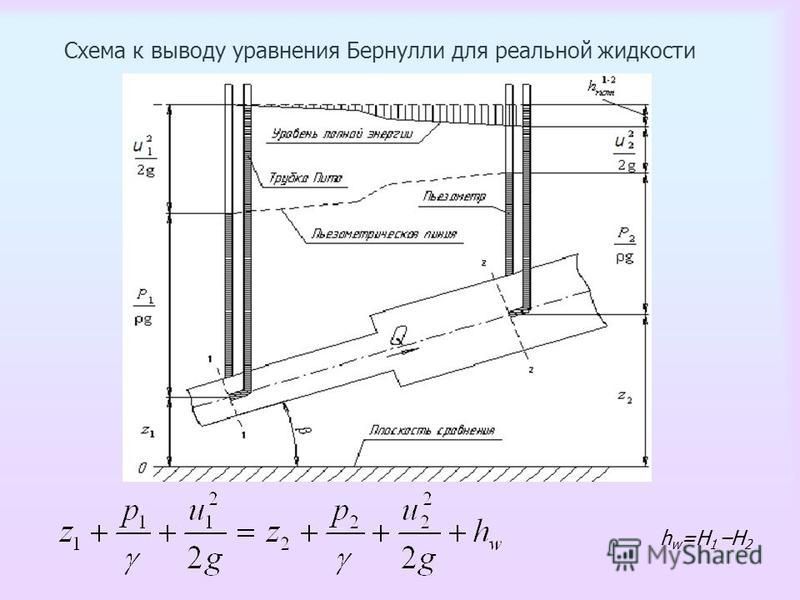 В обратном Эйлере рассматривается тот же сценарий, но учитывается линия, соединяющая две точки. Вместо того, чтобы брать наклон в предыдущей точке, берут наклон в новой точке. Это дает уравнение для обратного метода Эйлера.
В обратном Эйлере рассматривается тот же сценарий, но учитывается линия, соединяющая две точки. Вместо того, чтобы брать наклон в предыдущей точке, берут наклон в новой точке. Это дает уравнение для обратного метода Эйлера.
Пример: приведен примерно y (1)
Найти Y на T = 0
Приведен: на T = 0, Y = 1
. = 0,5
при T = 0,5,
при T = 0,5,
при T = 0,5,
при T = 0,5,
на T = 0,5,
на T = 0,5,
. г в т = 1
в T = 1,
в T = 1,
в T = 1,
в T = 1,
AT T = 1,
63636363636363636 3. Метод с примером Как и в усовершенствованном методе Эйлера, делается попытка найти лучшее соответствие определенному интегралу кривой. Один использует идею о том, что парабола будет покрывать наибольшую площадь под кривой (по сравнению с прямоугольником или трапецией других методов). Из этой идеи были найдены уравнения для следующих точек:
Из этой идеи были найдены уравнения для следующих точек:
, где
Пример: приведенный примерный Y (1)
Найти y при T = 0
Данный: по адресу 4 T = 0,00003
. 1
Find y at t = 0.5
Find y at t = 1
Анализ
Ответив на один и тот же вопрос с помощью обратного метода Эйлера и метода Рунге-Кутты, можно убедиться в точности результатов.
Точное решение для y(1) равно 0,6321205588.
Используя метод Эйлера, y(1) приблизительно равно 0,375.
При использовании обратного метода Эйлера значение y(1) приблизительно равно 0,8333333333.
Используя метод Рунге-Кутты, y(1) приблизительно равно 0,6328751629.
Обратный метод Эйлера обеспечивает лучшую аппроксимацию, чем метод Эйлера, с несколькими дополнительными шагами. Метод Рунге-Кутты обеспечивает наилучшее приближение, но требует больше вычислений.
Опубликовано 17 мая 2015 г. Йонасом Райцем | 2 комментария
Привет всем,
Я обновил ответ на задачу № 14 – правильный ответ:
Лучший,
Проф. 2 комментария
6.2 Преобразование Лапласа: решение задач с начальными значениями (обратное преобразование)
Преобразование Лапласа используется для преобразования функции в области t и переноса ее в область s. Практическое использование этого преобразования заключается в упрощении решения дифференциальных уравнений. Прочитав определения и зная, как работает преобразование Лапласа, мы перейдем к примеру того, как применить его к дифференциальному уравнению с начальными значениями.
Прочитав определения и зная, как работает преобразование Лапласа, мы перейдем к примеру того, как применить его к дифференциальному уравнению с начальными значениями.
1.Решить с помощью преобразования Лапласа
y”-y’-2y=0 с условием y(0)=1 y’=0
Шаг 1: Шаг 1 это дифференциальное уравнение? Да, потому что оно однородное и линейное
Шаг 2: Возьмем уравнение Лапласа с обеих сторон L{ y”-y’-2y=0}
Шаг 3: Решим алгебраически
, используя известную нам диаграмму преобразования Лапласа f”( t)= L{f(t)-sf(0)-f'(0)
f'(t)=sL{f(t)-f(0)
Возьмем Лапласа дифференциального уравнения, применив заданное начальное значение:
Y(s)-s(1)-0-{sY(s)-1}-2Y(s)
Фактор Y(s): Y(s)(-s-2)-s+1=0
Изолировать Y(s): Y(s)= 9000 и разделить из квадратного уравнения
Шаг 4. Упростите решение, применив дробь (s-2)(s+1)=B(s-2)
s-1= A(s+1)+B(s-2)
«” = as+a+bs-2b
«» = as+bs+a-2b
Объедините все буквы с s с s, и число с условиями, которые не имеют с на нем.
A+B=1, так как (1) стоит перед используемым s 1 -1=A-2B
Решите линейные уравнения: мы решим это, используя метод исключения :
A -2B = -1
2A+2B = 2
3A = 1 Следовательно, a = 1/3, затем заменив A в A+B = 1– (1/3)+ B=1
получаем B=2/3 и A=1/3
Наконец, ваша функция находится в области s:
Напоминание о решении дифференциального уравнения с использованием преобразования Лапласа:
1. Начните с дифференциальное уравнение
- Преобразование Лапласа из обеих частей уравнения
- Тогда вам придется упростить алгебраическое решение.
- Для этого потребуется метод, подобный частичной дроби
4. Сделайте обратное преобразование Лапласа решения, это будет ваше решение для дифференциального уравнения, в этот момент вы должны быть в области t с уравнением упрощения
Важное обозначение:
L{f(t) }: «L» используется для обозначения того, что применяется преобразование Лапласа функции {f(t)}.
F(s) : При работе с преобразованием Лапласа все, что написано с большой буквы, означает, что вы работаете в области s. Таким образом, F(s) означает, что функция f(t) уже перенесена в область s .
{F(S)}: используется при работе с обратным преобразованием Лапласа, поэтому возвращаемся к вашей функция в области t.
Опубликовано 17 мая 2015 г. автором BingJing Zheng | 11 комментариев
По мере прохождения курса нам обычно дают дифференциальное уравнение первого порядка, которое можно решить. Тем не менее, есть много проблем, которые не могут быть решены. Уравнения первого порядка можно разделить на линейное уравнение, сепарабельное уравнение, нелинейное уравнение, точное уравнение, однородное уравнение, уравнение Бернулли и неоднородные уравнения. Однако для большинства сепарабельных и точных уравнений не всегда можно представить решение в явном виде. Трудно найти значение для конкретной точки в функции. Есть некоторые уравнения, которые не попадают ни в одну из вышеперечисленных категорий. Итак, мы вводим метод, называемый методом Эйлера. Мы сможем использовать его для аппроксимации решений дифференциального уравнения. В методе Эйлера нам дадут дифференциальное уравнение, которое представляет собой наклон функции, и определим размер шага для интеграла (чем меньшие размеры шагов у вас есть, тем более точные значения аппроксимации вы получите). Мы создаем новую точку, начиная с начальной точки, мы подставляем эту точку в заданную функцию, это будет наклон начальной точки. Затем следующая новая точка будет иметь размер шага плюс h, умноженный на ранее рассчитанный наклон. общая формула: Однако погрешность метода Эйлера зависит от размера шага. единственный способ уменьшить ошибку — уменьшить размер шага, но это увеличит объем вычислений. это только примерно уменьшает ошибку наполовину.
Есть некоторые уравнения, которые не попадают ни в одну из вышеперечисленных категорий. Итак, мы вводим метод, называемый методом Эйлера. Мы сможем использовать его для аппроксимации решений дифференциального уравнения. В методе Эйлера нам дадут дифференциальное уравнение, которое представляет собой наклон функции, и определим размер шага для интеграла (чем меньшие размеры шагов у вас есть, тем более точные значения аппроксимации вы получите). Мы создаем новую точку, начиная с начальной точки, мы подставляем эту точку в заданную функцию, это будет наклон начальной точки. Затем следующая новая точка будет иметь размер шага плюс h, умноженный на ранее рассчитанный наклон. общая формула: Однако погрешность метода Эйлера зависит от размера шага. единственный способ уменьшить ошибку — уменьшить размер шага, но это увеличит объем вычислений. это только примерно уменьшает ошибку наполовину.
Теперь мы представляем усовершенствованный метод Эйлера. Этот метод очень похож на метод Эйлера. В методе Эйлера мы аппроксимируем функцию прямоугольной формой (см. график ниже):
В методе Эйлера мы аппроксимируем функцию прямоугольной формой (см. график ниже):
Однако это приближение не включает площадь под кривой. Для улучшения аппроксимации мы используем усовершенствованный метод Эйлера. В улучшенном методе мы используем среднее значение значений в изначально заданной точке и новой точке. Определим интеграл трапецией вместо прямоугольника. Площадь трапеции больше площади прямоугольника. Это также обеспечит более точное приближение.
Трудно предсказать, будет ли кривая решения вогнутой вверх или вогнутой вниз в действительности. Идеальная линия предсказания точно совпадет с кривой в следующей точке предсказания. Метод Эйлера создает наклон на основе начальной точки, и мы не знаем, будет ли следующая точка на этой линии наклона, если только мы не используем компьютер для построения уравнения. Иногда мы можем переоценивать значение или недооценивать значение. Усовершенствованный метод Эйлера решил эти проблемы, найдя среднее значение наклона на основе начальной точки и наклона новой точки, что даст среднюю точку для оценки значения. Это также уменьшает ошибки, которые мог бы иметь метод Эйлера. 92+2y, y(0)=1, оценка y(2), шаг 0,5.
Это также уменьшает ошибки, которые мог бы иметь метод Эйлера. 92+2y, y(0)=1, оценка y(2), шаг 0,5.
Свод
Примечание: Это очень важно написать и в начале каждого шага, потому что расчеты основаны на этих значениях. Этот метод связан с большим количеством вычислений, рекомендуется после каждой точки записывать значения в таблицу. Самому посмотреть и проверить будет несложно. Для каждой точки расчетный подход к следующей новой точке одинаков, поэтому, если вы настроите три шага, вам будет очень ясно перейти к следующему шагу.
Я думаю, что это видео очень полезно, и в нем четко указано на усовершенствованный метод Эйлера, а пример включен в видео. Пожалуйста, посмотрите это видео.
Posted on May 17, 2015 by kumar Прайс | 2 комментария
Обзор
Рассматриваются методы решения линейных уравнений второго порядка, когда коэффициенты являются функциями независимой переменной. Рассмотрим линейное однородное уравнение второго порядка
Рассмотрим линейное однородное уравнение второго порядка
P(x) d2 y/ dx2 + Q(x) dy/ dx + R(x)y = 0 (уравнение 1)
Поскольку процедура для неоднородного уравнения аналогична. Многие задачи математической физики приводят к уравнениям такого вида с полиномиальными коэффициентами; примеры включают уравнение Бесселя
X2 y’’ + xy’ + (x2 – a 22) y = 0
Где (a) – константа, а уравнение Лежандра
(1 – x 2 ) y» – 2xy’ + c(c + 1) y = 0 Где (c) – константа
Учитывая уравнение
P( x) d2 y/ dx2 + Q(x) dy /dx + R(x)y = 0
Уравнение
d2 y/ dx2 + Q(x) P(x) dy/ dx + R(x) P(x ) y = 0 или d2 y/ dx2 + p(x) dy/ dx + q(x)y = 0
Где p(x) = Q(x)/ P(x) и q(x) = R(x ) /P(x)
называется эквивалентной нормализованной формой уравнения. Точка (а) называется обыкновенной точкой уравнения (1). Другими словами, эти две величины имеют ряды Тейлора в районе x=x0. Мы будем иметь дело только с коэффициентами, которые являются многочленами, так что это будет эквивалентно утверждению, что 9n〗
, а затем попытайтесь определить, каким должен быть ан. Мы сможем сделать это только в том случае, если точка x=x0 будет обычной точкой. Обычно мы говорим, что это рядовое решение около x=x0.
Мы сможем сделать это только в том случае, если точка x=x0 будет обычной точкой. Обычно мы говорим, что это рядовое решение около x=x0.
Пример
y ”+y = 0
Предположим, что имеет серию Taylor около x = 0
y (x) =
y (x) = x
y (x) = 737373737373737373737373373 гг. 0 +а 1 х+а 2 х 2 +а 3 x 3 +a 4 x 4
Substitute into the differential equation and simplify by grouping together terms with similar powers of
We start with the assumption that
Y (x) = A 0 +A 1 x +A 2 x 2 +A 3 x 3 +A 4 X 4 +… . . x 4 +… .. x 4 +… .. Y'(x) = а 1 +2а 2 x +3a 3 x 2 +4a 4 x 3 +……
. x 4 +… .. x 4 +… .. Y'(x) = а 1 +2а 2 x +3a 3 x 2 +4a 4 x 3 +……
Y ”(x) = 2A 2 +6A 3 x +12a +6A 3 x +12A +12A +12a +6A 3 x +12a +6A 3 . x 2 +……
Now substitute and into the differential equation
Y»+y= 0:
( 2a 2 +6a 3 x+12a 4 x 2 +……) +( a 0 +a 1 x+a 2 x 2 +a 3 x 3 +a 4 x 4 + …..) = 0
Избавьтесь от скобок (не забудьте распределить знаки и перед вторыми и третьими скобками
2a 2 +6a 3 x +12a 4 x 2 +… +A 0 +A 1 x +A 2 x 2 +A 3 x 3 +A 4 77 4. 7 4. 4 7 4 7 4 7 4 7 4 7 4 7 4 7 4 4 7 4 7 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 .
7 4. 4 7 4 7 4 7 4 7 4 7 4 7 4 7 4 4 7 4 7 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 .
Теперь сгруппируем по степеням :
( 2a 2+ A 0 ) +(6A 3 +A 1 ) x +(12A 4 +A 2 ) x 2 +(20A 5 +A 3 ) x 399 399 399 399 399 399 399 399 399 399 399 399 399 399 399 399 399 399 3 . +…= 0
Наконец, мы сравниваем каждое слагаемое слева с соответствующим слагаемым справа – поскольку правая часть равна нулю, каждое из выражений в скобках (которые дают коэффициенты при степенях ) должны также равны нулю:
- 2а 2 +а 0 =0
- 6а 3 +а 1 =0
- 12а4+а2=0
- 20а 5 +а 3 =0
- ……
Затем вы найдете первые 5 слагаемых (коэффициенты)
- a 0 =0
- a 1 =0
- а 2 = а 0 /2
- a 3 = a 1 /6
- а 4 = а 0 / 24
Это дает нам коэффициенты для определения первых пяти членов ряда Тейлора, учитывая, что Y(x) = a 0 +a 1 x+a 2 x 2 +a 3 x 3 +a 4 x 4 +…. подставляем значения , чтобы получить
подставляем значения , чтобы получить
Y=a 0 +a 1 x+a 0 /2 x 2 +a 1 /6 x 90 60 + 0 8 903 /24 х 4
3. Если я недостаточно ясно выразился в объяснении или шагах, необходимых для решения уравнения, я добавлю пару видео, надеюсь, они помогут.
Опубликовано 16 мая 2015 г. Йонасом Райцем | Оставить комментарий
Привет всем,
Оценки за Экзамен 3 размещены на странице Оценки (напишите мне, если вы забыли пароль).
Этот экзамен включал в себя большой объем материала, и, хотя общие оценки были сопоставимы с первым экзаменом, я уверен, что не все справились так хорошо, как им хотелось бы. Вы можете улучшить свой результат на экзамене, заполнив специальное предложение ниже.
Вы можете улучшить свой результат на экзамене, заполнив специальное предложение ниже.
Дайте мне знать, если у вас есть какие-либо вопросы, и удачи в изучении!
Prof. Reitz
Экзамен 3 Специальное предложение – заработайте бонусные баллы . Вы можете улучшить свою оценку на экзамене, выполнив следующие действия:
- Выберите ТОЛЬКО ОДНУ задачу , за выполнение которой вы НЕ набрали полных баллов. Вы работаете над тем, чтобы вернуть (некоторые) баллы, которые вы упустили в этой задаче.
- Решите задачу заново, аккуратно и полностью , от начала до конца, на отдельном листе бумаги.
- Не забудьте свое имя, дату и номер проблемы.
- На том же листе напишите краткое заявление (одно или два полных предложения), объясняющее вашу ошибку (ошибки) . Цель состоит в том, чтобы сообщить мне, что вы понимаете, что вы сделали неправильно.
- Сдайте исходный экзамен и исправленную задачу и объяснение, скрепленные вместе, в классе в четверг (день выпускного экзамена).

- Бонусные баллы будут добавлены к вашей оценке за экзамен 3 в зависимости от количества баллов, которые вы пропустили в выбранной задаче, точности ваших исправлений и объяснений, а также вашей общей оценки за экзамен. Бонусные баллы ограничены следующим образом:
- Если вы набрали менее 60% на экзамене, вы можете заработать максимум 20 бонусных баллов.
- Если вы набрали от 60% до 69% на экзамене, вы можете заработать максимум 15 бонусных баллов.
- Если вы набрали от 70% до 79% на экзамене, вы можете заработать максимум 10 бонусных баллов.
- Если вы набрали от 80% до 89% на экзамене, вы можете заработать максимум 5 бонусных баллов.
- Если на экзамене вы набрали от 90 % и более, вы можете заработать максимум 2 бонусных балла.
Опубликовано 13 мая 2015 г. Кристианом Пинто | 7 комментариев
Преобразование Лапласа — это метод, используемый для перехода от одного домена к другому. В этом случае мы переходим от временной области (t) к частотной области (s).
Как и для большинства преобразований, если есть один способ перехода от одной единицы к другой, должен быть и способ вернуться назад. Это применимо и в этом случае, хотя это не обязательно единица. В этом случае это называется просто «обратное преобразование Лапласа». В этом случае мы переходим от частотной области (s) обратно к временной области (t).
Обозначение преобразования Лапласа:
Буква «L» используется для обозначения преобразования Лапласа. Внутри фигурных скобок находится функция, которую вы хотите преобразовать из временной области в частотную.
Иногда вы также можете видеть это обозначение, которое означает то же самое, что и предыдущее:
Что касается преобразования Лапласа, оно обозначается:
Это даст вам F(s).
Чтобы перейти к исходной временной области, необходимо выполнить обратное преобразование Лапласа для F(s), которое равно:
Теперь, когда мы записали преобразование Лапласа, мы можем углубиться в него.
Общая формула преобразования Лапласа, где ‘t’ больше или равно нулю:
Мы оцениваем, что t больше или равно нулю, потому что мы хотим удовлетворить два условия:
1. Функция f( t) должен быть кусочно-непрерывным из интервала [0,A]. Просто означает функцию, которая разбита на разные части, но все еще продолжается. Например: 9(at), когда t больше или равно M. В этом случае переменные K, M и a являются просто константами, а K, M положительны.
Что касается обратного преобразования Лапласа, то для него не существует заданного уравнения или метода. Обратное преобразование Лапласа обозначается следующим образом:
Это просто означает, что для получения функции f(t) вам потребуется выполнить обратное преобразование Лапласа F(s).
Основная причина, по которой мы используем преобразование Лапласа, заключается в том, что оно упрощает вычисление некоторых (не всех) дифференциальных уравнений.
Небольшое введение в шаги, которые необходимо предпринять при решении задачи преобразования Лапласа. Есть пять шагов, которые мы можем использовать для решения дифференциального уравнения с использованием преобразования Лапласа:
Есть пять шагов, которые мы можем использовать для решения дифференциального уравнения с использованием преобразования Лапласа:
1. Решить дифференциальное уравнение
2. Выполнить преобразование Лапласа для обеих частей уравнения. Это даст вам простое алгебраическое уравнение для решения.
3. Решите алгебраическое уравнение
4. Упростите алгебраическое уравнение, чтобы у вас было то, что вы решаете, в левой части и чему оно равно в правой части. Если вы можете упростить правую сторону, это сделает ее проще. После упрощения используйте частичные дроби для решения неизвестных. 9\простое}.\]
Мы видим, что левая часть уравнения становится производной произведения \(z\left( x \right)u\left( x \right)\) после умножения на \(\frac{1}{x}\ ).
Тогда общее решение линейного уравнения для \(z\left( x \right)\) определяется выражением
\[z = \frac{{\int {u\left(x\right)f\left(x\right)dx} + C}}{{u\left(x\right)}}
= \ frac {{\ int {\ frac {1} {x} \ cdot \ left ( { — 1} \ right) dx} + C} {\ frac {1} {x}}}
= \frac{{ — \ln \left| х \ справа | + С}}{{\ гидроразрыва {1} {х}}}
= x\left( {C — \ln \left| x \right|} \right).

 смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыСчетчик воды (4 ° C)МикробармикропаскальМиллибарМиллиметр Ртуть (0 ° С)Миллиметр воды (4 ° С)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футПаундаль / квадратный футФунт-сила / квадратный футФунт-сила / квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТон-сила (длинный) / кв. ФутТон-сила (длинный) / квадратный дюймТон-сила (короткое замыкание) / пл. ФутТон-сила (короткое замыкание) / пл. дюймторр
смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыСчетчик воды (4 ° C)МикробармикропаскальМиллибарМиллиметр Ртуть (0 ° С)Миллиметр воды (4 ° С)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футПаундаль / квадратный футФунт-сила / квадратный футФунт-сила / квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТон-сила (длинный) / кв. ФутТон-сила (длинный) / квадратный дюймТон-сила (короткое замыкание) / пл. ФутТон-сила (короткое замыкание) / пл. дюймторр ⓘ Базовая высота на сечении 2 [Z2]
ⓘ Базовая высота на сечении 2 [Z2]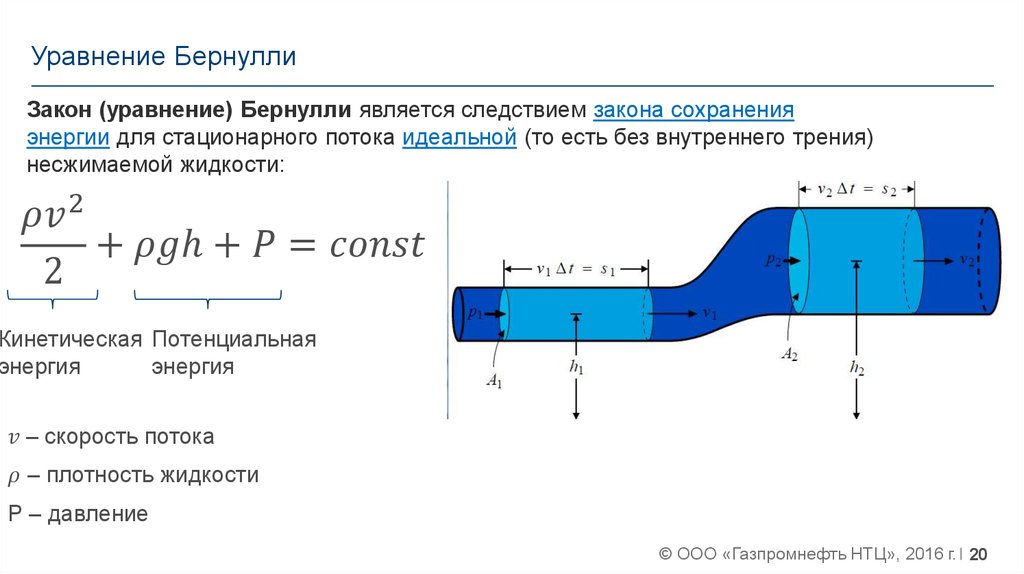 ⓘ Базовая высота на сечении 1 [Z1]
ⓘ Базовая высота на сечении 1 [Z1] ⓘ Скорость в точке 1 [V1]
ⓘ Скорость в точке 1 [V1] смэкса паскаль Фемто паскаль Foot морской воды (15 ° С)Нога воды (4 ° С)Нога воды (60 ° F)ГигапаскальГрамм-сила / кв. сантиметргектопаскальДюймовый Меркурий (32 ° F)Дюймовый Меркурий (60 ° F)КПа (4 ° С)КПа (60 ° F)кгс / кв. смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыСчетчик воды (4 ° C)МикробармикропаскальМиллибарМиллиметр Ртуть (0 ° С)Миллиметр воды (4 ° С)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футПаундаль / квадратный футФунт-сила / квадратный футФунт-сила / квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТон-сила (длинный) / кв. ФутТон-сила (длинный) / квадратный дюймТон-сила (короткое замыкание) / пл. ФутТон-сила (короткое замыкание) / пл. дюймторр
смэкса паскаль Фемто паскаль Foot морской воды (15 ° С)Нога воды (4 ° С)Нога воды (60 ° F)ГигапаскальГрамм-сила / кв. сантиметргектопаскальДюймовый Меркурий (32 ° F)Дюймовый Меркурий (60 ° F)КПа (4 ° С)КПа (60 ° F)кгс / кв. смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыСчетчик воды (4 ° C)МикробармикропаскальМиллибарМиллиметр Ртуть (0 ° С)Миллиметр воды (4 ° С)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футПаундаль / квадратный футФунт-сила / квадратный футФунт-сила / квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТон-сила (длинный) / кв. ФутТон-сила (длинный) / квадратный дюймТон-сила (короткое замыкание) / пл. ФутТон-сила (короткое замыкание) / пл. дюймторр Это именно тот случай, когда теория — если вывести за скобки доказательства утверждений — минимальна, но позволяет добиваться
Это именно тот случай, когда теория — если вывести за скобки доказательства утверждений — минимальна, но позволяет добиваться
 Далее составляется уравнение
Далее составляется уравнение Таким образом,
Таким образом,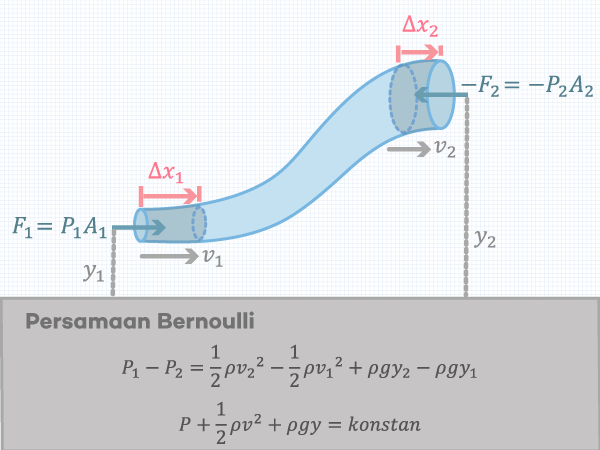 Напомним, что для нахождения ФСР составляется характеристическое
Напомним, что для нахождения ФСР составляется характеристическое Считается константой
Считается константой Вы должны ввести значения для невыбранного.
Вы должны ввести значения для невыбранного.