Элементы комбинаторики. Примеры комбинаторных задач
1. Элементы комбинаторики
2. Примеры комбинаторных задач
Задачи, решая которые приходится
составлять различные комбинации из
конечного числа элементов и
подсчитывать число комбинаций ,
называются
Раздел математики , в котором
рассматриваются подобные задачи,
называют комбинаторикой
Слово «комбинаторика» от латинского
combinare — «соединять , сочетать»
3. Пример 1
Из группы теннисистов, в которую входят четыречеловека-Антонов, Григорьев , Сергеев и Федоров ,
тренер выделяет пару для участия в соревнованиях .
Сколько существует вариантов выбора такой пары?
АГ, АС, АФ
ГС, ГФ
СФ
Значит, всего существует шесть вариантов выбора
Способ рассуждений , которым мы воспользовались ,
называют перебором возможных вариантов
4. Пример 2
Сколько трехзначных чисел можносоставить из цифр 1, 3, 5, 7 ,используя в
записи числа каждую из них не более
одного раза?
Чтобы ответить на вопрос задачи , выпишем все такие
числа .
 Полученные результаты запишем в четыре
Полученные результаты запишем в четырестроки , в каждой из которых шесть чисел:
135 137
153 157 173 175
315 317
351 357 371 375
513 517
531 537 571 573
713 715
731 735 751 753
5. Способ второй
Проведенныйперебор вариантов
проиллюстрирован на схеме
Такую
схему называют деревом
возможных вариантов
6. Способ третий
Первую цифру можно выбрать четырьмя способами . Так как послевыбора первой цифры останутся три , то вторую цифру можно
выбрать уже тремя способами. Наконец , третью цифру можно
выбрать двумя способами. Следовательно , общее число искомых
чисел равно произведению 4*3*2,т.е.24
Использовалось комбинаторное правило умножения:
Пусть имеется п элементов и требуется выбрать из них
один за другим k элементов. Если первый элемент
можно выбрать п1 способами, после чего второй
элемент можно выбрать п2 способами из оставшихся,
затем третий элемент можно выбрать п3 способами из
оставшихся и т.
 д., то число способов, которыми могут
д., то число способов, которыми могутбыть выбраны все k элементов, равно произведению
п1 · п2 · п2 · … · пk.
7. Пример 3
Из города А в город В ведут две дороги, из города В вгород С – три дороги , из города С до пристани-две
дороги . Туристы хотят проехать из города А через В и С
к пристани . Сколькими способами они могут выбрать
маршрут?
Решение: 2*3*2=12
8. Задачи
1. В кафе предлагают два первых блюда :борщ ,рассольник-и четыре вторых блюда: гуляш, котлеты,
сосиски, пельмени. Укажите все обеды из двух блюд,
которые может заказать посетитель . Построить
дерево возможных вариантов
2. Стадион имеет четыре входа: А, В, С, D. Укажите все
возможные способы, какими посетитель может войти
через один вход, а выйти через другой. Сколько таких
способов?
Ответ:12 способов
3. Используя цифры 0,2,4,6 составьте все возможные
трехзначные числа, в которых цифры не повторяются.
9. Задачи
4. В шахматном турнире участвуют 9 человек. Каждый
Каждыйиз них сыграл с каждым по одной партии. Сколько
всего партий было сыграно?
Ответ:36 партий
5. При встрече 8 человек обменялись рукопожатиями.
Сколько всего было сделано рукопожатий?
Ответ:28 рукопожатий
6. Учащиеся 9 класса решили обменяться
фотографиями. Сколько фотографий для этого
потребуется, если в классе 24 учащихся?
Ответ:552 фотографии
10. Задачи
7. В кафе имеются три первых блюда , пять вторыхблюд и два третьих. Сколькими способами посетитель
кафе может выбрать обед , состоящий из первого ,
второго и третьего блюд?
Ответ:30 способов
8. Петр решил пойти на новогодний карнавал в
костюме мушкетера. В ателье проката ему предложили
на выбор различные по фасону и цвету предметы:
пять видов брюк , шесть камзолов , три шляпы , две
пары сапог . Сколько различных карнавальных
костюмов можно составить из этих предметов?
Ответ:180 костюмов
11. Перестановки
Простейшими комбинациями , которые можносоставить из элементов конечного множества ,
являются перестановки
Число перестановок из n элементов обозначают
символом Рn(читается «Р из n»)
Для произведения первых n натуральных чисел
используют специальное обозначение: n! ( читается n
факториал)
2!=2; 5!=120; 1!=1
12.
 Примеры задачТаким образом , число всевозможных перестановок из
Примеры задачТаким образом , число всевозможных перестановок изn элементов вычисляется по формуле: Рn=n!
Пример 1. Сколькими способами могут быть
расставлены 8 участниц финального забега на восьми
беговых дорожках?
Р8=8!=40320
Пример 2. Сколько различных четырехзначных чисел, в
которых цифры не повторяются, можно составить из
цифр 0, 2, 4, 6?
Из цифр 0,2,4,6 можно получить Р4 перестановок. Из
этого числа надо исключить те перестановки , которые
начинаются с 0.Получаем: Р4-Р3=4!-3!=18
Пример 3. Имеется 9 различных книг, четыре из
которых- учебники . Сколькими способами можно
расставить эти книги на полке так , чтобы все
учебники стояли рядом?
Сначала будем рассматривать учебники как одну книгу.
Тогда на полке надо расставить не 9,а 6 книг . Это
можно сделать Р6 способами. В каждой из полученных
комбинаций можно выполнить Р4 перестановок
учебников. Значит , искомое число способов
расположения книг на полке равно произведению
Р6*Р4.
 Получаем:
Получаем:Р6*Р4=6!*4!=720*24=17280
14. Задачи
1. Сколькими способами 4 человека могут разместиться начетырехместной скамейке?
Ответ:24
2. Курьер должен разнести пакеты в 7 различных
учреждений. Сколько маршрутов может он выбрать?
Ответ:5040
3. Сколько шестизначных чисел(без повторения цифр)
можно составить из цифр: а)1,2,5,6,7,8; б)0,2,5,6,7,8 ?
Ответ : а)720;б)600
4. В расписании на понедельник шесть
уроков:алгебра,геометрия,биология,история,физкультура,х
имия.Сколькими способами можно составить расписание
уроков на этот день так , чтобы два урока математики
стояли рядом?
Ответ:240
15. Задачи
5. Делится ли число 14! На:А)168; б)136;в)147;г)132?
6.
7.
Ответ на 6) :15; 1/90; 1722; 40
16. Проверочная работа
1 ВАРИАНТ1. Комбинаторные задачи
2. Способы решения
комбинаторных задач
3. Вычислить
2 ВАРИАНТ
1. Перестановки , формула
2. Комбинаторика
3.
 Вычислить
Вычислить17. Размещения
Пусть имеется 4 шара и 3 пустых ячейки . В пустые ячейки можно поразному разместить три шара из этого набора шаров . Выбираяразными способами первый , второй и третий шары , будем получать
различные тройки шаров.
Каждую упорядоченную тройку , которую можно составить из
четырех элементов , называют размещением из четырех элементов
по три
Размещением из n элементов по к (к<n) называется любое
множество , состоящее из любых к элементов , взятых в
определенном порядке из данных n элементов
Число размещений из n элементов по к обозначают
Читают « А из n по к »
Формула для вычисления числа размещений из nэлементов по к
18. Примеры
1. Учащиеся второго класса изучают 8 предметов. Сколькимиспособами можно составить расписание на один день, чтобы в нем
было 4 различных предмета?
В этом примере речь идет о размещениях из 8 элементов по 4.
Имеем:
2. Сколько трехзначных чисел ( без повторения цифр в записи
числа) можно составить из цифр 0,1,2,3,4,5,6?
Среди данных цифр есть цифра 0, с которой не может начинаться
трехзначное число .
 Поэтому:
Поэтому:19. Задачи
1. Сколькими способами может разместиться семья из трехчеловек в четырехместном купе, если других пассажиров в купе
нет?
Ответ: 24
2. Из 30 участников собрания надо выбрать председателя и
секретаря. Сколькими способами это можно сделать?
Ответ: 870
3. Сколькими способами организаторы конкурса могут
определить, кто из 15 его участников будет выступать первым,
вторым и третьим?
Ответ: 2730
4. На странице альбома 6 свободных мест для фотографий.
Сколькими способами можно вложить в свободные места: а)2
фотографии; б) 4 фотографии; в) 6 фотографий?
Ответ: 30;360;720
20. Сочетания
Сочетанием из n элементов по к называется любоемножество , составленное из данных n элементов
В отличие от размещений в сочетаниях не имеет значения , в
каком порядке указаны элементы .Два сочетания из элементов по
к отличаются друг от друга хотя бы одним элементом
Обозначают
Читают «С из n по к»
Формула числа сочетаний из n элементов по к ,где к<n
21.
 Примеры1. Из 15 членов туристической группы надо выбрать трех
Примеры1. Из 15 членов туристической группы надо выбрать трехдежурных. Сколькими способами можно сделать этот выбор?
Каждый выбор отличается от другого хотя бы одним дежурным.
Значит , здесь речь идет о сочетаниях из 15 элементов по 3
Имеем:
2. Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо
выбрать 3 яблока и 2 груши. Сколькими способами можно сделать
такой выбор?
Имеем:
22. Задачи
1. В классе 7 человек успешно занимаются математикой.Сколькими способами можно выбрать из них двоих для участия в
математической олимпиаде?
Ответ:21
2. Учащимся дали список из 10 книг , которые рекомендуется
прочитать во время каникул. Сколькими способами ученик может
выбрать из них 6 книг?
Ответ:210
3. В классе учатся 16 мальчиков и 12 девочек. Для уборки
территории требуется выделить четырех мальчиков и трех
девочек. Сколькими способами это можно сделать?
Ответ:400400
4. В библиотеке читателю предложили на выбор из новых
поступлений 10 книг и 4 журнала.
 Сколькими способами он может
Сколькими способами он можетвыбрать из них 3 книги и 2 журнала?
Ответ:720
23. Домашняя работа Самостоятельная работа
1. Сколькими способами 9 участников конкурсамогут выступить в порядке очередности в
финале ?
2. Делится ли число 40! на: а)410;б)500;в)780?
3. Используя цифры 0,3,7,8 составьте все
возможные двузначные числа, в которых цифры
не повторяются
4. В городской думе 10 депутатов моложе 30 лет.
Сколькими способами можно выбрать из них
троих для работы в комитете по молодежной
политике?
Алгебра Примеры комбинаторных задач
Материалы к уроку
Конспект урока
В науке и на практике часто встречаются задачи, при решении которых нужно составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел, в котором они рассматриваются, — комбинаторикой. Методы комбинаторики применяются в физике, химии, биологии, экономике и других областях знаний.
Методы комбинаторики применяются в физике, химии, биологии, экономике и других областях знаний.
Рассмотрим некоторые комбинаторные задачи.
Пример первый. Из группы спортсменов по гребле, в которую входят четыре человека – Андреев, Гришин, Степанов и Николаев, тренер выделяет двоих для участия в соревнованиях пар. Сколько существует вариантов выбора такой пары?
Решение. Составим сначала пары, в которые входит Андреев. Для краткости будем писать первые буквы фамилий. Получим три пары: Андреев-Гришин, Андреев-Степанов, Андреев-Николаев.
Выпишем теперь пары, в которые входит Гришин, но не входит Андреев. Таких пар две: Гришин-Степанов, Гришин-Николаев.
Далее составим пары, в которые входит Степанов, но не входят Андреев и Гришин. Такая пара одна: Степанов-Николаев.
Других вариантов составления пар нет, потому что все пары, в которые входит Николаев, уже составлены.
Итак, получили шесть пар: Андреев-Гришин, Андреев-Степанов, Андреев-Николаев, Гришин-Степанов, Гришин-Николаев, Степанов-Николаев.
Значит, всего существует шесть вариантов выбора тренером пары спортсменов по гребле из данной группы.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
Второй пример. Сколько трехзначных чисел можно составить из цифр два, четыре, шесть, восемь, используя в записи числа каждую из них не более одного раза?
Чтобы ответить на вопрос задачи, выпишем все такие числа. Пусть на первом месте стоит цифра два, на втором месте может быть записана любая из цифр: четыре, шесть, восемь. Запишем, например, на втором месте цифру четыре. Тогда в качестве третьей цифры можно взять цифру шесть или восемь. Получим два числа двести сорок шесть и двести сорок восемь. Если на втором месте записать цифру шесть, то в качестве третьей цифры можно взять цифру четыре или восемь. В этом случае получим числа двести шестьдесят четыре и двести шестьдесят восемь. Если же на втором месте записать цифру восемь, то получим числа двести восемьдесят четыре и двести восемьдесят шесть.
Итак, мы составили все числа, которые начинаются с цифры два. Таких чисел шесть…..
Аналогичным способом можно составить числа, которые начинаются с цифры четыре, с цифры шесть, с цифры восемь.
Полученные результаты запишем в четыре строки, в каждой из которых шесть чисел…..
Таким образом, из цифр два, четыре, шесть, восемь можно составить двадцать четыре трехзначных числа, в записи которых цифры не повторяются.
Проведенный перебор вариантов проиллюстрирован на схеме. Такую схему называют деревом возможных вариантов….
Заметим, что ответ на вопрос, поставленный во втором примере, можно получить, не выписывая сами числа. Будем рассуждать так. Первую цифру можно выбрать четырьмя способами. После этого останутся три цифры, которые могут стоять на втором месте, и третью цифру можно выбрать из оставшихся двух. Следовательно, общее число искомых трехзначных чисел равно произведению четыре, три и два, то есть двадцати четырем.
Мы нашли ответ на поставленный во втором примере вопрос, используя комбинаторное правило умножения.
Сформулируем это правило в общем виде.
Пусть имеется эн элементов и требуется выбрать из них один за другим ка элементов. Если первый элемент можно выбрать (эн первое) способами, после чего второй элемент можно выбрать (эн второе) способами из оставшихся, затем третий элемент можно выбрать (эн третье) способами из оставшихся и так далее, то число способов, которыми могут быть выбраны все ка элементов равно произведению эн первого, эн второго, эн третьего и так далее до эн с индексом ка.
Пример третий. Из города А в город Бэ ведут три дороги, из города Бэ в город Цэ — четыре дороги, из города Це до пристани – две дороги. Туристы хотят проехать из города А через город Бэ и це к пристани. Сколькими способами они могут выбрать маршрут.
Путь из А в Бэ туристы могут добраться тремя способами. Далее в каждом случае они могут проехать из Бэ в Це четырьмя способами. Таким образом, имеются три умноженное на четыре вариантов маршрута из А в Це. Так из города Це на пристань можно попасть двумя способами, то всего существует три умноженное на четыре умноженное на два, то есть двадцать четыре способа выбора туристами маршрута из города А к пристани.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Элементы комбинаторики. Методы решения некоторых задач
1) Немного истории.
В математике и ее приложениях часто
приходится иметь дело с различного рода
множествами и подмножествами: устанавливать их
связь между элементами каждого, определять число
множеств или их подмножеств, обладающих заданным
свойством. Такие задачи приходится
рассматривать при определении наиболее выгодных
коммуникаций внутри города, при организации
автоматической телефонной связи, работы морских
портов, при выявлении связей внутри сложных
молекул, генетического кода, а также в
лингвистике, в автоматической системе
управления, значит и в теории вероятностей, и в
математической статистике со всеми их
многочисленными приложениями.
Поговорим об одном из разделов теории вероятности – комбинаторике.
Комбинаторика — ветвь математики,
изучающая комбинации и перестановки предметов.
Еще комбинаторику можно понимать как перебор
возможных вариантов. Комбинаторика возникла в 17
веке. Долгое время она лежала вне основного русла
развития математики.
С задачами, в которых приходилось выбирать те или
иные предметы, располагать их в определенном
порядке и отыскивать среди разных расположений
наилучшие, люди столкнулись еще в доисторическую
эпоху, выбирая наилучшее положение охотников во
время охоты, воинов – во время битвы,
инструментов — во время работы.
Комбинаторные навыки оказались полезными и в
часы досуга. Нельзя точно сказать, когда наряду с
состязаниями в беге, метании диска, прыжках
появились игры, требовавшие, в первую очередь,
умения рассчитывать, составлять планы и
опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.

Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе “ Об искусстве комбинаторики ”, опубликованной в 1666 году. Он также впервые ввел термин “комбинаторика”. Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов. В настоящее время в образовательный стандарт по математике включены основы комбинаторики, решение комбинаторных задач методом перебора, составлением дерева вариантов (еще его называют “дерево возможностей”) с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”.
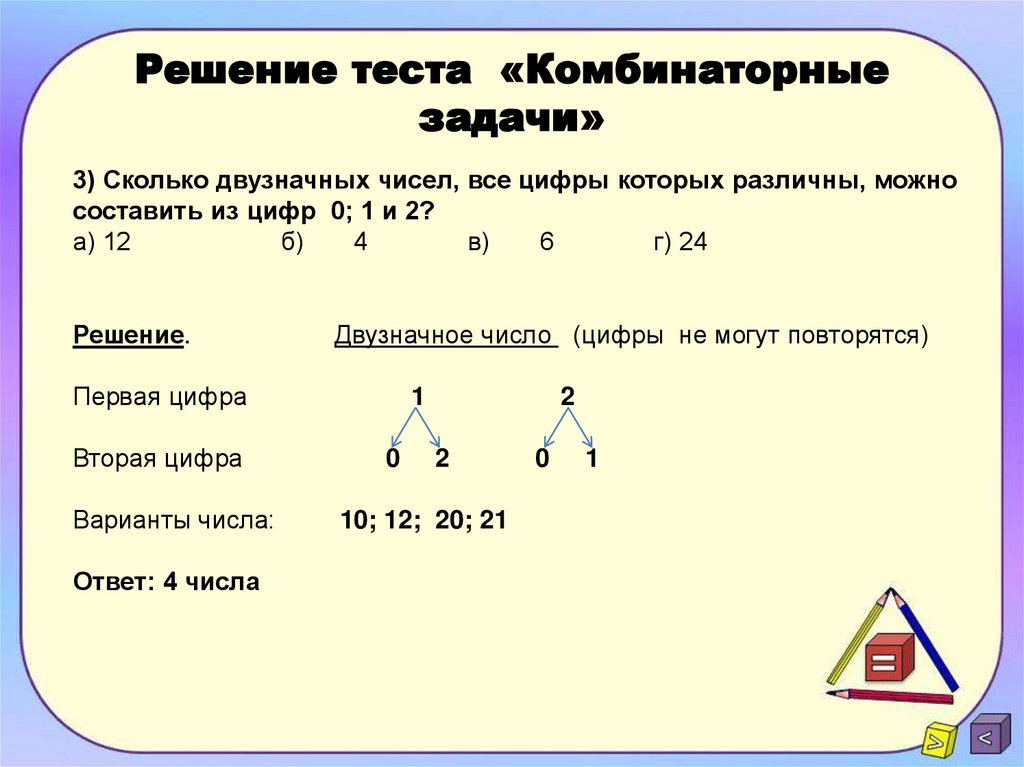 Правило
умножения заключается в том, что для того, чтобы
найти число всех возможных исходов независимого
проведения двух испытаний А и В, следует
перемножить число всех исходов испытания А и
число всех исходов испытания В. В задачах по
комбинаторике часто применяется такое понятие
как факториал (в переводе с английского “factor” -
“множитель”).
Правило
умножения заключается в том, что для того, чтобы
найти число всех возможных исходов независимого
проведения двух испытаний А и В, следует
перемножить число всех исходов испытания А и
число всех исходов испытания В. В задачах по
комбинаторике часто применяется такое понятие
как факториал (в переводе с английского “factor” -
“множитель”).Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут: n!=1 2 3 … (n-1) n
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
2) ЗАДАЧИ
1. В школьной столовой на первое можно
заказать борщ, солянку, грибной суп, на второе -
мясо с макаронами, рыбу с картошкой, курицу с
рисом, а на третье — чай и компот. Сколько
различных обедов можно составить из указанных
блюд?
Сколько
различных обедов можно составить из указанных
блюд?
1 способ. Перечислим возможные варианты
Чай(Ч) |
Мясо с макаронами(М) |
Рыба с картошкой(Р) |
Курица с рисом(Кр) |
Борщ (Б) |
БМЧ/ БМК |
БРЧ/БРК |
БКрЧ/БКрК |
Солянка(С) |
СМЧ/ СМК |
СРЧ/СРК |
СКрЧ/СКрК |
Грибной суп(Г) |
ГМЧ/ГМК |
ГРЧ/ГРК |
ГКрЧ/ГКрК |
18 вариантов.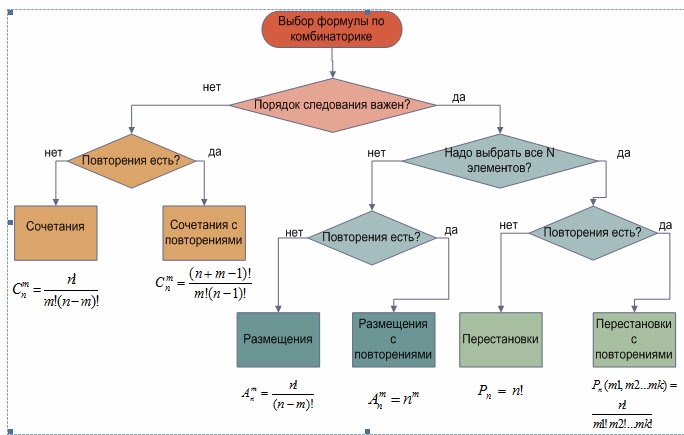
2 способ. Дерево возможностей.
3 способ. Используя правило умножения, получаем: 3х3х2=1
2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?
1 способ. Обозначим мячи — М1, М2,
игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5.
Перечислим возможные варианты:
М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
Ответ: 40 вариантов.
2 способ. Используя правило умножения,
получаем: 2х4х5= 40
3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
1 способ.
Перечислим возможные варианты.
0 |
2 |
6 |
|
2 |
20 |
22 |
|
3 |
30 |
32 |
36 |
6 |
60 |
62 |
66 |
7 |
70 |
72 |
76 |
9 |
90 |
92 |
96 |
2 способ. Дерево возможностей.
Дерево возможностей.
3 способ. Используя правило умножения, получаем: 5х3=15 .
4. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1,2,3,4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу?
1 способ. Перечислим возможные варианты номеров такси:
1 |
2 |
3 |
5 |
||
1 |
211 |
212 |
213 |
214 |
215 |
2 |
221 |
222 |
223 |
224 |
225 |
3 |
231 |
232 |
233 |
234 |
235 |
4 |
241 |
242 |
243 |
244 |
245 |
5 |
251 |
252 |
253 |
254 |
255 |
Ответ: 25 человек.
2 способ. Используя правило умножения, получаем: 5х5=25
5. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?
1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:
№1 — Саша — есть возможность выбрать из 5
вариантов (стульев)
№2 — Петя — 4 варианта
№3- Денис — 3 варианта
№4- Оля — 2 варианта
№5 — Настя- 1 вариант
Используя правило умножения, получаем: 5х4х3х2х1=120
2 способ. Решаем, используя понятие факториала: 5!=120
6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?
1 способ. Перечислим возможные
варианты состава пары:
Перечислим возможные
варианты состава пары:
11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д
Ответ: 10 пар.
2 способ. Из пяти классов нужно
выбрать 2 дежурных.
Число элементарных событий = = 10
7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать?
1 способ. Обозначим имена детей
первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.
Ответ: 6 пар.
2 способ. Мальчиков 3, из них 1 можно
выбрать ,
девочек 2, из них можно 1 выбрать , используя
правило умножения, получаем:
х = 6
8. В соревнованиях по фигурному
катанию принимали участие россияне, итальянцы,
украинцы, немцы, китайцы и французы.
В соревнованиях по фигурному
катанию принимали участие россияне, итальянцы,
украинцы, немцы, китайцы и французы.
Сколькими способами могут
распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве
страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 — имеют возможность занять с1-6 места, т.е. 6
вариантов
И2 — 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1=
720
2 способ. Используя понятие факториала, получаем: 6!=720
9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых?
Обозначим первыми заглавными буквами
имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В
2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно = 15
10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?
Вычислим, сколько четверок из 7 дисков
можно составить у Пети:
=35, число
четверок у Вали из 9 дисков -= 126
По правилу умножения находим число обменов 35х126=4410
11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?
Из 5 офицеров выбрать 2 можно с помощью
числа сочетаний =10 способами, из 8 сержантов 4 — =70, из 70 рядовых 15 -. По правилу
умножения находим число выбора отряда:
По правилу
умножения находим число выбора отряда:
10х70х= 700х
12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?
Из 6 изумрудов 3 он может выбрать =20 способами, из 9 алмазов 5 -=126, из 7 сапфиров 2 — =21. По правилу умножения находим число вариантов 20х126х21=52920
13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?
Здесь речь идет о размещениях
Можно было решать по-другому. На должность
председателя выбираем из 9 человек, на
заместителя — из 8, на профорга — из 7
По правилу умножения получаем 9х8х7=504
14. В районе построили новую школу. Из
пришедших 25 человек нужно выбрать директора
школы, завуча начальной школы, завуча среднего
звена и завуча по воспитательной работе.
Сколькими способами это можно сделать?
В районе построили новую школу. Из
пришедших 25 человек нужно выбрать директора
школы, завуча начальной школы, завуча среднего
звена и завуча по воспитательной работе.
Сколькими способами это можно сделать?
На должность директора выбираем из 25
человек, на завуча начальной — из 24, завуча
среднего звена — из 23, завуча по воспитательной
работе — 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем
15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?
Для Пети набор можно набрать 6х8х10=480
способами, для Васи — 5х7х9=315, для Коли — 4х6х8=192. По
правилу умножения получаем
По
правилу умножения получаем
480х315х192=29030400 способами.
16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?
В русском языке 9 гласных букв — а, е, е,
и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10
цифр выбрать 3 можно=120 способами. Применяя правило умножения,
получаем:
36х120=4320
17. Сколькими способами можно составить
трехцветный флаг из полос разной ширины, если
имеются материи из 8 тканей?
Эта задача на размещение
Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет — 6способами
Используя правило умножения, получаем 8х7х6=336
способов.
18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные?
Из 15 предметов 5 любых можно выбрать
19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?
1 способ. Обозначим белые — Б1, Б2, Б3,
алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3,
Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3,
Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3,
Б3-А2-Ч4
Ответ: 24 варианта.
2способ. Дерево возможностей
Дерево возможностей
3 способ. Используя правило умножения, получаем: 2х3х4=24
20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В — по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников?
1 способ. Обозначим СБ — путь из
Сосновки в Бытовку, ВГ — путь из Быковки в
Масловку, МВ — путь из Масловки в Видово.
По реке -Р, пешком — П, на автобусе — А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.
2 способ. Дерево возможностей
ЛИТЕРАТУРА
1) Еженедельное учебно-методическое приложение “Математика” Изд. Пресса. Москва.1999 г
2) Ю.Н.Макарычев и др. Алгебра 9. Учебник для класса с углубленным изучением математики. Изд. Мнемозина, Москва.2005 год.
3) Л.Г. Петерсон. Математика 4 класс. Изд. Баласс. Москва.1999 г.
4) Ю.Н. Тюрин и др. Теория вероятностей и статистика. МЦНМО. Москва. 2004 год.
Урок математики «Элементы комбинаторики» | Методическая разработка:
Тема урока: Элементы комбинаторики
Цели занятия.
Создать условия для:
Знакомства обучающихся с новым разделом математики: «Комбинаторика», применения основных понятий элементов комбинаторики при решении задач, использования комбинаторных навыков в практических целях и в жизни человека, опираясь на математические подсчеты.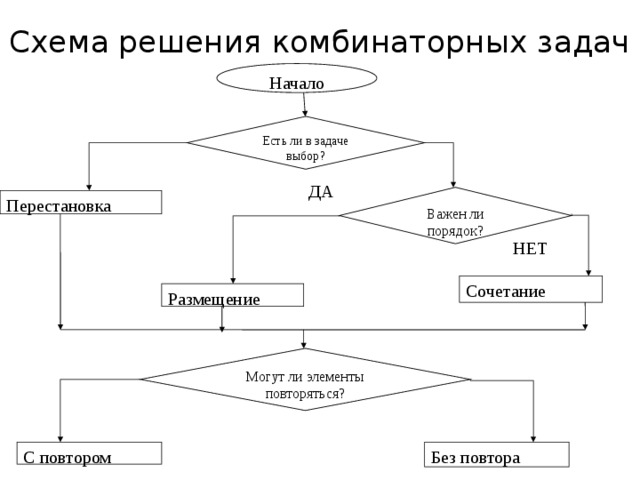
Развития у обучающихся умения решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, практических навыков и умений, аналитических способностей, логического мышления.
Формирования активности личности обучающегося, умения работать в группе, дл привития интереса обучающихся к данной науке, понимания того, что решения комбинаторных задач возникли из практических потребностей человека.
Тип урока: комбинированный
Оборудование: компьютер, проектор, экран, презентация, тесты, учебники математики Н.В. Богомолов..
Технологическая карта урока:
Этапы урока | Деятельность преподавателя | Деятель-ность обучаю-щихся |
Органи-зационный момент. | Взаимное приветствие преподавателя и обучающихся. Проверка отсутствующих. | |
Постановка целей урока. | Настроить на позитив. Математику, физику и психологу задают одну и ту же задачу: «Монету бросили 100 раз, и все 100 раз выпала решка. Что выпадет в 101-ый раз?» Математик:»С вероятностью 1/2 выпадет орёл» Физик: «Эксперимент показал, что должна выпасть решка» Психолог: «Выпадет орёл». Математик с физиком: «Но почему?» -Ну, как же, всё решка да решка! Орлу ведь тоже хочется! Задаёт вопросы обучающимся: Знакома ли вам тема урока? Какую цель можно поставить? (знакомство с новой темой, применение на практике и в жизни человека) | Слушают преподава-теля, проявляют интерес. Цель формули-руют обучаю- щиеся. |
Актуали-зация знаний. | Разминка Итак, начнем наш урок с разминки. Сегодня она будет в другой форме — в виде соревнования. Я задаю вопросы, и кто быстрее поднимет руку, тот и будет отвечать. 1) Портной имеет кусок сукна в 16 м, от которого он ежедневно отрезает по 2 метра. По истечении скольких дней он отрежет последний кусок? (7 дней) 2) Разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку, и одно осталось в корзине? (Один берет корзину вместе с яблоком) 3) Четыре коровы черной масти и три — рыжей масти за пять дней дали такой же надой молока, как 3 коровы черной масти и 5 рыжей за 4 дня. Какие коровы молочнее: черной или рыжей масти? (рыжей) 4) Как представить цифру 4 тремя пятерками? (4=5-5:5) 5) Шесть ног, а бежит не быстрее, чем на четырех. (всадник на коне) 6) Какие часы показывают верное время только два раза в сутки? (которые остановились) 7) В известной сказке «Поди туда — не знаю куда, принеси то — не знаю что» царь послал стрелка Андрея за «тридевять земель». Тридевять — это сколько? (27) 8) Шел Кондрат в Ленинград, а навстречу 12 ребят. У каждого по 3 лукошка, в каждом лукошке — кошка. У каждой кошки — 12 котят. В зубах по 4 мышонка. И задумался старый Кондрат: «Сколько мышат и котят ребята несут в Ленинград?» Как бы вы ответили на этот вопрос? (Один Кондрат шел в Ленинград) 9) В мешке лежат шарики белого и черного цвета. Сколько нужно взять шариков, чтобы 2 было одинакового цвета? (3) 10) Поехал мужик зимой на ярмарку, а базар далеко. Вот едет он лесом-полем, лесом-полем, лесом-полем. Встречает Бабу-Ягу и спрашивает: «Куда ехать?» Она ему показывает направо. И вот он снова едет лесом-полем, лесом-полем, лесом-полем, встречает Лешего. Спрашивает: «Как доехать до базара?» Он показывает налево. Вот он снова едет лесом-полем, лесом-полем, лесом-полем и выезжает к реке. А за рекой — базар. Как ему перебраться на тот берег, учитывая, что лодки нет и надо переправить весь груз? (Дело было зимой). Молодцы! | Отвечают на вопросы. |
Постановка проблемы. Мотивация. | Предлагает решить задачу. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? ВРФ ВФР РФВ РВФ ФРВ ФВР (6) Задачи такого типа называются комбинаторными. Сообщает тему урока. «Элементы комбинаторики». | Слушают преподава-теля, пытаются понять проблему урока. Записывают тему урока в тетрадях. |
Объяснение нового материала. | Лекция преподавателя (исторические данные) Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным. Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в XII веке. Долгое время она лежала вне основного русла развития математики. С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов — во время битвы, инструментов — во время работы. Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника. Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называется комбинаторикой. Комбинаторику можно рассматривать как часть теории множеств — любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях Раздел комбинаторики, в котором рассматривается лишь вопрос о подсчете числа решений комбинаторной задачи, теорией перечислений. Комбинаторика как наука стала развиваться в XIII веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Комбинаторные задачи делятся на несколько групп. Группы, составленные из каких-либо элементов называются соединениями.
Сколькими способами можно расставить 3 различные книги на книжной полке? abc acb bac bca cab cba ответ: 6. Это задача на перестановки Перестановками из n элементов называются такие соединения из n элементов, которые отличаются друг от друга лишь порядком следования элеметов. Pn =A= n(n-1) (n-2)…321 Pn = n! Произведение всех последовательных натуральных чисел от 1 до n обозначается n! n! = 1 · 2 · 3 · . Факториалы растут удивительно быстро (записывает на доске пример): n 1 2 3 4 5 6 7 8 9 10 n! 1 4 6 24 120 720 5040 40 320 362 880 3 628800
У нас имеется 5 книг, что у нас всего одна полка, и что на ней вмещается лишь 3 книги. Сколькими способами можно расставить на полке 3 книги? Выбираем одну из 5-ти книг и ставим на первое место на полке. Это мы можем сделать 5-ю способами. Теперь на полке осталось два места и у нас осталось 4 книги. Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых. Таких пар может быть 5·4. Осталось 3 книги и одно место. Одну книгу из 3-ёх можно выбрать 3-мя способами и поставить рядом с одной из возможных 5·4 пар. Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60. Это размещения. Размещением из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их следования. Число размещений из n элементов по m обозначаются символом: А= n(n-1) (n-2)… (n-(m-1)). А= n!m!
Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг? Книги внешне неразличимы. Но они различаются, и существенно! Эти книги разные по содержанию. Возникает ситуация, когда важен состав элементов выборки, но несущественен порядок их расположения. 123 124 125 134 135 145 234 235 245 345 ответ: 10 Это сочетания. Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Число сочетаний из n элементов по m обозначают символом C= | Слушают преподава-теля. Приложение (Презентация «Из истории комбинато-рики») Записывают определение в тетрадях. Пользуются учебником математики Н.В. Богомолов, с. 371 (формулы 16.2, 16.3,16.4, 16.5), с. 372 Записывают определение в тетрадях. Пользуются учебником математики Н.В. Богомолов, (формула 16.1), с. 371 Записывают определение в тетрадях. Пользуются учебником математики Н.В. Богомолов, (формулы16.6, 16.7, 16.8, 16.9, 16.10), с. 372 |
Закрепление полученных знаний. | 1 Задача. Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках? P8 = 8!= 1 ∙2∙ 3 ∙4∙ 5 ∙6∙ 7 ∙8 = 40320 2 Задача. Квартет Проказница Мартышка Осёл, Козёл, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой! – Кричит Мартышка, — погодите! Как музыке идти? Ведь вы не так сидите… И так, и этак пересаживались – опять музыка на лад не идет. Вот пуще прежнего пошли у них разборы И споры, Кому и как сидеть… Сколькими способами можно рассадить четырех музыкантов? P = 4! = 1 * 2 * 3 * 4 = 24 Задаёт вопрос: какой тип комбинаторной задачи? (перестановки). 3 Задача. Обучающиеся изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета? A =9!/5! = 6∙ 7∙ 8∙ 9 = 3024 Задаёт вопрос: какой тип комбинаторной задачи? (размещения). | Решение у доски. Записывают в тетрадях. Отвечают на вопрос. Решение у доски. Записывают в тетрадях. Отвечают на вопрос. |
Индиви-дуальная работа. Тест. | Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков? 1) 30 2) 100 3) 120 4) 5 2. 1) 128 2) 495 3) 36 4) 48 3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными? 1) 10 2) 60 3) 20 4) 30 № задания 1 2 3 № ответа 3 2 4 | Работают на месте. На экране (Тест). Взаимопро-верка с помощью мульти-медия, коррекция. |
Домашнее задание. | Раздает карточки с домашним заданием. Поясняет как решить. 1.В коробке находится 10 белых и 6 черных шаров. Сколькими способами из коробки можно вынуть один шар любого цвета? 2. 3. В магазине “Филателия” продается 8 разных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора? 4. Проект «История комбинаторики» | Слушают преподава-теля. |
Подведение итогов, рефлексия. | Задаёт вопросы обучающимся: Может ли нам комбинаторика помочь в реальной жизни? Решение комбинаторных задач развивает творческие способности. Области применения комбинаторики: учебные заведения ( составление расписаний) -сфера общественного питания (составление меню) -лингвистика (рассмотрение вариантов комбинаций букв) -спортивные соревнования (расчёт количества игр между участниками) -агротехника (размещение посевов на нескольких полях) -география (раскраска карт) -биология (расшифровка кода ДНК) -химия (анализ возможных связей между химическими элементами) -экономика (анализ вариантов купли-продажи акций) азартные игры (подсчёт частоты выигрышей) -криптография (разработка методов шифрования) -доставка почты (рассмотрение вариантов пересылки) -военное дело (расположение подразделений) Решение задачи с профессиональной направленностью (укроп, петрушка, редис). Как посадить растения, используя комбинаторные задачи: размещения, перестановки, сочетания? Как посадить растения с учетом солнца и образования тени (межпредметная связь с физикой). Какова была цель урока? Достигнута ли она? Чем обусловлен выбор правила комбинаторики? Чем обусловлен выбор формулы? Перспектива последующей работы. Настрой на позитив: «МАТЕМАТИКУ — сдам!» Оцените степень сложности урока Вам было на уроке:
Оцените степень вашего усвоения материала
| Отвечают с места. Выходят к доске и показывают применение формул на комбинато-рику. Отвечают с места. Отмечают в карточках. |
Литера-тура. | 1. «Математика» 1 сентября №1 2012г И.Р. Высоцкий «В10 –вероятность» «ЕГЭ 2012. Типовые тестовые задания» Электронные ресурсы: Открытый банк заданий по математике http://mathege.ru/or/ege/Main СтатГрад МИОО |
Решение комбинаторных задач с помощью таблицы вариантов, правило суммы и произведения
Таблица вариантов для комбинаций из двух элементов
Допустим, мы бросаем два игральных кубика, и нас интересуют все комбинации, когда сумма выпавших чисел кратна 5.
Каждый из кубиков имеет 6 возможных «состояний»: 1,2,3,4,5,6.
Для того, чтобы описать все возможные комбинации двух кубиков, нужно составить таблицу вариантов:
| Второй кубик | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Первый кубик | 1 | 11 | 12 | 13 | 14 | 15 | 16 |
| 2 | 21 | 22 | 23 | 24 | 25 | 26 | |
| 3 | 31 | 32 | 33 | 34 | 35 | 36 | |
| 4 | 41 | 42 | 43 | 44 | 45 | 46 | |
| 5 | 51 | 52 | 53 | 54 | 55 | 56 | |
| 6 | 61 | 62 | 63 | 64 | 65 | 66 | |
Сумма выпавших чисел на кубиках кратна 5 в 7 случаях (ячейки таблицы закрашены). Общее количество возможных комбинаций – 36. 2 = 3$ разными способами.
2 = 3$ разными способами.
По правилу суммы у нас 3+3 = 6 способов для выбора.
Например:
Сколько существует различных двузначных кодовых слов, состоящих из одной буквы И одной цифры, если разрешенные символы – это 5 букв «a,b,c,d,e» и 3 цифры «1,2,3»?
По правилу произведения число всех кодовых слов – всех возможных комбинаций: $m \cdot n = 5 \cdot 3 = 15$ слов.
Примеры
Пример 1. При составлении расписания завуч хочет на первый урок поставить алгебру или физику, а на второй – историю, географию или иностранный язык. Сколько существует вариантов расписания для первых двух уроков? Изобразите их с помощью таблицы вариантов.
Для первого урока есть m = 2 варианта.
Для второго урока n = 3 варианта.
По правилу произведения общее число вариантов для двух уроков
$mn = 2 \cdot 3 = 6$ вариантов.
2й урок | ||||
История | География | Иностранный язык | ||
1й урок | Алгебра | Алгебра История | Алгебра География | Алгебра Ин. |
Физика | Физика История | Физика Геграфия | Физика Ин. язык | |
Ответ: 6 вариантов
Пример 2. Из коробки с 12 фломастерами разного цвета один фломастер берет Коля, а за ним – один фломастер берет Петя. Сколько существует различных вариантов такого выбора фломастеров?
Перед Колей на выбор 12 фломастеров – у него m = 12 вариантов.
Перед Петей остаётся на выбор 11 фломастеров – у него n = 11 вариантов.
По правилу произведения общее число вариантов: $ mn = 12 \cdot 11 = 132$
Ответ: 132 варианта
Пример 3. Сколько различных трёхзначных чисел можно записать с помощью цифр 0,1,2,3,4,5, если а) цифры могут повторяться; б) цифры не повторяются.
а) цифры могут повторяться
В разряде сотен могут быть цифры 1,2,3,4,5, всего m=5 вариантов
В разряде десятков могут быть цифры 0,1,2,3,4,5, всего n=6 вариантов
В разряде единиц могут быть цифры 0,1,2,3,4,5, всего k=6 вариантов
По правилу произведения общее количество возможных трёхзначных чисел:
$$ mnk = 5 \cdot 6 \cdot 6 = 180 $$
б) цифры не повторяются
В разряде сотен могут быть цифры 1,2,3,4,5, всего m = 5 вариантов
В разряде десятков не цифра сотен, всего n = 5 вариантов
В разряде единиц не цифра десятков и не цифра сотен, всего k = 4 варианта
Всего $mnk = 5 \cdot 5 \cdot 4 = 100$
Ответ: а) 180; б) 100
Пример 4. Сколькими способами можно рассадить четырёх щенков по четырём углам комнаты?
Сколькими способами можно рассадить четырёх щенков по четырём углам комнаты?
У первого щенка $m_1 = 4$ варианта углов.
У второго щенка, т.к. один угол уже занят, остаётся $m_2 = 3$ варианта углов.
У третьего щенка, т.к. два угла уже заняты, остаётся $m_3 = 2$ варианта углов.
У четвертого щенка выбора нет, ему остался $m_4 = 1$ угол, без вариантов.
Общее количество способов по правилу произведения:
$$ m_1 \cdot m_2 \cdot m_3 \cdot m_4 = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $$
Ответ: 24 способа
Пример 5. Сколько существует способов занять 1,2 и 3 места на чемпионате, в котором участвуют 10 команд?
Для того, чтобы занять 1-е место существует $m_1 = 10$ претендентов.
Если 1-е место определено, для 2-го места остаётся $m_2 = 9$ претендентов.
Если 1-е и 2-е определено, для 3-го места остаётся $m_3 = 8$ претендентов.
Итого, по правилу произведения:
$m_1 \cdot m_2 \cdot m_3 = 10 \cdot 9 \cdot 8 = 720$ вариантов распределения призовых мест.
Ответ: 720 способов
Комбинаторика, элементы, решение задач и формулы. Алгебра 9 класс, урок и презентация
Дата публикации: .
Комбинаторика — знакомство
Ребята, мы переходим к изучению новой темы. На сегодняшнем уроке, мы будем изучать комбинаторные задачи. Раздел комбинаторики можно выделить как самостоятельный раздел, но он также является очень важным для изучения наших дальнейших тем математической статистики и теории вероятности.
Так что же такое комбинаторика? И какими задачами она занимается? Комбинаторика и слово комбинация очень похожи и имеют прямое отношение друг к другу. В комбинаторике изучают различные комбинации элементов множества и отношения на этих множествах. Впервые термин «комбинаторика» ввел Лейбниц, который в 1666 году опубликовал большой труд «Рассуждения о комбинаторном искусстве».
Примеры использовании комбинаторики
Давайте рассмотрим пример. Сколько чисел можно составить из цифр: 1,2,3?
Нужно найти количество комбинаций из трех чисел. Давайте найдем их. Напрямую переберем все цифры и возможные получающиеся числа. Подойдем к этой задаче осознано и последовательно составим числа от наименьшего к наибольшему.
Давайте найдем их. Напрямую переберем все цифры и возможные получающиеся числа. Подойдем к этой задаче осознано и последовательно составим числа от наименьшего к наибольшему.
Очевидно, что наименьшее число будет начинаться с единицы, тогда у нас два варианта: 123, 132. Теперь поставим на первое место цифру два и у нас также два варианта: 213, 231. У нас осталась цифра три: 312, 321. Мы получили шесть комбинаций: 123, 132, 213, 231, 312, 321. Метод, которым мы воспользовались, называется методом перебора, причем перебор организованный: мы брали числа не произвольно, а придумали правило, по которому будем составлять числа.
Пример. Из цифр 1,4,6 составить трехзначные числа, в которых одна цифра не может повторяться более двух раз.
а) Найти наименьшее число.
б) Найти наибольшее число.
в) Сколько чисел, начинающихся с 6, можно составить?
г) Сколько всего чисел можно составить?
Решение.
а) Чтобы получить наименьшее число, нам нужно на первое место поставить наименьшую цифру, потом на второе и третье — соответственно тоже.
 Наименьшим числом будет 114 так, как самая маленькая цифра у нас единица, и мы ее можем повторить два раза. А из цифр 4 и 6, которые нам надо поставить на третью позицию, очевидно, что 4 меньше 6.
Наименьшим числом будет 114 так, как самая маленькая цифра у нас единица, и мы ее можем повторить два раза. А из цифр 4 и 6, которые нам надо поставить на третью позицию, очевидно, что 4 меньше 6.б) Чтобы получить наибольшее число, нам нужно на первое место поставить наибольшую цифру, потом на второе и третье — соответственно тоже. Наибольшим числом будет 664 так, как самая большая цифра у нас 6, и мы ее можем повторить два раза. 4 больше 1, тогда на последнее место и выберем 4.
в) Назовем числа без повторяющихся цифр. Помним, что все числа должны начинаться с 6. 614 и 641 – без повторяющихся цифр. Теперь рассмотрим числа, в которых повторяется шестерка. 661, 664, 616, 646. Повторяется четверка: 644. Повторяется единица: 611. Всего у нас получилось 8 чисел.
г) Для того, чтобы подсчитать общее количество чисел, которые можно составить, применим тот же способ, что и в пункте в). На первое место поставим цифры 1 и 4, тогда у нас получится еще 16 комбинаций. Учтем, числа начинающиеся с шести, и того 24 комбинации.

Также для решения задачи под пунктом в) можно нарисовать дерево вариантов. Давайте так и поступим. Поместим цифру шесть в верхний прямоугольник, это будет первый уровень дерева. Тогда у нас существует три варианта, куда можно двигаться, соответственно записать — 66, 61 и 62. Таким образом, мы спустились вниз (на один уровень дерева). Далее для каждого из вариантов второго уровня составим возможные комбинации и запишем их в свои ячейки. На третьем уровне у нас получилось восемь ячеек, что и соответствует ответу.
Пример. В урне лежат два белых и один черный шар. На ощупь их различить невозможно. При вытаскивании белого шара его откладывают в сторону, если вытащили черный шар, то его кладут обратно. Шары вытаскивают три раза подряд.
а) Нарисовать дерево событий.
б) В скольких случаях вытащат шар одинакового цвета?
в) В скольких случаях вытащенных белых шаров будет больше?
Решение.
а) В вершине дерева обозначены шары, оставшиеся в урне. На ветвях дерева обозначены вытащенные шары. б) Как видно из рисунка три одинаковых шара можно вытащить только в одном случае, когда они все черные.
б) Как видно из рисунка три одинаковых шара можно вытащить только в одном случае, когда они все черные.
в) Три белых шара вытащить невозможно. Значит нам осталось посчитать количество комбинаций с двумя белыми шарами, нам подходят случаи когда на ветвях дерева встречаются две буквы Б. Такие комбинации: ЧББ, БЧБ, ББЧ. Получили, что всего три комбинации.
В нашем примере количество комбинаций сравнительно немного, но бывают случаи, когда комбинации исчисляются сотнями, и рисовать дерево очень проблематично. Как нам тогда поступить?
Для подсчета комбинаций существует правило умножения: Для того, чтобы найти количество возможных исходов двух независимо проведенных испытаний А и Б, нужно умножить число всех исходов испытания А на число всех исходов испытания Б.
Правила в комбинаторике
Давайте посмотрим правило умножения на примере.
Пример. Петя может доехать до школы четырьмя способами: на трамвае, на автобусе, на троллейбусе и маршрутке. Оплатить проезд можно тремя способами:
- купив билет на остановке,
- купив билет у кондуктора,
- воспользоваться проездным.

Решение.
Возможностей проезда у нас — четыре, способов оплаты — три. Тогда по правилу умножения у нас $4*3=12$ комбинаций. Давайте проверим с помощью таблицы все возможные комбинации. Выбор способа оплаты и способа проезда независимы. В каждую ячейку ставим по одному из событий, получаем 12 возможных ячеек. Наш ответ совпал с тем, что получили по правилу умножения.
Выбор способа решения задачи всегда остается за вами, ребята. Но правило умножения во многом облегчает решение многих задач, так как рисование дерева событий или таблицы возможных вариантов очень неудобно при большом количестве событий.
Правило умножения приводит к важному понятию факториала. Давайте на примере разберем это понятие.
Пример. Сколько существует комбинаций из шести букв: А, Б, В, Г, Д, Е. Буквы не повторяются.
Решение.
На первое место мы можем поставить шесть букв, на второе место — уже пять, так как буквы не повторяются, на третье — соответственно четыре, на четвертое — три, на пятое — две, и на шестое — букву.
Используем правило умножения: 6*5*4*3*2*1=720.
Ответ: 720 способов расстановки букв без повторения.
Определение. Произведение подряд идущих первых n натуральных чисел обозначают n! (n факториал): $n!=1*2*…*(n-1)*n$, n факториал – состоящий из n множителей.
Заметим важное свойство факториала: $n!=(n-1)!*n$.
Данное свойство значительно упрощает решение задач, где присутствует факториал.
Например, для вычисления задач вот такого типа: $\frac{4!*10!}{8!*3!}$.
Совсем необязательно вычислять все факториалы.
Можно все переписать вот в таком виде: $\frac{3!*4*8!*9*10}{8!*3!}$.
Сократив нашу дробь, получим гораздо более простое выражение: $4*9*10=360$.
Пример.
а) Сколько существует способов развесить на указанные места на елке пять различных шаров?
б) Вове надо выполнить четыре домашних задания: по математике, физике, русскому языку и истории. Сколько существует способов очередности выполнения домашнего задания?
Решение.
а) В нашей задаче шары не повторяются. Тогда на первое место претендуют пять шаров, на второе — уже четыре, на третье — соответственно три, на четвертое — два и на последнее — один.
$5*4*3*2*1=5!=120$.
Тогда на первое место претендуют пять шаров, на второе — уже четыре, на третье — соответственно три, на четвертое — два и на последнее — один.
$5*4*3*2*1=5!=120$.
б) Существует четыре варианта: с какого задания начать. Выполнив первое задание, Вове останется выбрать, что делать дальше из трех заданий, после — из двух и в конце останется только одно задание.
$4*3*2*1=4!=24$.
Условия наши задачи совершенно разные, но способ решения у них один.
Давайте выведем общее правило решения таких задач: N различных предметов можно расставить, без повторения элементов, на N различных места ровно N! способами.
Задачи для самостоятельного решения
1. Из цифр 2,7,9 составить двухзначные числа, в которых цифры не повторяются.
а) Найти наименьшее число.
б) Найти наибольшее число.
в) Сколько чисел, начинающихся с 2, можно составить?
г) Сколько всего чисел можно составить?
2. В урне лежат два белых и два черных шара. На ощупь их различить невозможно. При вытаскивании белого шара его откладывают в сторону, если вытащили черный шар, то его кладут обратно. Шары вытаскивают четыре раза подряд.
В урне лежат два белых и два черных шара. На ощупь их различить невозможно. При вытаскивании белого шара его откладывают в сторону, если вытащили черный шар, то его кладут обратно. Шары вытаскивают четыре раза подряд.
а) Нарисовать дерево событий.
б) В скольких случаях вытащат шары одинакового цвета?
в) В скольких случаях белые шары появятся раньше?
3) Саша может выбрать обед из трех блюд: суп, плов, рис с котлетой и из пяти напитков: сок, чай, кофе, лимонад, компот.
Сколько всего комбинаций из блюд может выбрать Саша?
4. Стрелок стреляет по шести мишеням из шести орудий. В одну мишень производится только один выстрел. Выстрелив один раз из орудия, стрелок откладывает его в сторону. Сколько комбинаций выстрелов по мишеням у него имеется?
комбинаторика — Обоснование использования «наивной» вероятности (подсчет элементов в пространстве) в подзадаче/этапе общего эксперимента?
Задавать вопрос
Спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 57 раз
$\begingroup$
Рассмотрим вопрос типа:
Есть урна с белыми шарами по 6$ и зелеными по 8$. Мы будем последовательно выбирать шары по $2$. В первом выборе, какой бы цветной шар мы ни выбрали, мы должны заменить его обратно в урну ДОПОЛНИТЕЛЬНЫМИ $2$ шарами этого цвета.
Мы будем последовательно выбирать шары по $2$. В первом выборе, какой бы цветной шар мы ни выбрали, мы должны заменить его обратно в урну ДОПОЛНИТЕЛЬНЫМИ $2$ шарами этого цвета.
Какова вероятность того, что для этого эксперимента вы выберете зеленый шар при втором выборе?
Мои трудности:
Несмотря на то, что я знаю, как решать такие задачи (условие первого выбора и использование методов подсчета), я не могу связать это с основными правилами вероятности. Математика довольно проста, но…
Я не совсем понимаю, почему мы можем использовать наивную вероятность (методы подсчета) на двух выборках по отдельности (далее, на 2-й выборке мы используем наивную вероятность на условной вероятности, что добавляет еще одну морщина).
Я решаю эти задачи, не особо задумываясь об этом, но меня это беспокоит.
Может ли кто-нибудь предоставить теорему или обоснование, позволяющее использовать наивные вероятности в таких вопросах из первых принципов? (законы вероятности, выборочные пространства и т. д.)
д.)
спасибо
- вероятность
- комбинаторика
$\endgroup$
2
$\begingroup$
Пока исходы на каждом этапе может быть оправдано как равновероятное , вы можете использовать «наивный» подход к измерению условной вероятности этого этапа как отношения подсчета исходов предпочтительного события к пространству выборки. Точно так же, как вы могли бы для более прямого senario; по той же причине.
Таким образом, вероятность того, что первым выбранным будет зеленый шар, равна: $\mathsf P(S_1=g)=\frac{8}{6+8}$, потому что в урне 6 белых и 8 зеленых шаров. и есть без предвзятости при выборе любого конкретного шара.
Аналогично, условная вероятность того, что второй выбор будет зеленым, при условии, что первый выбор будет зеленым, равна: $\mathsf P(S_2=g\mid S_1=g)=\frac{8+2}{6 +8+2}$, потому что в урну были добавлены два дополнительных зеленых шара (вместе с возвращенным первым выбором), и нет смещения – на тот момент – при выборе любого конкретного шара, который сейчас находится в урне.
И так далее для других частей пространства выборки. Тогда по закону полной вероятности:
$$\begin{align}\mathsf P(S_2=g)~=&~\mathsf P(S_1=g)\,\mathsf P(S_2=g\mid S_1=g)+\mathsf P(S_1 =w)\,\mathsf P(S_2=g\mid S_1=w)\\[1ex]=&~ \frac{8}{6+8}{\cdot}\frac{8+2}{6+ 8+2}+\frac{6}{6+8}{\cdot}\frac{8}{6+8+2}\\[1ex]=&~ \frac{4}{7}\end{ align}$$
Вот и все.
$\endgroup$
$\begingroup$
Если вам разрешено использовать понятие ожидаемого значения ,
, вычисления в таких задачах значительно упрощаются. 93$ в качестве модели для нашего пространства? Никто не мог этого доказать, это не математический вопрос. Но это кажется разумным, и это работает хорошо.
И в любом случае наивный подход к подсчету — это здравая модель, и она вполне применима, пока мы убеждены, что все события, которые мы подсчитываем, имеют одинаковую вероятность произойти.
Теперь к делу: при первом извлечении у нас есть вероятность $8/14$ вытащить зеленый шар, что просто означает, что более $14$ возможных случаев есть $8$, когда шар зеленый. Так как задача более сложная, с двумя извлечениями, то количество случаев на самом деле больше, но если хотите, мы все же можем сделать расчет из азов, без всякой формулы, и считая все шары разными (чтобы они все были одинаковыми). равновероятность выхода). Если вы подсчитаете это, у вас будет $6\times8=48$ случаев, в которых вы вынимаете дважды белый шар, 48$ – белый, а затем зеленый, 80$ – дважды зеленый и, наконец, 48$ – зеленый, а затем белый. Это означает, что у вас есть $128$ благоприятных случаев на общую сумму $224$, что дает вероятность $\frac{128}{224}=\frac{4}{7}$.
Так как задача более сложная, с двумя извлечениями, то количество случаев на самом деле больше, но если хотите, мы все же можем сделать расчет из азов, без всякой формулы, и считая все шары разными (чтобы они все были одинаковыми). равновероятность выхода). Если вы подсчитаете это, у вас будет $6\times8=48$ случаев, в которых вы вынимаете дважды белый шар, 48$ – белый, а затем зеленый, 80$ – дважды зеленый и, наконец, 48$ – зеленый, а затем белый. Это означает, что у вас есть $128$ благоприятных случаев на общую сумму $224$, что дает вероятность $\frac{128}{224}=\frac{4}{7}$.
Конечно, было бы нецелесообразно всегда подсчитывать каждый отдельный случай, так что вы просто определяете события, такие как «зеленое после белого», и вычисляете их вероятности с помощью известных формул. Но в глубине, если подумать, это действительно то же самое.
Надеюсь, это поможет 😉
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
примеров комбинаторики в реальной жизни | Виджай Гадре | Geek Culture
Для следующего набора задач определите, какую часть комбинаторики нам нужно использовать, и примените соответствующую формулу. Имейте в виду, что может быть более одного правильного подхода к некоторым (или ко всем) из этих вопросов.
Представьте, что вы работаете в офисе и у вас есть 5 задач, помеченных как «Критические» в Jira, которые нужно выполнить к концу дня. Сколькими способами вы можете выполнить указанные задачи до конца дня?
** «Jira» — это программа для управления проектами, которая позволяет создавать задачи и маркировать их в зависимости от их важности. «Критический» — это самый высокий уровень важности, и никакая задача с более низким уровнем не может быть запущена после запуска такой задачи.
Решение: —
Нам нужно устроить все 5 заданий; следовательно, мы ищем число Перестановка между 5 элементами. Таким образом, у нас 5! = 120 способов выполнения наших заданий.
Таким образом, у нас 5! = 120 способов выполнения наших заданий.
Представьте, что ваша компания пытается привлечь клиентов, проводя рекламную кампанию в Интернете. Идея состоит в том, чтобы сосредоточиться на определенной демографической группе, которая часто использует социальные сети. Ваша кампания будет показывать рекламу в Facebook, Messenger, Instagram, Twitter и Reddit (всего = 5). Ваши графические дизайнеры создали 8 различных версий баннера, которые вы можете использовать. Исходя из этой информации: —
- Подсчитайте, сколько различных вариантов у вас есть для всей кампании, при условии, что вы хотите использовать разные варианты для каждой платформы.
- Подсчитайте, сколько различных вариантов у вас есть для всей кампании, при условии, что вы можете использовать один и тот же баннер для некоторых или всех платформ.
- Подсчитайте, сколько способов мы можем выбрать, какой из 8 баннеров использовать, предполагая, что мы используем разные баннеры для каждой платформы.

- Подсчитайте, сколькими способами мы можем выбрать, какой из 8 баннеров использовать, предполагая, что мы можем использовать каждый из них несколько раз.
Решения: —
Теперь в нашем распоряжении 8 баннеров, их нужно разместить на 5 платформах.
- Использование разных баннеров для каждой платформы означает, что мы можем рассматривать каждую платформу социальных сетей как отдельную позицию. Следовательно, мы будем иметь дело с вариациями . Поскольку мы используем разные значения для каждого сайта/приложения, мы не можем повторять значения, поэтому наша формула V = n! / (н-р)! => 8!/3! => 6720.
- То же, что и 1., но мы 9р => 8⁵ => 32 768.
- Нам нужно выбрать 5 из 8 баннеров для использования. Мы используем разные для каждой платформы, поэтому повторение не допускается. Следовательно, мы используем формулу для комбинаций без повторений. Таким образом, C = n! / р!(н-р)! => 8!/5!*3! => 56.

- Теперь нам нужно выбрать 5 из 8 баннеров для использования. Тем не менее, мы можем выбрать несколько раз. Следовательно, нам нужно использовать комбинаций с повторениями, поэтому c = (n+p-1)!/p!(n-1) = 12!/5!*7! => 792.
В этом году вы помогаете организовать фестиваль карьеры в вашем колледже. Участвуют 11 компаний, и у вас достаточно места для всех. Сколькими способами вы можете расположить различные фирмы, предполагая: —
- Ни у одной фирмы нет предпочтений в том, где они хотят быть?
- Представители JP Morgan договорились, где они должны располагаться ровно посередине?
- JP Morgan, Citi Bank и Morgan-Stanley должны занимать средние 3 места?
- Представители Deutsche Bank отказываются от участия, поэтому вы можете предоставить дополнительное место одной из других компаний?
Решения: —
- Если ни один вид не имеет предпочтения, то нам нужно расставить весь набор из 11 фирм по комнате.
 Таким образом, нам нужно использовать перестановок , так что: n! = 11! => 39 916 800.
Таким образом, нам нужно использовать перестановок , так что: n! = 11! => 39 916 800. - Если JP Morgan нужно расположить посередине, то нам нужно всего лишь расположить оставшиеся 10 фирм по комнате. Таким образом, мы снова можем использовать Перестановка , но на этот раз n = 10. Следовательно, n! = 10! => 3 628 800.
- Один из подходов к этой проблеме заключается в рассмотрении двух отдельных групп фирм — JP Morgan, Citi Bank и MS как одной группы, а остальных 8 фирм как второй группы. Затем, если мы найдем количество способов, мы можем настроить каждую группу по комнате, у нас просто есть два события с разными примерными пространствами.
- Давайте начнем с размещения 3 банков в середине. Поскольку нам нужно разделить 3 средних точки на 3 банка, все, что нам нужно сделать, это вычислить количество перестановок среди 3 элементов. Поэтому 3! = 6,
- Теперь, поскольку ни одна из оставшихся 8 фирм не слишком заботится о том, где они расположены, мы снова полагаемся на перестановки, так что 8! = 40 320.

- Для любого из 40 320 способов, которыми мы расставляем 8 фирм по комнате, у нас есть 6 различных способов расположить 3 банка посередине. Таким образом, всего у нас есть 40 320 х 6 = 241 920 способов организовать праздник карьеры.
4. У нас 10 фирм, которым нужно заполнить 11 мест. Затем, если мы начнем заполнять комнату в определенном порядке, то будет 10 вариантов того, кто займет первое место. Поскольку любая фирма может получить дополнительное место, обеспечиваемое уходом DB, то снова есть 10 вариантов для второго места. Тогда будет 9разные варианты третьего и так далее. В результате получается 10 х 10! = 36 288 000 вариантов размещения фирм.
Темы по комбинаторике для учителей K-8: Заметки к занятию № 2
Темы по комбинаторике для учителей K-8: Заметки к занятию № 2Университет штата Иллинойс, математический факультет
MAT 305: Темы комбинаторики для K-8 Учителя Весна 1999 |
Некоторые методы подсчета
| ||||
Обзорная сессия 1
| ||||
Доказательство по индукции
| ||||
Подведение итогов Задание №1 | ||||
Задание №2 | ||||
Некоторые методы подсчета
Во время этого занятия мы начнем осмысливать счет. стратегии, кульминацией которых является широкое использование и применение
перестановки и комбинации. Сегодня мы снова обратимся к меню на
Бистро Блейза. Вопросы, которые следуют
все требуют, чтобы мы что-то считали, но каждый включает в себя различные
подход.
стратегии, кульминацией которых является широкое использование и применение
перестановки и комбинации. Сегодня мы снова обратимся к меню на
Бистро Блейза. Вопросы, которые следуют
все требуют, чтобы мы что-то считали, но каждый включает в себя различные
подход.
+ Принцип добавления
Если я закажу один овощ из меню, сколько выбор овощей предлагает Блейз?
Здесь мы выбираем один элемент из набора элементов. Потому что там нет общих предметов среди двух наборов, которые Блейз назвал Зелеными. и Картофель, мы можем объединить предметы в один большой набор. Мы используем Кроме того, здесь 4+5, чтобы определить общее количество элементов для выбора из.
Это иллюстрирует Дополнение Принцип :
Если выбор из группы I можно сделать n способами и выбор из группы II можно сделать m способами, тогда количество возможный выбор из группы I или группы II равен n+m. Состояние: Нет элементы группы I такие же, как и элементы группы II.
Это можно обобщить до одного выбора из более чем двух группы, опять же при условии, что все группы или наборы не пересекаются с , то есть не имеют ничего общего.
Примеры для иллюстрации принципа сложения:
Вот три набора букв, назовите их наборами I, II и III:
- Набор I: {a,m,r}
- Набор II: {b,d,i,l,u}
- Набор III: {c,e,n,t}
Сколькими способами можно выбрать одну букву из наборов? I, II или III? Обратите внимание, что три набора не пересекаются, или взаимно исключительный : среди трех наборов нет общих элементов.
Вот два набора положительных целых чисел:
- А={2,3,5,7,11,13}
- Б={2,4,6,8,10,12}.
Сколькими способами можно выбрать одно целое число из множества
А или Б? Обратите внимание, что эти два набора не являются непересекающимися. Какая модификация
Можем ли мы применить принцип сложения, чтобы учесть этот случай? Напишите
ту модификацию.
+ Принцип умножения
«Еда» в Бистро состоит одного супа, одного мясного блюда, одного зеленого овоща и одного десерт из меню a la carte. Если бы друг Блеза Пьер всегда заказывает такую еду, сколько разных блюд может быть созданный?
Мы можем перечислить возможные приемы пищи, предпочтительно в некоторых организованный способ убедиться, что мы рассмотрели все возможности. Вот набросок одного такого перечисления, где {V,O}, {K,R}, {S,P,B,I} и {L,A,C,F} представляют элементы, которые нужно выбрать из суповое, мясное, овощное и десертное меню соответственно.
ВКСЛ | ВКПЛ | ВКБЛ | ВКИЛ | ОРИЛ | |
ВКСА | ВКПА | ВКБА | ВКИА | ОРИА | |
ВКСЦ | ВКПЦ | ВКБК | ВКИЦ | ОРИК | |
ВКСФ | ВКПФ | ВКБФ | ВКИФ | ОРИФ |
Обратите внимание и будьте готовы описать процесс перечисления, который у меня есть
проиллюстрировано здесь.
Как еще мы могли бы завершить счет без определение всех возможных вариантов? Карта или дерево для иллюстрации процесса перечисления обеспечивает мост к такому методу.
У нас есть два способа выбрать суп, два способа выбрать мясо блюд, четыре зеленых овоща на выбор и четыре десерта Выбери из. Сочетание одного супа с каждым мясом, затем каждого из эти пары с каждым из четырех возможных зеленых овощей, и каждый из эти тройки с каждым из четырех возможных десертов приводят к использованию умножение как быстрый способ подсчитать все возможные приемы пищи, которые мы мог собраться у Блэза.
Это предполагает, что мы используем принцип умножения для опишите этот метод подсчета:
Если задача состоит из двух шагов и первый шаг можно выполнено n способами, а второй шаг — m способами, то найдутся нм способов выполнить задание. Условие: способы, которыми каждый шаг может быть завершены независимых друг от друга.
Это можно обобщить для выполнения задачи более чем за два
шагов, пока выполняется условие.
Пример, иллюстрирующий принцип умножения:
Вспомните наши три множества I, II и III: {a,m,r}, {b,d,i,l,u} и {с, д, н, т}. Определить количество трехбуквенных наборов, которые могут быть создан таким образом, что одна буква из набора I, одна буква из набора II, и одна буква из набора III. Обратите внимание, что наш выбор в каждом наборе не зависит от нашего выбора в других множествах. При необходимости мы мог бы перечислить возможные трехбуквенные или трехэлементные, наборы.
+ Перестановки
Сколькими способами могут буквы только одного набора из I,
II и III заказать? В наборе I у нас есть следующие возможности:
Мы используем принцип умножения, чтобы описать наш выбор. Мы
иметь три буквы на выбор при заполнении первой позиции, две
буквы остаются, чтобы заполнить вторую позицию, и осталась только одна буква
для последней позиции: 3x2x1=6 возможны различные порядки.
Точно так же для набора II есть 120 различных способов упорядочить пять
буквы и есть 24 различных способа заказать буквы в наборе
III.
Мы
иметь три буквы на выбор при заполнении первой позиции, две
буквы остаются, чтобы заполнить вторую позицию, и осталась только одна буква
для последней позиции: 3x2x1=6 возможны различные порядки.
Точно так же для набора II есть 120 различных способов упорядочить пять
буквы и есть 24 различных способа заказать буквы в наборе
III.
+ Факторная запись
Это вышеприведенное обсуждение иллюстрирует концепцию перестановки .
как упорядоченное расположение предметов. Мы также указываем на
наличие факториальной записи для компактного представления
конкретное умножение, которое мы только что выполнили: 3x2x1=3!, 5x4x3x2x1=5!,
и так далее. Итак, n(n-1)(n-2)…(2)(1)=n!.
Пример, иллюстрирующий использование перестановок:
Почти каждое утро или вечер в новостях я слышу о государстве
DCFS штата Иллинойс, Департамент по делам детей и семьи. я
запутаться, потому что на нашем факультете математики есть комитет
называется Комитетом по статусу факультета факультета, или DFSC. Видишь
почему я в замешательстве? Сколько различных упорядоченных последовательностей из 4 букв
существуют для набора букв {D, F, S, C}?
Видишь
почему я в замешательстве? Сколько различных упорядоченных последовательностей из 4 букв
существуют для набора букв {D, F, S, C}?
Думая о четырех должностях для заполнения, __ __ __ __ , у нас есть 4 буквы на выбор для первой позиции, 3 для следующей, 2 буквы для следующей позиции и 1 выбор для последней позиции. По принципу умножения получается 4x3x2x1=24 различных 4-буквенные упорядоченные расположения для набора букв {D, F, S, С}.
Мы можем расширить это приложение, чтобы рассмотреть упорядоченное расположение только некоторые элементы множества. Например, возвращение в меню напитков Blaise’s Бистро. Если Блейз опубликует только четыре возможных варианта газировки, как много разных упорядоченных композиций четырех газированных напитков?
Думаем о четырех позициях, которые нужно заполнить, __ __ __ __, у нас есть 6 газированных напитков
на выбор для первой позиции, 5 для следующей, 4 газировки для
следующий и 3 соды для последней позиции. Использование умножения
принципе, существует 6x5x4x3=360 различных способов выбора и заказа
четыре из шести газированных напитков в меню.
Обычно мы используем обозначение P(n,r) для представления число способов упорядочить r предметов из набора n предметов. в В первой задаче выше мы определили, что P(4,4)=24, а во второй мы рассчитали P(6,4)=360. Общее значение P(n,r) равно n(n-1)(n-2)…([n-(r-1)] или P(n,r)=n(n-1)(n-2)…(n-r +1). Обратите внимание, что n может быть любым неотрицательным целым числом. Есть ли какие-либо ограничения на значение r?
Есть шаг арифметики, который мы можем применить к общему шаблону для P(n,r), чтобы упростить вычисления перестановок. Во-вторых строку ниже, мы умножили на, это просто значение 1, потому что числитель и знаменатель равный. В четвертой строке ниже мы видим, как выражение может быть упрощено с использованием факториальной записи.
Таким образом, мы имеем P(6,2)=6!/4! И P(40,8)=40!/32!.
А как насчет P(4,4)? Приведенный выше результат предполагает P(4,4)=4!/0!. Мы
уже знаем, что P(4,4)=4x3x2x1=4!, поэтому имеем 4!=4!/0!. Для этого
быть правдой, должно быть так, что 0!=1. Как бы странно это ни было
появляются, нам нужно 0!=1, чтобы поддерживать согласованность в пределах
расчеты, которые мы хотим провести.
Для этого
быть правдой, должно быть так, что 0!=1. Как бы странно это ни было
появляются, нам нужно 0!=1, чтобы поддерживать согласованность в пределах
расчеты, которые мы хотим провести.
+ Комбинации
В чем разница между этими двумя вопросами?
(i) Сколькими способами можно раздать покерную комбинацию из 5 карт?(ii) Сколько существует различных 5-карточных комбинаций в покере?
Первый вопрос касается порядка или расположения карт как они раздаются. Во втором вопросе конечный результат при сдаче 2H, 4D, JC, 3S, 10D в этом порядке такие же, как и при розыгрыше. 4D,3S,JC,10D,2H именно в таком порядке. В каждом случае тот же 5-карточный покер рука существует.
Мы нашли P(52,5) как решение первой задачи. То есть мы
расставил 5 объектов, выбранных из 52 карт. Для второго
вопрос, есть много аранжировок, которые дают одну и ту же 5-карточную
рука. Мы должны учитывать это. Рассмотрим более простой
проблема.
Сколько существует упорядоченных расположений букв набора {А,Б,С,Г,Е}?
Используя перестановки, мы получаем P(5,5) = 5! = 120 способов расставить пять букв.
Сколько заказанных композиций из 3-х предметов из 5-элементный набор?
Имеем P(5,3) = 543 = 5!/2! = 60 аранжировок. Например, для три буквы {A,B,C} имеют такое расположение: ABC, ACB, BAC, БКА, КАБ, КБА. Это представляет 6 из 60 аранжировок, но каждая включает в себя тот же выбор трех букв. Так же и для трех буквы {A,C,E}: у нас есть ACE, AEC, CAE, CEA, EAC, ECA.
Кажется, что для каждого 3-буквенного подмножества {A,B,C,D,E} есть 6 аранжировки из тех же трех букв. Это полезное наблюдение при изучении следующего вопроса:
Сколькими способами мы можем выбрать три предмета из 5-элементный набор {A,B,C,D,E}, когда порядок трех элементов игнорируется?
Одним из способов является перечисление уникальных 3-элементных подмножеств {A,B,C,D,E}:
ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE. таких 10
3-элементные подмножества.
таких 10
3-элементные подмножества.
Еще один способ подсчета — использовать тот факт, что:
(i) имеется P(5,3) = 60 упорядоченных расположений набор из 5 элементов в подмножества из 3 элементов и
(ii) среди 60 упорядоченных композиций есть 10 групп по 6 аранжировки, в которых используется одно и то же трехбуквенное подмножество. То есть 60 ÷ 6 = 10 уникальных 3-элементных подмножеств. Используя комбинаторику, мы есть
В общем, у нас есть способ определить количество комбинаций
из n элементов, выбранных r за раз, где порядок выбора или
расположение r предметов не учитывается:
и заметим, что
Обзорная сессия 1
+ Открытые вопросы с сессии 1
+ Контрольные вопросы
Рассмотрите эти вопросы обзора:
- Вы использовали принцип Pigeonhole (PHP) для
решить задачу о том, что студенты покупают газировку в Blaise’s
Бистро, и вы решили проблему, связанную с распространением
пенни в 10 маркированных коробок.
 Какие ключевые компоненты вашего
стратегии решения были общими для ваших решений? Как мы можем
еще больше обобщить принцип голубятни? (Подсказка: подумайте
проблема копеек и коробок. Что, если этикетки на коробках не
последовательные целые числа от 0 до 9?). Сравнивать
Ваш ответ.
Какие ключевые компоненты вашего
стратегии решения были общими для ваших решений? Как мы можем
еще больше обобщить принцип голубятни? (Подсказка: подумайте
проблема копеек и коробок. Что, если этикетки на коробках не
последовательные целые числа от 0 до 9?). Сравнивать
Ваш ответ. - Мы кратко представили использование Нотация суммирования как средство краткого представления математические выражения, включающие сложение. Продукт обозначение служит той же цели для краткого представления математические выражения с умножением. Обозначить значение каждого из следующих выражений и проверить ваши решения.
Доказательство по индукции
Мы проиллюстрируем процесс доказательства по индукции, чтобы показать, что
+ Процесс
Шаг 1: Убедитесь, что желаемый результат справедлив для n=1.
Здесь, когда 1 заменяется на n как в левой, так и в правой части выражения в (I) выше, результат равен 1. В частности,
. Этот завершает шаг 1.
Шаг 2: Предположим, что желаемый результат верен для n=k.
В нашем примере это означает, что мы предполагаем сумму первых k положительные целые числа. Будет полезно показать это как
Шаг 2 завершен.
Шаг 3: Используйте допущение из шага 2, чтобы показать, что результат верно для n=(k+1).
То есть мы хотим это показать. Другими словами, покажите, что если предположить, что результат для n=k подразумевает результат для n=(k+1).
Здесь мы основываемся на уравнении, представленном в (II):
Если , добавление (k+1) в каждую сторону гарантирует, что
Левая часть (III) — это просто расширение выражения
, это
сумма первых (k+1) натуральных чисел.
Осталось показать, что правая часть (III) эквивалентна , что наш формула говорит нам, что это правильная сумма.
Перепишите правую часть (III) с общим знаменателем:
Теперь сложим числители и выразим над общим знаменателем:
В числителе (V) k+1 является общим для обоих членов, поэтому мы можем фактор числитель, в результате чего эквивалентная форма:
Выражение (VI) — это как раз тот результат, который мы искали.
Шаг 4: Подведите итоги своей работы.
По индукции мы показали, что сумма первых n положительных целые числа могут быть представлены выражением .
Уравнение имеет практическое применение каждый раз, когда мы ищем суммы последовательных положительных целые числа. Например, теперь мы можем использовать результат, чтобы сделать вывод, что . Мы также можем используйте результат, чтобы показать, что, например,.
+ Сводка
Индукция процесс основан на эффекте домино. Если мы сможем показать, что результат верно от k-го до (k+1)-го случая, и мы действительно можем показать это верно для первого случая (k=1), мы можем связать цепочку из выводы: истина для k=1 подразумевает истину для k=2, истина для k=2 подразумевает истинность для k=3 и так далее. Нажатие на первую костяшку вызывает все из оставшихся костяшек домино выпадают подряд.
+ практика
Вот практические задачи для закрепления процесса индукции.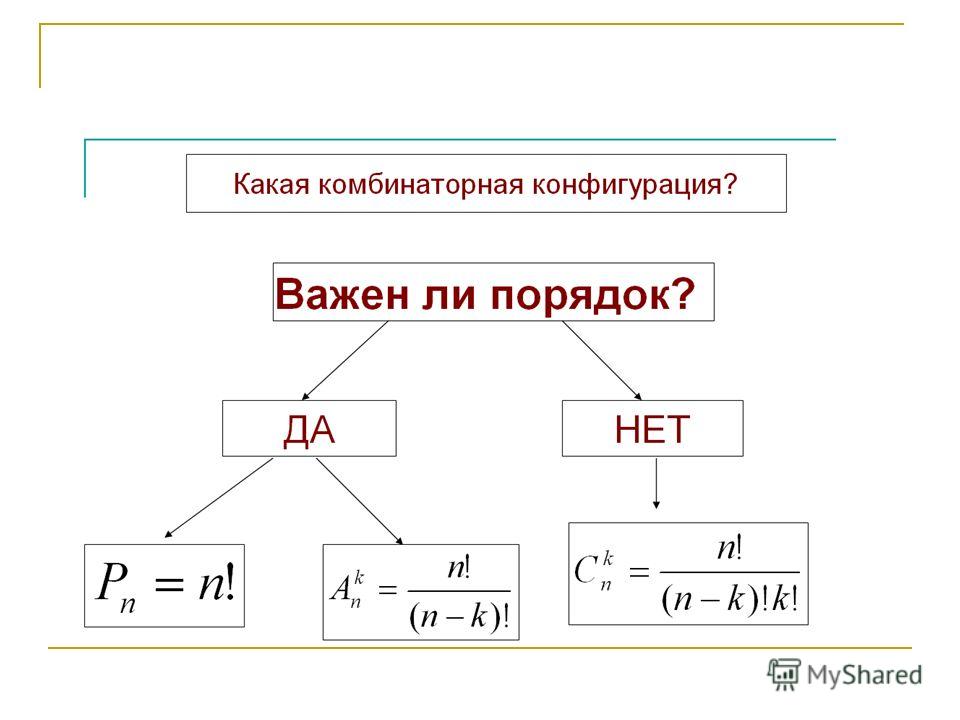
1. | Покажи это. |
2. | Покажи это. |
3. | Исследуйте закономерности в суммах и скоро. Используйте доказательство по индукции, чтобы оправдать предположение. |
4. | Покажите, что сумма первых n нечетных положительных целых чисел равна . |
Подведение итогов #1
Получив выполненное задание №1, мы отложим занятие
время для небольших групп, чтобы сравнить результаты и найти решения, которые будут
делились между классом. Текстовые задачи в задании №1 должны
быть прямолинейным. Обратите внимание, что большинство решений появляются в
оборотная сторона текста. Решения дополнительных задач будут
более вовлечены и, вероятно, потребуют обсуждения. я соберу
проблемы 8с и 16 из Проблема
Набор №1 и все три из дополнительных
Набор задач А.
Решения дополнительных задач будут
более вовлечены и, вероятно, потребуют обсуждения. я соберу
проблемы 8с и 16 из Проблема
Набор №1 и все три из дополнительных
Набор задач А.
Задание №2
- Наборы задач №2, №3, №4, №5, #6
Combinatorics на CocoaPods.org
Combinatorics содержит статические функции для генерации k — перестановки и k — комбинации (в обоих случаях с повторением или без) n элементов массива.
Совместимость
Комбинаторика требует iOS 8+ и совместима с проектами Swift 2.
Установка
Старая школа
Просто перетащите файл Combinatorics.swift в свой проект. Это все, что вам действительно нужно. Или, если вам просто нужна одна или две функции, скопируйте и вставьте эту функцию в свой проект. В конце дня Комбинаторика — это всего лишь набор статических функций, которые также могут быть определены как глобальные функции.
Немного теории
В естественном английском языке словосочетание используется для обозначения действия по взятию некоторых или всех элементов списка, с повторением или без него, с учетом или без учета их порядка. Но в математике существуют разные концепции для этих вещей в зависимости от того, разрешены или запрещены повторяющиеся элементы и имеет ли значение порядок элементов. Комбинаторика, а точнее перечислительная комбинаторика, концентрируется на подсчете количества определенных комбинаторных объектов, например, обеспечивая унифицированную основу для подсчета перестановок, комбинаций и разделов.
Комбинаторика (эта библиотека) включает функции для четырех различных сценариев:
- Если порядок элементов имеет значение и повторяющиеся элементы не допускаются, то это перестановка без повторения.
- Если порядок элементов имеет значение и разрешены повторяющиеся элементы, то это перестановка с повторением.
- Если порядок элементов не имеет значения и повторяющиеся элементы не допускаются, то это комбинация без повторения.
- Если порядок элементов не имеет значения и допускаются повторяющиеся элементы, то это комбинация с повторением.
Перестановки
Согласно Википедии, понятие перестановки относится к упорядочиванию всех членов множества в некоторой последовательности или порядке, или, если множество уже упорядочено, перестановке (переупорядочиванию) его элементов, процесс, называемый перестановка. Они отличаются от комбинаций, которые представляют собой выборки некоторых членов набора, где порядок не принимается во внимание. Например, записанные в виде кортежей, существует шесть перестановок множества {1,2,3}, а именно: (1,2,3), (1,3,2), (2,1,3), (2 ,3,1), (3,1,2) и (3,2,1). Это все возможные порядки этого набора из трех элементов. Другой пример: анаграмма слова, все буквы которого различны, представляет собой перестановку его букв. В этом примере буквы уже упорядочены в исходном слове, а анаграмма представляет собой переупорядочение букв. Изучение перестановок конечных множеств является предметом комбинаторики.
Например, записанные в виде кортежей, существует шесть перестановок множества {1,2,3}, а именно: (1,2,3), (1,3,2), (2,1,3), (2 ,3,1), (3,1,2) и (3,2,1). Это все возможные порядки этого набора из трех элементов. Другой пример: анаграмма слова, все буквы которого различны, представляет собой перестановку его букв. В этом примере буквы уже упорядочены в исходном слове, а анаграмма представляет собой переупорядочение букв. Изучение перестановок конечных множеств является предметом комбинаторики.
Более слабое значение термина «перестановка», иногда используемого в текстах по элементарной комбинаторике, обозначает такие упорядоченные расположения, в которых ни один элемент не встречается более одного раза, но без требования использования всех элементов из данного набора. Это не перестановки, за исключением особых случаев, а естественные обобщения концепции упорядоченного расположения. Действительно, это использование часто включает в себя рассмотрение комбинаций фиксированной длины 90 046 k 90 047 элементов, взятых из заданного набора размера 9. 0046 n , другими словами, эти k -перестановки n представляют собой различные упорядоченные расположения k -элементного подмножества n -множества (иногда называемые вариациями в старой литературе). также известны как частичные перестановки или последовательности без повторений, термины, которые позволяют избежать путаницы с другим, более распространенным значением «перестановки».
0046 n , другими словами, эти k -перестановки n представляют собой различные упорядоченные расположения k -элементного подмножества n -множества (иногда называемые вариациями в старой литературе). также известны как частичные перестановки или последовательности без повторений, термины, которые позволяют избежать путаницы с другим, более распространенным значением «перестановки».
Наконец, иногда встречаются термины «вариации без повторения» или «вариации с повторением». Это архаичные термины в комбинаторике, которые до сих пор широко используются неанглоязычными авторами для обозначения k — перестановки n (в этой библиотеке перестановки без повторения) и для n -кортежи (в этой библиотеке перестановки с повторением) соответственно.
Комбинации
И, опять же, согласно Википедии, комбинация — это способ выбора элементов из коллекции, при котором (в отличие от перестановок) порядок выбора не имеет значения. В меньших случаях можно подсчитать количество комбинаций. Например, даны три фрукта, скажем, яблоко, апельсин и груша, из этого набора можно извлечь три комбинации из двух: яблоко и груша; яблоко и апельсин; или груша и апельсин. Более формально, k — комбинация набора S является подмножеством k отдельных элементов S . Если в наборе n элементов, количество k -комбинаций равно биномиальному коэффициенту, индексированному n и k .
В меньших случаях можно подсчитать количество комбинаций. Например, даны три фрукта, скажем, яблоко, апельсин и груша, из этого набора можно извлечь три комбинации из двух: яблоко и груша; яблоко и апельсин; или груша и апельсин. Более формально, k — комбинация набора S является подмножеством k отдельных элементов S . Если в наборе n элементов, количество k -комбинаций равно биномиальному коэффициенту, индексированному n и k .
Использование
Как было сказано ранее, Комбинаторика (эта библиотека) включает функции для четырех различных сценариев:
- Если порядок элементов имеет значение и повторяющиеся элементы не допускаются, то это перестановка без повторения.
- Если порядок элементов имеет значение и допускаются повторяющиеся элементы, это перестановка с повторением.
- Если порядок элементов не имеет значения и повторяющиеся элементы не допускаются, то это комбинация без повторения.

- Если порядок элементов не имеет значения и допускаются повторяющиеся элементы, то это комбинация с повторением.
Все функции определены как общедоступные статические и вообще не зависят от других частных функций, поэтому на самом деле можно просто скопировать и вставить конкретную функцию в свой код. Для простоты и единообразия все функции принимают набор элементов в виде массива из 9 элементов.0950 T элементов, а также возвращает соответствующее подмножество в виде массива массивов из T элементов. Однако обратите внимание, что для комбинаций имеет значение только наличие элементов в массиве, а не их порядок.
Наконец, все функции определены как общие, поэтому можно легко вычислить перестановки и комбинации любого элемента.
Перестановка без повторения
перестановкиБез повторения из(элементы: [T], взятие: Int) -> [[T]]
Учитывая массив из элементов и сколько из них мы берем , возвращает массив со всеми возможными перестановками без повторения. Обратите внимание, что повторение запрещено, поэтому
Обратите внимание, что повторение запрещено, поэтому , принимающее , всегда должно быть меньше или равно elements.count .
Почти по соглашению, если , принимающее , равно 0, функция вернет [[]] (массив только с одной возможной перестановкой — перестановкой без элементов). В другом сценарии, если , принимая , больше, чем elements.count , функция вернет [] (пустой массив, поэтому вообще не включает перестановки).
Перестановка с повторением
permutationsWithRepetitionFrom(элементы: [T], принимая: Int) -> [[T]]
Учитывая массив из элементов и сколько из них мы принимая , возвращает массив со всеми возможными перестановками с повторением. Обратите внимание, что, поскольку повторение разрешено, с не обязательно должно быть меньше или равно elements.count .
Почти по соглашению, если , принимающее , равно 0, функция вернет [[]] (массив только с одной возможной перестановкой — перестановкой без элементов). В другом сценарии, если
В другом сценарии, если , принимающее , больше 0, но элементов не содержит элементов, функция вернет [] (пустой массив, поэтому вообще не включает перестановки).
Комбинация без повторения
комбинацииWithoutRepetitionFrom(элементы: [T], принимая: Int) -> [[T]]
Учитывая массив из элементов и сколько из них мы принимая , возвращает массив со всеми возможными комбинации без повторений. Обратите внимание, что повторение запрещено, поэтому , принимающее , всегда должно быть меньше или равно elements.count .
Почти по соглашению, если принимает равно 0, функция вернет [[]] (массив с единственной возможной комбинацией — комбинация без элементов). В другом сценарии, если , принимающее , больше, чем elements.count , функция вернет [] (пустой массив, поэтому комбинация вообще не включается).
Помните, что, поскольку комбинации не имеют значения в порядке, эти две комбинации представляют один и тот же набор элементов: [1,2,3] и [3,2,1].
Комбинации с повторением
комбинацииWithRepetitionFrom(элементы: [T], взятие: Int) -> [[T]]
Учитывая массив из элементов и сколько из них мы берем , возвращает массив со всеми возможными комбинациями с повторением. Обратите внимание, что поскольку повторение разрешено, , принимающее , не обязательно должно быть меньше или равно elements.count .
Почти по соглашению, если принимает равно 0, функция вернет [[]] (массив только с одной возможной комбинацией — комбинация без элементов). В другом сценарии, если , принимая , больше 0, но элементов не содержит элементов, функция вернет [] (пустой массив, поэтому вообще не включает комбинацию).
Помните, что, поскольку комбинации не имеют значения в порядке, эти две комбинации представляют один и тот же набор элементов: [1,2,2,3] и [3,2,1,2].
Некоторые примеры
Пример 1
// Все возможные способы расположения букв [abc].
пусть ps = Combinatorics.permutationsWithoutRepetitionFrom(["a", "b", "c"], принимая: 3)
для р в пс {
печать (p.joinWithSeparator (""))
} Вывод:
абв акб бак bca такси ЦБ
Пример 2
// Все возможные числа созданы путем выбора 5 разных цифр (принимая 0 в качестве первой цифры).
пусть ps = Combinatorics.permutationsWithoutRepetitionFrom(Array(0...9), принимая: 5)
для р в пс {
переменная exp = 100000
print(p.reduce(0) {exp /= 10; return $0 + $1 * exp})
} Вывод:
1234 1235 1236 1237 [еще много цифр] 98762 98763 98764 98765
Пример 3
// Все возможные двоичные числа, использующие ровно 3 бита.
let prs = Combinatorics.permutationsWithRepetitionFrom(["0", "1"], принимая: 3)
для пр в прс {
печать (pr.joinWithSeparator (""))
} Вывод:
000 001 010 011 100 101 110 111
Пример 4
// Вы можете заказать все возможные пиццы с 3 дополнительными ингредиентами.let cs = Combinatorics.combinationsWithoutRepetitionFrom(["бекон", "сыр", "помидор", "оливки", "лук"], взяв: 3) для c в cs { печать (с) }
Результат:
["бекон", "сыр", "помидор"] ["бекон", "сыр", "оливки"] ["бекон", "сыр", "лук"] ["бекон", "помидор", "оливки"] ["бекон", "помидор", "лук"] ["бекон", "оливки", "лук"] ["сыр", "помидор", "оливки"] ["сыр", "помидор", "лук"] ["сыр", "оливки", "лук"] ["помидор", "оливки", "лук"]
Пример 5
// Всеми возможными способами можно выбрать 6 номеров из 6 доступных.
пусть cs = Combinatorics.combinationsWithoutRepetitionFrom([4, 8, 15, 16, 23, 42], принимая: 6)
для c в cs {
печать (с)
} Вывод: не заблудитесь здесь, очевидно, есть только один способ — собрать их все, так как порядок не имеет значения!
[4, 8, 15, 16, 23, 42]
Пример 6
// Всеми возможными способами 4 человека могут заказать напитки в баре, где подают только газировку и пиво. let crs = Combinatorics.combinationsWithRepetitionFrom(["газировка", "пиво"], взяв: 4) для cr в crs { пусть сгруппировано = NSCountedSet (массив: cr) grouped.forEach({ print("\(grouped.countForObject($0)) × \($0)")}) Распечатать("") }
Выход:
4 × соды 3 × сода 1 × пиво 2 × сода 2 × пиво 1 × сода 3 × пиво 4 × пиво
Автор
Альберт Мата (@almata в Твиттере). Дополнительную информацию обо мне и моей работе можно найти на моем сайте albertmata.net.
Наймите меня
В настоящее время я живу в Барселоне и занимаюсь проектами (постоянными или подрядчиками) по всей Европе, если вы согласны с полной или частичной удаленной работой (скажем, я могу быть на месте одну или две недели в месяц, если вы нужно это). Для получения дополнительной информации, пожалуйста, проверьте мои проекты на albertmata.net/apps или свяжитесь со мной по телефону [электронная почта защищена] .
Лицензия
Комбинаторика доступна по лицензии MIT. См. файл LICENSE для получения дополнительной информации. Если у вас есть какие-либо вопросы или вы хотите поделиться тем, как вы используете этот инструмент, отправьте сообщение о проблеме.
См. файл LICENSE для получения дополнительной информации. Если у вас есть какие-либо вопросы или вы хотите поделиться тем, как вы используете этот инструмент, отправьте сообщение о проблеме.
Комбинаторика — История-компьютер
Что такое комбинаторика: полное объяснение
Комбинаторика — это наука о подсчете перестановок и комбинаций наборов элементов в конечной структуре. Полная сфера комбинаторики не была общепризнанной, однако наиболее распространенной формой упоминаемой является перечислительная комбинаторика, которая концентрируется на подсчете количества определенных комбинаторных объектов. Однако существует растущее подмножество подполей и подходов комбинаторики.
Вот известные в настоящее время подмножества комбинаторики математики:
- Перечислительная комбинаторика — классическая форма комбинаторики, широко используемая для последовательности Фибоначчи.
- Аналитическая комбинаторика. Перечислительная комбинаторика с использованием инструментов комплексного анализа и теории вероятностей.

- Теория разделов. Часть теории чисел и анализа, которая в настоящее время считается самостоятельной областью комбинаторики.
- Теория графов. Графы являются основой комбинаторики. Применение возможности и диапазона часто представляется визуально на графиках.
- Теория дизайна. Изучение комбинаторных планов, являющихся частями подмножеств с пересекающимися свойствами.
- Конечная геометрия – изучение геометрических систем с конечной структурой.
- Теория порядка – изучение частично упорядоченных множеств, конечных или бесконечных.
- Теория матроидов – Изучение свойств наборов векторов в векторном пространстве, которое не зависит от коэффициентов в линейной зависимости.
- Экстремальная комбинаторика. Изучение экстремальных вопросов о системах множеств.
- Вероятностная комбинаторика. Изучение вероятности появления определенного свойства у случайного дискретного объекта.
- Алгебраическая комбинаторика – использование теории групп и теории представлений или других методов абстрактной алгебры, которые применяют комбинаторные методы к задачам алгебры.

- Геометрическая комбинаторика. Применение комбинаторики к выпуклой и дискретной геометрии.
- Топологическая комбинаторика. Комбинаторные формулы часто используются при решении топографических задач или при изучении топологии.
- Арифметическая комбинаторика. Комбинаторные методы, использующие только сложение и вычитание.
- Бесконечная комбинаторика. Комбинаторная теория множеств, или бесконечная комбинаторика, представляет собой распространение методов комбинаторики на бесконечные множества.
- Комбинаторика слов – Использование комбинаторики для анализа шаблонов формального языка.
Комбинаторные задачи встречаются в исследованиях по всей математике. Комбинаторные решения часто пересекаются с несколькими исследованиями для создания анализа моделей и решений. Исследование существовало долгое время без конкретной ссылки как подмножество, используемое для графиков, еще до изобретения калькулятора. По мере того как теория графов и компьютерное моделирование развивались с течением времени, важность более подробных наборов данных, алгебры, информации о графах, баз данных и многого другого подтолкнула к изучению комбинаторных решений современных задач.
Комбинаторную теорию часто называют наукой о счете. Хотя может показаться, что с этим справилась чистая математика, творческий подход и использование методов комбинаторики перешли от подсчета вещей к подсчету возможности вещей и даже несуществующих вещей. Он даже начинает нарушать собственное определение, расширяясь от подсчета наборов элементов в пределах конечной структуры до подсчета наборов элементов или объектов в бесконечном окружении.
Комбинаторика — это наука о подсчете перестановок и комбинаций наборов элементов в конечной структуре.Комбинаторика: точное определение
Комбинаторика — это раздел математики, который в основном занимается подсчетом объектов в конечной дискретной структуре. Математики используют этот термин для обозначения большого подмножества дискретной математики. Он содержит изучение перестановок и комбинаций. Чаще всего он используется в информатике для создания формул и анализа алгоритмов. Хотя это не все, поскольку определение того, что рассматривает комбинаторика, расширяется.
В комбинаторике есть только три принципа:
- Сложение
- Умножение
- Включение-исключение
Некоторые могут считать перестановку/комбинацию четвертым принципом, но это функции умножения. Три принципа используются для подсчета и проверки исключений. Перестановка относится к тому, когда порядок подсчета или операции влияет на результат. Комбинация — это когда порядок подсчета или операции не влияет на результат.
Сначала предполагалось, что комбинаторика должна ответить на такие вопросы, как «Сколькими способами можно выполнить процесс?». Вот простой пример этого:
Сценарий: Организуйте буквы слова тонала, так что
- T всегда — L
- T и L всегда вместе
 N обозначает общее количество букв или размер всего списка объектов, а k представляет итерацию. Решите C(4, 4) = 4!(4!(4-4)!). В результате C(4, 4) = 24. Однако буквы L и T можно переставить в две позиции, или 2! Пути, либо «LT», либо «TL». Таким образом, итоговая сумма аранжировок 4!2! = 48,
N обозначает общее количество букв или размер всего списка объектов, а k представляет итерацию. Решите C(4, 4) = 4!(4!(4-4)!). В результате C(4, 4) = 24. Однако буквы L и T можно переставить в две позиции, или 2! Пути, либо «LT», либо «TL». Таким образом, итоговая сумма аранжировок 4!2! = 48,В этом примере перечислительной комбинаторики мы взяли целую последовательность и обнаружили, сколько аранжировок может быть при соблюдении простых требований.
Как работает комбинаторика?
Комбинаторика — это целое подмножество математики, посвященное подсчету множеств элементов в конечной дискретной структуре. Одним из часто используемых примеров комбинаторики является подсчет всех возможных способов решения задачи. Как растущая область исследования, она постоянно делится на дополнительные подмножества. Есть две формулы, используемые для вычисления комбинаторики; формула перестановки и формула сочетания.
Перестановка — это действие по упорядочиванию всех элементов набора или перестановке упорядоченного набора. Он часто используется, когда формула представляет рабочую операцию, где порядок выполнения действий имеет значение. Например, банки получают и ссужают деньги. Они должны получить деньги, в которых они нуждаются, чтобы одолжить больше денег. Это означает, что они должны организовывать транзакции таким образом, чтобы запрос на кредит не был отклонен, потому что у банка нет денег для кредита.
Он часто используется, когда формула представляет рабочую операцию, где порядок выполнения действий имеет значение. Например, банки получают и ссужают деньги. Они должны получить деньги, в которых они нуждаются, чтобы одолжить больше денег. Это означает, что они должны организовывать транзакции таким образом, чтобы запрос на кредит не был отклонен, потому что у банка нет денег для кредита.
Формула перестановки «x» объектов для выбора «a» объектов: Р(х,а) = а!/(а-х)!
Комбинированная формула используется, когда порядок элементов в наборе не имеет значения. Это используется больше для аналитических целей. Формула для комбинации «x» объектов для выбора «n» объектов: C(x, n) = n!/x!.(n-x)!
Большая часть комбинаторики используется в информатике. Поскольку информатика охватывает такую большую область влияния, это означает, что она используется почти везде. Более развлекательной целью комбинаторики является вычисление вероятности того или иного события. Формула для расчета вероятности (P) того, что событие «C» произойдет: P(C) = общее количество исходов, в которых происходит C / общее количество возможных исходов .
Формула для расчета вероятности (P) того, что событие «C» произойдет: P(C) = общее количество исходов, в которых происходит C / общее количество возможных исходов .
Как создать комбинаторику?
Идея комбинаторики состоит в том, чтобы выбрать определенные объекты из множества и/или количество способов их расположения. При работе с комбинаторикой нужно помнить лишь несколько основных правил. Предположим, есть два набора: A и B . Вот правила, которые нужно запомнить:
Правило произведения:
Правило произведения гласит, что если есть X количество способов выбрать один элемент из A и Y количество способов выбрать элемент из B , тогда X умножить на Y будет количество способов выбрать два элемента , один из A и один из B .
Правило суммы:
Правило суммы гласит, что если существует X количество способов выбрать элемент из A и Y количество способов выбрать элемент из B , тогда X плюс Y будет количеством способов выбрать один элемент, который может принадлежать либо группе A , либо B .
перестановки с повторением:
, если N Объекты N1 Объекты типа 1 , N2 . количество способов расположить эти N объектов определяется как: N!/(N1!N2!…Nk!)
Комбинации с повторением:
Если есть N элементов, из которых мы хотим выбрать K элементов, и нам разрешено выбрать один элемент несколько раз, то количество способов выбрать элемент определяется как:
C(N+K-1,K) = (N + K — 1)! / (К)!(Н – 1)!
Используя эти правила, вы можете опробовать метод комбинированного калькулятора на бумаге.
Кто создал комбинаторику?
Основные понятия о комбинировании и перечислении результатов были найдены в древней истории. Многим приписывают создание частей того, что сейчас составляет комбинаторику, но Массачусетский технологический институт называет Джан-Карло Рота отцом-основателем современной перечислительной комбинаторики. Они приписывают ему превращение методов из набора трюков в глубокую тему. Также следует отметить, что Полу Эрдосу часто приписывают разработку большей части современной комбинаторики благодаря его исследованиям в области теории чисел и теории графов.
Они приписывают ему превращение методов из набора трюков в глубокую тему. Также следует отметить, что Полу Эрдосу часто приписывают разработку большей части современной комбинаторики благодаря его исследованиям в области теории чисел и теории графов.
Самым современным поставщиком перечислительной комбинаторики является Ричард П. Стэнли. Стэнли опубликовал двухтомник, который используется в качестве стандартного введения в перечислительную комбинаторику математики в академической среде. До публикации Стэнли комбинаторика не считалась отдельной областью исследования и была взаимосвязана со многими другими разделами математики. Именно по этой причине трудно точно определить рождение комбинаторики в целом, поскольку тысячи математиков внесли свой вклад и расширили ее суть.
Каковы применения комбинаторики?
Комбинаторика — быстрорастущая область математики. По мере того, как компьютерные технологии собирают больше данных уникальных типов, возникает необходимость их анализа, организации, перечисления и многого другого. Вот список предметов, к которым уже применяется комбинаторика:
Вот список предметов, к которым уже применяется комбинаторика:
- Коммуникационные сети
- Криптография
- Сетевая безопасность
- Вычислительная молекулярная биология
- Компьютерная архитектура
- Научное открытие
- Язык
- Анализ паттернов
- Моделирование
- Базы данных
- Mining Data
- Национальная безопасность
- Операционные исследования
- Геометрические уравнения
- 3d. Computations
- Геометрические уравнения
- 3d. Computations
- Geometric Eavations
- . данные и требуют отслеживания, организации и применения данных, могут найти комбинаторные методы полезными для их анализа и решений. Почти все графические функции персональных компьютеров также используют комбинаторные методы. Простой пример, который используется в современных видеоиграх, — обнаружение столкновений. При обнаружении столкновений два набора элементов сравниваются друг с другом на предмет пересечения.
 Цель состоит в том, чтобы определить, столкнулись ли объекты или нет. Ограничение будет заключаться в том, что любая повторяющаяся позиция векторного графа считается коллизией. Это означает, что все рассчитанные точки, не соответствующие столкновению, игнорируются, а значения, соответствующие столкновению, используются для определения того, что делает объект, исходя из программирования игры.
Цель состоит в том, чтобы определить, столкнулись ли объекты или нет. Ограничение будет заключаться в том, что любая повторяющаяся позиция векторного графа считается коллизией. Это означает, что все рассчитанные точки, не соответствующие столкновению, игнорируются, а значения, соответствующие столкновению, используются для определения того, что делает объект, исходя из программирования игры.Варианты использования различных комбинаторных методов различаются в зависимости от того, что пытается найти исследователь/наблюдатель. Это означает, что существует бесконечное количество применений методов к математическим задачам и проблемам реального мира, которые влияют на повседневную жизнь. Это может быть столь же обыденным делом, как повышение безопасности банковского приложения или связи на вашем смартфоне.
Примеры комбинаторики в реальном мире
Комбинаторика встречается почти в каждом предмете, чего и следовало ожидать от такого обширного подмножества математики.
 Вот несколько примеров, которые помогут понять, где эти методы полезны:
Вот несколько примеров, которые помогут понять, где эти методы полезны:Военная стратегия:
Управление ресурсами и персоналом в опасных ситуациях имеет решающее значение для успеха миссии и выживания человечества. В то время как военные предпочитают получать надежные разведданные из надежных источников, стратегам все же необходимо просчитывать позиции и возможности. Используя информацию, которую они могут собрать, такую как размер подразделения, топология, доступность ресурсов, оборудование и транспорт, стратеги могут найти все возможные варианты и сузить круг лучших вариантов.
Графическое представление:
Компьютерная графика основана на буквальных графиках. Компьютер отслеживает позиционирование и рисует изображения в соответствии с массивным графиком с подробным описанием позиций и изменений. Даже в трехмерных представлениях графики используются для представления отображаемого изображения. Комбинаторные формулы используются программным обеспечением для 3D-моделирования и операционной системой компьютера.

Инженерное дело:
Анализ моделей и изображений помогает графически отображать такие материалы, как тепло, ветер, дождь и т. д. Затем эту информацию можно использовать для формирования деталей, которые лучше всего работают при воздействии определенных элементов. Это также помогает в создании прототипов для быстрого анализа требований к ограничениям.
Биомедицина:
Молекулярная биология требует многолетних исследований, прежде чем какие-либо тесты можно будет применить. Это требует, чтобы анализ и теоретические возможности рассматривались и намечались как можно полнее.
Планирование перевозок:
Простым, но важным применением комбинаторики является организация расписаний поездов, автобусов и самолетов. Организовать рейсы или поездки в соответствии с потребностями пассажиров, сохраняя при этом наиболее эффективные маршруты, сложно, но расчет перестановок помогает разобраться в этом.
Организация и дизайн:
Независимо от того, планируете ли вы мероприятие или проект кодирования, комбинаторная теория может помочь сформировать наилучший доступный дизайн в рамках установленных вами ограничений.

Объяснение комбинаторики: все, что вам нужно знать Часто задаваемые вопросы (часто задаваемые вопросы)
Что такое комбинаторика?
Комбинаторика — это целый раздел математики, посвященный изучению счетных множеств элементов в конечной дискретной структуре. Он неуклонно превращался в крупную математическую отрасль, включающую аспекты других математических теорий.
Для чего используется комбинаторика?
Комбинаторика используется для приложений информатики, таких как криптография, анализ данных, расчет вероятностей и программирование. Это позволяет математику анализировать информацию о шаблонах, возможностях, позициях, порядке операций и ограничениях. Это растущая область, которая находит все большее применение в анализе данных, криптографии, инженерии, информатике, биомедицине, бизнесе и коммуникации.
Почему комбинаторика так сложна?
Комбинаторика — сложный предмет, потому что он включает в себя обширную идею.
 Его можно использовать для простых процессов, но он был разработан для упрощения более сложных расчетов комбинаций/перестановок наборов данных. Часто комбинаторику трудно применить, потому что проблема, которую пытаются решить, сложна для понимания. Кроме того, полный объем того, что считается комбинаторикой, до сих пор не определен. Если вам не нужно глубоко погружаться в комбинаторику, но вам нужно использовать формулу комбинации, в Интернете доступны онлайн-калькуляторы комбинаций.
Его можно использовать для простых процессов, но он был разработан для упрощения более сложных расчетов комбинаций/перестановок наборов данных. Часто комбинаторику трудно применить, потому что проблема, которую пытаются решить, сложна для понимания. Кроме того, полный объем того, что считается комбинаторикой, до сих пор не определен. Если вам не нужно глубоко погружаться в комбинаторику, но вам нужно использовать формулу комбинации, в Интернете доступны онлайн-калькуляторы комбинаций.Что изучает комбинаторика?
Комбинаторика — это изучение комбинаций/перестановок объектов, принадлежащих конечному множеству с соблюдением определенных ограничений.
Что такое комбинаторика в кодировании?
Математические уравнения часто широко используются в кодировании как лучшее описание реальности, которое может понять компьютер. Комбинаторика не исключение. Он находит творческие возможности, которые могут быть полезны по мере того, как управление базами данных продолжает расти, но уже играет важную роль в создании кодов, исправляющих ошибки.
 Комбинаторная теория чаще всего применяется к кодированию на этапе проектирования как решение архитектуры инструкций.
Комбинаторная теория чаще всего применяется к кодированию на этапе проектирования как решение архитектуры инструкций.В чем разница между перестановкой и комбинацией?
Перестановка — это комбинация набора элементов, в которой порядок элементов имеет значение для результата, а комбинации не ограничены порядком элементов.
4 — Карточки по комбинаторике | Chegg.com
Какие четыре вещи имеют прямое отношение к элементам треугольника Паскаля?
- Блочные прогулки
- Биномиальные коэффициенты
- Комбинации/ «n выбирает k»
- Количество двоичных последовательностей длины n и k единиц
Что такое блуждание по блокам и как с ними связан треугольник Паскаля?
Блочный обход — это путь от одного перекрестка в плоскости решетки (Z2) до другого. Элементы треугольника Паскаля дают количество различных обходов кварталов, ведущих к определенному перекрестку.
Как треугольник Паскаля связан с биномиальными коэффициентами?
В n-й строке треугольника Паскаля даны коэффициенты для разложения n-й степени двучлена.

Чему соответствует каждая строка в треугольнике Паскаля?
Два в степени номера строки.
Что нужно помнить о расположении элементов треугольника Паскаля?
Вы всегда начинаете отсчет с нуля при нумерации строк и столбцов — т.е. первая строка называется 0-й строкой.
Что такое комбинации и как они связаны с треугольником Паскаля?
Комбинации «n выбирают k» относятся к числу способов выбрать подмножество k-элементов из множества n-элементов. N-я строка, k-я запись в треугольнике Паскаля дает n выбрать k.
Как записываются комбинации?
Комбинации заказаны?
Нет, два подмножества с одинаковыми элементами в разном порядке рассматриваются как одна комбинация.
Учитывают ли комбинации повторы?
Нет, два подмножества с разным повторением одних и тех же элементов считаются только одной комбинацией.
Как треугольник Паскаля соотносится с двоичными последовательностями?
Элементы треугольника Паскаля дают количество двоичных последовательностей длины n и k единиц.
 Обратите внимание, что обход блока может быть закодирован как двоичная последовательность левых и правых поворотов, и что комбинация также является двоичной последовательностью, если каждому элементу задана цифра, а элементам, выбранным для подмножества, задана единица, а не ноль.
Обратите внимание, что обход блока может быть закодирован как двоичная последовательность левых и правых поворотов, и что комбинация также является двоичной последовательностью, если каждому элементу задана цифра, а элементам, выбранным для подмножества, задана единица, а не ноль.В контексте комбинаций, почему треугольник Паскаля симметричен?
Потому что выбор k элементов для включения в подмножество аналогичен выбору n−k элементов для исключения из подмножества.
Почему n всегда выбирает ноль?
Потому что есть только один способ создать подмножество из нулевых элементов (пустое множество).
Почему n всегда равно n?
Потому что у вас есть n элементов на выбор, и вы должны выбрать только один из них.
Каков основной принцип счета?
Количество способов выполнения группы задач равно произведению количества способов выполнения каждой задачи по отдельности. Обратите внимание, что это всего лишь определение декартова произведения.

При подсчете некоторого количества результатов нескольких задач, как узнать, когда умножать отдельные числа результатов и когда их складывать?
Вы умножаете отдельные числа, когда происходит каждое из них для каждого результата другого. Вы добавляете отдельные числа, если имеете дело с отдельными случаями какого-то события.
Как тот факт, что сумма элементов в n-й строке треугольника Паскаля в сумме составляет 2n, относится к комбинациям?
Общее количество возможных подмножеств множества из n элементов равно 2n, поэтому понятно, что сумма всех комбинаций n равна 2n.
Что такое отбор с замещением и как вычисляется такая задача (используйте фундаментальный принцип подсчета)?
Выбор с заменой относится к задаче подсчета, в которой одинаковое количество вариантов доступно для каждого «слота» выбора. Таким образом, количество результатов равно количеству доступных вариантов в степени количества выборов.
Что такое перестановки?
Количество способов расположить определенное количество элементов из некоторого множества.

Как связаны комбинации и перестановки?
Перестановки подобны комбинациям, но умножаются на количество способов, которыми вы можете составить комбинацию, что равно k факториалу.
Какова формула перестановок?
Как повторяющиеся элементы обрабатываются в перестановках?
Повторы в перестановках запрещены.
Что такое отбор без замены и как вычисляется такая задача?
Выбор без замены — это тип задачи подсчета, в которой второй «слот» выбора имеет на один вариант меньше, чем первый, потому что он не может выбрать тот, который уже был выбран. Этот тип задач на самом деле представляет собой просто упорядоченный неповторяющийся список, также известный как перестановка.
Может ли задача на подсчет включать как комбинации, так и перестановки?
Да, например: клуб из 120 человек выбирает президента и вице-президента (120 человек переставляют 2) и комитет из пяти человек (118 выбирают 5).
Какие хорошие примеры демонстрируют разницу между перестановками и комбинациями?
Перестановки подсчитывают количество комбинаций велосипедных замков, а комбинации подсчитывают количество способов приготовить салат.

Что такое «полностью плохой» подход к подсчету результатов?
Определение количества желаемых исходов путем вычитания количества нежелательных исходов из общего числа исходов.
Что является предупредительным признаком того, что вы не сможете использовать фундаментальный принцип счета для решения задачи счета?
Если количество опций для некоторых слотов зависит от того, какие опции выбраны для других слотов, то проблема слишком сложна, чтобы решать ее методом грубой силы с использованием фундаментального принципа подсчета.
Каковы два подхода к задачам на подсчет, которые включают упорядоченные наборы, включая повторения (например, задача МИССИСИПИ)?
- Выбор местоположений
- Временное разделение повторений
Объясните метод выбора местоположений для решения задач упорядоченного счета с повторениями, таких как задача МИССИСИПИ.
Выбор местоположений включает в себя обработку «слотов» выбора как объектов, которые необходимо выбрать, так что вы выбираете определенное количество слотов для каждого повторяющегося объекта.
 Например, будет 11 вариантов выбора одного способа размещения буквы М, 10 вариантов выбора 4 способов размещения буквы I, 6 вариантов выбора 4 способов размещения буквы S и 2 выбора 2 способов размещения буквы P.
Например, будет 11 вариантов выбора одного способа размещения буквы М, 10 вариантов выбора 4 способов размещения буквы I, 6 вариантов выбора 4 способов размещения буквы S и 2 выбора 2 способов размещения буквы P.Объясните метод временного разделения повторяющихся элементов для решения упорядоченного счета с задачами на повторение, такими как задача МИССИСИПИ.
Во-первых, различайте все элементы, присваивая им индексы, такие как S1, S2 и т. д. Затем найдите количество расположений этих различных элементов (в данном случае 11!). Затем не различайте элементы, разделив их на количество способов расположения копий каждого элемента (4! для S, 4! для I, 2! для P и 1! для M).
Что известно как проблема «звезд и полос»?
Задача подсчета количества способов создания неупорядоченного множества с повторениями; то есть проблема выбора 8 хот-догов только трех вкусов. Обратите внимание, что такая проблема будет называться «3 multichooose 8».
Что такое метод «звезды и столбцы» для подсчета количества неупорядоченных подходов с повторениями?
Количество элементов в каждой категории можно выбрать, написав звездочки для элементов в целом, а затем поместив черточки между звездочками так, чтобы звездочки были разделены черточками на любое количество категорий.
 Тогда проблема становится вопросом размещения звездочек вокруг столбцов. Вы должны сложить количество звезд и баров, чтобы получить общее количество слотов, а затем найти (это число выбирает количество звезд).
Тогда проблема становится вопросом размещения звездочек вокруг столбцов. Вы должны сложить количество звезд и баров, чтобы получить общее количество слотов, а затем найти (это число выбирает количество звезд).Какова общая формула задачи «звезды-n-полосы»; то есть неупорядоченные наборы с повторением?
Факториал суммы звездочек и полос, деленный на отдельные факториалы числа звездочек и числа полосок. (Обратите внимание, что количество столбцов равно количеству категорий минус один).
Как дискретные вероятности связаны с комбинаторикой?
Вероятностные задачи — это просто дроби, в которых используется комбинаторика в числителе и знаменателе.
Как рассчитывается дискретная вероятность?
Это просто количество желаемых результатов, деленное на общее количество результатов.
Что за хитрость в решении задач с упорядоченными списками с повторением (задачи МИССИСИПИ), когда есть ограничение, что некоторые элементы не должны быть последовательными?
Сначала поместите другие элементы, затем поместите слоты между уже размещенными элементами для тех, которые не могут быть последовательными, и найдите количество аранжировок в этих слотах.




 У каждого котенка
У каждого котенка Ставит проблему.
Ставит проблему.

 Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер.
Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер. .. · n.
.. · n.


 В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде? Ольга помнит, что телефон подруги оканчивается тремя цифрами 5, 7, 8 но забыла, в каком порядке эти цифры расположены. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.
Ольга помнит, что телефон подруги оканчивается тремя цифрами 5, 7, 8 но забыла, в каком порядке эти цифры расположены. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.

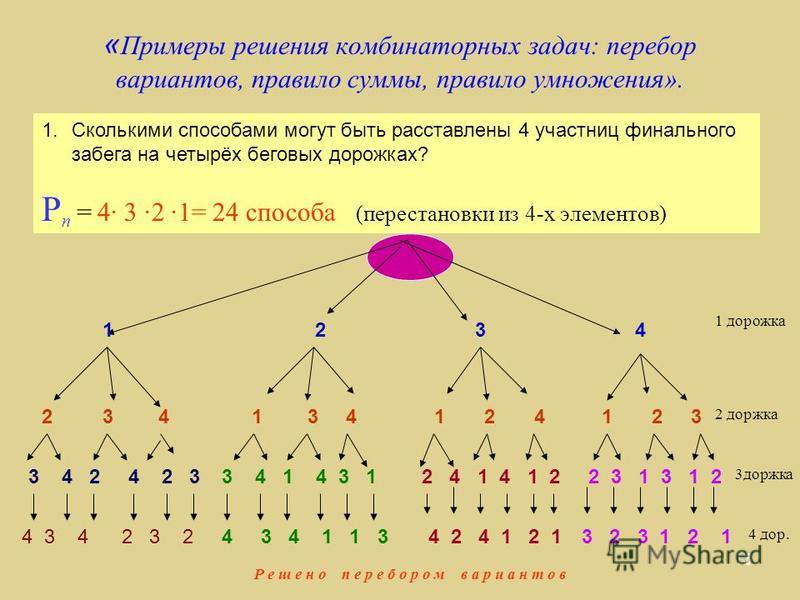 язык
язык

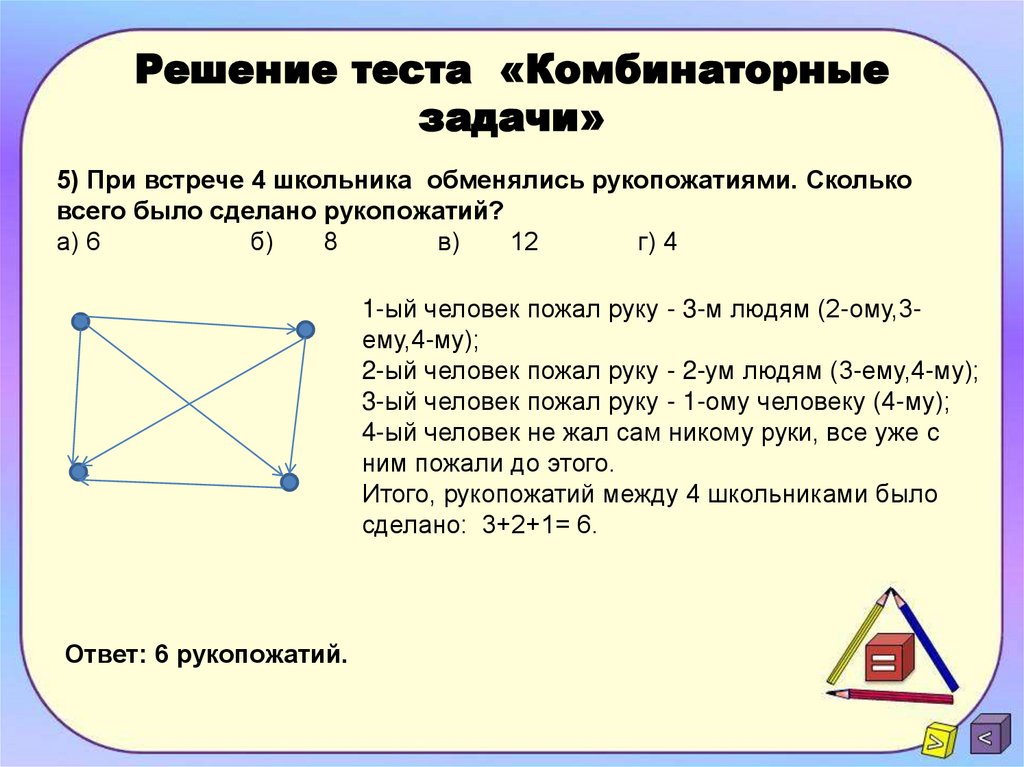
 Таким образом, нам нужно использовать перестановок , так что: n! = 11! => 39 916 800.
Таким образом, нам нужно использовать перестановок , так что: n! = 11! => 39 916 800.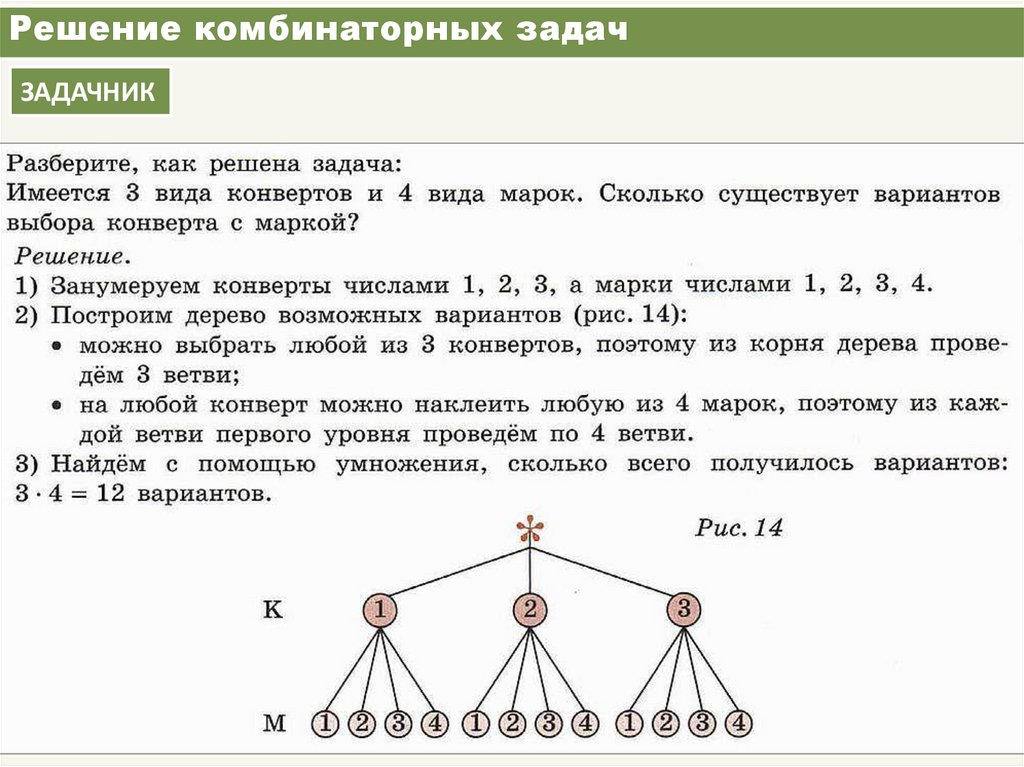
 edu)
edu)
 Какие ключевые компоненты вашего
стратегии решения были общими для ваших решений? Как мы можем
еще больше обобщить принцип голубятни? (Подсказка: подумайте
проблема копеек и коробок. Что, если этикетки на коробках не
последовательные целые числа от 0 до 9?). Сравнивать
Ваш ответ.
Какие ключевые компоненты вашего
стратегии решения были общими для ваших решений? Как мы можем
еще больше обобщить принцип голубятни? (Подсказка: подумайте
проблема копеек и коробок. Что, если этикетки на коробках не
последовательные целые числа от 0 до 9?). Сравнивать
Ваш ответ.
 let cs = Combinatorics.combinationsWithoutRepetitionFrom(["бекон", "сыр", "помидор", "оливки", "лук"], взяв: 3)
для c в cs {
печать (с)
}
let cs = Combinatorics.combinationsWithoutRepetitionFrom(["бекон", "сыр", "помидор", "оливки", "лук"], взяв: 3)
для c в cs {
печать (с)
}  combinationsWithRepetitionFrom(["газировка", "пиво"], взяв: 4)
для cr в crs {
пусть сгруппировано = NSCountedSet (массив: cr)
grouped.forEach({ print("\(grouped.countForObject($0)) × \($0)")})
Распечатать("")
}
combinationsWithRepetitionFrom(["газировка", "пиво"], взяв: 4)
для cr в crs {
пусть сгруппировано = NSCountedSet (массив: cr)
grouped.forEach({ print("\(grouped.countForObject($0)) × \($0)")})
Распечатать("")
} 

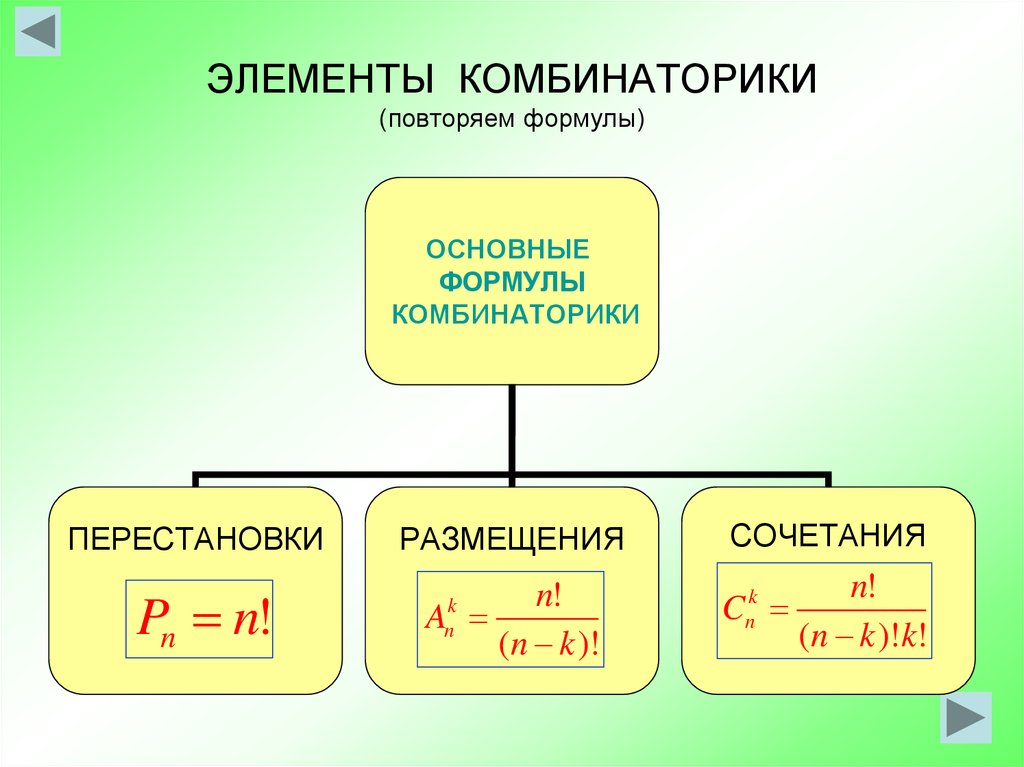 Цель состоит в том, чтобы определить, столкнулись ли объекты или нет. Ограничение будет заключаться в том, что любая повторяющаяся позиция векторного графа считается коллизией. Это означает, что все рассчитанные точки, не соответствующие столкновению, игнорируются, а значения, соответствующие столкновению, используются для определения того, что делает объект, исходя из программирования игры.
Цель состоит в том, чтобы определить, столкнулись ли объекты или нет. Ограничение будет заключаться в том, что любая повторяющаяся позиция векторного графа считается коллизией. Это означает, что все рассчитанные точки, не соответствующие столкновению, игнорируются, а значения, соответствующие столкновению, используются для определения того, что делает объект, исходя из программирования игры. Вот несколько примеров, которые помогут понять, где эти методы полезны:
Вот несколько примеров, которые помогут понять, где эти методы полезны:

 Его можно использовать для простых процессов, но он был разработан для упрощения более сложных расчетов комбинаций/перестановок наборов данных. Часто комбинаторику трудно применить, потому что проблема, которую пытаются решить, сложна для понимания. Кроме того, полный объем того, что считается комбинаторикой, до сих пор не определен. Если вам не нужно глубоко погружаться в комбинаторику, но вам нужно использовать формулу комбинации, в Интернете доступны онлайн-калькуляторы комбинаций.
Его можно использовать для простых процессов, но он был разработан для упрощения более сложных расчетов комбинаций/перестановок наборов данных. Часто комбинаторику трудно применить, потому что проблема, которую пытаются решить, сложна для понимания. Кроме того, полный объем того, что считается комбинаторикой, до сих пор не определен. Если вам не нужно глубоко погружаться в комбинаторику, но вам нужно использовать формулу комбинации, в Интернете доступны онлайн-калькуляторы комбинаций. Комбинаторная теория чаще всего применяется к кодированию на этапе проектирования как решение архитектуры инструкций.
Комбинаторная теория чаще всего применяется к кодированию на этапе проектирования как решение архитектуры инструкций.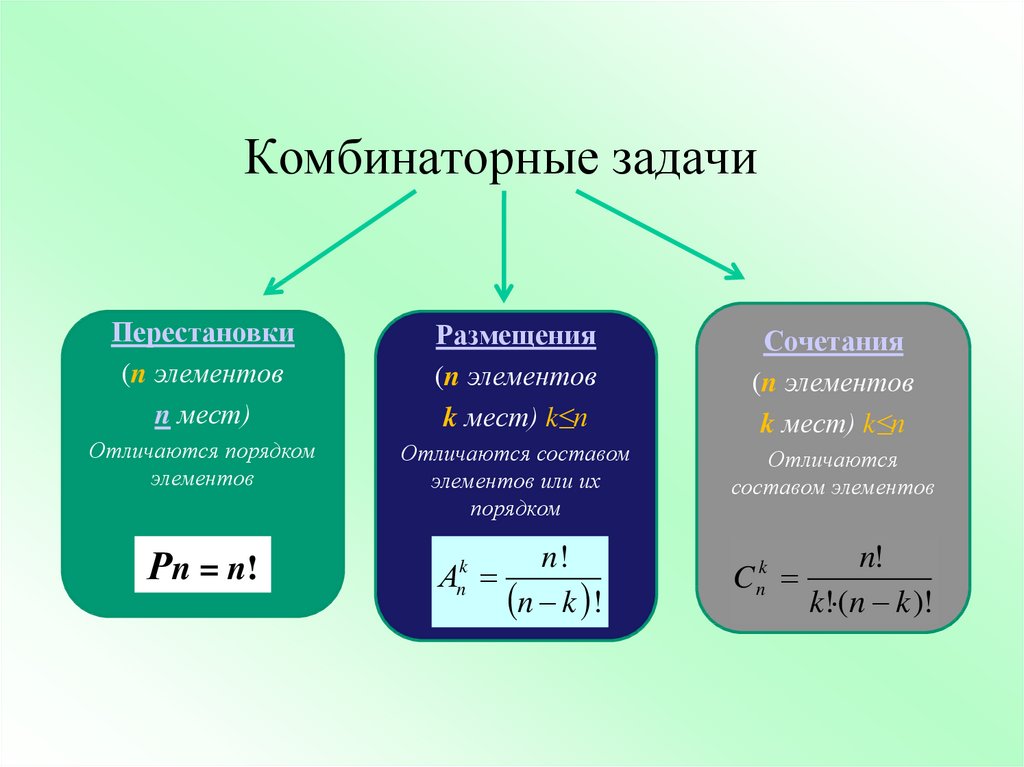
 Обратите внимание, что обход блока может быть закодирован как двоичная последовательность левых и правых поворотов, и что комбинация также является двоичной последовательностью, если каждому элементу задана цифра, а элементам, выбранным для подмножества, задана единица, а не ноль.
Обратите внимание, что обход блока может быть закодирован как двоичная последовательность левых и правых поворотов, и что комбинация также является двоичной последовательностью, если каждому элементу задана цифра, а элементам, выбранным для подмножества, задана единица, а не ноль.


 Например, будет 11 вариантов выбора одного способа размещения буквы М, 10 вариантов выбора 4 способов размещения буквы I, 6 вариантов выбора 4 способов размещения буквы S и 2 выбора 2 способов размещения буквы P.
Например, будет 11 вариантов выбора одного способа размещения буквы М, 10 вариантов выбора 4 способов размещения буквы I, 6 вариантов выбора 4 способов размещения буквы S и 2 выбора 2 способов размещения буквы P. Тогда проблема становится вопросом размещения звездочек вокруг столбцов. Вы должны сложить количество звезд и баров, чтобы получить общее количество слотов, а затем найти (это число выбирает количество звезд).
Тогда проблема становится вопросом размещения звездочек вокруг столбцов. Вы должны сложить количество звезд и баров, чтобы получить общее количество слотов, а затем найти (это число выбирает количество звезд).