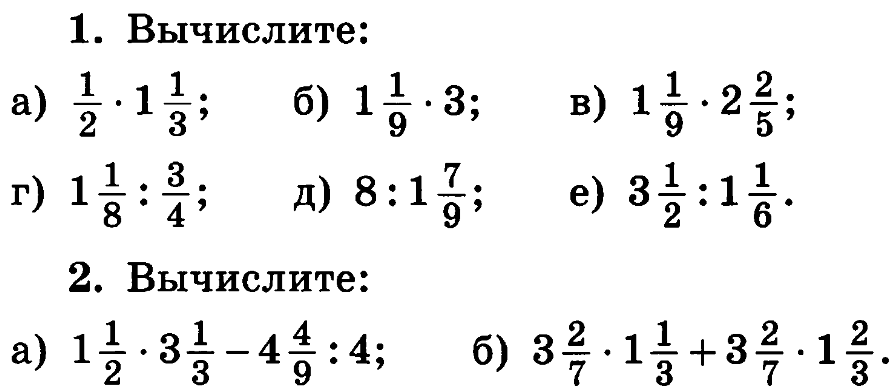Решить по действиям пример с дробями: Примеры и задачи с дробями

Математические действия с дробями: правила, решение задач

Действия с дробями общего вида

Для дробей общего вида характерно наличие числителя и знаменателя.

Значения которые, которыми выражены данные составляющие дроби, могут быть натуральными и числовыми выражениями.

Если рассмотреть подробно следующие дробные числа:

\[\frac{5}{4}, \frac{3,5}{5}, \frac{1+2,6}{4(6-1)}, \frac{\frac{3}{5}+\frac{7}{8}}{2,3-0,9}, \frac{1}{2 \sqrt{3}}\]

можно с уверенностью отметить, что и в числителе и знаменателе дробные выражения могут быть обозначены как:

• десятичная дробь;
• натуральный логарифм;
• сумма и разность выражений;
• дробь с постоянным значением числа.

Алгоритм решения задач с обыкновенной дробью общего вида

1. Когда необходимо произвести вычитание дробей с одинаковыми знаменателями, то в процессе решения суммируется только числитель дробей.
   \[\frac{a}{b} \pm \frac{c}{b}=\frac{a \pm c}{b}\]
   Где:
   \[a, c, d_{0}\] и равные некоторым числовым значениям.
   
2. При выполнении сложения или вычитания дробей для  различных значений в  знаменателях, нужно выполнить приведение к общему знаменателю. Далее осуществить сложение или вычитание преобразованных дробей с одинаковыми числовыми значениями.
   
3. При перемножении дробных значений, выполняются следующие действия:
   • произведение числителей;
   • аналогичные действия , но только с знаменателями.
     
4. При выполнении деления, необходимо первую дробь перемножить на вторую, но в обратном значении. Иными словами произвести замену числителя на значение знаменателя.

Основные показатели и свойства дроби:

• черта в дроби обозначает признак деления;
• деление на числовое значение характеризуется как перемножение его   на обратное значение;
• возможность применения свойств, которые относятся для действительных чисел;
• свойства для дробей и различного рода числовых неравенств.

Применяя данные свойства можно произвести преобразование дробных чисел:

---

Пример №1:

Для заданных значений дроби: \[\frac{8}{2,7}\] и \[\frac{1}{2,7}\] необходимо выполнить сложение.

используя алгоритм решения, необходимо значения в числителе сложить, а в знаменателе оставить без изменений и переписать.

Выполнив все действия получим дробь: \[\frac{8+1}{2,7}\].

Далее произведем сложение и получим дробное значение:

\[\frac{8+1}{2,7}=\frac{9}{2,7}=\frac{90}{27}=3 \frac{1}{3}\]

Следовательно: \[\frac{8}{2,7}+\frac{1}{2,7}=\frac{8+1}{2,7}=\frac{9}{2,7}=\frac{90}{27}=3 \frac{1}{3}\]

Ответ задачи: \[\frac{8}{2,7}+\frac{1}{2,7}=3 \frac{1}{3}\].

---

Пример №2

Необходимо найти разность дробей:  

\[\frac{1-\sqrt{2}}{3 \cdot\left(\log_{2} 3 \cdot \log_{2} 5+1\right)}\]

и

\[\frac{\sqrt[3]{2}}{3 \cdot\left(\log_{2} 3 \cdot \log_{2} 5+1\right)}\]

Так как в знаменателе данные являются равными между собой. вычисление будет производиться по принципу равного знаменателя.

Из этого следует:

\[\frac{1-\sqrt{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}-\frac{\sqrt[3]{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}=\frac{1-\sqrt{2} \sqrt{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}\]

Для решения данного типа задач важно помнить правило приведения к общему знаменателю. {-k}\]

Основные свойства дробей:

Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.

Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.

 Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей

• 0,900 = 0,9;
• 22,10200000 = 22,102;
• 0,45000=0,45;
• 0,12569000=0,12569;
• 0,780=0,78.

Основные характеристики десятичных дробей

1. Дробное число, не будет иметь какого-либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
2. Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — отсутствует.
3. Если значения, которые находятся в числителе и знаменателе разделить или перемножить на любое действительное число. То получится дробь равная ей по значении.
4. Если взять две дроби: \[\frac{a}{b}\] и \[\frac{c}{d}\] то они называться будут равными при \[a \cdot d \] или \[ b \cdot c .\]

Принцип умножения десятичных дробей

Для перемножения десятичных дробей необходимо, произвести следующие действия.

• Дробь записать в виде так называемого математического столбика. Далее рассмотреть заданное значение, как обыкновенные действительные числа и подсчитать их;
• Все знаки за запятой подсчитать и сложить сумму;
• Полученную сумму справа налево отложить и поставить запятую.

Для данного вида дробей характерны все те же действия, что и для остальных чисел.

Если переставить местами множители, на окончательный ответ это не повлияет.

если мы хотим умножить число на произведение двух и более. Сначала перемножаем данное число на первый множитель затем полученное значение на второй и так далее.

Чтобы умножить сумму на множитель. Нужно по отдельности перемножить числа и полученную сумму сложить.

Если проводим умножение на разность чисел. Для начала умножаем на уменьшаемое, а затем на вычитаемое. Следовательно, полученные значения вычитаем.

Также процесс умножения можно упростить. Десятичные дроби перемножить как действительные целые числа, и поставить запятую.

---

Пример №1:

Определить произведение чисел \[1,5 \cdot 0,75\].

Первым делом преобразуем дробь. Заменим десятичную. на обыкновенную.

\[0,75 = \frac{75}{100}\], \[1,5=\frac{15}{10}\]

Затем проводим сокращение дробных значений и выделяем, по уже изученным правилам целую часть.

\[\frac{125}{1000}\]  можно преобразовать и получить следующую дробь 1,125.

Ответ: 1,125.

---

Пример №2:

Определить произведение чисел \[5,382 \cdot 0,2\].

Первое значение является бесконечной дробью. Ее рекомендуется округлить до сотых значений. Получается \[5,382 \approx 5,38\].

Второй множитель округлять не требуется, это не имеет смысла.

\[5,38 \cdot 0,2=\frac{\frac{538}{100} \cdot 2}{10}=\frac{1,076}{1000}=1,076\]

Следовательно, получаем ответ к нашей задаче: 1,076.

---

Пример №3:

Необходимо перемножить две периодические дроби. \[0,(3) \cdot 2,(36)\]

Преобразуем заданные значения в обыкновенную дробь.

\[0,(3)=0,3+0,03+0,003+0,003+\ldots=\frac{0.3}{1-0,1}=\frac{0.3}{9}=\frac{3}{9}=\frac{1}{3}\]

\[2,(36)=2+(0,36+0,0036+\ldots)=2+\frac{0,36}{1-0,01}=2+\frac{36}{99}=2+\frac{4}{11}=\frac{2 \cdot 4}{11} \frac{26}{11}\]

\[\Rightarrow 0,(3) \cdot 2,(36)=\frac{\frac{1}{3} \cdot 26}{11}=\frac{26}{33}\]

Полученную в конечном итоге обыкновенную дробь приводим  к десятичной.  В столбик разделим числитель на знаменатель.

Окончательный ответ : \[0,(3) \cdot 2,(36)=0,(78)\]

Умножение десятичных дробей при помощи столбика

Перемножение столбиком выполняя на условии, что на запятые никакого внимания не уделяется (они игнорируются)

В итоговом результате ставится знак запятой справа. Отделяется столько запятых, сколько множители имеют десятичных знаков вместе.

Если не хватает цифр, то принято в окончательном ответе дописывать нули.

Рассмотрим примеры решения подобных задач.

---

Пример №1:

Нужно найти значение произведения, следующих чисел: 63,37 и 0,12.

Выполняем умножение, не обращая внимание на запятые.

Далее определяемся с запятой, где ее ставить.Она будет через четыре цифры справа. Потому что сумма десятичных знаков двух множителей равна  4.

Нули в данной ситуации не записываются. Это связано с достаточным количеством чисел.

Получаем окончательное значение равное 7,6044.

---

Пример №2:

Заданные числовые, дробные выражения 3,2601 и 0,0254. необходимо перемножить между собой.

Для этого применим умножение столбиком.

Мы будем ставить запятую, отделяющую 8  цифр с правой стороны.  Потому что заданные дроби, вместе, имеют восемь  знаков после запятой.

Нули в данной ситуации записываются. Это связано с  недостаточным количеством значений.

Получаем окончательное значение равное: 0 , 08280654

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Умножение десятичной дроби с обыкновенной и со смешанной дробью

Чтобы произвести данную операцию, необходимо выполнить следующие требования:

1. Десятичную дробь преобразовывают в обыкновенную и перемножаем с нужным числом.
2. В десятичную переводим обыкновенную или смешанную дробь  и далее перемножаем друг с другом.

---

Пример 1. Найти произведение \[\frac{3}{5} \text { на 0,9 }\].

Поэтапный процесс решения.

1. Записываем 0,9 в виде обыкновенной дроби, а именно \[0,9=\frac{9}{10}\].
2. Перемножаем цифры по правилам математики.
   \[\frac{\frac{3}{5}\cdot 9}{10}=\frac{27}{50}=0,54\]
   Ответ: \[\frac{3}{5} \cdot 0,9=0,54\]

---

Пример 2. Найти произведение чисел \[0,18 \text { на } 3 \frac{1}{4}\].

Выполняем следующие действия:

1. Записываем  \[3 \frac{1}{4}\] в виде десятичной дроби:
   \[3 \frac{1}{4}=3,25\].
2. Вычисляем известные нам значения:
   0,18 * 3,25 = 0,585.

Ответ: \[0,18 \quad 3 \frac{1}{4}=0,585\].

---

Пример 3:

Даны следующие значения \[0,4 \text { и } 3 \frac{3}{5} \text {. }\] По условию задач нужно найти их произведение, иными словами перемножить.

Первым делом 0,4 переведем в десятичную дробь и получим значение: \[0,4=\frac{4}{10}=\frac{2}{5}\]

Затем проводим вычисление:

\[0,4 \quad 3 \frac{3}{5}=\frac{\frac{2}{5} \cdot 23}{6}=\frac{23}{15}=1 \frac{8}{15}\]

Полученный ответ является смешанным значением. Его необходимо перевести в значение периодической дроби.  А именно: 1,5(3).

Следовательно, это и ответ задачи. 1,5(3).

Возведение в степень дробного числового выражения

Свойство произведения в степень в виде дроби

\[\frac{\left(z^{*} a\right)^{m}}{n}=\frac{z^{m}}{n} \cdot \frac{a^{m}}{n}, \text { при условии что: } \mathrm{z}>0, \mathrm{a}>0, \frac{m}{n}>0\]

В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный. {4}=3 x \frac{1}{(x+y)-4}=\frac{3}{(x+y)-4}\]

Преобразование дробных значений 0,1, 0,01, 0,001, где основанием степени является число 10

Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:

• указать отрицательный показатель степени;
• записать основание равным десяти.

---

Пример 1: Значение 0,01, где основание — число 10.

В числе 0,01  имеется два 0. Значит, оно будет представлено как 10 ^-2. Значение показателя равно значению нулей в числе 0,01.

0,01 = 10^-2

Число 0,01 это значение деления 1/100,  или  1/10²

---

Пример 2: Значение 0,00001 в виде степени с основанием 10.

0,00001 = 10^-5

Правила деления дробей

Выполнение деления дробных значений по своей аналогии одинаково с умножением.

При делении первую дробь необходимо перемножить со значениями дроби под номером два. {2.3} \cdot(\sqrt{x+1})-2}{\sin (2 \cdot x-\sqrt{x})}\]

Приведение дробей к наименьшему общему знаменателю

Наименьший общий знаменатель дробей

Определение

Общий знаменатель значения — это любое из положительных данных числа, которое является кратным для всех значений дробей.

Иными словами, можно сказать, что общим знаменателем дроби, будет характеризоваться натуральное простое числовое значение. Оно должно делиться без остатка на все значения знаменателей данных дробей. 

Натуральные числа имеют свойство бесконечности и поэтому ряд обыкновенных дробных значений имеет характерное множество общих значений знаменателя.  Чтобы определить общий знаменатель для дроби, нужно применить его основное определение. 

Рассмотри два значения дробных выражений: 16 и 35. Общим дробным знаменателем будет являться любое число с положительным значением. Оно должно быть кратным значениям 6 и 5. 

Перечислим подходящие значения: 30,35,65,95,125,155,185,215 и так далее.  

Данное определение звучит следующим образом: минимальное значение числа, на которое можно разделить знаменатель дроби, обязательно без остаточного значения.

Аббревиатура данного значения, выглядит как НОК.

В определенном перечне числовых значений, которые являются общими знаменателями данных дробей, будет иметь место наименьшее простое значение. Оно будет характеризоваться, как наименьший общий знаменатель. Сформулируем определение наименьшего общего знаменателя данных дробей.

Как правильно определить наименьший общий знаменатель числа дроби?

Так как НОК, будет иметь значение наименьшего положительного общего делителя данного набора чисел. Тогда  НОК знаменателей любых дробей, представлен, как минимальный общий знаменатель дроби.

Из этого следует, что определение наименьшего знаменателя дроби, будет сводиться к определению НОК знаменателя дроби.

Рассмотрим данное правило на примере решения.

---

Пример 1:

Задано два значения дроби: \[\frac{3}{10} и \frac{277}{28}\]

Знаменатели дробей равняются 10 и 28 соответственно.

Наименьший знаменатель будет определяться как НОК чисел 10 и 28.

Разложим числа на простые множители: 10=2*5, 28=2*2*7, следовательно НОК (15 и 28)=2*2*5*7=140.

Ответ задачи: 140

Когда  простые обыкновенные дроби, имеют одинаковые по значению  знаменатели, то это характеризуется как дроби приведены к общему знаменателю.

---

Пример 2: значения \[\frac{45}{76} \text { и } \frac{143}{76}\] приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей \[\frac{1}{3}, \frac{3}{3}, \frac{17}{3} \text { и } \frac{1000}{3}\] все эти значения приведены к общему знаменателю 3.

В случае, если знаменатели дробных чисел, являются разными по  значениям и не равны друг другу. Можно их привести к общему числовому  знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.

---

Например 3: \[\frac{2}{5} и \frac{7}{4}\] — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.

Применяя данные значения приведем и вычисления и получим общий множитель: значение равное 20.

При перемножении числителя и знаменателя дроби \[\frac{2}{5}\] на значение равное 4, получим дробь вида \[\frac{8}{20}\]. Проводим аналогичные действия, но только с дробью.

При перемножении числителя и знаменателя дроби \[\frac{7}{4}\] на 5 и приведем ее к дроби вида  \[\frac{35}{20}\].

Теперь можно сформулировать определение, приведение дробей к общему знаменателю.

Определение

Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.

В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.

Данное правило включает в себя три основных пункта.

Принцип приведения дробного значения к наименьшему общему знаменателю:

• Для начала определяется значение наименьшего общего знаменателя дробей.
• Затем для каждой дроби определяется дополнительный множитель. Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби.
• Перемножаем числитель и знаменатель на принятый дополнительный множитель.

Решение задач с приведением к наименьшему знаменателю

Пример 1:

Нужно привести к наименьшему знаменателю следующие дроби:

\[\frac{5}{14} и \frac{7}{18}\]

Для решения применим алгоритм решения, рассмотренный вышеприведенном пункте.

Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.

Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126.

Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения \[\frac{5}{14}\] и \[\frac{7}{18}\] будут приведены к числу 126.

Дробному значению \[\frac{5}{14}\] дополнительный множитель будет равняться 12614=9. Для значения второй дроби равной \[\frac{7}{18}\] , аналогичный множитель будет равняться 12918=7.

Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.

Записываем следующие выражения:

Итоги проведенных вычислений: Заданные дроби \[\frac{5}{14} и \frac{7}{18}\] приведены к общему знаменателю. Итоговое значение выражения \[\frac{45}{126} и \frac{49}{126}\].

---

Пример 2:

Нужно привести к наименьшему знаменателю следующие дроби:

\[\frac{3}{12} и \frac{5}{18}\]

В этом примере, также применим алгоритм решения, состоящий из трех главным действий.

Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.

Следующим шагом, разлом данные значения на множители: 12=2*6, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=216.

Произведем вычисление дополнительных множителей. С их помощью приведем дробные значения \[\frac{3}{12}\] и \[\frac{5}{18}\] будут приведены к числу 216.

Дробному значению \[\frac{3}{12}\] дополнительный множитель будет равняться 21612=18. Для значения второй дроби равной \[\frac{7}{18}\], аналогичный множитель будет равняться 21618=12.

Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.

Записываем следующие выражения:

Итоги проведенных вычислений: Заданные дроби \[\frac{5}{14} и \frac{7}{18}\] не приведены к общему знаменателю. Окончательное  значение выражения \[\frac{27}{108} и \frac{35}{126}\] и из этого следует, что знаменатели разные.

Ответ: значение 216 не будет являться наименьшим общем знаменателем.

Аналогичным способом, используя алгоритм решения, можно определить значение наименьшего знаменателя трех и более дробных значений.

Калькулятор вычисления НОД и НОК двух чисел

Обыкновенные дроби | СПАДИЛО

Определение

Обыкновенная дробь – это запись числа в виде:

где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби  можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби  можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.

• Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
• Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.

Сокращение дробей

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби – четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

Пример №4.

Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

Вычитание обыкновенной дроби из целого числа

Вычитание обыкновенной дроби из единицы

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

Вычитание обыкновенной дроби из бóльшего числа

Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

Пример №6.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное. Приём №1.

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

12=2×2×3

15=3×5

2. Затем найти одинаковые множители (подчеркиваем):

12=2×2×3

15=3×5

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.

Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 – видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Алгоритм сложения (вычитания)

1. Находим общий знаменатель данных дробей.
2. Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
3. Умножаем каждый числитель на дополнительный множитель.
4. Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.

Пример №10.

Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 – простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

Выполняем умножение в числителе: Выполняем сложение дробей с одинаковыми знаменателями:

Умножение обыкновенных дробей

Как перемножить дроби?

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

Пример №13. Нам даны смешанные дроби, переводим их  в неправильные для выполнения умножения.

Деление обыкновенных дробей

Как разделить одну дробь на другую?

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю. Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.

Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

Задание OM2004 Сократите дробь 36n4n−2∙32n−1 .

---

Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.

(3∙3∙4)n4n−2∙32n−1 ..

Теперь представим каждый множитель в виде степени:

3n∙3n∙4n4n−2∙32n−1 ..

Разложим знаменатель дроби на множители по свойству степеней

3n∙3n∙4n4n∙4−2∙32n∙3−1 ..

Теперь можно сократить числитель и знаменатель на 3n и в 4n степени

Получим дробь, которую преобразуем по свойству степеней:

..14−2∙3−1 ..= 42∙311..=16∙3=48

Ответ: 48

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1306o

Найдите значение выражения:

---

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1305o

Найдите значение выражения при x = 12:

---

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1304o

Найдите значение выражения

где a = 9, b = 36

---

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

9b² + 5a – 9b²

Приведем подобные слагаемые – это 9b² и  – 9b², в числителе остается 5a. Запишем конечную дробь:

5a/b

Вычислим её значение, подставив числа из условия:

5•9/36 = 1,25

Ответ: 1,25

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1303o

Найдите значение выражения:

при x = √45 , y = 0,5

---

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y

Подставим значение y = 0,5:  – 1 / (5 • 0,5) = – 1 / 2,5 =  – 0,4

Ответ: -0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1302o

Найдите значение выражения:

при a = 13, b = 6,8

---

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

 Сокращаем (a-b):

 И получаем:

a/2

Подставляем значение a = 13:

13 / 2 = 6,5

Ответ: 6,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0804o

Какое из данных ниже чисел является значением выражения?

---

Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:

16 – 14 = 2

Суммарно наши действия выглядят так:

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0603o Найдите значение выражения:

---

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Затем складываем:

4/84 + 3/84 = 7/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

84 / 7 = 12

Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0602o Найдите значение выражения:

---

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что   1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17  • 1/3, поэтому её можно легко вынести за скобку.

1/3 • (6 • (1/3)  — 17 )

Проведя вычисления в скобках, получим:

1/3 • ( 6 • (1/3)  — 17 ) = 1/3 • (6 /3  — 17 ) = 1/3 • ( 2  — 17 ) = 1/3 • ( -15 )

Теперь умножим полученное значение -15 на 1/3:

1/3 • ( -15 ) = -5

Ответ: -5

pазбирался: Даниил Романович | обсудить разбор | оценить

Алла Василевская | Просмотров: 19k

Решение уравнений с дробями | Алгебра

Продолжаем решать уравнения (важный аспект понимания алгебры и многих других разделов математики). В этом видео я рассматриваю сложение и вычитание дробей и то, как их понимание помогает нам понять, как решать уравнения с дробями.

Это второе видео из серии, посвященной решению уравнений. Мы продолжаем наше путешествие к пониманию уравнений с дробями и различных методов их решения. В видео представлены 2 примера на сложение и вычитание дробей и 2 примера на решение уравнений с дробями. Прежде чем ознакомиться с информацией в этом посте, мы советуем вам проверить предыдущий пост: Введение в решение уравнений | Алгебра | LThMath.

Во-первых, мы обсуждаем сложение и вычитание дробей. Самая важная часть об этом связана со знаменателем. Мы не можем складывать/вычитать дроби, если у них разные знаменатели. Чтобы получить общий знаменатель, нам нужно подумать о наименьшем общем кратном уже имеющихся знаменателей. Например, в первом вопросе нам нужно найти наименьшее общее кратное 3 и 4; во втором примере нам нужно наименьшее общее кратное 4 и 8. После нахождения l.c.m (наименьшее общее кратное) нам нужно фактически умножить дроби, чтобы получить общий знаменатель. Вы можете увидеть это в обоих вопросах.

В этих примерах мы также рассматриваем преобразование дроби 23/12 в смешанное число — это связано с упрощением дроби. Это можно сделать только тогда, когда числитель больше знаменателя.

Первый пример включает решение уравнения, которое на самом деле представляет собой вычитание двух дробей. Для этого вопроса вам нужно чувствовать себя уверенно при вычитании дробей в целом. Этапы решения:

1. Найдите наименьшее общее кратное 8 и 4 – это будет общий знаменатель.

2. Перемножьте дроби, чтобы получить общий знаменатель.

3. Вычтите 2 дроби.

4. Упростите числитель.

Приведенные выше шаги помогут вам решить часть, связанную с вычитанием двух дробей. Следующие шаги предназначены для продолжения решения и нахождения x:

5. Умножьте обе части на знаменатель.

6. Убедитесь, что в одной части уравнения есть только член, включающий x.

7. Найдите х.

8. (опционально) Упростите дробь – в этом случае замените ее на смешанное число.

Второй пример следует той же идее, с той лишь разницей, что мы складываем 2 дроби. Выполняем те же действия:

• Общий знаменатель
• Складываем дроби и упрощаем числитель
• Умножаем обе части на знаменатель
• Находим x
• (опционально) упрощаем дробь

Нам понравился наш пост по решению уравнений с дробями. Понимание и решение уравнений было (до сих пор) моей любимой темой в школе, и я до сих пор помню радость от понимания того, как решить одно из них. Раньше я тратил много времени, пытаясь найти разные методы решения одной из них. Это был такой расслабляющий процесс.

Посмотрите мое предыдущее видео, посвященное основам решения уравнений. В этом видео я рассматриваю порядок операций и то, как их понимание помогает нам понять, как решать уравнения:

---

Надеюсь, вам понравился этот пост и вы нашли его полезным. Хорошего дня. Если у вас есть идеи для будущих постов в блоге, дайте нам знать. Вы можете найти нас на Facebook, Tumblr, Twitter и Instagram. Мы постараемся выкладывать туда как можно чаще. Наслаждайся этим днем!

С любовью и не забывайте, что математика повсюду! Наслаждаться!

Нравится:

Нравится Загрузка…

Я смотрю в зеркало… Темно-карие глаза смотрят на меня и спрашивают, нравится ли мне лицо в зеркале… Эти глаза сначала смотрели вверх на черные кудрявые волосы, потом вниз…. Но эти глаза не могут заглянуть в мое сердце и разум… Они не могут узнать, что я чувствую или о чем я думаю… Они не могут видеть воду внутри меня, воду, которая кипит и делает меня таким, какой я есть.. , Упрямая вода, которая делает мою жизнь такой, какая она есть сейчас… Просмотреть все сообщения LThMath

18 мая 2021

Обучение

алгебра, уравнения, дробь, дроби, линейная алгебра, учитель математики, математическая красота, математика, новое видео, обучение, обучение математике, обучение математике, видео

Дроби единиц: определение, примеры — Turito

Возможно, вы знакомы с дробями. Если нет, то вы могли столкнуться с ситуациями, когда вы бы видели дроби. Например, во время поедания куска торта или пиццы. Кусок, который вы берете в первую очередь, является частью всего торта или пиццы. Следовательно, дробь — это числовое представление, показывающее часть целого. Верхняя часть дроби является числителем, а нижняя — знаменателем. Тогда что такое дробь единицы?

Содержание  

• Определение доли единицы измерения 
• Неединичная дробь 
• Свойства дробей 
• Элементарная арифметическая единица дробей
• Применение единиц дробей
• Единица измерения дробей
• Примеры дробей единиц измерения 

Дробная единица Определение

Теперь перейдем к тому, что такое дробная единица измерения. Единичные дроби — это те, в которых числитель всегда равен 1. Знаменатель может варьироваться и быть любым другим целым числом, но числитель должен быть равен 1, чтобы его можно было назвать единичной дробью. Хороший способ запомнить, что такое единичная дробь, — помнить, что единица означает 1. Следовательно, дробь с 1 вверху является единичной дробью. Пример единичной дроби – ½, ⅓, ⅕, ⅙ и многие другие.

Согласно Merriam-Webster, единичная дробь — это дробь, числитель которой равен единице, а знаменатель — целое число. Поисковая популярность этого слова находится в верхних 26% слов. Доля единицы слова помещается рядом со словами «фактор единицы» и «нагреватель».

Дроби единиц являются рациональными числами. 1/25, 1/100, 1/200 и многие другие — рациональные числа. Однако числа 7/33, 9/10, 67/96 и многие другие тоже являются рациональными числами, но не единичными дробями.

Каждая дробная единица является частью 1. Половина, третья, четвертая или любое другое число 1. Следовательно, вы можете называть их «пятыми», «одними четвертями» и т. д. Дроби единиц могут быть представлены на числовой прямой, как показано ниже.

⅖ = ⅕ + ⅕. Точно так же 5/5 = ⅕ + ⅕ + ⅕ + ⅕ + ⅕. Следовательно, каждая дробь представляет собой число единичных дробей.

Неединичные дроби 

Дроби, числитель которых не равен единице, называются неединичными дробями. Пример неединичных дробей – 2/6, ⅜, 5/7 и другие.

Возьмем еще один пример, чтобы понять дроби единиц. Рассмотрим прямоугольник, как показано ниже, с 10 маленькими квадратами.

Если вы выберете одну клетку из этих десяти, дробь будет 1/10. Если вы выберете 5 квадратов из этих 10, дробь будет 5/10, что также можно упростить до ½. Опять же, это дробная единица. Следовательно, упрощение дробей во многих случаях даст единичные дроби.

Свойства единичных дробей

Существуют различные свойства единичных дробей. Некоторые из них перечислены ниже. Будет полезно, если вы запомните эти свойства, так как это поможет вам ускорить расчеты и повысить уровень своей подготовленности.

• Единичные дроби всегда будут иметь числитель, равный единице. Знаменатель может быть любым положительным целым числом.
• Деление дробей единиц на целые числа дает дробь единиц. Например, если дробную единицу ¼ разделить на целое число, скажем, 5, полученная дробь будет равна 1/20, то есть дробной единице.
• Деление единичных дробей на рациональные числа даст неединичные дроби. Например, если вы разделите ⅙ на ⅝, в результате получится дробь 8/30, а не единичная дробь.
• Умножение двух долей единиц всегда дает дробь единиц. Например, 1/31, умноженное на 1/5, даст 1/155, то есть дробную часть.
• Умножение дробей единиц на целое число не приведет к дробям единиц. Например, 1/7, умноженная на целое число, скажем, 4, даст 4/7, неединичную дробь.

Элементарная арифметика единичных дробей

Вот арифметическое представление единичных дробей для справки, которое поможет вам повысить эффективность математических расчетов: 

• 1x x 1y = 1xy
• 1х + 1у = х + уху
• 1x – 1y= y – xxy
• 1х ÷ 1у= ух

Применение дробных единиц

Существуют различные области применения дробных единиц. Вот некоторые из них:

• Дробные единицы часто используются в теории вероятностей и статистике. Все вероятности равны единицам в равномерном распределении на дискретном пространстве. Вероятности такого вида часто возникают в статистических расчетах из-за принципа безразличия.
• Согласно закону Ципфа, многие наблюдаемые явления связаны с выбором элементов из упорядоченной последовательности. Вероятность выбора n-го члена пропорциональна доле единицы 1/n.
• Дробные единицы в основном также используются в физике. Энергетические уровни фотонов, которые могут быть поглощены или испущены атомом водорода, пропорциональны разнице между двумя долями единиц. Этот закон сформулирован Ридбергом и известен как формула Ридберга.
• В модели Бора также используются дробные единицы. Согласно закону Бора, энергетические уровни электронных орбиталей в атоме водорода обратно пропорциональны долям квадратных единиц. Энергия фотона квантуется как разница между двумя уровнями.
• Артур Эддингтон заявил, что постоянная тонкой структуры представляет собой долю единицы. Первая была 1/136, а вторая 1/137.

Курсы единиц с дробями

Вы видели, что такое дроби единиц в предыдущем разделе. При этом числитель был равен 1. Что, если знаменатель равен 1? Будет ли это называться дробью единицы? Ну нет!

Когда дроби имеют знаменатели, равные 1, они известны как удельные ставки с дробями. Следовательно, дробь со знаменателем, равным 1, является удельной ставкой этой дроби. Например, 60/6 может быть записано как 10, представляющее единичную ставку. Точно так же 57/8 является единичной ставкой и может быть записано как 7,125.

Единицы измерения полезны в повседневной жизни для определения относительной скорости, расчета расстояния и определения любых изменений в единицах измерения. Удельные ставки полезны для определения того, какой товар изменяется относительно другого товара. Например, найти время, расстояние изменяется относительно скорости. Следовательно, время — это единичная скорость изменения или просто скорость изменения расстояния по отношению к скорости.

Примеры дробей единиц

Давайте рассмотрим несколько примеров, чтобы глубже понять дроби единиц. Обязательно попрактикуйтесь в этих вопросах, чтобы укрепить свои основы.

Пример 1: Сколько единичных дробей в дроби ⅚?

Решение: Чтобы найти единичную дробь, приравняйте числитель к 1, а знаменатель оставьте без изменений. Следовательно, в данном случае доля единицы будет равна ⅙. Так как числитель в вопросе равен 5, то общее количество единичных дробей будет равно 5. 

⅚ = ⅙ + ⅙ + ⅙ + ⅙ + ⅙.

Пример 2: Как вы будете считать от ⅓ до 2 ⅓?

Решение. Как видно из числовой строки ниже, числа идут по порядку,

⅓, ⅔, 3/3 = 1, 4/3 = 1 ⅓, 5/3 = 1 ⅔ и так далее.

Опять же, это сумма. Следовательно, вы можете посчитать их как:

⅔ = 2 x ⅓ = ⅓ + ⅓

⅜ = 3 x ⅛ = ⅛ + ⅛ + ⅛ 

Пример 3. Сложите 2/8 и ⅜.

Решение: чтобы сложить их, следуйте схеме, показанной ниже:

2/8 = ⅛ + ⅛

⅜ = ⅛ + ⅛ + ⅛ 

Сложив все ⅛, указанные выше, вы получите ⅛ + ⅛ + ⅛ + ⅛ + ⅛ + ⅛ + ⅛ + ⅛ = ⅝.

В качестве альтернативы ответ можно найти напрямую, сложив числители. Это потому, что знаменатели равны, так что числители могут быть добавлены напрямую. Следовательно, ответ будет ⅝.

Пример 4: 1 в скольких пятых?

Решение: Чтобы найти ответ на этот вопрос, проверьте числовую строку, показанную ниже:

Из приведенной выше числовой строки вы можете увидеть пять пятых в одной. Следовательно, в 1 пять ⅕. 

Аналогично можно найти и остальные числа. В единице 3 терции, в единице 4 четверти и так далее.

Пример 5. Сложите заданную дробь и выразите ее в виде неправильной дроби: 5/9 + 1.

Решение: Чтобы решить эту задачу, переведите 1 в единичные дроби. Следовательно, 1 будет 9/9.