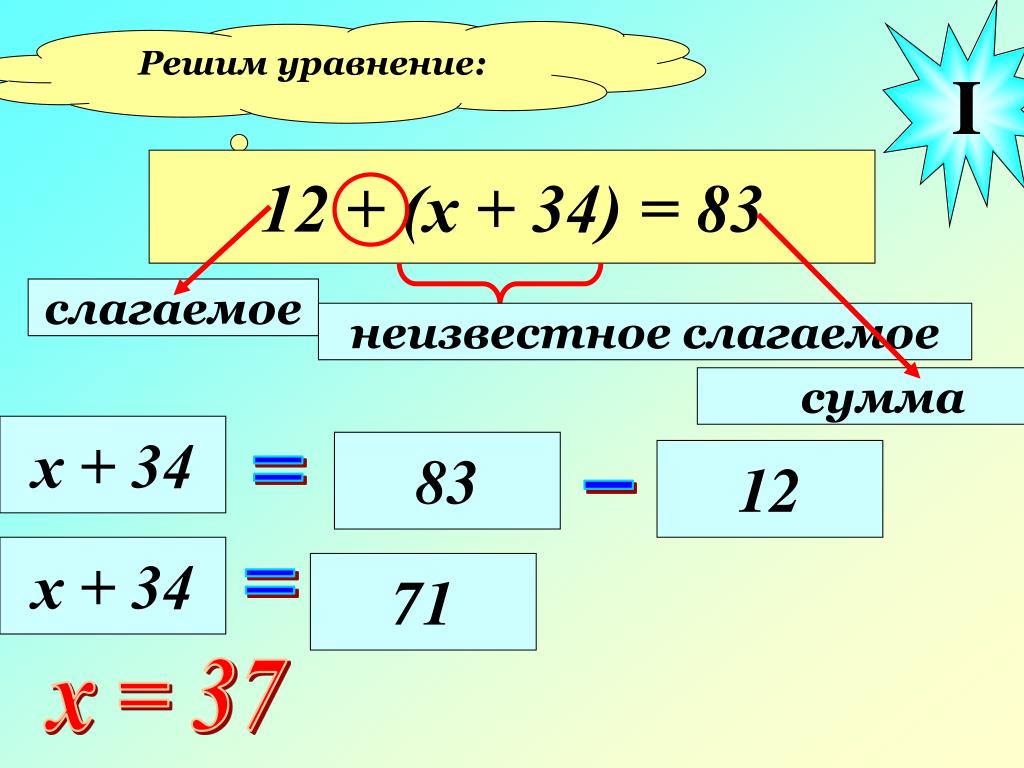
Этап урока, время этапа | Задачи этапа | Методы, приемы обучения | Формы учебного взаимодей-ствия | Деятельность учителя | Деятельность учащихся | Формируемые УУД и предметные действия |
Мотивационно-целевой этап | • вызвать эмоциональный настрой и познавательный интерес к теме; • организовать самостоятельное формулирование вопросов и постановку цели | Формирование информа-ционного запроса: «РИСК» | Фронталь-ная, индивиду-альная | 1. 2. Предъявляет фразу с информацией проблемного характера. 3. Предлагает задать вопросы, возникшие в связи с данной информацией, используя вопросительные слова | 1. Делятся мнениями на поставленную проблему 2. Записывают информацию. 3. Формулируют и записывают вопросы. | Личностные УУД: проявлять интерес к новому содержанию, осознавая неполноту своих знаний Познавательные УУД: формулировать информационный запрос Регулятивные УУД: определять цели учебной деятельности |
Ориентировоч-ный этап | • организовать самостоятельное планирование и выбор методов поиска информации | Беседа | фронталь-ная | Задает вопрос о способах получения нового знания, необходимого для ответа на возникшие вопросы, предлагает способ и последовательность действий | Называют известные им источники и методы поиска информации и знакомятся с предложенной учителем последовательностью действий | Регулятивные УУД: планировать, т. |
Поисково-исследователь-ский этап | • организовать осмысленное восприятие новой информации | Рассказ | Фронталь-ная, индивидуальная | 1. Сообщает 1 часть информации по теме урока 2. Предлагает ответить на вопросы, которые получены из 1 части рассказа. 3. Сообщает 2 часть информации. Предлагает записать выводы и решить уравнения. 4. Предлагает найти ответы на вопросы в ходе практической работы. | 1. Слушают новый материал. 2. Делают пометки, называют вопросы и дают на них ответы. 3. Слушают, записывают и решают. 4. Формулируют новые вопросы по изучаемой теме. | Познавательные УУД: извлекать необходимую информацию из прослушанных текстов; структурировать знания; Коммуникативные УУД: вступать в диалог, с достаточной полнотой и точностью выражать свои мысли. Предметные УУД: давать определения новым понятиям темы; называть способы решения уравнения. |
Практический этап | • обеспечить осмысленное усвоение и закрепление знаний | Практи-ческая работа | Индиви-дуальная, фронталь-ная | 1. Дает задание для учащихся №1, организует обсуждение результатов ее выполнения. 2. Помогает впомнить понятия «уравнение», «равенство»; «корень уравнения». 3. Дает задание для учащихся № 2, организует обсуждение ее результатов. | 1. Выполняют задания, сообщают о результатах. 2. Слушают объяснение учителя. 3. Выполняют задания № 2, сообщают о результатах. | Предметные УУД: Различать способы решения уравнений, правильно формулировать ход решения уравнений, находить неизвестные компоненты, применять на практике полученные выводы Познавательные УУД: анализировать и сравнивать объекты, подводить под понятие; |
Рефлексивно-оценочный этап | • осмысление процесса и результата деятельности | Беседа,письменное высказывание | Индиви-дуальная, фронталь-ная | 1. 2. Предлагает каждому учащемуся высказать свое мнение в виде 1 фразы: телеграммы | 1. Оценивают степень достижения цели, определяют круг новых вопросов. 2. Выборочно высказываются, делятся друг с другом мнением | Регулятивные УУД: констатировать необходимость продолжения действий Познавательные УУД: решать различные виды уравнений Коммуникативные УУД: адекватно отображать свои чувства, мысли в речевом высказывании |
Этапы урока | Деятельность | |||||
учителя | учащихся | |||||
Организационный этап | Учитель приветствует учащихся, проверяет их готовность к уроку. | Учащиеся готовы к началу работы. | ||||
Этап актуализация знаний. | Учитель: Девизом нашего урока будут слова Рено Декарта «Для того чтобы усовершенствовать ум, надо больше рассуждать чем заучивать» (1 слайд) 1.Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому начнем урок с устного счета:(2 слайд) У вас на столе лежат строки из таблиц, ваша задача найти соответствие между ними, то есть упростить выражение из левой таблицы и поставить ему в соответствие выражение из правой таблицы 2 слайд)( Ответы 1-В, 2-Е, 3-А, 4-Д, 5-Б. Следующее задание: решите уравнения а) x+3,8=2,7 x= – 1,1;б) х : 0,3=9 x=2,7; в) 5y + 3y=16 y=2; г) 3x – 1=5 x=2; д) 5z – 15=8z. (3 слайд) Все ли уравнения мы можем решить? ( Постановка проблемы) К последнему уравнению мы вернемся позже. 2. Открываем тетради, записываем число, классная работа. (4 слайд) -Обратите внимание на записи. 5(x-3)=20; a-4+b; x+8=-15; 4b; 7,5s-3k; 5x=2x+6; 6m -1. — Внимательно их изучите и ответьте на вопросы. — На какие две группы можно разделить написанное? — Как можно назвать каждую из групп?(5 слайд) — Интересна ли для нас 1 группа: выражения? — А вторая? Почему? – Кто догадался, какая тема сегодняшнего урока?(6 слайд) Альберт Эйнштейн, один из основателей современной физики сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».(7 слайд) -Да мы сегодня будем заниматься вечным – решать уравнения. — А вы разве не умеете их решать? Умеете. Что же нового мы можем узнать? — Какова же цель и задачи нашего урока? (8 слайд) | 1.Решают в уме, один из учеников проговаривает ответ 2. Находят соответствующие строки таблиц 3. Учащиеся внимательно смотрят на записи, отвечая на вопросы: На уравнения и выражения Уравнения, выражения Нет Да, потому что уравнения можно решить. 4. Ребята объявляют тему урока и записывают в тетради: « Решение уравнений». 5. Формулируют цель: познакомиться с более сложными уравнениями и найти новые способы их решения. 6. Формулируют задачи: вспомнить основные понятия, свойства, которые можно отнести к уравнениям; изучить материал учебника по этой теме; внимательно слушать учителя; делать необходимые записи в тетрадях. 7. Называют источники информации: учебник, учитель | ||||
Этап изучение нового материала | 1.Подготовительный этап. – А что значит «решить уравнение»? (9 слайд) – Итак, уравнение – это равенство. встречаемся с понятием равенство? В тетрадях запишем 1 уравнение и решим его. Какие существуют способы решения данного уравнения? — Хорошо! Давайте сначала решим уравнение, применив распределительное свойство умножения: 1 способ (10 слайд) 5(x-3) = 20 5x-15=20 5x=20+15 5x=35 x=35:5 x=7 — А сейчас по правилу отыскания неизвестных компонентов 2 способ (11 слайд) 5(x-3) = 20 — Что неизвестно в уравнении? — Как найти неизвестный множитель? (12 слайд) x-3=20:5 x-3=4 x=4+3 x=7 -Что мы получили в итоге? — Что называется корнем уравнения? -Число 7 является корнем уравнения x-3=4 и уравнения 5(x-3) = 20, так как 7-3=4 и 5(7-3)=20. (слайд 13) — Как из первого уравнения можно получить второе?(14 слайд) Мы с вами убедились, что корнем этих двух уравнений является одно и то же число. Давайте попробуем сделать вывод. Откройте учебники, прочитайте правило на странице 229. Вывод: Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число , не равное нулю. (15 слайд) Найдите уравнения равносильные данному (16, 17 слайды) 2. Дано уравнение: x+8= — 15. (18 слайд) Как его можно решить? Это уравнение решается с использованием зависимостей между компонентами и результатами математических действий. Но изучение отрицательных чисел дает возможность решить эти уравнения иначе. — Вспомним, чему равна сумма противоположных чисел? — Как можно получить в левой части уравнения только выражения с x? — Рассмотрим решение этого уравнения. x+8= — 15 x+8-8= -15-8 х=-15-8 x=-23 — Мы видим, что слагаемое без переменной перешло из левой части уравнения в правую с противоположным знаком. — А сейчас рассмотрим следующее уравнение и решим его: 5х=2х+6 (слайд 19) — Чем данное уравнение отличается от предыдущего? — Как его можно решить? — Нужно получить такое уравнение, чтобы слагаемые с x были только слева. 5х=2х+6 5x+ (-2x) = 2х+6+ (-2x) 5x+ (-2x) = 6 3x=6 x=6:3 x=2 Обратите внимание, слагаемое 2х перешло из правой части в левую с противоположным знаком. — Хорошо! Давайте рассмотрим такой вопрос: Вы собираетесь за границу. О чем в первую очередь вы должны подумать, когда пересечете границу? — Правильно, пересекая границу, вам обязательно надо поменять паспорт. — Давайте представим, что знак «=» — это граница, а знак числа – это ваш паспорт. Когда мы пересекаем границу, меняем паспорт, то есть, если число переносим из одной части в другую, мы должны поменять знак. Попробуйте сформулировать правило. А теперь прочитайте правило на странице 230. Корни уравнения не изменяются, если какое – нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. (20 слайд) | 1. Отвечают на вопросы: 1)Найти все значения неизвестных, при которых оно обращается в верное равенство или установить, что таких значений нет. 2) Называют возможные варианты, например, при взвешивании 3)Записывают уравнение в тетрадях, предлагают варианты решения. 4)Вспоминают распределительное свойство умножения и решают уравнение в тетрадях, комментируя вместе с учителем ход решения. 5)Отвечают на вопросы: Множитель 6)Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель 7) Корень уравнения x=7 Корнем уравнения называют то значение неизвестного, при котором это уравнение обращается в верное равенство 8) Это уравнение можно получить, разделив обе части данного уравнения на 5 или умножив обе части на 1\5. 9)Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число , не равное нулю. 10) Читают правило. 2. 1)Записывают уравнение в тетрадях, предлагают возможные варианты, решая уравнение 2)Прибавить или отнять числа, противоположные числам в левой части. 3) Неизвестное есть и в правой и в левой части уравнения. 4) Предлагают варианты решения уравнения 5) Для этого надо к обеим частям уравнения прибавить (-2 x). Решают уравнение 6) Слушают, отвечают на вопросы. 7) Формулируют правило. 8) Записывают в тетрадях вывод. | ||||
Этап первичное осмысление и закрепление знаний | 1. — Принято при решении уравнений переносить слагаемые так, чтобы в левой части уравнения были неизвестные числа, а в правой — известные числа. | |||||
Физпауза | Мы славно потрудились и славно отдохнем. На экране будут отображаться уравнения и их преобразования, если преобразования выполнены верно хлопаем в ладоши, если нет топаем ногами. 3х-6=5х+9; 3х-5х=9+6; 4х+12=2х-6; 4х+2х=-6-12; -7х=-21; х=3; -5х=1; х= -5 4х-7=х+6; 4х-х=6-7; 3(х-1)=6; х-1=2. | Выполняют упражнение Решают в тетрадях, один из учеников комментирует решение с места | ||||
Решить №1314 и 1315 с комментированием на месте. № 1314 8x+5,9=7x+20 2)6x-8=-5x-1,6 8x=7x+20-5,9 6x=-5x-1,6+8. № 1315 15y-8=-6y+4,6 2) -16z+1,7=2z-1 15y+6y=4,6+8 -16z-2z=-1-1,7 21y=12,6 -18z=-2,7 А сейчас давайте проговорим алгоритм решения уравнений новыми способами, итак: (22 слайд) По возможности упростить уравнение (раскрыть скобки). Слагаемые, содержащие переменную, перенести в левую часть уравнения, при этом меняя знак на противоположный. Числа перенести в правую часть уравнения, при этом изменив знак на противоположный. Привести подобные слагаемые в левой части уравнения. Привести подобные слагаемые в правой части уравнения. Разделить число правой части на коэффициент при переменной. Записать ответ. Вернемся к началу урока и решим уравнение, вызвавшее затруднение: 5Z – 8Z = 15 3Z =15 Z = 15: (-3) Z = — 5 (23 слайд) | ||||||
Историческая справка | Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом. Вот примеры задач из этого папируса. 1) «Неизвестное, его седьмая часть, его целое составляет 19». В современном виде задача запишется так: Общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми. В своем сочинении «Аль-джебр и аль-мукабала» он дает два приема, применяемых при решении уравнений. Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными. Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению. Пусть, например, дано уравнение: 5x – 17 = 2x – 5. Применим «аль-джебр»: прибавляем к каждой части уравнения 5 и 17. Получим: 5x + 5 = 2x + 17. Применим «аль-мукабала»: вычитаем из каждой части 2x и 5. Получим: 3x = 12. Отсюда легко находится x. Появление этого замечательного сочинения аль-Хорезми можно считать началом выделения алгебры как самостоятельной, отдельной отрасли математики. Само название «алгебра» взято из заглавия этого сочинения («Аль-джебр») | |||||
Этап закрепление изученного материала | Решить уравнение №1316( а- г) на доске и в тетрадях, проговаривая правила. ( 30 слайд) №1316( а- г) 6x-12=5x+4 б) -9a+8=-10a-2 в) 7m+1=8m+9 6x-5x=4+12 -9a+10a=-2-8 7m-8m=9-1 X=16 a=-10 -m=8 г) -12n-3=11n-3 -12n-11n=-3+3 -23n=0 3. Решить уравнение №1319(а;б) с комментариями на месте. №1319(а;б) 0,5x+3=0,2x б) -0,4a-14=0,3a 0,5x-0,2x= -3 -0,4a-0,3a=14 0,3x=-3 -0,7a=14 x=-3:0,3 a=14:(-0,7) x=-10 a=-20 | 1)Осмысливают и приступают применять новый способ решения на практике. 2)Делают записи в тетрадь. После выполнения задания сверяют с доской. Один из учеников решает у доски с комментарием. 3)Решают самостоятельно, сверяют с доской, один из учеников решает у доски. | ||||
Этап подведение итогов. Домашнее задание. | -Наш урок подходит к концу, с начала запишем домашнее задание, затем подведем итоги. (26 слайд) Домашнее задание каждый из вас выбирает сам. — На доске: Домашнее задание: п. 42, выучить правила; решить №1342(а; б; в; г) – на оценку «3», №1346 – на оценку «4», №1349– на оценку «5» — Ваши вопросы по домашнему заданию. А теперь оцените свою работу на уроке. ( — А теперь давайте вспомним Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы? — Давайте еще раз повторим, какие правила мы с вами вывели на уроке. А сейчас я попрошу вас выразить ваше отношение к уроку в виде телеграммы, она лежит у вас на парте. Закончите предложения. — Итог урока каждый из вас подведет закончив предложения на листах которые лежат на ваших столах, которое выразит ваше отношение к уроку. (32 слайд) Закончить урок я хочу словами С. Я. Моршака Желаю вам цвести, расти, Копить, крепить здоровье, Оно для дальнего пути – Главнейшее условие. Пусть каждый день и каждый час Вам новое добудет, Пусть добрым будет ум у вас, А сердце умным будет. Вам от души желаю я, Друзья, всего хорошего. А всё хорошее, друзья, Даётся нам недешево. С. Я. Маршак | 1) Ребята записывают домашнее задание в дневниках. 2) Просматривают домашнее задание, задают вопросы 3)Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение уравнения, корня уравнения. 4) В конце своей работы каждый ученик пишет на листах окончание предложений. По желанию зачитывают на весь класс | ||||
Конспект урока «Решение уравнений с неизвестным вычитаемым».
Предмет: математика
УМК «Школа России».
Тема: Решение уравнений с неизвестным вычитаемым.
Тип: Урок открытия нового знания.
Цель урока: способствовать развитию умений решать уравнения с неизвестным вычитаемым
Задачи: 1.Учить решать уравнения способом, основанным на связи между компонентами и результатом действия вычитания;
2.Совершенствовать вычислительные навыки и умения решать текстовые задачи.
3.Способствовать воспитанию активности обучающихся.
Планируемые результаты.
Предметные:
- научатся решать уравнения на нахождение неизвестного вычитаемого на основе взаимосвязи чисел при вычитании, объяснять решение уравнений, пользуясь изученной математической терминологией, выполнять проверку.
- совершенствовать вычислительные навыки и умения решать текстовые задачи
- закреплять приемы письменного сложения и вычитания, сравнивать именованные числа
Метапредметные :
- Регулятивные: принимать и сохранять учебную задачу, планировать совместно с учителем свои действия в соответствии с поставленной задачей, осуществлять пошаговый контроль и оценивать правильность выполнения работы по результату, адекватно воспринимать словесную оценку учителя и товарищей.

- Познавательные: осуществлять поиск и выделять конкретную информацию с помощью учителя, строить речевые высказывания в устной форме, оформлять свою мысль по типу рассуждения, проводить сравнения по заданным критериям, устанавливать причинно — следственные связи.
- Коммуникативные: формулировать собственное мнение, допускать возможность существования различных точек зрения договариваться и приходить к общему решению в совместной деятельности, строить понятные для партнёра высказывания.
Личностные:
- проявят мотивацию учебно-познавательной деятельности и личностного смысла учения, которые базируются на необходимости постоянного расширения знаний для решения новых учебных задач и на интересе к учебному предмету
- будут понимать значение математических знаний в собственной жизни,
- освоят позитивный стиль общения со сверстниками.
Ресурсы урока: Рабочая программа, учебник «Математика» ч. 1. С. 9, М. И. Моро.
9, М. И. Моро.
Ход урока:
- Организационный момент
Ну-ка проверь,дружок,
Ты готов начать урок?
Все ли правильно сидят?
Все ль внимательно глядят?
Всё ль на месте?
Всё ль в порядке
Ручка, книжка и тетрадка?
Соберись и улыбкой поделись!
- Актуализация знаний
Чистописание ( на слайде)
«Найди лишнее» Число 52
-Почему лишнее? Что ещё можете рассказать об этом числе?
Пишем число 52
2 ЧЕЛ. К ДОСКЕ
1.- карточка с заданием:
Реши столбиком :25 + 67 84 – 48 29 + 38 71- 37
2. – расставь названия компонентов при сложении, при вычитании
Математический диктант
— Чему равна сумма чисел 53 и 8? — 61
-На сколько 68 больше 13? -55
-Увеличь 54 на 20? -74
-К какому числу прибавили 35, если получилось 70? -35
-Найдите разность чисел 86 и 70 — 16
-Какое число больше 65 на 12? 77
-Сумма двух чисел = 74, 1-ое слагаемое — 60. Чему равно 2 слагаемое? — 14
Чему равно 2 слагаемое? — 14
Примените правило нахождения неизвестного слагаемого…
— Разность двух чисел = 60 Чему равно уменьшаемое, если вычитаемое = 10 — 70
Примените правило нахождения неизвестного уменьшаемого
III. Самоопределение к деятельности
1. На доске карточки: а +7 70 – 8= 62 х – 30 = 47
Х +61 = 84 90 – с 86 +4 = 90 64 – х = 20
-на какие группы можно разделить данные записи?
1 гр- буквенные выражения
2 гр.- числовые выражения
3 гр- уравнения
-Нас интересует группа уравнений..
— Что такое уравнение? ( равенство, с неизвестным числом, которое надо найти)
-Что значит решить уравнение? ( (найти значение неизвестного числа, чтобы равенство стало верным)
2. Вспомним правила решения уравнений и решим их.
У доски 1 чел. х +61 = 84
Чем явл. неизвестное число? Правило нахождения слагаемого…
_ Каким действием мы нашли неизвестное число?
ВАЖНА ЛИ ПРОВЕРКА? Найденное ЗНАЧЕНИЕ НЕИЗВЕСТНОГО ЧИСЛА ОБРАЩАЕТ УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО.
3. У доски 2 ученик х – 30 = 47
Чем явл. неизвестное число? Правило нахождения уменьшаемого…
_ Каким действием мы нашли неизвестное число?
ВАЖНА ЛИ ПРОВЕРКА? Найденное ЗНАЧЕНИЕ НЕИЗВЕСТНОГО ЧИСЛА ОБРАЩАЕТ УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО.
3. -КАКОЕ УРАВНЕНИЕ ОСТАЛОСЬ?
64 – Х = 20
— Чем является неизвестное число?
-Можно ли к этому уравнению применить известные нам правила?
-Почему возникло затруднение? Есть ли у нас знания по решению таких уравнений?
-Нам нужно новое правило!!
-Значит, какова цель нашего урока? ( составить новое правило к уравнениям на нахождение вычитаемого, научиться решать эти уравнения)
-Как мы сформулируем ТЕМУ НАШЕГО УРОКА!
РЕШЕНИЕ УРАВНЕНИЙ НА НАХОЖДЕНИЕ ВЫЧИТАЕМОГО
(вешаю лист с темой урока)
3 ученик. 64 – х =20
Каким действием попробуем решить? (пробуют сложением)
Верное равенство получилось? ВАЖНОСТЬ ПРОВЕРКИ!
(пробуют вычитанием)
Верное равенство получилось? Проверка это показала
Сформулируйте правило нахождения неизвестного вычитаемого.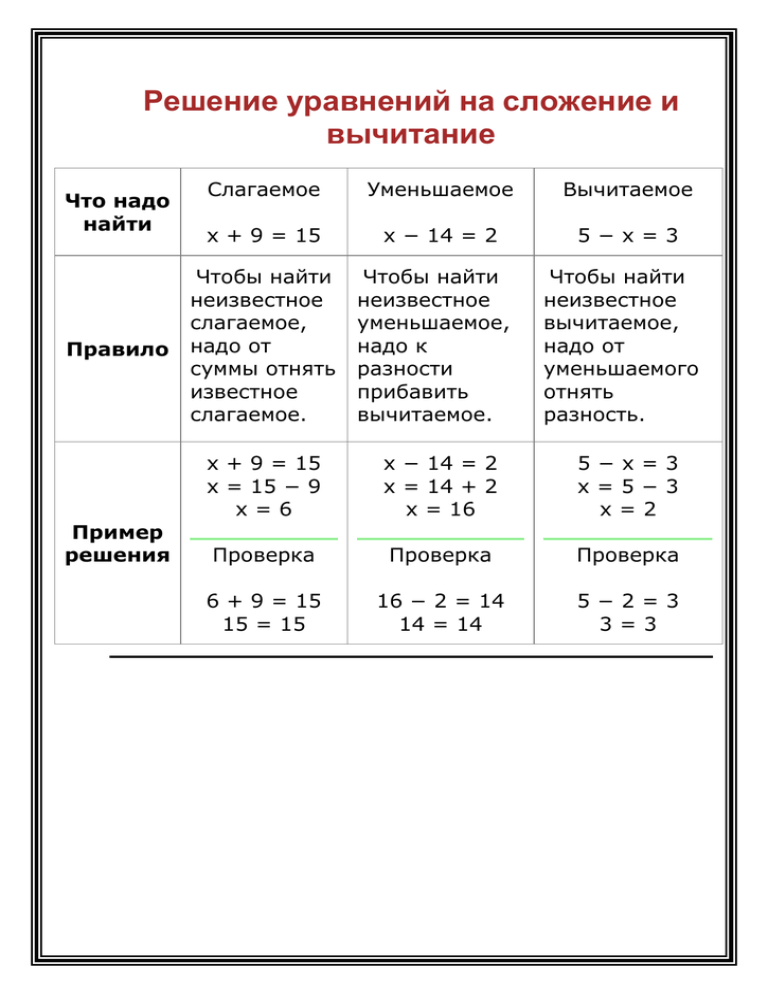
Слайд.. –Мы сказали правило нахождения вычитаемого.
Работа по теме урока
Работа в группах
1. Нам нужно вывести общий алгоритм решения уравнений. Пронумеруйте правильную последовательность действий
|
|
РЕШИТЬ УРАВНЕНИЕ И СДЕЛАТЬ ПРОВЕРКУ |
|
|
ВСПОМНИТЬ НАЗВАНИЕ КОМПОНЕНТОВ ДАННОГО УРАВНЕНИЯ |
|
|
ПРИМЕНИТЬ ПРАВИЛО |
|
|
ОПРЕДЕЛИТЬ НЕИЗВЕСТНЫЙ КОМПОНЕНТ |
|
|
ВСПОМНИТЬ ПРАВИЛО НАХОЖДЕНИЯ НЕИЗВЕСТНОГО КОМПОНЕНТА |
Проверка
Работа в группах
2. Раздать листочки в группы
Раздать листочки в группы
Составить самим и решить по 2 уравнения с неизвестным вычитаемым.
Проверка. Выходят к доске с листочком и отчитываются. Я вешаю листочки на доску.
Ещё раз спрашиваю правило…
-Как можно использовать правило, которое сегодня разобрали?
( для проверки вычислений, для решения уравнений, для решения задач)
Работа в парах.
На каждой парте лист с заданием
Найдите уравнение и решите его каждый в свою тетрадь.
48 – 25 =23
30 + х > 40
36 – х = 12
Х • 2
Обсудите в парах задание и приступайте к выполнению.
Назад к основам — решение линейного уравнения | by Hybesis — H.urna
Многие думают, что уравнения и алгебра непонятны, и используют какие-то эзотерические языки. Правда в том, что уравнения на самом деле являются относительно простыми понятиями ; зная основные правила игры и немного практики, вы можете научиться манипулировать ими и решать их в одно мгновение.
Линейное уравнение — это простейшая форма уравнения, с которой вы можете иметь дело ; это ограничивает проблему уникальной неизвестной переменной (обычно называемой x ) и без показателя степени (например, x — 30 = 15).
Общий вид такого уравнения (после перемещения всего в левую часть):
ax + b = 0
Нам всем приходится решать такое уравнение каждый день, даже не уведомляя об этом. Допустим, я сейчас тренируюсь, я просто знаю, что я бегаю уже 30 минут, а тренер сказал нам, что у нас осталось еще 15 минут бега. Сколько всего мы пробежим? Эту задачу можно записать следующим образом:
?Общее время? − TimeAlreadyRun = TimeLeft
x − 30 = 15 минут
Результат может быть уже решен, но давайте поиграем в уравнение:
TotalTime = TimeAlreadyRun + TimeLeft
30 + 15 = 45 минут
Мы точно знаем, что собираемся в общей сложности пробежал 45 минут (кроме случаев, когда на нас играет тренер). Теперь давайте заглянем в правила игры, вот увидите: их совсем немного (даже с самыми сложными задачами)!
Уравнение похоже на утверждение, говорящее «это равно тому». Предыдущее уравнение, x — 30 = 15 спрашивает: сколько x сделает это уравнение верным?
Предыдущее уравнение, x — 30 = 15 спрашивает: сколько x сделает это уравнение верным?
Таким образом, цель состоит в том, чтобы найти x; в алгебраическом мире, что означает получить:
x = что-то без x .
Следующая часть представляет вам правила и полезные инструменты, предназначенные для достижения этой цели. Имейте в виду, что решение уравнения похоже на решение головоломки : есть вещи, которые мы можем делать, и некоторые другие, которые запрещены.
Необходимо выполнить только два правила:
Что бы вы ни делали с одной стороной уравнения, вы должны делать с другой стороной.
Вам запрещено делить что-либо на 0.
Основы
- a+b)(c+d) = ac + ad + bc + bd
- a * 1 = a
- − (a−b) = −a + b
- a * (b + c) = ab + ac
Дроби
- 0 / а = 0, а ≠ 0
- а / а = 1
- (-а) / б = — (а / б)
- а / ( б / с ) = (а ⋅ с) / б
- а / 1 = а
- -а / −b = a / b
- a / (−b) = − (a / b)
- (b / c) / a = b / (c * a)
Вы должны всегда проверять, что ваше «решение ” действительно является решением, нет ничего проще: замените ‘x’ значением решения в уравнении и убедитесь, что равенство верно.
Убедитесь, что ваш раствор никогда не делится на 0!
В предыдущем примере мы нашли x = 45.
Если мы поместим это в уравнение, мы получим: 45−30=15
Что верно: решение проверено.
Это не оптимальный способ, но всегда выигрывающий робот всегда достигает цели этим методом! Вот как он это делает:
Есть ли в уравнении дроби?
Да → Умножить каждое слагаемое (с обеих сторон) на знаменатель.
Есть ли в уравнении круглые скобки?
Да → Расширьте уравнение с помощью инструментов.
С обеих сторон одинаковые термины?
Да → Объединить похожие термины. (Не забывайте знак перед каждым членом!)
Имеются ли переменные в обеих частях уравнения?
Да → Добавьте или вычтите члены, чтобы получить все переменные в левой части и все константы в правой части.
На данный момент у робота есть базовое двухшаговое уравнение (если нет, то он будет прослушиваться).
Добавьте или вычтите, чтобы удалить любые константы из левой части уравнения.
Умножьте или разделите, чтобы удалить любые коэффициенты из левой части уравнения.
!РЕШЕНИЕ НАЙДЕНО!
В конце робот не забывает проверять свой ответ, чтобы обнаружить возможную проблему :).
Любое линейное выражение (левая или правая часть уравнения) может быть отображено в виде линии в 2D-графике. График очень прост: у нас есть y на вертикальной оси (результат) и для диапазона значений x (горизонтальная абсцисса) мы вычисляем и нанесите точки (x, y).
Самая простая линия, константа: y=-3 (для всех x: y=-3). Другая основная линия, которую нужно знать: y=x (для всех x, y как одно и то же значение). Рисунок здесь y = 2xУмножение x на константу делает поворот на линии. Рисуем здесь все вместе y = 2x — 3
Добавление или вычитание выражения на постоянное значение — это просто добавление смещения.

Линейное уравнение можно изобразить в виде двух пересекающихся линий. Точка пересечения этих двух линий является решением уравнения (если линии параллельны, это означает, что уравнение не имеет решения). Действительно, ответ на вопрос тот же, что и в алгебраическом мире:
Сколько x сделает это уравнение верным, когда эти прямые равны?
Преимущество построения графика уравнения в том, что вы можете использовать его для визуализации значения y для любого заданного значение x или даже x для любого заданного значения y.
Здесь мы проиллюстрировали взаимосвязь между алгебраическим уравнением и его графиками, что дает вам альтернативный способ понимания уравнений.
Запустите Hurna Explorer, чтобы попрактиковаться и визуализировать любые уравнения.
Следующая статья будет посвящена квадратным уравнениям и всем мощным вещам, с которыми вы можете работать 🙂
Каковы 4 основных правила решения уравнения?
У нас есть 4 способа решения одношаговых уравнений: Сложение, вычитание, умножение и деление . Если мы прибавим одно и то же число к обеим частям уравнения, обе стороны останутся равными.
Если мы прибавим одно и то же число к обеим частям уравнения, обе стороны останутся равными.
|
Посмотреть полный ответ на mathplanet.com
Что такое правило 4 в математике?
Правило четырех гласит, что темы в математике должны быть представлены четырьмя способами: геометрически, численно, аналитически и словесно. Внедрение правила четырех помогает учащимся овладеть всеми четырьмя типами репрезентации, а также оказывает поддержку учащимся, которые учатся по-разному.
Запрос на удалениеЧто такое правило уравнений?
Главное правило алгебры — баланс. Уравнение имеет знак равенства, и все, что находится по одну сторону знака равенства, должно равняться тому, что находится по другую сторону знака равенства. Имея это в виду, мы можем делать с уравнением все, что захотим, до тех пор, пока мы сохраняем баланс по обе стороны от знака равенства.
|
Посмотреть полный ответ на сайте Study.com
Какие существуют четыре типа уравнений?
Различные типы уравнений
- Линейное уравнение.
- Радикальное уравнение.
- Экспоненциальное уравнение.
- Рациональное уравнение.
|
Посмотреть полный ответ на byjus.com
Как решить 4 квадратных уравнения?
Решение квадратных уравнений
- Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
- Фактор.
- Установить каждый коэффициент равным нулю.
- Решите каждое из этих уравнений.
- Проверьте, вставив свой ответ в исходное уравнение.
|
Просмотреть полный ответ на Cliffsnotes.com
Основы алгебры — Решение основных уравнений — Краткий обзор!
youtube.com/embed/kWOTmyoaWJg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Как называется уравнение с 4 членами?
Многочлен из четырех членов, известный как четырехчлен, можно разложить на множители, сгруппировав его в два двучлена, которые являются многочленами из двух членов. 92+k y=a(x−h)2+k. Запрос на удаление
|
Посмотреть полный ответ на albert.io
Каковы 4 состояния вещества химических уравнений?
Этими состояниями являются:
- Твердое, обозначенное символом (s)
- Жидкое, обозначенное символом (l)
- Газообразное, обозначенное символом (g)
- Водное, то есть растворенное в воде, и обозначенное символом (водный)
|
Посмотреть полный ответ на Studypug. com
com
Каковы 3 метода решения уравнений?
Для решения систем уравнений используются три метода: построение графика, замена и исключение. Чтобы решить систему с помощью графика, вы просто рисуете заданные уравнения и находите точку (точки), где они все пересекаются.
Запрос на удаление |
Посмотреть полный ответ на mathnasium.com
Какое правило важно при решении уравнений?
Следуйте обратному порядку операций — сначала ищите сложение/вычитание, затем умножение/деление, затем возведение в степень и скобки. Важное правило при решении уравнения — всегда делать с одной стороной знака равенства то, что мы делаем с другой.
Запрос на удаление |
Посмотреть полный ответ на hood.edu
Каковы 3 правила математики?
Существует множество законов, определяющих порядок выполнения операций в арифметике и алгебре. Три наиболее широко обсуждаемых закона — это коммутативный, ассоциативный и распределительный законы. С годами люди обнаружили, что когда мы складываем или умножаем, порядок чисел не влияет на результат.
Три наиболее широко обсуждаемых закона — это коммутативный, ассоциативный и распределительный законы. С годами люди обнаружили, что когда мы складываем или умножаем, порядок чисел не влияет на результат.
|
Посмотреть полный ответ на whatcom.edu
Каковы основные математические правила?
Правила упорядочения в математике — BODMAS
- Скобки (части вычислений внутри скобок всегда идут первыми).
- Порядки (числа со степенями или квадратными корнями).
- Подразделение.
- Умножение.
- Дополнение.
- Вычитание.
|
Полный ответ см. на сайте skillsyouneed.com
В чем польза четырех правил?
«4 правила» (сложение, вычитание, умножение и деление) лежат в основе расчетов и решения задач. За прошедшие годы в школах был принят ряд методов обучения, и иногда бывает так, что опыт родителей не совпадает с опытом их детей.
|
Посмотреть полный ответ на blsschool.co.uk
Что такое правило кратности 4?
Правило делимости числа 4
Если последние две цифры числа делятся на 4, то это число кратно 4 и полностью делится на 4. Пример: возьмем число 2308. Рассмотрим две последние цифры, т. е. 08. Поскольку 08 делится на 4, исходное число 2308 также делится на 4.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Каковы 4 основных типа материи?
- Материя определяется как все, что занимает пространство и имеет массу, и это все вокруг нас. …
- Твердые тела, жидкости и газы — это три состояния вещества, обычно встречающиеся на Земле (рис. 1.6). …
- Четвертое состояние вещества, плазма, естественным образом встречается в недрах звезд.
|
Посмотреть полный ответ на openstax. org
org
Каковы 4 характеристики материи?
(b) Характеристики материи:
- Материя состоит из мельчайших частиц.
- Частицы вещества притягиваются друг к другу.
- Частицы вещества имеют промежутки между ними.
- Частицы вещества постоянно движутся.
|
Посмотреть полный ответ на toppr.com
Каковы 4 свойства состояния вещества?
Четыре основных состояния материи — твердое, жидкое, газообразное и плазменное, но есть и другие, такие как конденсат Бозе-Эйнштейна и кристаллы времени, созданные руками человека. Перейти к: Твердые тела, жидкости и газы.
Запрос на удаление |
Посмотреть полный ответ на сайте livecience.com
Может ли квадратное уравнение иметь 4 решения?
Но уравнение в квадратной форме является более общим объектом, и мы не можем обязательно сказать, что оно имеет не более двух решений. ax4+bx2+c=0, и это уравнение имеет не более четырех решений (а на самом деле ровно четыре комплексных решения, как вы узнаете позже).
ax4+bx2+c=0, и это уравнение имеет не более четырех решений (а на самом деле ровно четыре комплексных решения, как вы узнаете позже).
|
Посмотреть полный ответ на math.stackexchange.com
Каковы 4 ключевые особенности квадратного числа?
В квадратичном графе есть много ключевых особенностей, таких как нули (х-пересечения, также известные как корни), у-пересечение, ось симметрии и вершина.
Запрос на удаление |
Посмотреть полный ответ на prezi.com
Может ли квадратное уравнение иметь 4 корня?
Следовательно, квадратное уравнение не может иметь более двух корней.
Запрос на удаление |
Посмотреть полный ответ на toppr.com
Что такое уравнение 4 класс?
Что такое уравнение? Уравнение — это математическое предложение, в котором две равные стороны разделены знаком равенства.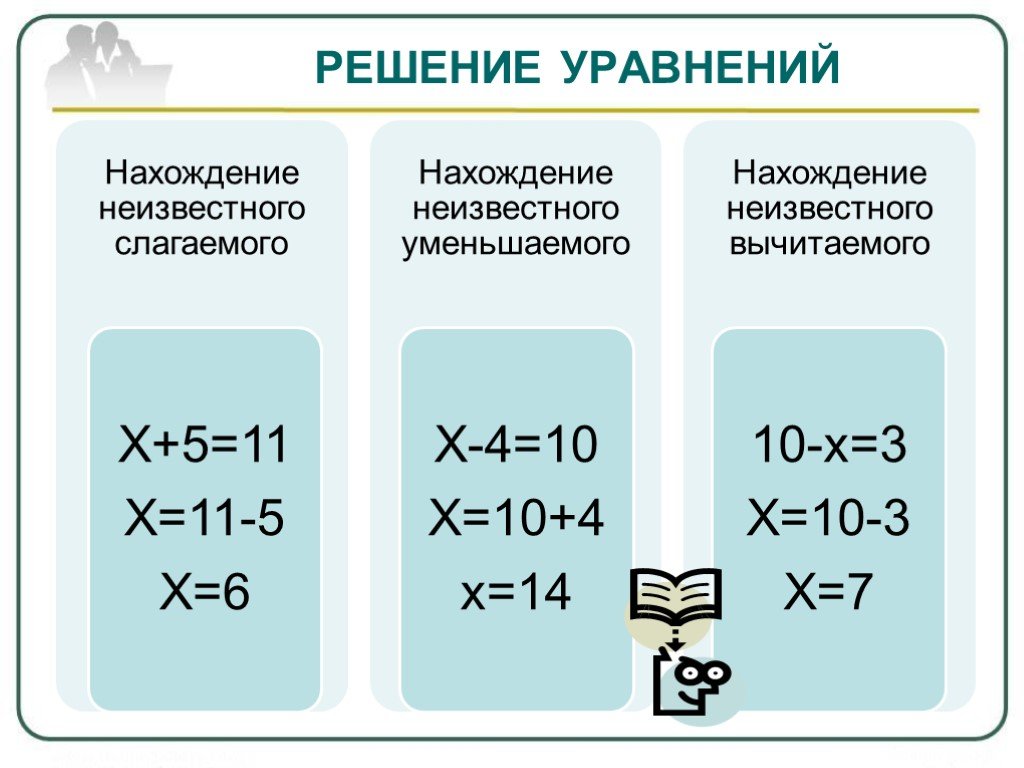

 Проводит беседу о том, что знают про уравнения, где встречаются в жизни равенства.
Проводит беседу о том, что знают про уравнения, где встречаются в жизни равенства. е. составлять план действий с учетом конечного результата.
е. составлять план действий с учетом конечного результата.
 Предлагает оценить факт достижения цели урока: на все ли вопросы найдены ответы.
Предлагает оценить факт достижения цели урока: на все ли вопросы найдены ответы.

 Решают уравнения, устно говоря ответы
Решают уравнения, устно говоря ответы А в жизни мы
А в жизни мы
 Что для этого необходимо сделать?
Что для этого необходимо сделать?

 (25 слайд)
(25 слайд)
 (слайд 24)
(слайд 24)