4*. В пространстве расположен параллелограмм ABCD и произвольный четырехугольник… Геометрия Зив Б.Г. 10 класс. Контрольные работы 5. Вариант 4
4*. В пространстве расположен параллелограмм ABCD и произвольный четырехугольник… Геометрия Зив Б.Г. 10 класс. Контрольные работы 5. Вариант 4 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
4*.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
1. Точки А, С, М и Р лежат в плоскости а, а точка B ¢ α (рис. 66). Постройте… Геометрия 10 класс Зив Б.Г. Контрольные работы. Вариант 1
1. Точки А, С, М и Р лежат в плоскости а, а точка B ¢ α (рис. 66). Постройте точку пересечения прямой МР с плоскостью АВС. (Подробнее…)
ГДЗГеометрияЗив Б. Г.10 класс
3*.
В указанной выше пирамиде найдите угол между гранями ВМС и DMC. Геометрия 10 класс Зив Б.Г. Контрольные работы 4. Вариант 2
3*. В указанной выше пирамиде найдите угол между гранями ВМС и DMC.
ГДЗГеометрияЗив Б. Г.10 класс
Решите пожалуйста Дополнительное задание а) б) в) г)
(Подробнее…)
ГДЗЭкзамены
Помогите определить перевод. Lesson 13. № 4. ГДЗ Английский язык 4 класс Верещагина.
Read the words and guess their meaning.
sandals [‘sændəlz], hospital [‘hɒspɪtl], Canada [‘kænədə], rock- (Подробнее…)
ГДЗАнглийский язык4 классВерещагина И.Н.
Задание 2. 3a Reading Skills. Spotlight. Английский язык. 10 класс. О.В. Афанасьева ГДЗ
Какие заголовки подходят, а какой нет? Как указать правильно?
ГДЗАнглийский языкSpotlightАфанасьева О. В.
10 класс
что значит произвольный четырехугольник — Знания.site
Последние вопросы
Математика
5 минут назад
Яка з нерівностей є правильною, якщо х=-3? а) -7-х<2; б) 3,5 +х >5;в) х-2,3>7;г)х+4,1<-10; д)11-х<3.Математика
10 минут назад
Помогите пожалуйста !!!Надо очень срочно.Математика
10 минут назад
ПОМОГИТЕ ПОЖАЛУСТАААААААААААААААААААААААААААААААААААААААМатематика
15 минут назад
Помогите решить :((((Математика
15 минут назад
одну сторону прямоугольника уменьшили на 30% ,а другую увеличили на 80% .
как изменилась прямоугольники и на сколько процентов? решите плиз . СРОЧНО НУЖНО Математика
15 минут назад
ОЧЕНЬЬЬЬЬЬЬЬ СРОЧНОООООООО!!!!!!!!!! ПОМОГИТЕ ПОЖАЛУСТАМатематика
40 минут назад
Помогите с дзМатематика
44 минут назад
На диаграмме показаны результаты проверочный работы, проведённой в 6 «Б» классе. По вертикальной оси указано числоМатематика
1 час назад
решить. 2 x- 9cos x+4=0
помогите решить Тригонометрическое уравнениеМатематика
2 часа назад
Алгебра помогите пожалуйста-
Математика
2 часа назад
Помогите, пожалуйста, с алгеброй!!!!
как изменилась прямоугольники и на сколько процентов? решите плиз . СРОЧНО НУЖНО 
2 x- 9cos x+4=0
помогите решить Тригонометрическое уравнениеВсе предметы
English
United States
Polski
Polska
Bahasa Indonesia
Indonesia
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Português
Brasil
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
многомерное исчисление — Преобразование произвольного четырехугольника в единичный квадрат
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 1к раз
$\begingroup$
В этом ответе Педро Химено он предложил следующее преобразование для отображения точек любого произвольного четырехугольника в единичный квадрат
$$\pmatrix{x’\\y’} = > \pmatrix{u_x&v_x&w_x\\u_y&v_y&w_y}\pmatrix{x\\y\\xy}$$
$$x’=u_xx+v_xy+w_xxy\\ y’=u_yx+v_yy+w_yxy$$
Он преобразует единичный квадрат способом, контролируемым векторами $u=(u_x,u_y), v=(v_x,v_y), w=(w_x,w_y)$ следующим образом:
Геометрическая интерпретация u, v, w (извините, я не могу размещать изображения)
Однако я хотел бы сделать наоборот.
Мне нужно интегрировать произвольный четырехугольник, и я хотел бы определить свой интеграл на единичном квадрате, а затем отобразить координаты единичного квадрата на исходном четырехугольнике.
Матрица, предложенная Педро, однако, необратима, и я не уверен, что мне нужна псевдообратная матрица.
Как получить обратное преобразование?
- многомерное исчисление
- аналитическая геометрия
$\endgroup$
5
$\begingroup$
Одна из возможных стратегий.
Параметризуйте каждую сторону вашего (выпуклого) четырехугольника $ABCD$, используя
$A + t(B-A)$,
$D + t(C-D)$,
$A + s(D-A)$,
$B + s(C-B)$
с $P = (s,t)$ в единичном квадрате. Чтобы отобразить $P$ в четырехугольник, соедините точки, определенные $t$ на $AB$ и $DC$, точки, определенные $s$ на двух других ребрах, и найдите пересечение этих двух отрезков.
$\endgroup$
3
$\begingroup$
Этот ответ преобразует единичный квадрат в произвольный четырехугольник . Если вам нужен только прямоугольник, вы можете просто использовать: $$\begin{pmatrix}x’ \\ y’ \end{pmatrix} = \begin{pmatrix} u_x & v_x \\ u_y & v_y \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix }$$ которое обратимо в предположении, что $u$ и $v$ линейно независимы. Это предполагает, что один из углов вашего прямоугольника находится в начале координат, в противном случае вам также потребуется выполнить перевод.
$\endgroup$
1
$\begingroup$
Возможно, вы могли бы использовать матрицу перспективной проекции в однородных координатах.
Для обращения этой операции достаточно найти обратную матрицу преобразования.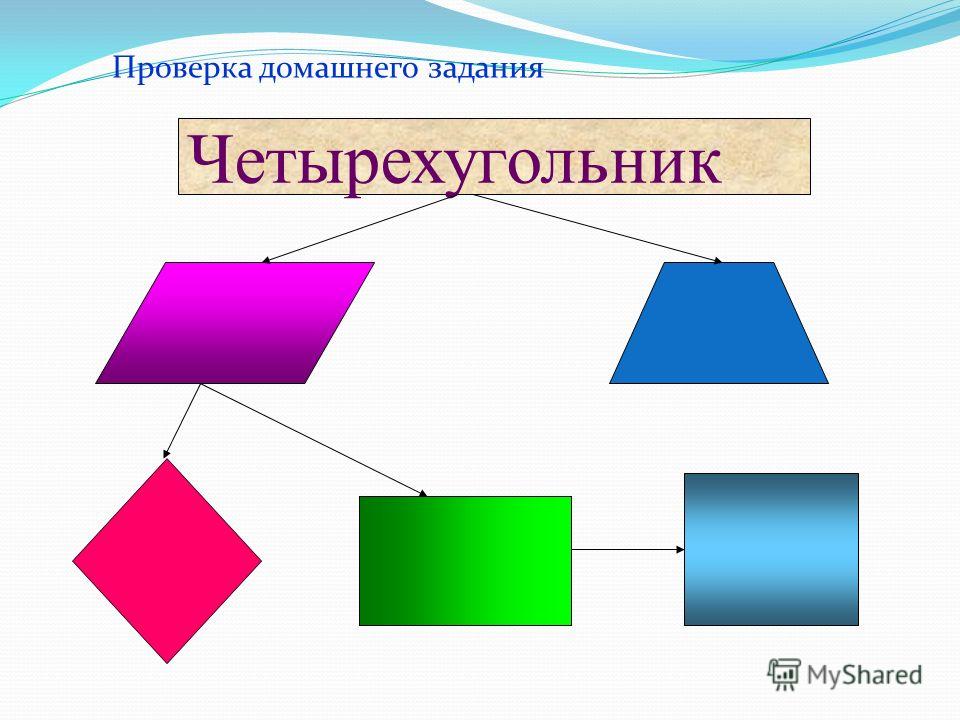
Это будет работать во многих случаях. Однако он не соответствует ни одному четырехугольнику . Во-первых, я думаю, что четырехугольник все же должен быть выпуклым.
(Источник изображения: Wikimedia Commons, Автор: Д.стебани, Лицензия: CC BY-SA 4.0)
$\endgroup$
Середины четырехугольника образуют параллелограмм
2 февраля 2012 г.
Возьмите любой четырехугольник, например этот
, затем отметьте середины и соедините их.
Похоже, мы построили параллелограмм, не так ли? Удивительный факт заключается в том, что независимо от того, с какого четырехугольника вы начнете, вы всегда получите параллелограмм, если соедините середины .
Такой результат кажется случайным и удивительным. Вы должны нарисовать несколько четырехугольников только для того, чтобы убедиться, что это даже кажется верным. Как вы собираетесь это доказывать в целом?
Несколько студентов недавно спросили меня, почему это так.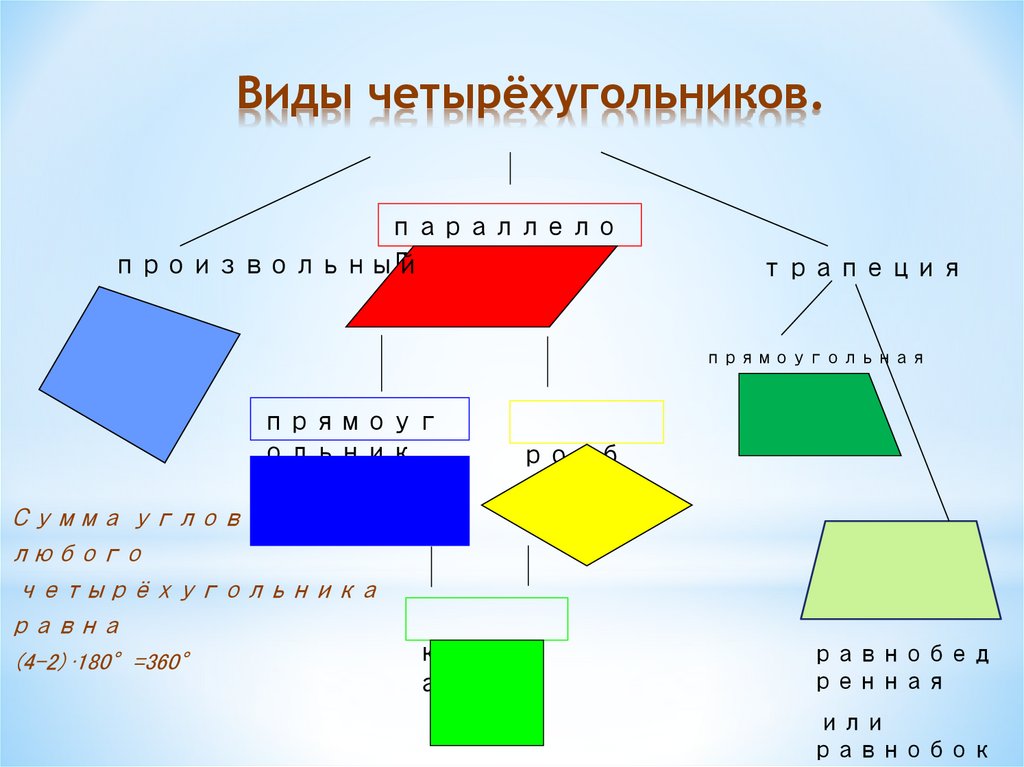
Я совершенно забыл, как подходить к проблеме, поэтому у меня появилась возможность поэкспериментировать с ней по-новому. У меня было две идеи, как начать. Первый заключался в том, чтобы нарисовать еще одну линию на чертеже и посмотреть, поможет ли это.
Не кажется ли вам, что синяя линия параллельна оранжевым линиям над и под ней? Если бы это было правдой, это дало бы нам мощный путь вперед. Это также предвещает мою вторую идею: попробуйте соединить середины треугольника, а не четырехугольника.
Вот как это выглядит для произвольного треугольника.
Похоже, что соединение этих средних точек образует четыре конгруэнтных треугольника, не так ли? На самом деле, это не так уж сложно доказать. Зная это, мы можем видеть, что любая пара соприкасающихся треугольников образует параллелограмм. Это означает, что две синие линии ниже параллельны.
Итак, мы можем заключить:
Лемма. Синие линии выше параллельны.
Теорема.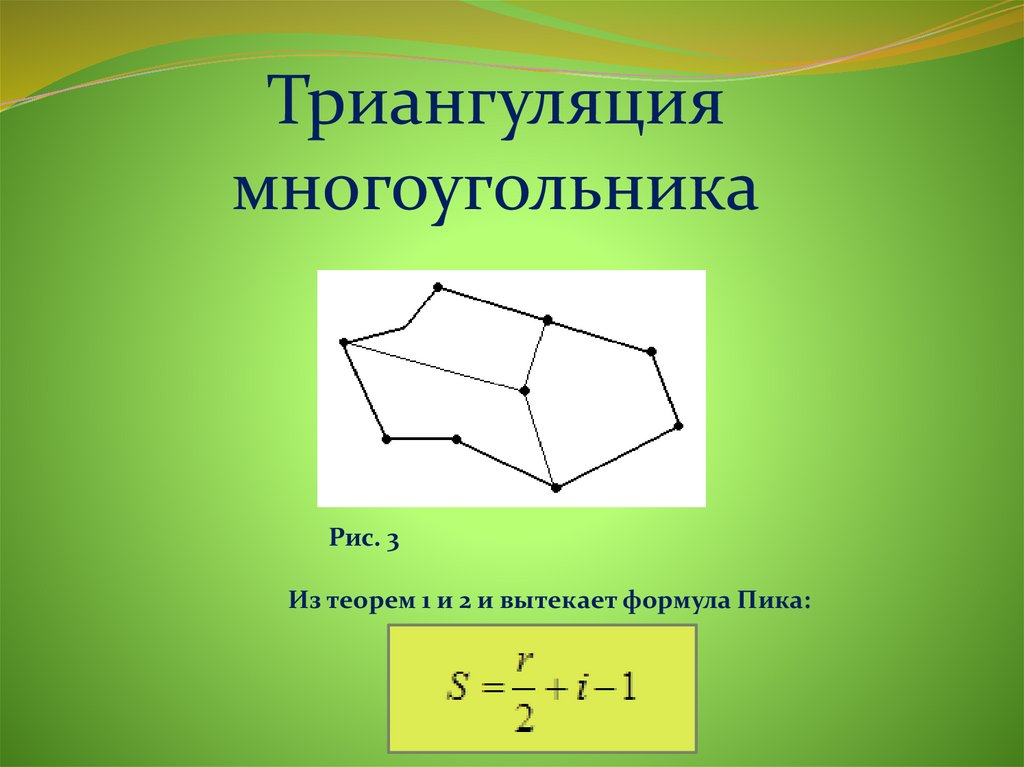
Оранжевая фигура выше — параллелограмм.
Доказательство. Снова нарисуйте эту синюю линию.
У нас та же ситуация, что и на треугольной картинке сверху! Видишь?
Давайте сотрем нижнюю половину изображения и сделаем параллельные линии одного цвета:
Видите, что синие линии параллельны? Верхняя линия соединяет середины треугольника, так что мы можем применить нашу лемму!
Но то же самое относится и к нижней, и к средней линии! Таким образом, все синие линии ниже должны быть параллельны.
То же верно и для оранжевых линий по тому же принципу.
Итак, четырехугольник все-таки параллелограмм!
Я нашел довольно симпатичный аргумент: рисование линий из противоположных углов превращает непостижимое в (надеюсь) очевидное. Это решение от путаницы к ясности для меня является одним из величайших удовольствий при занятиях математикой.
Следующий вопрос заключается в том, можем ли мы сломать результат, изменив первоначальную настройку.