Темы проектов по алгебре — Презентации по проектной деятельности
Учащихся 7-11 классов, интересующихся математикой, безусловно, привлекут темы проектов по алгебре, выбрав которые, школьники получат возможность проводить исследования на темы: статистика, иррациональные числа, интеграл и т.д.
Темы проектов по математике для 5 и 6 кл. на ЭТОЙ СТРАНИЦЕ, по геометрии на ЭТОЙ СТРАНИЦЕ.
Содержание
Темы проектов по алгебре
7 классАликвотные дроби в нашей жизни
Анализ учебных достижений учащихся моего класса
В мире формул сокращённого умножения
Вклад Диофанта в развитие алгебры
Геометрическая алгебра и формулы сокращённого умножения
Графики вокруг нас
Если я буду жить в кредит
Жизнь и деятельность среднеазиатского учёного Аль-Хорезми
Задачи на переливание жидкости
Использование процентных расчетов в жизнедеятельности современного человека
История возникновения степени числа
Сборник заданий на тему «Одночлены и многочлены»
История развития вычислительной техники
Линейная функция в механике
Мой край через математические понятия
Парабола и её применение
Практическое применение знаний о функциях
Среднее арифметическое, размах, мода
Статистическое исследование на тему «Какие профессии выбирают выпускники моей школы?»
Увлекательные способы умножения чисел
Всё о рациональных дробях
Женский след в математике
Извлечение квадратных корней без калькулятора
Интересные факты о действительных числах
История возникновения алгебры
Математическая обработка экспериментальных данных
История иррациональных чисел
Математические модели реальных процессов в природе и обществе
Множества и операции над ними
Неравенства с параметром
Нестандартные приёмы решения квадратных уравнений
Обратная пропорциональность в математике и в жизни
Парабола, гипербола, эллипс
Представление дроби в виде суммы дробей
Преобразование двойных радикалов
Приближённые вычисления в жизненных ситуациях
Системы уравнений в задачах экономики
Степень с целым показателем
Текстовые задачи на работу и производительность
Франсуа Виет и его теорема
Функции у=х^-1 и у=х^-2 и их свойства
Этот простой, сложный параметр
Арифметическая прогрессия на клетчатой бумаге
Биография параболы
Возможности метода Крамера
Геометрическая вероятность
Движение по замкнутой трассе: как решать задачи?
Загадки арифметической прогрессии
Как решать квадратные неравенства?
Квадратный трёхчлен и его приложения
Комбинаторика в примерах
Метод математической индукции как эффективный метод доказательства гипотез
Невероятное вероятно
Нетрадиционные методы решения иррациональных уравнений
Почему парабола такого вида?
Прогрессии в нашей жизни
Пушкин в зеркале математики
Реальная математика: насколько это реально?
Системы неравенств в ОГЭ
Теория вероятностей в игре
Фракталы и математический хаос
Функции в природе и технике
Тематика исследовательских проектов по алгебре и началам анализа
10 классЗамечательные кривые: спирали и розы
Значения степенных и показательных выражений
Кредит, вклады и оптимизация в задачах
Кредиты и проценты в жизни современного человека
Кривые второго порядка
Малая и большая теорема Ферма
Математические методы в экономике
Математический цветник: розы Гвидо Гранди
Матричная алгебра в экономике
Обратные тригонометрические функции
Производная в физике и технике
Решение задач с использованием тригонометрических функций
Производная и её геометрический смысл
Решение логических задач с помощью кругов Эйлера
Рисуем графиками функций
Способы решения тригонометрических неравенств
Текстовые задачи и производная: в чём связь?
Тригонометрические выражения и их преобразования
Тригонометрическое домино
Тригонометрия в окружающем мире
Уравнения в целых числах
Экономический смысл производной
Бином Ньютона
В поисках логарифма
Интеграл и его история
Использование элементов математической логики при решении задач
История возникновения логарифмов
Комплексные числа и их роль в математике
Логарифмическая линейка
Логарифмы в музыке и поэзии
Логарифмическая спираль Архимеда
Логарифмы и банковское дело
Метод Гауса для СЛАУ
Методы доказательства неравенств
От показательных уравнений к показательным неравенствам
Показательная функция и её применение в жизни, науке и технике
Практическое применение интеграла
Природа и история мнимых чисел
Решение неравенств с параметром методом областей
Текстовые задачи из ЕГЭ
Теория вероятностей или искусство предположений
Финансовая математика
Функционально-графические методы при решении уравнений
СКАЧАТЬ ТЕМЫ ПРОЕКТОВ ПО АЛГЕБРЕ 7-11 КЛАССЫ
Темы, входящие в ГИА (ОГЭ) по курсу математики
Темы, входящие в ГИА (ОГЭ) по курсу математики- Числа и вычисления
- Натуральные числа
- Десятичная система счисления.
 Римская нумерация
Римская нумерация - Арифметические действия над натуральными числами
- Степень с натуральным показателем
- Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители
- Признаки делимости на 2, 3, 5, 9, 10
- Наибольший общий делитель и наименьшее общее кратное
- Деление с остатком
- Десятичная система счисления.
- Дроби
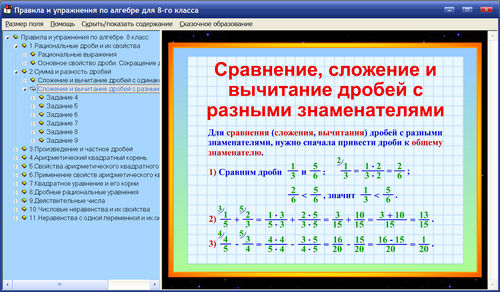
- Обыкновенная дробь, основное свойство дроби. Сравнение дробей
- Арифметические действия с обыкновенными дробями
- Нахождение части от целого и целого по его части
- Десятичная дробь, сравнение десятичных дробей
- Арифметические действия с десятичными дробями
- Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной
- Целые числа
- Модуль (абсолютная величина) числа
- Сравнение рациональных чисел
- Арифметические действия с рациональными числами
- Степень с целым показателем
- Числовые выражения, порядок действий в них, использование скобок.
 Законы арифметических действий
Законы арифметических действий
- Действительные числа
- Квадратный корень из числа
- Корень третьей степени
- Нахождение приближенного значения корня с помощью калькулятора
- Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби
- Сравнение действительных чисел
- Измерения, приближения, оценки
- Единицы измерения длины, площади, объема, массы, времени, скорости
- Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире
- Представление зависимости между величинами в виде формул
- Проценты. Нахождение процента от величины и величины по ее проценту
- Отношение, выражение отношения в процентах
- Пропорция. Пропорциональная и обратно пропорциональная зависимости
- Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя – степени десяти в записи числа
- Натуральные числа
- Алгебраические выражения
- Буквенные выражения (выражения с переменными)
- Буквенные выражения.
 Числовое значение буквенного выражения
Числовое значение буквенного выражения - Допустимые значения переменных, входящих в алгебраические выражения
- Подстановка выражений вместо переменных
- Равенство буквенных выражений, тождество. Преобразования выражений
- Свойства степени с целым показателем
- Буквенные выражения.
- Многочлены
- Многочлен. Сложение, вычитание, умножение многочленов
- Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов
- Разложение многочлена на множители
- Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители
- Степень и корень многочлена с одной переменной
- Алгебраическая дробь
- Алгебраическая дробь. Сокращение дробей
- Действия с алгебраическими дробями
- Рациональные выражения и их преобразования
- Свойства квадратных корней и их применение в вычислениях
- Буквенные выражения (выражения с переменными)
- Уравнения и неравенства
- Уравнения
- Уравнение с одной переменной, корень уравнения
- Линейное уравнение
- Квадратное уравнение, формула корней квадратного уравнения
- Решение рациональных уравнений
- Примеры решения уравнений высших степеней.
 Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители
Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители - Уравнение с двумя переменными; решение уравнения с двумя переменными
- Система уравнений; решение системы
- Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением
- Уравнение с несколькими переменными
- Решение простейших нелинейных систем
- Неравенства
- Числовые неравенства и их свойства
- Неравенство с одной переменной. Решение неравенства
- Линейные неравенства с одной переменной
- Системы линейных неравенств
- Квадратные неравенства
- Текстовые задачи
- Решение текстовых задач арифметическим способом
- Решение текстовых задач алгебраическим способом
- Числовые последовательности
- Понятие последовательности
- Арифметическая и геометрическая прогрессии
- Арифметическая прогрессия.
 Формула общего члена арифметической прогрессии
Формула общего члена арифметической прогрессии - Формула суммы первых нескольких членов арифметической прогрессии
- Геометрическая прогрессия. Формула общего члена геометрической прогрессии
- Формула суммы первых нескольких членов геометрической прогрессии
- Сложные проценты
- Арифметическая прогрессия.
- Уравнения
- Функции и графики
- Числовые функции
- Понятие функции. Область определения функции. Способы задания функции
- График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства, чтение графиков функций
- Примеры графических зависимостей, отражающих реальные процессы
- Функция, описывающая прямую пропорциональную зависимость, ее график
- Линейная функция, ее график, геометрический смысл коэффициентов
- Функция, описывающая обратно пропорциональную зависимость, ее график. Гипербола
- Квадратичная функция, ее график. Парабола. Координаты вершины параболы, ось симметрии
- График функции
- График функции
- График функции
- Использование графиков функций для решения уравнений и систем
- Числовые функции
- Координаты на прямой и плоскости
- Координатная прямая
- Изображение чисел точками координатной прямой
- Геометрический смысл модуля
- Числовые промежутки: интервал, отрезок, луч
- Декартовы координаты на плоскости
- Декартовы координаты на плоскости; координаты точки
- Координаты середины отрезка
- Формула расстояния между двумя точками плоскости
- Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых
- Уравнение окружности
- Графическая интерпретация уравнений с двумя переменными и их систем
- Графическая интерпретация неравенств с двумя переменными и их систем
- Координатная прямая
- Геометрия
- Геометрические фигуры и их свойства.
 Измерение геометрических величин
Измерение геометрических величин- Начальные понятия геометрии
- Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства
- Прямая. Параллельность и перпендикулярность прямых
- Отрезок. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой
- Понятие о геометрическом месте точек
- Треугольник
- Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений
- Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника
- Прямоугольный треугольник. Теорема Пифагора
- Признаки равенства треугольников
- Неравенство треугольника
- Сумма углов треугольника. Внешние углы треугольника
- Зависимость между величинами сторон и углов треугольника
- Теорема Фалеса
- Подобие треугольников, коэффициент подобия.
 Признаки подобия треугольников
Признаки подобия треугольников - Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от до
- Решение прямоугольных треугольников. Основное тригонометрическое тождество. Теорема косинусов и теорема синусов
- Многоугольники
- Параллелограмм, его свойства и признаки
- Прямоугольник, квадрат, ромб, их свойства и признаки
- Трапеция, средняя линия трапеции; равнобедренная трапеция
- Сумма углов выпуклого многоугольника
- Правильные многоугольники
- Окружность и круг
- Центральный, вписанный угол; величина вписанного угла
- Взаимное расположение прямой и окружности
- Касательная и секущая к окружности; равенство отрезков касательных, проведенных из одной точки
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Вписанные и описанные окружности правильного многоугольника
- Измерение геометрических величин
- Длина отрезка, длина ломаной, периметр многоугольника.
 Расстояние от точки до прямой
Расстояние от точки до прямой - Длина окружности
- Градусная мера угла, соответствие между величиной угла и длиной дуги окружности
- Площадь прямоугольника
- Площадь параллелограмма
- Площадь трапеции
- Площадь треугольника
- Площадь круга, площадь сектора
- Формулы объема прямоугольного параллелепипеда, куба, шара
- Длина отрезка, длина ломаной, периметр многоугольника.
- Векторы на плоскости
- Вектор, длина (модуль) вектора
- Равенство векторов
- Операции над векторами (сумма векторов, умножение вектора на число)
- Угол между векторами
- Коллинеарные векторы, разложение вектора по двум неколлинеарным векторам
- Координаты вектора
- Скалярное произведение векторов
- Геометрические фигуры и их свойства.
- Статистика и теория вероятностей
- Описательная статистика
- Представление данных в виде таблиц, диаграмм, графиков
- Средние результатов измерений
- Вероятность
- Частота события, вероятность
- Равновозможные события и подсчет их вероятности
- Представление о геометрической вероятности
- Комбинаторика
- Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения
- Описательная статистика
Алгебра 1 — Что такое Алгебра 1? Задачи, темы, формулы
Алгебра 1 или элементарная алгебра включает в себя традиционные темы, изучаемые в курсе современной элементарной алгебры.
Алгебра помогает представить различные ситуации или проблемы в виде математических выражений. Понятия, относящиеся к алгебре 1 или элементарной алгебре, включают в себя переменные, оценку выражений и уравнений, свойства равенств и неравенств, решение алгебраических уравнений и линейных уравнений с одной или двумя переменными и так далее.
| 1. | Что такое Алгебра 1? |
| 2. | Алгебра 1 Темы |
| 3. | Законы алгебры 1 |
| 4. | Алгебра 1 Формулы |
| 5. | Разница между Алгеброй 1 и Алгеброй 2 |
6. | Алгебра 1: советы и рекомендации |
| 7. | Часто задаваемые вопросы по алгебре 1 |
Что такое Алгебра 1?
Алгебра 1 состоит из общих/основных понятий алгебры. Он вводит оценочные уравнения и неравенства, действительные числа и их свойства, которые включают аддитивные и мультипликативные тождества, обратные операции, а также дистрибутивные и коммутативные свойства. В алгебре 1 мы также познакомимся с концепцией многочленов, а также включим немного геометрии для вычисления площади, объема и периметров фигур с использованием алгебраических выражений вместо чисел.
Алгебра 1 или элементарная алгебра связана с решением алгебраических выражений для правильного ответа. В алгебре 1 простые переменные, такие как x, y, представлены в виде уравнения. В зависимости от степени переменной уравнения можно разделить на различные типы, а именно линейные уравнения, квадратные уравнения, кубические уравнения и так далее. Линейные уравнения имеют вид ax + b = c, ax + by + c = 0, ax + by + cz + d = 0. Элементарная алгебра, основанная на степени переменных, разветвляется на квадратные уравнения и полиномы. Общая форма представления квадратного уравнения: ax 2 + bx + c = 0, а для полиномиального уравнения это ax n + bx n-1 + cx n-2 + …..k = 0.
Линейные уравнения имеют вид ax + b = c, ax + by + c = 0, ax + by + cz + d = 0. Элементарная алгебра, основанная на степени переменных, разветвляется на квадратные уравнения и полиномы. Общая форма представления квадратного уравнения: ax 2 + bx + c = 0, а для полиномиального уравнения это ax n + bx n-1 + cx n-2 + …..k = 0.
Правила для различных свойств в алгебре 1 можно лучше понять, как показано ниже,
Алгебра 1 Темы
Алгебра разделена на многочисленные темы, чтобы помочь в детальном изучении. Алгебра 1 разделена на 12 глав, и каждая глава разделена на несколько уроков. Эти 12 глав в Алгебре 1 даны как:
Глава 1. Вещественные числа и операции с ними
- Целые числа
- Дроби
- Экспоненты
- ПЕМДАС
Глава 2. Линейные уравнения и неравенства
- Переменные выражения
- Линейные уравнения
- Соотношение
- Пропорция
Глава 3. Введение в функции
Введение в функции
- Что такое функции?
- Полиномиальные функции
- Визуализация функций с помощью графиков
- Арифметические и геометрические прогрессии
Глава 4: Линии графика
- Декартова система
- Графики линейных уравнений
- Перпендикулярная линия
- Параллельные линии
Глава 5. Решение линейных систем
- Решение линейных систем методом замены
- Решение линейных систем методом перекрестного умножения
- Решатель системы уравнений
- Решения линейного уравнения
Глава 6. Многочлены и их операции
- Многочлены
- Полиномиальные выражения
- Полином энной степени
- Умножение многочленов
Глава 7. Факторинг и решение методом факторизации
- Что такое фактор?
- Методы факторинга
- Факторизация алгебраических выражений
- Факторизация квадратных уравнений
Глава 8. Экспоненты и экспоненциальные функции
Экспоненты и экспоненциальные функции
- Экспоненты
- Экспоненциальные функции
- Иррациональные Показатели
- Операции с экспоненциальными членами
Глава 9. Рациональные выражения и уравнения
- Рациональные числа
- Рациональная функция
- Нецелочисленные рациональные показатели
- Упрощение рациональных выражений
Глава 10. Подкоренные выражения и уравнения
- Сурды
- Квадрат и квадратный корень
- Рационализация
- Рационализировать знаменатель
Глава 11. Решение квадратных уравнений и построение графиков парабол
- Квадратные и квадратные корни
- Квадратичная формула
- График квадратичной функции
- Комплексные числа и комплексные решения
Глава 12: Анализ данных и вероятность
- Обработка данных
- Вероятность и статистика
- Категориальные данные
- Перестановки и комбинации
Законы алгебры 1
Основными законами алгебры являются ассоциативные, коммутативные и дистрибутивные законы, представленные в таблице ниже:
| Имя свойства | Определение | Пример |
|---|---|---|
| Коммутативное право на добавление | (а + б) = (б + а). | Если (4x + 3x) = 7x, то (3x + 4x) = 7x |
| Коммутативный закон для умножения | (а × б) = (б × а). Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат. | Если (2x × 4) = 8x, то (4 × 2x) = 8x |
| Ассоциативный закон Для Дополнения | а + (б + в) = (а + б) + в. Эта группировка слагаемых не влияет на сумму. | Если 3у + (4у + 5у) = (3у + 9у) = 12у, тогда (3у + 4у) + 5у = 7у + 5у = 12у |
| Ассоциативный закон умножения | а × (б × с) = б × (а × с). Эта группа факторов не влияет на продукт. | Если 3a × (2b × 5c) = 3a × (10bc) = 30abc, то (3a × 2b) × 5c = 6ab × 5ac = 30abc |
| Дистрибутивное право Дополнение | а × (б + с) = (а × б) + (а × с). | Если 4x × (3y + 2y) = (4x × 5y) = 20xy, то (4x × 3y) + (4x × 2y) = 12xy + 8xy = 20xy |
Распределительный закон для вычитания | а × (б — с) = (а × б) — (а × с). Вычитание двух чисел и последующее их умножение на третье дает тот же результат, что и умножение двух чисел по отдельности на третье с последующим вычитанием полученного результата. | Если 4x × (3y — 2y) = (4x × y) = 4xy, то (4x × 3y) — (4x × 2y) = 12xy — 8xy = 4xy |
Алгебра 1 Формулы
Вот список формул, которые очень полезны при решении задач по алгебре 1.
- Algebraic identities:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
( a + b)(a — b) = a 2 — b 2
(x + a)(x + b) = x 2 + x(a + b) + ab
(a + b) 3 = а 3 + 3а 2 б + 3аб 2 + б 3
(A- B) 3 = A 3 — 3A 2 B + 3AB 2 — B 3
A 3 + B 3 = (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B) (A + B). а 2 — ab + b 2 )
а 2 — ab + b 2 )
а 3 — b 3 = (a — b)(a 2 + ab + b 2 ) 1 90 а + b 8 2 = а 2 + b 2 + c 2 + 2ab + 2bc + 2ca - Свойства показателей:
a m . а н = а m + n
a m /a n = a m — n
(a m ) n = an
(ab) м = a м . б м
а 0 = 1
а -м = 1/а м - Формулы линейных уравнений:
Общая форма: ax + by = c
Форма пересечения наклона: y = mx + b
Двухточечная форма: y−y 1 =m(x−x 1 )
Форма пересечения: x/a + y/ б = 1
Вертикальная линия через (p, q): x = p
Горизонтальная линия через (p, q): y = q - Формулы квадратных уравнений:
Стандартная форма квадратного уравнения: ax 2 + bx + c = 0
Вершинная форма квадратного уравнения: a (x — h) 2 + k = 0
Квадратная формула: Корни квадратного уравнения ax 2 + bx + c = 0 определяются как x = [-b ± √(b² — 4ac)]/2a.
- Формулы арифметической последовательности:
n -й член, a n =a 1 +(n−1)d
Сумма = n/2 [2a + (n — 1) d] (OR) n/2 [a 1 + a п ] - Формулы геометрической последовательности:
n -й -й член геометрической прогрессии равен a n = a · r n — 1 .
Сумма n слагаемых, S n = a (r n – 1)/(r–1)
Сумма бесконечных слагаемых, S = a/(1–r) - Формула средней скорости изменения: [f(b) — f(a)] / (b — a)
- Формула сложных процентов: A = P (1 + r / n) n t
- Статистические формулы:
Среднее значение = (Сумма наблюдений) ÷ (Общее количество наблюдений)
Среднее значение сгруппированных данных = Σf i /N
Медиана, когда n нечетно: [(n + 1)/2] срок; Медиана, когда n четное: [(n/2) th term + ((n/2) + 1) th term]/2
Диапазон = Максимум — Минимум
Межквартильный диапазон = Верхний квартиль — Нижний квартиль
Разница между Алгеброй 1 и Алгеброй 2
Алгебру 1 и Алгебру 2 можно отличить по сложности и использованию алгебраических выражений. В следующей таблице поясняются важные различия между алгеброй 1 и алгеброй 2.
В следующей таблице поясняются важные различия между алгеброй 1 и алгеброй 2.
| Алгебра 1 | Алгебра 2 |
|---|---|
| Алгебра 1 знакомит вас с общими понятиями алгебры. Вы узнаете о переменных, функциях и самых важных понятиях во всей алгебре. | Алгебра 2 гораздо более продвинутая. Это также гораздо более разнообразно: вы узнаете обо всем, от логарифмов и комплексных чисел до неявных функций и коник до фундаментальной теоремы алгебры. |
| Алгебра 1 помогает учащимся получить базовые знания по темам алгебры. | Алгебра 2 повышает сложность и понимание тем, изучаемых в алгебре 1. |
| На этом уроке учащиеся узнают, как манипулировать показателями степени или полиномами, записывать их в более простой форме и т. д. | В нем учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные техники. |
| Алгебра 1 сосредоточена на решении уравнений и неравенств | Алгебра 2 концентрируется на дополнительных типах уравнений, таких как экспоненциальные и логарифмические уравнения. |
| Алгебра 1 необходима для понимания алгебры 2. | Алгебра 2 необходима для понимания концепций исчисления. |
Советы и рекомендации по алгебре 1
- Чтобы понять Алгебру 1, нам нужно быть знакомым с предалгебраическими темами, такими как целые числа, одношаговые уравнения, многошаговые уравнения, неравенства и уравнения, графики и функции, проценты, вероятности, введение в геометрию и, правильно треугольники. Как только мы пройдем переподготовку, мы сможем перейти к алгебре 1.
- При умножении двух рациональных выражений в алгебре всегда есть риск получить ложные решения или посторонние решения, поэтому будьте осторожны с расчетной частью.
- Мы можем складывать многочлены, просто добавляя одинаковые члены, чтобы объединить два многочлена в один.

Важные замечания по алгебре 1:
- Свойство неравенства сложения: прибавление одного и того же числа к каждой стороне неравенства дает эквивалентное неравенство.
- Отрицательные показатели: обратные величины положительных показателей в экспоненциальных функциях.
- Свойство отношения степеней: оно говорит нам, что при делении степеней с одинаковым основанием нам просто нужно вычесть степени.
- Константы имеют мономиальную степень 0.
☛ Похожие темы:
- Математический калькулятор
- Калькулятор алгебры
- Калькулятор алгебраических формул
Задачи по алгебре 1
Пример 1: Используя законы и свойства алгебры 1, оцените выражение (4 × (x + 2)), где x = 5.
Решение:
Дано x = 5. x в 4 × (x + 2), мы получаем, 4 × (5 + 2) = 4 × 7 = 28,
Ответ: 28
Пример 2: Решите данное выражение для значения x, 4 + 3 = x.

Решение:Дано, 4 + 3 = х. Мы просто сделаем сложение данного выражения и получим значение x. 4 + 3 равно 7 или x = 4 + 3 = 7.
Ответ: Следовательно, значение x равно 7.
Пример 3: Решите данное выражение, используя правила алгебры 1 для значения y, 2y + 16 = 32,
Решение:
Дано, 2y + 16 = 32. Решим уравнение относительно y.
2y = 32 — 16 дает 2y = 16, y = 8.
Ответ: Следовательно, значение y равно 8.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по алгебре 1
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по алгебре 1
Чему вы научитесь на уроке алгебры 1?
Алгебра 1 или Элементарная алгебра включает основные традиционные темы, изучаемые в курсе современной элементарной алгебры. Основные арифметические операции включают числа наряду с математическими операциями, такими как +, -, x, ÷. В то время как алгебра включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения.
Основные арифметические операции включают числа наряду с математическими операциями, такими как +, -, x, ÷. В то время как алгебра включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения.
Что считается алгеброй 1?
Алгебра 1 состоит из общих понятий алгебры. Он вводит оценочные уравнения и неравенства, действительные числа и их свойства, которые включают аддитивные и мультипликативные тождества, обратные операции, а также дистрибутивные и коммутативные свойства.
В чем разница между алгеброй 1 и алгеброй 2?
Разницу между Алгеброй 1 и Алгеброй 2 можно понять, используя следующие пункты:
- Алгебра 1 помогает учащимся получить базовые знания по темам алгебры, в то время как алгебра 2 повышает сложность и понимание тем, изучаемых в алгебре 1.
- В алгебре 1 учащиеся учатся работать с показателями степени или многочленами и записывать их в более простых формах и т.
 д., в то время как в алгебре 2 учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные приемы.
д., в то время как в алгебре 2 учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные приемы. - Алгебра 1 сосредоточена на решении уравнений и неравенств. Но алгебра 2 концентрируется на дополнительных типах уравнений, таких как показательные и логарифмические уравнения.
- Алгебра 1 необходима для понимания алгебры 2, тогда как алгебра 2 необходима для понимания понятий, возникающих в исчислении.
Что такое стандартная форма в алгебре 1?
Стандартная форма в Алгебре 1 — это форма записи данного математического понятия, такого как уравнение, число или выражение, в форме, которая следует определенным правилам.
Как быстро выучить алгебру 1?
Понятия алгебры 1 можно освоить, следуя определенным инструкциям. Ключевые моменты, приведенные ниже, помогут вам обеспечить тщательное графическое изображение элементарной алгебры.
- Сосредоточьтесь на основных арифметических понятиях.

- Помните правило PEMDAS.
- Научитесь четко различать роли переменных, констант, показателей степени, отрицательных и положительных чисел.
- Проведите тщательную ревизию формул.
- Работа над практическими задачами.
Какой класс алгебры 1?
Алгебра 1 или элементарная алгебра — это первый математический предмет, который вы должны пройти в средней школе. В этой части алгебры мы изучаем действительные числа, изучаем решение, написание и графическое отображение линейных уравнений. Также в Алгебру 1.9 включены многочлены, а также квадратные уравнения и функции.0003
Какие темы рассматриваются в Алгебре 1?
Темы, затронутые в алгебре 1, разделены на разные главы. Эти главы можно разделить на следующие категории:
- Вещественные числа и их операции
- Линейные уравнения и неравенства
- Введение в функции
- Графические линии
- Решение линейных систем
- Многочлены и их операции
- Факторинг и решение методом факторинга
- Экспоненты и экспоненциальные функции
- Рациональные выражения и уравнения
- Основные выражения и уравнения
- Решение квадратных уравнений и построение графиков парабол
- Анализ данных и вероятность
Алгебра 1 или 2 сложнее?
Алгебра 1 является структурным элементом алгебры 2. Алгебра 2 — более высокий и сложный курс, поэтому алгебра 2 намного сложнее, чем алгебра 1.
Алгебра 2 — более высокий и сложный курс, поэтому алгебра 2 намного сложнее, чем алгебра 1.
Что такое Алгебра 1 Уравнения?
Уравнения алгебры 1 включают только линейные уравнения и квадратные уравнения. Кубические уравнения и другие уравнения более высокого порядка НЕ являются частью алгебры 1.
Что вы изучаете в первую очередь на уроке алгебры 1?
Первое, чему учащиеся изучают алгебру 1, — это вещественные числа и операции с ними.
Что необходимо для лучшего понимания алгебры 1?
Для понимания Алгебры 1 полезно знать основы арифметики, целые числа, дроби, десятичные дроби, проценты, отношения, пропорции, вероятности, введение в геометрию и прямоугольные треугольники.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по алгебре
Темы и понятия по алгебре 1
Ищете все темы по алгебре 1?
Алгебра 1 — это математический курс, изучающий, как использовать переменные, числа и математические операции для решения задач.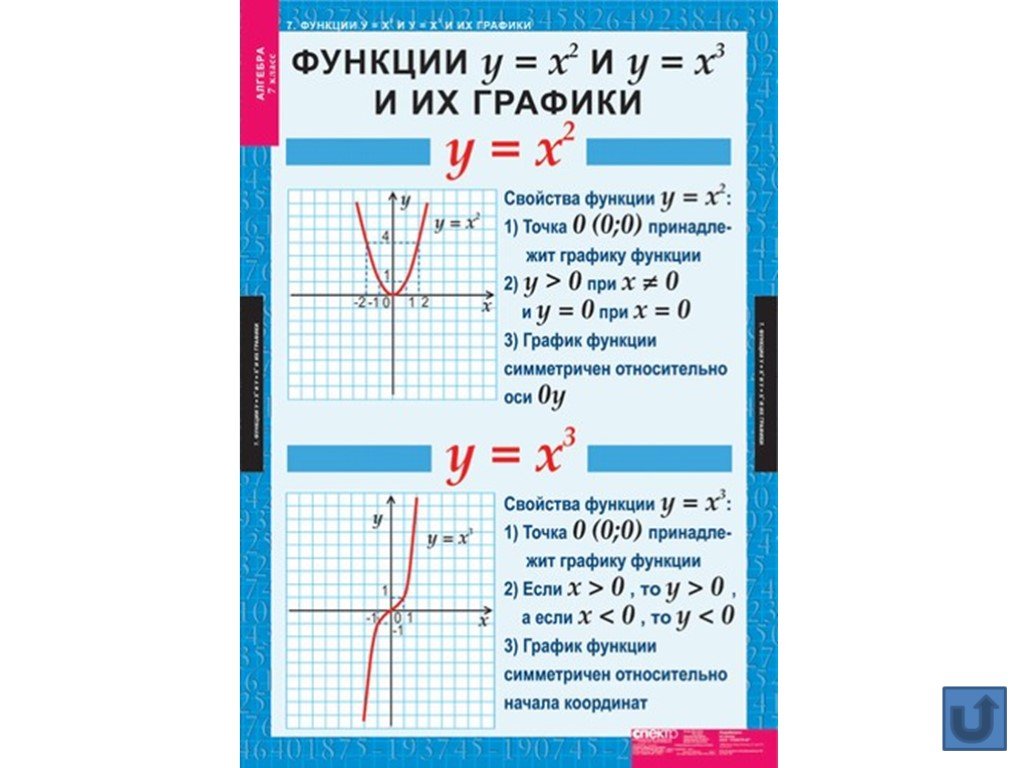 Ниже вы найдете список всех тем Алгебры 1, краткое изложение типичного курса Алгебры 1 и обсуждение того, что делает Алгебру 1 уникальной.
Ниже вы найдете список всех тем Алгебры 1, краткое изложение типичного курса Алгебры 1 и обсуждение того, что делает Алгебру 1 уникальной.
Что мы просматриваем
Какие темы есть в Алгебре 1?
Приведенная ниже последовательность тем, понятий и навыков охватывает все наиболее часто изучаемые темы Алгебры 1. В качестве бонуса многие темы содержат прямые ссылки на практические задачи Альберта по алгебре 1 .
Введение в выражения
Экспоненты и радикалы
Полиномы
Линейные уравнения
Линейные неравенства
Введение в функции
Последовательности и экспоненциальные функции
Квадратные уравнения
Описательная статистика
- Представление данных
- Статистические данные с одной переменной
- Вариация
- Стандартное отклонение
- Двухсторонние таблицы
- Диаграммы рассеяния
Что такое Алгебра 1?
Алгебра 1 — это математический курс средней школы, в котором изучается, как использовать буквы (называемые переменными) и числа с математическими символами для решения задач.
Алгебра 1 обычно включает в себя вычисление выражений, написание уравнений, построение графиков функций, решение квадратичных уравнений и понимание неравенств. Алгебра 1 фокусируется на множестве различных типов функций, таких как линейные, квадратичные и кубические, — все они представлены в традиционных «обозначениях функций», а также графически на координатной плоскости.
Учащиеся, изучающие Алгебру 1, как правило, формируют концептуальное понимание и получают процедурное беглое понимание понятий, которые необходимы для более сложных математических предметов, таких как геометрия и исчисление. Абстрагирование ситуаций из реальной жизни в математические модели (выражения, уравнения, функции) является ключевой частью успеха в Алгебре 1.
Какой класс алгебры 1?
Алгебра 1 обычно преподается в конце средней школы или в начале старшей школы .
В Соединенных Штатах 9-й класс (первый год обучения), по-видимому, является наиболее распространенным классом, в котором учащиеся изучают алгебру 1. Некоторые средние школы также предлагают алгебру для учащихся 1-10 классов.
Некоторые средние школы также предлагают алгебру для учащихся 1-10 классов.
С другой стороны, многие средние школы предлагают учащимся курс алгебры 1 уже в 8-м классе или даже в 7-м классе для более продвинутых учеников по математике.
Алгебра 1 сложная?
Невозможно точно сказать, насколько легкая или сложная Алгебра 1 для каждого отдельного ученика. Учащиеся, хорошо разбирающиеся в математических темах средней школы (дроби, десятичные числа, отношения, проценты, отрицательные числа), должны найти курс Алгебры 1 относительно доступным.
Тем не менее, для многих студентов Алгебра 1 будет довольно сложной задачей.
В Алгебре 1 есть десятки быстро меняющихся тем и навыков, которые дополняют друг друга по мере прохождения учебного плана. Наличие сильных арифметических навыков является невероятно важной предпосылкой для обретения уверенности в курсе Алгебры 1. Если учащийся начинает немного отставать от конкретной концепции, вполне вероятно, что эти неправильные представления довольно быстро перерастут в дальнейшую путаницу.
Если вы ищете возможность попрактиковаться в учебе на самых разных уровнях сложности, подумайте о том, чтобы попробовать практические вопросы Albert’s Algebra 1.
В чем разница между алгеброй 1 и 2?
Как следует из названий, между Алгеброй 1 и Алгеброй 2 есть много общего. Оба курса интенсивно работают с переменными и функциями, а также с использованием математических операций для нахождения неизвестных величин.
Студенты, изучающие Алгебру 1, как правило, должны овладеть широким спектром методов решения линейных и квадратных уравнений. Алгебра 1 фокусируется на том, чтобы «делать одно и то же с обеими частями уравнения» для решения уравнений. Используя линзу линейных и квадратичных функций, Алгебра 1 подталкивает учащихся к поиску корней (решений) с использованием нескольких методов (включая квадратичную формулу), построению графиков отношений функций на координатной плоскости и преобразованию между различными формами квадратичных уравнений.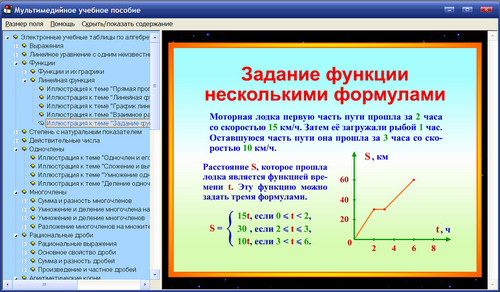
Алгебра 2 является расширенным развитием идей Алгебры 1. Учащиеся Алгебры 2 знакомятся с гораздо более широким набором функций, включая логарифмы, радикалы и рациональные функции. Тригонометрические функции часто становятся важной новой областью изучения алгебры 2, когда учащиеся начинают изучать единичный круг. Алгебра 2 обычно включает в себя решения с действительными и комплексными числами, включая арифметику с мнимыми числами, а также конические сечения, такие как гиперболы, параболы и эллипсы. Основные параболы, которые студенты привыкли считать не имеющими решений на курсе Алгебра 1, на самом деле имеют два «воображаемых» решения на курсе Алгебра 2.
В общем, Алгебра 2 включает в себя более широкий и сложный набор типов функций, чем те, которые рассматриваются в темах Алгебры 1.
Заинтересованы в школьной лицензии?
Пригласите Альберта в свою школу и предоставьте всем учителям лучший в мире банк вопросов для:
➜ SAT® и ACT®
➜ AP®
➜ ELA, математика, естествознание и социальные науки
➜ Государственные оценки
Варианты для учителей, школы, районы.

 Римская нумерация
Римская нумерация Законы арифметических действий
Законы арифметических действий Числовое значение буквенного выражения
Числовое значение буквенного выражения Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители
Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители Формула общего члена арифметической прогрессии
Формула общего члена арифметической прогрессии Измерение геометрических величин
Измерение геометрических величин Признаки подобия треугольников
Признаки подобия треугольников Расстояние от точки до прямой
Расстояние от точки до прямой Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат.
Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат. Сложение двух чисел и последующее их умножение на третье дает тот же результат, что и умножение двух чисел по отдельности на третье с последующим сложением полученного результата.
Сложение двух чисел и последующее их умножение на третье дает тот же результат, что и умножение двух чисел по отдельности на третье с последующим сложением полученного результата.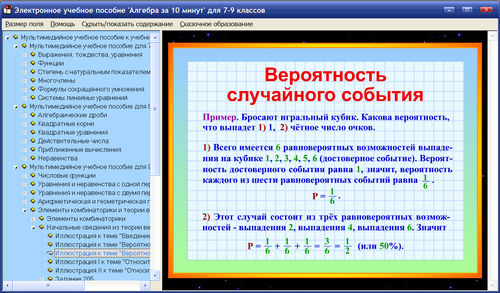 а 2 — ab + b 2 )
а 2 — ab + b 2 ) 

 д., в то время как в алгебре 2 учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные приемы.
д., в то время как в алгебре 2 учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные приемы.