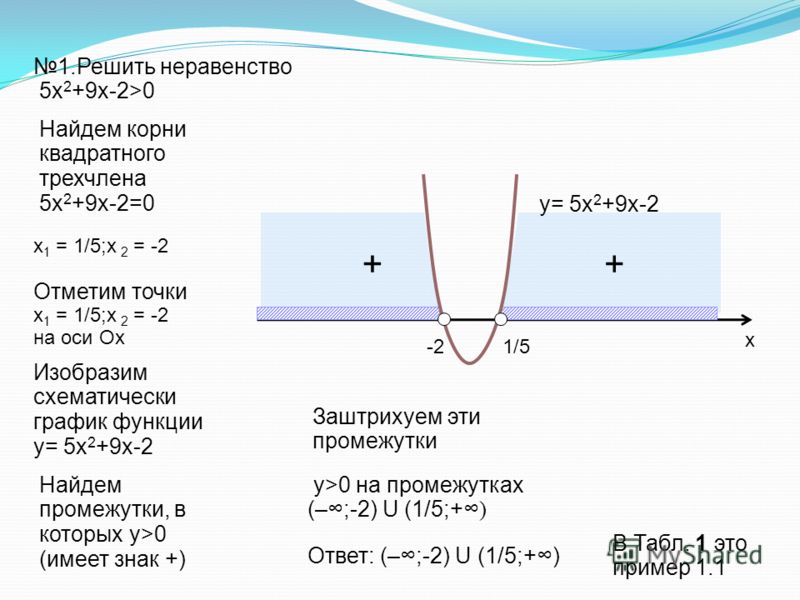
2+n-72)=1/(n+9)§2. Иррациональные неравенства — ЗФТШ, МФТИ
Иррациональными называют неравенства, в которых переменные входят под знаком корня. Так как корень чётной степени существует только у неотрицательных чисел, то при решении неравенств, содержащих такое выражение, прежде всего удобно найти ОДЗ.
Сначала приведём уже выведенные в 10-ом классе условия равносильности для уравнений (в частности, для того, чтобы была понятна приведённая уже здесь нумерация условий равносильности для корней `(`УР К`)`):
ПУНКТ 2. НЕРАВЕНСТВО ВИДА `sqrt(f(x)) <= sqrt(g(x))`
Рассмотрим неравенство вида `sqrt(f(x)) <= sqrt(g(x))`.
Докажем, что
1. Если `sqrt(f(x)) <= sqrt(g(x))`, то `f(x) >= 0`, `g(x) >= 0` и `f(x) <= g(x)`, т. е. `x` является решением системы неравенств fx≤gx,fx≥0.\left\{\begin{array}{l}f\left(x\right)\leq g\left(x\right),\\f\left(x\right)\geq0.
\end{array}\right.
2. Если `x` является решением системы неравенств fx≤gx,fx≥0,\left\{\begin{array}{l}f\left(x\right)\leq g\left(x\right),\\f\left(x\right)\geq0,\end{array}\right.
то `f(x) >= 0`, `g(x) >= 0`, `sqrt(f(x))` и `sqrt(g(x))` существуют.
При этом `f(x) <= g(x) iff sqrt(f(x)) <= sqrt(g(x))`, т. е. неравенство выполнено.
ПУНКТ 3. НЕРАВЕНСТВА ВИДА `(sqrtf(x) — g(x))/(h(x))>=0` `(<= 0)`
Роль сопряжённых выражений
Обычно при решении неравенств, имеющих ОДЗ, надо сначала найти ОДЗ. При нахождении ОДЗ такого сложного неравенства, как `(sqrtf(x) — g(x))/(h(x)) >= 0`, учителя и школьники обычно решают систему fx≥0,hx≠0\left\{\begin{array}{l}f\left(x\right)\geq0,\\h\left(x\right)\neq0\end{array}\right.. Затем школьники иногда ошибочно опускают знаменатель и решают неравенство `sqrt(f(x)) — g(x) >= 0`.
Мы в ОДЗ дроби не будем записывать условие `h(x) != 0`, и тем более не будем тратить время и силы на решение этого неравенства.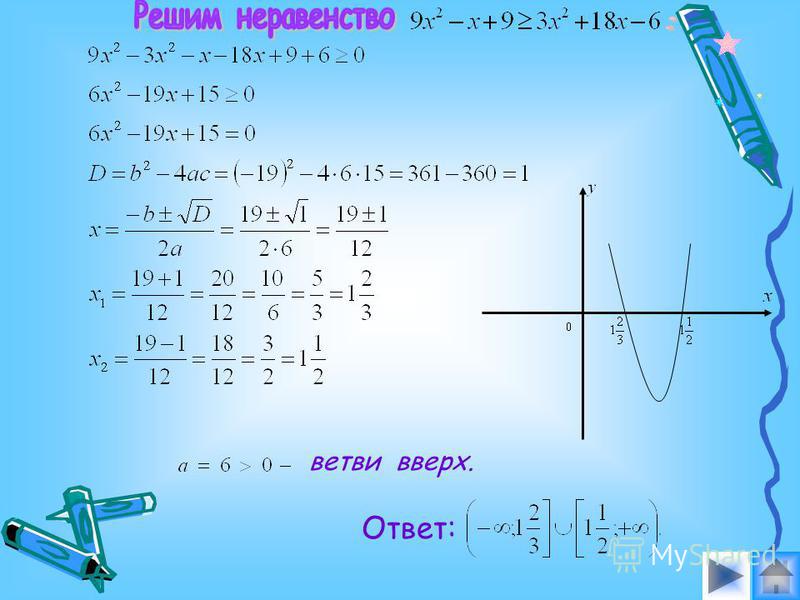
Оправдывается это тем, что в дальнейшем используем только классический метод интервалов для рациональных функций, в котором условие `h(x) != 0` автоматически выполняется, ибо нули знаменателя наносятся на числовую ось кружочками («дырками»), т. е. ограничение `h(x) != 0` заложено в самом методе. Это ОДЗ, которое отличается от привычного школьного (с `h(x) != 0`), по предложению самих учителей, будем обозначать не ОДЗ, а ОДЗ*. Итак, например, для неравенств вида `(sqrtf(x) — g(x))/(h(x)) >= 0` будем искать ОДЗ*: `f(x) >= 0`.
Рассмотрим довольно часто встречающееся неравенство вида
В методической литературе предлагается рассмотреть две системы в зависимости от знака знаменателя `h(x)`, причём в каждой есть неравенство с корнем. Энтузиазм решать задачу при этом быстро «испаряется».
Мы поступим иначе: рассмотрим два случая в зависимости не от знака `h(x)`, а от знака `g(x)`, и неравенств с корнем решать не придётся.
2 (x)`
имеет тот же знак, что и `(sqrt(f(x)) — g(x))` в ОДЗ. Новое выражение уже не содержит радикалов (корней), а выражение `(sqrt(f(x)) + g(x))` называется сопряжённым для `(sqrt(f(x)) — g(x))` выражением. Отсюда следует важное правило П К1:
Теперь используем эти свойства для решения довольно сложных неравенств вида
Сейчас мы покажем, что можно обойтись, хотя и двумя случаями, но без корней.
Рассмотрим, для определённости, неравенство `(sqrt(f(x)) — g(x))/(h(x)) >= 0`.
1. Мы уже заметили, что, если `g(x) < 0`, то числитель положителен в ОДЗ. Но тогда fx-gxhx≥0⇔ОДЗhx>0\dfrac{\sqrt{f\left(x\right)}-g\left(x\right)}{h\left(x\right)}\geq0\overset{\mathrm{ОДЗ}}\Leftrightarrow h\left(x\right)>0.
2. Если же `g(x) >= 0`, то разность может менять знак в зависимости от значений `x`, но сумма `sqrt(f(x)) + g(x)` всегда неотрицательна в ОДЗ, и умножение обеих частей неравенства на это сопряжённое выражение приводит к равносильному неравенству, т.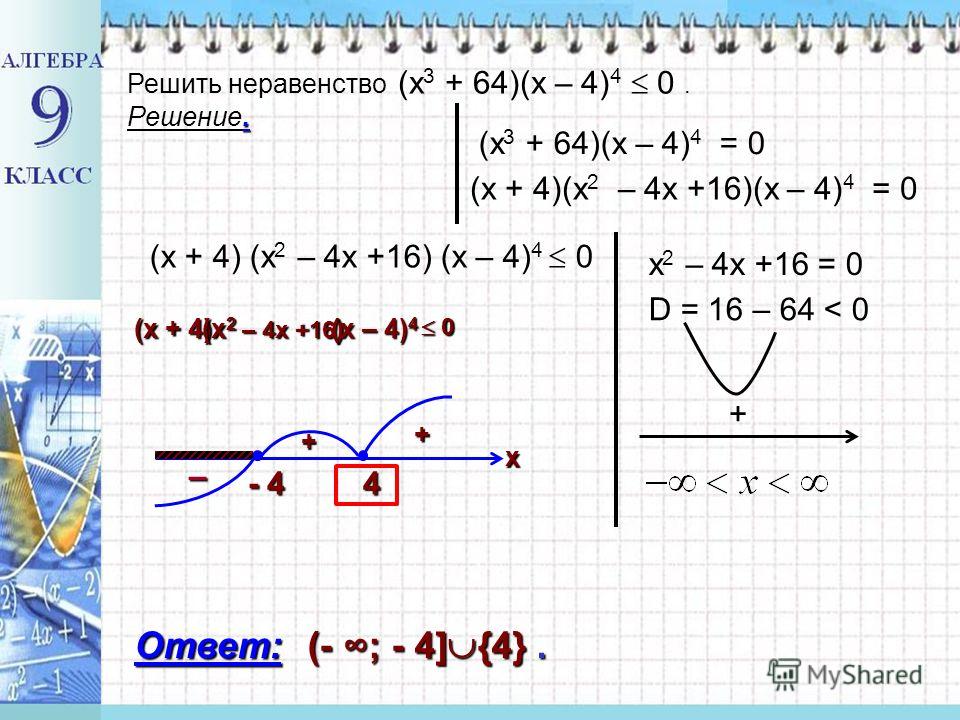
2\left(x\right)}{h\left(x\right)}\geq0.
Для неравенства другого знака меняется лишь знак неравенства. Объединив оба условия, получаем новое замечательное условие равносильности в ОДЗ:
Найденные в результате исследования совокупности (УР К9) решения следует сравнить с ОДЗ.
ПУНКТ 4. НЕРАВЕНСТВО ВИДА `(sqrt(f(x)) — sqrt(g(x)))/(h(x)) >= 0 (<= 0)`.
Роль сопряжённых выражений
Теперь рассмотрим неравенство вида `(sqrt(f(x)) — sqrt(g(x)))/(h(x)) >= 0 (<= 0)`.
На вид довольно сложное неравенство. Разность `sqrt(f(x)) — sqrt(g(x))` где-то на числовой оси положительна, где-то отрицательна, но сумма корней `sqrt(f(x)) + sqrt(g(x))` всегда неотрицательна в ОДЗ. Поэтому умножение обеих частей неравенства на это сопряжённое выражение приводит к равносильному в ОДЗ неравенству, и имеет место условие равносильности в ОДЗ
или полное условие равносильности, включающее ОДЗ:
Отсюда, в частности, следует полезное правило (П К2):
ПУНКТ 5.
НЕСТРОГОЕ НЕРАВЕНСТВО `(sqrt(f(x)))/(g(x)) >= 0 (<= 0)`.
Воспользуемся определением нестрогого неравенства и особенностью иррациональных неравенств.
Получим
2(3х+7)-8(х+3)
Новые вопросы
Ответы
2(3x+7)-8(x+3)≤0
6x+14-8x-24≤0
-2x≤24-14
-2x≤10
x≥-5
2(3x+7)-8(x+3)≤0
6x+14-8x-24≤0
-2x≤24-14
-2x≤10
x≥-5
Похожие вопросы
Найдите 2 числа, если известно что первое меньше чем второе на 3, а второе больше за первое в три раза…
Найдите 2 числа, если известно что первое меньше чем второе на 3, а второе больше за первое в три раза…
Помогите решить, пожалуйста!Решите уравнения:
1) √х=10
2) √х=0,09
3) √х-2=8
4) √х+5=17.
..
Дкажите тождество : (x3+5×2)-(2x-1)-(x2+3x)+(5x-x3)=4×2+1…
Укажите две последовательные десятичные дроби с одним знаком после запятой между которыми заключино число √28…
(корень из 27 +корень из 12+ 5) *(1-корень из 3)…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
ИнформатикаЭкономика
Музыка
Право
Французский язык
Немецкий язык
МХК
Психология
3-82.
Решение линейных неравенствПроцедура решения линейных неравенств с одной переменной похоже на решение основных уравнений. (См. Решение уравнений.)
Нам нужно быть осторожными с смыслом равенства при умножении или делении на отрицательные числа.
Ниже приведены несколько примеров решения уравнений, содержащих неравенства.
Пример 1
Решить x + 2
Ответить
Нам нужно вычесть `2` из обеих частей неравенства.
`х+2<4`
`x<4-2`
`x<2`
График этого решения выглядит следующим образом:
12340-1xОткрыть изображение на новой страницеПример 2
Решите `x/2>4`
Ответить
Нам нужно умножить обе части неравенства на `2`.
`x/2>4`
`x>4xx2`
`х>8`
Вот график этого решения:
123456780xОткрыть изображение на новой страницеПример 3
Решите 2 x ≤ 4
Ответить
Нам нужно разделить обе части неравенства на `2`.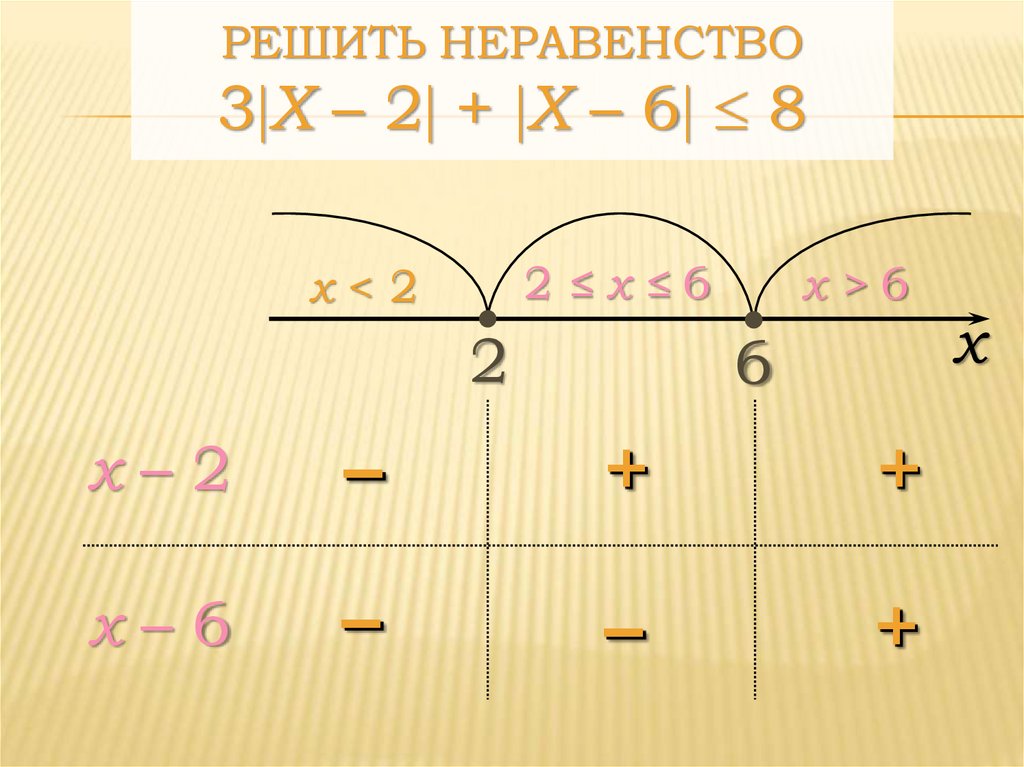
`2x<=4`
`x<=4/2`
`х<=2`
Вот график этого решения:
1230-1-2xОткрыть изображение на новой страницеПример 4
Решите неравенство 3 − 2 x ≥ 15
Ответить
В этом примере нам нужно вычесть 3 с обеих сторон; затем разделите обе части на «-2» (не забывая изменить направление неравенства).
`3-2x>=15`
`-2x>=15-3`
`-2x>=12`
`x<=12/(-2)`
`х<=-6`
Вот график этого решения:
10-1-2-3-4-5-6-7-8xОткрыть изображение на новой странице(Обратите внимание на изменение смысла из-за деления на отрицательный номер)
Проверить: Всегда проверяйте свое решение, и вы можете быть уверены, что ваш ответ правильный.
В этом случае любое число меньше `-6` должно «работать» в исходном уравнении, а любое число больше `-6` не должно работать.
Возьмем `x = -10` (удобное число меньше, чем `-6`)
LHS `= 3 − 2 (-10) = 3 + 20 = 23`.
Это больше, чем «15», так что это правда.
Это больше, чем «15», так что это правда.Теперь возьмем `x = 0` (удобное число больше, чем `-6`)
LHS `= 3 − 2(0) = 3`. Это НЕ больше, чем «15», на что мы и надеялись.
Таким образом, мы можем быть уверены, что наш ответ правильный.
Пример 5
Решите неравенство `3/2(1-x)>1/4-x`
Ответить
`3/2(1-x)>1/4-x`
Умножение обеих частей на 4 дает нам:
`6(1-x)>1-4x`
`6-6x>1-4x`
`-6x+4x>1-6`
`-2x> -5`
`x<5/2`
(Обратите внимание на изменение смысла в последней строке из-за деления на отрицательный количество).
Вот график этого решения:
12340-1-2-3-4×2.5Открыть изображение на новой страницеПроверить: Принимая x = 0 (что должно работать):
`»LHS» = 3/2(1 − 0) = 3/2`
`»RHS» = 1/4`
ВЕРНО, что `3/2 > 1/4`, так что это хорошо.
Теперь возьмем x = 3 (удобное число больше 5/2, которое не должно работать):
`»LHS» = 3/2(1 − 3) = -3`
`»RHS» = 1/4 − 3 = -2 3/4`
Это НЕ правда, что `-3 > -2 3/4` и поэтому `x=3` не работает, как мы надеялись.
Мы можем быть уверены, что наш ответ (`x<5/2`) правильный.
Пример 6
Решите −1 < 2 x + 3 < 6
Ответить
`- 1 < 2x + 3 < 6`
Вычтите «3» со всех трех сторон
`- 1 — 3 < 2x + 3 - 3 < 6 - 3`
`- 4 < 2x < 3`
Разделить все стороны на «2»
`-2 < x < 3/2`
График решения:
12340-1-2-3-4×1.5Открыть изображение на новой страницеПример 7
Решить 2 x < x − 4 ≤ 3 x + 8
Ответ
Другой способ решения более сложных неравенств с 3 членов (сторон) состоит в том, чтобы переписать неравенство в виде
`2x < x - 4` и `x — 4 ≤ 3x + 8`
Тогда, решив каждое из этих неравенств, получим:
Неравенство LHS:
`х < - 4`
Правая сторона неравенства:
`x — 4 ≤ 3x + 8`
`- 4 ≤ 2x + 8`
`- 12 ≤ 2x`
`x ≥ -6 `
Принимая во внимание, что окончательное решение должно удовлетворять неравенств, получаем:
`x < -4` и `x ≥ -6`
Эти две части выглядят как:
0-1-2-3-4-5-6-7xОткрыть изображение на новой страницеПри рассмотрении области, где пересекаются две части, мы получаем
`-6 ≤ x < -4`
Это окончательный график решения:
0-1-2-3-4-5-6-7xОткрыть изображение на новой страницеУпражнения
Решите следующие неравенства для x :
1.
Решите 3 − 3 x < − 1
Ответить
`3 — 3x < -1`
`- 3x < -4 `
`x> 4/3 ~~ 1.333…`
Вот график решения:
12340-1×1.33Открыть изображение на новой странице2. Решить −2( x + 4) > 1 − 5 х
Ответить
`-2(x + 4) > 1 — 5x`
`-2x — 8 > 1 — 5x `
`3x — 8 > 1`
`3x > 9`
`x > 3`
Граф решений:
12340-1xОткрыть изображение на новой странице3. Решить `x/5-5 >2/3(х+3)`
Ответить
`х/5-2>2/3(х+3)`
Умножить на 5:
`x-10>10/3(x+3)`
Умножить на 3:
`3x-30>10(x+3)`
`3x-30>10x+30`
`3x>10x+60`
`-7x>60`
`x<(-60)/7~~-8,57`
График решения:
-5-6-7-8-9-10-11x-8.
57Открыть изображение на новой странице4. Решить x − 1 < 2 x + 2 < 3 x + 1
Ответить
Нам нужно найти пересечение «истинных» значений.
`x — 1 < 2x + 2` и `2x + 2 < 3x + 1`
`x < 2x + 3` и `2x < 3x - 1`
`x > -3` и `x > 1`
Эти 2 неравенства на одной оси выглядят следующим образом:
1230-1-2-3-4xОткрыть изображение на новой страницеПересечение этих двух областей `x > 1`.
Всегда проверяйте свои ответы!
Вот окончательный график решения:
1230-1-2-3-4xОткрыть изображение на новой страницеIXL | Изучайте математику для 8-го класса
IXL | Изучайте математику в 8 классе.1
Факторы
2
Правила делимости
3
Основной или составной
4
простые множители
5
Наибольший общий делитель
6
Наименьший общий множитель
7
GCF и LCM: текстовые задачи
8
Коэффициенты сортировки числовых выражений
1
Целые числа на числовых линиях
2
Графические целые числа на горизонтальных и вертикальных числовых линиях
3
Абсолютное значение и противоположные целые числа
4
Сравнивать и упорядочивать целые числа
5
Целочисленные неравенства с абсолютными значениями
1
Правила сложения и вычитания целых чисел
2
Складывать и вычитать целые числа с помощью счетчиков
3
Складывать и вычитать целые числа
4
Сложение и вычитание трех или более целых чисел
5
Складывать и вычитать целые числа: текстовые задачи
6
Правила умножения и деления целых чисел
7
Умножать и делить целые числа
8
Вычислять числовые выражения, включающие целые числа
1
Понимание показателей
2
Оценить показатели
3
Решите уравнения с переменными показателями
4
Экспоненты с отрицательными основаниями
5
Показатели с десятичной и дробной базой
6
Понимание отрицательных показателей
7
Оценить отрицательные показатели
8
Оценить отрицательные и нулевые показатели
9
Умножение с показателями
10
Деление с показателями
11
Умножение и деление с показателями
12
Силовое правило
13
Оцените выражения, используя свойства экспонент
14
Определите эквивалентные выражения, включающие показатели I
15
Определите эквивалентные выражения, включающие показатели степени II
Контрольная точка: целочисленные показатели
1
Преобразование между стандартной и научной нотацией
2
Научное обозначение на калькуляторах
3
Сравните числа, записанные в экспоненциальном представлении.
4
Сложение и вычитание чисел, записанных в экспоненциальном представлении
5
Умножать числа, записанные в экспоненциальном представлении
6
Разделить числа, записанные в экспоненциальном представлении
Контрольная точка: научное обозначение
1
Квадратные корни полных квадратов
2
Оцените положительные квадратные корни
3
Положительные и отрицательные квадратные корни
4
Оцените положительные и отрицательные квадратные корни
5
Связь между квадратами и квадратными корнями
6
Решите уравнения, используя квадратные корни
7
Кубические корни положительных совершенных кубов
8
Кубические корни положительных и отрицательных совершенных кубов
9
Решение уравнений с использованием кубических корней
10
Оцените кубические корни
Контрольная точка: квадратные и кубические корни
1
Запишите дроби в меньших терминах
2
Наименьший общий знаменатель
3
Круглые десятичные и смешанные числа
4
Запишите повторяющуюся десятичную дробь
5
Преобразование между десятичными дробями и дробями или смешанными числами
6
Абсолютное значение рациональных чисел
7
Сравните рациональные числа
8
Расставь рациональные числа по порядку
1
Обратные и мультипликативные обратные
2
Складывать и вычитать рациональные числа
3
Сложение и вычитание рациональных чисел: текстовые задачи
4
Применение правил сложения и вычитания
5
Умножать и делить рациональные числа
6
Умножение и деление рациональных чисел: текстовые задачи
7
Применение правил умножения и деления
8
Применение правил сложения, вычитания, умножения и деления
9
Оценивать числовые выражения, включающие рациональные числа
1
Определите рациональные и иррациональные квадратные корни
2
Различать рациональные и иррациональные числа
3
Классифицировать числа
4
Иррациональные числа на числовых рядах
Контрольная точка: Рациональные и иррациональные числа
Контрольная точка: приблизительные иррациональные числа
1
Понимание коэффициентов
2
Определить эквивалентные отношения
3
Напишите эквивалентное отношение
4
Равнозначные соотношения: текстовые задачи
5
Ставки за единицу
6
Словесные задачи с соотношениями
7
Соотношения образуют пропорцию?
8
Образуют ли пропорции пропорцию: текстовые задачи
9
Решить пропорции
10
Решить пропорции: текстовые задачи
11
Оцените численность населения, используя пропорции
12
Чертежи в масштабе: текстовые задачи
13
Чертежи в масштабе: текстовые задачи с коэффициентом масштаба
1
Найдите константу пропорциональности по таблице
2
Напишите уравнения пропорциональных отношений по таблицам
3
Определите пропорциональные отношения с помощью графика
- г.
4
Найдите константу пропорциональности по графику
5
Напишите уравнения пропорциональных отношений по графикам
6
Определите пропорциональные отношения из графиков и уравнений
- г.
7
Определение пропорциональных отношений из таблиц
8
Определить пропорциональные отношения: текстовые задачи
9
График пропорциональных отношений и найти наклон
- г.
10
Интерпретировать графики пропорциональных отношений
11
Напишите и решите уравнения пропорциональных отношений.
12
Найдите постоянную вариации
13
Определить прямую вариацию
14
Напишите уравнения прямой вариации
15
Напишите и решите уравнения прямой вариации
Контрольная точка: пропорциональные отношения
1
Преобразование между процентами, дробями и десятичными дробями
2
Сравните проценты с дробями и десятичными дробями
3
Найдите, сколько процентов составляет одно число от другого
4
Найти, сколько процентов составляет одно число от другого: текстовые задачи
5
Оценить проценты чисел
6
Проценты чисел и денежных сумм
7
Проценты чисел: текстовые задачи
8
Сравните проценты чисел
9
Решите процентные уравнения
10
Процент изменения
- г.
11
Процент изменений: текстовые задачи
12
Процент изменения: найти исходное количество словесных задач
1
Прайс-листы
2
Цены за единицу
3
Цены за единицу с преобразованием единиц
4
Цены за единицу: найти общую цену
5
Процент от числа: налог, скидка и т.
д.6
Найдите процент: налог, скидка и т. д.
7
Цены продажи: найти первоначальную цену
8
Многошаговые задачи с процентами
9
Советы по оценке
10
Простой интерес
11
Сложные проценты
д.1
Преобразование ставок и измерений: общепринятые единицы
2
Преобразование ставок и измерений: метрические единицы
3
Смешанные обычные единицы
4
Преобразование между обычной и метрической системами
5
Точность
6
Преобразование между градусами Цельсия и Фаренгейта
1
Многоступенчатые текстовые задачи
2
Проблемы со словами на угадывание и проверку
3
Используйте диаграммы Венна для решения задач
4
Проблемы со словами за прошедшее время
1
Обзор координатной плоскости
2
Квадранты и оси
3
Следуйте указаниям на координатной плоскости
4
Найдите расстояние между двумя точками
1
Идентифицировать и классифицировать полигоны
2
Классифицировать треугольники
3
Определить трапеции
4
Классифицировать четырехугольники I
5
Классифицировать четырехугольники II
6
Графические треугольники и четырехугольники
7
Найдите недостающие углы в треугольниках
8
Найдите недостающие углы в треугольниках, используя отношения
9
Теорема о сумме углов треугольника
10
Найдите недостающие углы в четырехугольниках I
11
Найдите недостающие углы в четырехугольниках II
12
Теорема о внешнем угле
13
Внутренние углы многоугольников
14
Назовите дополнительные, дополнительные, вертикальные, смежные и конгруэнтные углы.
15
Найдите меры дополнительных, дополнительных, вертикальных и смежных углов.
16
Определите альтернативные внутренние и альтернативные внешние углы
17
Сечения параллельных прямых: назовите пары углов.
18
Трансверсали параллельных прямых: найти меру угла
19
Пересечения параллельных прямых: найти x
20
Найдите длины и меры отрезков и углов, разделенных пополам.
21
Части круга
Контрольная точка: треугольники и трансверсали
1
Линейная симметрия
2
Вращательная симметрия
3
Вращательная симметрия: величина вращения
4
Определение отражений, поворотов и переводов
5
Опишите последовательность преобразований
6
Переводы: граф изображения
7
Переводы: найти координаты
8
Переводы: написать правило
9
Отражения по осям x и y: графическое изображение изображения
10
Отражения по осям x и y: найти координаты
11
Отражения: нарисуйте изображение
12
Отражения: найти координаты
13
Вращения: график изображения
14
Вращения: найти координаты
15
Последовательности преобразований конгруэнтности: графическое изображение
16
Определите конгруэнтные фигуры
17
Операторы сравнения и соответствующие части
18
Длины сторон и меры углов конгруэнтных фигур
19
Конгруэнтные треугольники: SSS, SAS и ASA.
Контрольная точка: преобразование конгруэнтности
1
Подобные и конгруэнтные фигуры
2
Расширения: графическое изображение
3
Дилатации: найти координаты
4
Расширения: найдите масштабный коэффициент
5
Определите подобные треугольники
6
Критерий угла-угла для подобных треугольников
7
Длины сторон и меры углов подобных треугольников
8
Длины сторон и меры углов подобных фигур
9
Найдите недостающие длины сторон в пропорциональных треугольниках
Контрольная точка: преобразования подобия
Контрольная точка: Преобразования на координатной плоскости
1
Теорема Пифагора: найти длину гипотенузы
2
Теорема Пифагора: найти недостающую длину ноги
3
Теорема Пифагора: найти недостающий катет или длину гипотенузы
4
Теорема Пифагора: найти периметр
5
Теорема Пифагора: текстовые задачи
6
Обратная теорема Пифагора: прямоугольный треугольник?
Контрольная точка: теорема Пифагора и ее обращение
Контрольная точка: приложения теоремы Пифагора
1
Части объемных фигур
2
Сетки трехмерных фигур
3
Вид спереди, сбоку и сверху
4
Базовые планы
5
Подобные твердые вещества
1
Периметр
2
Область
3
Площадь и периметр: текстовые задачи
4
Площадь и окружность кругов
5
Круги: словесные задачи
6
Площадь и периметр полукруга и четверти круга
7
Площадь между двумя фигурами
8
Объем кубов, призм и пирамид
9
Площадь поверхности кубов, призм и пирамид
10
Объем цилиндров
11
Объем конусов
12
Площадь поверхности цилиндров
13
Площадь поверхности конусов
14
Объем сфер
15
Площадь поверхности сфер
16
Объем и площадь поверхности подобных твердых тел
17
Периметр и площадь: изменение масштаба
Контрольная точка: объем
1
Определять арифметические и геометрические прогрессии
2
Арифметические последовательности
3
Геометрические последовательности
4
Номерные серии: смешанный обзор
5
Числовые последовательности: проблемы со словами
6
Вычислить переменные выражения для числовых последовательностей
7
Напишите переменные выражения для арифметических последовательностей
1
Запись переменных выражений: одна операция
2
Запись переменных выражений: две или три операции
3
Напишите выражения переменных из диаграмм
4
Напишите переменные выражения: текстовые задачи
5
Вычислить выражения с одной переменной
6
Оценка выражений с несколькими переменными
7
Вычислить выражения абсолютного значения
8
Оценить радикальные выражения
9
Оценивать рациональные выражения
10
Определите термины и коэффициенты
11
Факторы сортировки переменных выражений
12
Свойства сложения и умножения
13
Умножьте, используя распределительное свойство
14
Напишите эквивалентные выражения, используя свойства
15
Складывать и вычитать похожие термины
16
Сложение и вычитание линейных выражений
17
Коэффициенты линейных выражений
18
Определите эквивалентные линейные выражения I
19
Определите эквивалентные линейные выражения II
20
Определите эквивалентные линейные выражения: текстовые задачи
1
Какой x удовлетворяет уравнению?
2
Напишите уравнение из слов
3
Моделируйте и решайте уравнения, используя плитки алгебры
4
Напишите и решите уравнения, которые представляют диаграммы
5
Свойства равенства
6
Определите эквивалентные уравнения
7
Решите одношаговые уравнения
8
Решите двухшаговые уравнения
9
Решите двухшаговые уравнения: завершите решение
10
Решите одношаговые и двухшаговые уравнения: текстовые задачи
11
Решите уравнения, содержащие одинаковые члены
12
Решите уравнения с переменными с обеих сторон
13
Решите уравнения с переменными с обеих сторон: дробные коэффициенты
14
Решите уравнения с дистрибутивным свойством
15
Решение многошаговых уравнений
16
Решите многошаговые уравнения с дробными коэффициентами
17
Решить уравнения: смешанный обзор
18
Решите многошаговые уравнения: завершите решение
19
Найдите количество решений
20
Создавайте уравнения без решений или с бесконечным количеством решений
Контрольная точка: решение линейных уравнений
1
Решения неравенства
2
Графические неравенства на числовых линиях
3
Запишите неравенства из числовых линий
4
Решите одношаговые неравенства
5
Графические решения одношаговых неравенств
6
Решите двухшаговые неравенства
7
Графические решения двухшаговых неравенств
8
Решите многошаговые неравенства
9
Графические решения многошаговых неравенств
10
Решите неравенства с целыми числами: переменные с обеих сторон
11
Решите неравенства с десятичными дробями: переменные с обеих сторон
1
Найдите наклон графика
2
Найдите наклон из двух точек
3
Найдите недостающую координату, используя наклон
4
Форма пересечения наклона: найти наклон и пересечение по оси Y
5
Нарисуйте линию, используя наклон
6
Нарисуйте линию из уравнения в форме пересечения наклона
7
График линии из уравнения в форме точка-наклон
8
Напишите линейное уравнение, используя наклон и точку пересечения с осью Y.
9
Напишите линейное уравнение по графику
10
Напишите линейное уравнение из наклона и точки
11
Напишите линейное уравнение по двум точкам
12
Преобразование линейного уравнения в стандартной форме в форму пересечения наклона
13
График линии из уравнения в стандартной форме
14
Нарисуйте горизонтальную или вертикальную линию
15
Уравнения горизонтальных и вертикальных линий
16
Наклоны параллельных и перпендикулярных линий
Контрольная точка: наклон и линейные уравнения
1
Определить функции
2
Определить функции: графики
3
Удовлетворяет ли (x, y) линейной функции?
4
Свяжите график уравнения с его решениями
5
Определите независимые и зависимые переменные
6
Скорость изменения: таблицы
7
Скорость изменения: графики
8
Постоянная скорость изменения
9
Оцените линейную функцию
10
Заполните таблицу для линейной функции
11
Заполните таблицу и начертите линейную функцию
12
Интерпретировать точки на графике линейной функции
13
Интерпретируйте наклон и точку пересечения оси Y линейной функции
14
Запишите линейную функцию из таблицы
15
Сравните линейные функции: графики и уравнения
16
Сравните линейные функции: таблицы, графики и уравнения
17
Напишите линейные функции: текстовые задачи
18
Оцените линейную функцию: текстовые задачи
19
Определение линейных и нелинейных функций: графики и уравнения
20
Определение линейных и нелинейных функций: таблицы
21
Удовлетворяет ли (x, y) нелинейной функции?
22
Оцените нелинейную функцию
23
Найдите значения, используя графики функций
24
Заполните таблицу для графика функции
25
Домен и набор функций
Контрольная точка: понимание функций
Контрольная точка: сравнение функций
Контрольная точка: линейные и нелинейные функции
Контрольная точка: создание и интерпретация линейных функций
Контрольная точка: набросайте и опишите графики
1
Является ли (x, y) решением системы уравнений?
2
Решите систему уравнений, построив график
3
Решите систему уравнений с помощью графика: текстовые задачи
4
Найдите количество решений системы уравнений, построив график
5
Найдите количество решений системы уравнений
6
Классифицировать систему уравнений по графику
7
Классифицировать систему уравнений
8
Решите систему уравнений с помощью замены
9
Решите систему уравнений с помощью замены: текстовые задачи
10
Решите систему уравнений методом исключения
11
Решите систему уравнений методом исключения: текстовые задачи
12
Решите систему уравнений любым способом
13
Решите систему уравнений любым методом: текстовые задачи
Контрольная точка: Системы уравнений
1
Определить мономы
2
Модельные полиномы с плитками алгебры
3
Сложение и вычитание полиномов с помощью плиток алгебры
4
Сложение и вычитание многочленов
5
Добавьте многочлены, чтобы найти периметр
6
Умножить одночлены
7
Разделить одночлены
8
Умножать и делить одночлены
9
Степени мономов
10
Квадратные и кубические корни одночленов
11
Умножение многочленов с использованием плиток алгебры
12
Умножить многочлены
13
Умножьте многочлены, чтобы найти площадь
1
Интерпретировать таблицы
2
Интерпретация гистограмм
3
Создание гистограмм
4
Интерпретировать линейные графики
5
Создание линейных графиков
6
Интерпретировать линейные графики
7
Создание линейных графиков
8
Создание и интерпретация линейных графиков с дробями
9
Интерпретация сюжетов «стебель-листья»
10
Создание участков стебля и листьев
11
Интерпретация гистограмм
12
Создание гистограмм
13
Создание частотных диаграмм
14
Коробчатые графики
15
Интерпретировать графики рассеяния
16
Создание точечных диаграмм
17
Определение тенденций с помощью точечных диаграмм
18
Делайте прогнозы с помощью точечных диаграмм
19
Интерпретация круговых диаграмм
20
Круговые диаграммы и центральные углы
1
Вычислить среднее значение, медиану, моду и диапазон
2
Интерпретируйте диаграммы и графики, чтобы найти среднее значение, медиану, моду и диапазон
3
Среднее значение, медиана, мода и диапазон: найдите пропущенное число
4
Изменения среднего, медианы, режима и диапазона
5
Рассчитать среднее абсолютное отклонение
6
Вычислить квартили и межквартильный диапазон
7
Определите выброс
8
Определите выброс и опишите эффект от его удаления.
