что это такое, чему равно, история, как округлить
Даже если вы давно закончили школу и из всего курса математики помните только таблицу умножения, мы уверены: про число пи вы знаете. Скажете сходу, чему оно равно? Помните, для чего нужно число пи и как его посчитать? Если нет, читайте наш урок
Мария Макулова
Редактор раздела «Образование»
Вячеслав Смольняков
Учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике
Ирина Ходакова
Учитель математики
Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.
От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.
Что такое число пи
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности. То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных. Например, число пи необходимо, чтобы посчитать площадь круга.
Число пи — это результат деления длины окружности на ее диаметр
Чему равно число пи
Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.
Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении. Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби). Итак:
π = 3,14
или
π = 3,1415926535
Как посчитать число пи самостоятельно
Возьмите несколько круглых предметов разного размера, например тарелку, блюдце и крышку от кастрюли. Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета. Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру. Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли. Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Измерьте окружность каждого. Для этого используйте сантиметровую ленту. Или можно обернуть их по окружности ниткой или веревкой, а потом полученную длину нитки или веревки измерить линейкой. С помощью сантиметровой ленты или линейки измерьте и диаметр каждого предмета. Длина окружности и диаметры у каждого будут разные, ведь предметы разные по размеру. Теперь для каждого предмета разделите его длину окружности на диаметр. Вы увидите, что во всех случаях, какого бы размера ни был круглый предмет, полученное значение будет 3 целых и далее десятые и сотые доли. Оно необязательно соответствует принятому значению в 3,14, но всегда будет около него.
Какого бы размера ни был круглый предмет, при делении длины его окружности на диаметр получится 3 целых и далее десятые и сотые доли — приблизительно 3,14
Практическое применение числа пи
В школе нас учат использовать число пи для вычисления площади круга. Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Рассчитывается она по следующей формуле: S = πr², где S — площадь, π — число пи, r² — радиус в квадрате. Можно использовать эту формулу: S = d²/4*π, где d² — диаметр.
Зная число пи и диаметр, можно посчитать длину окружности. Для этого вспомним школьные уравнения. Если π = C/d, то C (длина окружности) высчитывается по формуле C = π*d.
Но применение числа пи в науке гораздо шире. Оно используется практически для любых расчетов в любой области, будь то архитектура, авиация и даже статистика. Например, число π нужно для расчета времени полета самолета и расстояния, которое он должен преодолеть. А в статистике с помощью числа пи рассчитывают значения ниже так называемой кривой нормального распределения. Это нужно для того чтобы, например, выяснить, как распределялись голоса респондентов при опросе.
S (площадь круга) = πr²
История числа пи
Считается, что первым обозначать число пи буквой греческого алфавита π (pi) стал британский математик Уильям Джонс в 1706 году, а популяризировал обозначение его швейцарский коллега Леонард Эйлер в 1737 году. Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Есть версия, что эта буква выбрана не случайно, а как начальная в греческом слове perijereia, что означает «окружность», «периферия».
Как и на многие явления, известные науке сегодня, на существование некой постоянной, с помощью которой можно посчитать площадь круга, обратили внимание еще в Древнем мире. Но ученые того времени приходили к разному мнению относительно значения этой постоянной: одни использовали значение 3,125, другие — 3,16, третьи — 3,139. Но всегда это значение было 3 с небольшим.
На точное вычисление числа пи ушли тысячелетия. Первым, кто определил более-менее приблизительное значение π, был древнегреческий ученый Архимед. По его расчетам пи равно 3,142857142857143. Как мы знаем сейчас, верными оказались только первые два десятичных числа.
Точнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.
В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).
В ТЕМУ
Популярные вопросы и ответы
Как округлить число пи?
Чтобы не запоминать число пи с большим количеством десятичных значений, его принято округлять. В математике все округления проводятся по строгим правилам. Для округления значения числа пи применяют метод округления к ближайшему целому. Если перед округляемым числом стоит число 5 и большее, то число округляется в большую сторону. Например, 12,513. Другой пример: 12,5812,613.
Если перед округляемым числом стоит число менее 5, то число округляется в меньшую сторону. Например, 12,412. Или: 12,3412,312.
Например, 12,412. Или: 12,3412,312.
Итак, возьмем π — 3,1415. Округление начинают с последнего значения, в данном случае это 5. Значит, следующая за ним единица округляется до двух: 3,14153,142. Последнее число 2 меньше пяти, значит, последующее 4 остается неизменным: 3,1423,14. Вот мы и пришли к общепринятому значению числа пи.
По тому же принципу давайте продолжим округление до целого числа: 3,143,23. И вот у нас получилось значение числа пи 3.
Как запомнить число пи?
Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике:
На практике мы часто используем округление числа пи до сотых — 3,14. Чуть реже нам нужна большая точность, и мы уже берем значение 3,14159. Чтобы запомнить дробную часть, можно воспользоваться нехитрым приемом: выучить одну фразу «Это я знаю и помню прекрасно». Количество букв в словах соответствует первым цифрам числа пи: «это» — 3, «я» — 1, «знаю» — 4 и так далее.
Количество букв в словах соответствует первым цифрам числа пи: «это» — 3, «я» — 1, «знаю» — 4 и так далее.
Для запоминания большего количества цифр есть специальные стихотворения, это называется мнемонический метод запоминания.
Ирина Ходакова, учитель математики:
Чтобы запомнить значение числа π используют один из самых популярных способов — запомнить фразу, в которой количество букв в каждом слове совпадает с цифрами числа π.
Например, «Что(3) я(1) знаю(4) о(1) круге(5)?»
Чтобы запомнить больше знаков числа π, пользуются различными приемами мнемотехники (совокупность приемов, облегчающих запоминание информации). Например, существует стихотворение С. Боброва «Волшебный двурог» для запоминания числа π, которое совсем не сложно выучить:
«Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь»
Где используется число пи?
Вячеслав Смольняков:
В школе ученики впервые знакомятся с числом пи в 6 классе, и я обычно привожу разные примеры того, где это можно использовать в реальной жизни. Например, девочки на уроках технологии часто шьют круглые изделия, и число пи поможет им рассчитать, какое количество тесьмы необходимо для того, чтобы обшить по краю круглую салфетку. Мальчикам часто бывает интересно, как рассчитать, какое расстояние они преодолели на уроке физкультуры, бегая по кругу в спортзале. А еще все любят подарки… Сколько нужно упаковочной бумаги, чтобы обернуть подарок, который находится в коробке цилиндрической формы? Для всего этого нужно знать про число пи. В более старших классах мы используем знание о числе пи уже для решения геометрических задач (однако оно используется не только в геометрии).
Например, девочки на уроках технологии часто шьют круглые изделия, и число пи поможет им рассчитать, какое количество тесьмы необходимо для того, чтобы обшить по краю круглую салфетку. Мальчикам часто бывает интересно, как рассчитать, какое расстояние они преодолели на уроке физкультуры, бегая по кругу в спортзале. А еще все любят подарки… Сколько нужно упаковочной бумаги, чтобы обернуть подарок, который находится в коробке цилиндрической формы? Для всего этого нужно знать про число пи. В более старших классах мы используем знание о числе пи уже для решения геометрических задач (однако оно используется не только в геометрии).
В науке число пи используется в множестве геометрических формул, прежде всего для нахождения объемов тел, площадей фигур, которые содержат круг. В тригонометрии это число является одним из основных. Также мы можем его встретить при расчете интегралов в высшей математике, встречается оно и в формулах математической статистики и физики.
Если же рассказывать про то, откуда человечество вообще заинтересовалось данной темой, то стоит переместиться в древность. Получение знаний в ту эпоху, как и сейчас, носило практический характер. Сколько нужно каменных блоков, чтобы построить круглую башню? Вопросы, подобные этому, интересовали и Архимеда, и древних правителей, которым нужно было рассчитать ресурсы для обороны собственных владений.
Получение знаний в ту эпоху, как и сейчас, носило практический характер. Сколько нужно каменных блоков, чтобы построить круглую башню? Вопросы, подобные этому, интересовали и Архимеда, и древних правителей, которым нужно было рассчитать ресурсы для обороны собственных владений.
В XX веке при помощи компьютеров человечество смогло рассчитать уже несколько десятков триллионов знаков после запятой, причем, как и в древности, это имеет практическое значение — при помощи данного расчета можно оценить производительность компьютерных систем.
Ирина Ходакова:
Изначально число π было необходимо для применения в строительстве. Ведь порой из-за погрешности в значении числа π падали башни и рушились целые дворцы. Сейчас π используется в различных сферах нашей жизни.
Мы уже выяснили, что число π позволяет нам рассчитывать и создавать окружности. Если колеса на вашем автомобиле будут немного отличаться друг от друга, то поездки для вас станут как минимум не очень удобными. Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
Но применение числа π этим не ограничивается. Например, без числа π нельзя было бы обеспечить качественную работу телевизоров, радио и телефонов, так как инженеры используют π для расчета и оптимизации звуковых волн. Также π играет важную роль в расчете времени и расстояния путешествия на самолете, так как на большие расстояния самолеты летят по округлой дуге. Не было бы даже многих игр, таких как футбол, баскетбол, теннис, ведь мячи должны быть абсолютно круглыми.
Что вы знаете про число пи?
Посмотрим, насколько хорошо вы разобрались в теме. Потренируйтесь в несложных расчетах и ответьте на простые вопросы для самопроверки.
| Пройти тест |
Примерно 3,14
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых. Это 3,14.
Ровно 3
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых. Это 3,14.
Это 3,14.
Около 3
У числа пи нет точного значения. Но для расчетов принято округленное значение до сотых. Это 3,14.
| Дальше |
| Проверить |
| Узнать результат |
Это сумма длины окружности и диаметра окружности
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
Это отношение длины окружности к диаметру окружности
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
Это произведение радиуса окружности и длины окружности
Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
Обозначается оно буквой греческого алфавита π. То есть π — это результат деления длины окружности на ее диаметр.
| Дальше |
| Проверить |
| Узнать результат |
3,1415927
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения. В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
3,1415
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения. В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
3,14159
Один из методов запоминания числа пи — это подсчет количество букв в каждом слове предложения. В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
В нашем предложении «Это я знаю и помню прекрасно» в каждом слове такое количество букв: 3, 1, 4, 1, 5, 9. То есть по предложению мы запоминаем, что число пи равно 3,14159.
| Дальше |
| Проверить |
| Узнать результат |
14 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см. 2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
12,56 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см. 2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
16,09 см
Вычисляем площадь круга по формуле S = πr². Нам известно, что радиус равен 2 см. 2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
2 в квадрате — это 4. Теперь 4 умножаем на число пи — 3,14. Получаем 12,56 см — это площадь нашего круга.
| Дальше |
| Проверить |
| Узнать результат |
8,87 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
12,48 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
18,84 см
Используем формулу С = πd, где С — длина окружности, а d — диаметр. Мы знаем, что он равен 6 см. Число пи нам тоже известно — 3,14. Умножаем 6 на 3,14 — получаем 18,84 см.
| Дальше |
| Проверить |
| Узнать результат |
5,73 см
Для расчетов нам поможет та же формула С = πd. Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
6,05 см
Для расчетов нам поможет та же формула С = πd. Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
5,13 см
Для расчетов нам поможет та же формула С = πd. Только в этом случае нам известна длина окружности (С) и число пи. Чтобы по этим данным вычислить диаметр, немного изменим нашу формулу — d = С/π, то есть 18 делим на 3,14. Это равно 5.73248408. Далее используем метод округления к ближайшему целому — округляем до сотых. Получаем 5,73.
Получаем 5,73.
| Дальше |
| Проверить |
| Узнать результат |
21,13 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два. В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
43,96 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два. В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
35,56 см
Для этого расчета вспомним, чему равен диаметр: d = 2r. То есть диаметр равен радиусу, умноженному на два. В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
В нашей задаче радиус окружности — 7 см. Значит, диаметр — 14 см. Далее используем уже знакомую формулу С = πd. Считаем. 3,14 умножаем на 14, получаем 43,96 см.
| Дальше |
| Проверить |
| Узнать результат |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Прочитайте статью еще раз и пройдите тест повторно.
| Пройти еще раз |
Вы хорошо разобрались в материале, но ошибки еще есть.
| Пройти еще раз |
Вы хорошо разобрались в материале, но ошибки еще есть.
| Пройти еще раз |
Вы изучили правило и умеете его применять.
| Пройти еще раз |
Фото на обложке: shutterstock.com
Как выставляются отметки в аттестат по математике и истории (дополнение 2019) – МОСКОВСКИЙ УЧИТЕЛЬ
Ярослав Галкин/ 29 апреля, 2019/ Блог/ 30 комментариев
В последнее время мой блог набрал популярность по запросам «как выставляется оценка в аттестат за 9 класс в 2017 году». Под постами начали появляться комментарии с вопросами, а иногда даже претензиями о том как интерпретирован закон, на каждый из них я стараюсь дать исчерпывающий ответ. Теперь о самом камне преткновения – отметки по предметам: алгебра, геометрия, история России, всеобщая история.
Конечно уже многие школы выписали аттестаты, но считаю, что пост этот нужен для того, чтобы еще раз понять как школа принимала решение об учете экзаменационных отметок в аттестате.
Рассмотрим информацию с сайтов
- Министерства науки и образования РФ
- Региональный центр обработки информации города Москвы
- Федеральный Институт Педагогических Измерений
- Департамента образования города Москвы
Рассмотрим документы:
- Письмо от 1 апреля 2019 г.

- Приказ Министерства образования и науки РФ от 14 февраля 2014 г. N 115 «Об утверждении Порядка заполнения, учета и выдачи аттестатов об основном общем и среднем общем образовании и их дубликатов» (с изменениями и дополнениями)
- Приказ Министерства образования и науки РФ от 25 декабря 2013 г. N 1394
- «Об утверждении Порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования»
- «Порядок проведения государственной итоговой аттестации по образовательным программам среднего общего образования»
- приказ министерства науки и образования России №3 от 09.01.2017 «О ВНЕСЕНИИ ИЗМЕНЕНИЯ В ПОРЯДОК ЗАПОЛНЕНИЯ, УЧЕТА И ВЫДАЧИ АТТЕСТАТОВ ОБ ОСНОВНОМ ОБЩЕМ И СРЕДНЕМ ОБЩЕМ ОБРАЗОВАНИИ И ИХ ДУБЛИКАТОВ, УТВЕРЖДЕННЫЙ ПРИКАЗОМ МИНИСТЕРСТВА ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ОТ 14 ФЕВРАЛЯ 2014 Г. № 115»
- ст.
 59 закона об образовании 273-ФЗ
59 закона об образовании 273-ФЗ - Рекомендации для образовательных организаций по выставлению итоговых отметок в аттестат об основном общем образовании в городе Москве в 2015–2016 учебном году
Для того, чтобы понять как будут выставляться отметки в аттестат за 9 класс в 2018/2019 учебном году, нужно внимательно прочитать письмо Министерства Просвещения от 1 апреля 2019.
В этом письме даются разъяснения как записывается название предмета в аттестат и как рассчитывается отметка по предмету.
| Названия предметов в аттестате | |
| ФК ГОС | ФГОС |
| Математика | Математика |
| История | История России. Всеобщая история |
Отметка по истории складывается как среднее арифметическое годовых отметок по истории России, Всеобщей истории и экзамену.
Каждая отметка должна быть не ниже 3 (тройки)
Таблица соответствия баллов по предметам и в аттестате
| № | Алгебра / История России | Геометрия / Всеобщая история | Экзамен | Аттестат |
| 1 | 3 (удовл.) | 3 (удовл. ) ) | 3 (удовл.) | 3 (удовл.) |
| 2 | 3 (удовл.) | 3 (удовл.) | 4 (хор.) | |
| 3 | 3 (удовл.) | 3 (удовл.) | 5 (отл.) | )"}»>4 (хор.) |
| 4 | 3 (удовл.) | 4 (хор.) | 3 (удовл.) | 3 (удовл.) |
| 5 | 3 (удовл.) | 4 (хор.) | 4 (хор.) | 4 (хор.) |
| 6 | )"}»>3 (удовл.) | 4 (хор.) | 5 (отл.) | |
| 7 | 3 (удовл.) | 5 (отл.) | 3 (удовл.) | 4 (хор.) |
| 8 | 3 (удовл.) | 5 (отл.) | )"}»>4 (хор.) | 4 (хор.) |
| 9 | 3 (удовл.) | 5 (отл.) | 5 (отл.) | 4 (хор.) |
| 10 | 4 (хор.) | 3 (удовл.) | 3 (удовл.) | 3 (удовл. |
| 11 | 4 (хор.) | 3 (удовл.) | 4 (хор.) | 4 (хор.) |
| 12 | 4 (хор.) | 3 (удовл.) | 5 (отл.) | 4 (хор.) |
| 13 | )"}»>4 (хор.) | 4 (хор.) | 3 (удовл.) | 4 (хор.) |
| 14 | 4 (хор.) | 4 (хор.) | 4 (хор.) | 4 (хор.) |
| 15 | 4 (хор.) | )"}»>5 (отл.) | 4 (хор.) | |
| 16 | 4 (хор.) | 5 (отл.) | 3 (удовл.) | 4 (хор.) |
| 17 | 4 (хор.) | 5 (отл.) | 4 (хор.) | 4 (хор.) |
| 18 | )"}»>4 (хор.) | 5 (отл.) | 5 (отл.) | 5 (отл.) |
| 19 | 5 (отл.) | 3 (удовл.) | 3 (удовл.) | 4 (хор.) |
| 20 | 5 (отл.) | 3 (удовл.) | )"}»>4 (хор.) | 4 (хор.) |
| 21 | 5 (отл.) | 3 (удовл.) | 5 (отл.) | 4 (хор.) |
| 22 | 5 (отл.) | 4 (хор.) | 3 (удовл.) | 4 (хор.) |
| 23 | )"}»>5 (отл.) | 4 (хор.) | 4 (хор.) | 4 (хор.) |
| 24 | 5 (отл.) | 4 (хор.) | 5 (отл.) | 5 (отл.) |
| 25 | 5 (отл.) | 5 (отл.) | )"}»>3 (удовл.) | 4 (хор.) |
| 26 | 5 (отл.) | 5 (отл.) | 4 (хор.) | 5 (отл.) |
| 27 | 5 (отл.) | 5 (отл.) | 5 (отл.) | 5 (отл.) |
ШКАЛА ПЕРЕВОДА БАЛЛОВ ОГЭ 2019
Читать статью в редакции 2017 годаПочему молчит департамент?
Школам дали свободу действий, в соответствии с 273-ФЗ, а она не знает, что с ней теперь делать. На самом деле департамент дал свои рекомендации еще в прошлом году:
На самом деле департамент дал свои рекомендации еще в прошлом году:
В соответствии с Приказом Минобрнауки России от 14.02.2014 No115 «Об утверждении Порядка заполнения, учета и выдачи аттестатов об основном общем и среднем общем образовании и их дубликатов». Аттестат об основном общем образовании и приложение к нему выдаются лицам, завершившим обучение по образовательным программам основного общего образования и успешно прошедшим государственную итоговую аттестацию. Итоговые отметки за 9 класс по русскому языку и математике определяются как среднее арифметическое годовой и экзаменационной отметок выпускника и выставляются в аттестат целыми числами в соответствии с правилами математического округления. Итоговые отметки за 9 класс по другим учебным предметам выставляются на основе годовой отметки выпускника за 9 класс. Итоговые отметки по алгебре и геометрии выставляются на основе годовых отметок выпускника за 9 класс.
С учетом того, что пункт про учет отметок по математике и русскому языку в приказе не изменился, то и это письмо продолжает быть актуальным, а следовательно нет никаких оснований делать напоминание об этом. Аналогичная ситуация с историей России и всеобщей историей.
Аналогичная ситуация с историей России и всеобщей историей.
Справедливо ли это?
Мы добрались до самого интересного! Справедливым решением учащиеся и родители, обычно считают только то, что работает в их пользу. Но тут сразу отметается принцип объективности. Что справедливо для одних, далеко несправедливо для других. Кто-то хочет учета экзамена, а кто-то нет.
Давайте обратимся к рекомендованным и утвержденным шкалам оценивания по математике.
ФИПИ рекомендует:
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении Федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика»
РЦОИ Москвы утвердил шкалу оценивания:
Общий балл по предмету: | Отметка по пятибалльной шкале | |||
| «2» | «3» | «4» | «5» | |
| Русский язык | 0-14 | 15-24 | 25-33* | 34-39** |
| Математика | 0-7 | 8-14 | 15-21 | 22-32 |
* Из них не менее 4 баллов за грамотность (по критериям ГК-1 – ГК-4).
Если по критериям ГК1–ГК4 обучающийся набрал менее 4 баллов, выставляется отметка «3».
**Из них не менее 6 баллов за грамотность (по критериям ГК-1 – ГК-4). Если по критериям ГК1–ГК4 обучающийся набрал менее 6 баллов, выставляется отметка «4».
Получается, что для математики в этом году сняты минимальные требования по модулям «Алгебра», «Геометрия», «Реальная математика» (поправьте в комментариях, если не прав)
А официальной интерпретации баллов по отдельным модулям на этот год я вообще не нашел.
Пример:
Возьмем шкалу оценивания 2016 года из Интернета с любого профильного сайта
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» в отметку по алгебре
- 0—4 баллов — отметка «2»
- 5—10 баллов — отметка «3»
- 11—15 баллов — отметка «4»
- 16—20 баллов — отметка «5»
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» в отметку по геометрии
- 0—2 баллов — отметка «2»
- 3—4 баллов — отметка «3»
- 5—7 баллов — отметка «4»
- 8—12 баллов — отметка «5»
Ученик набирает 15 баллов на модуле алгебра, 0 – геометрия, 0 – реальная математика. Итоговая отметка по математике 4 (хорошо), что дает ему основание получить аттестат.
Итоговая отметка по математике 4 (хорошо), что дает ему основание получить аттестат.
При этом модуль «Алгебра» – 4 (хорошо), а «Геометрия» – 2 (неудовлетоворительно). И тут же ученик попадает под действие ст. 59 закона об образовании 273-ФЗ. Неудовлетворительные результаты на итоговой аттестации не позволяют получить аттестат об основном общем образовании.
Остается добавить, что по состоянию на 2018 год по рекомендациям ФИПИ нет разделения отметки по математике на алгебру и геометрию, есть только рекомендованное условие, что в сумму баллов должно включаться не менее 2х по геометрии. Но окончательная шкала перевода формируется региональными центрами обработки информации при сопровождении ОГЭ.
P.S. Надеюсь, что дал исчерпывающий, обоснованный и объективный ответ по этому сложному вопросу.
Что учитывать в аттестате решать самой школе, ей же нести ответственность за свое решение.
3.3 3 Голосов
Рейтинг публикации
АттестацияДокументыМнениеОбзор
Основы реляционной алгебры / Хабр
Реляционная алгебра базируется на теории множеств и является основой логики работы баз данных.
Когда я только изучал устройство баз данных и SQL, предварительное ознакомление с реляционной алгеброй очень помогло дальнейшим знаниям правильно уложиться в голове, и я постараюсь что бы эта статья произвела подобный эффект.
Так что если вы собираетесь начать свое обучение в этой области или вам просто стало интересно, прошу под кат.
Реляционная база данных
Для начала введем понятие реляцинной базы данных, в которой будем выполнять все действия.
Реляционной базой данных называется совокупность отношений, содержащих всю информацию, которая должна хранится в базе. В данном определении нам интересен термин отношение, но пока оставим его без строго определения.
Лучше представим себе таблицу продуктов.
таблица PRODUCTS
| ID | NAME | COMPANY | PRICE |
| 123 | Печеньки | ООО ”Темная сторона” | 190 |
| 156 | Чай | ООО ”Темная сторона” | 60 |
| 235 | Ананасы | ОАО ”Фрукты” | 100 |
| 623 | Томаты | ООО ”Овощи” | 130 |
Таблица состоит из 4х строк, строка в таблице является кортежем в реляционной теории. Множество упорядоченных кортежей называется отношением.
Множество упорядоченных кортежей называется отношением.
Перед тем как дать определение отношения, введем еще один термин — домен. Домены применительно к таблице это столбцы.
Для ясности, теперь введем строгое определение отношения.
Пусть даны N множеств D1,D2, …. Dn (домены), отношением R над этими множествами называется множество упорядоченных N-кортежей вида <d1,d1,…dn>, где d1 принадлежит D1 и тд. Множества D1,D2,..Dn называются доменами отношения R.
Каждый элемент кортежа представляет собой значение одного из атрибутов, соответствующего одному из доменов.
Ключи в отношениях
В отношении требованием является то, что все кортежи должны различаться. Для однозначной идентификации кортежа существует первичный ключ. Первичный ключ это атрибут или набор из минимального числа атрибутов, который однозначно идентифицирует конкретный кортеж и не содержит дополнительных атрибутов.
Подразумевается, что все атрибуты в первичном ключе должны быть необходимыми и достаточными для идентификации конкретного кортежа, и исключение любого из атрибутов в ключе сделает его недостаточным для идентификации.
Например, в такой таблице ключом будет сочетание атрибутов из первого и второго столбца.
таблица DRIVERS
| COMPANY | DRIVER |
| ООО ”Темная сторона” | Владимир |
| ООО ”Темная сторона” | Михаил |
| ОАО ”Фрукты” | Руслан |
| ООО ”Овощи” | Владимир |
Видно, что в организации может быть несколько водителей, и чтобы однозначно идентифицировать водителя необходимо и значение из столбца “Название организации” и из “Имя водителя”. Такой ключ называется составным.
В реляционной БД таблицы взаимосвязаны и соотносятся друг с другом как главные и подчиненные. Связь главной и подчиненнной таблицы осуществляется через первичный ключ (primary key) главной таблицы и внешний ключ ( foreign key ) подчиненной таблицы.
Внешний ключ это атрибут или набор атрибутов, который в главной таблице является первичным ключем.
Этой подготовительной теории будет достаточно для знакомства с основными операциями реляционной алгебры.
Операции реляционной алгебры
Основные восемь операций реляционной алгебры были предложены Э.Коддом.
- Объединение
- Пересечение
- Вычитание
- Декартово произведение
- Выборка
- Проекция
- Соединение
- Деление
Первая половина операций аналогична таким же операциям над множествами. Часть операций можно выразить через другие операции. Рассмотрим большую часть операций с примерами.
Для понимания важно запомнить, что результатом любой операции алгебры над отношениями является еще одно отношение, которое можно потом так же использовать в других операциях.
Создадим еще одну таблицу, которая нам пригодится в примерах.
таблица SELLERS
| ID | SELLER |
| 123 | OOO “Дарт” |
| 156 | ОАО ”Ведро” |
| 235 | ЗАО “Овоще База” |
| 623 | ОАО ”Фирма” |
Условимся, что в этой таблице ID это внешний ключ, связанный с первичным ключом таблицы PRODUCTS.
Для начала рассмотрим самую простую операцию — имя отношения. Её результатом будет такое же отношение, то есть выполнив операцию PRODUCTS, мы получим копию отношения PRODUCTS.
Проекция
Проекция является операцией, при которой из отношения выделяются атрибуты только из указанных доменов, то есть из таблицы выбираются только нужные столбцы, при этом, если получится несколько одинаковых кортежей, то в результирующем отношении остается только по одному экземпляру подобного кортежа.
Для примера сделаем проекцию на таблице PRODUCTS выбрав из нее ID и PRICE.
Синтаксис операции:
π(ID, PRICE) PRODUCTS
В результате этой операции получим отношение:
| ID | PRICE |
| 123 | 190 |
| 156 | 60 |
| 235 | 100 |
| 623 | 130 |
Выборка
Выборка — это операция, которая выделяет множество строк в таблице, удовлетворяющих заданным условиям. ID<300) PRODUCTS
ID<300) PRODUCTS
| ID | NAME | COMPANY | PRICE |
| 123 | Печеньки | ООО ”Темная сторона” | 190 |
| 235 | Ананасы | ОАО ”Фрукты” | 100 |
Совместим операторы проекции и выборки. Мы можем это сделать, потому что любой из операторов в результате возвращает отношение и в качестве аргументов использует также отношение.
Из таблицы с продуктами выберем все компании, продающие продуты дешевле 110.
πCOMPANYσ(PRICE<100 ) PRODUCTS
| COMPANY |
| ООО ”Темная сторона” |
| ОАО ”Фрукты” |
Умножение
Умножение или декартово произведение является операцией, производимой над двумя отношениями, в результате которой мы получаем отношение со всеми доменами из двух начальных отношений. Кортежи в этих доменах будут представлять из себя все возможные сочетания кортежей из начальных отношений. На примере будет понятнее.
Кортежи в этих доменах будут представлять из себя все возможные сочетания кортежей из начальных отношений. На примере будет понятнее.
Получим декартово произведения таблиц PRODUCTS и SELLERS.
Синтаксис операции:
PRODUCTS × SELLERS
Можно заметить, что у двух этих таблиц есть одинаковый домен ID. В подобной ситуации домены с одинаковыми названиями получают префикс в виде названия соответствующего отношения, как показано ниже.
Для краткости перемножим не полные отношения, а выборки с условием ID<235
(цветом выделены одни и те же кортежи)
| PRODUCTS.ID | NAME | COMPANY | PRICE | SELLERS.ID | SELLER |
| 123 | Печеньки | ООО ”Темная сторона” | 190 | 123 | OOO “Дарт” |
| 156 | Чай | ООО ”Темная сторона” | 60 | 156 | ОАО ”Ведро” |
| 123 | Печеньки | ООО ”Темная сторона” | 190 | 156 | ОАО ”Ведро” |
| 156 | Чай | ООО ”Темная сторона” | 60 | 123 | OOO “Дарт” |
Для примера использования этой операции представим себе необходимость выбрать продавцов с ценами меньше 90. PRICE<90) PRODUCTS × SELLERS
PRICE<90) PRODUCTS × SELLERS
В результате этой операции получим отношение:
| SELLER |
| ОАО ”Ведро” |
Соединение и естественное соединение
Операция соединения обратна операции проекции и создает новое отношение из двух уже существующих. Новое отношение получается конкатенацией кортежей первого и второго отношений, при этом конкатенации подвергаются отношения, в которых совпадают значения заданных атрибутов. В частности, если соединить отношения PRODUCTS и SELLERS, этими атрибутами будут атрибуты доменов ID.
Также для понятности можно представить соеднинение как результат двух операций. Сначала берется произведение исходных таблиц, а потом из полученного отношения мы делаем выборку с условием равенства атрибутов из одинаковых доменов. В данном случае условием явлется равенство PRODUCTS.ID и SELLERS.ID.
Попробуем соединить отношения PRODUCTS и SELLERS и получим отношение.
| PRODUCTS.ID | NAME | COMPANY | PRICE | SELLERS.ID | SELLER |
| 123 | Печеньки | ООО ”Темная сторона” | 190 | 123 | OOO “Дарт” |
| 156 | Чай | ООО ”Темная сторона” | 60 | 156 | ОАО ”Ведро” |
| 235 | Ананасы | ОАО ”Фрукты” | 100 | 235 | ЗАО “Овоще База” |
| 623 | Томаты | ООО ”Овощи” | 130 | 623 | ОАО ”Фирма” |
Натуральное соединение получает схожее отношение, но в случае, если у нас корректно настроена схема в базе ( в данном случае первичный ключ таблицы PRODUCTS ID связан с внешним ключем таблицы SELLERS ID), то в результирующем отношении остается один домен ID.
Синтаксис операции:
PRODUCTS ⋈ SELLERS;
Получится такое отношение:
PRODUCTS. ID ID |
NAME | COMPANY | PRICE | SELLER |
| 123 | Печеньки | ООО ”Темная сторона” | 190 | OOO “Дарт” |
| 156 | Чай | ООО ”Темная сторона” | 60 | ОАО ”Ведро” |
| 235 | Ананасы | ОАО ”Фрукты” | 100 | ЗАО “Овоще База” |
| 623 | Томаты | ООО ”Овощи” | 130 | ОАО ”Фирма” |
Пересечение и вычитание.
Результатом операции пересечения будет отношение, состоящее из кортежей, полностью входящих в состав обоих отношений.
Результатом вычитания будет отношение, состоящее из кортежей, которые являются кортежами первого отношения и не являются кортежами второго отношения.
Данные операции аналогичны таким же операциям над множествам, так что, я думаю, нет необходимости подробно их расписывать.
Источники информации
- Основы использования и проектирования баз данных — В. М. Илюшечкин
- курс лекций Introduction to Databases — Jennifer Widom, Stanford University
Буду благодарен за аргументированные замечания
Темы исследовательских работ по математике
Внимание! Для повторения и закрепления таблицы умножения и таблицы деления предлагаем наши игровые программы Таблица умножения в мультиках и Таблица деления в мультиках.
На этой странице представлен общий список тем исследовательских работ по математике для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11 класса, перейти к которым можно по ссылкам и далее на страницах выбрать наиболее подходящую уровню знаний и умений ребенка тему проекта. Проектная деятельность учащегося начинается только после того, как тема научно-исследовательской работы будет одобрена руководителем (учителем).
Приведенные разнообразные темы проектов по математике на этой странице можно брать за основу, дополнять и изменять в соответствии с поставленными целями исследования и идеей проекта.
- Темы проектов по математике для 1, 2, 3, 4 класса
- Темы проектов по математике для 5 класса
- Темы проектов по математике для 6 класса
- Темы проектов по математике для 7 класса
- Темы проектов по математике для 8 класса
- Темы проектов по математике для 9 класса
- Темы проектов по математике для 10 класса
- Темы проектов по математике для 11 класса
Правильно выбранные темы проектов по математике для учащихся 5, 6, 7, 8, 9, 10 или 11 класса способствует тому, что работа над ними будет, действительно, увлекательна, познавательна и интересна. Особенно, если данный исследовательский проект по математике выполняется группой детей.
- Темы исследовательских работ по истории математики
- Темы исследовательских работ по алгебре
- Темы исследовательских работ на логику
- Темы исследовательских работ по геометрии
- Темы исследовательских работ по стереометрии
- Темы исследовательских работ по комбинаторике
- Темы исследовательских работ на математические игры
- Темы исследовательских работ по математике в предметах
Приведенные ниже темы исследовательских работ и проектов по математике являются примерными, некоторые из них можно объединить в одну тему при наличии общих задач и цели исследования.
Темы исследовательских проектов по математике
Темы проектных работ по математике:
Авторские задачи.
Аликвотные дроби
Арифметика остатков. Сравнения по модулю.
Без мерной линейки
Без мерной линейки, или измерение голыми руками.
Бесконечный мир чисел.
Божественное число
Буква в кубе.
Быстрый счет — легко и просто!
Быстрый счет без калькулятора.
В глубь веков, или Как считали древние.
В мире времени (сборник творческих задач).
В мире ребусов и лабиринтов.
В мире удивительных чисел.
В поисках оптимальных решений.
В царстве чисел-великанов.
Вездесущая математика.
Великие задачи
Великолепная семерка
Великолепные цифры.
Виды задач на логическое мышление.
Виды и свойства движений.
Виды текстовых задач и их решение.
Влияние скорости падения дождевых капель на скорость движения человека во время дождя.
Во всем царит гармонии закон…
Время и его измерение
Время остановить нельзя, а измерить?
Время работать и время отдыхать.
Все есть число
Все о «тройке» и чуть больше…
Все о числе 13
Все о числе 7
Всегда ли 2 х 2 = 4?
Вычисление скорости течения реки.
Галерея замечательных чисел.
Галерея числовых диковинок.
Гармония и математика
Генетический код и квадрат Пифагора.
География чисел
Гипотеза об истоках золотого сечения.
Головоломки со спичками
Графические методы и геометрические соображения при решении задач по математике Графические приемы при решении задач по математике.
Графический метод решения сюжетных задач.
Графический способ умножения чисел.
Два способа решения логических задач
Действия над числами в различных системах счисления.
День рождения нуля
День рождения числа «пи»
Детские задачи для взрослых детей.
Древнерусские задачи
Древние системы счисления.
Древние, но вечно юные простые числа
Дружественные тройки чисел.
Дружественные числа
Жар холодных чисел
Живая математика
Живая природа и симметрия.
Загадка бумажной полоски.
Загадка Рамануджана
Загадки числового ряда
Загадочный мир чисел.
Задачи из старинного учебника.
Задачи из Эфиопии
Задачи на все случаи жизни
Задачи на движение двух объектов.
Задачи на движение по реке
Задачи на клетчатой бумаге. Формула Пика.
Задачи на местном материале
Задачи на наибольшее и наименьшее значение величин и методы их решения.
Задачи на оптимизацию
Задачи на переливание жидкости.
Задачи на разрезание
Задачи на свежем воздухе.
Задачи на чётность
Задачи о лабиринтах
Задачи о четырех красках.
Темы исследовательских работ по математике
Темы исследовательских проектов по математике:
Задачи повышенной трудности «на движение».
Задачи с ограничениями.
Задачи с одинаковыми цифрами.
Задачи с параметрами
Задачи со спичками
Задачи старинные и старые.
Задачи, которые могли бы стать теоремами.
Замечательные числа. Дружественные числа и простые числа-близнецы.
Дружественные числа и простые числа-близнецы.
Занимательная логика в математике
Занимательные задачи
Занимательные задачи далекого прошлого.
Занимательные задачи по математике.
Занимательные числа
Заниматика
Занятные стайки простых чисел.
Зарождение и эволюция математической задачи.
Зачем человеку нужны измерения в разные времена?
Знакомое и незнакомое магическое число Пи.
Знакомство с симметрией
Измерение времени.
Изопериметрическая проблема, или Задача Дидоны.
Изучение возможности использования рисунка на уроках математики.
Интересные и быстрые способы и приемы вычислений.
Интересные и интеллектуальные задачки.
Искусство отгадывать числа
Использование математических разрезных игр.
Использование некоторых положений теории чисел для решения задач повышенной трудности.
Использование старинных мер длины и веса для решения и составления задач.
Исследование математических способностей.
Исследование метода решения задач различными способами.
Исследование ряда натуральных чисел.
Исчисление времени
Как велик миллион?
Как измерить время?
Как измерить расстояние между родственниками.
Как найти решение задачи
Как разрезать пирог?
Как считать без компьютера и калькулятора.
Календари времени
Календарная даль веков
Калькуляторы.
Квадратное колесо — правда или миф?
Контактные числа и проблема тринадцати шаров.
Копилка нестандартных задач по математике.
Королева математики
Красивые и быстрые способы вычислений
Красота в симметрии
Красота и математика
Красота через призму науки
Криптограммы — тайнопись прошлого, настоящего и будущего
Криптография
Криптография и криптоанализ.
Криптография и математика
Криптография и стеганография.
Криптография как метод кодирования и декодирования информации.
Криптография, математические алгоритмы при шифровании.
Криптография. Азы шифрования и история развития.
Криптография. Методы ее практического применения.
Криптография. Наука о шифрах
Кристаллография и математика
Крылатые математические выражения.
Курьезы, софизмы, парадоксы в математике.
Ловкий циркуль
Магические тайны числа 7
Магические числа
Магические числа в природе
Магические числа и фигуры
Магическое число «Пи»
Магическое число Шахерезады.
Магия чисел
Магия чисел 3, 11, 13
Математика в жизни: расчёт ремонтных работ помещения.
Математика в моей будущей профессии.
Математика вокруг нас
Математика на шахматной доске.
Математики-вундеркинды
Математическая обработка экспериментальных данных.
Математическая формула прекрасного.
Математические жемчужины
Математические презентации
Математические софизмы.
Математические термины.
Математический бильярд.
Математический календарь школьникам.
Математический маятник
Математический помощник
Математическое моделирование глобального развития человечества.
Математическое моделирование и его практическое применение.
Математическое моделирование как способ решения задач (проблем).
Математическое моделирование окружающей среды.
Математическое моделирование.
Математическое описание случайных явлений.
Математическое путешествие в мир гармонии.
Материалы для математического досуга.
Мир чисел, звуков и цвета
Моделирование составных задач.
Мир больших чисел.
Моделирование текстовых задач.
Наглядная топология
Неизвестное об известном, или Как сделать открытие. Число Пи равно 4?
Некоторые интересные зависимости.
Необычное в обычных числах
Нестандартные задачи
Нестандартные задачи на олимпиадах по математике.
Нуль в математике занимает особое место.
Нумерации и системы счисления.
Нумерология
Нумерология — магия чисел
Нумерология — миф или реальность?
Нумерология — наука о числах в нашей жизни.
Нумерология — современная наука
Нумерология в жизни человека
Нумерология: наука или заблуждение?
Одним росчерком
Описание красоты и гармонии природы математическим отношением.
Определение в курсе математики
Оптические иллюзии и их применение
Орнамент как отпечаток души народа.
Орнаментальное и геометрическое искусство М. Эшера.
Орнаменты
От пальцев до калькулятора
Открытие: случайность или закономерность?
Очарование простых чисел.
Палиндромы в математике
Параметр. Динамические иллюстрации к решению задач.
Письмо с секретом
Планета чисел
По страницам нестареющих русских учебников по математике.
Практические советы математиков.
Преданья старины далёкой (решение старинных задач)
Приборы, инструменты и приспособления для вычислений.
Прикладные задачи
Применение графических методов при решении текстовых задач.
Применение космических снимков на уроке математики.
Проверка вычисления числа «пи».
Проверка на четность
Простые числа
Противоречие непротиворечивого утверждения.
Путешествие к истокам геометрии.
Развитие понятия «бесконечность» в математике.
Разговор о нуле
Различные способы решения текстовых задач.
Реальный мир воображаемых чисел.
Рекуррентные соотношения и их применение.
Решение диофантовых уравнений
Решение задач методом оценки
Решение задач на смеси и сплавы.
Решение задач на соответствие и исключение неверных ответов.
Решение задач по готовым чертежам.
Решение задач по теме «Движение по реке».
Решение оптимизационных задач по математике.
Решение старинных задач
Решение текстовых задач
Решение уравнений в целых числах.
Самое интересное число
Секрет успешного решения задач.
Семь величайших загадок математики.
Серьезное и курьезное в числах
Симметрические простые числа.
Системы счисления
Скрытые модули
Совершенные числа
Совершенные числа. Дружественные числа.
Совершенные числа. Простые числа Мерсенна.
Сокращенное деление с помощью схемы Горнера.
Сохранить здоровье помогут задачи
Способы и приемы быстрых вычислений.
Способы представления чисел в различных системах счисления.
Способы решения задач на движение тел
Способы устного возведения чисел в квадрат.
Сравнительный анализ устойчивости некоторых известных шифров.
Старинные задачи
Старинные задачи древних народов.
Старинные занимательные задачи
Считаем без калькулятора
Тайна чётных чисел
Тайна числа «Пи»
Текстовые задачи в школьном курсе математики.
Текстовые задачи и моделирование.
Текстовые задачи на движение
Текстовые задачи на смеси, сплавы и растворы.
Текстовые задачи на совместную работу.
Учебник математики: вчера, сегодня, завтра
Фигурные числа
Философская тайна чисел
Философские аспекты математики
Финно-угорская система счисления в ряду других систем.
Фольклорные задачи
Целые числа и измерение температуры.
Цена одной минуты
Цепные дроби
Цифра «9» в тувинской нумерологии.
Цифровые корни
Числа в нашей жизни.
Числа вокруг нас
Числа Пифагора и красота мира.
Числа правят миром
Числа правят миром. Можно ли представить себе мир без чисел?
Можно ли представить себе мир без чисел?
Числа с собственными именами.
Число П.
Число, которое больше Вселенной.
Числовые неравенства
Шестое математическое действие.
Шесть математических действий.
Шифры и криптограммы.
Шифры и математика
Эти удивительные кватернионы.
Перейти к разделам:
Исследовательские работы по математике
Методы исследования
Если Вы хотите разместить ссылку на эту страницу, установите у себя на сайте или форуме один из следующих кодов:
Код ссылки на страницу с темами проектов по математике:
<a href=»http://obuchonok.ru/node/431″ target=»_blank»>Темы исследовательских работ по математике</a>
Код ссылки на форум с темами исследовательских работ по математике:
[URL=http://obuchonok.ru/node/431]Темы исследовательских работ по математике[/URL]
Если страница Вам понравилась, поделитесь в социальных сетях:
Как подтянуть свои знания по математике
Учите математику в школе, колледже или университете? Или просто хотите подтянуть знания по алгебре и геометрии? Тригонометрические функции, уравнения и графики кажутся слишком сложными? Нужен совет, как прокачать математику?
Хотите ли вы подтянуть свои знания по математике как можно быстрее или, напротив, заняться планомерной ревизией всего пройденного материала, чтобы заполнить возможные пробелы, наши советы могут вам пригодиться в любом случае.
В математике важно уметь думать быстро: это понадобится для того, чтобы запоминать формулы, доказательства теорем, многочисленные правила и таблицы. Поэтому первое, что вы можете сделать, это заняться ментальной арифметикой — она позволит вам быстро считать в уме.
На сайте Superprof вы найдёте порядка двадцати советов и приёмов для эффективной ревизии всего пройденного материала по математике. Речь идёт в том числе и о советах, которым обычно не учат в школах. Так что приготовьтесь — мы научим, как преуспеть в математике!
Как прокачать ментальную арифметику?
Конечно, теорема Пифагора важна, как и разница между равнобедренными и прямоугольными треугольниками, однако, не стоит забывать и о ментальной арифметике! Вам может показаться, что это не так важно, как геометрические функции, дифференциальные уравнения и логарифмы, но мы вас убедим в обратном!
Не нужно быть Эйнштейном, чтобы понимать математикуИсточник: Unsplash
Вам не стоит браться за квадратные уравнения, работу со сложными числами и квадратными корнями прежде, чем вы разберётесь с ментальной арифметикой.
Вы можете возразить, что для обычных вычислений существует калькулятор, и он действительно хорош в решении сложных алгебраических задач, однако, если вы не способны самостоятельно в уме или на листе бумаги решить уравнение (а также умножить, поделить, сложить и вычесть числа), то вам наверняка будет сложно прогрессировать в математике.
Так что займитесь обучением ментальной арифметике уже сегодня!
Репетитор может вам в этом помочь. Преимущества дополнительных занятий по математике, онлайн или офлайн, от именитых профессоров или репетиторов, заключаются в том, что они встраиваются в вашу повседневную жизнь легко и естественно. Результат вас впечатлит:
- Вы сможете решать упражнения по математике быстрее,
- Финальная стоимость покупок в магазине станет понятной и предсказуемой,
- Подсчёт пропорций перестанет вводить вас в ступор,
- Вы прокачаете собственную память.
Цель любого учащегося, который хочет стать лучше в математике, это достичь того уровня, когда решение обычных математических задач станет рефлекторным. Если каждый день, то есть регулярно, заниматься ментальной арифметикой, вы непременно достигнете этой цели. Для этого не нужно решать полиномиальные или линейные уравнения, достаточно всего лишь 10 минут упражнений в день.
Если каждый день, то есть регулярно, заниматься ментальной арифметикой, вы непременно достигнете этой цели. Для этого не нужно решать полиномиальные или линейные уравнения, достаточно всего лишь 10 минут упражнений в день.
Есть несколько пунктов, на которые нужно обратить внимание при занятиях математикой. Прежде всего, подготовьте базу — таблицу умножения надо знать наизусть. Желательно заучить и возведение в квадрат, хотя бы до 10. Кроме того, добавьте в ваш арсенал следующие приёмы:
- Всегда смотрите на последнюю цифру числа,
- Научитесь переводить обычную дробь в десятичную,
- Разбирайте числа на составляющие для более лёгкого сложения,
- Упрощайте числа для вычитания,
- Меняйте порядок слагаемых для более удобного сложения,
- Группируйте слагаемые.
Лучшие преподаватели по математике доступны для занятий
Поехали!
Как прокачать навыки счёта
Умение быстро считать может пригодиться где угодно. Речь не только об уроках математики — в школе или дома с репетитором, но и в других дисциплинах. Математика тесно связана с химией и физикой, например. Кроме того, быстрый счёт нужен, как никогда, во время экзаменов, ведь на кону каждая минута.
Математика тесно связана с химией и физикой, например. Кроме того, быстрый счёт нужен, как никогда, во время экзаменов, ведь на кону каждая минута.
Источник: Unsplash
Пробовали ли вы научиться считать быстрее? Начните с самого начала: умножения, деления, сложения и вычитания, квадратных корней и возведения в степень. Заучите соответствующие таблицы хотя бы до 15. Мы также рекомендуем обратиться к репетитору по математике, который сможет заниматься с вами дополнительно онлайн или на дому, решая вместе с вами многочисленные задачи. Репетитор также поделится с вами дополнительными приёмами и техниками.
Репетитор может помочь вам прокачать ваш мозг. Кстати, исследование, проведённое в Калифорнии, показало, что объём человеческого мозга равен примерно одному квадриллиону байт (1 млн Гб). Представляете, как много информации можно там разместить! Добавляя понемногу каждый день, вы сможете существенно продвинуться в математике.
Повторите основы ментальной арифметики и математики. Вы также можете заняться решением прошлогодних экзаменационных работ. Главное, не забывать получать удовольствие от процесса!
Сколько времени требуется, чтобы усовершенствовать свои знания по математике?
После того, как вы разобрались с ментальной арифметикой, время заняться полноценной программой по математике. Подробнее — в нашей статье о том, сколько времени потребуется на то, чтобы прокачать свои математические скиллы.
Сколько уроков потребуется в общей сложности? Это вопрос с подвохом, ведь многое зависит от вашего изначального уровня и целей. Некоторым хватит обычного академического подхода — им достаточно уроков в школе, чтобы добиться нужного результата. Другим необходимо полноценное сопровождение в виде дополнительных занятий по математике с участием репетитора.
Математика — это наука, требующая от учащегося высокого уровня организации. Если же ученик не слишком организован, то вмешательство репетитора попросту необходимо. Мы рекомендуем также сначала разобраться с темой — понять её — прежде, чем заучивать формулы и теоремы. Понять идею и концепт — очень важно, а зубрёжка без понимания не принесёт нужного результата. Кроме того, не подглядывайте в ответы при решении примеров и не списывайте у одноклассников — в этом нет никакого смысла.
Мы рекомендуем также сначала разобраться с темой — понять её — прежде, чем заучивать формулы и теоремы. Понять идею и концепт — очень важно, а зубрёжка без понимания не принесёт нужного результата. Кроме того, не подглядывайте в ответы при решении примеров и не списывайте у одноклассников — в этом нет никакого смысла.
В конце концов, будьте внимательны и любознательны, задавайте вопросы и не забывайте про практику. Всё это — обязательные составляющие прогресса в математике. Помните также о том, что совершенствование в математике мало отличается от совершенствования в чтении. Фокусируйтесь на терминах и используемых дефинициях. Постарайтесь не отвлекаться, не будьте слишком самоуверенны, не пытайтесь выучить всю математику в ночь перед экзаменом и не надейтесь на калькулятор в любой непонятной ситуации.
Несколько стратегий, чтобы преуспеть в математике
Взглянем на более важные вещи. Какая цель у всех этих дополнительных материалов, репетиторов и практических занятий? Для обычного ученика целью будут, конечно, хорошие оценки по математике!
Но как их заполучить?
Неважно, учитесь ли вы в начальных классах школы или старших, в профильном лицее или университете, вам помогут вот эти 10 советов:
- Убедитесь, что вы поняли тему прежде, чем приступить к следующей главе,
- Тренируйте свою память, регулярно выполняя упражнения по математике,
- Если вы не понимаете, как решить задачу, запишите на бумаге все этапы для её решения,
- Работайте в спокойной тихой обстановке: дома или в библиотеке,
- Не пренебрегайте помощью друзей: решайте вместе дифференциальные уравнения, обсуждайте тему интегралов, теорию вероятностей, тригонометрию и так далее.
 Вы можете вместе решать прошлогодние экзаменационные работы или разбирать сложные темы,
Вы можете вместе решать прошлогодние экзаменационные работы или разбирать сложные темы, - Пошагово записывайте ваши решения. Это поможет вам в будущем,
- Никогда не пишите сразу на чистовик,
- Используйте черновики и карандаши,
- Никогда не учитесь допоздна — это негативно скажется на ваших успехах,
- Визуализируйте задачи, если не понимаете, как приступить к решению.
Математические приёмы, которым не научат в школе
Можете перечислить цифры числа Пи, что следуют сразу за 3.14?
Как много цифр числа Пи вы помните?Источник: Unsplash
Чтобы дополнить вашу Олимпийскую подготовку к математике, мы собрали 10 классных математических приёмов, которым вас не научат в школе, но которые способны существенно облегчить повседневную жизнь:
- Перевод градусов Фаренгейта в градусы Цельсия и наоборот. Идеально для путешествий!
- Способность вычислить день недели, зная полную дату. Вы сможете по-настоящему впечатлить друзей!
- Умножение и деление больших чисел в уме,
- Умножение на 11,
- Запоминание цифр числа Пи,
- Возведение чисел в квадрат,
- Сложение и вычитание дробей,
- Нахождение кратных чисел,
- Перевод зарплаты из годовой в почасовую,
- Возведение в квадрат чисел, кратных 5.

Тесты по математике для 4 класса онлайн
Таблица умножения
-
ВПР 4 класс, математика. 22 вариант
25.04.2017 233634
Проверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий.
-
1 вариант ВПР 4 класс, математика.
12.05.2017 90595
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.Обязательные ответы на все вопросы теста.
-
2 вариант ВПР 4 класс, математика
12.
 05.2017
39814
05.2017
39814
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.Обязательные ответы на все вопросы теста.
-
Таблица умножения
08.07.2017 295785
Тест предназначен для закрепления изученного материала и его повторения. Удачи в прохождении!
-
4 сынып тест №1
27.11.2021 130468
Қазақ тілі, математика, әдебиеттік оқу пәндері бойынша тестте 30 сұрақ берілген
-
Математика решение задач
30.
 01.2021
58293
01.2021
58293
тест для учащихся 3-4 классов по математике задания не простые. Пожелаем удачи.
-
3 вариант ВПР 4 класс, математика
12.05.2017 18430
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.Обязательные ответы на все вопросы теста.
-
На сколько хорошо ты знаешь таблицу умножения?
10.09.2015 122890
Проверим на сколько хорошо ты знаешь (или недавно выучил) таблицу умножения? Всю таблицу спрашивать не будем. А вот 25 примеров порешаем?!
-
5 вариант ВПР 4 класс, математика
13.
 05.2017
11071
05.2017
11071
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
ВПР 4 класс, математика. 21 вариант
25.04.2017 40721
Проверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий.
-
таблица умножения от 2 до 15
04.10.2020 23121
13 заданий. Критерии: «5» — 13 баллов, «4» — 11-12 баллов, «3» — 9-10 баллов.
-
Тест по математике 4 класс
25.
 09.2015
191677
09.2015
191677
Проверочная работа по математике за курс начального общего образования
-
ВПР 4 класс, математика. 24 вариант
25.04.2017 12442
Проверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий.
-
перевод единиц измерения величин
05.05.2020 4467
Тест по математике для учащихся 4-5 классов. Тест включает в себя как задания на перевод величин в различные единицы измерения, так и на действия с ними. В тесте 15 вопросов, из них 11 с открытым ответом и 4 с множественным выбором.

-
7 вариант ВПР 4 класс, математика
14.05.2017 5899
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
4 вариант ВПР 4 класс, математика
13.05.2017 183894
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.Обязательные ответы на все вопросы теста.
-
10 вариант ВПР 4 класс, математика
14.
 05.2017
6867
05.2017
6867
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
6 вариант ВПР 4 класс, математика
13.05.2017 8684
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
8 вариант ВПР 4 класс, математика
14.05.2017 7010
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
 Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста. -
4-SINF O’QUVCHILARI UCHUN MATEMATIKA FANIDAN ONLAYN OLIMPIADA
11.01.2022 4098
4-SINF O’QUVCHILARI UCHUN MATEMATIKA FANIDAN ONLAYN OLIMPIADA.
-
Математика задание 3.8
06.02.2021 11708
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Олимпиада для Начальной школы 4 класс Математика
16.
 04.2020
5725
04.2020
5725
Тест предназначен для учеников 4 классов.
-
12 вариант ВПР 4 класс, математика
16.05.2017 6004
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
11 вариант ВПР 4 класс, математика
15.05.2017 4680
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
 Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста.
-
9 вариант ВПР 4 класс, математика
14.05.2017 5537
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
13 вариант ВПР 4 класс, математика
16.05.2017 5613
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста.
-
МАТЕМАТИКА 4-СИНФ
12.
 05.2020
2444
0
05.2020
2444
0
Тестҳои мазкур барои хонандагони синфи 4-уми мактабҳои тоҷикӣ ва ӯзбекӣ тайёр карда шудааст
-
Тест по математике для учащихся 4 класса по теме: Периметр.Площадь. Единицы площади
24.11.2014 22622
Тест включает задания на нахождение площади и периметра прямоугольников. В тесте размещены задания базового и программного уровня. Задания базового уровня оцениваются в 1 балл, программного в 2 балла.
-
ВПР математика 4 кл
06.01.2022 588
Тренировочный тест по математике для подготовки к впр.
 Включает в себя выражения для вычисления, решение арифметических и геометрических задач.
Включает в себя выражения для вычисления, решение арифметических и геометрических задач. -
Готовимся к ВПР. Задание № 3 «Арифметический метод».
31.07.2022 558
Готовимся к ВПР: задание № 3. Тест по теме: «Арифметический метод». Предназначен для проверки умения решать практико-ориентированные задачи.
-
Задачи на движение. 4 класс. Вариант 1.
26.08.2017 12156
Тесты для учащихся 4 классов состоящие из всех видов задач на движение
-
Нумерация многозначных чисел
10.
 12.2020
469
0
12.2020
469
0
Задания в тестовой форме по теме: «Нумерация многозначных чисел» для обучающихся 4 класса. Проверяемые предметные умения: Читать натуральные числа в пределах миллиона Сравнивать числа в пределах миллиона Представлять многозначное число в виде суммы разрядных слагаемых. В тест включено 12 вопросов с одним вариантом ответа. Для успешного прохождения необходимо ответить правильно не менее 70% вопросов.
-
Готовимся к ВПР. Задание № 2 «Арифметические действия с числами»
29.07.2022 543
Готовимся к ВПР: задание № 2. Тест по теме: «Арифметические действия с числами». Предназначен для проверки знаний обучающихся о порядке действий в выражениях со скобками и без на основе четырех арифметических действий.

-
Математика. Устный счет 4 класс
25.03.2020 7225
Математика. Устный счет . 4 класс 4 четверть.
-
Математический диктант для учащихся 4 класса. Нумерация многозначных чисел
26.11.2014 20102
Математический диктант направлен на формирование устного счета и повторение материала по теме «Нумерация многозначных чисел»
-
Финансовая грамотность 4 класс
19.
 04.2022
279
04.2022
279
Тест предназначен для учащихся 4-го класса по теме «Финансовая грамотность»
-
Математика 4 класс ВПР
11.05.2020 5372
Решение разных типов заданий заданий из ВПР по математике 4 класса, для проверки своих знанийи закрепления тем.
-
ВПР по математике 4 класс. 2020
21.05.2020 400
Проверочная работа по математике Демоверсии ВПР 2020 года для 4 класса Образец
-
ВПР 4 класс
07.
 03.2022
571
03.2022
571
С помощью теста вы сможете понять готовы ли вы к ВПР. А также потренероваться перед экзаменом!
-
Итоговый тест по математике для 4 класса №1.
25.02.2014 182986
Итоговый тест за курс 4 класса по математике. Содержит 20 заданий. Выполнение теста ограничено по времени.
-
Математика 4 класс ВПР 2020
11.04.2020 46829
Проверочная работа по математике Демоверсии ВПР 2020 года для 4 класса Образец
-
31.
 03.2020 математика ВПР
03.2020 математика ВПР
31.03.2020 646
Тест ВПР по математике предназначен для учащихся 4 класса. Подготовка к ВПР
-
Дистанционная олимпиада для обучающихся 4 класса
26.01.2018 3774
Дистанционная олимпиада. Задания по математике, русскому языку, литературному чтению, математике
-
Математический диктант 4 класс
12.02.2022 107
Математический диктант, 4 класс, программа 21 век. Инструкция по работе с тестом: Тест расчитан на 10 мин.
 Время прохождения ограничено. Внимательно прочитайте пример и отметьте галочкой ответ в окошечке. Дальнейшее прохождение не возможно если ответ не введён. По окончанию теста вы получите сертификат о прохождении, в котором фиксируется ваши результаты. Удачи в прохождении!
Время прохождения ограничено. Внимательно прочитайте пример и отметьте галочкой ответ в окошечке. Дальнейшее прохождение не возможно если ответ не введён. По окончанию теста вы получите сертификат о прохождении, в котором фиксируется ваши результаты. Удачи в прохождении! -
МОДО 4 класс
08.04.2022 7837
Тест для подготовки к МОДО в 4 классе. Тест по математической, читетнльской и естественно-научной грамотности.
-
Решение задач
02.04.2014 21582
Данный тест для учащихся 4 класса поможет провести повторение и закрепление умений решать задачи, поможет привить любовь к математике
-
Тест по математике для 4 класса по теме: Деление многозначного числа на однозначное
12.
 03.2015
6949
03.2015
6949
Проверь свои знания по математике по теме: Деление многозначного числа на однозначное. Внимательно читай задания и у тебя всё получится. Успехов тебе!
-
5 класс. Математика. Сложение и вычитание натуральных чисел №5
30.06.2016 220 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на сложение и вычитание натуральных чисел
-
Таблица умножения 2
02.02.2021 3731
Это тест по таблице умножения 2. Тут более все усложненноё и для 3 класса и выше.
 Удачи в прохождении и надеемся что наш тест вам понравится.
Удачи в прохождении и надеемся что наш тест вам понравится. -
устный счёт «Сложение и вычитание в пределах 100″
20.09.2020 1285 0
Задания для устного счета на сложение и вычитание натуральных чисел с переходом через десяток. В тесте 20 заданий, которые выбираются случайным образом из базы заданий. Оценка «5» — за 91-100%, «4» — за 70-90%, «3» — за 50-69% верных ответов.
-
Математика 3 класс задание 3.4
02.02.2021 324
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Таблица умножения 4
05.
 02.2021
807
02.2021
807
Это таблица умножения 4, от 1 до 100. Самая усложнённая венрсия на данный момент.
-
Входная контрольная работа по математике 4 класс
04.03.2021 606
Входная контрольная работа по математике в 4 классе с ответами для УМК «Школа России» (авт: М.И.Моро и др.)
-
Математика. Входной тест по теме «Сложение и вычитание многозначных чисел».
03.06.2017 818
Тест предназначен для диагностики предметных умений по математике, тема «Сложение и вычитание многозначных чисел»
-
ЧИСЛА, КОТОРЫЕ БОЛЬШЕ 1000.
 НУМЕРАЦИЯ
НУМЕРАЦИЯ
21.03.2021 527 0
Тест по математике для 4 класса начальной школы. Составлен в соответствии с программой и УМК для 4 класса авторского коллектива под руководством М. И. Моро
-
Умножение и деление многозначных чисел
10.06.2021 254
Тест для 4 класса по математике на тему «Умножение и деление многозначных чисел»
-
4 класс — итоговый по стандартной программе.
13.06.2015 12027
Итоговый тест для выпускников стандартной начальной школы 1-4 классов.
 Оценивается по 5-бальной шкале.
Оценивается по 5-бальной шкале. -
5 класс. Математика. Действия с натуральными числами №2
02.07.2016 2298
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
Контрольный тест за курс начальной школы
06.10.2016 2536
Диагностический разноуровневый тесты является одним из способов проверки знаний и умений учащихся, направленных на выявление степени усвоения изученного материала, пробелов в знаниях учащихся 4 классов и проведения более тщательной коррекции.
-
Решение задач в 4 классе
18.
 10.2016
8436
10.2016
8436
Тест предназначен для контроля знаний обучающихся 4 класса по теме «Решение задач»
-
Умножение и деление на однозначные числа (4 класс)
23.10.2016 2029
Тест предназначен для контроля базовых знаний по математике на тему «Умножение и деление на однозначные числа» за курс начальной школы в форме ЕГЭ
-
Математика, 4 класс. Доли.
08.12.2018 1761
Тест предназначен для контроля качества усвоения материала по теме «Доли».
-
Математика задание 3.
 1
1
02.02.2021 295
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Тест по таблице умножения
08.02.2021 981
Тест по математике. Проверим ваше знание таблицы умножения! Мой тест можно узнать по начальной картинке⬆️
-
Меры величин
05.10.2021 516 0
Тема: «Меры величин» Класс: 4
-
Чтение и запись многозначных чисел (миллионы, миллиарды)
09.
 11.2021
139
0
11.2021
139
0
Тест по математике по теме: «Чтение и запись многозначных чисел» 4 класс
-
Вспомним первый класс
18.12.2013 22379
Вспомним первый класс. Такие простые были примеры, но если оно так и есть, тогда сейчас проверим. Начнем?
-
Многозначные числа
07.09.2014 2424
Тест проверяет умение читать и записывать многозначные числа.
-
Тест по математике для 4 класса «Четыре арифметических действий»
19.
 02.2015
886
02.2015
886
Тест по математике для 4 класса по теме «Четыре арифметических действия»
-
Итоговый тест по математике для 4 класса
11.10.2016 11835
Итоговый тест за курс 4 класса по математике. Содержит 11 заданий. Выполнение теста ограничено по времени.
-
Периметр и площадь геометрических фигур (4 класс)
17.10.2016 4876
Тест для контроля знаний по теме «Периметр и площадь геометрических фигур» для 4 класса, для любого УМК
-
Арифметические действия.
 Устные вычисления (математика 4 класс)
Устные вычисления (математика 4 класс)
17.10.2016 955
Тест для контроля знаний по математике по теме «Арифметические действия. Устные вычисления» для обучающихся 4 класса
-
Четыре арифметических действия (4 класс)
23.10.2016 519
Тест предназначен для контроля базовых знаний по математике на тему «Четыре арифметических действия» за курс начальной школы в форме ЕГЭ
-
Нумерация (4 класс)
23.10.2016 1853
Тест предназначен для контроля базовых знаний по математике на тему «Нумерация» за курс начальной школы в форме ЕГЭ
-
Величины (4 класс)
23.
 10.2016
6930
10.2016
6930
Тест предназначен для контроля базовых знаний по математике на тему «Величины» за курс начальной школы в форме ЕГЭ
-
Умножение и деление на двухзначное и трехзначное число (4 класс)
24.10.2016 6283
Тест предназначен для контроля базовых знаний по математике на тему «Умножение и деление на двухзначное и трехзначное число» за курс начальной школы в форме ЕГЭ
-
Тест по математике №4, 4 класс
30.01.2019 4922
Проверочная работа по математике 4 класс. Цель: проанализировать результаты усвоения основных тем программы.

-
Математика задание 4.1
06.02.2021 435
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 4.2
06.02.2021 305
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
ИТОГОВЫЙ ТЕСТ ЗА КУРС НАЧАЛЬНОЙ ШКОЛЫ
21.03.2021 1436 0
Тест по математике для 4 класса начальной школы.
 Составлен в соответствии с программой и УМК для 4 класса авторского коллектива под руководством М. И. Моро
Составлен в соответствии с программой и УМК для 4 класса авторского коллектива под руководством М. И. Моро -
Математический диктант
02.02.2014 28254
Тест проводится на этапе устного счёта урока математика в 4 классе. Тема умножение многозначного числа на на круглое число.
-
Итоговый тест по математике для 4 класса №2.
10.03.2014 39507
Итоговый тест по математике на конец 4 класса. Тест состоит из 20 заданий, с выбором одного правильного ответа из предложенных вариантов. Выполнение теста ограничено по времени.
-
Математика.
 4 класс. Числа и величины.
4 класс. Числа и величины.
22.03.2014 4960
Тест составлен на основе примерных заданий для итоговой оценки достижения планируемых результатов. Раздел «Числа и величины».
-
Тест по математике (4 класс) 3 четверть
14.03.2015 8774
Тест по математике за 3-ю четверть 4 класса. Время не ограничено. В тесте всего 7 простых заданий.
-
5 класс. Математика. Сложение и вычитание натуральных чисел №2
26.06.2016 516
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на сложение и вычитание натуральных чисел
-
5 класс.
 Математика. Сложение и вычитание натуральных чисел №3
Математика. Сложение и вычитание натуральных чисел №3
30.06.2016 267 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на сложение и вычитание натуральных чисел
-
5 класс. Математика. Сложение и вычитание натуральных чисел №4
30.06.2016 829
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на сложение и вычитание натуральных чисел
-
5 класс. Математика. Сложение и вычитание натуральных чисел №6
30.06.2016 281
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на сложение и вычитание натуральных чисел
-
5 класс.
 Математика. Умножение и деление натуральных чисел №1
Математика. Умножение и деление натуральных чисел №1
30.06.2016 1357 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс. Математика. Умножение и деление натуральных чисел №2
30.06.2016 442 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс. Математика. Умножение и деление натуральных чисел №3
30.06.2016 655
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс.
 Математика. Умножение и деление натуральных чисел №4
Математика. Умножение и деление натуральных чисел №4
30.06.2016 387 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс. Математика. Умножение и деление натуральных чисел №5
30.06.2016 661
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс. Математика. Умножение и деление натуральных чисел №6
30.06.2016 607
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на умножение и деление натуральных чисел
-
5 класс.
 Математика. Действия с натуральными числами №1
Математика. Действия с натуральными числами №1
02.07.2016 985
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
5 класс. Математика. Действия с натуральными числами №3
02.07.2016 285 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
5 класс. Математика. Действия с натуральными числами №4
02.07.2016 239
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
5 класс.
 Математика. Действия с натуральными числами №5
Математика. Действия с натуральными числами №5
02.07.2016 1169 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
5 класс. Математика. Действия с натуральными числами №6
02.07.2016 280 0
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
Устные и письменные приемы вычислений. Сложение и вычитание (4 класс)
23.10.2016 517 0
Тест предназначен для контроля базовых знаний по математике на тему «Устные и письменные приемы вычислений.
 Сложение и вычитание» за курс начальной школы в форме ЕГЭ
Сложение и вычитание» за курс начальной школы в форме ЕГЭ
| n value | n-sided polygon | Approximation Pi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 2.8284271247461 | 6033774484193961571393437507539|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 8 | 3.061467458 81738276798722431 0499885 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 16 | 3.12144515225805228555725578956323558548430658840312 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 32 | 3.1365484 | 9314258044436535637354136|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 64 | 3.140331156954752 | 71185243316|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 128 | 3.1412772509327728680620197707882144083796632626497 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 256 | 3.1415138011443010763285150594568223079353138154929 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 512 | 3.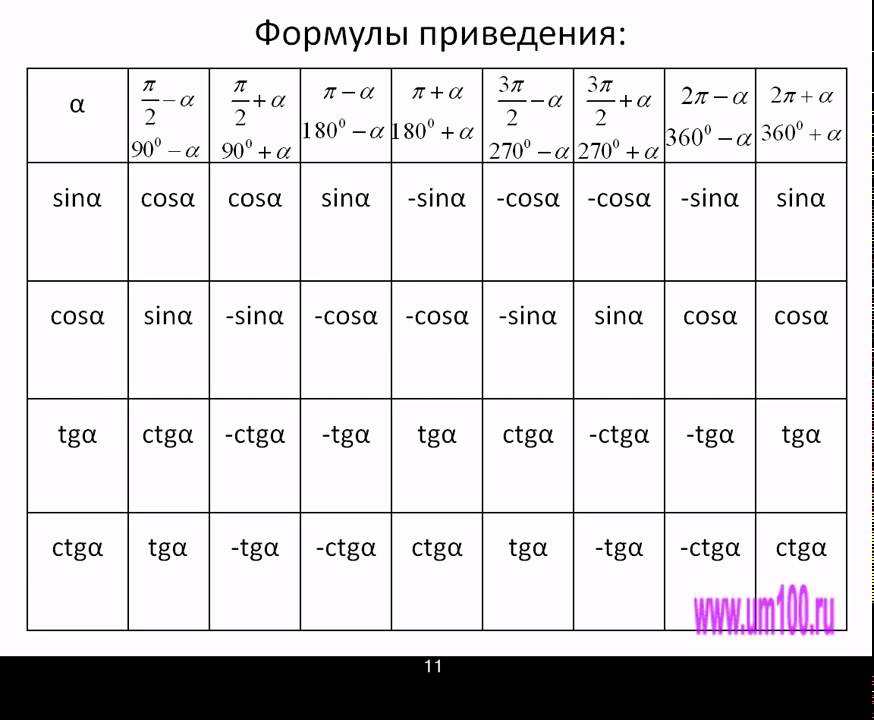 1415729403670 1415729403670 | 1358001102707614295336377945043 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 1,024 | 3.141587725277159700628854262701939585748 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 2,048 | 3.14155111999739979717637408339557475626500861 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 4,096 | 3.14155701177423403759941573699303052060756511 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 8,192 | 3.141558487266568160608753097320532784311 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 16,384 | 3.141533856298| 14 | 32,768 | 3.141577698566948510796 | 770756977660019063 15 | 65,536 | 3.14153865 | 8035255210579638843386552441744 16 | 131,072 | 3.1415 | 28892719430421737400034605760375256 17 | 262,144 | 3. |  1415 14155145931201633482432810804326516595198228 18 | 524,288 | 3.1415 | 57099320888771834485977211465153507 19 | 1,048,576 | 3.1415 | 533581234081942333585093231068 20 | 2,097,152 | 3.1415 | 588618236614208540788498096272 | 21 | 4,194,304 | 3.1415 | 5894994880005346604326558615457887249375 22 | 8,388,608 | 3.1415 | 589719800847116201022786548981288773909 23 | 16,777,216 | 3.1415 | 61587618761014171133317717258977487 24 | 33,554,432 | 3.1415 | 5897886486116729343582822425517812397356 25 | 67,108,864 | 3.1415 | 5897920 26 | 134,217,728 | 3. |  1415 14155897929515969577302218087195994326561128 27 | 268,435,456 | 3.1415 | 5897931667462219700150778696165489637681 28 | 536,870,912 | 3.1415 | 5897932205335380299633965384625651498614 29 | 1,073,741,824 | 3.1415 | 589793233980367044950476257084 30 | 2,147,483,648 | 3.1415 | 58979323734207429869724623575802529 | 31 | 4,294,967,296 | 3.1415 | 58979323818250111213393872207292754 32 | 8,589,934,592 | 3.1415 | 58979323838154931118436647038557834 33 | 17,179,869,184 | 3.1415 | 589793238445134440639651 | 7 | 34 | 34,359,738,368 | 3.1415 | 5897932384582661602928534441638628581061 35 | 68,719,476,736 | 3. |  1415 141558979323846154328405241888424209979 36 | 137,438,953,472 | 3.1415 | 5897932384623698068428372941950876333395 37 | 274,877,906,944 | 3.1415 | 58979323846257498364866966489565261 38 | 549,755,813,888 | 3.1415 | 5897932384626262847522112848220392885791 39 | 1,099,511,627,776 | 3.1415 | 58979323846263476799843533868716709 | 40 | 2,199,023,255,552 | 3.1415 | 58979323846264231462154715237674487 41 | 4,398,046,511,104 | 3.1415 | 55897932384626431161150139529569329 42 | 8,796,093,022,208 | 3.1415 | 5897932384626433164883806513871102973797 43 | 17,592,186,044,416 | 3.1415 | 5897932384626433665817223259946546238762 44 | 35,184,372,088,832 | 3. | 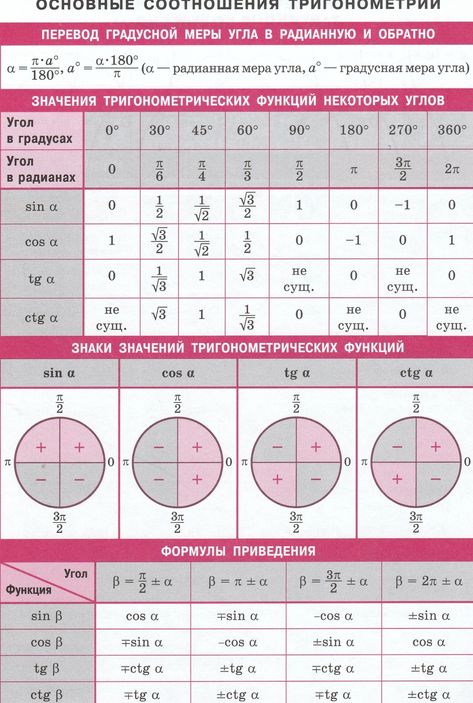 1415 141558979323846264337577446465407055004 45 | 70,368,744,177,664 | 3.1415 | 58979323846264338223583095122259064 46 | 140,737,488,355,328 | 3.1415 | 5897932384626433830186000629752551060079 47 | 281,474,976,710,656 | 3.1415 | 58979323846264338321427717889160333 | 48 | 562,949,953,421,312 | 3.1415 | 5897932384626433832631964578707997560397 49 | 1,125,899,906,842,624 | 3.1415 | 5897932384626433832754262776155769885413 50 | 2,251,799,813,685,248 | 3.1415 | 5897932384626433832784837325517712966667 51 | 4,503,599,627,370,496 | 3.1415 | 5897932384626433832796285819873698 52 | 9,007,199,254,740,992 | 3.1415 | 58979323846264338327943193320179558 53 | 18,014,398,509,481,984 | 3. | 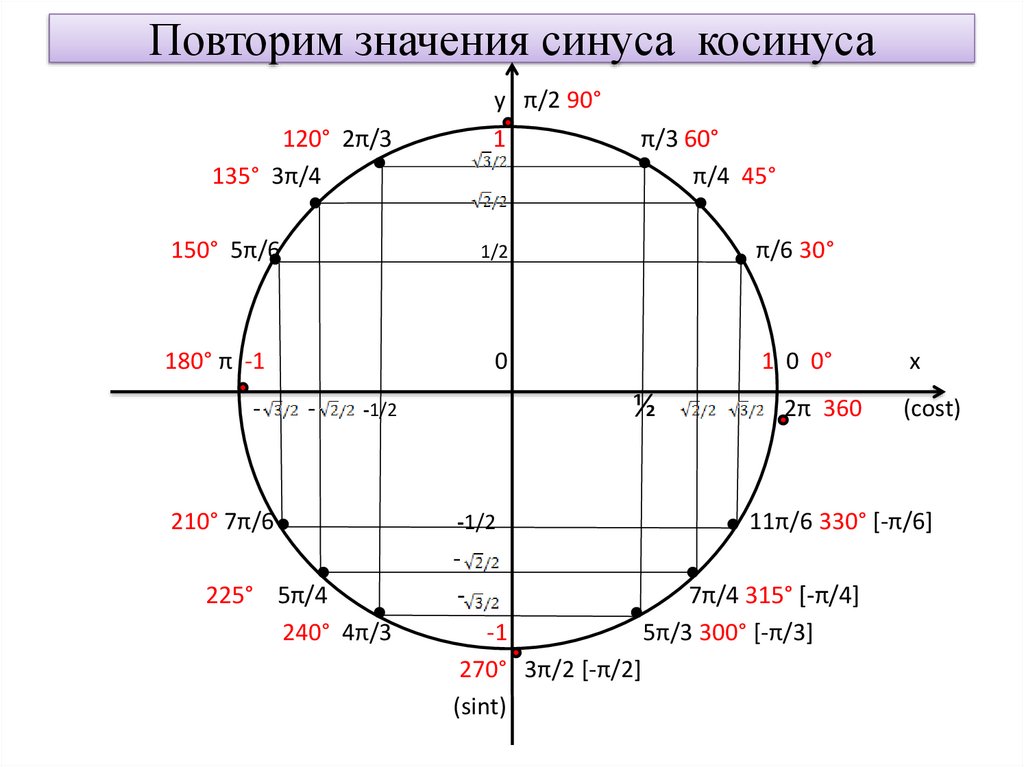 1415 14155897932384626433832794869599527100540203 54 | 36,028,797,018,963,968 | 3.1415 | 60545630364589793238462643383279498 55 | 72,057,594,037,927,936 | 3.1415 | 58979323846264338327950188893189065 | 56 | 144,115,188,075,855,872 | 3.1415 | 589793238462643383279502635380849722104 57 | 288,230,376,151,711,744 | 3.1415 | 5897932384626433832795028219930894800573 58 | 576,460,752,303,423,488 | 3.1415 | 5897932384626433832795028686461494195457 59 | 1,152,921,504,606,846,976 | 3.1415 | 5897932384626433832795028803094144044178 60 | 2,305,843,009,213,693,952 | 3.1415 | 5897932384626433832795028832252306506358 61 | 4,611,686,018,427,387,904 | 3. |  1415 14155897932384626433832795028839541847121903 62 | 9,223,372,036,854,775,808 | 3.1415 | 5897932384626433832795028841364232275789 63 | 18,446,744,073,709,551,616 | 3.1415 | 5897932384626433832795028841819828564261 64 | 36,893,488,147,419,103,232 | 3.1415 | 5897932384626433832795028841933727636379 65 | 73,786,976,294,838,206,464 | 3.1415 | 5897932384626433832795028841962202404408 66 | 147,573,952,589,676,412,928 | 3.1415 | 5897932384626433832795028841969321096416 67 | 295,147,905,179,352,825,856 | 3.1415 | 5897932384626433832795028841971100769418 68 | 590,295,810,358,705,651,712 | 3.1415 | 5897932384626433832795028841971545687668 69 | 1,180,591,620,717,411,303,424 | 3. |  1415 141558979323846264338327950288419716561 70 | 2,361,183,241,434,822,606,848 | 3.1415 | 5897932384626433832795028841971684724622 71 | 4,722,366,482,869,645,213,696 | 3.1415 | 58979323846264338327950288419716469 72 | 9,444,732,965,739,290,427,392 | 3.1415 | 5897932384626433832795028841971693414431 73 | 18,889,465,931,478,580,854,784 | 3.1415 | 5897932384626433832795028841971693848922 74 | 37,778,931,862,957,161,709,568 | 3.1415 | 5897932384626433832795028841971693957544 75 | 75,557,863,725,914,323,419,136 | 3.1415 | 58979323846264338327950288419716939847 76 | 151,115,727,451,828,646,838,272 | 3.1415 | 58979323846264338327950288419716939 77 | 302,231,454,903,657,293,676,544 | 3. | 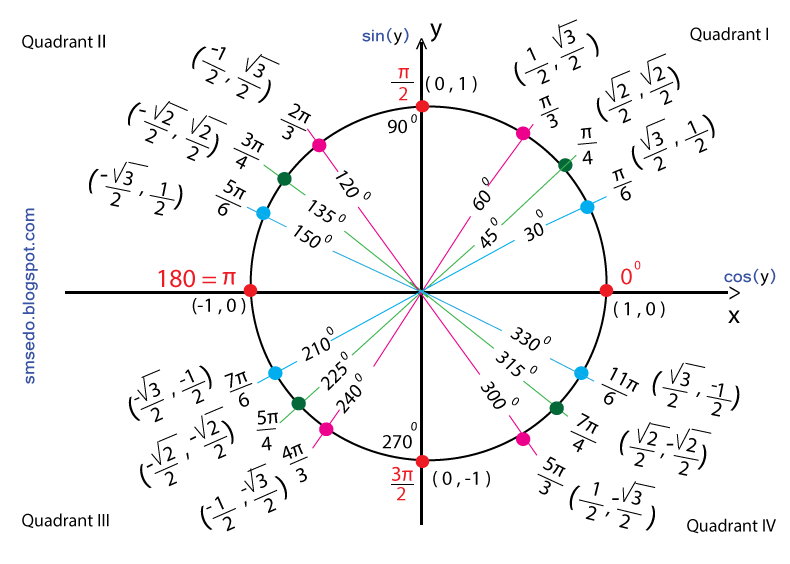 1415 14155897932384626433832795028841971693993186 78 | 604,462,909,807,314,587,353,088 | 3.1415 | 5897932384626433832795028841971693993611 79 | 1,208,925,819,614,629,174,706,176 | 3.1415 | 5897932384626433832795028841971693993717 80 | 2,417,851,639,229,258,349,412,352 | 3.1415 | 5897932384626433832795028841971693993743 81 | 4,835,703,278,458,516,698,824,704 | 3.1415 | 589793238462643383279502884197169399375 82 | 9,671,406,556,917,033,397,649,408 | 3.1415 | 5897932384626433832795028841971693993752 83 | 19,342,813,113,834,066,795,298,816 | 3.1415 | 5897932384626433832795028841971693993752Формула Виете — это бесконечное произведение вложенных радикалов, представляющее математическую константу π | ||
Значение числа Пи — символ, примеры, значения числа Пи
Значение числа Пи — это отношение длины окружности к ее диаметру .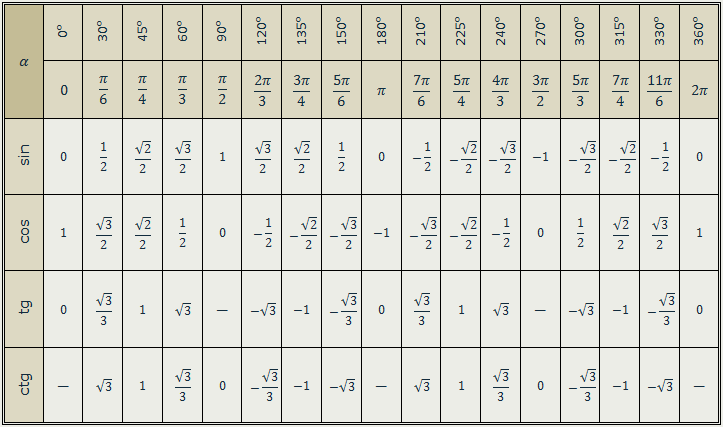 Символ пи обозначается как π. Ее также называют константой Архимеда, которая была названа в честь греческого математика Архимеда, который создал алгоритм для аппроксимации значения числа пи. Значение числа пи иррационально, а это означает, что количество цифр после запятой бесконечно. Он используется как 3.1415929 или 22/7. В геометрии он используется для вычисления площади поверхности, объема и длины окружности различных трехмерных фигур.
Символ пи обозначается как π. Ее также называют константой Архимеда, которая была названа в честь греческого математика Архимеда, который создал алгоритм для аппроксимации значения числа пи. Значение числа пи иррационально, а это означает, что количество цифр после запятой бесконечно. Он используется как 3.1415929 или 22/7. В геометрии он используется для вычисления площади поверхности, объема и длины окружности различных трехмерных фигур.
| 1. | Каково значение числа Пи? |
| 2. | Символ для Пи |
| 3. | Формула для Пи |
| 4. | Как рассчитать число Пи? |
| 5. | Значение числа Пи в десятичных дробях |
| 6. | Значение числа Пи в дробях |
| 7. | Значение числа Пи в градусах |
| 8. | Часто задаваемые вопросы о значении Pi |
Каково значение числа Пи?
Значение «пи» является постоянным, что означает, что его нельзя изменить. Это иррациональное число, обычно приближающееся к 3,14. Он используется в различных формулах для измерения площади поверхности и объема различных твердых тел. «Пи» определяется как отношение длины окружности к диаметру окружности. Мы знаем, что диаметр окружности — это самый длинный отрезок, проходящий через центр окружности. Представьте, что линия диаметра изогнута так, что она охватывает часть окружности круга. Теперь π определяется как общее количество раз, когда диаметр оборачивается вокруг окружности, что примерно равно 3,14 раза.
Это иррациональное число, обычно приближающееся к 3,14. Он используется в различных формулах для измерения площади поверхности и объема различных твердых тел. «Пи» определяется как отношение длины окружности к диаметру окружности. Мы знаем, что диаметр окружности — это самый длинный отрезок, проходящий через центр окружности. Представьте, что линия диаметра изогнута так, что она охватывает часть окружности круга. Теперь π определяется как общее количество раз, когда диаметр оборачивается вокруг окружности, что примерно равно 3,14 раза.
Если длину окружности разделить на диаметр, то получится примерно 3,14. Следует отметить, что какого бы размера круг мы ни рисовали, отношение длины окружности к его диаметру всегда будет одинаковым.
Символ числа Пи
Символ, используемый для обозначения числа пи в математике, это π, , который используется в греческих буквах. Он известен как математическая константа, поскольку его значение не меняется. Символ пи представляет 22/7 в дробях или 3,14 (приблизительно) в десятичных дробях.
Символ пи представляет 22/7 в дробях или 3,14 (приблизительно) в десятичных дробях.
Формула для Пи
Число Пи можно получить, разделив длину окружности на ее диаметр. Поскольку пи — это отношение длины окружности к ее диаметру, формула для вычисления π выглядит следующим образом:
π = длина окружности/диаметр
Одно интересное утверждение, которое помогает нам запомнить значение числа пи, звучит так: «Как бы я хотел Я мог вычислить число пи». Подсчитав количество букв в каждом слове, мы можем легко записать значение числа пи. Так как «Как» имеет 3 письма; «Я» — 1 буквы, «желание» — 4 буквы, «Я» — 1 буквы, «мог» — 5 буквы, «вычислить» — 9 буквы, «пи» — 2 письма. Следовательно, значение числа пи, округленное до 6 знаков после запятой, равно 3,141592.
Как рассчитать число Пи?
Значение числа Пи можно рассчитать с помощью простого действия.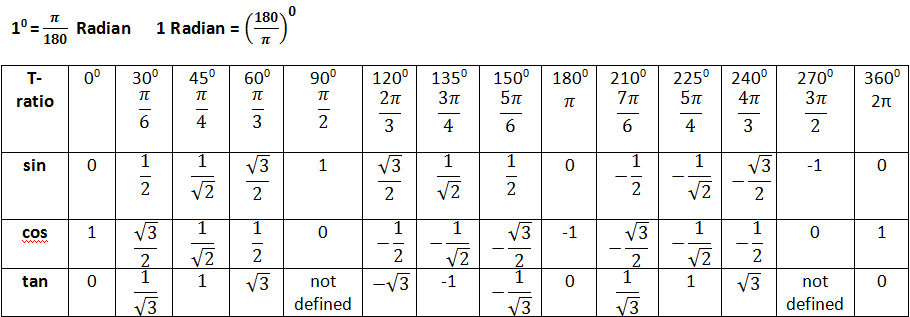 Следуйте шагам, приведенным ниже, чтобы узнать, почему значение числа пи является отношением длины окружности к диаметру круга:
Следуйте шагам, приведенным ниже, чтобы узнать, почему значение числа пи является отношением длины окружности к диаметру круга:
- Шаг 1: Нарисуйте круг диаметром 1 единица.
- Шаг 2: После этого шага возьмите нитку и проложите ее по границе круга (окружности).
- Шаг 3: Теперь поместите нить на линейку и отметьте длину.
Повторите процесс с диаметрами 2 единиц, 3 единиц, 4 единиц, 5 единиц и запишите свои наблюдения в таблицу.
| Диаметр | Окружность | Длина окружности/диаметр |
|---|---|---|
| 1 шт. | 3,1 шт. | 3.1/1 |
| 2 шт. | 6,2 шт. (прибл.) | 6,2/2 = 3,1 |
| 3 шт. | 9,3 шт. (прибл.) | 9,3/3 = 3,1 |
| 4 шт. | 12,4 шт. (прибл.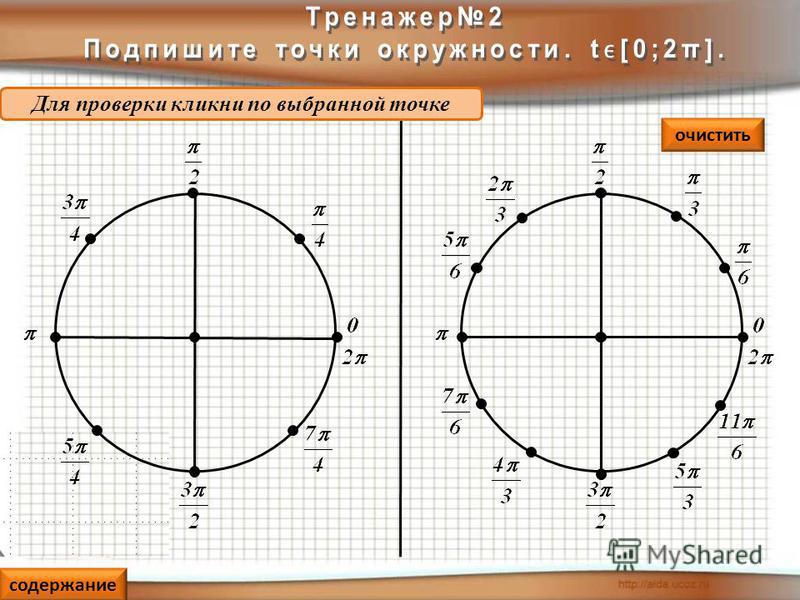 ) ) | 12,4/4 = 3,1 |
| 5 шт. | 15,5 шт. (прибл.) | 15,5/5 = 3,1 |
Мы можем заметить, что отношение длины окружности к диаметру всегда одинаково и равно 3,1.
Значение числа Пи в десятичных дробях
Как обсуждалось выше, значение числа пи является иррациональным числом, что означает бесконечность десятичных знаков после числа 3. 100 десятичных знаков числа пи состоят из всех цифр от 0 до 9.. Есть восемь нулей, восемь единиц, двенадцать двоек, одиннадцать троек, десять четверок, восемь пятерок, девять шестерок, восемь семерок, двенадцать восьмерок и четырнадцать девяток. Обратите внимание на приведенный ниже рисунок, который показывает, что значение пи в десятичных дробях начинается с 3, а 100 -я десятичная цифра содержит число 9.
округлено до 100 знаков после запятой:. Для простоты расчетов его часто округляют до 3,14.
Значение числа Пи в дробях
Число пи в дроби равно 22/7.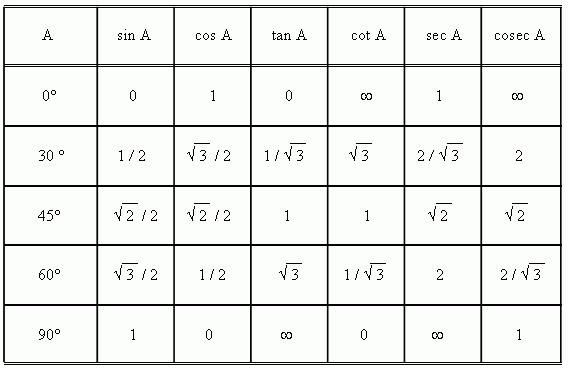 Мы знаем, что значение числа пи — это иррациональное число, в котором цифры после запятой бесконечны. Поэтому для облегчения расчетов значение числа пи также определяется в виде дроби и выражается как 22/7.
Мы знаем, что значение числа пи — это иррациональное число, в котором цифры после запятой бесконечны. Поэтому для облегчения расчетов значение числа пи также определяется в виде дроби и выражается как 22/7.
Значение числа Пи в градусах
Значение пи в градусах равно 180 градусам, так как π радиан равно 180°. Чтобы понять это, мы рассмотрим понятие радиан, которое является единицей измерения углов в системе СИ. Мы знаем, что в круге один полный оборот составляет окружность круга. Это означает, что если мы повернем на 360° вокруг точки (известной как центр окружности) на фиксированном расстоянии (радиусе), мы получим длину окружности, равную 2πr, где r обозначает радиус окружности. Итак, мы можем написать: Окружность = 2πr = 360 градусов. А для полукруга угол равен 180°, а длина дуги будет 2πr/2 = πr. Формула радианов – длина дуги/радиус. Итак, для половины окружности длина дуги равна πr, а радиус равен r.
⇒ πr/r радиан = 180°
⇒ π радиан = 180°
Следовательно, число Пи в градусах равно 180 градусам.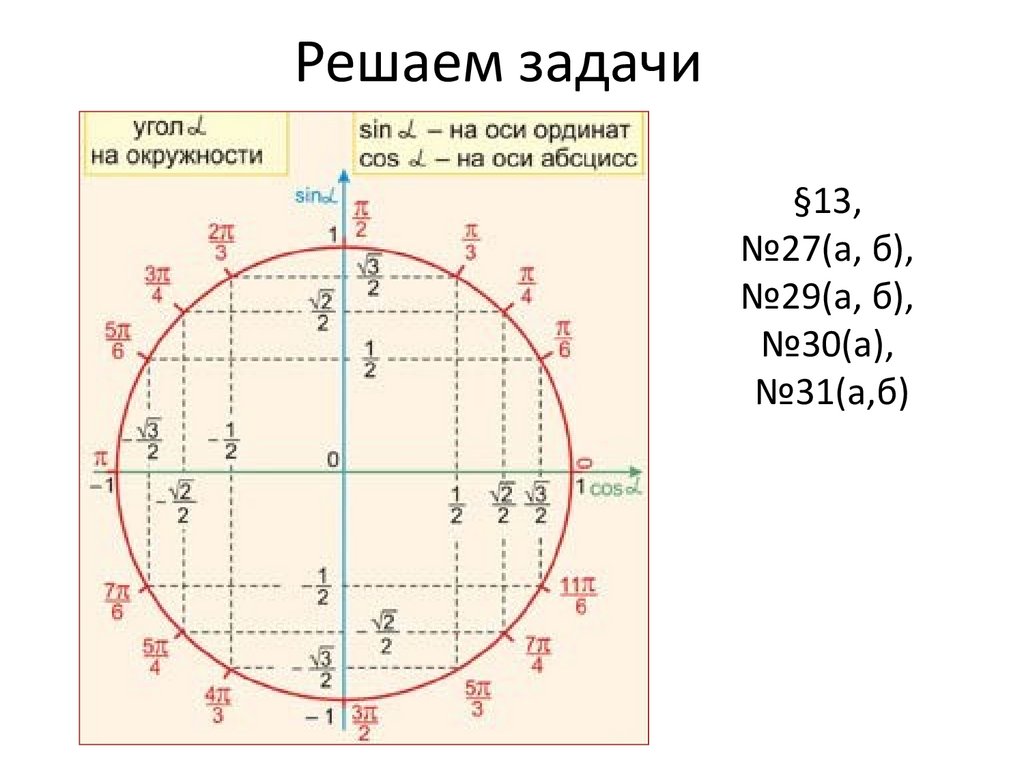
Важные примечания:
Некоторые важные моменты, касающиеся символа Пи и его значения, приведены ниже:
- «Пи» — это математическая константа, представляющая собой отношение длины окружности к ее диаметру. Это иррациональное число, которое часто приближается к 3,14159.
- Исходя из задачи, для простоты вычислений мы используем значение числа пи как 22/7 или 3,14.
- Несколько основных формул окружности с использованием числа пи:
а) Окружность = π × диаметр
б) Площадь = πr 2
► Похожие темы
Ознакомьтесь с интересными статьями, посвященными значению числа пи в математике.
- Калькулятор Пи
- Объем цилиндра в единицах Пи
- Объем конуса в единицах числа Пи
Часто задаваемые вопросы о стоимости Pi
Что такое Пи в математике?
Пи в математике — это константа, представляющая собой отношение длины окружности к ее диаметру.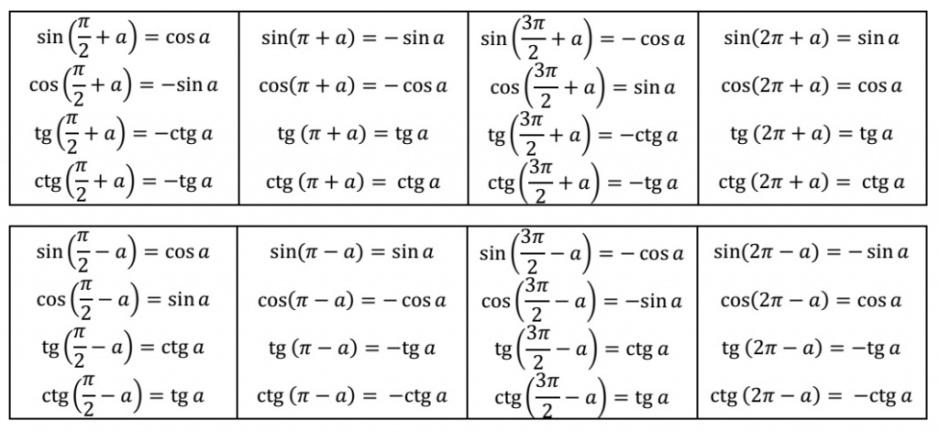 Это иррациональное число, которое часто приближается к 3,14159. Он обозначается греческой буквой «π» и пишется как «пирог». Иногда для облегчения вычислений значение числа Пи используют в виде дроби 22/7.
Это иррациональное число, которое часто приближается к 3,14159. Он обозначается греческой буквой «π» и пишется как «пирог». Иногда для облегчения вычислений значение числа Пи используют в виде дроби 22/7.
Что означает символ Пи?
Символ «пи» обозначается как «π», что является греческим алфавитом. Символ пи в основном используется для вычисления окружности кругов, площади поверхности и объема трехмерных фигур.
Каково число Пи?
Значение числа пи равно 3,1415929.. или 22/7. Это иррациональное число, что означает, что десятичные разряды после 3 бесконечны. Число Пи широко используется в понятиях измерения площади поверхности, объема трехмерных фигур и т. д.
Каковы первые 100 цифр числа Пи?
Первые 100 цифр числа пи равны 3,1415
5 8979323846 2643383279 5028841971 6939937510 5820974944 5
8164 0628620899 9628034125 8628034125. Значение числа пи начинается с цифры 3, за которой следует десятичная точка. Поскольку пи — иррациональное число, цифры после запятой бесконечны.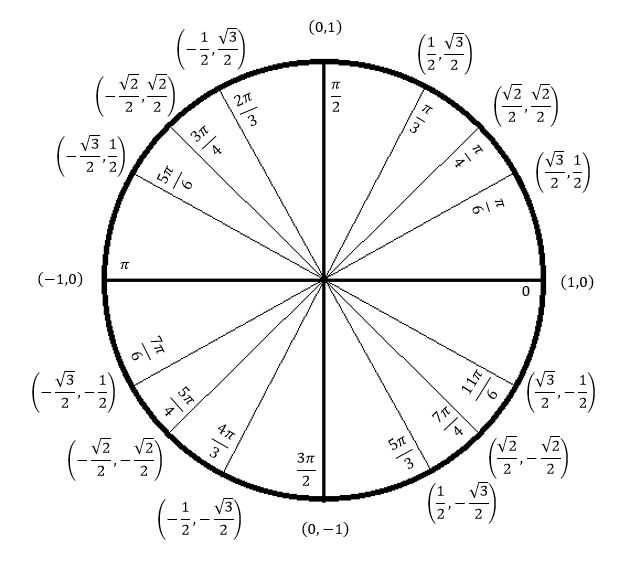 Сотая цифра после запятой равна 9.
Сотая цифра после запятой равна 9.Заканчивается ли когда-нибудь значение числа Пи?
Число «пи» никогда не заканчивается, потому что это иррациональное число. Это непрерывающийся и неповторяющийся номер, который примерно записывается как 3.14. Количество десятичных знаков после запятой простирается до бесконечности.
Почему значение числа Пи важно?
Значение числа Пи важно по следующим причинам:
- Пи в математике используется для вычисления площади и длины окружности.
- π используется во многих формулах тригонометрии для изучения отношений между длинами и углами треугольников и в геометрии, где мы изучаем формы, размеры, взаимное расположение и свойства пространства.
- Он также широко используется в области архитектуры и робототехники.
- Пи (π) считается очень важным, поэтому 14 марта отмечается как «день Пи», чтобы признать эту константу.
Что такое формула Пи?
Формула числа пи представляет собой отношение длины окружности к ее диаметру. В форме отношения это представлено как π = Окружность/Диаметр.
В форме отношения это представлено как π = Окружность/Диаметр.
Для чего используется число Пи?
Значение числа пи используется в различных формулах, используемых для расчета площади и длины окружности, объема цилиндров и т.д. Значение числа пи указано как 3,14 или 22/7.
Как было обнаружено число Пи?
Число Пи было получено путем деления длины окружности на диаметр. Это отношение, приблизительно равное 3,14, остается неизменным даже при изменении диаметра или длины окружности. Древние вавилоняне и египтяне рассчитывали значение числа пи для практических целей. Затем, около 250 г. до н.э., греческий математик создал для него алгоритм. Позднее китайские математики аппроксимировали значение до семи, а затем и до пяти знаков.
Как найти число Пи?
Число Пи вычисляется путем деления длины окружности на ее диаметр. Простое действие, показанное ниже, может доказать, что отношение или значение пи остается неизменным, даже если диаметр и длина окружности изменяются.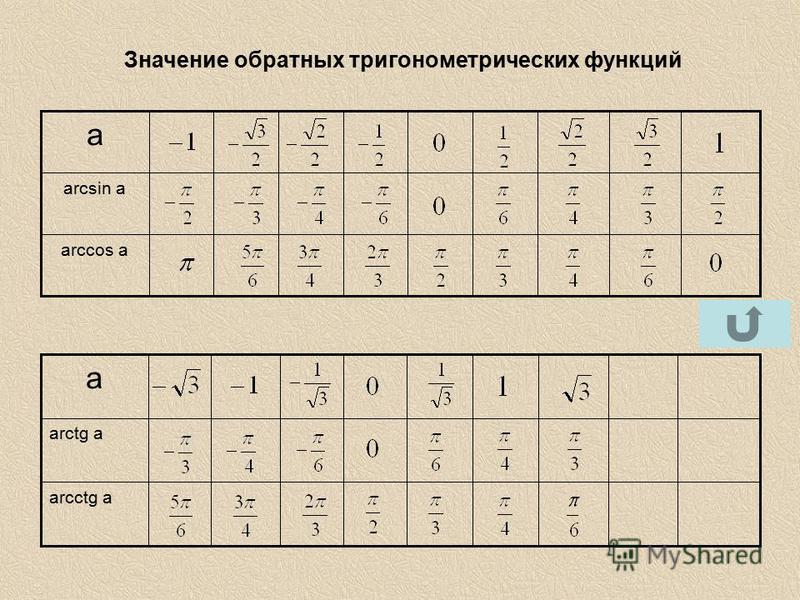
- Шаг 1: Нарисуйте круг диаметром 1 единица.
- Шаг 2: После этого шага возьмите нитку и проложите ее по границе круга (окружности).
- Шаг 3: Теперь поместите нить на линейку и отметьте длину.
- Шаг 4: Повторите процесс с диаметрами 2 единиц, 3 единиц, 4 единиц, 5 единиц и запишите свои наблюдения в таблицу. Мы можем заметить, что отношение длины окружности к диаметру всегда одинаково и составляет 3,1:1.
Какое число Пи в градусах?
Значение пи в градусах равно 180°. Здесь понятие радиана поможет нам понять это. Радиан — это единица измерения углов в системе СИ. Один радиан определяется как угол, который вытягивается из центра окружности, пересекающей дугу, длина которой равна радиусу данной окружности. Величина одного полного оборота (360°) в радианах равна длине окружности, деленной на радиус, или 2πr/r = 2π. Следовательно, 2π (радиан) = 360°, что дает π = 180°.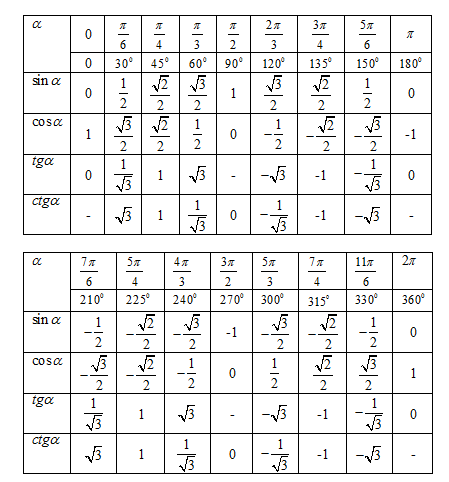
Какое число Пи в дробях?
Значение числа пи в виде дроби равно 22/7. Это значение используется в формулах для облегчения расчета.
Какими двумя способами мы можем использовать значение числа Пи?
Значение числа пи может быть использовано как 3,1415929 или 22/7 в зависимости от удобства расчета некоторых измерений, таких как площадь поверхности и объем. Оба значения дают одинаковый результат. Для преобразования радиан в градусы значение π радиан равно 180 градусам.
Вычисление числа пи Архимедом « Ученый-математик
MathJax TeX Test PageАвторы и права: Ancient Origins
Введение
Архимед широко известен как величайший математик древности. Он был пионером прикладной математики, например, с его открытием принципа плавучести, и мастером инженерных расчетов, например, с его «винтом», чтобы поднимать воду с одного уровня на другой. Но самым далеко идущим его открытием был «метод исчерпывания», который он использовал для вывода площади круга, площади поверхности и объема сферы и площади под параболой. Действительно, с помощью этого метода Архимед почти на 2000 лет предвосхитил современное развитие исчисления, которое началось в 17 веке с Лейбница и Ньютона. Дополнительные сведения см. в статье в Википедии.
Действительно, с помощью этого метода Архимед почти на 2000 лет предвосхитил современное развитие исчисления, которое началось в 17 веке с Лейбница и Ньютона. Дополнительные сведения см. в статье в Википедии.
В этой статье мы представляем оригинальный метод Архимеда для вычисления периметра и площади круга, используя при этом гораздо более простую систему обозначений (алгебру), гораздо более простую систему вычислений (десятичная арифметика и компьютерные технологии). ) и гораздо лучше развитая основа для строгого математического доказательства. Пошаговое представление реальных вычислений Архимеда см. в этой статье Чака Линдси.
Отрицание числа Пи
Одной из причин написания этой статьи является ответ некоторым недавним авторам, которые отвергают основы математической теории и принятое значение $\pi$, утверждая вместо этого, что они обнаружили, что $\pi$ является другим значением. Например, один автор утверждает, что $\pi = 17 – 8 \sqrt{3} = 3,1435935394\ldots$. Другой автор утверждает, что $\pi = (14 – \sqrt{2})/4 = 3,1464466094\ldots$. Третий автор обещает указать «точное» значение $\pi$, существенно отличающееся от общепринятого. Другие примеры см. в этом блоге Math Scholar. Конечно, $\pi$ не может быть задано каким-либо подобным алгебраическим выражением, поскольку трансцендентность $\pi$ была доказана Линдеманном в 1882 году, и с тех пор его доказательство было тщательно проверено многими тысячами математиков.
Другой автор утверждает, что $\pi = (14 – \sqrt{2})/4 = 3,1464466094\ldots$. Третий автор обещает указать «точное» значение $\pi$, существенно отличающееся от общепринятого. Другие примеры см. в этом блоге Math Scholar. Конечно, $\pi$ не может быть задано каким-либо подобным алгебраическим выражением, поскольку трансцендентность $\pi$ была доказана Линдеманном в 1882 году, и с тех пор его доказательство было тщательно проверено многими тысячами математиков.
В этой статье максимально просто и лаконично показано, почему $\pi = 3,1415
5\ldots$ и, конечно же, ни одно из этих вариантов значений. С этой целью этот материал не требует математической подготовки, кроме очень базовой алгебры, тригонометрии и теоремы Пифагора, и тщательно избегает вычислений, расширенного анализа или любых рассуждений, которые зависят от предварительных знаний о $\pi$. В соответствии с этим для углов используется традиционная запись в градусах вместо радианной меры, принятой в профессиональной исследовательской работе, как для облегчения понимания презентации, так и для того, чтобы избежать любых концепций или методов, которые могут рассматриваться как зависящие от $\pi$.
 9\circ$ из-за неоднозначности знака при извлечении квадратного корня.
9\circ$ из-за неоднозначности знака при извлечении квадратного корня.Кредит: Викимедиа
Доказательство : Сначала мы установим некоторые более общие результаты: $$\sin (\alpha + \beta) = \sin (\alpha) \cos (\beta) + \cos (\ альфа) \sin (\beta),$$ $$\cos (\alpha + \beta) = \cos (\alpha) \cos (\beta) – \sin (\alpha) \sin (\beta),$ $ $$\tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 — \tan(\alpha)\tan(\beta)}.$$ формула для $\sin(\alpha + \beta)$ имеет простое геометрическое доказательство, основанное только на формуле Пифагора и простых правилах прямоугольных треугольников, которое проиллюстрировано справа (здесь $OP = 1$). Сначала обратите внимание, что $RPQ = \alpha, \, PQ = \sin(\beta)$ и $OQ = \cos (\beta)$. Кроме того, $AQ/OQ = \sin(\alpha)$, поэтому $AQ = \sin(\alpha) \cos(\beta)$ и $PR/PQ = \cos(\alpha)$, поэтому $PR = \cos(\alpha)\sin(\beta)$. Объединяя эти результаты, $$\sin(\alpha + \beta) = PB = RB + PR = AQ + PR = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta ).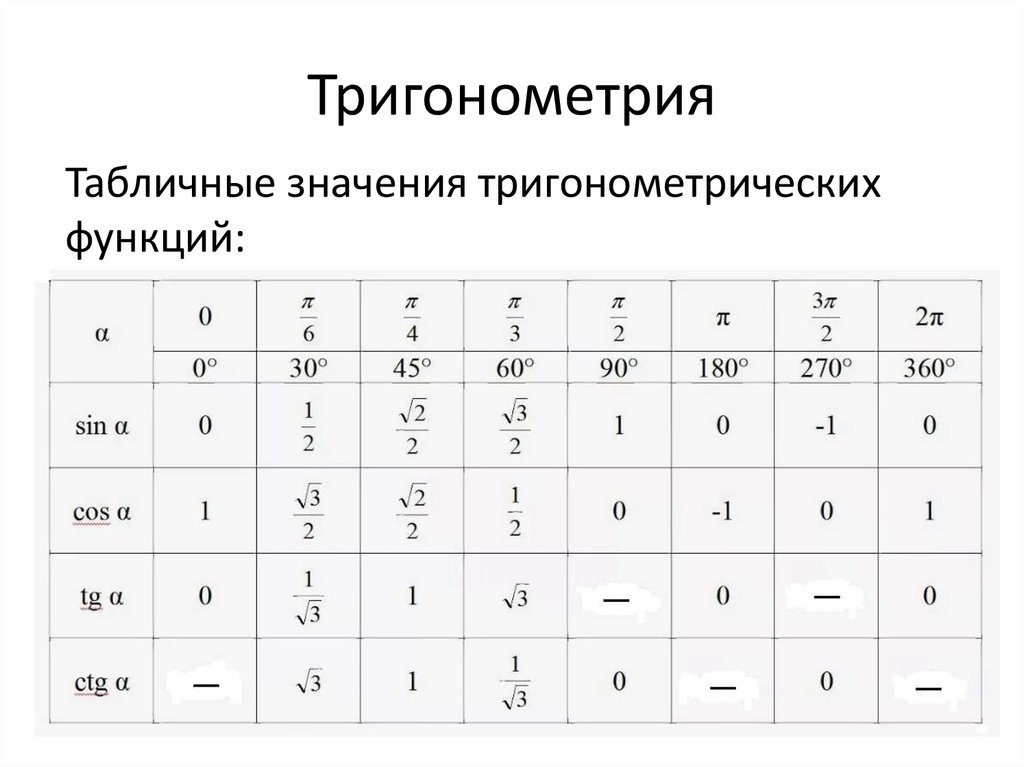 $$ Доказательство формулы для косинуса суммы двух углов совершенно аналогично, а формула для $\tan(\alpha + \beta)$ получается делением формулы для $\sin(\alpha + \beta)$ по формуле для $\cos(\alpha + \beta)$ с последующей простой алгеброй. Дополнительные сведения см. в этой статье в Википедии, из которой были взяты приведенные выше иллюстрация и доказательство. 9\circ$ из-за неоднозначности знака при извлечении квадратного корня). Формулу для $\tan(\alpha/2)$ можно найти, разделив формулы для $\sin(\alpha/2)$ и $\cos(\alpha/2)$ плюс немного алгебры, но следующее еще проще и позволяет избежать квадратных корней: $$\tan(\alpha/2) = \frac{\sin(\alpha/2)}{\cos(\alpha/2)} = \frac{\sin(\ альфа/2)\cos(\alpha/2)}{\cos(\alpha/2)\cos(\alpha/2)} = \frac{1/2 \cdot \sin(\alpha)}{1/ 2 \cdot (1 + \cos(\alpha))} = \frac{\sin(\alpha)}{1 + \cos(\alpha)}.$$
$$ Доказательство формулы для косинуса суммы двух углов совершенно аналогично, а формула для $\tan(\alpha + \beta)$ получается делением формулы для $\sin(\alpha + \beta)$ по формуле для $\cos(\alpha + \beta)$ с последующей простой алгеброй. Дополнительные сведения см. в этой статье в Википедии, из которой были взяты приведенные выше иллюстрация и доказательство. 9\circ$ из-за неоднозначности знака при извлечении квадратного корня). Формулу для $\tan(\alpha/2)$ можно найти, разделив формулы для $\sin(\alpha/2)$ и $\cos(\alpha/2)$ плюс немного алгебры, но следующее еще проще и позволяет избежать квадратных корней: $$\tan(\alpha/2) = \frac{\sin(\alpha/2)}{\cos(\alpha/2)} = \frac{\sin(\ альфа/2)\cos(\alpha/2)}{\cos(\alpha/2)\cos(\alpha/2)} = \frac{1/2 \cdot \sin(\alpha)}{1/ 2 \cdot (1 + \cos(\alpha))} = \frac{\sin(\alpha)}{1 + \cos(\alpha)}.$$
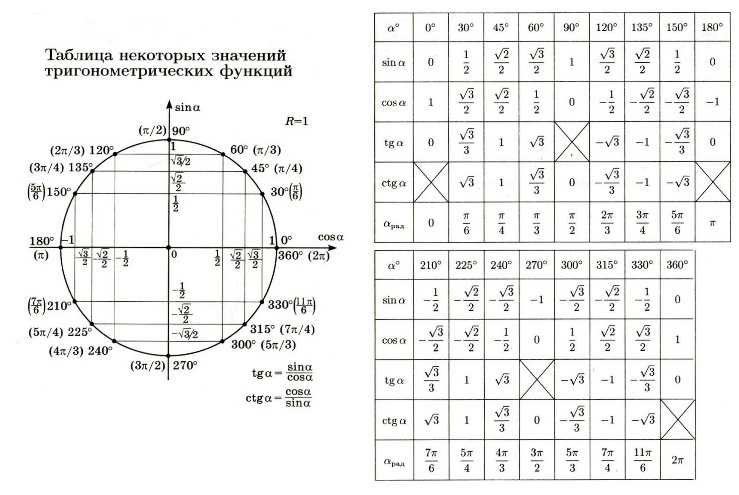 {k+1} \tan(\theta_{k+1}) = a_{k+1}.$$ Аналогично, вспоминая тождество $\sin(2\alpha) = 2 \ sin(\alpha) \cos(\alpha)$ из леммы 1, так что $\sin(\theta_k) = 2 \sin(\theta_{k+1}) \cos(\theta_{k+1})$ , мы можем написать $$B_{k+1} = \sqrt{A_{k+1} B_k} = \sqrt{9{k+1} \sin(\theta_{k+1}) = b_{k+1}.$$
{k+1} \tan(\theta_{k+1}) = a_{k+1}.$$ Аналогично, вспоминая тождество $\sin(2\alpha) = 2 \ sin(\alpha) \cos(\alpha)$ из леммы 1, так что $\sin(\theta_k) = 2 \sin(\theta_{k+1}) \cos(\theta_{k+1})$ , мы можем написать $$B_{k+1} = \sqrt{A_{k+1} B_k} = \sqrt{9{k+1} \sin(\theta_{k+1}) = b_{k+1}.$$В качестве исторического комментария отметим, что Архимед определенно не использовал это обозначение и явно не вывел ни формулы Архимеда, ни итерация. Но его конструкция эквивалентна этим результатам.
Вычисления с использованием архимедовой итерации
Теперь мы можем напрямую вычислять некоторые приближения к $\pi$, используя только формулы теоремы 1 или теоремы 2. Эти результаты показаны в таблице до 16 знаков после запятой. точка, но были выполнены с использованием арифметики с точностью до 50 цифр, чтобы исключить любую возможность ошибки числового округления, искажающей результаты таблицы. Имейте в виду, что полупериметры и площади описанных многоугольников представляют собой завышенные оценки $\pi$, а полупериметры и площади вписанных многоугольников — заниженные оценки $\pi$. 9 тысяч долларов
9 тысяч долларов
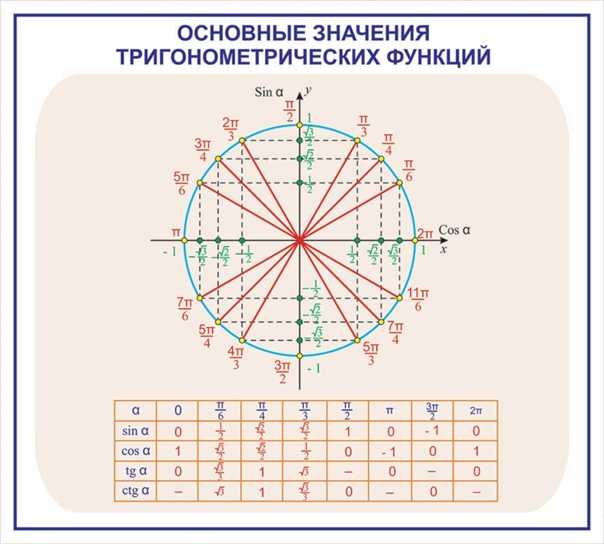 1418730499798238
14187304997982384
0386138
 14153653839
14153653839 0386138
4
0336908
8678444
8678444
0336908
0550368
8571714
4561041
8571714
0550368
6566377
5563709
6566377
4561041
6065043
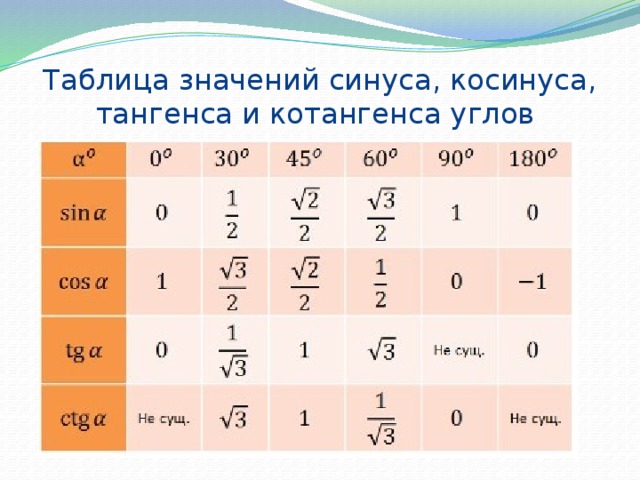 1415
1415 5814376
6065043
5563709
5939710
5877043
5939710
5814376
5
58
5
5877043
Как легко заметить, каждый из этих столбцов быстро сходится к хорошо известному значению $\pi$. В последней строке таблицы, где представлены результаты для описанных и вписанных многоугольников с 3 145 728 сторонами, все четыре записи совпадают с точностью до десяти знаков после запятой: $3,14159.26535\ldots$. Обратите внимание, кстати, что оба из двух вариантов значений $\pi$, упомянутых выше в разделе об отрицании числа Пи, исключаются на четвертой итерации . От этих вычислений никуда не деться — значения вариантов для $\pi$ просто неверны.
Теперь мы строго докажем, что формулы Архимеда (или, что то же самое, архимедова итерация) сходятся к $\pi$ как в смысле длины окружности, так и в смысле площади, снова опираясь только на рассуждения из первых принципов.
АКСИОМА 1 (аксиома полноты): . Каждое ограниченное сверху множество действительных чисел имеет наименьшую верхнюю границу; каждый набор вещественных чисел, ограниченный снизу, имеет наибольшую нижнюю границу.
Комментарий : Эта фундаментальная аксиома действительных чисел просто утверждает свойство, согласно которому множество действительных чисел, в отличие, скажем, от множества рациональных чисел, не имеет «дыр». Эквивалентное утверждение аксиомы полноты: «Каждая последовательность действительных чисел Коши имеет предел в действительных числах». Подробности см. в статье Википедии «Полнота действительных чисел» и в этой главе. 9k$ сторон, значение которых в точности равно $\pi$, определенному в теореме 3а.
Комментарий : Строго говоря, с современной точки зрения, $\pi$ теперь обычно определяется как длина окружности, деленная на ее диаметр (или как полуокружность окружности радиуса один), где длина окружности окружность определяется как предел периметров описанных или вписанных правильных многоугольников с $n$ сторонами при неограниченном увеличении $n$.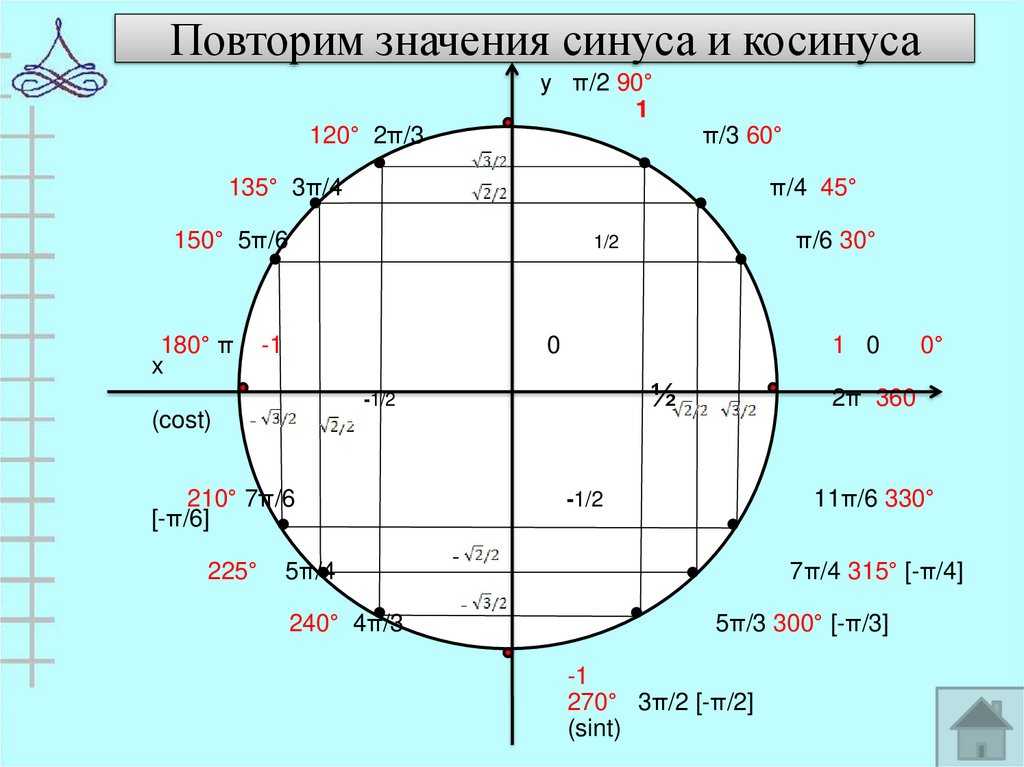 k$. Следуя современному соглашению, мы представляем в отдельном блоге полное доказательство того, что $\pi$, определенное Архимедом, совпадает с $\pi$, основанным на общих $n$-сторонних правильных многоугольниках для окружности радиуса один, и, как бонус, доказательство того, что пределы площадей этих многоугольников также равны $\pi$. Подробности смотрите в отдельном блоге.
k$. Следуя современному соглашению, мы представляем в отдельном блоге полное доказательство того, что $\pi$, определенное Архимедом, совпадает с $\pi$, основанным на общих $n$-сторонних правильных многоугольниках для окружности радиуса один, и, как бонус, доказательство того, что пределы площадей этих многоугольников также равны $\pi$. Подробности смотрите в отдельном блоге.
Стратегия доказательства : Мы покажем, что (a) последовательность описанных полупериметров $(a_k)$ строго убывает; б) последовательность вписанных полупериметров $(b_k)$ строго возрастает; (c) все $(a_k)$ строго больше всех $(b_k)$; и (d) расстояние между $a_k$ и $b_k$ становится сколь угодно малым для больших $k$. Таким образом, наибольшая нижняя граница описанных полупериметров равна наименьшей верхней границе вписанных полупериметров, а общий предел может быть определен как $\pi$. Аналогичный аргумент приводит к тому же выводу для последовательности описанных и вписанных областей. 9k},$$, так что разница между описанным и вписанным полупериметрами уменьшается примерно в четыре раза с каждой итерацией (как также видно из таблицы выше).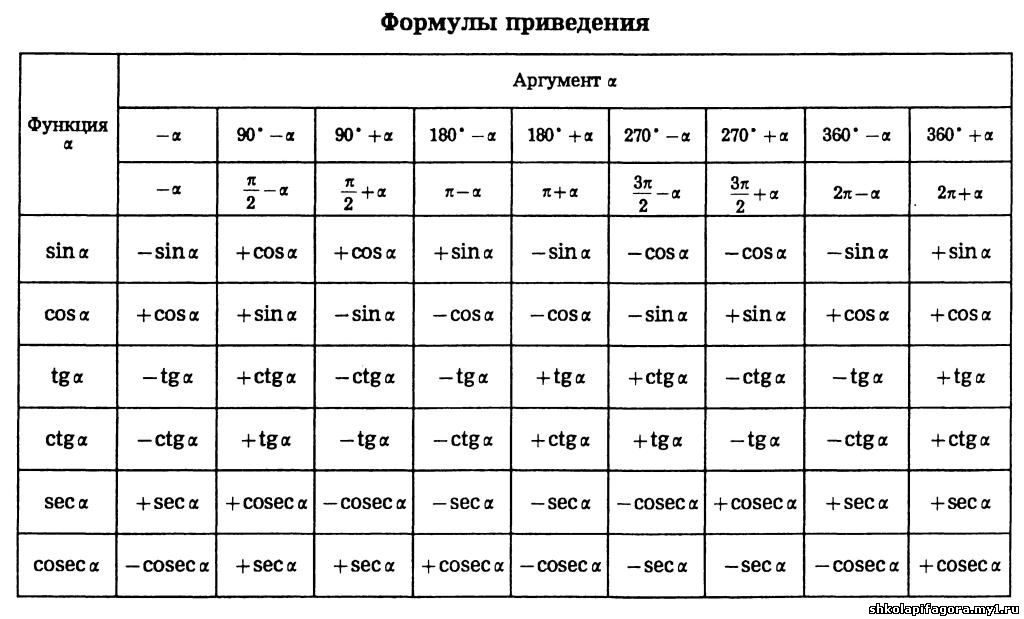
Напомним из предыдущего, что все $a_k \gt 3$, так что последовательность описанных полупериметров $(a_k)$ ограничена снизу. Таким образом, по аксиоме 1 последовательность $(a_k)$ имеет точную нижнюю границу $L_1$. На самом деле, поскольку все $a_k$ больше всех $b_k$, любое $b_k$ является нижней гранью последовательности $(a_k)$, так что мы можем написать для любого $k$ $a_k \geq L_1 \geq b_k$. Кроме того, все $b_k \lt 4$, так что последовательность $(b_k)$ вписанных полупериметров ограничена сверху и, следовательно, имеет наименьшую верхнюю границу $L_2$. И, как и ранее, поскольку любое $a_k$ является оценкой сверху для последовательности $(b_k)$, для каждого $k$ также следует, что $a_k \geq L_2 \geq b_k$. Таким образом, и $L_1$, и $L_2$ «зажаты» между $a_k$ и $b_k$, которые при достаточно больших $k$ сколь угодно близки друг к другу (в соответствии с последним показанным уравнением выше), так что $ L_1$ должен быть равен $L_2$. Это завершает доказательство теоремы 3а. 9k},$$, так как финальное неравенство было установлено несколькими строками выше. Как и прежде, отсюда следует, что точная нижняя граница вписанных площадей $c_k$ в точности равна точной верхней границе вписанных площадей $d_k$. Кроме того, поскольку последовательность $(a_k)$ полупериметров описанных многоугольников точно такая же последовательность , что и последовательность $(c_k)$ площадей описанных многоугольников, мы заключаем, что общий предел площадей равен совпадает с общим пределом полупериметров, а именно $\pi$. Это завершает доказательство теоремы 3b. 92).$$ Тогда $1/a_k$ ежеквартально сходится к $\pi$: каждая итерация примерно увеличивает вчетверо число правильных цифр. Just three iterations yield 171 correct digits, which are as follows: $$3.1415
Как и прежде, отсюда следует, что точная нижняя граница вписанных площадей $c_k$ в точности равна точной верхней границе вписанных площадей $d_k$. Кроме того, поскольку последовательность $(a_k)$ полупериметров описанных многоугольников точно такая же последовательность , что и последовательность $(c_k)$ площадей описанных многоугольников, мы заключаем, что общий предел площадей равен совпадает с общим пределом полупериметров, а именно $\pi$. Это завершает доказательство теоремы 3b. 92).$$ Тогда $1/a_k$ ежеквартально сходится к $\pi$: каждая итерация примерно увеличивает вчетверо число правильных цифр. Just three iterations yield 171 correct digits, which are as follows: $$3.1415
5897932384626433832795028841971693993751058209749445
81640628620899862803482$$ $$534211706798214808651328230664709384460955058223172535940812848111745028410270193\ldots$$Other posts in the “Simple proofs” series
The other posts in the “Simple proofs of great theorems” серии доступны здесь.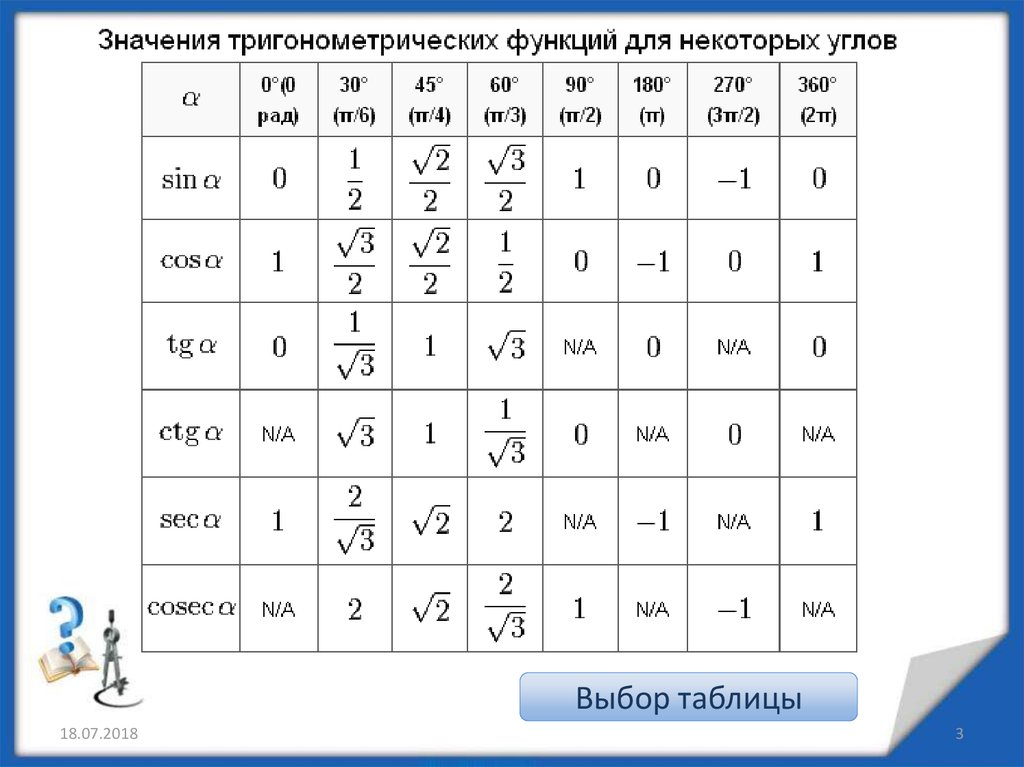
Как использовать число Пи в Google Таблицах [3 простых примера]
Пи — важное иррациональное число для множества приложений. Пи - это отношение диаметра и длины окружности. Пи всегда имеет значение, приблизительно равное 3,14159. Поскольку это число бесконечно, его чаще всего обозначают греческой буквой π.
Google Таблицы – это отличный инструмент для работы с электронными таблицами, который используется аналитиками данных во всем мире благодаря фантастическому набору функций и онлайн-резервному копированию в реальном времени. Все эти функции бесплатны для частных лиц и малого бизнеса.
Он может выполнять множество сложных задач и расчетов. Некоторые из них включают анализ с использованием функции Pi. Например, вы можете захотеть выполнить некоторые расчеты на красивой круговой диаграмме.
В этой статье рассказывается о формуле Пи в Google Таблицах и о том, как ее использовать, с несколькими примерами и способами ввода символа Пи в ваши электронные таблицы.
Содержание
Как вставить Pi в Google Таблицы
Существует два основных способа использования функции Google Sheets Pi.
- Чтобы ввести функцию Пи, щелкните ячейку, в которую вы хотите поместить функцию Пи, и перейдите на вкладку Вставить . В раскрывающемся меню нажмите Функция . Вы должны увидеть несколько вариантов на выбор, нажмите Math и выберите оттуда Pi .
- Если вы знакомы с формулами, просто нажмите на ячейку и введите =PI()
Функция Pi не имеет аргументов, поэтому в скобки ничего не помещается. Это приведет к ошибке. Это связано с тем, что функция представляет число Пи, а не реальную формулу. Итак, рассмотрим это номер , а не формула, при использовании его в ваших таблицах.
Круговые вычисления с помощью функции Пи
Вот несколько итераций синтаксиса, которые вы можете использовать в некоторых круговых вычислениях с примерами.
Как использовать число Пи в Google Таблицах для расчета диаметра
Вы можете рассчитать диаметр круга, разделив длину окружности на число Пи. Синтаксис для этого вычисления:
= (окружность) / PI ( )
Предположим, что значение окружности равно 20. Чтобы найти диаметр, вам просто нужно написать это в ячейке:
= 20 / PI()
Радиус окружности также можно рассчитать, разделив диаметр окружности на 2.
Электронная таблица Пи — Окружность
Вы вычисляете неизвестную длину окружности, умножая диаметр на число Пи. Синтаксис этого вычисления:
= (диаметр) * PI ( )
Предположим, что значение диаметра равно 20. Чтобы найти длину окружности, просто напишите это в ячейке:
= 20 * PI( ) 92
Как ввести Pi в Google Sheets
Использование функции CHAR — лучший способ создать символ Pi в Google Sheets. Эта функция позволяет преобразовывать числа в символы. Это делается с помощью таблицы Unicode, которая является отраслевым стандартом для обработки текста на компьютере.
Эта функция позволяет преобразовывать числа в символы. Это делается с помощью таблицы Unicode, которая является отраслевым стандартом для обработки текста на компьютере.
Вы можете ввести функцию CHAR в свои Google Таблицы двумя способами.
Метод 1
- Щелкните ячейку, в которой вы хотите использовать функцию CHAR
- Нажмите «Вставить» в верхней панели, а затем нажмите «Функция».
- Перейдите в подменю «Текст» и нажмите «СИМВОЛ».
- Введите номер и нажмите Enter. Должен появиться символ Пи. Код символа числа Пи — 960. .
Метод 2
Для экономии времени можно использовать формулу. Просто выберите ячейку и введите: =CHAR(960)
Часто задаваемые вопросы
Как вставить Pi в Google Sheets?
Вы можете использовать функцию CHAR, которая используется для преобразования чисел в символы в соответствии с таблицей Unicode. Используйте эту формулу для ввода символа числа Пи на листах:
=CHAR(960)
Обязательно используйте номер Unicode 960 для числа Пи, а не 129383 , так как это может не дать желаемых результатов.
Что такое Pi в Google Таблицах?
Функцию Pi в Sheets можно использовать для вычисления окружности. Пи можно определить как отношение длины окружности к ее диаметру. Математическое значение Пи приблизительно равно 3,14159.2654.
Как умножить число Пи в Google Таблицах?
Вы можете умножить числа Пи, введя синтаксис функции числа Пи и используя символ «*» для умножения любого числа на Число Пи.
Как вставить математические символы в Google Sheets?
Чтобы вставить специальные символы в свои Google Таблицы, вы можете найти Unicode символа через Google и использовать функцию CHAR для ввода кода, который превратит его в специальный символ.
Вы также можете сделать это с помощью Google Docs, для этого:
- Откройте новый файл Документа Google.
- Нажмите Вставьте в верхнюю строку и нажмите Специальные символы . Это покажет вам меню, в котором вы можете найти своего персонажа, используя панель поиска или просматривая список, чтобы найти его.

- Как только вы выберете символ, он появится в вашем документе. Просто скопируйте его с помощью Ctrl + C и вставьте в электронную таблицу с помощью Ctrl + V.
Вы также можете использовать метод копирования и вставки, выполнив поиск символа X в Google и скопировав результат.
Завершение работы с функцией Pi
Использование Pi в Google Sheets становится таким же простым, как несколько нажатий на клавиатуре, если вы знаете сочетания клавиш. Если вы нашли эту статью полезной, ознакомьтесь с другими нашими руководствами, чтобы улучшить свои навыки работы с электронными таблицами. Более того, вы можете записаться на курс, чтобы стать мастером Google Таблиц.
Другие полезные функции в Google Таблицах:
- Краткое руководство по функциям СЧЁТЕСЛИ и СЧЁТЕСЛИМН в Google Таблицах
- Функция GOOGLEFINANCE: простое руководство для начинающих
- Как использовать функцию QUERY Google Таблиц (пошаговая инструкция)
- Функция ADDRESS в Google Таблицах 101 [Краткое руководство]
- Функция прогнозирования Google Таблиц: руководство для начинающих
Все математические и статистические функции Power Apps (с примерами)
Математические и статистические функции являются одними из наиболее часто используемых функций в Power Apps. К счастью, они также являются одними из самых простых функций для изучения. Выполнение математических операций в Power Apps имеет много общего с Microsoft Excel. Многие основные функции, такие как SUM и COUNT, абсолютно одинаковы. В этой статье я перечислю все математические и статистические функции Power Apps и покажу примеры их использования.
К счастью, они также являются одними из самых простых функций для изучения. Выполнение математических операций в Power Apps имеет много общего с Microsoft Excel. Многие основные функции, такие как SUM и COUNT, абсолютно одинаковы. В этой статье я перечислю все математические и статистические функции Power Apps и покажу примеры их использования.
Содержание: Математические функции Функция АБС МОД Функция ПИ-функция ПИТАНИЕ Функция Функция SQRT Функция СУММ Статистические функции СРЕДНЯЯ функция СЧЁТ Функция Функция МАКС. МИН Функция Функция СТАНДОТКЛОН Функция ВАРП Функции округления ОКРУГЛ Функция Функция ОКРУГЛВВЕРХ Функция ОКРУГЛВНИЗ Функция INT ТРАНК Функция Функции счета Функция СЧЁТ СЧЁТЕСЛИ Функция СЧЕТЧИК Функция Случайные функции СЛУЧАЙ Функция СЛУЧАЙ МЕЖДУ Функция Логарифмические функции Функция EXP Функция LN ЖУРНАЛ Функция
Математические функции
Абс. функция
Назначение
Получает абсолютное значение числа (без знаков). Отрицательное число становится положительным. Положительные числа остаются положительными.
Отрицательное число становится положительным. Положительные числа остаются положительными.
Синтаксис
Abs(число)
Аргументы
Число – числовое значение для удаления знаков из
9069 Абс(-3) // Результат: 3
Абс(5) // Результат: 5
Abs(0) // Результат: 0 Mod Function
Purpose
Returns the remainder of a number divided by another number
Syntax
Mod(number, divisor)
Arguments
number – a number value to divide.
делитель – число, на которое делится другое число.
Пример
Mod(10, 3) // Результат: 1
Mod(10, 7) // Результат: 3
Mod(10, 5) // Результат: 0 Функция Пи
Purpose
Returns the mathematical constant Pi ( π )
Syntax
Pi()
Example
Pi() // Result: 3. 1415
1415 59
Power Function
Purpose
Raises a number to the power of another number
Syntax
Power(base, exponent)
Arguments
base – the base number to raise
exponent – показатель степени увеличения основания на
Пример
Степень (10, 2) // Результат: 100
Мощность(10, 3) // Результат: 1000
Мощность(5, 3) // Результат: 125 Квадратная функция
Назначение
Получить квадратный корень из числа.
Синтаксис
SQRT (номер)
Аргументы
№ - значение для получения квадратного root из
№ - ряд. Sqrt(16) // Результат: 4 Sqrt(1) // Результат: 1
Функция суммирования
Purpose
Calculates the sum for a table of numbers
Syntax
Sum(source, expression)
Arguments
source – a table of numbers to be added
expression — формула, вычисляемая для каждой строки таблицы, которая предоставляет набор чисел, которые нужно сложить вместе
Пример
Sum([1,2,3,4,5], Value) // Результат: 15
Сумма(
Стол(
{Буква: "А", Значение: 1},
{Буква: "В", Значение: 2},
{Буква: "С", Значение: 3},
{Буква: "Д", Значение: 4},
{Буква: "Е", Значение: 5}
),
Ценность
)
// Результат: 15 Статистические функции
Функция усреднения
Цель
Рассчитывает среднее (среднее значение арифметики) для таблицы чисел
Синтаксис
Средний (источник, экспрессия)
7
Средний (источник, экспрессия)
7
7
7 Argimment
77903 7 Arding Arding). среднее из
среднее из
выражение – формула, вычисляемая для каждой строки таблицы, которая предоставляет набор чисел для усреднения
Пример
Среднее([1,2,3,4,5], Значение) // Результат: 3
Среднее([3,4,6,9], Значение) // Результат: 5,5 Функция подсчета
Purpose
Counts the number values in a single column table
Syntax
Count(source, expression)
Arguments
source – a single-column table of numbers to count
выражение – логическое выражение, определяющее, какие числа включать в счет
Пример
Count([2,4,6]) // Результат: 3
Счетчик([2,4,6,8]) // Результат: 4
Count([2,4,6,8,Blank()]) // Результат: 4 Максимальная функция
Назначение
Возвращает максимальное значение из таблицы чисел
Синтаксис
Max(source, expression)
Аргументы
источник – таблица чисел для получения максимального значения из
выражение – формула, рассчитанная для каждой строки таблицы, которая обеспечивает набор чисел для расчета максимального значения
7 Пример
Среднее([1,2,3,4,5], Значение) // Результат: 5
Среднее ([-2-1,0,1,2], значение) // Результат: 2 Минимальная функция
Назначение
Возвращает минимальное значение из таблицы чисел
Синтаксис
мин. — формула, оцениваемая для каждой строки таблицы, которая предоставляет набор чисел для расчета минимального значения
Мин([-2-1,0,1,2], Значение) // Результат: -2
— формула, оцениваемая для каждой строки таблицы, которая предоставляет набор чисел для расчета минимального значения
Мин([-2-1,0,1,2], Значение) // Результат: -2
Функция StdevP
Цель
Рассчитывает стандартное отклонение для таблицы чисел
Синтаксис
STDEVP (источник, выражение)
ARADP (источник, выражение)
3333333333. Ardevp (источник, выражение). from
выражение – формула, рассчитанная для каждой строки таблицы, которая предоставляет набор чисел для расчета стандартного отклонения
Пример
StdevP([1,2,3,4,5], Значение) // Результат: 1.41421356
StdevP([1,3,7,11], Value) // Результат: 3.84057287 Функция VarP
Цель
Расчета дисперсии для таблицы чисел
Синтаксис
VARP (источник, выражение)
Argp (источник, выражение)
Argp (источник, выражение)
 0678
0678выражение – формула, рассчитанная для каждой строки таблицы, которая предоставляет набор чисел для расчета дисперсии Результат: 3.84057287 VarP([1,3,7,11], Value) // Результат: 14.75
Функции округления
Функция округления
Назначение
Округляет число до ближайшего числа с выбранным количеством цифр
Syntax
Round(number, num_digits)
Arguments
number – a number to round
num_digits – the number of decimal places in the rounded number
Example
Раунд(3.2, 0) // Результат: 3
Раунд(5.75, 1) // Результат: 5.8
Round(1.355, 2) // Результат: 1.36 Функция RoundUp
Назначение
раунды ряд до следующего числа с выбранным количеством цифр
Синтаксис
Раунда (номер, num_digits)
Argument num_digits – количество знаков после запятой в округленном числе
Пример
RoundUp(3. 2, 0) // Результат: 4
RoundUp(5.75, 1) // Результат: 5.8
RoundUp(1.355, 2) // Результат: 1.36
2, 0) // Результат: 4
RoundUp(5.75, 1) // Результат: 5.8
RoundUp(1.355, 2) // Результат: 1.36 Функция округления вниз
Purpose
Rounds a number down to the next number with the chosen number of digits
Syntax
RoundDown(number, num_digits)
Arguments
number – a number to round вниз
num_digits – количество знаков после запятой в округленном числе
Пример
RoundDown(3.2, 0) // Результат: 3
RoundDown(5.75, 1) // Результат: 5.7
RoundDown(1.355, 2) // Результат: 1.35 Функция Int
Цель
раунды десятичного числа или текстовое значение для ближайшего целого числа (число без десятичных дел)
Синтаксис
Int (номер)
INT (номер)
77779
INT (номер)
7777779
. число для преобразования в целое число
число для преобразования в целое число
Пример
Int(3.2) // Результат: 3
Целое(5.75) // Результат: 6
Int("1") // Результат: 1 Функция Trunc
Purpose
Removes the decimals from a number
Syntax
Trunc(number)
Arguments
number – a number to truncate
Example
Trunc( 3.2) // Результат: 3
Trunc(5.75) // Результат: 5
Trunc(1) // Результат: 1 Функции подсчета
Функция подсчета
Назначение
Подсчитывает числовые и текстовые значения в таблице с одним столбцом. Пустая строка «считается не блунковым значением
Синтаксис
Counta (число, num_digits)
аргументы
. выражение – логическое выражение, определяющее, какие числа включать в счет Функция CountIf Назначение CountIf(источник, условие1 [ условие2, …]) источник – таблица значений для подсчета решает, какие строки считать Функция CountRows CountRows(source) source – a table whose rows will be counted Случайные функции Функция ранда Purpose Syntax Rand() Функция RandBetween Purpose Syntax RandBetween(bottom, top) Syntax bottom – the lowest random number in the range top – наибольшее случайное число в диапазоне Логарифм Эксп Функция Назначение Exp(число) число – число e возведено в степень Ln Функция Цель 7 LN (номер) 7 (номер) 7 (номер) 7 (номер) 7 (номер) 7 (номер) 7 (номер) – число для нахождения натурального логарифма Функция журнала Purpose Log(number, base) number – the number to calculate the logarithm for база – основание логарифма Подпишитесь на БЕСПЛАТНУЮ рассылку новых статей Power Apps на ваш почтовый ящик каждую неделю Введите ваш адрес электронной почты Есть вопросы? Если у вас есть какие-либо вопросы или отзывы о Все математические и статистические функции Power Apps (с примерами) , оставьте сообщение в разделе комментариев ниже. Книги по математике заставили меня поверить в математику! Математика не должна быть доступна только для студентов, изучающих математику, потому что математика может быть чрезвычайно интересной для всех. Если мы сможем найти правильный аппарат, то сможем показать красоту математики любому человеку в этом мире. Но что мы можем сделать, чтобы люди полюбили математику? Я думаю, что пресловутое число пи — лучший кандидат, чтобы показать красоту математики, и у него так много интересных свойств, что они поражают людей. Но с чего начать изучение числа Пи? Ответ очевиден; Вы должны получить правильные книги! Я подобрал для вас 7 очень хорошо написанных математических книг о числе Пи! Каждая из этих книг заставит вас полюбить математику! Я люблю их читать. История числа Пи, по словам автора, хотя и является небольшой частью истории математики, тем не менее является зеркалом истории человека. Петр Бекман держит это зеркало, показывая предысторию того, когда число Пи достигло прогресса, а когда нет, потому что науку душил милитаризм или религиозный фанатизм. Эта книга — одна из лучших математических книг о числе Пи. Посмотрите отзывы на Amazon. Что такое математика? Как именно это работает? И при чем здесь трое братьев и сестер, пытающихся разделить торт? В How to Bake Pi , профессор математики Юджиния Ченг предлагает доступное введение в логику и красоту математики, неожиданно основанное на знаниях с кухни: мы узнаем, например, как беамель в лазанья может быть очень похожа на число 5, и почему приготовление хорошего заварного крема доказывает, что математика проста, а жизнь сложна. Конечно, дело не только в кулинарии. мы также пробежим нью-йоркский и чикагский марафоны, поближе познакомимся с собором Святого Павла, нанесем визиты Золушке и Льюису Кэрроллу и даже разберемся, почему мы думаем о томате как о овоще. В основе всего этого лежит работа Ченга по теории категорий, передовой «математике математики» о выяснении того, как работает математика. Это не математика наших школьных классов, рассматриваемая через теорию категорий; математика становится не столько о числах и формулах, сколько о том, как мы что-то знаем, во что верим и понимаем, в том числе о том, съел ли наш брат слишком много пирога. Многие из нас думают, что математика сложна, но, как поясняет Ченг, математика предназначена для того, чтобы делать сложные вещи более простыми. В сочетании с ее заразительным энтузиазмом в кулинарии и истинным интересом к жизни взгляд Ченг на математику становится этой уникальной книгой: забавным, живым и понятным путешествием по огромной территории, которую ранее не исследовала ни одна популярная книга по математике. Проверьте отзывы на Amazon! Весь наш мир построен на математике, от кода веб-сайта до уравнений, позволяющих проектировать небоскребы и мосты. Большую часть времени эта математика работает тихо за кулисами, пока не перестанет работать. Всевозможные, казалось бы, невинные математические ошибки могут иметь серьезные последствия. Математику легко игнорировать до тех пор, пока неуместная десятичная запятая не перевернет фондовый рынок, единицу Математику легко игнорировать до тех пор, пока неуместная десятичная запятая не перевернет фондовый рынок, ошибка преобразования единиц не приведет к падению самолета или кто-то не поделит на ноль и останавливает линкор посреди океана. Изучение и объяснение множества сбоев, потенциальных промахов и математических ошибок, связанных с Интернетом, большими данными, уличными знаками, лотереями, Римской империей, и объяснение множества сбоев, потенциальных промахов и математических ошибок, раскрытых Мэттом Паркером причудливые способы, которыми математика сбивает нас с толку, и что это говорит о ее важном месте в нашем мире. Делать ошибки еще никогда не было так весело. Проверьте отзывы на Amazon! Бенуа Мандельброт, родившийся в Варшаве и выросший во Франции во время прихода к власти Гитлера, нашел спасение от жестокости окружающего мира с помощью математики. Логика иногда создает монстров, и Мандельброт рано начал охотиться на монстров. Втянутый в бесконечные обнародования формул, он погружается в тайные измерения и неведомые чудеса. Однако его дары не облегчают ему жизнь. Когда нацисты отказываются от притворства марионеточного правительства в Виши, Франция, ревность одноклассников Мандельброта приводит к доносам и катастрофе. Молодой математик должен спасти свою семью с помощью открытых им секретных пространств, иначе его гений уничтожит их. Проверьте отзывы на Amazon! Мы все узнали, что отношение длины окружности круга к его диаметру называется π и что значение этого алгебраического символа примерно равно 3,14. Однако нам не сказали, что за этим, казалось бы, обыденным фактом скрывается мир тайн, который очаровывал математиков с древних времен до наших дней. Проще говоря, π — это странно. В этом восхитительном введении неспециалиста в одно из самых интересных явлений математики, доктора. Позаментье и Леманн рассматривают историю числа Пи с добиблейских времен до 21 века, множество забавных и ошеломляющих способов оценки π на протяжении веков, причудливые примеры одержимости числом Пи (включая попытку законодательно установить его точное значение) и полезные сведения. применения пи в повседневной жизни, включая статистику. Этот поучительный и освежающий подход к математике развлечет непрофессиональных читателей и повысит их математическую грамотность. Проверьте отзывы на Amazon! Входят сэр Камференс, его жена леди Ди из Аметра и их сын Радиус. С помощью плотника Гео из Метри эта проницательная команда проектирует идеальный стол, способствующий обсуждению идеального мирного плана. Первый в серии Sir Cumference, SIR CUMFERENCE AND THE FIRST ROUND TABLE, делает математику увлекательной и доступной для всех. Проверьте отзывы на Amazon! Никакое число не привлекало внимание и воображение людей на протяжении веков так сильно, как отношение длины окружности к ее диаметру. Радость Пи это книга из многих частей. Свежие повествования рассказывают об истории числа π и причудливых историях тех, кто им одержим. На боковых панелях документированы увлекательные факты о пи (включая отрывок из судебного процесса над О. Дж. Симпсоном). Десятки фрагментов и фактов раскрывают замечательное влияние числа Пи на протяжении веков. Мнемонические устройства учат, как запоминать π до многих сотен цифр (или больше, если вы так склонны). Мультфильмы, стихи, лимерики и шутки, вдохновленные числом пи, предлагают восхитительный «квадратный» юмор числа пи.
Пример CountA([2,4,6]) // Результат: 3
CountA(["A","B","C","D"]) // Результат: 4
CountA(["A","B","C","D",""]) // Результат: 5
Подсчитывает количество строк в таблице, удовлетворяющих набору условий
Синтаксис
Аргументы
Пример CountIf(["A","B","A","A","B"], Value="A") // Результат: 3
CountIf(["A","B","A","A","B"], Value="B") // Результат: 2
Считатьесли(
Стол(
{Тест: "Английский", Оценка: 90},
{Тест: "Английский", оценка: 55},
{Тест: "Математика", Оценка: 73},
{Тест: "Математика", оценка: 85}
),
Оценка>=65
)
// Результат: 3
Purpose
Counts the number of rows in a table
Syntax
Arguments
Пример Счетные ряды(
Стол(
{Значение: "А"},
{Значение: "В"},
{Значение: "С"}
)
)
// Результат: 3
Generates a psuedo-random decimal number between 0 and 1
Example // Result: 0.
 18009472
// Результат: 0,25365866
// Результат: 0,52303658
18009472
// Результат: 0,25365866
// Результат: 0,52303658
Generates a random number within a range
Пример // RandBetween(3, 7) // Результат: 4
// RandBetween(3, 7) // Результат: 3
// RandBetween(3, 7) // Результат: 6
Возвращает e в степени заданного числа. Математическая константа e (также известная как число Эйлера) равна 2,71828182845904, основанию натурального логарифма.
Синтаксис
Аргументы
Пример Exp(1) // Результат: 2,71828182845
Exp(2) // Результат: 7.
 38
389893
Возвращает естественный логарифм ряд — логарифм к базе E -номера E (номер Эйлера)
Пример Ln(2.71828182845) // Результат: 1
Ln(7.38
9893) // Результат: 2
Calculates the logarithm of a number for a given base
Syntax
Arguments
Пример Log(10, 10) // Результат: 1
Лог(10, 15) // Результат: 0,85027415
Log(10, 20) // Результат: 0,76862179
Вам понравилась эта статья? 😺 Вы можете размещать сообщения, используя свой адрес электронной почты, и вам не нужно создавать учетную запись, чтобы присоединиться к обсуждению.
Вы можете размещать сообщения, используя свой адрес электронной почты, и вам не нужно создавать учетную запись, чтобы присоединиться к обсуждению. 7 Великолепно написанных математических книг о Пи
Чтение математических книг — лучший способ выучить математику!

Через Amazon.com История числа Пи Петра Бекмана 
«История числа пи — это лишь малая часть истории математики, которая сама по себе является лишь зеркалом истории человека. Эта история полна закономерностей и тенденций, частота и сходство которых слишком поразительны, чтобы их можно было отбросить как случайность. Подобно законам квантовой механики, а в конечном счете и всей природы, законы истории носят явно статистический характер. Но что это за законы, никто не знает. Видны лишь отдельные обрывки. И из них то, что Хейселей Кливленда больше, чем Архимедов Сиракуз».
― Петр Бекманн, История числа π
Как испечь пи, автор Евгения Ченг Через Amazon.com
 How to Bake Pi предлагает совершенно новый способ осмысления области, которую, как мы все думаем, мы знаем; она ослепит постоянного читателя популярной математики, а также развеселит и просветит даже самых закоренелых математикофобов.
How to Bake Pi предлагает совершенно новый способ осмысления области, которую, как мы все думаем, мы знаем; она ослепит постоянного читателя популярной математики, а также развеселит и просветит даже самых закоренелых математикофобов. «В школе, если вы напишете 10 + 4 = 2, вам скажут, что это неправильно, но на самом деле это правильно в некоторых случаях, например, когда вы говорите время — четыре часа позже 10 часов — это действительно 2 часа. Часы.
― Юджиния Ченг, Как испечь число Пи: съедобное исследование математики математики
Скромный Пи: Когда математика идет не так в реальном мире, Мэтт Паркер Через Amazon.com
«Даже после целой жизни образования, связанного с малыми числами, остается рудиментарный инстинкт, что большие числа являются логарифмическими; что разрыв между триллионом и миллиардом ощущается примерно так же, как скачок между миллионом и миллиардом, потому что и то, и другое в тысячу раз больше.
 На самом деле скачок к триллиону намного больше: разница между жизнью до тридцати лет и временем, когда человечество может больше не существовать».
― Мэтт Паркер, Humble Pi: Когда математика идет не так в реальном мире
На самом деле скачок к триллиону намного больше: разница между жизнью до тридцати лет и временем, когда человечество может больше не существовать».
― Мэтт Паркер, Humble Pi: Когда математика идет не так в реальном мире
Мандельброт Великолепный: новелла Лиз Зимской Через Amazon убегает в глубокую математику, чтобы избежать возвышения Гитлера.
Все, что я видел — деревья, здания, холмы, окружающие город, — имело дополнительное мерцание возможности вокруг этого. Как прекрасен был мир, как полон тайн! Может быть, сегодня я перестану прятаться в конце класса. Возможно, если бы я сказал что-нибудь блестящее, Эмиль Валла и его друзья не заметили бы форму моего лица. Возможно, мы могли бы даже начать делать домашнее задание вместе.
― Лиз Зимска , Мандельброт Великолепный: новелла
Пи: Биография самого загадочного числа в мире Альфреда С. Позаментье Через Amazon.com Математики называют его «трансцендентным числом», потому что его значение нельзя вычислить с помощью любой комбинации сложения, вычитания, умножения, деления и извлечения квадратного корня.
Математики называют его «трансцендентным числом», потому что его значение нельзя вычислить с помощью любой комбинации сложения, вычитания, умножения, деления и извлечения квадратного корня. Где-то в прошлом, после того, как было изобретено колесо (или любой действительно круглый объект), длина окружности, вероятно, была измерена для сравнения.
 Возможно, в первые дни было важно измерить, какой путь проедет колесо за один оборот. Это можно было сделать, покатив колесо по земле и отметив расстояние, которое оно проедет ровно за один оборот (конечно, без проскальзывания) или с помощью чего-то, похожего на струну, надетую вдоль него. Вероятно, также был отмечен диаметр, размер, который гораздо легче измерить, поскольку для этого требовалось просто положить рядом с ним прямую палку или линейку и отметить его длину.
― Альфред С. Позаментье, Пи: биография самого загадочного числа в мире , и их сына Радиуса за игру слов, каламбуры и решение задач в этом математическом приключении, наполненном геометрией. Король Артур был хорошим правителем, но теперь ему нужен хороший правитель. Что бы вы сделали, если бы соседнее королевство угрожало войной? Естественно, вы созовете своих самых сильных и храбрых рыцарей вместе, чтобы найти решение. Но когда ваш конференц-стол создает больше проблем, чем угроза вашего врага, вам нужна помощь специалиста.
Возможно, в первые дни было важно измерить, какой путь проедет колесо за один оборот. Это можно было сделать, покатив колесо по земле и отметив расстояние, которое оно проедет ровно за один оборот (конечно, без проскальзывания) или с помощью чего-то, похожего на струну, надетую вдоль него. Вероятно, также был отмечен диаметр, размер, который гораздо легче измерить, поскольку для этого требовалось просто положить рядом с ним прямую палку или линейку и отметить его длину.
― Альфред С. Позаментье, Пи: биография самого загадочного числа в мире , и их сына Радиуса за игру слов, каламбуры и решение задач в этом математическом приключении, наполненном геометрией. Король Артур был хорошим правителем, но теперь ему нужен хороший правитель. Что бы вы сделали, если бы соседнее королевство угрожало войной? Естественно, вы созовете своих самых сильных и храбрых рыцарей вместе, чтобы найти решение. Но когда ваш конференц-стол создает больше проблем, чем угроза вашего врага, вам нужна помощь специалиста.
Рыцари мчались так быстро, как только могли, к Королевскому замку. Рядом жил сэр Камференс, поэтому его семья приехала вместе с ним. Сэр Камференс был женат на леди Ди, которая была родом из города Аметр. У них родился сын Радиус. Радиус был очень маленьким и довольно молодым, но его острый ум и безграничная энергия с лихвой компенсировали недостаток роста и возраста.
- Синди Нойшвандер , Сэр Камференс и первый круглый стол: математическое приключение
Радость числа Пи Дэвида Блатнера Через Amazon Пи-или? как это символически известно, — бесконечно, и в «Радость пи» оно оказывается бесконечно интригующим. Обладая острым историческим пониманием и освежающим чувством юмора, Дэвид Блатнер исследует многие грани π и увлечение им человечества — от древних египтян и Архимеда до Леонардо да Винчи и современных братьев Чудновских. Они вычислили число Пи до восьми миллиардов цифр с помощью самодельного суперкомпьютера.
Пи-или? как это символически известно, — бесконечно, и в «Радость пи» оно оказывается бесконечно интригующим. Обладая острым историческим пониманием и освежающим чувством юмора, Дэвид Блатнер исследует многие грани π и увлечение им человечества — от древних египтян и Архимеда до Леонардо да Винчи и современных братьев Чудновских. Они вычислили число Пи до восьми миллиардов цифр с помощью самодельного суперкомпьютера.


 59 закона об образовании 273-ФЗ
59 закона об образовании 273-ФЗ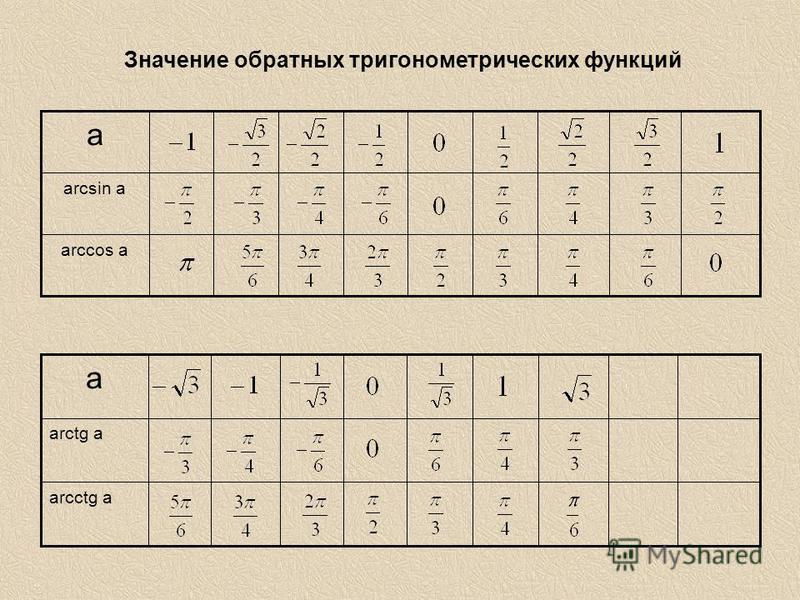 Если по критериям ГК1–ГК4 обучающийся набрал менее 4 баллов, выставляется отметка «3».
Если по критериям ГК1–ГК4 обучающийся набрал менее 4 баллов, выставляется отметка «3».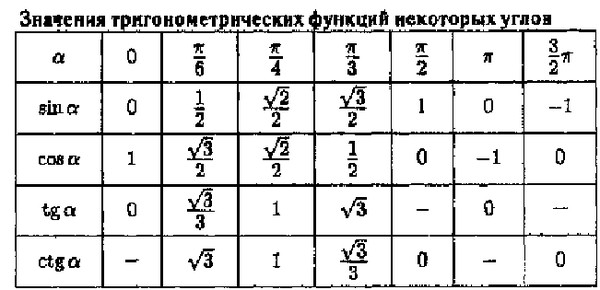 Вы можете вместе решать прошлогодние экзаменационные работы или разбирать сложные темы,
Вы можете вместе решать прошлогодние экзаменационные работы или разбирать сложные темы,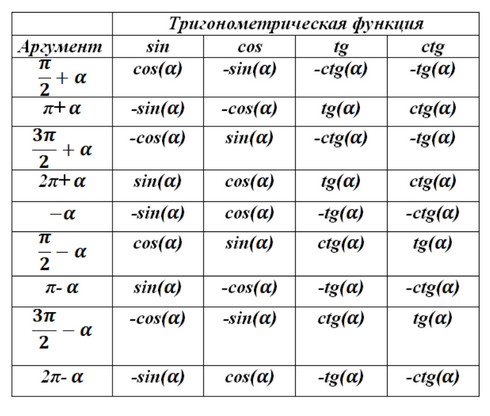
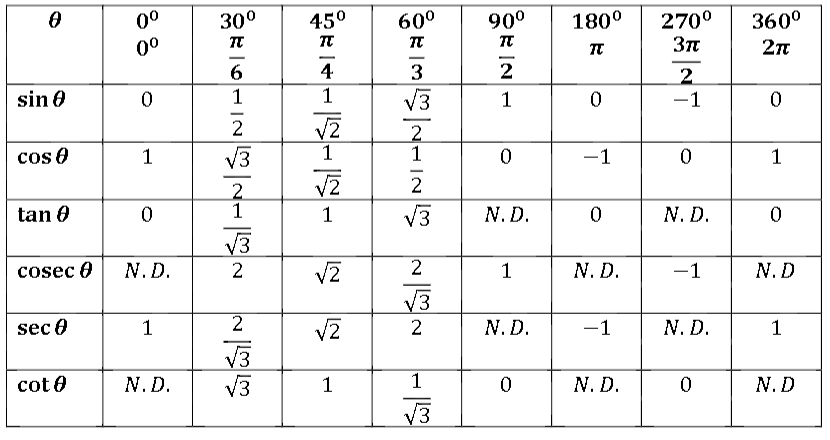 05.2017
39814
05.2017
39814
 01.2021
58293
01.2021
58293
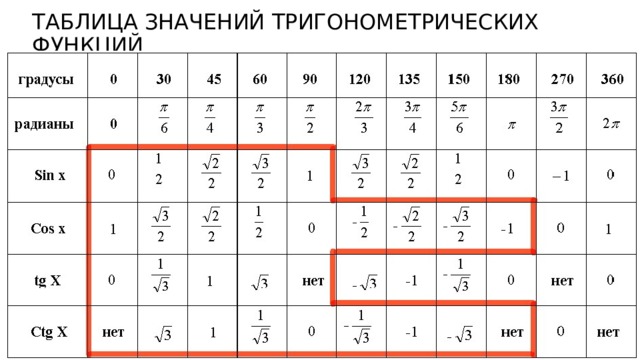 05.2017
11071
05.2017
11071
 09.2015
191677
09.2015
191677
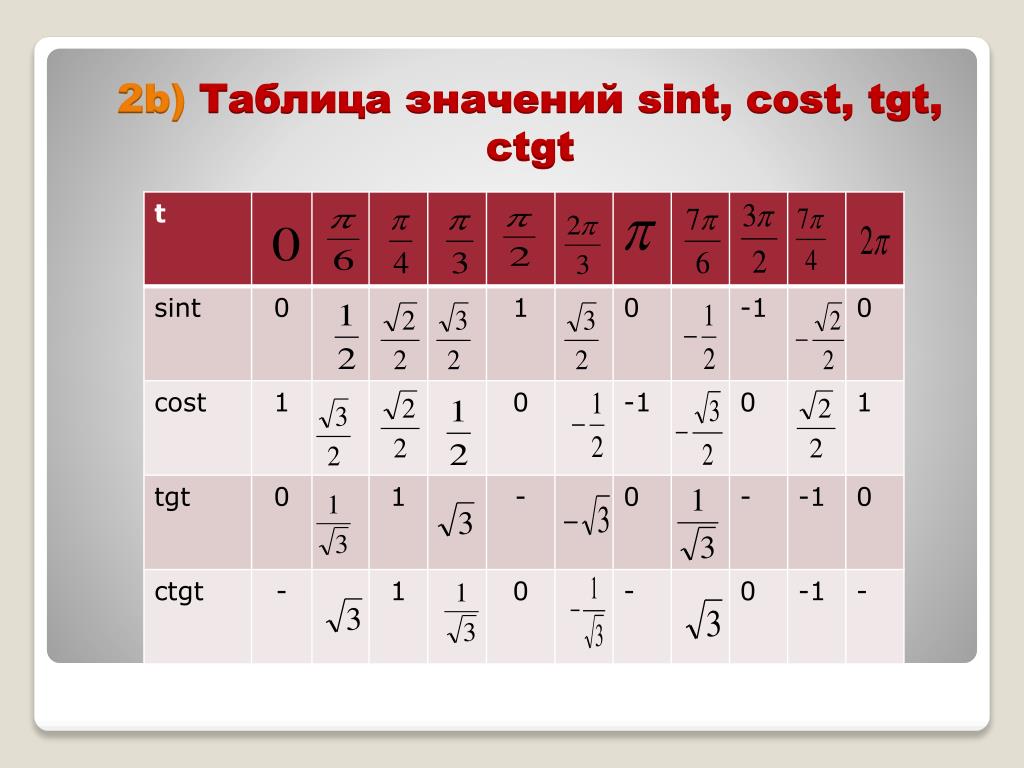
 05.2017
6867
05.2017
6867
 Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста. 04.2020
5725
04.2020
5725
 Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста. 05.2020
2444
0
05.2020
2444
0
 Включает в себя выражения для вычисления, решение арифметических и геометрических задач.
Включает в себя выражения для вычисления, решение арифметических и геометрических задач.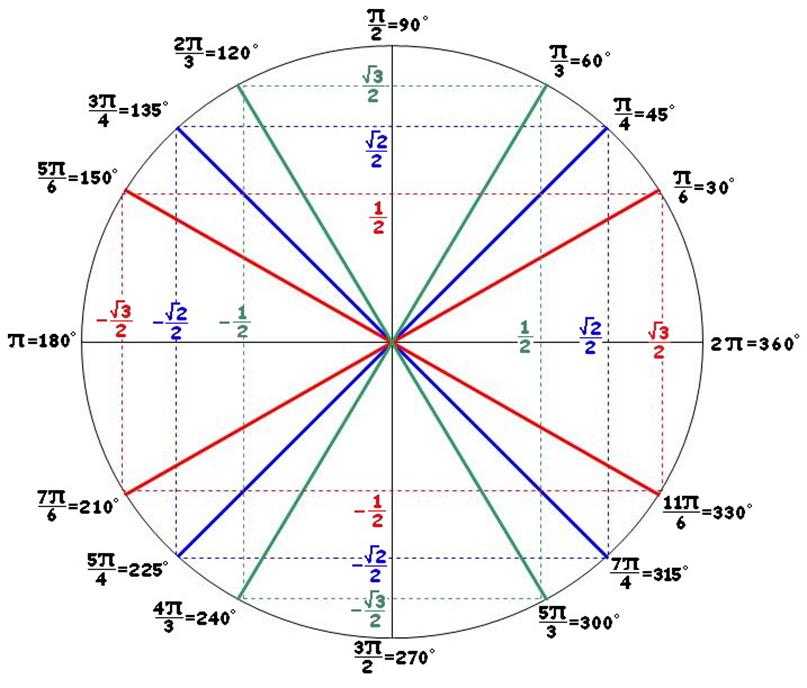 12.2020
469
0
12.2020
469
0

 04.2022
279
04.2022
279
 03.2022
571
03.2022
571
 03.2020 математика ВПР
03.2020 математика ВПР
 Время прохождения ограничено. Внимательно прочитайте пример и отметьте галочкой ответ в окошечке. Дальнейшее прохождение не возможно если ответ не введён. По окончанию теста вы получите сертификат о прохождении, в котором фиксируется ваши результаты. Удачи в прохождении!
Время прохождения ограничено. Внимательно прочитайте пример и отметьте галочкой ответ в окошечке. Дальнейшее прохождение не возможно если ответ не введён. По окончанию теста вы получите сертификат о прохождении, в котором фиксируется ваши результаты. Удачи в прохождении!  03.2015
6949
03.2015
6949
 Удачи в прохождении и надеемся что наш тест вам понравится.
Удачи в прохождении и надеемся что наш тест вам понравится. 02.2021
807
02.2021
807
 НУМЕРАЦИЯ
НУМЕРАЦИЯ
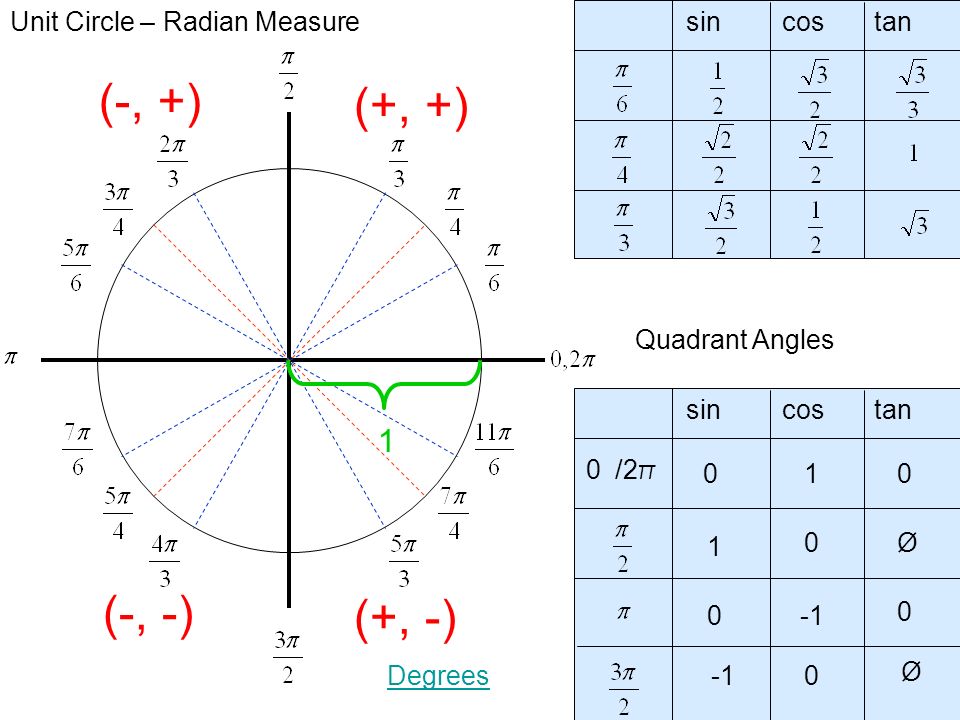 Оценивается по 5-бальной шкале.
Оценивается по 5-бальной шкале. 10.2016
8436
10.2016
8436
 1
1
 11.2021
139
0
11.2021
139
0
 02.2015
886
02.2015
886
 Устные вычисления (математика 4 класс)
Устные вычисления (математика 4 класс)
 10.2016
6930
10.2016
6930

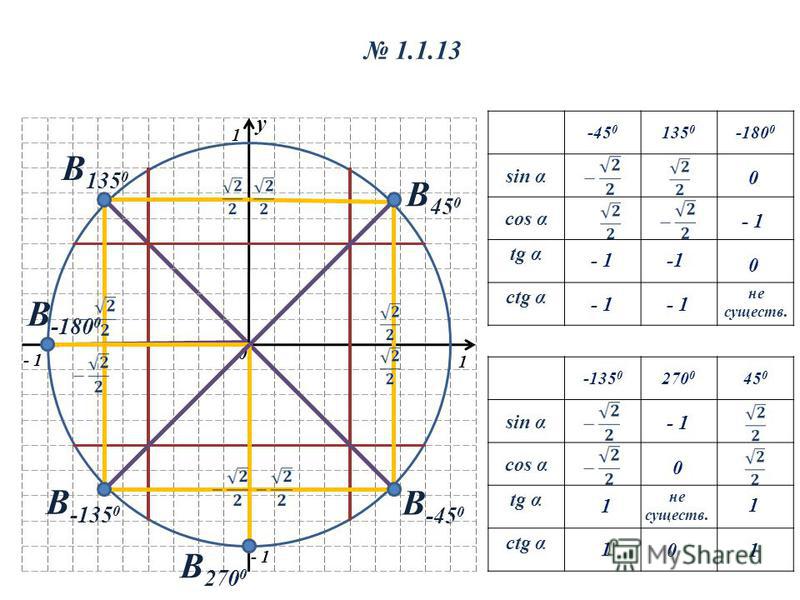 Составлен в соответствии с программой и УМК для 4 класса авторского коллектива под руководством М. И. Моро
Составлен в соответствии с программой и УМК для 4 класса авторского коллектива под руководством М. И. Моро 4 класс. Числа и величины.
4 класс. Числа и величины.
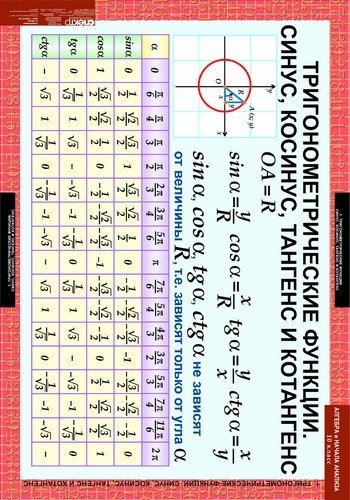 Математика. Сложение и вычитание натуральных чисел №3
Математика. Сложение и вычитание натуральных чисел №3
 Математика. Умножение и деление натуральных чисел №1
Математика. Умножение и деление натуральных чисел №1
 Математика. Умножение и деление натуральных чисел №4
Математика. Умножение и деление натуральных чисел №4
 Математика. Действия с натуральными числами №1
Математика. Действия с натуральными числами №1
 Математика. Действия с натуральными числами №5
Математика. Действия с натуральными числами №5
 Сложение и вычитание» за курс начальной школы в форме ЕГЭ
Сложение и вычитание» за курс начальной школы в форме ЕГЭ