Решение кубических уравнений: примеры, метод Виета-Кардано
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида Ax3+B=0
Кубическое уравнение, содержащее двучлен, имеет вид Ax3+B=0 . Его необходимо приводить к x3+BA=0 с помощью деления на А, отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x3+BA=0x+BA3x2-BA3x+BA23=0
Результат первой скобки примет вид x=-BA3, а квадратный трехчлен — x2-BA3x+BA23, причем только с комплексными корнями.
Пример 1Найти корни кубического уравнения 2×3-3=0.
Решение
Необходимо найти х из уравнения. Запишем:
2×3-3=0x3-32=0
Необходимо применить формулу сокращенного умножения.
Тогда получим, что
x3-32=0x-3326×2+3326x+923=0
Раскроем первую скобку и получим x=3326. Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x=3326.
Решение возвратного кубического уравнения вида Ax3+Bx2+Bx+A=0
Вид квадратного уравнения — Ax3+Bx2+Bx+A=0, где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
Ax3+Bx2+Bx+A=Ax3+1+Bx2+x==Ax+1×2-x+1+Bxx+1=x+1Ax2+xB-A+A
Корень уравнения равен х=-1, тогда для получения корней квадратного трехчлена Ax2+xB-A+A необходимо задействовать через нахождение дискриминанта.
Пример 2Решить уравнение вида 5×3-8×2-8x+5=0.
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5×3-8×2-8x+5=5×3+1-8×2+x==5x+1×2-x+1-8xx+1=x+15×2-5x+5-8x==x+15×2-13x+5=0
Если х=-1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5×2-13x+5:
5×2-13x+5=0D=(-13)2-4·5·5=69×1=13+692·5=1310+6910×2=13-692·5=1310-6910
Ответ:
x1=1310+6910×2=1310-6910×3=-1
Решение кубических уравнений с рациональными корнями
Если х=0, то он является корнем уравнения вида Ax3+Bx2+Cx+D=0.
При свободном члене D=0 уравнение принимает вид Ax3+Bx2+Cx=0. При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид xAx2+Bx+C=0.
Найти корни заданного уравнения 3×3+4×2+2x=0.
Решение
Упростим выражение.
3×3+4×2+2x=0x3x2+4x+2=0
Х=0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3×2+4x+2. Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D=42-4·3·2=-8. Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х=0.
Когда коэффициенты уравнения Ax3+Bx2+Cx+D=0 целые, то в ответе можно получить иррациональные корни. Если A≠1, тогда при умножении на A2 обеих частей уравнения проводится замена переменных, то есть у=Ах:
Ax3+Bx2+Cx+D=0A3·x3+B·A2·x2+C·A·A·x+D·A2=0y=A·x⇒y3+B·y2+C·A·y+D·A2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными.
Найти корни заданного уравнения 2×3-11×2+12x+9=0.
Решение
Необходимо произвести преобразование с помощью умножения на 22 обеих частей, причем с заменой переменной типа у=2х. Получаем, что
2×3-11×2+12x+9=023×3-11·22×2+24·2x+36=0y=2x⇒y3-11y2+24y+36=0
Свободный член равняется 36, тогда необходимо зафиксировать все его делители:
±1,±2,±3,±4,±6,±9,±12,±36
Необходимо произвести подстановку y3-11y2+24y+36=0, чтобы получить тождество вида
13-11·12+24·1+36=50≠0(-1)3-11·(-1)2+24·(-1)+36=0
Отсюда видим, что у=-1 – это корень. Значит, x=y2=-12.
Далее следует деление 2×3-11×2+12x+9 на x+12 при помощи схемы Горнера:
| xi | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | -11 | 12 | 9 | |
-0. 5 | 2 | -11+2·(-0.5)=-12 | 12-12·(-0.5)=18 | 9+18·(-0.5)=0 |
Имеем, что
2×3-11×2+12x+9=x+122×2-12x+18==2x+12×2-6x+9
После чего необходимо найти корни квадратного уравнения вида x2-6x+9. Имеем, что уравнение следует привести к виду x2-6x+9=x-32, где х=3 будет его корнем.
Ответ: x1=-12, x2,3=3.
ЗамечаниеАлгоритм можно применять для возвратных уравнений. Видно, что -1 – это его корень, значит, левая часть может быть поделена на х+1. Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A0x3+A1x2+A2x+A3=0 необходимо найти B1=A1A0, B2=A2A0, B3=A3A0.
После чего p=-B123+B2 и q=2B1327-B1B23+B3.
Полученные p и q в формулу Кардано. Получим, что
y=-q2+q24+p3273+-q2-q24+p3273
Подбор кубических корней должен удовлетворять на выходе значению -p3.
Тогда корни исходного уравнения x=y-B13. Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2×3-11×2+12x+9=0.
Решение
Видно, что A0=2, A1=-11, A2=12, A3=9.
Необходимо найти B1=A1A0=-112, B2=A2A0=122=6, B3=A3A0=92.
Отсюда следует, что
p=-B123+B2=—11223+6=-12112+6=-4912q=2B1327-B1B23+B3=2·-112327—112·63+92=343108
Производим подстановку в формулу Кордано и получим
y=-q2+q24+p3273+-q2—q24+p3273==-343216+34324·1082-49327·1233+-343216-34324·1082-49327·1233==-3432163+-3432163
-3432163 имеет три значения. Рассмотрим их ниже.
-3432163=76cosπ+2π·k3+i·sinπ+2π·k3, k=0, 1, 2
Если k=0, тогда -3432163=76cosπ3+i·sinπ3=7612+i·32
Если k=1, тогда -3432163=76cosπ+i·sinπ=-76
Если k=2, тогда -3432163=76cos5π3+i·sin5π3=7612-i·32
Необходимо произвести разбиение по парам, тогда получим -p3=4936.
Тогда получим пары: 7612+i·32 и 7612-i·32, -76 и -76, 7612-i·32 и 7612+i·32.
Преобразуем при помощи формулы Кордано:
y1=-3432163+-3432163==7612+i·32+7612-i·32=7614+34=76y2=-3432163+-3432163=-76+-76=-146y3=-3432163+-3432163==7612-i·32+7612+i·32=7614+34=76
Значит,
x1=y1-B13=76+116=3×2=y2-B13=-146+116=-12×3=y3-B13=76+116=3
Ответ:
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Кубическим уравнением называется уравнение вида
где a, b,c ,d — постоянные коэффициенты, а х — переменная. Мы рассмотрим случай, когда коэффициенты являются веществеными числами. Корни кубического уравнения. Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство. Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) .
Итак, возможны только 3 следующих случая:
На практике часто , решение кубических уравнений упирается в разложении их на множители. Формула Кардано. Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел). Канонической формой кубического уравнения называется уравнение вида
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
Итак, приступим к вычислению корней.
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y1, y2, y3 и подставьте их в (3). Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем α = β, и y1=2α, y2= y3 = — α. Аналогично подставляем в (3) и получаем ответ. Тригонометрическая формула Виета. Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а. Итак, алгоритм применения этой формулы: 1. Вычисляем
2. Вычисляем
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
б) Если S<0, то заменим тригонометрические функции гиперболическими.
Тогда
Для тех, кого интересуют также и мнимые корни: x2= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i x3= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i
| |
Дополнительная информация от TehTab. | |
И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Найдем следующие величины:
(если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
ru:Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Системы уравнений. Формулы. Методы. / / Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
(В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
Найдем следующие величины:
Введите свой запрос:Решение кубических уравнений — методы и примеры вычислений
Всё, что окружает человека, в какой-то мере связано с математикой. Пожалуй, не одно значимое открытие в физике, химии не обходится без составления формул. Особое место при расчётах занимают кубические уравнения. Решение практических задач очень важно, поэтому необходимо уметь проводить вычисления. Существуют различные подходы, позволяющие довольно быстро найти ответ. Поэтому нужно не только знать принцип решения, но и правильно подобрать метод.
Содержание
- История и формулировки
- Формула квадратного уравнения
- Разложение на множители
- Использование дискриминанта
- Теорема Виета и двучлен
- Подробный онлайн-калькулятор
История и формулировки
Кубические уравнения составлялись ещё в Древней Греции и Египте. Археологами были найдены клинописные таблицы XVI века до нашей эры, содержащие описание возможного их решения.
Вычислением кубов занимался Гиппократ, пытавшийся свести задачу к нахождению отрезков с помощью чертёжных инструментов. Архимед использовал для поиска ответа пересечение двух конусов.
Впервые методы решения такого рода уравнений были описаны в китайском учебнике «Математика в девяти книгах», составленном во втором столетии до нашей эры. В седьмом веке Омар Хайям на основании своих работ приходит к выводу, что решение уравнений третьей степени может иметь более одного ответа.
Математик Шараф ад-Дин публикует тракт об уравнениях, в котором описывает восемь различных типов кубических выражений, имеющих положительное решение. В своих вычислениях он использует численную аппроксимацию. Учёный не только разработал подход для решения с использованием производной функции и экстремумов, но и понял важность дискриминанта многочлена при нахождении кубов.
В 1530 году итальянский математик Никколо Тарталья разрабатывает методику решения, которой он после поделился с Джероламо Кардано.
Согласно этому способу нужно было извлекать квадратный корень из отрицательного числа. Параллельно с этими исследованиями, основоположник символической алгебры Франсуа Виет, предлагает свой способ решения кубического равенства с тремя корнями. Позднее его работу описал и обосновал Рене Декарт.
Уравнением третьей степени называют выражение вида: a*y 3 + d*y 2 + c*y + n = 0. В математике оно называется кососимметрическим. Число y, значение которого необходимо найти, при подстановке превращает формулу в тождество. Называется оно корнем уравнения или просто решением. Кроме этого, y ещё является и корнем многочлена куба.
Таким образом, в кубических уравнениях стоит только одна переменная в третьей степени. Они всегда имеют три корня. При этом ответы могут быть равны друг другу и даже быть комплексными (но не более двух).
Формула квадратного уравнения
Используется при решении простейшего равенства методом разложения кубического уравнения на множители.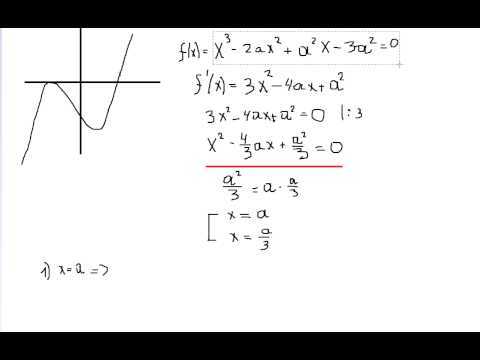
Когда последний член равен нулю, решить такую задачу можно по методу квадратных уравнений. При n = 0, уравнение примет вид :
a*y 3 + d*y 2 + c*y + n = 0.
В полученном выражении каждый член представлен произведением на неизвестное, поэтому переменную y можно вынести за скобки: y*(d*y 2 + c) = 0. Уравнение в скобках является классическим квадратным, которое можно решать несколькими способами:
- разложением на множители;
- с использованием формулы корней квадратного уравнения;
- методом дополнения.
При выборе первого варианта разложение выполняют следующим образом. Например, необходимо решить равенство вида: *y 2 — 11*y — 16 = 0. Квадратный член можно записать в виде двух множителей: 3*y и y. Поэтому их можно записать сразу как произведение в скобках: (3 * + n) * (y + n) = 0. Так как определённый член можно записать в виде произведения 2*2 или 1*4, то формулу можно представить как (3 *y +1) * (y — 16).
Если раскрыть скобки, то получится равенство 3*y 2 — 12 *y + y + 16. Решением (-12*y + y) будет (-11*y). Как раз тот член, который нужен. Используя же произведение 2*2 — искомый член найти не получится.
Равенство раскладывают на два множителя: (3*y +1) (х — 16) = 0. Согласно аксиоме произведение двух членов равно нулю только тогда, когда хотя бы один из них равен нулю. Приравняв каждое выражение в скобках к нулю, можно записать два равенства: 3*y + 1 = 0 и y — 16 = 0. При решении каждого из них получится два ответа: y = 1/3 и y = 16.
Для проверки результата необходимо оба возможных решения подставить в формулу. Так как для квадратного уравнения существует только два решения, а для кубического три, то в этом случае третьим ответом будет ноль. Поэтому решением уравнения будет три корня: 0, 1/3, 16.
Но проще и нагляднее всего использовать второй вариант. Формула корней кубического уравнения имеет вид: y = ((-d + (d 2 — 4*a*c) ½ ) / 2*a и y = ((-d — (d 2 — 4*a*c) ½ ) / 2*a.
Корни квадратного уравнения и будут ответом для кубического. Например, 5*y 2 — 7*y — 14 = 0. Приняв, что a = 5, d = -7, c = — 14 и подставив числовые значения, будет верным запись: y = 1 4 / 5 и y = -1. Дробное решение и отрицательное будет являться корнями кубического равенства.
Разложение на множители
Если определённый член не равен нулю, то посчитать игрек при помощи квадратных уравнений невозможно. В этом случае используется метод разложения на свободные множители. Например, 2 * y 3 + 9 * y 2 +13 * y + 6 = 0. Чтобы разложить кубическое уравнение на множители и определить неизвестное, придерживаются следующего порядка:
Коэффициентом кубического члена является двойка, соответственно её множители — цифры один и два.Вычисление рационального числа операция долгая и требующая внимания. Поэтому для быстрого нахождения ответа используется деление по схеме Горнера. По этой схеме выполняют деление целых цифр на коэффициенты всех членов равенства. Если в ответе получается только целая часть, то эти числа считаются вариантами решения.
Таким методом можно находить и иррациональные выражения.
Чтобы освоить способ Горнера, необходимо тщательно в нём разобраться. Способ заключается в делении коэффициентов многочлена без учёта степенных показателей. Вычитание заменяется сложением как при делении в столбик. То есть уравнение, впрочем, как и неравенство, вида y 3 + 2*y 2 — 4 *y + 8, записывается как 1 2 -4 8 с необходимым делимым. В результате должен получиться многочлен с остатком. Если он будет нулевым, то одним из ответов уравнения и будет делимое .
Использование дискриминанта
Дискриминант степенного выражения представляет произведение квадратов разностей корней в различных сочетаниях. Другими словами, берут пару, состоящую из любых корней уравнения, вычитают друг из друга и возводят в квадрат. Это и будет один множитель. Затем берут другую пару и повторяют действия.
Таким образом, перебирают все варианты.
При решении кубических равенств используют значения коэффициентов. Например, для уравнения y 3 — 3* y 2 + 3* y — 1, они будут равны: a = 1, d = -3, c = 3, n = -1. Затем вычисляют дельта нулевое. Это ключевая величина, которая после подставляется в формулу. В примере, Δ0 = d 2 — 3 * a * c, определяют как (-3) 2 — 3 * (1) * (3) = 9 − 3 * 3 = 0 .
Затем находят дельта один. Δ1 = 2 * d 3 — 9 * a * d * c + 27 * a 2 * n. Подставив значения в формулу, вычисляют Δ1:
2 (-3) 3 — 9 (1)(-3)*(3) + 27 (1) 2 * (-1) = 2 (-27) — 9 (-9) + 27 (-1) = -54 + 81 — 27 = 81 − 81 = 0 = Δ 1.
Используя найденное, по аналогии с квадратичным равенством находят дискриминант: d 2 — 4 * a * c. Применительно к кубическому виду применяется правило, что показатель отрицательный, когда уравнение может иметь только одно решение. Если же его значение равно нулю — одно или два.
Уравнение кубического вида всегда должно иметь хотя бы одно решение, так как его график должен проходить через ось икс.
Так как в примере дельта-ноль и один равны нулю, то можно использовать следующее выражение:
- Δ1 2 — 4 * Δ0 3 / — 27 *a 2;
- (0) 2 — 4 * (0) 3 / — 27 * (1) 2;
- (0−0) / 27;
- Δ = 0.
Исходя из этого, уравнение имеет два решения. Вычислив С, можно определить возможные решения уравнения. Заменив по мере необходимости дельты, решается равенство:
C = ((Δ 1 2 — 4 Δ 0 3 ) +Δ) / 2) ½ = (((0 — 0) + 0)/2) ½ = 0.
Корни куба определяются по формуле: u n C + Δ0/(u n C)) / 3*a, где u = (-1 + √(-3))/2, а n равно одному, двум или трём. Если подставить эти значения в равенство, и оно будет верным, то эта цифра и является возможным решением уравнения.
Этот способ показательный, но довольно сложный. Но если его понять, то проблем с решением уравнений любой сложности возникнуть не должно.
Теорема Виета и двучлен
Выражение вида: a*y 3 + d = 0 называется двухчленным или неполным уравнением. Для его решения нужно равенство привести к виду: y 3 + d/a = 0. Затем используя формулу сокращённого умножения для суммы кубов можно записать:
(y + 3 √ d/a) * (y 2 − ( 3 √ d/a)* y + 3 √ (d/a) 2 ) = 0.
Из первого множителя и находят значение игрека. Оно будет равно 3 √ d/a, ведь второй множитель — это квадратный трёхчлен с корнями комплексного вида.
Для проверки рациональных равенств удобно применять теорему Виета. Согласно ей корни уравнения связаны с коэффициентами выражениями:
- y1 + y2 + y3 = — d/a;
- y1 * y2 + y2 * y3 + y1 * y3 = c/a;
- y1 * y2 * y3 = — n/a.
Используя теорему, некоторые уравнения можно решить даже устно. Например, y3 + 2y — 24 = 0. Решение выполняется в следующей последовательности:
- записывают теорему применительно к равенству;
- определяют знаки корней;
- раскладывают определённый член.
Частным случаем применения теоремы являются тригонометрические формулы для кубического равенства:
S = Q 3 — R 2 , где Q = (a2 — 3d)/9, а R = (2 а 3 — 9ad + 27c) / 54.
В зависимости от знака S применяется одна из следующих формул : φ = (arcos (R/Q 3/2 ))/3 и φ = (arcos (ЇRЇ/Q 3/2 ))/3. Первое выражение справедливо при S > 0 и имеет три корня: y 1 = -2 (Q) ½ * cos (φ) — a/3; y 2 = — (Q) ½ cos (φ + 2p /3) — a/3; y 3 = -2 (Q) ½ * cos (φ — 2p/3) — a/3. А второе при S < 0 и имеет только одно решение: y = -2sgn®*[q] ½ * ch (φ) — a/3. В случае же когда S=0,то уравнение имеет следующие корни: y 1= -2*R1 /3 — a/3; y 2= y 3 =R1/3 — a/3.
Теорему Виета можно использовать и для наивысшей, четвёртой степени, при которой ещё существует аналитическое решение.
Подробный онлайн-калькулятор
Вычисление корней требует внимательности и усердия. Чтобы быстро находить решение, нужно не только знание теории, но и практические занятия. Конечно же, знать формулы и уметь решать уравнения нужно самому.
Но при самостоятельном вычислении существует вероятность допущения ошибки. Поэтому на помощь приходят своего рода решебники-онлайн. Они умеют не только точно и быстро определять корни равенства, но и показывать подробное вычисление. Благодаря этому можно не просто получить правильный ответ, но и разобраться в решении, понять различные нюансы, проверить свои знания.
Из наиболее популярных интернет-порталов, позволяющих найти корни кубического уравнения онлайн, можно выделить: mathforyou.
net, allcalc.ru, wedmath.ru, kontrolnaya-radota.ru. Воспользоваться такими сайтами-решателями сможет любой пользователь, даже не имеющий представление о методах решения уравнений.
Для этого нужно просто заполнить предлагаемые на странице поля и нажать кнопку «Рассчитать» или «Решить». Калькулятор сам на основании запрограммированных формул, чаще всего по методу Вието — Кардано, выполнит расчёт и выведет на экран ответ. Кроме этого, будет предложено подробное решение с описанием. На этих сайтах также можно посмотреть и примеры решений, формулы, теоремы.
Предыдущая
МатематикаЗнаки тригонометрических функций по четвертям — примеры определения
Следующая
МатематикаБиквадратные уравнения — примеры с решениями
Решение кубических уравнений с примерами решения
Содержание:
- Рассмотрим вопрос о количестве корней кубического уравнения
В этом разделе мы не будем решать кубические уравнения, а, в основном, будем рассматривать задачу о нахождении количества корней уравнения в зависимости от значений параметров.
Начнем с довольно простых примеров.
Пример 1:
Уравнение имеет корень Найти остальные корни этого уравнения.
Решение:
I способ. Поскольку известен один корень кубического уравнения, подставим его значение в уравнение, которое должно обратиться в верное равенство или Решим полученное уравнение относительно и получим
При имеем уравнение Разделив многочлен третьей степени «уголком» или по схеме Горнера на
получим квадратное уравнение при этом
Возможна группировка и разложение на множители:
При получаем уравнение Вновь разделив левую часть уравнения на получим квадратное уравнение которое дает
Возможна группировка и разложение на множители:
Ответ: при
при
Примечание. Обратим внимание на то, что по условию задачи необходимо найти корни, отличные от единицы, при таких значениях параметра, при которых является корнем заданного уравнения.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
II способ. Для кубического уравнения имеет место зависимость между его возможными корнями
и коэффициентами В нашем случае Дальнейшее решение системы не представляет труда и приводит к уже полученным результатам.
Пример 2:
Известно, что уравнение имеет своими корнями числа -1 и 2. Найти третий корень этого уравнения.
Решение:
Укажем наиболее простой способ решения. Подставляя в данное уравнение получим уравнения и
Решая систему получим и
Тогда данное уравнение принимает вид
Поскольку и
являются корнями уравнения, многочлен в левой части урав-ненияделится на Ясно,что тогда третий корень исходного уравнения
Ответ:
Возможно вам будут полезны данные страницы:
Прямая в пространстве |
Прямые и плоскости в пространстве |
Область значения функции |
Формулы приведения |
Пример 3:
Определить, при каких значениях уравнение имеет ровно два корня.
Решение:
I способ. Перепишем исходное уравнение в виде и построим график функции Для того чтобы найти число уравнения часто бывает достаточно представить схематический график функции не проводя полных исследований.
При решении данной задачи достаточно найти экстремумы функции и промежутки монотонности:
1. поскольку функция является многочленом.
2. Находим производную функции и критические точки из уравнения поскольку
3. Определяем промежутки монотонности и экстремумы функции. На промежутках функция убывает, а на промежутке функция возрастает,
— точка минимума;
— точка максимума;
Строим график функции и находим точки пересечения графика этой функции с прямой Покажем схематичное решение на рисунке:
Ясно, что данное уравнение имеет ровно два корня при и при
II способ. Применим теорему Виета. Поскольку уравнение имеет два равных корня, будем считать тогда, применительно к нашему уравнению, получаем систему уравнений
Решая систему уравнений, находим но тогда
Для определения имеем два уравнения:
III способ.
Воспользуемся методом неопределенных коэффициентов. Любое кубическое уравнение имеет либо один действительный корень, либо три действительных корня. Если оно имеет ровно два корня, то уравнение имеет три корня, два из которых равны, а поэтому
корни уравнения.
Два многочлена одной степени от одного и того же переменного равны только при равенстве коэффициентов при равных степенях. Это дает нам систему уравнений
Эта система была решена при решении задачи вторым способом.
Ответ:
Рассмотрим вопрос о количестве корней кубического уравнения
Любое кубическое уравнение заменой неизвестного сводится к каноническому виду (мы
сохранили обозначение переменной). Будем считать, что отличны от нуля. Если то для функции имеем поэтому функция возрастает на и уравнение имеет ровно один действительный корень.
Пример 4:
Определить все значения при которых уравнение имеет ровно один корень.
Решение:
Очевидно, исходя из приведенных рассуждений, уравнение имеет один корень, если
Ответ:
Если то функция имеет две критические точки
точка максимума
точка минимума
Если то уравнение при имеет один корень:
Например, уравнение будет иметь один корень, если то есть откуда Подтверждение можно получить, построив график функции
Пример 5:
Определить все значения при которых уравнение имеет один корень.
Решение:
Здесь решаем неравенство
Ответ: при
Если числа разных знаков, то уравнение имеет три корня. Очевидно, что в этой ситуации должны удовлетворять неравенству
Например, уравнение имеет три действительных корня, поскольку
Пример 6:
При каких значениях параметра уравнение имеет три корня?
Решение:
Здесь получаем неравенство
Ответ: при
Пример 7:
В зависисмости от параметра указать те значения для которых уравнение имеет три различных корня.
Решение:
Если то при всех уравнение имеет один корень, поэтому далее считаем, что но тогда, поделив обе части уравнения на получаем ему равносильное уравнение
то решений нет, поскольку при Получаем
Ответ:
Если же то кубическое уравнение имеет кратный корень, совпадающий с точкой максимума или точкой минимума: В первом случае но тогда во-втором но тогда вновь то есть в обоих случаях имеем, что есть необходимое условие для уравнения иметь корень кратности 2.
Вернемся к примеру 3.
Уравнение имеет ровно два корня. Найти Сделаем замену тогда
Сделаем еще одну замену тогда получаем уравнение но тогда В нашем случае Откуда И окончательно имеем Найденные значения совпадают с полученными ранее результатами.
Исследовательская работа «Прогрессивное решение кубических уравнений. От простого до сложного» • Наука и образование ONLINE
Автор: Юсупова Гавхархон Джахонгировна
Место работы/учебы (аффилиация): СООУ 16 Б Гафуровский район, Таджикистан,
Научный руководитель: Шарипова Гулбахор Халимджановна
Актуальность. Практически всё, что окружает человека так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Множество различных алгебраических и геометрических задач сводятся к какому-либо уравнению.
Линейные уравнения мы знаем с самых ранних лет, с начальной школы. С квадратными знакомимся в 8 классе, а вот кубические уравнения решаем в старших классах, делаем это обычно графическим способом или методом разложения на множители.
Проблема: Отсутствие навыков решения уравнений высших степеней вызывает затруднение при подготовке к итоговой аттестации на профильном уровне.
Объект: Кубическое уравнение
Предмет исследования: Способы решения кубических уравнений.
Гипотеза: Существует связь между коэффициентами кубического уравнения и его корнями, при решении таких уравнений можно применять разнообразные способы.
Цель: Изучение способов решения кубических уравнений.
Задачи:
- Подобрать необходимую литературу;
- Отобрать материал для исследования, выбрать главную, интересную, понятную информацию;
- Проанализировать и систематизировать полученную информацию;
- Найти различные методы и приёмы решения кубических уравнений;
- Классифицировать исследуемые уравнения;
- Сравнить степень сложности каждого из них;
- Познакомить одноклассников со способами решения уравнений;
- Создать электронную презентацию работы для представления собранного материала.
Методы исследования:
- Изучение литературных и Интернет-ресурсов;
- Анализ и классификация информации;
- Сравнение способов решения; -Обобщение.
Структура работы: Работа состоит из двух глав. Первая глава азбука кубического уравнения и уравнений n-ой степени. Вторая-. В третьей главе рассмотрены различные приёмы решения кубических уравнений.
Новизна работы: Мной было придумана новая тема с названием «Прогрессия корней уравнений n-ой степени», где там есть доказательства о возможности решение уравнений 7 степени. А также теорема Виета для уравнений пятого, шестого и седьмого степени.
Выводы:
- Теория уравнений занимает ведущее место в математике. Имеет не только теоретическое значение, но и служит практическим целям. Изучив учебную и научную литературу, интернет-ресурсы по теме «Кубические уравнения и его корни» удалось выяснить, что современной науке известно множество способов решения уравнений.
- На мой взгляд, самые надежные и практичные способы — это теорема Виета и схема Горнера, они позволяют быть уверенным в своем ответе.
- Выдвинута гипотеза о существовании связи между коэффициентами кубического уравнения и его корнями. Действительно — такая формула существует.
- В данной работе достигнута цель и выполнены основные задачи: показаны и изучены новые, ранее неизвестные формулы. Рассмотрено много примеров. Исследованы различные методы решения уравнений третьей степени. Не все способы удобны для решения, но каждый из них интересен. Предлагаемая работа рассчитана на учеников 9 — 11 классов, желающих повысить уровень математической подготовки, узнать больше о кубических уравнениях и способах их решения.
Практическая значимость: в зависимости от вида уравнения умение определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод. Продолжение работы вижу в изучении уравнений высших степеней.
Загрузка…
Мероприятие завершено
Исследовательская работа «Влияют ли числа на судьбу человека»
Мир нас восхищает многообразием, как мы с вами постоянно говорим, различных загадок. Мало кто знает, что пароль к загадкам вселенной — это числа. Разумеется, ученые в глубочайшей древности увидели связь личности и числа. Конечно же, все мы знаем, что…
Посмотреть работу
Исследовательская работа «Сравнительный анализ аэродинамических свойств легковых автомобилей с различными видами кузова»
При современных условиях жизни приходится признать, что необходимо экономить практически на всем. А, как, известно, одной из самых существенных позиций в колонке расходов является автомобиль. Есть некоторые бытовые хитрости, которые способны помочь…
Посмотреть работу
4″>Исследовательская работа «Взаимосвязь музыки и математики»Всем известно, что математика — это царица наук и предполагает точность, а музыка -это душевное состояние и одинакового мнения у всех быть не может. Однако, и то и другое — это творческий процесс. Возникает ряд вопросов: Какая связь может быть между…
Посмотреть работу
Комплексные числа: квадратные и кубические уравнения
Комплексные числа: квадратные и кубические уравнения Математика пробудилась в Западной Европе в 13 веке. В то время работы по математике были переведены с арабского на латынь, что позволило западноевропейским ученым узнать о средневековой арабоязычной математике и более старой греческой математике, такой как « элемента » Евклида. Во всей этой математике числами считались только положительные числа. Отрицательные числа еще не принимались в качестве сущностей. (Некоторые древние культуры, в том числе китайская и индийская, принимали отрицательные числа, но не упомянутые выше.
)Решение квадратичных уравнений.
С отрицательными числами мы понимаем, что каждое квадратное уравнение с переменной х можно записать в видегде a, b, и c — константы. Мы также знаем, что общее решение дается квадратичной формулой:
где имеются два различных действительных решения, если дискриминант b 2 4 ac положительное, одно двойное действительное решение, если дискриминант равен 0, и никаких действительных решений, если дискриминант отрицательный.
Еще в 15 веке этого не понимали. Вместо этого квадратные уравнения были разделены на четыре вида в зависимости от знаков коэффициентов а, b, и с. Поскольку старший коэффициент a не равен нулю в квадратном уравнении, вы всегда можете разделить на него, чтобы получить эквивалентное квадратное уравнение, где a равно 1, то есть x 2 + bx + c = 0.
Эта одна форма порождает четыре формы, когда вы перемещаете отрицательные члены в другую часть уравнения и когда вы отбрасываете нулевые члены из уравнения:
| x 2 | = | c |
| x 2 + bx | = | c |
| x 2 + c | = | bx |
| x 2 | = | bx + c |
Есть и другие формы, но либо они не имеют решений среди положительных чисел, либо их можно свести к линейным уравнениям. Каждая из этих форм требовала другой формы решения. Оглядываясь назад, мы видим, что решения 15-го века — это всего лишь частные случаи квадратичной формулы.
Можно подумать, что объединение четырех случаев в один может быть достаточным основанием для принятия отрицательных чисел, но, по-видимому, это не так. Кажется, что пройдет много времени, прежде чем люди расширят свою концепцию числа, включив в нее новые сущности.
Решение кубиков.
Уравнения третьей степени называются кубическими уравнениями. Общий вид кубика после деления на старший коэффициент:Как и в случае с квадратным уравнением, для кубического есть несколько форм, когда отрицательные члены переносятся на другую сторону уравнения, а нулевые члены опускаются.
Еще в 16 веке решать кубические уравнения было большим делом. В Италии разгорелся большой спор между Кардано (1501–1576) и Тартальей (1499–1557) о том, кому следует присудить решение кубического уравнения. В любой книге по истории математики можно найти подробности этого увлекательного спора.
Однако для нас интересно то, что отрицательные числа узаконивались, развивалось более глубокое понимание уравнений и появилось первое подозрение на комплексное число. Между прочим, в то время еще не была развита символическая алгебра, поэтому все уравнения записывались не символами, а словами!
Кардано в своем Artiss Magnæ или Great Art нашел отрицательные решения уравнений и назвал эти числа «фиктивными». Он также отметил важный факт, связывающий решения кубического уравнения с его коэффициентами, а именно, что сумма решений есть отрицание b, коэффициент члена x 2 . В другом месте он упоминает, что задача разделить 10 на две части так, чтобы их произведение было равно 40, должна быть равна 5 + √(15) и 5 √(15).
Исследования Бомбелли комплексных чисел
Кардано не углублялся в то, что позже стали называть комплексными числами, чем это наблюдение, но несколько лет спустя Бомбелли (1526–1572) привел несколько примеров с участием этих новых зверей.
Вот один пример.
Одна из кубических формул Кардано дает решение уравнения
где е = ( d /2) 2 ( c /3) 3 ). Бомбелли использовал это, чтобы решить уравнение x 3 = 15 x + 4, чтобы получить решение
Итак, квадратный корень из 121 не является действительным числом; это ни положительное, ни отрицательное, ни ноль. Бомбелли продолжал работать с этим выражением, пока не нашел уравнения, которые привели его к решению 4. Он определил, что
и, следовательно, решение x = 4. Вы можете проверить правильность этих уравнений, возложив в куб 2 ± √1, чтобы получить 2 ± 11√1.
Этот пример приведен не для того, чтобы показать, что Бомбелли знал все, что нужно знать о комплексных числах, а только то, что он начал их понимать.
линейная алгебра — Решение кубических уравнений в терминах квадратных уравнений
Вопрос задан
Изменено 1 год, 92+(а+б) х+(а+б+в)=0$$
$\endgroup$
0
$\begingroup$
Как только вы найдете один корень кубического, вы можете вычесть линейный множитель по теореме о множителях, оставив квадратный для решения других корней.
3/27}}{2}}$. (Обратите внимание, что вы должны правильно определить эти кубические корни, чтобы их произведение было равно $-p/3$; мы не хотим ошибаться в $\exp\tfrac{\pm2\pi i} {3}$.)
$\endgroup$
0
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Методы решения кубических выражений и поиска корней
Печать
Надеемся, мы убедили вас в том, что использование кубических уравнений состояния может представлять собой очень значимый и выгодный способ моделирования поведения PVT нефтяных флюидов. Что нам сейчас нужно, так это инструменты, которые позволят нам получать от них нужную нам информацию. Несмотря на то, что кубические уравнения состояния явны для давления, давление не является обычным неизвестным, вычисляемым в типичной задаче. В наиболее распространенной задаче давление и температура известны, и нам нужен либо молярный объем (или его обратная величина, молярная плотность), либо коэффициент сжимаемости (наиболее вероятный случай). Поэтому мы очень часто сталкиваемся с необходимостью найти корни кубического выражения. Здесь мы представляем ряд подходов, которым можно следовать.
Аналитическая схема
Учитывая кубический многочлен с действительными коэффициентами: x 3 + ax 2 + bx + c = 0, первым шагом является вычисление параметров:
Q=a2−3b9 и R=2a3 −9ab+27c54Это уравнение отображается неправильно из-за несовместимого браузера.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.5)
Пусть теперь M = R 2 – Q 3 будет дискриминантом . Затем рассмотрим следующие случаи:
Если M < 0 (R 2 < Q 3 ), многочлен имеет три действительных корня . В этом случае вычислите θ=arccos(RQ3) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. и вычислить три различных действительных корня как:
x1=−(2Qcosθ3)−a3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.6а)
x2=−(2Qcosθ+2π3)−a3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(11.6б)x3=−(2Qcosθ−2π3)−a3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.6с)
Обратите внимание, что x 1 , x 2 , x 3 не даны в каком-либо особом порядке, и что θЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. должен быть исчислен в радианах.
Если M > 0 (R 2 > Q 3 ), полином имеет только один действительный корень . Вычисление:
S=−R+M3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.7а)
T=-R-M3Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см.
и вычислить действительный корень следующим образом: в разделе «Технические требования» в руководстве. (11.7б)x1=S+T−a3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.7с)
(11.6б)
в разделе «Технические требования» в руководстве. (11.7б)Также могут встречаться два сложных корня (комплексные сопряжения). Однако для наших целей они не представляют интереса, поэтому формулы не приводятся. Такие формулы можно найти в следующих рекомендуемых чтениях:
- W.H. Пресс, С.А. Теукольский, В.Т. Феттерлинг, Б.П. Фланнери, Numerical Recipes in Fortran, 2 nd Edition, Cambridge Univ. Пресса, (1992), с. 179.
- Spiegel, M., Liu, J., Математический справочник формул и таблиц , 2 nd Edition, Schaum’s Outline Series, McGraw Hill, p.10.
Иногда приведенные выше уравнения для S и T вызывают проблемы при программировании. Обычно это происходит всякий раз, когда компьютер/калькулятор вычисляет кубический корень из отрицательной величины.
Если вы хотите избежать такой ситуации, вы можете вместо этого вычислить S’ и T’:
S’=−sign(R)abs(R)+M3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. T’=Q/S’Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (что делает T’=0, когда S’=0)
где:
абс(R) = абсолютное значение R
и
sign(R) = (+1) или (– 1), если R положительный или отрицательное соответственно.
Оно может быть определено как:
sign(R) = R/Abs(R)
и тогда действительный корень:
x1=S’+T’−a3Это уравнение не отображается правильно из-за несовместимости браузер. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
Имейте в виду следующие полезные отношения между корнями любого кубического выражения:
x1+x2+x3=-aЭто уравнение отображается неправильно из-за несовместимого браузера.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.8а)
x1x2+x2x3+x3x1=+bЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.8b)
x1x2x3=-cЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.8c)
Самопроверка
Проверьте свое понимание вычисления кубического корня с помощью аналитических средств, решив следующие примеры.
С общими кубическими выражениями,
x3−6×2+11x−6=0⇒x1=1×2=2×3=3Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
x3+7×2+49x+343=0x1=-7×2=0+7ix3=0-7iЭто уравнение отображается неправильно из-за несовместимого браузера.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
x3+2×2+3x+4=0⇒x1=-1,65063×2=-0,174685+1,54687ix3=-0,174685-1,54687iЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
с EOS в терминах объема (v), для чистого компонента,
v3−7.8693v2+13.3771v−6.5354=0Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
=> Один действительный корень (одна фаза),
v1=5,7357
Другой пример,
v3−15,6368v2+30,315v−14,8104=0
=> Две возможные фазы (три действительных корня),
3
2 v1 = 0,807582 (жидкая фаза) v2 = 1,36174 (отвергнутая) v3 = 13,4675 (газовая фаза)
с EOS с точки зрения коэффициента сжимаемости (z), для чистого компонента
z3−1,0595z2+0,2215z−0,01317=0Это уравнение отображается неправильно из-за несовместимого браузера.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
=> Один фаза,
z = 0,8045
Еще один пример,
Z3 -Z2+0,089Z — 0,0013 = 0
=> Две возможные фазы,
Zliquid = 0,01830112Zx = 0,07607070707076078606078607860786096096096096096096096096096096096096096076ERSHOR). 0,
8Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
Численная схема
Метод Ньютона-Рафсона предоставляет полезную схему для решения неявной переменной из любой формы уравнения (не только кубического). Ньютона-Рафсона является итеративной процедурой с быстрой сходимостью, хотя она не всегда может дать ответ, потому что должно быть предоставлено первое предположение, достаточно близкое к фактическому ответу.
При нахождении «x» в любом уравнении типа f(x)=0 метод дает новую оценку (новое предположение), более близкую к фактическому ответу, основанную на предыдущей оценке (старое предположение).
Это записывается следующим образом:
xnew=xold-f(xold)f'(xold) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.9)
Рассмотрение кубического уравнения f(x)=x3+ax2+bx+c=0Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. , предыдущее уравнение принимает вид:
xnew=xold-xold3+axold2+bxold+c3xold2+2axold+bЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.10)
Итерации продолжаются до тех пор, пока не будет достигнуто существенное улучшение для «x new », т. е. | х новый – х старый | < терпимость. Обоснованное предположение должно быть предоставлено в качестве начального значения для итераций.
Если вы решаете кубическое уравнение относительно Z (коэффициент сжимаемости), обычно рекомендуется принимать Z = bP/RT в качестве начального предположения для сжимаемости жидкой фазы и Z = 1 для парового корня.
Полуаналитическая схема
Если вы использовали предыдущий численный подход для вычисления одного из корней кубического выражения, полуаналитическая схема может дать вам два других действительных корня (если они существуют). Используя приведенные выше отношения со значением «x 1 » в качестве уже известного корня, два других корня вычисляются путем решения системы уравнений:
x2+x3=−a−x1Это уравнение отображается неправильно. из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.11а)
x2x3=−c/x1Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(11.11б)
что приводит к квадратному выражению.
Эту процедуру можно сократить до следующих шагов:
Пусть x3+ax2+bx+c=0Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. — исходный кубический многочлен, а «E» — уже известный корень (x 1 = Е). Затем мы можем разложить на множители такое кубическое выражение, как:
.(x−E)(x2+Fx+G)=0Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.12а)
где:F=a+EЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.12б)
G=−c/EЭто уравнение отображается неправильно из-за несовместимого браузера.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.12с)Найдите x 2 , x 3 , используя формулы квадратного выражения,
x1=EЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.13а)
x2=−F+F2−4G2Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.13б)
x3=-F-F2-4G2Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.13с)
Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (11.12с)‹ Преимущества использования кубических уравнений состояния вверх Действие ›
Битва кубического уравнения и рассвет комплексных чисел | Каспер Мюллер
Охота за давно разыскиваемым математическим оружием
Изображение с Wikimedia Commons — фрактал Джулии, созданный из кубического уравнения с использованием комплексных чисел.
История алгебры более остросюжетная, чем самый остросюжетный американский фильм. Может быть, никакой древний грек не разгромил большую часть Парижа из-за того, что его дочь похитили, но я могу заверить вас, что эта история еще более удивительна.
Мы увидим, как личные секреты превратились в целое математическое поле, которое теперь используется во всех дисциплинах математики и физики.
Все дело в полиномиальных уравнениях. Эти уравнения изучались с древних времен и до сих пор являются важной частью современной алгебры.
Вавилоняне знали, как решать квадратные уравнения, которые напоминают уравнения вида ax² + bx + c = 0 , и использовали эти формулы для вычисления площадей. В настоящее время мы преподаем формулы и доказательства решений этих уравнений в средних школах и даже в некоторых начальных школах по всему миру в качестве стандартной части стандартной учебной программы.
Спустя более 2000 лет первая попытка решить кубическое уравнение появилась у персидского математика Омар Хайям .
Кубическое уравнение представляет собой уравнение вида ax³ + bx² + cx + d = 0 .
Хайям был блестящим математиком и внес несколько вкладов в науку и математику, включая календарь, способный измерять количество дней в году до 365,24219858156 дней. Для сравнения, сегодня мы измеряем год как 365,242190 дней, и, по-видимому, шестой десятичный знак изменяется в течение всей жизни! Довольно удивительная вещь.
Хайям нашел геометрический подход к кубическому уравнению. Рассчитав конические сечения, он фактически смог найти положительные решения этих уравнений. Все эти решения были геометрическими, и нет сомнений, что Хайям предпочел бы вместо них найти алгебраические решения.
Прошло около 400 лет, прежде чем кто-либо нашел алгебраическую формулу для кубического уравнения. В 1400-х годах центр математики снова переместился в Европу, теперь вооруженную арабскими цифрами и алгебраическими методами.
Раньше в Европе предпочтительным способом расчета были римские цифры, но вскоре стало очевидным преимущество арабских цифр.
В конце концов, что логичнее LXX+XXX = C или 70 + 30 = 100?
Однако церковь придерживалась римских цифр, и в темный период истории арабские цифры были фактически запрещены в Италии. Это, вероятно, имело какое-то отношение к культуре, а также. Начнем с того, что только иностранные продавцы использовали эту темную магию, которая позволяла им рассчитывать призы и проценты за секунды. Представьте, что вы разговариваете с вашим банком, а затем наблюдаете, как ваш консультант записывает какую-то тарабарщину, которую вы не можете прочитать и поэтому просто должны доверять. Они боялись быть обманутыми.
Но благодаря здравому смыслу и важным ранним влиятельным лицам, таким как Фибоначчи, эту синтаксическую битву выиграли арабские цифры (индийско-арабские цифры), и через пару сотен лет после того, как Фибоначчи популяризировал этот синтаксис в Европе, математическое сообщество наконец созрело. достаточно, чтобы решить кубическое уравнение алгебраически.
Следует отметить, что арабские цифры были введены в Европу до Фибоначчи, но долгое время не получали распространения.
Прежде чем перейти к следующей части повествования, нужно вспомнить, как математики в то время работали с уравнениями. Поскольку математики того времени не знали об отрицательных числах, они всегда писали уравнения так, чтобы коэффициенты были положительными.
Поэтому они разделили полиномиальное уравнение на категории или классы. Например, квадратное уравнение ax² + bx + c = 0 имело три связанных с ним класса, а именно:
- ax² + bx = c ,
- ax² = bx +c и 92644 ax² + 90 c = bx ,
, где a , b и c — положительные числа.
На самом деле было еще хуже, потому что европейцы в то время не знали о числе 0 , поэтому для уравнений, в которых «отсутствовали» некоторые члены, приходилось соблюдать особые правила. К каждому из классов был прикреплен свой собственный алгоритм/формула, который нужно было использовать для его решения.
Это, конечно, относится и к кубическому уравнению, и говорят, что Хайям рассматривал 14 различных типов классов уравнений, каждый из которых имел разные геометрические подходы.
Первым, кто нашел формулу для класса кубических уравнений, был Шипионе дель Ферро . Преподавал математику в Болонском университете. Где-то в начале 1500-х годов он открыл формулу для решения кубических уравнений вида x³ + bx + c = 0,, где b, c > 0,.
Если бы дель Ферро нашел эту формулу сегодня, нет сомнения, что он немедленно опубликовал бы ее, но тогда она была совсем другой. Если вы нашли формулу, то вы держите ее при себе, как если бы вы нашли рецепт золота!
Причину такого загадочного поведения можно найти в том, как новые профессора подали заявки на должности в университетах Европы эпохи Возрождения.
Видите ли, в то время кандидат на эту работу должен был бросить вызов другим кандидатам в своего рода публичной математической дуэли, где вы задавали другим кучу математических вопросов или задач, и кто бы ни решил больше задач, когда время истекло вышел, получил работу. Кандидат также должен продемонстрировать, что он, конечно же, может решить свои собственные проблемы.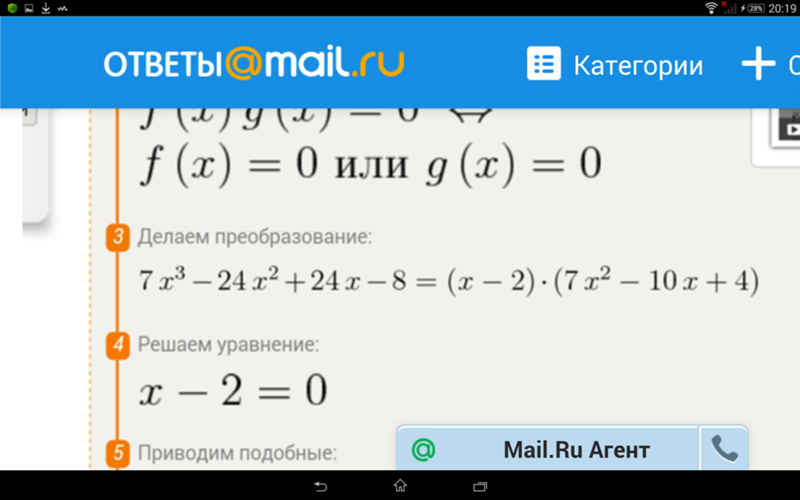
В некоторых университетах можно было даже бросить вызов профессору, занимающему в настоящее время должность.
Неудивительно, что если бы вы нашли новую формулу, вы бы сохранили ее в секрете, который затем можно было бы использовать в качестве математического ядерного оружия в такой дуэли и, таким образом, обеспечить себе хорошую работу профессора математики!
Дель Ферро никогда не публиковал свое открытие. Однако перед смертью он рассказал свой секрет своему преемнику Аннибале делла Неф и своему ученику Антонио Мария Фиор .
Вооружившись этим оружием, Фиор был убежден, что сможет сокрушить на дуэли любого математика, и в 1535 году вызвал на дуэль уже работавшего математика Никколо Тарталья . Излишне говорить, что он не должен был этого делать.
Тарталья был умен и поэтому быстро понял, что происходит. Многие из вопросов, заданных Фиором, имели ту же основную форму и вращались вокруг приведенного выше кубического уравнения, решение которого нашел дель Ферро.
Он рассудил, что должна быть общая формула (или метод/алгоритм) для ее решения.
Он яростно работал день и ночь, а вечером перед тем, как истекло время дуэли, заново открыл формулу дель Ферро и выиграл дуэль.
Тем временем дуэль привлекла большое внимание внешнего мира, и вскоре после этого Тарталья получил письмо от не кого иного, как Джероламо Кардано с вопросом, может ли он увидеть формулу. Начнем с того, что Тарталья отказался, но Кардано уже был солидным ученым и одним из лучших врачей Европы того времени. Поэтому у него были важные связи. Он предложил представить Тарталью и некоторые из его изобретений суду в Милане, и Тарталья согласился показать формулу, если Кардано пообещал никогда ее не публиковать. Кардано согласился.
В частном порядке Кардано начал работать над решениями других классов кубических уравнений, и через пару лет он рассмотрел все классы уравнений для кубического уравнения.
Кардано решил поехать в Болонью, где Нав позволил ему изучить оригинальные каракули дель Ферро.
В то время ходили слухи, что решение на самом деле нашел дель Ферро, а не Тарталья. Кардано выяснил, что это действительно так.
После этого Кардано решил опубликовать, несмотря на обещание, данное Тарталье.
Тем временем Кардано уговорил своего блестящего ученика Лодовико Феррари дать ему недавно открытую формулу для решения уравнения четвертой степени (полиномиальное уравнение четвертой степени).
В 1545 году вышла знаменитая книга Кардано Ars Magna , в которой он не только опубликовал формулу Тартальи вместе со всеми другими вариантами, но и формулу Феррари для уравнения четвертой степени.
Несмотря на то, что Тарталья был признан за его вклад в открытие, он был в ярости. Кардано каким-то образом уговорил Феррари защитить его, и в 1548 году Феррари победил Тарталью в еще одной математической дуэли.
Ars Magna называют первым значительным математическим достижением в Европе со времен античности.
Удивительно, чего добились эти первые пионеры, учитывая условия их работы.
У них не было не только отрицательных чисел и числа 0, но и того символического языка, который есть у нас сегодня. На самом деле им приходилось записывать свои формулы словами. Как рецепт блюда. У них также не было систем координат, с которыми они могли бы связать свои полиномиальные уравнения.
В настоящее время мы рассматриваем решение этих уравнений как пересечение оси x с графиком соответствующего полинома. Конечно, у них не было этой геометрической картины.
Если мы переведем их слова в формулы, мы найдем кое-что интересное. Одной из формул, которую Кардано нашел на основе открытий Ферро и Тартальи, были положительные решения класса кубических уравнений вида x³ — ax — b = 0 . Оказывается, они всегда имеют (действительное) положительное решение, и формула Кардано выглядит следующим образом:
, где a и b — положительные числа.
Рассмотрим уравнение x³ — 15x — 4 = 0 . Если мы воспользуемся формулой Кардано, мы получим интересный результат
, и в этом выражении мы увидим некоторые «запрещенные» квадратные корни отрицательных чисел.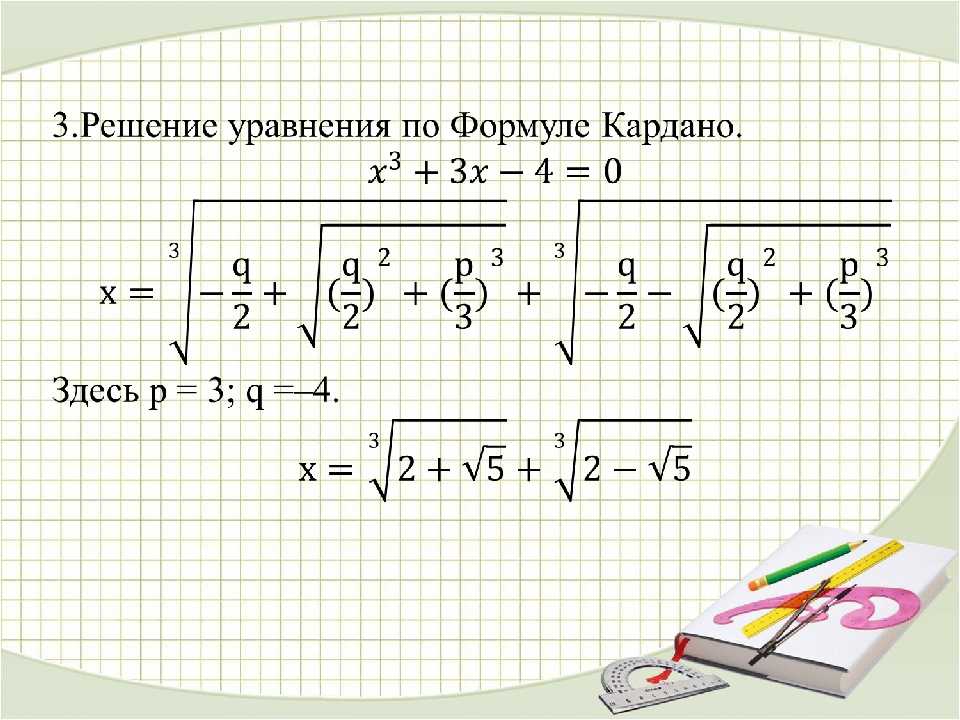
В то время они не знали, как это интерпретировать. Кардано знал, что это выражение должно дать положительное решение, и в данном случае он знал, что это решение равно x = 4 . Так что же делают эти странные символы в его формуле?
Рафаэлло Бомбелли показал, что
и
, и если мы вместо этого используем эти выражения в формуле для x , приведенной выше, чуждые квадратные корни компенсируют друг друга, и мы остаемся с x = 4 , поскольку мы должен.
Математики того времени быстро поняли, что если бы только нам разрешили использовать эти инопланетные числа, как если бы они были реальными, то мы могли бы использовать формулы Кардано для нахождения реальных положительных решений уравнений кубической и четвертой степени.
По какой-то магии все числа инопланетян всегда уравновешивались и, в конце концов, раскрывали истинное решение. Многие математики того времени думали об этих странных квадратных корнях, как будто они не были настоящей математикой, и использовали их только в случае необходимости.
Многие, конечно, отказывались их использовать и видели в этом своего рода ковбойскую математику.
Они боялись, что эти расчеты непоследовательны и что однажды они столкнутся с неприятными противоречиями.
Несмотря на то, что математики пытались скрыть использование этих чисел, им приходилось использовать их время от времени, и так было до 18 века, когда блестящая Леонард Эйлер связал эти числа с теорией функций.
Эйлер, однако, не имел геометрического представления о комплексных числах и не знал точно, что они представляют. Он также считал, что основная теорема алгебры ( n многочленов -й степени имеют n комплексных корней с учетом кратности) верна, но никогда не приводил убедительного доказательства.
Многие великие математики пытались доказать основную теорему алгебры, но потерпели неудачу. Первым, кто доказал это формальное удовлетворение, был Карл Фридрих Гаусс .
Только в конце 18-го века эти инопланетные числа оказались такими же законными и реальными, как и настоящие числа.
Это показал великий норвежско-датский математик Каспар Вессель . Оказалось, что они просто жили в другом измерении, которое математики того времени не могли видеть.
Эти инопланетные числа называются комплексными числами, и в настоящее время они считаются частью нашей системы счисления, и было доказано, что они согласуются с другими нашими числами. Фактически, действительные числа теперь считаются частью комплексных чисел.
Изначальный суп комплексных чисел был наполнен конкуренцией, экономикой, религией и культурой.
Иногда в математике нам нужно экспериментировать и быть «математическими гангстерами», как выразился математик Эдвард Френкель . У Эйлера не было проблем с использованием комплексных чисел повсюду, и он оказал большое влияние на весь предмет.
К счастью, Вессель , Гаусс , Коши , Риман , Вейерштрасс и другие помогли поставить комплексные числа на прочную основу и показали, как и Кардано, что они нужны нам для решения задач о действительных и даже целых числах.
Риман показал, что мы можем использовать их, например, для изучения простых чисел, и теперь мы знаем, что они также нужны нам в квантовой физике, радиолокационной технологии и т. д. . Ведь они тоже считались чуждыми для Кардано и его современников.
На создание этой истории вдохновил норвежский математик Том Линдстрем . Спасибо за оживление этой темы, Том!
Если у вас есть какие-либо вопросы, комментарии или замечания по поводу этой статьи или в целом, вы можете связаться с нами по телефону LinkedIn .
Каспер Мюллер — старший консультант по данным и аналитике, FS, технологический консалтинг — EY | LinkedIn
Программирование и математика — одни из моих самых больших интересов. Наука о данных, машинное обучение, программирование и…
www.linkedin.com
Если вам нравится читать подобные статьи на Medium, вы можете легко получить членство для полного доступа: просто нажмите здесь .
Спасибо за внимание.
Кубическое уравнение
Кубическое уравнение Кубическое уравнение — это полиномиальное уравнение третьей степени. Учитывая общее кубическое уравнение
| (1) |
(Коэффициент можно принять за 1 без ограничения общности путем деления всего уравнения на ), первая попытка устранить член, сделав замену формы
| (2) |
затем
| (3) | |
| (4) | |
| (5) |
| (6) |
затем
| (7) | |||
| (8) | |||
| (9) |
поэтому уравнение (1) становится
| (10) |
| (11) |
| (12) |
Определение
| (13) | |||
| (14) |
то позволяет записать (12) в стандартной форме
| (15) |
Самый простой способ продолжить — сделать замену Виеты.
| (16) |
которое сводит кубику к уравнению
| (17) |
которое легко превратить в квадратное уравнение путем умножения на, чтобы получить
| (18) |
(Биркхофф и Мак Лейн, 1965, стр. 106). Результат квадратного уравнения
где и иногда полезнее иметь дело, чем и . Таким образом, имеется шесть решений для (по два, соответствующих каждому знаку для каждого корня из ). Подключение обратно к (17) дает три пары решения, но все пары равны, так что есть три решения кубического уравнения.
Уравнение (12) можно также явно разложить на множители, если попытаться извлечь член формы из кубической
уравнение, оставляя после себя квадратное уравнение, которое затем можно разложить на множители с помощью квадратной формулы.
Этот процесс
эквивалентно замене Виеты, но немного лучше мотивирует «волшебство» Виеты.
замены, а также при выводе явных формул для решений. Сначала определим промежуточные переменные
| (20) | |||
| (21) |
(которые идентичны и с точностью до постоянного множителя). Тогда общее кубическое уравнение (12) принимает вид
| (22) |
Пусть и будут на данный момент произвольными константами. Идентичность, удовлетворяющая Perfect Cubic уравнения в том, что
| (23) |
Таким образом, общая кубика была бы факторизуема непосредственно, если бы она не имела члена (т.
е. если ). Однако, поскольку
в общем, добавьте кратное —say —к обеим сторонам (23), чтобы получить немного беспорядочный
личность | (24) |
что после перегруппировки членов равно
| (25) |
Теперь мы хотели бы сопоставить коэффициенты и с коэффициентами уравнения (22), поэтому мы должны иметь
| (26) |
| (27) |
Подключение первого ко второму дает
| (28) |
Следовательно, если мы можем найти значение, удовлетворяющее приведенному выше тождеству, мы выделим линейный член из кубического, тем самым сводя его к квадратному уравнению.
Пробным решением, совершающим это чудо, оказывается симметричное выражение | (29) |
Взятие второй и третьей степени дает
| (30) | |||
| (31) |
Подключение и к левой части (28) дает
| (32) |
так что мы действительно нашли множитель (22), и теперь нам нужно только факторизовать квадратичную часть.
подключение
в квадратичную часть (25) и решение полученного | (33) |
затем дает решения
Их можно упростить, определив
| (35) | |||
| (36) |
так что решения квадратичной части можно записать
| (37) |
Определение
| (38) | |||
| (39) | |||
| (40) |
где Дискриминант (который определяется немного по-другому, в том числе противоположный Знак, Биркхофф и Маклейн, 1965), дает очень простые выражения для и , а именно
| (41) | |||
| (42) |
Поэтому, наконец, корни исходного уравнения в затем даются
| (43) | |||
| (44) | |||
| (45) |
с Коэффициентом в исходном уравнении и как определено выше.
Эти три уравнения
дающие три корня кубического уравнения, иногда называют формулой Кардано. Обратите внимание, что если уравнение
находится в стандартной форме Vieta | (46) |
в переменной , то , и , а промежуточные переменные имеют простой вид (ср. Бейер 1987)
| (47) | |||
| (48) | |||
| (49) |
Уравнение для в Формуле Кардано не имеет явного появления в нем while и do,
но это ничего не говорит о количестве действительных и комплексных корней
(поскольку и сами, в общем-то, Комплексные).
Однако, определяя, какой
Корни вещественны, а сложные могут быть достигнуты с помощью
отметив, что если дискриминант, один корень действителен
и два являются комплексными сопряженными; если , то все Корни Действительны и по крайней мере два равны; а если , то все корни действительны и неравны. Если
, определять
| (50) |
Тогда Вещественные решения имеют вид
| (51) | |||
| (52) | |||
| (53) |
Эту процедуру можно обобщить для нахождения действительных корней любого уравнения в стандартной форме.
(46) с помощью тождества | (54) |
(Диксон, 1914) и установка
| (55) |
(Биркхофф и Мак Лейн, 1965, стр. 90–91), затем
| (56) |
| (57) |
| (58) |
Если , то используйте
| (59) |
чтобы получить
| (60) |
Если и , используйте
| (61) |
а если и , используйте
| (62) |
чтобы получить
| (63) |
Тогда решения исходного уравнения
| (64) |
Альтернативный подход к решению кубического уравнения заключается в использовании резольвент Лагранжа.
Позволять , определять
| (65) | |||
| (66) | |||
| (67) |
где корни
| (68) |
и рассмотрим уравнение
| (69) |
где и — комплексные числа.
Тогда корни | (70) |
для , 1, 2. Умножение дает
| (71) |
или же
| (72) |
куда
| (73) | |||
| (74) |
Решения удовлетворяют тождествам Ньютона.
| (75) | |||
| (76) | |||
| (77) |
В стандартной форме , , и , поэтому мы имеем тождества
| (78) | |||
| (79) | |||
| (80) |
Некоторые любопытные тождества с корнями кубического уравнения, принадлежащие Рамануджану, приведены Берндтом (1994).
Каталожные номера
Абрамовиц М. и Стегун С. А. (ред.). Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, с. 17, 1972.
Бергер, М. §16.4.1-16.4.11.1 в Geometry I. Нью-Йорк: Springer-Verlag, 1994.
Берндт, Британская Колумбия, Записные книжки Рамануджана, часть IV. Нью-Йорк: Springer-Verlag, стр. 22-23, 1994.
Beyer, WH Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 9-11, 1987.
Биркгоф, Г. и Мак Лейн, С. Обзор современной алгебры, 3-е изд. Нью-Йорк: Macmillan, стр. 90–91, 106-107 и 414-417, 1965.
Диксон Л. Э. «Новое решение кубического уравнения». Amer. Мат. Ежемесячно 5 , 38-39, 1898.
Диксон, Л. Э. Элементарная теория уравнений.
Нью-Йорк: Wiley, стр. 36-37, 1914.
Данхэм, В. «Кардано и решение куба». Гл. 6 дюймов Путешествие через гениев: Великие теоремы математики. Нью-Йорк: Wiley, стр. 133–154, 1990.
Эрлих, Г. §4.16 в основных понятиях абстрактной алгебры. Бостон, Массачусетс: PWS-Кент, 1991.
Джонс, Дж. «Омар Хайям и геометрическое решение куба». http://jwilson.coe.uga.edu/emt669/Student.Folders/Jones.June/omar/omarpaper.html.
Кеннеди, Э. К. «Заметка о корнях кубического». Amer. Мат. Ежемесячно 40 , 411-412, 1933.
Кинг, Р. Б. За пределами уравнения четвертой степени. Бостон, Массачусетс: Биркхойзер, 1996.
Press, WH; Фланнери, Б. П.; Теукольский, С. А.; и Феттерлинг В. Т. «Квадратные и кубические уравнения». §5.6 в Численные рецепты на FORTRAN: Искусство научных вычислений, 2-е изд. Кембридж, Англия: Издательство Кембриджского университета, стр. 178–180, 1992.
Спаниер, Дж.
и Олдхэм, К. Б. «Кубическая функция и высшие полиномы».
Ч. 17 в Атлас функций. Вашингтон, округ Колумбия: Hemisphere, стр. 131–147, 19.87.
ван дер Варден, Б. Л. §64 в Алгебра. Нью-Йорк: Фредерик Унгар, 1970.
© 1996-9 Эрик В. Вайсштейн
1999-05-25
Кубическое уравнение как поэзия
Апрель. Это не только самый жестокий месяц (или, в обозначениях логики первого порядка, ∀m (a≤ C m), но также Месяц математической грамотности и Месяц национальной поэзии. За последние несколько лет я принял предложение Стивена Орнса и сделал его Месяцем математической поэзии.0023
В этом месяце я наткнулся на ранний пример математической поэзии в решении кубического уравнения. Кубическое уравнение представляет собой многочлен с 3 в качестве наибольшего показателя. Более известное квадратное уравнение имеет форму ax 2 +bx+c=0, тогда как кубическое уравнение обычно имеет вид ax 3 +bx 2 +cx+d=0.
Многие из нас выучили квадратичную формулу в средней или старшей школе (возможно, на мелодию «Поп, ласка»). Но вы когда-нибудь изучали кубическую формулу? Вероятно, нет — это довольно сложно и не так легко вывести. В то время как версии квадратной формулы были известны древним вавилонянам и средневековым исламским математикам, кубическое уравнение упорно сопротивлялось общему решению еще много лет.
Окончательное решение кубического уравнения — одна из самых ярких историй в истории математики. Вы можете прочитать расширенные (иногда приукрашенные) отчеты об этом в другом месте, но нас беспокоит то, что Никколо Тарталья (ок. 1500–1557) открыл способ решения некоторых видов кубических уравнений. Другой математик, Джироламо Кардано (1501-1576), хотел узнать формулу и обещал не публиковать ее. Тарталья поделился формулой с Кардано в виде стихотворения, и в итоге Кардано опубликовал его. (Подробнее об их споре можно прочитать здесь.)
Convergence, журнал, издаваемый Математической ассоциацией Америки, является отличным ресурсом для изучения математики на протяжении ее истории.
Я зашел в статью «Конвергенция» Фридриха Качера «Как Тарталья решил кубическое уравнение», чтобы узнать больше о стихотворении, которое Тарталья отправил Кардано.
Если вы сомневаетесь, что по-итальянски все звучит более романтично, вот оригинальное итальянское стихотворение Тартальи.
Quando chel cubo con le cose appresso
Se agguaglia à qualche numero discreto
Trouan dui altri Differenti in esso.Dapoi terrai questo per consuto
Chellor produtto semper sia eguale
Alterzo cubo delle cose neto,El residuo poi suo generale
делли лор лати куби бен соттратти
Varra la tua cosa Principale.In el secondo de cotestiatti
Quando che’l cubo restasse lui solo
Tu osseruarai quest’altri contratti,Del numer farai due tal part’à uolo
Che l’una in l’altra si produca schietto
El terzo cubo delle cose in stoloDelle qual poi, per communprecetto
Torrai li lati cubi insieme gionti
Et cotal somma il tuo consetto.El terzo poi de questi nostri conti
Se solue col secondo se ben guardi
Че за natura сына квази congionti.Questi trouai, & non con paßi tardi
Nel mille cinquecentè, quatroe trenta
Con Fondamenti ben sald’è gagliardiNella citta dal mar’intorno centa.
Между прочим, схема рифмовки — терцинная рима (aba bcb cdc и т. д.), которая впервые появилась в Данте в Инферно . Возможно, Тарталья подсознательно убеждал Кардано оставить всякую надежду на решение кубического уравнения.
Это начало перевода стихотворения Катчера на английский язык:
Когда куб с конусом рядом с ним
Приравнивает себя к другому целому числу,
Найдите два других, из которых это различие.В дальнейшем вы будете считать это обычным
Что их произведение всегда будет равно
К третьему кубу сети Коуза.Общий остаток от
Из их сторон куба, хорошо вычтенных,
Будет значение вашего основного неизвестного.
Полный перевод стихотворения на английский и символическую нотацию см. в статье Катчера. Он даже указывает на ошибку в стихотворении Тартальи. (Третий куб — это не то же самое, что куб третьего.)
Кстати, одна из моих любимых вещей в истории кубического уравнения — его связь с комплексными числами, которые включают квадратные корни из отрицательные числа. Я оставлю вас с этим тизером: уравнение x 3 =15x+4 имеет три действительных решения, но если вы используете кубическую формулу для ее решения, вы в конечном итоге совершите экскурсию на комплексную плоскость, прежде чем снова получите действительные числа. Попытки Рафаэля Бомбелли разобраться с квадратными корнями из отрицательных чисел, которые возникли таким образом, в конечном итоге заложили основу для комплексного анализа.
Чтобы узнать больше о решении кубического уравнения, ознакомьтесь с другой статьей о сходимости «Решение кубического уравнения с помощью Кардано» Уильяма Б.