а)1-3х 3-х в)5(y-1,2)-4,6> 3y+1
Алгебра, 2020-01-23 07:52:22, marivenkova
Ответ
Ответ разместил: den111111111113
а)-3х<-1
х>1/3
б) 4х>5
х>5/4
в) 5у-10,6>3у+1
2у>11,6
у>5,8
Ответ
Ответ разместил: Comalia
а)1-3х<0
-3х<-1 до множим на (-1)
3х<1
х<1/3
б)
3х-2>3-х
3х+х>3+2
4х>5
х>1,25
в)
5(у-1,2)-4,6>3y+1
5y-6-4,6>3y+1
5y-3y>1+4,6+6
2y>11,6
y>5,8
Ответ
Ответ разместил: nata506
1/6х<5
х<5:1/6
x<5*6
x<30
1-3х<0
-3x<-1
x>1/3
5(y-1,2)-4,6>3y+1
5y-6-4,6>3y+1
2y-10.6>1
2y>11.6
y>5.8
Ответ
Ответ разместил: Natiman
5 (у-1,2)-4,6》3у+1
5у-6-4,6》3у+1
5у-10,6》3у+1
5у-3у》10,6+1
2у》11,6
у=11,6÷2
у=5,8
Ответ
Ответ разместил: lemyana2017
5(y-1,2)-4. 6>3y+1
6>3y+1
5y-6-4,6>3y+1
5y-3y>1+6+4,6
2y>11,6
y>5,8
внизу рисует рисунок и пишешь тот же ответ
Ответ
Ответ разместил: лехакек
5(у -1,2)-4,6>3у+1
5у -6-4,6>3у +1
2у >11,6
у >5,8
ответ : (5,8;+ бесконечность)
Ответ
Ответ разместил: Artem22011
5y-6-4,4>3y+1
5y-10,4>3y+1
5y-3y>1+10,4
2y>11,4
y>5,7
Ответ
Ответ разместил: helpme163
5у -6-4,6-3у-1> 0 2у-11,6> 0 2у> 11,6 у> 5,8
Ответ
Ответ разместил: катяkfrr
1) 1-3х меньше или равно 0. -3х меньше или равно -1 меняем знаки х больше или равно 1/3. ответ: [1/3; +бесконечности). 2) 1/6х меньше 5. х меньше 30. ответ: (-бесконечности; 30). 3)5 (y-1,2)-4,6 больше 3y+1. 5y-6-4,6-3y-1 больше 0. 2y больше 11,6. y больше 11,6. y больше 5,8. ответ: (5,8;+бесконечности)
Ответ
Ответ разместил: alexksyx
1)Приведем к общему знаменателю и его отбросим x<30
2) нет х, наверное, ошибка или -2<=0 ответ: любые значения х
3) 5у-6-4,6>3y+1
5y-3y>1+10,6
2y>11,6
y>5,8
4) 6-2x<3x-6
6-x>=2x
-5x<-12 x>2,4
-3x>=-6 x<2
ответ: нет решений
Другие вопросы по: Алгебра
Рушить уравнение: 3х-2\2х+5=х+4\х+10. 2-х=4 ,а то завтра экзамен, а я это все !)….
2-х=4 ,а то завтра экзамен, а я это все !)….
Опубликовано: 28.02.2019 16:00
Ответов: 3
В4 кусках ткани было по5 метров, пятая часть всей ткани пошла на пошив штор, сколько ткани осталось?…
Опубликовано: 28.02.2019 21:00
Ответов: 3
Народ мне что такое приложения? ? как их находят в объясните простым не сильно научным ! умоляю*…
Опубликовано: 01.03.2019 11:30
Ответов: 1
Масса 3 л керосина равна 2 кг 415г. найти массу 8 л керосина…
Опубликовано: 02.03.2019 04:20
Ответов: 3
Популярные вопросы
Опрос всех жителей тучково показал, что 46% о учатся, 64%-работают, 17%- не учатся и не работают. каков процент жителей поселка, которые одновременно и учатся и работают?…
Опубликовано: 28.02.2019 09:30
Ответов: 3
Какое наименьшее число точек определяет прямую в пространстве. ..
..
Опубликовано: 01.03.2019 19:40
Ответов: 3
Сделать крассворд по музыке. 1(6 букв), 10(5букв). — части песен. 2(10 букв), 3(11 букв) 7(11 букв) — название форм по кол-ву частей. 4(9 букв) — форма используемая в песнях. 5(8 б…
Опубликовано: 02.03.2019 13:50
Ответов: 1
Напишите сочинение (15-20) предл. на тему: «я в этот мир пришла,» отразите в нем свои главые жизненные ценности…
Опубликовано: 02.03.2019 14:20
Ответов: 2
Дно бассейна имеет форма прямоугольника со сторонами 5м и 10м. дно бассейна выложино квадратными плитками со стороной 20см верно дно бассейна израсходовано меньше чем 1200 плиток…
Опубликовано: 02.03.2019 23:30
Ответов: 2
Споиснением : у двух мышек родилось 15 детенышей. сколько детенышей родилось у каждой мышки, если у одной из них детенышей в два раза больше, чем у другой?. ..
..
Опубликовано: 03.03.2019 08:50
Ответов: 1
Фермер расчитав что корова стоит вчетверо дороже собаки а лошадб вчетверо дороже кооровы захватил 200 руб и на всё купил собаку две коровы и лошадь сколько стоит каждое из купленых…
Опубликовано: 03.03.2019 17:50
Ответов: 2
Важным признаком в определении названия группы водорослей является цвет их основного…
Опубликовано: 07.03.2019 16:10
Ответов: 3
Натуральные числа х и y таковы, что 12х и 18у являются точными квадратами. чему равно наименьшее возможное значение суммы х+у…
Опубликовано: 07.03.2019 18:40
Ответов: 3
22. дан фрагмент программы, обрабатывающий массив а из 10 элементов: n : = 10; for i: =1 tо n do a[i] : = i; j : = 1; for i: =1 tо n-1 do if a[i] < a[i+1] then j : = j + 1; чему…
Опубликовано: 07.03.2019 19:20
Ответов: 3
Больше вопросов по предмету: Алгебра Случайные вопросы
| 1 | Найти производную — d/dx | бревно натуральное х | ||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | ||
| 3 | Найти производную — d/dx | |||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | ||
| 22 | Найти производную — d/dx | грех(2x) | ||
| 23 | Найти производную — d/dx | |||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | ||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | ||
| 43 | Оценка интеграла 9бесконечность | |||
| 45 | Найти производную — d/dx | х/2 | ||
| 46 | Найти производную — d/dx | -cos(x) | ||
| 47 | Найти производную — d/dx | грех(3x) | ||
| 68 | Оценить интеграл | интеграл от sin(x) по x | ||
| 69 | Найти производную — d/dx | угловой синус(х) | ||
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | ||
| 85 | Найти производную — d/dx | лог х | ||
| 86 | Найти производную — d/dx | арктан(х) | ||
| 87 | Найти производную — d/dx | бревно натуральное 5х93-8 | ||
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Уравнения и неравенства
Принцип сложения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида x + b = c, используя принцип сложения.
Решать уравнения вида x + b = c, используя принцип сложения.
2. Использование принципа сложения
Когда мы используем знак равенства (=), мы указываем, что два выражения равны по значению. Это называется уравнением . Например, x + 5 = 23 — это уравнение. Выбирая определенные процедуры, можно шаг за шагом перейти от заданного уравнения к уравнению x = некоторому числу. Число является решением уравнения.
Одна из первых процедур, используемых при решении уравнений, нашла применение в нашем повседневном мире. Предположим, мы поместили 10-килограммовый ящик с одной стороны качелей и 10-килограммовый камень с другой стороны. Если центр ящика находится на таком же расстоянии от точки баланса, как и центр камня, мы ожидаем, что качели будут балансировать. Коробка и камень не выглядят одинаково, но имеют одинаковую ценность по весу. Если мы добавим 2-килограммовый свинцовый груз к центру веса каждого объекта одновременно, качели все равно должны балансировать. Результаты равны.
Результаты равны.
Похожий принцип есть и в математике. Мы можем выразить это такими словами.
Принцип сложения
Если к обеим частям уравнения прибавить одно и то же число, результаты каждой стороны будут равны по значению.
Мы можем переформулировать это в символах таким образом.
Для действительных чисел a, b, c, если a=b thenat+tc=b+ec
Вот пример.
Если 3=6/2, то 3+5=6/2+5
Поскольку мы добавили одинаковое количество 5 к обеим сторонам, каждая сторона имеет одинаковую ценность.
3+5=6/2+5
8 =6/2+10/2
8 = 16/2
8=8
Мы можем использовать принцип сложения для решения уравнения.
ПРИМЕР 1 Решите для x. x + 16 = 20
x + 16 + (-16) = 20 + (-16) Используйте принцип сложения, чтобы добавить -16 к обеим частям.
x+0=4 Упростить.
x=4 Значение x равно 4.
Мы только что нашли решение уравнения. Решение — это значение переменной, которая делает уравнение верным. Затем мы говорим, что значение 4 в нашем примере удовлетворяет уравнению. Мы можем легко проверить, что 4 является решением, подставив это значение в исходное уравнение. Этот шаг называется проверка решения.
Затем мы говорим, что значение 4 в нашем примере удовлетворяет уравнению. Мы можем легко проверить, что 4 является решением, подставив это значение в исходное уравнение. Этот шаг называется проверка решения.
Чек . x + 16 = 20
4 + 16 ≟ 20
20 = 20 ✔
Когда одно и то же значение появляется с обеих сторон знака равных, мы называем уравнение Identity . Поскольку две части уравнения в нашей проверке имеют одинаковое значение, мы знаем, что исходное уравнение было решено правильно. Мы нашли решение.
Когда вы пытаетесь решить эти типы уравнений, вы замечаете, что вы должны добавить определенное число к обеим частям уравнения. Какой номер выбрать? Посмотрите на число, которое находится на той же стороне уравнения, что и х, то есть на число, прибавленное к х. Затем подумайте о числе, которое равно напротив знака . Это называется добавкой , обратной числа. Аддитивное значение, обратное 16, равно -16. Аддитивное обратное значение -3 равно 3. Число, которое нужно добавить к обеим частям уравнения, и есть это аддитивное обратное.
Аддитивное обратное значение -3 равно 3. Число, которое нужно добавить к обеим частям уравнения, и есть это аддитивное обратное.
Неважно, в какой части уравнения стоит переменная. Термин x может быть справа или слева. В следующем примере член x будет справа.
ПРИМЕР 2 Решите для x. 14 =x- 3
14+3=x-3 +3 Добавьте 3 к обеим частям, так как 3 является аддитивной инверсией к -3. Это устранит -3 справа и изолирует x.
17 =x+0 Упростить.
17=x Значение x равно 17.
Проверить . 14 = x-3
14 ≟ 17-3 Замените x на 17.
14 =14 ✔ Упрощение. Это проверяет. Решение x = 17.
Прежде чем прибавлять число к обеим частям, всегда следует упростить уравнение. В следующем примере показано, как объединение чисел путем сложения по отдельности в обеих частях уравнения упрощает уравнение.
ПРИМЕР 3 Решите для х. 15 +2=3+x+2
17=x+5 Упростите, добавив.
17+ (-5) =x+5+(-5) Добавьте значение -5 к обеим частям, так как -5 является аддитивной величиной, обратной 5.
12=x Упростите. Значение x равно 12.
Чек . 15+2 = 3+x+2
15+2 ≟ 3+12+2 Замените x на 12 в исходном уравнении.
17=17 ✔ Проверено.
В примере 3 мы добавили -5 к каждой стороне. Вы можете вычесть по 5 с каждой стороны и получить тот же результат. В предыдущем уроке мы обсуждали, что вычитание 5 равносильно прибавлению минус 5. Понимаете, почему?
Мы можем определить, является ли значение решением уравнения, выполнив те же шаги, что и для проверки ответа. Подставьте проверяемое значение переменной в исходное уравнение. Мы получим тождество, если значение является решением.
ПРИМЕР 4 Является ли x = 10 решением уравнения -15 + 2 = x-3? Если это не так, найдите решение.
Подставим 10 вместо x в уравнение и посмотрим, получится ли тождество.
-15+2=х-3
-15+2=10-3
-13 ≠ 7 Это неправда. Это не личность.
Таким образом, x = 10 не является решением. Теперь возьмем исходное уравнение и решим, чтобы найти решение.
-15+2=x-3
-13=x-3 Упростите, добавив.
-13+3=x-3+3 Прибавьте 3 к обеим сторонам. 3 является аддитивной инверсией -3.
-10=x
Проверить, является ли решение x = -10. Значение x = 10 было неверным из-за ошибки знака. Мы должны быть особенно внимательны, чтобы писать правильный знак для каждого числа при решении уравнений.
ПРИМЕР 5 Найдите значение x, удовлетворяющее уравнению 1/5+x = −1/10+1/2
Чтобы объединить дроби, дроби должны иметь общие знаменатели. Наименьший общий знаменатель (LCD) дробей равен 10.
(1*2)/(5*2)+x = −1/10+(1*5)/(2*5) Замените каждую дробь на эквивалентная дробь со знаменателем 10.
2/10 + x = −1/10+5/10 Это эквивалентное уравнение.
2/10+x = 4/10 Упростите, добавив.
2/10+(-2/10)+x = 4/10+(-2/10) Добавьте добавку, обратную 2/10, к каждой стороне
x=2/10 Сложите дроби.
x= 1/5 Упростите ответ.
Чек . Подставим 1/5 вместо x в исходное уравнение и посмотрим, получим ли мы тождество.
1/5+x = −1/10+1/2
1/5+1/5 ≟ −1/10+1/2 Подставьте 1/5 вместо x
2/5 ≟ −1/10 +1/2
2/5 = 4/10
2/5 = 2/5 ✔ Проверено.
Принцип умножения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида 1/ax=b.
2. Решить уравнения вида ax = b.
Решение уравнений вида 1/ax=b
Принцип сложения позволяет нам добавлять одно и то же число к обеим частям уравнения. Что произойдет, если мы умножим каждую часть уравнения на одно и то же число? Например, что произойдет, если мы умножим каждую часть уравнения на 3?
Чтобы ответить на этот вопрос, вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Если мы утроим количество грузов с каждой стороны (мы умножаем каждую сторону на 3), качели все равно должны балансировать. «Значение веса» каждой стороны остается равным.
«Значение веса» каждой стороны остается равным.
На словах мы можем сформулировать этот принцип так.
Принцип умножения
Если обе части уравнения умножить на одно и то же число, результаты на каждой стороне
равны по значению.
В символах мы можем переформулировать принцип умножения таким образом.
|
Для действительных чисел a,b,c с #0 [email protected]=b thenca=cb |
Давайте посмотрим на уравнение, в котором было бы полезно умножить каждую часть уравнения на 3.
ПРИМЕР 1 Решите для х. 1/3x=-15
Мы знаем, что (3)(1/3) = 1. Мы умножим каждую часть уравнения на 3, потому что мы хотим изолировать переменную x.
(3)(1/3x)=3(-15) Умножьте каждую часть уравнения на 3, так как (3)(1/3) = 1.
(3/1)(1/3)(x )=-45
1x=-45 Упрощение.
x= -45
Проверить . 1/3(-45) ≟ -15 Замените x на -45 в исходном уравнении.
-15=-15 ✔ Проверяет.
Обратите внимание, что 1/5x можно записать как x/5. Чтобы решить уравнение x/5=3, мы могли бы умножить каждую часть уравнения на 5. Попробуйте. Затем проверьте свое решение.
Чтобы решить уравнение x/5=3, мы могли бы умножить каждую часть уравнения на 5. Попробуйте. Затем проверьте свое решение.
Решение уравнений вида ax = b
Мы можем видеть, что использование принципа умножения для умножения каждой стороны уравнения на 1/2 равносильно делению каждой стороны уравнения на 2. Таким образом, было бы кажется, что принцип умножения позволил бы нам разделить каждую часть уравнения на любое ненулевое действительное число. Есть ли реальный пример этой идеи?
Вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Предположим, что мы должны были разрезать два объекта пополам (так, чтобы количество веса каждого было разделено на 2). Затем мы возвращаем предметы на те же места на качелях. Качели все равно будут балансировать. «Значение веса» каждой стороны остается равным.
На словах мы можем сформулировать этот принцип так:
Принцип деления
Если обе части уравнения разделить на одно и то же ненулевое число, результаты
с каждой стороны равны по значению.
Примечание : Мы накладываем ограничение на число, на которое мы делим. Мы не можем разделить на ноль. Мы говорим, что такие выражения, как 2/0, не определены. Таким образом, мы ограничиваем наш делитель ненулевыми числами. Мы можем переформулировать принцип деления таким образом.
a b
Для действительных чисел a, b, c, где c ~ 0, если a=b, то — = —
coc
ПРИМЕР 2 Найдите x. 5x = 125
(5x)/5=125/5 Поделите обе части на 5.
x = 25 Упростите. Решение 25.
Чек . 5x = 125
5(25) ≟ 125 Замените x на 25.
125 = 125 ✔ Это проверка.
Для уравнений вида ax = b (число, умноженное на x, равно другому числу), мы решаем уравнение, разделив обе части на определенное число. Какой номер выбрать? Смотрим на ту часть уравнения, которая содержит х. Мы замечаем число, которое умножается на х. Делим на это число. Принцип деления говорит нам, что у нас все еще может быть истинное уравнение, если мы разделим на это число 9. 2055 с обеих сторон уравнения.
2055 с обеих сторон уравнения.
Решением уравнения может быть правильная или неправильная дробь.
ПРИМЕР 3 Решите для x. 4x = 38
(4x)/4= 38/4 Поделите обе части на 4.
x=19/2 Упростите. Решение 19/2.
Если оставить решение в виде дроби, будет легче проверить это решение в исходном уравнении.
Проверить : 4x = 38 Заменить x на 19/2.
4(19/2) ≟ 38
38 = 38 ✔ Проверено.
В примерах 2 и 3 мы делили на число, умноженное на х (коэффициент при х). Эта процедура выполняется независимо от того, положительный или отрицательный знак этого числа.
ПРИМЕР 4 Найдите x. -3x = 48
(-3x)/-3=48/-3 Поделите обе части на -3.
x=-16 Решение равно -16.
Коэффициент x может быть равен 1 или -1. Возможно, вам придется переписать уравнение так, чтобы коэффициент 1 или -1 был очевиден. С практикой вы сможете «увидеть» коэффициент, фактически не переписывая уравнение.
ПРИМЕР 5 Найдите x. -x = -24
-1x = -24 Перепишите уравнение. -1x совпадает с -x. Теперь коэффициент -1 очевиден.
(-1x)/-1=-24/-1 Поделите обе части на -1
x= 24 Решение будет 24.
Используйте вместе принципы сложения и умножения
умеет:
1. Решать уравнения вида ax + b =c.
2. Решите уравнения, в которых переменная присутствует в обеих частях уравнения.
3. Решите уравнения со скобками.
Решение уравнений вида ax +b=c
Для решения многих уравнений мы должны использовать как принцип сложения, так и принцип умножения.
ПРИМЕР 1 Найдите x и проверьте свое решение. 5x +3 = 18
5x + 3 + (-3)= 18+ (-3) Добавьте -3 к обеим частям, используя принцип сложения.
5x = 15 Упрощение.
(5x)/5=15/5 Поделите обе части на 5, используя принцип деления.
x=3 Решение 3.
Проверить . 5(3)+3 ≟ 18
Чек . 15+3 ≟ 18
15+3 ≟ 18
Чек . 18=18 ✔ Проверил.
Переменная в обеих частях уравнения
В некоторых случаях переменная появляется в обеих частях уравнения. Мы хотели бы переписать уравнение так, чтобы все члены, содержащие переменную, оказались с одной стороны. Для этого применим принцип сложения к переменному члену.
ПРИМЕР 2 Решите для x. 9x = 6x + 15
9x + (-6x) = 6x + (-6x) + 15 Добавьте -6x к обеим сторонам. Обратите внимание, что 6x + (-6x) исключает переменную с правой стороны.
3x = 15 Соберите одинаковые члены.
(3x)/3=15/3 Поделите обе части на 3.
x=5 Решение равно 5.
Многие задачи имеют переменные и постоянные члены в обеих частях уравнения. Вы захотите получить все переменные члены с одной стороны и все постоянные члены с другой стороны.
ПРИМЕР 3 Найдите x и проверьте свое решение. 9х + 3 = 7х -2.
9x + (-7x) + 3 = 7x + (-7x) — 2 Добавьте -7x к обеим частям уравнения.
2x+3=-2 Объедините подобные термины.
2x + 3+ (-3) = -2 + (-3) Добавьте -3 к обеим сторонам.
2x = -5 Упростить.
(2x)/2=-5/2 Поделите обе части на 2.
x = -5/2 Решение равно −5/2.
Чек . 9x + 3 = 7x -2
Чек . 9(-5/2)+3 ≟ 7(-5/2)-2 Замените x на −5/2.
Чек . −45/2+3 ≟ −35/2-2 Упростить.
Чек . −45/2+6/2 ≟ −35/2-4/2 Переведите в эквивалентные дроби с общим знаменателем.
Чек . −39/2 = −39/2 ✔ Это проверка. x = −5/2 является решением.
В нашем следующем примере мы изучим уравнения, которые необходимо упростить, прежде чем предпринимать какие-либо другие шаги. 2, попытайтесь собрать их на одной стороне уравнения. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. 92 = 0.
6y+y-2=-y+y+12 Добавьте y к каждой стороне.
7y-2= 12 Упростить.
7y-2+2=12+2 Добавьте по 2 с каждой стороны.
7y=14 Упрощение.
(7y)/7 = 14/7 Разделите каждую сторону на 7.
y=2 Упростите. Решение 2.
Решение уравнений со скобками
Уравнения, которые вы только что решили, представляют собой более простые версии уравнений, которые мы сейчас обсудим. Эти уравнения содержат круглые скобки. Если скобки сначала удалить, проблемы становятся такими же, как те, с которыми мы сталкивались ранее. Мы используем распределительное свойство, чтобы удалить круглые скобки.
ПРИМЕР 6 Найдите x и проверьте свое решение. 4(x + 1)- 3(x-3) = 25
4(x + 1)- 3(x-3) = 25
4x +4-3x+9 = 25 Умножьте на 4 и -3, чтобы убрать скобки. Будьте осторожны со знаками. Помните, что (-3)(-3) = 9.
После удаления скобок важно собрать одинаковые члены с каждой стороны уравнения. Сделайте это, прежде чем переходить к изоляции переменной.
x + 13 = 25 Соберите одинаковые термины.
x+ 13-13 = 25-13 Добавьте -13 к обеим сторонам, чтобы изолировать переменную.
x = 12 Решение 12.
Проверить . 4(12+1)-3(12-3) ≟ 25 Замените x на 12.
4(13)-3(9) ≟ 25 Объедините числа в скобках.
52-27 ≟ 25 Умножить.
25=25 ✔ Упрощение. Это проверяет.
В задачах с десятичными дробями следует проявлять большую осторожность. На некоторых шагах вы будете умножать десятичные числа, а на других шагах вы будете их складывать.
ПРИМЕР 7 Найдите x. 0,3(1,2x-3,6) = 4,2x-16,44
0,36x-1,08 = 4,2x -16,44 Удалите скобки.
0,36x-0,36x-1,08 = 4,2x-0,36x-16,44 Вычтите 0,36x с обеих сторон.
-1,08 = 3,84x -16,44 Соберите одинаковые члены.
-1,08 + 16,44 = 3,84x-16,44 + 16,44 Прибавьте 16,44 к обеим сторонам.
15,36 = 3,84x Упростить.
15,36/3,84=(3,84x)/3,84 Поделите обе части на 3,84.
4=x Решение: x = 4.
ПРИМЕР 8 Найдите z и проверьте. 2(3z-5) + 2 = 4z -3(2z + 8)
2(3z-5) + 2 = 4z -3(2z + 8)
6z-10 + 2 = 4z-6z-24 Удалите скобки.
6z- 8 = -2z-24 Соберите одинаковые термины.
6z-8 + 2z = -2z + 2z-24 Добавьте по 2z с каждой стороны.
8z-8 = -24 Упростить.
8z-8 +8 = -24+ 8 Добавьте 8 с каждой стороны.
8z =-16 Упрощение.
(8z)/8=-16/8 Разделите каждую сторону на 8.
z=-2 Упростите. Решение -2.
Чек . 2[3(-2)-5] +2 ≟ 4(-2)-3[2(-2) + 8] Замените z на -2.
2[-6-5] +2 ≟ -8 -3[-4 + 8] Умножить.
2[-11] +2 ≟ -8 -3[4] Упрощение.
-22 +2 ≟ -8 -12
-20 = -20 ✔ Проверяет.
Уравнения с дробями
Изучив этот раздел, вы сможете:
1. Решать уравнения с дробями.
Решение уравнений с дробями
Уравнения с дробями решить довольно сложно. Эта трудность просто из-за особой осторожности, которую мы обычно должны проявлять при вычислениях с дробями. Фактические процедуры решения уравнений одинаковы, с дробями или без них. Чтобы избежать лишней работы, преобразуем данное уравнение с дробями в эквивалентное уравнение, не содержащее дробей. как нам это сделать? Умножаем каждую часть уравнения на наименьший общий знаменатель всех дробей, содержащихся в уравнении. Затем мы используем распределительное свойство, так что LCD умножается на каждый член уравнения.
Фактические процедуры решения уравнений одинаковы, с дробями или без них. Чтобы избежать лишней работы, преобразуем данное уравнение с дробями в эквивалентное уравнение, не содержащее дробей. как нам это сделать? Умножаем каждую часть уравнения на наименьший общий знаменатель всех дробей, содержащихся в уравнении. Затем мы используем распределительное свойство, так что LCD умножается на каждый член уравнения.
ПРИМЕР 1 Найдите x. 1/4x-2/3=5/12x
Сначала находим, что LCD = 12.
12(1/4x-2/3)=12(5/12x) Умножаем каждую сторону на 12
(12 /1)(1/4)(x)-(12/1)(2/3)=(12/1)(5/12)(x) Используйте распределительное свойство.
3x-8 = 5x Упростить.
3x + (-3x)-8 = 5x + (-3x) Добавьте -3x к каждой стороне.
-8 = 2x Упростить.
-8/2=(2x)/2 Поделить каждую сторону на 2.
-4= x Упростить.
Чек . 1/4(-4)-2/3 ≟ 5/12(-4)
-1-2/3 ≟ −5/3
−3/3-2/3 ≟ −5/3
− 5/3 = -5/3 ✔ Проверяет.
В примере 1 мы умножили каждую часть уравнения на LCD. Обычной практикой является немедленно перейти ко второму шагу и умножить каждое слагаемое на LCD, а не
ПРИМЕР 2 Решить x. (x+5)/7=x/4+1/2
x/7+5/7=x/4+1/2 Сначала запишем отдельными дробями
(28)(x/7)+( 28)(5/7)=(28)(x/4)+(28)(1/2) Мы видим, что LCD равно 28, поэтому мы умножаем каждое слагаемое на 28.
4x + 20 = 7x + 14 Упрощение.
4x-4x + 20 = 7x-4x + 14 Добавьте -4x к обеим сторонам.
20 = 3x + 14 Соберите одинаковые члены.
20-14=3x + 14- 14 Добавьте -14 к обеим сторонам.
6 = 3x Соберите одинаковые члены.
6/3=(3x)/3 Разделите обе части на 3.
2=x Решение: x = 2.
Если задача содержит и скобки, и дроби, лучше сначала удалить скобки. Многие студенты считают полезным иметь письменную процедуру решения этих более сложных уравнений.
Процедура решения линейных уравнений
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на наименьший общий знаменатель всех дробей.
3. Соберите одинаковые термины, если это возможно. Если возможно, упростите числовую работу.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с переменной на одной стороне уравнения.
5. Добавьте или вычтите значение в обеих частях уравнения, чтобы получить все члены, не содержащие переменную в другой части уравнения.
6. Разделите обе части уравнения на коэффициент при переменной.
7. Упростите решение (если возможно).
8. Проверьте свое решение.
Давайте используем каждый шаг в решении этого примера.
ПРИМЕР 3 Найдите x и проверьте свое решение. 1/3(x-2)= 1/5(x+4)+2
Шаг 1 x/3-2/3=x/5+4/5+2 Удалите скобки.
Шаг 2 15(x/3)-15(2/3) = 15(x/5) +15(4/5) +15(2) Умножить на ЖК-дисплей, 15.
Шаг 3 5x-10 = 3x + 12 + 30 Упростить.
5x-10 = 3x + 42 Упростить.
Шаг 4 5x-3x-10 = 3x-3x + 42 Добавьте -3x к обеим сторонам.
2x-10 = 42 Упростить.
Шаг 5 2x-10+ 10 = 42+ 10 Прибавьте 10 к обеим сторонам.
2x = 52 Упростить.
Шаг 6 (2x)/2=52/2 Разделите обе части на 2.
Шаг 7 x = 26 Упростите решение.
Шаг 8 Проверка . 1/3(26-2) ≟ 1/5(26 +4)+2 Замените x на 26.
1/3(24) ≟ 1/5(30)+2 Объедините значения в скобках.
8 ≟ 6+2 Упростить.
8 = 8 ✔ x=26 — это решение.
Следует помнить, что не каждый шаг будет необходим в каждой задаче. Вы также можете комбинировать некоторые шаги, если вы постоянно получаете правильное решение. Тем не менее, вам рекомендуется записывать каждый шаг, чтобы избежать ошибок по невнимательности.
Важно помнить, что когда мы пишем десятичные дроби, эти числа на самом деле представляют собой дроби, записанные особым образом. Таким образом, 0,3 = 7 и 0,07 = 745. Можно взять линейное уравнение, содержащее десятичные дроби, и умножить каждый член на соответствующее значение, чтобы получить целые коэффициенты.
Таким образом, 0,3 = 7 и 0,07 = 745. Можно взять линейное уравнение, содержащее десятичные дроби, и умножить каждый член на соответствующее значение, чтобы получить целые коэффициенты.
Формулы
Изучив этот раздел, вы сможете:
1. Решать формулы для заданной переменной.
Решение указанной переменной в формуле
Формулы — это уравнения с одной или несколькими переменными, которые используются для описания реальных ситуаций. Формула описывает отношения, существующие между переменными. Например, в формуле d = rt расстояние (d) связано с показателем скорости (r) и временем (t). Мы можем использовать эту формулу, чтобы найти расстояние, если мы знаем скорость и время. Иногда, однако, нам дают расстояние и скорость, и нас просят найти время.
ПРИМЕР 1 Джозеф проехал 156 миль со средней скоростью 52 мили в час. Сколько времени понадобилось Иосифу, чтобы совершить путешествие?
d= rt Используйте формулу расстояния.
156 = 52t Подставьте известные значения переменных.
156/52=52/52t Поделите обе части уравнения на 52, чтобы найти t.
3=t Мы нашли t.
Джозефу потребовалось 3 часа, чтобы проехать 156 миль со скоростью 52 мили в час.
Если у нас есть много задач, требующих нахождения времени по расстоянию и скорости, может оказаться целесообразным переписать формулу с точки зрения времени.
ПРИМЕР 2 Решите для t. d=rt
d/r=(rt)/r Мы хотим изолировать t. Поэтому мы делим обе части уравнения на коэффициент при t, который равен r.
d/r=t Вы решили для указанной переменной.
Простое уравнение первой степени с двумя переменными можно рассматривать как уравнение прямой. Часто полезно найти у, чтобы упростить построение графика.
ПРИМЕР 3 Решите для y. 3x-2y = 6
-2y = 6-3x Мы хотим изолировать член, содержащий y, поэтому мы вычитаем 3x с обеих сторон.
(-2y)/(-2)= (6-3x)/(-2) Поделите обе части на коэффициент y.
y=6/-2+(-3x)/-2 Перепишите дробь.
y= 3/2x-3 Упростите и перегруппируйте.
Это известно как форма уравнения прямой с пересечением наклона.
Наша процедура решения уравнения первой степени может быть переписана так, чтобы получить процедуру решения формулы для заданной переменной.
Процедура решения формулы для указанной переменной
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на ЖКИ всех дробей.
3. Соберите одинаковые термины или упростите их, если возможно.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с нужной переменной на одной стороне уравнения.
5. Прибавьте или вычтите соответствующую величину, чтобы получить все члены, в которых нет нужной переменной на другой стороне уравнения.
6. Разделите обе части уравнения на коэффициент при нужной переменной.
7. Если возможно, упростите.
ПРИМЕР 4 Трапеция – четырехсторонняя фигура с двумя параллельными сторонами. Если параллельные стороны равны a и b, а высота равна h, площадь определяется как
Если параллельные стороны равны a и b, а высота равна h, площадь определяется как
A=h/2(a+b)
Решите это уравнение для a.
A=h/2(a+b)
A=(ha)/2+(hb)/2 Удалите скобки.
2(A) = 2((ha)/2)+2((hb)/2) Умножьте все члены на LCD на 2.
2A = ha + hb Упростите.
2A-hb = ha Мы хотим выделить член, содержащий a. Поэтому мы вычитаем hb с обеих сторон.
(2A-hb)/h= (ha)/h Поделите обе части на h (коэффициент при a).
(2A-hb)/h=a Решение получено.
Примечание : Хотя решение представлено в простой форме, его можно записать другим способом. Поскольку
(2A-hb)/h=(2A)/h-(hb)/h=(2A)/h-b
, мы могли бы иметь (2A)/h-b = a в качестве альтернативного способа записи ответа.
Написание и графическое отображение неравенств
Изучив этот раздел, вы сможете:
1. Интерпретировать утверждение о неравенстве.
2. Нарисуйте неравенство на числовой прямой.
Заявления о неравенстве
Мы часто говорим, что одно значение больше или меньше другого значения. Мы говорим, что «5 меньше 7» или «9 больше 4». Эти соотношения называются неравенствами . Мы можем записать неравенства в математике, используя символы. Мы используем символ для представления слов «больше чем».
Мы говорим, что «5 меньше 7» или «9 больше 4». Эти соотношения называются неравенствами . Мы можем записать неравенства в математике, используя символы. Мы используем символ для представления слов «больше чем».
Заявление в словах в алгебре
5 меньше 7. 5
9 больше 4. 9> 4
Примечание . «5 меньше 7» и «7 больше 5» имеют одинаковый смысл. Точно так же 5 5 имеют одинаковый смысл. Они представляют собой два эквивалентных способа описания одной и той же связи между двумя числами 5 и 7.
Мы можем проиллюстрировать концепцию неравенства графически, если рассмотрим числовую прямую.
+++ +—_ +++ +_+_+—_—_+_¢_ _ +>
-5 -4 -3 -—2 -] 0 I 2 3 4 5 6 7 8
Мы говорим, что одно число больше другого, если оно находится справа от другого на числовой прямой. Таким образом, 7 > 5, так как 7 правее 5.
А как насчет отрицательных чисел? Мы можем сказать: «-1 больше, чем -3» и записать это символами -1 > -3, потому что мы знаем, что -1 лежит справа от -3 на числовой прямой.
ПРИМЕР 1 Замените вопросительный знак символом в каждом утверждении.
(а) 3 ? -1 (б) -2 ? 1 (в) -3 ? -4 (г) 0 ? 3
(a) 3>-1 Используйте >, так как 3 находится справа от -1.
(b) -2 (Или, что то же самое, мы могли бы сказать, что 1 находится справа от -2.)
(c) -3 > -4 Так как -3 справа от -4.
(d) 0
Построение графика неравенства на числовой прямой
Иногда мы будем использовать неравенство, чтобы выразить связь между переменной и числом. x > 3 означает, что x может иметь значение любого числа больше 3. Это можно изобразить на числовой прямой на графике следующим образом:
-5 -4 -3 -2 -1 0 l 2 3 4 5
Обратите внимание, что незаштрихованный кружок под цифрой 3 означает, что мы не включаем точку для числа 3. -2 следующим образом:
$$ —} fj —_ + —_;_+_+_+_ + > x
-5 -4 -3 -2 -l 0 I 2 3 #4 = =# §
Иногда переменная больше или равна определенному числу. В утверждении «x больше или равно 3» мы подразумеваем, что x может иметь значение 3 или любое число больше 3. Мы запишем это как x >= 3. Мы представим это графически следующим образом:
В утверждении «x больше или равно 3» мы подразумеваем, что x может иметь значение 3 или любое число больше 3. Мы запишем это как x >= 3. Мы представим это графически следующим образом:
—+—. >! 4H_{_AH_ ee ee et
—2 -1 0 l 2 3 4 5 6 7
Обратите внимание, что замкнутый кружок у 3 означает, что мы do включаем точку для числа 3.
x
—— t+. et Ht HH HH
-5 -4 -3 -2 -1 0 1 2 3 4 5
ПРИМЕР 2 Назовите каждое математическое соотношение словами, а затем проиллюстрируйте его графически.
(а) x
(а) Мы утверждаем, что «х меньше -2».
x -4 -3 -2 -!1 0 ] 2
(б) Мы можем утверждать, что -3 меньше x» или, эквивалентное утверждение, »x больше -3». Убедитесь, что вы видите, что -3 -3. Хотя оба способа верны, мы обычно записываем сначала переменную в простом линейном неравенстве, содержащем переменную и числовое значение.
(c) Мы утверждаем, что «x меньше или равно -6».
_-—od—_tH¥!_t—_t*—_+—_ +t +
-7 -6 -5 -4 -3 -2 -1 0 л 2
Есть много повседневных ситуаций с участием неизвестного значение и неравенство. Мы можем перевести эти ситуации в алгебраические утверждения. Это первый шаг в решении текстовых задач с использованием неравенств.
Мы можем перевести эти ситуации в алгебраические утверждения. Это первый шаг в решении текстовых задач с использованием неравенств.
ПРИМЕР 3 Переведите каждое английское выражение в алгебраическое выражение.
(a) Прибывшая на место полиция сообщила, что машина двигалась со скоростью более 80 миль в час (используйте переменную s для скорости).
(b) Владелец автотранспортной компании сказал, что полезная нагрузка грузовика никогда не должна превышать 4500 фунтов (используйте переменную p для полезной нагрузки).
(a) Поскольку скорость должна быть больше 80, мы имеем s > 80.
(b) Если полезная нагрузка грузовика никогда не может превышать 4500 фунтов, то полезная нагрузка всегда должна быть меньше или равна 4500 фунтов. Таким образом, мы пишем p
Решить неравенства
Изучив этот раздел, вы сможете:
1. Решить неравенство.
Решение неравенств
Возможные значения, которые делают неравенство верным, называются его решениями . Таким образом, когда мы решим неравенство , мы найдем все значений, которые делают его верным. Чтобы решить неравенство, мы упрощаем его до такой степени, что можем ясно видеть возможные значения переменной. Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями.
Таким образом, когда мы решим неравенство , мы найдем все значений, которые делают его верным. Чтобы решить неравенство, мы упрощаем его до такой степени, что можем ясно видеть возможные значения переменной. Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями.
Сначала мы рассмотрим закономерность, которая имеет место, когда мы выполняем данную операцию с обеих сторон неравенства.
Пример 1
Оригинальное неравенство Новое неравенство
(a) 3
(b) -2
(B) -2
(c) 0>-4 → Поделить обе части на 2. → 0>-2
(d) 8 >4 → Вычтите 6 с обеих сторон. → 2>-2
Обратите внимание, что мы избегали умножения или деления на отрицательное число !
Теперь посмотрим, что произойдет, если мы умножим или разделим на отрицательное число. Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство.
Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство.
Оригинальное неравенство Новое неравенство
3
Какой правильный знак неравенства? Поскольку -6 находится справа от -10, мы знаем, что новое неравенство должно быть -6 > -10, если мы хотим, чтобы утверждение оставалось верным. Обратите внимание, как мы меняем направление неравенства с (больше). Таким образом, мы получили бы новое неравенство -6 > -10. Таким образом,
3-10
Знак (-6 > -10). Аналогичное обращение имеет место в следующем примере.
Пример 2
Оригинальное неравенство Новое неравенство
(a) -2 3
(b) 0>-4 → Поделите обе части на -2. → 0
(c) 8 >4 → Поделите обе части на -4. → -2
Обратите внимание, что мы выполняем арифметические действия с числами со знаком так же, как всегда. Но новое неравенство имеет обратный знак неравенства (по сравнению с исходным неравенством). Всякий раз, когда обе части неравенства умножаются или делятся на отрицательное число, направление неравенства меняется на противоположное.
Всякий раз, когда обе части неравенства умножаются или делятся на отрицательное число, направление неравенства меняется на противоположное.
Процедура решения неравенств
| Вы можете использовать те же процедуры для решения неравенств, что и для решения уравнений, за исключением того, что направление неравенства меняется на противоположное, если вы умножаете или делите
обе части на отрицательное число.
ПРИМЕР 3 Решите и начертите 3x + 7 >= 13.
3x +7-7>=13-7 Вычтите 7 с обеих сторон.
3x>= 6 Упростить.
(3x)/3>=6/3 Обе части разделить на 3.
x>=2 Упростить. Обратите внимание, что направление неравенства не изменилось, так как мы разделили на положительное число.
Графическое представление en ee
—2 -Il 0 I 2 3 4
ПРИМЕР 4 Решите и начертите 5-3x > 7.
5-5-3x>7-5 Вычтите 5 с обеих сторон.
-3x>2 Упростить.
(-3x)/-3
x
Графическое представление Ht Ht
-1_2_1 0 l
3 3
Как и уравнения, некоторые неравенства содержат круглые скобки и дроби. Начальные шаги для решения этих неравенств будут такими же, как и для решения уравнений со скобками и дробями. Когда переменная появляется в обеих частях неравенства, целесообразно собрать члены x в левой части символа неравенства. 9ПРИМЕР 5 )(15/8) Умножить все члены на LCD = 8. Мы делаем , а не , меняем направление символа неравенства, поскольку мы умножаем на положительное число, 8.
Начальные шаги для решения этих неравенств будут такими же, как и для решения уравнений со скобками и дробями. Когда переменная появляется в обеих частях неравенства, целесообразно собрать члены x в левой части символа неравенства. 9ПРИМЕР 5 )(15/8) Умножить все члены на LCD = 8. Мы делаем , а не , меняем направление символа неравенства, поскольку мы умножаем на положительное число, 8.
-52x
-52x-4x
-56x
(-56x)/56>= -15/-56 Поделите обе части на -56. мы изменить направление неравенства, если мы разделим обе части на отрицательное число.
x>=15/56
Графическое представление 0 15 28 l
56 56
. ]
Наиболее распространенная ошибка, которую учащиеся допускают при решении неравенств, — это забывание изменить направление символа неравенства на противоположное при умножении или делении на отрицательное число.
Алгебраическое решение уравнений
Алгебраическое решение уравнений
|
Содержание: Эта страница соответствует § 2. 4
4
(стр. 200) текста.
Предполагаемые проблемы из текста:
р. 212 #7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87,
88, 95, 97
Квадратные уравнения
Уравнения с радикалами
Полиномиальные уравнения высшей степени
Уравнения с дробными выражениями или абсолютными значениями
г.
Квадратные уравнения
Квадратное уравнение имеет форму ax 2 + bx + c = 0, где a, b и c — числа, a —
не равно 0,
Факторинг
Такой подход к решению уравнений основан на том, что если произведение двух величин равно нулю, то
хотя бы одна из величин должна быть равна нулю. Другими словами, если a*b = 0, то либо a = 0, либо b = 0, либо и то, и другое.
Подробнее о факторинговых полиномах см. в обзорном разделе P.3 (стр. 26) текста.
г.
Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3)(x — 4) = 0,
2x + 3 = 0 или x — 4 = 0.
х = -3/2 или х = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt(k).
Пример 2.
х 2 — 9 = 0,
х 2 = 9,
х = 3 или х = -3.
Пример 3.
Пример 4.
х 2 + 7 = 0,
х 2 = -7.
х = ± .
Обратите внимание, что = = ,
так что решенияx = ± , два комплексных числа.
г.
Завершение квадрата
Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, позволяющей применить квадрат
принцип корня.
Пример 5.
x 2 +6x — 1 = 0,
х 2 +6х = 1.
х 2 +6х + 9 = 1 + 9.
9, добавленное к обеим сторонам, получено в результате возведения в квадрат половины коэффициента x, (6/2) 2 = 9.
Причина
выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (многочлена с двумя членами).
Вот почему эта процедура называется , завершающей квадрат . [Заинтересованный читатель может видеть, что это
верно, если учесть (x + a) 2 = x 2 + 2ax + a 2 . Чтобы получить «а», нужно всего лишь
разделить x-коэффициент на 2. Таким образом, чтобы завершить квадрат для x 2 + 2ax, нужно добавить 2 .](х + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня и найти x.
х = -3 ± кв. м (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Способ заполнения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент
(коэффициент х 2 ) равно 1.В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив
обе части уравнения на 2.х 2 + 3х = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат,
(3/2) 2 = 9/4. Это константа, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.х 2 + 3х + 9/4 = 5/2 + 9/4.
Левая часть равна квадрату (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь воспользуемся принципом квадратного корня и найдем x.
91 812 х + 3/2 = ± кв. м (19/4) = ± кв. м (19)/2.
x = -3/2 ± sqrt(19)/2 = (-3 ± sqrt(19))/2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от
проблема и ваши личные предпочтения. Уравнение, имеющее правильную форму для применения принципа квадратного корня
можно переставить и решить с помощью факторизации, как мы видим в следующем примере.
г.
Пример 7.
х 2 = 16.
х 2 — 16 = 0,
(х + 4)(х — 4) = 0,
х = -4 или х = 4.
В некоторых случаях уравнение можно решить с помощью факторизации, но факторизация не очевидна.
Метод заполнения квадрата будет работать всегда, даже если решения представляют собой комплексные числа, и в этом случае
мы возьмем квадратный корень из отрицательного числа. Кроме того, шаги, необходимые для завершения квадрата,
всегда одинаковы, поэтому их можно применить к общему квадратному уравнению
г.
ах 2 + Ьх + с = 0.
Результатом заполнения квадрата этого общего уравнения является формула решений уравнения
называется квадратичной формулой.
Квадратичная формула
Решения уравнения ax 2 + bx + c = 0 равны
Мы говорим, что заполнение квадрата всегда работает, и мы заполнили квадрат в общем случае,
где у нас есть a, b и c вместо чисел. Итак, чтобы найти решение любого квадратного уравнения, запишем его
Итак, чтобы найти решение любого квадратного уравнения, запишем его
в стандартной форме, чтобы найти значения a, b и c, а затем подставить эти значения в квадратичную формулу.
г.
Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения.
Однако процесс заполнения квадрата важен и по другим причинам, поэтому вам все же нужно знать, как
сделай это!
Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В этом случае a = 2, b = 6, c = -5. Подстановка этих значений в квадратичную формулу дает
г.
Обратите внимание, что ранее мы решили это уравнение, заполнив квадрат.
Примечание : Есть два реальных решения. С точки зрения графиков, есть два перехвата для графика
функции f(x) = 2x 2 + 6x — 5,
Пример 9.
4х 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует обратить внимание на две вещи.
- Есть только одно решение. С точки зрения графиков это означает, что существует только один x-пересечение.
- Решение упрощено таким образом, что в нем не используется квадратный корень. Это означает, что уравнение могло быть
решается факторингом. (Все квадратные уравнения можно решить факторингом! Я имею в виду, что это могло быть
решить легко с помощью факторинга.)4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0,
х = -1/2.
Пример 10.
х 2 + х + 1 = 0
а = 1, б = 1, с = 1
г.
Примечание: Реальных решений нет. С точки зрения графиков, для графика нет перехватов
функции f(x) = x 2 + x + 1.Таким образом, решения комплексные, поскольку график y = x 2
+ x + 1 не имеет x-перехватов.
Выражение под радикалом в квадратной формуле, b 2 — 4ac, называется дискриминантом
уравнение. Последние три примера иллюстрируют три возможности для квадратных уравнений.
1. Дискриминант > 0. Два действительных решения.
2. Дискриминант = 0. Одно действительное решение.
3. Дискриминант
Примечания по проверке растворов
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения. (см. пример
3 из раздела «Линейные уравнения и моделирование».) Тем не менее, рекомендуется проверить свои решения,
потому что очень легко допустить ошибки по невнимательности при решении уравнений.г.
Алгебраический метод, заключающийся в подстановке числа обратно в уравнение и проверке того, что
результирующее утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда
решение включает радикал.Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4(-1/2) 2 +4(-1/2) + 1 = 0,
г.
4(1/4) — 2 + 1 = 0.
1 — 2 + 1 = 0.
0 = 0. Решение проверяется.
В предыдущем примере 2x 2 + 6x — 5 = 0 мы нашли два действительных решения, x = (-3 ± sqrt(19))/2.
Проверить это алгебраически, конечно, можно, но не очень просто. В этом случае либо графический
проверить или использовать калькулятор для алгебраической проверки быстрее.Сначала найдите десятичные приближения для двух предложенных решений.
г.
(-3 + кв.(19))/2 = 0,679449.
(-3 — кв.(19))/2 = -3,679449.
Теперь используйте графическую утилиту, чтобы построить график y = 2x 2 + 6x — 5, и проследите график, чтобы примерно найти, где
x-перехваты. Если они близки к приведенным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
одинаковые значения. Тем не менее, вам все равно нужно быть осторожным, заявляя, что ваше решение правильное, поскольку оно
не точное решение.г.
Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и перешли непосредственно к графику
утилиты для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя
(алгебраически) два числа, которые вы считаете решениями, если графическая утилита показывает, что перехваты очень
рядом с найденными вами числами, то вы, вероятно, правы!
Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3х 2 -5х — 2 = 0. Ответ
(б) (х + 1) 2 = 3. Ответ
(в) х 2 = 3х + 2. Ответ
Вернуться к содержанию
Уравнения с радикалами
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень, возведя в квадрат, если радикал
является квадратным корнем, кубирование для кубического корня и т. д. Эта операция может ввести посторонние корни, поэтому все решения
д. Эта операция может ввести посторонние корни, поэтому все решения
должны быть проверены.
г.
Если в уравнении только один радикал, то перед возведением в степень следует договориться, чтобы
радикальный член сам по себе на одной стороне уравнения.
Пример 11.
Теперь, когда мы выделили радикальный член в правой части, мы возводим обе части в квадрат и решаем полученное уравнение
для х.Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно
решение .Решение : x = 3.
Примечание: Решением является координата x точки пересечения графиков y = x и
у = кврт(х+1)+1.
Посмотрите, что произошло бы, если бы мы возвели в квадрат обе части уравнения перед , выделив радикал
срок.
Это хуже, чем то, с чего мы начали!
Если в уравнении более одного радикального члена, то, вообще говоря, мы не можем исключить все радикалы с помощью
возведение в степень один раз. Однако мы можем уменьшить количество радикальных членов путем возведения в степень.
Если уравнение включает более одного радикального члена, то мы все равно хотим выделить один радикал с одной стороны и
возвести в степень. Затем мы повторяем этот процесс.
Пример 12.
Теперь возведите в квадрат обе части уравнения.
В этом уравнении всего один радикал, так что мы добились прогресса! Теперь изолируйте радикальный член, а затем возведите его в квадрат.
обе стороны снова.г.
Чек:
Подстановка x = 5/4 в исходное уравнение дает
кв (9/4) + кв (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание по проверке растворов:
Алгебраическую проверку в этом случае выполнить несложно. Однако графическая проверка имеет то преимущество, что показывает, что
нет решений, которые мы не нашли, по крайней мере, в рамках прямоугольника просмотра. Решение
является x-координатой точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).г.
Упражнение 2:
Решите уравнение sqrt(x+2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) с одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух более сложны. Когда мы сталкиваемся
такой задачи, то либо полином имеет особый вид, позволяющий нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой.
г.
Нулевая постоянная
Одним из частых случаев является отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько степеней
x, чтобы начать задачу.
Пример 13.
2x 3 + 3x 2 -5x = 0,
х (2х 2 + 3х -5) = 0,
Теперь у нас есть произведение x и квадратного многочлена, равное 0, поэтому у нас есть два более простых уравнения.
г.
x = 0, или 2x 2 + 3x -5 = 0.
Первое уравнение несложно решить. x = 0 является единственным решением. Второе уравнение может быть решено факторингом.
Примечание: Если бы мы не могли учесть квадратное выражение во втором уравнении, то мы могли бы прибегнуть к
использовать квадратную формулу. [Убедитесь, что вы получаете те же результаты, что и ниже.]х = 0 или (2х + 5)(х — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1,
г.
Примечание: Решение находится из пересечений графиков f(x) = 2x 3
+ 3x 2 -5x.
Фактор по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0,
Коэффициент x 2 в -2 раза больше, чем x 3 , и такое же соотношение существует между
коэффициенты третьего и четвертого членов. Сгруппируйте термины один и два, а также термины три и четыре.г.
х 2 (х — 2) — 9 (х — 2) = 0,
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить на множители левую часть уравнения.
(х — 2)(х 2 — 9) = 0,
Всякий раз, когда мы находим произведение, равное нулю, мы получаем два более простых уравнения.
х — 2 = 0 или х 2 — 9 = 0.
х = 2, или (х + 3)(х — 3) = 0,
Итак, есть три решения, x = 2, x = -3, x = 3.
г.
Примечание: Эти решения находятся из точек пересечения графика f(x) = x 3
-2x 2 -9x +18.
Квадратичный в форме
Пример 15.
х 4 — х 2 — 12 = 0,
Этот многочлен не квадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x 2 .
(х 2 ) 2 — (х 2 ) — 12 = 0.
Вам может помочь замена x на z 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(г — 4) (г + 3) = 0,
z = 4 или z = -3.
Мы не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение верным. Теперь замените z на
x 2 и решить полученные уравнения.г.
х 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i или x = — i.
Итак, есть четыре решения, два действительных и два комплексных.
Примечание: Эти решения находятся из точек пересечения графика f(x) = x 4
— х 2 — 12.График функции f(x) = x 4 — x 2 — 12 и масштабирование, показывающее местное
экстремумы.
Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения с дробными выражениями или абсолютными значениями
Пример 16.
Наименьший общий знаменатель равен x(x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. С помощью графической утилиты мы
убедитесь, что оба этих решения проверяются. Решением является координата x точки пересечения графиков
y = 1 и y = 2/x-1/(x+2).г.
Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями состоит в том, чтобы помнить, что величина внутри абсолютного значения
бары могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности,
и все решения должны быть проверены.Дело 1 . Предположим, что x — 1 >= 0. Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
г.
5(х — 1) = х + 11.
5х — 5 = х + 11.
4x = 16.
x = 4, и это решение верно, потому что 5*3 = 4 + 11.
Случай 2. Предположим, что x — 1
г.
Теперь наше уравнение становится
-5(х — 1) = х + 11.
-5х + 5 = х + 11.
-6х = 6.
x = -1, и это решение верно, потому что 5*2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs() является абсолютным значением, так что вы будете
графически отображать
5*abs(x — 1) — x — 11 и посмотрите на x-перехваты, или вы можете найти решение как x-координаты
точки пересечения графиков y = x+11 и y = 5*abs(x-1).г.
Упражнение 4:
(a) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — х/3 Ответ
Вернуться к содержанию
|
Законы показателей
Экспоненты также называются Степенями или Индексами
Показатель степени числа говорит сколько раз использовать число в умножение.
В этом примере: 8 2 = 8 × 8 = 64
Прописью: 8 2 можно назвать «8 во второй степени», «8 в степени 2» или
просто «8 в квадрате»
Попробуйте сами:
изображений/exponent-calc. js
js
Таким образом, экспонента избавляет нас от записи большого количества умножений!
Пример: a
7
a 7 = a × a × a × a × a × a × a = aaaaaaa
г.
Обратите внимание, как мы написали буквы вместе, чтобы означать умножение? Мы будем делать это много здесь.
Пример: x
6 = xxxxxx
Ключ к законам
Написание всех букв — ключ к пониманию Законов
Пример: х
2 х 3 = (хх)(ххх) = ххххх = х 5
Что показывает, что х 2 х 3 = х 4 на 9 больше, чем 9 потом!
г.
Итак, если вы сомневаетесь, просто не забудьте записать все буквы (столько, сколько вам говорит показатель степени) и посмотреть, сможете ли вы понять это.
Все, что вам нужно знать…
«Законы экспонентов» (также называемые «Правилами экспонентов») исходят из трех идей :
Показатель степени говорит сколько раз использовать число в умножении . | |||
| Отрицательный показатель степени означает, что делит , потому что деление | |||
|
Если вы их понимаете, то понимаете и экспоненты!
И все законы ниже основаны на этих идеях.
Законы экспонентов
Вот законы
(пояснения следуют):
| Право | Пример |
|---|---|
| х 1 = х | 6 1 = 6 |
| х 0 = 1 | 7 0 = 1 |
| х -1 = 1/х | 4 -1 = 1/4 |
| x м x n = x м+n | х 2 х 3 = х 2+3 = х 5 |
| x м /x n = x м-n | x 6 /x 2 = x 6-2 = x 4 |
| (х м ) н = х мн | (х 2 ) 3 = х 2×3 = х 6 |
| (ху) п = х п г п | (ху) 3 = х 3 у 3 |
| (x/y) n = x n /y n | (х/у) 2 = х 2 / у 2 |
| x -n = 1/x n | х -3 = 1/х 3 |
| И закон о дробных показателях: | |
х м/н = | х 2/3 = |
Объяснение законов
Первые три приведенных выше закона (x 1 = x, x 0 = 1 и x -1 = 1/x) являются лишь частью естественной последовательности показателей степени. Взгляните на это:
Взгляните на это:
г.
| Пример: Степени числа 5 | |||
|---|---|---|---|
| .. и т.д.. | |||
| 5 2 | 1 × 5 × 5 | 25 | |
| 5 1 | 1 × 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 ÷ 5 | 0,2 | |
| 5 -2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| .. и т.д.. | |||
Посмотрите на эту таблицу некоторое время. .. обратите внимание, что положительные, нулевые или отрицательные показатели степени на самом деле являются частью одного и того же шаблона, то есть в 5 раз больше (или в 5 раз меньше) в зависимости от того, увеличивается (или уменьшается) показатель степени.
Закон, что x
m x n = x m+n
С x m x n , сколько раз мы в итоге умножаем «x»? Ответ: сначала «m» раз, затем еще «n» раз, всего «m+n» раз.
Пример: х
2 х 3 = (хх)(ххх) = ххххх = х 5
Итак, х 2 х 3 = х (2+904) 929
Закон, что х
m /x n = x m-n
Как и в предыдущем примере, сколько раз мы должны умножить «x»? Ответ: «m» раз, тогда уменьшите это в «n» раз (потому что мы делим), итого в «m-n» раз.
г.
Пример: x
4 /x 2 = (xxxx) / (xx) = xx = x 2
х 2
(Помните, что x / x = 1, так что каждый раз, когда вы видите x «над чертой» и одну «ниже черты», вы можете отменить их. )
Этот закон также может показать вам, почему x 0 = 1 :
Пример: х
2 /x 2 = x 2-2 = x 0 =1
Закон того, что (x
m ) n = x mn
Сначала вы умножаете «m» раз. Тогда у вас есть , чтобы сделать это «n» раз , всего m×n раз.
Тогда у вас есть , чтобы сделать это «n» раз , всего m×n раз.
Пример: (x
3 ) 4 = (xxx) 4 = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x 12
Итак (x 3 3) 9 = х 3×4 = х 12
Закон того, что (xy)
n = x n y n
Чтобы показать, как это работает, просто подумайте о перестановке всех «x» и «y», как в этом примере:
Пример: (xy)
3 = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x 3 y 3
Закон того, что (x/y)
n = x n /y n
Как и в предыдущем примере, просто переставьте «x» и «y»
г.
Пример: (x/y)
3 = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x 3 /y 3
Закон, который
х
м/н =
п√х м
знак равно
(n√x) м
Хорошо, это немного сложнее!
Я предлагаю вам сначала прочитать дробные экспоненты, так это имеет больше смысла.
В любом случае, важная идея заключается в следующем:
x 1/ n = n- корень x
Таким образом, дробная экспонента, такая как 4 3/2 , на самом деле говорит о том, что нужно сделать куб (3) и квадратный корень из (1/2) в любом порядке.
Просто запомните из дробей, что m/n = m × (1/n) :
Пример:
x
( м n ) =
x (м × 1 n ) =
(х м ) 1/n =
n√x м
Порядок не имеет значения, поэтому он также работает для m/n = (1/n) × m :
Пример:
x
( м n ) =
x ( 1 n × m) =
(x 1/n ) м =
(n√x) м
Экспоненты экспонентов .
..
Что насчет этого примера?
4 3 2
Мы делаем показатель степени в сверху сначала , поэтому мы вычисляем его следующим образом:
| Начните с: | 4 3 2 | |
| 3 2 = 3×3: | 4 9 | |
| 4 9 = 4×4×4×4×4×4×4×4×4: | 262144 |
И все!
Если вам сложно запомнить все эти правила, то запомните это:
, вы сможете понять их, когда поймете три идеи
в верхней части этой страницы:
- Показатель степени говорит сколько раз использовать число при умножении
- A отрицательный показатель степени означает деление
- Дробная экспонента, такая как 1/n означает взять корень n-й степени :
х ( 1 п ) =
п√х
О, еще кое-что.

.. Что, если x = 0?
| Положительный показатель степени (n>0) | 0 n = 0 | |
| Отрицательная экспонента (n | 0 -n равно undefined (поскольку деление на 0 не определено) | |
| Показатель степени = 0 | 0 0 … ммм … см. ниже! |
Странный случай 0
0
Существуют разные аргументы в пользу правильного значения 0 0
0 0 , которое может быть 1 или, возможно, 0, поэтому некоторые говорят, что оно действительно «неопределенно»:
| х 0 = 1, значит… | 0 0 = 1 | |
| 0 n = 0, значит. .. | 0 0 = 0 | |
| Если есть сомнения… | 0 0 = «неопределенный» |
323, 2215, 2306, 324, 2216, 2307, 371, 2217, 2308, 2309
Как найти набор решений
Все математические ресурсы ACT
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 Следующая →
ACT Math Help »
Алгебра »
Уравнения / Неравенства »
Наборы решений »
Как найти набор решений
|2x – 25| – 3 = 7. У этой задачи есть два решения. Какова сумма этих решений?
У этой задачи есть два решения. Какова сумма этих решений?
Возможные ответы:
10
17
25
7,5
Правильный ответ:
251912 46
Объяснение:
Во-первых, упростим уравнение, чтобы в левой части уравнения осталось только абсолютное значение:
|2 x – 25| = 10
Теперь создайте два равенства, одно для 10, а другое для –10.
2 x – 25 = 10 и 2 x — 25 = –10
2 x = 35 и 2 x = 15
x = 17,5 и x = 7,5
. Два соль. 17.5 + 7.5 = 25
Report an Error
Find the roots of the equation x 2 + 5 x + 6.
Possible Answers:
2, –3
–2, 3
2, 3
1, 4
–2, –3
Правильный ответ:
–2, –3
Объяснение:
Факторинг дает нам ( x + 2)( x + 3). Это дает x = –2, –3.
Это дает x = –2, –3.
Сообщить об ошибке
Когда вы делите число на 3, а затем прибавляете 2, результат будет таким же, как если вы умножаете то же число на 2, а затем вычитаете 23. Что это за число?
Возможные ответы:
7
15
2
3
9
Правильный ответ:
15
Объяснение:
Вы составляете уравнение и получаете: ( x /3) + 2 = 2 x – 23.
Прибавьте 23 к обеим частям: ( x /3) + 25 = 2 x
Умножьте обе части на 3: x + 75 = 6 x
Вычтите x из обеих сторон: 75 = 5 x и получите
Разделите на x = 15
Report an Error
Find the sum of the solutions to the equation:
2x 2 – 2x – 2 = 1 – x
Possible Answers:
Правильный ответ:
Объяснение:
Во-первых, нам нужно получить все с одной стороны, чтобы уравнение равнялось нулю.
2x 2 — 2x -2 = 1-x
Нам нужно прибавить x слева, а затем вычесть 1.
2x 2 — 2x -2 +x — 1 = 0
2x 2 — x — 3 = 0
Теперь нам нужно разложить бином на множители. Для этого нам нужно перемножить два внешних коэффициента, что даст нам 2(-3) = -6. Нам нужно найти два числа, которые при перемножении дадут нам -6. Нам также нужно, чтобы эти два числа равнялись -1, когда мы их складываем, потому что -1 — это коэффициент члена x.
Если мы используем +2 и -3, то эти два числа перемножатся, чтобы дать нам -6 и сложить, чтобы дать нам -1. Теперь мы можем переписать уравнение следующим образом:
2x 2 — x — 3 = 2x 2 + 2x — 3x — 3 = 0
2x 2 + 2x — 3x — 3 = 0
Теперь мы можем сгруппировать первые два и последние два члена. два термина. Затем мы можем факторизовать первые два члена и два последних члена.
2x(x+1) -3(x+1) = 0
(2x-3)(x+1) = 0
Это означает, что либо 2x — 3 = 0, либо x + 1 = 0. Таким образом, значения x, которые решают уравнение, равны 3/2 и -1.
Таким образом, значения x, которые решают уравнение, равны 3/2 и -1.
Вопрос требует от нас суммы решений, поэтому мы должны добавить 3/2 и -1, что даст нам 1/2.
Сообщить об ошибке
Если 3y = 2x – 7, то какое из следующих утверждений верно?
Возможные ответы:
x больше
недостаточно информации
y больше
они равны
Правильный ответ:
недостаточно информации 4
Объяснение:
Если мы присвоим одной переменной другую, мы получим y = (2x – 7)/3 или x = (3y + 7)/2, но нам не дано никаких указаний на то, каковы значения x и y есть, и мы можем предположить, что их может быть любое число. Если x = 7/2, то y = 0. Если y = -7/3, то x = 0. Попробуем другие числа. Если у = –10, то х = –37/2. Итак, для первых двух примеров x больше, чем y. В последнем примере у больше, чем х. Нам нужно больше информации, чтобы определить, что больше x или y. Правильный ответ — недостаточно информации.
Правильный ответ — недостаточно информации.
Сообщить об ошибке
|10 – 2| – |1 – 9| знак равно
Возможные ответы:
Правильный ответ:
0
Объяснение:
При взятии абсолютного значения мы понимаем, что обе операции абсолютного значения дают 8, что дает нам разницу 0.
Сообщить об ошибке
Когда вы умножаете число на 5, а затем вычитаете 23, результатом будет так же, как если бы вы умножили то же число на 3, а затем добавили 3. Что это за число?
Возможные ответы:
13
6
10
5
7
Правильный Ответ:
Правильный Ответ:
.
Объяснение:
Вы составляете уравнение 5x – 23 = 3x + 3, затем решаете для x, что дает вам 13.
Сообщить об ошибке
Каково произведение двух значений , которые удовлетворяют следующему уравнению?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите значения x путем факторизации.
или
Затем умножьте растворы, чтобы получить произведение.
Сообщить об ошибке.
Объяснение:
Сбор терминов оставляет
И деление на дает
Сообщить об ошибке
Решить для x .
Возможные ответы:
Ни один из других ответов
18.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | ||
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | ||
| 3 | Оценить | 5+5 | ||
| 4 | Оценить | 7*7 | ||
| 5 | Найти простую факторизацию | 24 | ||
| 6 | Преобразование в смешанный номер | 52/6 | ||
| 7 | Преобразование в смешанный номер | 93/8 | ||
| 8 | Преобразование в смешанный номер | 34/5 | ||
| 9 | График | у=х+1 | ||
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | ||
| 11 | Найдите площадь поверхности | сфера (3) | | |
| 12 | Оценить | 54-6÷2+6 | ||
| 13 | График | г=-2x | ||
| 14 | Оценить | 8*8 | ||
| 15 | Преобразование в десятичное число | 5/9 | ||
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | ||
| 17 | График | у=2 | ||
| 18 | Преобразование в смешанный номер | 7/8 | ||
| 19 | Оценить | 9*9 | ||
| 20 | Решите для C | С=5/9*(Ф-32) | ||
| 21 | Упростить | 1/3+1 1/12 | ||
| 22 | График | у=х+4 | ||
| 23 | График | г=-3 | ||
| 24 | График | х+у=3 | ||
| 25 | График | х=5 | ||
| 26 | Оценить | 6*6 | ||
| 27 | Оценить | 2*2 | ||
| 28 | Оценить | 4*4 | ||
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | ||
| 30 | Оценить | 1/3+13/12 | ||
| 31 | Оценка | 5*5 | ||
| 32 | Решить для d | 2д=5в(о)-вр | ||
| 33 | Преобразование в смешанный номер | 3/7 | ||
| 34 | График | г=-2 | ||
| 35 | Найдите склон | у=6 | ||
| 36 | Преобразование в проценты | 9 | ||
| 37 | График | у=2х+2 | ||
| 38 | 92+5х+6=0||||
| 41 | Преобразование в смешанный номер | 1/6 | ||
| 42 | Преобразование в десятичное число | 9% | ||
| 43 | Найти n | 12н-24=14н+28 | ||
| 44 | Оценить | 16*4 | ||
| 45 | Упростить | кубический корень из 125 | ||
| 46 | Преобразование в упрощенную дробь | 43% | ||
| 47 | График | х=1 | ||
| 48 | График | у=6 | ||
| 49 | График | г=-7 | ||
| 50 | График | у=4х+2 | ||
| 51 | Найдите склон | у=7 | ||
| 52 | График | у=3х+4 | ||
| 53 | График | у=х+5 | ||
| 54 | График | 92-9=0|||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | ||
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | ||
| 60 | Найти простую факторизацию | 14 | ||
| 61 | Преобразование в смешанный номер | 7/10 | ||
| 62 | Решите для | (-5а)/2=75 | ||
| 63 | Упростить | х | ||
| 64 | Оценить | 6*4 | ||
| 65 | Оценить | 6+6 | ||
| 66 | Оценить | -3-5 | ||
| 67 | Оценить | -2-2 | ||
| 68 | Упростить | квадратный корень из 1 | ||
| 69 | Упростить | квадратный корень из 4 | ||
| 70 | Найди обратное | 1/3 | ||
| 71 | Преобразование в смешанный номер | 20. 11. 11. | ||
| 72 | Преобразование в смешанный номер | 7/9 | ||
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , | |
| 76 | График | 3x+4y=12 | ||
| 77 | График | 3x-2y=6 | ||
| 78 | График | у=-х-2 | ||
| 79 | График | у=3х+7 | ||
| 80 | Определить, является ли многочлен | 2x+2 | ||
| 81 | График | у=2х-6 | ||
| 82 | График | у=2х-7 | ||
| 83 | График | у=2х-2 | ||
| 84 | График | у=-2х+1 | ||
| 85 | График | у=-3х+4 | ||
| 86 | График | у=-3х+2 | ||
| 87 | График | у=х-4 | ||
| 88 | Оценить | (4/3)÷(7/2) | ||
| 89 | График | 2x-3y=6 | ||
| 90 | График | х+2у=4 | ||
| 91 | График | х=7 | ||
| 92 | График | х-у=5 | ||
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | |||
| 95 | Найдите площадь поверхности | конус (12)(9) | | |
| 96 | Преобразование в смешанный номер | 3/10 | ||
| 97 | Преобразование в смешанный номер | 7/20 | 93||
| 6 | Решить для ? | cos(x)=1/2 | ||
| 7 | Найти x | sin(x)=-1/2 | ||
| 8 | Преобразование градусов в радианы | 225 | ||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | ||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | ||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | |
| 14 | Преобразование градусов в радианы | 120 градусов | ||
| 15 | Преобразование градусов в радианы | 180 | ||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4||
| 38 | Найти точное значение | грех(255) | ||
| 39 | Оценить | лог база 27 из 36 | ||
| 40 | Преобразовать из радианов в градусы | 2 шт. | 92-3sin(x)+1=0||
| 43 | Найти x | tan(x)+ квадратный корень из 3=0 | ||
| 44 | Найти x | sin(2x)+cos(x)=0 | ||
| 45 | Упростить | (1-cos(x))(1+cos(x)) | 92=25||
| 59 | График | f(x)=- натуральный логарифм x-1+3 | ||
| 60 | Найдите значение с помощью единичного круга | угловой синус(-1/2) | ||
| 61 | Найти домен | квадратный корень из 36-4x^2 92=0 | ||
| 66 | Найти x | cos(2x)=(квадратный корень из 2)/2 | ||
| 67 | График | у=3 | ||
| 68 | График | f(x)=- логарифмическая база 3 x-1+3 | 92 | |
| 71 | Найти x | квадратный корень из x+4+ квадратный корень из x-1=5 | ||
| 72 | Решить для ? | cos(2x)=-1/2 | ||
| 73 | Найти x | логарифмическая база x из 16=4 | 9х||
| 75 | Упростить | (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) | ||
| 76 | Упростить | сек(х)sin(х) | ||
| 77 | Упростить | кубический корень из 24 кубический корень из 18 | 92=0||
| 96 | Найти x | 3x+2=(5x-11)/(8г) | ||
| 97 | Решить для ? | sin(2x)=-1/2 | ||
| 98 | Найти x | (2x-1)/(x+2)=4/5 | 92 — 1| — 1 = 3x — 2$ без построения графика | |
 Test a value in each interval. The factor, x plus 2, is negative when negative 3 is substituted for x in the interval negative infinity to negative 2. The factor, x minus 6, is negative when negative 3 is substituted for x in the interval negative infinity to negative 2. The factor, x plus 2, is positive when 0 is substituted for x in the interval negative 2 to 6. The factor, x minus 6, is negative when 0 is substituted for x in the interval negative 2 to 6. The factor, x plus 2, is positive when 7 is substituted for x in the interval 6 to infinity. The factor, x minus 6, is positive when 0 is substituted for x in the interval 6 to infinity. Above the number line, show the sign of each factor of the rational expression in each interval. Below the number line, show the sign of the quotient. The number line is divided into intervals by critical points at negative 2 and 6. An open parenthesis is used at negative 2 and a closed parenthesis is used at 6. The number line is shaded between negative 2 and 6.
Test a value in each interval. The factor, x plus 2, is negative when negative 3 is substituted for x in the interval negative infinity to negative 2. The factor, x minus 6, is negative when negative 3 is substituted for x in the interval negative infinity to negative 2. The factor, x plus 2, is positive when 0 is substituted for x in the interval negative 2 to 6. The factor, x minus 6, is negative when 0 is substituted for x in the interval negative 2 to 6. The factor, x plus 2, is positive when 7 is substituted for x in the interval 6 to infinity. The factor, x minus 6, is positive when 0 is substituted for x in the interval 6 to infinity. Above the number line, show the sign of each factor of the rational expression in each interval. Below the number line, show the sign of the quotient. The number line is divided into intervals by critical points at negative 2 and 6. An open parenthesis is used at negative 2 and a closed parenthesis is used at 6. The number line is shaded between negative 2 and 6. The factors x plus 2 and x minus 6 are marked as negative above the number line for the interval negative infinity to negative 2. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as positive below the number line for the interval negative infinity to negative 2. The factor x plus 2 is marked as positive and the factor x minus 6 is marked as negative above the number line for the interval negative 2 to 6. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as negative below the number line for the interval negative 2 to 6. The factors x plus 2 and x minus 6 are marked as positive above the number line for the interval 6 to infinity. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as positive below the number line for the interval 6 to infinity. Determine the intervals where the inequality is correct. Write the solution in interval notation. The solution is the interval negative 2 and 6 with negative 2 and 6 not included.
The factors x plus 2 and x minus 6 are marked as negative above the number line for the interval negative infinity to negative 2. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as positive below the number line for the interval negative infinity to negative 2. The factor x plus 2 is marked as positive and the factor x minus 6 is marked as negative above the number line for the interval negative 2 to 6. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as negative below the number line for the interval negative 2 to 6. The factors x plus 2 and x minus 6 are marked as positive above the number line for the interval 6 to infinity. The quotient of the quantity x plus 2 and the quantity x minus 6 is marked as positive below the number line for the interval 6 to infinity. Determine the intervals where the inequality is correct. Write the solution in interval notation. The solution is the interval negative 2 and 6 with negative 2 and 6 not included. » data-label=»»>
» data-label=»»>разница над общим знаменателем.

Частное не определено, когда знаменатель равен нулю.
Под числовой чертой показывается знак частного.
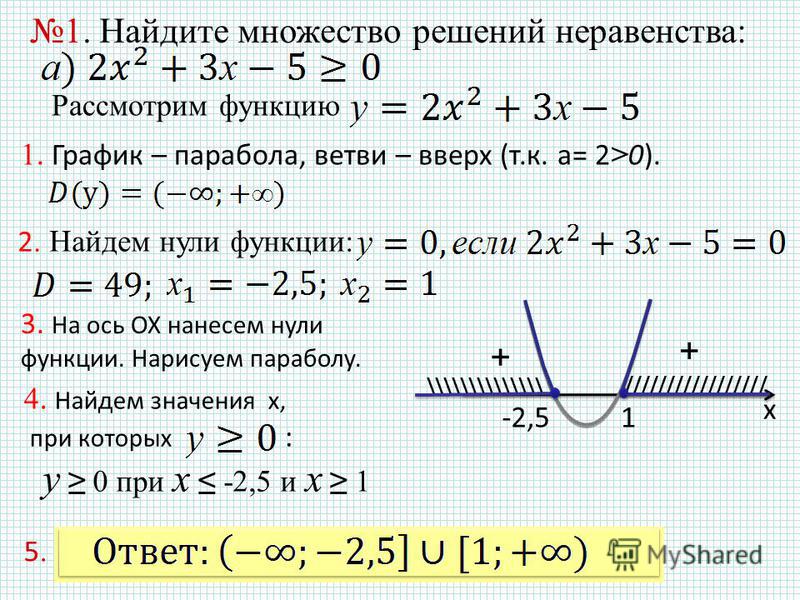 Мы хотим, чтобы частное было отрицательным, поэтому решение включает точки от −2 до 6. Поскольку неравенство строго меньше, конечные точки не учитываются.
Мы хотим, чтобы частное было отрицательным, поэтому решение включает точки от −2 до 6. Поскольку неравенство строго меньше, конечные точки не учитываются.Решите и запишите решение в интервальной записи:
Решите и запишите решение в интервальной записи:
В следующем примере числитель всегда положителен, поэтому знак рационального выражения зависит от знак знаменателя.
Решите и запишите решение в интервальной записи:
 The factor x plus 3 is marked as positive and the factor x minus 5 is marked as negative above the number line for the interval negative 3 to 5. The quotient of 4 and the product of the quantity x plus 3 and the quantity x minus 5 is marked as negative below the number line for the interval negative 3 to 5. The factors x plus 3 and x minus 5 are marked as positive above the number line for the interval 5 to infinity. The quotient of 4 and the product of the quantity x plus 3 and the quantity x minus 5 is marked as positive below the number line for the interval 5 to infinity. Write the solution in interval notation. The solution is the union of the interval negative infinity to negative 3 and the interval 5 to infinity, with 3 and 5 not included» data-label=»»>
The factor x plus 3 is marked as positive and the factor x minus 5 is marked as negative above the number line for the interval negative 3 to 5. The quotient of 4 and the product of the quantity x plus 3 and the quantity x minus 5 is marked as negative below the number line for the interval negative 3 to 5. The factors x plus 3 and x minus 5 are marked as positive above the number line for the interval 5 to infinity. The quotient of 4 and the product of the quantity x plus 3 and the quantity x minus 5 is marked as positive below the number line for the interval 5 to infinity. Write the solution in interval notation. The solution is the union of the interval negative infinity to negative 3 and the interval 5 to infinity, with 3 and 5 not included» data-label=»»>
Частное равно 0, когда числитель равен 0.
Поскольку числитель всегда равен 5, частное не может быть равно 0.
знаменатель равен нулю.
Над числовой строкой покажите знак каждого
.множителей знаменателя в каждом интервале.
Под числовой прямой покажите знак частного.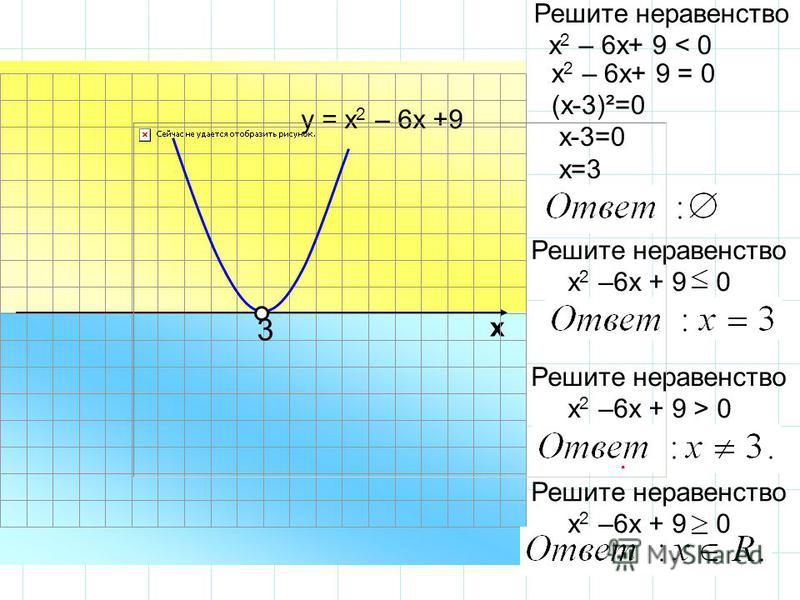
Решите и запишите решение в интервальной записи:
Решите и запишите решение в интервальной записи:
Следующий пример требует некоторой работы, чтобы привести его в нужную форму.
Решите и запишите решение в интервальной записи:
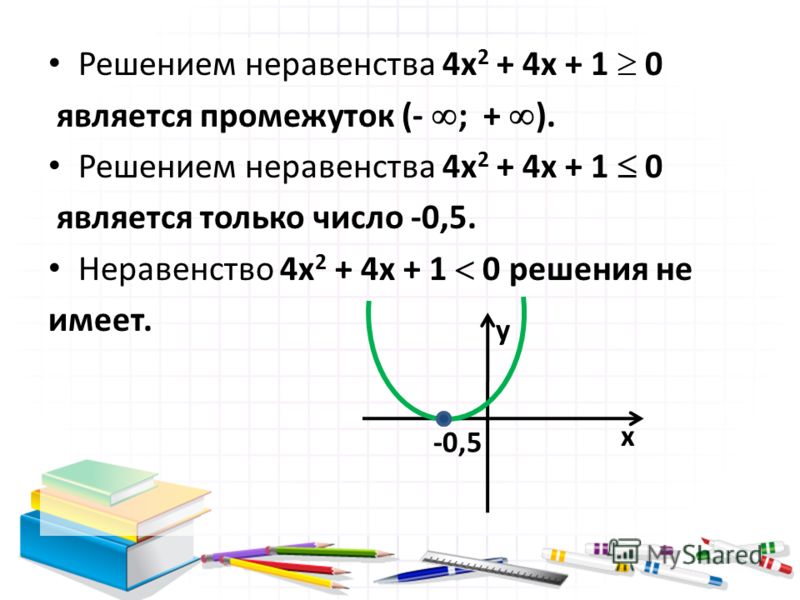 The number line is shaded between negative 1 and 0 and between 0 and 6. The factors x minus 6 and x plus 1 are marked as negative above the number line for the interval negative infinity to negative 1. The factor x squared is marked as positive above the number line for the interval negative infinity to negative 1. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as positive below the number line for the interval negative infinity to negative 1. The factor x minus 6 is marked as negative above the number line for the interval negative 1 to 0. The factors x plus 1 and x squared are marked as positive above the number line for the interval negative 1 and 0. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as negative below the number line on the interval negative 1 to 0. The factor x minus 6 is marked as negative above the number line on the interval 0 to 6.
The number line is shaded between negative 1 and 0 and between 0 and 6. The factors x minus 6 and x plus 1 are marked as negative above the number line for the interval negative infinity to negative 1. The factor x squared is marked as positive above the number line for the interval negative infinity to negative 1. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as positive below the number line for the interval negative infinity to negative 1. The factor x minus 6 is marked as negative above the number line for the interval negative 1 to 0. The factors x plus 1 and x squared are marked as positive above the number line for the interval negative 1 and 0. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as negative below the number line on the interval negative 1 to 0. The factor x minus 6 is marked as negative above the number line on the interval 0 to 6.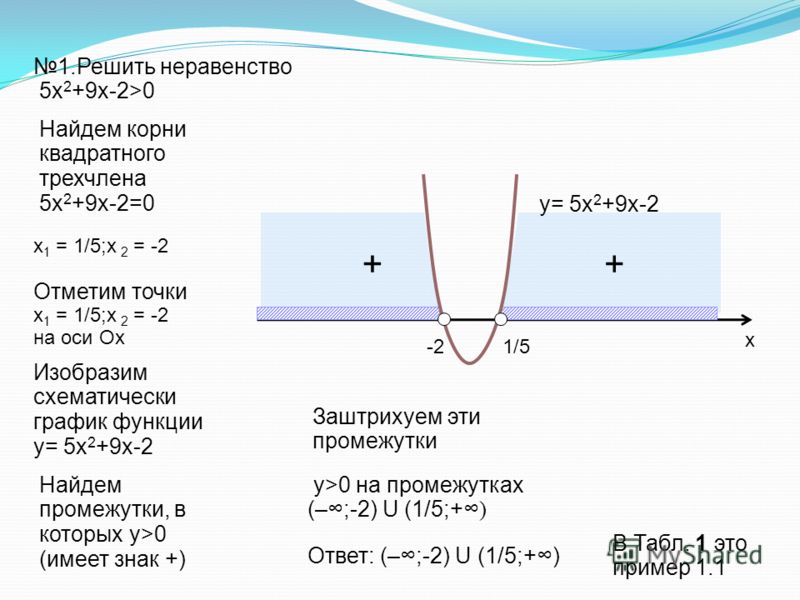 The factors x plus 1 and x squared are marked as positive above the number line on the interval 0 to 6. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as negative below the number line on the interval 0 to 6. The factors x minus 6, x plus 1 and x squared are marked positive above the number line on the interval 6 to infinity. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as positive below the number line on the interval 6 to infinity. Since 0 is excluded, the solution is the two intervals negative 1 to 0 and 0 to 6, or the union of the intervals negative 1 to 0 and 0 to 6.» data-label=»»>
The factors x plus 1 and x squared are marked as positive above the number line on the interval 0 to 6. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as negative below the number line on the interval 0 to 6. The factors x minus 6, x plus 1 and x squared are marked positive above the number line on the interval 6 to infinity. The quotient of the product of the quantity x minus 6 and the quantity x plus 1 all divided by 3 x squared is marked as positive below the number line on the interval 6 to infinity. Since 0 is excluded, the solution is the two intervals negative 1 to 0 and 0 to 6, or the union of the intervals negative 1 to 0 and 0 to 6.» data-label=»»>
разность над общим знаменателем.
строки на интервалы.
коэффициентов в каждом интервале. Под числовой прямой покажите знак частного.
интервалов и
Решите и запишите решение в интервальной записи:
Решите и запишите решение в интервальной записи:
Решение неравенства с рациональными функциями
При работе с рациональными функциями иногда полезно знать, когда функция больше или меньше определенного значения. Это приводит к рациональному неравенству.
Для данной функции найдите значения x , которые делают функцию меньше или равной 0.
Мы хотим, чтобы функция была меньше или равна 0.
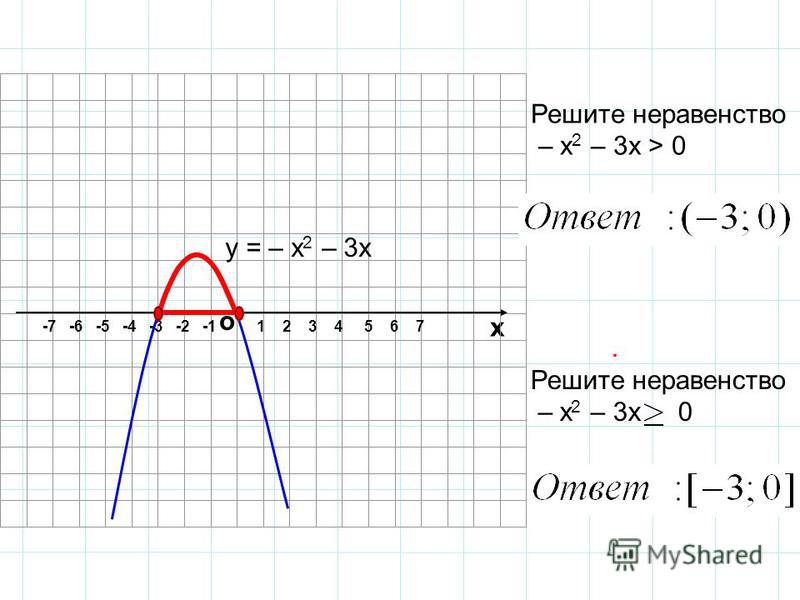 The quotient of the quantity x plus 3 and the quantity x minus 5 is marked as negative below the number line on the interval negative 3 to 5. The factors x plus 3 and x minus 5 are marked as positive above the number line on the interval 5 to infinity. The quotient of the quantity x plus 3 and the quantity x minus 5 is marked as positive below the number line on the interval 5 to infinity. Write the solution in interval notation. Since 5 is excluded, we do not include it in the interval. The solution is the interval negative 3 to 5, with negative 3 included.» data-label=»»>
The quotient of the quantity x plus 3 and the quantity x minus 5 is marked as negative below the number line on the interval negative 3 to 5. The factors x plus 3 and x minus 5 are marked as positive above the number line on the interval 5 to infinity. The quotient of the quantity x plus 3 and the quantity x minus 5 is marked as positive below the number line on the interval 5 to infinity. Write the solution in interval notation. Since 5 is excluded, we do not include it in the interval. The solution is the interval negative 3 to 5, with negative 3 included.» data-label=»»>
числовая строка, покажите знак каждого множителя
в каждом интервале. Ниже числовой строки
.показать знак частного
5 исключено, не включаем в интервал.
Для заданной функции найдите значения x , при которых функция меньше или равна 0,
Для заданной функции найдите значения x , которые делают функцию меньше или равной 0.
В экономике функция используется для представления затрат на производство x единиц товара. Среднюю стоимость единицы продукции можно найти, разделив ее на количество изделий. Тогда средняя стоимость единицы продукции будет равна
Среднюю стоимость единицы продукции можно найти, разделив ее на количество изделий. Тогда средняя стоимость единицы продукции будет равна
. Функция представляет затраты на производство определенного количества изделий. Найдите ⓐ функцию средней стоимости, ⓑ сколько изделий нужно произвести, чтобы средняя стоимость была меньше 40 евро.
ⓐ
ⓑ
Необходимо произвести более 100 единиц товара, чтобы средняя стоимость не превышала 40 евро за единицу.
Функция представляет затраты на производство определенного количества изделий. Найдите ⓐ функцию средней стоимости, ⓑ сколько изделий нужно произвести, чтобы средняя стоимость была меньше 60?
ⓐ
ⓑ Необходимо произвести более 150 единиц продукции, чтобы средняя стоимость не превышала 60 евро за единицу.
Функция представляет затраты на производство определенного количества изделий. Найдите ⓐ функцию средней стоимости, ⓑ сколько изделий нужно произвести, чтобы средняя стоимость была меньше 20?
ⓐⓑ Необходимо произвести более 60 единиц продукции, чтобы средняя стоимость не превышала 20 евро за единицу.
Ключевые понятия
- Решите рациональное неравенство.
- Запишите неравенство в виде одного частного слева и нуля справа.
- Определите критические точки — точки, в которых рациональное выражение будет равно нулю или не определено.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Проверка значения в каждом интервале. Над числовой прямой показывают знак каждого множителя рационального выражения в каждом интервале. Ниже числовой строки укажите знак частного. г.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Раздел Упражнения
Практика делает совершенным
Решение рациональных неравенств
В следующих упражнениях решите каждое рациональное неравенство и запишите решение в интервальной записи.
6
Решение неравенства с рациональными функциями
В следующих упражнениях решите каждое неравенство с рациональными функциями и запишите решение в интервальной записи.
Для заданной функции найдите значения, при которых функция меньше или равна 0.
Для заданной функции найдите значения, при которых функция меньше или равна 0.
Для заданной функции найдите значения x, которые делают функцию меньше или равной 0,
Для заданной функции найдите значения x, при которых функция меньше или равна 0.
Написание упражнений
Напишите шаги, которые вы использовали бы, чтобы объяснить своему младшему брату решение рациональных неравенств.
Ответы будут разными.
Составьте рациональное неравенство, решение которого
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ Изучив этот контрольный список, что вы сделаете, чтобы уверенно выполнять все задачи?
Упражнения на обзор глав
Упрощение, умножение и деление рациональных выражений
Определение значений, для которых рациональное выражение не определено
В следующих упражнениях определите значения, для которых рациональное выражение не определено.
Упрощение рациональных выражений
В следующих упражнениях упрощайте.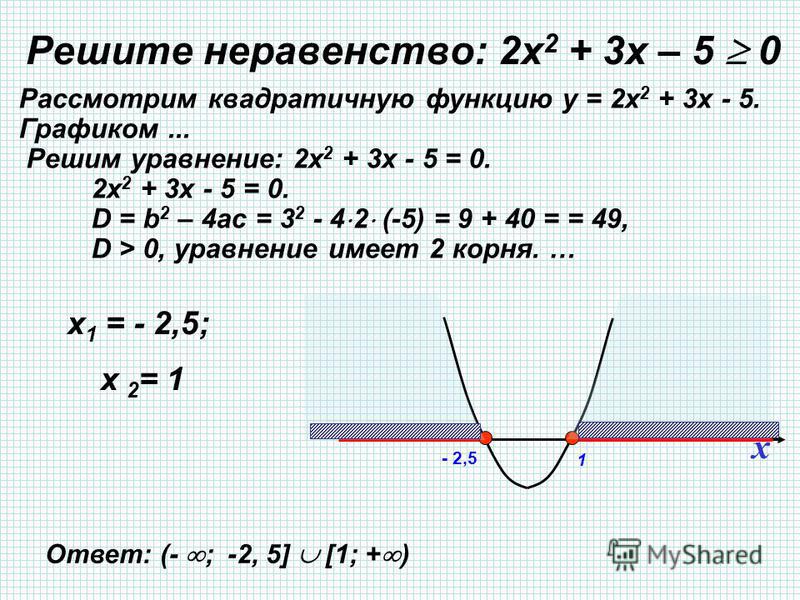
Умножение рациональных выражений
В следующих упражнениях умножайте.
Разделение рациональных выражений
В следующих упражнениях разделите.
Multiply and Divide Rational Functions
Find where and
Find where and
Add and Subtract Rational Expressions
Add и Вычитание рациональных выражений с общим знаменателем
В следующих упражнениях выполните указанные операции.
Add and Subtract Rational Expressions Whose Denominators Are Opposites
In the following exercises, add and subtract.
Найдите наименьший общий знаменатель рациональных выражений
Сложение и вычитание рациональных выражений с разными знаменателями
В следующих упражнениях выполните указанные операции.
Add and Subtract Rational Functions
В следующих упражнениях найдите, где даны и .
В следующих упражнениях найдите, где даны и .
Упростить комплексное рациональное выражение
Упростить сложное рациональное выражение, записав его в виде деления
В следующих упражнениях упростите.
Упрощение сложного рационального выражения с помощью ЖК-дисплея
В следующих упражнениях упрощайте.
.1813 Для рациональной функции ⓐ найти область определения функции ⓑ решить ⓒ найти точки на графике при этом значении функции.
ⓐ Область определения – все действительные числа, кроме и ⓑ
ⓒ
Для рациональной функции ⓐ найти область определения функции ⓑ решить ⓒ найти точки на графике при этом значении функции.
Решение рационального уравнения для определенной переменной
В следующих упражнениях найдите решение для указанной переменной.
на
для
Решение приложений с рациональными уравнениями
Решение пропорций
В следующих упражнениях решите.
Решение с использованием пропорций
В следующих упражнениях решите.
Рэйчел выпила клубничный коктейль на 21 унцию, содержащий 739 калорий. Сколько калорий в коктейле на 32 унции?
калорий
Лео отправился в Мексику на рождественские каникулы и обменял 525 долларов на мексиканские песо. В то время по обменному курсу 1 доллар США был равен 16,25 мексиканских песо. Сколько мексиканских песо он получил за поездку?
Решите приложения с похожими фигурами
В следующих упражнениях решите.
аналогично Длины двух сторон каждого треугольника даны на рисунке. Найдите длины третьих сторон.
На карте Европы Париж, Рим и Вена образуют треугольник, стороны которого показаны на рисунке ниже. Если фактическое расстояние от Рима до Вены равно 700 милям, найдите расстояние от
ⓐ Париж-Рим
ⓑ Париж-Вена
Рост Франчески 5,75 фута. Однажды вечером ее тень была 8 футов в длину. В то же время тень соседнего дерева была 32 фута в длину. Найдите высоту дерева.
Найдите высоту дерева.
23 фута
Высота маяка в Пенсаколе, штат Флорида, составляет 150 футов. Стоя рядом со статуей, Наташа ростом 5,5 футов отбрасывала тень длиной 1,1 фута. Какой длины будет тень маяка?
Решение задач равномерного движения
В следующих упражнениях решите.
Возвращаясь в 5 часах езды от родителей, Лоло попала в плохую погоду. Она смогла проехать 176 миль, пока погода была хорошей, но затем, двигаясь на 10 миль в час медленнее, проехала 81 милю, когда погода испортилась. С какой скоростью она ехала в плохую погоду?
миль в час
Марк летит на самолете, который может пролететь 490 миль при попутном ветре 20 миль в час и 350 миль при попутном ветре 20 миль в час. Какова скорость самолета?
Джосу может ехать на велосипеде со скоростью 8 миль в час быстрее, чем Арджун может ехать на своем велосипеде. Люку требуется на 3 часа больше времени, чем Джосу, чтобы проехать 48 миль. Как быстро Джон может ездить на велосипеде?
Как быстро Джон может ездить на велосипеде?
миль в час
Кертис готовился к триатлону. Он пробежал 8 километров и проехал на велосипеде 32 километра за 3 часа. Его скорость бега была на 8 километров в час меньше скорости езды на велосипеде. Какова была его скорость бега?
Решение рабочих приложений
В следующих упражнениях решите.
Брэнди может обрамить комнату за 1 час, а Джейк за 4 часа. Как долго они смогут создать комнату, работая вместе?
час
Прем косит газон 3 часа, а ее двоюродная сестра Барб — 2 часа. Как долго они будут работать вместе?
Джеффри может покрасить дом за 6 дней, но если у него есть помощник, он может сделать это за 4 дня. Сколько времени понадобится помощнику, чтобы покрасить дом в одиночку?
дней
Марта и Деб вместе пишут книгу, которая занимает их 90 дней. Если бы Сью работала одна, это заняло бы у нее 120 дней. Сколько времени потребуется Деб, чтобы написать книгу в одиночку?
Решение задач с прямыми вариациями
В следующих упражнениях решите.
Если изменяется прямо пропорционально времени и найти время
Если изменяется обратно пропорционально времени и найти время
Ванесса едет навестить своего жениха. Расстояние, прямо зависит от скорости, которую она проезжает. Если она проедет 258 миль со скоростью 60 миль в час, как далеко она проедет со скоростью 70 миль в час?
mph
Если стоимость пиццы напрямую зависит от ее диаметра, и если пицца диаметром 8 дюймов стоит 12 фунтов стерлингов, то сколько будет стоить пицца диаметром 6 дюймов?
Расстояние до остановки автомобиля зависит от квадрата его скорости. Чтобы остановить автомобиль, движущийся со скоростью 50 миль в час, требуется 200 футов. Сколько футов потребуется, чтобы остановить автомобиль, движущийся со скоростью 60 миль в час?
футов
Решение обратных вариационных задач
В следующих упражнениях решите.
Если изменяется обратно пропорционально квадрату времени и найдите, когда
Количество билетов на музыкальный сбор средств обратно пропорционально цене билетов. Если у Мадлен достаточно денег, чтобы купить 12 билетов по 6 фунтов стерлингов, сколько билетов Мадлен может позволить себе купить, если цена вырастет до 8 фунтов стерлингов?
Если у Мадлен достаточно денег, чтобы купить 12 билетов по 6 фунтов стерлингов, сколько билетов Мадлен может позволить себе купить, если цена вырастет до 8 фунтов стерлингов?
билеты
На струнном инструменте длина струны изменяется обратно пропорционально частоте ее колебаний. Если 11-дюймовая струна на скрипке имеет частоту 360 циклов в секунду, какую частоту имеет 12-дюймовая струна?
Решение рациональных неравенств
Решение рациональных неравенств
В следующих упражнениях решите каждое рациональное неравенство и запишите решение в интервальной записи.
Solve an Inequality with Rational Functions
In the following exercises, solve each rational function inequality and write the solution in interval notation
Для заданной функции найдите значения, при которых функция больше или равна 0.
Для заданной функции найдите значения, при которых функция меньше или равна 0.
Функция
представляет собой затраты на производство определенного количества изделий. Найдите ⓐ функцию средней стоимости, ⓑ сколько изделий необходимо произвести, чтобы средняя стоимость была меньше 160 евро.
ⓐ
ⓑ Необходимо произвести более 10 000 единиц продукции, чтобы средняя стоимость единицы продукции оставалась ниже средней.
Тиллман начинает свой собственный бизнес по продаже тако на пляже. С учетом стоимости его грузовика с едой и ингредиентов для тако функция представляет затраты Тиллмана на производство тако. Найдите ⓐ функцию средней стоимости для тако Тиллмана ⓑ сколько тако должен произвести Тиллман, чтобы средняя стоимость была меньше ?4.
Практический тест
В следующих упражнениях упрощайте.
В следующих упражнениях выполните указанную операцию и упростите.
.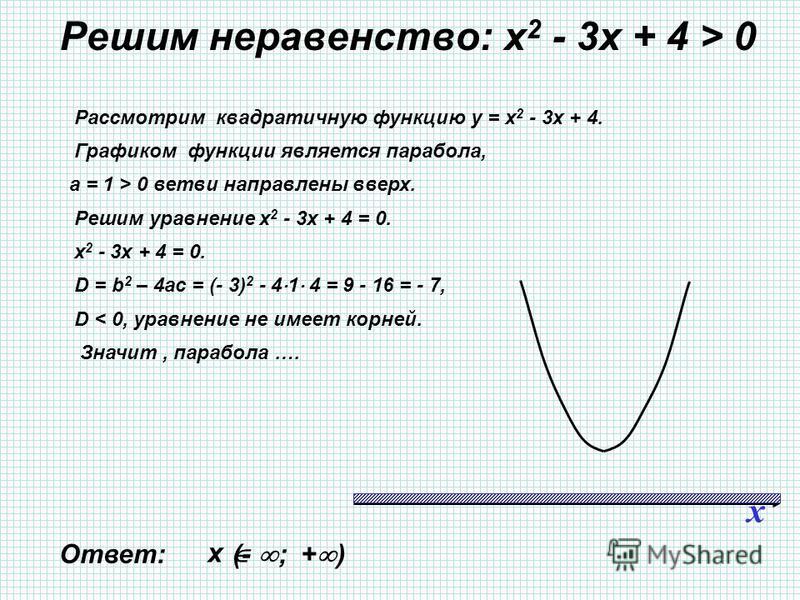
В следующих упражнениях решите каждое рациональное неравенство и запишите решение в интервальной записи.
В следующих упражнениях найдите данное и
Учитывая функцию,
найдите значения, при которых функция меньше или равна 0.
В следующих упражнениях решите.
Если зависит прямо от , и когда найти, когда
Если зависит обратно пропорционально квадрату и когда найти, когда
Матеус может проехать на велосипеде 30 миль при ветре за то же время, что и 21 миль против ветра. Если скорость ветра 6 миль в час, какова скорость Матеуса на его велосипеде?
Оливер может расколоть грузовик с бревнами за 8 часов, но, работая с его отцом, они могут сделать это за 3 часа. Сколько времени потребуется отцу Оливера, работающему в одиночку, чтобы расколоть бревна?
Отцу Оливера потребовалось несколько часов, чтобы самому расколоть бревна.

 Уравнения, содержащие модуль. Рациональные уравнения
Уравнения, содержащие модуль. Рациональные уравнения Ответ не принадлежит промежутку, следовательно нет решений.
Ответ не принадлежит промежутку, следовательно нет решений.
 Решите уравнение:
Решите уравнение: Решите уравнение:
Решите уравнение:
 Решите уравнение:
Решите уравнение:
 Решите уравнение:
Решите уравнение:
 е. x2>x1 → f(x2)>f(x1)
е. x2>x1 → f(x2)>f(x1)
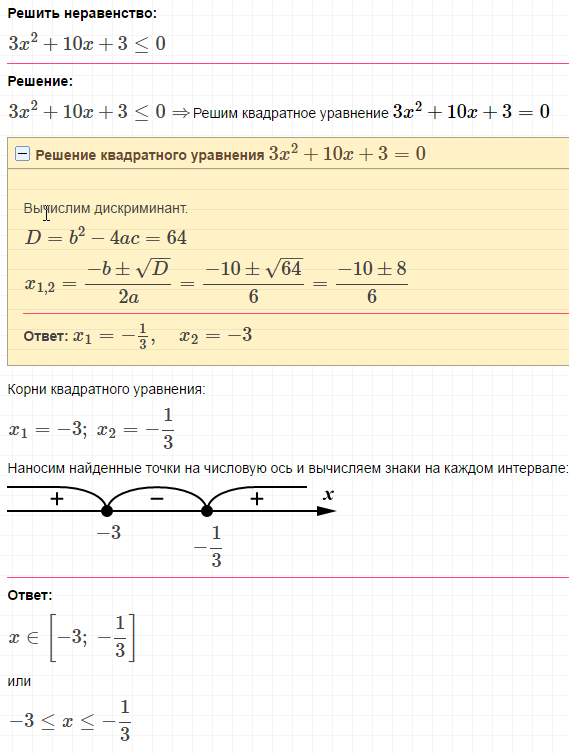
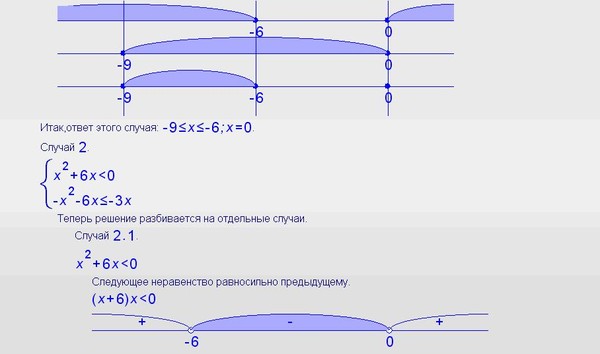

 2}}\right|.$$
2}}\right|.$$ $
$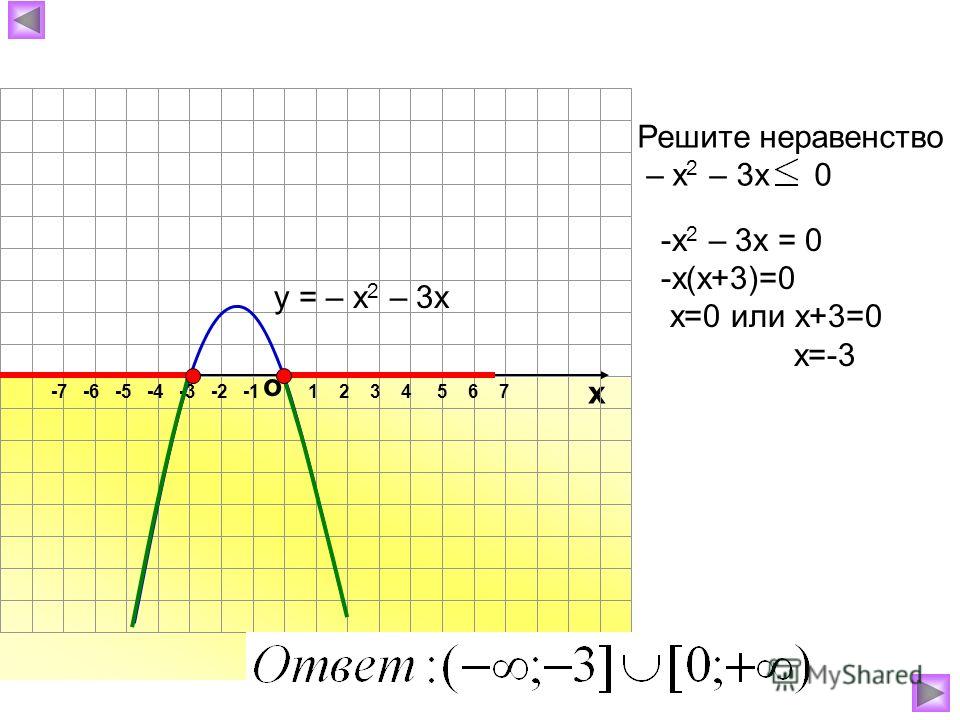 $
$ 183.
183.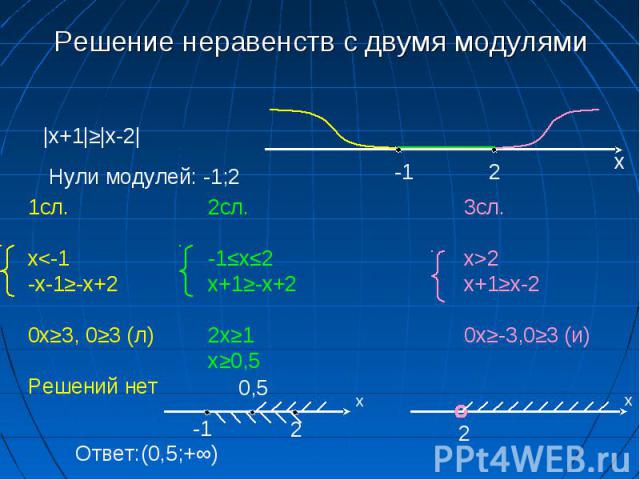 $
$
 Причина
Причина В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив
В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив Таким образом, решения комплексные, поскольку график y = x 2
Таким образом, решения комплексные, поскольку график y = x 2 


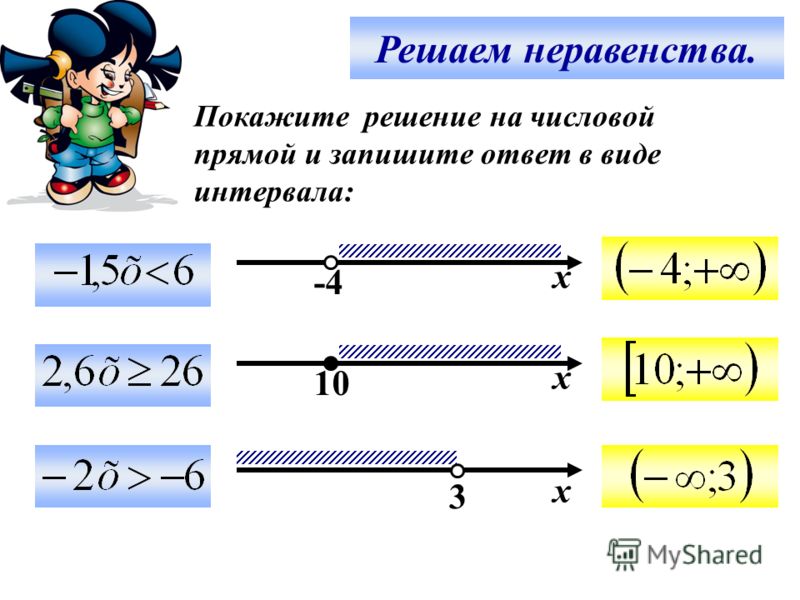



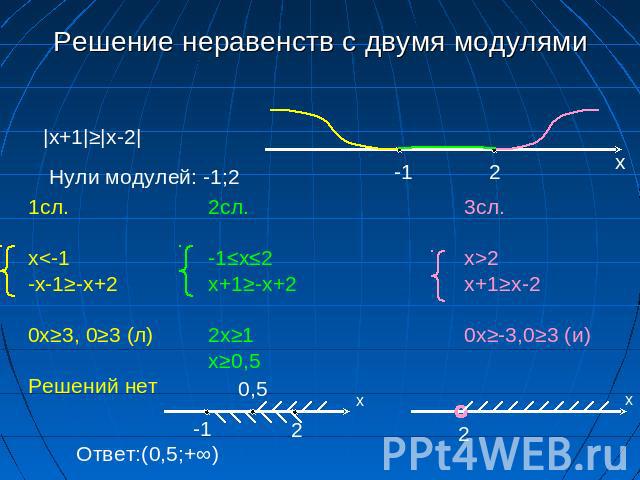
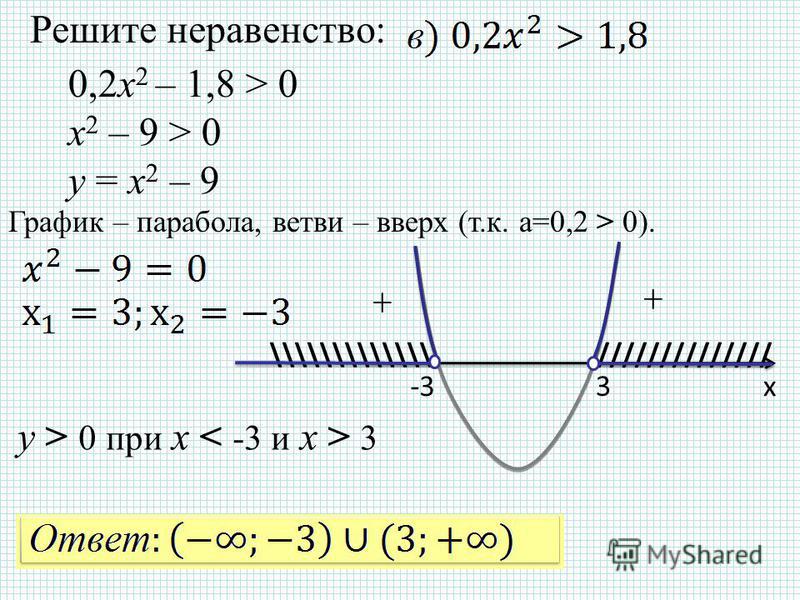 02.15
02.15


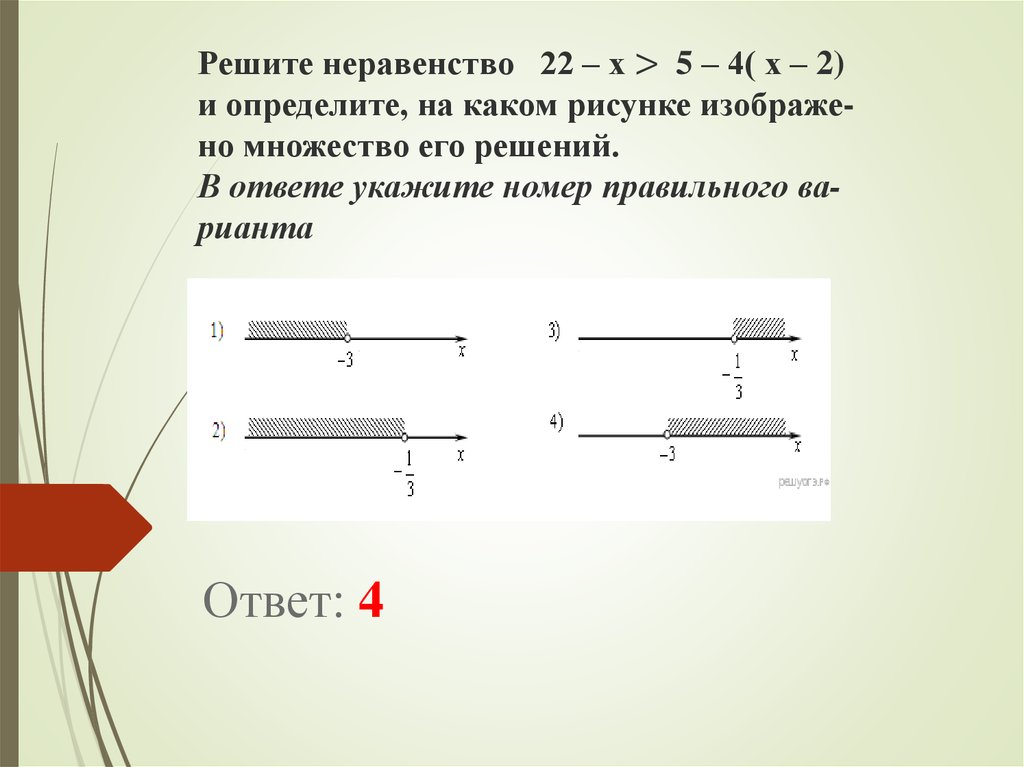 2 — 1 &= 3x — 1 \\ x(x — 3)& = 0 \\ \Longleftrightarrow \boxed { х = 0 \ {\ rm or} \ x = 3} \ end {выровнено} $ $ 92 — 1 &= -3x + 1 \\ \Longleftrightarrow \boxed{x = {-3 \pm \sqrt{17} \over 2}} \end{aligned}$$У нас есть четыре решения.
2 — 1 &= 3x — 1 \\ x(x — 3)& = 0 \\ \Longleftrightarrow \boxed { х = 0 \ {\ rm or} \ x = 3} \ end {выровнено} $ $ 92 — 1 &= -3x + 1 \\ \Longleftrightarrow \boxed{x = {-3 \pm \sqrt{17} \over 2}} \end{aligned}$$У нас есть четыре решения.


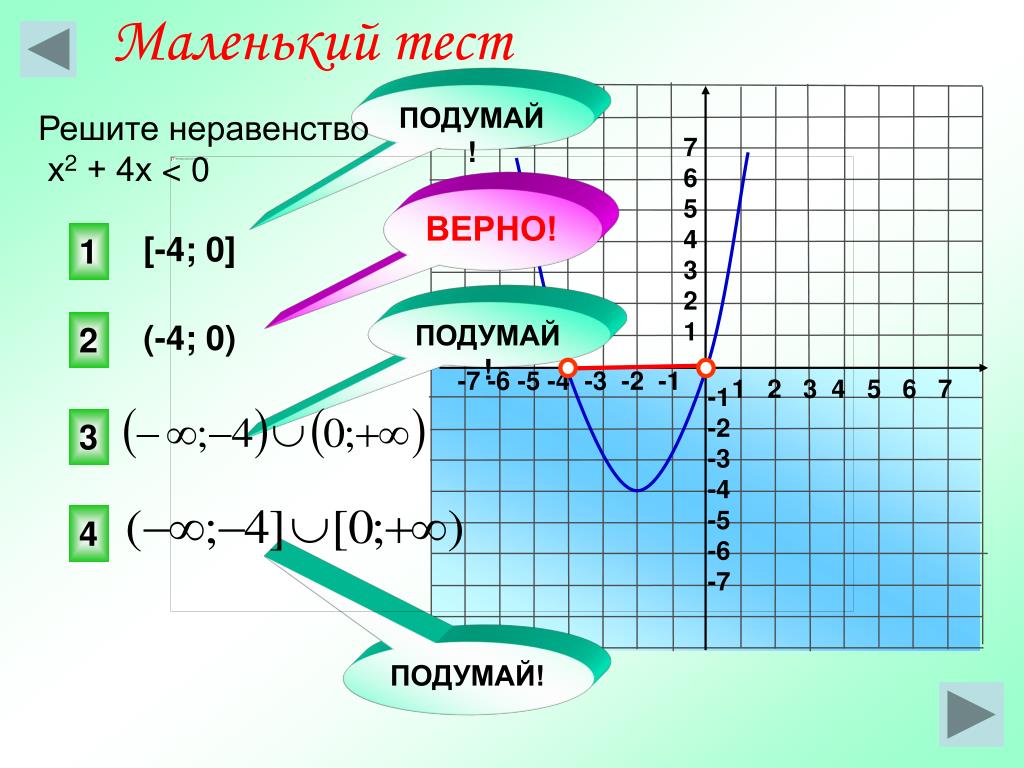







 Ниже числовой строки укажите знак частного.
Ниже числовой строки укажите знак частного.