Векторы и матрицы в квантовых вычислениях — Azure Quantum
- Статья
- Чтение занимает 5 мин
Для понимания квантовых вычислений нужно хотя бы в общих чертах разбираться в векторах и матрицах. В этой статье представлено краткое введение в эту тему, а заинтересованным читателям рекомендуем ознакомиться с обычным справочником по линейной алгебре, например Strang, G. (1993). Introduction to linear algebra (Vol. 3). Wellesley, MA: Wellesley-Cambridge Press (Г. Странг, Введение в линейную алгебру, том 3, изд-во Wellesley-Cambridge Press, Уэллсли, штат Массачусетс, США, 1993 г.) или к интернет-ресурсам по линейной алгебре, например этому справочнику.
Такая нотация позволяет выразить норму вектора $v$ как $\sqrt{\langle v, v\rangle}$.
При умножении вектора на число $c$ мы получим новый вектор, все элементы которого умножены на $c$. При сложении двух векторов $u$ и $v$ мы получим новый вектор, все элементы которого являются суммами соответствующих элементов $u$ и $v$. К этим операциям относятся:
$$\mathrm{Если}~u =\begin{bmatrix} u_1\\ u_2\\ \vdots\\ u_n \end{bmatrix}~\mathrm{and}~ v =\begin{bmatrix} v_1\\ v_2\\ \vdots\\ v_n \end{bmatrix},~\mathrm{то}~ au+bv =\begin{bmatrix} au_1+bv_1\\ au_2+bv_2\\ \vdots\\ au_n+bv_n \end{bmatrix}. $$
Матрица размером $m \times n$ представляет собой набор из $mn$ комплексных чисел, организованных в $m$ строк и $n$ столбцов, как показано ниже:
$$M =\begin{bmatrix} M_{11}~~ M_{12}~~\cdots~~ M_{1n}\\ M_{{21}~~ M_{22}~~\cdots~~ M_{2n}\\\ddots\\ M_{m1}~~ M_{m2}~~\cdots~~ M_{mn}\\\end{bmatrix}.$$
Обратите внимание, что вектор с размерностью $n$ полностью идентичен матрице $n \times 1$.
Умножение матриц
При умножении двух матриц $M$ с размером $m\times n$ и $N$ с размером $n \times p$ мы получим новую матрицу $P$ с размером $m \times p$ по такой формуле:
\begin{\begin{align}&\begin{bmatrix} M_{{11}~~ M_{12}~~\cdots~~ M_{1n}\\ M_{21}~~ M_{22}~~\cdots~~ M_{2n}\\\ddots\\ M_{m1}~~ M_{m2}~~\cdots~~ M_{mn}\end{bmatrix}\begin{bmatrix} N_{{11}~~ N_{12}~~\cdots~~ N_{1p}\\ N_{{21}~~ N_{{22}~~\cdots~~ N_{2p}\\\ddots\\ N_{n1}~~ N_{n2}~~\cdots~~ N_{np}\end{bmatrix}=\begin{bmatrix} P_{{11}~~ P_{{12}~~\cdots~~ P_{1p}\\ P_{{21}~~ P_{22}~~\cdots~~ P_{2p}\\\ddots\\ P_{m1}~~ P_{m2}~~\cdots~~ P_{mp}\end{bmatrix}\end{align}
где элементы $P$ обозначены как $P_{ik}=\sum_j M_{ij}N_{jk}$. Например, элемент $P_{11}$ является скалярным произведением первой строки $M$ и первого столбца $N$. \dagger$.
\dagger$.
Тензорное произведение
Еще одной важной операцией является кронекерово произведение, также именуемое прямым произведением матриц или тензорным произведением. Обратите внимание, что кронекерово произведение коренным образом отличается от обычного умножения матриц. В теории квантовых вычислений для обозначения кронекерового произведения широко применяется термин тензорное произведение.
Для примера рассмотрим два вектора $v=\begin{bmatrix}a \\ b \end{bmatrix}$ и $u =\begin{bmatrix} c \\ d \\ e \end{bmatrix}$. Тензорное произведение этих векторов обозначается как $v \otimes u$, а его результатом является блочная матрица. $$\begin{bmatrix} a \\ b \end{bmatrix}\otimes\begin{bmatrix} c \\ d \\ e \end{bmatrix}=\begin{bmatrix} a \begin{bmatrix} c \\ d \\ e \end{bmatrix}\\[1.5em] b \begin{bmatrix} c \\ d \\ e\end{bmatrix}\end{bmatrix}=\begin{bmatrix} a c \\ a d \\ a e \\ b c \\ b d \\ be\end{bmatrix}$$
Обратите внимание, что операцию для получения тензорного произведения можно применить к любым матрицам и (или) векторам произвольных размеров. Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле:
Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле:
\begin{align} M \otimes N &=\begin{bmatrix} M_{11}~~\cdots~~ M_{1n}\\\ddots\\ M_{m1}~~\cdots~~ M_{mn}\end{bmatrix}\otimes\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\\&=\begin{bmatrix} M_{{11}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}~~\cdots~~ M_{1n}\begin{bmatrix} N_{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\\\ddots\\ M_{m1}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}~~\cdots~~ M_{mn}\begin{bmatrix} N_{{11}~~\cdots~~ N_{1q}\\\ddots\\ N_{p1}~~\cdots~~ N_{pq}\end{bmatrix}\end{bmatrix}. \end{align}
Лучше всего продемонстрировать это на конкретном примере: $$\begin{bmatrix} a\ b \\ c\ d \end{bmatrix}\otimes\begin{bmatrix} e\ f\\g\ h \end{bmatrix}=\begin{bmatrix} a\begin{bmatrix} e\ f\\ g\ h \end{bmatrix} b\begin{bmatrix} e\ f\\ g\ h \end{bmatrix}\\[1em] c\begin{bmatrix} e\ f\\ g\ h \end{bmatrix} d\begin{bmatrix} e\ f\\ g\ h \end{bmatrix}\end{bmatrix}=\begin{bmatrix} ae\ af\ be\ bf \\ ag\ ah\ bg\ bh \\ ce\ cf\ de\ df \\ cg\ ch\ dg\ dh \end{bmatrix}.
Next Steps
- Расширенные концепции матриц
- Кубит в квантовых вычислениях
- Операции с несколькими кубитами
- Нотация Дирака
- Измерения Паули
- Квантовые схемы
- Квантовые оракулы
§6. Алгебра матриц
Материал этого раздела особенно полезен тем, кто хочет хорошо освоить дисциплину «Алгебра и геометрия» и успешно сдать экзамен.
6.1. Транспонирование матриц
Для транспонирования матрицы нужно ввести какой-либо идентификатор, затем ввести оператор присваивания и в появившийся слот ввести идентификатор транспонируемой матрицы. Этот идентификатор окажется охваченным синим контуром. Не снимая контур, нажмите клавиши <Ctrl>+<1>. Введется символ транспонирования (рис. 2.19). Просмотрите результат: строки и столбцы поменяются местами.
Транспонирование изучено.
2
A= 5
1
C := AT
4 | 5 | 6 |
| Исходная матрица. | |
7 | 8 | 9 |
| Число строк | =3, |
| число столбцов | =4 | |||
−7 | 6.8 | 9.3 |
|
| |
Операция транспонирования
(клавиши <Ctrl>+<1>)
| 2 | 5 | 1 |
| Транспонированная матрица. | |
| 4 | 7 | −7 | |||
C = | Число строк | =4, | ||||
|
|
|
| число столбцов | =3 | |
| 5 | 8 | 6. |
|
|
|
| 6 | 9 | 9.3 |
|
|
|
Рис. 2.19. Транспонирование матрицы.
6.2. Умножение матрицы на скаляр
Согласно аксиомам алгебры матриц умножение на скаляр состоит в том, что на него умножается каждый элемент матрицы. Например, введите операцию умножения на скаляр как на параметр (рис. 2.20). Затем выведите идентификатор матрицы-произведения с каким-либо значением параметра. Вы увидите результат умножения.
Умножение на скаляр изучено.39
2 | 4 | 5 | 6 |
|
| Исходная |
A = 5 | 7 | 8 | 9 |
|
| матрица-сомножитель |
|
| |||||
|
|
|
|
|
|
|
1 | −7 | 6. |
|
| ||
Ввод операции умножения на скаляр D(α) := α A | ||||||
| 20 | 40 | 50 | 60 | Результат умножения | |
D(10) = |
|
|
|
|
| матрицы на скаляр 10 |
50 | 70 | 80 | 90 | |||
| 10 | −70 | 68 | 93 |
| |
Рис. 2.20. Умножение матрицы на скаляр.
6.3. Операции умножения матриц
Запомните общее простое правило проверки размерностей мат-
риц, при которых умножение возможно.
Подпишите размерности под матрицами и проследите, чтобы внут-
ренние цифры были одинаковыми Внешние цифры дадут размерность результата (рис.
Рис. 2.21. Правило размерностей для умножения матриц.
6.3.1. Умножение матрицы на вектор справа и слева. Согласно правилам матричной алгебры возможно умножение матрицы на вектор справа. В результате получится вектор, содержащий столько же строк, сколько исходная матрица. Умножение возможно только тогда, когда число столбцов матрицы-сомножителя точно совпадает с числом элементов вектора (при попытке умножить матрицы, не согласованные по размерности, выведется сообщение об ошибке – такое же, как показано на рис. 2.17).
40
Для умножения матрицы на вектор слева его нужно предварительно транспонировать. Результат умножения – строка с таким же числом элементов, сколько столбцов у исходной матрицы. Умножение слева возможно только тогда, когда число элементов вектора точно совпадает с числом строк матрицы-сомножителя. Сделайте упражнение, показанное на рис. 2.22.
Умножение матрицы на вектор изучено.
 |
|
| 2 | 4 | 5 | 6 |
|
| 1 | ||
Сомножители: матрица А и вектор В. | A := |
| 5 | 7 | 8 | 9 |
| B := |
| −1 | |
Размерности согласованы: |
|
|
| 1 | |||||||
число столбцов А = числу элементов В = 4 |
|
| 1 | −7 | 6.8 | 9.3 |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| −1 |
Формула произведения матриц: F := A B |
|
|
|
|
|
|
| ||||
Результат: произведения |
| −3 |
|
|
|
|
|
|
| ||
матрицы на вектор есть вектор | F = | −3 |
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
Попытка умножить матрицу на вектор слева. |
| 5.5 |
|
|
|
|
|
|
| ||
|
| F1 := BT A |
|
|
|
| |||||
Несогласованность размерностей: число элементов |
|
|
|
|
| ||||||
вектора НЕ равночислу строк матрицы. |
|
|
|
|
|
|
|
|
|
| |
Сообщение об ошибке. |
|
|
|
|
| The number of rows and/or column | |||||
|
|
|
|
| in these array do not match | ||||||
|
|
|
|
|
| ||||||
Умножение слева с согласованными размерностями: G := BT AT
Результат умножения — строка: | G = ( −3 −3 5. |
Рис. 2.22. Умножение матрицы на вектор справа и слева.
6.3.2.Умножение вектора на вектор (частный случай п. 6.3.1).
Размерности векторов могут не совпадать. Второй вектор-сомножитель должен транспонироваться. Результат умножения – матрица, число ее строк равно числу элементов первого вектора-сомножителя, а число столбцов – числу элементов второго вектора-сомножителя. Сделайте упражнение, показанное на рис. 2.23.
Умножение вектора на вектор изучено.
6.3.3.Скалярное произведение векторов. Операция может быть вы-
полнена только с векторами одинаковой размерности. Первый векторсомножитель нужно транспонировать. Результат умножения – скаляр. Важное замечание: Mathcad выводит результат не в форме числа, а в
форме матрицы размерности 1×1. При некоторых вычислениях нужно указывать номер элементаэтой«матрицы». Сделайте упражнение порис. 2.23.
Скалярное произведение изучено.
41
Неудачная попытка умножить матрицу на скаляр (особенности Mathcad: скалярное произведение трактуется как матрица, поэтому Mathcad считает что не соблюдается
правило размерностей)
Так нужно «обмануть» Mathcad: указать номер элемента «матрицы» — скалярного произведения (индекс вводится скобкой [ )
Рис. 2.23. Умножение вектора на вектор. Скалярное произведение векторов.
2.23. Умножение вектора на вектор. Скалярное произведение векторов.
6.3.4. Умножение матриц совершается аналогично умножению матрицы на вектор (п. 6.3.1). Важнейшее требование – соблюдение правила размерностей матриц-сомножителей. При работе со сложными формулами не поленитесь подписать размерности под матрицами, как показано на рис. 2.21: это спасет Вас от многих ошибок.
Упражнение – в разделе 6.6.
Умножение матриц изучено.
6.4. Сложение матриц
Сложение матриц может быть выполнено только с матрицами одинаковой размерности. При нашей работе с Mathcad выявилась ошибка, допущенная его авторами: Mathcad считает возможной операцию сложения матрицы со скаляром (прибавляет этот скаляр к каждому элементу матрицы). Такая операция в алгебре матриц запрещена.
Упражнение – в разделе 6.6.
Сложение матриц изучено.
42
Скалярное произведение двух матриц — Dudom
С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Матрица и число
Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:
Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т. д.
Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:
- a11 × 3 = 18. Это значение записываем в матрицу B в то место, где пересекаются столбец № 1 и строка № 1.

- a21 × 3 = 15. Мы получили элемент b21.
- a12 × 3 = –6. Мы получили элемент b12. Записываем его в матрицу B в место, где пересекаются столбец № 2 и строка № 1.
- a22 × 3 = 9. Данный результат – это элемент b22.
- a13 × 3 = 12. Данное число вносим в матрицу на место элемента b13.
- a23 × 3 = –3. Последнее полученное число – это элемент b23.
Таким образом, мы получили прямоугольный массив с числовыми элементами.
| 18 | –6 | 12 |
| 15 | 9 | –3 |
Векторы и условие существования произведения матриц
В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Векторы можно называть матрицами:
- вектор-столбец – это матрица, построенная из одного столбца;
- вектор-строчка – это матрица, которая включает в себя только одну строку.
При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.
При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
Умножение на вектор-столбец
При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.
Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:
где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.
Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.
Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.
Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:
- Вычислим y1. 1 × 4 + (–1) × 2 + 0 × (–4). Итоговое значение равно 2.
- Вычислим y2. 0 × 4 + 2 × 2 + 1 × (–4). При расчете получим 0.
- Вычислим y3. 1 × 4 + 1 × 2 + 0 × (–4). Сумма произведений указанных множителей равна 6.
- Вычислим y4. (–1) × 4 + 0 × 2 + 1 × (–4). Координата равна –8.
Умножение вектор-строки на матрицу
Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:
где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.
Произведение прямоугольных матриц
Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:
- Матрица C будет состоять из 2 строк и 3 столбцов.
- Рассчитаем элемент c11. Для этого выполним скалярное произведение строки № 1 из матрицы A и столбца № 1 из матрицы B. c11 = 0 × 7 + 5 × 3 + 1 × 1 = 16. Далее поступаем аналогичным образом, меняя только строки, столбцы (в зависимости от индекса элемента).
- c 12 = 12.
- c13 = 9.
- c21 = 31.
- c22 = 18.
- c23 = 36.
Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.
| 16 | 12 | 9 |
| 31 | 18 | 36 |
Умножение трех матриц: теоретическая часть
Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:
- Умножить сначала A и B. Результат затем умножить на C.
- Найти сначала произведение B и C. Далее матрицу A умножить на полученный результат.
Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.
Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).
Умножение трех матриц: практика
Квадратные матрицы
Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.
Ниже на рисунке представлена задача № 4, которую нам предстоит решить.
Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.
Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:
- d11 = 0 × 1 + 5 × 6 = 30;
- d12 = 0 × 4 + 5 × 2 = 10;
- d21 = 3 × 1 + 2 × 6 = 15;
- d22 = 3 × 4 + 2 × 2 = 16.
Промежуточный результат готов.
| 30 | 10 |
| 15 | 16 |
Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:
Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:
- g11 = 30 × 8 + 10 × 1 = 250;
- g12 = 30 × 5 + 10 × 3 = 180;
- g21 = 15 × 8 + 16 × 1 = 136;
- g22 = 15 × 5 + 16 × 3 = 123.
Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.
| 250 | 180 |
| 136 | 123 |
Прямоугольные матрицы
Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.
Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.
Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:
Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:
- d11 = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
- d12 = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.
Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.
| 0 | 7 |
| 0 | 19 |
| 1 | 11 |
Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:
- f11 = 2 × 0 + 6 × 0 + 1 × 1 = 1;
- f12 = 2 × 7 + 6 × 19 + 1 × 11 = 139;
- f21 = 0 × 0 + 1 × 0 + 3 × 1 = 3;
- f22 = 0 × 7 + 1 × 19 + 3 × 11 = 52.

Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.
| 1 | 139 |
| 3 | 52 |
Знакомство с прямым произведением
Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.
У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.
Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.
Определитель произведения
При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:
Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:
det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.
У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:
Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.
Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.
Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.
Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:
Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.
Числа одинаковые. Вышеуказанная теорема верна.
Ранг произведения
Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:
- перестановку местами двух параллельно лежащих рядов;
- умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
- прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.
После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.
Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.
Рассмотрим практическую задачу. Пусть нам надо определить затраты рабочего времени на одном из рабочих мест, если нам известно следующее:
1. Нормативы на выполнение каких то стандартных работ.
| сменить катридж | удалить бумагу | заменить клавиатуру | удалить вирус | поставить программу | подключить к сети | |
| Затраты | 10 | 15 | 12 | 50 | 25 | 20 |
2. По месячной отчетности нам известно сколько раз было та или иная стандартная работа
| Количество | |
| сменить катридж | 12 |
| удалить бумагу | 7 |
| заменить клавиатуру | 1 |
| удалить вирус | 3 |
| поставить программу | 21 |
| подключить к сети | 5 |
Задача решается достаточно легко, нам надо взять время затраченное например на смену катриджа, умножить его на количество таких событий, потом сделать то же самое по другой работе и в конце концов все результаты сложить между собой.
Вот то, что мы с Вами только что проделали, это и называется скалярным умножением векторов, в том случае если эти две таблицы мы представим в виде двух векторов/матриц.
Задача, как видите простая, и нет проблемы решать вручную, даже если вектора большие. Единственная загвоздка, если матрицы имеют комплексные значения. Умножать и складывать комплексные результаты, это значит подвергать Ваш ответ, человеческой невнимательности.
Если обобщить вышесказанное, то если первый вектор или матрица представлена рядом
а второй вектор рядом
То скалярное произведение равно
Созданный бот, позволит Вам правильно выполнять скалярное умножение двух матриц.
Примеры
Умножить скалярно два вектора
Очень важно оговорить что произведение скалярное, так как, два таких же вектора можно умножить обычным способом.
вторник, 14 июня 2016 г.
Скалярное произведение матриц
Книга о преобразованиях гиперкомплексных чисел после ее выхода продолжает дописываться и в ней появились интересные параграфы, один из которых представляю здесь.
2$ задает построение отношения в полной мере.
Но такое определение скалярного произведения для матриц не является коммутативным по аргументам $$ (A,B)
eq (B,A) $$ и не может быть отнесено к не квадратным матрицам и следовательно к векторам как частному случаю матрицы.НОУ ИНТУИТ | Лекция | Программная система ПараЛаб для изучения и исследования методов параллельных вычислений
< Лекция 12 || Лекция 12: 123456789101112
Аннотация: В лекции описывается программная система Параллельная Лаборатория (сокращенное наименование – ПараЛаб), которая предназначена для учебного применения студентами и преподавателями вузов в целях исследования и изучения параллельных алгоритмов решения сложных вычислительных задач в рамках лабораторного практикума по различным учебным курсам в области параллельного программирования
Ключевые слова: вычислительная задача, вычислительная система, топология сети передачи данных, операции передачи данных, windows 2000, Windows, доступ, вычислительный эксперимент, анализ, обмен данными, матрица, метод решения, топология, производительность, индикатор, затраты, меню, пункт, латентность, типовая топология, конвейерное вычисление, floating point operation, FLOPS, пропускная способность, длина маршрута, сортировка, обработка графов, размерность, алгоритм Шелла, скалярное умножение, матричные вычисления, горизонтальное разбиение, виртуальные топологии, частичный результат, MXM, коэффициентами системы, алгоритм Гаусса, графовая модель, активный эксперимент, выделенная вершина, алгоритм Прима, процессор, алгоритмы Фокса и Кэннона, информация, операции, приостановка процесса, приостановка выполнения
12.
1. Введение
Программная система Параллельная Лаборатория (сокращенное наименование – ПараЛаб) обеспечивает возможность проведения вычислительных экспериментов с целью изучения и исследования параллельных алгоритмов решения сложных вычислительных задач. Система может быть использована для организации лабораторного практикума по различным учебным курсам в области параллельного программирования, в рамках которого обеспечивается возможность:
- моделирования многопроцессорных вычислительных систем с различной топологией сети передачи данных;
- получения визуального представления о вычислительных процессах и операциях передачи данных, происходящих при параллельном решении разных вычислительных задач ;
- построения оценок эффективности изучаемых методов параллельных вычислений.
Проведение такого практикума может быть организовано на «обычных» однопроцессорных компьютерах, работающих под управлением операционных систем MS Windows 2000 или MS Windows XP (режим многозадачной имитации параллельных вычислений). Кроме режима имитации, в системе ПараЛаб может быть обеспечен удаленный доступ к многопроцессорной вычислительной системе для выполнения экспериментов в режиме «настоящих» параллельных вычислений для сопоставления результатов имитации и реальных расчетов.
В целом система ПараЛаб представляет собой интегрированную среду для изучения и исследования параллельных алгоритмов решения сложных вычислительных задач. Широкий набор имеющихся средств визуализации процесса выполнения эксперимента и анализа полученных результатов позволяет изучить эффективность использования тех или иных алгоритмов на разных вычислительных системах, сделать выводы о масштабируемости алгоритмов и определить возможное ускорение процесса параллельных вычислений.
Реализуемые системой ПараЛаб процессы изучения и исследований ориентированы на активное усвоение основных теоретических положений и способствуют формированию у обучаемых собственных представлений о моделях и методах параллельных вычислений путем наблюдения, сравнения и сопоставления широкого набора различных визуальных графических форм, демонстрируемых в ходе выполнения вычислительного эксперимента.
Основной сферой использования системы ПараЛаб является учебное применение студентами и преподавателями вузов для исследования и изучения параллельных алгоритмов решения сложных вычислительных задач в рамках лабораторного практикума по различным учебным курсам в области параллельного программирования. Система ПараЛаб может применяться также и при проведении научных исследований для оценки эффективности параллельных вычислений.
Пользователи, начинающие знакомиться с проблематикой параллельных вычислений, найдут систему ПараЛаб полезной для освоения методов параллельного программирования, опытные вычислители могут использовать систему для оценки эффективности новых разрабатываемых параллельных алгоритмов.
12.2. Общая характеристика системы
ПараЛаб — программная система, которая позволяет как проводить реальные параллельные вычисления на многопроцессорной вычислительной системе, так и имитировать такие эксперименты на одном последовательном компьютере с визуализацией процесса параллельного решения сложной вычислительной задачи.
При проведении имитационных экспериментов ПараЛаб предоставляет для пользователя возможность:
- определить топологию параллельной вычислительной системы для проведения экспериментов, задать число процессоров в этой топологии, установить производительность процессоров, выбрать характеристики коммуникационной среды и способ коммуникации ;
- осуществить постановку вычислительной задачи, для которой в составе системы ПараЛаб имеются реализованные параллельные алгоритмы решения, выполнить задание параметров задачи;
intuit.ru/2010/edi»> выбрать параллельный метод для решения выбранной задачи;- установить параметры визуализации для выбора желаемого темпа демонстрации, способа отображения пересылаемых между процессорами данных, степени детальности визуализации выполняемых параллельных вычислений;
- выполнить эксперимент для параллельного решения выбранной задачи; при этом в системе ПараЛаб может быть сформировано несколько различных заданий для проведения экспериментов с отличающимися типами многопроцессорных систем, задач или методов параллельных вычислений, для которых выполнение эксперимента может происходить одновременно (в режиме разделения времени). Одновременное выполнение эксперимента для нескольких заданий позволяет наглядно сравнивать динамику решения задачи различными методами, на разных топологиях, с разными параметрами исходной задачи. При выполнении серии экспериментов, требующих длительных вычислений, в системе имеется возможность их проведения в автоматическом режиме с запоминанием результатов для организации последующего анализа полученных данных;
intuit.ru/2010/edi»> накапливать и анализировать результаты выполненных экспериментов ; по запомненным результатам в системе имеется возможность построения графиков зависимостей характеристик параллельных вычислений ( времени решения, ускорения, эффективности ) от параметров задачи и вычислительной системы.Одной из важнейших характеристик системы является возможность выбора способов проведения экспериментов. Эксперимент может быть выполнен в режиме имитации, т.е. проведен на одном процессоре без использования каких-либо специальных программных средств типа библиотек передачи сообщений. Кроме того, в рамках системы ПараЛаб обеспечивается возможность проведения реального вычислительного эксперимента.
При построении зависимостей временных характеристик от параметров задачи и вычислительной системы для экспериментов, выполненных в режиме имитации, используются теоретические оценки в соответствии с имеющимися моделями параллельных вычислений (см.
, например, [ [ 2 ] , [ 94 ] ]). Для реальных экспериментов на многопроцессорных вычислительных системах зависимости строятся по набору результатов проведенных вычислительных экспериментов.
Важно отметить, что в системе ПараЛаб обеспечена возможность запоминания результатов проведенных экспериментов в специальной области памяти. Запомненные результаты позволяют выполнить анализ полученных данных; по имеющейся информации любой из проведенных ранее экспериментов может быть восстановлен для повторного выполнения или продолжения расчетов.
Реализованные таким образом процессы изучения и исследований позволят усвоить теоретические положения и помогут формированию представлений о методах построения параллельных алгоритмов, ориентированных на решение конкретных прикладных задач.
intuit.ru/2010/edi»>Демонстрационный примерДля выполнения примера, имеющегося в комплекте поставки системы:
- выберите пункт меню Начало и выполните команду Загрузить ;
- выберите строку first.prl в списке имен файлов и нажмите кнопку Открыть ;
- выберите пункт меню Выполнение и выполните команду В активном окне.
В результате этих действий на экране дисплея будет представлено окно для выполнения вычислительного эксперимента (рис. 12.1). В этом окне демонстрируется решение задачи умножения матриц при помощи ленточного алгоритма.
В области «Выполнение эксперимента» представлены процессоры вычислительной системы и структура линий коммутации.
Рядом с каждым процессором изображены те данные, которые он обрабатывает в каждый момент выполнения алгоритма (для ленточного алгоритма умножения матриц это несколько последовательных строк матрицы А и несколько последовательных столбцов матрицы В ). При помощи перемещающихся прямоугольников (пакетов) желтого цвета изображается обмен данными, который осуществляют процессоры.
В области «Результат умножения матриц» изображается текущее состояние матрицы – результата умножения. Поскольку результатом перемножения полос исходных матриц А и В является блок матрицы С, получаемая результирующая матрица имеет блочную структуру. Темно-синим цветом обозначены уже вычисленные блоки, голубым цветом выделены блоки, еще подлежащие определению.
В списке «Выполняемая задача» представлены параметры решаемой задачи: название, метод решения, объем исходных данных. В списке » Вычислительная система » приводятся атрибуты выбранной вычислительной системы: топология, количество и производительность процессоров, характеристики сети.
Рис. 12.1. Окно вычислительного эксперимента
Ленточный индикатор «Эксперимент» отображает текущую стадию выполнения алгоритма. В строках «Общие затраты времени» и «Затраты на передачу данных» представлены временные характеристики алгоритма.
После выполнения эксперимента (восстанавливается главное меню системы) можно завершить работу системы. Для этого выберите пункт меню Архив и выполните команду Завершить.
Дальше >>
< Лекция 12 || Лекция 12: 123456789101112
Умножение матриц | это… Что такое Умножение матриц?
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.
Содержание
- 1 Определение
- 2 Иллюстрация
- 3 Мотивировка
- 4 Свойства
- 5 Обратная матрица
- 6 Алгоритмы быстрого перемножения матриц
- 7 См.
также
- 8 Литература
- 9 Примечания
Определение
Пусть даны две прямоугольные матрицы и размерности и соответственно:
Тогда матрица размерностью называется их произведением:
где:
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Следует заметить, что из существования произведения вовсе не следует существование произведения
Иллюстрация
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B.
Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.
Значения на пересечениях отмеченных кружочками будут:
В общем случае, произведение матриц не является коммутативной операцией. К примеру:
Элемент произведения матриц приведённых выше вычисляется следующим образом
Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент на пересечении строки и столбца результирующей матрицы является скалярным произведением -й строки первой матрицы и -го столбца второй матрицы.
Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Мотивировка
Описанное правило матричного умножения прозрачнее всего мотивируется исходя из умножения вектора на матрицу.
Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A дает выражение компонент вектора v’ = Av:
-то есть линейный оператор оказывается представлен матрицей, векторы — векторами-столбцами, а действие оператора на вектор — матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц — вектор-столбец — имеет размер 1хn).
(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом — элементы матрицы перехода к новому базису).
Далее, рассмотрев последовательное действие на вектор двух операторов: сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), имеем, дважды применив нашу формулу:
откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по рецепту произведения соответствующих матриц:
Определенное таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (дает простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).
Свойства
Сочетательное свойство:
Распределительное свойство:
- .
Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:
Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:
Если и — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
Умножение матриц в целом некоммутативно:
Если , то матрицы и называются перестановочными или коммутирующими между собой.
Определитель и след произведения не зависят от порядка умножения матриц:
Обратная матрица
Основная статья: Обратная матрица
Квадратная матрица называется неособенной (невырожденной), если она имеет единственную обратную матрицу такую, что выполняется условие:
В противном случае матрица называется особенной (вырожденной).
Матрица порядка является невырожденной в том и только в том случае, если в этом случае есть квадратная матрица того же порядка
где — алгебраическое дополнение элемента в определителе
Алгоритмы быстрого перемножения матриц
Сложность вычисления произведения матриц по определению составляет Θ(n3), однако существуют более эффективные алгоритмы[1], применяющиеся для больших матриц.
- Алгоритм Штрассена (1969)
- Первый алгоритм быстрого умножения матриц был разработан В. Штрассеном[2] в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки. На каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате сложность этого алгоритма составляет . Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, численная неустойчивость и большой объём используемой памяти.
- Разработано большое количество алгоритмов на основе метода Штрассена, которые улучшают его численную устойчивость и уменьшают объём используемой памяти.
- Алгоритм Пана (1978)
- В 1978 Пан[3] предложил свой метод умножения матриц, сложность которого составила Θ(n2.78041).
- Алгоритм Бини (1979)
- В 1979 группа итальянских учёных во главе с Бини[4] разработала алгоритм умножения матриц с использованием тензоров.
Его сложность составляет Θ(n2.7799).
- Алгоритмы Шёнхаге (1981)
- В 1981 Шёнхаге[5] представил метод, работающий со сложностью Θ(n2.695), который он назвал частичным матричным умножением. Позже ему удалось получить оценку Θ(n2.6087).
- Затем Шёнхаге создал метод, названный методом прямых сумм, сложность которого составляет Θ(n2.548). Романи сумел понизить оценку до Θ(n2.5166), а Пан — до Θ(n2.5161).
- Алгоритм Копперсмита — Винограда (1990)
- В 1990 Копперсмит и Виноград[6] опубликовали алгоритм, умножающий матрицы со сложностью O(n2.3727).[7] Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день алгоритм Копперсмита-Винограда является наиболее асимптотически быстрым, но он эффективен только на очень больших матрицах и поэтому не применяется.
- Алгоритмы с использованием теории групп (2003)
- В 2003 Кох и др. рассмотрели в своих работах[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали возможность существования алгоритмов умножения матриц со сложностью Θ(n2)[9].
См. также
- Произведение Кронекера
Литература
- Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 392—394..
Примечания
- ↑ Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983 — 1985 гг.: Пер. с англ. — М.: Мир, 1988 — В.Б. Алекссев. Сложность умножения матриц. Обзор.
- ↑ Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969
- ↑ Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations.
— Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
- ↑ Bini D., Capovani M., Lotti G., Romani F. — complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
- ↑ Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251–280, 1990.
- ↑ Williams, Virginia (2011), Breaking the Coppersmith-Winograd barrier.
- ↑ Group-theoretic Algorithms for Matrix Multiplication
- ↑ Toward an Optimal Algorithm for Matrix Multiplication
Узнаем как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц
С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц.
Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Матрица и число
Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:
bij = e × aij.
Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т. д.
Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:
- a11 × 3 = 18. Это значение записываем в матрицу B в то место, где пересекаются столбец № 1 и строка № 1.
- a21 × 3 = 15. Мы получили элемент b21.
- a12 × 3 = –6. Мы получили элемент b12. Записываем его в матрицу B в место, где пересекаются столбец № 2 и строка № 1.
- a22 × 3 = 9. Данный результат – это элемент b22.
- a13 × 3 = 12. Данное число вносим в матрицу на место элемента b13.
- a23 × 3 = –3. Последнее полученное число – это элемент b23.
Таким образом, мы получили прямоугольный массив с числовыми элементами.
18 –6 12 15 9 –3 Векторы и условие существования произведения матриц
В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца.
Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Векторы можно называть матрицами:
- вектор-столбец – это матрица, построенная из одного столбца;
- вектор-строчка – это матрица, которая включает в себя только одну строку.
При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.
При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т.
е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
Умножение на вектор-столбец
При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.
Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:
y1 = a11x1 + a12x2 + … + a1nxn,
y2 = a21x1 + a22x2 + … + a2nxn,
…………………………………,
ym = am1x1 + am2x2 + … + amnxn,
где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.
Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.
Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:
- Вычислим y1. 1 × 4 + (–1) × 2 + 0 × (–4). Итоговое значение равно 2.
- Вычислим y2. 0 × 4 + 2 × 2 + 1 × (–4). При расчете получим 0.
- Вычислим y3. 1 × 4 + 1 × 2 + 0 × (–4). Сумма произведений указанных множителей равна 6.
- Вычислим y4. (–1) × 4 + 0 × 2 + 1 × (–4). Координата равна –8.
Умножение вектор-строки на матрицу
Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно.
Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:
yk = a1kx1 + a2kx2 + … + amkxm,
где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.
Произведение прямоугольных матриц
Это вычислительное действие может показаться сложным.
Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:
- Матрица C будет состоять из 2 строк и 3 столбцов.
- Рассчитаем элемент c11. Для этого выполним скалярное произведение строки № 1 из матрицы A и столбца № 1 из матрицы B. c11 = 0 × 7 + 5 × 3 + 1 × 1 = 16. Далее поступаем аналогичным образом, меняя только строки, столбцы (в зависимости от индекса элемента).
- c12 = 12.
- c13 = 9.
- c21 = 31.
- c22 = 18.
- c23 = 36.
Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.
16 12 9 31 18 36 Умножение трех матриц: теоретическая часть
Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:
- Умножить сначала A и B. Результат затем умножить на C.
- Найти сначала произведение B и C. Далее матрицу A умножить на полученный результат.
Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна.
Должны существовать произведения A × B и B × C.
Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).
Умножение трех матриц: практика
Квадратные матрицы
Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.
Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.
Ход решения.
Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:
- d11 = 0 × 1 + 5 × 6 = 30;
- d12 = 0 × 4 + 5 × 2 = 10;
- d21 = 3 × 1 + 2 × 6 = 15;
- d22 = 3 × 4 + 2 × 2 = 16.
Промежуточный результат готов.
30 10 15 16 Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:
- g11 = 30 × 8 + 10 × 1 = 250;
- g12 = 30 × 5 + 10 × 3 = 180;
- g21 = 15 × 8 + 16 × 1 = 136;
- g22 = 15 × 5 + 16 × 3 = 123.
Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.
250 180 136 123 Прямоугольные матрицы
Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.
Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение.
Приступим к решению задачи.
Ход решения.
Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:
- d11 = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
- d12 = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.
Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.
0 7 0 19 1 11 Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:
- f11 = 2 × 0 + 6 × 0 + 1 × 1 = 1;
- f12 = 2 × 7 + 6 × 19 + 1 × 11 = 139;
- f21 = 0 × 0 + 1 × 0 + 3 × 1 = 3;
- f22 = 0 × 7 + 1 × 19 + 3 × 11 = 52.
Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.
1 139 3 52 Знакомство с прямым произведением
Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.
У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.
Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок.
Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.
Определитель произведения
При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц».
Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:
det A = a11 × a22 – a12 × a21.
Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:
det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.
У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:
det A = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.
Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.
Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.
Ход решения.
Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1.
Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:
- c11 = 2 × 4 + 3 × 1 = 11;
- c12 = 2 × 5 + 3 × 2 = 16;
- c21 = 1 × 4 + 1 × 1 = 5;
- c22 = 1 × 5 + 1 × 2 = 7.
Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.
Ранг произведения
Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:
- перестановку местами двух параллельно лежащих рядов;
- умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
- прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.
После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.
Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись.
Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.
Умножить матрицу на вектор в R
Просмотреть обсуждение
Улучшить статью
Сохранить статью
- Последнее обновление: 26 мар, 2021
Читать Обсудить Посмотреть обсуждение
Улучшить статью
Сохранить статью
Матрица — это двумерная структура, а вектор — одномерная структура.
В этой статье мы собираемся умножить данную матрицу на заданный вектор, используя язык программирования R. Умножение между ними происходит, когда элементы вектора умножаются на элементы матрицы по столбцам.
Подход:
- Создать матрицу
- Создать вектор
- Умножить их
- Показать результат.
Метод 1: Наивный метод
Когда структуры готовы, мы напрямую умножаем их, используя оператор умножения (*).
Пример:
R
VECTOR1 =C(1,2,3,4,5,6,7,8,9,11,11,12)
MATRIX1 <-Матрикс(Vector1, NROW = 2, NCOL = 6)
MUL_VEC =
MUL_VEC =
7.
(matrix1*mul_vec)Output:
Example 2:
R
vector1=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)
матрица1 <-matrix(vector1, nrow=4,ncol=4)
(matrix1)
mul_vec=c(1,2,3,4)
печать("Результат")
печать(matrix1*mul_vec)Output:
Example 3:
This code has both matrix and vector has equal size
R
vector1 =c(1,2,3,4)
matrix1 <-matrix(vector1,nrow=2,ncol=2)
( матрица1)
MUL_VEC =C(1,2,3,4)
(
(
PRIN(matrix1*mul_vec)Вывод:
Метод 2: Используя метод развертки()
, мы можем использовать методы развертки() для умножения вектора на матрицу2.
Функция развертки () используется для применения операции «+ или – или «*» или «/» к строке или столбцу в данной матрице.
Синтаксис:
развертка(данные, MARGIN, FUN)
Параметр:
- data=input matrix
- MARGIN означает строку 2; MARGIN = 1 означает столбец.
- Веселье: операция, которая должна быть выполнена (например, + или - или * или /)
Здесь мы выполняем « *». матрица1 <-
матрица(c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15),
, by row= =True)
Печать(MATRIX1)
Печать("-------------------------------------------------
вектор1 <-c(1,2,3,4,5)
печать0058(развертка(matrix1, MARGIN=2,vector1, `*`))
печать("-----------------")
Vector2 <-C(1,2,3)9003
ПЕЧАТА., `*`))
Вывод:
Пример 2:
R
MATRIX1 <-MATRIX(C(1,2,3,4,4,5,6 8,6 8.7),C(1,2,3,4,4,5,6 8,68,C(1,2,3,4,4,6,68C(1,2,3,4,4,6,68C(1,2,3,4,4,6,68C(1,2,3,4,4,6,68C(1,2,3,4,4,6,
NROW = 2, Byrow =True)
Печать(MATRIX1)
. Печать(
7778(
7778(
77(
7(
7(
7(
7.----"
)
Vector1 <-C(1,2,3,4)
Печать(Sweep(MATRIX1, MARINE = 2, 2, 2, 2, 2, 1, 1, `‘ veer1).
Печать(»-------------------")
Vector2 <-C(1.2 <-C(1.2 <-C(1.2 <-C(1.2 <-C(1.2 <-C(1.2. )
печать(развертка(Matrix1, Margin = 1, Vector2, `*`))Выход:
Multiclickation and Lineear Combination Произведение двух матрицы можно рассматривать как результат взятия линейные комбинации их строк и столбцы.
Такой способ интерпретации матричного умножения часто помогает понимать важные результаты матричной алгебры.
Table of contents
Terminology
Post-multiplying a matrix by a vector
Pre-multiplying a matrix by a vector
Post-multiplying a matrix by another matrix
Pre -умножение матрицы на другую матрицу
Терминология
Рассмотрим две матрицы а также и их продукт . Помните, что умножение матриц не является коммутативным, так что не то же самое, что .
Когда мы выполняем умножение мы скажи это:
предварительно умножает , или же предварительно умножается на ;
пост-умножает , или же умножается на .
В качестве альтернативы мы говорим, что:
левое умножение , или же умножается слева на ;
право-умножает , или же умножается справа на .
Пост-умножение матрицы на вектор
Начнем со случая, когда матрица постумножается на вектор.
Предложение Позволять быть матрица и а вектор. Тогда где обозначает -й столбец .
Доказательство
Продукт это вектор. Применяя определение матричного произведения, -й запись находится в бытьЭто также является -й ввод линейной комбинации
Другими словами, пост-умножение матрицы по вектору это то же самое, что взять линейную комбинацию столбцов , где коэффициенты линейной комбинации являются элементами .
Пример Пусть и Тогда, формула умножения двух матриц даетПо вычисляя тот же продукт как линейную комбинацию столбцов , мы получить
Предварительное умножение матрицы на вектор
Теперь обсудим случай, когда матрица предварительно умножается на вектор.
Предложение Позволять быть вектор и а матрица. Тогда где обозначает -й ряд .
Доказательство
Продукт это вектор. Применяя определение произведения матриц, получаем -й элемент как который равно -й запись
Таким образом, предварительное умножение матрицы по вектору это то же самое, что взять линейную комбинацию строк . Коэффициенты комбинации являются элементами .
Пример Пусть и Тогда, формула умножения двух матриц даетПо вычисляя тот же продукт как линейную комбинацию строк , мы получить
Пост-умножение матрицы на другую матрицу
Давайте теперь рассмотрим более общий случай, когда матрица постумножается.
по другой матрице.
Предложение Позволять быть матрица и ан матрица. Затем -й столбец продукта это здесь обозначает -й столбец .
Доказательство
Применяя определение матрицы умножение, т. -й запись находится в бытьЭто также является -й запись вектора-столбца
Итак -й столбец продукта является линейной комбинацией столбцов , с коэффициентами, взятыми из -й столбец .
Пример Пусть и Тогда, формула умножения двух матриц даетПо вычисление первого столбца как линейная комбинация столбцов , мы получить второй столбец можно вычислить как
Предварительное умножение матрицы на другую матрицу
В предыдущем разделе столбцы интерпретировались как линейные комбинации столбцов . Теперь интерпретируем ряды как линейные комбинации строк .
Предложение Позволять быть матрица и ан матрица. Затем -й ряд продукта это здесь обозначает -й ряд .
Доказательство
Применяя определение матрицы умножение, т. -й запись находится в бытьЭто также является -й запись вектора-строки
Итак -й ряд продукта представляет собой линейную комбинацию строк , с коэффициентами, взятыми из -й ряд .
Пример Рассмотрим две матрицы а потом, формула умножения двух матриц даетПо вычисление первой строки в виде линейной комбинации строк , мы получить вторая строка может быть вычислена как
Как указывать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Умножение матриц и линейные комбинации», Лекции по матричной алгебре. https://www.statlect.
com/matrix-алгебра/matrix-multiplication-and-linear-combinations.
Как сделать умножение матриц
Изображение ARENA Creative на Shutterstock
Линейная алгебра может быть сложной для изучения. Однако очень важно, чтобы вы понимали это, а не просто запоминали, как выполняется каждая операция в линейной алгебре.
Понимание того, почему и как выполняются операции в линейной алгебре, требует логики и практики. Умножение матриц — это лишь одна из операций, охватываемых при изучении линейной алгебры в колледже, и для сдачи экзаменов требуется понимание того, как выполнять эту операцию вручную.
Давайте посмотрим, как выполнить матричное умножение между матрицей и скалярным числом, вектором или матрицей.
Что такое умножение матриц?
Линейная алгебра — относительно новая область изучения математики. В 1812 году французский математик Жак Филипп Мари Бине первым описал умножение матриц.
Однако некоторые ученые ставят эту дату под сомнение, поскольку первая матрица не была полностью описана до 1857 года Артуром Кейли в Великобритании.
Чтобы понять, насколько «молодой» является линейная алгебра, приведем теорему Пифагора в геометрии, которая была описана между 400 и 800 годами до нашей эры.
Матрица — это прямоугольный массив чисел или выражений. Он расположен в строках и столбцах. Количество строк представлено «m», а количество столбцов — «n».
Каждый элемент в матрице может быть представлен как «ai,j», где «j» увеличивается по отношению к столбцу, а «i» увеличивается по количеству строк, как вы можете видеть на рисунке ниже.
Фото кредит
Как умножить матрицу на число
Умножить матрицу на число очень просто. Просто каждый элемент в матрице умножается на число. Стратегия не меняется в зависимости от количества строк и столбцов.
Когда число умножается на матрицу, это называется скалярным умножением.
Скаляр — это величина, полностью описываемая одной величиной или числовым значением. В приведенном выше примере 3 является скаляром.
Как умножить матрицу на матрицу
Умножение между матрицами более сложное. Хотя вычисление результата умножения матриц вручную, вероятно, нецелесообразно в реальном мире, понимание процесса углубит ваше понимание линейной алгебры.
При умножении матрицы на матрицу количество столбцов в первой матрице должно равняться количеству строк во второй матрице, иначе операция не может быть определена.
Результатом будет матрица с m столбцами и p строками. Это представлено следующим уравнением:
[mn ][np] [mp]
Чтобы вычислить результат умножения матрицы на матрицу, вычислите «точечный продукт» каждой строки и столбца.
Скалярное произведение — это алгебраическая операция, при которой два списка чисел (векторов), равных по длине, возвращают одно число.
Скалярный продукт также называется скалярным произведением, поскольку в результате вычисления получается одно число.
Матрицы разных размеров можно перемножать. Здесь у нас есть матрица A с «m» строками и «n» столбцами и матрица B с «n» строками и «p» столбцами.
Результатом матричного произведения является матрица C с m строками и p столбцами.
Для вычисления каждого элемента в матрице C используются приведенные ниже формулы.
Давайте сделаем пример. Здесь у нас есть матрица с 2 строками и 3 столбцами, умноженная на матрицу с 3 столбцами и 2 строками. В результате получится матрица с 2 строками и 2 столбцами.
Чтобы вычислить c1,1, мы должны определить скалярное произведение 1-й строки 1-й матрицы и 1-го столбца 2-й матрицы.
Формула выглядит следующим образом:
c1,1=2 (-1) +(-2) 3 +7 1 =-1
Аналогично вычисляется c1,2 путем определения скалярного произведения 1-го строку и 2-й столбец 2-й матрицы.
Формула выглядит следующим образом:
c1,2=2 5 +(-2)7 +7 9 =59
Для расчета c2,1 и c2,2 используются следующие уравнения:
c2,1=1 (-1) +8 3 +4 1 =27
c2,2=1 5 +8 7 +4 9 =97
Произведение матрицы на матрицу:
Как умножить матрицу на вектор
Вектор — это матрица только с одной строкой или только с одним столбцом. Умножение матрицы на вектор выполняется аналогично процедуре умножения матрицы на матрицу.
Здесь у нас есть вектор x=(4,-2,1), и мы умножаем его на матрицу A.
Вычислите c1,1, определив скалярное произведение 1-й строки, умноженное на вектор.
См. приведенное ниже уравнение для расчета c1,1.
c1,1=64 +2(-2) +41=24
Аналогично, вот уравнения для расчета c2,1 и c3,1.
c2,1 =-14 +4(-2) +31 =-9
c3,1 =-24 +9(-2) +31 =-23
Решение умножения матрицы на вектор выглядит следующим образом следующим образом:
В целом, умножение матрицы на вектор следует той же процедуре, что и умножение матрицы на матрицу.
Тем не менее, важно соблюдать соглашения об именах.
Каков порядок действий?
В отличие от умножения действительных чисел, умножение матриц не является коммутативным. Например, результат не зависит от порядка элементов.
Например, в приведенном ниже расчете:
123=312=36
Обе части уравнения равны 36 независимо от порядка чисел. Это верно не для всех матриц. Коммутативные матрицы возникают, когда матрица умножается сама на себя или когда она умножается на единичную матрицу.
Например, у нас есть матрица A, умноженная на матрицу B, в результате получается матрица C.
Но если у нас есть матрица B, умноженная на матрицу A, конечным результатом будет другая матрица D.
Давайте сравним вычисление первого скалярного произведения, чтобы понять, почему существует разница.
При вычислении первого значения c1,1 используется формула: 23 =0
Из того, как вычисляется скалярное произведение, ясно, что порядок имеет значение при умножении матриц.
Обратите внимание, как подсвечиваются разные числа в матрицах при переключении порядка умножения матриц.
Как применять умножение матриц к реальным задачам
Умножение матриц имеет применение в реальном мире, даже если мы не можем думать об этих ситуациях как об умножении матриц.
Например, умножение матриц можно использовать для расчета прибыли магазина.
В таблице ниже указана стоимость каждого предмета, выставленного на продажу в магазине одежды.
В таблице ниже показано, сколько рубашек, свитеров и брюк было продано в понедельник, вторник и среду.
Прибыль в понедельник можно рассчитать по следующей формуле.
Прибыль за понедельник = Цена проданных рубашек + Цена проданных свитеров и свитеров
+ Цена проданных брюк Брюки
=122 + 304 + 604 =384
Знакомо? Мы только что рассчитали скалярный продукт для продаж в понедельник.
Представим эти данные в виде матрицы и вектора.
После умножения матриц мы можем рассчитать продажи в понедельник, вторник и среду ниже.
Приведенное ниже уравнение можно использовать для расчета прибыли во вторник.
Прибыль во вторник = c2,1=412 +1530 +1160 =1158
Аналогично, прибыль в среду можно рассчитать по приведенной ниже формуле.
Прибыль среды = c3,1= 412 + 230 + 160 = 168
Результирующая матрица 1 на 3 приведена ниже.
Матрицы и их операции также играют фундаментальную роль в понимании логики между массивами в программировании. Матрицы хранятся в виде массива массивов в программировании. Их также называют многомерными массивами.
Линейная алгебра лежит в основе многих передовых математических инструментов, таких как ряды Фурье и решение линейных уравнений. Он также играет ключевую роль в других областях, таких как статистика.
Краткий обзор специальных матриц
Некоторые матрицы неоднократно появляются в ходе исследований, и им присвоены определенные имена, чтобы их можно было легко идентифицировать.
Например, в нулевой матрице все значения просто равны 0.
Единичная матрица — это еще одна специальная матрица. Это квадратная матрица, в которой количество столбцов и строк равно. Диагональные значения, где «m» и «m» равны, равны 1.
Конкретные условия для единичной матрицы обозначаются:
Квадратная матрица, умноженная на единичную матрицу, не приведет к изменению квадратной матрицы. Например:
Для демонстрации расчета скалярного произведения первого значения используется следующее уравнение:
c1,1=91 + 40 + (-2)0 = 9
Продолжайте практиковаться базовое упражнение по линейной алгебре и является обязательным курсом для большинства специальностей STEM.
Освоение этой операции позволяет учащимся глубже понять линейную алгебру.
Убедитесь, что вы практикуете умножение матриц вручную. Легко пропустить число при вычислении скалярного произведения во время экзамена или теста. Практика должна помочь вам снизить вероятность ошибок, которых можно было бы избежать, если бы вы лучше знали метод расчета.
Если у вас проблемы с линейной алгеброй, онлайн-курсы охватывают различные операции и линейные преобразования, чтобы вы были готовы к экзаменам. Эти курсы знакомят с новыми обозначениями и абстрактными способами мышления, которые могут быть чужды некоторым студентам.
Чтобы получить индивидуальную помощь в умножении матриц, вы можете найти лучших преподавателей на HeyTutor.
Умножение вектора на матрицу
где r и s a (действительные) скаляры и x , y ∈R 2 . При работе над такими преобразований английский математик Артур Кэли (1821-1895) разработал в 1857 г.
Матричная алгебра.
Из определений сложения векторов и покомпонентного умножения на скаляр ,
(2) x = (x 1 ,x 2 ) = x 1 (1,0) + x 2 (0,1) Применить теперь (1) к (2): f( x ) = x 1 f(1,0) + x 2 f(0,1), где f(1,0), что правильнее записывать как f((1,0)), это результат применения f к вектору (1,0). Похожий замечание справедливо для f(0,1) и f(x 1 ,x 2 ) в следующем. Пусть f(1,0)=(f 11 ,f 21 ) и f(0,1)=(f 12 , ф 22 ). затем
(3) F ( x ) = F (x 1 , x 2 ) = x 1 (F 11 , F 21 ) + x 2 (F 12 ) + x 2 (F 12 ) + x 2 (F 12 ) + x 2 (F 12 ) + x 2 (F 12 ) + x 2 (F 12 ). ) = (x 1 f 11 + x 2 f 12 , x 1 f 21 + x 2 f 32)
Предположим, что g — другое линейное преобразование и g(1,0)=(g 11 , g 21 ) и g(0,1)=(g 12 , g 22 ). Затем по (3),
(4) g(f( x )) = ((x 1 f 11 + x 2 f 12 )g 11 + (x 1 f 21 + x 2 f 22 ) G 12 , (x 1 F 11 + x 2 F 12 ) G 12 + (x 1 ) F 2 22 21112 2 21112 2 21112 2 21912 21112 2 21112 2 21112 2 21112 2 21112 2 21112 2 21112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112 2112. )г 22 ) или после перегруппировки
(4') G (F ( x ) = (x 1 (F 11 G 11 + F 21 G 12 ) + x 2 (F 12 ) + x 2 (F 12 ) + x 2 (F 12 ). 22 G 12 ), x 1 (F 11 G 12 + F 21 G 22 ) + x 2 (F 22 22 ) + x 2 (F 22 22 ) + x 2 (F 22 ) + x 2 G 22 22 ) + x 2 G 22 ). г 22 ))
Мы видим, что композиция g(f( x )) двух линейных преобразований, в свою очередь, является линейным. Кроме того,
(5) g(f(1,0)) = (f 11 g 11 + f 21 g 12 , f 11 g 21 + f 21 g), g(f(0,1)) = (f 12 g 11 + f 22 g 12 , f 12 g 21 + f 9 22 g) 232 g) Теперь пара чисел x 1 ,x 2 может быть записан как вертикальный (матрица 2x1) или горизонтальный (матрица 1x2) вектор .
Учитывая ограничения HTML, горизонтальное соглашение реально спасает жизнь и используется до сих пор. Однако я должен отметить, что вертикальные обозначения гораздо более распространены. В зависимости от обозначений (3) и (5) можно по-разному переписать в векторно-матричном формате:
х (х 1 , х 2 ) F f( x ) x F F x g(f( x )) x FG GF x Мы пришли к тому, что линейное преобразование векторного пространства может быть выражено как произведение матрицы и вектора. Представлена композиция двух линейных преобразований произведением соответствующих матриц.
Заявление является более общим, чем то, что было показано на самом деле. р 2 известно как арифметическое векторное пространство. Набор всех комбинаций rsin(x) + scos(x), где x изменяется в течение некоторого интервала, — еще один пример двумерного вектора. пространство, элементы которого выглядят иначе, чем элементы R 2 . Однако, как мы уже отмечали, векторные пространства той же размерности изоморфны , и один из способов установить соответствие ( изоморфизм ) между ними заключается в выборе оснований и идентификации их векторы с кортежами координат. Например, вектор rsin(x) + scos(x) может быть идентифицирован с упорядоченной парой (r,s). При этом соответствии sin(x) и cos(x) появляются как (1,0) и (0,1) соответственно.
Таким образом, выбор оснований в векторных пространствах приводит к идентификации векторов с кортежами координат (горизонтальные или вертикальные). Горизонтальные кортежи обычно называются векторами-строками , тогда как вертикальные они известны как вектора-столбца .
Матрицы появляются как представляющие линейные преобразования для фиксированной пары оснований. Чтобы получить результат применения преобразования к вектору, умножьте соответствующую матрицу и кортеж. Произведение двух матриц представляет собой композицию (произведение) двух преобразований (функций)
- H.Eves, Великие моменты в математике после 1650 года , MAA, 1983
Что можно умножить?
- Что такое умножение?
- Умножение уравнений
- Умножение функций
- Умножение матриц
- Умножение чисел
- Пасьянс "Кошка" и теория групп
- Умножение перестановок
- Умножение наборов
- Умножение векторов
- Умножение вектора на матрицу
- Векторное пространство и пространства со скалярным произведением
- Таблицы сложения и умножения в различных основаниях
- Умножение точек на окружности
- Умножение точек на эллипсе
|Контакты| |Главная страница| |Содержание| |Геометрия| |Вверх|
Copyright © 1996-2018 Александр Богомольный69989803
Linear Transformations и размножение матрицы
Что представляет собой линейные преобразования?
Что такое векторное пространство?
Как выполнить умножение матриц?Этот пост является продолжением предыдущего поста, что является обязательным условием для прочтения этого.
В последнем посте я рассмотрел базисные векторы, интервалы и линейные комбинации.
Концептуализация линейных преобразований
A Линейное преобразование — это просто функция, функция $f(x)$. Он принимает ввод, число x, и дает нам вывод для этого числа. Однако в линейной алгебре мы используем букву T для преобразования.
$$T(input_x) = output_x$$
Или с векторными координатами на входе и соответствующими векторными координатами на выходе
$$ \begin{bmatrix} х_{ввод}\\ у_ {ввод} \end{bmatrix} = \begin{bmatrix} х_{выход}\\ у_ {выход} \end{bmatrix} $$
Мы могли бы думать о преобразовании в терминах преобразования вектора, когда мы существенно преобразуем координаты вектора или даже базисные векторы для некоторого вектора. Идея состоит в том, что мы даем некоторые векторные координаты в качестве входных данных, а затем получаем выходные данные из этих векторных координат.
Каждый раз, когда мы это делаем, мы можем визуализировать преобразование, представляя вектор, перемещающийся из одного положения в другое — каждый вектор в пространстве перемещается с преобразованием.
Преимущество трансформаций в том, что нам нужно всего
- Координаты любого вектора в нашем пространстве и
- Базисные векторы
Затем, если мы сделаем преобразование, мы преобразуем все векторы в нашем пространстве вместе с базисными векторами. Это означает, что нам просто нужно найти преобразованные базисные векторы, чтобы вычислить любой преобразованный вектор в нашем пространстве.
Как выполнить линейное преобразование?
Мы можем написать подобное общее уравнение для вектора $\vec{v}$ с векторными координатами $\begin{bmatrix}x\\y\end{bmatrix}$ и базисными векторами $\hat{i} = \ begin{bmatrix}i_1\\i_2\end{bmatrix}$ и $\hat{j} = \begin{bmatrix}j_1\\j_2\end{bmatrix}$
$$ T\left(\begin{bmatrix}x\\y\end{bmatrix}\right)= х \ начало {bmatrix} я_1\\ i_2 \end{bmatrix} + у \ начало {bmatrix} j_1\\ j_2 \end{bmatrix} $$
Таким образом, это означает, что нам просто нужно заменить $\hat{i}$ и $\hat{j}$ после преобразования, и мы можем просто выполнить умножение, как описано в Основах линейной алгебры 1.
An Альтернативный способ представления вышеизложенного и, возможно, более интуитивный способ численного понимания преобразования будет примерно таким:
$$ преобразовано _ {\ vec {v}} = x (преобразовано _ {\ hat {i}}) + y (преобразовано _ {\ hat {j}}) $$
Чтобы получить преобразованный вектор (выходной), мы берем координаты входного вектора x и y и масштабируем с преобразованными базисными векторами $\hat{i}$ и $\hat{j}$. Тогда то, что x и y заканчиваются, является преобразованными векторными координатами для вектора $\vec{v}$.Что происходит численно
— т.е. что происходит между вводом и выводом?Все, что происходит численно, заключается в том, что мы определяем правило, которое диктует, как мы преобразовываем любой вектор — именно так вы выполняете численное преобразование. Такое правило может быть неправильным, но держись за меня; Так что же может быть за правило? Часто бывает так, что мы определяем, в какое измерение должно преобразоваться наше текущее векторное пространство.
9{2}$ означает все действительные числа в двумерном пространстве.
Прежде чем двигаться дальше, мы не коснулись умножения векторов. Так как же нам перемножать матрицы? Позвольте мне расширить то, что вы узнали в Основах линейной алгебры 2 — масштабирование вектора по числу.
Допустим, у нас есть матрица A , определенная как таковая, где a, b, c и d — действительные числа
$$ А = \begin{bmatrix} а и б\\ CD \end{bmatrix} $$
И вектор $\vec{v}$, определенный как
$$ \vec{v} = \begin{bmatrix} Икс\\ у \end{bmatrix} $$
Затем мы могли бы перемножить их вместе, точно так же, используя векторное умножение:
$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} Икс\\ у \end{bmatrix} = х \begin{bmatrix} а\\ с \end{bmatrix} + у \begin{bmatrix} б\\ д \end{bmatrix} = \begin{bmatrix} топор + по\\ сх + ду \end{bmatrix} $$
Обратите внимание, что мы можем определить вектор как матрицу, поэтому мы также можем назвать это умножением матриц.
Умножение матриц: Умножаем строки на столбцы . Это означает, что вы берете первое число в первой строке второй матрицы и масштабируете (умножаете) его на первый столбец в первой матрице. Вы делаете это с каждым числом в строке и столбце, затем переходите к следующей строке и столбцу и делаете то же самое.Теперь мы можем определить линейное преобразование. Мы можем начать с задания матрицы A чисел, а затем пусть вектор $\vec{v}$ будет любым возможным вектором в нашем векторном пространстве
$$ А = \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bmatrix} Икс\\ у \end{bmatrix} $$
Тогда мы можем выбрать и сказать, что мы определяем наше линейное преобразование как $T(\vec{v}) = A \vec{v}$. Это означает, что для каждой векторной координаты в нашем векторе $\vec{v}$ мы должны умножить ее на матрицу A .
$$ Т(\vec{v}) = А \vec{v} \rightarrow \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bmatrix} Икс\\ у \end{bmatrix} $$
Как я только что показал вам выше, где мы определили матрицу A с помощью a, b, c и d, мы можем выполнить умножение следующим образом
$$ Т(\vec{v}) = А \vec{v} \rightarrow \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bmatrix} Икс\\ у \end{bmatrix} = х \begin{bmatrix} -2\\ 3 \end{bmatrix} + у \begin{bmatrix} 6\\ 1 \end{bmatrix} = \begin{bmatrix} -2х + 6у\\ 3x + 1г \end{bmatrix} $$
Вычисление преобразованного вектора?
Чтобы вычислить любой вектор после преобразования, все, что нам нужно сделать, как описано выше в этом посте, — это записать базисные векторы.
Если мы знаем, где находятся базисные векторы после преобразования, вычисление любого преобразованного вектора становится до бешенства простым.
Я подчеркивал эту матрицу A на протяжении всего поста по очень конкретной причине. Представьте, что первый столбец матрицы равен $\hat{i}$, а второй столбец равен $\hat{j}$ 9.0003
$$ А = \begin{bmatrix} \шляпа{i}_x и \шляпа{j}_x\\ \шляпа{i}_y и \шляпа{j}_y \end{bmatrix} $$
Теперь становится очевидным, что мы можем по любому вектору вычислить любой вектор в преобразованном векторном пространстве. Итак, если у нас есть преобразованные $\hat{i}$ и $\hat{j}$, мы можем просто передать любой вектор в эту формулу вместе с преобразованными базисными векторами, и это даст нам преобразованный вектор (где T означает для преобразованных):
$$ \begin{bmatrix} T _ {\ шляпа {i} _x} и T _ {\ шляпа {j} _x} \\ T _ {\ шляпа {i} _y} и T _ {\ шляпа {j} _y} \end{bmatrix} \begin{bmatrix} \vec{v}_x \\ \vec{v}_y \end{bmatrix} $$
Как насчет умножения матриц 2x2?
Этот случай тоже несложный.
Предположим, у нас есть матрицы A (слева) и B (справа). Мы бы просто умножили строки в первой матрице на столбцы во второй матрице:
$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} е & ж \\ г и ч \end{bmatrix} = \begin{bmatrix} ае + бг и аф + бч \\ ce + dg и cf + dh \end{bmatrix} $$
НО! Это нелегко запомнить, поэтому здесь есть интуитивный способ, как я показал ранее. Разделим процесс на 2:
- Умножим матрицу A на первый столбец в матрице B
- Умножим матрицу A на второй столбец в матрице B
9006 Этот сценарий известен I показывал вам это ранее:$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} е \\ грамм \end{bmatrix} = е \begin{bmatrix} а \\ с \end{bmatrix} + г \begin{bmatrix} б\ д \end{bmatrix} = \begin{bmatrix} ае+бг\ се + дг \end{bmatrix} $$
$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} ф\ час \end{bmatrix} = f \begin{bmatrix} а \\ с \end{bmatrix} + ч \begin{bmatrix} б\ д \end{bmatrix} = \begin{bmatrix} аф+бч\ ср + дч \end{bmatrix} $$
Сложив два результата вместе, мы получим уравнение выше:
$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} е & ж \\ г и ч \end{bmatrix} = \begin{bmatrix} ае + бг и аф + бч \\ ce + dg и cf + dh \end{bmatrix} $$
Очевидно, этому нужно было многому научиться.
Но мы могли бы также пойти дальше и задать надвигающийся вопрос, что может быть неправильным линейным преобразованием? Потому что мы только что определили некоторое линейное преобразование и предположили, что оно правильное. Пока я не буду углубляться в тему, но, как предлагает WolframAlpha, нам нужно, чтобы 2 условия были истинными, прежде чем мы сможем назвать это линейным преобразованием.
Резюме (из вопросов вверху):
- Что такое линейные преобразования?
Линейные преобразования — это функция $T(x)$, в которой мы получаем входные данные и преобразуем их по некоторому определению правила. Примером является $T(\vec{v})=A \vec{v}$, где для каждой векторной координаты в нашем векторе $\vec{v}$ мы должны умножить это на матрицу A.- Что такое векторное пространство?
Векторное пространство — это набор всех векторов в нашем пространстве, которые мы определяем в измерениях. Мы можем выполнять операции над этими векторами, например.сложение векторов или масштабирование.
- Как выполнять умножение матриц?
С матрицей $A = \begin{bmatrix}a & b\\c & d \end{bmatrix}$, где a, b, c и d - действительные числа.
Только запомните: Мы умножаем строки на столбцы . Это означает, что вы берете первое число в первой строке второй матрицы и масштабируете (умножаете) его на первый столбец в первой матрице. Вы делаете это с каждым числом в строке и столбце, затем переходите к следующей строке и столбцу и делаете то же самое.
Это могут быть два вектора, где a и c — один вектор, а b и d — другой вектор. Во-вторых, с вектором $\vec{v}=\begin{bmatrix}x\\y \end{bmatrix}$ (подразумевается, что $\vec{v}$ является матрицей), мы бы умножали их вот так.$$ \begin{bmatrix} а и б\\ CD \end{bmatrix} \begin{bmatrix} Икс\\ у \end{bmatrix} = х \begin{bmatrix} а\\ с \end{bmatrix} + у \begin{bmatrix} б\\ д \end{bmatrix} = \begin{bmatrix} топор + по\\ сх + ду \end{bmatrix} $$
3Blue1Brown — Умножение матриц как композиция
Опубликовано 8 августа 2016 г.
Обновлено 4 октября 2022 г.1493 Урок Гранта Сандерсона
Текстовая адаптация River Way
Исходный код
«По моему опыту, доказательства с использованием матриц можно сократить на 50%, если выбросить матрицы».
\qquad — Эмиль Артин
Резюме
В предыдущем уроке мы показали, что линейные преобразования — это просто функции с векторами в качестве входных данных и векторами в качестве выходных данных. Однако часто удобнее думать о линейных преобразованиях как о перемещении пространства таким образом, чтобы линии сетки оставались параллельными и равномерно расположенными.
Полноту преобразования можно определить по месту расположения базисных векторов после преобразования, формирующих столбцы матрицы. Чтобы найти, куда попадает любой произвольный вектор после преобразования, существует операция, называемая умножением матрицы на вектор. Вот вычисление для двумерной матрицы и вектора:
[abcd][xy]=x[ac]+y[bd]=[ax+bycx+dy]\begin{bmatrix} \color{green}a & \ color{red}b \\ \color{green}c & \color{red}d \end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} = x\begin{bmatrix}\color{green }a\\ \color{green}c\end{bmatrix} +y\begin{bmatrix}\color{red}b\\ \color{red}d\end{bmatrix} = \begin{bmatrix} \color{ зеленый}a\цвет{черный}x+\цвет{красный}b\цвет{черный}y \\ \color{зеленый}c\цвет{черный}x+\цвет{красный}d\цвет{черный}y \end{ bmatrix}[acbd][xy]=x[ac]+y[bd]=[ax+bycx+dy] 9в конечном итоге заканчивается на [−10]\begin{bmatrix}-1\\0\end{bmatrix}[−10], так что сделайте это вторым столбцом матрицы.
Эта новая матрица фиксирует общий эффект применения вращения, а затем сдвига, но как одно действие, а не два последовательных.
Композиция — это умножение
Вот один из способов представить эту новую матрицу. Если бы вы взяли какой-то вектор и прокачали его через вращение, а затем сдвиг, долгий путь вычислить, где он приземлится, сначала умножив слева на матрицу вращения, а затем умножив результат слева на матрицу сдвига. Это, в численном выражении, то, что это означает , чтобы применить вращение, а затем сдвиг к заданному вектору. Но все, что вы получите, должно быть таким же, как простое умножение этой новой матрицы композиции, которую мы нашли, на вектор, независимо от того, какой вектор вы выбрали, поскольку предполагается, что эта новая матрица захватывает тот же общий эффект, что и действие вращения, затем сдвига.
Основываясь на том, как все здесь записано, я думаю, что разумно назвать эту новую матрицу произведением двух исходных матриц, не так ли?
[1101]⏟Сдвиг [0−110]⏟Вращение=[1−110]⏟Композиция\цвет{фиолетовый} \underbrace{ \begin{bmatrix}1&1\\0&1\end{bmatrix} }_{\large \ text{Сдвиг}} \ \color{оранжевый} \underbrace{ \begin{bmatrix}0&-1\\1&0\end{bmatrix} }_{\large \text{Вращение}} \color{black} = \color{ красный} \underbrace{ \begin{bmatrix}1&-1\\1&0\end{bmatrix} }_{\large \text{Композиция}}Сдвиг
[1011]Вращение
[01−10]= Состав
[11−10]
Мы можем подумать о том, как вычислить это произведение в более общем виде, просто мгновение, но легко заблудиться в лесу чисел.
Всегда помните, что такое умножение двух матриц имеет геометрический смысл применения одного преобразования за другим.
Странно то, что здесь мы читаем справа налево. Сначала вы применяете преобразование, представленное матрицей справа, затем применяете преобразование, представленное матрицей слева. Это проистекает из обозначения функций, поскольку мы пишем функции слева от переменной, поэтому композиция всегда должна читаться справа налево. Хорошие новости для читателей на иврите и плохие новости для всех нас.
f(g(x)) Читать справа налево ←[1101]⏟Сдвиг [0−110]⏟Rotation=[1−110]⏟Composition\begin{align*} &\qquad f(g(x)) \\ &\underleftarrow{\text{Читать справа налево}} \\ &\color{purple} \underbrace{ \begin{bmatrix}1&1\\0&1\end{bmatrix} }_{\large\text{Сдвиг} } \ \color{orange} \underbrace{ \begin{bmatrix}0&-1\\1&0\end{bmatrix} }_{\large\text{Rotation}} \color{black} = \color{red} \underbrace { \begin{bmatrix}1&-1\\1&0\end{bmatrix} }_{\large\text{Композиция}} \end{align*}f(g(x))
Чтение справа налево Сдвиг
[1011]Вращение
[01−10]= Композиция
[11−10]
Вычисление новой матрицы
Давайте посмотрим на другой пример.
Есть две матрицы M1M_1M1 и M2M_2M2, которые выполняют разные преобразования:
Суммарный эффект от применения M1M1M1, затем M2M2M2 дает новое преобразование, поэтому найдем его матрицу.
Но давайте посмотрим, сможем ли мы сделать это без каких-либо изображений, а вместо этого просто используя числовые элементы в каждой матрице. 9))=[0120][11−20][01]=−2[01]+0[20]=[0–2]
Умножение этих двух матриц дает [0210][1−210]=?\begin{bmatrix}0&2\\1&0\end{bmatrix}\begin{bmatrix}1&-2\\1&0\end{bmatrix}=?[0120][11 −20]=?
[02−21]\begin{bmatrix}0&2\\-2&1\end{bmatrix}[0−221]
[201−2]\begin{bmatrix}2&0\\1&-2\ end{bmatrix}[210−2]
[−2102]\begin{bmatrix}-2&1\\0&2\end{bmatrix}[−2012]
[1−220]\begin {bmatrix}1&-2\\2&0\end{bmatrix}[12−20]
Общая форма
Давайте повторим тот же процесс еще раз, но на этот раз записи будут переменными в каждой матрице, просто чтобы показать, что один и тот же ход рассуждений работает для любых матриц.
Это более тяжелый символ и потребует больше места, но это должно удовлетворить любого, кто ранее учился матричному умножению традиционным способом.
[abcd]⏟M2 [efgh]⏟M1=[????]⏟M2M1\color{purple} \ underbrace{ \begin{bmatrix}a&b\\c&d\end{bmatrix} }_{\large M_2} \ \color{orange} \underbrace{ \begin{bmatrix}e&f\\g&h\end{bmatrix} }_{\large M_1} \color{black} = \color{red} \underbrace{ \begin{bmatrix}? &?\\?&?\end{bmatrix} }_{\large M_2M_1}M2 9заканчивается после применения второго преобразования. Таким образом, первый столбец матрицы произведения всегда будет равен левой матрице, умноженной на первый столбец правой матрицы.
[abcd][eg]=e[ac]+g[bd]=[ae+bgce+dg]\color{purple} \begin{bmatrix}a&b\\c&d\end{bmatrix} \color{orange} \begin{bmatrix}e\\g\end{bmatrix} \color{black} = \color{orange} e \color{purple} \begin{bmatrix}a\\c\end{bmatrix} \color{black} + \color{orange} g \color{purple} \begin{bmatrix}b\\d\end{bmatrix} \color{black} = \begin{bmatrix} \color{purple} a \color{orange} e \ color{black} + \color{purple} b \color{orange} g \\ \color{purple} c \color{orange} e \color{black} + \color{purple} d \color{orange} g \ end{bmatrix}[acbd][eg]=e[ac]+g[bd]=[ae+bgce+dg] 9и, следовательно, второй столбец матрицы продукта.
[abcd][fh]=f[ac]+h[bd]=[af+bhcf+dh]\color{purple} \begin{bmatrix}a&b\\c&d\end{bmatrix} \color{orange} \begin{bmatrix}f\\h\end{bmatrix} \color{black} = \color{orange} f \color{purple} \begin{bmatrix}a\\c\end{bmatrix} \color{black} + \color{orange} h \color{purple} \begin{bmatrix}b\\d\end{bmatrix} \color{black} = \begin{bmatrix} \color{purple} a \color{orange} f \ color{black} + \color{purple} b \color{orange} h \\ \color{purple} c \color{orange} f \color{black} + \color{purple} d \color{orange} h \ end{bmatrix}[acbd][fh]=f[ac]+h[bd]=[af+bhcf+dh]
Обычно эту формулу учат как нечто, что нужно запомнить, наряду с определенным алгоритмическим процессом для ее запоминания.
[abcd]⏟M2 [efgh]⏟M1=[ae+bgaf+bhce+dgcf+dh]⏟M2M1\color{purple} \underbrace{ \begin{bmatrix}a&b\\c&d\end{bmatrix} }_ {\ large M_2} \ \ color {orange} \ underbrace { \ begin {bmatrix} e&f \\ g&h \ end {bmatrix} } _ {\ large M_1} \ color {black} = \ color {red} \ underbrace { \ begin{bmatrix} \color{purple} a \color{orange} e \color{black} + \color{purple} b \color{orange} g & \color{purple} a \color{orange} f \color{ черный} + \color{purple} b \color{orange} h \\ \color{purple} c \color{orange} e \color{black} + \color{purple} d \color{orange} g & \color {purple} c \color{orange} f \color{black} + \color{purple} d \color{orange} h \end{bmatrix} }_{\large M_2M_1}M2
[acbd]M1
[egfh]=M2M1
[ae+bgce+dgaf+bhcf+dh]
Умножение этих двух матрицы дают [−3125][537−3]=?\begin{bmatrix}-3&1\\2&5\end{bmatrix}\begin{bmatrix}5&3\\7&-3\end{bmatrix}=?[−32 15][573−3]=?
[45−9−8−12]\begin{bmatrix}45&-9\\-8&-12\end{bmatrix}[45−8−9−12]
[−12−8− 945]\begin{bmatrix}-12&-8\\-9&45\end{bmatrix}[−12−9−845]
[−945−12−8]\begin{bmatrix}-9&45\\- 12&-8\end{bmatrix}[−9−1245−8]
[−8−1245−9]\begin{bmatrix}-8&-12\\45&-9\end{bmatrix}[−845−12−9]
Я действительно считаю, что прежде чем запоминать этот процесс, вы должны привыкнуть думать о том, что на самом деле представляет собой умножение матриц: применение одного преобразования за другим.
Поверьте мне, это даст вам концептуальную основу, облегчающую понимание свойств матричного умножения.
Некоммутативность
Вот важный вопрос: имеет ли значение, в каком порядке мы располагаем две матрицы? 9\circ90∘ вращение.
Общий эффект совсем другой, так что может показаться, что порядок имеет значение! Думая с точки зрения преобразований, это то, что вы можете делать в своей голове, визуализируя, без необходимости умножения матриц!
При умножении этих двух матриц [0-110][-200-2]=?[-200-2][0-110]\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{ bmatrix}-2&0\\0&-2\end{bmatrix}\stackrel{?}{=}\begin{bmatrix}-2&0\\0&-2\end{bmatrix}\begin{bmatrix}0&-1\\1&0 \end{bmatrix}[01−10][−200−2]=?[−200−2][01−10]
Да, матрицы коммутируют.
Нет, матрицы не коммутируют.
Ассоциативность. Это означает, что если у вас есть три матрицы, A, B и C, и вы их все умножаете, не имеет значения, вычисляете ли вы сначала A, умноженное на B, а затем умножаете результат на C, или если вы сначала умножаете B на C, а затем умножаете результат по матрице A слева.

 8
8 8 9.3
8 9.3
 5)
5)

 2$ задает построение отношения в полной мере.
2$ задает построение отношения в полной мере. 1. Введение
1. Введение


 , например, [
[
2
]
,
[
94
]
]). Для реальных экспериментов на
многопроцессорных вычислительных системах зависимости строятся по
набору результатов проведенных вычислительных экспериментов.
, например, [
[
2
]
,
[
94
]
]). Для реальных экспериментов на
многопроцессорных вычислительных системах зависимости строятся по
набору результатов проведенных вычислительных экспериментов. Рядом с каждым процессором изображены те данные, которые он
обрабатывает в каждый момент выполнения алгоритма (для ленточного
алгоритма умножения матриц это несколько последовательных строк
матрицы А и несколько последовательных столбцов матрицы В ). При
помощи перемещающихся прямоугольников (пакетов) желтого цвета
изображается обмен данными, который осуществляют процессоры.
Рядом с каждым процессором изображены те данные, которые он
обрабатывает в каждый момент выполнения алгоритма (для ленточного
алгоритма умножения матриц это несколько последовательных строк
матрицы А и несколько последовательных столбцов матрицы В ). При
помощи перемещающихся прямоугольников (пакетов) желтого цвета
изображается обмен данными, который осуществляют процессоры.
 также
также
 Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.


 Его сложность составляет Θ(n2.7799).
Его сложность составляет Θ(n2.7799).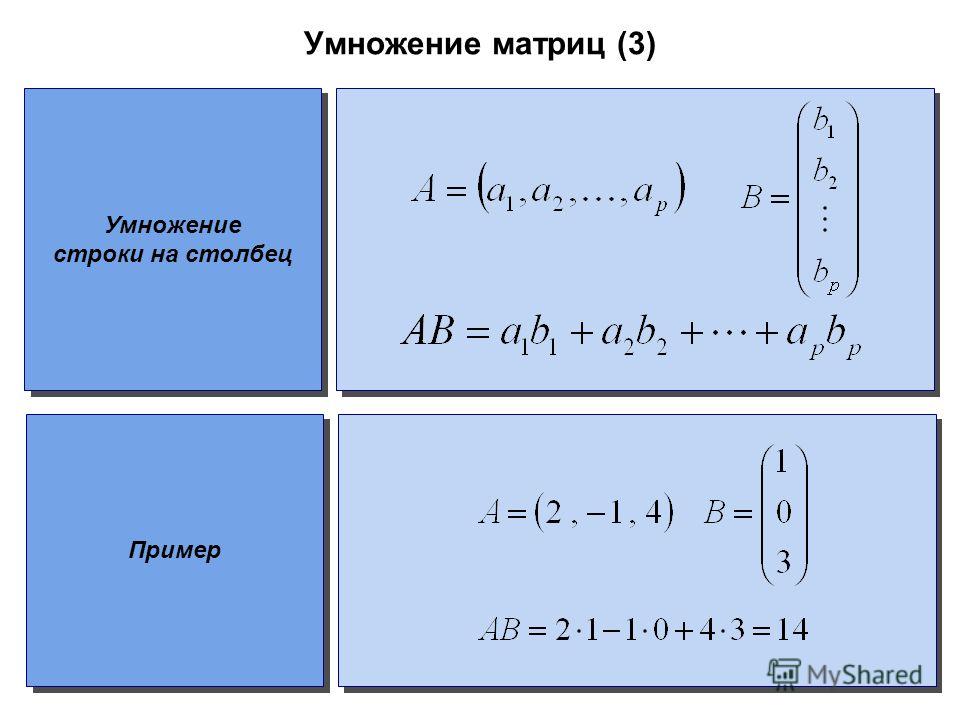
 — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
— Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978 Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.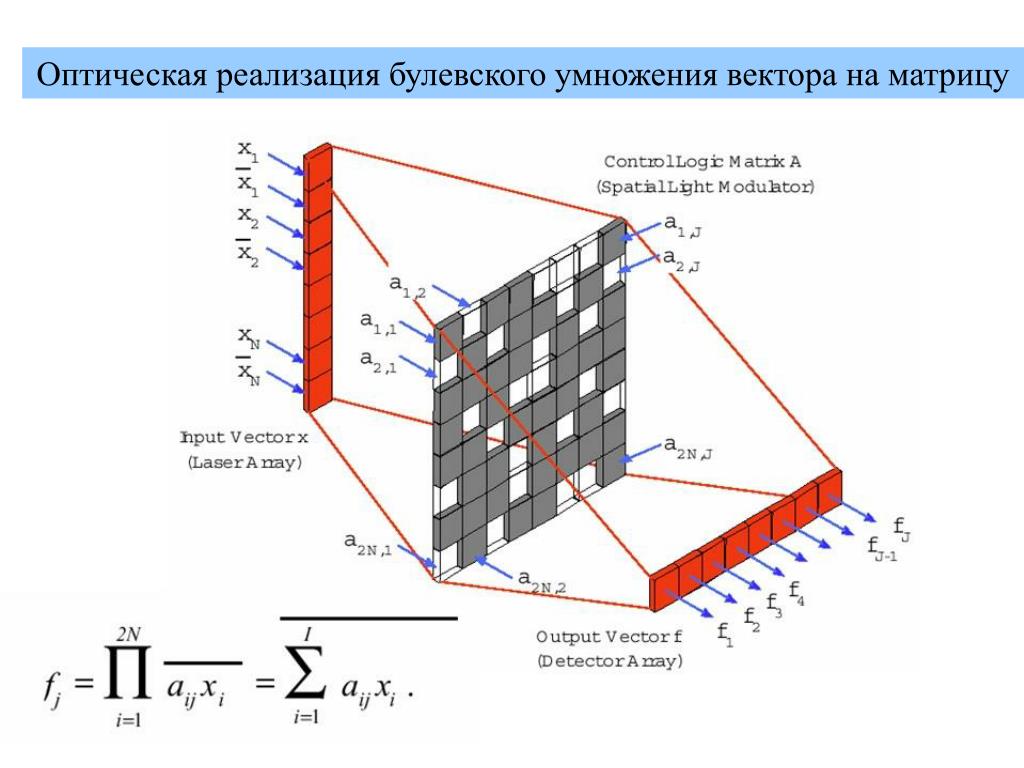
 Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.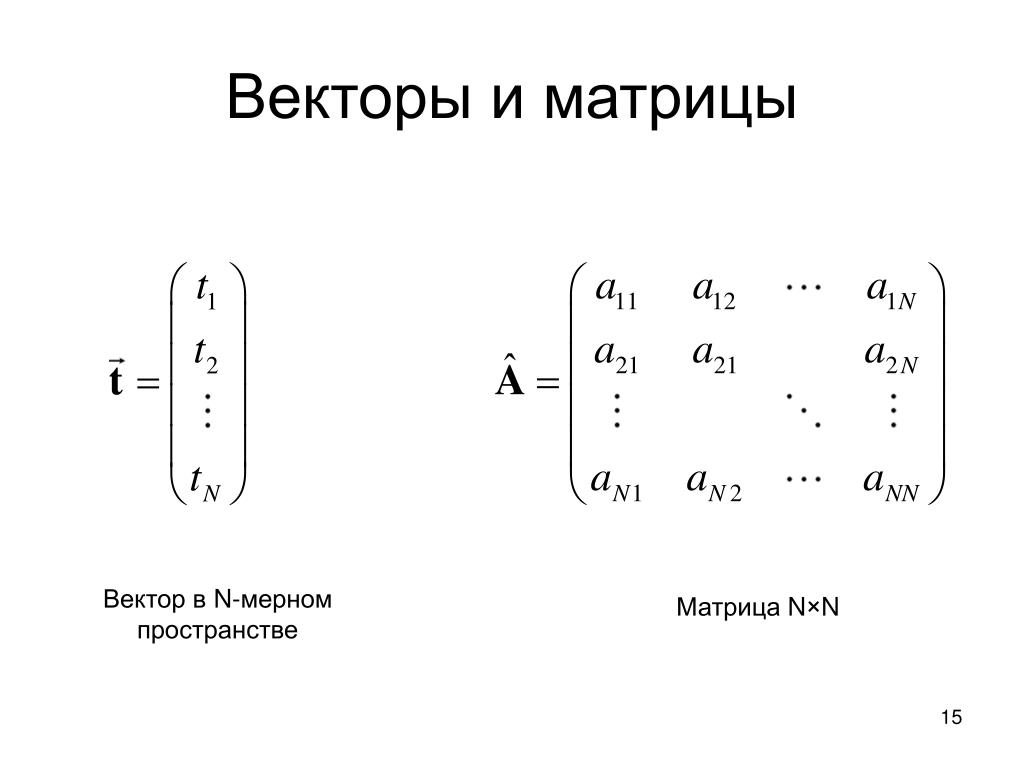
 Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
 Должны существовать произведения A × B и B × C.
Должны существовать произведения A × B и B × C.
 Приступим к решению задачи.
Приступим к решению задачи.
 Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B. Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
 Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
 Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B). В этой статье мы собираемся умножить данную матрицу на заданный вектор, используя язык программирования R. Умножение между ними происходит, когда элементы вектора умножаются на элементы матрицы по столбцам.
В этой статье мы собираемся умножить данную матрицу на заданный вектор, используя язык программирования R. Умножение между ними происходит, когда элементы вектора умножаются на элементы матрицы по столбцам.
 Функция развертки () используется для применения операции «+ или – или «*» или «/» к строке или столбцу в данной матрице.
Функция развертки () используется для применения операции «+ или – или «*» или «/» к строке или столбцу в данной матрице.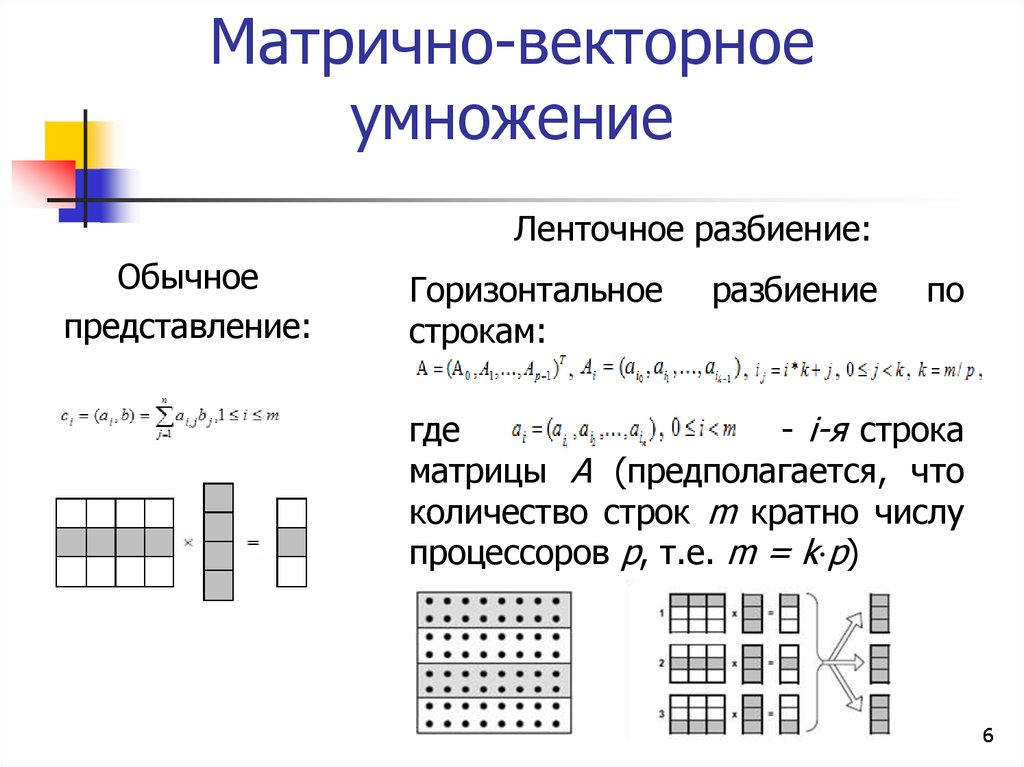 , `*`))
, `*`))  ----"
----"  Такой способ интерпретации матричного умножения часто помогает
понимать важные результаты матричной алгебры.
Такой способ интерпретации матричного умножения часто помогает
понимать важные результаты матричной алгебры.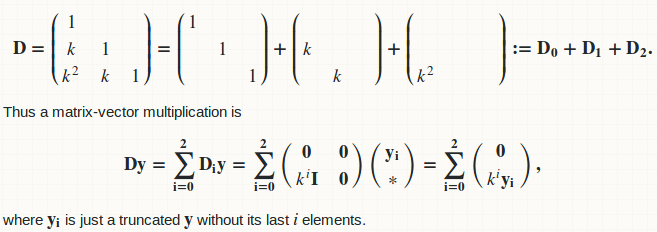

 по другой матрице.
по другой матрице.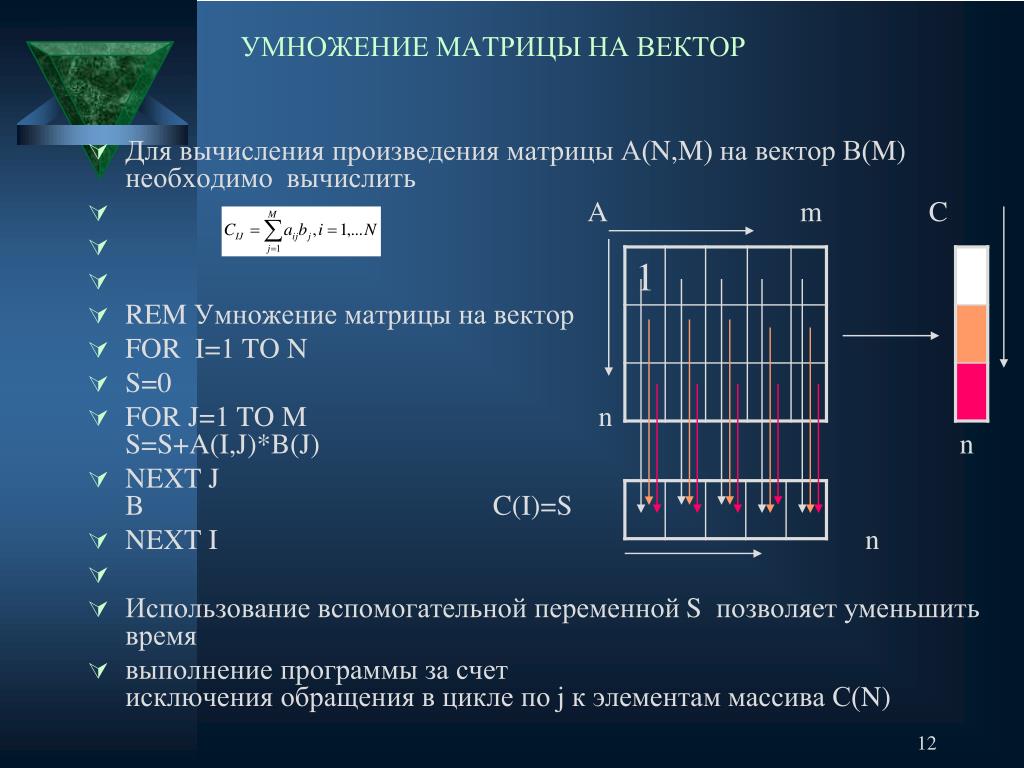
 com/matrix-алгебра/matrix-multiplication-and-linear-combinations.
com/matrix-алгебра/matrix-multiplication-and-linear-combinations. Однако некоторые ученые ставят эту дату под сомнение, поскольку первая матрица не была полностью описана до 1857 года Артуром Кейли в Великобритании.
Однако некоторые ученые ставят эту дату под сомнение, поскольку первая матрица не была полностью описана до 1857 года Артуром Кейли в Великобритании.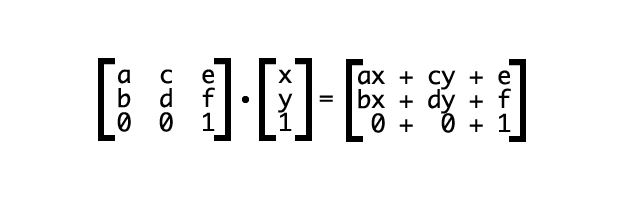 Скаляр — это величина, полностью описываемая одной величиной или числовым значением. В приведенном выше примере 3 является скаляром.
Скаляр — это величина, полностью описываемая одной величиной или числовым значением. В приведенном выше примере 3 является скаляром. Скалярный продукт также называется скалярным произведением, поскольку в результате вычисления получается одно число.
Скалярный продукт также называется скалярным произведением, поскольку в результате вычисления получается одно число.
 Тем не менее, важно соблюдать соглашения об именах.
Тем не менее, важно соблюдать соглашения об именах. Обратите внимание, как подсвечиваются разные числа в матрицах при переключении порядка умножения матриц.
Обратите внимание, как подсвечиваются разные числа в матрицах при переключении порядка умножения матриц.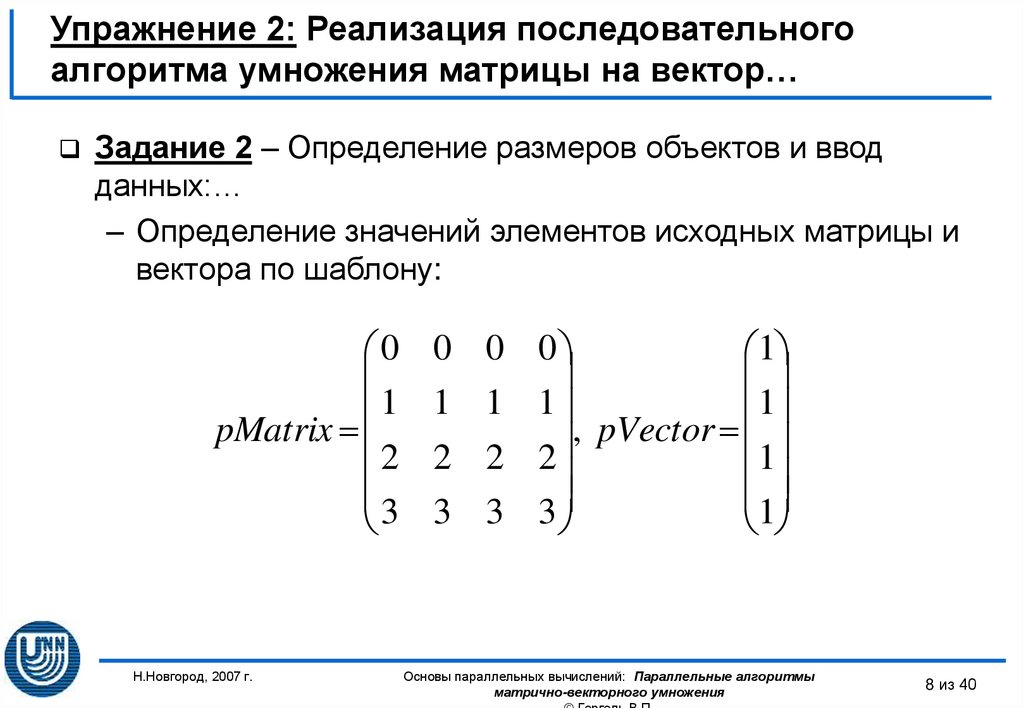
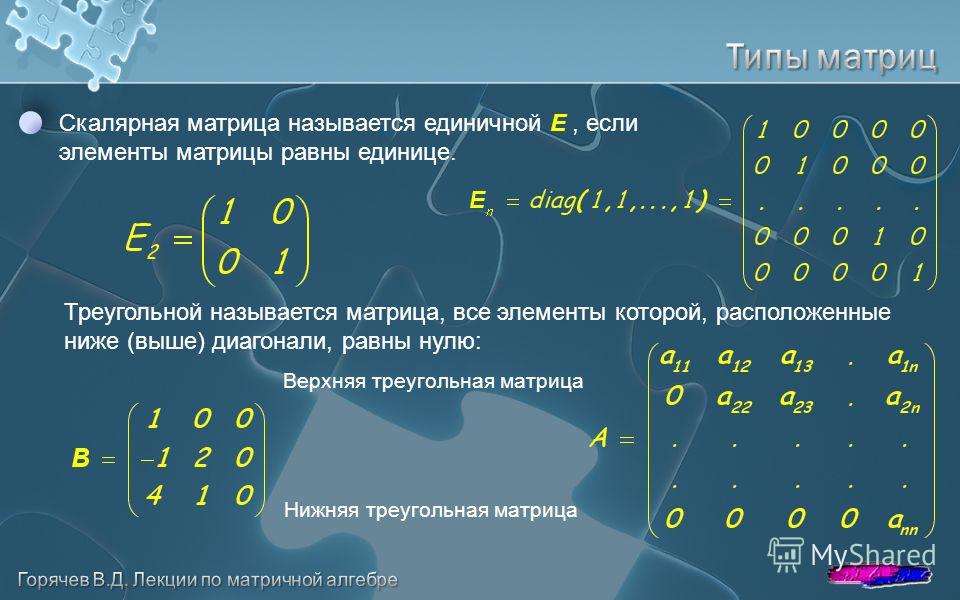
 Освоение этой операции позволяет учащимся глубже понять линейную алгебру.
Освоение этой операции позволяет учащимся глубже понять линейную алгебру. Матричная алгебра.
Матричная алгебра. ) = (x 1 f 11 + x 2 f 12 , x 1 f 21 + x 2 f 32)
) = (x 1 f 11 + x 2 f 12 , x 1 f 21 + x 2 f 32)