Тест по теме: «Квадратичная функция»
Тест по теме: «Квадратичная функция» для 9 класса
Цели: проверить знания, умения и навыки учащихся по теме; выявить степень усвоения пройденного материала.
Тест содержит 2 варианта по 17 заданий, из них 7 заданий с выбором ответа, 3 задания на соответствие, 3 задания с кратким ответом, 5 заданий с краткой записью решения. (В №14 необходимо записать краткое решение, но ответ выбрать из предложенных). После каждого номера есть специально отведенное место для ответа, и при необходимости для записи решения. Часть заданий, предложенных в тесте, взяты из банка заданий ОГЭ по математике для 9 класса.
Задания №1, 2, 4, 5, 6, 7, 8, 9, 10, 12, 16 оцениваются по 1 баллу.
Задания №3, 11, 13, 14, 15, 17 оцениваются до 2 баллов.
Тест рассчитан на 25 минут для учащихся 9 классов.
Критерии оценивания:
Оценка | Баллы |
«5» | 20-23 |
«4» | 15-19 |
«3» | 8-14 |
«2» | 0-7 |
Тест по теме: «Квадратичная функция»
Вариант 1
№1 Запишите номера квадратичных функций(возожно несколько вариантов ответа):
;
ОТВЕТ: ___________________________
№2 Установите соответствия между графиком квадратичной функции и алгоритмом построения.
А) Смещение параболы на 2 единичных отрезка вправо и на 3 единичных отрезка вниз | |
Б) Смещение параболы на 2 единичных отрезка влево и на 3 единичных отрезка вниз; | |
В) Смещение параболы на 2 единичных отрезка влево и на 3 единичных отрезка вверх; | |
Г) Смещение параболы на 2 единичных отрезка вправо и на 3 единичных отрезка вверх; |
А | Б | В | Г |
ОТВЕТ:
№3 Схематически постройте график функции , предварительно представив его в виде
Запишите необходимые преобразования тут: ОТВЕТ: ___________________________ | ||||||||||
№4 На рисунке изображены графики функций вида .
А) | Б) | В) | Г) |
А | Б | В | Г |
ОТВЕТ:
№5 Найдите значение с по графику функции изображенному на рисунке.
ОТВЕТ: ___________________________
№6 На рисунке изображены графики функций вида . Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.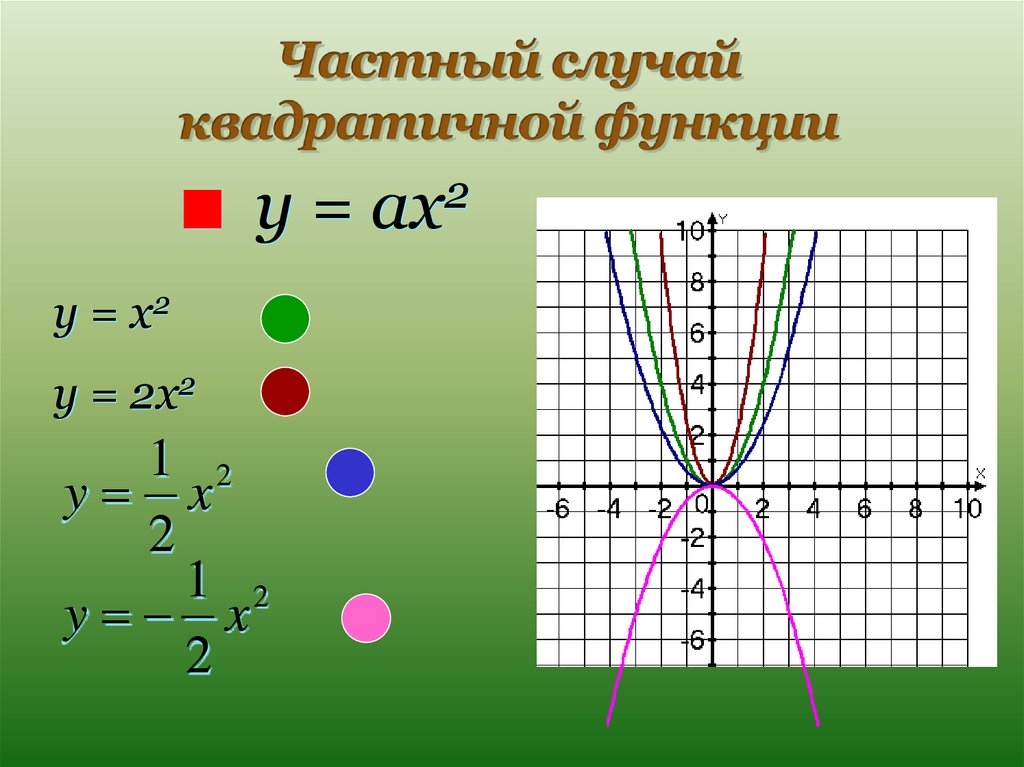
А) | Б) | В) | Г) |
А | Б | В | Г |
Ответ:
№7 Запишите номер, под которым записаны координаты вершины параболы .
1) (3; -80); | 2) (-3; 28); | 3) (3; -28); | 4) (-3; 82). |
ОТВЕТ: __________________________________________________________
№8 Укажите номер прямой относительно которой симметричен график
.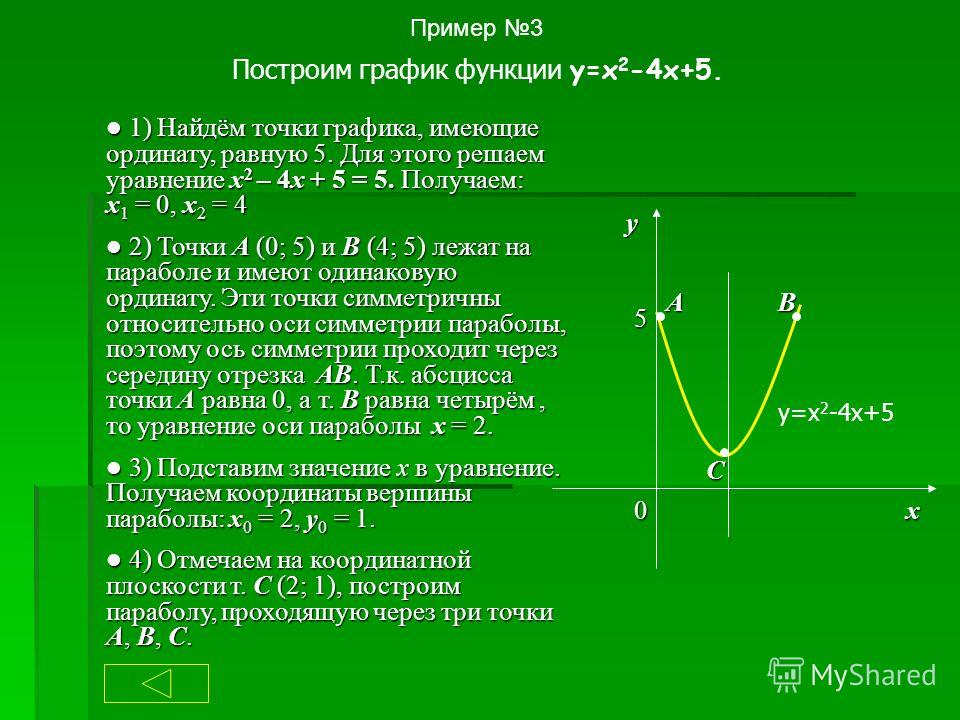
1) | 2) | 3) | 4) |
ОТВЕТ: __________________________________________________________
№ 9 Укажите область значений функции .
1) | 2) | 3) | 4) |
ОТВЕТ: __________________________________________________________
№10 Найдите наибольшее значение функции
ОТВЕТ: __________________________________________________________
№11 Найдите значение коэффициентов а и b по графику функции изображенному на рисунке.
Запишите необходимые вычисления тут: |
№12 Найдите промежуток возрастания функции .
1) | 2) | 3) | 4) |
ОТВЕТ: __________________________________________________________
№13 Найдите нули функции .
Запишите необходимые вычисления тут:
ОТВЕТ: __________________________________________________________
№14 При каких значениях x значения функции .
1) | 2) | 3) | 4) |
Запишите необходимые вычисления или объяснения тут: | |||
ОТВЕТ: __________________________________________________________
№15 Найдите точки пересечения парабол В ответе укажите наименьшую ординату.
Запишите необходимые вычисления тут:
ОТВЕТ: __________________________________________________________
№16 График какой из функции изображен на рисунке.
1) | 2) | 3) | 4) |
ОТВЕТ: ___________________________
№17 При каких значения m прямая имеет с графиком одну общую точку.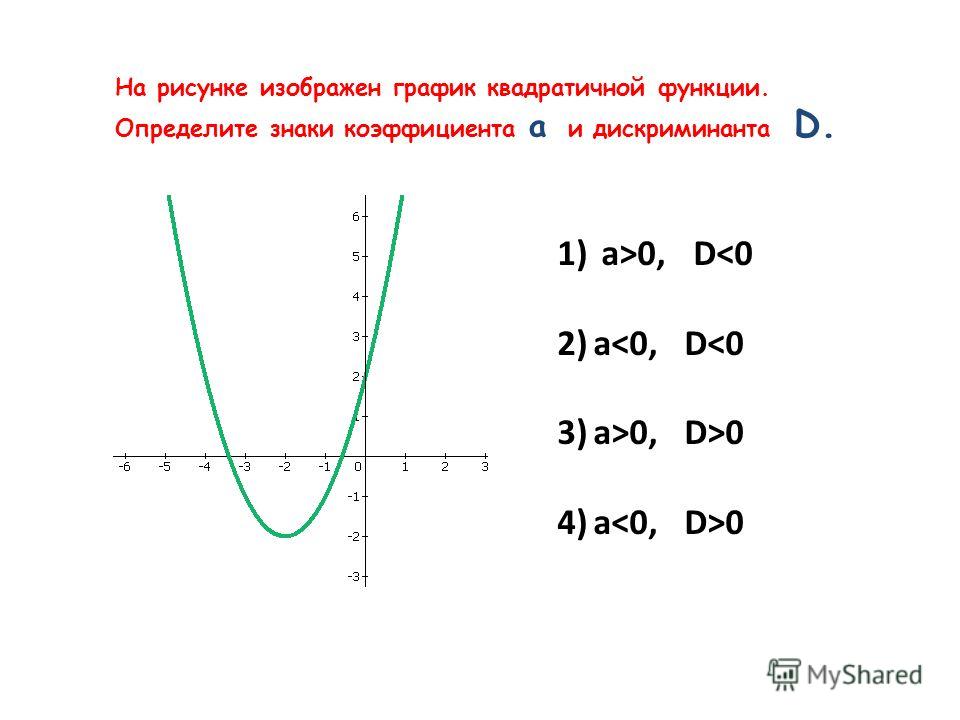
ОТВЕТ: ___________________________
Тест по теме: «Квадратичная функция»
Вариант 2
№1 Запишите номера квадратичных функций (возможно несколько вариантов ответа):
ОТВЕТ: ___________________________
№2 Установите соответствия между графиком квадратичной функции и алгоритмом построения.
А) Смещение параболы на 3 единичных отрезка влево и на 2 единичных отрезка вверх; | |
Б) Смещение параболы на 3 единичных отрезка влево и на 2 единичных отрезка вниз; | |
В) Смещение параболы на 3 единичных отрезка вправо и на 2 единичных отрезка вниз | |
Г) Смещение параболы на 3 единичных отрезка вправо и на 2 единичных отрезка вверх; |
А | Б | В | Г |
ОТВЕТ:
№3 Схематически постройте график функции , предварительно представив его в виде
Запишите необходимые преобразования тут: ОТВЕТ: ___________________________ | ||||||||||
№4 На рисунке изображены графики функций вида .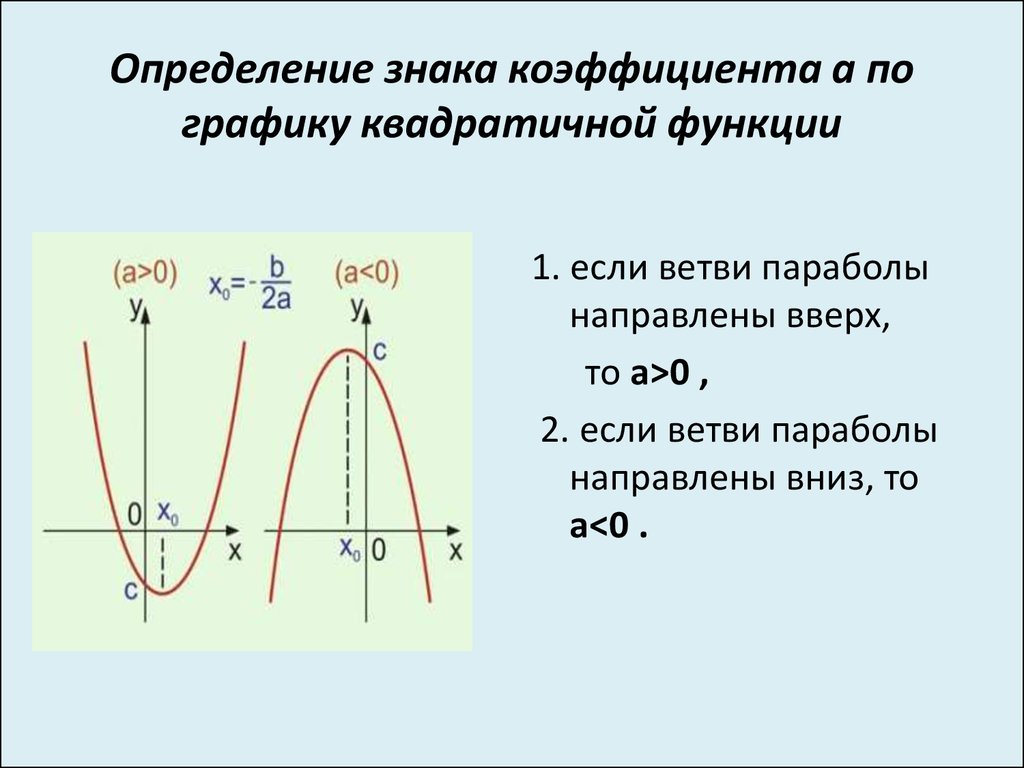 Установите соответствие между графиками функций и знаками коэффициентов a и c.
Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) | Б) | В) | Г) |
А | Б | В | Г |
ОТВЕТ:
№5 Найдите значение с по графику функции изображенному на рисунке.
ОТВЕТ: ___________________________
№6 На рисунке изображены графики функций вида . Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.
А) | Б) | В) | Г) |
А | Б | В | Г |
Ответ:
№7 Запишите номер, под которым записаны координаты вершины параболы .
1) (-3; -28); | 2) (-3; 28); | 3) (3; 80); | 4) (-3; -82). |
ОТВЕТ: __________________________________________________________
№8 Укажите номер прямой относительно которой симметричен график
.
1) | 2) | 3) | 4) y |
ОТВЕТ: __________________________________________________________
№9 Укажите область значений функции .
1) | 2) | 3) | 4) |
ОТВЕТ: __________________________________________________________
№10 Найдите наименьшее значение функции .
ОТВЕТ: __________________________________________________________
№11 Найдите значение коэффициентов а и b по графику функции изображенному на рисунке.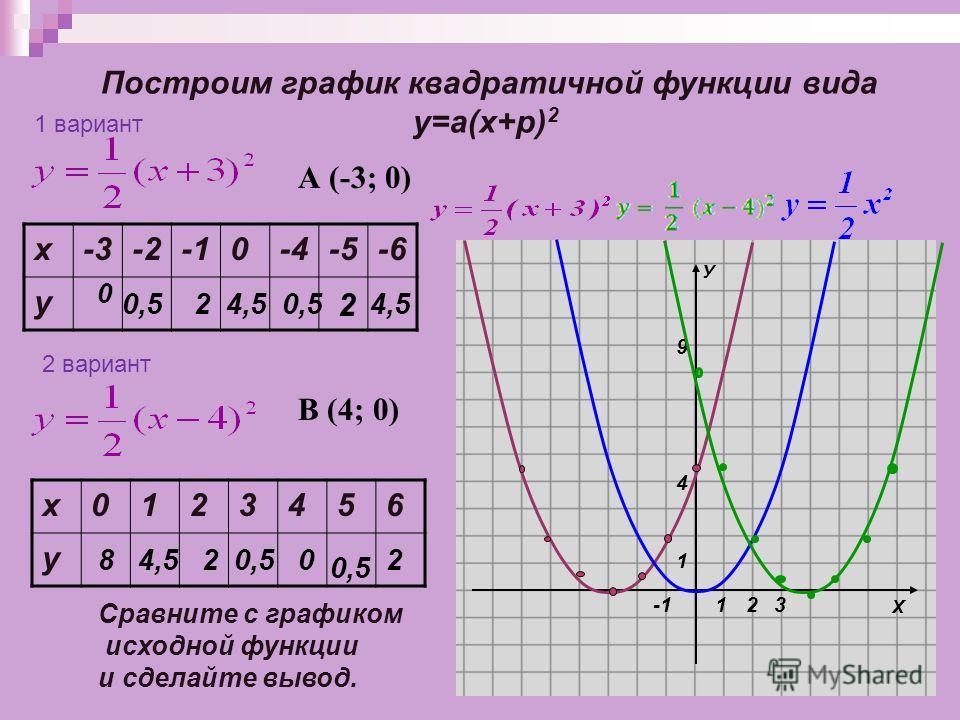
Запишите необходимые вычисления тут: ОТВЕТ: ___________________________ |
№12 Найдите промежуток убывания функции .
1) | 2) | 3) | 4) |
ОТВЕТ: __________________________________________________________
Запишите необходимые вычисления тут:
№13 Найдите нули функции .
ОТВЕТ: __________________________________________________________
№14 При каких значениях x значения функции .
1) | 2) | 3) | 4) |
Запишите необходимые вычисления или объяснения тут: | |||
ОТВЕТ: __________________________________________________________
№15 Найдите точки пересечения парабол В ответе укажите наибольшую ординату.
Запишите необходимые вычисления тут:
ОТВЕТ: __________________________________________________________
№16 График какой из функции изображен на рисунке.
1) | 2) | 3) | 4) |
ОТВЕТ: _________________________
№17 При каких значения m прямая имеет с графиком две общие точки. ОТВЕТ: ___________________________
ОТВЕТ: ___________________________
Ответы
Вариант 1 | Вариант 2 | ||
1 | 2,3,4 | 1 | 2,3,5 |
2 | А-4, Б-2, В-1, Г-3 | 2 | А-3, Б-1, В-2, Г-4 |
3 | 3 | ||
4 | А-2, Б-1, В-4, Г-3 | 4 | А-4, Б-2, В-3, Г-1 |
5 | -2 | 5 | 1 |
6 | А-4, Б-3, В-1, Г-2 | 6 | А-3, Б-2, В-1, Г-4 |
7 | 2 | 7 | 1 |
8 | 4 | 8 | 2 |
9 | 1 | 9 | 3 |
10 | -0,25 | 10 | 10 |
11 | 11 | ||
12 | 3 | 12 | 3 |
13 | 13 | ||
14 | т. Ответ: 1 | 14 | т.к a=-4<0, то ветки параболы направлены вниз. Ответ: 2 |
15 | Ответ: 0 | 15 | Ответ: 18 |
16 | 1 | 16 | 4 |
17 | 17 | ||
/data/files/k1594744081. docx (ТЕСТ)
docx (ТЕСТ)
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
3.3.3 Квадратичная функция, её график
Видеоурок 1: Квадратичная функция. Часть 1
Видеоурок 2: Квадратичная функция. Часть 2
Видеоурок 3: Построение графика квадратичной функции
Лекция: Квадратичная функция, её график
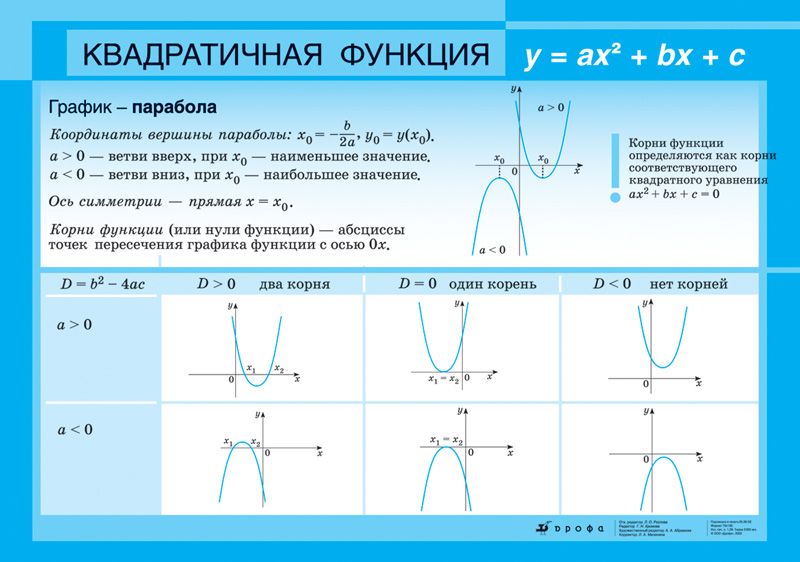
Квадратичная функцияЕсли перед Вами появилась функция вида у = ах2 + bx + c, то такая функция будет иметь название квадратичной.
Обратите внимание, функция будет квадратичной только в том случае, если коэффициент а ≠ 0.
Итак, в данной функции а, b и с — это коэффициенты:
а — коэффициент при старшем члене,
b — второй коэффициент,
с — свободных член.

Любая квадратичная функция на координатной плоскости изображается в виде параболы, однако функция у = х2 имеет вид:
При с = 0 график всегда начинается в начале координат, а остальные 4 точки определяются самостоятельно:
Если коэффициент а < 0, то данный график будет иметь немного другой вид — ветки параболы будут направлены вниз:
Характеристика функции у = х2
1. Область значения функции — существует для всех действительных чисел.
2. Область значения функции — функция не может принимать отрицательные значения.
3. Парная функция, симметрична относительно оси ОУ.
4. Монотонно убывает на промежутке от минус бесконечности до нуля, монотонно возрастает на промежутке от нуля до бесконечности.
5. Минимум функции на все рассматриваемом промежутке в точке [0; 0].
Решение квадратного уравнения
Как мы знаем, при решении квадратного уравнения может существовать несколько случаев, которые влияют на количество корней.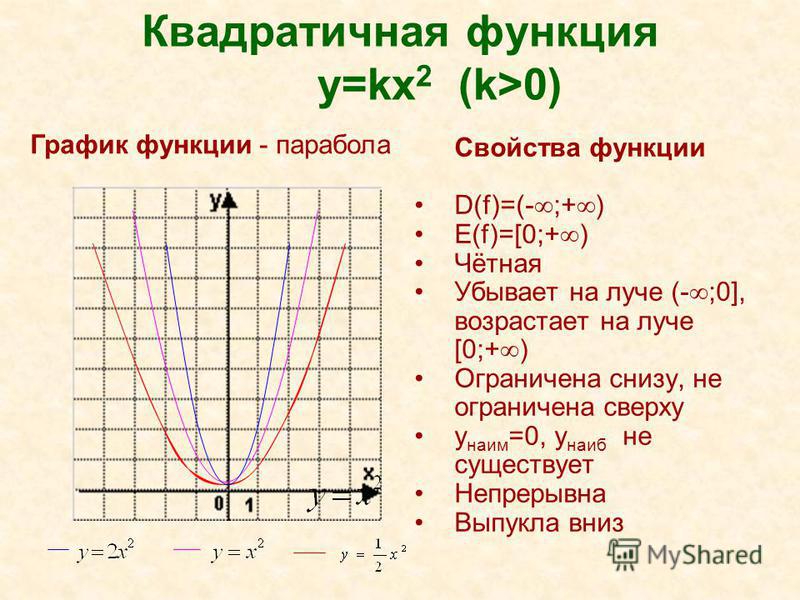 Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.
Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.
1. Если мы имеем уравнение вида у = ах2 + bx + c, то решая его по дискриминанту, можем получить D < 0. С точки зрения графика квадратичной функции это значит, что вершина параболы находится над осью ОХ, а её ветки направлены вверх. Именно из-за того, что не существует пересечения с осью ОХ, решений данное уравнение не имеет.
2. Если дискриминант равен нулю D = 0, то это означает, что уравнение имеет один корень. Следовательно, на графике это можно показать в качестве вершины, которая лежит на оси ОХ.
3. Если дискриминант больше нуля D > 0, это значит, что уравнение имеет два корня. На графике это можно показать, как пересечение оси ОХ ветвями параболы.
Алгоритм построения квадратичной функции
Давайте рассмотри алгоритм построение параболы по квадратичной функции на примере следующей функции: у = 2х2 + 3х — 5.
1. Первым делом следует определиться с направлением ветвей параболы. Для этого необходимо обратить внимание на коэффициент, который стоит перед старшим членом. Если коэффициент положительный, то ветви параболы направлены вверх. Следовательно, 2 > 0, а значит, в нашей функции ветви параболы направлены вверх.
2. Дальше следует приравнять функцию к нулю для нахождения дискриминанта. В данном получившемся уравнении дискриминант больше нуля, а это значит, что мы будем иметь два решения, а значит, два пересечение графика с осью ОХ.
3. Теперь давайте определим, в каких точках график будет пересекать ось ОХ. Для этого необходимо решить получившееся уравнение.
В данном случае мы получили корни:
х1 = 1, х2 = -2,5.
4. Находим координату вершины параболы. Для этого необходимо воспользоваться формулой:
5. Еще дополнительные две симметричные точки находятся через подстановку вместо «х» нуля. В нашем уравнении мы получили, что при х = 0, у = -5.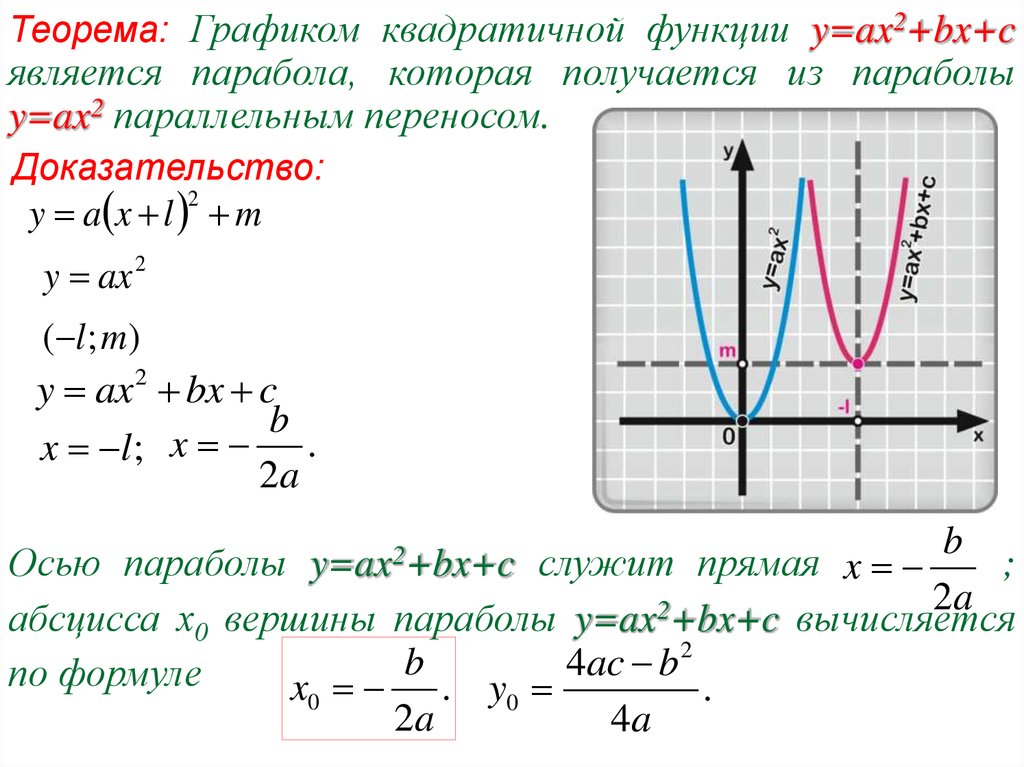
6. А теперь нанесем вершину, точки пересечения с осью ОХ и ОУ на график. В результате этого получим:
- Вконтакте
- Сайт
Учебник по алгебре в колледже 34
Колледж Алгебра
Учебник 34: Графики квадратичных Функции
WTAMU > Виртуальная математическая лаборатория> Алгебра колледжа
> Цели обученияПосле завершения этого руководства вы сможете:
- Найдите вершину квадратичной функции.

- Определите, является ли вершина максимальной или минимальной точкой квадратичного функция.
- График квадратичной функции.
Введение
В этом уроке мы рассмотрим графики квадратичных функций.
График квадратичной функции называется параболой и имеет кривую
форма. Одной из главных точек параболы является ее вершина.
Это самая высокая или самая низкая точка на его графике. Вы можете думать
как конец параболы. Я покажу вам, как найти
вершина, а также ось симметрии, проходящая через эту точку.
Я также освежу вашу память о том, как найти х —
и у — перехваты. Если вам нужен обзор
о том, что такое перехваты на графике, смело переходите к Tutorial
26: Уравнения линий. При обнаружении x перехватов
вам придется решать квадратное уравнение. Если вы
нужен обзор по решению квадратных уравнений, смело переходите к Tutorial
17: Квадратные уравнения.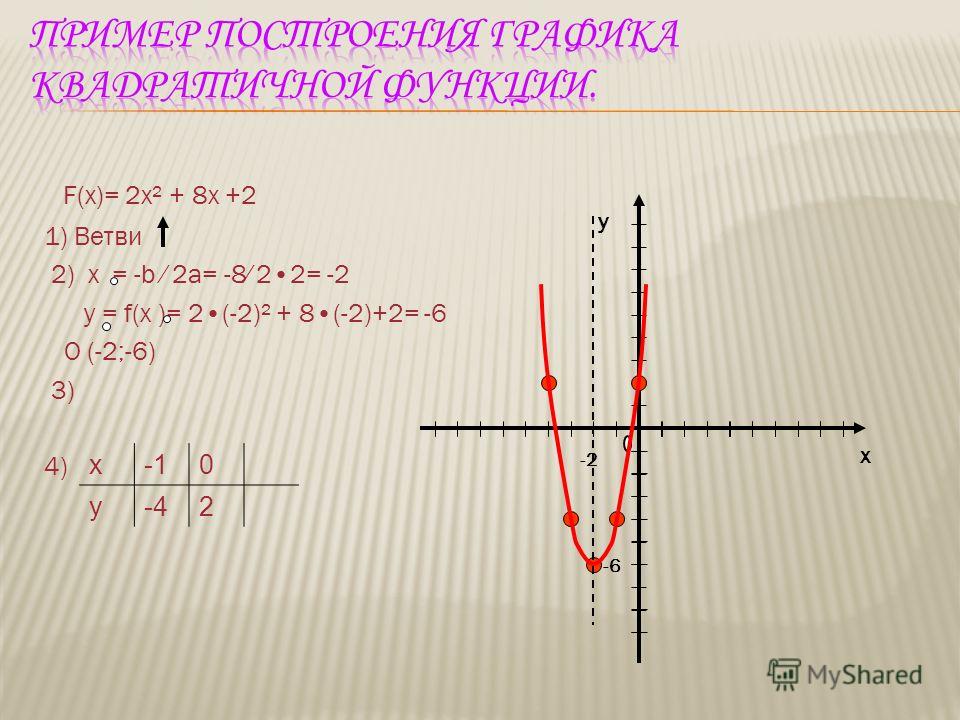 Если вы учитесь в колледже по алгебре
класс, работа с квадратичными функциями неизбежна, даже если это против
твоя религия. Так что, я думаю, вам лучше начать.
Если вы учитесь в колледже по алгебре
класс, работа с квадратичными функциями неизбежна, даже если это против
твоя религия. Так что, я думаю, вам лучше начать.
Учебник
Квадратичная функция
Квадратичная функция — это функция, которую
можно записать в виде
где а , б ,
и с
константы и
Обратите внимание, что в квадратичной функции есть степень двойки на вашей независимой переменная, и это высшая степень.
Стандартная форма
Квадратичная функция
Иногда квадратичная функция записывается в стандартной форме.
Можно оставить его в таком виде при работе с вашей проблемой.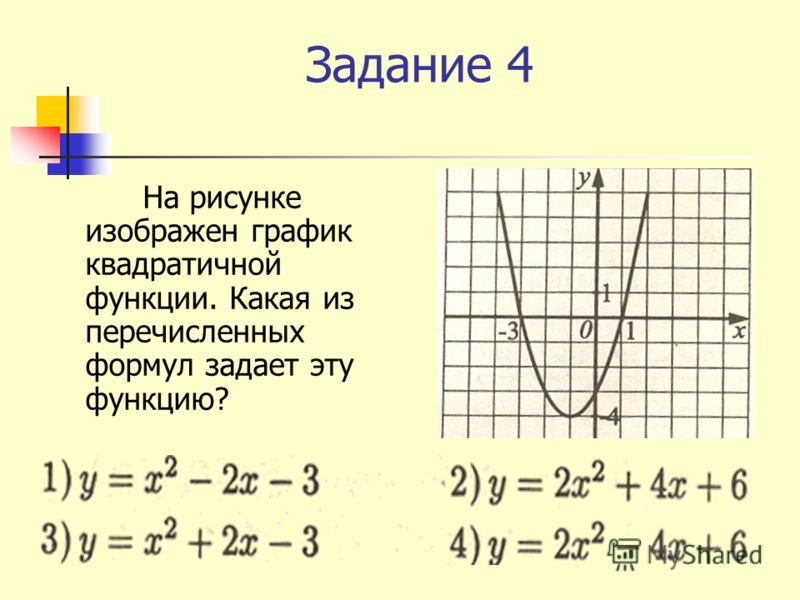 Я покажу вам, как построить параболу, используя любую форму.
Я покажу вам, как построить параболу, используя любую форму.
График квадратичной функции
График квадратичной функции называется параболой . Это в основном изогнутая форма, открывающаяся вверх или вниз.
О чем говорят нам числа и ?
Если у вас есть квадратичная функция в любой форме, ИЛИ,
если a > 0, то парабола открывается вверх ,
если a < 0, то парабола открывается вниз .
Вершина
Вершина — самая низкая или самая высокая точка (в зависимости от направления)
на графике квадратичной функции.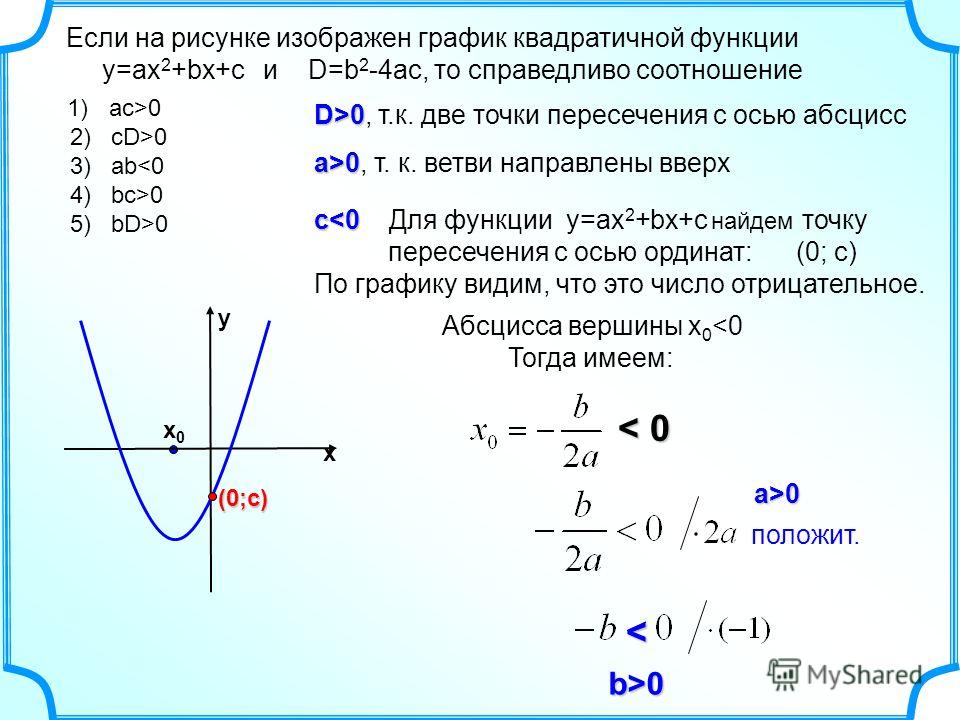
Нахождение вершины с помощью формы
, :
Если ваша квадратичная функция имеет вид
, ,
затем
вершина = .
В основном вы найдете x значение сначала вершину, а затем просто вставьте это значение в функцию, чтобы получить y или функциональное значение вершины.
Нахождение вершины с помощью формы :
Если ваша квадратичная функция имеет вид , затем
вершина = ( ч , к ).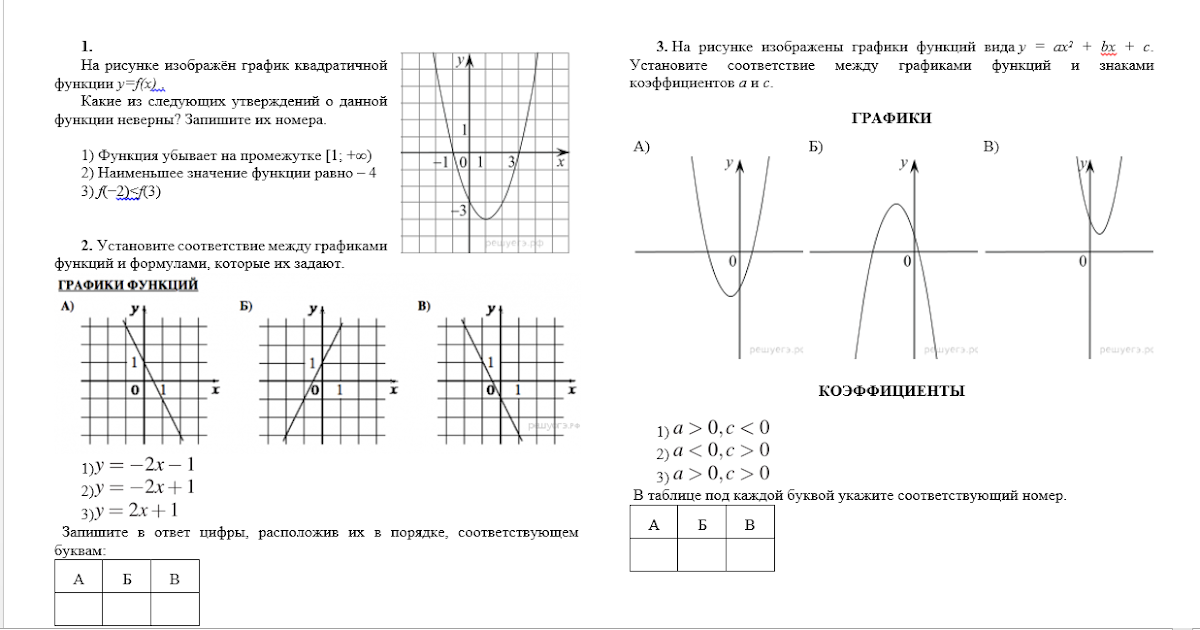
Ось симметрии
Каждая парабола симметрична относительно вертикальной линии, называемой осью симметрии. Эта вертикальная линия проходит через вершину.
Думайте об этом как о зеркальном отображении этой вертикальной линии.
Следующие три графика иллюстрируют различные аспекты графика квадратичной функции или параболы.
Ниже приведен график функции :
Я хочу, чтобы вы обратили внимание на некоторые особенности этого
график:
Прежде всего, посмотрите, как вершина является
самая нижняя точка на графике.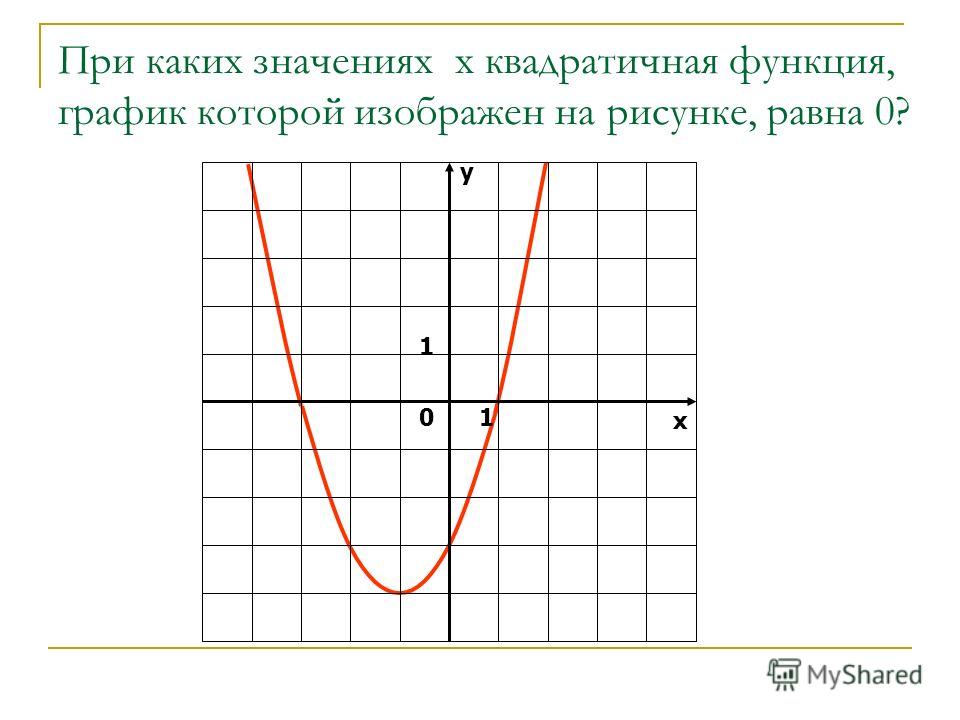 Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, как есть один y -intercept
но нет x — перехват . квадратичный
функция может не иметь ни одного, одного или двух x -перехватов.
Ниже приведен график функции :
Я хочу, чтобы вы обратили внимание на некоторые особенности этого
график:
Прежде всего, посмотрите, как вершина является
самая нижняя точка на графике. Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Он либо будет самым низким, либо
наивысшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, как есть один y -intercept
и один x -перехват . квадратичный
функция может не иметь ни одного, одного или двух x -перехватов.
Ниже приведен график функции :
Я хочу, чтобы вы кое-что заметили по этому поводу. график:
график:
Прежде всего, посмотрите, как вершина является наивысшая точка на графике. Он либо будет самым низким, либо наивысшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . это не на самом деле часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, как есть один y -intercept
и два x -перехваты . квадратичный
функция может не иметь, одну или две x -перехваты.
Пример
1 : Найдите координаты вершины .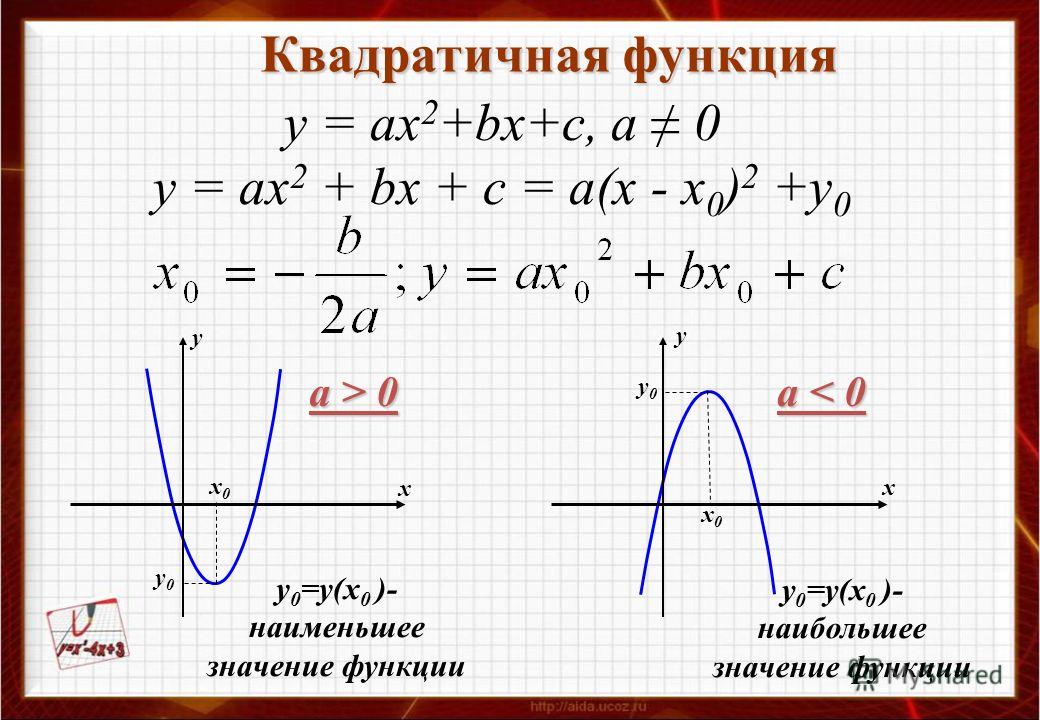 Без построения графика определите, является ли вершина максимальной или минимальной точкой
квадратичной функции.
Без построения графика определите, является ли вершина максимальной или минимальной точкой
квадратичной функции.
Вершина
Обратите внимание, как эта квадратичная функция записывается в стандартной форме.
Это значит, что мы можем найти вершину, выровняв ее
с общей стандартной формой и идентифицируйте ( h , k ).
*Стандартная форма четверки. функция
С ( ч , к ) является вершиной в стандартной форме, как вы думаете, что наша вершина для этого проблема?
Если вы сказали (1, -3), вы правы.
Будьте осторожны со своими знаками по этой проблеме. это реально заманчиво
сказать, что вершина (1, 3). Однако внимательно посмотрите на
стандартная форма. Обратите внимание, что знак перед h — минус, а перед k — плюс.
Итак, ч — это число, которое мы вычитаем из х ,
что в нашем случае равно 1. к это номер
мы добавляем в конце, что в нашем случае мы добавляем минус 3.
это реально заманчиво
сказать, что вершина (1, 3). Однако внимательно посмотрите на
стандартная форма. Обратите внимание, что знак перед h — минус, а перед k — плюс.
Итак, ч — это число, которое мы вычитаем из х ,
что в нашем случае равно 1. к это номер
мы добавляем в конце, что в нашем случае мы добавляем минус 3.
Максимум или минимум?
Далее мы хотим определить, является ли вершина,
мы нашли, (1, -3), является точкой максимума или минимума, без построения графика.
Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.
Начиная с и = 4 и 4 больше 0, эта парабола развернется .
Значит ли это, что вершина является максимальной или минимальной? точка?
Если вы сказали минимальный балл, вы правы.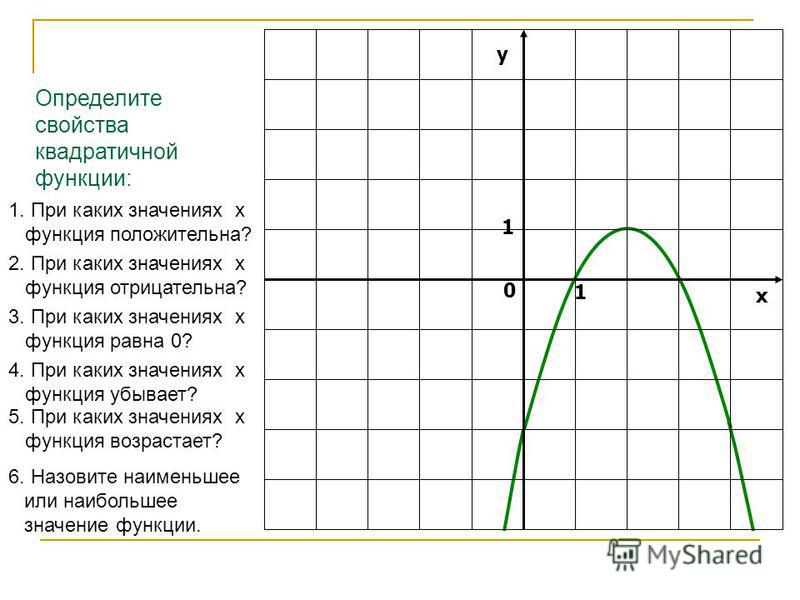
Итак, наша вершина (1, -3) является точкой минимума.
Пример 2 : Найдите координаты вершины . Без построения графика определите, является ли вершина максимальной или минимальной точкой квадратичной функции.
Вершина
Обратите внимание, как эта квадратичная функция записывается в виде .
Это означает, что мы можем найти вершину, используя
формула .
*Укажите a , b ,
и с
*Подставить значения в вершинную форму. для а , б ,
и с
для а , б ,
и с
*Подставьте -5/4 дюйма для x , чтобы найти значение y для вершины
Вершина будет .
Максимум или минимум?
Далее мы хотим определить, является ли вершина,
мы нашли, , является максимальным
или точка минимума, без построения графика.
Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.
Начиная с и = -2, и -2 меньше 0, эта парабола развернулась бы вниз .
Значит ли это, что вершина является максимальной или минимальной? точка?
Если вы сказали максимальное количество баллов, вы правы.
Итак, наша вершина — точка максимума.
График квадратичной функции
Шаг 1: Выполняется кривая графика вверх или вниз?
Шаг 2: Найдите вершина.
Шаг 3: Найдите точки пересечения.
Если вам нужен обзор перехватов, смело переходите к Tutorial 26: Уравнения линий .
Шаг 4: Постройте параболу.
Нанесите точки, найденные в шагах 2 и 3, и проведите кривую через их.
Пример
3 : Используйте вершину и точки пересечения, чтобы нарисовать график
квадратичная функция.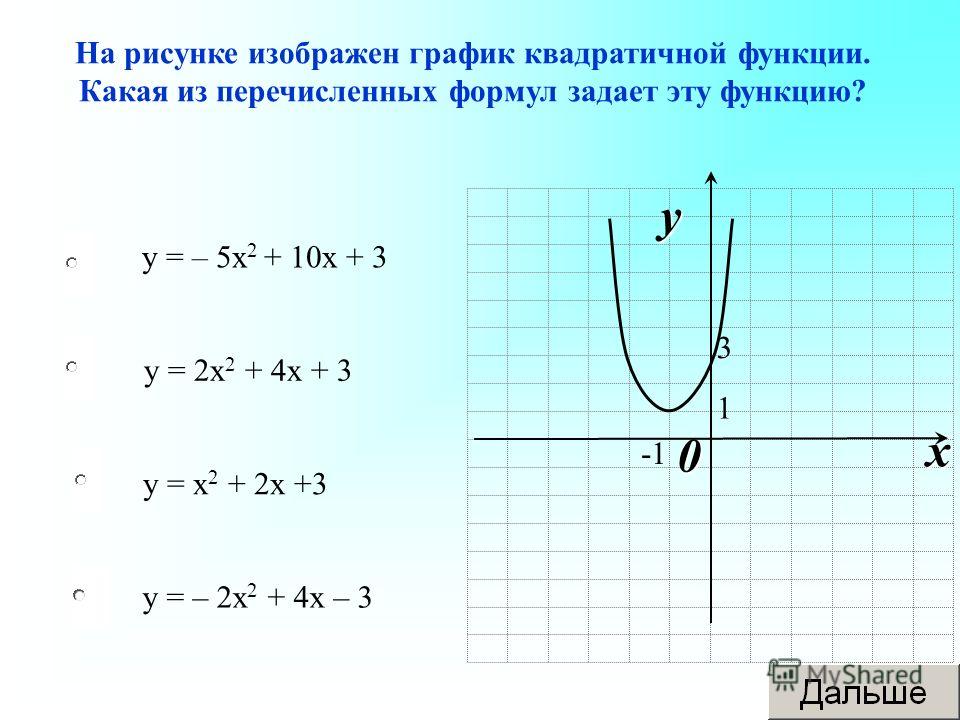 Найдите уравнение для оси симметрии этой функции.
Найдите уравнение для оси симметрии этой функции.
Шаг 1: Выполняется кривая графика вверх или вниз?
Поскольку a = -1 и -1 < 0, то это выглядит как и , он будет изгибаться вниз.
Это дает нам хорошее представление о том, что мы идем в правильном направлении.
Шаг 2: Найдите вершина.
Как и в примере 1 выше, эта квадратичная функция записывается в стандартной форме. Это означает, что мы можем найти вершину, сопоставив ее с общей стандартной формой, и выявить ( ч , к ).
*Стандартная форма четверки. функция
С ( ч , к ) Вершина имеет стандартную форму, как вы думаете, что это за вершина?
Если вы сказали (-1, 4), вы правы.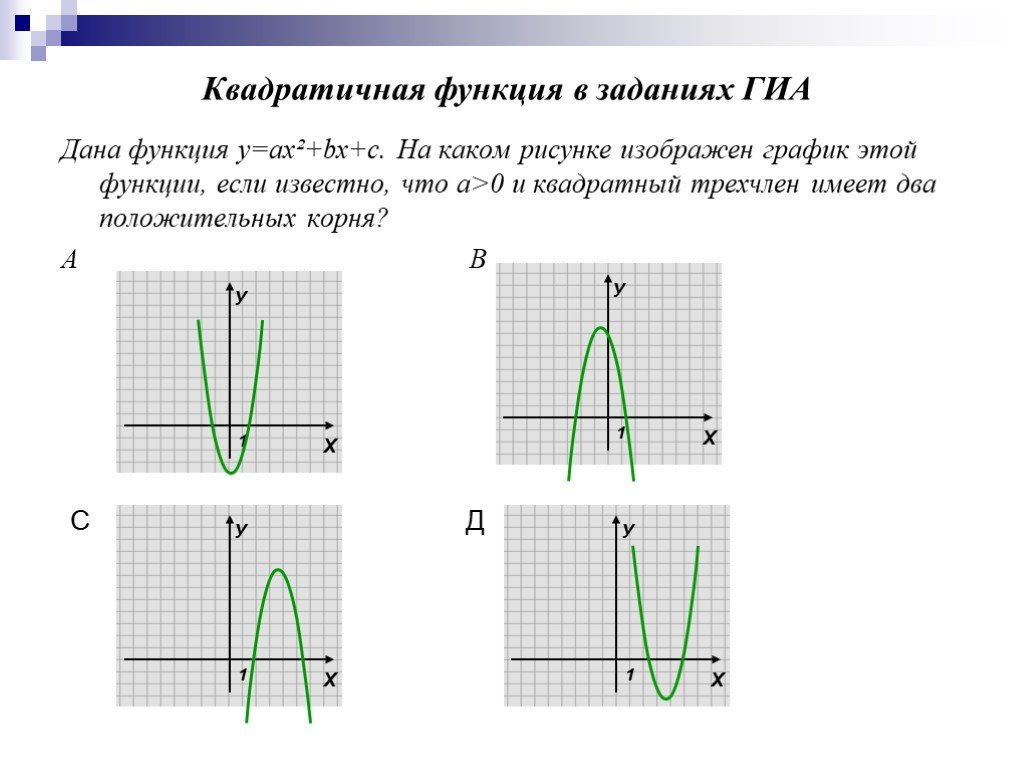
Будьте осторожны со своими знаками по этой проблеме. Обратите внимание, как
знак перед ч это минус, но
один перед k положительный. Итак, ч
число, которое мы вычитаем из x , что
в нашем случае -1. k — это число, которое мы
добавляем в конце, что в нашем случае мы добавляем 4.
Шаг 3: Найдите перехваты.
у -перехват
Напоминаем, что y -перехват всегда
где график пересекает ось y , что означает x = 0:
*Замените x на
0
Пересечение и равно (0, 3).
x — точка пересечения
Напоминаем, что перехват x всегда
где график пересекает ось x , что означает y = 0:
*Замените y (или
f(x)) с 0
*Решить
квадратичный факторизацией
x -пересечений (-3, 0) и (1,
0).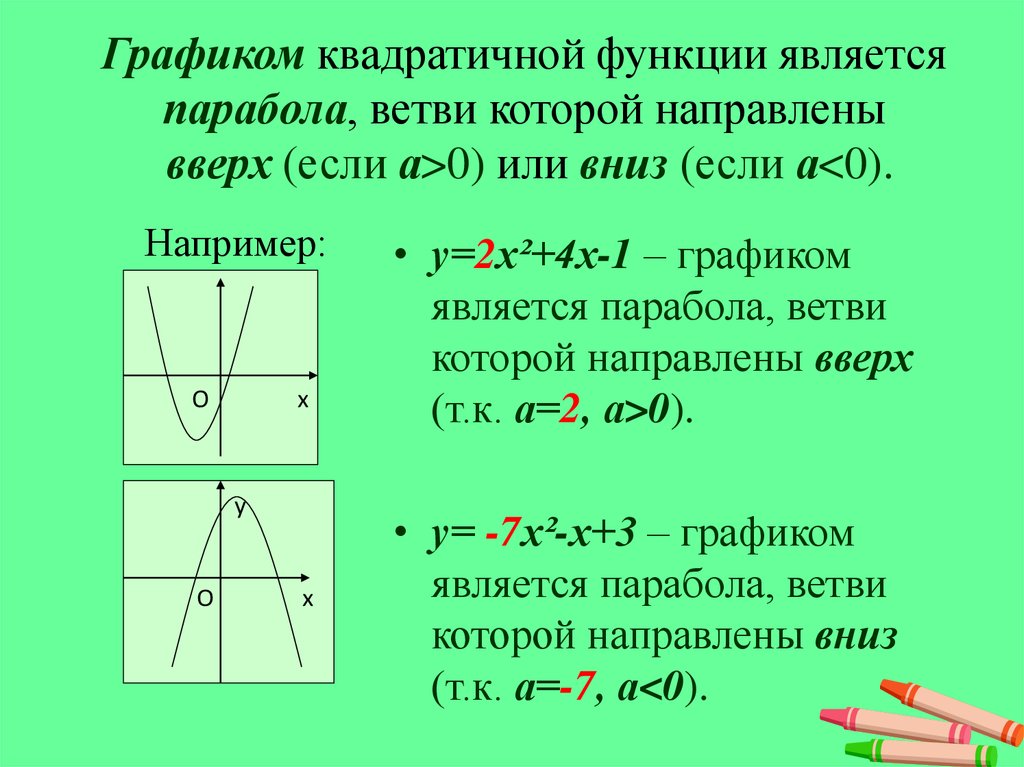
Шаг 4: График парабола.
Ось симметрии
Как показано на графике, ось симметрии равна x = -1.
Пример 4 : Используйте вершину и точки пересечения, чтобы нарисовать график квадратичная функция. Найдите уравнение для оси симметрии этой функции.
Шаг 1: Выполняется кривая графика вверх или вниз?
Поскольку a = 1 и 1 > 0, то это выглядит как it собирается изогнуться.
Это дает нам хорошее представление о том, что мы идем в правильном направлении.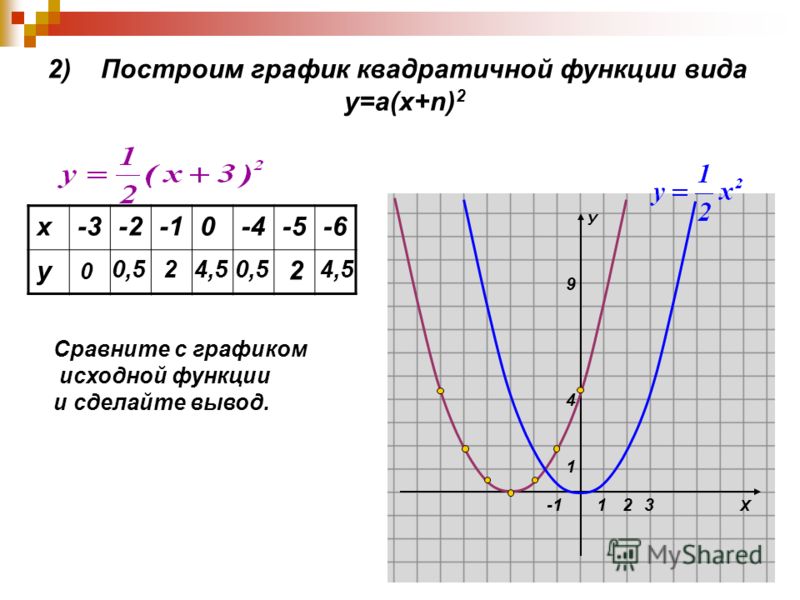
Шаг 2: Найдите вершина.
Как и в примере 2 выше, эта квадратичная функция записывается в виде . Это означает, что мы можем найти вершину, используя формула .
*Укажите a , b ,
и с
*Подставить значения в вершинную форму. для а , б ,
и с
*Подставьте -1 для x , чтобы найти значение y для вершины
Итак, вершина равна (-1, 1).
Шаг 3: Найдите
перехваты.
у -перехват
Напоминаем, что y -перехват всегда
где график пересекает ось y , что означает x = 0:
*Замените x на
0
Пересечение y равно (0, 2).
x — точка пересечения
Напоминаем, что перехват x всегда
где график пересекает ось x , что означает y = 0:
*Заменить и (или f(x)) с 0
Обратите внимание, что это не учитывается. Попробуем решить с помощью квадратичная формула:
*Квадратичный
формула
*Подставьте значения для a , b ,
и с
Обратите внимание, что мы получили отрицательное число под квадратным корнем. Это означает, что нет действительного числового решения. Это также означает, что
НЕТ x -перехватов.
Это означает, что нет действительного числового решения. Это также означает, что
НЕТ x -перехватов.
Шаг 4: График парабола.
Ось симметрии
Как показано на графике, ось симметрии равна x = -1.
Практические задачи
Это практические задачи, которые помогут вам перейти на следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы эти
виды проблем. Математика работает так же, как и все
в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться.
Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этого, вам следует решить проблему на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения для этой задачи . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1а — 1б: Найти координаты вершины заданного квадратичная функция. Без построения графика определите, является ли вершина точка максимума или минимума квадратичной функции.
1а.
(ответ/обсуждение
к 1а)
1б.
(ответ/обсуждение
к 1б)
Практика Задачи 2a–2b: Используйте вершину и точки пересечения, чтобы нарисовать график заданной квадратичной функции.
Найдите уравнение для этого ось симметрии функции.
2а.
(ответ/обсуждение
к 2а)
2б.
(ответ/обсуждение
к 2б)
Нужна дополнительная помощь по этим темам?
Ниже представлена веб-страница, которая может помочь вас в темах, которые были освещены на этой странице:
http://www.purplemath.com/modules/grphquad.htm
Эта веб-страница поможет вам построить график парабол.
Обратитесь за помощью за пределами Класс, найденный в Учебнике 1: Как преуспеть в математическом классе для некоторых больше предложений.
WTAMU > Виртуальная математическая лаборатория > Алгебра колледжа
Последняя редакция Ким Сьюард от 10 июля 2010 г.
Авторские права на все содержимое (C) 2002–2010, WTAMU и Ким Сьюард. Все права защищены.
Квадратичные функции и их графики — Алгебра
Как определить вершину и направление квадратичной функции? 92 +k#)
1. Направление параболы можно определить по значению a. Если а положительно, то парабола направлена вверх (делает букву U). Если a отрицательно, то парабола обращена вниз (перевернутая u).
2. Вершина (h,k).
Вот пример:
#y = -3(x-2)+6# Лицевой стороной вниз, так как a = -3 и вершина (2, 6).Как найти x точек пересечения квадратичной функции? 92+bx+c#, что является уравнением второй степени.
Решив это уравнение, вы найдете два значения x (x1 и x2), которые вместе с y=0 дадут вам точки пересечения:Помните, что уравнение второй степени также может иметь решения:
— совпадающие (точка пересечения есть ВЕРШИНА параболы)
— мнимые (парабола не пересекает ось x)
В зависимости от дискриминанта уравнения.

 к a=6>0, то ветки параболы направлены вверх.
к a=6>0, то ветки параболы направлены вверх.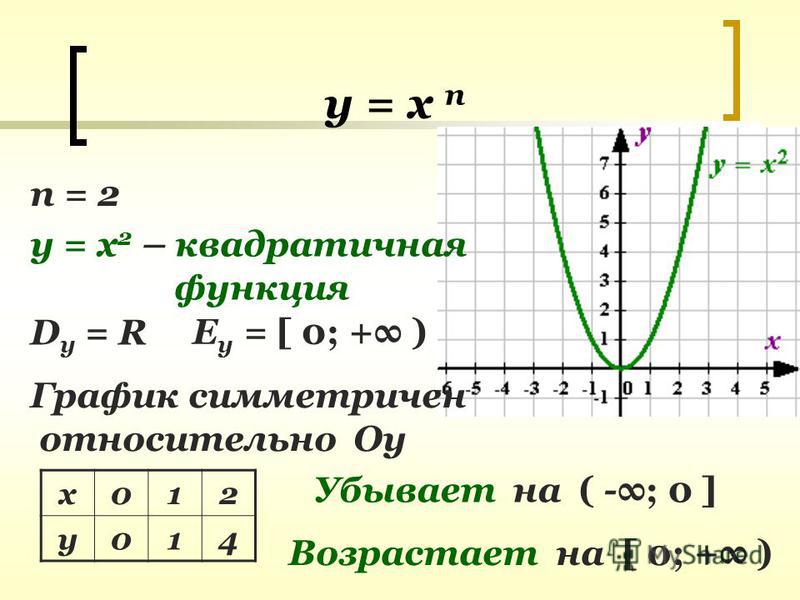

 Найдите уравнение для этого
ось симметрии функции.
Найдите уравнение для этого
ось симметрии функции. 