Решите ту же задачу для прямоугольника не являющегося квадратом 4 класс: Решите задачу Квадрат и прямоугольник имеют равные площади,соседние стороны прямоугольника равны 3 см 12 см…

Циклы в программировании. Цикл while. Урок 10 курса «Python. Введение в программирование»

Циклы являются такой же важной частью структурного программирования, как условные операторы. С помощью циклов можно организовать повторение выполнения участков кода. Потребность в этом возникает довольно часто. Например, пользователь последовательно вводит числа, и каждое из них требуется добавлять к общей сумме. Или нужно вывести на экран квадраты ряда натуральных чисел и тому подобные задачи.

Цикл while

«While» переводится с английского как «пока». Но не в смысле «до свидания», а в смысле «пока имеем это, делаем то».

Можно сказать, while является универсальным циклом. Он присутствует во всех языках, поддерживающих структурное программирование, в том числе в Python. Его синтаксис обобщенно для всех языков можно выразить так:

while логическое_выражение {
    выражение 1;
    …
    выражение n;
}

Это похоже на условный оператор if. Однако в случае циклических операторов их тела могут выполняться далеко не один раз. В случае

if, если логическое выражение в заголовке возвращает истину, то тело выполняется единожды. После этого поток выполнения программы возвращается в основную ветку и выполняет следующие выражения, расположенные ниже всей конструкции условного оператора.

В случае while, после того как его тело выполнено, поток возвращается к заголовку цикла и снова проверяет условие. Если логическое выражение возвращает истину, то тело снова выполняется. Потом снова возвращаемся к заголовку и так далее.

Цикл завершает свою работу только тогда, когда логическое выражение в заголовке возвращает ложь, то есть условие выполнения цикла больше не соблюдается. После этого поток выполнения перемещается к выражениям, расположенным ниже всего цикла. Говорят, «происходит выход из цикла».

Рассмотрите блок-схему цикла while.

На ней ярко-голубыми прямоугольниками обозначена основная ветка программы, ромбом – заголовок цикла с логическим выражением, бирюзовым прямоугольником – тело цикла.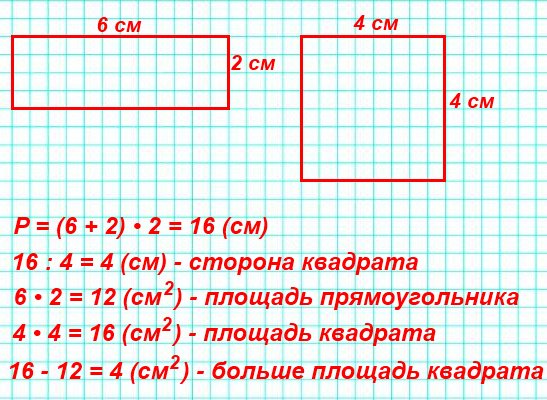

С циклом while возможны две исключительные ситуации:

• Если при первом заходе в цикл логическое выражение возвращает False, то тело цикла не выполняется ни разу. Эту ситуацию можно считать нормальной, так как при определенных условиях логика программы может предполагать отсутствие необходимости в выполнении выражений тела цикла.

• Если логическое выражение в заголовке while никогда не возвращает False, а всегда остается равным True, то цикл никогда не завершится, если только в его теле нет оператора принудительного выхода из цикла (break) или вызовов функций выхода из программы – quit()

  , exit() в случае Python. Если цикл повторяется и повторяется бесконечное количество раз, то в программе происходит зацикливание. В это время она зависает и самостоятельно завершиться не может.

Вспомним наш пример из урока про исключения. Пользователь должен ввести целое число. Поскольку функция input() возвращает строку, то программный код должен преобразовать введенное к целочисленному типу с помощью функции int(). Однако, если были введены символы, не являющиеся цифрами, то возникает исключение ValueError, которое обрабатывается веткой except. На этом программа завершается.

Другими словами, если бы программа предполагала дальнейшие действия с числом (например, проверку на четность), а она его не получила, то единственное, что программа могла сделать, это закончить свою работу досрочно.

Но ведь можно просить и просить пользователя корректно вести число, пока он его не введет. Вот как может выглядеть реализующий это код:

n = input("Введите целое число: ")
 
while type(n) != int:
    try:
        n = int(n)
    except ValueError:
        print("Неправильно ввели!")
        n = input("Введите целое число: ")
 
if n % 2 == 0:
    print("Четное")
else:
    print("Нечетное")

Примечание 1. Не забываем, в языке программирования Python в конце заголовков сложных инструкций ставится двоеточие.

Примечание 2. В выражении type(n) != int с помощью функции type() проверяется тип переменной n. Если он не равен int, то есть значение n не является целым числом, а является в данном случае строкой, то выражение возвращает истину. Если же тип

n равен int, то данное логическое выражение возвращает ложь.

Примечание 3. Оператор % в языке Python используется для нахождения остатка от деления. Так, если число четное, то оно без остатка делится на 2, то есть остаток будет равен нулю. Если число нечетное, то остаток будет равен единице.

Проследим алгоритм выполнения этого кода. Пользователь вводит данные, они имеют строковый тип и присваиваются переменной n. В заголовке while проверяется тип n. При первом входе в цикл тип n всегда строковый, то есть он не равен int. Следовательно, логическое выражение возвращает истину, что позволяет зайти в тело цикла.

Здесь в ветке try совершается попытка преобразования строки к целочисленному типу. Если она была удачной, то ветка except пропускается, и поток выполнения снова возвращается к заголовку

while.

Теперь n связана с целым числом, следовательно, ее тип int, который не может быть не равен int. Он ему равен. Таким образом логическое выражение type(n) != int возвращает False, и весь цикл завершает свою работу. Далее поток выполнения переходит к оператору if-else, находящемуся в основной ветке программы. Здесь могло бы находиться что угодно, не обязательно условный оператор.

Вернемся назад. Если в теле try попытка преобразования к числу была неудачной, и было выброшено исключение ValueError, то поток выполнения программы отправляется в ветку except и выполняет находящиеся здесь выражения, последнее из которых просит пользователя снова ввести данные. Переменная

n теперь имеет новое значение.

После завершения except снова проверяется логическое выражение в заголовке цикла. Оно даст True, так как значение n по-прежнему строка.

Выход из цикла возможен только тогда, когда значение n будет успешно конвертировано в число.

Рассмотрим следующий пример:

total = 100
 
i = 0
while i < 5:
    n = int(input())
    total = total - n
    i = i + 1
 
print("Осталось", total)

Сколько раз «прокрутится» цикл в этой программе, то есть сколько итераций он сделает? Ответ: 5.

1. Сначала переменная i равна 0. В заголовке цикла проверяется условие i < 5, и оно истинно. Тело цикла выполняется. В нем меняется значение i, путем добавления к нему единицы.

2. Теперь переменная i равна 1. Это меньше пяти, и тело цикла выполняется второй раз.

   В нем i меняется, ее новое значение 2.

3. Два меньше пяти. Тело цикла выполняется третий раз. Значение i становится равным трем.

4. Три меньше пяти. На этой итерации i присваивается 4.

5. Четыре по прежнему меньше пяти. К i добавляется единица, и теперь ее значение равно пяти.

Далее начинается шестая итерация цикла. Происходит проверка условия i < 5. Но поскольку теперь оно возвращает ложь, то выполнение цикла прерывается, и его тело не выполняется.

«Смысловая нагрузка» данного цикла – это последовательное вычитание из переменной total вводимых чисел. Переменная i в данном случае играет только роль счетчика итераций цикла. В других языках программирования для таких случаев предусмотрен цикл

for, который так и называется: «цикл со счетчиком». Его преимущество заключается в том, что в теле цикла не надо изменять переменную-счетчик, ее значение меняется автоматически в заголовке for.

В языке Python тоже есть цикл for. Но это не цикл со счетчиком. В Питоне он предназначен для перебора элементов последовательностей и других сложных объектов. Данный цикл и последовательности будут изучены в последующих уроках.

Для while наличие счетчика не обязательно. Представим, что надо вводить числа, пока переменная total больше нуля. Тогда код будет выглядеть так:

total = 100
 
while total > 0:
    n = int(input())
    total = total - n
 
print("Ресурс исчерпан")

Сколько раз здесь выполнится цикл? Неизвестно, все зависит от вводимых значений. Поэтому у цикла со счетчиком известно количество итераций, а у цикла без счетчика – нет.

Самое главное для цикла while – чтобы в его теле происходили изменения значений переменных, которые проверяются в его заголовке, и чтобы хоть когда-нибудь наступил случай, когда логическое выражение в заголовке возвращает False. Иначе произойдет зацикливание.

Примечание 1. Не обязательно в выражениях total = total - n и i = i + 1 повторять одну и ту же переменную. В Python допустим сокращенный способ записи подобных выражений: total -= n и i += 1.

Примечание 2. При использовании счетчика он не обязательно должен увеличиваться на единицу, а может изменяться в любую сторону на любое значение. Например, если надо вывести числа кратные пяти от 100 до 0, то изменение счетчика будет таким

i = i - 5, или i -= 5.

Примечание 3. Для счетчика не обязательно использовать переменную с идентификатором i. Можно назвать переменную-счетчик как угодно. Однако так принято в программировании, что счетчики обозначают именами i и j (иногда одновременно требуются два счетчика).

Практическая работа

1. Измените последний код из урока так, чтобы переменная total не могла уйти в минус. Например, после предыдущих вычитаний ее значение стало равным 25. Пользователь вводит число 30. Однако программа не выполняет вычитание, а выводит сообщение о недопустимости операции, после чего осуществляет выход из цикла.

2. Используя цикл while, выведите на экран для числа 2 его степени от 0 до 20. Возведение в степень в Python обозначается как **. Фрагмент вывода:

   ...
     32
     64
    128
    256
    512
   1024
   ...

Примеры решения и дополнительные уроки в pdf-версии курса

Формула площади прямоугольника (Слупко М.В.) | Математика | 5 класс

Введение

Представьте ситуацию. Мама хочет испечь торт. Но у неё осталось мало глазури, которой она его покроет сверху. На какой из этих трёх тортов уйдёт меньше всего глазури (Рис. 1)?

Рис. 1. Торты разной формы

Казалось бы, все просто: какая фигура меньше, на ту меньше глазури и понадобится.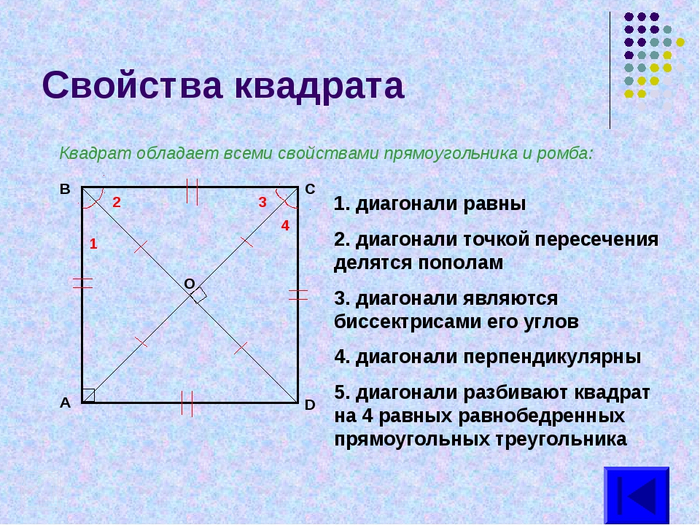 Но что такое «меньше»? Для отрезков было понятно: сравнивали длины. А что можно сравнивать у фигур? Для этого используют другую характеристику – площадь. Чем меньше будет площадь торта, тем меньше глазури понадобится маме.

А как определить площадь фигуры? Как сравнивать площади разных фигур? На этом уроке мы поговорим о том, как посчитать площадь прямоугольника.

Почему мы начинаем именно с него? Во-первых, прямоугольники в нашей жизни встречаются часто, поэтому возникает много практических задач, связанных с вычислением площади прямоугольника: сколько стекла надо, чтобы застеклить оконный проём, сколько лака надо, чтобы покрыть дверь, сколько бумаги надо, чтобы обернуть подарок и т.д. (Рис. 2).

Рис. 2. Примеры практических задач на вычисление площади прямоугольника

Во-вторых, прямоугольники легко укладывать плотно друг к другу (сравните: чем проще заполнить коробку – прямоугольными плитками или, например, круглыми, при условии, что пустого места должно оставаться как можно меньше) (Рис. 3).

Рис. 3. Заполненные прямоугольные коробки

Поэтому площадь любой фигуры можно посчитать достаточно точно, «разрезав» эту фигуру на прямоугольники (Рис. 4).

Рис. 4. Фигура разбита на прямоугольники

То есть если уметь находить площадь прямоугольников, то можно приближенно посчитать площади других фигур.

---

 

Аксиомы площади

На самом деле площадь прямоугольника важна не только для того, чтобы научиться считать площади других фигур. Она нужна, чтобы вообще дать определение: а что же такое площадь.

Интуитивно каждый из нас понимает, что такое площадь. Но сформулировать определение не так просто. Обычно говорят, что площадь – это место, которое фигура занимает на плоскости (чем больше площадь, тем больше места она занимает и наоборот).

Давайте попробуем строго определить, что же такое площадь фигуры, каким требованиям она должна удовлетворять, чтобы результат согласовывался с нашим жизненным опытом и здравым смыслом.

Итак, пусть у нас есть фигура (Рис. 1).

Рис. 1. Произвольная фигура

Чтобы найти её площадь, надо задать какой-то стандарт, то есть определить площадь известной фигуры. В математике такой фигурой считается единичный квадрат (квадрат со стороной ). Его площадь считается равной  (Рис. 2).

Рис. 2. Единичный квадрат

Теперь, если фигура состоит из двух квадратов, логично считать, что она занимает в  раза больше места, то есть её площадь равна сумме площадей двух квадратов, или равна  (Рис. 3).

Рис. 3. Фигура площадью 

Это свойство площади можно обобщить: если фигура состоит из двух фигур, то её площадь равна сумме площадей этих фигур (Рис. 4). Действительно, эта фигура занимает столько же места, сколько те две фигуры вместе взятые.

Рис. 4. Фигура состоит из двух фигур

Наконец, совсем очевидно, что у одинаковых фигур (под одинаковыми мы имеем в виду те, которые можно совместить при наложении) площади должны быть равны, так как они занимают одинаковое место (Рис. 5).

Рис. 5. Одинаковые фигуры совместились при наложении

---

 

Этих свойств достаточно, чтобы научиться считать площадь любой известной нам фигуры.

Площадь прямоугольника

Площадь фигуры равна количеству единичных квадратов, которые укладываются внутрь фигуры.

Возьмем прямоугольник: высота  см, а длина  см. Заполним его квадратами со стороной  см. Площадь каждого такого квадрата . Всего поместилось  квадратов (Рис. 5).

Рис. 5. Площадь данного прямоугольника

Значит, по определению площади фигуры, площадь нашего прямоугольника равна .

Обязательно ли нужно выкладывать все единичные квадраты внутри прямоугольника, чтобы понять, сколько их поместится? Давайте посмотрим еще раз. Выложим внизу прямоугольника один ряд единичных квадратов. Длина прямоугольника  см, а длина стороны квадрата  см. Их поместится  штук (Рис. 6).

Рис. 6. Первый ряд

Выложим второй ряд. Он будет содержать тоже  квадратов (Рис. 7).

Рис.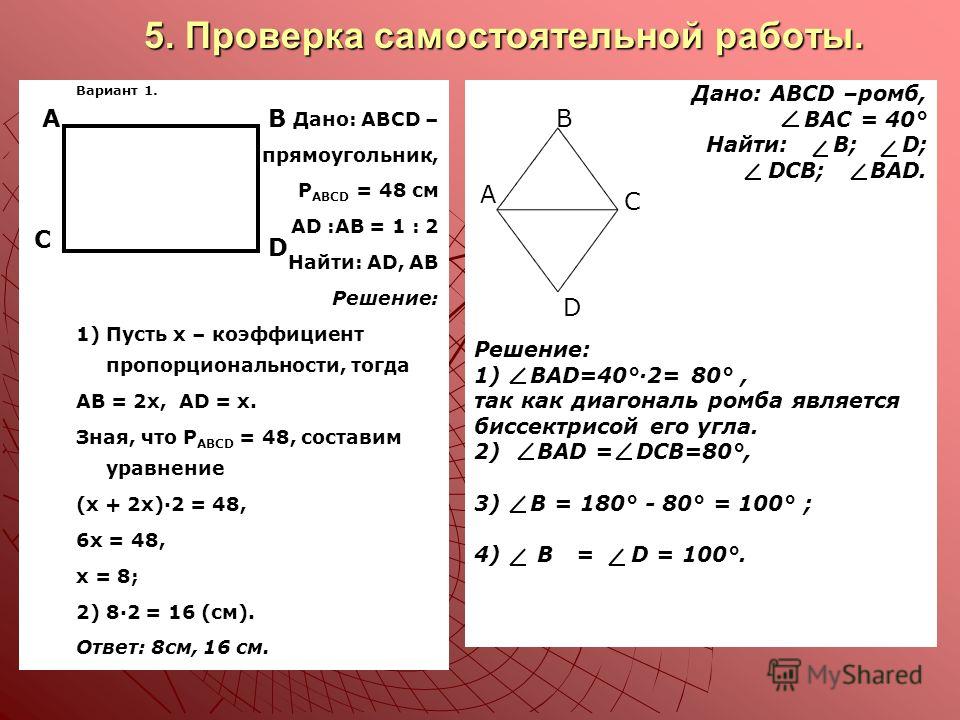 7. Второй ряд

Сколько всего таких рядов? Так как высота прямоугольника  см, то поместится  ряда (Рис. 8).

Рис. 8.  ряда

Итак,  ряда по  штук в каждом. Всего  квадратов. То есть, чтобы понять, сколько квадратов поместится, не обязательно их рисовать.

А если бы мы считали ряды по-другому? Каждый вертикальный ряд содержит  квадрата, и всего помещается  таких рядов (Рис. 9): .

Рис. 9.  рядов

Рассмотрим прямоугольник побольше. Если бы мы стали рисовать единичные квадраты, то получилось бы  рядов по  штук в каждом (Рис. 10), или, наоборот,  столбиков по  в каждом.

Рис. 10.  рядов

Рис. 11.  рядов

Но этого делать необязательно. Достаточно умножить длину одной стороны на длину другой, причем в любом порядке: .

Итак, мы получили основной вывод: площадь прямоугольника равна произведению длин двух соседних сторон:  (Рис. 12).

Рис. 12. Прямоугольник

Если длины сторон измерены в сантиметрах, то площадь по этой формуле получится в: . Если длины в метрах, то значение площади получатся в: .

Примеры

Пример 1. Найти площадь прямоугольника со сторонами  м и  м (Рис. 13).

Рис. 13. Иллюстрация к примеру 

Решение

Ответ: .

Пример 2. Найти площадь прямоугольника со сторонами  мм и  мм.

Решение

Чтобы найти площадь, нам необязательно рисовать прямоугольник. Все нужные данные у нас есть: .

Ответ: .

Может оказаться, что стороны будут измерены в разных единицах.

Пример 3. Найти площадь прямоугольника со сторонами  м и  см (Рис. 14).

Рис. 14. Иллюстрация к примеру 3

В такой ситуации нужно выразить длины сторон в одних и тех же единицах измерения.

Переведем  м в сантиметры: . Так как теперь длины у нас в см, то площадь мы получим в : .

Ответ: .

Площадь квадрата

Прямоугольник, у которого все стороны равны, называется квадратом (Рис. 15).

Рис. 15. Квадрат

К нему тоже применима формула площади прямоугольника.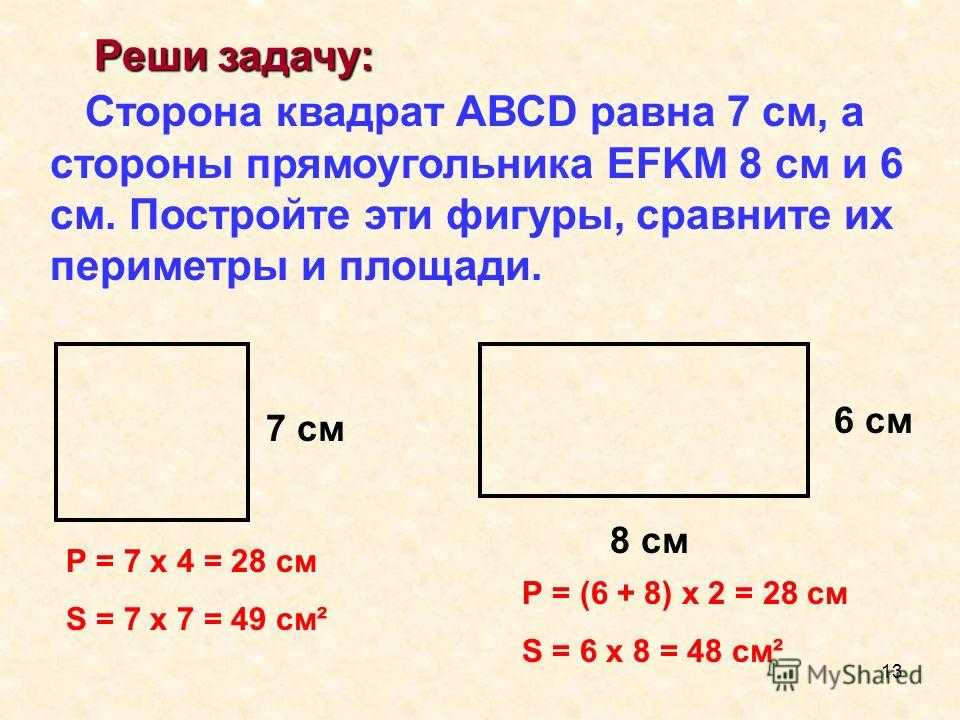 Но так как стороны равны, то формулу можно записать короче: .

Пример: найти площадь квадрата со стороной  м  см.

Решение

Запишем длину стороны в одних единицах, в сантиметрах: .

Найдем площадь квадрата: .

Ответ: .

Другой тип задач

Встречаются задачи, где уже известна площадь прямоугольника и длина одной стороны. Требуется найти другую сторону. Разберем этот случай на конкретном примере.

Пример: поле имеет ширину  метров. Какова должна быть длина поля, что площадь поля получилась  га (Рис. 16)?

Рис. 16. Иллюстрация к примеру

Решение

Начнем с единиц, в которых нам дана площадь. Вспомним, что такое  га. Гектар – мера площади, используемая в сельском хозяйстве. Она равна площади квадратного участка земли со стороной  м. Вычислим эту площадь в : . То есть площадь в  и называют  га.

Теперь вернемся к условию задачи. Требуемая площадь поля  га. Переведем ее в : . Итак, нам известны ширина поля и его площадь.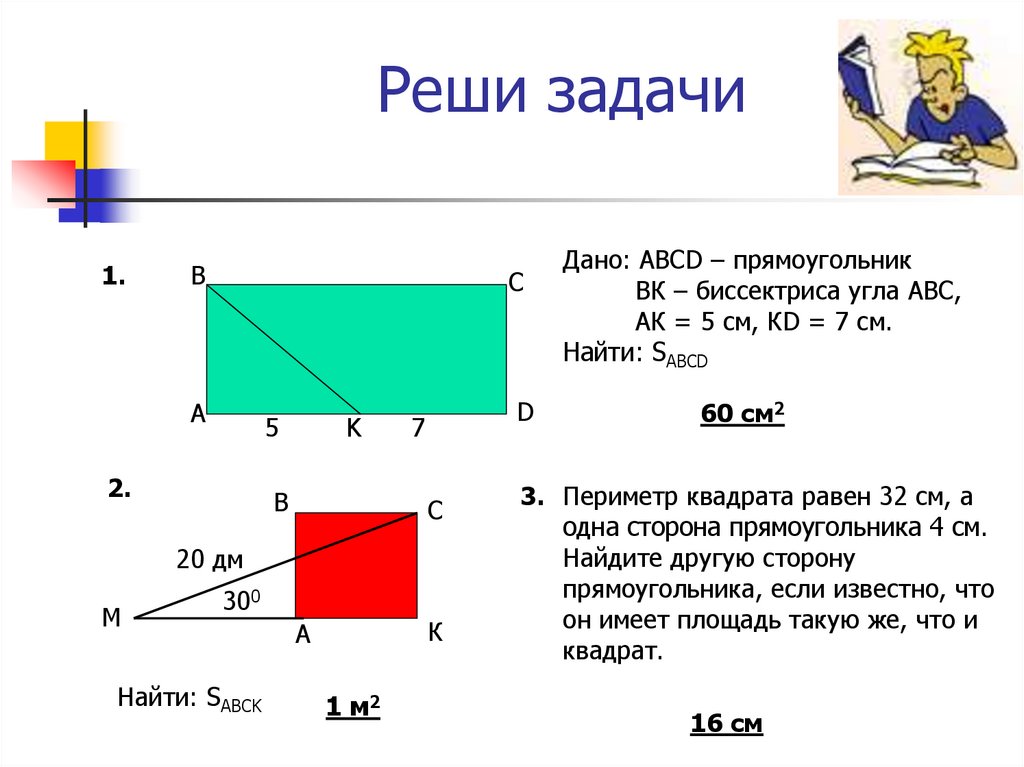 Не известна длина поля. Обозначим ее  (Рис. 17).

Рис. 17. Характеристики поля в 

Воспользуемся формулой площади прямоугольника. Площадь прямоугольника равна произведению длин его сторон: . Площадь и одну длину мы знаем. Подставим в формулу: .

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель: .

Ответ:  м.

Заключение

Итак, подведем итоги.

• Если нам известны две стороны прямоугольника (длина и ширина), то площадь прямоугольника находится по формуле  (Рис. 18).

Рис. 18. Произвольный прямоугольник

• Если длины сторон даны в м, то площадь получится в , если в мм, то площадь в , если длины в км, то площадь в .
• Если длины сторон указаны в разных единицах измерения (например, в метрах и километрах), то, прежде чем применять формулу, нужно выразить длины в одних и тех же единицах измерения (например, только в метрах).
• Формулу площади квадрата можно записать короче: .
• Если известна площадь и одна сторона прямоугольника, то мы можем найти другую сторону. Для этого площадь нужно разделить на длину известной стороны: .

Нахождение площади прямоугольника – простая, но очень важная задача. В дальнейшем мы будем ее использовать, чтобы получить формулы площадей других фигур.

 

Список рекомендованной литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 5 класс. М.: Мнемозина, 2013.
2. Ерина Т.М. Математика 5 класс. Рабочая тетрадь к учебнику Виленкина Н.Я. М.: Экзамен, 2013.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С. Математика 5 класс. М.: Вентана-Граф, 2013.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «school-assistant.ru» (Источник)
2. Интернет портал «school-assistant.ru» (Источник)
3. Интернет портал «edufuture.biz» (Источник)

 

Домашнее задание

1. Стороны прямоугольника равны  см и  см. Чему равна его площадь?
2. Сторона квадрата равна  метров. Чему равна его площадь?
3. Площадь прямоугольника равна . Чему равна ширина, если его длина равна  см?

Является ли квадрат прямоугольником? Да или нет? — Мэшап Математика

Сегодня тот день, когда вы, наконец, узнаете ответ на спорный вопрос, может ли квадрат быть прямоугольником. Прежде чем мы найдем окончательный ответ на этот вопрос, давайте рассмотрим два очень важных определения:

Что такое квадрат?

Квадрат – это замкнутая фигура с четырьмя сторонами одинаковой длины и четырьмя прямыми углами.

Что такое прямоугольник?

Прямоугольник – это замкнутая фигура с четырьмя прямыми сторонами и четырьмя прямыми углами.

Тонкое различие в определениях между квадратом и прямоугольником чрезвычайно важно. Почему? Потому что это тонкое различие является ключом к определению того, является ли квадрат прямоугольником.

Итак, является ли квадрат прямоугольником?

Быстрый ответ: ДА! Квадрат может быть прямоугольником по определению.

Теперь давайте рассмотрим причины, по которым квадрат всегда является прямоугольником, используя аналогию с печеньем, что сделает ответ очень простым!

Все квадраты — прямоугольники, но не все прямоугольники — квадраты (точно так же, как все печенья — печенье, но не все печенье — печенье).

Аналогия с печеньем

По определению, печенье — это небольшое выпечное лакомство, обычно круглое, плоское и хрустящее.

И все мы знаем, что Oreo — это тип печенья (и, безусловно, подходит под это определение).

Но каждое ли печенье — Oreo?

Определенно нет! Орео — это особый тип печенья, но существует множество других видов печенья, включая сахарное печенье, печенье с шоколадной крошкой, печенье для девочек-скаутов и имбирное печенье.

И, кроме того, мы можем сделать вывод, что:

Теперь давайте расширим тот же самый тип мышления из аналогии с печеньем, чтобы понять, почему квадрат является прямоугольником.

Каждый квадрат является прямоугольником. И вот почему:

Помните, что прямоугольник — это замкнутая фигура с четырьмя прямыми сторонами и четырьмя прямыми углами.

Квадрат подходит под это определение? ДА! Квадрат — это особый вид замкнутой фигуры с четырьмя прямыми сторонами и четырьмя прямыми углами, у которых и имеют стороны одинаковой длины.

Следовательно, мы можем сделать вывод, что:

Вывод: квадрат всегда прямоугольник, но прямоугольник не всегда квадрат.

Однако важно помнить, что хотя все квадраты являются прямоугольниками, не все прямоугольники являются квадратами. Как и в примере с файлами cookie, все Oreo являются файлами cookie, но не все файлы cookie являются файлами Oreo. И то же самое верно для квадратов и прямоугольников. Таким образом, хотя все квадраты являются прямоугольниками, не все прямоугольники являются квадратами.

Хотите узнать больше о том, почему все квадраты являются прямоугольниками? Посмотрите наши Является ли квадрат прямоугольником? Видео на YouTube, сопровождающее этот пост:

Хотите больше увлекательных математических загадок, головоломок и головоломок?

Было весело? Если вы хотите решить еще больше головоломных математических головоломок, чтобы отточить свой ум и улучшить свои навыки решения задач, перейдите по ссылкам ниже:

Другие посты, которые вам понравятся:

Игра «Бумажный самолетик»: забавный проект для школьников

Какая самая простая математика в колледже?

Как вовлечь учащихся в уроки математики — 5 идей

Где находится Бермудский треугольник?—Карта Бермудского треугольника

4 комментария

Площадь и периметр прямоугольника

Горячая математика

Прямоугольник – это параллелограмм с четырьмя прямыми углами. Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.

периметр п прямоугольника находится по формуле п «=» 2 л + 2 ж , где л это длина и ж это ширина прямоугольника.

область А прямоугольника находится по формуле А «=» л ж , где л это длина и ж это ширина.

Вы часто будете сталкиваться с текстовыми задачами, когда заданы два значения в одной из этих формул, а вам нужно найти третье.

Пример 1:

Периметр прямоугольного бассейна равен 56 метров. Если длина бассейна 16 метров, затем найдите его ширину.

Здесь заданы периметр и длина прямоугольного бассейна. Нам нужно найти ширину бассейна.

Периметр п прямоугольника находится по формуле п «=» 2 л + 2 ж , где л это длина и ж это ширина прямоугольника.

Учитывая, что периметр 56 метров, а длина 16 метров. Итак, подставляем эти значения в формулу.

56 «=» 2 ( 16 ) + 2 ж

Упрощать.

56 «=» 32 + 2 ж

Вычесть 32 с обеих сторон.

24 «=» 2 ж

Разделите каждую сторону на 2 .

12 «=» ж

Следовательно, ширина прямоугольного бассейна равна 12 метров.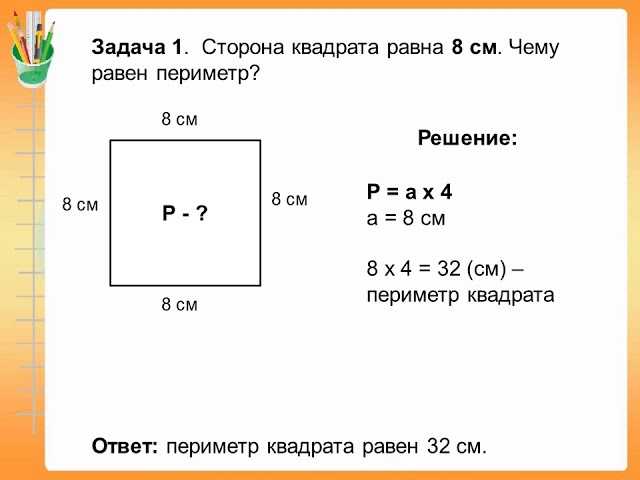

Пример 2:

Площадь прямоугольного забора равна 500 квадратный фут. Если ширина забора 20 футов, затем найдите его длину.

Здесь даны площадь и ширина прямоугольного забора. Нам нужно найти длину забора.

Площадь А прямоугольника находится по формуле А «=» л ж , где л это длина и ж это ширина.

Учитывая, что площадь 500 квадратных метров, а ширина 20 ноги. Итак, подставляем эти значения в формулу.

500 «=» л × 20

Разделите каждую сторону на 20 изолировать л .

25 «=» л

Следовательно, длина прямоугольного забора равна 25 ноги.