Самые сложные уравнения: Математика. Примеры решения сложных систем уравнений.

Сложные квадратные уравнения примеры с решением. Квадратные уравнения

Уравнение вида

Выражение D = b 2 — 4 ac называют дискриминантом квадратного уравнения. Если D = 0, то уравнение имеет один действительный корень; если D > 0, то уравнение имеет два действительных корня.
В случае, когда D = 0 , иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение D = b 2 — 4 ac , можно переписать формулу (2) в виде

Если b = 2 k , то формула (2) принимает вид:

где k = b / 2 .
Последняя формула особенно удобна в тех случаях, когда b / 2 — целое число, т.е. коэффициент b — четное число.
Пример 1: Решить уравнение 2 x 2 — 5 x + 2 = 0 .

Здесь a = 2, b = -5, c = 2 . Имеем D = b 2 — 4 ac = (-5) 2- 4*2*2 = 9 . Так как D > 0 , то уравнение имеет два корня. Найдем их по формуле (2)

Итак x 1 =(5 + 3) / 4 = 2, x 2 =(5 — 3) / 4 = 1 / 2 ,
то есть x 1 = 2 и x 2 = 1 / 2 — корни заданного уравнения.
Пример 2: Решить уравнение 2 x 2 — 3 x + 5 = 0 . Здесь a = 2, b = -3, c = 5 . Находим дискриминант D = b 2 — 4 ac = (-3) 2- 4*2*5 = -31 . Так как D 0 , то уравнение не имеет действительных корней.

Неполные квадратные уравнения. Если в квадратном уравнении ax 2

+ bx + c =0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным . Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Пример 1: решить уравнение 2 x 2 — 5 x = 0 .
Имеем x (2 x — 5) = 0 . Значит либо x = 0 , либо 2 x — 5 = 0 , то есть x = 2.5 . Итак, уравнение имеет два корня: 0 и 2.5
Пример 2: решить уравнение 3 x 2 — 27 = 0 .
Имеем 3 x 2 = 27 . Следовательно корни данного уравнения — 3 и -3 .

Теорема Виета.

Если приведенное квадратное уравнение x 2 + px + q =0 имеет действительные корни, то их сумма равна — p , а произведение равно q , то есть

x 1 + x 2 = -p ,
x 1 x 2 = q

(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.

Что называют квадратным уравнением

Важно!

Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.

Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.

Примеры квадратных уравнений

• 5x 2 − 14x + 17 = 0
• −x 2 + x + = 0
• x 2 + 0,25x = 0
• x 2 − 8 = 0

Важно! Общий вид квадратного уравнения выглядит так:

A x 2 + b x + c = 0

«a », «b » и «c » — заданные числа.

• «a » — первый или старший коэффициент;
• «b » — второй коэффициент;
• «c » — свободный член.

Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».

Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.

5x 2 − 14x + 17 = 0 −7x 2 − 13x + 8 = 0 −x 2 + x + = 0 x 2 + 0,25x = 0

Уравнение	Коэффициенты
a = −7 b = −13 с = 8
x 2 − 8 = 0

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная

формула для нахождения корней .

Запомните!

Чтобы решить квадратное уравнение нужно:

• привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
• использовать формулу для корней:

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

X 2 − 3x − 4 = 0

Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .

Определим коэффициенты «a », «b » и «c » для этого уравнения.

x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =

С её помощью решается любое квадратное уравнение.

В формуле «x 1;2 = » часто заменяют подкоренное выражение

«b 2 − 4ac » на букву «D » и называют дискриминантом . Более подробно понятие дискриминанта рассматривается в уроке «Что такое дискриминант ».

Рассмотрим другой пример квадратного уравнения.

x 2 + 9 + x = 7x

В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».

X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0

Теперь можно использовать формулу для корней.

X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =

x = 3
Ответ: x = 3

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.

Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах.

Приступим! Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a, b и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти.

Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1: Решить 2x 2 +8 x –192=0

а=2 b=8 c= –192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2: Решить x 2 –22 x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3: Решить x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а x 2 + bx + c =0 выполняется равенство

a + b + с = 0, то

— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство

a + с = b , то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001 x 2 –4995 x – 6=0

Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит

Пример 2: 2501 x 2 +2507 x +6=0

Выполняется равенство a + с = b , значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.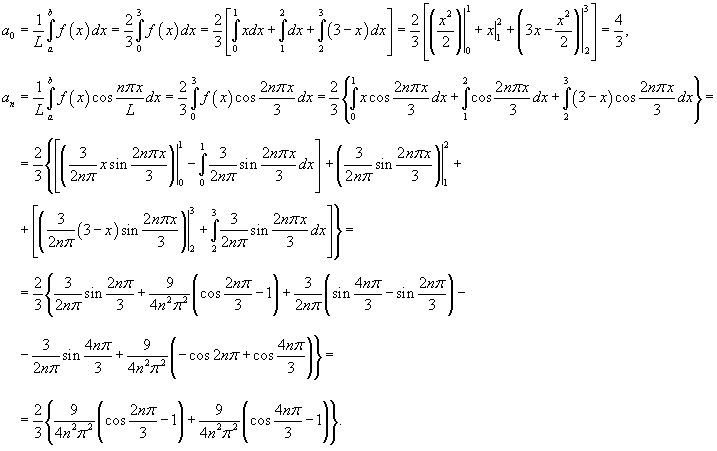

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а ± b+c ≠ 0, то используется прием переброски, например:

2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1 = 5 х 2 = 0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.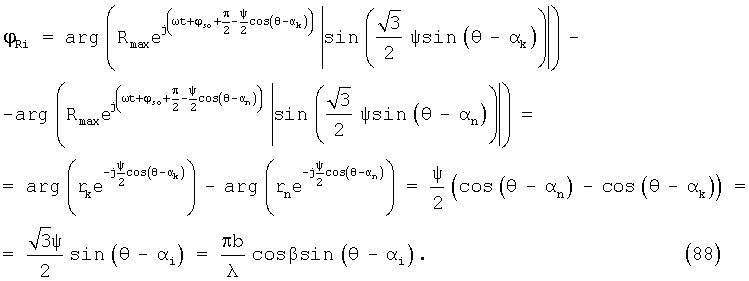

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже. ..»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример.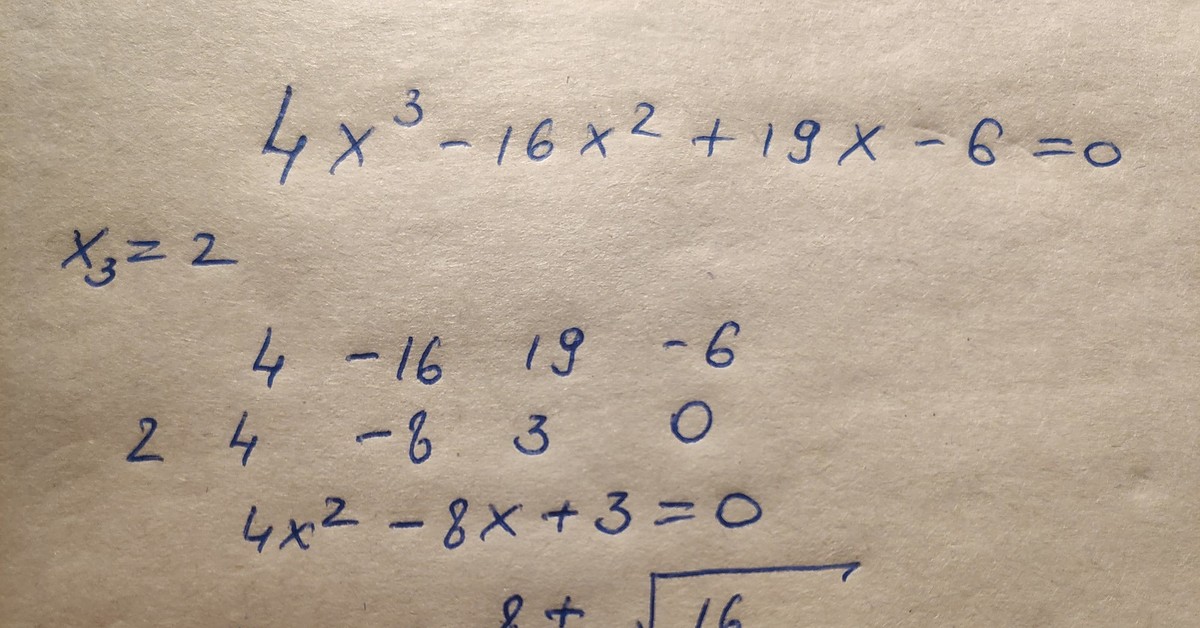 Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Эта тема поначалу может показаться сложной из-за множества не самых простых формул. Мало того что сами квадратные уравнения имеют длинные записи, еще и корни находятся через дискриминант. Всего получается три новые формулы. Не очень просто запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы будут вспоминаться сами собой.

Общий вид квадратного уравнения

Здесь предложена их явная запись, когда самая большая степень записана первой, и дальше — по убыванию. Часто бывают ситуации, когда слагаемые стоят вразнобой. Тогда лучше переписать уравнение в порядке убывания степени у переменной.

Введем обозначения. Они представлены в таблице ниже.

Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.

Причем коэффициент а ≠ 0. Пусть эта формула будет обозначена номером один.

Когда уравнение задано, то непонятно, сколько корней будет в ответе. Потому что всегда возможен один из трех вариантов:

• в решении будет два корня;
• ответом будет одно число;
• корней у уравнения не будет совсем.

И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в конкретном случае.

Виды записей квадратных уравнений

В задачах могут встречаться их разные записи. Не всегда они будут выглядеть как общая формула квадратного уравнения. Иногда в ней будет не хватать некоторых слагаемых. То что было записано выше — это полное уравнение. Если в нем убрать второе или третье слагаемое, то получится нечто другое. Эти записи тоже называются квадратными уравнениями, только неполными.

Причем исчезнуть могут только слагаемые у которых коэффициенты «в» и «с». Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:

Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет иметь номер два, а вторая — три.

Дискриминант и зависимость количества корней от его значения

Это число нужно знать для того, чтобы вычислить корни уравнения. Оно может быть посчитано всегда, какой бы ни была формула квадратного уравнения. Для того чтобы вычислить дискриминант, нужно воспользоваться равенством, записанным ниже, которое будет иметь номер четыре.

После подстановки в эту формулу значений коэффициентов, можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два различных корня. При отрицательном числе корни квадратного уравнения будут отсутствовать. В случае его равенства нулю ответ будет один.

Как решается квадратное уравнение полного вида?

По сути, рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.

Поскольку в ней стоит знак «±», то значений будет два. Выражение под знаком квадратного корня — это дискриминант. Поэтому формулу можно переписать по-другому.

Формула номер пять. Из этой же записи видно, что если дискриминант равен нулю, то оба корня примут одинаковые значения.

Если решение квадратных уравнений еще не отработано, то лучше до того, как применять формулы дискриминанта и переменной, записать значения всех коэффициентов. Позже этот момент не будет вызывать трудностей. Но в самом начале бывает путаница.

Как решается квадратное уравнение неполного вида?

Здесь все гораздо проще. Даже нет необходимости в дополнительных формулах. И не понадобятся те, что уже были записаны для дискриминанта и неизвестной.

Сначала рассмотрим неполное уравнение под номером два. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.

Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Потом нужно разделить на коэффициент, стоящий перед неизвестной. Останется только извлечь квадратный корень и не забыть записать его два раза с противоположными знаками.

Далее записаны некоторые действия, помогащие научиться решать всевозможные виды равенств, которые превращаются в квадратные уравнения. Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недочеты бывают причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет постоянно выполнять. Потому что появится устойчивый навык.

• Сначала нужно записать уравнение в стандартном виде. То есть сначала слагаемое с самой большой степенью переменной, а потом — без степени и последним — просто число.

• Если перед коэффициентом «а» появляется минус, то он может усложнить работу для начинающего изучать квадратные уравнения. От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.

• Таким же образом рекомендуется избавляться от дробей. Просто умножить уравнение на соответствующий множитель, чтобы знаменатели сократились.

Примеры

Требуется решить следующие квадратные уравнения:

х 2 − 7х = 0;

15 − 2х − х 2 = 0;

х 2 + 8 + 3х = 0;

12х + х 2 + 36 = 0;

(х+1) 2 + х + 1 = (х+1)(х+2).

Первое уравнение: х 2 − 7х = 0. Оно неполное, поэтому решается так, как было описано для формулы под номером два.

После вынесения за скобки получается: х (х — 7) = 0.

Первый корень принимает значение: х 1 = 0. Второй будет найден из линейного уравнения: х — 7 = 0. Легко заметить, что х 2 = 7.

Второе уравнение: 5х 2 + 30 = 0. Снова неполное. Только решается оно так, как описано для третьей формулы.

После перенесения 30 в правую часть равенства: 5х 2 = 30. Теперь нужно выполнить деление на 5. Получается: х 2 = 6. Ответами будут числа: х 1 = √6, х 2 = — √6.

Третье уравнение: 15 − 2х − х 2 = 0. Здесь и далее решение квадратных уравнений будет начинаться с их переписывания в стандартный вид: − х 2 − 2х + 15 = 0. Теперь пришло время воспользоваться вторым полезным советом и умножить все на минус единицу. Получается х 2 + 2х — 15 = 0. По четвертой формуле нужно вычислить дискриминант: Д = 2 2 — 4 * (- 15) = 4 + 60 = 64. Он представляет собой положительное число. Из того, что сказано выше, получается, что уравнение имеет два корня. Их нужно вычислить по пятой формуле. По ней получается, что х = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда х 1 = 3, х 2 = — 5.

Четвертое уравнение х 2 + 8 + 3х = 0 преобразуется в такое: х 2 + 3х + 8 = 0. Его дискриминант равен такому значению: -23. Поскольку это число отрицательное, то ответом к этому заданию будет следующая запись: «Корней нет».

Пятое уравнение 12х + х 2 + 36 = 0 следует переписать так: х 2 + 12х + 36 = 0. После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.

Шестое уравнение (х+1) 2 + х + 1 = (х+1)(х+2) требует провести преобразования, которые заключаются в том, что нужно привести подобные слагаемые, до того раскрыв скобки. На месте первой окажется такое выражение: х 2 + 2х + 1. После равенства появится эта запись: х 2 + 3х + 2. После того как подобные слагаемые будут сосчитаны, уравнение примет вид: х 2 — х = 0. Оно превратилось в неполное. Подобное ему уже рассматривалось чуть выше. Корнями этого будут числа 0 и 1.

Трудные задания ЕГЭ по химии

Как показали результаты репетиционного экзамена по химии, наиболее трудными оказались задания, направленные на проверку знаний химических свойств веществ. К числу таких заданий можно отнести задание С3 – «Цепочка органических веществ», С2 – «Реакции между неорганическими веществами и их растворами».

При решении задания С3 «Цепочка органических веществ» учащийся должен написать пять уравнений химических реакций, среди которых одно является окислительно-восстановительным.

Рассмотрим составление одного из таких окислительно-восстановительных уравнений:

СН₃СНО X₁

Чтобы составить уравнение окислительно-восстановительной реакции с участием органических веществ, нужно научиться определять степень окисления в органическом веществе по его структурной формуле. Для этого нужно иметь знания о химической связи, знать, что такое электроотрицательность.

Структурная формула помогает оценить смещение электронов по каждой из связей. Так атом углерода метильной группы (–СН₃) сместит электрон по каждой из связей к себе. Таким образом, степень окисления углерода метильной группы будет равна (-3). Атом углерода карбонильной группы (СО) отдаст 2 электрона атому кислорода, но частично компенсирует недостачу, приняв 1 электрон от атома водорода. Следовательно, его степень окисления будет равна +1:

 

 

 

 

 

 

В продукте реакции степень окисления углерода метильной группы не изменится. Карбонильная группа атомов превратится в карбоксильную с замещенным водородом на натрий, вследствие щелочной среды (-СООNa). Атом углерода карбоксильной группы сместит два электрона в сторону карбонильного кислорода и один электрон в сторону кислорода замещенной гидроксильной группы. Таким образом, степень окисления атома углерода карбоксильной группы будет равна (+3):

 

 

 

 

 

 

 

Следовательно, одна молекула этаналя отдает 2 электрона:

С⁺¹-2е=С⁺³

Рассмотрим теперь процессы, происходящие с перманганатом натрия. Обращает внимание, что в схеме дан перманганат натрия, а не калия. Свойства перманганата натрия должны быть аналогичны свойствам перманганта калия, который в зависимости от кислотности среды способен давать различные продукты:

  Так как в нашем случае перманганат натрия используется в щелочной  среде, то продуктом реакции будет манганат ион – MnO₄^2-.

Определим степень окисления иона марганца в перманганате калия NaMnO₄ пользуясь правилом равенства числа положительных и отрицательных зарядов в нейтральной структурной единице вещества. Четыре кислорода каждый по (-2) дадут восемь отрицательных зарядов, так как степень окисления у калия +1, то у марганца будет +7:

Na⁺¹Mn⁺⁷O₄^-2

Записав формулу манганата натрия Na₂MnO₄, определим степень окисления марганца:

Na₂⁺¹Mn⁺⁶O₄^-2

Таким образом, марганец принял один электрон:

Mn⁺⁷+1e=Mn⁺⁶

Полученные уравнения позволяют определить множители перед формулами в уравнении химической реакции, которые называют коэффициентами:

С⁺¹-2е=С⁺³  ·1

Mn⁺⁷+1e=Mn⁺⁶ ·2

Уравнение реакции приобретет следующий вид:

2NaMnO₄+CH₃CHO+3NaOH=CH₃COONa+2Na₂MnO₄+2H₂O

Задание С2 требует от участника ЕГЭ знание свойств разнообразных свойств неорганических веществ, связанных с протеканием как окислительно-восстановительных реакций между веществами, находящимися как в одном, так и в различных агрегатных состояниях, так и обменных реакций протекающих в растворах. Такими свойствами могут быть некоторые индивидуальный свойства простых веществ и их соединений, например, реакция лития или магния с азотом:

2Li+3N₂=2Li₃N

2Mg+N₂=Mg₂N₂

горение магния в углекислом газе:

Mg+CO₂=MgO+CO

2Mg+CO₂=2MgO+C

Особую трудность у учащихся вызывают сложные случаи взаимодействия растворов веществ солей подвергающихся гидролизу. Так для взаимодействия раствора сульфата магния с карбонатом натрия можно записать целых три уравнения возможных  процессов:

MgSO₄+Na₂CO₃=MgCO₃+Na₂SO₄

 

2MgSO₄+2Na₂CO₃+H₂O=(MgOH)₂CO₃¯+2Na₂SO₄+CO₂

2MgSO₄+2Na₂CO₃+2H₂O=2Mg(OH)₂¯+2Na₂SO₄+2CO₂

Традиционно трудны для написания уравнения с участием комплексных соединений. Так растворы амфотерных гидроксидов в избытке щелочи обладают всеми свойствами щелочей. Они способны вступать в реакции с кислотами и кислотными оксидами:

Na[Al(OH)₄]+HCl=NaCl+Al(OH)₃¯+H₂O

 Na[Al(OH)₄]+2HCl=NaCl+Al(OH)₂Cl+2H₂O

Na[Al(OH)₄]+3HCl=NaCl+Al(OH)Cl₂+3H₂O

Na[Al(OH)₄]+4HCl=NaCl+AlCl₃+4H₂O

Na[Al(OH)₄]+CO₂=NaHCO₃+Al(OH)₃¯

2Na[Al(OH)₄]+CO₂=Na₂CO₃+2Al(OH)₃¯+H₂O

Растворы солей, имеющие кислую реакцию среды, вследствие гидролиза, способны растворять активные металлы, например, магний или цинк:

Mg+MgCl₂+2H₂O=2MgOHCl+H₂­

На экзамене желательно помнить об окислительных свойствах солей трехвалентного железа:

2FeCl₃+Cu=CuCl₂+2FeCl₂

Могут пригодиться знания об аммиачных комплексах:

CuSO₄+4NH₃=[Cu(NH₃)₄]SO₄

AgCl+2NH₃=[Ag(NH₃)₂]Cl

Традиционно вызывают затруднения, связанные с проявлением  основных  свойств раствором аммиака. В результате чего могут протекать обменные реакции в водных растворах:

MgCl₂+2NH₃+2H₂O=Mg(OH)₂+2NH₄Cl

В заключение приведем серию уравнений химических реакций, которые нужно знать участникам ЕГЭ по химии:

 

 

  Кислотные оксиды (кроме SiO₂) реагируют с водой, как амфотерным оксидом с образованием кислот:

P₂O₅ + 3H₂O = 2H₃PO₄

SO₃ + H₂O = H₂SO₄

Для получения азотной кислоты азот оксид азота (IV) должен быть доокислен, например кислородом воздуха:

4NO₂ + O₂ + 2H₂О = 4HNO₃

Лабораторный способ получения хлороводорода: к твердому хлориду натрия приливают концентрированную серную кислоту:

NaCl + H₂SO₄ = NaHSO₄ + HCl­

Для получения бромоводорода из бромида натрия, концентрированная серная кислота не подойдет, так как выделяющийся бромоводород будет загрязнен парами брома. Можно использовать концентрированную фосфорную кислоту:

NaBr+ H₃PO₄ = NaH₂PO₄ + HBr­

Кислоты реагируют с металлами, стоящими в ряду напряжений до водорода:

Fe + 2 HCl = FeCl₂ + H₂­

И их оксидами:

Fe₂O₃ + 6HCl = 2FeCl₃ + 3H₂O

Обратите внимание на валентность переходных элементов в солях.

Щелочные и щелочноземельные металлы взаимодействуют с водой:

K + H₂O = KOH + ½ H₂­

В условиях избытка кислоты могут образовываться и кислые соли:

2Н₃РО₄ + 2Na = 2NaH₂PO₄ + Н₂­

Органические кислоты также проявляют кислотные свойства:

2СН₃СООН + 2Na = 2CH₃COONa + Н₂­

СНзСООН + NaOH = CH₃COONa + Н₂О

Комплексные гидроксиды реагируют с кислотами с образованием солей и воды:

Na[Al(OH)₄] + HCl = AlCl₃ + 4H₂O + NaCl

LiOH + HNO₃ = LiNO₃ + H₂O

Многоосновные кислоты в реакции с гидроксидами могут образовывать кислые соли:

Н₃РО₄ + КОН = КН₂РО₄ + Н₂О

Продуктом реакции аммиака с фосфорной кислотой может также быть кислая соль:

NH₃ + H₃PO₄ = NH₄H₂PO₄

Обратим внимание на свойства оснований, их взаимодействие с кислотами:

2Н₃РО₄ + ЗСа(ОН)₂ = Са₃(РО₄)₂¯ + 6Н₂О

с кислотными оксидами:

Ca(OH)₂ + CO₂ = CaCO₃¯ + H₂O

2Ca(OH)₂ + CO₂=(СaOH)₂CO₃+H₂O

Реакция гидроксидов с кислотными оксидами может приводить и к кислым солям:

KOH + CO₂ = KHCO₃

Основные  оксиды реагируют с амфотерными оксидами:

CaO + H₂O = Ca(OH)₂

Средние соли в воде реагируют с кислотными оксидами с образованием кислых солей:

CaCO₃ + CO₂ + H₂O = Ca(HCO₃)₂

Более сильные кислоты вытесняют более слабые из их солей:

CH₃COONH₄ + HCl  = CH₃COOH + NH₄Cl

K₂CO₃ + H₂SO₄ = K₂SO₄ + H₂O + CO₂­

Кислоты в присутствии серной кислоты реагируют со спиртами с образованием сложных эфиров:

CH₃COOH + C₂H₅OH = CH₃COOC₂H₅ + H₂O

Более сильное основание вытесняет более слабое из его солей:

AlCl₃ + 3NaOH = Al(OH)₃ + 3NaCl

MgCl₂ + KOH = MgOHCl + KCl

NH₄С1 + NaOH = NaCl + NH₃ + H₂O

Чтобы получить из основной соли получить среднюю соль нужно подействовать кислотой:

MgOHCl + HCl = MgCl₂ + H₂O

Гидроксиды металлов (кроме щелочных металлов) разлагаются при нагревании в твердом виде до оксидов:

2Al(OH)₃ = Al₂O₃ + 3H₂O

2Fe(OH)₃ = Fe₂O₃ + 3H₂O

Гидрокарбонаты при нагревании разлагаются до карбонатов:

2KHCO₃ = K₂CO₃ + H₂O + CO₂­

Нитраты обычно разлагаются до оксидов (обратите внимание на повышение степени окисления переходного элемента находящегося в промежуточной степени окисления):

2Fe(NO₃)₂ = Fe₂O₃ + 4NO₂­ + 0,5O₂­

2Fe(NO₃)₃ ® Fe₂O₃ + 6NO₂­ + 1,5 O₂­

2Cu(NO₃)₂ = 2CuO + 4NO₂­ + О₂­

Нитраты щелочных металлов разлагаются до нитритов:

NaNO₃ = NaNO₂ + ½ O₂­

Карбонаты металлов (кроме щелочных) разлагаются до оксидов:

CaCO₃ = CaO + CO₂­

При составлении уравнений реакций ионного обмена пользуйтесь таблицей растворимости:

K₂SO₄ + BaCl₂ = BaSO₄¯ + 2KCl

[C₆H₅-NH₃]C1 + AgNО₃ = [C₆H₅NH₃]NO₃ + AgCl¯

 

Электролиз расплавов солей:

2KCl = 2K + Cl₂­

Электролиз растворов солей металлов, стоящих в ряду напряжения после водорода:

2HgSO₄ + 2H₂O  = 2Hg + О₂­ + 2H₂SO₄

1) на катоде: Hg²⁺ + 2e = Hg°

2) на аноде: 2Н₂О – 4е = О₂ + 4Н⁺

 

Электролиз раствора сульфата натрия

1) на катоде: 2H₂O + 2e = H₂ + 2OH^–

2) на аноде: 2H₂O – 4e = O₂ + 4H⁺

3) Составлено общее уравнение электролиза:

2H₂O = 2H₂­ + O₂­

до водорода:

СаI₂ + 2Н₂О  =  Н₂­ + I₂ + Са(ОН)₂

1) на катоде: 2Н₂О + 2e = 2ОН + Н₂

2) на аноде: 2I^— — 2e = I₂ 

Сравните свойства одноэлементных и кислородсодержащих анионов.

Химические реакции, возможные при электролизе сульфата хрома (III):

1)Сг³⁺ + e = Сг²⁺

2) Cr²⁺ + 2e = Сг°  

3) Сг³⁺ + 3 e= Сг°

4) 2Н⁺ + 2e = Н₂

Электролиз водных растворов солей карбоновых кислот:

2CH₃COONa + 2H₂O  = CH₃CH₃­ + 2CO₂­ + H₂­ + 2NaOH

 

 

Пример взаимного гидролиза солей:

A1₂(SO₄)₃ + 3K₂CO₃ + 3H₂O = 2A1(OH)₃ + 3CO₂­ + 3K₂SO₄

Амфотерные гидроксиды растворяются в водных растворах щелочей:

A1(OH)₃ + 3KOH = K₃[A1(OH)₆]

A1(OH)₃ + KOH = K[Al(OH)₄]

реагируют с твердыми щелочами при сплавлении:

Al(OH)₃  + KOH KAlO₂ + 2H₂O

Амфотерные металлы реагируют с водными растворами щелочей:

Al + NaOH + 3H₂O = Na[Al(OH)₄] + 3/2 H₂­

Продукт сплавления амфотерного гидроксида со щелочью легко разлагается водой:

KAlO₂ + 2H₂O = KOH + Al(OH)₃¯

Комплексные гидроксиды реагируют с кислотами:

K[Al(OH)₄] + HCl =KCl + Al(OH)₃¯ + H₂O

Способ получения:

СаО + 3С = СаС₂ + СО­

Бинарные соединения реагируют с кислотами:

Al₂S₃ + 3H₂SO₄ ^:= Al₂(SO₄)₃ + 3H₂S­

Mg₃N₂ + 8HNO₃ = Mg(NO₃)₂ + 2NH₄NO₃

и водой:

A1₄C₃ + 12Н₂О = 4А1(ОН)₃ + ЗСН₄­

PCl₃ + H₂O = 3H₃PO₃ + 3HCl

 

Азотная кислота является сильным окислителем:

окисляют неметаллы:

ЗР + 5HNO₃ + 2Н₂О = Н₃РО₄ + 5NO­

P + 5HNO₃ = H₃PO₄ + 5NO₂­ + H₂O

металлы:

Cu + 4HNO₃ = Cu(NO₃)₂ + 2NO₂­ + 2H₂O

4Mg + 10HNO₃ = 4Mg(NO₃)₂ + N₂O­ + 5H₂O

оксиды переходных металлов в промежуточных степенях окисления:

3Cu₂O + 14HNO₃ = 6Cu(NO₃)₂ + 2NO+ 7H₂O (возможно выделение NО₂)

оксиды азота также проявляют окислительные свойства:

5N₂O + 2P = 5N, + P₂O

но по отношению к кислороду являются восстановителями:

2NO + O₂ = 2NO₂

Азот реагирует с некоторыми простыми веществами:

N₂+3H₂= 2NH₃

N₂ + O₂ = 2NO

3Mg + N₂ = Mg₃N₂

 

обычно проявляют окислительные свойства:

PH₃ + 4Br₂ + 4Н₂О = Н₃РО₄ + 8НВг

2P + 5Cl₂ = 2PCl₅

2P + 3PCl₅ = 5PCl₃

PH₃ + 4Br₂ + 4H₂O = H₃PO₄ + 8HBr

Cl₂ + H₂ = 2HCl

2HCl + F₂ = 2HF + Cl₂

2NH₃ + 3Br₂ = N₂ + 6HBr

Галогены в растворах щелочей диспропорционируют при комнатной температуре:

Cl₂ + 2KOH = KCl + H₂O + KClO

и при нагревании:

Cl₂ + 6KOH = 5KCl + KClO₃ + 3H₂O

2NH₃ + 2KMnO₄ = N₂ + 2MnO₂ + 2KOH + 2H₂O

реагирует с простыми веществами:

S + O₂ = SO₂

3S + 2А1 = A1₂S₃

оксид серы (IV) может быть доокислен кислородом:

2SO₂ + O₂ = 2SO₃

2SO₂ + O₂ + 2H₂O = 2H₂SO₄

и выступать в роли окислителя:

SO₂ + 2H₂S = 3S + 2H₂O

Концентрированная серная кислота проявляет окислительные свойства:

Cu + H₂SO₄ = CuSO₄ + SO₂ +2H₂O

4Mg + 5H₂SO₄ = 4MgSO₄ + H₂S + 4H₂O

получение фосфора:

 

реагируют с галогенами:

2Fe + 3Cl₂ = 2FeCl₃

Алюминий без оксидной пленки растворяется в воде:

Al (без оксидной пленки) + Н₂О = Al(OH)₃ + 3/2 H₂­

методы получения металлов:

Fe₂O₃ + CO = 2FeO + CO₂­

FeO + CO = Fe + CO₂­

CuO + H₂ = Cu + H₂O

Гидроксид железа (II) может быть легко доокислен пероксидом водорода:

2Fe(OH)₂ + H₂O₂ = 2Fe(OH)₃

обжиг пирита:

2FeS₂ + O₂ = Fe₂O₃ + 4SO₂­

          

2С₁₀Н₂₂ + 31O₂ = 20CО₂ + 22H₂О

Методы получения алканов из простых веществ:

С + 2H₂ = CH₄

сплавлением солей щелочных металлов с щелочами:

СН₃СООК + КОН ® СН₄ + К₂СО₃

Химические свойства алканов — промышленное окисление метана:

CH₄ + O₂ = CH₂O + H₂O

Взаимодействие алканов с галогенами:

С₂Н₆ + Сl₂ С₂Н₅Сl + НСl

Изомеризация алканов:

 

с водными растворами щелочей:

С₆Н₅-СНВг-СН₃ + КОН (водн.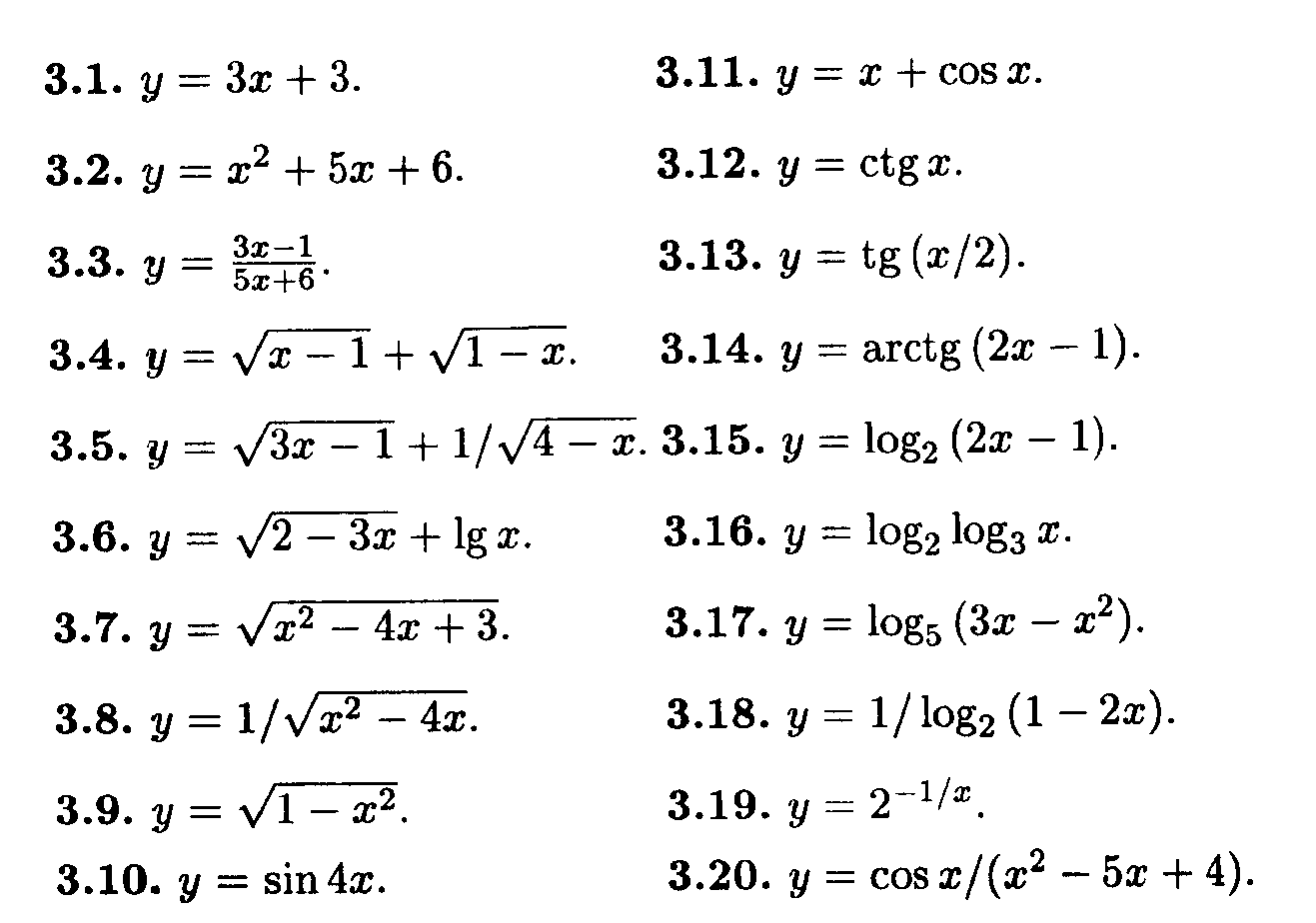 ) ® С₆Н₅-СНОН-СН₃ + KBr

C₆H₅Br + KOH ® C₆H₅OH + KBr

По правилу Зайцева водород отщепляется от наименее гидрированного атома

Из дигалогеналканов можно получить алкины:

 

Реакция Вюрца:

 

 

Присоединяют водород:

присоединяют галогены:

присоединяют галогенводороды:

присоединят воду:

СН₂=СН₂ + Н₂О ® СН₃СН₂ОН

С водным раствором перманганата калия без нагревания образуют гликоли (двухатомные спирты)

ЗС₆Н₅СН=СН₂ + 2КМnО₄ + 4Н₂О ® ЗС₆Н₅СН(ОН)-СН₂ОН + MnO₂¯ + 2KOH

 

промышленный способ получения ацетилена

2СН₄ ® С₂Н₂ + ЗН₂

карбидный способ получения ацетилена:

CaC₂ + 2H₂O = Ca(OH)₂ + C₂H₂

реакция Кучерова — альдегид можно получить только из ацетилена:

С₂Н₂ + Н₂О СН₃СНО

Реакция алкинов с концевой тройной связью с аммиачным раствором оксида серебра:

2CH₃-CH₂-CºCH + Ag₂O 2CH₃-CH₂-CºCAg +H₂O

использование полученных продуктов в органическом синтезе:

CH₃-CH₂-CºCAg  + C₂H₅Br  ®  CH₃-CH₂-CºC-C₂H₅ + AgBr

Получение бензола из алкенов:

из ацетилена:

3C₂H₂  C₆H₆

Нитрование бензола и его производных в присутствие серной кислоты

C₆H₆ + HNO₃ ® C₆H₅-NO₂ + H₂O

карбоксильная группа является ориентантом второго рода

реакция бензола и его производных с галогенами:

C₆H₆ + Cl₂ C₆H₅Cl   + HCl

С₆Н₅С₂Н₅ + Вг₂ С₆Н₅-СНВг-СН₃ + НВг

галогеналканами:

C₆H₆ + С₂Н₅С1 C₆H₅C₂H₅ + НС1

алкенами:

C₆H₆ + CH₂=CH-CH₃ ® C₆H₅-CH(CH₃)₂

Окисление бензола перманганатом калия в присутствии серной кислоты при нагревании:

5C₆H₅-CH₃ + 6KMnO₄ + 9H₂SO₄ = 5C₆H₅-COOH + 3K₂SO₄ + 6MnSO₄ + 14H₂O

Промышленный способ получения метанола:

CO + 2H₂ = CH₃OH

при нагревании с серной кислотой в зависимости от условий могут образовываться простые эфиры:

2С₂Н₅OH C₂Н₅ОС₂Н₅ + Н₂О

или алкены:

2С₂Н₅OH CH₂=CH₂ + H₂O

спирты реагируют с щелочными металлами:

С₂Н₅OH + Na ® C₂H₅ONa + ½ H₂

с галогенводородами:

СН₃СН₂ОН + НСl ® CH₃CH₂Cl + H₂O

с оксидом меди (II):

СН₃СН₂ОН + СuO ® CH₃CHO + Cu + H₂O

более сильная кислота вытесняет более слабые из их солей:

C₂H₅ONa + HCl ® C₂H₅OH + NaCl

при нагревании смеси спиртов с серной кислотой образуются несимметричные простые эфиры:

Образуют с аммиачным раствором оксида серебра серебряное зеркало:

CH₃CHO + Ag₂O CH₃COONH₄ + 2Ag

реагируют со свежеосажденным гидроксидом меди (II):

CH₃CHO + 2Cu(OH)₂ ® CH₃COOH + 2CuOH + H₂O

могут быть восстановлены до спиртов:

CH₃CHO + H₂  ® CH₃CH₂OH

окисляются перманганатом калия:

ЗСН₃СНО + 2КМnО₄® 2СН₃СООК + СН₃СООН + 2МnО₂ + Н₂О

можно получить восстановлением нитросоединений в присутствии катализатора:

C₆H₅-NO₂ + 3H₂   = C₆H₅-NH₂ + 2H₂O

реагируют с кислотами:

C₆H₅-NH₂ + HC1 =[C₆H₅-NH₃]C1

Глюкозу можно получить гидролизом крахмала или целлюлозы:

(С₆Н₁₀О₅)_n + n H₂O = nC₆H₁₂O₆

Для глюкозы характерно спиртовое брожение:

C₆H₁₂O₆ ® 2C₂H₅OH + 2CO₂

молочнокислое брожение:

C₆H₁₂O₆ ® 2СН₃СН(ОН)СООН

реакция серебряного зеркала:

C₆H₁₂O₆+Ag₂O 2Ag¯+C₆H₁₂O₇

Аминокислоты реагируют как с кислотами:

H₂N-CH-COOH+HCl ®  Cl^— H₃N⁺-CH-COOH

так и c щелочами:

H₂N-CH-COOH+NaOH ® H₂N-CH-COONa+H₂O

соли аминокислот также способны участвовать в реакциях обмена в водном растворе:

Cl^— H₃N⁺-CH-COOH+NaOH ® H₂N-CH-COOH +NaCl + H₂O

Cl^— H₃N⁺-CH-COOH+2NaOH ® H₂N-CH-COONa +NaCl + 2H₂O

H₂N-CH-COONa+HCl ® H₂N-CH-COOH +NaCl

H₂N-CH-COONa+2HCl ® Cl^— H₃N⁺-CH-COOH +NaCl

МЦКО

Химия – предмет, не относящийся к обязательным для сдачи ЕГЭ, и выбирают его выпускники, которые хорошо в нем разбираются. Но и у них даже, казалось бы, самые легкие задания могут вызвать затруднения. На каких моментах часто спотыкаются участники экзамена и как можно избежать ошибок, рассказывает Наталия Покровская, эксперт Московского центра качества образования, ответственный секретарь предметной комиссии ЕГЭ по химии.

Вариант контрольно-измерительных материалов единого государственного экзамена по химии состоит из 35 заданий: 29 в первой части – с выбором ответа или кратким ответом, и 6 во второй – высокого уровня сложности с развернутым ответом.

Задания 1–3

– Первые три задания не относятся к разряду трудных, но и в них выпускники могут допустить ошибки: иногда ребят сбивает с толку простое изменение формулировки вопроса, – рассказывает Наталия Покровская. – Например, если в задании 3 написано «Выберите элементы, проявляющие высшую степень окисления +5», всем ясно, о чем идет речь. А нестандартная формулировка вроде «Выберите элементы, которые имеют одинаковую разность между значениями их высшей и низшей степеней окисления» вызывает непонимание, хотя суть задания не изменилась! Таким образом, старшеклассники должны быть готовы к тому, что вопрос может звучать по-разному.

Задание 7

Это задание также нельзя назвать трудным. Главное при его выполнении быть внимательными. Например, в условии может быть сказано: «Добавили раствор вещества Х». Значит, выбирая из предложенного списка вещество Х, сразу нужно исключить все нерастворимые вещества. Поскольку задание чаще всего направлено на проверку знаний о реакциях, протекающих в растворах, следует вспомнить, в каких случаях выделяются газы: разложение получившихся непрочных кислот (сернистой, угольной) или гидрата аммиака, появление в продуктах сероводорода, совместный полный гидролиз, вытеснение водорода из кислоты металлом. Всю информацию, касающуюся осадков, можно найти в таблице растворимости. Написание схемы реакции поможет визуализировать условие задания и не допустить ошибок.

Задания 8, 30, 31 и 32

Задания 8, 30, 31 и 32 направлены на проверку знаний свойств неорганических веществ. Изменившийся формат заданий 30 и 31 ограничивает экзаменуемых в выборе веществ, между которыми идет реакция. Теперь уравнение должно соответствовать указанным в условии признакам: меняется ли цвет раствора, образуется или не образуется осадок либо газ. Поэтому не любое правильно написанное уравнение будет считаться верным: оценивается уравнение только той реакции, которая полностью соответствует условию. Для выполнения задания 30 нужно хорошо знать, какие конкретно вещества являются окислителями и восстановителями, а для задания 31 – вспомнить формулы малодиссоциирующих веществ (их нельзя записывать в виде ионов).

Важно помнить: если в исходных веществах есть кислота, то в продуктах не может получиться основание или основная соль, и наоборот. Следует проверять, чтобы получившиеся продукты реакции не реагировали между собой и с реагентами. Если есть возможность дальнейшего протекания реакции, значит, уравнение неверно. Больше информации о выполнении этих заданий можно найти на сайте Московского образовательного телеканала в видеоролике «Учимся вместе. Я сдам ЕГЭ!».

Задания 8 и 32 различаются тем, что первое предполагает только выбор возможных реакций, а во втором требуется написание уравнений (при этом даются подсказки в виде признаков протекания реакций). Приступая к выполнению задания 8, нужно рассмотреть предложенные формулы веществ с двух позиций: их кислотно-основных и окислительно-восстановительных свойств. Это позволит сразу понять, от какого списка реагентов можно отказаться: например, кислота не реагирует с кислотой, а восстановитель – с восстановителем. Для выполнения задания 32 особенно важно знать цвета осадков и растворов – это может быть хорошей подсказкой для определения продуктов реакции. Выучить палитру довольно просто, если раскрасить таблицу растворимости, отмечая все известные цветовые признаки соединений. Дополнительную информацию о задании 32 можно посмотреть по ссылке.

Задание 13

Очень много ошибок выпускники делают в задании 13 (свойства углеводородов), особенно если вопрос заключается в определении механизма реакции. Рекомендую обратить внимание на то, что ионный механизм всегда связан с присутствием ионов, то есть разноименно заряженных частиц. Но есть вещества, которые при разных условиях могут образовывать и частицы-ионы, и частицы-радикалы. Например, молекула хлора при облучении распадается на радикалы, а вот катализатор поляризует молекулу галогена, в результате чего происходит гетеролитический разрыв связи, и получаются ионы.

Гораздо легче запомнить свойства углеводородов, если учитывать возможность веществ с определенным типом связи вступать в соответствующие реакции: кратная связь – реакции присоединения, одинарная связь – реакции замещения. Но не следует забывать также, что при изменении условий могут быть исключения даже в основных законах: с перекисью водорода в качестве катализатора реакция присоединения идет вопреки правилу Марковникова, а если хлорирование алкена проводить при температуре 600 0С, то вместо реакции присоединения пойдет замещение у атома углерода в sp3-гибридизации.

Задания 15 и 17

Не менее сложны задания 15 (азотсодержащие органические вещества и углеводы) и 17 (кислородсодержащие органические вещества). При изучении свойств этих соединений нужно обратить внимание, что реакции могут идти как по функциональной группе, так и по радикалу. Чтобы выучить как можно больше свойств органических соединений, можно составить конспект, выписать побольше уравнений для каждого класса. И конечно же, нужно выполнять цепочки на взаимосвязь органических веществ. Рекомендую посмотреть видеоролики по этим заданиям на Московском образовательном телеканале – «Химия, ЕГЭ. Задание № 15» и «Химия, ЕГЭ. Задание № 17», а также видео «Химия, 10 класс. Взаимосвязь классов органических веществ».

Затруднения вызывают и вопросы по окислительно-восстановительным реакциям в органической химии, особенно если нужно расставить коэффициенты. Справиться с такими заданиями поможет консультация эксперта: «Химия, 11 класс. Окислительно-восстановительные реакции в органической химии».

Задания 34 и 35

Самыми трудными для выполнения являются задания 34 и 35 – это расчетные задачи с химическим содержанием.

Ошибки в задании 35 чаще всего случаются из-за неправильного определения структурной формулы. Обычно это связано с недостаточным знанием химических свойств органических веществ. Поэтому здесь только один совет: стараться каждый день выполнять хотя бы одну цепочку превращений, писать уравнения реакций.

Задание 34 сложно тем, что для него нет единого алгоритма решения. Есть задачи на электролиз, смеси, атомистику, а бывает, что в условии переплетается несколько типов задач. Я бы советовала сначала отработать какой-то один тип задач, разобраться в его логике. Потом подключить задачи другого типа и понять, в чем отличие, определить последовательность действий.

При решении этих задач требуется повышенное внимание: лучше прочитать условие несколько раз, возвращаться к нему по мере выполнения задания, отмечать массы веществ, которые уходят из раствора, чтобы исключить их при нахождении массы конечного раствора. Формулы, применяемые для решения задачи 34, простые и хорошо известные, например: массовая доля равна массе растворенного вещества, деленной на массу раствора. Сложности – в деталях: при вычислении массы раствора нужно не забыть сложить все массы добавляемых веществ, вычесть массы осадков и выделившихся газов. Важно помнить, что амфотерные гидроксиды в избытке щелочи растворяются, и если в начале задачи трудно определить избыток или недостаток щелочи, можно написать два возможных уравнения – образования гидроксида и образования комплексной соли.

Полезные ссылки

Для успешной сдачи экзамена по химии нужно готовиться, повторять теорию и выполнять упражнения. Найти их можно в открытом банке заданий на сайте Федерального института педагогических измерений.

Также я рекомендую посмотреть видеоролики Московского образовательного телеканала, где в рубриках «Субботы московского выпускника» (совместный проект с Московским центром качества образования), «Спроси эксперта», «Учимся вместе. Я сдам ЕГЭ!» ведущие эксперты предметных комиссий разбирают задания ЕГЭ и дают рекомендации, как лучше подготовиться. А все новости, касающиеся ЕГЭ, можно найти на сайте Московского центра качества образования.

Источник: Activityedu.ru

Все сложные реакции заданий 32 из банка ФИПИ.

Все реакции из заданий 32, которые могут вызвать затруднения при составлении. На ЕГЭ 99% реакций в заданиях 32 будут либо они, либо аналогичные.

1) Si + 2Cl₂ SiCl₄

2) SiCl₄ + 3H₂O H₂SiO₃ + 4HCl

3) Ca₃(PO₄)₂ + 5C + 3SiO₂ 2P + 5CO + 3CaSiO₃

4) Ca₃N₂ + 6H₂O 3Ca(OH)₂ + 2NH₃↑

5) 2NH₃ + 3CuO  3Cu + 3H₂O + N₂↑

6) Cu + 4HNO₃(конц.) Cu(NO₃)₂ + 2NO₂↑ + 2H₂O

7) 2Cu(NO₃)₂ 2CuO + 4NO₂ + O₂↑

8) 4FeS + 7O₂ 2Fe₂O₃ + 4SO₂↑

9) 2H₂S + SO₂ 3S↓ + 2H₂O

10) S + 6HNO₃ H₂SO₄ + 6NO₂↑ + 2H₂O

11) 4Al(NO₃)₃ 2Al₂O₃ + 12NO₂↑ + 3O₂↑

12) 2Al₂O₃ 4Al + 3O₂↑ (электролиз раствора Al₂O₃ в расплаве криолита)

13) 3KNO₃ + 8Al + 5KOH + 18H₂O  3NH₃↑ + 8K[Al(OH)₄]

14) CrO₃ + 2KOH K₂CrO₄ + H₂O

15) 2K₂CrO₄ + H₂SO₄ K₂Cr₂O₇ + K₂SO₄ + H₂O

16) 14HBr + K₂Cr₂O₇ 2CrBr₃ + 3Br₂ + 7H₂O + 2KBr

17) H₂S + Br₂ S↓ + 2HBr

18) 3Mg + N₂ Mg₃N₂

19) Mg₃N₂ + 6H₂O 3Mg(OH)₂↓ + 2NH₃↑

20) Cr₂(SO₄)₃ + 6NH₃ + 6H₂O 2Cr(OH)₃↓ + 3(NH₄)₂SO₄

21) 2Cr(OH)₃ + 4KOH + 3H₂O₂ 2K₂CrO₄ + 8H₂O

22) 2Ag + 2H₂SO₄(конц.) Ag₂SO₄ + SO₂↑ + 2H₂O

23) 2KClO₃ 2KCl + 3O₂↑ (в присутствии кат-ра)

24) 3Fe + 2O₂  Fe₃O₄

25) Fe₃O₄ + 8HCl FeCl₂ + 2FeCl₃ + 4H₂O

26) 6FeCl₂ + 14HCl + K₂Cr₂O₇ 6FeCl₃ + 2CrCl₃ + 2KCl + 7H₂O

27) 2Na + H₂ 2NaH

28)  NaH + H₂O NaOH + H₂↑

29) 2NO₂ + 2NaOH NaNO₂ + NaNO₃ + H₂O

30) 2Al + 2NaOH + 6H₂O 2Na[Al(OH)₄] + 3H₂↑

31) Cu + 2H₂SO₄  CuSO₄ + SO₂↑ + 2H₂O

32) 2CuSO₄ + 4KI 2CuI↓ + I₂↓ + 2K₂SO₄

33) 2NaCl + 2H₂O H₂↑ + Cl₂↑ + 2NaOH (электролиз раствора)

34) Fe₂O₃ + 6HI 2FeI₂ + I₂↓ + 3H₂O

35) Na[Al(OH)₄]  + CO₂ NaHCO₃ + Al(OH)₃↓

36) Al₂O₃ + Na₂CO₃ (тв.) 2NaAlO₂ + CO₂↑ (сплавление)

37) Al₄C₃ + 12HBr 4AlBr₃ + 3CH₄↑

38) 2AlBr₃ + 3K₂SO₃ + 3H₂O 2Al(OH)₃↓ + 3SO₂↑ + 6KBr

39) 3SO₂ + K₂Cr₂O₇ + H₂SO₄ K₂SO₄ + Cr₂(SO₄)₃ + H₂O

40) Zn + 2KOH + 2H₂O K₂[Zn(OH)₄] + H₂↑

41) K₂[Zn(OH)₄]  K₂ZnO₂ + 2H₂O

42) K₂ZnO₂ + 4HCl 2KCl + ZnCl₂ + 2H₂O

43) HI + KHCO₃ KI + H₂O + CO₂↑

44) 6KI + K₂Cr₂O₇ + 7H₂SO₄ 4K₂SO₄ + 3I₂↓ + Cr₂(SO₄)₃ + 7H₂O

45) 2AlI₃ + 3Na₂S + 6H₂O 2Al(OH)₃↓ + 3H₂S↑ + 6NaI

46) Fe₃O₄ + 10HNO₃ 3Fe(NO₃)₃ + NO₂↑ + 5H₂O

47) Fe₂O₃ + Fe  3FeO

48) 2Na + O₂ Na₂O₂ (горение)

49)  Na₂O₂ + 4HCl 2NaCl + 2H₂O + Cl₂↑

50) 3Cl₂ + 10KOH + Cr₂O₃ 2K₂CrO₄ + 6KCl + 5H₂O

51) K₂CrO₄ + BaCl₂ BaCrO₄↓ + 2KCl

52) 2Cu(NO₃)₂ + 2H₂O 2Cu + O₂↑ + 4HNO₃ (электролиз раствора)

53) 6KOH + 3S K₂SO₃ + 2K₂S + 3H₂O

54) 6KHCO₃ + Fe₂(SO₄)₃ 2Fe(OH)₃↓ + 3K₂SO₄ + 6CO₂↑

55) KH + H₂O KOH + H₂↑

56) K₂ZnO₂ + 2H₂SO₄ K₂SO₄ + ZnSO₄ + 2H₂O

57) FeSO₄ + 2NH₃ + 2H₂O Fe(OH)₂↓ + (NH₄)₂SO₄

58)  Fe(OH)₂ + 4HNO₃(конц.) Fe(NO₃)₃ + NO₂↑ + 3H₂O

59) 2Fe(NO₃)₃ + 3K₂CO₃ + 3H₂O 2Fe(OH)₃↓ + 3CO₂↑ + 6KNO₃

60) 4NO₂ + 2Ca(OH)₂ Ca(NO₃)₂ + Ca(NO₂)₂ + 2H₂O

61) 3Ca + 2P Ca₃P₂

62) Ca₃P₂ + 6H₂O 3Ca(OH)₂ + 2PH₃↑

63) PH₃ + 8NaMnO₄ + 11NaOH 8Na₂MnO₄ + Na₃PO₄ + 7H₂O

64) Na₂MnO₄ + Na₂SO₃ + H₂O MnO₂↓ + Na₂SO₄ + 2NaOH

65) P + 5HNO₃ H₃PO₄ + 5NO₂↑ + H₂O

66) 4Zn + 2NO₂ 4ZnO + N₂↑

67) 2NaNO₃   2NaNO₂ + O₂↑

68) NaNO₂ + NH₄I  NaI + N₂↑ + 2H₂O

69) 2NaI + H₂O₂ + H₂SO₄ Na₂SO₄ + I₂↓ + 2H₂O

70) 3I₂ + 6NaOH(р−р)  NaIO₃ + 5NaI + 3H₂O

71) H₂O₂ + Ag₂O 2Ag↓ + O₂↑ + H₂O

72) 2ZnS + 3O₂ 2ZnO + 2SO₂↑

73) Na₂[Zn(OH)₄]  Na₂ZnO₂ + 2H₂O

74) 3Cu₂O + Na₂Cr₂O₇ + 10H₂SO₄ 6CuSO₄ + Cr₂(SO₄)₃ + Na₂SO₄ + 10H₂O

75) NaHCO₃ + NaOH Na₂CO₃ + H₂O

76) K₂Cr₂O_7(тв.) + 14HCl_(конц.) 2CrCl₃ + 2KCl + 3Cl₂↑ + 7H₂O

77) 3NaNO₂ + 2KMnO₄ + H₂O 2MnO₂↓ + 2KOH + 3NaNO₃

78) MnO₂ + 4HCl_(конц.) MnCl₂ + Cl₂↑ + 2H₂O

79) 2Fe(OH)₃ + 6HI 2FeI₂ + I₂↓ + 6H₂O

80) 3Na₂CO₃ + 2CrBr₃ + 3H₂O 2Cr(OH)₃↓ + 6NaBr + 3CO₂↑

81) 5FeCl₂ + KMnO₄ + 8HCl 5FeCl₃ + MnCl₂ + KCl + 4H₂O

82) K₂SiO_3(р—р) + 2H₂O + 2CO₂ H₂SiO₃↓ + 2KHCO₃

83)  Ba(OH)₂ + 2NaHCO₃ = Na₂CO₃ + BaCO₃↓ + 2H₂O (при избытке NaHCO₃)
либо
Ba(OH)₂ + NaHCO₃ = BaCO₃ + NaOH + H₂O (при избытке Ba(OH)₂)

84) 6KOH + 3Cl₂ KClO₃ + 5KCl + 3H₂O

85) Cr₂O₃ + KClO₃ + 4KOH 2K₂CrO₄ + KCl + 2H₂O

86) 4NH₃ + 5O₂ 4NO + 6H₂O (кат. Pt, Cr₂O₃, t, p)

87) 2NO + O₂ 2NO₂

88) NaNO₂ + 2KMnO₄ + 2KOH 2K₂MnO₄ + NaNO₃ + H₂O

89) 8KI_(тв.) + 9H₂SO_4(конц.) 8KHSO₄ + 4I₂↓ + H₂S↑ + 4H₂O

90) Al₂O₃ + 2NaOH + 3H₂O 2Na[Al(OH)₄]

91) Na[Al(OH)₄] + 4HNO₃ NaNO₃ + Al(NO₃)₃ + 4H₂O

92) 2Ca(OH)₂ + 4NO₂ + O₂ 2Ca(NO₃)₂ + 2H₂O

93) K[Al(OH)₄] + SO₂ KHSO₃ + Al(OH)₃↓

94) 8KOH + PCl₅ K₃PO₄ + 5KCl + 4H₂O

95) 2KBr(тв) + 2H₂SO₄(конц., гор.) K₂SO₄ + Br₂ + SO₂↑ + 2H₂O

96) 3Br₂ + 6KOH 5KBr + KBrO₃ + 3H₂O

97) Br₂ + K₂SO₃ + 2NaOH 2NaBr + K₂SO₄ + H₂O

98) Fe₂O₃ + 6HI 2FeI₂ + I₂ + 3H₂O

99) Fe₂O₃ + 2NaOH(тв.) 2NaFeO₂ + H₂O (сплавление)

100) 4NO₂ + O₂ + 2H₂O 4HNO₃

101) NaFeO₂ + 4HNO₃(изб.) NaNO₃ + Fe(NO₃)₃ + 2H₂O

102) FeO + 4HNO₃(конц.) Fe(NO₃)₃ + NO₂↑ + 2H₂O

103) Ca₂Si + 4H₂O 2Ca(OH)₂ + SiH₄↑

104) 3Na₂SO₃ + Na₂Cr₂O₇ + 4H₂SO₄ Cr₂(SO₄)₃ + 4Na₂SO₄ + 4H₂O

105) 4Mg + 5H₂SO₄(конц.) 4MgSO₄ + H₂S↑ + 4h3O

106) CuS + 10HNO₃  Cu(NO₃)₂ + H₂SO₄ + 8NO₂ + 4H₂O
либо (одинаково верно)
CuS + 8HNO₃(конц.) CuSO₄ + 8NO₂↑ + 4h3O

107) 3Cu + 8HNO₃(разб.) 3Cu(NO₃)₂ + 2NO↑ + 4H₂O

108) 2Cu(NO₃)₂ + 2H₂O 2Cu↓ + O₂↑ + 4HNO₃ (электролиз раствора)

109) Cu₂O + 3H₂SO₄(конц.) 2CuSO₄ + SO₂↑ + 3H₂O

110) 2NaI + 2NaMnO₄ I₂↓ + 2Na₂MnO₄ (в щелочном растворе)

111) 2Na₂O₂ + 2CO₂ 2Na₂CO₃ + O₂

112) 8NaOH(р-р, изб.) + Al₂S₃ 2Na[Al(OH)₄] + 3Na₂S

113) 4Ca + 5H₂SO_4(конц.)  H₂S↑ + 4CaSO₄↓ + 4H₂O

114) 2Fe(OH)₂ + H₂O₂ 2Fe(OH)₃

115) Na₂O₂ + 2H₂O_(хол.)  H₂O₂ + 2NaOH

116) Ag₂S + 10HNO₃(конц.) = 2AgNO₃ + H₂SO₄ + 8NO₂ + 4H₂O
либо (одинаково верно)
Ag₂S + 8HNO₃ → Ag₂SO₄ + 8NO₂ + 4H₂O

7 величайших математических загадок тысячелетия.

Часто, беседуя со старшеклассниками об исследовательских работах по математике, слышу следующее: «Что можно нового открыть в математике?» А действительно: может быть все великие открытия сделаны, а теоремы доказаны?

8 августа 1900 года на международном математическом конгрессе в Париже математик Дэвид Гилберт (David Hilbert) изложил список проблем, которые, как он полагал, предстояло решить в ХХ веке. В списке было 23 пункта. Двадцать один из них на данный момент решены. Последней решенной проблемой из списка Гилберта была знаменитая теорема Ферма, с которой ученые не могли справиться в течение 358 лет. В 1994 году свое решение предложил британец Эндрю Уайлз. Оно и оказалось верным.

По примеру Гилберта в конце прошлого века многие математики пытались сформулировать подобные стратегические задачи на ХХI век. Один из таких списков приобрел широкую известность благодаря бостонскому миллиардеру Лэндону Клэю (Landon T. Clay). В 1998 году на его средства в Кембридже (Массачусетс, США) был основан Математический институт Клэя (Clay Mathematics Institute) и установлены премии за решение ряда важнейших проблем современной математики. 24 мая 2000 года эксперты института выбрали семь проблем — по числу миллионов долларов, выделенных на премии. Список получил название Millennium Prize Problems:

1. Проблема Кука (сформулирована в 1971 году)

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.

Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема также является одной из нерешенных задач из области логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.

2. Гипотеза Римана (сформулирована в 1859 году)

Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например 2, 3, 5, 7 и так далее. Такие числа называются простыми и играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди ряда всех натуральных чисел не подчиняется никакой закономерности. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.

3. Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)

Связана с описанием множества решений некоторых алгебраических уравнений от нескольких переменных с целыми коэффициентами. Примером подобного уравнения является выражение x2 + y2 = z2. Эвклид дал полное описание решений этого уравнения, но для более сложных уравнений поиск решений становится чрезвычайно трудным.

4. Гипотеза Ходжа (сформулирована в 1941 году)

В ХХ веке математики открыли мощный метод исследования формы сложных объектов. Основная идея заключается в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких «кирпичиков» и объектов.

5. Уравнения Навье — Стокса (сформулированы в 1822 году)

Если плыть в лодке по озеру, то возникнут волны, а если лететь в самолете, в воздухе возникнут турбулентные потоки. Предполагается, что эти и другие явления описываются уравнениями, известными как уравнения Навье — Стокса. Решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Решение этой проблемы позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.

6. Проблема Пуанкаре (сформулирована в 1904 году)

Если натянуть резиновую ленту на яблоко, то можно, медленно перемещая ленту без отрыва от поверхности, сжать ее до точки. С другой стороны, если ту же самую резиновую ленту соответствующим образом натянуть вокруг бублика, то никаким способом невозможно сжать ленту в точку, не разрывая ленту или не ломая бублик. Говорят, что поверхность яблока односвязна, а поверхность бублика — нет. Доказать, что односвязна только сфера, оказалось настолько трудно, что математики ищут правильный ответ до сих пор.

7. Уравнения Янга — Миллса (сформулированы в 1954 году)

Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга — Миллса следовало существование частиц, которые действительно наблюдались в лабораториях во всем мире, поэтому теория Янга — Миллса принята большинством физиков несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.

Думаю, что этот материал, опубликованный в блоге

интересен не только студентам, но и школьникам, серьёзно занимающимся математикой. Есть над чем подумать, выбирая темы и направления исследовательских работ.

Показательные уравнения (уровень С) — Колпаков Александр Николаевич

Банк заданий на показательные уравнения для подготовки к ЕГЭ по математике и внутреннего экзамена в МГУ. Коллекция моих любимых уравнений. Обычно сильные репетиторы по математике ведут работу со способными выпускниками, поступающими на серьезные факультеты главного ВУза страны, за границами традиционных ЕГЭ задач. Хороший репетитор предложит Вам подборку классических показательно — логарифмических уравнений на разные виды и способы решений. Учебные планы репетитора по математике, занятого исключительно подготовкой к ЕГЭ, обычно не затрагивают подобные головоломки. Они предлагаются в случае занятий для поступления МГУ или разбираются на уроках с любознательным учеником, заинтересованном в дополнительных знаниях.

Показательный вид — наиболее простой из всех конкурсных уравнений, поэтому собрать номера с высоким уровнем сложности оказалось делом нелегким. Здесь опубликована только часть материалов моей базы. Она постоянно пополняется новыми заданиями. Появится время — размещу остальное.

Уважаемые репетиторы по математике и школьные преподаватели, присылайте понравившиеся Вам сложные показательные уравнения мне на почту (принимается сканер или фото условия). С удовольствием включу их в комплект.

Коллекция показательных уравнений репетитора по математике

Приведите к простейшему показательному уравнению:

=====================================================
Однородные уравнения:

=====================================================
На преобразования и замену:

Отв: x=2,5

Отв: x=4

Отв:

Отв:

Отв:

======================================================
Уравнения с квадратным трехчленом:

Отв:

Отв:

======================================================
На метод оценки значений:

======================================================
На монотонность

Колпаков А.Н. Репетитор по математике — составитель комплекта. Москва, Строгино

Топ-5 приложений для решения задач по математике

Мы отобрали для вас лучшие приложения для Android, которые созданы для решения практически любых задач по математике в два счета.

Математику по праву можно назвать царицей наук, которую в равной степени можно как любить, так и ненавидеть. Если задуматься всерьез, то мы используем знания по математике каждый день. Повсюду сталкиваемся с числами – на циферблате часов, на денежных банкнотах, в расписании уроков. Нам все время приходится выполнять простые и сложные математические операции – посчитать, через сколько минут начнется любимый фильм, сколько сдачи должны дать в магазине, когда приедет автобус.

Но для многих математика — это непонятные действия, числа, правила и задачи. Говорят, все познается в сравнении. Математика позволяет нам узнать, насколько что-то больше, длиннее, шире, дороже другого. Без знания математики невозможно построить дом, автомобиль. Если бы не математика, у нас бы никогда не было ни компьютеров, ни планшетов и смартфонов. Математическими расчетами пользуются все другие науки в мире. 

Простая арифметика, превращающаяся в дальнейшем в сложную алгебру и геометрию, заставляла многих ненавидеть эти дисциплины. Кому-то математика в школе давалась легко, а для кого-то она так и осталась чем-то далеким и непостижимым. Как ни крути, иногда умение считать деньги не спасает от необходимости решения сложных математических уравнений и неравенств. «Смартфон» дословно переводится как «умный телефон», и благодаря стороннему софту ему можно доверить даже самые сложные задачи. В век информационных технологий дела с этим обстоят совсем иначе. На помощь школьникам и студентам пришли смартфоны и планшеты с «умными» приложениями-калькуляторами, речь о которых пойдет в этой статье. Оговоримся сразу, что приложения не могут быть панацеей. Вам всё равно придется учить математику, а они лишь помогут вам, подскажут ход решения. Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.

Photomath

Одно из самых известных приложений для решения математических задач с первого же дня назвали ужасом для учителей математики. А разработчики просто называют его «камерой-калькулятором». Photomath интересно тем, что способно решить практически любую математическую задачу. Вам тяжело разобраться в решении логарифмических, квадратных, тригонометрических уравнений и неравенств? Трудно решать задачи с корнями, модулями, степенями, дробями, интегралами и факториалами? Теперь с помощью приложения Photomath решать такие задания не составит большого труда. Но самое интересно — приложение не просто решает математические задачи, а подробно расписывает ход расчетов. Это понравится не только учащимся и студентам, а также родителям, которые захотят проверить домашнее задание своего чада.

Пользователю понравится, что приложение Photomath способно работать в автоматическом режиме. Достаточно просто открыть его и сразу же активируется встроенный интерфейс камеры с заданной областью распознавания. Для того, что начать работу, необходимо расположить камеру так, чтобы математическая задача вместилась в эту область. Буквально через мгновение умные алгоритмы программы начнут анализировать данные на экране и практически моментально выдадут ответ. Если захотите увидеть весь ход решения вашей задачи, то просто нажмите на результат в красном прямоугольнике. В истории приложения сохраняются 10 последних записей, поэтому в любой момент сможете просмотреть решение предыдущей задачи. 

Иногда случается, что программа некорректно распознала те или иные математические символы в задании, решив неправильно при этом задачу. Но не отчаивайтесь. В Photomath у вас есть возможность отредактировать их в режиме калькулятора. Стоит отметить, разработчики очень хорошо продумали эту функцию. Здесь доступен калькулятор со всевозможными операторами, есть цифровая, текстовая и символьная раскладки. 

Долгое время приложение умело распознавать только напечатанное задание. Причем из книги было намного легче отсканировать его, чем с экрана ноутбука. Теперь же, наконец-то, появилась долгожданная функция распознавания рукописного текста. Все работает почти безупречно, но для лучшего результата желательно, чтобы запись была аккуратным почерком. 

Мне очень понравилось пользоваться приложением. Оно практически справляется с любым заданием со всей школьной программы по математике и алгебре, включая старшую и высшую школы. Да, приложение стоящее, абсолютно бесплатное, не содержит рекламы, как обычно бывает с такими приложениями, есть русский язык интерфейса, способно работать без подключения к Интернету, но и ошибок предостаточно. 

MalMath: Step by step solver

С помощью данного приложения вы сумеете решить математические задачи не только получив пошаговое описание процесса вычисления, но и построение необходимых графиков. Само приложение MalMath для Android полностью бесплатное, к тому же совершенно не содержит рекламы. Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.

Интерфейс MalMath представлен на русском языке, выполнен в классическом стиле и оптимизирован под экраны смартфонов. У вас есть возможность в настройках изменить размер шрифта и скорость анимации. Открыв боковое меню, увидите, что оно включает пять пунктов: главный экран, рабочий лист, график, генератор задач, избранное. Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.

Сам процесс добавления задачи очень похож на вставку формул в Microsoft Word. Из собственного опыта отмечу, что, вроде бы все понятно и просто, но иногда довольно неудобно, особенно, что касается ввода сложных комбинаций с дробями и корнями. Придется потратить немного времени, чтобы привыкнуть к определенному принципу набора, но все же оно того стоит.

Mathway

Еще одно весьма заслуживающее внимания приложение, которое поможет справиться с математическими заданиями. Приложение является своеобразным инструмент для решения задач, который, помимо школьного курса математики, охватывает математический анализ, статистику, тригонометрию, линейную алгебру и даже химию. Если вы когда-то использовали веб-версию сервиса Mathway, то сразу же узнаете внешний вид и функциональные возможности данного приложения. Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником. 

Стоит заметить, что именно данное приложение из рассматриваемых в этой статье является одним из самых интересных в плане качества решения. Вам понравится, что получите, пожалуй, наиболее развернутые пошаговые решения задач, к тому же на понятном русском языке. Немного странным выглядит тот факт, что в описании указано, что для просмотра пошагового решения, нужна платная подписка, хотя все функциональные возможности приложения совершенно бесплатны. Mathway поможет вам не только с решением уравнений, неравенств и прочих сложных выражений, но также сумеет построить графики, может найти число молекул в определенной массе тела. 

Mathway для Android тоже решает задачи с помощью камеры устройства, правда, реализована эта функция не самым лучшим образом. Для такого вывода у нас есть несколько веских причин. Во-первых, интерфейс камеры в программе крайне минималистичный, в нем почему-то нет даже области распознавания. Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение. Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.

Мне очень понравилось, что Mathway предлагает пользователю самому выбрать способ решения задачи, в зависимости от этого результаты могут меняться. Если не подходит один из способов, достаточно снова тапнуть на математическое выражение и выбрать другой вариант решения. Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится. 

Mathpix

Mathpix — первое приложение, которое позволяет вам решать и визуализировать решения, распознавая рукописный текста, включая сложные формулы. Mathpix стремится заменить дорогие и устаревшие графические калькуляторы, чтобы обеспечить бесплатное и интересное учебное пособие для студентов-математиков по всему миру.

Я и вовсе хотел написать его первым среди всех приложений, так как это один из старожилов подобных приложений для решения математических задач. Оно намного раньше, в отличие от Photomath, получило способность распознавать рукописные математические задачи. Стоит заметить, что  суть и принцип работы обоих приложений очень похожи, но в целом сервис Mathpix рассчитан на более взрослую аудиторию. Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т. д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.

Вам очень понравится работа алгоритмов распознавания текстов и условий у Mathpix. Программа практически в считанные секунды сканирует и считывает условие задачи. Тут же отправляет на сервер данные условия и почти мгновенно выдает ответ. Но ошибки тоже случаются, хотя довольно редко. При этом пользователю доступны инструменты для работы с задачами в режиме графика: редактирование вводных данных, добавление таблиц, заметок и дополнительных функций для нескольких графиков.

Я тут так пафосно расписал возможности приложения, но отмечу, что оно хорошо справляется только с несложными задачами. Если еще с построением элементарных графиков приложение справится, то с более сложными заданиями, которые включают тригонометрические и логарифмические уравнения, неравенства, а также уравнения с модулем, возникали большие проблемы. Приложение просто игнорировало их решение. Так что разработчикам еще необходимо потрудиться над возможностями своей программы.

Большинству пользователей не понравится, что отсутствует интерфейс на русском языке, а также подробное описания решения задач. Да и само приложение довольно-таки сложновато в использовании, элементы управления неудобны на смартфоне с небольшим экраном. Создалось впечатление,что это веб-версия приложения. Но решение всё же остается за вами.

MyScript Calculator

Ну и, наконец, самое интересное приложение MyScript Calculator, которое впервые появилось в начале 2013 года. К тому же, сразу получило признание на международной выставке CES и было отмечено за инновации. Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные. В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.

Вам понравится, что приложение автоматически сумеет распознать написанное вручную, переведет записи в нормальный цифровой вид и буквально в то же мгновение выдаст результат. Стоит отметить, что алгоритмы распознавания MyScript Calculator просто великолепные. На практике программа умудряется определить даже самые откровенные каракули. Также вы сможете отменить или повторить последние действия и полностью очистить экран от написанного. К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.

Основным недостатком MyScript Calculator для Android можно считать отсутствие подробного описания решений, программа выдает только итоговый результат. Хотя, учитывая концепцию приложения, возможно оно было бы лишним. А вот то, что здесь не хватает различных удобных мелочей, так это скорее пожелание разработчикам на будущее. К примеру, хотелось бы увидеть историю вычислений, возможность масштабировать экран и сохранять введенные задачи. Но, если все это отбросить в сторону, приложение действительно полезное, простое и оригинальное. 

Вместо тысячи слов…

Ну и в заключение все же хочется сказать, что хоть приведенные приложения и помогут вам справиться с математическими заданиями, но не забывайте, что это всего лишь программа. Она призвана помочь вам, а не добавлять вам знаний. Но еще раз повторюсь, данные приложения не являются панацеей для решения задач. Так, с некоторыми заданиями оно и вовсе не справится. К тому же иногда ошибаются в самых простейших случаях. Поэтому не стоит доверять им всецело, а все-таки учить математику.

Будем признательны, если в комментариях поделитесь своим опытом использования подобных приложений, которые облегчают изучение математики.

сложнейших математических задач и уравнений

Вместе с гипотезой Гольдбаха гипотеза о простых числах-близнецах является наиболее известной в теории чисел — или исследовании натуральных чисел и их свойств, часто с использованием простых чисел. Поскольку вы знаете эти числа с начальной школы, высказывать предположения легко.

Когда два простых числа имеют разность, равную 2, они называются двойными простыми числами. Итак, 11 и 13 — простые числа-близнецы, как и 599 и 601. Итак, это факт теории чисел первого дня, что существует бесконечно много простых чисел.Итак, существует ли бесконечно много близнецов простых чисел? Гипотеза Twin Prime говорит «да».

Пойдем немного глубже. Первое в паре простых чисел-близнецов, за одним исключением, всегда на 1 меньше кратного 6. Итак, второе простое число-близнец всегда на 1 больше, чем кратное 6. Вы можете понять почему, если готовы к следуйте пьянящей теории чисел.

Все простые числа после 2 нечетны. Четные числа всегда на 0, 2 или 4 больше, чем кратные 6, в то время как нечетные числа всегда на 1, 3 или 5 больше, чем кратные 6.Что ж, одна из этих трех возможностей для нечетных чисел вызывает проблему. Если число на 3 больше, чем кратное 6, то оно имеет множитель 3. Наличие множителя 3 означает, что число не является простым (за единственным исключением самого 3). Вот почему каждое третье нечетное число не может быть простым.

Как твоя голова после этого абзаца? А теперь представьте себе головную боль каждого, кто пытался решить эту проблему за последние 170 лет.

Хорошая новость в том, что за последнее десятилетие мы добились многообещающего прогресса.Математикам удавалось подходить к все более и более близким версиям гипотезы о простом близнеце. Это была их идея: проблема с доказательством того, что существует бесконечно много простых чисел с разницей в 2? Как насчет доказательства того, что существует бесконечно много простых чисел с разницей в 70 000 000? Это было хорошо доказано в 2013 году Итангом Чжаном из Университета Нью-Гэмпшира.

За последние шесть лет математики улучшили это число в доказательстве Чжана с миллионов до сотен. Уменьшение числа до 2 и будет решением гипотезы о простом близнеце.Самое близкое, что мы подошли — с учетом некоторых тонких технических предположений — 6. Время покажет, не за горами ли последний шаг от 6 до 2, или эта последняя часть будет бросать вызов математикам еще на десятилетия.

5 самых сложных нерешенных математических задач в мире

Открытые задачи математической физики — это список самых чудовищных математических загадок физики. Вот пять основных проблем, которые остаются нерешенными

Физика 7 февраля 2019 г.

Бенджамин Скусе

Майк Даннинг / Гетти

1.Разделение сепаратрисы

Движущийся маятник может либо качаться из стороны в сторону, либо вращаться по непрерывному кругу. Точка, в которой он переходит от одного типа движения к другому, называется сепаратрисой, и ее можно вычислить в самых простых ситуациях. Однако, когда маятник толкают с почти постоянной скоростью, математика разваливается. Есть ли уравнение, которое может описать такую ​​сепаратрису?

изображений истории науки / Alamy Stock Photo

2.Навье – Стокса

Уравнения Навье-Стокса, разработанные в 1822 году, используются для описания движения вязкой жидкости. Такие вещи, как воздух, проходящий над крылом самолета или вода, вытекающая из крана. Но есть определенные ситуации, в которых неясно, ошибочны ли уравнения или вообще нет ответа. Многие математики пытались — и потерпели неудачу — решить эту проблему, в том числе Мухтарбай Отелбаев из Евразийского национального университета в Астане, Казахстан. В 2014 году он потребовал решения, но позже отозвал его.Это проблема, которая стоит больше, чем просто престиж. Это также одна из задач Премии тысячелетия, что означает, что любой, кто ее решит, может претендовать на призовой фонд в размере 1 миллиона долларов.

Cecile Lavabre / Getty

3. Экспоненты и размеры

Представьте себе брызги духов, разливающиеся по комнате. Движение каждой молекулы является случайным, этот процесс называется броуновским движением, даже если движение газа в целом предсказуемо. Есть математический язык, который может описывать подобные вещи, но не идеально.Он может предоставить точные решения, изменяя свои собственные правила, или он может оставаться строгим, но никогда не прийти к точному решению. Может ли он когда-нибудь поставить оба флажка? Это то, что задает проблема экспонент и размеров. Помимо квантовой проблемы холловской проводимости, это единственная проблема в списке, которая хотя бы частично решена. В 2000 году Грегори Лоулер, Одед Шрамм и Венделин Вернер доказали, что точные решения двух проблем броуновского движения могут быть найдены без нарушения правил. Это принесло им медаль Филдса, математический эквивалент Нобелевской премии.Совсем недавно Станислав Смирнов из Женевского университета в Швейцарии решил связанную с этим проблему, в результате чего в 2010 году он был награжден медалью Филдса.

Godong / Alamy Stock Photo

4. Теоремы о невозможности

Существует множество математических выражений, не имеющих точного решения. Возьмем одно из самых известных чисел, пи, которое представляет собой отношение длины окружности к ее диаметру. Доказательство того, что число Пи после десятичной точки не может заканчиваться, было одним из величайших достижений в математике.Физики также говорят, что невозможно найти решения определенных проблем, таких как определение точной энергии электронов, вращающихся вокруг атома гелия. Но можем ли мы доказать эту невозможность?

Tetra Images / Getty

5. Бокал

Чтобы понять эту проблему, вам нужно знать о спине, квантовомеханическом свойстве атомов и частиц, таких как электроны, которое лежит в основе магнетизма. Вы можете думать об этом как о стрелке, которая может указывать вверх или вниз. Электроны внутри блоков материалов наиболее счастливы, если они сидят рядом с электронами с противоположным спином, но есть некоторые устройства, где это невозможно.В этих фрустрированных магнитах вращения часто случайным образом переворачиваются, что, как оказалось, является полезной моделью других неупорядоченных систем, включая финансовые рынки. Но у нас есть ограниченные способы математического описания поведения подобных систем. Этот вопрос с вращающимся стеклом спрашивает, можем ли мы найти хороший способ сделать это.

• См. Полный список нерешенных задач: Открытые задачи математической физики

Подробнее по этим темам:

10 самых важных уравнений в истории

Уравнения — важный инструмент для описания того, сколько вещей в естественном мире функционируют и взаимодействуют.Но одни уравнения оказали более сильное влияние, чем другие.

Здесь мы представляем 10 таких уравнений, а также помогаем ответить на некоторые общие вопросы об уравнениях в сети.

СВЯЗАННЫЕ: 15 НАИБОЛЕЕ ВАЖНЫХ АЛГОРИТМОВ, ПОМОГЛИ ОПРЕДЕЛЕНИЕ МАТЕМАТИКИ, ВЫЧИСЛЕНИЙ И ФИЗИКИ

Какое уравнение является самым длинным в мире?

Согласно Sciencealert, самое длинное математическое уравнение содержит около 200 терабайт текста. Эта задача, получившая название булевой проблемы троек Пифагора, была впервые предложена калифорнийским математиком Рональдом Грэхемом еще в 1980-х годах.

Почему уравнения важны?

Уравнения используются каждый день для многих, многих вещей. Они помогают вам искать в Интернете, заставляют ваш компьютер функционировать и удерживают самолеты в воздухе, и это лишь некоторые из них.

Что такое уравнение теории хаоса?

«Теория хаоса — это раздел математики, в котором основное внимание уделяется поведению динамических систем, которые очень чувствительны к начальным условиям. Теория хаоса — это междисциплинарная теория, утверждающая, что в пределах очевидной случайности хаотических сложных систем существуют лежащие в основе закономерности, постоянные петли обратной связи. , повторение, самоподобие, фракталы и самоорганизация.»- Википедия.

Уравнение выглядит следующим образом: —

Изменено с news.bitofnews.com

Эта теория эффективно помогает нам иметь дело со сложными системами, поведение которых очень чувствительно к незначительным изменениям условий, так что небольшие изменения могут вызвать к непредвиденным последствиям.

Теория хаоса — наука сюрпризов, но не всегда приятных сюрпризов.

10 уравнений, которые изменили мир

Вот десять самых важных уравнений, которые изменили мир.Этот список далеко не исчерпывающий и в нем нет определенного порядка.

1. Теорема Пифагора

Источник: Maxpixel

Являясь основным продуктом школьных уроков математики, это уравнение фактически изменило мир. Это позволило нам составить более точные карты и помочь найти кратчайшее расстояние между объектами; среди других вещей.

Он также широко используется в архитектуре, деревообработке и многих других областях.

2. Исчисление

«Исчисление, первоначально называвшееся исчислением бесконечно малых или« исчислением бесконечно малых », представляет собой математическое исследование непрерывных изменений, точно так же, как геометрия — это изучение формы, а алгебра — это математическое исследование. изучение обобщений арифметических операций.»- Википедия.

Он был разработан независимо великим Исааком Ньютоном и сэром Готфридом Лейбницем. После его изобретения он объединил алгебру и геометрию в качестве одного из столпов математики.

3. Логарифмы

Логарифмы есть еще один тип уравнения, который изменил мир. Они помогли нам делать утомительные вычисления до того, как появились калькуляторы.

Логарифм — это величина, представляющая степень, до которой необходимо возвести фиксированное число (основание), чтобы получить заданное число.Использование таблиц логарифмов позволило исключить многие утомительные шаги в вычислениях в таких областях, как геодезия, навигация и инженерия.

4. Относительность

Источник: Peat Bakke / Flickr

Знаменитые уравнения Эйнштейна по теории относительности не только ответили на многие ранее нерешенные вопросы, но также помогли изменить наш взгляд на время, пространство и гравитацию.

Он используется для объяснения всего, от черных дыр до Большого взрыва и ядерной энергетики, а также GPS на наших телефонах.

5. Нормальное распределение

Сегодня мы все знакомы с графиками колоколообразной кривой. Они помогают описать распределение данных в заданном наборе.

Его можно использовать для чего угодно, от IQ в популяции до результатов экзамена в группе студентов. В рамках нормального распределения большинство точек данных попадают где-то посередине, с меньшим количеством людей в каждую крайность.

6. Уравнение Шредингера

Источник: YassineMrabet / Wikimedia Commons

Уравнение Шредингера необходимо для современных компьютерных микросхем и лазеров.По-видимому, это также помогает удерживать кошек в состоянии анабиоза между жизнью и смертью.

А если серьезно, это уравнение буквально навсегда изменило область квантовой физики. Это линейное уравнение в частных производных, которое описывает волновую функцию квантово-механической системы. Его открытие стало важной вехой в развитии квантовой механики.

7. Закон всемирного тяготения Ньютона

«Закон всемирного тяготения Ньютона гласит, что каждая частица притягивает каждую другую частицу во Вселенной с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату. расстояния между их центрами.»- Википедия.

Закон всемирного тяготения Ньютона — одно из самых фундаментальных уравнений в физике.

8. Волновое уравнение

« Волновое уравнение описывает поведение волн — вибрирующая струна гитары, рябь в пруду за камнем. брошен или свет выходит из лампы накаливания. Волновое уравнение было ранним дифференциальным уравнением, и методы, разработанные для его решения, открыли дверь для понимания и других дифференциальных уравнений », — businessinsider.com.

Он эффективно образует важный компонент электромагнетизма, оптики, гидродинамики и теплопередачи.

9. Второй закон термодинамики

«Это означает, что в закрытой системе энтропия (S) всегда устойчива или возрастает. Термодинамическая энтропия, грубо говоря, является мерой того, насколько неупорядочена система. Система, которая запускается в упорядоченном, неравномерном состоянии — скажем, в горячей области рядом с холодной — всегда будет иметь тенденцию к выравниванию, при этом тепло будет течь из горячей области в холодную до тех пор, пока не будет равномерно распределено.»- businessinsider.com.

Это помогает нам, среди прочего, понять направление теплопередачи. Эта теория может быть выражена в терминах изменения энтропии системы (dS). В этом уравнении рассчитывается dS путем измерения количества тепла, поступившего в замкнутую систему (δQ), деленного на общую температуру (T) в точке, где произошла теплопередача.

10. Преобразование Фурье

Это уравнение лежит в основе современной сигнальной обработки.Это также важно для анализа сигналов и сжатия данных.

«Преобразование Фурье необходимо для понимания более сложных волновых структур, таких как человеческая речь. Учитывая сложную беспорядочную волновую функцию, такую ​​как запись разговора человека, преобразование Фурье позволяет нам разбить беспорядочную функцию на комбинацию чисел. простых волн, что значительно упрощает анализ ». — businessinsider.com.

15 самых сложных вопросов по SAT математике

Хотите проверить себя, отвечая на самые сложные вопросы по математике SAT? Хотите знать, что делает эти вопросы такими сложными и как их лучше всего решать? Если вы готовы по-настоящему погрузиться в математический раздел SAT и нацелиться на этот высший балл, то это руководство для вас.

Мы собрали то, что мы считаем , из 15 самых сложных вопросов для текущего SAT , со стратегиями и ответами на каждый из них. Все это сложные вопросы SAT Math из практических тестов SAT College Board, а это значит, что их понимание — один из лучших способов учиться для тех из вас, кто стремится к совершенству.

Изображение: Соня Севилья / Викимедиа

Краткий обзор SAT Math

Третий и четвертый разделы SAT всегда будут математическими разделами .Первый математический подраздел (с меткой «3») позволяет использовать калькулятор , не , а второй математический подраздел (с меткой «4») разрешает использование калькулятора. Однако не беспокойтесь о разделе без калькулятора: если вам не разрешено использовать калькулятор для ответа на вопрос, это означает, что вам не нужен калькулятор, чтобы ответить на него.

Каждый математический подраздел расположен в порядке возрастания сложности (где чем больше времени требуется на решение задачи и чем меньше людей ответят на нее правильно, тем сложнее).В каждом подразделе вопрос 1 будет «легким», а вопрос 15 — «сложным». Однако возрастающая сложность сбрасывается с простого на сложный на сетке.

Таким образом, вопросы с несколькими вариантами ответов расположены по возрастающей сложности (вопросы 1 и 2 будут самыми легкими, вопросы 14 и 15 будут самыми сложными), но уровень сложности сбрасывается для секции сетки (то есть вопросы 16 и 17 снова будут будьте «легкими», и вопросы 19 и 20 будут очень сложными).

Таким образом, за очень немногими исключениями, наиболее сложные математические задачи SAT будут сгруппированы в конце сегментов с несколькими вариантами ответов или во второй половине вопросов сетки. Однако, помимо места в тесте, у этих вопросов есть еще несколько общих черт. Через минуту мы рассмотрим примеры вопросов и способы их решения, а затем проанализируем их, чтобы выяснить, что общего у этих типов вопросов.

Но сначала: стоит ли вам прямо сейчас сосредоточиться на самых сложных математических вопросах?

Если вы только начинаете свою подготовку к учебе (или если вы просто пропустили этот первый, важный шаг), обязательно остановитесь и пройдите полный практический тест, чтобы определить свой текущий результат. Ознакомьтесь с нашим руководством по всем бесплатным практическим тестам SAT, доступным в Интернете, а затем сядьте, чтобы пройти все сразу.

Абсолютно лучший способ оценить свой текущий уровень — просто пройти практический тест SAT, как если бы он был настоящим, соблюдая строгий график и работая без перерывов только с разрешенными перерывами (мы знаем — вероятно, это не ваш любимый способ провести субботу) . Как только вы получите хорошее представление о своем текущем уровне и процентильном рейтинге, вы можете установить контрольные точки и цели для получения окончательного результата по SAT Math.

Если вы в настоящее время набираете баллы в диапазоне 200–400 или 400–600 по SAT Math, лучше всего сначала ознакомиться с нашим руководством по повышению своего балла по математике , чтобы он постоянно был на уровне 600 или выше, прежде чем начать. в попытке решить самые сложные математические задачи на тесте.

Если, однако, вы уже набрали больше 600 баллов по математике и хотите проверить свои способности на реальном SAT, то обязательно переходите к остальной части этого руководства. Если вы стремитесь к совершенству (или близкому к нему), вам необходимо знать, как выглядят самые сложные вопросы по математике SAT и как их решать.И, к счастью, именно этим мы и займемся.

ПРЕДУПРЕЖДЕНИЕ: Поскольку количество официальных практических тестов SAT ограничено, вы можете подождать, чтобы прочитать эту статью, пока не попробуете все или большую часть первых четырех официальных практических тестов (поскольку большинство вопросов, приведенных ниже, были приняты. из этих тестов). Если вы беспокоитесь о том, чтобы испортить эти тесты, прекратите читать это руководство сейчас; вернитесь и прочтите, когда вы их закончите.

Теперь перейдем к нашему списку вопросов (уууу)!

Изображение: Niytx / DeviantArt

15 самых сложных вопросов SAT по математике

Теперь, когда вы уверены, что вам следует попытаться ответить на эти вопросы, давайте приступим прямо к делу! Мы собрали 15 самых сложных вопросов по SAT Math, которые вы можете попробовать ниже, а также пошаговые инструкции, как получить ответ (если вы в тупике).

Нет калькулятора Вопросы по SAT по математике

Вопрос 1

$$ C = 5/9 (F-32) $$

Приведенное выше уравнение показывает, как температура $ F $, измеренная в градусах Фаренгейта, соотносится с температурой $ C $, измеренной в градусах Цельсия. Основываясь на уравнении, какое из следующих утверждений должно быть верным?

1. Повышение температуры на 1 градус по Фаренгейту эквивалентно повышению температуры на 5/9 градусов Цельсия.
2. Повышение температуры на 1 градус Цельсия эквивалентно повышению температуры на 1.8 градусов по Фаренгейту.
3. Повышение температуры на 5 долларов / 9 градусов по Фаренгейту эквивалентно повышению температуры на 1 градус Цельсия.

A) только I
B) только II
C) только III
D) только I и II

ОБЪЯСНЕНИЕ ОТВЕТА: Думайте об уравнении как об уравнении для линии

$$ y = mx + b $$

, где в данном случае

$$ C = {5} / {9} (F − 32) $$

или

$$ C = {5} / {9} F — {5} / {9} (32) $$

Вы можете видеть, что наклон графика составляет $ {5} / {9} $, что означает, что при увеличении на 1 градус по Фаренгейту увеличение составляет $ {5} / {9} $ на 1 градус Цельсия.

$$ C = {5} / {9} (F) $$

$$ C = {5} / {9} (1) = {5} / {9} $$

Следовательно, утверждение I верно. Это эквивалентно тому, что увеличение на 1 градус Цельсия равно увеличению на $ {9} / {5} $ градусов по Фаренгейту.

$$ C = {5} / {9} (F) $$

$$ 1 = {5} / {9} (F) $$

$$ (F) = {9} / {5} $$

Поскольку $ {9} / {5} $ = 1.8, утверждение II верно.

Единственный ответ, в котором и утверждение I, и утверждение II являются истинными, — это D , но если у вас есть время и вы хотите быть абсолютно внимательными, вы также можете проверить, соответствует ли утверждение III (увеличение на $ {5} / { 9} $ градус Фаренгейта равен увеличению температуры на 1 градус Цельсия) верно:

$$ C = {5} / {9} (F) $$

$$ C = {5} / {9} ({5} / {9}) $$

$$ C = {25} / {81} (\ which \ is ≠ 1) $$

Увеличение на 5 долларов / 9 градусов по Фаренгейту приводит к увеличению на {25} / {81} долларов, а не на 1 градус Цельсия, и поэтому утверждение III неверно. 2 $
D) Значение не может быть определено на основе предоставленной информации.12 $$

Окончательный ответ: A.

Вопрос 4

Точки A и B лежат на окружности радиуса 1, а длина дуги $ {AB} ↖⌢ $ равна $ π / 3 $. Какая часть окружности окружности равна длине дуги $ {AB} ↖⌢ $?

ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы выяснить ответ на этот вопрос, вам сначала нужно знать формулу для определения длины окружности круга.

Длина окружности $ C $ равна $ C = 2πr $, где $ r $ — радиус окружности.Для данной окружности радиусом 1 длина окружности равна $ C = 2 (π) (1) $ или $ C = 2π $.

Чтобы узнать, какая часть окружности составляет длину $ {AB} ↖⌢ $, разделите длину дуги на длину окружности, что даст $ π / 3 ÷ 2π $. Это деление можно представить как $ π / 3 * {1/2} π = 1/6 $.

Дробь $ 1/6 $ также может быть переписана как $ 0,166 $ или 0,167 $.

Окончательный ответ: 1/6 доллара, 0,166 доллара или 0,167 доллара.

Вопрос 5

$$ {8-i} / {3-2i} $$

Если приведенное выше выражение переписать в форме $ a + bi $, где $ a $ и $ b $ — действительные числа, каково значение $ a $? (Примечание: $ i = √ {-1} $)

ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы переписать $ {8-i} / {3-2i} $ в стандартной форме $ a + bi $, вам нужно умножить числитель и знаменатель $ {8-i} / {3- 2i} $ сопряженным, $ 3 + 2i $.2 = -1 $, последняя дробь может быть уменьшена упрощенно до

$$ {24 + 16i-3i + 2} / {9 — (- 4)} = {26 + 13i} / {13} $$

, что упрощается до 2 + i $. Следовательно, когда $ {8-i} / {3-2i} $ переписывается в стандартной форме a + bi, значение a равно 2.

Окончательный ответ: A.

Вопрос 6

В треугольнике $ ABC $ мера $ ∠B $ равна 90 °, $ BC = 16 $ и $ AC $ = 20. Треугольник $ DEF $ похож на треугольник $ ABC $, где вершины $ D $, $ E $ и $ F $ соответствуют вершинам $ A $, $ B $ и $ C $ соответственно, а также каждой стороне треугольника $. DEF $ составляет $ 1/3 $ длины соответствующей стороны треугольника $ ABC $.2} = √ {400-256} = √ {144} = 12 $$

Поскольку треугольник DEF подобен треугольнику ABC, с вершиной F, соответствующей вершине C, мера $ \ angle ∠ {F} $ равна мере $ \ angle ∠ {C} $. Следовательно, $ sin F = sin C $. От сторон треугольника ABC,

$$ sinF = {\ Against \ side} / {\ hypotenuse} = {AB} / {AC} = {12} / {20} = {3} / {5} $$

Следовательно, $ sinF = {3} / {5} $.

Окончательный ответ: {3} / {5} $ или 0,6.

Вопросы SAT по математике, разрешенные калькулятором

Вопрос 7

Неполная таблица выше суммирует количество учащихся-левшей и учащихся-правшей с разбивкой по полу для учащихся восьмых классов средней школы им. Кейзеля.Учениц-правшей в 5 раз больше, чем учениц-левшей, и учеников-правшей в 9 раз больше, чем учениц-левшей. Если в школе 18 учеников-левшей и 122 учащихся-правшей, что из следующего наиболее близко к вероятности того, что случайно выбранный ученик-правша будет женщиной? (Примечание: предположим, что ни один из восьмиклассников не является одновременно правшой и левшой.)

А) 0.410
B) 0,357
C) 0,333
D) 0,250

ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы решить эту проблему, вы должны создать два уравнения, используя две переменные ($ x $ и $ y $) и предоставленную вам информацию. Пусть $ x $ будет количеством учениц-левшей и пусть $ y $ будет количеством учениц-левшей. Используя информацию, приведенную в задаче, количество учащихся-правшей будет составлять 5 долларов США, а количество учащихся-правшей будет составлять 9 лет.Поскольку общее количество студентов-левшей составляет 18, а общее количество студентов-правшей — 122, система уравнений ниже должна быть верной:

$$ x + y = 18 $$

$$ 5x + 9y = 122 $$

Когда вы решаете эту систему уравнений, вы получаете $ x = 10 $ и $ y = 8 $. Таким образом, из 122 учащихся-правшей 5 * 10, или 50, — девушки. Следовательно, вероятность того, что случайным образом выбранный студент-правша будет женщиной, составляет {50} / {122} $, что с точностью до тысячных составляет 0,410.

Окончательный ответ — А.

Вопросы 8 и 9

Используйте следующую информацию как для вопроса 7, так и для вопроса 8.

Если покупатели входят в магазин со средней скоростью $ r $ покупателей в минуту и ​​каждый остается в магазине в течение среднего времени T $ минут, среднее количество покупателей в магазине, N $, в любой момент времени равно задается формулой $ N = rT $. Эта связь известна как закон Литтла.

По оценкам владельца магазина Good Deals Store, в рабочее время в магазин заходит в среднем 3 покупателя в минуту, и каждый из них остается в среднем на 15 минут.Владелец магазина использует закон Литтла, чтобы оценить, что в магазине одновременно находится 45 покупателей.

Вопрос 8

Закон Литтла может применяться к любой части магазина, например к определенному отделу или кассовым линиям. Владелец магазина определяет, что в рабочее время примерно 84 покупателя в час совершают покупку, и каждый из этих покупателей проводит в очереди в кассе в среднем 5 минут. Сколько в среднем покупателей в любое время в рабочее время ожидают в очереди у кассы, чтобы совершить покупку в магазине Good Deals Store?

ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку в вопросе говорится, что закон Литтла может применяться к любой отдельной части магазина (например, только к кассе), тогда среднее количество покупателей, $ N $, в очереди к кассе в любой time равно $ N = rT $, где $ r $ — это количество покупателей, заходящих в кассу в минуту, а $ T $ — это среднее количество минут, которое каждый покупатель проводит в очереди.

Поскольку 84 покупателя в час совершают покупку, 84 покупателя в час входят в кассу. Однако это необходимо преобразовать в количество покупателей в минуту (для использования с $ T = 5 $). Поскольку в часе 60 минут, тариф составляет $ {84 \ shoppers \ per \ hour} / {60 \ minutes} = 1,4 $ покупателя в минуту. Используя данную формулу с $ r = 1,4 $ и $ T = 5 $, получаем

$$ N = rt = (1.4) (5) = 7 $$

Таким образом, среднее количество покупателей, $ N $, в очереди на кассу в любое время в рабочее время равно 7.

Окончательный ответ 7.

Вопрос 9

Владелец магазина Good Deals Store открывает новый магазин в другом конце города. По оценкам владельца нового магазина, в рабочее время в него заходят в среднем 90 покупателей в час, и каждый из них остается в среднем на 12 минут. Среднее количество покупателей в новом магазине в любой момент времени на какой процент меньше среднего количества покупателей в исходном магазине в любое время? (Примечание: игнорируйте символ процента при вводе ответа.Например, если ответ 42,1%, введите 42,1)

ОБЪЯСНЕНИЕ ОТВЕТА: Согласно исходной информации, предполагаемое среднее количество покупателей в исходном магазине в любой момент времени (N) составляет 45. В вопросе говорится, что в новом магазине менеджер оценивает, что в среднем 90 покупателей в час (60 минут) заходят в магазин, что эквивалентно 1,5 покупателям в минуту (r). Менеджер также подсчитал, что каждый покупатель остается в магазине в среднем 12 минут (T).Таким образом, по закону Литтла в каждый момент времени в новом магазине в среднем находится $ N = rT = (1.5) (12) = 18 $ покупателей. Это

$$ {45-18} / {45} * 100 = 60 $$

На

процента меньше, чем среднее количество покупателей в исходном магазине в любое время.

Окончательный ответ — 60.

Вопрос 10

На плоскости $ xy $ точка $ (p, r) $ лежит на прямой с уравнением $ y = x + b $, где $ b $ — константа. Точка с координатами $ (2p, 5r) $ лежит на прямой с уравнением $ y = 2x + b $.Если $ p ≠ 0 $, каково значение $ r / p $?

A) 2/5 долларов США

B) 3/4 $

C) 4/3 долл. США

D) $ 5/2 $

ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку точка $ (p, r) $ лежит на прямой с уравнением $ y = x + b $, точка должна удовлетворять уравнению. Подстановка $ p $ вместо $ x $ и $ r $ вместо $ y $ в уравнение $ y = x + b $ дает $ r = p + b $, или $ \ bi b $ = $ \ bi r- \ bi p $.

Аналогично, поскольку точка $ (2p, 5r) $ лежит на прямой с уравнением $ y = 2x + b $, точка должна удовлетворять уравнению.Замена $ 2p $ на $ x $ и $ 5r $ на $ y $ в уравнении $ y = 2x + b $ дает:

$ 5r = 2 (2p) + b $

$ 5r = 4p + b $

$ \ bi b $ = $ \ bo 5 \ bi r- \ bo 4 \ bi p $.

Затем мы можем установить два уравнения, равных $ b $, равным друг другу и упростить:

$ б = р-п = 5р-4п $

$ 3p = 4r $

Наконец, чтобы найти $ r / p $, нам нужно разделить обе части уравнения на $ p $ и на $ 4 $:

$ 3p = 4r $

3 доллара США = {4r} /

доллара США на человека

$ 3/4 = р / п $

Правильный ответ: B , 3/4 доллара.

Если вы выбрали варианты A и D, возможно, вы неправильно сформировали свой ответ из коэффициентов в пункте $ (2p, 5r) $. Если вы выбрали вариант C, возможно, вы перепутали $ r $ и $ p $.

Обратите внимание, что пока он находится в разделе калькулятора теста SAT, вам совершенно не нужен калькулятор для его решения!

Вопрос 11

Зерновой бункер состоит из двух правых круглых конусов и правого круглого цилиндра с внутренними размерами, представленными на рисунке выше. 2h $$

можно использовать для определения общего объема силоса.2) (5) = ({4} / {3}) (250) π $$

, что примерно равно 1047,2 кубических футов.

Окончательный ответ — D.

Вопрос 12

Если $ x $ — среднее (среднее арифметическое) для $ m $ и $ 9 $, $ y $ — это среднее значение для $ 2m $ и $ 15 $, а $ z $ — это среднее значение для $ 3m $ и $ 18 $, то что есть среднее значение $ x $, $ y $ и $ z $ в пересчете на $ m $?

A) млн. Долл. + 6
B) млн. Долл. + 7
C) 2 млн. Долл. + 14
D) 3 млн. Долл. + 21

ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку среднее (среднее арифметическое) двух чисел равно сумме двух чисел, разделенных на 2, уравнения $ x = {m + 9} / {2} $, $ y = {2m +15} / {2} $, $ z = {3m + 18} / {2} $ верны.2-x- {11} / {4} $$

и

$$ y = k $$

Реальное решение системы двух уравнений соответствует точке пересечения графиков этих двух уравнений на плоскости $ xy $.

График $ y = k $ — это горизонтальная линия, которая содержит точку $ (0, k) $ и трижды пересекает график кубического уравнения (поскольку оно имеет три действительных решения). Учитывая график, единственная горизонтальная линия, которая трижды пересекала бы кубическое уравнение, — это линия с уравнением $ y = −3 $ или $ f (x) = −3 $.2 $$

Динамическое давление $ q $, создаваемое жидкостью, движущейся со скоростью $ v $, можно найти с помощью приведенной выше формулы, где $ n $ — постоянная плотность жидкости. Инженер-авиастроитель использует формулу для определения динамического давления жидкости, движущейся со скоростью $ v $, и той же жидкости, движущейся со скоростью 1,5 $ v $. Каково отношение динамического давления более быстрой жидкости к динамическому давлению более медленной жидкости?

ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы решить эту проблему, вам необходимо задать уравнения с переменными.2 = (2.25) q_1 $$

Следовательно, коэффициент динамического давления более быстрой жидкости равен

$$ {q2} / {q1} = {2.25 q_1} / {q_1} = 2.25 $$

Окончательный ответ — 2,25 или 9/4.

Вопрос 15

Для полинома $ p (x) $ значение $ p (3) $ равно $ -2 $. Что из следующего должно быть истинным относительно $ p (x) $?

A) $ x-5 $ — множитель $ p (x) $.
B) $ x-2 $ — множитель $ p (x) $.
C) $ x + 2 $ является множителем $ p (x) $.
D) Остаток от деления $ p (x) $ на $ x-3 $ равен -2 $.1 $ и не выше), остаток — действительное число.

Следовательно, $ p (x) $ можно переписать как $ p (x) = (x + k) q (x) + r $, где $ r $ — действительное число.

В вопросе указано, что $ p (3) = -2 $, поэтому должно быть верно, что

$$ — 2 = p (3) = (3 + k) q (3) + r $$

Теперь мы можем ввести все возможные ответы. Если ответ A, B или C, $ r $ будет $ 0 $, а если ответ D, $ r $ будет $ -2 $.

A. $ -2 = p (3) = (3 + (-5)) q (3) + 0 $ 90 305 $ -2 = (3-5) q (3) 90 305 $ -2 = (- 2 ) q (3) $

Это могло быть правдой, но только если $ q (3) = 1 $

Б.$ -2 = p (3) = (3 + (-2)) q (3) + 0 $
$ -2 = (3-2) q (3) $
$ -2 = (-1) q ( 3) $

Это могло быть правдой, но только если $ q (3) = 2 $

C. $ -2 = p (3) = (3 + 2) q (3) + 0 $ 90 305 $ -2 = (5) q (3)

$

Это может быть правдой, но только если $ q (3) = {- 2} / {5} $

D. $ -2 = p (3) = (3 + (-3)) q (3) + (-2) $ 90 305 $ -2 = (3 — 3) q (3) + (-2) $
-2 = (0) q (3) + (-2) 9000 3 долл. США

Это всегда будет истинным независимо от того, что такое $ q (3) $.

Из вариантов ответа единственное, что должно быть истинным относительно $ p (x) $, — это D, а остаток от деления $ p (x) $ на $ x-3 $ равен -2.

Окончательный ответ — D.

Хотите улучшить свой результат SAT на 160 баллов? Мы написали руководство о 5 лучших стратегиях, которые вы должны использовать, чтобы улучшить свой результат. Скачать бесплатно сейчас:

Вы заслуживаете того, чтобы вздремнуть, задав эти вопросы.

Что общего у самых сложных вопросов по SAT Math?

Важно понимать, что делает эти сложные вопросы «сложными». Таким образом, вы сможете понять и решить похожие вопросы, когда увидите их в день тестирования, а также получите лучшую стратегию выявления и исправления ваших предыдущих математических ошибок SAT.

В этом разделе мы рассмотрим, что общего у этих вопросов, и приведем примеры каждого типа.Некоторые из причин, по которым самые сложные вопросы по математике являются самыми сложными вопросами по математике, заключаются в том, что они:

# 1: Проверьте несколько математических понятий одновременно

Здесь мы должны иметь дело с мнимыми числами и дробями одновременно.

Секрет успеха: Подумайте, какую применимую математику вы могли бы использовать для решения задачи, выполняйте пошагово и пробуйте каждую технику, пока не найдете тот, который работает!

# 2: задействовать множество шагов

Помните: чем больше шагов вам нужно предпринять, тем легче где-то напортачить!

Мы должны решить эту проблему поэтапно (используя несколько средних значений), чтобы разблокировать остальные ответы в эффекте домино.Это может сбивать с толку, особенно если вы в стрессе или у вас не хватает времени.

Секрет успеха: Не торопитесь, делайте шаг за шагом и перепроверяйте свою работу, чтобы не ошибиться!

# 3: Тестируйте концепции, с которыми вы мало знакомы

Например, многие учащиеся менее знакомы с функциями, чем с дробями и процентами, поэтому большинство функциональных вопросов считаются задачами «высокой сложности».

Если вы не разбираетесь в функциях, это может быть сложной проблемой.

Секрет успеха: Просмотрите математические концепции, с которыми вы не так хорошо знакомы, например, функции. Мы предлагаем использовать наши отличные бесплатные руководства по тестированию SAT Math.

# 4: написаны необычно или запутанно

Может быть сложно точно определить, какие вопросы задает , не говоря уже о том, как их решить. Это особенно актуально, когда вопрос находится в конце раздела, а у вас не хватает времени.

Поскольку в этом вопросе содержится так много информации без диаграммы, может быть сложно разобраться в этом за ограниченное время.

Секрет успеха: Не торопитесь, проанализируйте, что от вас просят, и нарисуйте диаграмму, если это вам поможет.

# 5: Используйте много разных переменных

При таком большом количестве различных переменных очень легко запутаться.

Секрет успеха: Не торопитесь, проанализируйте, что от вас просят, и подумайте, является ли включение цифр хорошей стратегией для решения проблемы (это не относится к вопросу выше, но может быть ко многим другим. SAT переменные вопросы).

На вынос

SAT — это марафон, и чем лучше вы к нему подготовитесь, тем лучше вы будете себя чувствовать в день теста. Знание того, как отвечать на самые сложные вопросы, которые может бросить вам тест, сделает сдачу настоящего SAT намного менее сложной задачей.

Если вы считаете, что эти вопросы были легкими, не стоит недооценивать влияние адреналина и усталости на вашу способность решать проблемы. Продолжая учиться, всегда придерживайтесь надлежащих рекомендаций по времени и старайтесь проходить полные тесты, когда это возможно. Это лучший способ воссоздать реальную среду тестирования, чтобы вы могли подготовиться к реальной сделке.

Если вы считаете, что эти вопросы были сложными, обязательно укрепит свои математические знания, ознакомившись с нашими индивидуальными руководствами по математическим темам для SAT. Здесь вы увидите более подробные объяснения рассматриваемых тем, а также более подробную разбивку ответов.

Что дальше?

Почувствовали, что эти вопросы оказались сложнее, чем вы ожидали? Взгляните на все темы, затронутые в разделе SAT по математике, а затем отметьте, какие разделы были для вас особенно трудными.Затем взгляните на наши индивидуальные руководства по математике, которые помогут вам укрепить любую из этих слабых сторон.

Не хватает времени на сдачу экзамена по математике? Наш гид поможет вам выиграть время и увеличить свой счет.

Хотите набрать наивысший балл? Ознакомьтесь с нашим руководством о том, как получить отличные 800 баллов по математике в разделе SAT, написанном отличником.

Хотите улучшить свой результат SAT на 160 баллов?

Посетите наши лучшие в своем классе онлайн-классы подготовки к SAT.Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.

Наши классы полностью онлайн, и их ведут эксперты SAT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую индивидуальную программу, которой вы будете следовать, чтобы вы никогда не запутались, что изучать дальше.

Попробуйте без риска сегодня:

Самые сложные математические задачи. Шесть сложных способов стать… | Франческо Ди Лалло

Можно ли быстро решить любую проблему, решение которой можно быстро проверить?

Проблемы можно разделить на разные классы сложности. Здесь нас интересуют классы P и NP. Они обозначают олиномиальное время P и детерминированное P олиномиальное время N , соответственно.

По сути, проблема P может быть решена «быстро» и проверена «быстро». В то время как проблема NP (в настоящее время) не имеет «быстрого» решения. В частности, для задачи с размером входных данных n, время, необходимое для ее решения, если она относится к классу P, растет в соответствии с некоторым полиномом. А если это NP, то он будет расти быстрее.

Пример проблемы, которая считается NP (я говорю, что думала , поскольку она зависит от истинности гипотезы) — это задача коммивояжера (версия проблемы решения):

Учитывая список городов и расстояние между ними, можете ли вы построить маршрут, проходящий через каждый город, общая длина которого меньше заданного расстояния?

Решение этой проблемы сложно и требует больших затрат, но решение легко проверить — решение представляет собой список городов для посещения по порядку, и можно проверить, что это действительное решение, просто сложив расстояния и сравнивая его с заданной границей.Важно отметить, что при увеличении длины списка городов время на решение будет намного быстрее, чем при использовании любого полинома.

С другой стороны, пример проблемы P — это проверка того, находится ли номер в данном списке. Его легко решить и легко проверить, и если вы увеличите размер списка вдвое, затраченное время также удвоится (так что затраченное время не будет расти слишком быстро).

Проблема P vs NP заключается в том, действительно ли проблемы NP отличаются от проблем P. Иначе говоря, существует ли какой-то секретный или скрытый алгоритм, который может быстро решить ранее рассмотренные сложные проблемы?

В трех измерениях пространства и времени, при заданной начальной скорости, существуют ли векторная скорость и скалярное поле давления, которые являются как гладкими, так и глобально определенными, которые решают уравнения Навье – Стокса?

Уравнения Навье-Стокса представляют собой два нелинейных уравнения в частных производных , которые описывают движение жидкости в трехмерном пространстве.Это система из двух уравнений, которые связывают векторное поле скорости и скорость его изменения с полем давления, внешними силами, приложенными к жидкости. Уравнения записываются следующим образом:

Мы не будем углубляться в то, что означает каждый термин, но, по сути, первое уравнение представляет собой (вязкую) версию жидкости Ньютона F = ma — силы, участвующие в сумме давления, вязкие стресс и внешние силы. Второе уравнение — это очень просто сохранение массы и требует, чтобы жидкость была несжимаемой.

Для того, чтобы решение было «действительным», у нас есть два условия:

1. Векторное поле v и скалярное поле p глобально определены и непрерывны во всем пространстве.
2. Полная кинетическая энергия ограничена. (Интеграл от квадрата нормы v по всему пространству ограничен.)

Итак, проблема Навье-Стокса сводится к доказательству одного из двух случаев:

Утвердительный : дан f = 0 и начальное поле скорости (которое должно удовлетворять определенным условиям) существует поле скорости и давления, которое удовлетворяет (1) и (2).

Пробой: Существует начальное векторное поле и внешнее силовое поле, где нет решения, удовлетворяющего (1) и (2). Уравнения

N-S управляют диффузией молока в чае — Фото Alex Boyd на Unsplash

Имеют ли все нетривиальные нули дзета-функции Римана действительную часть, равную 1/2?

Опять же, давайте разберемся с этим. Во-первых, дзета-функция Римана определяется следующим уравнением

, которое справедливо для с> 1. Обратите внимание, что для s = 1, функция сводится к гармоническому ряду, который увеличивается. Мы можем проделать некоторые причудливые математические вычисления, чтобы аналитически продолжить (существенно расширить) функцию до комплексной плоскости (кроме с = 0 и 1 ) со следующей функциональной зависимостью:

Теперь мы хотим найти, для каких с , ζ (s) = 0. Теперь, поскольку косинус равен 0 для нечетных отрицательных целых чисел, ζ (-2n) для положительного целого n равно 0. Они называются тривиальными нулями, поскольку они равны нулю из-за природы косинуса.Вместо этого нас интересует, когда ζ само по себе равно нулю.

Известно, что все нетривиальные нули имеют действительную часть от 0 до 1, известную как критическая полоса. Как оказалось, кажется, что если с является нетривиальным нулем (т.е. если ζ (s) = 0 и с не является отрицательным четным числом), то с = 1/2 + iy для некоторого значения y . т.е. действительная часть с равна 1/2 , это называется критической линией.

Для эллиптической кривой E над всегда ли совпадает алгебраический ранг с аналитическим рангом?

Эллиптическая кривая E — это набор решений уравнения вида y² = x³ + Ax + B с ограничением, что дискриминант ∆ = -16 (4A³ + 27B²) ≠ 0. Ограничение просто гарантирует, что кривая будет достаточно хорошей.

Две эллиптические кривые. Слева: y² = x³-1.5x + 1, справа: y² = x³-4x + 1

Теперь мы ограничиваем решения эллиптической кривой, требуя, чтобы x и y были рациональными.Вот что мы подразумеваем под кривой над over. Теперь мы можем использовать эту кривую E, чтобы сформировать группу, обозначенную E (ℚ). Мы проделали довольно аккуратную бинарную операцию: по двум точкам мы проводим через них линию, находим третье пересечение с E и отражаем его через ось x.

Как сложить две точки A и B, чтобы найти C

Чтобы полностью превратить ее в группу, нам нужно добавить бесконечно удаленную точку, которая действует как идентичность группы (для читателя, знакомого с проективной геометрией, E — неособая проективная кривая, поэтому мы получаем тождество бесплатно из амбиантного пространства).

Первый естественный вопрос, который задают, — что мы можем сделать вывод о структуре E (ℚ)?

Результат Морделла и Вейля говорит нам, что E (ℚ) конечно порождено и может быть записано как

, где E (ℚ) _tors — это все точки в E (ℚ), которые имеют конечный порядок. r известен как алгебраический ранг кривой E.

Отлично, теперь у нас есть первая половина. Теперь нам нужно понять аналитический ранг.

Давайте теперь еще больше ограничим решения, рассмотрев E в конечном поле размером p , где p — простое число

Мы определяем следующие значения

и, наконец, L-серию E при с как таковой

напомним, что ∆ — дискриминант эллиптической кривой.Затем мы можем разложить L в ряд Тейлора около с = 1:

Здесь r_an — аналитический ранг кривой. Те, кто знаком с комплексным анализом, узнают, что r_an — это порядок исчезновения нуля.

Наконец-то! Мы можем записать гипотезу Берча и Суиннертона-Дайера очень просто как

Хорошо, что все это означает? Как оказалось, вычислить алгебраический ранг довольно сложно, тогда как аналитический ранг несколько проще. Эта гипотеза обеспечивает мост между страной анализа и страной алгебры.

Для любой компактной простой калибровочной группы G существует ли нетривиальная квантовая теория Янга – Миллса на, которая имеет щель масс Δ> 0?

Небольшой отказ от ответственности: я вряд ли специалист в области физики элементарных частиц, поэтому я изложу здесь свое лучшее поверхностное понимание.

Задача состоит в том, чтобы сделать современную физику математически строгой.

Мы начинаем с идеи калибровочных симметрий: это, по сути, свободы в том, как мы описываем физическую систему.Например, не имеет значения, как и где мы ориентируем нашу систему координат.

Изящная теорема Эмми Нётер гласит, что для каждой симметрии существует соответствующий закон сохранения. Например:

• Временная инвариантность (т.е. не имеет значения, начинаете ли вы свой эксперимент сейчас или через 5 минут после того, как выпили чашку чая) непосредственно ведет к сохранению энергии
• Трансляционная инвариантность дает начало сохранение импульса

Далее переходим к теории Янга-Миллса.

Лучшее объяснение, которое я смог найти, дает Лоуренс Краусс. Представьте себе шахматную доску, если вы поменяете каждый белый квадрат на черный квадрат и каждый черный квадрат на белый, тогда игра будет практически идентичной. Немногое произошло, но произошли изменения, так что это довольно простая симметрия.

А теперь представьте, что я локально переключаю цвет определенного квадрата и делаю это столько, сколько хочу, по всей доске. Доска будет выглядеть очень странно, но я могу написать книгу правил, в которой будут учтены все сделанные мною свопы.Эта книга правил затем диктует, как играть в игру.

Теперь свод правил — это фактически поле, а игра — теория Янга-Миллса, и локальная перестановка цветов является калибровочной симметрией.

Фото Хассана Паши на Unsplash

Итак, давайте пройдемся по нему:

Калибровочная группа — это группа (возможно, очень причудливых) симметрий системы, это дает начало закону сохранения, и мы можем написать «свод правил» это поле, которое определяет, как взаимодействуют частицы, что является теорией Янга-Миллса.

Это уже было сделано в случае электромагнитного взаимодействия и сильного ядерного взаимодействия, которые полностью описаны с помощью квантовой электродинамики и квантовой хромодинамики.

Существование Янга-Миллса (мы перейдем к разнице масс через секунду) спрашивает, существует ли это описание для всех четырех фундаментальных сил? И что еще интереснее, можно ли их объединить?

Фотография israel palacio на Unsplash

Касательно разрыва масс: возбуждение в одном из этих полей на самом деле является частицей. Массовый разрыв — это, по сути, условие, что масса этих частиц должна быть ограничена снизу, чтобы вы не могли найти частицу, которая была бы сколь угодно легкой. Это то, что мы наблюдаем в природе.Это называется зазором массы, поскольку существует зазор между 0 и самой легкой частицей.

Итак, чтобы теория Янга-Миллса «хорошо» описывала реальность, должна также присутствовать эта разница в массах.

Пусть X — неособое комплексное проективное многообразие. Тогда может ли каждый класс Ходжа на X быть записан как линейная комбинация с рациональными коэффициентами классов когомологий комплексных подмногообразий X?

Этот дурацкий. Я собираюсь вдаваться в гораздо меньшие подробности здесь, потому что, черт возьми, это трудно понять.

Существует естественный обмен между алгебраическими уравнениями и геометрическими фигурами. Решение x² + y²-1 = 0 образует круг, а x + y-1 = 0 образует линию.

Итак, мы можем придумать несколько сумасшедших уравнений, и решение будет иметь форму (иногда очень сложную), это называется алгебраических циклов. Если эти алгебраические циклы достаточно гладкие, то их можно назвать многообразиями (напомним, это из гипотезы Пуанкаре).

Итак, алгебраические циклы (читай решения уравнений) могут образовывать многообразия, если мы добавим больше уравнений, мы получим алгебраические циклы на многообразии.

Добавляя z = 0 к уравнению x² + y² + z² = 1, мы получаем круг.

Теперь с топологической точки зрения мы можем рисовать сумасшедшие формы на многообразии, а затем группировать эти формы вместе, если они могут быть деформированы друг в друга. Они сгруппированы в классы гомологии.

Два разных класса гомологии на торе

Теперь это выглядит точно так же, как обмен, который мы рассмотрели выше: мы переходим от алгебраического описания формы к геометрическому описанию. Проблема в том, для данного многообразия, когда класс гомологии содержит одну фигуру, которую можно описать как алгебраический цикл на этом многообразии?

К сожалению, мы имели дело с многообразиями, живущими в регулярном евклидовом пространстве.Гипотеза Ходжа имеет дело с многообразиями, живущими в проективном комплексном n-мерном пространстве (имеющем вещественную размерность 2n). Так что здесь все поражает. Многообразие неособое, если нет «заостренных битов».

Ходжу пришла в голову изящная и элегантная идея сказать, эквивалентен ли класс гомологии алгебраическому циклу, и это, по сути, гипотеза Ходжа. Я предоставляю заинтересованным читателям возможность получить степень магистра по алгебраической геометрии, если они хотят понять больше.

6 математических задач, которые еще не решены | Андрей Тапалага ✒️

Приз за решение — 1 миллион долларов США.

Фото Франка В. на Unsplash

Эти проблемы были названы проблемами тысячелетия, поскольку они до сих пор не решены в течение 2000 года. Они кажутся невозможными даже для самых ярких умов, которые может предложить мир. Даже по сей день многие ученые проводят свою жизнь, пытаясь разгадать ответы на эти вопросы.Эти вопросы были предоставлены Кембриджским математическим институтом Клэя, и тот, кому удастся их решить, получит приз в размере 1 миллиона долларов США. Эти вопросы являются вершиной математики и исходят из самых темных уголков древней математики, которые кажутся почти невозможными. Вы можете спросить, почему рядом с умом математика предусмотрено, что у невозможного есть число, следовательно, нет ничего невозможного.

Это самая сложная и нерешенная компьютерная проблема в мире, проще говоря, P обозначает проблемы, которые легко решить для компьютера, а NP обозначает проблемы, которые трудно решить для компьютера, но которые легко решить. проверить компьютер.Причина, по которой этот вопрос настолько сложен, заключается в том, что это скорее игра в угадайку, она заставляет вас перебирать все возможные комбинации, и есть более 100 миллионов различных комбинаций, которые можно попробовать, чтобы найти правильный ответ. Это займет слишком много времени, поскольку возможности сложны даже для человека с докторской степенью по математике, поэтому ученые пытаются придумать другой способ решения этого уравнения.

Это вопрос, который все еще остается нерешенным с 1859 года. Проблема заключается в том, что использование дзета-функции с нулевой степенью дает неочевидный ответ.Таким образом, вы, по сути, складываете последовательные растущие числа, из которых, по логике, вы должны получить бесконечное число, но это не так. Итак, мы ищем ответ, чтобы объяснить, почему сложение бесконечного количества чисел не дает нам бесконечного результата.

Это вопрос, в котором используются законы квантовой физики. Использование теории Янга-Миллса для описания сильных взаимодействий элементарных частиц зависит от тонкого квантово-механического свойства, называемого «разрыв масс»: квантовые частицы имеют положительные массы, хотя классические волны движутся со скоростью света.Комбинация двух может быть объяснена с помощью новой революционной идеи, которая описывает новые стороны математики, а также физики.

То, что Навье пытался объяснить всю свою жизнь, было предсказанием турбулентности воздуха, возникающей в воздухе во время полета. Многие считают, что эти турбулентности вызваны колебаниями воздуха, вызванными предыдущими струями, которые пересекали ту же космическую область. Он также попытался дать лучший прогноз волн, обрушивающихся на лодку в озере.Он придумал очень сложное уравнение, которое до сих пор заставляет блестящие умы ломать голову.

Этот гениальный человек искал способ исследовать и измерять формы сложных объектов. Его идея была проста, он хотел увидеть, в какой степени мы можем приблизить форму данного объекта, комбинируя простые геометрические строительные блоки. Проблема в том, что в некоторых случаях форма некоторых объектов все еще не может быть аппроксимирована даже всеми возможными попытками, оставляя пробелы в теории, которые все еще необходимо решить.

Этот вопрос может быть одним из «самых простых» из 6-го, однако до сих пор нет подсказки о том, как его решить, чтобы дать вам представление, это то уравнение, на которое мы смотрим:

x2 + y2 = z2

Это небольшое уравнение было исчерпано, чтобы его проработать на 134 страницах, но все еще не близко к ответу. Эти два мудрых человека пытались описать все решения в виде целых чисел, а также x, y, z алгебраических уравнений.

В целом, я попытался дать простое объяснение упомянутых выше вопросов, эти вопросы требуют целых дней, чтобы объяснять и понимать ретроспективно.Ученым, которые занимаются математикой 30 или 40 лет, все еще трудно ответить на эти вопросы. Мы все еще ждем

10 математических уравнений и формул, которые изменили мир

Математика всегда вокруг нас , куда бы мы ни пошли.

И это потому, что математика настолько широка, она охватывает сложение и вычитание, деление, дроби, графики, округление, решение уравнений, алгебру, неравенства, переменные, статистику, подстановку, триггер, вычисление, распределительное свойство, симметрию, целые числа, простые числа, вероятность, значение, векторы, формы, последовательность, пропорции и многое другое!

Будь то строительство вашего дома, планировка улиц в вашем районе, простой процесс запуска машины или включения посудомоечной машины, когда вы занимаетесь своими руками или играете на пианино, сложная и базовая математика действительно повсюду.

Не существует объекта, который не являлся бы каким-то образом результатом математики в действии , который вы будете изучать во время школьной математики и за ее пределами на уроках математики дальнейшего образования.

Сложные уравнения со многими неизвестными, радикальные математические теоремы, восходящие к древности и открытиям конца двадцатого века, сформировали наш мир.

И с каждой новой концепцией наше понимание физического мира вокруг нас растет.

В 2013 году известный британский математик и ученый Ян Стюарт опубликовал книгу под названием «17 уравнений, изменивших мир» (ред.Роберт Лаффонт).

Сколько лет математическим формулам?

Поскольку математика — это широкое применение материи , а не открытие, мы не можем доверять одному человеку изобретение самой математики (если только вы не хотите быть очень глубокими и сказать, что создатель нашей вселенной несет ответственность за рождение математики!). Тем не менее, мы можем оглянуться назад на , когда математика начала играть роль в жизни людей.

Неудивительно, что свидетельства показывают, что даже у тех, кто жил в доисторические времена, было некоторое понимание математических концепций , записи о которых были обнаружены на многих предметах, таких как кости и резные фигурки на стенах.

Отметки показали бы, что они использовали рациональное мышление при обучении тому, как решать простые математические задачи , например, складывать вещи на поверхности. Так что же в первую очередь могло побудить их заинтересоваться математикой? Например, их заинтриговало бы время. Может быть, подсчитать, сколько времени им осталось на охоту за пропитанием до заката, на что они бы посмотрели на астрономию, чтобы ответить.

Звездный сад утверждает, что:

«Кости Ишанго около 20 000 лет, и на ней есть ряд зазубрин в трех колоннах.Образцы в этих числах могут показывать, что они были созданы кем-то, кто разбирался в сложении, вычитании, умножении, делении и простых числах ».

Далее они говорят, что:

« Люди понимали геометрию и алгебру примерно к 2000 г. до н.э. […] Примерно в это время и вавилоняне, и древние египтяне знали число π (пи) — отношение длины окружности к ее диаметру. Примерно к 1500 г. до н.э. вавилоняне также знали о теореме Пифагора, которая показывает, как связаны длины сторон прямоугольных треугольников.»

Теорема названа в честь древнегреческого математика Пифагора (хотя некоторые говорят, что эта концепция предшествовала ему), что показывает, что, хотя все математические теоремы и формулы просто существуют и ждут своего открытия, мы можем по крайней мере похвалить некоторых людей за то, что они их нашли.

В их краткой истории математики веб-сайт Звездного сада добавляет, что: «Кеплер также был вдохновлен Пифагором и считал, что движение планет производит музыку. Он использовал математику, чтобы показать, что планеты вращаются вокруг Солнца по эллипсам, и к 1619 году он смог определить время, необходимое каждой планете для обращения по орбите, и их относительные расстояния от Солнца.

В 1687 году Ньютон опубликовал свой закон всемирного тяготения. Это было новаторским, потому что оно показало, что не только абстрактные математические принципы, такие как недавно изобретенное исчисление, могут быть применены к тому, что мы наблюдаем в природе, но и что законы, отвечающие за движение планет, также несут ответственность за движение объектов. на земле. Ньютон также считал, что Вселенную можно понимать как математический объект, и описывал Бога как «опытного в механике и геометрии».

Современник Ньютона, Лейбниц, обнаружил еще одну связь между математикой и природой, когда впервые рассмотрел идею фракталов. […] Математики двадцатого века, такие как французский математик Гастон Жюлиа и польско-французско-американский математик Бенуа Мандельброт, были вдохновлены Лейбницем на создание собственных сложных фракталов.

К этому времени квантовая механика и теории специальной и общей теории относительности немецко-швейцарско-американского физика Альберта Эйнштейна показали, что природа подчиняется законам математики, даже когда это противоречит нашему здравому смыслу пониманию мира.»

Итак, как мы видим, математика всегда присутствовала на протяжении всей истории человечества, однако ряд из значительных достижений произошел благодаря опытным математикам, которые пришли, чтобы их найти. Мы рассмотрим некоторые из них. самые известные математические уравнения ниже.

В заключение по истории математики важно отметить, что, несмотря на то, что люди не развивали математические концепции, математика всегда играла важную роль на планете. существование людей, математика продиктовала бы всю природу, а также источники энергии и животных, которые украшали Землю, благодаря ее потребности в воспроизводстве и жизни в целом.

10 знаменитых математических уравнений

Если вам интересно, почему математика так важна и какое влияние оказало каждое из основных уравнений, читайте дальше, чтобы открыть для себя 10 революционных формул , которые поднимут ваш курс обучения математике на новый уровень. Конечно, нет конца количеству существующих математических формул и выражений (некоторые могут сказать, что список бесконечен!), Но здесь мы сосредоточимся на некоторых из наиболее известных алгебраических уравнений и предложим некоторые полезные обозначения.

Не забывайте, Superprof может помочь вам найти идеального репетитора по математике, если вы захотите получить помощь по математике с помощью учителя математики или онлайн-справки по математике!

Теорема Пифагора

Это, несомненно, одна из самых известных теорем.Его название легко приходит на ум даже спустя годы после вашего последнего урока математики.

Доказательство из «Элементов Евклида» (Источник: Wikipedia.org)

Вы можете знать это наизусть, но давайте быстро напомним: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратных корней из длин. двух других сторон.

Эта теорема, восходящая к 530 году до нашей эры, является одной из основ математики по сей день и с момента своего открытия внесла свой вклад в историю математики.

Это уравнение необходимо для понимания геометрии и тригонометрии, и оно действительно сформировало наше понимание этих разделов математики.

Говорят, что мы перешли от евклидовой геометрии к неевклидовой геометрии.

Когда теорема Пифагора встречается с искусством (Источник: commons.wikimedia.org)

С тех пор, благодаря Пифагору и его знаменитому уравнению, теперь легко вычислить длины, углы и продемонстрировать, что данный треугольник прямоугольный .

Эту концепцию часто можно встретить в сфере строительства и архитектуры.

Логарифмы

Логарифмы, популяризированные Джоном Напье в 1610 году, объединяют обратные и экспоненциальные функции, а также противоположности.

Логарифмы распространены в формулах, используемых в науке, для измерения сложности алгоритмов и фракталов, и появляются в формулах для подсчета простых чисел.

Логарифм продукта — это сумма логарифмов факторов (Источник: Википедия.org)

До появления современного компьютера логарифмическое вычисление было самым обычным способом умножения больших чисел и позволяло производить более быстрые вычисления, но, прежде всего, помогало совершать скачки в областях математики, физики, инженерии и Астрономия .

Существует 3 типа логарифмов:

• Натуральные логарифмы — фундаментальная основа математического анализа
• Десятичные логарифмы используются в математических вычислениях
• Двоичные логарифмы используются в теории вычислений и в прикладных вычислениях

Логарифм числа — это показатель степени, до которого необходимо возвести другое фиксированное число, основание, для получения этого числа.

Например, в случае с основанием 10 логарифм (log) равен: Log (1) = 0, log (10) = 1, log (100) = 2.

Такие вычисления полезны в следующих случаях: Например, покер, а в решении головоломок .

Закон всемирного тяготения

Кто никогда не слышал о знаменитом законе всемирного тяготения Исаака Ньютона ? Вы знаете историю о яблоке, которое упало на голову великого мыслителя, когда он размышлял о луне в ночном небе, в 1687 году.

Закон всемирного тяготения в его современной форме (Источник: Википедия.org)

Ньютон затем задался вопросом: почему луна не падает с неба, проводя связь между этими двумя телами (луной и яблоком)?

Ответ очевиден — сейчас: он «удерживается» гравитационной силой .

Дерево Ньютона, Тринити-колледж, Кембридж (Источник: проект Geography, Великобритания и Ирландия — Н. Чедвик)

Так родился знаменитый закон всемирного тяготения Ньютона : «Астральные тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональны квадрату расстояния между их центрами.»

Через 200 лет после Ньютона Эйнштейн заменил эту теорию гравитации своей теорией относительности.

Теория относительности

Сведен ли человек в математике или физике или ничего не знает о математическом словаре, все знают Альберт Знаменитая формула Эйнштейна: E = mc² .

E представляет энергию, m — массу тела, c — скорость света (Источник: publicdomainpictures.net — Даниэле Пеллати)

Эта формула, которая иллюстрирует теорию относительности (ограничено относительность и общая теория относительности) до этого момента революционизировали наше понимание физики.

Это остается важным и по сей день, поскольку показывает, что материя может быть преобразована в энергию и наоборот.

Ограниченная теория относительности ввела идею о том, что скорость света — это универсальная постоянная, которая не меняется, и что течение времени не одинаково для тел, движущихся с разными скоростями.

Общая теория относительности Эйнштейна описывает гравитацию, в которой пространство и время искривлены и свернуты: главное изменение в нашем понимании закона всемирного тяготения Ньютона.

Даже сегодня Теория относительности Эйнштейна остается важной в нашем понимании происхождения, структуры и предназначения нашей Вселенной.

Математика помогает нам лучше понимать мир вокруг нас и является вездесущей силой в нашей повседневной жизни.

Теория хаоса

Теория хаоса показала нам, что невозможно с уверенностью предсказать, что произойдет в будущем. Это исследование поведения динамических систем .Отличная тема для изучения математики.

Эта теория доказывает, что никакие реально существующие процессы нельзя предсказать с уверенностью. Теория Роберта Мэя более свежая, датируется 1975 годом. Она описывает процесс, который постоянно развивается с течением времени.

В своей формуле Мэй хотел объяснить, что хаотическое поведение (например, климат, который время от времени подвергается многочисленным изменениям погоды) может через несколько дней привести к изменениям в других совершенно иных системах.

Самая известная иллюстрация — это так называемый «эффект бабочки», который показывает, что взмах крыльев бабочки в Бразилии может привести к урагану или торнадо в Азии.

Другими словами, самые незначительные вещи могут иметь неожиданные последствия для нашей окружающей среды, ближнего и дальнего.

Турбулентность в концевом вихре от крыла самолета (Источник: Национальное управление по аэронавтике и исследованию космического пространства (НАСА))

Множество факторов, связанных с событием, делает его непредсказуемым.

Идентичность Эйлера

Идентичность Эйлера считается « лучшим из уравнений » в математических классах, потому что она описывает маловероятную комбинацию пяти математических констант.

Тождество Эйлера — это равенство, где e — число Эйлера, основание натурального логарифма, i — мнимая единица, которая удовлетворяет условию i2 = −1, а π — это число пи, отношение длины окружности к ее диаметру (Источник: Wikipedia.org)

Уравнение Эйлера (опубликованное Леонардом Эйлером в 1755 году) применимо в случае идеальной жидкости.

Почему это уравнение имеет значение? Потому что использует три основных арифметических операции: сложение, умножение и возведение в степень. .

Пять представленных констант — это «0», аддитивная идентичность; «1» — мультипликативное тождество; сказочный пи; «е» — основание натурального логарифма и числа, которое широко используется в математическом анализе; и «i», мнимая единица комплексных чисел, найденных в уравнениях с 3 неизвестными.

Это уравнение, которое украшает Дворец Декуверт в Париже, проложило путь к развитию топологии, ветви современной математики .

Преобразование Фурье

Преобразование Фурье делит время на несколько частот и простые волны, точно так же, как призма разделяет свет на составляющие его цвета.

Преобразование Фурье (Источник: Wikipedia.org)

Преобразование Фурье позволяет нам иметь дело с непериодическими функциями.

Другим примером может быть магнитное поле или акустическое поле , которое определяется как сигнал. Преобразование Фурье — это его спектр, поскольку он деконструирует такое поле.

Обложка «Темной стороны луны» Pink Floyd (Источник: Flickr.com — El Silver)

Эта теория была настолько потрясающей, потому что внезапно стало возможным понять структуру более сложных волн, таких как Соловьева .

Сегодня эта теория, восходящая к 1822 году, лежит в основе современной обработки и анализа сигналов, а также обработки данных .

Уравнения Максвелла

Уравнения Максвелла описывают взаимодействие электрических зарядов, а также объясняют электрические токи и магнитные поля.

Уравнения Максвелла, также называемые уравнениями Максвелла-Лоренца, являются фундаментальными законами физики.

Они лежат в основе нашего понимания взаимосвязи между электричеством и магнетизмом и входят в число основных, фундаментальных законов современной физики.

Уравнения Максвелла составляют основу классического электромагнетизма (Источник: commons.wikimedia.org)

Есть 4 формы уравнений Максвелла:

• Уравнение Максвелла-Гаусса
• Уравнение Максвелла-Томсона
• Уравнение Максвелла-Фарадея
• Уравнение Максвелла-Ампера

Второй закон термодинамики

Второй закон термодинамики (также известный как принцип Карно по имени его первооткрывателя в 1824 году) неопровержимо доказывает, что физические явления необратимы, особенно когда происходят тепловые изменения.

Принципы термодинамики — это основные законы, управляющие термодинамикой.

Этот принцип несколько раз модифицировался и переформулировался и получил широкую популярность в 1873 году благодаря Людвигу Больцманну и Максу Планку.

Сади Карно, первый, кто сформулировал второй закон термодинамики (Источник: архив истории математики MacTutor)

В то время как первый закон термодинамики определяет, что энергии могут передаваться между физическими системами в виде тепла и работы .Второй закон вводит другую величину, известную как энтропия .

Это принцип изменения и эволюции, поскольку он определяет, в каком направлении возможны потенциальные преобразования энергии .

Следовательно, одни химические превращения возможны, а другие невозможны. Вы можете с уверенностью заявить, например, что если вы положите кубик льда в чашку горячего кофе, кубик льда растает, а кофе никогда не замерзнет.

Уравнение Шредингера

Уравнение Шредингера, придуманное австрийским физиком Эрвином Шредингером в 1925 году, представляет собой фундаментальное уравнение в квантовой механике .

Зависящее от времени уравнение Шредингера (Источник: wikipedia.org)

Поскольку общая теория относительности Эйнштейна помогла объяснить Вселенную в крупном масштабе, это уравнение проливает свет на поведение атомов и субатомных частиц .

Уравнение Шредингера объясняет изменения частицы во времени. Он описывает состояния частицы, из которых можно описать любое состояние.

Это уравнение ставит настоящий философский вопрос: состоит ли материя из наличия возможных физических состояний (твердые тела, жидкости, газы)?

Эрвин Шредингер, австрийский физик, лауреат Нобелевской премии (Источник: commons.wikimedia.org)

Применение этого уравнения можно найти в современной технологии , включая ядерную энергию, твердотельные компьютеры и лазеры.

Как мы видим, на протяжении всей истории человечества и особенно с XVIII века математические уравнения трансформировали наше понимание мира, в котором мы живем, и нашу способность решать математические задачи. Они служат нам каждый день в нашей повседневной жизни, на уроках математики или более или менее непосредственно.

F формулы и уравнения, о которых вы можете узнать на уроках алгебры. уравнения.

Призы и награды по математике

Есть ряд неотъемлемых наград, присуждаемых людям, часто называемым гениями, которые преуспели в различных областях математики , обычно предлагая решение математической задачи. Это престижные награды, имеющие абсолютную ценность и ценность, некоторые из которых даже считаются приравненными к получению Нобелевской премии. Таким образом, лишь очень немногие избранные получают эти награды, подчеркивая их математические способности.

Ниже приведены некоторые из этих наград.

Медаль Филдса

Медаль Филдса — одна из самых известных наград, присуждаемых математикам , которые достигли чего-то удивительного за свою карьеру, работая с числами, уравнениями или другими вещами, например, открыв важную теорию или концепцию.

Официально победители этой премии награждаются Международной медалью за выдающиеся открытия в математике (вы можете понять, почему ее чаще называют просто медалью Филдса), и она вручается только один раз в четыре года максимум четырем математикам. моложе 40 лет.Это означает, что большинство лауреатов этой престижной награды можно отнести к категории молодых, многообещающих математиков с большими перспективами на будущее.

Премия Абеля

Еще одна уважаемая номинация, Премия Абеля вручается королем Норвегии математику, выдающемуся в своей области математических исследований .

Он назван в честь Нильса Хенрика Абеля, который еще в 2001 году, когда он был впервые создан, был популярным норвежским математиком.

Премия Вольфа по математике

Израильский фонд Вольфа ежегодно присуждает шесть различных премий, одна из которых — Премия Вольфа по математике.

Эта награда существует с 1978 года и считается большой честью для номинанта. Некоторые известные имена, получившие эту награду, включают Эндрю Уайлс, Джон Милнор и другие.

Медаль Черна

Одной из новых наград по математике является Медаль Черна, которая отмечает достижения в математике с 2010 года.

Она присуждается каждые четыре года, поэтому пока что лишь несколько математиков получили в свои руки одну из этих престижных наград. Он вручается на Международном конгрессе математиков, и он включает денежную премию в размере 250 000 долларов (очевидно, чтобы помочь финансировать дальнейшие исследования или увеличить плату за обучение в других областях математики).

Первым получателем в 2010 году стал Луис Ниренберг, а победителем в 2014 году стал Филипп Гриффитс.

Так почему же нет Нобелевской премии для математиков ?

В мире математических фактов некоторые скажут, что причина этого в том, что у жены Альфреда Нобеля был роман с известным математиком, но теперь мы знаем, что это неправда, поскольку Нобель даже не женился при жизни.Проще говоря, его работа, связанная с научными вопросами, означала, что эти предметы были ему ближе к сердцу, чем математическое выражение.

Найдите репетитора по математике на сайте Superprof.

Математики, изменившие мир

Если вы, как и мы, задаетесь вопросом, почему в истории математики не было упоминания о женщинах-математиках , то этот раздел для вас! Поговорим об уравнениях и неравенствах …!

Несмотря на то, что многие женщин принимали участие в математических открытиях , как и их сверстники-мужчины, их способность решать задачи редко упоминалась.Ниже приведены лишь некоторые из женщин, у которых помогли сформировать математику с течением времени .

Гипатия

Гипатия была дочерью греческого математика Теона и стала главой школы платоников в Александрии, Египет, где преподавала астрономию и философию.

Эта высокоинтеллектуальная женщина была убита в 415 году нашей эры, и религиозные группы заклеймили ее как сатанистку, однако считается, что она была влиятельным гением , внесшим значительный вклад в опубликованные тексты своего знаменитого отца в то время, когда она у нее была.

Софи Жермен

Говорят, что Мария-Софи Жермен одержима теориями чисел и исчислением , вдохновленная чтением об Архимеде.

Это был 18 век, и некоторые учреждения не позволяли женщинам учиться под их крышей. Поэтому Жермен приняла личность студента, чтобы учиться в мужской математической академии в Париже.

К сожалению, хотя некоторые знают о ее блестящей работе над Великой теоремой Ферма, она никогда не была официально признана, и она умерла, известная лишь как незамужняя, не имеющая профессии женщина.

Узнайте больше о Софи Жермен с онлайн-репетитором по математике.

Кэролайн Гершель

Кэролайн Гершель была первой женщиной, получившей золотую медаль Королевского астрономического общества в 1828 году после того, как она обнаружила семь новых комет.

Гершель стала оплачиваемым помощником своего брата-астронома Уильяма, и пара открыла планету Уран в 1781 году, прежде чем сделать многочисленных важных открытий, своих собственных открытий перед ее смертью в возрасте 97 лет.

Ада Лавлейс

Со знаменитым отцом, поэтом лордом Байроном, неудивительно, что Лавлейс прозвали Чародейкой! Тем не менее, в отличие от отца, она была гораздо более талантливой, когда ее просили координировать систему счисления, а не решать любые задачи со словами.

Лавлейс по профессии был викторианским пионером компьютеров , который сотрудничал с Чарльзом Бэббиджем над первыми программируемыми компьютерами в середине 19 века. Даже сейчас можно увидеть, что ее идеи так далеко опередили ее время, что может быть причиной того, что ее вклад в область математики не был признан до 1950-х годов — более чем через 100 лет после того, как она выполняла эту работу.

Софья Ковалевская

И последнее, но не менее важное: Ковалевская, родившаяся в Москве в 1850 году, внесла очень важный вклад в математический анализ в Германии.

Поскольку ее способности были замечены ее дядей в первую очередь, она получила частные уроки, однако позже была вынуждена выйти замуж.

Она наконец преодолела неравенство и разрыв между мужчинами и женщинами и стала первой женщиной, получившей профессуру в Северной Европе.

Другие влиятельные женщины-математики

Посмотрите ниже на еще несколько женщин, которые исторически занимались математикой, и почему.

Имя	Математическая идентичность
Эмми Нётер	Новатор в высшей алгебре
Флоренс Найтингейл	Изобретатель графических1674		способов отображения статистики Джоус выключатель
Дама Джоселин Белл Бернелл	Пионер астрономии
Радиа Перлман	Лидер в области информатики

Математика в будущее

Что будет дальше? ?

Какое новое математическое открытие перевернет наши нынешние представления о жизни, как мы ее знаем? Могли бы вы стать известным математиком квадратного уравнения, алгебраической функции, тригонометрическим прорывом или даже открытием новой концепции, такой как теорема Пифагора?

В качестве альтернативы, возможно, вы внесете что-то совершенно новое в таблицу , открыв новое целое число, о существовании которого мы даже не подозревали, разработав интеллектуальный графический калькулятор или упростив математику с помощью устройства для решения уравнений или приложения для системы уравнений.

No related posts.