Простейшие задачи в координатах | План-конспект урока по геометрии (9 класс) по теме:
Тема урока: Простейшие задачи в координатах
(урок введения новых знаний)
Цели урока:
- рассмотреть простейшие задачи в координатах (нахождение координат середины отрезка, определение длины вектора, определение расстояния между точками) и показать, как они применяются при решении задач;
- развивать у учащихся умения сопоставлять, анализировать, выделять главное, обобщать, формулировать выводы;
- воспитывать познавательную активность, умение самостоятельно добывать знания, формировать культуру общения.
Ход урока
1. Организационный момент
Здравствуйте. Садитесь.
Как у вас настроение? Давайте настроимся на работу. Глубоко вдохните. Выдохните вчерашнюю обиду и беспокойство. Вдохните в себя тепло солнечных лучей. Повернитесь друг к другу и улыбнитесь, а теперь улыбнитесь мне, а я улыбнусь вам. Если день начинается с улыбки, то можно надеяться, что он пройдет удачно.
А я желаю вам плодотворной и успешной работы на протяжении всего урока.
Взгляните на иллюстрацию. Распознайте в изображении цифры и найдите сумму чисел.
(Ответ: 63)
2.Проверка домашнего задания
Откройте тетради с домашней работой. Выполните самопроверку сравнив свое решение с моим.
Оцените свою домашнюю работу и поставьте отметку в лист самооценки.
3. Актуализация знаний
Давайте повторим те геометрические понятия, которые вам знакомы и сегодня понадобятся на уроке. Согласны ли вы с утверждениями, если нет обоснуйте свое мнение и сформулируйте верное утверждение.
Оцените свою устную работу и поставьте отметку в лист самооценки.
4. Постановка учебной задачи
Вы смогли ответить на последние два вопроса однозначно? (ответы учащихся)
В чем затруднение? (ответы учащихся)
Чему на уроке должны научиться? (Научиться определять координаты середины отрезка и длины вектора).
Ответы на эти вопросы можно объединить, сформулировав тему нашего урока.
5. Открытие нового знания
Тема урока: Простейшие задачи в координатах
Откройте тетради и запишите тему урока
Какие цели можно поставить для себя на урок? (продолжить фразу)
Узнать…
Познакомиться со ….
Научиться применять …
Цель урока: рассмотреть простейшие задачи в координатах и научиться применять их на практике.
Чтобы познакомиться с данными задачами, мы проведем мини исследование. Но сначала разделимся на группы.
1. Деление на группы. Я попрошу вас взять синие карточки, поднимите их вверх, покажите друг другу. Спасибо.
Вы сейчас по моему сигналу должны будете встать и двигаться по классу, общаясь между собой создать некие группы. Но принцип построения групп вы выбираете сами. Я об этом вам ничего не говорю. Единственное, что хочу сказать, что вы ограничены во времени, у вас ребята на это есть всего 1,5 минуты. Тихонечко встаньте и подойдите ко мне в центр класса. Через две минуты я хочу увидеть группы. Сколько я не знаю.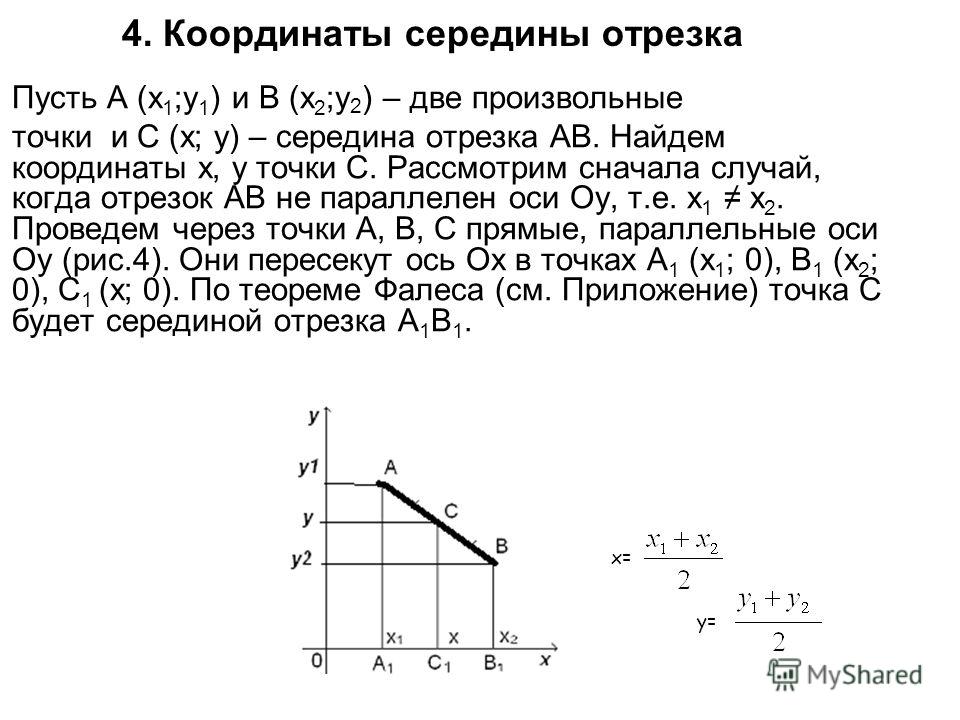
Начали.
Почему вы объединились в одну группу?
Почему вы вместе?
Скажите, пожалуйста, почему вы вместе?
А почему вы объединились в группу?
Вы разбились на группы. Посмотрите друг на друга. Вам комфортно в таком составе. Хорошо.
Прошу группы для дальнейшей работы занять свои места. Пожалуйста, садитесь.
Перед вами листы, на которых сформулировано задание. Ваша задача выполнив полученные задания сделать вывод о простейших задачах в координатах.
2. Работа в группах 4 минуты.
3. Вывод по работе в группах.
4. Мы с вами знаем как координаты вектора, зная координаты его начала и конца (сформулировать, спросить ученика) и знали как найти длину вектора (сформулировать, спросить ученика). Что можно еще узнать, по вашему мнению, соединив эти две задачи вместе. ( длину отрезка, расстояние между двумя точками зная координаты этих точек).
Вывод формулы.
Пусть точка М имеет координаты (х1; у1), а точка N имеет координаты (х2; у2).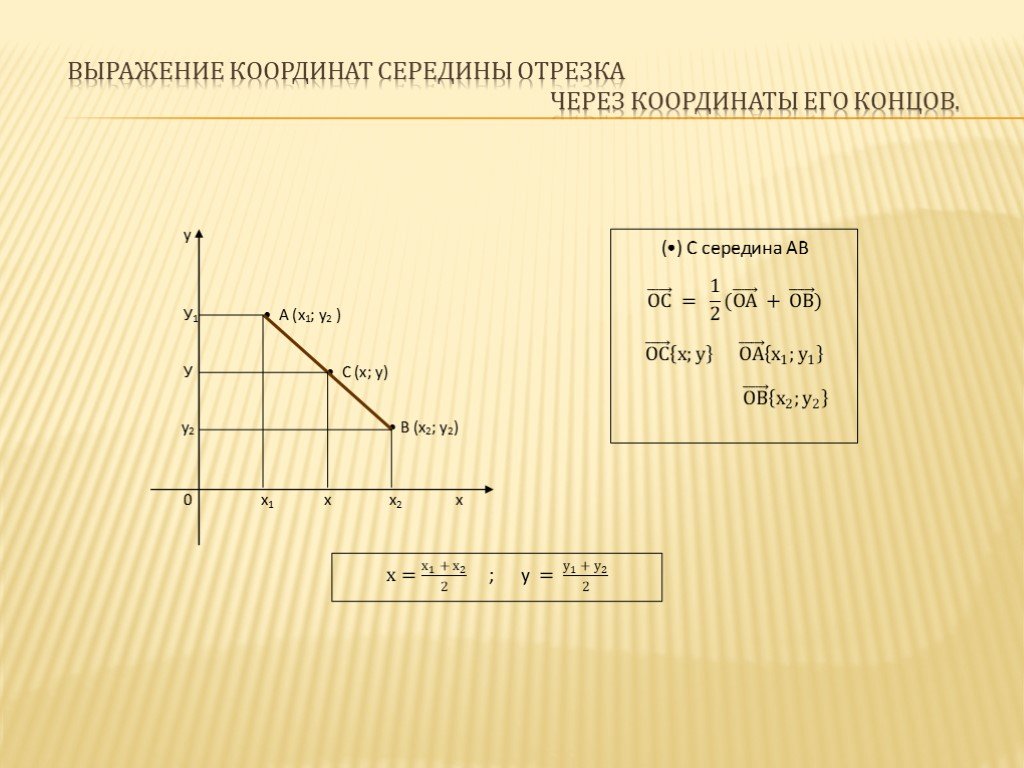 Найдите координаты вектора MN {x2-x1; y2-y1}. Тогда длина вектора
Найдите координаты вектора MN {x2-x1; y2-y1}. Тогда длина вектора
│MN│=
Я вам хочу подарить закладки, с основными формулами сегодняшнего урока.
6. Первичное усвоение материала. Устное решение задач.
Теория без практики – мертва, практика без теории невозможна.
Теперь мы готовы решать задачи.
Оцените свою активность при выполнении работы по овладению новыми знаниями и поставьте отметку в лист самооценки.
7. Первичная проверка усвоение материала:
Как мы можем проверить усвоен ли материал? (Выполнить самостоятельную)
(самостоятельная работа с самопроверкой в классе).
Но для начала дадим своим глазам отдохнуть.
Зарядка для глаз.
-Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа вернитесь в исходное положение. Закройте глаза, сосчитайте до 5, откройте глаза и …
Выполнение теста: возьмите зеленые карточки и выполните предложенные задания.
Тест
— Обменяйтесь работами и выполните взаимопроверку. Поставьте оценку, используя критерии
«5» — без ошибок
«4» — 1 ошибка
«3» — 2 ошибки
Перенесите оценку за тест в лист самооценки.
Поднимите руки:
— Кто получил «5»?
— Кто получил «4»?
8. Включение знаний в систему
9.Домашнее задание
1. п. 89, № 937, № 938(а, в), № 940 (а, в)
2. № 947 (а)
3. Подготовить сообщение о Рене Декарте.
Попытайтесь ответить на вопрос: Почему я взяла имя данного ученого?
10. Итог урока.
Вот и закончился урок
Нам надо подвести итог
— Каким сегодня был для нас урок (закрепление или открытие)?
— Что узнали на уроке? (простейшие задачи в координатах: длина вектора, длина отрезка, координаты середины)
— Вернемся к листу самооценки. В начале нашего урока вы поставили свою цель, ответьте себе на вопрос: Достиг ли я своей цели? Сделайте соответствующую отметку в листе самооценки.
— Кто достиг своей цели, поднимите руки.
— А теперь поставьте себе оценку за урок ( найдите среднее арифметическое своих оценок).
— Кто получил «5»?
— Кто получил «4»?
— Рефлексия «Оцени себя на уроке». (спросить двух — трех учеников)
Учащимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям.
Урок Я на уроке Итог
1. интересно 1. работал 1. понял материал
2. скучно 2. отдыхал 2. узнал больше, чем знал
3.безразлично 3.помогал другим 3. не понял
— Вы сегодня хорошо работали, помогали друг другу и справились со всеми заданиями. Благодарю всех за активную работу.
Говорю вам большое спасибо. Урок окончен. До свидания.
Найти длину отрезка по координатам точек формула. Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 .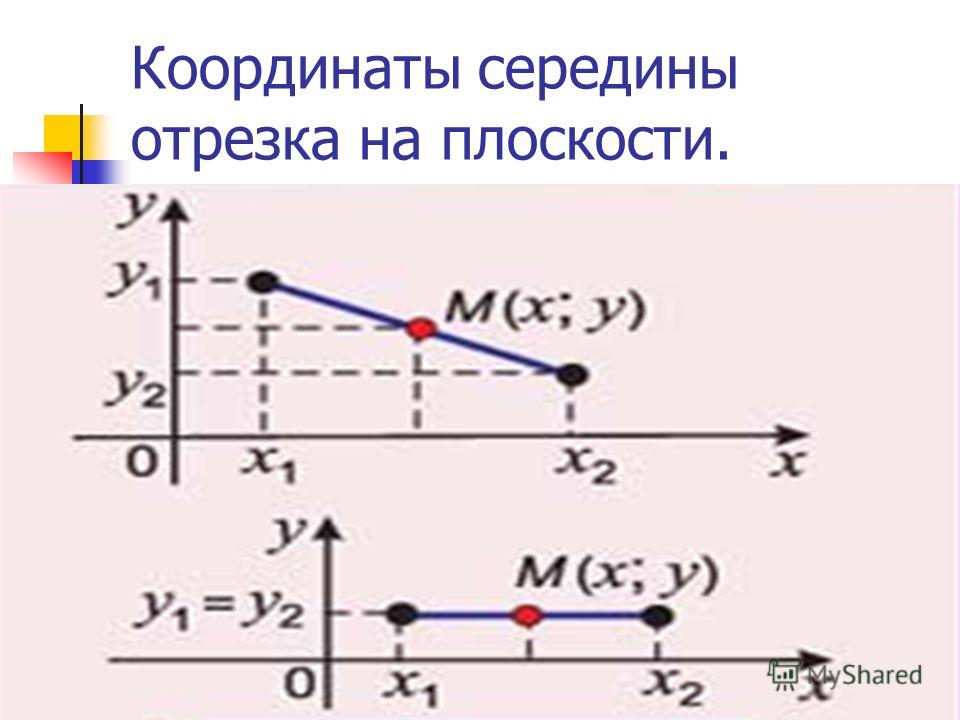
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам.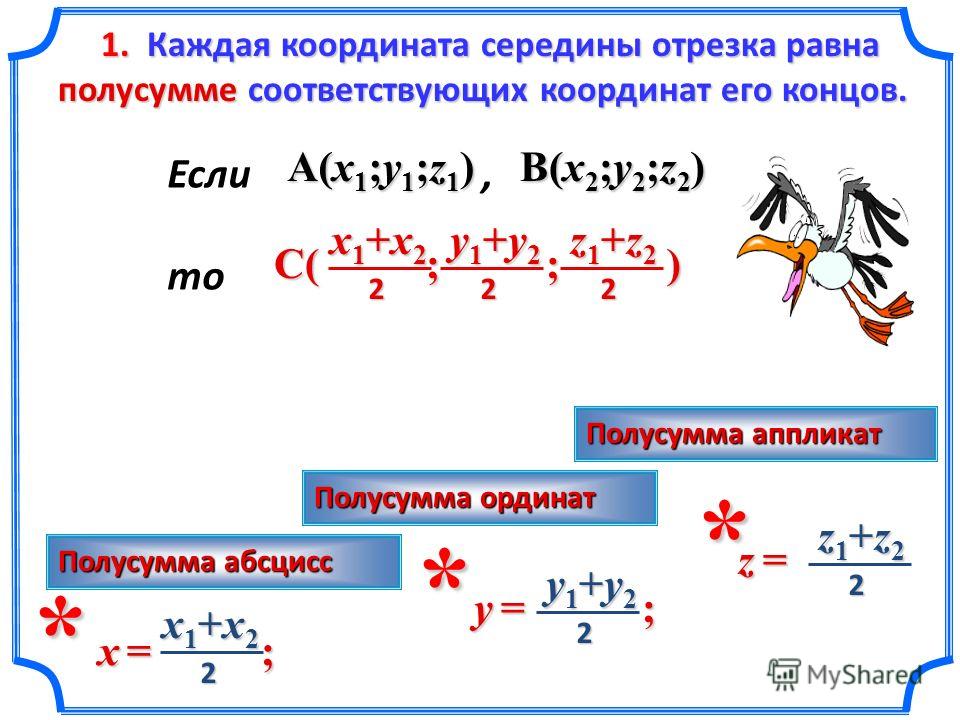 Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
(рис. 3
).
Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.
Длины отрезков MN
и EF
мы измерили единичным отрезком , длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC = 8 − 3 = 5 (см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC =
8
+ 5
= 13
(см).
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Математическая задача: Середина отрезка
Точка А имеет координаты [4; -11], а середина отрезка AB – точка [17; -7]. Каковы координаты точки В?
Правильный ответ:
Bx = 30By = -3
Пошаговое объяснение:
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Чтобы решить эту математическую задачу со словами, вам необходимо знать следующие знания:
- Геометрия
- Аналитическая геометрия
- Сегмент линии
Оценка слова Проблема:
- Практика для 12 -летнего возраста
- .
- Отрезок
Вычислить длину отрезка AB, если координаты конечных вершин равны A[10, -4] и B[5, 5]. - Координаты шестиугольника
Дан правильный шестиугольник ABCDEF. Точка А имеет координаты [1; 3], а точка D имеет координаты [4; 7]. Вычислите сумму координат центра его описанной окружности.
Вычислите сумму координат центра его описанной окружности. - Хорда BC
Окружность k имеет центр в точке S = [0; 0]. Точка А = [40; 30] лежит на окружности k. Какой длины хорда ВС, если центр Р этой хорды имеет координаты: [- 14; 0]? - Центр
В треугольнике ABC есть точка D[1,-2,6], являющаяся центром |BC|, и точка G[8,1,-3], являющаяся центром тяжести треугольник. Найдите координаты вершины A[x,y,z]. - Координаты 80452
A (a1, 4) B(7, -2) отрезок AB имеет центр, в котором обе координаты равны - Координаты 65224
Линия PQ определяется точками с координатами P = [- 2; 4] и Q = [4; 0]. Каковы координаты центра S отрезка PQ? - Середины треугольника
Определить координаты вершин треугольника ABC, если известны середины сторон треугольника SAB [0;3] SBC [1;6] SAC [4;5], его стороны AB, BC, AC. - Прямоугольный 3478
В прямоугольной системе координат проведен отрезок AB с концами A [1;6] и B [5;2]. Центр симметрии является началом системы координат. Найдите координаты центра этого отрезка в этой проекции симметрии.
Найдите координаты центра этого отрезка в этой проекции симметрии. - треугольник 5420
Даны две пары параллельных прямых, AB к CD и AC к BD. Точка E лежит на прямой BD, точка F — середина отрезка BD, точка G — середина отрезка CD, площадь треугольника ACE равна 20 см². Определить площадь треугольника - Отрезок
Для отрезка, конечными точками которого являются L[-1, 13] и M[18, 2], найти значение x и y для точки, расположенной 4 над 7, расстояние от L до M. - Координаты 2
Координаты вершин показанного треугольника: A(1,7), B(5,2) и C(5,7). Какова длина отрезка АВ в единицах? - Вектор — основные операции
Заданы точки A [-9; -2] Б [2; 16] С [16; -2] и Д [12; 18] а. Определить координаты векторов u=AB v=CD s=DB b. Вычислить сумму векторов u + v c. Вычислить разность векторов u-v d. Определить координаты векто - Пересечение 3486
В прямоугольной системе координат есть точка A [-2; -4] и точку S [0; -2]. Определить координаты точек B, C и D так, чтобы ABCD был квадратом, а S — пересечением их диагоналей.
- Координаты середины
Если середина отрезка — (6,3), а другой конец — (8,4), какова координата другого конца? - Центр
Вычислить координаты центра тяжести T [x, y] треугольника ABC; А[-17,9] В[-26,-19] С[-7,7]. - Разделить отрезок
Найти точку P на отрезке AB такую, что |AP| = г |АВ|. Координаты конечных точек: A = (−2, 0, 1), B = (10, 8, 5), отношение r = 1/4. - Три точки 2
Три точки: A(3, 8), B(6, 2) и C(10, 2). Точка D такова, что прямая DA перпендикулярна AB, а DC параллельна AB. Вычислите координаты D.
- all math problems16767
- algebra 4875
- arithmetic 3457
- basic functions 5179
- combinatorics 880
- geometry 2762
- goniometry and trigonometry 496
- numbers 5250
- physical quantity 5416
- planimetrics 3022
- solid геометрия 2082
- статистика 647
- темы, темы 2549
-
- новые математические задачи
- популярные математические задачи
- Более сложные математические задачи
- Самые простые задачи со словами
Формула средней точки — УРОКИ МАТЕМАТИИ КЕЙТ
Сопутствующие ресурсы: Что такое средняя точка? Середина двух точек — это точка, которая находится ровно посередине между ними. Допустим, вы стоите в точке А, а я стою в точке Б. Если я скажу, что встречу вас на полпути, где я вас встречу?
Хорошо, это тоже было немного очевидно. Чтобы усложнить задачу, предположим, что у вас не было миллиметровой бумаги, и я просто дал вам координаты. Как можно было найти середины двух разных отрезков без использования графика? Не могли бы вы еще понять это? В последнем примере у нас были точки C(0,5) и D(0,1). Поскольку обе конечные точки имеют координату x, равную 0, логично, что средняя точка также имеет координату x, равную 0. Но как насчет 3? 3 это всего лишь среднее из 5 и 1 (чтобы найти среднее двух чисел, их нужно сложить и разделить на 2: (5 + 1)/2 = 6/2 = 3). Пример 1 Допустим, у вас есть точки H(2,2) и K(6,4). Сможете ли вы найти середину между H и K? Пример 2 Найдите середину между точками P(-3,5) и Q(2,-1). Делаем то же самое, что и раньше. Найдите среднее значение координат x и среднее значение координат y. Просто будьте особенно осторожны при сложении положительных и отрицательных чисел! Что такое формула средней точки?Формула средней точки — это просто более формальный способ записать шаги, которые мы предприняли выше. Вот официальная формула (или, по крайней мере, ее версия): . Пример 3Найдите середину между точками (-3,8) и (10,-2). Если это поможет, вы можете сначала пометить точки. Помните, что координаты x всегда указываются первыми в упорядоченной паре. Неважно, какой из них вы назовете пунктом 1 или пунктом 2. Вы можете поменять их местами, и вы все равно получите тот же ответ. | Добро пожаловать на уроки математики у Кейт! Учителя, обязательно ознакомьтесь с учебными пособиями и заданиями. |
Это не обязательно, но было бы неплохо сделать быстрый набросок точек, чтобы увидеть, разумен ли ваш ответ для средней точки (или, по крайней мере, попытаться визуализировать его в уме). Легко допустить ошибку при сложении отрицательных чисел (Как вы складываете отрицательные числа?), поэтому грубый набросок часто может помочь вам обнаружить ошибку.
Точка (3.5,3) кажется мне прямо посередине!
Поиск отсутствующей конечной точки
Если вы изучаете формулу средней точки на уроке математики, скорее всего, вы столкнетесь с некоторыми проблемами, требующими поиска отсутствующей конечной точки отрезка по одной конечной точке и средней точке . Эти типы задач немного сложнее, поэтому давайте рассмотрим пример.
Пример
M(3,-1) – это середина между точками A(2,-8) и B. Найдите координаты точки B.
Вы можете взять миллиметровку и попытаться начертить сегмент, чтобы увидеть, где будет лежать B. Или вы можете использовать формулу средней точки и работать в обратном направлении! Начнем с координат x. Мы знаем, что если мы возьмем две конечные точки отрезка и усредним их x-координаты, мы получим x-координату средней точки. Это означает, что среднее значение 2 и какое-то число должно быть равно 3. Мы обозначим координаты точки B маленьким нижним индексом b.
Или вы можете использовать формулу средней точки и работать в обратном направлении! Начнем с координат x. Мы знаем, что если мы возьмем две конечные точки отрезка и усредним их x-координаты, мы получим x-координату средней точки. Это означает, что среднее значение 2 и какое-то число должно быть равно 3. Мы обозначим координаты точки B маленьким нижним индексом b.
Если мы знаем среднее значение 2 и координата x точки B должна быть равна 3, мы можем записать это в виде уравнения. Когда мы делаем этот шаг, мы используем первую половину формулы средней точки.
Вы знаете, как решить это уравнение? Один из способов — подумать о шагах, которые вы обычно предпринимаете, чтобы найти среднюю точку и двигаться в обратном направлении. Обычно вы сначала складываете две координаты x, а затем делите на 2. Если вы идете назад, вам нужно использовать обратные операции, чтобы отменить эти шаги. Чтобы отменить деление обеих сторон на 2, нам нужно сначала умножить обе стороны на 2.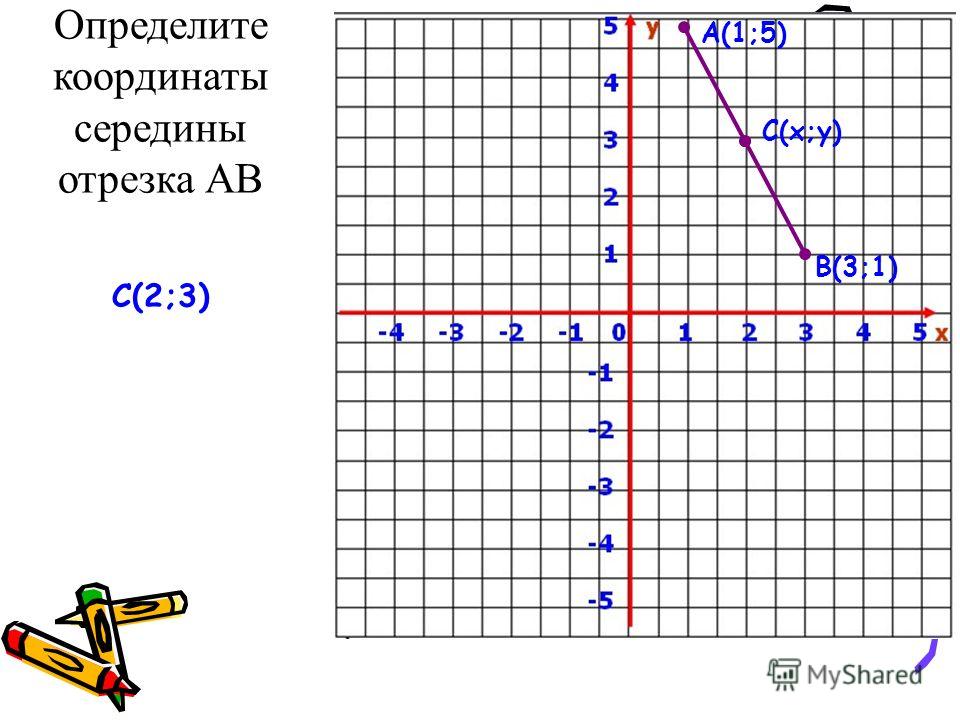 (Еще один вариант — преобразовать правую часть уравнения в дробь, поставив 1 в знаменателе. Затем вы можете выполнить перекрестное умножение. Оба варианта дают один и тот же результат.)
(Еще один вариант — преобразовать правую часть уравнения в дробь, поставив 1 в знаменателе. Затем вы можете выполнить перекрестное умножение. Оба варианта дают один и тот же результат.)
Мы обнаружили, что x-координата отсутствующей конечной точки должна быть равна 4. Мы можем легко проверить это дважды. Равно ли среднее из 2 и 4 3? (2 + 4)/2 = 6/2 = 3.
Если вы будете достаточно решать задачи этого типа, вы сможете визуализировать их без необходимости составлять уравнение. Вы можете попрактиковаться в этом с миллиметровой бумагой или попытаться представить в уме, как далеко должны быть точки друг от друга.
Не забудьте про координату y! Мы собираемся повторить процесс, на этот раз с координатами y. Мы знаем, что координата y точки A равна -8, а координата y средней точки M равна -1. Это говорит нам о том, что среднее значение -8 и какое-то число должно получиться равным -1.
Мы можем использовать вторую часть формулы средней точки, чтобы составить другое уравнение для нахождения отсутствующей координаты y.


 Вычислите сумму координат центра его описанной окружности.
Вычислите сумму координат центра его описанной окружности.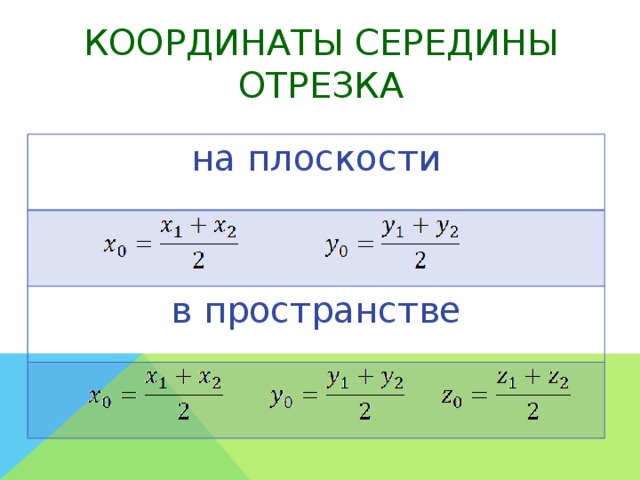 Найдите координаты центра этого отрезка в этой проекции симметрии.
Найдите координаты центра этого отрезка в этой проекции симметрии.
 Как найти середину? Давайте посмотрим на пример и посмотрим, сможем ли мы понять это.
Как найти середину? Давайте посмотрим на пример и посмотрим, сможем ли мы понять это. Теперь вы можете найти середину?
Теперь вы можете найти середину? Это даст нам координаты точки прямо посередине.
Это даст нам координаты точки прямо посередине. Он просто предлагает сложить две координаты x вместе и разделить на 2, затем сложить две координаты y вместе и разделить на 2. Не зацикливайтесь на том, какая точка является точкой 1 или точкой 2. Вы получите тот же ответ. независимо от того, какую точку вы решите назвать точкой 1.
Он просто предлагает сложить две координаты x вместе и разделить на 2, затем сложить две координаты y вместе и разделить на 2. Не зацикливайтесь на том, какая точка является точкой 1 или точкой 2. Вы получите тот же ответ. независимо от того, какую точку вы решите назвать точкой 1.