Обозначение область определения функции: Какой буквой обозначается множество значений функции и область определения функции?

Практическая тетрадь по теме «Функция и её свойства»

ПРАКТИЧЕСКАЯ ТЕТРАДЬ

по теме «Функция и её свойства»

Пояснительная записка:

Практическая тетрадь «Функция и её свойства» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанной теме. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.

Тема: ФУНКЦИЯ, ЕЕ СВОЙСТВА

СПРАВОЧНЫЙ МАТЕРИАЛ

Определение: Закономерность, при которой каждому значению х из множества Х соответствует единственное значение у из множества Y, называется функцией.

Обозначение функции: y=f (x).y=g(x). y=(x).., где х — независимая переменная, или аргумент; у- зависимая переменная ,или функция.

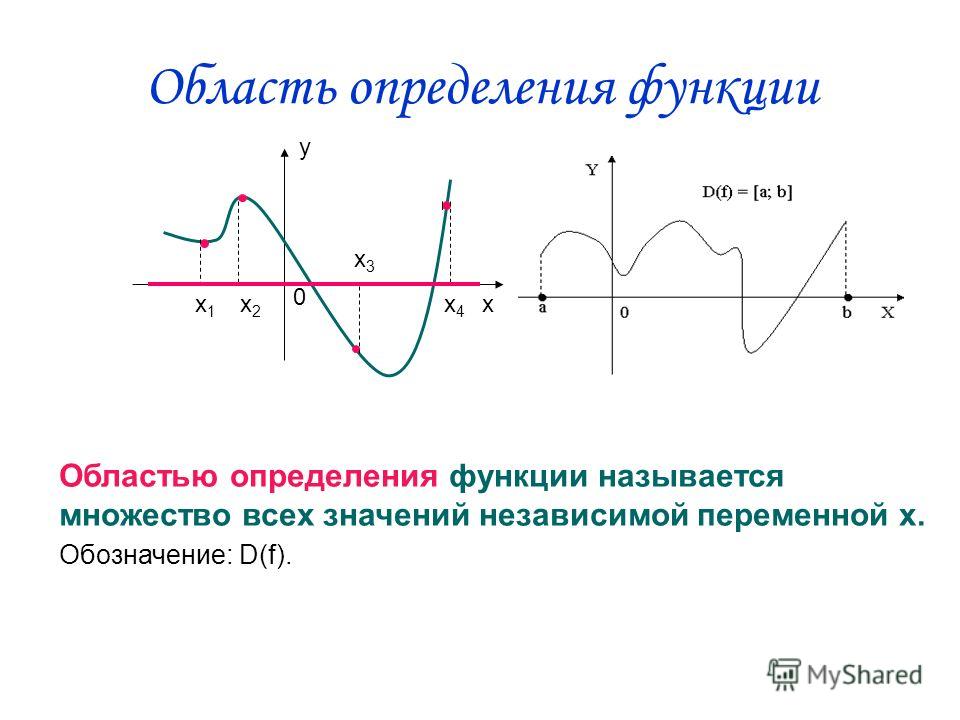
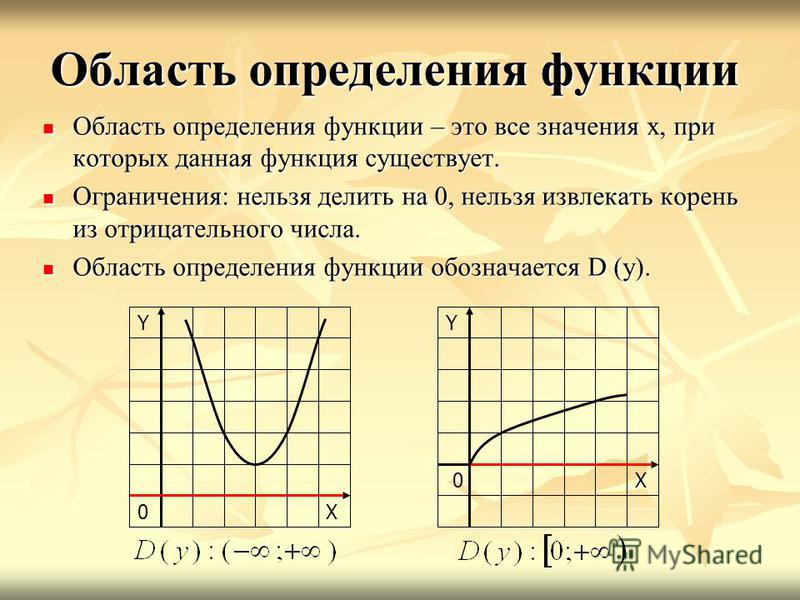
Множество значений переменной, при которых функция имеет смысл, называют областью определения функции, обозначение Д (f), а значение функции, соответствующее каждому значению независимой переменной из области определения, называют множеством значения функции, обозначение Е(f).

 

Понятие о четности, нечетности функции

Определение: Функция f называется четной, если для любого х из ее области определения f (-x)= f (x)

Определение: Функция f называется нечетной, если для любого х из ее области определения f (-x)= — f (x)

Понятие периодичности функции

Определение: Функцию f называют периодической с периодом Т0, если для любого х из области определения значение этой функции в точке х,

х-Т, х+Т равны, т.е. f (х+Т)= f(х)= f(х-Т)

Определение периода любой периодической функции основано на следующем свойстве: если функция f (x) является периодической и ее период равен числу Т, то периодической будет функция у=kf`(ax+b), (где k0, а0 и b – постоянные) и ее период равен числу .

 

УПРАЖНЕНИЯ С РЕШЕНИЯМИ

 

Пример 1. Найдите область определения функции

а) у=2 б) у= в)у= г) у= +

Решение:

а) у=2 функция заданная в виде многочлена, поэтому можно вычислять ее значения при любых значениях аргумента. Область определения все действительные числа.

Ответ: Д(f) =R

 

б) у= функция дробно-рациональная х .

 

Ответ: Д(f) =()

в)у= , необходимо взять подкоренное выражение неотрицательным, т.е.

2х-1.

Ответ: Д(f) =;+

г) у= + найдем область определения для х т.е ;+

для знаменатель х+2 х т.е ()

Д(f)=;+()=;+.

 

Ответ: Д(f)=;+

 

 

Пример 2. Найдем множество значений функций у=2

Решение: Известно, что Е(f) для у= есть отрезок

Рассмотрим -1 / умножим на 2

-2 / прибавим -5

-7

Ответ: Д(f)=

 

 

Пример 3. Определим четность или нечетность функций:

а) f(х)= б) f(х)=- +х в) f(х)=+

Решение: а) f(-х)= = f(х) – четная функция

 

б) f(-х)=- +(-х)= -х = — (- +х )= — f(х)- нечетная функция

 

в) f(-х)=+=-+ функция ни четная, ни нечетная (общего вида)

 

 

Пример 4. Найдем период для функции у=

Решение: Период функции у=, а по условию а=2 Тогда по формуле получаем, что =. Следовательно период данной функции равен .

Ответ:

 

 

Пример 5. Найдем наименьший положительный период функции у=tg

Решение: По определению период функции у=tg х равен по условию

а =, тогда по формуле получаем, что ==3 .

Ответ: 3

 

 

 

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

 

Найдите область определения функции:

а) у= б) у=

Ответ: Д(f) = (-2) Ответ: Д(f) ;0)

в) у = arcsin (2х-5)

Ответ: Д(f) = (2)

 

2. Найдите множество значений функции:

а) у=2 б) у=

Ответ: Е(f)=Ответ: Е(f)=

в) у= 1-2

Ответ: Е(f)=

3. Найдите область определения и множество значений функции:

а) у = б) у=

Ответ: Д(f)= , Е(f)= (0;+) Ответ: Д(f)= R, Е(f)=

в) у =-

Ответ: Д(f)=(-), Е(f)= (-)

4. Выясните четность, или нечетность следующих функций:

а) у = б) у =3+ в) у =+tgх

г) у = д) у = х —

5. Найдите наименьший положительный период функций

а) у = б) у = 5tg в) у =

Ответ: Ответ: Ответ: 16

г) у =ctg (5х — ) д) у = tg(2-5х) е) у = 2

Ответ: Ответ:Ответ:

 

ТЕСТ №1

1. Какая из функций в области определения является нечетной?

2. Что можно сказать о функции:

А) Ни четная, ни нечетная. В) Четная. С) Периодическая.

D) Нечетная. Е) Общего вида.

3. Найдите наименьший положительный период функции

4. Найдите область определения функции

5. Найдите множество значений функции

6. Найдите функцию, обратную данной

 

7. Найдите наименьшее значение функции у = х2 — 6х + 11

8. Найдите область определения функции:

9. Найдите множество значений функции

10. Найдите область определения функции:

ТЕСТ №2

1. Какая из функций является нечетной?

2. Какая из функций является четной?

3. Найдите наименьший положительный период функции

4. Найдите область определения функции:

5. Найдите множество значений функции

6. Дана функция у = 5 – 4х. Найдите ей обратную.

 

 

7. Дана функция у = х2-4х+3. Найдите значение х, при котором функция

принимает наименьшее значение.

8. Найдите область определения функции:

9. Найдите наименьшее значение функции

10 .Найдите область определения функции:

4.5. Логические функции

Логическая функция– это логическое выражение, состоящее из логических переменных связанных между собой с помощью операций алгебры логики.

В соответствии с вышеприведенными аксиомами (1)-(5) функция может принимать в зависимости от значений переменных x_pтолько два значения0и1.

Для функции nпеременныхx_n-1,…,x₀будем использовать общее обозначениегдеv=(x_n-1,…,x₀)каждая переменнаяx_p (p=0,1,2,…,n)может принимать только два значения0и1. Поэтому число всех возможных комбинаций значенийx_n-1,…,x₀конечно и равно2ⁿ.

В общем виде конкретное значение переменной x_p (0 или 1) будем обозначать черезe_p. Символамиi, jи т.п. будем обозначать порядковые десятичные числа.e_n-1…e_p…e₀ – обобщающая запись двоичного числа, гдеe_p = 0 или 1, и являются элементами алгебры логики если они используются в качестве значений переменных, для этих элементов не существует соотношений больше или меньше.

4.6. Область определения логических функций

Областью определения функции n переменныхx_n-1,…,x₀ является совокупность точекn-мерного пространства, причем каждая из точек задается определенной комбинацией значений этих переменныхгдеe_p

=0или1,(p=0,1,2,…,n-1).

Например,пусть есть некая функция 4х переменныхn=4то одна из точек определения этой функцииV_i =(e_n-1…e_p…e₀)гдеi=e_n-1…e_p…e₀ (например,V_i=1100).

Из этих соотношений видно, что точки определения можно посчитать по порядку от 0до2ⁿкак в двоичном счете, так и десятичном и в любом другом. Поэтому область определения функцииf(v) nпеременных имеет2ⁿточек т.е.

Для задания функции

f(v) следует указать ее значения во всех точках области определения т.е. следует задать значенияf(v_i)=0или1гдеi=0,1,2,…,2ⁿ-1. В совокупности эти значения представляют некое двоичное число из2ⁿразрядов т.к. имеется всегоразличных2ⁿ разрядных двоичных чисел, то и число различных функцийnпеременных равно.

Функции n переменных могут зависеть не от всех переменныхx_n-1…x₀. Такие функции называютсявырожденными.

Так же функция может быть задана как во всех точках определения, так и не во всех:

— функция nпеременныхf(v) называетсяполностью определенной,если ее значения

f(v_i)=0или1 заданы во всех2ⁿ точкахV_i области определения;

— если же значение функции не задано хотя бы в одной точки V_i, то она называетсяне полностью определенной, это означает, что функция в этой точке может иметь значение 1 или 0 – и это не важно – такое значение будем называть коэффициентомс;

— если значения функции не заданы во всех точках V_i, то она называетсяполностью неопределенной.

4.6. Таблица истинности

Так как область определения любой функции nпеременных конечна2ⁿточек она может быть задана таблицей значенийf(v_i)=0или1которые она принимает в точках

v_i, гдеi=0,1,…,2^n-1. Такие таблицы называютсятаблицами истинности.

Например: функция двух переменных

Vi— точки определения функции	Значения точек определения функции (значения e0, e1 переменных функции x0, x1)	Значение функции f(v) в точках определения
V0	0 0	1
V1	0 1	0
V2	1 0	0
V3	1 1	0

3$.

15-112: Основы программирования

---

1. Переменные
2. Функции
3. Операторы и выражения
4. Встроенные функции
5. Переменная область видимости
6. Отчеты о возврате
7. Печать против возврата
8. Функциональная композиция
9. Вспомогательные функции
10. Рекомендуемые функции
11. Тестовые функции

---

1. Переменные

• Переменная — это именованное значение, которое ссылается на часть данных или хранит ее.

  # мы помещаем значение в переменную, используя знак = х = 5 print(x) # x оценивается как 5 print(x*2) # оценивается как 10



• В отличие от математики, переменным могут быть присвоены новые значения, даже значения разных типов.

  г = 10 печать (у — 2) у = Истина print(y)



• Переменным можно давать любое имя, если оно начинается с буквы и не содержит специальных символов.

  количество кроликов = 40 курсIs15112 = Истина 99problems = 0 # произойдет сбой, потому что он начинается с числа



• Переменные можно обновлять с помощью операций присваивания.

  х = 5 x += 2 # то же, что и x = x + 2 print(x) # должно быть 7 # Это можно сделать с помощью любой арифметической операции. у = 350 у //= 10 print(y) # должно быть 35

Функции

• Функция — это процедура (последовательность операторов), хранящаяся под именем, которое можно использовать повторно, вызывая это имя.

  # Функция состоит из двух частей: заголовка и тела. # Заголовок определяет имя и параметры. # Заголовок функции записывается следующим образом: def functionName(parameters): # Параметры — это переменные, которые будут предоставлены при вызове функции. # Заголовок заканчивается двоеточием, чтобы указать, что за ним последует тело. # Тело содержит действия (инструкции), которые выполняет функция. # Тело пишется под функцией с отступом. # Когда строки больше не имеют отступа, тело функции заканчивается. # Функции обычно содержат оператор return. Это обеспечит результат при вызове функции. # Пример: защита двойной (х): print(«Я в двойной функции!») возврат 2 * х # Для вызова функции мы используем имя функции, # за которыми следуют круглые скобки, содержащие значения данных, которые мы хотим использовать, называемые аргументами функции. # Этот вызов функции будет оцениваться как выражение. print(double(2)) # напечатает 4 print(double(5)) # напечатает 10 print(double(1) + 3) # напечатает 5



• Функции могут иметь столько параметров, сколько им нужно, или вообще не иметь их.

  по определению f(x, y, z): вернуть х + у + г print(f(1, 3, 2)) # возвращает 6 деф г(): вернуться 42 print(g()) # возвращает 42 # Обратите внимание: количество предоставленных аргументов должно совпадать с количеством параметров! print(g(2)) # произойдет сбой print(f(1, 2)) # также вылетит, если запустится

Операторы и выражения

• Выражение — это значение данных или операция, результатом которой является значение.

  # Примеры выражений. # Обратите внимание, что при запуске в редакторе ни одно из этих значений не отображается. 4 «Привет, мир» # Если бы вы могли заменить некоторый код одним значением данных без изменения # поведение вашей программы (как и любая из строк ниже), этот код является выражением. 7 + 2 Правда или ложь (2 < 3) и (9 > 0) # Python может печатать только значения и выражения, поэтому, если вы можете напечатать это, это выражение print((2 < 3) и (9 > 0))



• Операторы, напротив, не возвращают значения, и мы не можем их распечатать. Однако обычно они выполняют какое-то действие.

  # Определение функции является примером оператора: защита f(x): возврат 5*х # Присвоение значения переменной является оператором # Заявления могут содержать выражения, как показано ниже # справа от знака равенства x = 5 + 4 # Вся строка является оператором. 5 + 4 — это выражение. # Условные операторы (о которых мы скоро узнаем) также являются утверждениями если 10 >

  5: у = 5 + 3

Встроенные функции

# Некоторые функции уже предоставлены Python print(«Функции преобразования типов:») print(bool(0)) # преобразовать в логическое значение (True или False) print(float(42)) # преобразовать в число с плавающей запятой print(int(2. 8)) # преобразовать в целое число (int) print(«И некоторые основные математические функции:») print(abs(-5)) # абсолютное значение print(max(2,3)) # вернуть максимальное значение print(min(2,3)) # вернуть минимальное значение print(pow(2,3)) # возвести в заданную степень (pow(x,y) == x**y) print(round(2.354, 1)) # раунд с заданным количеством цифр

Область действия переменной

• Переменные существуют в определенной области в зависимости от того, когда они определены. Это означает, что они невидимы и не могут использоваться за пределами этой области. в других частях кода.

  по определению f(x): печать(«х:», х) у = 5 распечатать(«у:», у) вернуть х + у печать (f (4)) print(x) # произойдет сбой! print(y) # также рухнет, если мы его достигнем!



• Переменные в функциях имеют локальную область видимости. Они существуют только внутри непосредственной функции и не имеют отношения к одноименным переменным в разных функциях.

  по определению f(x): print(«В е, х =», х) х += 5 вернуть х определение г (х): у = е (х * 2) print(«В г, х =», х) г = е (х * 3) print(«В г, х =», х) вернуть у + г печать (г (2)) # Другой пример защита f(x): print(«В е, х =», х) х += 7 обратный раунд (x / 3) определение г (х): х *= 10 вернуть 2 * f (х) определение ч(х): х += 3 вернуть f(x+4) + g(x) распечатать (ч (ф (1)))



• При определении вне функций переменные имеют глобальную область действия и могут использоваться где угодно.

  # В общем, вам следует избегать использования глобальных переменных. # Вы даже потеряете очки стиля, если будете их использовать! # Тем не менее, вам нужно понять, как они работают, так как другие # будет их использовать, а также может быть несколько очень редких случаев # где вы также должны их использовать! г = 100 защита f(x): вернуть х + г печать (f (5)) # 105 печать (f (6)) # 106 печать(г) # 100 # Другой пример защита f(x): # Если мы модифицируем глобальную переменную, мы должны объявить ее глобальной. # В противном случае Python будет считать, что это локальная переменная. глобальный г г += 1 вернуть х + г печать (f (5)) # 106 печать (f (6)) # 108 печать(г) # 102

Отчеты о возврате

• Базовый пример

  по определению является положительным (x): возврат (х > 0) print(isPositive(5)) # Истинно print(isPositive(-5)) # Ложь print(isPositive(0)) # False



• Возврат немедленно завершает функцию:

  по определению является положительным (x): print(«Привет!») # запускается возврат (х > 0) print(«До свидания!») # не запускается («мертвый код») print(isPositive(5)) # печатает Hello, затем True



• Нет оператора возврата —> return Нет:

  по определению f(x): х + 42 print(f(5)) # Нет



• Другой пример:

  по определению f(x): результат = х + 42 print(f(5)) # Нет

Печать против возврата

• Путать печать и возврат — распространенная ошибка на ранних этапах.

  по определению в кубе (x): print(x**3) # Вот ошибка! cubed(2) # вроде работает! print(cubed(3)) # типа работает (но печатает None, что странно) print(2*cubed(4)) # Ошибка!



• Еще раз (правильно):

  по определению в кубе (x): return (x**3) # Так лучше! cubed(2) # похоже игнорируется (почему?) print(cubed(3)) # работает! print(2*cubed(4)) # работает!

Функциональный состав

Для вложенных вызовов функций мы должны сначала оценить самые внутренние функции

def f(w): возврат 10*ш определение г (х, у): return f(3*x) + y # f(3*x) должно быть вычислено, прежде чем мы сможем вернуться определение ч(г): return f(g(z, f(z+1))) # Самая внутренняя f(z+1) должна быть вычислена первой print(h(1)) # подсказка: попробуйте функцию «визуализировать»

Вспомогательные функции

# Обычно мы пишем функции для решения проблем. # Мы также можем написать функции для хранения действия, которое используется несколько раз! # Это так называемые вспомогательные функции.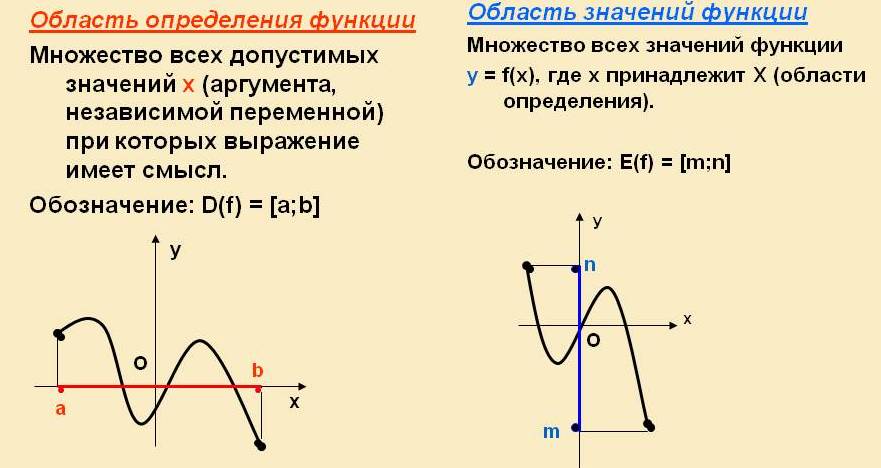 def oneDigit(n): вернуть n%10 определение более крупного OnesDigit (x, y): вернуть max (onesDigit (x), oneDigit (y)) print(largerOnesDigit(134, 672)) # 4 print(largerOnesDigit(132, 674)) # Еще 4

Рекомендуемые функции

# Есть несколько функций из модулей, которые вы обязательно захотите использовать в заданиях # Во-первых: встроенная функция округления ведет себя странно при округлении до 0,5. # Используйте нашу функцию roundHalfUp, чтобы исправить это. Def roundHalfUp(d): # Округлить до ближайшего числа, начиная с нуля. # Вам не нужно понимать, как работает эта функция. импортировать десятичный округление = десятичное.ROUND_HALF_UP вернуть int (десятичный. Десятичный (d). to_integral_value (округление = округление)) print(round(0.5)) # Это оценивается как 0 — что! print(round(1.5)) # И это будет 2 — так запутанно! print(roundHalfUp(0.5)) # Теперь это всегда будет округлять 0,5 в большую сторону (до 1) print(roundHalfUp(1.5)) # Это тоже округление! # Второе: при сравнении чисел с плавающей запятой == работает некорректно.