В эксперименте симметричную монету бросают дважды. Математика и мы. Ршение задачи с симметричной монетой
Условие
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет хотя бы один раза.
Решение
- Данную задачу будем решать по формуле:
Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.
- Применим данную теорию к нашей задаче:
А – событие, когда орел выпадет хотя бы 1 раза;
Р(А) – вероятность того, что орел выпадет хотя 1 раза.
- Определим m и n:
m — число благоприятствующих этому событию исходов, то есть число исходов, когда орел выпадет 1 раза. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы выпал орел хотя бы один раз, а это возможно тогда, когда выпадут следующее комбинации: ОР, РО и ОО, то есть получается, что
m = 3, так как возможно 3 варианта выпадения хотя бы 1-го орла;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды.
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.
Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять
перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Задача 3 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
Из таблицы видим, что число возможных элементарных исходов n=8.
Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Орел | Решка | Орел |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Решка | |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | Орел |
| 6 | Орел | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение . При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6 . Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4.
Решение . При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
В задачах по теории вероятностей, которые представлены в ЕГЭ номером №4, кроме , встречаются задачи на подбрасывание монеты и о бросках кубика. Их сегодня мы и разберем.
Задачи о подбрасывании монеты
Задача 1. Симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
В таких задачах удобно выписать все возможные исходы, записывая их при помощи букв Р (решка) и О (орел). Так, исход ОР означает, что при первом броске выпал орел, а при втором – решка. В рассматриваемой задаче возможны 4 исхода: РР, РО, ОР, ОО. Благоприятствуют событию «решка выпадет ровно один раз» 2 исхода: РО и ОР. Искомая вероятность равна .
Ответ: 0,5.
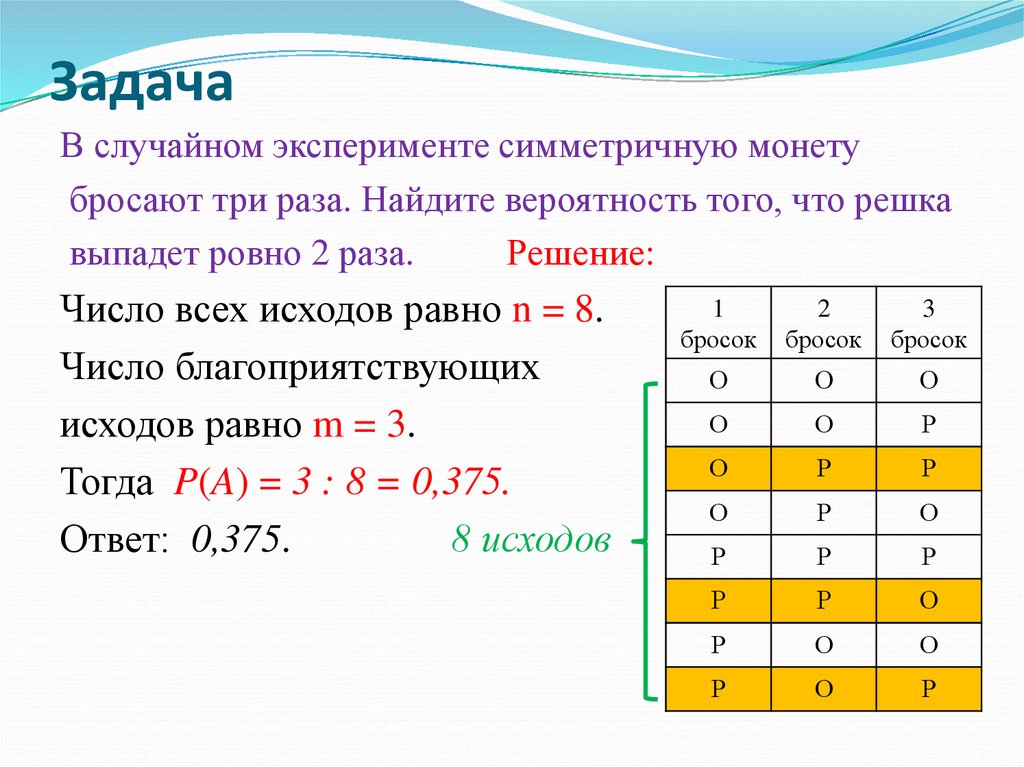
Задача 2. Симметричную монету бросают трижды, Найдите вероятность того, что орел выпадет ровно два раза.
Всего возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «орёл выпадет ровно два раза» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .
Ответ: 0,375.
Задача 3. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.
Эта задача аналогична предыдущей. Пусть каждый раз выпадение решки означает выигрыш жребия «Изумрудом» (такое предположение не влияет на вычисление вероятностей). Тогда возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «решка выпадет ровно один раз» 3 исхода: РОО,ОРО,ООР. Искомая вероятность равна .
Ответ: 0,375.
Задача 4 . Симметричную монету бросают трижды. Найдите вероятность того, что наступит исход РОО (в первый раз выпадает решка, во второй и третий — орёл).
Как и в предыдущих задачах, здесь имеется 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Вероятность наступления исхода РОО равна .
Ответ: 0,125.
Задачи о бросках кубикаЗадача 5. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 8»?
Задача 6 . Одновременно бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
Вообще, если бросают игральных костей (кубиков), то имеется равновозможных исходов. Столько же исходов получается, если один и тот же кубик бросают раз подряд.
Событию «в сумме выпало 4» благоприятствуют следующие исходы: 1 – 3, 2 – 2, 3 – 1.
Их количество равно 3. Искомая вероятность равна .
Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Таким образом, приблизительно равна 0,083…, округлив до сотых имеем 0,08.
Ответ: 0,08
Задача 7 . Одновременно бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Исходом будем считать тройку чисел: очки, выпавшие на первой, второй и третьей игральной кости. Всего имеется равновозможных исходов. Событию «в сумме выпало 5» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1. Их количество равно 6. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Приблизительно получаем 0,027…, округлив до сотых, имеем 0,03.Источник “Подготовка к ЕГЭ. Математика. Теория вероятностей”. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
В качестве предисловия.
Все знают, что монета имеет две стороны — орёл и решку.
Нумизматы считают, что монета имеет три стороны — аверс, реверс и гурт.
И среди тех, и среди других, мало кто знает, что такое симметричная монета. Зато об этом знают (ну, или должны знать:), те, кто готовится сдавать ЕГЭ.
В общем, в этой статье речь пойдёт о необычной монете, которая, к нумизматике никакого отношения не имеет, но, при этом, является самой популярной монетой среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и пр. Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой звучит так — «В случайном эксперименте симметричную монету бросают дважды (трижды, четырежды и т.д.). Требуется определить вероятность того, что одна из сторон выпадет определённое количество раз.
Ршение задачи с симметричной монетой
Понятно, что в результате броска монета упадёт либо орлом, либо решкой. Сколько раз — зависит от того, сколько бросков совершить. Вероятность выпадения орла или решки вычисляется делением количества удовлетворяющих условию исходов на общее количество возможных исходов.
Одн бросок
Здесь всё просто. Выпадет либо орёл, либо решка. Т.е. имеем два возможных исхода, один из которых нас удовлетворяет — 1/2=50%
Дваброска
За два броска могут выпасть:
два орла
две решки
орёл, затем решка
решка, затем орёл
Т.е. возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, нужно найти вероятность того, что орёл выпадет один раз, требуется просто подсчитать количество подходящих вариантов в таблице — т.
е. тех строк, где орёл встречается один раз. Таких строк две. Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Вероятность того, что орёл в двух бросках выпадет дважды равна 1/4=25%
Три роска
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные цифры от «0» до «7». Так проще не запутаться с вариантами.
Решим задачу из предыдущего пункта — вычислим вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна 3/8=37,5%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 3/8=37,5%, т.е. абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.
Четыр броска
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл выпадет один раз.
Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна 3/16=18,75%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%,.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.
Итак с увеличением количества бросков, принцип решения задачи совершенно не меняется — только, в соответствующей прогрессии, увеличивается количество вариантов.
Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды.
Найдите вероятность того, что орёл не выпадет ни разу.
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды.
Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
P = 3 / 4 = 0.75
|
Найдите вероятность того, что орел не выпадет ни разу.
Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых. 
Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Результат округлите до сотых.
Таких благоприятных исходов 150 – 9 = 141. Видео-вопрос: определение вероятности выпадения решки хотя бы один раз при трехкратном подбрасывании монеты
Какова вероятность того, что хотя бы один раз выпадет решка, если монету подбросить три раза?
Стенограмма видео
Какова вероятность получения решка хотя бы один раз, если монета подбрасывается три раза?
Существует множество способов
подход к этой проблеме.
Какой бы метод мы ни решили использовать,
нам нужно напомнить, что каждый бросок или подбрасывание монеты является независимым событием. Результат первого броска делает
не влияет на результат других. Один из способов решения этой проблемы
будет перечислять все возможные комбинации при трехкратном подбрасывании монеты. Возможно, что все три монеты
мог приземлиться на решку. Другой возможностью было бы
приземлиться на решку для наших первых двух бросков и решку на третий. Мы могли бы получить два хвоста и голову
двумя другими способами. Решки, головы, решки или головы, решки,
хвосты. Получение одного хвоста и двух голов
может случиться решка, орел, орел. Также может случиться орел, решка,
головы или головы, головы, решки.
Наконец-то все три монеты смогли приземлиться
на головах. Это означает, что существует восемь
различные комбинации, которые могут возникнуть.
Нам нужна вероятность получения
хвост хотя бы один раз. Наша топ-комбинация состоит из трех
хвосты. Следующие три имеют два хвоста. Три комбинации после этого
иметь одну монету, приземлившуюся на решку. Это означает, что семь из
восемь комбинаций завершаются получением решки хотя бы один раз. Вероятность того, что это произойдет
следовательно, семь из восьми или семь восьмых.
Альтернативным методом может быть
вычислить вероятность единственной комбинации, которая нам не нужна в первую очередь,
вероятность трех решек. Вероятность приземления головой
в любом отдельном броске монеты половина. Поскольку каждое из событий или бросков
независимыми, мы можем перемножить эти дроби, чтобы вычислить вероятность получения
три головы. Вероятность выпадения трех орлов равна
одна восьмая. Как вероятность выпадения решки
по крайней мере один раз все остальное, мы можем вычесть этот ответ из единицы, как мы знаем
сумма вероятностей равна единице.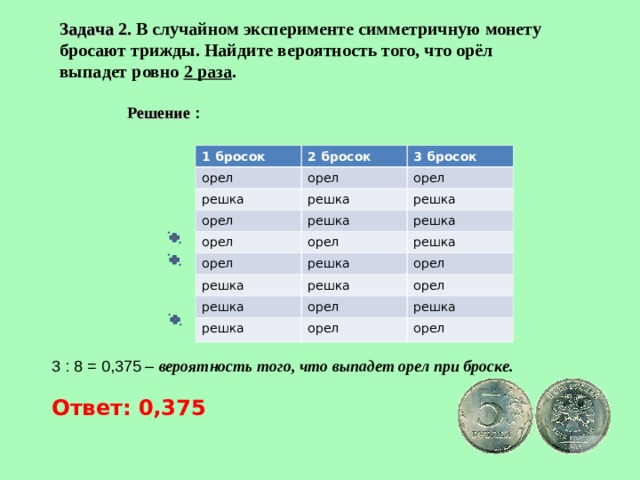
Вычитая из единицы одну восьмую,
еще раз дает нам ответ семь восьмых. При трехкратном подбрасывании монеты
вероятность того, что хотя бы раз выпадет решка, составляет семь восьмых.
Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.
Вероятность того, что при подбрасывании монеты выпадет больше орла, чем решки
Задавать вопрос
спросил
Изменено 5 лет, 6 месяцев назад
Просмотрено 32к раз
$\begingroup$
Правильная монета должна быть подброшена 8$ раз.
Какова вероятность того, что орел выпадет чаще, чем решка?
98)$\textbf{Угадай:}$ Я предполагаю, что по симметрии мы можем записать вероятность $x$ выпадения ровно $4$ орла и $4$ решки, а затем вычислить $\dfrac{1}{2}(1-x)$.
$\endgroup$
$\begingroup$
Число в числителе должно быть $\displaystyle \left( \begin{array}{c} 8 \\ 4 \end{array} \right) = \frac{8!}{4! ( 8-4)!} = 70$.
Почему? Потому что у нас есть 8$ бросков, и из этих бросков у нас есть 4$ орла.
$\endgroup$
1
$\begingroup$
Поскольку число исходов с 4H и 4T равно C(8,4)=70, существует равная вероятность того, что остальные исходы выпадут больше орлов, чем решек, или больше решек, чем орлов.
Зная, что общее количество результатов подбрасывания монеты 8 раз равно 256, разница 256-70 разделится поровну.