2.Квадратичная функция y=x² — Функции и их графики
В уравнении квадратичной функции: a – старший коэффициент b – второй коэффициент с — свободный член. Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид: Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу: Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов. График функции имеет вид: Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ. Итак, мы заметили: Если старший коэффициент a>0, то ветви параболы напрaвлены вверх. Если старший коэффициент a<0, то ветви параболы напрaвлены вниз. Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ. Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение . В случае квадратичной функции нужно решить квадратное уравнение . В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения. И здесь возможны три случая: 1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так: 2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. 3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ: , Если ,то график функции выглядит примерно так: Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы. И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY. Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: . То есть точка пересечения параболы с осью OY имеет координаты (0;c). Итак, основные параметры графика квадратичной функции показаны на рисунке: |
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
1. Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если угол MNP=80 градусов.
2.На стороне ВС параллелограмма ABCD взята точка М так, что АВ=ВМ.
Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если угол MNP=80 градусов.
2.На стороне ВС параллелограмма ABCD взята точка М так, что АВ=ВМ.
Длина сухопутной границы России с Китаем,Монголией и Казахстаном составляет 15293 километра.Найдите длину границы России с каждым из этих государств,если длина границы с Китаем и Монголией равна 7649
Лист бумаги квадратной формы со стороной 8 см. разрезали на 4 равных треугольника. Найдите площадь одного треугольника.
Сделать анализ стихотворения на выбор: Д. С. Мережковского («Парки», «Дети ночи», «Двойная бездна»), З. Н. Гиппиус («Песня», «Посвящение», «Пауки», «Все, кругом»), В. Брюсова («Юному поэту»,
Дан вектор m{1;2;2}.Найдите координаты единичного вектора е ,сонаправленного с вектором
Пользуйтесь нашим приложением
Mathscene — Функции 1 — Урок 3
Mathscene — Функции 1 — Урок 3| 2007 Расмус Эф и Джанн Сак | Функции я | Печать |
Урок 3
Функции второй степени
Давайте еще раз посмотрим на многочлены второй степени. Простейшая форма функции – f(x)
= х 2 . График представляет собой
парабола часто называется основной параболой.
Простейшая форма функции – f(x)
= х 2 . График представляет собой
парабола часто называется основной параболой.
Обратите внимание, что график симметричен относительно y- ось. Ось у называется осью симметрии этой функции.
Теперь посмотрим, как коэффициенты влияют на вид графика.
Коэффициент x 2 обычно называется а. Если мы посмотрим на парабол с разными значениями a мы видим, что некоторые из них шире, а некоторые уже, чем основная парабола, где a = 1,
Вот графики парабол, где а = 4, 2, ог .
а = 4 а = 2 а = а =
Вот параболы с отрицательные значения
а = −4 а = -2 а = — а = —
Если значение a равно положительный график изгибается вверх (как улыбка!) Чем больше значение a, тем сузить график.
Когда становится мало
график становится все более и более плоским, пока, когда a не станет отрицательным, он не повернется вниз (
как хмурый! ).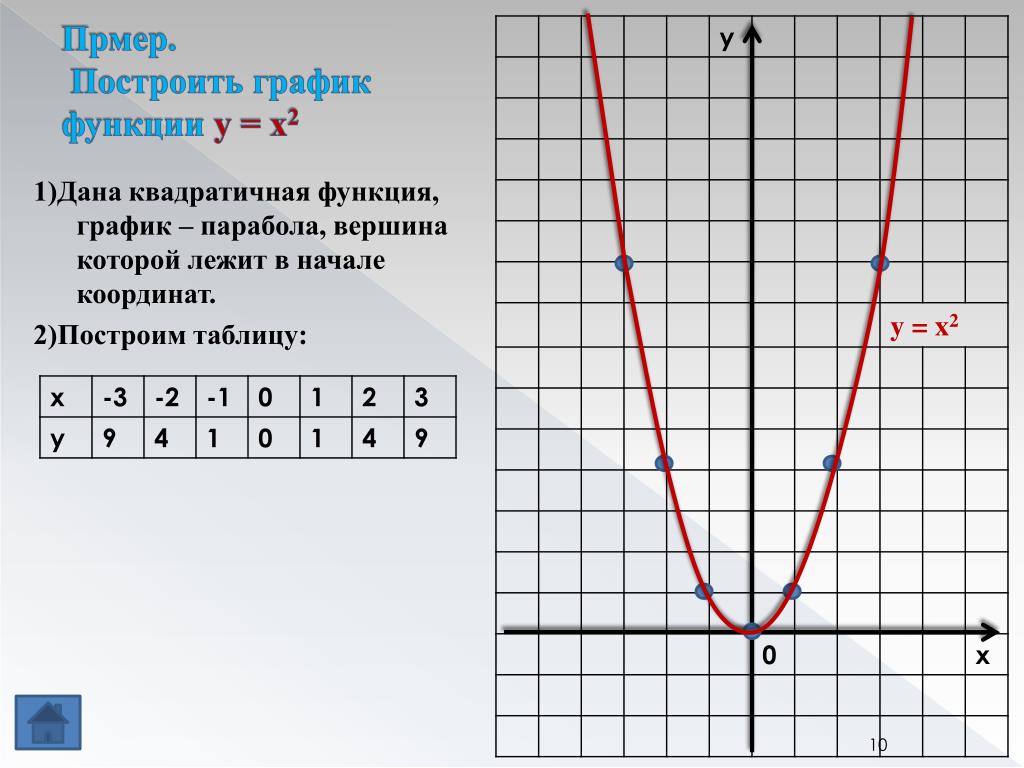
Пример 1
Теперь нарисуем график f(x) = x 2 + 1 и сравните это с g(x) = x 2 .
| х | ф(х) = х 2 + 1 | |
| -2 | (-2) 2 + 1 = 5 | |
| -1 | (-1) 2 + 1 = 2 | |
| 0 | 0 + 1 = 1 | |
| 1 | 1 2 + 1 = 2 | |
| 2 | 2 2 + 1 = 5 |
Значения функции (
значения y ) в таблице значений для f(x) = x 2 +1 все
на единицу больше соответствующих значений в таблице значений для g(x) = x 2 и график сместился по вертикали на 1 единицу.
Обратите внимание, что график f(x) = x 2 + 1 не пересекает ось х. Это говорит нам о том, что уравнение x 2 + 1 = 0 не имеет решения. Мы это уже знаем, поскольку квадрат числа никогда не отрицательно, поэтому x 2 никогда не может быть равно -1.
Пример 2
Нарисуйте график f(x) = x 2 − 1 и сравните его с g(x) = х 2 .
| х | ф(х) = х 2 — 1 | |
| -2 | (-2) 2 — 1 = 3 | |
| -1 | (-1) 2 — 1 = 0 | |
| 0 | 0 — 1 = -1 | |
| 1 | 1 2 — 1 = 0 | |
| 2 | 2 2 — 1 = 3 |
Теперь значения функции в
таблица f(x) на единицу ниже, чем соответствующие значения в таблице для
g(x) = x 2 и график
сместился на одну единицу.
Обратите внимание, что в этом примере график f(x) = x 2 − 1 пересекает ось x в двух местах.
Это означает, что уравнение х 2 − 1 = 0 имеет два решения,
х 2 — 1 = 0
х 2 = 1
х = 1
, которые равны x = −1 и x = 1.
Пример 3
Нарисуйте график f(x) = (x + 1) 2 ( или f(x) = х 2 + 2х + 1) и сравните к основной параболе g(x) = x 2 .
| х | ф(х) = (х+1) 2 | |
| -3 | (-3 + 1) 2 = 4 | |
| -2 | (-2 + 1) 2 = 1 | |
| -1 | (-1 + 1) 2 = 0 | |
| 0 | (0 + 1) 2 = 1 | |
| 1 | (1 + 1) 2 = 4 |
Здесь мы добавили 1 к x
и мы видим, что функция
значения в таблице значений переместились на одну строку вверх по сравнению с базовым
функция.
График функции f(x) представляет собой то же самое, если мы переместим график g(x) = x 2 на одну единицу Слева.
Мы говорим, что базовый граф был переведен на -1 единиц по горизонтали. Ось симметрии теперь x = −1.
Пример 4
Нарисуй график f(x) = (x − 2) 2 − 1 (или f(x) = x 2 − 4x + 3) и сравните его с базовым графом g(x) = x 2 .
Если мы используем тот же метод, что и в предыдущем Например, мы можем предположить, что график сместился на две единицы вправо и на одну единица вниз. Теперь проверим это, составив таблицу значения, начиная с x = 0 и рисование графика.
| х | ф(х) = (х — 2) 2 — 1 | |
| 0 | (0–2) 2 — 1= 3 | |
| 1 | (1 — 2) 2 — 1= 0 | |
| 2 | (2 — 2) 2 — 1 = -1 | |
| 3 | (3 — 2) 2 — 1 = 0 | |
| 4 | (4 — 2) 2 — 1 = 3 |
Обратите внимание, что ось симметрии теперь x = 2.
Мы можем найти, где график проходит по оси Y без рисования графика. Мы делаем это, вычисляя f(0) = 3 или путем умножения скобок и видя, что постоянный член (термин без x) равен 3.
f(x) = (x − 2) 2 − 1 = x 2 — 4х + 4 — 1 = х 2 − 4x + 3 или
f(0) = (x − 2) 2 − 1 = 4 − 1 = 3
Пример 5
Найдите, где график f(x) = (x − 2) 2 − 1 пересекает ось x. Положим y = f(x) = 0 и решим уравнение для х.
| (х — 2) 2 − 1 = 0 | Первый переместите -1 на знак равенства. |
| (х — 2) 2 = 1 | Далее, возьми квадратный корень из обеих частей уравнения. Запомните + и −. |
| х — 2 = 1 = 1 | Наконец
переместите 2 на другую сторону и упростите результат. |
| х = 2 1 |
Точки пересечения х = 2 −1 = 1 и х = 2 + 1 = 3.
Легко видеть, что запись функции в виде f(x) = (x − 2) 2 − 1 дает нам много информации.
Это говорит нам, как переводится базовый график вертикально и горизонтально.
Это также говорит нам, где находится ось симметрии.
Наконец, мы можем легко найти точки пересечение с осями x и y.
Общий вид уравнения, записанного в этом способ:
f(x) = a(x + r) 2 + s
а — коэффициент x 2 как мы уже видели.
ось симметрии имеет уравнение x = −r (или, можно сказать, имеет такое же значение как r, но с обратным знаком).
В связи с этим важно знать, как переписать функцию
ф(х) = топор 2 + bx + c в виде f(x) = a(x + r) 2 + s
Пример 6
Теперь давайте посмотрим, как мы можем изменить секунду
степень функции от одной формы к другой.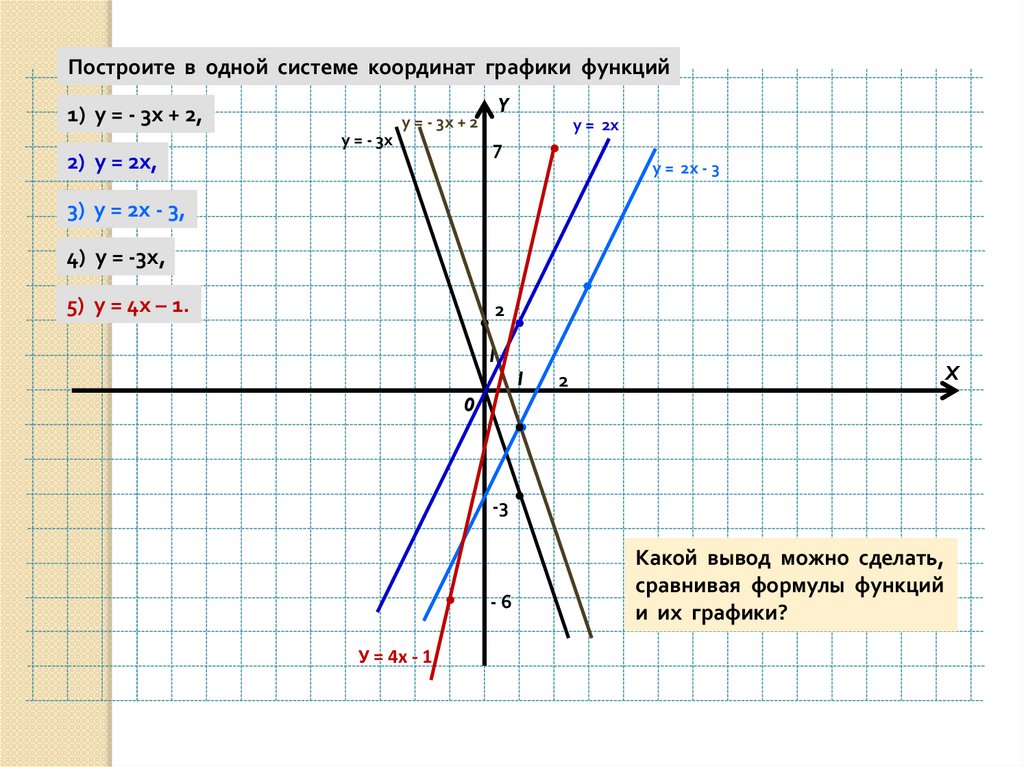
Перепишем f(x) = x 2 − 4x + 3 в виде f(x) = (x − 2) 2 − 1.
По сравнению с общей формой:
f(x) = ах 2 + бх + с
f(x) = x 2 − 4x + 3
Вот = 1
огб = -4
и c = 3 (поэтому график пересекает ось y в 3).
Посмотрите на правило возведения скобки в квадрат:
(x q) 2 = p 2 2xq + q 2 .
Мы видим, что коэффициент x составляет 2 кв.
В нашем примере коэффициент x равен −4, что означает 2q = − 4 и, следовательно, д = -2.
Если мы посчитаем (х − 2) 2 получаем х 2 − 4x + 4.
(х − 2) 2 = х 2 − 4x + 4.
Если вычесть 1 с обеих сторон мы получаем :
(х — 2) 2 -1 = х 2 — 4х + 4-1 = х 2 — 4х + 3
Подведение итогов метода:
| f(x) = x 2 − 4x + 3 | Половина
коэффициент x равен −4 / 2 = −2, что мы возводим в квадрат (4 ) и
добавить в уравнение.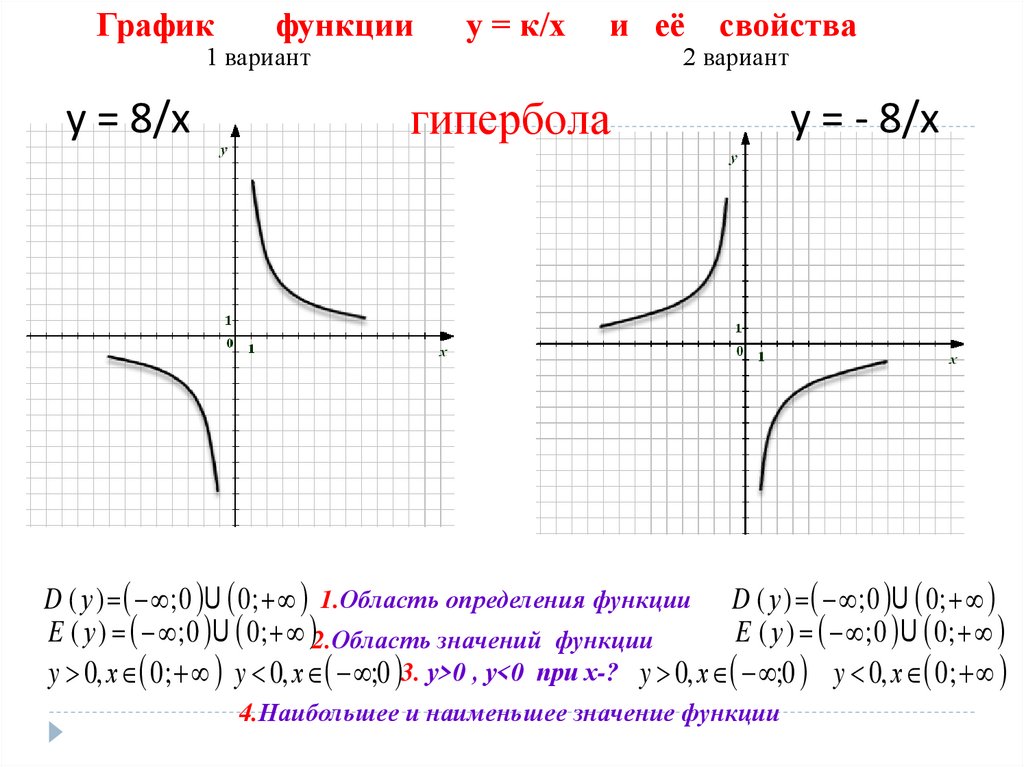 |
| = (x 2 − 4x + 2 2 ) − 2 2 + 3 | |
| = (x − 2) 2 − 4 + 3 | Если мы
добавить 4 к уравнению, мы также должны вычесть 4, так что уравнение
остается без изменений Теперь упростим -4+3 = -1 |
| = (x − 2) 2 − 1 |
Из вышеприведенного примера можно сделать вывод, что график полинома второй степени, где a = 1 (f(x) = x 2 + bx + c) имеет ось симметрии в:
x = −b / 2 и разрезает y ось, где y = c.
Пример 7
Найдите ось симметрии графика f(x) = 2x 2 − 12x + 10.
В этом случае a = 2 , поэтому правило из предыдущего примера не применяется. Ни один
так же легко переписать функцию, как и раньше.
Вместо этого мы переводим функцию вниз на 10 единиц, вычитая 10 из уравнения. Перемещение графика по вертикали не изменить положение оси симметрии.
Мы называем эту новую функцию g(x) и находим, где g(x) пересекает ось x.
2x 2 − 12x = 0
2х(х — 6) = 0
Это уравнение имеет решения x = 0 и 6, поэтому график g(x) пересекает ось x в 0 и 6. Ось симметрии должна быть посередине этих двух точек, т.е. находится в х = 3 .
Пример 8
Перепишите функцию f(x) = 2x 2 − 12x + 10 в виде
f(x) = a(x + r) 2 + с.
| f(x) = 2x 2 − 12x + 10 | Дубль 2
за скобками. Половина коэффициента x
равно −6 / 2 = −3, поэтому в скобках прибавь 3 2 .
Мы действительно добавили 18, так что теперь нам нужно вычесть 23 2 = 18 вне скобок. |
| = 2(x 2 − 6x + 3 2 ) − 2 3 2 + 10 | |
| = 2(x 2 − 6x + 9) − 18 + 10 | |
| = 2 (х — 3) 2 − 8 |
Теперь мы видим, как и прежде, что ось симметрии находится в х = 3,
Коэффициенты x В приведенном выше примере (f(x) = 2x 2 − 12x + 10) a = 2, b = −12 и c = 10. Чтобы найти ось симметрии, мы вынесли множитель 2 за скобки. Это соответствует делению на 2. Тогда мы дополнил квадрат делением коэффициента при x (−6) на 2,
Общая формула для оси симметрии
функция
f(x) = ax 2 + бх + с есть
поэтому:
Пример 9
Найдите вершину параболы f(x) = 2x 2 − 12x + 10.
Вершина (где парабола поворачивается) лежит
на оси симметрии, поэтому мы знаем x-значение вершины (3).
Мы нашли значение y путем вычисления f (3).
f(3) = 23 2 − 123 + 10 = 18 − 36 + 10 = −8.
Вершина параболы (3, −8).
Примечание. Если a>0, вершина является точкой минимума. Если a<0 вершина является точкой максимума. 92-2x-1 график квадратичной функции. обозначьте вершину и ось полутри.
Вы можете разместить это решение на ВАШЕМ сайте!
Содержание:
Шаг 1: Нахождение вершины
Шаг 2: Нахождение двух точек слева от оси симметрии
Шаг 3: Отражение двух точек для получения точек справа от оси симметрии
Шаг 4: Нанесение точек на график (с таблицей)
Шаг 5: График параболы
Чтобы построить график, мы можем выполнить следующие шаги:
Шаг 1) Найдите вершину (вершина — это либо самая высокая, либо самая низкая точка на графике). Также вершина находится на оси симметрии параболы (т.е. делит ее пополам).
Шаг 2) Получив вершину, найдите две точки слева от оси симметрии (линия, которая вертикально проходит через вершину).
Шаг 3) Отразите эти две точки относительно оси симметрии, чтобы получить еще две точки справа от оси симметрии.
Шаг 4) Нанесите на график все найденные точки (включая вершину).
Шаг 5) Проведите кривую через все точки, чтобы построить параболу.
Давайте подробно рассмотрим эти шаги
Перейти к началу страницы
Шаг 1)
Нахождение вершины:
Чтобы найти вершину, нам сначала нужно найти x-координату вершины.
Чтобы найти x-координату вершины, используйте эту формулу: .
Начните с данной формулы.
Из , мы можем видеть, что , и .
Подключить и .
Отрицайте, чтобы получить .
Умножьте 2 и получите .
Разделить.
Таким образом, x-координата вершины равна . Примечание: это означает, что ось симметрии также .
Теперь, когда мы знаем координату x вершины, мы можем использовать ее, чтобы найти координату y вершины.
Начните с данного уравнения.
Подключить .
Квадрат для получения.
Умножь и получи .
Умножь и получи .
Объедините похожие термины.
Итак, координата y вершины равна .
Итак, вершина .
———————————————— ———————
Перейти к началу страницы
Шаг 2)
Найдите две точки слева от оси симметрии:
Найдем значение y, когда
Начните с данного уравнения.
Подключить .
Квадрат для получения.
Умножь и получи .
Умножь и получи .
Объедините похожие термины.
Итак, первая точка слева от оси симметрии равна (-1,2)
———————
Давайте найдем значение y, когда
Начните с данного уравнения.
Подключить .
Квадрат для получения.
Умножь и получи .
Умножь и получи .
Объедините похожие термины.
Итак, вторая точка слева от оси симметрии равна (0,-1)
———————————————— ———————
Перейти к началу страницы
Шаг 3)
Отражение двух точек относительно оси симметрии:
Теперь помните, что парабола симметрична относительно оси симметрии (которая равна )
Это означает, что значение y для (которое составляет одну единицу от оси симметрии) равно значению y (которое также составляет одну единицу от оси симметрии).


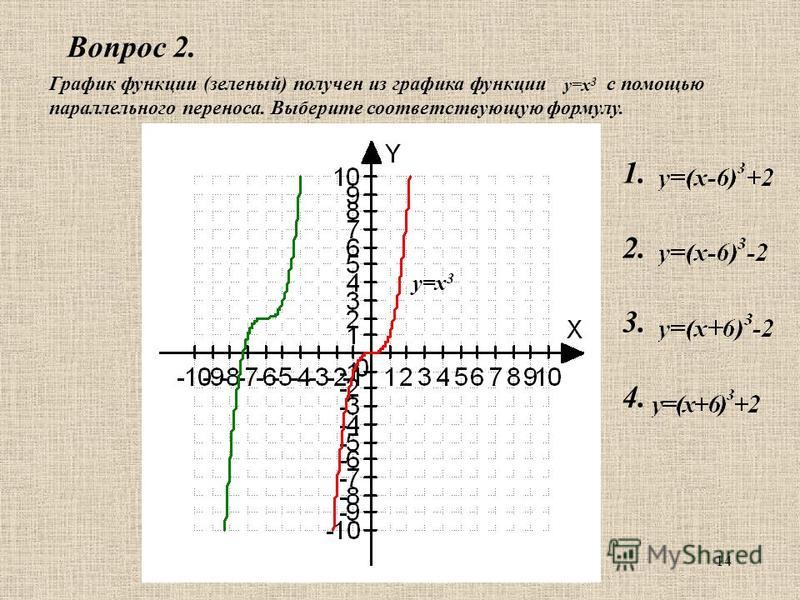
 Найдите с помощью графика :
a)Значение y при x = -1,5;
б) Значение х при которых у=3;
в) Нули функции;промежутки в которых у>0 и в которых у
Найдите с помощью графика :
a)Значение y при x = -1,5;
б) Значение х при которых у=3;
в) Нули функции;промежутки в которых у>0 и в которых у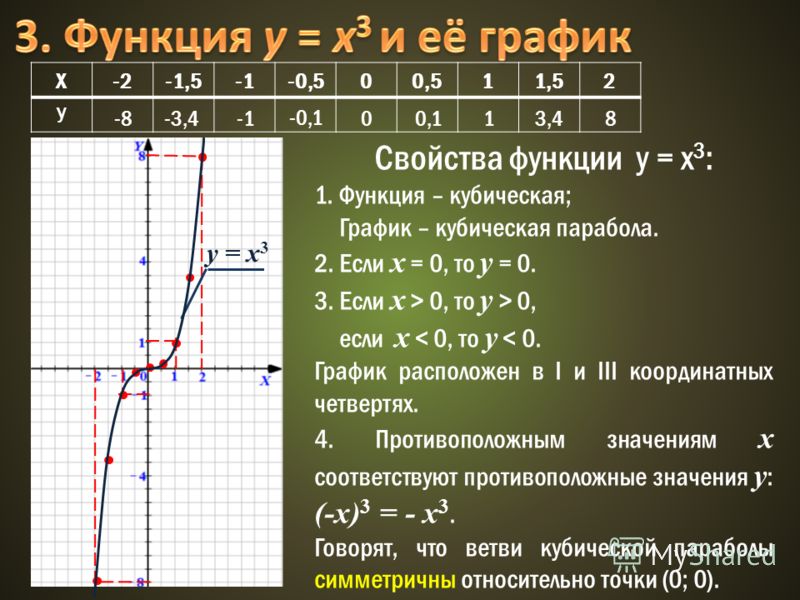 10.17
10.17