Симплекс метод что такое: Симплекс-метод онлайн

Линейное программирование. Симплекс-метод | Решатель

Рассмотрим симплекс-метод для решения задач линейного программирования (ЛП). Он основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает.
 

Алгоритм симплекс-метода следующий:
 

1. Исходную задачу переводим в канонический вид путем введения дополнительных переменных. Для неравенства вида ≤ дополнительные переменные вводят со знаком (+), если же вида ≥ то со знаком (—). В целевую функцию дополнительные переменные вводят с соответствующими знаками с коэффициентом, равным 0, т.к. целевая функция не должна при этом менять свой экономический смысл.
2. Выписываются вектора P_i из коэффициентов при переменных и столбца свободных членов. Этим действием определяется количество единичных векторов. Правило – единичных векторов должно быть столько, сколько неравенств в системе ограничений.
3. После этого исходные данные вводятся в симплекс-таблицу. В базис вносятся единичные вектора, и исключая их из базиса, находят оптимальное решение. Коэффициенты целевой функции записывают с противоположным знаком.
4. Признак оптимальности для задачи ЛП – решение оптимально, если в f – строке все коэффициенты положительны. Правило нахождения разрешающего столбца – просматривается f – строка и среди ее отрицательных элементов выбирается наименьшее. Вектор P_i его содержащий становится разрешающим. Правило выбора разрешающего элемента – составляются отношения положительных элементов разрешающего столбца к элементам вектора Р₀ и то число, которое дает наименьшее отношение становится разрешающим элементом, относительно которого будет произведен пересчет симплекс-таблицы. Строка, содержащая этот элемент называется разрешающей строкой.
   Если в разрешающем столбце нет положительных элементов, то задача не имеет решения. После определения разрешающего элемента переходят к пересчету новой симплекс – таблицы.
5. Правила заполнения новой симплекс – таблицы. На месте разрешающего элемента проставляют единицу, а другие элементы полагают равными 0. Разрешающий вектор вносят в базис, из которого исключают соответствующий нулевой вектор, а остальные базисные вектора записывают без изменений. Элементы разрешающей строки делят на разрешающий элемент, а остальные элементы пересчитывают по правилу прямоугольников.
6. Так поступают до тех пор, пока в f – строке все элементы не станут положительными.

 

Рассмотрим решение задачи с использованием рассмотренного выше алгоритма.
Дано:

Приводим задачу к каноническому виду:

Составляем вектора:

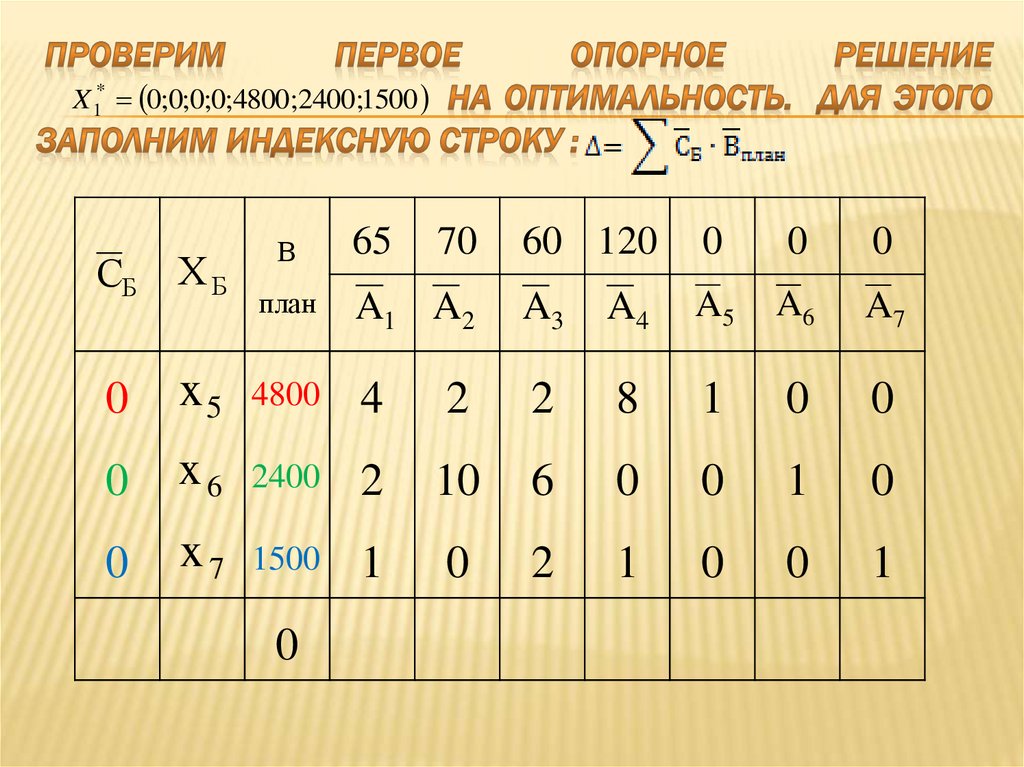
Заполняем симплекс – таблицу:

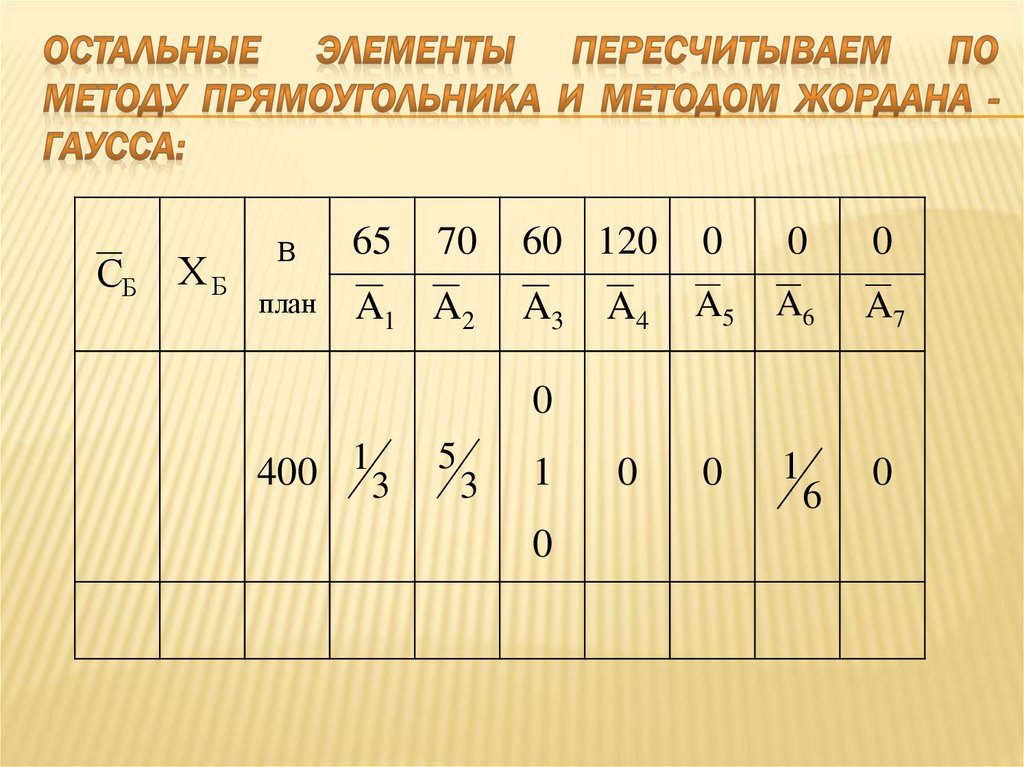
Правило прямоугольников:
Пересчитаем первый элемент вектора Р₀, для чего составляем прямоугольник из чисел: и получаем: .

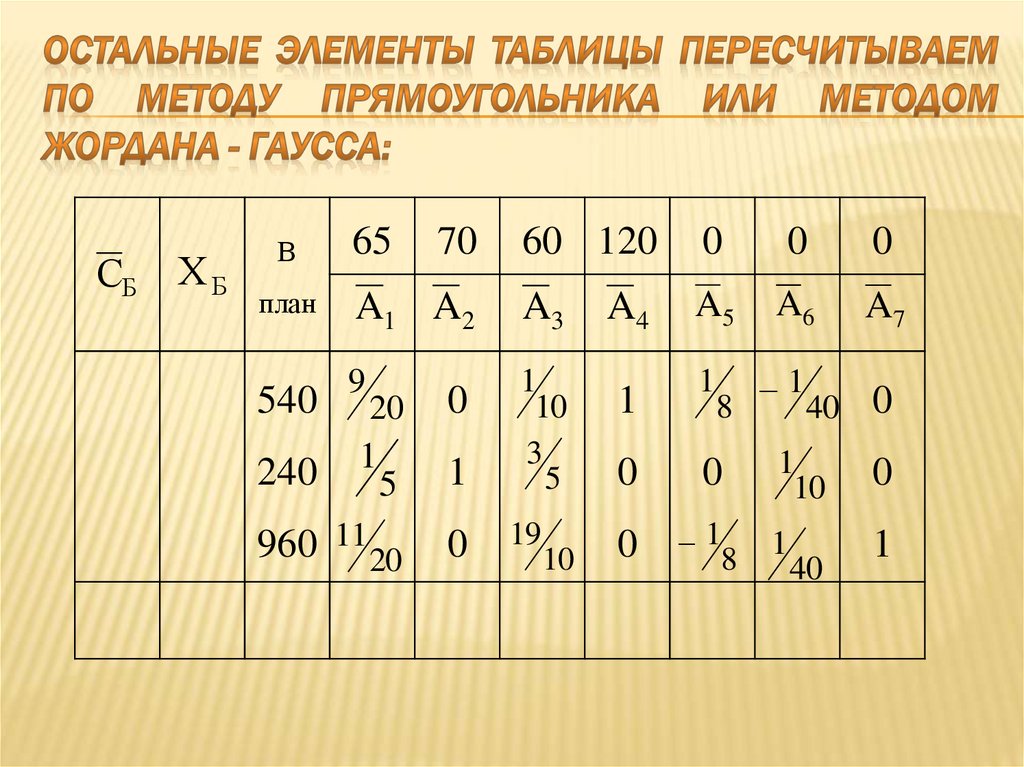
Аналогичные расчеты выполним для всех остальных элементов симплекс – таблицы:

В полученном плане f – строка содержит один отрицательный элемент – (-5/3), вектора P₁. Он содержит в своем столбце единственный положительный элемент, который и будет разрешающим элементом. Сделаем пересчет таблицы относительно этого элемента:

Отсутствие отрицательных элементов в f – строке означает, что найден оптимальный план:
F* = 36/5, Х = (12/5, 14/5, 8, 0, 0).
 

Рекомендуемая литература

• Ашманов С. А. Линейное программирование, М: Наука, 1998г.,
• Вентцель Е.С. Исследование операций, М: Советское радио, 2001г.,
• Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическое программирование, М: Высшая школа, 1986г.

 
 

Решение линейного программирования на заказ

Заказать любые задания по этой дисциплине можно у нас на сайте. Прикрепить файлы и указать сроки можно на странице заказа.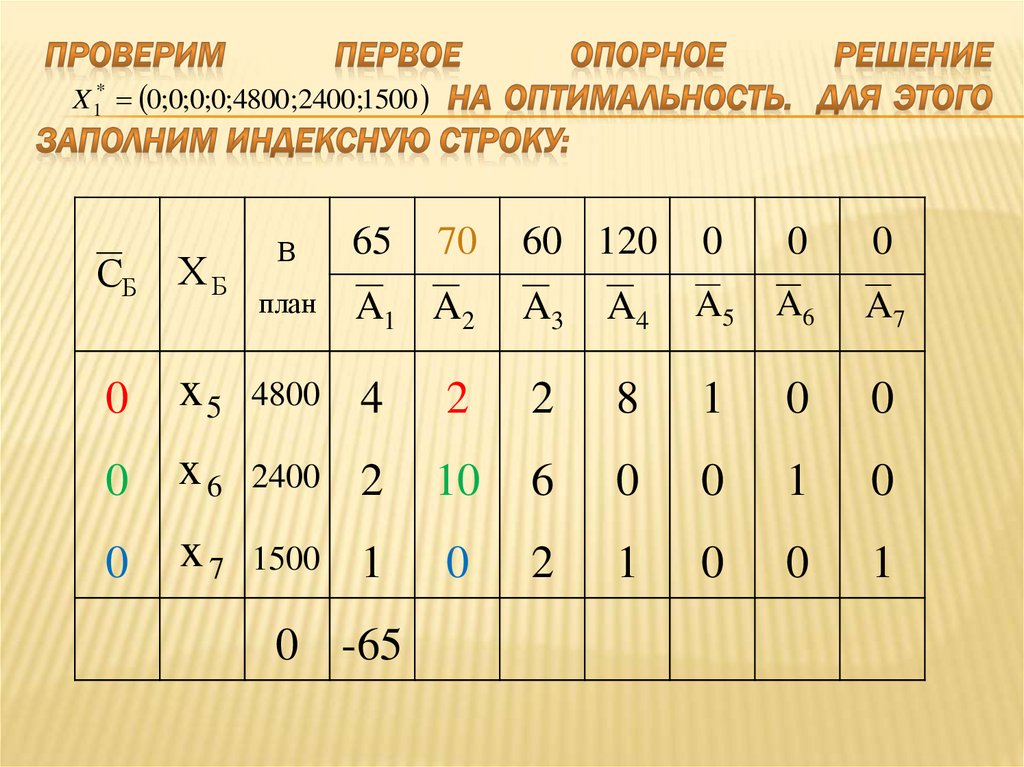

НОУ ИНТУИТ | Лекция | Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность

< Лекция 13 || Лекция 6: 123

Аннотация: В данной лекции широко рассматривается такой метод решения двойственной задачи линейного программирования, как двойственный симплекс – метод. Также рассматриваются его основные свойства и характеристики, проводится сравнительный анализ с обычным симплекс – методом. Кроме того, проводится исследование моделей задач на чувствительность с использованием экономической интерпретации обычной задачи линейного программирования.

Ключевые слова: симплекс-метод, двойственный симплекс-метод, оптимальный план, двойственная задача, сопряженный базис, базисное решение, псевдоплан прямой задачи, оптимальное решение прямой задачи, метод полного исключения, разложение вектора, симплекс-таблица, симплекс, метод искусственных переменных, оптимальные значения двойственных переменных, базисными векторами

1.

Двойственный симплекс – метод

Использование идей двойственности в сочетании с общей идеей симплекс-метода позволило разработать еще один метод решения задач ЛП — двойственный симплекс-метод. Впервые этот метод был предложен Лемке в 1954г. Решение задачи ЛП двойственным симплекс-методом сводится к отысканию оптимального плана прямой задачи последовательным переходом от одного базиса к другому.

Задача ЛП в канонической форме имеет вид:

( 1.1)

при условиях

( 1. 2)

или .

Предположим, что и ранг матрицы А равен m.

Двойственная задача к задаче (1.1), (1.2) записывается так:

( 1.3)

при условиях

( 1.4)

Назовем сопряженным базисом, или базисом двойственной задачи такую систему из m линейно-независимых векторов матрицы ограничений прямой задачи , для которой базисное решение y соответствующей системы линейных уравнений вида

( 1. 5)

удовлетворяет всем ограничением (1.4).

Разложим вектор b по сопряженному базису

( 1.6)

Решив систему (1.6), получим некоторое ее базисное решение , которое называется псевдопланом прямой задачи, так как для него может выполняться условие неотрицательности переменных x_i0.

Таким образом, псевдоплан прямой задачи есть базисное решение относительно сопряженного базиса.

Как известно, оценки для небазисных векторов определяется в соответствии с

( 1. 7)

Псевдоплан можно найти и независимо от двойственной задачи. Пусть — произвольная система линейно-независимых векторов прямой задачи.

Выразим все небазисные векторы {A_j} через базисные:

( 1.8)

( 1.9)

Обозначим решение (1.9) через х₀. Тогда можно дать дополнительное определение псевдоплана: n —

мерный вектор X, для которого x_i = x_i0при , и x_j=0 при , является псевдопланом тогда и только тогда, когда все .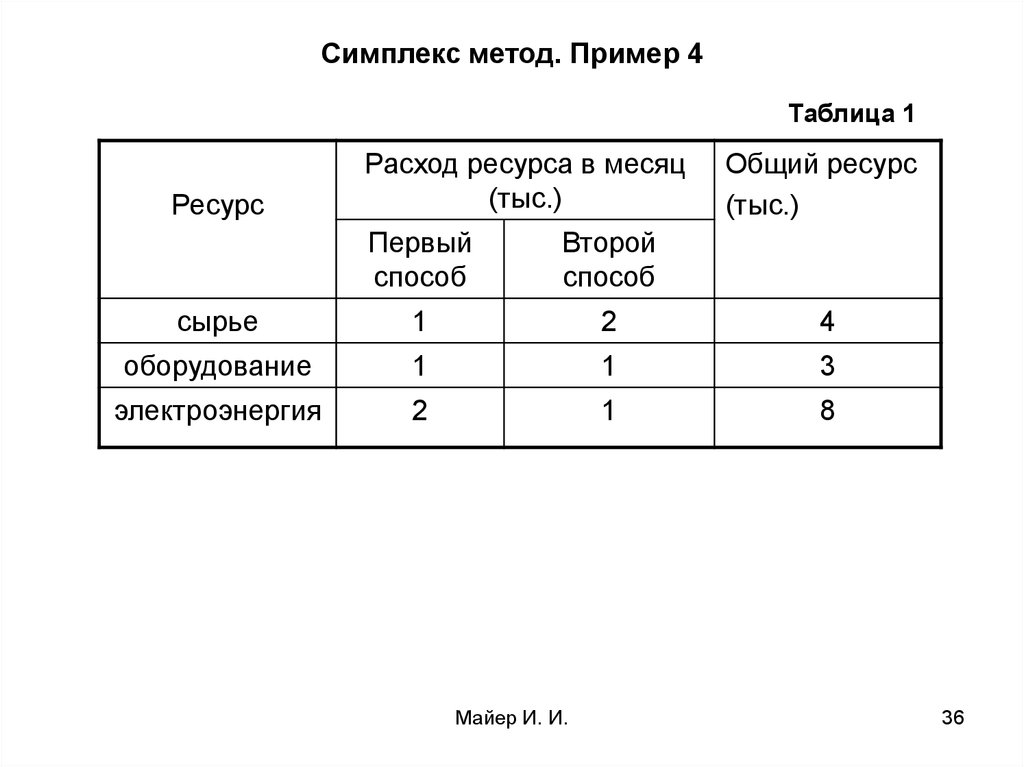

Доказательство. Векторы , линейно независимы.

Поэтому можно вычислить такой y={y₁,y₂,…,y_m}, для которого

( 1.10)

Тогда

С учетом (1.4) получим

( 1.11)

что и требовалось доказать.

Рассмотрим некоторый сопряженный базис и соответствующий ему псевдоплан.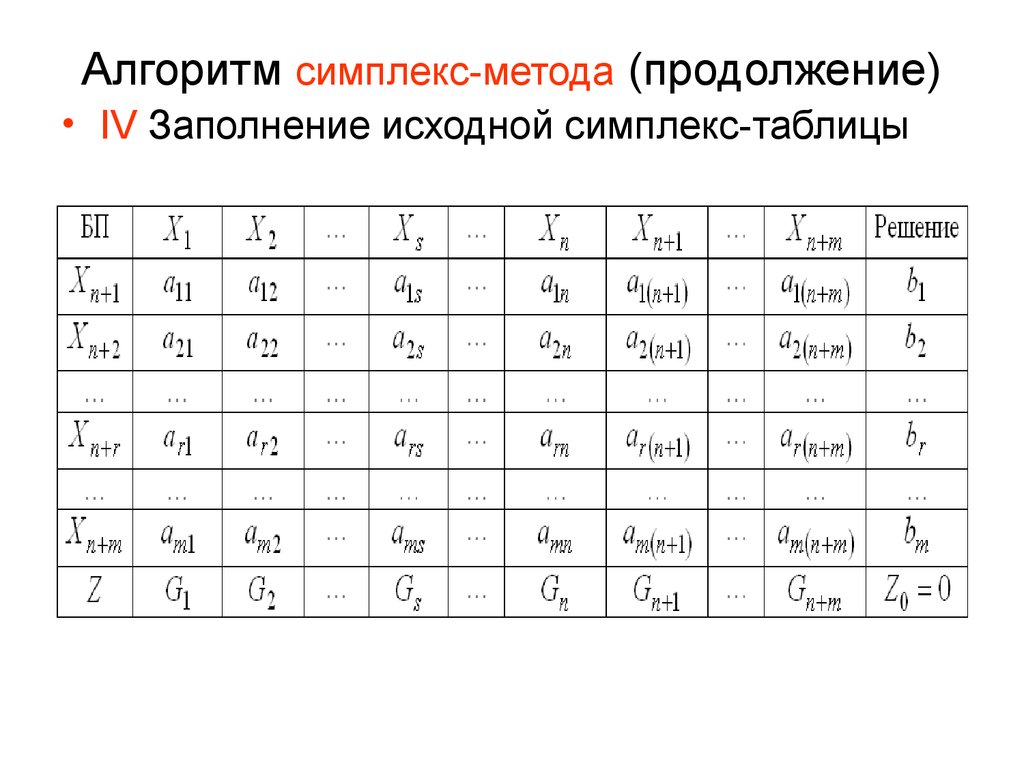

Справедлив следующий признак оптимальности: если среди базисных компонентов псевдоплана Х нет отрицательных, то псевдоплан Х={x_i0} оказывается оптимальным решением прямой задачи.

Доказательство. Имеет место такая цепочка равенств:

Равенство (1) следует из (1.2), равенство (2) получено переменой порядка суммирования, равенство (3) следует из (1.10).

Так как

( 1.12)

то

( 1. 13)

Таким образом, , что и является признаком оптимальности планов х и у, если .

Этот признак является необходимым и достаточным условием оптимальности в случае невыродженности базисного решения y двойственной задачи .

Пусть известен некоторый сопряженный базис , которому соответствует псевдоплан х. Очевидно, . При этом в зависимости от знаков {x_i} и {x_ij} может иметь место один из трех случаев:

1. базисные компоненты для всех ;
2. среди х_i имеются отрицательные, причем для некоторого i: х_i0<0, а все ;
3. псевдоплан содержит отрицательные компоненты х_i0<0, но для каждой из них среди элементов {х_ij}, j=1,. ..,n, имеются отрицательные. В первом случае, как следует из достаточного признака оптимальности, псевдоплан х — оптимальное решение. Во втором случае задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному базису и, следовательно, к новому псевдоплану с меньшим значением L.

Дальше >>

< Лекция 13 || Лекция 6: 123

Теория симплекс-метода

Теория симплекс-метода

 

Симплекс-метод — итерационная процедура, позволяющая улучшать решение на каждом шаге. Эта процедура завершается, когда невозможно улучшить решение.

Начиная со случайного значения вершины целевой функции, Симплекс-метод пытается повторно найти другое значение вершины, которое улучшает предыдущее. Поиск осуществляется по стороне многоугольника (или по ребрам многогранника, если количество переменных больше). Поскольку количество вершин (и ребер) конечно, всегда можно будет найти результат. (См. Графический метод)

Симплекс-метод основан на следующем свойстве: если целевая функция F не принимает максимальное значение в вершине A, то существует ребро, начинающееся в A, вдоль которого значение функции растет.

Обратите внимание, что симплекс-метод работает только с неравенством типа «≤» и независимыми коэффициентами, большими или равными нулю, и вам придется стандартизировать ограничения для алгоритма. В случае, если после этой процедуры появляются (или не изменяются) ограничения типа «≥» o «=», следует попробовать другие способы, лучшим выбором является двухфазный симплексный метод.

 

Подготовка модели к адаптации к симплекс-методу

Стандартный вариант модели:

Целевая функция:	c1·x1 + c2·x2 + … + cn·xn
Тема:	a11·x1 + a12·x2 + … + a1n·xn = b1 a21·x1 + a22·x2 + … + a2n·xn = b2 … am1·x1 + am2·x2 + . .. + amn·xn = bm x1,…, xn ≥ 0

Для этого необходимо соблюдать следующие правила:

1. Цель должна состоять в максимизации или минимизации функции.
2. Все ограничения должны быть одинаковыми.
3. Все переменные не являются отрицательными.
4. Независимые термины не являются отрицательными.

Изменение типа оптимизации.

Если мы хотим минимизировать нашу модель, мы можем ее сохранить, но мы должны учитывать новые критерии для условия остановки (остановить итерации, когда все коэффициенты в строке целевой функции значения меньше или равны нулю) и условие выхода строка. Чтобы не менять критерии, мы можем преобразовать целевую функцию минимизации F в целевую функцию максимизации F·(-1).

Преимущества: нам не придется беспокоиться о критериях остановки или условиях выхода строк, поскольку они продолжаются.

Неудобства: В случае если у функции все основные переменные положительны, а далее ограничения неравенства «≤», при замене они становятся отрицательными и в строке значения целевой функции остаются знаки плюс, то Симплексный метод подчиняется условию остановки, и оптимальное значение, которое будет получено, равно 0 по умолчанию.

Решение: На самом деле такой задачи не существует, так как для того, чтобы решение было больше 0, любое ограничение должно иметь условие «≥», и тогда мы перешли бы к модели двухфазного симплексного метода.

 

Преобразование знака независимого члена (константы справа от ограничений)

Придется расположить нашу модель так, чтобы независимые члены ограничений были больше или равны 0, иначе симплекс-метод использовать нельзя. Единственное, что необходимо сделать, это умножить на «-1» ограничения, где независимые члены меньше 0.

Преимущества: С помощью этой простой модификации знаков в ограничении мы можем использовать симплекс-метод.

Неудобства: Это может сработать в ограничениях, где мы должны изменить знаки констант, знаки неравенств будут («=», «≤»), став («=»,»≥»), что в любом случае мы будем должны разработать двухфазный симплексный метод. Это неудобство неуправляемо, хотя оно могло бы принести нам пользу только в том случае, если члены неравенства существуют («≤», «≥»), а члены «≥» совпадают с ограничениями, где независимый член отрицателен.

 

Ограничения нормализации.

Если в нашей модели появляется неравенство типа «≥», то должны ли мы добавить новую переменную, называемую избыточной переменной si , с ограничением si ≥ 0. Новая переменная появляется с коэффициентом, равным нулю, в объективе функцию и вычитание в неравенствах.

Перед нами возникает задача, посмотрим, как решать неравенства, содержащие неравенство типа «≥» :

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 — 1·xs = b1

Поскольку все наши модели основаны на том, что все его переменные больше или равны нулю, когда мы делаем первую итерацию в симплексной модели, базовые переменные не будут базы, и они примут нулевое значение, а все остальные сохранят свои значения. В этом случае наша переменная xs после обнуления x1 и x2 примет значение — b1. Условие неотрицательности не будет выполняться, поэтому необходимо будет добавить новую переменную xr, которая появится в целевой функции с нулевым коэффициентом, и добавить в неравенство соответствующее ограничение. Осталось бы следующим образом:

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 — 1·xs + 1 ·xr = b1

Переменные такого типа называются искусственными переменными, и они появляются при наличии неравенств с неравенством ( «=»,»≥»). Это обязательно заставит нас выполнить метод двухфазного симплекса, который будет объяснен позже.

Сам режим, если неравенство имеет тип «≤», нам придется добавить новую переменную, называемую резервной переменной si, с ограничением si «≥» 0. Новая переменная появляется с нулевым коэффициентом в целевой функции, а суммирование в неравенствах.

Подводя итоги, мы можем позволить этой доске, согласно появившемуся неравенству, и со значением, с которым должны быть новые переменные.

Тип неравенства	Тип переменной
≥	— избыточный + искусственный
=	+ искусственный
≤	+ провисание

 

Запуск симплекс-метода

После стандартизации нашей модели может произойти переход к симплекс-методу или двухфазному симплекс-методу. Посмотрите сами на рисунке, как мы должны действовать, чтобы достичь решения нашей задачи.

 

 

Мы объясним каждый метод шаг за шагом, конкретизируя аспекты, которые необходимо учитывать.

Симплексный метод

— Построение первой доски: В первом столбце доски появится то, что мы будем называть базой, во втором — коэффициент, который каждая переменная, которая появляется в базе, имеет в целевой функции (мы будем называть этот столбец Cb), в третьем столбце независимый член каждого ограничения (P0), и из этого столбца будет появляться каждая переменная целевой функции (Pi). Чтобы иметь более наглядное представление о доске, мы добавим строку, в которую мы поместим каждое из названий столбцов. На этой доске мы добавим две новые строки: одну, которая будет вести доску, где появятся константы коэффициентов целевой функции, и еще одна, которая будет последней строкой, где будет принимать значение целевая функция. Наша итоговая доска будет иметь такие строки как ограничения.

 

Таблица
			С1	С2	…	Сп
Основание	Кб	Р0	Р1	Р2	…	Пн
Р1	Кб1	б1	а11	а12	…	и
Р2	Кб2	б2	а21	а22	…	а2н
. ..	…	…	…	…	…	…
Вечер	куб.м	бм	утра1	утра2	…	утра
З		З0	З1-С1	З2-С2	…	Цинк-Сn

Значения строки Z получаются так: Значение Z0 будет результатом подстановки Cim в целевую функцию (иначе ноль появляется в базе). Левые столбцы получаются путем вычитания из этого значения коэффициента, стоящего в первой строке доски.

При реализации симплекс-метода будет видно, что в базе, в этой первой таблице, будут переменные резерва.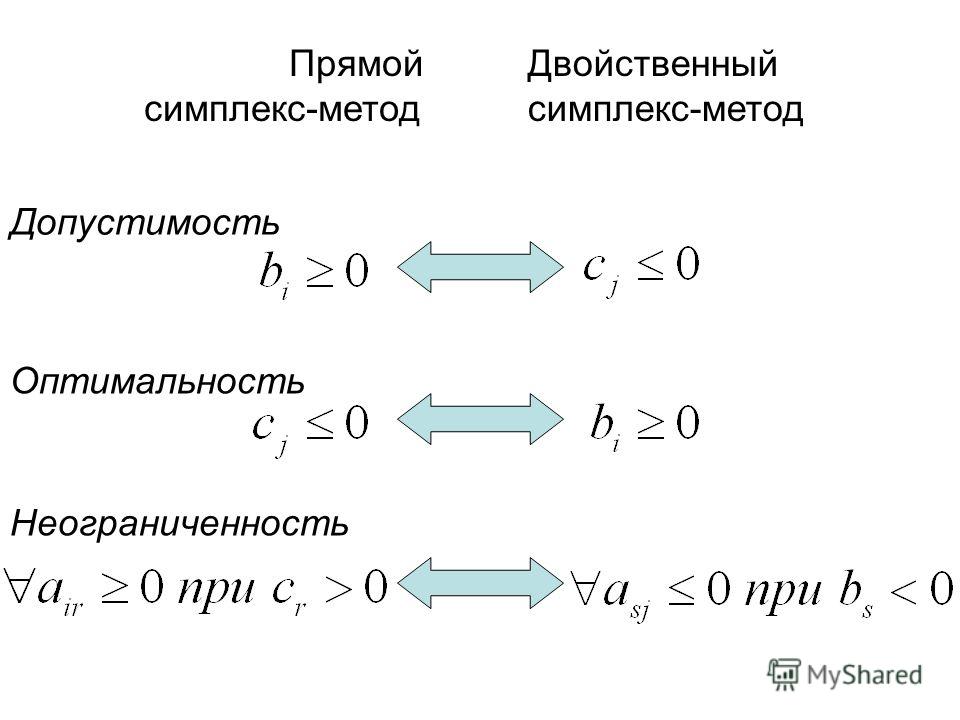

— Условие остановки: будет проверять, должны ли мы делать новую итерацию или не делать, чтобы было известно, появится ли в строке Z какое-либо отрицательное значение. Если это не так, значит, мы достигли оптимального решения задачи.

— Выбор входящей переменной: Если условие остановки не выполнено, мы должны выбрать одну переменную для входа в базу в следующей доске. Для него ищем строго отрицательные значения строки Z, а младшими будут те, которые дают нам входящую переменную.

— Выбор переменной, которая выскальзывает: как только мы получили входящую переменную, будет достигнута исходящая переменная, и нам больше нечего делать, кроме как выбрать ту строку, частное которой P0/Pj будет наименьшим среди строго положительных (учитывая, что только будет выполнено, когда Pj больше 0). Пересечение между входящим столбцом и исходящей строкой определит нам опорный элемент.

— Обновление доски: Соответствующие строки целевой функции и заголовки останутся в новой доске без изменений.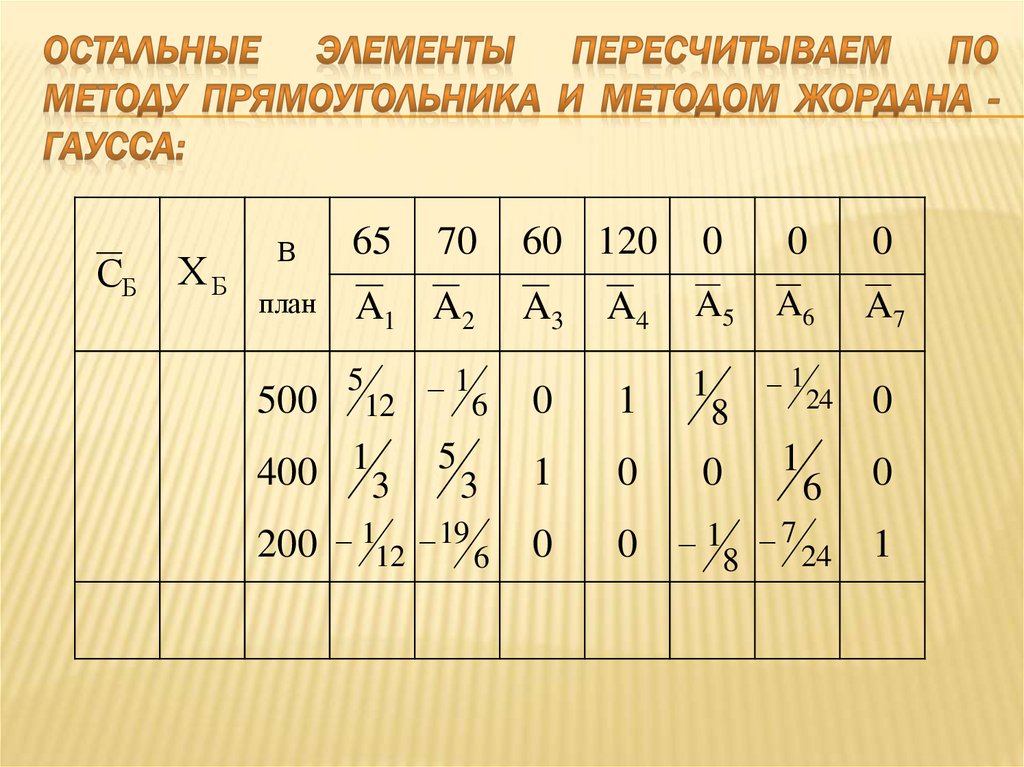 Левые строки будут рассчитываться двумя способами:

• Если мы пытаемся использовать сводную строку, каждый элемент будет получен из:

   

  Новый элемент сводной строки = фактически элемент сводной строки / сводная точка.

   

• Левые элементы строк будут достигнуты так:

   

  Новый элемент строки = Фактический элемент сводной строки — (Элемент сводной колонки из фактической строки * Новый элемент строки).
  

Двухфазный симплекс-метод

Этот метод отличается от симплекс-метода тем, что сначала необходимо решить вспомогательную задачу, которая должна минимизировать сумму искусственных переменных. Как только эта первая проблема решена и реорганизована окончательная плата, мы начинаем со второй фазы, которая состоит в создании обычного Симплекса.

1-я фаза

На этой первой фазе все можно сделать так же, как и в симплексном методе, за исключением построения первой доски, состояния остановки и подготовки доски, которая будет использоваться во второй фазе.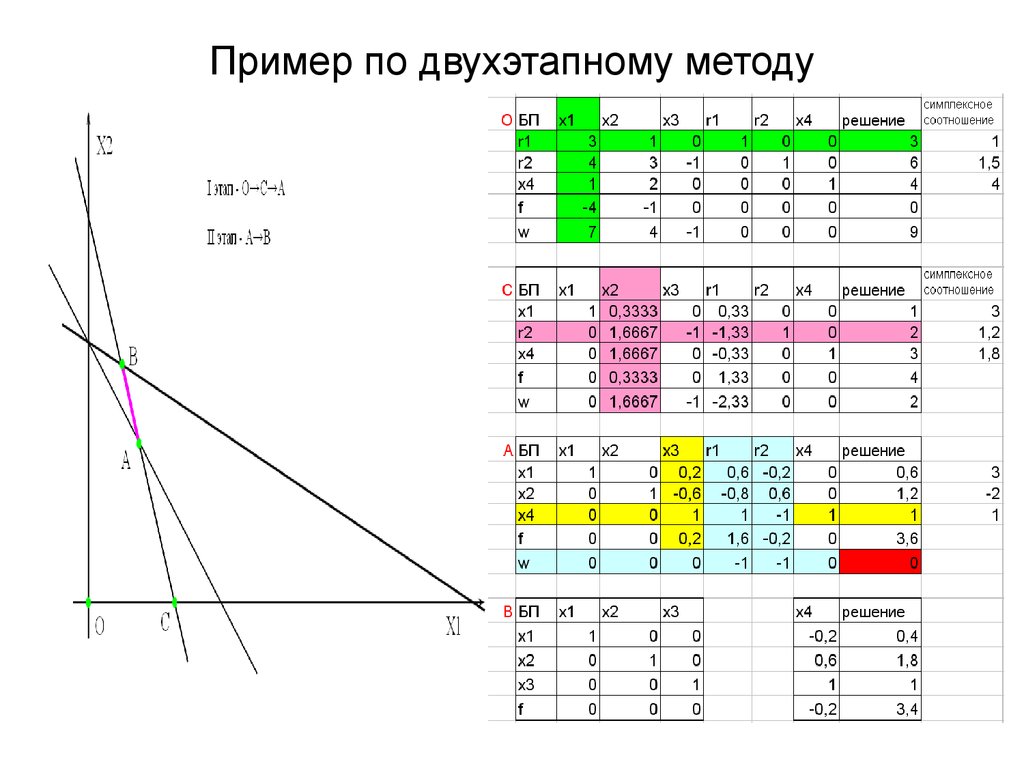

— Сборка первой доски: Мы работаем так же, как метод симплекса, но с некоторыми отличиями. Строка целевой функции отличается на первом этапе, потому что целевая функция изменяется, из-за этого будет появляться каждый член с нулевым значением, но это искусственные переменные, которые имеют значение «-1», потому что мы минимизируем сумму этих переменных. (помните, что минимизировать F — это то же самое, что максимизировать F·(-1)).

Другое отличие для этой первой доски состоит в способе вычисления строки Z. Его нужно будет вычислить следующим образом: Произведения Cb·Pj будут добавлены для всех строк, и к этой сумме мы должны вычесть значение, которое появляется (согласно столбцу, который мы делаем) в строке целевой функции.

 

Таблица
		С0	С1	С2	. ..	Сп-к	…	Сп
Основание	Кб	Р0	Р1	Р2	…	Пн-к	…	Пн
Р1	Кб1	б1	а11	а12	…	ан-к	…	и
Р2	Кб2	б2	а21	а22	…	а2н-к	…	а2н
. ..	…	…	…	…	…	…	…	…
Вечер	куб.м	бм	утра1	утра2	…	амн-к	…	утра
З		З0	Z1	Z2	…	Цинк-к	…	Цинк

Существование Zj = Σ(Cb·Pj) — Cj, где Cj = 0 для всех переменных решений, резервов и излишков и Cj = -1 для искусственных переменных.

 

— Условия остановки: Условия остановки такие же, как и в симплексном методе. Отличие заключается в том, что при достижении условия остановки может возникнуть два случая: функция принимает нулевое значение, что означает, что исходная задача имеет решение, или функция принимает другое значение, что говорит о том, что наша модель не имеет решения.

— Удаление столбцов с искусственными переменными: если мы пришли к выводу, что исходная задача имеет решение, мы должны подготовить нашу доску ко второму этапу. Столбцы искусственных переменных будут удалены, строка целевой функции будет изменена вместо исходной, а строка Z будет рассчитана так же, как и на первой доске 1-й фазы.

 

Обнаружение аномальных случаев и решений

Получение решения: При достижении условия остановки вы можете увидеть значения основных переменных, которые находятся в базе, и оптимальное значение, которое принимает функция, глядя на столбец P0. В случае минимизации это оптимальное значение нужно умножить на «-1».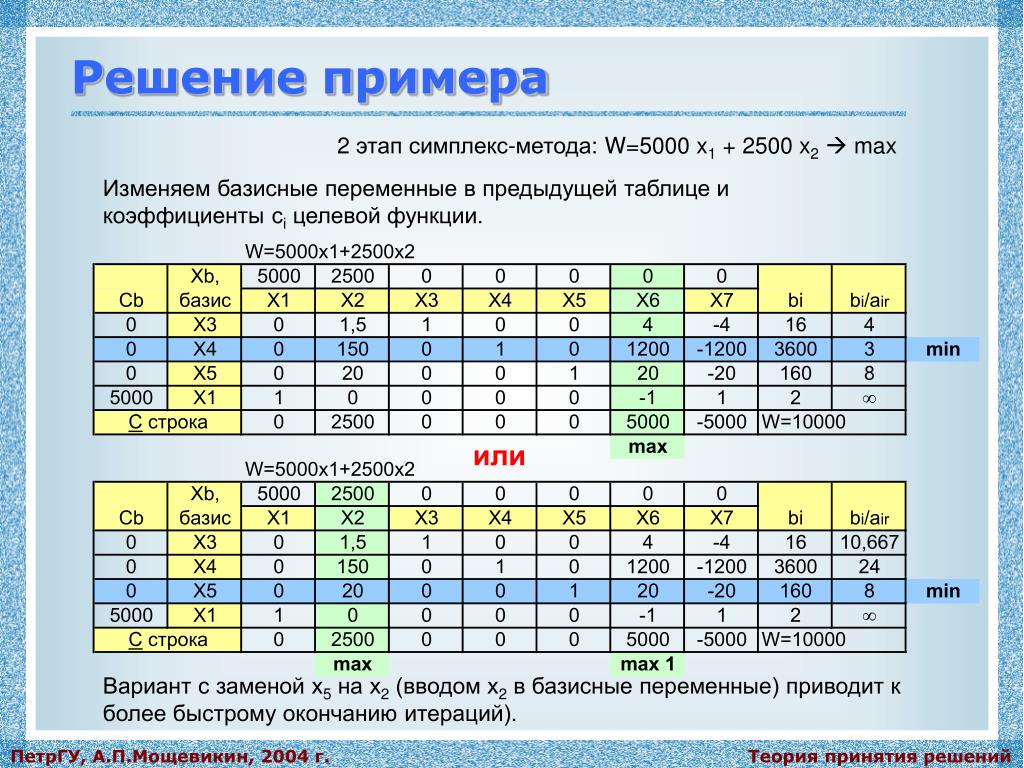

Бесконечные решения: если после выполнения условия остановки вы заметите, что какая-либо переменная, не фигурирующая в базе, имеет значение 0 в строке Z, это означает, что существуют другие решения, дающие такое же оптимальное значение для целевая функция. Это задача, которая допускает бесконечное число решений, все они находятся среди отрезка (или плоской части, или области пространства и т. д., в зависимости от числа переменных), который определяет Ax+By=Z0. Вы можете сделать больше итераций, используя в качестве входящей переменной любую переменную в строке Z, которая имеет нулевое значение, и у вас будут другие решения.

Неограниченное решение: при поиске исходящей переменной заметите ли вы, что каждая переменная в столбце входящей переменной имеет все элементы отрицательные или недействительные, это проблема, которая имеет неограниченное решение. Таким образом, оптимального конкретного значения не существует. Если значения переменных растут, то значение целевой функции также растет без нарушения каких-либо ограничений.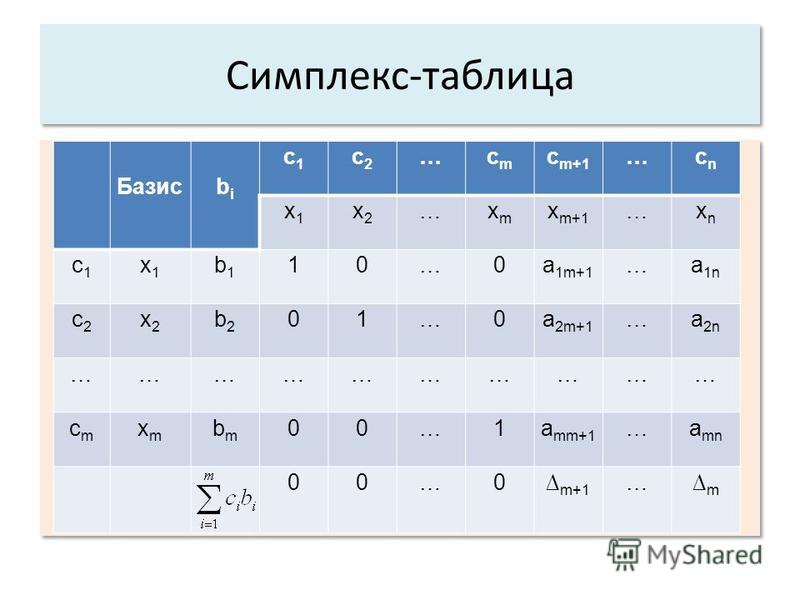

Решение не существует: В случае, если кажется, что решения нет, нам придется решить его с помощью метода двухфазного симплекса, поэтому в конце 1-й фазы мы узнаем, находимся ли мы в такой ситуации.

Привязка входящей переменной: Вы можете выбрать любую из них, если это не повлияет на окончательное решение, неудобство, которое это представляет, заключается в том, что в зависимости от этого выбора вам придется делать больше или меньше итераций. Рекомендуется выбирать в пользу основных переменных, так как это те, которые останутся в базе в конце метода.

Связь выходной переменной: Снова можно выбрать любую из них, хотя может возникнуть вырожденный случай и зацикливание циклов. Чтобы избежать их, насколько это возможно, у нас будет предубеждение в пользу того, что базовые переменные делают так, чтобы они оставались в базе. В случае, если речь идет о первой фазе (метода двухфазного симплекса), мы выберем в случае ничьей искусственные переменные.

Любопытство на 1-м этапе: Когда первый этап завершается, если исходная задача имеет решение, все искусственные переменные в строке Z должны иметь значение «1».

Может ли точка опоры быть 0?: Она не может быть 0, потому что частные должны быть больше 0.

Оптимизация — Почему этот алгоритм/метод называется «симплексным»?

$\begingroup$

Я пытался узнать больше об симплексном алгоритме/методе. В частности, Мне интересно узнать, почему этот алгоритм называется «симплексным алгоритмом».

Например, при чтении страницы Википедии (https://en.wikipedia.org/wiki/Simplex_algorithm): «Название алгоритма происходит от концепции симплекса и было предложено Т. С. Моцкиным. Симплексы на самом деле не используются в методе, но одна из его интерпретаций состоит в том, что он работает с симплициальными конусами, которые становятся правильными симплексами с дополнительным ограничением. Рассматриваемые симплициальные конусы представляют собой углы (т. геометрический объект, называемый многогранником. Форма этого многогранника определяется ограничениями, применяемыми к целевой функции».

Это немного сбивает меня с толку. Вот что я думаю, причина в следующем:

• «Симплекс» — это «многоугольник треугольной формы». Несколько «симплексов» можно комбинировать вместе для создания уникальных форм. Они называются «симплициальными комплексами».

• В задачах линейного программирования целевые функции и их ограничения образуют неправильную форму (т. е. комбинацию перекрывающихся плоскостей). Однако из-за линейного характера этих функций и ограничений результирующие формы будут иметь разные вершины.

• Таким образом, система целевых функций и ограничений из задачи линейного программирования образуют «симплициальный комплекс».

• В задачах линейного программирования нас интересует оптимизация целевых функций относительно некоторых ограничений, поскольку система уравнений и ограничение образуют «симплициальный комплекс», мы могли бы сказать, что нас интересует оптимизация симплициального комплекса.

• В результате алгоритм, используемый для оптимизации симплексного комплекса, называется «Алгоритм симплекса». Этот алгоритм (стратегически) «обходит» вершины симплициального комплекса (соответствующего системе линейных уравнений и ограничений), пока не найдет вершину, расположенную в самой низкой точке высоты.

Мой вопрос: Может ли кто-нибудь помочь мне понять, правильно ли я понял, почему симплекс-алгоритм называется «симплекс-алгоритмом?»

• оптимизация
• линейное программирование
• симплекс

$\endgroup$

2

$\begingroup$

В статье с открытым доступом Джордж Б. Данциг, (2002) Линейное программирование. Operations Research 50(1):42-47, математик, стоящий за симплекс-методом, пишет: 9{m \times n}$, то допустимое базовое решение соответствует нахождению $m+1$ столбцов матрицы $A$, таких что симплекс , порожденный этими $m+1$ столбцами, содержит $b$.