Sin 105 градусов — sin 15 градусов… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
Вынести общий множитель за скобки 2b-5c…
Санжар и булат одновременно выехали на велосипедах из посылка к реке через 20 минут санжар ехавший со скоростью 250 м мин был у реки на каком расстоянии от него находится булат если он ехал со скоростью 200 м мин решите задачу разными способами по
…
Практическая работа 22…
№1
Из двух городов расстояние между которыми 390 км,навстречу друг другу одновременно выехали два поезда и встретились через 3 часа.
№2
Площадь пруда прямоугольной формы 17200м2 а его длина 200м.Найди его периметр.
№3
В одном бочонке было 20 кг меда.После того,как винни пух в…
В 2 кувшина налили молоко. В 1 — ом кувшине было 5,4 л молока. Когда из 1-ого кувшина перелили 1,2 молока во 2-ой то в нем стало на 2,8 л больше чем осталось в первом сколько литров молока было во втором кувшине?
ПОЖАЛУЙСТА НАПИШИТЕ РЕШЕНИЕ И ОТВЕТ, МНЕ УЖЕ ИТДИ НАДО ПОБЫСТРЕЙ!…
Помогите, пожалуйста с решением! очень срочно!!! даю 10 баллов!
1)a < b, b = m, m < k
2)a < b, b = m, m > k
сравните a и k, если это возможно!!!…
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Немецкий язык
МХК
ОБЖ
Психология
Sin 15 решение
Обновлено: 29. 09.2022
09.2022
Здравствуйте!
Нужно вычислить значение тригонометрического выражения sin 15 * cos 15. Помогите, пожалуйста. Объясните, как решаются подобные задания.
Спасибо!
При вычислении значений вида необходимо внимательно посмотреть на тригонометрическое выражение и обратить внимание на то, что аргументы под знаком тригонометрических функций одинаковые (равны 15) и необходимо найти произведение функций синус и косинус.
1-й способ.
Рассмотрим формулу двойного аргумента, которая для функции синус выглядит следующим образом:
В нашем случае х равен 15. Подставим это значение в формулу двойного аргумента функции синус и получим:
Выразим из этого уравнения искомое выражение:
Найдем правую часть уравнения, используя таблицу значений основных аргументов тригонометрических функций.
2-й способ.
Рассмотрим тригонометрическую формулу для синуса суммы:
В нашем случае значения х1 и x2 равны 15. Подставим значения в формулу и получим:
Мы пришли к тому же уравнению, что и в первом способе. Следовательно, и результат получим тот же:
Здравствуйте!
Какими способами можно вычислить sin 15 градусов? Помогите, пожалуйста.
Спасибо!
Самым простым способом вычисления синуса 15 градусов является использование калькулятора. Но часто встречаются случаи, когда необходимо вычислить sin 15 без использования технических средств.
Данный способ не является единственным. Можно также использовать таблицы Брадиса, из которых можно узнать значение многих тригонометрических функций от практически любого угла. Из этих таблиц искомое значение синуса 15 градусов = 0,2588.
Рассмотрим один способ, который заключается в применении тригонометрических тождеств.
Будем рассматривать формулу синуса разницы аргументов. Для ее использования нужно 15 градусов представить в виде разности таких аргументов, синус от которых можно найти из таблицы значения функции синус.
Запишем аргумент 15 градусов как разность указанных аргументов:
По формуле sin разности распишем:
Теперь можно найти значения функций, которые присутствуют в данном выражении, в выше упомянутой таблице значений функции синус, а также и функции косинус:
Открыть таблицы значениц функций тригонометрических функций. Все уже давно посчитано с высокой точностью.
Для практических применений нужны не столько точные формулы, сколько приближенные значения синусов и косинусов конкретных углов. В прежние времена эти значения собирались в таблицы тригонометрических функций. Пример такой таблицы мы приводим ниже. Излишне объяснять, что таблицы, использовавшиеся на практике, давали значения тригонометрических функций не через , а с гораздо более мелким шагом. В настоящее время тригонометрические таблицы утратили былое значение: чтобы приближенно найти синус или косинус угла, достаточно нажать несколько клавиш на микрокалькуляторе или компьютере.
Табл. 1: Значения тригонометрических функций (с двумя знаками после запятой)
Если ты школьник, то никак 🙂
Если студент, то формула Тэйлора тебе в руки
sin15=sin(45-30)=sin45cos30-cos45sin30, а дальше подставляй табличные значения. А приближенное значение можно найти по таблицам Брадиса
Есть формула синуса половинного угла через синус какого то там угла (в нашем случае 15 половина от 30) написать не могу поищи в нет а если на словах то синус одной второй альфа равен плюс минус корень квадратный из 1 минус косинус альфа
sovremennye kal’kuliatory (graficheskie) eto delo schitaiut. ia shkolu zakonchila 11 let nazad, v shkole u menia byl kal’kuliator TI-85 — vse eti dela schital, i risoval grafiki bol’shinstva uravnenii. tak zhe schital komplexnye tsifry. sovetuiu preobresti — budet men’she golovnoi boli.
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
Таблица синусов для 181°-360°
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Таблица синусов для 0°-180°
Читайте также:
- Kings bounty принцесса в доспехах или перекрестки миров
- Арбат я хочу чтоб ты стала моею женой
- Civilization beyond earth концовки
- Достижение активный игрок варфейс
- Driver hub не устанавливается на windows 10
Как вычислить синус без таблицы
Содержание
- Линии тригонометрических функций
- Значения основных функций тригонометрии
- Сведение к углу
- Использование формул
- Частные случаи
- Вычисление синуса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
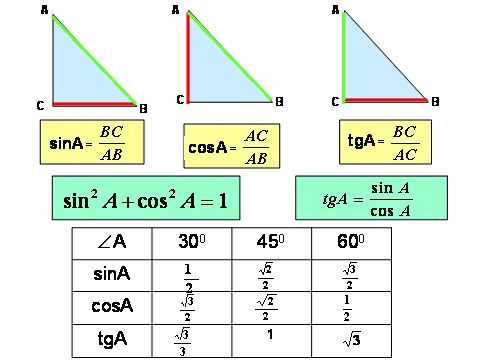
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Вычисление синуса
В этой главе будет показано, как можно вычислять стороны треугольника с точностью до 2% и углы с точностью до 1°, пользуясь одним лишь понятием синуса и не прибегая ни к таблицам, ни к формулам. Такая упрощенная тригонометрия может пригодиться во время загородной прогулки, когда таблиц под рукой нет, а формулы полузабыты. Робинзон на своем острове мог бы успешно пользоваться такой тригонометрией.
Итак, вообразите, что вы еще не проходили тригонометрии или же забыли се без остатка, — состояние, которое иным из читателей, вероятно, нетрудно себе представить. Начнем знакомиться с ней сызнова. Что такое синус острого угла? Это— отношение противолежащего катета к гипотенузе в том треугольнике, который отсекается от угла перпендикуляром к одной из его сто-
рон. Например, синус угла а (рис. 87) есть , или ,
или —, или —.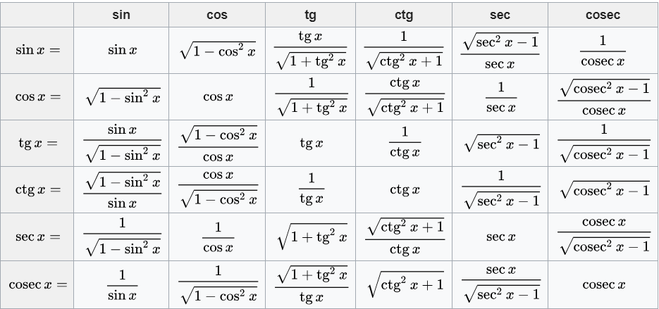 Легко видеть, что вследствие по-
Легко видеть, что вследствие по-
добил образовавшихся здесь треугольников все эти отношения равны одно другому.
Чему же равны синусы различных углов от 1 до 90°? Как узнать это, не имея под рукой таблиц? Весьма просто: надо составить таблицу синусов самому. Этим мы сейчас и займемся.
Начнем с тех углов, синусы которых нам известны из геометрии. Это, прежде всего, угол в 90°, синус которого, очевидно, равен 1. Затем угол в 45°, синус которого
легко вычислить по Пифагоровой теореме; он равен ,
т.е. 0,707. Далее нам известен синус 30°; так как катет, лежащий против такого угла, равен половине гипотенузы, то синус 30° = V2.
Рис. 87. Что такое синус острого угла?
Итак, мы знаем синусы (или, как принято обозначать, sin) трех углов
Этого, конечно, недостаточно; необходимо знать синусы и всех промежуточных углов, по крайней мере через каждый градус. Для очень малых углов можно при вычислении синуса вместо отношения катета к гипотевычислить.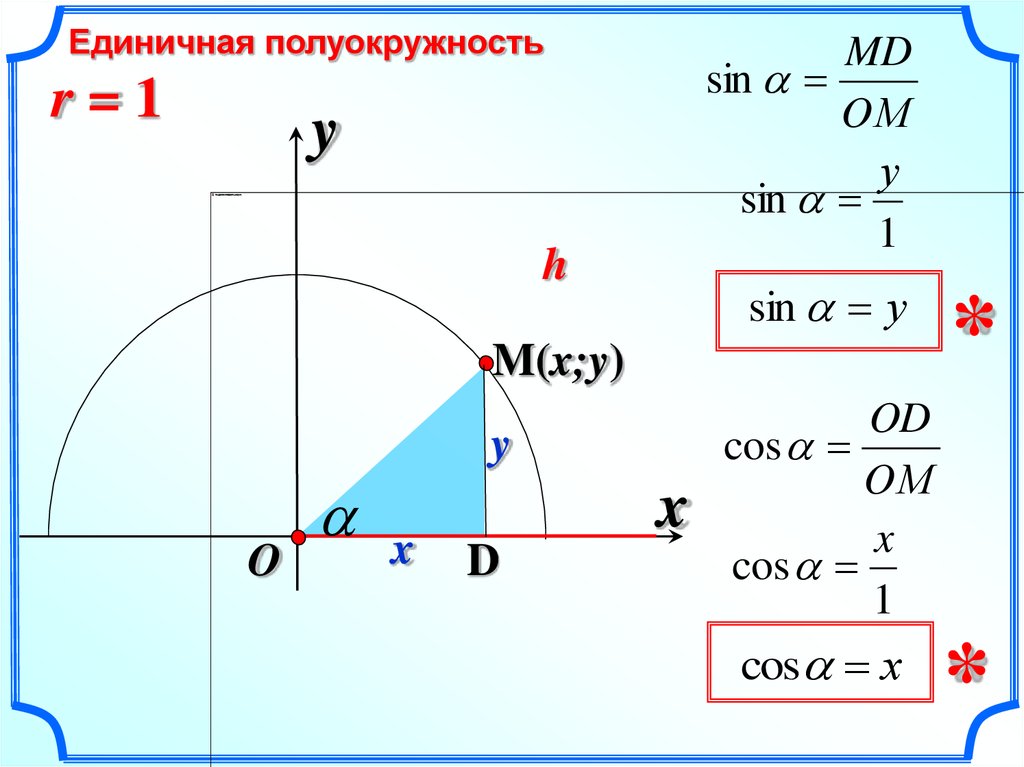 Например, для угла в 1° дуга следовательно, sin 1° можно принять равным
Например, для угла в 1° дуга следовательно, sin 1° можно принять равным
нузе брать без большой погрешности отношение дуги к
радиусу: из рис. 87 (справа) видно, что отношение —
мало отличается от отношения . Последнее же легко
вычислить. Например, для угла в 1° дуга и,
следовательно, sin 1° можно принять равным
Таким же образом находим:
Но надо убедиться, как далеко можно продолжать эту табличку, не делая большой погрешности. Если бы мы вычислили по такому способу sin 30°, то получили
Рис. 88. Как вычислить sin 15°?
бы 0,524 вместо 0,500; разница была бы уже во второй значащей цифре, и погрешность со- й 24
ставляла бы -, т.е. около
- 500
- 5%. Это чересчур грубо даже для нетребовательной походной тригонометрии. Чтобы найти границу, до которой позволительно вести вычисление синусов по указанному приближенному способу, постараемся найти точным приемом sin 15°.
 Для этого воспользуемся следующим не особенно замысловатым построением (рис. 88). Пусть
Для этого воспользуемся следующим не особенно замысловатым построением (рис. 88). Пусть
sin 15° = Продолжим ВС на равное расстояние до
точки D; соединим А с D, тогда получим два равных треугольника: ADC и АВС, и угол BAD, равный 30°. Опустим на AD перпендикуляр BE; образуется прямоугольный треугольник ВАЕ с углом 30° ( = 0,016. Строго говоря, это,
конечно, не так, но отступление от указанного правила обнаруживается только в третьей значащей цифре, которую мы все равно отбрасываем. Итак, прибавляя последовательно по 0,016 к sin 15°, получим синусы 16°, 17°, 18° ит.д.:
Все эти синусы верны в первых двух десятичных знаках, т.е. с достаточною для наших целей точностью: они отличаются от истинных синусов менее чем на половину единицы последней цифры.
Таким же способом поступают при вычислении углов в промежутках между 30 и 45°. Разность sin 45°- -sin 30° = 0,707 -0,5 = 0,207. Разделив ее на 15, имеем 0,014. Эту величину будем прибавлять последовательно к синусу 30°; тогда получим:
Эту величину будем прибавлять последовательно к синусу 30°; тогда получим:
Остается найти синусы острых углов больше 45°. В этом поможет нам Пифагорова теорема. Пусть, например, мы желаем найти sin 53°,
т.е. (рис. 89) отношение -.
Так как угол В = 37°, то синус его мы можем вычислить по предыдущему: он равен 0,5 +
+ 7 • 0,014 = 0,6. С другой стороны, мы знаем, что sin В =
=-. Итак, -= 0,6, откуда
АС = 0,6 • АВ. Зная АС, легко вычислить ВС. Этот отрезок Рис. 89. К вычислению равен синуса угла, большего 45°
Расчет в общем нетруден; надо только уметь вычислять квадратные корни.
Тригонометрическая окружность наглядно показывает отношения синуса и косинуса при различных значениях угла α . Угол α начинает раскрываться с правой стороны оси косинуса.
Если исследовать значения синуса, то в первой и второй четверти графика они будут положительны, так как находятся выше оси косинуса, то есть выше нуля, а в третьей и четвертой четверти графика синус станет отрицательным, так как точки окружности опускаются ниже нуля.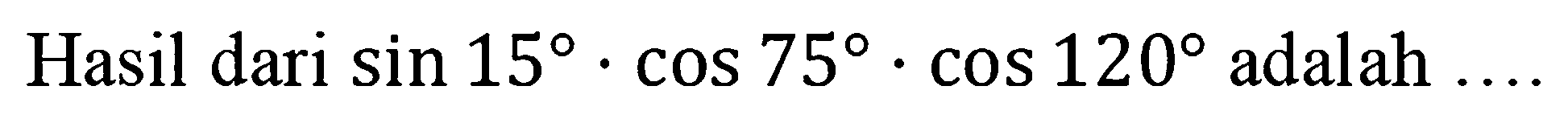 Поэтому синус угла от 0° до 180° будет со знаком плюс, а синус угла от 180° до 360° будет со знаком минус, как видно из таблицы ниже. В таблице приведены все значения синусов углов от 0° до 360° с точностью до 1 градуса.
Поэтому синус угла от 0° до 180° будет со знаком плюс, а синус угла от 180° до 360° будет со знаком минус, как видно из таблицы ниже. В таблице приведены все значения синусов углов от 0° до 360° с точностью до 1 градуса.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Sin 15 градусов — Найти значение Sin 15 градусов
LearnPracticeDownload
Значение с точностью до 15 градусов равно 0,2588190. . . . Sin 15 градусов в радианах записывается как sin (15° × π/180°), то есть sin (π/12) или sin (0,261799…). В этой статье мы обсудим способы нахождения значения sin 15 градусов на примерах.
. . . Sin 15 градусов в радианах записывается как sin (15° × π/180°), то есть sin (π/12) или sin (0,261799…). В этой статье мы обсудим способы нахождения значения sin 15 градусов на примерах.
- Sin 15°: 0,2588190. . .
- Sin 15° в дробях: (√6 — √2)/4
- Sin (-15 градусов): -0,2588190. . .
- Sin 15° в радианах: sin (π/12) или sin (0,2617993 . . .)
Каково значение греха 15 градусов?
Значение sin 15 градусов в десятичной системе равно 0,258819045. . .. Sin 15 градусов также можно выразить с помощью эквивалента заданного угла (15 градусов) в радианах (0,26179 . . .).
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180°)
⇒ 15 градусов = 15° × (π/180°) рад = π/12 или 0,2617. . .
∴ sin 15° = sin(0,2617) = (√6 — √2)/4 или 0,2588190. . .
Объяснение:
Для sin 15 градусов угол 15° лежит между 0° и 90° (первый квадрант). Поскольку функция синуса положительна в первом квадранте, значение sin 15° = (√6 — √2)/4 или 0,2588190. . .
Поскольку функция синуса положительна в первом квадранте, значение sin 15° = (√6 — √2)/4 или 0,2588190. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 15° как sin 15 градусов = sin(15° + n × 360°), n ∈ Z.
⇒ sin 15° = sin 375° = sin 735° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-15°) = -sin(15°).
Методы нахождения значения Sin 15 градусов
Функция синуса положительна в 1-м квадранте. Значение sin 15° равно 0,25881. . .. Мы можем найти значение sin 15 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Sin 15 градусов с использованием единичной окружности
Чтобы найти значение sin 15 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 15° с положительной осью x.
- Грех в 15 градусов равен координате y (0,2588) точки пересечения (0,9659, 0,2588) единичной окружности и r.

Следовательно, значение sin 15° = y = 0,2588 (приблизительно)
Sin 15° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 15 градусов как:
- ± √(1-cos² (15°))
- ± тангенс 15°/√(1 + тангенс²(15°))
- ± 1/√(1 + раскладушка²(15°))
- ± √(сек²(15°) — 1)/сек 15°
- 1/косек 15°
Примечание: Поскольку 15° лежит в 1-м квадранте, конечное значение sin 15° будет положительным.
Мы можем использовать тригонометрические тождества для представления sin 15° как
- sin(180° — 15°) = sin 165°
- -sin(180° + 15°) = -sin 195°
- cos(90° — 15°) = cos 75°
- -cos(90° + 15°) = -cos 105°
☛ Также проверьте:
- грех 2 степени
- грех 45 градусов
- грех 0 градусов
- грех 95 градусов
- грех 48 градусов
- грех 933 градуса
Примеры использования Sin 15 градусов
Пример 1: Используя значение sin 15°, найдите: (1-cos²(15°)).

Решение:
Мы знаем, (1-cos²(15°)) = (sin²(15°)) = 0,067
⇒ (1-cos²(15°)) = 0,067Пример 2. Найдите значение sin 15°, если cosec 15° равно 3,8637.
Решение:
Так как sin 15° = 1/csc 15°
⇒ sin 15° = 1/3,8637 = 0,2588Пример 3. Найдите значение 5 sin(15°)/7 cos(75°).
Решение:
Используя тригонометрические тождества, мы знаем, что sin(15°) = cos(90° — 15°) = cos 75°.
⇒ sin(15°) = cos(75°)
⇒ Значение 5 sin(15°)/7 cos(75°) = 5/7
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Sin 15 Degrees
Что такое Sin 15 Degrees?
Sin 15 градусов — значение тригонометрической функции синуса для угла, равного 15 градусам. Значение sin 15° равно (√6 — √2)/4 или 0,2588 (приблизительно).
Каково значение Sin 15 градусов в пересчете на Tan 15°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 15° как tan 15°/√(1 + tan²(15°)). Здесь значение тангенса 15° равно 0,267949.
Как найти Sin 15° с точки зрения других тригонометрических функций?
Используя тригонометрическую формулу, значение sin 15° можно выразить через другие тригонометрические функции следующим образом:
- ± √(1-cos²(15°))
- ± тангенс 15°/√(1 + тангенс²(15°))
- ± 1/√(1 + раскладушка²(15°))
- ± √(сек²(15°) — 1)/сек 15°
- 1/косек 15°
☛ Также проверьте: тригонометрическую таблицу
Как найти значение Sin 15 градусов?
Значение sin 15 градусов можно рассчитать, построив угол 15° с осью x и затем найдя координаты соответствующей точки (0,9659, 0,2588) на единичной окружности. Значение sin 15° равно координате y (0,2588). ∴ sin 15° = 0,2588.
Значение sin 15° равно координате y (0,2588). ∴ sin 15° = 0,2588.
Каково значение Sin 15° в пересчете на Sec 15°?
Поскольку функцию синуса можно представить с помощью функции секанса, мы можем записать sin 15° как √(sec²(15°) — 1)/sec 15°. Значение sec 15° равно 1,035276.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Sin 15 — значение, расчет, вывод, методы и часто задаваемые вопросы треугольника. Тригонометрические соотношения дают отношение между сторонами и углами прямоугольного треугольника. В прямоугольном треугольнике сторона, противоположная прямому углу, является наибольшей стороной, которая называется гипотенузой. Две другие стороны являются основанием и перпендикулярны рассматриваемому опорному углу. Понятие теоремы Пифагора очень важно для лучшего понимания тригонометрии. Тригонометрия используется для измерения высот и расстояний в строительстве, навигации и других реальных приложениях.

Тригонометрические соотношения
Существует шесть тригонометрических соотношений.
Шесть тригонометрических соотношений определяются следующим образом:
Синус угла θ,
sin θ = \[\frac{Противоположность}{Гипотенуза}\]
- Косинус угла θ, 91
cos θ = \[\frac{Adjacent}{Гипотенуза}\]
Тангенс угла θ,
tan θ = \[\frac{Opposite 90\}{Adjacent]1160
Котангенс угла θ,
ctg θ = \[\frac{Adjacent}{Противоположный}\]
Секанс угла θ,
Косеканс угла θ,
Другие тригонометрические отношения числа 150 можно определить, используя соотношение других тригонометрических отношений с синусом угла 150.
 можно вычислить.
можно вычислить.- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x) `
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x) `
- Производная синуса
- Первообразная синуса
- Свойства функции синуса
- Уравнение с синусом
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус: синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: рыжевато-коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
- Tan (15xb0) можно найти, если мы знаем значение sin 15 градусов и cos 15 градусов.
- Из приведенной выше таблицы у нас есть значения tan, sin и cos для 0 30 45 60xb0 и 90xb0.
- загар (15xb0) и221а3 1/ и221а3 + 1.
- Следовательно, значение tan (15xb0) равно u221a3 1/u221a3 + 1,
- u2234 Тан (15xb0) (1,732 1)/(1,732 + 1) 0,2679.
- Tan (15xb0) можно найти, если мы знаем значение sin 15 градусов и cos 15 градусов.
- Из приведенной выше таблицы у нас есть значения tan, sin и cos для 0 30 45 60xb0 и 90xb0.
- коричневый (15xb0) и221а3 1/ и221а3 + 1.
- Следовательно, значение tan (15xb0) равно u221a3 1/u221a3 + 1,
- u2234 Тан (15xb0) (1,732 1)/(1,732 + 1) 0,2679.
- Sin 15° = Sin(60°-45°)
- = Sin60cos45°-Cos60°sin45°
- (√3/2)(1/√2) – (1/2)(1/√2)
- = (√3 -1)/2√2
- Итак, Sin15° = (√3 — 1)/2√2
- Cos 15° = Cos (60°-45°)
- использование Cos(A-B) = CosA cosB + SinA sinB формула
- Cos60° cos45° + Sin60° sin45°
- ( 2)(1/√2)+ (√3/2)(1/√2)
- Cos 15° = 1/2√2 + √3/2√2
- Cos 15° = (√3+1)/(2√2)
- sin(45 – 30) + cos(45- 30)
- sin(45)cos(30) – cos(45)sin(30) + cos(45)cos(30) ) + sin(45)sin(30)
- (1/√2)(√3/2) – (1/√2)(1/2) + (1/√2)(√3/2) + (1/√2)(1/2) 9
- √6/2
- cos θ = соседняя сторона/гипотенуза
- tan θ = противоположная сторона/соседняя сторона
- сек θ = гипотенуза/соседняя сторона
- cosec θ = гипотеновая/противоположная сторона
- Cosec θ = гипотенос/противоположность/противоположная сторона
- .
 Сторона/Противоположная сторона
Сторона/Противоположная сторона - cosec θ = 1/sin θ
- СЕД θ = 1/cos θ
- Cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- Tan θ = 1/cot θ 16
- tan θ = 1/cot θ
- Tan θ = 1/cot θ
- Table
Часто задаваемые вопросыAngles (In Degrees) 0° 30° 45° 60° 90° 180° 270° 360° Angles (In Radians) 0° π/6 π/4 π/3 π/2 π 3π/2 2π sin 0 1/2 1/√2 √3/2 1 0 — 1 0 COS 1 √3/2 1/√2 1/2 0 -1 0 1 11
TAN 0 1/√3 1 √3 ∞ 0 ∞ 0 cot ∞ √3 1 1/√3 0 ∞ 0 ∞ csc ∞ 2 √2 2/√3 1 ∞ -1 ∞ sec 1 2/√3 √2 2 ∞ -1 ∞ 1 Как найти значение cos 15 и sin 15?
В этом посте мы объяснили возможные способы нахождения значений sin15 и cos 15 градусов
Каково значение sin 15?
(√3 -1)/2√2
Каково значение 2 sin 15 градусов cos 15 градусов?
2 × sin 15° × cos 15° = sin 30°
Значение cos равно 15?
(√3+1)/(2√2)
Как найти грех 15?
(√3 -1)/2√2 .

Гипотенуза}{Смежный}\]
cosec θ = \[\frac{Гипотенуза}{Противоположный}\]
Тригонометрические отношения угла 150
0 Шесть тригонометрических отношений угла 150
0 синус, косинус, тангенс, котангенс, секанс и косеканс любого угла. Для расчета тригонометрических отношений числа 150 обязательно знание тригонометрических соотношений стандартных углов и половинных углов. Кроме того, необходимо знать несколько важных тригонометрических формул. Синус угла — это отношение длины стороны, противоположной углу, называемому противоположной стороной или перпендикуляром, к длине стороны, противоположной прямому углу в прямоугольном треугольнике, который является наибольшей стороной, называемой гипотенузой. Чтобы найти sin 15 градусов, важны значения синуса и косинуса стандартных углов.
Для расчета тригонометрических отношений числа 150 обязательно знание тригонометрических соотношений стандартных углов и половинных углов. Кроме того, необходимо знать несколько важных тригонометрических формул. Синус угла — это отношение длины стороны, противоположной углу, называемому противоположной стороной или перпендикуляром, к длине стороны, противоположной прямому углу в прямоугольном треугольнике, который является наибольшей стороной, называемой гипотенузой. Чтобы найти sin 15 градусов, важны значения синуса и косинуса стандартных углов.
sin 00 = 0 | cos 00 = 1 |
sin 300 = 1/2 | cos 300 = √3/2 |
SIN 45 0 = 1/√2 | COS 450 = 1/√2 |
SIN 600 = √3/2 | COS 600 = ½ | COS 600 = ½ | 8888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888 8 . | соз 900 = 0 |
Получение значения Sin 15 градусов
Чтобы найти значение Sin 15 градусов, используется понятие половины угла.
150 можно записать как \[\frac{300}{2}\].
Рассмотрим угол ‘P’ (sin \[\frac{P}{2}\] + cos \[\frac{P}{2}\])2 = sin2 (\[\frac{P}{ 2}\]) + cos2 (\[\frac{P}{2}\]) + 2 sin (\[\frac{P}{2}\]) cos (\[\frac{P}{2} \])
Согласно тригонометрическим формулам sin² A + cos² A = 1.
Подставляя это значение в приведенное выше уравнение,
(sin \[\frac{P}{2}\] + cos \[\frac{P}{2}\])² = 1 + 2 sin (\[\frac{P}{2}\] ) cos (\[\frac{P}{2}\])
Из суммы в тригонометрическую формулу произведения sin A + sin B = \[\frac{2 sin (C + D)}{2}\] . \[\frac{cos (C + D)}{2}\]
Используя это уравнение, 2 sin \[\frac{P}{2}\] cos \[\frac{P}{2}\] = sin \[\frac{P}{2}\] + sin \[\frac{P}{2}\] = sin P
Таким образом, уравнение можно переписать как:
(sin \[\frac{ P}{2}\] + cos \[\frac{P}{2}\])2 = 1 + sin P sin \[\frac{P}{2}\] + cos \[\frac{P} {2}\] = \[\sqrt{(1 + sin P)}\] → (1)
(sin \[\frac{P}{2}\] — cos \[\frac{P}{2}\])² = sin² \[\frac{P}{2}\] + cos² \[ \frac{P}{2}\] — 2 sin \[\frac{P}{2}\] cos \[\frac{P}{2}\]
(Sin \[\frac{P}{ 2}\] — Cos \[\frac{P}{2}\])²= 1 — sin P
(sin \[\frac{P}{2}\] — cos \[\frac{P} {2}\]) = \[\sqrt{(1 — sin P)}\] → (2)
Рассмотрим значение P = 300.
Подставляя значение P в уравнения 1 и 2,
=> sin (\[\frac{300}{2}\]) + cos (\[\frac{300}{2}\]) = \[\sqrt{(1 + sin 300)}\] sin 150 + cos 150 = \[\sqrt{(1 + \frac{1}{2})}\] sin 150 + cos 150 = \[\frac{\sqrt{3}}{\sqrt{2}} \] → (3)
=> sin (\[\frac{300}{2}\]) — cos (\[\frac{300}{2}\]) = \[\sqrt{(1 — sin 300)}\] sin 150 — cos 150 = \[\sqrt{(1 — \frac{1}{2})}\] sin 150 — cos 150 = \[\frac{1}{\sqrt{2}}\] → ( 4)
Сложение уравнений (3) и (4),
sin 150 + cos 150 + sin 150 — cos 150 = \[\frac{\sqrt{3}}{\sqrt{2}}\] — 1 /√22 sin 150 = (√3 — 1)/√2sin 150 = \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\]
Значение sin 15 градусов = \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\]
Альтернативный метод определения значений Sin 15
Угол 150 можно записать как разность 450 и 300. sin 150 можно записать как sin (450 — 300).
Значение можно определить по формуле разности:
sin (A — B) = sin A cos B — cos A sin B
sin (450 — 300) = sin 450 cos 300 — cos 450 sin 300
= \[\frac{1}{\sqrt{2}}\] x \[\frac{\sqrt{3}}{2}\] — \[\frac{1}{\sqrt{2}} \] x \[\frac{1}{2}\] = \[\frac{\sqrt{3}}{2\sqrt{2}}\] — \[\frac{1}{2\sqrt{ 2}}\]
= \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\]
Забавные факты:
Упрощенный метод нахождения значения Sin 15°
Здесь приведен простейший метод нахождения значения Sin 15°:
sin 15° = Sin (45 – 30)°
Sin (45-30)° = Sin 45° cos 30° – cos 45° sin 30°
Sin 15° = (\[\frac{1}{\sqrt{2}}\])(\[ \frac{\sqrt{3}}{2}\])-(\[\frac{1}{\sqrt{2}}\])(\[\frac{1}{2}\])
sin 15° = (\[\frac{\sqrt{3}}{2\sqrt{2}}\])-(\[\frac{1}{2\sqrt{2}}\])
sin 15° = \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\]
Значение Sin 15 в десятичной форме
Как известно, sin 15° = \[\ frac{(\sqrt{3-1})}{2\sqrt{2}}\].
Теперь мы рационализируем знаменатель в правой части приведенного выше выражения.
= \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\]
Умножить и разделить √2.
⇒ \[\frac{(\sqrt{3-1})}{2\sqrt{2}}\] x \[(\frac{\sqrt{2}}{\sqrt{2}})\ ]
⇒ \[\frac{\sqrt{2}(\sqrt{3-1})}{4}\]
⇒ \[\frac{(\sqrt{6}-\sqrt{2}) }{4}\]
⇒ 0,2588 (до четырех знаков после запятой)
Таким образом, значение sin 15° равно = 0,2588
Калькулятор — sin(15) — Solumaths
Грех, онлайн-исчисление
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах,
градусов или градианов.
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Синус тригонометрической функции отметил грех , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
Вычисление синуса угла в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы рассчитать синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :
| sin(`2*pi`) | `0` | ||||||||||
| sin(`pi`) | `0` | ||||||||||
| sin(`pi/2`) | `1` | ||||||||||
| sin(`pi/4`) | `sqrt(2)/2` 03 03 | 5 90(0) `pi/3`) | `sqrt(3)/2` | ||||||||
| sin(`pi/6`) | `1/2` | ||||||||||
| sin(`2*pi/3`) | `sqrt(3)/2` | ||||||||||
| sin(`3*pi/4`) | `sqrt(2)/2` | ||||||||||
| sin(`5*pi/6`) | ` 1/2` | ||||||||||
| sin(`0`) | `0` | ||||||||||
| sin(`-2*pi`) | `0` | ||||||||||
| sin(`-pi`) | `0` | ||||||||||
| sin(`-pi/4`) | `-sqrt(2)/2` | ||
| sin(`-pi/3`) | `-sqrt(3)/2` | ||
| sin(`-pi/6`) | `-1/2` | ||
| sin(`-2*pi/3`) | `-sqrt(3)/2` | sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
Производная синуса равна cos(x).
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производный синус:
Чтобы дифференцировать функцию синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) является производной(`sin(x)`)=`cos(x)`
Первообразная синуса :
Калькулятор первообразной позволяет вычислить первообразную функции синуса.
Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`
Предельный синус:
Калькулятор пределов позволяет вычислять пределы функции синуса.
предел sin(x) is limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса есть функция арксинуса, отмеченная как arcsin.
График синуса :
Графический калькулятор может отображать синусоидальную функцию в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Расчет онлайн с помощью sin (синуса)
См. также
Список связанных калькуляторов:
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Что такое sin 15 градусов? – Книга Веа
по jai
Содержание
Что такое sin 15 градусов?
0,2588
Как решить sin 15 градусов?
Значение Tan 15
Каково точное значение греха 15 градусов?
0,2588
Как найти sin 15 без калькулятора?
0,9659
Чему равен cos 15 градусов?
примерно 0,269 градуса
Как найти sin 15 градусов?
Значение sin 15 градусов можно вычислить, построив угол 15xb0 с осью x, а затем найдя координаты соответствующей точки (0,9659, 0,2588) на единичной окружности. Значение sin 15xb0 равно координате y (0,2588). u2234 sin 15xb0 0,2588.
u2234 sin 15xb0 0,2588.
Как посчитать 15 градусов?
Значение Tan 15
Каково значение 15 градуса в тригонометрии?
0,267949192
Каково точное значение cos 15 градусов?
Ответ: Значение cos 15xb0 (u221a3+1)/2u221a2.
Как найти значение sin 15?
Значение sin 15xb0 равно y-координате (0,2588). u2234 sin 15xb0 0,2588.
Что такое COS 15 как дробь?
Значение cos 15 градусов в десятичном виде равно 0,965925826. . .. Cos 15 градусов также можно выразить с помощью эквивалента данного угла (15 градусов) в радианах (0,26179 . . .) u21d2 15 градусов 15xb0 xd7 (u03c0/180xb0) рад u03c0/12 или 0,2617 . . . u2234 cos 15xb0 cos(0,2617) (u221a6 + u221a2)/4 или 0,9659258. . .
. .) u21d2 15 градусов 15xb0 xd7 (u03c0/180xb0) рад u03c0/12 или 0,2617 . . . u2234 cos 15xb0 cos(0,2617) (u221a6 + u221a2)/4 или 0,9659258. . .
Что такое точное значение sin 15 градусов?
Sin 15 градусов — значение тригонометрической функции синуса для угла, равного 15 градусам. Значение sin 15xb0 равно (u221a6 – u221a2)/4 или 9.1694 0,2588 (приблизительно)
Как найти 15 градусов?
Значение sin 15 градусов можно вычислить, построив угол 15xb0 с осью x и затем найдя координаты соответствующей точки (0,9659, 0,2588) на единичной окружности. Значение sin 15xb0 равно координате y (0,2588). u2234 sin 15xb0 0,2588.
Сколько процентов составляет 15 градусов?
26,80%
Как найти значение тангенса 15 градусов?
Sin 15 градусов — значение тригонометрической функции синуса для угла, равного 15 градусам. Значение sin 15xb0 равно (u221a6 – u221a2)/4 или 0,2588 (приблизительно)
Как мы можем найти значение sin 15?
Фактическое значение sin 15 градусов равно (u221a3u22121)/(2u221a2).
Как найти cos 15 без калькулятора?
Часто задаваемые вопросы по Sin 15 Degrees Sin 15 градусов — это значение тригонометрической функции синуса для угла, равного 15 градусам. Значение sin 15xb0 равно (u221a6 – u221a2)/4 или 9.1694 0,2588 (приблизительно)
Что такое sin 15 как дробь?
В формате дроби значение cos(30xb0) равно u221a3/2. Поскольку это иррациональное число, его значение в десятичной форме равно 0,8660254037.
Что такое cos как дробь?
у221а3/2. Cos 30.FormFormulaValueСистема сотенных Cos 33 (u2153) g 0,8660254037 еще 2 строки
Как найти точное значение cos 15?
0,267949192
Как упростить грех 15?
Ответ: Значение cos 15xb0 (u221a3+1)/2u221a2.
Как считать градусы?
Значение sin 15 градусов можно вычислить, построив угол 15xb0 с осью x и затем найдя координаты соответствующей точки (0,9659, 0,2588) на единичной окружности. Значение sin 15xb0 равно координате y (0,2588). u2234 sin 15xb0 0,2588.
Значение sin 15xb0 равно координате y (0,2588). u2234 sin 15xb0 0,2588.
Какой угол равен 15 градусам?
Каждый градус равен , разделенному на 60 равных частей, называемых минутами. Таким образом, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7xb0 30′. Каждая минута далее делится на 60 равных частей, называемых секундами, и, например, 2 градуса 5 минут 30 секунд записывается как 2xb0 5′ 30.
Как решить тангенс 15 градусов?
острый угол
Сколько градусов составляет процент?
Окружность имеет 360 градусов, поэтому, если вы хотите выразить угол в процентах, просто разделите измерение угла (в градусах) на 360 и умножьте на 100. В обратном порядке разделите процент на 100 и умножьте на 360.
Значение Sin 15 cos 15 градусов
Присоединяйтесь к нам на канале Telegram Каково значение Sin 15+Cos 15 градусов?Содержание
Мы должны использовать тригонометрические тождества, чтобы найти значение Sin 15 cos 15 градусов. Мы можем узнать значения Sin 15+Cos 15 и многими другими способами. Давайте обсудим подробно –
Мы можем узнать значения Sin 15+Cos 15 и многими другими способами. Давайте обсудим подробно –
Сначала мы объясним, как найти значение sin 15 cos 15 градусов. нет формулы для нахождения значения sin 15 градусов, но мы должны использовать одну из тригонометрических тождеств (формулу сложного угла) Sin(AB) = SinA cosB -CosA sinB. Теперь положим A = 60 и B = 45
Итак, мы можем сказать, что Sin 15° = Sin(60°-45°). Используя формулу составного угла Sin(AB) = SinA cosB -CosA sinB, мы можем решить эту проблему. Вы можете перейти по этой ссылке, чтобы найти другие объяснения формул и математические заметки .
Значение Sin 15 градусов sСначала нужно переписать Sin 15° как Sin (60°-45°), после чего применить формулу составного угла Sin(A-B) = SinA cosB -CosA sinB
Сначала вы должны переписать Cos 15° как Cos (60°-45°), после чего вы должны применить формулу составного угла Cos(AB) = CosA cosB + SinA sinB
Мы можем переписать sin(15) + cos(15) как sin(45 – 30) + cos(45- 30), после чего мы можем применить формулу составного угла Sin(A-B) = SinA cosB -CosA sinB и Cos(A-B ) = CosA cosB + SinA sinB
- 6

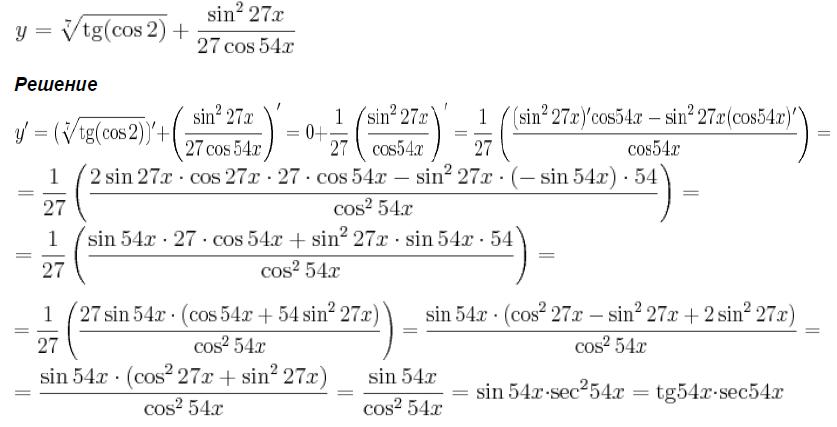 Для этого воспользуемся следующим не особенно замысловатым построением (рис. 88). Пусть
Для этого воспользуемся следующим не особенно замысловатым построением (рис. 88). Пусть

 = 1
= 1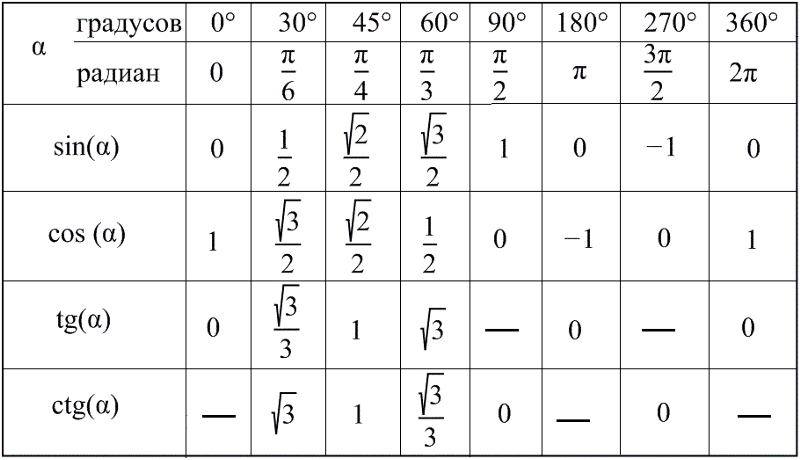 можно вычислить.
можно вычислить. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. Сторона/Противоположная сторона
Сторона/Противоположная сторона