Обобщение понятия степени и решение примеров со степенями
Здравствуйте. Многие ученики испытывают сложности при решении заданий, в которых встречаются выражения с корнями. В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!
1. Свойства степеней и корней
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равняется а.
Степень числа а с показателем n обозначают an, например:
В общем случае при n > 1 имеем
Число a называется основой степени

Приведем основные свойства действий со степенями.
Приведенные свойства обобщаются для любых показателей степени
Часто в вычислениях используются степени с рациональным показателем. При этом удобным оказалось такое обозначение:
Корнем n— ой степени из числа а называется число b, n— я степень которого равняется a:
Корень также называется радикалом.
Корень нечетной степени n всегда существует. Корень четной степени 2n из отрицательного числа не существует. Существуют два противоположных числа, которые являются корнями четной степени из положительного числа а > 0. Положительный корень n— ой степени из положительного числа называют арифметическим корнем.
Из формул (3), (4) вытекают такие свойства радикалов
Если степень корня n = 2, то показатель корня обычно не пишется.
Пример 1.1. Найти значение выражения
Подкоренное выражение разложим на простые множители:
Пример 1.2. Упростить выражение
Имеем:
Пример 1.3. Извлечь корень
Имеем:
Пример 1.4. Упростить выражение
Поскольку при
2. Действия с радикалами
1) Преобразование корня по формуле называется внесением множителя под знак радикала.
Исходя из формулы (7) получим
Пример 2.2. Внести множитель под знак радикала x√y при x< 0.
Имеем равенство
2) Преобразование корня исходя из формулы называется вынесением множителя из-под знака радикала.
Пример 2.3. Вынести множитель из-под знака корня в выражении
Получим:
Пример 2.4. Вынести множитель из-под знака корня
Имеем:
Пример 2.5. Вынести множитель из-под знака корня:
Радикалы вида , где a, b — рациональные числа, называются подобными
. Их можно прибавлять и отнимать:Пример 2.6. Упростить:
Пример 2.7. Сложить радикалы:
Пример 2.8. Выполнить действие:
Заметим, что равенство не выполняется. В этом можно убедиться на таком примере:
Приведем примеры умножения радикалов.
Пример 2.9.
Аналогично освобождаются от кубических иррациональностей в знаменателе:
Рассмотрим более сложные примеры рационализации знаменателей:
Чтобы перемножить радикалы с разными степенями, их сначала превращают в радикалы с одинаковыми степенями.
Пример 2.10. Перемножим радикалы:
Во время умножения радикалов можно использовать формулы сокращенного умножения. Например:
Если радикалы находятся в знаменателе дроби, то, используя свойства радикалов, можно избавиться от иррациональности.
Пример 2.11. Рационализируем знаменатели дробей
Выражения называются сопряженными. Произведение сопряженных выражений не содержит радикалов:
Это свойство используется для рационализации знаменателей.
Пример 2.12. Избавиться от иррациональности в знаменателе:
Избавимся от иррациональности в знаменателе дроби:
3. Вычисление иррациональных выражений
С помощью свойств корней можно упрощать и вычислять иррациональные выражения.
Пример 3.1. Вычислить
Выполним последовательно действия:
Пример 3. 2. Вычислить:
2. Вычислить:
Выполним действия.
Часто используется формула двойного радикала:
Пример 3.3. Исходя из формулы (8) находим:
Пример 3.4. Вычислить
Исходя из формулы (8) находим:
Окончательно получаем:
Аналогично вычисляются кубические корни. Имеем:
Возводим обе части равенства в куб:
Сравнивая выражения при √с, получаем однородную систему уравнений:
Поделив уравнение почленно, приходим к уравнению для z = y/x:
Пример 3.5. Вычислить значение радикала
После возведения в куб уравнения приходим к системе уравнений:
Поделив почленно первое уравнение на второе, получим уравнение для z= y/x:
По схеме Горнера находим корень z = — ½
Из системы уравнений и уравнения y/x = — ½ находим x = 2, y = -1. Итак,
Итак,
Пример 3.6. Вычислить .
Возьмем .
Возведя обе части уравнения в куб, получаем откуда вытекает система уравнений
Система уравнений имеет очевидное решение x= 1, y= 1.
Поэтому .
Вычисляем радикал
Окончательно имеем a = — 1.
Пример 3.7. Вычислить
Поскольку
Дальше имеем:
Итак, a = — 2.
Пример 3.8. Вычислить
Возведем уравнение в куб, воспользовавшись равенством .
Получили для x кубическое уравнение
или x3 – 3x – 18 = 0,
имеет корни
Во множестве действительных чисел имеем корень x = 3.
4. Оценки для радикалов
Если
Это неравенство можно использовать для доведения неровностей, которые содержат радикалы.
Пример 4.1. Доказать, что .
Возведя неравенство в шестую степень, получим очевидное неравенство
Можно приводить радикалы к одной и то й же самой степени :
Пример 4.2. Оценим .
Поскольку
При преобразовании неравенств можно использовать символ V, понимая под ним знаки « > », « < », или « ».
Пример 4.3. Какое число больше
.
Поскольку
На этом все. Напоминаю, что Вы можете записываться ко мне на занятия в расписании, я с радостью помогу Вам с любыми вопросами по математике или высшей математике.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Вычислить значение выражения с корнями
Умение работать с числовыми выражениями, содержащими квадратный корень, необходимо для успешного решения ряда задач из ОГЭ и ЕГЭ. Как правило, на этих экзаменах достаточно базового представления о том, что такое извлечение корня и как оно осуществляется на практике.
Как правило, на этих экзаменах достаточно базового представления о том, что такое извлечение корня и как оно осуществляется на практике.
Определение
Корень степени n из числа X — это такое число x, для которого верно равенство: x n = X.
Найти значение выражения с корнем — это значит найти x при известных X и n.
Квадратный корень или, что то же самое, корень второй степени из X — число x, для которого выполнено равенство: x 2 = X.
Обозначение: ∛Х. Здесь 3 — степень корня, Х — подкоренное выражение. Знак ‘√’ часто называют радикалом.
Если над корнем не стоит число, указывающее на степень, то по умолчанию подразумевается степень 2.
В школьном курсе для четных степеней обычно не рассматривают отрицательные корни и подкоренные выражения. Например, не существует √-2, а для выражения √4 верным ответом считается 2, несмотря на то, что (-2) 2 тоже равняется 4.
Рациональность и иррациональность корней
Наиболее простое из возможных заданий c корнем — найти значение выражения либо проверить его на рациональность.
Например, вычислить значения √25; ∛8; ∛-125:
- √25 = 5, так как 5 2 = 25;
- ∛8 = 2, так как 2 3 = 8;
- ∛ — 125 = -5, так как (-5) 3 = -125.
Ответы в приведенных примерах — это рациональные числа.
При работе с выражениями, не содержащими буквенных констант и переменных, рекомендуется всегда выполнять подобную проверку с помощью обратной операции возведения в натуральную степень. Нахождение числа x в n-й степени эквивалентно вычислению произведения n множителей x.
Существует множество выражений с корнем, значение которых иррационально, то есть записывается в виде бесконечной непериодической дроби.
По определению рациональные — это те, что можно выразить обыкновенной дробью, а иррациональные — все остальные действительные числа.
К таким относятся √24, √0,1, √101.
Если в задачнике сказано: найдите значение выражения с корнем из 2, 3, 5, 6, 7 и т. д., то есть из тех натуральных чисел, которые не содержатся в таблице квадратов, то в правильном ответе √2 может присутствовать (когда не оговорено обратное).
Проведение оценки
В задачах с открытым ответом, если найти значение выражения с корнем и записать его рациональным числом невозможно, результат следует оставить в виде радикала.
Некоторые задания могут потребовать проведения оценки. Например, сравнить 6 и √37. Для решения требуется возвести оба числа в квадрат и сравнить результаты. Из двух чисел больше то, чей квадрат больше. Данное правило работает для всех положительных чисел:
Точно так же решаются задачи, в которых несколько чисел надо расставить в порядке возрастания или убывания.
Пример: расставить по возрастанию 5, √6, √48, √√64.
После возведения в квадрат имеем: 25, 6, 48, √64. Можно было бы еще раз возвести все числа в квадрат, для того чтобы сравнить их с √64, но он равен рациональному числу 8. 6 15 декабря, 2018
Чему равно значение выражения (frac<sqrt<343>><sqrt<7>>) ?
Данное выражение можно пеперисать в виде:
Чему равно значение выражения (frac<sqrt<243>><sqrt<9>>) ?
Данное выражение можно пеперисать в виде:
Какое из данных чисел является значением выражения (frac<(3sqrt<5>)^2><25>) ?
Преобразуем числитель: ((3sqrt<5>)^2 = 3^2 cdot <sqrt<5>>^2 = 9 cdot 5 = 45) . 2 = 4 cdot 7 = 28) .
2 = 4 cdot 7 = 28) .
Найдите значение выражения (frac <sqrt<12>cdot sqrt<540>><sqrt<30>>) .
Перепишем исходное выражение, занеся все числа под один корень:
Разложим выражение под корнем на множители так, чтобы среди них были полные квадраты:
(sqrt <216>= sqrt <4 cdot 9 cdot 6>= 2 cdot 3 cdot sqrt <6>= 6sqrt<6>) .
Найдите значение выражения (frac <sqrt<150>cdot sqrt<216>><sqrt<90>>) .
Перепишем исходное выражение, занеся все числа под один корень:
Разложим выражение под корнем на множители так, чтобы среди них были полные квадраты:
Найдите значение выражения (4sqrt <3>cdot sqrt <2>cdot 4sqrt<6>) .
Преобразуем (sqrt <6>= sqrt <2>cdot sqrt<3>) .
Найдем произведение множителей без корня, а множители с корнем сгруппируем:
(4sqrt <3>cdot sqrt <2>cdot 4 sqrt <2>cdot sqrt <3>=16 cdot sqrt<3>^2 cdot sqrt<2>^2 = 16 cdot 3 cdot 2 = 96) .
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Повторение свойств квадратных корней
Вкратце повторим теорию и напомним основные свойства квадратных корней.
Свойства квадратных корней:
1. 2.
;
3.
;
4.
.
Примеры на упрощение выражений с корнями
Перейдем к примерам использования этих свойств.
Пример 1. Упростить выражение
.
Решение. Для упрощения
число 120 необходимо разложить на простые множители:
. Квадрат суммы раскроем по соответствующей формуле:
.
Пример 2. Упростить выражение
.
Решение. Учтем, что данное выражение имеет смысл не при всех возможных значениях переменной, т. к. в данном выражении присутствуют квадратные корни и дроби, что приводит к «сужению» области допустимых значений. ОДЗ: Ответ. Пример 3. Упростить выражение
к. в данном выражении присутствуют квадратные корни и дроби, что приводит к «сужению» области допустимых значений. ОДЗ: Ответ. Пример 3. Упростить выражение
.
Решение. Видно, что вторая скобка числителя имеет неудобный вид и нуждается в упрощении, попробуем разложить ее на множители с помощью метода группировки.
. Для возможности выносить общий множитель мы упростили корни путем их разложения на множители. Подставим полученное выражение в исходную дробь:
. После сокращения дроби применяем формулу разности квадратов.
Пример на избавление от иррациональности
Пример 4. Освободиться от иррациональности (корней) в знаменателе: а)
.
б) выполним аналогичные действия:
.
Ответ.Пример на доказательство и на выделение полного квадрата в сложном радикале
Пример 5. Докажите равенство
Докажите равенство
.
Доказательство. Воспользуемся определением квадратного корня, из которого следует, что квадрат правого выражения должен быть равен подкоренному выражению:
. Раскроем скобки по формуле квадрата суммы:
, получили верное равенство.
Пример 6. Упростить выражение
.
Решение. Указанное выражение принято называть сложным радикалом (корень под корнем). В данном примере необходимо догадаться выделить полный квадрат из подкоренного выражения. Для этого заметим, что из двух слагаемых
. Подставим это выражение под корень:
Ответ.
.
На этом занятии мы заканчиваем тему «Функция
. Свойства квадратного корня», а на следующем уроке начинаем новую тему «Действительные числа».
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал xenoid.ru (Источник).
2. Математическая школа (Источник).
3. Интернет-портал XReferat.Ru (Источник).
Домашнее задание
1. №357, 360, 372, 373, 382. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Избавьтесь от иррациональности в знаменателе: а) 3. Упростите выражение: а) 4. Докажите тождество
.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
«>
Счет, степени, корни — Математика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений
- Формулы сокращенного умножения
- Квадратный трехчлен и теорема Виета
- Основные свойства степеней
- Основные свойства математических корней
- Основные свойства квадратного корня
Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений
К оглавлению…
При выполнении численных вычислений с большим количеством операций и дробей желательно выполнять следующие рекомендации:
- Переводите десятичные дроби в обыкновенные, т.е. такие у которых есть числитель и знаменатель.
- Не старайтесь посчитать сразу все выражение. Выполняйте вычисления по одному действию, пошагово.
 При этом учтите, что:
При этом учтите, что:
- сначала выполняют операции в скобках;
- затем считают произведения и/или деления;
- потом суммируют или вычитают;
- и в последнюю очередь, если это была многоэтажная дробь, делят уже полностью упрощенный числитель на тоже полностью упрощенный знаменатель;
- причем выполняя в первую очередь операции в скобках также соблюдают ту же последовательность, сначала произведения или деления внутри скобок, потом суммирование или вычитание в скобках, а если внутри скобки есть другая скобка то действия в ней выполняются прежде всего.
- Не спешите умножать и делить «страшные числа». Скорее всего, в одном из следующих действий что-то сократится. Чтобы проще было сократить можно числа раскладывать на простые множители.
- При сложении и вычитании выделяйте в дробях целую часть (если это возможно). При умножении и делении, наоборот, приводите дробь к виду без целой части.
От корней в знаменателе принято избавляться. Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (a — b) является выражение (a + b) и наоборот).
Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (a — b) является выражение (a + b) и наоборот).
При преобразовании или упрощении алгебраических выражений последовательность действий такова:
- Разложить на множители все, что можно разложить на множители.
- Сократить все, что можно сократить.
- И только потом приводить к общему знаменателю. Ни в коем случае не пытайтесь сразу сломя голову приводить к общему знаменателю. Пример будет становиться чем дальше, тем страшнее.
- Снова разложить на множители и сократить.
Для того чтобы перевести десятичную периодическую дробь в обыкновенную (с числителем и знаменателем) необходимо:
- Из числа, стоящего до второго периода в исходной периодической дроби вычесть число, стоящее до первого периода в этой же дроби и записать полученную разность в числитель будущей обыкновенной дроби.

- В знаменателе же записать столько девяток, сколько цифр в периоде исходной дроби, и столько нулей, сколько цифр между запятой и первым периодом.
- Не забыть про целую часть, если она есть.
При решении задач из данной темы также необходимо помнить много сведений из предыдущих тем. Приведём далее основные из них.
Формулы сокращенного умножения
К оглавлению…
При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения:
Последние две формулы также часто удобно использовать в виде:
Квадратный трехчлен и теорема Виета
К оглавлению. ..
..
В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:
Итак, еще раз о теореме Виета:
- Если D < 0 (дискриминант отрицателен), то уравнение корней не имеет и теорему Виета применять нельзя.
- Если D > 0 (дискриминант положителен), то уравнение имеет два корня и теорема Виета прекрасно работает.
- Если D = 0, то уравнение имеет единственный корень, для которого бессмысленно вводить понятие суммы или произведения корней, поэтому теорему Виета тоже не применяем.

Основные свойства степеней
К оглавлению…
У математических степеней есть несколько важных свойств, перечислим их:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:
Основные свойства математических корней
К оглавлению…
Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:
Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:
Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):
Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):
Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:
Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение. Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:
Основные свойства квадратного корня
К оглавлению…
Квадратным корнем называется математический корень второй степени:
Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:
Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:
Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:
При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:
8.1 Упрощение выражений с помощью корней — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Упрощение выражений с корнями
- Оценка и приблизительные корни
- Упрощение переменных выражений с корнями
Приготовься 8.1
Прежде чем начать, пройдите этот тест на готовность.
Упрощение: ⓐ (−9)2(−9)2 ⓑ −92−92 ⓒ (−9)3.(−9)3.
Если вы пропустили эту проблему, просмотрите пример 2.21.
Приготовься 8.2
Округлите 3.8463.846 до сотых.
Если вы пропустили эту проблему, просмотрите пример 1.34.
Приготовься 8.3
Упрощение: ⓐ x3·x3x3·x3 ⓑ y2·y2·y2y2·y2·y2 ⓒ z3·z3·z3·z3.z3·z3·z3·z3.
Если вы пропустили эту проблему, просмотрите пример 5.12.
Упрощение выражений с корнями
В разделе «Основы» мы кратко рассмотрели квадратные корни. Помните, что когда действительное число n умножается само на себя, мы пишем n2n2 и читаем ‘ N в квадрате». Это число называется квадратом х , а х называется квадратным корнем. Например,
Помните, что когда действительное число n умножается само на себя, мы пишем n2n2 и читаем ‘ N в квадрате». Это число называется квадратом х , а х называется квадратным корнем. Например,
132 читается как «13 в квадрате» 169 называется квадратом из 13, так как 132=16913 является квадратным корнем из 169132 читается как «13 в квадрате» 169 называется квадратом из 13, так как 132=16913 является квадратным корнем из 169
Квадрат и квадратный корень числа
Квадрат
Если n2=m, то квадрат n. Если n2=m, то квадрат n.
Квадратный корень
Если n2=m, то это квадратный корень из m. Если n2=m, то это квадратный корень из m.
Обратите внимание (−13) 2 = 169, поэтому −13 также является квадратным корнем из 169. Следовательно, и 13, и −13 являются квадратными корнями из 169.
Итак, каждое положительное число имеет два квадратных корня — положительный и отрицательный. Что, если бы нам нужен был только положительный квадратный корень из положительного числа? Мы используем подкоренной знак и пишем m,m, что обозначает положительный квадратный корень из 9.0034 м . Положительный квадратный корень также называют главным квадратным корнем. Этот символ, как и другие радикалы, которые будут введены позже, являются группирующими символами.
Мы также используем знак радикала для квадратного корня из нуля. Потому что 02=0,02=0,0=0,0=0. Обратите внимание, что ноль имеет только один квадратный корень.
Обозначение квадратного корня
неправильно читается как «квадратный корень из m». Если n2=m, то nn=m, при n≥0. mis читается как «квадратный корень из m». Если n2=m, то nn=m, при n≥0.
Мы знаем, что каждое положительное число имеет два квадратных корня и знак подкореня указывает на положительный. Мы пишем 169=13,169=13. Если мы хотим найти отрицательный квадратный корень числа, мы помещаем минус перед знаком радикала. Например, −169=−13,−169=−13.
Мы пишем 169=13,169=13. Если мы хотим найти отрицательный квадратный корень числа, мы помещаем минус перед знаком радикала. Например, −169=−13,−169=−13.
Пример 8.1
Упрощение: ⓐ 144144 ⓑ −289,−289.
Решение
ⓐ
| Поскольку 122=144,122=144. | 1212 |
ⓑ
| −289−289 | |
| Поскольку 172=289172=289 и перед знаком корня стоит минус. | −17−17 |
Попытайся 8.1
Упрощение: ⓐ −64−64 ⓑ 225,225.
Попытайся 8.2
Упрощение: ⓐ 100100 ⓑ −121.−121.
Можем ли мы упростить -49?-49? Существует ли число, квадрат которого равен −49?−49?
()2=-49()2=-49
Любое положительное число в квадрате является положительным. Любое отрицательное число в квадрате положительно. Не существует действительного числа, равного −49..−49. Квадратный корень из отрицательного числа не является действительным числом.
Любое отрицательное число в квадрате положительно. Не существует действительного числа, равного −49..−49. Квадратный корень из отрицательного числа не является действительным числом.
Пример 8.2
Упрощение: ⓐ −196−196 ⓑ −64,−64.
Решение
ⓐ
| Не существует действительного числа, квадрат которого равен −196,−196. | -196 не является действительным числом. -196 не является действительным числом. |
ⓑ
| Негатив перед радикалом. | −8−8 |
Попытайся 8.3
Упрощение: ⓐ −169−169 ⓑ −81,−81.
Попытайся 8.4
Упрощение: ⓐ −49−49 ⓑ −121,−121.
До сих пор мы говорили только о квадратах и квадратных корнях. Давайте теперь расширим нашу работу, включив в нее высшие силы и высшие корни.
Давайте сначала рассмотрим словарь.
Пишем:Говорим:n2nsквадратn3nкуб n4в четвертой степениn5в пятой степениМы пишем:Говорим:n2nsквадрат n3nкуб n4в четвертой степениn5в пятой степени
Термины «квадрат» и «куб» происходят от формул площади квадрата и объема куба.
Будет полезно иметь таблицу степеней целых чисел от −5 до 5. См. рис. 8.2.
Рисунок 8.2
Обратите внимание на знаки в таблице. Все степени положительных чисел, конечно, положительны. Но когда у нас есть отрицательное число, четные степени положительны, а нечетные степени отрицательны. Мы скопируем строку со степенью −2, чтобы вам было проще это увидеть.
Теперь мы расширим определение квадратного корня на более высокие корни.
Если bn=a, то bi является корневым корнем a. Главный корень a записывается и называется индексом подкореня. Если bn=a, то bi является корнем a. Главный корень a записывается и называется индексом подкореня.
Точно так же, как мы используем слово «куб» для b 3 , мы используем термин «кубический корень» для a3.a3.
Мы можем обратиться к рисунку 8.2, чтобы найти более высокие корни.
43=6434=81(-2)5=-32643=4814=3-325=-243=6434=81(-2)5=-32643=4814=3-325=-2
Можем ли мы получить четный корень из отрицательного числа? Мы знаем, что квадратный корень из отрицательного числа не является действительным числом. То же верно для любого четного корня. Даже корней отрицательных чисел не являются действительными числами. Нечетные корней отрицательных чисел являются действительными числами.
Свойства anan
Когда n — четное число, а
- a≥0,a≥0, то anan — действительное число.
- a<0,a<0, то anan не является действительным числом.
Когда n является нечетным числом, anan является действительным числом для всех значений от до .
Мы применим эти свойства в следующих двух примерах.
Пример 8.3
Упрощение: ⓐ 643643 ⓑ 814814 ⓒ 325,325.
Решение
ⓐ
| 643643 | |
| Поскольку 43=64,43=64. | 44 |
ⓑ
Так как (3)4=81. (3)4=81. (3)4=81. | 33 |
ⓒ
| Так как (2)5=32.(2)5=32. | 22 |
Попытайся 8,5
Упрощение: ⓐ 273273 ⓑ 25642564 ⓒ 2435,2435.
Попытайся 8,6
Упрощение: ⓐ 1000310003 ⓑ 164164 ⓒ 10245,10245.
В этом примере обратите внимание на отрицательные знаки, а также на четные и нечетные степени.
Пример 8.4
Упрощение: ⓐ −1253−1253 ⓑ −164−164 ⓒ −2435.−2435.
Решение
ⓐ
| −1253−1253 | |
| Поскольку (−5)3=−125.(−5)3=−125. | −5−5 |
ⓑ
| −164−164 | |
Подумайте, (?)4=-16. (?)4=-16. Ни одно действительное число, возведенное в четвертую степень, не является отрицательным. (?)4=-16. Ни одно действительное число, возведенное в четвертую степень, не является отрицательным. | Не настоящее число. |
ⓒ
| −2435−2435 | |
| Поскольку (−3)5=−243.(−3)5=−243. | −3−3 |
Попытайся 8,7
Упрощение: ⓐ −273−273 ⓑ −2564−2564 ⓒ −325,−325.
Попытайся 8,8
Упрощение: ⓐ −2163−2163 ⓑ −814−814 ⓒ −10245.−10245.
Оценка и приблизительные корни
Когда мы видим число со знаком радикала, мы часто не задумываемся о его числовом значении. Хотя мы, наверное, знаем, что 4=2,4=2, каково значение 2121 или 503?503? В некоторых ситуациях имеет смысл быстрая оценка, а в других удобно использовать десятичную аппроксимацию.
Чтобы получить числовую оценку квадратного корня, мы ищем совершенные квадратные числа, ближайшие к подкоренному. Чтобы найти оценку 11,11, мы видим, что 11 находится между числами в точном квадрате 9 и 16, ближе к 9. Тогда его квадратный корень будет между 3 и 4, но ближе к 3.
Чтобы найти оценку 11,11, мы видим, что 11 находится между числами в точном квадрате 9 и 16, ближе к 9. Тогда его квадратный корень будет между 3 и 4, но ближе к 3.
Точно так же, чтобы оценить 913 913, мы видим, что 91 находится между числами в совершенном кубе 64 и 125. Тогда кубический корень будет между 4 и 5.
Пример 8,5
Оцените каждый корень между двумя последовательными целыми числами: ⓐ 105105 ⓑ 433,433.
Решение
ⓐ Подумайте о числах в идеальном квадрате, ближайших к 105. Составьте небольшую таблицу этих идеальных квадратов и их квадратных корней.
Найдите 105 между двумя последовательными правильными квадратами. | |
| 105105 находится между их квадратными корнями. |
ⓑ Точно так же мы находим 43 между двумя числами в совершенном кубе.
| Найдите 43 между двумя последовательными совершенными кубами. | |
| 433433 находится между их кубическими корнями. |
Попытайся 8,9
Оценить каждый корень между двумя последовательными целыми числами:
ⓐ 3838 ⓑ
3
Попытайся 8.
 10
10Оценить каждый корень между двумя последовательными целыми числами:
ⓐ 8484 ⓑ 15231523
Существуют математические методы аппроксимации квадратных корней, но в настоящее время большинство людей используют калькулятор для нахождения квадратных корней. Чтобы найти квадратный корень, вы будете использовать клавишу xx на вашем калькуляторе. Чтобы найти кубический корень или любой корень с более высоким индексом, вы будете использовать ключ xyxy.
При использовании этих клавиш вы получаете приблизительное значение. Это приближение, точное к количеству цифр, отображаемых на дисплее вашего калькулятора. Символ приближения ≈≈ и читается «приблизительно».
Предположим, ваш калькулятор имеет 10-разрядный дисплей. Вы бы увидели, что
5,2.2360679788888888 г.
Откуда мы знаем, что эти значения являются приблизительными, а не точными? Посмотрите, что произойдет, если мы возведем их в квадрат:
.(2,236067978)2=5,000000002(2,24)2=5,0176(3,105422799)4=92,999999991(3,11)4=93,54
1(2,236067978)2=5,000000002(2,24)2=5,0176(3,105422799)4=92,999999991(3,11)4=93,545 Их квадраты близки к 5, но не равны в точности 5. Четвертые степени близки к 93, но не равны 93.
Четвертые степени близки к 93, но не равны 93.
Пример 8,6
Округлить до двух знаков после запятой: ⓐ 1717 ⓑ 4
ⓒ 514,514.
Решение
ⓐ
| Используйте ключ квадратного корня калькулятора. | 4,123105626…4,123105626… |
| Округлить до двух знаков после запятой. | 4.124.12 |
| 17≈4,1217≈4,12 |
ⓑ
| 4 | |
| Используйте клавишу калькулятора xyxy. | 3,6510…3,6510… |
| Округлить до двух знаков после запятой. | 3. 663.66 663.66 |
| 493≈3,66493≈3,66 |
ⓒ
| 514514 | |
| Используйте клавишу калькулятора xyxy. | 2,6723451177…2,6723451177… |
| Округлить до двух знаков после запятой. | 2.672.67 |
| 514≈2,67514≈2,67 |
Попытайся 8.11
Округлить до двух знаков после запятой:
ⓐ 1111 ⓑ 713713 ⓒ 1274,1274.
Попытайся 8.12
Округлить до двух знаков после запятой:
ⓐ 1313 ⓑ 843843 ⓒ 984,984.
Упрощение выражений переменных с помощью корней
Нечетный корень числа может быть как положительным, так и отрицательным. Например,
А как же четный корень? Нам нужен основной корень, поэтому 6254=5,6254=5.
Но заметьте,
Как убедиться, что корень четвертой степени из −5, возведенный в четвертую степень, равен 5? Мы можем использовать абсолютное значение. |−5|=5.|−5|=5. Поэтому мы говорим, что когда n четно ann=|a|.ann=|a|. Это гарантирует, что главный корень положителен.
Упрощение нечетных и четных корней
Для любого целого числа n≥2,n≥2,
когда индекс нечетный=когда индекс четныйann=|a|когда индекс нечетный=когда индекс четныйann=|a|
Мы должны использовать знаки абсолютного значения, когда берем четный корень выражения с переменной в радикале.
Пример 8,7
Упрощение: ⓐ x2x2 ⓑ n33n33 ⓒ p44p44 ⓓ y55.y55.
Решение
ⓐ Мы используем абсолютное значение, чтобы получить положительный корень.
Поскольку индекс nn четный, ann=|a|. ann=|a|. ann=|a|. | |х||х| |
ⓑ Это корень с нечетным индексом, поэтому знак абсолютного значения не нужен.
| Поскольку индекс nn нечетный, ann=a.ann=a. | нн |
ⓒ
| р44р44 | |
| Так как индекс nis evenann=|a|.nis evenann=|a|. | |р||р| |
ⓓ
| y55y55 | |
| Поскольку индекс nn нечетный, ann=a.ann=a. | г.г. |
Попытайся 8.13
Упрощение: ⓐ b2b2 ⓑ w33w33 ⓒ m44m44 ⓓ q55. q55.
q55.
Попытайся 8.14
Упрощение: ⓐ y2y2 ⓑ p33p33 ⓒ z44z44 ⓓ q55.q55.
А как насчет квадратных корней из высших степеней переменных? Свойство Степени Экспонент говорит (am)n=am·n. (am)n=am·n. Таким образом, если возвести в квадрат м , показатель степени станет 2 м .
(ам)2=а2м(ам)2=а2м
Глядя теперь на квадратный корень,
a2mSince(am)2=a2m.(am)2Sincenisevenann=|a|.|am|Soa2m=|am|.a2mSince(am)2=a2m.(am)2Sincenisevenann=|a|.|am|Soa2m =|ам|.
Мы применяем эту концепцию в следующем примере.
Пример 8,8
Упрощение: ⓐ x6x6 ⓑ y16.y16.
Решение
ⓐ
| х6х6 | |
| Поскольку (x3)2=x6.(x3)2=x6. | (x3)2(x3)2 |
Поскольку индекс nn четен, an=|a|. an=|a|. an=|a|. | |x3||x3| |
ⓑ
| Так как (y8)2=y16.(y8)2=y16. | (у8)2(у8)2 |
| Поскольку индекс nn четен, ann=|a|.ann=|a|. | y8y8 |
| В этом случае знак абсолютного значения не нужен, так как y8y8 положителен. |
Попытайся 8.15
Упрощение: ⓐ y18y18 ⓑ z12.z12.
Попытайся 8.16
Упрощение: ⓐ m4m4 ⓑ b10.b10.
В следующем примере используется та же идея для более высоких корней.
Пример 8,9
Упрощение: ⓐ y183y183 ⓑ z84.z84.
Решение
ⓐ
| y183y183 | |
Так как (y6)3=y18. (y6)3=y18. (y6)3=y18. | (у6)33(у6)33 |
| Поскольку nn нечетно, ann=a.ann=a. | y6y6 |
ⓑ
| Поскольку (z2)4=z8.(z2)4=z8. | (з2)44(з2)44 |
| Так как z2z2 положительно, нам не нужен знак абсолютного значения. | з2з2 |
Попытайся 8.17
Упрощение: ⓐ u124u124 ⓑ v153.v153.
Попытайся 8.18
Упрощение: ⓐ c205c205 ⓑ d246d246
В следующем примере у нас теперь есть коэффициент перед переменной. Понятие a2m=|am|a2m=|am| работает примерно так же.
16r22=4|r11|потому что (4r11)2=16r22.16r22=4|r11|потому что (4r11)2=16r22.
Но обратите внимание, что 25u8=5u425u8=5u4 и знак абсолютного значения не требуется, так как u 4 всегда положительно.
Пример 8.10
Упрощение: ⓐ 16n216n2 ⓑ −81c2.−81c2.
Решение
ⓐ
| 16н216н2 | |
| Поскольку (4n)2=16n2.(4n)2=16n2. | (4н)2(4н)2 |
| Поскольку индекс nn четен, ann=|a|.ann=|a|. | 4|n|4|n| |
ⓑ
| Так как (9c)2=81c2.(9c)2=81c2. | −(9с)2−(9с)2 |
| Поскольку индекс nn четен, ann=|a|.ann=|a|. | −9|с|−9|с| |
Попытайся 8.19
Упрощение: ⓐ 64x264x2 ⓑ −100p2.−100p2.
Попытайся 8.20
Упрощение: ⓐ 169y2169y2 ⓑ −121y2. −121y2.
−121y2.
Этот пример просто развивает идею, поскольку имеет корни с более высоким индексом.
Пример 8.11
Упрощение: ⓐ 64p6364p63 ⓑ 16q124.16q124.
Решение
ⓐ
| Перепишите 64p664p6 как (4p2)3.(4p2)3. | (4п2)33(4п2)33 |
| Извлеките кубический корень. | 4p24p2 |
ⓑ
| Перепишите подкоренное число в четвертой степени. | (2q3)44(2q3)44 |
| Возьми четвертый корень. | 2|q3|2|q3| |
Попытайся 8.
 21
21Упрощение: ⓐ 27x27327x273 ⓑ 81q284,81q284.
Попытайся 8.22
Упрощение: ⓐ 125qq93 ⓑ 243q255.243q255.
В следующих примерах есть две переменные.
Пример 8.12
Упрощение: ⓐ 36x2y236x2y2 ⓑ 121a6b8121a6b8 ⓒ 64p63q93.64p63q93.
Решение
ⓐ
| 36x2y236x2y2 | |
| Поскольку (6xy)2=36x2y2(6xy)2=36x2y2 | (6xy)2(6xy)2 |
| Извлеките квадратный корень. | 6|ху|6|ху| |
ⓑ
| 121a6b8121a6b8 | |
| Поскольку (11a3b4)2=121a6b8(11a3b4)2=121a6b8 | (11a3b4)2(11a3b4)2 |
Извлеките квадратный корень. | 11|а3|б411|а3|б4 |
ⓒ
| 64p63q9364p63q93 | |
| Поскольку (4p21q3)3=64p63q9(4p21q3)3=64p63q9 | (4p21q3)33(4p21q3)33 |
| Извлеките кубический корень. | 4p21q34p21q3 |
Попытайся 8.23
Упрощение: ⓐ 100a2b2100a2b2 ⓑ 144p12q20144p12q20 ⓒ 8x30y1238x30y123
Попытайся 8.24
Упрощение: ⓐ 225m2n2225m2n2 ⓑ 169x10y14169x10y14 ⓒ 27w36z15327w36z153
Раздел 8.1 Упражнения
Практика ведет к совершенству
Упрощение выражений с помощью корней
В следующих упражнениях упрощайте.
1.
ⓐ 6464 ⓑ −81−81
2.
ⓐ 169169 ⓑ −100−100
3.
ⓐ 1
ⓑ −1−14.
ⓐ 144144 ⓑ −121−121
5.
ⓐ 4949 ⓑ −0,01−0,01
6.
ⓐ 6412164121 ⓑ −0,16−0,16
7.
ⓐ −121−121 ⓑ −289−289
8.
ⓐ −400−400 ⓑ −36−36
9.
ⓐ −225−225 ⓑ −9−9
10.
ⓐ −49−49 ⓑ −256−256
11.
ⓐ 21632163 ⓑ 25642564
12.
ⓐ 273273 ⓑ 164164 ⓒ 24352435
13.
ⓐ 51235123 ⓑ 814814 ⓒ 1515
14.
ⓐ 12531253 ⓑ 12
964 ⓒ 1024510245 15.
ⓐ −83−83 ⓑ −814−814 ⓒ −325−325
16.
ⓐ −643−643 ⓑ −164−164 ⓒ −2435−2435
17.
ⓐ −1253−1253 ⓑ −12964−12964 ⓒ −10245−10245
18.
ⓐ −5123−5123 ⓑ −814−814 ⓒ −15−15
Оценка и приблизительные корни
В следующих упражнениях оцените каждый корень между двумя последовательными целыми числами.
19.
ⓐ 7070 ⓑ 713713
20.
ⓐ 5555 ⓑ 11
3
21.
ⓐ 200200 ⓑ 13731373
22.
ⓐ 172172 ⓑ 20032003
В следующих упражнениях аппроксимируйте каждый корень и округлите его до двух знаков после запятой.
23.
ⓐ 1919 ⓑ 8
ⓒ 4
24.
ⓐ 2121 ⓑ
3 ⓒ 10141014
25.
ⓐ 5353 ⓑ 14731473 ⓒ 45244524
26.
ⓐ 4747 ⓑ 16331633 ⓒ 52745274
Упрощение выражений переменных с помощью корней
В следующих упражнениях при необходимости упростите использование абсолютных значений.
27.
ⓐ u55u55 ⓑ v88v88
28.
ⓐ a33a33 ⓑ b99b99
29.
ⓐ y44y44 ⓑ m77m77
30.
ⓐ k88k88 ⓑ p66p66
31.
ⓐ x6x6 ⓑ y16y16
32.
ⓐ a14a14 ⓑ w24w24
33.
ⓐ x24x24 ⓑ y22y22
34.
ⓐ a12a12 ⓑ b26b26
35.
ⓐ x93x93 ⓑ y124y124
36.
ⓐ a105a105 ⓑ b273b273
37.
ⓐ m84m84 ⓑ n205n205
38.
ⓐ r126r126 ⓑ s303s303
39.
ⓐ 49x249x2 ⓑ −81×18−81×18
40.
ⓐ 100y2100y2 ⓑ −100m32−100m32
41.
ⓐ 121m20121m20 ⓑ −64a2−64a2
42.
ⓐ 81x3681x36 ⓑ −25×2−25×2
43.
ⓐ 16x8416x84 ⓑ 64y12664y126
44.
ⓐ −8c93−8c93 ⓑ 125d153125d153
45.
ⓐ 216a63216a63 ⓑ 32b20532b205
46.
ⓐ 128r147128r147 ⓑ 81s24481s244
47.
ⓐ 144x2y2144x2y2 ⓑ 169w8y10169w8y10 ⓒ 8a51b638a51b63
48.
ⓐ 196a2b2196a2b2 ⓑ 81p24q681p24q6 ⓒ 27p45q9327p45q93
49.
ⓐ 121a2b2121a2b2 ⓑ 9c8d129c8d12 ⓒ 64x15y66364x15y663
50.
ⓐ 225x2y2z2225x2y2z2 ⓑ 36r6s2036r6s20 ⓒ 125y18z273125y18z273
Письменные упражнения
51.
Почему не существует действительного числа, равного -64?-64?
52.
В чем разница между 9292 и 9?9?
53.
Объясните, что означает n th корень числа.
54.
Объясните разницу между нахождением n th корня числа при четном индексе и при нечетном.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Если большинство ваших чеков было:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими источниками информации. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет — не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Упрощение подкоренных выражений — ChiliMath
Подкоренное выражение состоит из трех частей:
подкоренной символ , подкоренное число и подкоренное число и индекс
В этом руководстве основное внимание уделяется упрощению подкоренных выражений с индексом 2. Этот тип подкореня широко известен как квадратный корень.
Компоненты подкоренного выражения
Начав с одного подкоренного выражения, мы хотим разбить его на части «меньших» подкоренных выражений. Мы надеемся, что некоторые из этих фрагментов можно еще больше упростить, потому что подкоренные члены (элементы внутри символа) представляют собой идеальные квадраты. Помните, квадратный корень из идеальных квадратов получается очень красиво!
Нам нужно понять, как может выглядеть идеальное квадратное число или выражение. Давайте сделаем это, пройдясь по конкретным примерам.
Давайте сделаем это, пройдясь по конкретным примерам.
Examples of Perfect Squares
| Numbers that are perfect squares: |
|---|
| 4 |
| 9 |
| 16 |
| 25 |
| 36 |
| 49 |
Что делает их идеальными квадратами?
Обратите внимание, что квадратный корень из каждого приведенного выше числа дает ответ в виде целого числа. Думайте о них как о совершенно благопристойных числах.
Кроме того, эти числа являются полными квадратами, потому что все они могут быть выражены в виде экспоненциальных чисел с четными степенями. Полномочия не обязательно должны быть «2» все время. Пока степени являются четными числами, такими как 2, 4, 6, 8 и т. д., они считаются полными квадратами. Если подумать, пара любых чисел — это идеальный квадрат!
Пока степени являются четными числами, такими как 2, 4, 6, 8 и т. д., они считаются полными квадратами. Если подумать, пара любых чисел — это идеальный квадрат!
Более того, приведенные выше выражения переменных также являются полными квадратами, потому что все переменные имеют четные степени или степени.
Примеры упрощения подкоренных выражений
Пример 1: Упростить подкоренное выражение \sqrt {16} .
Это просто! Число 16, очевидно, является идеальным квадратом, потому что я могу найти целое число, которое при умножении само на себя дает целевое число. Должно быть 4, так как (4)(4) = 4 2 = 16. Таким образом, ответ равен 9.0005
Ниже приведен скриншот ответа калькулятора , который подтверждает наш ответ.
Пример 2: Упростите подкоренное выражение \sqrt {60}.
Вы можете методом проб и ошибок найти число, которое в квадрате дает 60. Пройдя некоторые квадраты натуральных чисел…
Ответ должен быть некоторым числом n , найденным между 7 и 8. Таким образом, мы ожидаем, что квадратный корень из 60 должен содержать десятичные значения. Чтобы упростить это радикальное число, попробуйте разложить его на множители так, чтобы один из множителей был полным квадратом. При беглом рассмотрении число 4 — это идеальный квадрат, который может делить 60.
Таким образом, мы ожидаем, что квадратный корень из 60 должен содержать десятичные значения. Чтобы упростить это радикальное число, попробуйте разложить его на множители так, чтобы один из множителей был полным квадратом. При беглом рассмотрении число 4 — это идеальный квадрат, который может делить 60.
Итак, наш ответ…
И для проверки нашего калькулятора…
Какое правило я использовал, чтобы разбить их как произведение квадратных корней? Вот!
Запомните приведенное ниже правило, так как вы будете использовать его снова и снова.
ПРАВИЛО ПРОИЗВЕДЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- Это означает, что квадратный корень из произведения из a и b равен 903 903 произведению их отдельных квадратных корней.
Пример 3: Упростите подкоренное выражение \sqrt {72} .
Всегда ищите совершенный квадратный множитель подкоренного числа. После некоторых проб и ошибок я обнаружил, что любой из идеальных квадратов 4, 9 и 36 может разделить 72. Итак, какой из них мне выбрать? На самом деле, любой из трех коэффициентов идеального квадрата должен работать. Однако лучший вариант — максимально возможный, поскольку это значительно сокращает количество шагов в решении.
Итак, какой из них мне выбрать? На самом деле, любой из трех коэффициентов идеального квадрата должен работать. Однако лучший вариант — максимально возможный, поскольку это значительно сокращает количество шагов в решении.
Сравните, что произойдет, если я упрощу подкоренное выражение, используя каждый из трех возможных множителей совершенного квадрата. Выбор самого большого делает решение очень коротким и точным.
- Начните с 4
- Начните с 9
- Начните с
Введение
Корни как степени, свойства степеней, важное свойство, произведение и частное корней
Решенные упражнения: упрощение выражений с корнями
Корень степени n = 2 известен как квадратный корень .
Пример:
Квадратный корень из 9 равен 3, потому что 3 в степени двойки равно 9.
$$ \sqrt{9} = 3 $$
Корень степени n = 3 известен как кубический корень .
Пример:
Кубический корень из -8 равен -2, потому что -2 в степени три равно -8.

$$ \sqrt[3]{-8} = -2 $$
- Нахождение квадратных корней.
- Найдите кубический корень.
- Найти n -го корня.
- Упростите выражения, используя правила произведения и частного для радикалов.
- Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Когда подкоренное число a положительно, a2=a. Когда подкоренное число отрицательное, результат не является действительным числом.
- Кубический корень числа — это число, которое при трехкратном использовании в качестве множителя само с собой дает исходное число.
 Кубический корень может быть положительным или отрицательным в зависимости от знака подкоренного числа. Следовательно, для любого действительного числа a , мы имеем свойство a33=a.
Кубический корень может быть положительным или отрицательным в зависимости от знака подкоренного числа. Следовательно, для любого действительного числа a , мы имеем свойство a33=a. - При работе с корнями n th, n определяет применимое определение. Мы используем ann=a, когда n нечетно и ann=|a| когда n четно. Когда n четно, отрицательный корень n обозначается знаком минус перед знаком корня.
- Чтобы упростить квадратные корни, найдите наибольший совершенный квадратный множитель подкоренного числа, а затем примените правило произведения или частного для радикалов.
- Чтобы упростить кубические корни, найдите наибольший совершенный кубический множитель подкоренного числа и затем примените правило произведения или частного для радикалов.
- Чтобы упростить корни n , найдите множители, мощность которых равна индексу n , а затем примените правило произведения или частного для радикалов.
 Как правило, процесс упрощается, если вы работаете с простой факторизацией подкоренного числа.
Как правило, процесс упрощается, если вы работаете с простой факторизацией подкоренного числа. - Упростить радикальные выражения, используя правило произведения и частного для радикалов.
- Используйте формулы, содержащие радикалы.
- Оценить данные функции квадратного корня и кубического корня.
- В начале алгебры мы обычно предполагаем, что все переменные выражения в радикале являются положительными. Это позволяет нам сосредоточиться на упрощении радикалов без технических проблем, связанных с принципом 9.1574 н -й корень.
- Чтобы упростить подкоренные выражения, найдите множители подкоренного числа со степенями, соответствующими индексу. Если они найдены, их можно упростить, применяя правила произведения и частного для радикалов, а также свойство ann=a, где a положительно.
- . 8. 4.4a4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3c4b3.
10. 50x6y4
11. 64R2S6T5
12. 144R8S6T2
13. (x+1) 2
14. (2x+3) 2
15. 4 (3x-1) 2
16. 9000 (2x+3)2
17. 9x325y2
18. 4x59y4
19. m736n4
20. 147m9n6
21. 2r2s525t4
22. 36r5s2t6
23. 27a33
24. 125b33
25. 250x4y33
26. 162a3b53
27. 64x3y6z93
28. 216x12y33
29. 8x3y43
30. 27x5y33
31. a4b5c63
32. a7b5c33
33. 8x427y33
34. x5125y63
35. 360r5s12t133
36. 540r3s2t93
37. 81×44
38. x4y44
39. 16x4y84
40. 81x12y44
41. a4b5c64
42. 54a6c84
43.
 128×64
128×6444. 243y74
45. 32m10n55
46. 37m9n105
47. −34×2
48. 79y2
49. −5x4x2y
50 . −3y16x3y2
51. 12ABA5B3
52. 6A2B9A7B2
53. 2xтарный 8×63
54. −5x2trot27x33
55. 2Ab> — 8A4B53
956. 5A27BTRIT. как подкоренное выражение с коэффициентом 1.57. 52x
58. 23y
59. 2×3
60. 3Y2
61. AB10A
62. 2AB2A
63. M2NMN
64. 2M2N333N
65. 5 2 2×3
. 3 5y3
67. 2x⋅33
68. 3y⋅23
Предположим, что переменная может представлять любое действительное число, а затем упростить.
69. 4×2
70. 25y2
71. 8y33
72. 125a33
73. 64×44
740005
75. 36A4
76. 100A8
77. 4A6
78. A10
79. 18A4B5
80. 48A5B3
81. 128x6y86
82. A6B86
S
S
S
S
S
S
S
s
s
s
s
s
s
s
s
s
s
9 y -отрезки для любого графа будут иметь форму (0, y ), где y — действительное число.
 Следовательно, чтобы найти у -перехваты, задаем х = 0 и найти y . Найдите и -перехваты для следующего.
Следовательно, чтобы найти у -перехваты, задаем х = 0 и найти y . Найдите и -перехваты для следующего. 83. y=x+4−1
84. y=x+1−3
85. y=x−13+2
86. y=x+13−3
Используйте формула расстояния для расчета расстояния между заданными двумя точками.
87. (5, –7) и (3, –8)
88. (–9, 7) и (–8, 4)
89. (–3, –4) и (3, −6)
90. (−5, −2) и (1, −6)
91. (-1, 1) и (-4, 10)
92. (8, -3) и (2, -12)
Факторами подкоренное число и затем упрощение. ( Предположим, что все выражения положительны. )
93. x2−6x+9
94. x2−10x+25
95. 4×2+1+12x+9
96,000
97. Скорость транспортного средства до включения тормозов можно оценить по длине следов заноса на дороге. На сухом асфальте скорость v в милях в час можно оценить по формуле v=5d, где d представляет длину следов заноса в футах.
 Оцените скорость автомобиля перед торможением на сухом асфальте, если следы заноса остаются на расстоянии 36 футов.
Оцените скорость автомобиля перед торможением на сухом асфальте, если следы заноса остаются на расстоянии 36 футов.98. Радиус r сферы можно рассчитать по формуле r=6π2V32π, где V представляет объем сферы. Каков радиус сферы, если объем равен 36π кубических сантиметров?
Период T маятника в секундах определяется формулой
T=2πL32
, где L представляет длину в футах. Вычислите период, зная следующие длины. Укажите точное значение, а приблизительное значение округлить до десятых долей секунды.
99. 8 футов
100. 32 фута
101. 1/2 фута
102. 1/8 фута
Время,
за
t t 9 секунд свободного падения объекта определяется по формуле т=s4, где s представляет собой расстояние падения в футах. Рассчитайте время, за которое объект упадет, зная следующие расстояния.
 Укажите точное значение, а приблизительное значение округлить до десятых долей секунды.
Укажите точное значение, а приблизительное значение округлить до десятых долей секунды. 103. 48 футов
104. 80 футов
105. 192 фута
106. 288 футов
Часть C: радикальные функции
915 вычислить следующую функцию.
107. f(x)=x−1, найти f(1), f(2) и f(5)
108. f(x)=x+5, найти f(−5), f( −1), и f(20)
109. f(x)=x+3, найти f(0), f(1) и f(16)
110. f(x)=x−5 , найти f(0), f(1) и f(25)
111. g(x)=x3, найти g(−1), g(0) и g(1)
112. g (x)=x+73, найти g(−15), g(−7) и g(20)
113. g(x)=x3−2, найти g(−1), g(0) , и g(8)
114. g(x)=x−13+2, найти g(0), g(2) и g(9)
Для каждой функции заполнить таблицу.
115. f(x)=x+1
116. f(x)=x−2
117. f(x)=x3+1
118. f(x)=x+23
Часть D: Дискуссионная доска
119. Задайте значение для x так, чтобы x2≠x. Объясните, почему важно предполагать, что переменные представляют положительные числа.

120. Изучите и обсудите достижения Кристофа Рудольфа. За что ему приписывают?
121. Исследуйте и обсудите методы, использовавшиеся для вычисления квадратных корней до повсеместного использования электронных калькуляторов.
122. Что такое сурд и откуда произошло это слово?
Ответы
1: 6A
3: XY
5: 6x5x
7: 7Aba
9: 3x2y5xy
11: 8RS3T2T
13: x+1
15: 2 (3x — 1).
17: 3xx5y
19: m3m6n2
21: rs22s5t2
23: 3a
25: 5xy⋅2×3
27: 4xy2z3
29: 2xy⋅y3
31: abc2⋅ab23
33: 2x⋅x33г
35: 2rs4t4⋅45r2t3
37: 3x
39: 2xy2
41: abc⋅bc24
43: 2x⋅8×24
45: 2m2n
47: −6x
49: −10x2y
51 : 12a3b2ab
53: 4×3
55: −4a2b2⋅ab23
57: 50x
59: 12×2
61: 10a3b2
63: m5n3
65: 250×3
67: 24×33
69: 2 |х|
71: 2у
73: 2|х|
75:6а2
77:2|а3|
79: 3A2B22B
81: 2 | xy | ⋅2y26
83: (0, 1)
85: (0, 1)
87: 5
89: 210
91: 310
4 89: 210
91: 310
44 89: 210
91: 310
40004: 210
91: 310
40004: 210
91: 310
93: x−3
95: 2x+3
97: 30 миль в час
99: π≈3,1 секунды
101: π/4≈0,8 секунды
100:5:000 3≈90,1 секунды 90,1 секунды 23≈3,5 секунды
107: f(1)=0, f(2)=1 и f(5)=2
109: f(0)=3, f(1)=4 и f( 16)=7
111: g(−1)=−1, g(0)=0 и g(1)=1
113: g(−1)=−3, g(0)=−2 и g(8)=0
115:
117:
8.
 3 Сложение и вычитание подкоренных выражений
3 Сложение и вычитание подкоренных выраженийЦели обучения
- Сложение и вычитание подкоренных выражений.
- Упростите радикальные выражения, включающие одинаковые радикалы.
Сложение и вычитание подкоренных выражений
Сложение и вычитание подкоренных выражений аналогично сложению и вычитанию одинаковых терминов. Радикалы считаются похожими на радикалы Радикалы, которые имеют один и тот же индекс и подкоренное число, или похожие радикалы. Термин, используемый при обращении к подобным радикалам, когда они имеют один и тот же индекс и подкоренное число. Например, термины 35 и 45 содержат одинаковые радикалы и могут быть добавлены с использованием распределительного свойства следующим образом:
Обычно мы не показываем шаг, связанный с распределительным свойством, а просто пишем
При добавлении членов с одинаковыми корнями добавляйте только коэффициенты; коренная часть остается прежней.
Пример 1: Добавить: 32+22.

Решение: Термины содержат одинаковые радикалы; поэтому добавляем коэффициенты.
Ответ: 52
Вычитание выполняется аналогичным образом.
Пример 2: Вычесть: 27−37.
Решение:
Ответ: −7
Если подкоренное число и индекс не совсем совпадают, то подкоренные числа не подобны, и мы не можем их объединить.
Пример 3: Упрощение: 105+62−95−72.
Решение:
Дальнейшее упрощение невозможно, потому что 5 и 2 не похожи на радикалы; подкоренные не совпадают.
Ответ: 5−2
Осторожно
Важно отметить, что 5−2≠5−2. Мы можем убедиться в этом, рассчитав значение каждой стороны с помощью калькулятора.
В общем, обратите внимание, что an±bn≠a±bn.
Пример 4: Упрощение: 3 63+26−63−36.
Решение:
Дальнейшее упрощение невозможно, потому что 63 и 6 не похожи на радикалы; индексы не совпадают.

Ответ: 2 63−6
≥
Часто нам приходится упрощать, прежде чем мы сможем идентифицировать одинаковые радикалы в терминах.
Пример 5: Вычесть: 12−48.
Решение: На первый взгляд радикалы не похожи. Однако после полного упрощения мы увидим, что можем их комбинировать.
Ответ: −23
Пример 6: Упрощение: 20+27−35−212.
Решение:
Ответ: −5−3
Попробуйте! Вычесть: 250−68.
Ответ: −22
Решение для видео
(нажмите, чтобы посмотреть видео)Далее мы работаем с радикальными выражениями, включающими переменные. В этом разделе предполагается, что все подкоренные числа, содержащие переменные выражения, не являются отрицательными.
Пример 7: Упрощение: −6 2×3−3×3+7 2×3.
Решение:
Дальнейшее объединение невозможно, потому что оставшиеся подкоренные выражения не имеют одного и того же корня; они не такие, как радикалы.
 Обратите внимание, что 2×3−3×3≠2x−3×3.
Обратите внимание, что 2×3−3×3≠2x−3×3.Ответ: 2×3−3×3
Нам часто приходится вычитать подкоренное выражение с несколькими членами. Если это так, не забудьте применить распределительное свойство перед объединением подобных терминов.
Пример 8: Упрощение: (9x−2y)−(10x+7y).
Решение:
Ответ: −x−9y
Пока мы не упростим, часто неясно, какие термины, содержащие радикалы, подобны.
Пример 9: Упрощение: 5 2y3−(54y3−163). Пример 10:
Решение:
Ответ: 14a25b
Попробуйте! Упрощение: 45×3−(20×3−80x).
Ответ: x5x+45x
Решение для видео
(нажмите, чтобы посмотреть видео)Подсказка
Обратите внимание на различия между произведениями и суммами внутри радикала.
Продукция Сумм x2y2=xyx3y33=xy х2+у2≠х+ух3+у33≠х+у Свойство a⋅bn=an⋅bn говорит о том, что мы можем упростить радикалы, когда операция в подкоренном выражении является умножением.
 Соответствующего свойства для сложения нет.
Соответствующего свойства для сложения нет.Ключевые выводы
- Складывать и вычитать термины, содержащие одинаковые радикалы, так же, как и термины. Если индекс и подкоренное число совпадают, то радикалы подобны и могут быть объединены. Это включает добавление или вычитание только коэффициентов; коренная часть остается прежней.
- Полностью упростите каждый радикал, прежде чем объединять похожие термины.
Тематические упражнения
Часть A: Сложение и вычитание одинаковых радикалов
Упрощение.
1. 93+53
2. 126+36
3. 45–75
4. 310–810
5. 6–46+26
6. 510–1510–210
7 . )−(10+35)
12. (−83+615)−(3−15)
13. 4 63−3 53+6 63
14. 103+5 103−4 103
15,0004 (7 93−4 33)−(93−3 33)16. (−8 53+253)−(2 53+6 253)
Упростить. ( Предположим, что все радикалы, содержащие переменные выражения, положительны.
 )
) 17. 9x+7x
18. −8y+4y
19. 7xy — 3xy+xy
20. 10y2x —12y2x — 2y2x
21. 2Ab — 5A+6AB -100009
9
21. 2AB -5A+6AB -100009
9
22. −3xy+6y−4xy−7y
23. 5xy−(3xy−7xy)
24. −8ab−(2ab−4ab)
25. (32x−3x)−(2x−73x)
26. (y−42y)−(y−52y)
27. 5 x3−12 x3
28. −2 y3−3 y3
29. a⋅3b5+4a⋅3b5−a⋅3b5
0004 30. −8 ab4+3 ab4−2 ab431. 62a−4 2a3+72a−2a3
32. 4 3a5+3a3−9 3a5+3a3
5
33. (4x 3xy4) −xy3)
34. (5 6y6−5y)−(2 6y6+3y)
Часть B: Сложение и вычитание рациональных выражений
Упростить.
35. 75−12
36. 24−54
37. 32+27−8
38. 20+48−45
39. 28−27+903−12 24−40−54
41. 45−80+245−5
42. 108+48−75−3
43. 42-(27-72)
44.
 -35-(20-50)
-35-(20-50)45. 163-543
46. 813-243
47. 1353+400-53 900 −323−43
49. 227−212
50. 350−432
51. 3243−218−48
52. 6216−224−296
53. 218−375−298+448
54 .
58. 4 1623−2 3843−3 7503
Упростить. ( Предположим, что все радикалы, содержащие переменные выражения, положительны. )
59. 81b+4b
60. 100a+A
61. 9A2B — 36A2B
62. 50A2-18A2
63. 49x — 9Y+X-4Y
64.
. −25x — Y
65. 78x- (316y — 218x)
66. 264y- (332y — 81y)
67. 29m2n — 5m9n+M2N
68. 418n2m-2n8m+N2M
69. 4x2y — 418n2m — 2n8m+N2M
- 69. 4x2y — 418n2m — 2n8m+N2M
69. 409. 418. 418n2m — 2n8m+n2m
69. 418. 418n2m-2n8m+n2m 9000 69. 418. 418n2m-2n8m+n2m 9000 69. 418. 418n2m-2n8m+n2m 9000 69. 418. 418n2m-2n8M+ 9xy2−16x2y+y2x
70. 32x2y2+12x2y−18x2y2−27x2y
71. (9x2y−16y)−(49x2y — 4y)
72. (72x2y2–18x2y) — (50x2y2+x2y)
73.
 12m4n — M75M2n+227m4n
12m4n — M75M2n+227m4n74. 5n27mn2+212mn4–n3mn2 2
75.27a3b3b3b3b — A — Абл. 298A4B — 2A162A2B+A200B
77. 125A3-27A3
78. 1000A23–64A23
79. 2x 54×3-2 16×43+5 2×43
80. x> +81y24
82. 32y45−y45
83. 32a34−162a34+5 2a34
84. 80a4b4+5a4b4−a⋅5b4
9053×3 83. 1−92x3x3x 85.000586. 24×3–128×3-81×3
87. 27x4y3-8xy33+x>64xy3 -etet yt3
88. 125xy33+8x3y3–216xy33+10x>
89. (162x4y3 — 3550x.3533+10xt3
9000 89. 384x4y3)90. (32x2y65−243x6y25)−(x2y65−x⋅xy25)
Часть C: Дискуссионная доска
91. Выберите значения для x и y+y и используйте калькулятор ≠х+у.
92. Выберите значения для x и y и используйте калькулятор, чтобы показать, что x2+y2≠x+y.
Ответы
1: 143
3: -25
5: -6
7: 87–2
9: 95–43
11: -5110
13: 10 63-3 53 53
15: 6 93–33
17: 16x
19: 5xy
21: 8ab — 15a
23: 9xy
25: 22x+63x
27: —7 x3
29: 4Aet.
 3B5
3B531: 132a — 5 2a3
33: −4xy4
35: 33
37: 22+33
39: 57–53
41: 55
43: 102-33
41: 5543: 102-33
45: −23
47: 4 53
49: 23
51: 233–62
53: −82+3
55: 83–66
57: 26 23
59: 11B.
61: −3ab
63: 8x -5y
65: 202x -12y
67: −8mn
69: −2xy -2yx
71: -4xy
73: 3m23n
7: 21547: 2: 2: 2: 2: 2: 2: 2: 2: 2,
71: 2,
7,
71: 4000 −12A2AB
77: 2 A3
79: 7x>2×3
81: 5 Y24
83: 4 2A34
85: −2x+2 x3
87: 7xt3-3-3Yx3
89: 7x⋅6xy3−6x⋅2xy23
8.4 Умножение и деление подкоренных выражений
Цели обучения
- Умножение подкоренных выражений.
- Разделить подкоренные выражения.
- Рационализируйте знаменатель.
Умножение радикальных выражений
При умножении радикальных выражений с одинаковым индексом мы используем правило произведения для радикалов.
 Если a и b представляют положительные действительные числа,
Если a и b представляют положительные действительные числа,Пример 1: Умножьте: 2⋅6.
Решение: Эта задача представляет собой произведение двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножьте: 93⋅63.
Решение: Эта задача является произведением кубических корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами стоят коэффициенты.
Пример 3: Умножьте: 23⋅52.
Решение: Используя правило произведения для радикалов и тот факт, что умножение коммутативно, мы можем умножить коэффициенты и подкоренные числа следующим образом.
Обычно первый шаг, связанный с применением свойства коммутативности, не показан.
Ответ: 106
Пример 4: Умножьте: −2 5×3⋅3 25×23.

Решение:
Ответ: −30x
Используйте свойство дистрибутивности при умножении рациональных выражений, содержащих более одного члена.
Пример 5: Умножьте: 43(23−36).
Решение: Примените свойство распределения и умножьте каждый член на 43.
Ответ: 24−362
Пример 6: Умножьте: 4×23(2×3−5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x−10x⋅2×3
Процесс умножения радикальных выражений с несколькими членами аналогичен процессу умножения многочленов. Примените распределительное свойство, упростите каждый радикал, а затем объедините одинаковые члены.
Пример 7: Умножьте: (5+2)(5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножить: (3x−y)2.

Решение:
Ответ: 9x−6xy+y
Попробуйте! Умножить: (23+52)(3−26).
Ответ: 6−122+56−203
Video Solution
(нажмите, чтобы посмотреть видео)Выражения (a+b) и (a−b) называются сопряженнымиМножители (a+b) и (a−b) являются сопряженными.. При умножении сопряженных чисел сумма произведений внутренний и внешний члены дают 0.
Пример 9: Умножить: (2+5)(2−5).
Решение: Примените распределительное свойство, а затем скомбинируйте подобные термины.
Ответ: −3
Важно отметить, что при умножении сопряженных подкоренных выражений мы получаем рациональное выражение. Это верно в целом и часто используется в нашем изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b мы имеем следующее свойство:
Деление подкоренных выражений (рационализация знаменателя)
Чтобы разделить подкоренные выражения с одинаковым индексом, мы используем правило отношения подкоренных.
 Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеемПример 10: Разделим: 8010.
Решение: В этом случае мы можем увидеть, что имеют общие факторы. Если мы применим правило отношения для радикалов и запишем его в виде одного квадратного корня, мы сможем уменьшить дробное подкоренное число.
Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Решение:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Решение:
Ответ: 3b⋅a32
Когда делитель подкоренного выражения содержит подкорень, общепринятой практикой является поиск эквивалентного выражения, в котором знаменатель является рациональным числом. Нахождение такого эквивалентного выражения называется рационализацией знаменателя. Процесс определения эквивалентного подкоренного выражения с рациональным знаменателем.
 .
.Для этого умножьте дробь на 1 особой формы, чтобы подкоренное число в знаменателе можно было записать со степенью, совпадающей с индексом. После этого упростите и удалите радикал в знаменателе. Например,
Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой множитель.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без корня в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Объясните знаменатель: 123x.
Решение: Подкоренное число в знаменателе определяет факторы, которые необходимо использовать для его рационализации. В этом примере умножьте на 1 в виде 3x3x.
Ответ: 3x6x
Как правило, мы обнаружим необходимость уменьшить или отменить после рационализации знаменателя.

Пример 15: Рационализируем знаменатель: 525ab.
Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b в этом примере не отменяются. Не отменяйте факторы внутри радикала с теми, что снаружи.
Ответ: 10abab
Попробуйте! Рационализируйте знаменатель: 4a3b.
Ответ: 23ab3b
Видеорешение
(нажмите, чтобы посмотреть видео)До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одинаковыми подкоренными дает рациональный знаменатель. В общем случае это верно только тогда, когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не оправдывает его. В этом случае, если мы умножаем на 1 в виде x23x23, то мы можем записать подкоренное число в знаменателе как степень числа 3.
 Упрощение результата дает рационализированный знаменатель. Например,
Упрощение результата дает рационализированный знаменатель. Например,Таким образом, чтобы рационализировать знаменатель подкоренных выражений с одним подкоренным членом в знаменателе, начните с разложения подкоренной части знаменателя. Множители этого подкоренного числа и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на n -й корень из множителей, которые дают n -й степени всех множителей в подкоренном члене знаменателя.
Пример 16: Рационализируем знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один делитель 5. Поэтому умножьте на 1 в виде 5353.
Ответ: 535
Пример 17: Рационализируем знаменатель: 27a2b23.
Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Объясните знаменатель: 1 4×35.

Решение: В этом примере мы умножим на 1 в виде 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена, содержащие квадратные корни, мы можем рационализировать это, используя очень специальную технику. Этот метод включает умножение числителя и знаменателя дроби на сопряженную часть знаменателя. Напомним, что умножение подкоренного выражения на его сопряженное дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13−2.
Решение: В этом примере сопряжение знаменателя равно 3+2. Поэтому умножьте на 1 в виде (3+2)(3+2).
Ответ: 3+2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, исключаются путем умножения на сопряженное. Мы можем использовать свойство (a+b)(a−b)=a−b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62+6.

Решение: Умножьте на 1 в виде 2−62−6.
Ответ: −2+3
Пример 21: Рационализируем знаменатель: x+yx−y.
Решение: В этом примере мы умножим на 1 в форме x−yx−y.
Ответ: x−2xy+yx−y
Попробуйте! Рационализируйте знаменатель: 35+525−3.
Ответ: 195+4511
Видео решение
(нажмите, чтобы посмотреть видео)Ключевые выводы
- Чтобы умножить два одночленных радикальных выражения, умножьте коэффициенты и умножьте подкоренные. Если возможно, упростите результат.
- Применить распределительное свойство при умножении подкоренных выражений с несколькими терминами. Затем упростите и объедините все как радикалы.
- Умножение двухчленного подкоренного выражения, содержащего квадратные корни, на его сопряженное дает рациональное выражение.
- Подкоренные выражения принято записывать без подкоренных в знаменателе.
 Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя.
Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя. - Если в выражении есть один член в знаменателе, содержащий радикал, то рационализируйте его, умножив числитель и знаменатель на n -й корень из множителей подкоренного и так, чтобы их степени были равны индексу.
- Если подкоренное выражение имеет в знаменателе два члена, содержащих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на их сопряженные.
Упражнения по теме
Часть A. Умножение радикальных выражений
Умножение. ( Предположим, что все переменные неотрицательны. )
1. 3ac5
2. 7ac3
3. 2=6
4. 5om
5. 7t7
6. 12=12
7. 25 порядка 710
8. 315om 26
9. (25) 2
10. (62) 2
11. 2x порядка 2x
12. 5y порядка
13. 3а⋅12
14.
 3а⋅2а
3а⋅2а15. 42x> 36x
16. 510y порядка 22y
17. 53 порядка 253
18. 43=23
19. 43 ОТДЫХА103
20. 183 порядка63
21. (5 93)) (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23t9a3
26. 7b3t49b23
27. 6×23 порядка4×23
28. 12y3t9y23
29. 20x2y3 порядка10x2y23
30. 63xy3⋅12x4y23
31. 5 (3-5)
32. 2 (3–2)
33. 37(27−3)
34. 25(6−310)
35. 6(3−2)
36. 15(5+3)
37. х(х+ху)
38. у(ху+у)
39. 2ab(14a−210b)
40. 6ab(52a−3b)
41. (2−5)(3+7)
42. (3+2)(5−7)
43 , (23−4)(36+1)
44. (5−26)(7−23)
45. (5−3)2
46. (7−2)2
47. ( 23+2)(23−2)
48. (2+37)(2−37)
49. (a−2b)2
50. (ab+1)2
51. Какие периметр и площадь прямоугольника, длина которого 53 сантиметра, а ширина 32 сантиметра?
52. Каковы периметр и площадь прямоугольника, длина которого 26 сантиметров, а ширина 3 сантиметра?
53.
 Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?54. Если основание треугольника 63 м, а высота 36 м, то какова его площадь?
Часть B: Деление подкоренных выражений
Разделить.
55. 753
56. 36010
57. 7275
58. 9098
59. 90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16A5B232A2B23
.- 15.9000
63.
65. 15
66. 16
67. 23
68. 37
69. 5210
70. 356
71. 3-53
72. 6-22
73. 17x 17x.
74. 13 лет
75. a5ab
76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25n3 25m2n3
85. 327x2y5
86. 216xy25
87. AB9A3B5
88. ABCAB2C35
89. 310–3
90. 26-2
91. 15+3
92.
 17-2
17-291. 15+3
92. 17-2
91. 15+3
92. 17 — 2
91. 6
94. 55+15
95. 105−35
96. −224−32
97. 3+53−5
98. 10−210+2
99. 23−3243+2
100. 65+225−2
101. x+yx−y
902.004 1xy +y103. a-ba+b
104. ab+2ab-2
105. x5-2x
106. 1x-y
Часть C: Обсуждение
107. причины, по которым принято рационализировать знаменатель.
108. Объясните своими словами, как рационализировать знаменатель.
Ответы
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6A
15: 24×3
17: 5
19: 2 53
21: 30 23
23: 16
25: 3A
27: 2x порядка 3×3
29: 2xyцать 25×3
31: 35–5
33: 42-321
35: 32-23
37 37 : x+xy
39: 2a7b−4b5a
41: 6+14−15−35
43: 182+23−126−4
45: 8−215
47: 47: 182+23−126−4
0005
49: a−22ab+2b
51: Периметр: (103+62) сантиметров; Площадь: 156 квадратных сантиметров
53: 18 квадратных метров
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2A
65: 55
67: 63
44464 40004 60004 60004 60004 60004 60004 65: 55
9000 67: 634 40004 40004 60004 60004 65: 55
9000 67: 634 40004 60004 60004 65: 55
9000 67: 6340004 60004 60004 65: 55
9000: 634 40004 60004 6504: 55
9000: 63: 2a.
 : 104
: 10471: 3–153
73: 7x7x
75: AB5B
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9AB32B
9 855. 855. 855. 855. 855. 855. 855. 855. 855. 855.0004 87: 27A2B45389: 310+
91: 5–32
93: −1+2
95: −5–352
97: −4–15
99: 15-7623
97: −4-1599: 15-7623
597: −4-1599: 15-7623
97: −4-1599: 15-7623
97:101: x2+2xy+yx2−y
103: a−2ab+ba−b
105: 5x+2×25−4x
8.5 Рациональные показатели
Цели обучения
- Написать выражения с рациональными показателями в подкоренной форме.
- Напишите подкоренные выражения с рациональными показателями.
- Выполнять операции и упрощать выражения с рациональными показателями.
- Выполнить операции над радикалами с разными индексами.
Определение рациональных показателей
До сих пор показатели степени ограничивались целыми числами.
 В этом разделе мы определим, какие рациональные (или дробные) показатели степени. Дробный показатель степени m / n указывает на радикал с индексом n и показателем степени m : am/n=amn. средства и как с ними работать. Применяются все правила для экспонент, разработанные до этого момента. В частности, вспомним правило произведения показателей. Даны любые рациональные числа m и n , затем
В этом разделе мы определим, какие рациональные (или дробные) показатели степени. Дробный показатель степени m / n указывает на радикал с индексом n и показателем степени m : am/n=amn. средства и как с ними работать. Применяются все правила для экспонент, разработанные до этого момента. В частности, вспомним правило произведения показателей. Даны любые рациональные числа m и n , затемНапример, если у нас есть показатель степени 12, то правило произведения показателей степени подразумевает следующее:
Здесь 51/2 является одним из двух равных делителей 5; следовательно, это квадратный корень из 5, и мы можем записать
Кроме того, мы можем видеть, что 21/3 является одним из трех равных делителей 2.
Следовательно, 21/3 является кубическим корнем из 2, и мы можем записать
В общем случае это верно для любого ненулевого действительного числа a ,
Другими словами, знаменатель дробного показателя степени определяет индекс n -го корня.

Пример 1: Переписать как радикал.
а. 71/2
б. 71/3
Решение:
а. 71/2=7
б. 71/3=73
Пример 2: Перепишите как радикал, а затем упростите.
а. 811/2
б. 811/4
Решение:
а. 811/2=81=9
б. 811/4=814=344=3
Пример 3: Перепишите как радикал, а затем упростите.
а. (125×3)1/3
б. (−32y10)1/5
Решение:
а.
б.
Далее рассмотрим дробные показатели степени, где числитель — целое число, отличное от 1. Например, рассмотрим следующее:
Это показывает, что 52/3 является одним из трех равных множителей числа 52. Другими словами, 52/3 — это кубический корень из 52 и мы можем написать:
В общем, для любого действительного числа a ,
Выражение с рациональным показателем степени эквивалентно радикалу, где знаменатель — индекс, а числитель — показатель степени.
 Любое подкоренное выражение может быть записано с рациональным показателем, который мы называем экспоненциальной формой. Эквивалентное выражение, записанное с использованием рационального показателя.
Любое подкоренное выражение может быть записано с рациональным показателем, который мы называем экспоненциальной формой. Эквивалентное выражение, записанное с использованием рационального показателя.а. 72/5
б. 23/4
Решение:
а. 72/5=725=495
б. 23/4=234=84
Пример 5: Перепишите как радикал, а затем упростите.
а. 82/3
б. (32)3/5
Решение:
а.
б. Мы часто можем избежать очень больших целых чисел, работая с их простой факторизацией.
Для подкоренного выражения нас попросят найти эквивалент в экспоненциальной форме. Предположим, что все переменные положительны.
Пример 6: Перепишите с использованием рациональных показателей: x23.
Решение: Здесь индекс равен 3, а мощность равна 2. Мы можем написать
Ответ: x2/3
Пример 7: Перепишем, используя рациональные показатели: y36.

Решение: Здесь индекс равен 6, а мощность равна 3. Мы можем записать
Ответ: y1/2
Важно отметить, что следующие утверждения эквивалентны.
Другими словами, не имеет значения, применяем ли мы силу сначала или сначала корень. Например, мы можем применить силу перед корнем:
Или мы можем применить n -й корень перед властью:
Результаты те же.
Пример 8: Перепишите как радикал, а затем упростите: (−8)2/3.
Решение: Здесь индекс равен 3, а мощность равна 2. Мы можем записать
Ответ: 4
Попробуйте! Перепишите как радикал, а затем упростите: 253/2.
Ответ: 125
Решение для видео
(нажмите, чтобы посмотреть видео) 9(2/3)≈1,587, мы бы набралиОперации с использованием правил экспонент
В этом разделе мы рассмотрим все правила экспонент, которые распространяются на рациональные экспоненты.
 Если даны рациональные числа m и n , то мы имеем
Если даны рациональные числа m и n , то мы имеемПравило произведения: хм⋅хн=хм+п Частное правило: xmxn=xm−n , x≠0 Силовое правило: (xm)n=xm⋅n Правило мощности для продукта: (ху)n=xnyn Степенное правило для частного: (xy)n=xnyn , y≠0 Отрицательные степени: х-n=1xn Нулевой показатель: х0=1, х≠0 Эти правила позволяют выполнять операции с рациональными показателями.

Пример 9: Упрощение: 22/3⋅21/6.
Решение:
Ответ: 25/6
Пример 10: Упростить: x1/2×1/3.
Решение:
Ответ: x1/6
Пример 11: Упростить: (y3/4)2/3.
Решение:
Ответ: y1/2
Пример 12: Упростите: (16a4b8)3/4.
Решение:
Ответ: 8a3b6
Пример 13: Упростите: 25−3/2.
Решение:
Ответ: 1/125
Попробуйте это! Упрощение: (8a3/4b3)2/3a1/3.
Ответ: 4a1/6b2
Решение для видео
(нажмите, чтобы посмотреть видео)Выражения радикалов с разными индексами
Чтобы применить правило произведения или частного для радикалов, индексы задействованных радикалов должны быть одинаковыми.
 Если индексы разные, то сначала переписать радикалы в экспоненциальной форме, а затем применить правила для показателей.
Если индексы разные, то сначала переписать радикалы в экспоненциальной форме, а затем применить правила для показателей.Пример 14: Умножить: 2⋅23.
Решение: В этом примере индекс каждого радикального фактора разный. Следовательно, правило произведения для радикалов не применяется. Начните с преобразования радикалов в эквивалентную форму с использованием рациональных показателей. Затем примените правило произведения для показателей.
Ответ: 256
Пример 15: Разделить: 4325.
Решение: В этом примере индекс радикала в числителе отличается от индекса радикала в знаменателе. Следовательно, частное правило для радикалов не применяется. Начните с преобразования радикалов в эквивалентную форму с использованием рациональных показателей, а затем примените правило частных для показателей.
Ответ: 2715
Пример 16: Упрощение: 43 .

Решение: Здесь корень квадратного корня является кубическим корнем. Переписав это выражение с использованием рациональных показателей, мы увидим, что применяется степенное правило для показателей.
Ответ: 23
Ключевые выводы
- При преобразовании дробных показателей степени в радикалы используйте числитель как степень, а знаменатель как индекс радикала.
- Все правила степеней применяются к выражениям с рациональными степенями.
Упражнения по теме
Часть A: Рациональные показатели
Выразите, используя рациональные показатели.
1. 6
2. 10
3. 113
4. 24
5. 523
6. 234
7. X5
8. X6
9. X76
10. x45
Экспресс в радикальной форме.
11. 21/2
12. 51/3
13. 72/3
14. 23/5
15. x3/4
16. x5/6
17. x−1/2
18.
 0004 900 /4
0004 900 /419. (1x)−1/3
20. (1x)−3/5
Пишите как радикал, а затем упрощайте.
21. 251/2
22. 361/2
23. 1211/2
24. 1441/2
25. (14)1/2 09 5 5
27. 4-1/2
28. 9-1/2
29. (14)-1/2
30. (116)-1/2
31. 81/3
32. 1251/3
33. (127)1/3
34. (8125)1/3
35. (−27)1/3
36,00 ( −64)1/3
37. 161/4
38. 6251/4
39. 81−1/4
40. 16−1/4
41. 100,0004 4 9004 9004 , (−32)1/5
43. (132)1/5
44. (1243)1/5
45. 93/2
46. 43/2
47. 85/3
48. 272/3
49. 163/2
50. 322/5
51. (116)3/4 9(2/3) лет». Помогите Марку определить, сколько лет Марси.
Часть B: Rational Exponents
Выполните операции и упростите. Оставляйте ответы в экспоненциальной форме.
65. 22/3⋅24/3
66.
 33/2⋅31/2
33/2⋅31/267. 51/2⋅51/3
68. 21/6⋅23/4 90.001 90.001 /4⋅y2/5
70. x1/2⋅x1/4
71. 57/351/3
72. 29/221/2
73. 2a2/3a1/6
9.003b 74/ 2b1/375. (81/2)2/3
76. (36)2/3
77. (x2/3)1/2
78. (y3/4)4/5
79. (4x2y4)1/2
80. (9x6y2)1/2
81. (2×1 /3y2/3)3
82. (8×3/2y1/2)2
83. (a3/4a1/2)4/3
84. (b4/5b1/10)10/3
85. (4×2/3y4)1/2
86. (27×3/4y9)1/3
87. y1/2⋅y2/3y1/6
88. x2/5⋅x1/2×1/10
89. xyx1/2y1/3
90. x5/4yxy2/5
91. 49a5/7b3/27a3/7b1/4
92. 16a5/6b5/48a1/2b2/3
93. (9×2/3y6)3/2×1/2y
94. (125x3y3/5)2/3xy1/3
95. (27a1/4b3/2)2/3a1/6b1/2
96. (25a2 /3b4/3)3/2a1/6b1/3
Часть C: Смешанные индексы
Выполните операции.
97. 93 порядка 35
98. 5=255
99. X> X3
100. Y⋅Y4
101. X23⋅x4
102. x35 x3
103.
 100310
100310. 104. 16543
105. a23a
106. b45b3
107. x23x35
108. x34x23
109. 165
110. 93
111. 253
112. 553
113. 73
114 экспоненты? Каковы некоторые из его других достижений?
116. При использовании текста лучше всего передавать n -й корень, используя рациональные показатели степени. Приведите пример.
Ответы
1: 61/2
3: 111/3
5: 52/3
7: x1/5
9: x7/6
11: 2
13: 723
15: x34
17: 1x
19: X3
21: 5
23: 110005
25: 1/2
27: 1/2
29: 2
31: 2
33: 1/3
35: -3
37: 2
39: 1/3
41: 10
43: 1/2
45: 27
47: 32
49: 64
51: 1/8
5:8 5 : 9
0005
57: 1.68
59: 1.38
61: Не действительное число
63: В первом выражении квадратный корень из отрицательного числа создает условие ошибки на калькуляторе.
 Квадратный корень из отрицательного числа не является реальным. Во втором выражении, из-за порядка операций, после возведения числа 4 в степень (3/2) к ответу применяется знак минус.
Квадратный корень из отрицательного числа не является реальным. Во втором выражении, из-за порядка операций, после возведения числа 4 в степень (3/2) к ответу применяется знак минус.65: 4
67: 55/6
69: y13/20
71: 25
73: 2a1/2
75: 2
77: x1/3
79: 2xy2
81: 8xy2
83: A1/3
85: 2×1/3y2
87: Y
89: x1/2y2/3/3/3/3/3/3/3.
91: 7×2/7y5/4
93: 27×1/2y8
95: 9B1/2
97: 31315
99: X56
101: x1112
103: 106
05: A6
- 55: A6
- 5: A6
- 5: A6
- 5: A6
- 5: A6
- 5: A6 9000 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6 9000: A6. 107: x15
109: 45
111: 215
113: 76
8.6 Решение радикальных уравнений
Цели обучения
- Решение уравнений с квадратными корнями.

- Решите уравнения с кубическими корнями.
Радикальные уравнения
Радикальное уравнениеЛюбое уравнение, которое содержит один или несколько радикалов с переменной в подкоренной величине. это любое уравнение, которое содержит один или несколько радикалов с переменной в подкоренной величине. Ниже приведены некоторые примеры радикальных уравнений, все из которых будут решены в этом разделе:
Начнем со свойства возведения в квадрат равенства Данных действительных чисел a и b , где a=b, тогда a2=b2.; учитывая действительные числа a и b , мы имеем следующее:
Другими словами, равенство сохраняется, если мы возводим в квадрат обе части уравнения.
Обратное, с другой стороны, не обязательно верно:
Это важно, потому что мы будем использовать это свойство для решения радикальных уравнений. Рассмотрим очень простое радикальное уравнение, которое можно решить путем проверки:
Здесь мы видим, что x=9является решением.
 Чтобы решить это уравнение алгебраически, используйте свойство возведения в квадрат равенства и тот факт, что (a)2=a2=a, когда a положительно. Удалите квадратный корень, возведя в квадрат обе части уравнения следующим образом:
Чтобы решить это уравнение алгебраически, используйте свойство возведения в квадрат равенства и тот факт, что (a)2=a2=a, когда a положительно. Удалите квадратный корень, возведя в квадрат обе части уравнения следующим образом:В качестве проверки мы видим, что 9=3, как и ожидалось. Поскольку свойство равенства, обратное квадрату, не обязательно верно, решения уравнения в квадрате могут не быть решениями оригинала. Следовательно, возведение в квадрат обеих частей уравнения вводит возможность появления посторонних решений. Решение, которое не решает исходное уравнение, или решения, которые не решают исходное уравнение. По этой причине мы должны проверять ответы, полученные в результате возведения в квадрат обеих частей уравнения.
Пример 1: Решите: x−1=5.
Решение: Мы можем исключить квадратный корень, применив свойство равенства в квадрате.
Далее надо проверить.
Ответ: Решение: 26.
Пример 2: Решите: 5−4x=x.

Решение: Начните с возведения в квадрат обеих частей уравнения.
У вас осталось квадратное уравнение, которое можно решить с помощью факторизации.
Поскольку вы возвели обе стороны в квадрат, вы должны проверить свои решения.
После проверки видно, что x=−5 было лишним; это не решало исходное радикальное уравнение. Не обращайте внимания на этот ответ. Это оставляет x=1 как единственное решение.
Ответ: Решение x=1.
Обратите внимание, что в двух предыдущих примерах радикал изолирован с одной стороны уравнения. Как правило, это не так. Шаги для решения радикальных уравнений с квадратными корнями показаны в следующем примере.
Пример 3: Решите: 2x−5+4=x.
Решение:
Шаг 1: Извлеките квадратный корень. Начните с вычитания 4 из обеих частей уравнения.
Шаг 2: Подровняйте обе стороны. Возведение обеих сторон в квадрат исключает квадратный корень.

Шаг 3: Решите полученное уравнение. Здесь у вас осталось квадратное уравнение, которое можно решить с помощью факторизации.
Шаг 4: Проверьте решения в исходном уравнении. Квадрат обеих сторон вводит возможность посторонних решений; поэтому проверка обязательна.
После проверки видим, что x=3 — посторонний корень; это не решает исходное радикальное уравнение. Это оставляет x=7 как единственное решение.
Ответ: Решение x=7.
Пример 4: Решите: 3x+1−2x=0.
Решение: Начните с выделения термина с корнем.
Несмотря на то, что член в левой части имеет коэффициент, он все же считается изолированным. Напомним, что термины разделяются операторами сложения или вычитания.
Решите полученное квадратное уравнение.
Так как мы возвели обе стороны в квадрат, мы должны проверить наши решения.
После проверки мы видим, что x=−34 было лишним.

Ответ: Решение 3.
Иногда оба возможных решения лишние.
Пример 5: Решите: 4−11x−x+2=0.
Решение: Начните с выделения радикала.
Так как мы возвели обе стороны в квадрат, мы должны проверить наши решения.
Поскольку оба возможных решения являются посторонними, уравнение не имеет решений.
Ответ: Нет решения, Ø
Свойство равенства в квадрате распространяется на любую степень положительного целого числа n . Для действительных чисел a и b мы имеем следующее: , то an=bn.. Используйте это свойство вместе с тем фактом, что (an)n=ann=a, когда a положителен, чтобы решить радикальные уравнения с индексами больше 2.
Пример 6: Решите: x2+43−2=0.
Решение: Выделите радикал, а затем возведите в куб обе части уравнения.
Чек.
Ответ: решения равны −2 и 2.

Попробуйте! Решите: 2x−1+2=x.
Ответ: x=5 (x=1 лишнее)
Видеорешение
(нажмите, чтобы посмотреть видео)Возможно, уравнение имеет два радикальных выражения.
Пример 7: Решите: 3x−4=2x+9.
Решение: Оба радикала считаются изолированными в разных частях уравнения.
Проверка x=13.
Ответ: Решение: 13.
Пример 8: Решите: x2+x−143=x+503.
Решение: Удалите радикалы, кубируя обе стороны.
Чек.
Ответ: Решения равны −8 и 8.
Мы научимся решать некоторые из более сложных радикальных уравнений в следующем курсе «Алгебра среднего уровня».
Попробуйте! Решите: 3x+1=2x−3.
Ответ: 13
Решение для видео
(щелкните, чтобы посмотреть видео)Ключевые выводы
- Решите уравнения, содержащие квадратные корни, сначала выделив радикал, а затем возведя в квадрат обе стороны.
 Возведение квадратного корня в квадрат устраняет радикал, оставляя нам уравнение, которое можно решить с помощью методов, изученных ранее при изучении алгебры. Однако возведение в квадрат обеих частей уравнения приводит к возможности посторонних решений, поэтому проверьте свои ответы в исходном уравнении.
Возведение квадратного корня в квадрат устраняет радикал, оставляя нам уравнение, которое можно решить с помощью методов, изученных ранее при изучении алгебры. Однако возведение в квадрат обеих частей уравнения приводит к возможности посторонних решений, поэтому проверьте свои ответы в исходном уравнении. - Решите уравнения с кубическими корнями, сначала выделив радикал, а затем возведя в куб обе части. Это устраняет радикал и приводит к уравнению, которое можно решить с помощью методов, которыми вы уже овладели.
Упражнения по теме
Часть A. Решение радикальных уравнений
Решить.
1. x=2
2. x=7
3. x+7=8
4. x+4=9
5. x+6=3
6. x+2= 1
7. 5x-1=0
8. 3x-2=0
9. x-3=3
10. x+5=6
11. 3x+1=2
12. 5x −4=4
13. 7x+4+6=11
14. 3x−5+9=14
15. 2x−1−3=0
16. 3x+1−2=0
17. x3=2
18.
 x3=5
x3=519. 2x+93=3
20. 4x−113=1
21. 5x+73+3=1
22. 3x−63+5 =2
23. 2 x+23−1=0
24. 2 2x−33−1=0
25. 8x+11=3x+1
26. 23x−4=2(3x+1 )
27. 2(x+10)=7x−15
28. 5(x−4)=x+4
29. 5x−23=4×3
30. 9(x−1)3=3 (x+7)3
31. 3x+13=2(x−1)3
32. 9×3=3(x−6)3
33. 4x+21=x
34. 8x+9 =x
35. 4(2x−3)=x
36. 3(4x−9)=x
37. 2x−1=x
38. 32x−9=x
39. 9x+ 9=x+1
40. 3x+10=x+4
41. x−1=x−3
42. 2x−5=x−4
43. 16−3x=x−6
44. 7−3x=x−3
45. 32x+10=x+9
46. 22x+5=x+4
47. 3x−1−1=x
48. 22x+2−1=x
49. 10x+41−5=x
50. 6( x+3)−3=x
51. 8×2−4x+1=2x
52. 18×2−6x+1=3x
53. 5x+2=x+8
54. 42(x+1 )=x+7
55. x2−25=x
56. x2+9=x
57. 3+6x−11=x
58. 2+9x−8=x
59. 4x +25−x=7
60. 8x+73−x=10
61.
 24x+3−3=2x
24x+3−3=2x62. 26x+3−3=3x
63. 2x−4=14−10x
64. 3x−6=33−24x
65. x2−243=1
66. x2−543=3
67. x2+6×3+1=4
68. x2+2×3+5=7
69. 25×2-10x-73=-2
70. 9×2-12x-233=-3
71. 2×2-15x+25=(x+5)(x-5)
72. x2- 4x+4=x(5−x)
73. 2(x2+3x−20)3=(x+3)23
74. 3×2+3x+403=(x−5)23
75. x1/2−10=0
76. x1/2−6=0
77. x1/3+2=0
78. x1/3+4=0
79. (x−1)1 /2−3=0
80. (x+2)1/2−6=0
81. (2x−1)1/3+3=0
82. (3x−1)1/3−2=0
83. (4x+15)1/2−2x=0
84. (3x+2)1/2−3x=0
85. (2x+12)1/2−x=6
86. (4x+36)1/2−x=9
87. 2(5x+26)1/2=x+10
88. 3(x−1)1/2=x+1
89. Квадратный корень из удвоенного числа на 1 меньше числа равен на 2 меньше число. Найдите число.
90. Квадратный корень из 4 меньше удвоенного числа равен на 6 меньше числа. Найдите число.
91. Квадратный корень из удвоенного числа равен половине этого числа.
 Найдите число.
Найдите число.92. Квадратный корень из удвоенного числа равен одной трети этого числа. Найдите число.
93. Расстояние, d , измеренное в милях, на котором человек может увидеть предмет, определяется по формуле d=6h3
, где h представляет собой рост человека над уровнем моря, измеренный в футах. На какой высоте должен находиться человек, чтобы увидеть объект на расстоянии 5 миль?
94. Текущая, I , измеряемое в амперах, находится по формуле I=PR
, где P — потребляемая мощность, измеренная в ваттах, а R — сопротивление, измеренное в омах. Если лампочке требуется 1/2 ампера тока и она потребляет 60 Вт мощности, то каково сопротивление лампочки?
Период T маятника в секундах определяется формулой T=2πL32
где L представляет длину в футах. Для каждой приведенной ниже задачи рассчитайте длину маятника, учитывая период. Укажите точное значение, а приблизительное значение округлить до ближайшей десятой доли фута.

95. 1 секунда
96. 2 секунды
97. 1/2 секунды
98. 1/3 секунды
Время, объект в свободном падении, в секундах и
определяется по формуле t=s4 где с представляет расстояние в футах, на которое упал объект. Для каждой приведенной ниже задачи рассчитайте расстояние, на которое падает объект, учитывая количество времени.
99. 1 Второй
100. 2 секунды
101. 1/2 Второй
102. 1/4 Вторая секунду
. , 0), где x — действительное число. Следовательно, чтобы найти x — перехваты, установить y = 0 и найти x . Найдите x -перехватов для каждого из следующих. Часть B: Дискуссионная доска
107. Обсудите причины, по которым мы иногда получаем посторонние решения при решении радикальных уравнений.
 Существуют ли какие-либо условия, когда нам не нужно проверять наличие посторонних решений? Почему?
Существуют ли какие-либо условия, когда нам не нужно проверять наличие посторонних решений? Почему?Ответы
1: 4
3: 1
5: Ø
7: 1/25
9: 12
11: 1
13: 3
15: 13/4
17 17 : 8
19: 9
21: −3
23: -15/8
25: 2
27: 7
29: 2
31: -3
33: 7
35
43: Ø
45: −3, 3
47: 2, 5 5
4 49: −4, −4
51: 1/2
53: 2, 7
55: Ø
57: 10
59: −6, −4
6,004 6, 3/2
63: Ø
65: −5, 5
67: −9, 3
69: 1/5
71: 5, 10
7 5: 9004 7 5: 900, 7 100
77: −8
79: 10
81: −13
83: 5/2
85: -6, -4
87: -2, 2
89: 5
91 : 8
93: 1623 фута
95: 8/π2≈0,8 фута
97: 2/π2≈0,2 фута
99: 16 футов
101: 4 фута
103: (4, 0)
10,5:04 10
8.
 7 Повторные упражнения и образец экзамена
7 Повторные упражнения и образец экзаменаПовторные упражнения
( Предположим, что все переменные представляют неотрицательные числа. )
Радикалы
Упрощение.
1. 36
2. 425
3. −16
4. −9
5. 1253
6. 3 −83
0004 7. 16438. −5 −273
9. 40
10. −350
11. 9881
12. 1121
13. 5 1923
14. 2 — 543
Выражения
Упростить.
15. 49×2
16. 25a2b2
17. 75x3y2
18. 200m4n3
19. 18x325y2
20. 108x349y4
21. 216×33
22. −125x6y33
23. 27a7b5c33
24 120x9y43
Используйте формулу расстояния для расчета расстояния между заданными двумя точками.
25. (5, –8) и (2, –10)
26. (–7, –1) и (–6, 1)
27. (–10, –1) и (0 , -5)
28. (5, -1) и (-2, -2)
Сложение и вычитание радикальных выражений
Упростить.

29. 83+33
30. 1210-210
31. 143+52-53-62
32. 22ab-5ab+7ab-2ab
9(0+7x) 33.33.0004 34. (8yx-7xy)-(5xy-12yx)
35. 45+12-20-75
36. 24-32+54-232
37. 23×2+45x-x27+20x
5 90 80 . 56A2B+8A2B2-224A2B — A18B2
39. 5y4x2y- (x16y3–29x2y3)
40. (2B9A2C — 3A16B2C) — (64A2B2C -9000.92.12.116×3 — 216×3 — (64A2B2C–9BA2C)
41.116×3 — 216×3 — 216×3 — 2. ⋅543+3 2×3343. 8x3y3-2x сердие3++27x3y3+xomy3
44. 27a3b3-3 8ab33+a⋅64b3-B порядко
45. 3⋅6
46. (35)2
47. 2(3−6)
48. (2−6)2
49. (1−5)(1+5)
50. (23+5)(32−25)
51. 2a23⋅4a3
52. 25a2b3⋅5a2b23
Разделить.
53. 724
54. 104864
55. 98x4y236x2
56. 81x6y738y33
Рационализируйте знаменатель.
57. 27
58. 63
59. 142x
60. 1215
61. 12×23
62. 5a2b5ab23
63.
 13−2
13−264. 2−62+6
Рациональные показатели
Выразите в радикальной форме.
65. 71/2
66. 32/3
67. x4/5
68. y−3/4
Запишите как радикал, а затем упростите.
69. 41/2
70. 501/2
71. 42/3
72. 811/3
73. (14)3/2
1)1−1−34Выполните операции и упростите. Оставляйте ответы в экспоненциальной форме.
75. 31/2⋅33/2
76. 21/2⋅21/3
77. 43/241/2
78. 93/491/4
/49.4 280. (8x6y9)1/3
81. (a4/3a1/2)2/5
82. (16×4/3y2)1/2
Решение радикальных уравнений
Решить.
83. x=5
84. 2x−1=3
85. x−8+2=5
86. 3x−5−1=11
87. 5x−3=2x+15
88. 8x−15=x
89. x+41=x−1
90. 7−3x=x−3
91. 2(x+1)=2(x+1)
92. x(x+6)=4
93. x(3x+10)3=2
94. 2×2−x3+ 4=5
95. 3(x+4)(x+1)3=5x+373
96.
 3×2−9x+243=(x+2)23
3×2−9x+243=(x+2)2397. y1/2−3=0
98. y1/3+3=0
99. (x−5)1/2−2=0
100. (2x−1)1/3−5=0
Пример экзамена
В задачах 1–18 предположим, что все переменные представляют собой неотрицательные числа.
1. Упрощение.
- 100
- −100
- −100
2. Упрощение.
- 273
- −273
- −273
3. 12825
4. 13
5. 512x2y3z
6. 250x2y3z53
Выполните операции.
7. 524−108+96−327
8. 38x2y−(x200y−18x2y)
9. 2ab(32a−b)
10. (x−5y)1без деминации 5 5
11. 102x
12. 14xy23
13. 1x+5
14. 2−32+3
Выполните операции и упростите. Оставляйте ответы в экспоненциальной форме.
15.
 22/3⋅21/6
22/3⋅21/616. 104/5101/3
17. (121a4b2)1/2
18. (9y1/3×6)1/2y1/6 9.0075
19. x−7=0
20. 3x+5=1
21. 2x−1+2=x
22. 31−10x=x−4
23. (2x+1) (3x+2)=3(2x+1)
24. x(2x−15)3=3
25. Период T маятника в секундах определяется по формуле T=2πL32, где L представляет длину в футах. Вычислите длину маятника, если период равен 1,5 секунды. Округлите до десятых.
Обзорные упражнения Ответы
1: 6
3: Не реальное число
5: 5
7: 1/4
9: 210
11: 729
13: 20 33
15:
7x
17: 5xy3x
19: 3x2x5y
21: 6x
23: 3A2BCtab23
25: 13
27: 229
29: 113
31: 93–2
33: 4x-2y
35: 5–33
: 37: −x3+55x
39: 12xyy
41: 4 x3–5 XY3
43: 2x порядка 3
45: 32
47: 6-23
49: −4
51: 2A.

53: 32
55: 7xy26
57: 277
59: 72xx
61: 4x32x
63: 05 054 90
5
67: x45
69: 2
71: 2 23
73: 1/8
75: 9
77: 4
79: 6x2y
81: A1/3
83: 25: 25: 25: 25: 25: 25: 25: 25: 25: 25: 25: 25
85: 17
87: 6
89: 8
91: −1/2, −1
93: 2/3, −4
95: −5, 5/3 90 9
99: 9
Примеры ответов на экзамен
1:
- 10
- Не настоящее число
- −10
3: 825
5: 10xy3yz
7: 146–153
9: 6A2B — 2BA
11: 52xx
13: X — 5x — 25
15: 25/6
17: 11A2B2B2B 25.
19: 49
21: 5
23: −1/2, 1/3
25: 1,8 фута
Раздел 1: Упрощение радикальных выражений с использованием правила произведения и правила частного | Хьюстонский общественный колледж
Важно, чтобы вы сначала посмотрели видео.

Обзор радикальных выражений
Мы начнем обсуждение в этом разделе со следующего: Что такое 7 в квадрате? Ответ, конечно,72 = 7 · 7 = 49
Итак, когда мы возводим 7 в квадрат, мы получаем 49. Теперь мы хотим пойти в противоположном направлении.
Противоположное (обратное) действие возведения числа в квадрат называется извлечением его квадратного корня. Например,
- квадратный корень из 100 равен 10, потому что 10 2 = 100,
- другой квадратный корень из 100 равен -10, потому что (-10) 2 = 100.
Пусть c – действительное число. Если a 2 = c , то a является квадратным корнем из c .
Действительные числа имеют два квадратных корня, один положительный и один отрицательный. Положительный или главный квадратный корень записывается с помощью символа , а отрицательный квадратный корень – с помощью символа .
 Символ называется радикальным знаком и всегда представляет главный квадратный корень, за исключением того
Символ называется радикальным знаком и всегда представляет главный квадратный корень, за исключением того Распространенной ошибкой является утверждение, что . Это неправда. Правильный ответ:
. Квадратный корень числа всегда положителен.Число внутри подкоренного знака называется подкоренным числом и . Все выражение называется радикалом .
Пример 1. Найдите квадратный корень.
Раствор.
Использование правил произведения и частного для радикалов
Когда мы сталкиваемся с такой задачей, как √4 , нам нетрудно сказать, что ответ равен 2 (поскольку 2 × 2 = 4). Даже такую задачу, как ³√ 27 = 3 , легко решить, если мы поймем, что 3 × 3 × 3 = 27.Наши проблемы обычно возникают, когда мы либо не можем легко увидеть ответ, либо если число под нашим подкоренным знаком не является идеальным квадратом или идеальным кубом.

Задача вроде √24 может показаться сложной, потому что нет числа, которое можно умножить само на себя и получить 24. Однако задачу можно упростить. Таким образом, хотя 24 не является идеальным квадратом, его можно разбить на более мелкие части, где одна из этих частей может быть идеальным квадратом. Итак, теперь у нас есть √24 = √ 4 × 6 = √ 4 · √ 6 = 2√ 6 .
Следующие правила очень полезны для упрощения радикалов.
Правила радикалов
Если n — натуральное число больше 1, а a и b — положительные действительные числа, то
1. Обратное свойство n√ an = a, если n нечетное или
н√ ан = | а | если n равно
2. Правило продукта н √ аб = н √ а · н √ б 3. Правило частных Обратите внимание, что иногда мы можем позволить a или b быть отрицательными, и эти свойства все равно будут работать. 
Также обратите внимание, что, хотя мы можем «разбивать» произведения и частные под радикалом, мы не можем делать то же самое для сумм или разностей. Другими словами,
Если «разбить» корень на сумму двух частей, то мы явно получим разные ответы! Так что будьте осторожны, чтобы не совершить эту очень распространенную ошибку!
Вскоре мы собираемся упрощать радикалы, поэтому теперь нам нужно определить упрощенную радикальную форму. Говорят, что радикал находится в упрощенной радикальной форме (или просто в упрощенной форме), если верно каждое из следующих утверждений.
- Все показатели степени в подкоренном члене должны быть меньше индекса.
- Любые показатели степени в подкоренном члене не могут иметь общих делителей с индексом.
- Под радикалом дроби не появляются.
- В знаменателе дроби нет корней.
Упрощение подкоренного выражения может включать не только числа, но и переменные.
 Точно так же, как вы могли разбить число на более мелкие части, вы можете сделать то же самое с переменными. Когда радикал представляет собой квадратный корень, вы должны попытаться возвести члены в четную степень (2, 4, 6, 8 и т. д.).
Точно так же, как вы могли разбить число на более мелкие части, вы можете сделать то же самое с переменными. Когда радикал представляет собой квадратный корень, вы должны попытаться возвести члены в четную степень (2, 4, 6, 8 и т. д.).Когда радикал представляет собой кубический корень, вы должны попытаться возвести члены в степень три (3, 6, 9, 12 и т. д.). Например, . Эти типы упрощений с переменными будут полезны при выполнении операций с радикальными выражениями.
Пример 2. Упростите следующий радикал.Раствор.
Пример 3. Сократите радикальное выражение до меньших членов.
Раствор.
Пример 4. Упростите следующий радикал.
∛ 320
Решение.∛320 = ∛ 64 · 5 = ∛ 64 · ∛ 5 = 4 ∛ 5
Пример 5.
 Упростите следующее. Предположим, что все переменные положительны.
Упростите следующее. Предположим, что все переменные положительны.
Раствор.
В этом случае показатель степени (7) больше, чем индекс (2), поэтому нарушается первое правило упрощения. Чтобы исправить это, мы будем использовать первое и второе свойства радикалов выше. Итак, заметим, что мы можем записать подкоренное число следующим образом:у7 = у6у = (у3)2у
Итак, у нас есть подкоренное число, записанное как совершенный квадрат, умноженный на член, показатель которого меньше индекса. Тогда радикал становится
Теперь используйте второе свойство радикалов, чтобы разбить радикал, а затем используйте первое свойство радикалов в первом члене.
Теперь это удовлетворяет правилам упрощения, и мы закончили.Прежде чем двигаться дальше, давайте кратко обсудим, как мы выяснили, как разбить экспоненту. Для этого мы отметили, что индекс равен 2. Затем мы определили наибольшее кратное 2, меньшее 7, показатель степени подкоренного числа.
 Это 6. Далее мы заметили, что 7 = 6 + 1,
Это 6. Далее мы заметили, что 7 = 6 + 1,Наконец, помня несколько правил возведения в степень, мы можем переписать подкоренное число как
Пример 6. Упростите следующее. Предположим, что все переменные положительны.
Решение.Здесь более одного термина, но все работает точно так же. Мы разобьем подкоренное число на совершенные квадраты, умноженные на члены, показатели которых меньше 2 (т.е. 1).
18x 6 y 11 = 9x 6 Y 10 (2y) = 9 (x 3 ) 2 (у 5 ) 2 ( 2Y) .
Не забывайте также искать правильные квадраты в числе.Теперь вернитесь к радикалу и затем используйте второе и первое свойство радикалов, как в первом примере.
Обратите внимание, что мы использовали тот факт, что второе свойство может быть расширено до такого количества членов, которое имеется в произведении под радикалом.
 Кроме того, не волнуйтесь, что в окончательном ответе нет крестиков под радикалом. Иногда это будет происходить.
Кроме того, не волнуйтесь, что в окончательном ответе нет крестиков под радикалом. Иногда это будет происходить.Проверьте свои знания, открыв действие «Проверь себя».
Упрощение подкоренных выражений — примеры, определение, переменные, шаги
Упрощение подкоренных выражений в алгебре — это понятие в алгебре, при котором мы упрощаем выражение с подкоренным элементом в более простую форму и удаляем подкоренное, если это возможно. Напомним теперь значение подкоренных выражений. Радикальные выражения — это алгебраические выражения, включающие радикалы. Подкоренные выражения состоят из корня алгебраического выражения (числа, переменных или их комбинации). Корень может быть квадратным, кубическим или вообще n -й корень. Упрощение подкоренных выражений подразумевает приведение алгебраических выражений к простейшему виду и, по возможности, полное исключение подкоренных выражений из выражений.

В этой статье мы изучим шаги по упрощению подкоренных выражений с переменными и показателями, правила, используемые для упрощения подкоренных выражений с помощью решенных примеров.
1. Что такое упрощение подкоренных выражений? 2. шагов для упрощения подкоренных выражений 3. Упрощение радикальных выражений с переменными 4. Правила упрощения подкоренных выражений 5. Часто задаваемые вопросы об упрощении подкоренных выражений Что такое упрощение подкоренных выражений?
Упрощение подкоренных выражений — это процесс приведения подкоренных выражений к простейшей форме и полного удаления подкоренных выражений, если это возможно. Если в знаменателе алгебраического выражения присутствует подкоренное выражение, то умножаем числитель и знаменатель на соответствующее подкоренное выражение (например, сопряженное в случае двучлена и тот же подкоренной в случае одночлена) для упрощения подкореня выражение.

Рассмотрим пример упрощения подкоренных выражений. Рассмотрим f(x) = √(4x 2 у 6 ). Чтобы упростить f(x), нам нужно найти пары одинаковых множителей 4x 2 y 6 . f(x) = √(2 × 2 × x × x × y 3 × y 3 ) = √(2 2 × x 2 × (y 3 × y 3 )) = 2 |х| |у 3 | (Поскольку √x 2 всегда неотрицательно, то есть |x|). Ниже приведено изображение примера радикального выражения и его компонентов.
шагов для упрощения радикальных выражений
Упрощение подкоренных выражений — это процесс исключения подкоренных выражений или приведения выражений, состоящих из квадратных корней, кубических корней или вообще корня n-й степени, к простейшей форме. Рассмотрим несколько примеров пошагового упрощения подкоренных выражений. Мы вспомним некоторые приемы, которые мы используем для упрощения подкоренных выражений, такие как умножение и деление с сопряженными, нахождение множителей в парах для квадратного корня и т.
 д.
д.Упрощение подкоренных выражений с помощью квадратного корня
Для упрощения подкоренных выражений с квадратным корнем рассмотрим пример. Рассмотрим подкоренное выражение √486. Мы будем упрощать это радикальное выражение до самой простой формы, пока дальнейшее упрощение не станет невозможным.
- Шаг 1: Найдите множители числа под радикалом.
486 = 3 × 3 × 3 × 3 × 3 × 2 - Шаг 2: Запишите число под радикалом как произведение его множителей в степени двойки.
486 = 3 2 × 3 2 × 3 × 2 - Шаг 3: Запишите множители вне радикала, имеющие мощность 2.
√486 = √(3 2 × 3 2 × 3 × 2) = 3 × 3 √(3 × 2) = 9√(3 × 2) - Шаг 4: Упрощайте радикал до тех пор, пока не станет невозможно дальнейшее упрощение
√486 = 9√(3 × 2) = 9√6. Дальнейшее умножение теперь невозможно.
Следовательно, мы упростили подкоренное выражение √486 как 92\times 11} = 6\sqrt[5]{4\times 11} = 6\sqrt[5]{44}\)
Упрощение радикальных выражений с помощью переменных
Процесс упрощения подкоренных выражений с переменными подобен процессу упрощения чисел.
 Мы факторизуем переменные вместе с числами. Рассмотрим пример упрощения подкоренных выражений с переменными для лучшего понимания. Рассмотрим подкоренное выражение √(100x 4 y 6 z 3 ).
Мы факторизуем переменные вместе с числами. Рассмотрим пример упрощения подкоренных выражений с переменными для лучшего понимания. Рассмотрим подкоренное выражение √(100x 4 y 6 z 3 ).- Шаг 1: Запишите число под радикалом как произведение его простых множителей и раскройте переменные.
√100x 4 y 6 z 3 = √(2 × 2 × 5 × 5 × x × x × x × x × y × y × y × y × y × y × z × z × z) - Шаг 2: Объедините факторы в пары одинаковых факторов.
√(2 × 2 × 5 × 5 × x × x × x × x × y × y × y × y × y × y × z × z × z) = √(2 2 × 5 2 × x 2 × х 2 × у 2 × y 2 × y 2 × z 2 × z) = √ (2 2 × 5 2 × (x 2 ) 2 × (x 2 ) 2 × (x 3 ) 2 × (x 3 ) 2 × (x 2 ) 2 × (x 2 ) 2 × (x 2 ) 2 × (x 2 ) 2 × г 2 × г) - Шаг 3: Выведите из радикала множители со степенью 2.
 Обратите внимание, что √x 2 всегда неотрицательно. Итак, используйте символ абсолютного значения, чтобы сделать значение неотрицательным.
Обратите внимание, что √x 2 всегда неотрицательно. Итак, используйте символ абсолютного значения, чтобы сделать значение неотрицательным.
√100x 4 y 6 z 3 = √(2 2 × 5 2 × (x 2 ) 2 × (Y 3 ) 2 × Z 2 × Z) = 2 × 5 × x 2 × | Y 3 | 3 | × |г| × √z - Шаг 4: Упрощайте радикал до тех пор, пока дальнейшее упрощение не станет единственным
√100x 4 y 6 z 3 = 10 x 2 |y 3 | |г| √z
Правила упрощения подкоренных выражений
Теперь, когда мы научились упрощать различные виды подкоренных выражений. Давайте рассмотрим некоторые правила упрощения подкоренных выражений, которые можно использовать для упрощения сложных подкоренных выражений. Если a, b — действительные числа, то имеем:
- √ab = √a√b
- √(а/б) = √а/√б, б ≠ 0
- √а + √б ≠ √(а + б)
- √а — √б ≠ √(а — б)
Советы и рекомендации по упрощению подкоренных выражений
- Чтобы упростить подкоренное выражение с подкоренным в знаменателе, умножьте числитель и знаменатель на сопряженную часть знаменателя.
 Например, упростите подкоренное выражение (√2 + √3)/(√5 — √2). Мы умножим числитель и знаменатель этого выражения на сопряженное √5 — √2, которое равно √5 + √2, и воспользуемся алгебраическим тождеством a 2 — б 2 = (а — б)(а + б).
Например, упростите подкоренное выражение (√2 + √3)/(√5 — √2). Мы умножим числитель и знаменатель этого выражения на сопряженное √5 — √2, которое равно √5 + √2, и воспользуемся алгебраическим тождеством a 2 — б 2 = (а — б)(а + б).
(√2 + √3)/(√5 — √2) = (√2 + √3) × (√5 + √2)/(√5 — √2) × (√5 + √2)
= (√2√5 + √3√5 + √2√2 + √3√2)/((√5) 2 — (√2) 2 )
= (√10 + √15 + 2 + √6)/(5 — 2)
= (√10 + √15 + 2 + √6)/3
Следовательно, мы упростили радикальное выражение с радикалами в знаменателе, и дальнейшее упрощение не может быть сделано. - Поскольку квадрат отрицательного числа равен квадрату положительного числа той же величины, поэтому нам нужно помнить, что квадратный корень числа всегда будет неотрицательным. Поэтому мы берем абсолютное значение.
Темы, относящиеся к упрощению радикальных выражений
- Формула радикалов
- Калькулятор упрощения подкоренных выражений
- Рабочие листы радикальных выражений
Часто задаваемые вопросы об упрощении радикальных выражений
Что такое упрощение подкоренных выражений в алгебре?
Упрощение подкоренных выражений — это процесс приведения подкоренных выражений к простейшей форме и полного удаления подкоренных выражений, если это возможно.

Когда вы используете абсолютное значение при упрощении радикальных выражений?
Четная степень любого числа всегда положительна, поэтому любой четный корень должен быть положительным числом (иначе он мнимый), и, следовательно, при упрощении подкоренных выражений с переменными необходимо использовать абсолютное значение, что гарантирует ответ положительный. При работе с радикальными выражениями с нечетными радикалами это требование не применяется, поскольку для отрицательных чисел существуют нечетные корни.
Как упростить подкоренные выражения?
Упрощение подкоренных выражений — это процесс исключения подкоренных выражений или приведения выражений, состоящих из квадратных корней, кубических корней или вообще корня n-й степени, к простейшей форме.
Какие математические понятия важны для упрощения радикальных выражений?
Все математические понятия, включая сложение, вычитание, умножение и деление, важны для упрощения подкоренных выражений наряду с порядком операций.

- Решение уравнений с квадратными корнями.
. Вам просто нужно убедиться, что вы еще больше упростили оставшееся подкоренное число (вещи внутри подкоренного символа). Повторяйте процесс до тех пор, пока подкоренное число больше не будет иметь совершенный квадратный множитель.
Похоже, калькулятор согласен с нашим ответом. Большой!
Пример 4: Упростите подкоренное выражение \sqrt {48} .
Еще один способ решить эту проблему — разложить на простые множители подкоренное число. Затем как можно чаще выражайте простые числа парами. Парные простые числа выйдут из символа квадратного корня, а одно простое останется внутри.
Затем как можно чаще выражайте простые числа парами. Парные простые числа выйдут из символа квадратного корня, а одно простое останется внутри.
И проверяет при решении на калькуляторе.
Пример 5: Упростите подкоренное выражение \sqrt {200} .
94}} .Подкорень содержит как числа, так и переменные. Разберемся с ними отдельно.
Для числового члена 12 его наибольший совершенный квадратный коэффициент равен 4. Теперь, что касается переменных, мне нужно разбить их на пары, поскольку квадратный корень любой парной переменной — это просто сама переменная. Решение этой задачи должно выглядеть примерно так…
Стандартный способ написания окончательного ответа состоит в том, чтобы поместить все термины (как числа, так и переменные), которые находятся вне подкоренного символа 97}}.
Эту задачу мы решим двумя способами. Цель состоит в том, чтобы показать, что есть более простой способ приблизиться к этому, особенно когда показатели степени переменных становятся больше.
Метод сопряжения : это обычный способ, когда мы группируем переменные по две, а затем применяем операцию извлечения квадратного корня , чтобы вывести переменную за пределы радикального символа. Вы увидите, что для больших мощностей этот метод может быть утомительным и трудоемким.
«Разделение равных полномочий» Метод : Вы не найдете этого имени ни в одном учебнике по алгебре, потому что я его выдумал. Тем не менее, ключевая концепция здесь. Основной подход состоит в том, чтобы выразить каждую переменную как произведение членов с четными и нечетными показателями. Если термин уже имеет четную мощность, то вам нечего делать. В противном случае вам нужно выразить как некоторую четную степень плюс 1 .
Помните, что получение квадратного корня из «чего-то» эквивалентно возведению этого «чего-то» в дробную степень {1 \over 2}. 9{13}}}.
Вы можете быть заинтересованы в:
Решение радикальных уравнений
Добавление и вычитание радикальных выражений
Умножение радикальных выражений
Рационализация конфессии
Корни и экспоненты: решающие упражнения: символизирующие коренные костюмы: элементарные и высокие школы
9. эта страница:
эта страница:Введение
Power является выражением этого типа
A B = A · A · · A · A · A. , сам по себе столько раз, сколько показатель степени , b , указывает. Мы читаем это как « a в степени b ».
На этой странице мы рассмотрим случаи, когда показатель степени b является дробью. Другими словами, мы будем работать с корнями и их полномочиями.
Корни как степени
Пусть n — натуральное число, отличное от нуля (1, 2, 3, 4,. ..),
..),
Мы будем называть корень степени n 9n = a$$ Другими словами, n корень числа a есть
число b , что в степени n равно a (так, b n = a ). Число n называется степенью корня и называется подкоренной и корня. Рассмотрим некоторые частные случаи: Важно: Нет корней с четной степенью
(2, 4, 6, 8..) отрицательных чисел
(это комплексные числа), но есть
являются корнями отрицательных чисел, если степень
нечетное число.
9б} $$ СВОЙСТВА ПОЛНОМОЧИЙ Продукт Мощность Частное Отрицательный показатель степени Обратный Инверсия инверсии
Произведение и частное корней
Произведение двух корней с одинаковыми степень — это корень (той же степени) произведения подкоренных, это,
$$ \sqrt[n]{a}\cdot \sqrt[n]{b} = \sqrt[n]{a\cdot b} $$
То же самое происходит с частным:
$$ \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}} $$
Упрощение выражений с дробными показателями
Упражнение 1
Показ раствор
Упражнение 2
Показать раствор
.
Упражнение 4
Показать решение
Упражнение 5
Показать решение
Exercise 6
Show solution
Exercise 7
Show solution
Exercise 8
Show solution
Exercise 9
Показать решение
Упражнение 10
Показать решение
Упражнение 110049
Show solution
Exercise 12
Show solution
Exercise 13
Show solution
Exercise 14
Show solution
Упражнение 15
Показать решение
Matesfacil. com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
Основные выражения и уравнения
8.1 Радикалы
Цели обучения
Квадратные корни
Квадратный кореньЧисло, которое при умножении само на себя дает исходное число. числом называется такое число, которое при умножении само на себя дает исходное число. Например, 4 — это квадратный корень из 16, потому что 42=16. Поскольку (−4)2=16, мы можем сказать, что −4 также является квадратным корнем из 16. Каждое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. По этой причине мы используем подкоренной знак для обозначения главного (неотрицательного) квадратного корняПоложительный квадратный корень из действительного числа, обозначаемый символом . и знак минус перед радикалом — для обозначения отрицательного квадратного корня.
и знак минус перед радикалом — для обозначения отрицательного квадратного корня.
Ноль — единственное действительное число, имеющее один квадратный корень.
Если подкоренное выражение a в подкоренном знаке, число внутри подкоренного знака, неотрицательно и может быть разложено на множители как квадрат другого неотрицательного числа, то квадратный корень из числа очевиден. В этом случае имеем следующее свойство:
Пример 1: Найдите квадратный корень.
а. 36
б. 144
г. 0,04
г. 19
Решение:
а. 36=62=6
б. 144=122=12
в. 0,04=(0,2)2=0,2
д. 19=(13)2=13
Пример 2: Найдите отрицательный квадратный корень.
а. −4
б. −1
Решение:
а. −4=−22=−2
б. −1=−12=−1
Подкоренное число не всегда может быть правильным квадратом. Если натуральное число не является полным квадратом, то его квадратный корень будет иррациональным.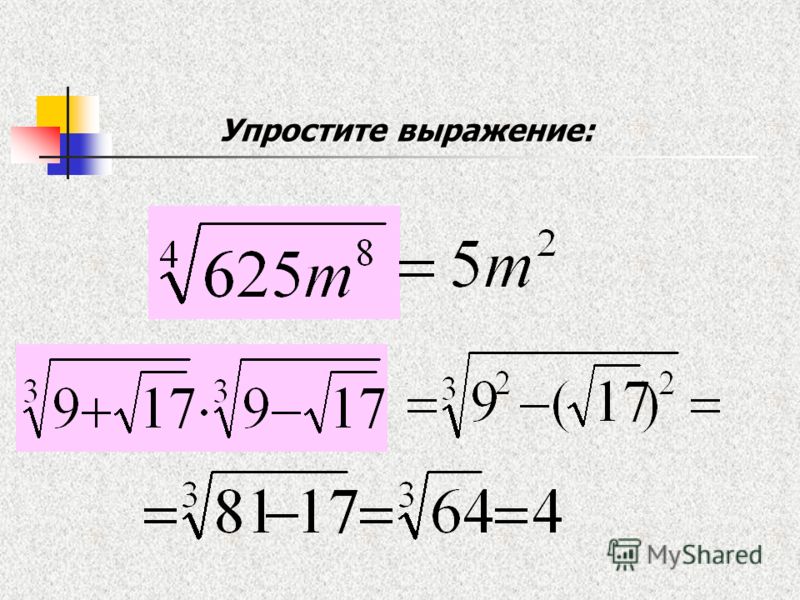 Например, 2 — иррациональное число, и на большинстве калькуляторов его можно приблизить с помощью кнопки квадратного корня.
Например, 2 — иррациональное число, и на большинстве калькуляторов его можно приблизить с помощью кнопки квадратного корня.
Далее рассмотрим квадратный корень из отрицательного числа. Чтобы определить квадратный корень из -9, вы должны найти число, которое при возведении в квадрат дает -9:
Однако любое действительное число в квадрате всегда дает положительное число:
Квадратный корень из отрицательного числа в настоящее время не определен. А пока скажем, что −9 не является действительным числом.
Кубические корни
Кубический кореньЧисло, которое при трехкратном использовании в качестве множителя дает исходное число; оно обозначается символом 3. числом называется такое число, которое при трехкратном умножении само на себя дает исходное число. Кроме того, мы обозначаем кубический корень с помощью символа 3, где 3 называется индексом. Положительное целое число n в обозначении n, которое используется для обозначения n -го корня. . Например,
. Например,
Произведение трех равных множителей будет положительным, если множитель положительный, и отрицательным, если множитель отрицательный. По этой причине любое действительное число будет иметь только один действительный кубический корень. Следовательно, технические особенности, связанные с главным корнем, не применяются. Например,
В общем, для любого действительного числа a мы имеем следующее свойство:
При упрощении кубических корней ищите множители, которые являются совершенными кубами.
Пример 3: Найдите кубический корень.
а. 273
б. 643
г. 03
д. 183
Решение:
а. 273=333=3
б. 643=433=4
в. 03=033=0
д. 183=(12)33=12
Пример 4: Найдите кубический корень.
а. −83
б. −13
в. −1273
Решение:
а. −83=(−2)33=−2
б. −13=(−1)33=−1
−13=(−1)33=−1
в. −1273=(−13)33=−13
Возможно, подкоренное число не является совершенным кубом. Если целое число не является совершенным кубом, то его кубический корень будет иррациональным. Например, 23 — это иррациональное число, которое можно приблизить на большинстве калькуляторов с помощью основной кнопки. В зависимости от калькулятора мы обычно вводим индекс перед нажатием кнопки, а затем подкоренное число следующим образом:
Следовательно, у нас есть
.
n th КорниДля любого целого числа n≥2 мы определяем корень nЧисло, которое при возведении в степень n дает исходное число. положительного действительного числа как число, которое при возведении в n -ю степень дает исходное число. Для любого неотрицательного действительного числа a мы имеем следующее свойство:
Здесь n называется индексом , а an называется подкоренным числом и . Более того, мы можем обращаться ко всему выражению an как к радикалу. Используется при обращении к выражению формы an.. Когда индекс представляет собой целое число, большее 3, мы говорим «корень четвертой степени», «корень пятой степени» и т. д. n -й корень любого числа очевиден, если мы можем записать подкоренное число с показателем степени, равным индексу.
Используется при обращении к выражению формы an.. Когда индекс представляет собой целое число, большее 3, мы говорим «корень четвертой степени», «корень пятой степени» и т. д. n -й корень любого числа очевиден, если мы можем записать подкоренное число с показателем степени, равным индексу.
Пример 5: Найдите n -й корень.
а. 814
б. 325
г. 17
д. 1164
Решение:
а. 814=344=3
б. 325=255=2
в. 17=177=1
д. 1164=(12)44=12
Если индекс равен n=2, то радикал указывает на квадратный корень, и его принято записывать без индекса, как показано ниже:
Мы уже позаботились о том, чтобы определить главный квадратный корень числа. Теперь мы расширим эту идею до n корней, когда n четно. Например, 3 — это корень четвертой степени из 81, потому что 34=81. А поскольку (−3)4=81, мы можем сказать, что −3 также является корнем четвертой степени из 81. Следовательно, мы используем радикальный знак n для обозначения главного (неотрицательного) корня n. Положительный корень n , когда n четно. когда n четно. В этом случае для любого действительного числа a , воспользуемся следующим свойством:
Следовательно, мы используем радикальный знак n для обозначения главного (неотрицательного) корня n. Положительный корень n , когда n четно. когда n четно. В этом случае для любого действительного числа a , воспользуемся следующим свойством:
Например,
Отрицательный корень n -й, когда n четное, будет обозначаться знаком минус перед радикалом −n.
Мы видели, что квадратный корень из отрицательного числа не является действительным, потому что любое действительное число при возведении в квадрат дает положительное число. Фактически аналогичная проблема возникает для любого четного индекса:
Здесь корень четвертой степени из −81 не является действительным числом, потому что четвертая степень любого действительного числа всегда положительна.
Пример 6: Упрощение.
а. −164
б. −164
Решение:
а. Подкоренное число отрицательное, а индекс четный. Следовательно, не существует действительного числа, которое при возведении в четвертую степень равно −16.
Следовательно, не существует действительного числа, которое при возведении в четвертую степень равно −16.
б. Здесь подкоренное положительное. Более того, 16=24, и мы можем упростить его следующим образом:
Когда n нечетно, таких проблем не возникает. Произведение нечетного числа положительных множителей положительно, а произведение нечетного числа отрицательных множителей отрицательно. Следовательно, когда индекс n нечетно, существует только один действительный корень n -го для любого действительного числа a . И у нас есть следующее свойство:
Пример 7: Найдите n -й корень.
а. −325
б. −17
Решение:
а. −325=(−2)55=−2
б. −17=(−1)77=−1
Попробуйте! Найдите корень четвертой степени: 6254.
Ответ: 5
Видео Решение
(нажмите, чтобы посмотреть видео) Резюме: Когда n является нечетным , корень n -го числа равен положительному или отрицательному в зависимости от знака подкоренного числа.
Когда n четно , корень n -го числа равен положительному или недействительному в зависимости от знака подкоренного числа.
Упрощение использования правила произведения и частного для радикалов
Не всегда подкоренное выражение является совершенной степенью данного индекса. Если нет, мы используем следующие два свойства, чтобы упростить их. Если a и b представляют собой положительные действительные числа, тогда мы имеем
Упрощенный радикал Радикал, в котором подкоренное число не состоит из какого-либо множителя, который может быть записан как совершенная степень индекса. если он не содержит ни одного множителя, который можно записать в виде совершенной степени индекса.
Пример 8: Упростим: 12.
Решение: Здесь 12 можно записать как 4 ⋅ 3, где 4 — полный квадрат.
Мы можем проверить наш ответ на калькуляторе:
Также стоит отметить, что
Ответ: 23
Пример 9: Упрощение: 135.
Решение: Начните с поиска наибольшего идеального квадратного коэффициента 135.
,
4 Ответ: 315
Пример 10: Упростим: 50121.
Решение: Начнем с нахождения простых факторизаций как 50, так и 121. Это позволит нам легко определить наибольшие совершенные квадратные множители.
Следовательно,
Ответ: 5211
Пример 11: Упрощение: 1623.
Решение: Используйте основную факторизацию 162, чтобы найти самый большой идеальный коэффициент кубика:
Замените Radicand на этот фактор а затем применить правило произведения для радикалов.
Мы можем проверить наш ответ на калькуляторе.
Ответ: 3 63
Попробуйте! Упростить: 2 963.
Ответ: 4 123
Решение для видео
(нажмите, чтобы посмотреть видео)
Пример 12: Упрощение: −965.
Решение: Здесь мы отмечаем, что индекс нечетный, а подкоренное число отрицательное; следовательно, результат будет отрицательным. Мы можем разложить подкоренное число следующим образом:
Тогда упростим:
Ответ: −2 35
Пример 13: Упростим: −8643.
Решение: В этом случае рассмотрим эквивалентную дробь с −8=(−2)3 в числителе, а затем упростим.
Ответ: −1/2
Попробуйте! Упростить −1083.
Ответ: −3 43
Решение для видео
(нажмите, чтобы посмотреть видео)Ключевые выводы
Тематические упражнения
Часть A: радикалы
Упрощение.
1. 81
2. 100
3. 64
4. 121
5. 0
6. 1
7. 0.25
8. 0.01
9. 1,21
10. 2.25
11. 14
12. 136
13. 2516
14. 925
15. -25
16. −9
17. −36
18. 100
20. −1
21. 273
22. 1253
23. 643
24. 83
25. 183
26. 1643
27. 8273
28. 641253
29. 0.0013
30. 10003
31. −13
32. −83
33. −273
34. −643
35. −183
36. −27643
37. −8273
38. −11253
39. 814
40. 6254
41. 164
42. 10 0004
43. 325
44. 15
45. 2435
46. 100 0005
47. −164
−164
48. -16
49. −325
50. −15
51. -1
52 53. −5 −273
54. −2 −83
55. 5 −1 0003
56. 3 −2435
57. 10 −164
58. 2 −646
59. 325
58. 2 −646
59.
60. 64
61. 2 273
62. 8 2435
63. −7 83
64. -4 6254
65. 6 100 0005
66. 5 1287
Часть B: Упрощение радикалов
Упрощение.
67. 32
68. 250
69. 80
70. 150
71. 160
72. 60
73. 175
74. 216
75. 5112
9000 7664. 1013577. 5049
78. −2120
79. −3162
80. 89
81. 45121
82. 9681
83. 543
84. 243
85. 483
86. 813
87. 403
88. 1203
89. 1623
90. 5003
91. 541253
92. 403433
93. 5 −483
94. 2 −1083
95. 8 964 Упрощение Дайте точный ответ и примерный ответ, округлив его до сотых.
101. 8
102. 200
103. 45
104. 72
105. 34
106. 59
107. 3225
108. 4849
109. 803
110. 3203
111. 483
112. 2703
777777477774777477477774774774777747747747774774774774774774774hRITE. Следуя как радикальное выражение с коэффициентом 1.
113. 215
114. 37
115. 510
116. 103
117. 2 73
118. 3 63
119. 2 54
. 120. 3 24
121. Формула площади квадратов A=s2. Если площадь равна 18 квадратных единиц, то какова длина каждой стороны?
122. Вычислите длину стороны квадрата площадью 60 квадратных сантиметров.
123. Формула объема V куба: V=s3. Если объем куба 112 кубических единиц, то какова длина каждой стороны?
124. Вычислите длину стороны куба объемом 54 кубических сантиметра.
Часть C: Дискуссионная доска
125. Объясните, почему из любого ненулевого действительного числа существует два квадратных корня.
126. Объясните, почему для любого действительного числа существует только один кубический корень.
127. Чему равен квадратный корень из 1 и чему равен кубический корень из 1? Объяснить, почему.
128. Объясните, почему -1 не является действительным числом и почему -13 является действительным числом.
Ответы
1: 9
3: 8
5: 0
7: 0,5
9: 1,1
11: 1/2
13: 5/4
15: Не реальное число
17: −6
19: -10
21: 3
23: 4
25: 1/2
27: 2/3
29: 0,1
31: −1
33: −3
35: −1/2
37: −2/3
39: 3
41: 2
43: 2
45: 3
47: −2
49: −2
51: Ненастоящее число
53: 15
55: −50
57: Ненастоящее число
59: 15
61: 6
63: −14
65: 60
67: 42
69: 45
71: 410
73: 57
75: 207
77: 527
79: −272
81: 3511
83: 3 23
85: 2 63
87: 2 53
89: 3 63
91: 3 235
93: — 103
95: 1645
93: — 103
95: 1645
: — 103
95: 1645
: — 103
91: 165
997:2 55
99:2 753
101:22≈2,83
103:35≈6,71
105:32≈90,830005
107: 425,1,13
109: 2 103,4. 31
31
111: 2 63,3.63
113: 60
115: 250
117: 563
119: 804
121: 32 units
119: 804
121: 32.
123: 2 143 шт.
8.2 Упрощение радикальных выражений
Цели обучения
Упрощение радикальных выражений
Алгебраическое выражение, содержащее радикалы, называется радикальным выражением. Алгебраическое выражение, содержащее радикалы.. Мы используем правила произведения и частного, чтобы упростить их.
Пример 1: Упрощение: 8y33.
Решение: Используйте тот факт, что ann=a, когда n нечетно.
Ответ: 2 года
Пример 2: Упрощение: 9х2.
Решение: Квадратный корень имеет индекс 2; использовать тот факт, что ann=|a| когда n четно.
Поскольку x является переменной, она может представлять отрицательное число. Таким образом, нам нужно убедиться, что результат положительный, включив оператор абсолютного значения.
Ответ: 3|x|
Важное примечание
Обычно в начале текстов по алгебре отмечается, что все переменные считаются положительными. Если это так, то x в предыдущем примере является положительным, и оператор абсолютного значения не требуется. Пример можно упростить следующим образом:
9×2=32×2 =32⋅x2=3x
В этом разделе предполагается, что все переменные положительны. Это позволяет нам сосредоточиться на вычислении корней n -й без технических деталей, связанных с основной проблемой n -го корня. По этой причине мы будем использовать следующее свойство для остальной части раздела:
ann=a, if a≥0 n-й корень
При упрощении подкоренных выражений ищите множители со степенями, соответствующими индексу.
Пример 3: Упрощение: 18x3y4.
Решение: Начните с определения квадратных множителей 18, x3 и y4.
Сделайте эти замены, а затем примените правило произведения для радикалов и упростите.
Ответ: 3xy22x
Пример 4: Упрощение: 4a5b6.
Решение: Начните с определения квадратных множителей чисел 4, a5 и b6.
Сделайте эти замены, а затем примените правило произведения для радикалов и упростите.
Ответ: 2a2ab3
Пример 5: Упрощение: 80x5y73.
Решение: Начните с определения кубических коэффициентов 80, x5 и y7.
Сделайте эти замены, а затем примените правило произведения для радикалов и упростите.
Ответ: 2xy2⋅10x2y3
Пример 6: Упростить 9x6y3z93.
Решение: Коэффициент 9=32 и, следовательно, не имеет совершенных кубических множителей.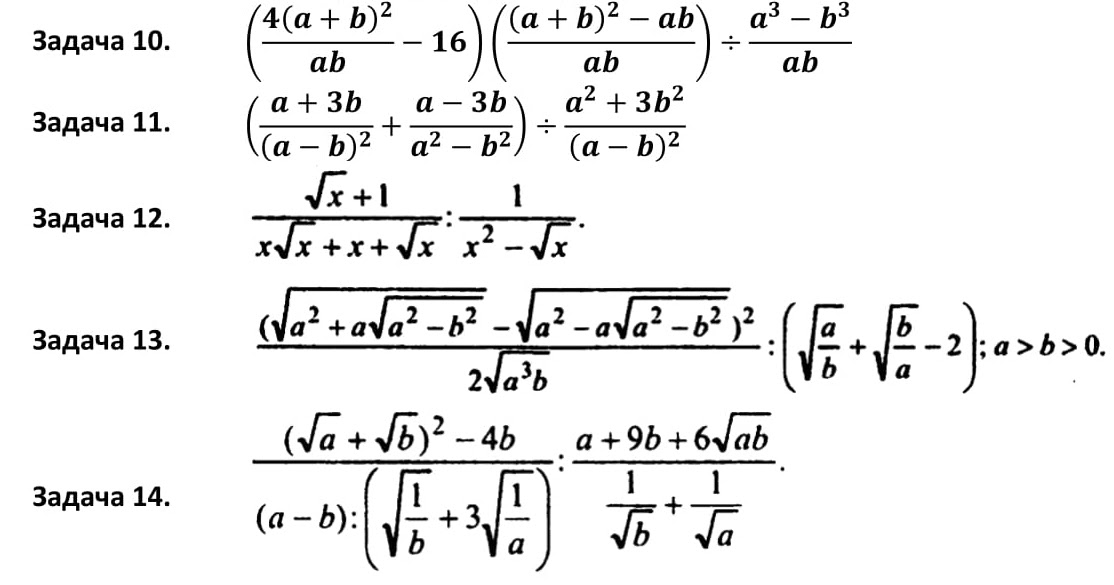 Он останется единственным оставшимся подкоренным числом, поскольку все остальные множители являются кубами, как показано ниже:
Он останется единственным оставшимся подкоренным числом, поскольку все остальные множители являются кубами, как показано ниже:
Замените переменные этими эквивалентами, примените правило произведения и частного для радикалов, а затем упростите.
Ответ: x2⋅93yz3
Пример 7: Упрощение: 81a4b54.
Решение: Определите все множители, которые можно записать в виде совершенных степеней числа 4. Здесь важно заметить, что b5=b4⋅b. Следовательно, множитель b останется внутри радикала.
Ответ: 3ab⋅b4
Пример 8: Упрощение: −32x3y6z55.
Решение: Обратите внимание, что переменный множитель x нельзя представить в виде степени числа 5, и поэтому он останется внутри радикала. Кроме того, для y6=y5⋅y; множитель y также останется внутри радикала.
Ответ: −2yz⋅x3y5
Попробуйте! Упростить: 192x6y7z12. ( Предположим, что все переменные положительны. )
( Предположим, что все переменные положительны. )
Ответ: 8x3y3z63y
Решение для видео
(нажмите, чтобы посмотреть видео)Подсказка
Чтобы упростить корень n th, мы можем разделить степени на индекс.
a6=a3, что равно a6÷2=a3b63=b2, что равно b6÷3=b2c66=c , что равно c6÷6=c1
частное и остаток упростить. Например,
A5 = A2⋅A, который составляет A5 ÷ 2 = A2 R 1B53 = B порядка, который составляет B5 ÷ 3 = B1 R 2C145 = C2omC45, который C14 ÷ 5 = C2 R 4
Частное — это показатель степени множителя вне радикала, а остаток — это показатель степени множителя, оставшегося внутри радикала.
Формулы с радикалами
Далее мы рассмотрим формулу расстояния. Даны две точки (x1, y1) и (x2, y2),
Расстояние d между ними определяется следующей формулой:
Напомним, что эта формула была получена из теоремы Пифагора.
Пример 9: Вычислите расстояние между (−4, 7) и (2, 1).
Решение: Используйте формулу расстояния со следующими точками.
Рекомендуется включать формулу в ее общем виде перед заменой значений переменных; это улучшает читаемость и снижает вероятность ошибок.
Ответ: 62 ед.0005
, где L представляет собой длину маятника в футах. Если длина маятника равна 6 футам, рассчитайте период, округлив его до ближайшей десятой доли секунды.
Решение: Подставьте 6 вместо L и упростите.
Ответ: Период составляет примерно 2,7 секунды.
Функции извлечения квадратного и кубического корня
Начнем с функции извлечения квадратного корня. Функция f(x)=x.:
Мы знаем, что квадратный корень не является вещественным числом, если1574 x — это минус. Следовательно, мы заключаем, что область состоит из всех действительных чисел, больших или равных 0. Здесь мы выбираем 0 и некоторые положительные значения для x , вычисляем соответствующие значения y и строим получившиеся упорядоченные пары.
Здесь мы выбираем 0 и некоторые положительные значения для x , вычисляем соответствующие значения y и строим получившиеся упорядоченные пары.
После нанесения точек мы можем нарисовать график функции извлечения квадратного корня.
Пример 11: Для заданной функции f(x)=x+2 найдите f(−2), f(2) и f(6).
Решение: Замените x каждым из заданных значений.
Ответ: f(−2)=0, f(2)=2 и f(6)=22
Далее рассмотрим функцию кубического корня. Функция f(x)=x3.:
Поскольку кубический корень может быть как отрицательным, так и положительным, мы заключаем, что область определения состоит из всех действительных чисел. Для полноты выберите некоторые положительные и отрицательные значения для x , а также 0, а затем вычислите соответствующие значения y .
Нанесите точки и нарисуйте график функции кубического корня.
Пример 12: Для заданной функции g(x)=x−13 найдите g(−7), g(0) и g(55).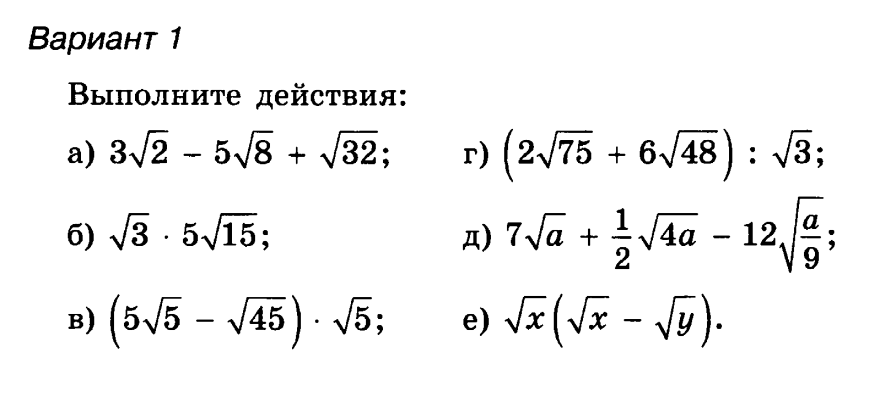
Решение: Замените x каждым из заданных значений.
Ответ: g(−7)=−2, g(0)=−1 и g(55)=3 23
Ключевые выводы
Тематические упражнения
Часть A: Упрощение подкоренных выражений
Упрощение. ( Предположим, что все переменные представляют собой положительные числа. )
1. 36A2
2. 121B2
3. X2Y2
4. 25x2y2z2
25x2y2z2
5. 180×3
6. 150y3
7. 49a3b2


 При этом учтите, что:
При этом учтите, что:



 Кубический корень может быть положительным или отрицательным в зависимости от знака подкоренного числа. Следовательно, для любого действительного числа a , мы имеем свойство a33=a.
Кубический корень может быть положительным или отрицательным в зависимости от знака подкоренного числа. Следовательно, для любого действительного числа a , мы имеем свойство a33=a. Как правило, процесс упрощается, если вы работаете с простой факторизацией подкоренного числа.
Как правило, процесс упрощается, если вы работаете с простой факторизацией подкоренного числа. 128×64
128×64 Следовательно, чтобы найти у -перехваты, задаем х = 0 и найти y . Найдите и -перехваты для следующего.
Следовательно, чтобы найти у -перехваты, задаем х = 0 и найти y . Найдите и -перехваты для следующего.  Оцените скорость автомобиля перед торможением на сухом асфальте, если следы заноса остаются на расстоянии 36 футов.
Оцените скорость автомобиля перед торможением на сухом асфальте, если следы заноса остаются на расстоянии 36 футов. Укажите точное значение, а приблизительное значение округлить до десятых долей секунды.
Укажите точное значение, а приблизительное значение округлить до десятых долей секунды. 
 3 Сложение и вычитание подкоренных выражений
3 Сложение и вычитание подкоренных выражений

 Обратите внимание, что 2×3−3×3≠2x−3×3.
Обратите внимание, что 2×3−3×3≠2x−3×3. Соответствующего свойства для сложения нет.
Соответствующего свойства для сложения нет. )
)  -35-(20-50)
-35-(20-50) 12m4n — M75M2n+227m4n
12m4n — M75M2n+227m4n 3B5
3B5 Если a и b представляют положительные действительные числа,
Если a и b представляют положительные действительные числа,

 Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем .
.
 Упрощение результата дает рационализированный знаменатель. Например,
Упрощение результата дает рационализированный знаменатель. Например,

 Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя.
Процесс нахождения такого эквивалентного выражения называется рационализацией знаменателя. 3а⋅2а
3а⋅2а Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь? 17-2
17-2 : 104
: 104 В этом разделе мы определим, какие рациональные (или дробные) показатели степени. Дробный показатель степени m / n указывает на радикал с индексом n и показателем степени m : am/n=amn. средства и как с ними работать. Применяются все правила для экспонент, разработанные до этого момента. В частности, вспомним правило произведения показателей. Даны любые рациональные числа m и n , затем
В этом разделе мы определим, какие рациональные (или дробные) показатели степени. Дробный показатель степени m / n указывает на радикал с индексом n и показателем степени m : am/n=amn. средства и как с ними работать. Применяются все правила для экспонент, разработанные до этого момента. В частности, вспомним правило произведения показателей. Даны любые рациональные числа m и n , затем
 Любое подкоренное выражение может быть записано с рациональным показателем, который мы называем экспоненциальной формой. Эквивалентное выражение, записанное с использованием рационального показателя.
Любое подкоренное выражение может быть записано с рациональным показателем, который мы называем экспоненциальной формой. Эквивалентное выражение, записанное с использованием рационального показателя.
 Если даны рациональные числа m и n , то мы имеем
Если даны рациональные числа m и n , то мы имеем
 Если индексы разные, то сначала переписать радикалы в экспоненциальной форме, а затем применить правила для показателей.
Если индексы разные, то сначала переписать радикалы в экспоненциальной форме, а затем применить правила для показателей.
 0004 900 /4
0004 900 /4 33/2⋅31/2
33/2⋅31/2 100310
100310 Квадратный корень из отрицательного числа не является реальным. Во втором выражении, из-за порядка операций, после возведения числа 4 в степень (3/2) к ответу применяется знак минус.
Квадратный корень из отрицательного числа не является реальным. Во втором выражении, из-за порядка операций, после возведения числа 4 в степень (3/2) к ответу применяется знак минус.
 Чтобы решить это уравнение алгебраически, используйте свойство возведения в квадрат равенства и тот факт, что (a)2=a2=a, когда a положительно. Удалите квадратный корень, возведя в квадрат обе части уравнения следующим образом:
Чтобы решить это уравнение алгебраически, используйте свойство возведения в квадрат равенства и тот факт, что (a)2=a2=a, когда a положительно. Удалите квадратный корень, возведя в квадрат обе части уравнения следующим образом: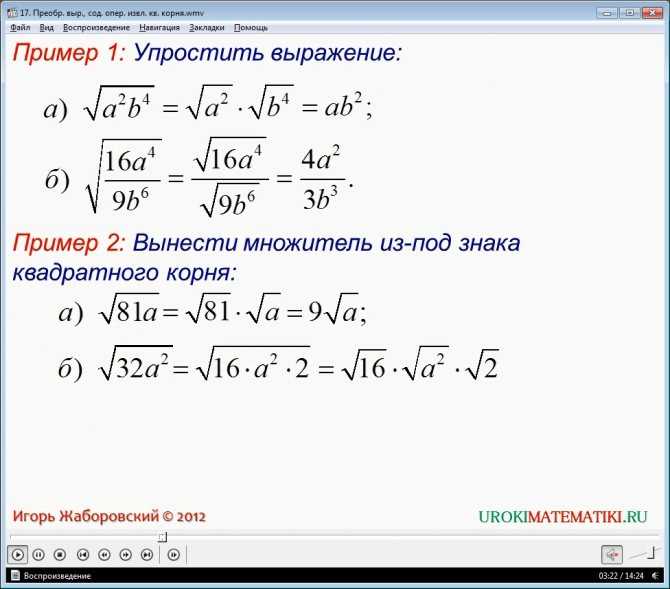



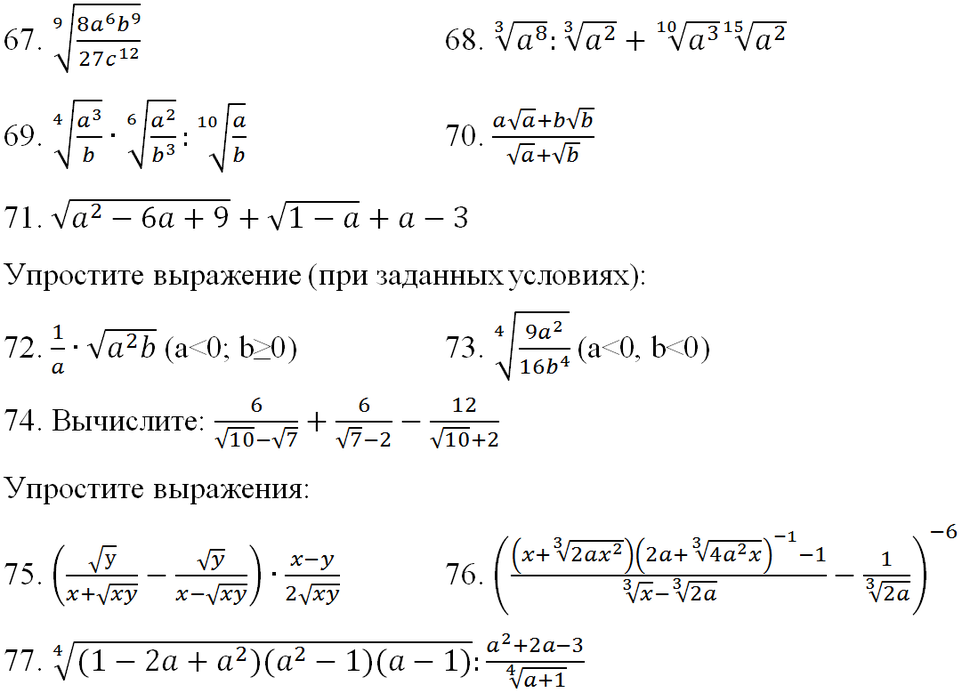 Возведение квадратного корня в квадрат устраняет радикал, оставляя нам уравнение, которое можно решить с помощью методов, изученных ранее при изучении алгебры. Однако возведение в квадрат обеих частей уравнения приводит к возможности посторонних решений, поэтому проверьте свои ответы в исходном уравнении.
Возведение квадратного корня в квадрат устраняет радикал, оставляя нам уравнение, которое можно решить с помощью методов, изученных ранее при изучении алгебры. Однако возведение в квадрат обеих частей уравнения приводит к возможности посторонних решений, поэтому проверьте свои ответы в исходном уравнении. x3=5
x3=5 24x+3−3=2x
24x+3−3=2x Найдите число.
Найдите число.
 Существуют ли какие-либо условия, когда нам не нужно проверять наличие посторонних решений? Почему?
Существуют ли какие-либо условия, когда нам не нужно проверять наличие посторонних решений? Почему?