| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.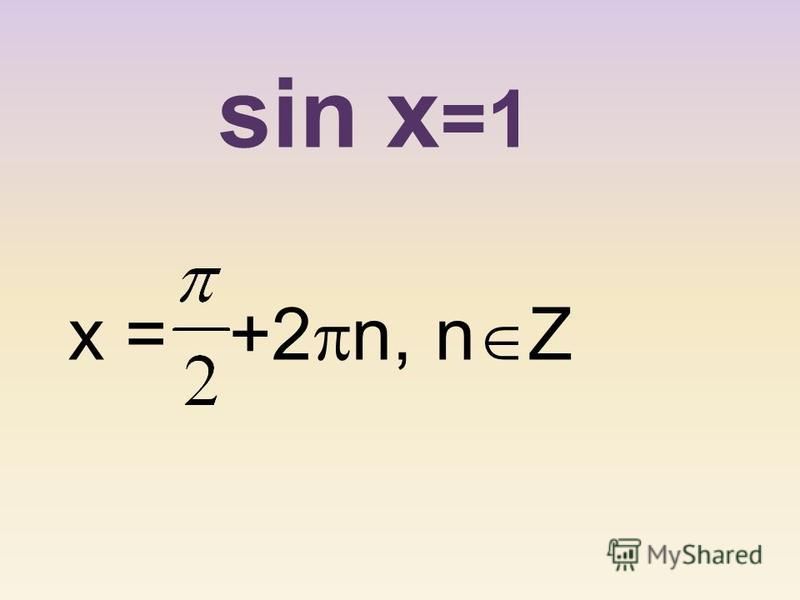 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.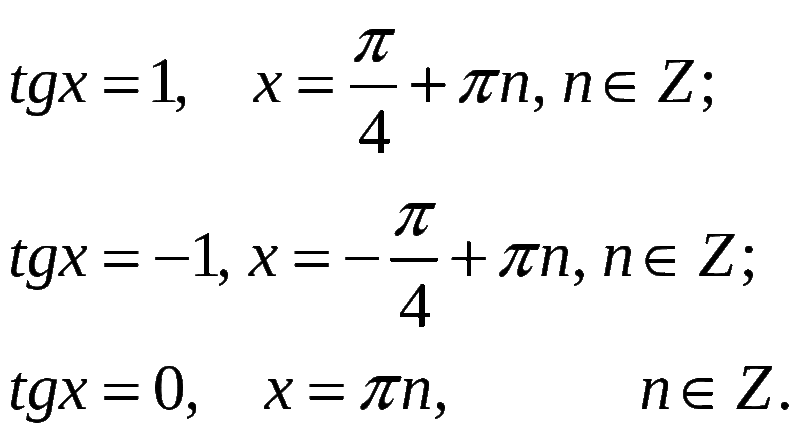 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.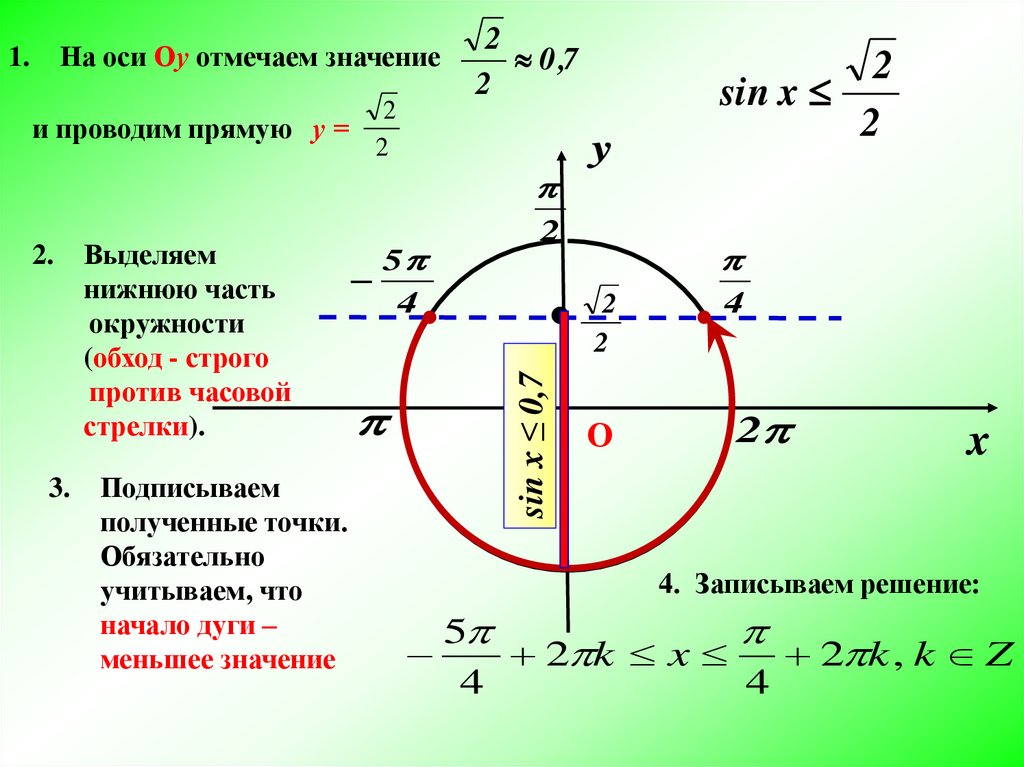 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
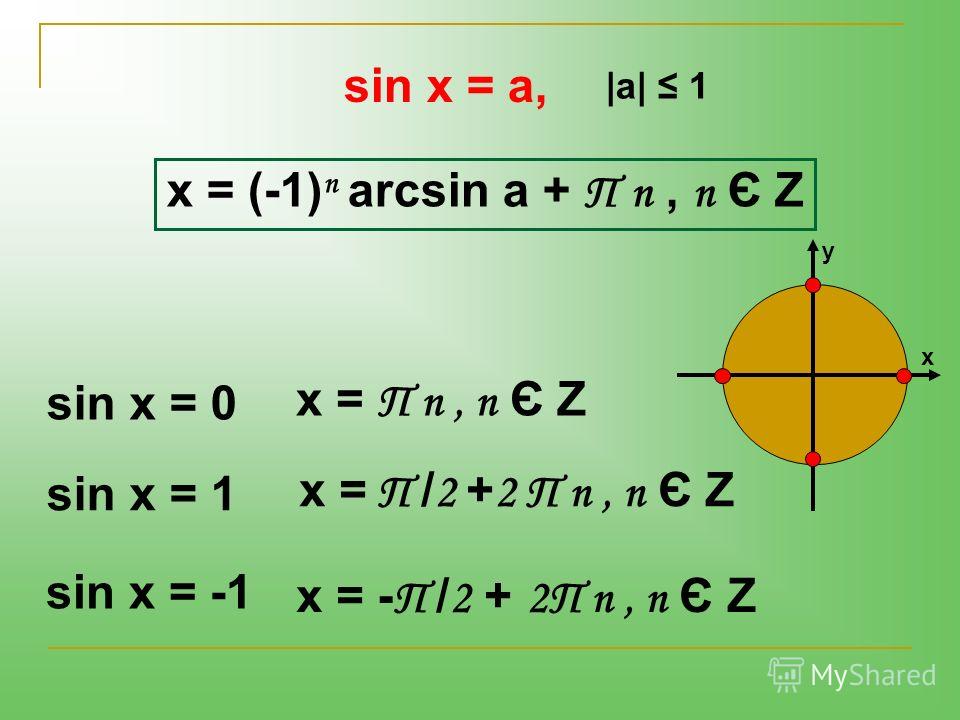
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн для чайников 🫖🤓
Учитель очень удивится увидев твоё верное решение😉
Введите уравнение с неизвестным, для которого требуется найти корни.
 2
2Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства — Урок 5 2008 Расмус Эхф | Печать |
Пример 1
Решите уравнение sin x = cos x и затем неравенство
грех x > cos x на интервале 0 x < 2,
Из единичного круга мы видим, что sin x и cos x
может иметь одинаковое значение только в двух местах, в x = /4
и х = 5/4
(45 и 225 ).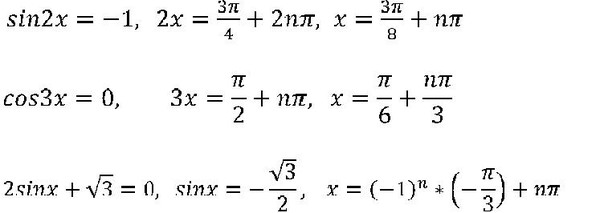
Уравнение sin x = cos x также можно решить путем деления на cos x.
тангенс х = 1
x = тангенс −1 (1)
х = 45 ∙ /180 + к∙
x = /4 + k∙ (k — любое целое число, положительное или отрицательное)
Если положить k = 0 и k = 1, получим решения /4 (45 ) и /4 + = 5/4 (45 + 180 = 225 ).
Чтобы решить неравенство sin x > cos x, нам нужно увидеть, что больше sin x или cos x на интервалах между решениями /4 и 5/4. Решения можно увидеть, если мы нарисуем графики f(x) = sin x и g(x) = cos Икс. График sin x лежит над графиком cos x на интервале /4 x 5x/4 (см. заштрихованную область на диаграмме).
sin x cos x на интервале /4 x 5x/4.
Пример 2
Решить уравнение sin x ∙ cos x = 0 и затем неравенство
sin x ∙ cos x > 0 на интервале 0 x < 2.
Неравенство не имеет решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения уравнение sin x ∙ cos x = 0 на интервале 0 x < 2, поэтому 0, /2 и 3/2 (0 , 90 , 180 и 270 ).
Решение sin x
∙ cos x > 0 можно найти, взглянув на единичный круг. Нам нужно найти
где sin x, умноженный на cos x, является положительным. Другими словами, sin x и cos x имеют
иметь один и тот же знак, оба должны быть
положительный или оба отрицательные. Это происходит в первом и третьем квадранте.
поэтому решения
0 < х < /2 и р < х < 3/2.
Мы также можем увидеть это по
построение графика
f(x) = sin x ∙ cos x.
Пример 3
Решите уравнение sin x ∙ cos x − sinx = 0 и тогда неравенство sin x ∙ cos x − sin x > 0 на интервале 0 x < 2,
sin x ∙ cos x − sinx = 0 sin x (cos x − 1) = 0 | Нам нужно
чтобы разложить уравнение на множители, взяв sin x за скобки. |
Уравнение имеет решения когда sin x = 0 или скобка (cos x − 1) = 0,
sin x = 0
x = 0 или (180 ).
или
потому что х — 1 = 0
потому что х = 1
х = 0
Единственные решения уравнение поэтому 0 и .
Неравенство sin x ∙ cos x − sin x > 0 можно переписать как sin x (cos x − 1) > 0,
Теперь полезно сделать таблицу знаков и посмотрите на знаки sin x и cos x − 1.
Решение
Мы видим, что оба фактора
отрицательно на интервале
< x < 2,
Теперь давайте посмотрим, как это подходит
в с графиком
f(x) = sin x ∙ cos x − sin x
Заштрихованная область над крестиком
ось показывает, где
sin x (cos x − 1) > 0, что согласуется с нашими расчетами.
Пример 4
Найти все решения уравнения cos 2 x − cos x = 0,
cos 2 x − cos х = 0
потому что х ∙ (кос х — 1) = 0
Решения можно найти, когда cos x = 0 или cos x − 1 = 0
cos х = 0
x =/ 2 или 3/ 2 (90 или 270 )
х = / 2 + к∙
или
потому что х — 1 = 0
потому что х = 1
x = 0 + k∙2 = k∙2
Все решения укладываются в шаблон x = /2 + к∙
Пример 5
Найти все решения уравнения sin 2 x − 5 sin x + 4 = 0,
Это квадратное уравнение с sin x в качестве
переменная. Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Синус мы не можем принять значение 4 поэтому нам не нужно рассматривать sin x = 4. Другая возможность — sin x = 1, решение которой /2 (90 ). Таким образом, полное решение:
х = / 2 + к∙2
Пример 6
Решите уравнение sin 5x = грех х .
Возможно, что позиция 5х на единичном круге совпадает с позицией x и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее уравнение:
1) 5x = x + к∙360
4x = к∙360
х = к∙90
Мы показываем эту возможность в диаграмма.
Появляется вторая возможность
от того что
грех x = грех (180 − х ). Это дает нам следующее решение:
5 х = 180 — х + к∙360
6x = 180 + к∙360
х = 30 + к∙60
Это решение показано на
схему справа.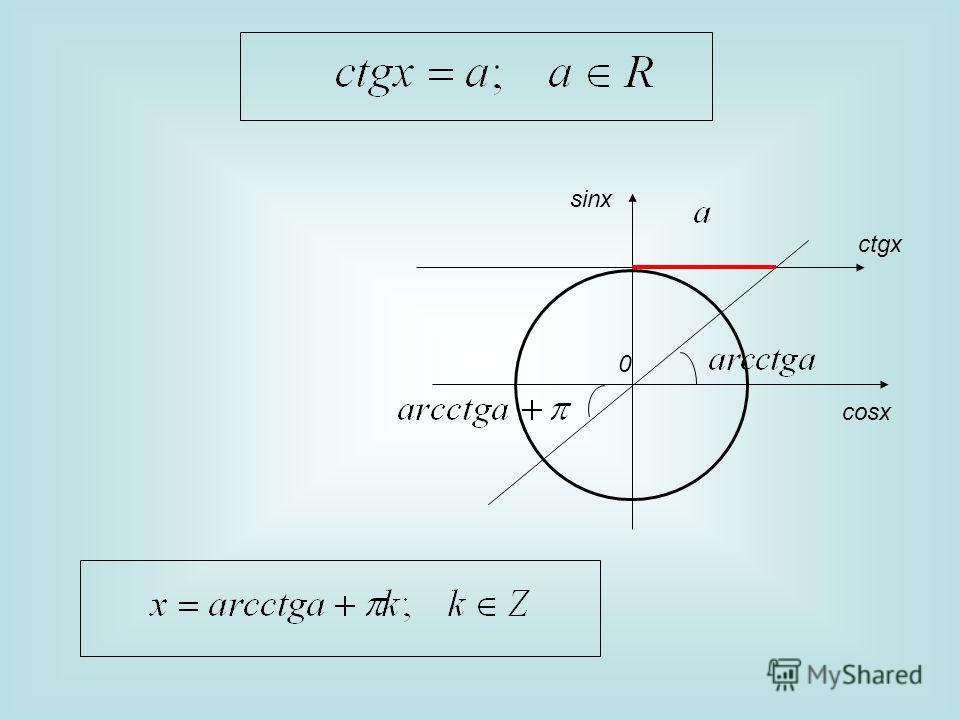
Но мы замечаем, что первое решение содержится в второе решение, поэтому достаточно дать второе решение
х = 30 + к∙60
Пример 7
Решите уравнение cos 2x = cos x на интервале 0 x < 2,
1) Сначала рассмотрим вероятность того, что x и 2x находятся в одном и том же месте на единичной окружности.
2x = x + k∙2 x = k∙2 х = 0 | Вычесть x из обеих частей уравнения, а затем выберите k = 0 (k = 1 дает 2, которое находится вне интервала |
2) Второй вариант.
с факта
потому что v = cos (-v). Тогда решение будет следующим:
2x = −x + к∙2
3x = k∙2
x = k∙2/ 3
Это дает решения 2/3 (120 )
для k = 1 и 4/3 (240 ) для k = 2.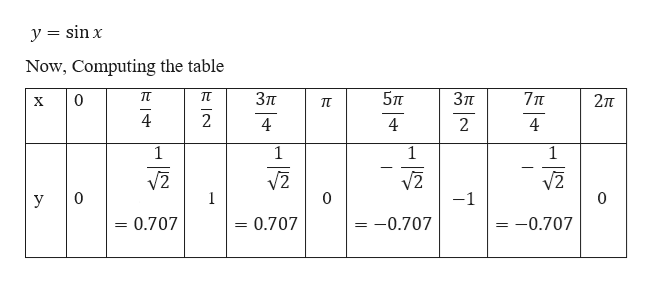 поэтому полное решение:
поэтому полное решение:
0, 2/3 или 4/3.
Пример 8
Решите уравнение tan 3x = загар 2x.
Уравнения Тана во многих способов самое простое из тригонометрических уравнений, так как есть только возможность учтите, что это повторяется с интервалом 180 .
3x = x + k∙180
2x = к∙180
х = к∙90
или в радианах
х = к∙/ 2
Попробуйте викторину 5 по триггерным функциям.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
— Есть ли способ решить $\sin(x)=x$?
спросил
Изменено 10 месяцев назад
Просмотрено 34к раз
$\begingroup$
Примечание. Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов.
Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов.
При попытке решить $\sin(x)=x$ первым очевидным решением является $x=0$. Однако существует бесконечное количество комплексных значений $x$, которые мы можем попытаться найти. Однако мы собираемся игнорировать их.
Мне интересно, есть ли способ аналитического решения для $x$ в $\sin(x)=x$. Это кажется невозможным, точно так же, как мы не можем решить $\cos(x)=x$ аналитически или легко, но поскольку $\sin(x)=x$ имеет такой простой точный ответ, я подумал, есть ли это способ, которым вы могли бы это сделать.
Итак, существует ли аналитический способ решить эту проблему? Если да, то как? Если нет, то как еще мы могли бы решить это, кроме как графически?
- алгебра-предварительное исчисление
- анализ
- тригонометрия
- трансцендентальные уравнения
$\endgroup$
19
$\begingroup$
Если бы задачу можно было решить чисто алгебраическими средствами (с конечным числом шагов), это означало бы, что $\sin(x)$ можно было бы задать полиномиальным представлением, из которого вы могли бы перейти к своей обычной процедуре факторизации к найти нули многочлена. 7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
Итак, теперь у нас есть наше «алгебраическое решение», состоящее в том, что $x = 0$.
$\endgroup$
4
$\begingroup$
Поскольку вы рассматриваете только действительные числа, я думаю, что самый простой способ решить эту проблему — разделить случаи и использовать неравенства в каждом случае:
$x=0$ — явное решение, поскольку $\sin 0=0 $.
Если $x\in]0,1[$, то из МВТ следует, что $\exists c\in]0,1[: \cos c=\frac{\sin x-\sin 0}{x-0 }$.
Так как $x,c\in]0,1[$, то $1>\frac{\sin x}{x} \Leftrightarrow x>\sin x$.
Если $x=1$, то $\sin 1 \neq 1$.
Если $x>1$, то очевидно $x>\sin x$.
Теперь ясно, что если $a$ является решением, то $-a$ также является решением (поскольку $\sin(-x) = -\sin x$). Следовательно, нет решений с $x<0$
$\endgroup$
$\begingroup$
Подсказка: покажите, что если $x\neq 0$ ($x$ действительное), $\left|\frac{\sin(x)}{x}\right|<1.

 3
3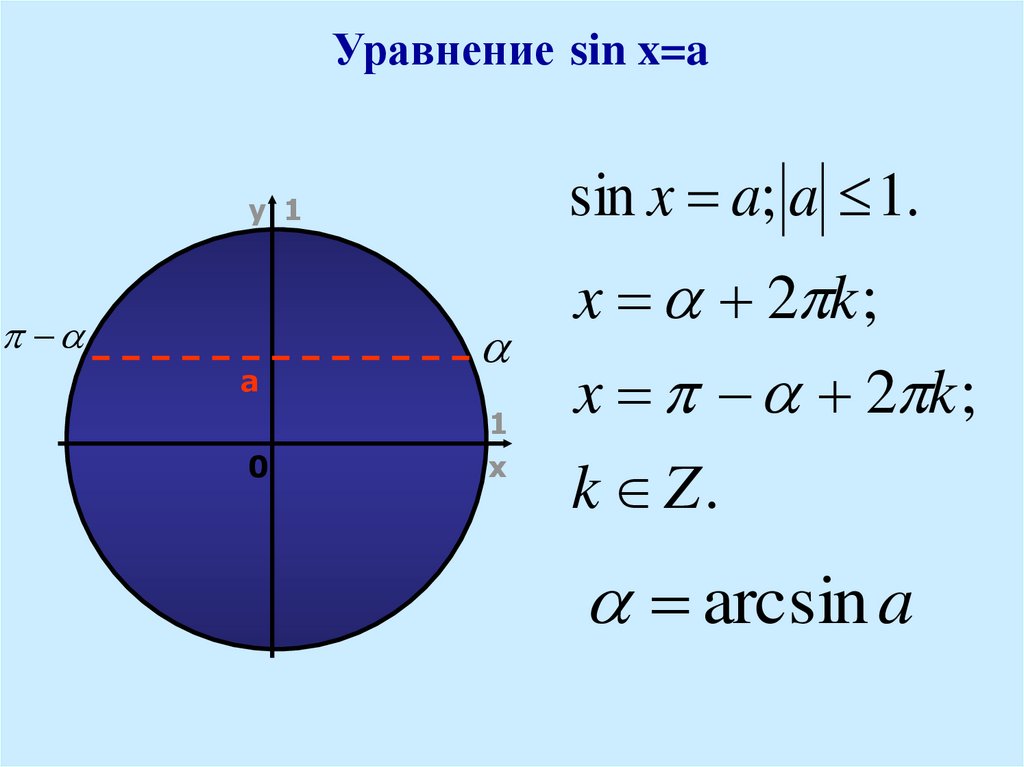 14159..
14159..