Sin x п 4: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74 Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

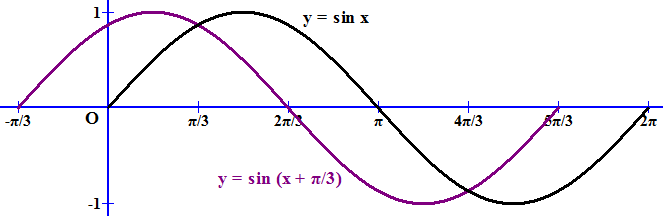
y = sin(x+pi/4)

Графики функций, Построение графиков Работа проверена: Rassy Время решения: 10 мин Сложность: 3.7

Дано

$$f{left (x right )} = sin{left (x + frac{pi}{4} right )}$$

График функции

Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$sin{left (x + frac{pi}{4} right )} = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_{1} = – frac{pi}{4}$$
$$x_{2} = frac{3 pi}{4}$$
Численное решение
$$x_{1} = 99. 7455667515$$
$$x_{2} = 21.2057504117$$
$$x_{3} = 90.3207887907$$
$$x_{4} = -69.9004365424$$
$$x_{5} = -38.4845100065$$
$$x_{6} = -73.042029196$$

$$x_{7} = 96.6039740979$$
$$x_{8} = 62.0464549084$$
$$x_{9} = 74.6128255228$$
$$x_{10} = -63.6172512352$$
$$x_{11} = 77.7544181763$$
$$x_{12} = -76.1836218496$$
$$x_{13} = -22.7765467385$$
$$x_{14} = 18.0641577581$$
$$x_{15} = 33.7721210261$$
$$x_{16} = 49.480084294$$
$$x_{17} = 36.9137136797$$
$$x_{18} = -13.3517687778$$
$$x_{19} = -88.7499924639$$
$$x_{20} = -16.4933614313$$
$$x_{21} = -85.6083998103$$
$$x_{22} = -82.4668071567$$
$$x_{23} = -47.9092879672$$
$$x_{24} = 71.4712328692$$
$$x_{25} = -10.2101761242$$
$$x_{26} = 80.8960108299$$
$$x_{27} = -0.785398163397$$
$$x_{28} = 24.3473430653$$
$$x_{29} = -54.1924732744$$
$$x_{30} = 93.4623814443$$
$$x_{31} = -29.0597320457$$
$$x_{32} = 43.1968989869$$
$$x_{33} = 14.9225651046$$
$$x_{34} = -98. 1747704247$$
$$x_{35} = -95.0331777711$$
$$x_{36} = 40.0553063333$$
$$x_{37} = 65.188047562$$
$$x_{38} = -66.7588438888$$
$$x_{39} = 1745.94011723$$
$$x_{40} = 11.780972451$$
$$x_{41} = -3.92699081699$$
$$x_{42} = 68.3296402156$$
$$x_{43} = -25.9181393921$$
$$x_{44} = 52.6216769476$$
$$x_{45} = -19.6349540849$$
$$x_{46} = -32.2013246993$$
$$x_{47} = 5.49778714378$$
$$x_{48} = -79.3252145031$$
$$x_{49} = 58.9048622548$$
$$x_{50} = -44.7676953137$$
$$x_{51} = 30.6305283725$$
$$x_{52} = -60.4756585816$$
$$x_{53} = 391.913683535$$
$$x_{54} = 87.1791961371$$
$$x_{55} = -57.334065928$$
$$x_{56} = -107.599548385$$
$$x_{57} = -35.3429173529$$
$$x_{58} = -41.6261026601$$
$$x_{59} = 55.7632696012$$
$$x_{60} = 84.0376034835$$
$$x_{61} = 46.3384916404$$
$$x_{62} = -51.0508806208$$
$$x_{63} = 27.4889357189$$
$$x_{64} = 2.35619449019$$
$$x_{65} = 8.63937979737$$
$$x_{66} = -7. 06858347058$$
$$x_{67} = -91.8915851175$$

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в sin(x + pi/4).
$$sin{left (frac{pi}{4} right )}$$
Результат:
$$f{left (0 right )} = frac{sqrt{2}}{2}$$
Точка:

(0, sqrt(2)/2)

Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение
$$frac{d}{d x} f{left (x right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac{d}{d x} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = frac{pi}{4}$$
$$x_{2} = frac{5 pi}{4}$$
Зн. экстремумы в точках:

pi /pi pi
(–, sin|– + –|)
4 4 4 /

5*pi /pi pi
(—-, -sin|– + –|)
4 4 4 /

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{2} = frac{5 pi}{4}$$
Максимумы функции в точках:
$$x_{2} = frac{pi}{4}$$
Убывает на промежутках

(-oo, pi/4] U [5*pi/4, oo)

Возрастает на промежутках

[pi/4, 5*pi/4]

Точки перегибов

Найдем точки перегибов, для этого надо решить уравнение
$$frac{d^{2}}{d x^{2}} f{left (x right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$frac{d^{2}}{d x^{2}} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = – frac{pi}{4}$$
$$x_{2} = frac{3 pi}{4}$$

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках

(-oo, -pi/4] U [3*pi/4, oo)

Выпуклая на промежутках

[-pi/4, 3*pi/4]

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty} sin{left (x + frac{pi}{4} right )} = langle -1, 1rangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = langle -1, 1rangle$$

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции sin(x + pi/4), делённой на x при x->+oo и x ->-oo
$$lim_{x to -infty}left(frac{1}{x} sin{left (x + frac{pi}{4} right )}right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$sin{left (x + frac{pi}{4} right )} = cos{left (x + frac{pi}{4} right )}$$
– Нет
$$sin{left (x + frac{pi}{4} right )} = – cos{left (x + frac{pi}{4} right )}$$
– Нет
значит, функция
не является
ни чётной ни нечётной

   

3(x)=\sin(3x)$$

по желанию.

$\endgroup$

$\begingroup$

Вам, вероятно, понадобится «формула сложения углов» для синуса, так как вы, вероятно, не должны знать «формулы множественных углов». (Вам понадобятся « двойные -формулы углов»…)

$$ \sin 3x \ + \ \sin x \ = \ \sin(2x + x ) \ + \ \sin x $$

$$ = \ (\sin 2x \\\cos x \ + \ \\cos 2x \\sin x) \ + \ \sin x $$ 92x)$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Предварительное исчисление алгебры

— элегантный способ решить $\frac {\sqrt3 — 1}{\sin x} + \frac {\sqrt3 + 1}{\cos x} = 4\sqrt2 $

спросил

Изменено 6 лет, 8 месяцев назад

Просмотрено 3к раз

$\begingroup$

Нужно найти $x\in\left(0,\frac{\pi}{2}\right)$:

$$\frac {\sqrt3 — 1}{\sin x} + \frac {\ sqrt3 + 1} {\ cos x} = 4 \ sqrt2 $ $

Я перевел дробь $\cos x$ вправо и попытался упростить ;

Но это выглядело очень грязно, и попытка записать $\sin x$ в терминах $\cos x$ не помогла.

Есть ли более простой (элегантный) способ сделать это.

  • алгебра-предварительное исчисление
  • тригонометрия

$\endgroup$

2

$\begingroup$

$\sin(\frac{\pi}{12}) = \frac{\sqrt{3}-1}{2\sqrt{2}}$ и $\cos(\frac{\pi}{12 }) = \frac{\sqrt{3}+1}{2\sqrt{2}}$.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *