Бинарная операция | это… Что такое Бинарная операция?
Бинарная операция (от лат. bi — два) — математическая операция, принимающая два аргумента и возвращающая один результат (то есть с арностью два).
Содержание
|
Определение
Пусть — тройка непустых множеств. Бинарной операцией или двуме́стной опера́цией в паре со значениями в называется отображение , где
Если , то действие называется внутренним, если или — внешним. В частности, любое внутреннее действие является внешним.
Замечание
Бинарную операцию принято обозначать знаком действия, который ставится между операндами (инфиксная форма записи). Например, для произвольной бинарной операции результат её применения к двум элементам и записывается в виде .
Это не значит, что не используются другие формы записи бинарных операций. Существуют и другие виды записи:
- префиксная (польская запись) — ;
- постфиксная (обратная польская запись) — .
Типы бинарных операций
Коммутативная операция
Основная статья: Коммутативная операция
Бинарная операция называется коммутативной, если её результат не зависит от перестановки операндов, то есть
Ассоциативная операция
Основная статья: Ассоциативная операция
Бинарная операция называется ассоциативной, если
Для ассоциативной операции результат вычисления не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи.
Для неассоциативной операции выражение при однозначно не определено.
Альтернативная операция
Бинарная операция называется альтернати́вной если
- и .
Примеры
Примерами бинарных операций могут служить сложение, умножение и вычитание на поле вещественных чисел. Сложение и умножение чисел являются коммутативными и ассоциативными операциями, а вычитание — нет.
Записи
Мультипликативная запись
Если абстрактную бинарную операцию на называют умноже́нием
, то её результат для элементов называют их произведе́нием и обозначают или . В этом случае нейтральный элемент , то есть элемент удовлетворяющий равенствамназывается едини́чным элеме́нтом относительно выбранной бинарной операции.
Аддитивная запись
Если бинарную операцию называют сложе́нием, то образ пары элементов называют су́ммой и обозначают . Обычно, если бинарную операцию называют сложением, то она предполагается коммутативной.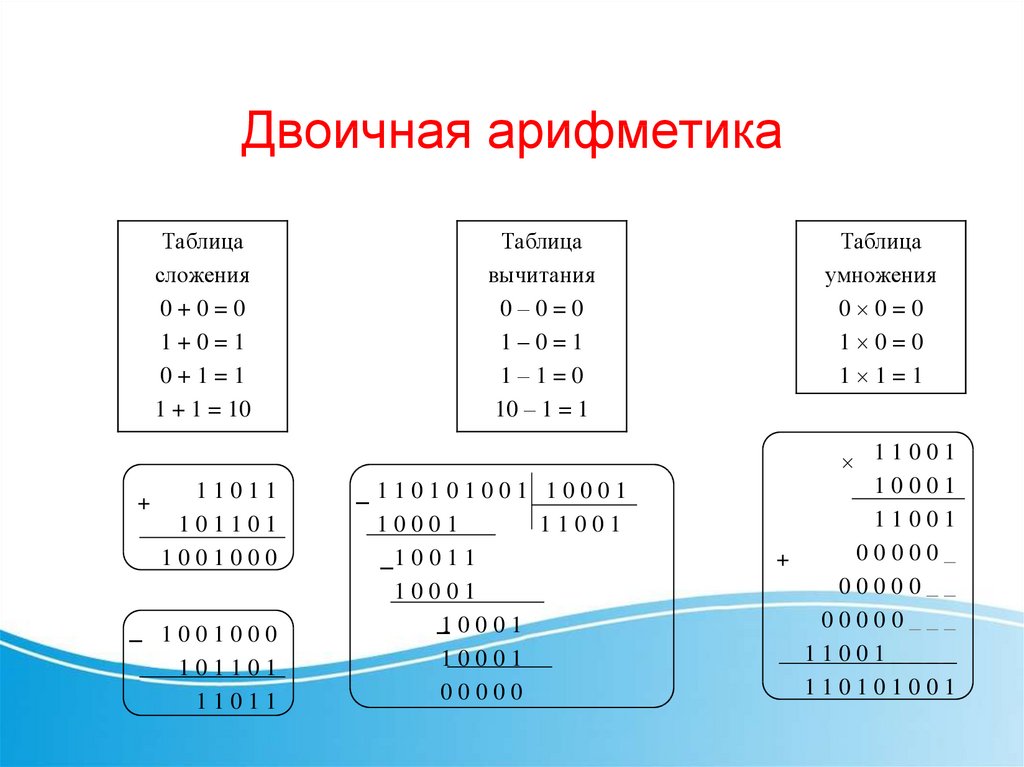
Нейтральный элемент в аддитивной записи обозначают символом 0, называют нулевы́м элеме́нтом и пишут
Обратная операция
Если операция обладает биективностью, то у неё существуют обратные операции. Для бинарной операции может быть до двух обратных операций (левая и правая), в случае коммутативной операции — они совпадают.
Теорема 1
Для любой бинарной операции, существует не более одного нейтрального элемента
Теорема 2
Если бинарная операция ассоциативна, то для каждого элемента существует не более одного обратного
См. также
- арность
- унарная операция
- тернарная операция
Литература
- Цыпкин А. Г. Справочник по математике для средних и учебных заведений. — М.: Наука, 1988. — 430 с. — ISBN 5-02-013792-8.
Введение в алгебру — тест 1
Главная / Математика / Введение в алгебру / Тест 1
Упражнение 1:
Номер 1
Какое действие лежит в основе алгебраической операции на множестве?
Ответ:
 (1) конъюнкция 
 (2) отображение 
 (3) ассоциация 
Номер 2
Верно ли то, что в основе алгебраической операции на множестве лежит операция отображения элементов?
Ответ:
 (1) нет, в основе лежит инъекция 
 (2) да, утверждение верно 
 (3) нет, в основе лежит конъюнкция 
Номер 3
Количество элементов множества, участвующих в алгебраической операции называют
Ответ:
 (1) четность 
 (2) размерность 
 (3) арность 
Упражнение 2:
Номер 1
Бинарная операция - это
Ответ:
 (1) алгебраическая операция на множестве, в которой участвуют два элемента 
 (2) операция с двоичными числами на множестве 
 (3) процесс нахождения двоичного кода любого элемента множества 
Номер 2
Унарная операция - это
 (1) система правил, которые используют для сведения элементов множества к одному виду 
 (2) алгебраическая операция на множестве, в которой участвует один элемент 
 (3) нахождение зависимости порядка действий при алгебраических операциях на множестве от размера поля 
Номер 3
Верно ли то, что в бинарных операциях на множестве не может участвовать более двух элементов?
Ответ:
 (1) нет, это неверно, количество элементов такой операции не ограниченно 
 (2) да, это верно 
 (3) все зависит от размера поля и типов данных 
Упражнение 3:
Номер 1
Нульарная операция - это
Ответ:
 (1) процесс нахождения контекстной зависимости между ненулевыми элементами при операциях на множестве 
 (2) фиксированный элемент множества 
 (3) нахождение зависимости количества элементов множества от типа его поля и относительной размерности 
Номер 2
Верно ли утверждение, что нульарные операции являются фиксированными элементами множества?
Ответ:
 (1) утверждение неверно 
 (2) верно обратное утверждение — эти операции являются нефиксированными элементами 
 (3) да, это действительно так 
Номер 3
Под нулевым множеством принято понимать
Ответ:
 (1) бесконечное множество 
 (2) пустое множество 
 (3) одноэлементное множество 
Упражнение 4:
Номер 1
Непустое множество с любой бинарной операцией называют
Ответ:
 (1) моноидом 
 (2) полиномом 
 (3) группоидом 
Номер 2
Группоид - это
Ответ:
 (1) непустое множество с любой бинарной операцией 
 (2) совокупность элементов, которые объединены общим признаком 
 (3) формальное определение, обозначающее порядок элементов в алгебраическом выражении 
Номер 3
Имеется непустое множество с определенной бинарной операцией.Можно ли утверждать, что это группоид?
Можно ли утверждать, что это группоид?Ответ:
 (1) нет, это неверно 
 (2) да, это так и есть 
 (3) это может быть только полином 
Упражнение 5:
Номер 1
Может ли бинарная операция обладать свойством ассоциативности?
Ответ:
 (1) да, может 
 
 (3) теоретически это не противоречит определению, но практически невозможно 
Упражнение 6:
Номер 1
Бинарная операция разности целых чисел является ассоциативной. Верно ли это?
Ответ:
 (1) да, это верно для всех чисел 
 (2) утверждение неверно 
 (3) это верно, только для отрицательных чисел 
Номер 2
Верно ли утверждение, что бинарная операция разности целых чисел является коммутативной?
Ответ:
 (1) да, это абсолютно верно 
 (2) нет, это неверно 
 (3) она является как коммутативной, так и ассоциативной 
Номер 3
Бинарная операция разности целых чисел коммутативна, но не ассоциативна.
Верно ли это?Ответ:
 (1) да, это верно 
 (2) верно обратное утверждение 
 (3) нет, это неверно вообще 
Упражнение 7:
Номер 1
Сложение, как и умножение натуральных чисел коммутативно, но не ассоциативно. Так ли это?
Ответ:
 (1) да, это так 
 (2) нет, это неверно 
 
Номер 2
Пересечение, как и объединение подмножеств коммутативно, но не ассоциативно. Верно ли это?
Ответ:
 (1) верно обратное утверждение 
 (2) да, это верно 
 (3) нет, это неверно 
Номер 3
Симметрическая разность подмножеств является
Ответ:
 (1) конъюнктивной 
 (2) коммутативной 
 (3) ассоциативной 
Упражнение 8:
Номер 1
Композиция отображений является
Ответ:
 (1) ассоциативной во всех случаях 
 (2) коммутативной во всех случаях 
 (3) ассоциативной только в редких случаях 
Номер 2
Композиция отображений коммутативна только тогда, когда
Ответ:
 (1) она не является ассоциативной 
 (2) она производится в одноэлементном множестве 
 (3) она производится независимо от поля подмножества 
Номер 3
Бинарная операция возведения в степень коммутативна, но не ассоциативна.
Так ли это?Ответ:
 (1) да, это так 
 (2) верно обратное утверждение 
 (3) это неверно 
Упражнение 9:
Номер 1
Подмножество группоида с бинарной операцией, замкнутое относительно этой операции, называется
Ответ:
 (1) подгруппа 
 (2) подгруппоид 
 (3) метагруппа 
Номер 2
Биективный гомоморфизм группоидов называется
Ответ:
 (1) изоморфизмом группоидов 
 (2) полиморфизмом группоидов 
 (3) группоидным мономорфизмом 
Номер 3
Группоид с бинарной операцией называется полугруппой, если эта бинарная операция является
Ответ:
 (1) биективной 
 (2) ассоциативной 
 (3) коммутативной 
Упражнение 10:
Номер 1
Подгруппоид полугруппы является
Ответ:
 (1) группой 
 (2) моногруппой 
 (3) полугруппой 
Номер 2
Подгруппоид полугруппы называется
Ответ:
 (1) подполугруппой 
 (2) подгруппой 
 (3) метагруппой 
Номер 3
К вспомогательным элементам элемента моноида относят
Ответ:
 (1) правый обратный 
 (2) левый обратный 
 (3) двусторонний обратный 
Упражнение 11:
Номер 1
Если в моноиде элемент имеет и правый обратный, и левый обратный, то такой элемент называется
Ответ:
 (1) обратным 
 (2) обратимым 
 (3) независимым 
Номер 2
Какой элемент моноида считается обратимым?
Ответ:
 (1) элемент, имеющий правый обратный 
 (2) элемент, имеющий левый обратный 
 (3) элемент, имеющий как правый, так и левый обратный 
Номер 3
Обратный элемент обратного элемента моноида
Ответ:
 (1) равен самому элементу 
 (2) является обратимым 
 (3) является обратным 
Упражнение 12:
Номер 1
Сколько ассоциативных расстановок скобок существует для трех сомножителей?
Ответ:
 (1) 2 
 (2) 3 
 (3) 4 
Номер 2
Для трех сомножителей результат применения ассоциативной операции не зависит от расстановки скобок.
Верно ли это?Ответ:
 (1) нет, это противоречит принципу ассоциативности 
 (2) да, это верно 
 (3) это верно только в очень редких случаях 
Номер 3
Два элемента являются инъекциями. Является ли инъекцией их произведение?
Ответ:
 (1) только в очень редких случаях 
 (2) нет, не является 
 (3) да, является 
Главная / Математика / Введение в алгебру / Тест 1
Двоичные цифры
| Двоичная цифра может быть только 0 или 1 |
Двоичный номер Двоичное число состоит из двоичных цифр. |
В компьютерном мире « b inary dig it » часто сокращается до слова « бит »
Более одной цифры
Итак, есть только два способа получить двоичную цифру ( «0» и «1» или «Вкл.» и «Выкл.» ) … но как насчет 2 или более двоичных цифр ?
Запишем их все, начиная с 1 цифры (вы сами можете проверить с помощью переключателей):
| 2 способа получить одну цифру… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| … 4 способа получить две цифры … |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. .. 8 способов получить три цифры … |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. .. и 16 способов получить четыре цифры. |
|
Вот этот последний список сбоку:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
И (без ведущих нулей) у нас есть первые 16 двоичных чисел:
| Двоичные: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Это полезно! Чтобы запомнить последовательность двоичных чисел, просто подумайте:
- «0» и «1» {0,1}
- , затем снова повторите «0» и «1», но с «1» впереди: {0,1,10,11}
- , затем повторите те с «1» впереди: {0,1,10,11,100,101,110,111}
- и так далее!
На каждом этапе мы повторяем все, что у нас есть до сих пор, но с 1 впереди.
Теперь узнайте, как использовать Binary для счета на пальцах после 1000:
Активность: Binary Fingers
| Также поиграйте с разными барабанами. |
Двоичные цифры… Они удваиваются!
Также обратите внимание, что каждый раз, когда мы добавляем еще одну двоичную цифру, мы двойной возможные значения.
Почему двойной ? Потому что мы берем все предыдущие возможные значения и сопоставляем их с «0» и «1», как указано выше.
- Таким образом, всего одна двоичная цифра имеет 2 возможных значения (0 и 1)
- Две двоичные цифры имеют 4 возможных значения (0, 1, 10, 11)
- Три имеют 8 возможных значений
- Четыре имеют 16 возможных значений
- Пять имеют 32 возможных значения
- Шесть имеют 64 возможных значения
- и т. д.
Используя показатели степени, это может быть представлено как:
| Число из цифр | Формула | Настройки |
|---|---|---|
| 1 | 2 1 | 2 |
| 2 | 2 2 | 4 |
| 3 | 2 3 | 8 |
| 4 | 2 4 | 16 |
| 5 | 2 5 | 32 |
| 6 | 2 6 | 64 |
и т. д… | и т.д. .. | и т.д… |
Пример: когда у нас есть 50 двоичных цифр (или 50 вещей, каждая из которых может иметь только две позиции), сколько существует различных способов?
Ответ: 2 50 = 2 × 2 × 2 × 2 × 2 … (пятьдесят из них)
= 1 125 899 906 842 624
Итак, двоичное число из 50 цифр может иметь 1 125, 29, 84, 25, 8, 84, 25, 8, 125, 8, 125, 8, 84,
Или, другими словами, он может показать число до 1 125 899 906 842 623 (примечание: это на единицу меньше, чем общее количество значений, потому что одно из значений равно 0).
Пример: Начните месяц с 1 доллара и удваивайте его каждый день, через 30 дней у вас будет
миллиардер ! 2 30 = 2 × 2 × 2 × 2 … (тридцать из них)
= 1 073 741 824
Шахматная доска
Игра о короле шахмат приехавшим мудрецом. Король спросил: «Какой приз, если вы выиграете?».
Мудрец сказал, что ему просто нужно несколько зернышек риса: одно на первом квадрате, 2 на втором, 4 на третьем и так далее, удваивая на каждом квадрате.
Король был удивлен этой скромной просьбой.
Ну, Мудрец победил, так сколько зернышек риса он должен получить?
На первом квадрате: 1 зерно, на втором квадрате: 2 зерна (всего 3) и так далее:
| Квадрат | Зерно | Всего |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 4 | 7 |
| 4 | 8 | 15 |
| 10 | 512 | 1 027 |
| 20 | 524 288 | 1 048 575 |
| 30 | 53 6870 912 | 1 073 741 823 |
| 64 | ??? | ??? |
К 30-му квадрату видно, что риса уже много! Миллиард зерен риса составляет около 25 тонн (1000 зерен — это около 25 г… Я взвесил немного!)
Обратите внимание, что Итого любого квадрата на 1 меньше, чем зерен в следующем квадрате (пример: в квадрате 3 всего 7, а в квадрате 4 8 зерен).
Таким образом, сумма всех квадратов представляет собой формулу: 2 n −1 , где n — номер квадрата. Например, для клетки 3 сумма равна 2 3 -1 = 8 — 1 = 7
Таким образом, для заполнения всех 64 клеток на шахматной доске потребуется:
2 64 9056 1 = 18 446 744 073 709,551 615 зерен (460 миллиардов тонн риса),
во много раз больше риса, чем во всем королевстве.
Итак, силу бинарного удвоения нельзя воспринимать легкомысленно (460 миллиардов тонн — это не свет!)
Зерна риса на каждом квадрате с экспоненциальной записью
Значения округлены, поэтому
53 6870 912 отображается как 5×10 8
, что означает 5 с 8 нулями
(Кстати, в легенде Мудрец оказывается Господь Кришна и говорит королю, что он не обязан платить долг сразу, но может платить ему со временем, просто подавайте рис паломникам каждый день, пока долг не будет погашен.
)
Шестнадцатеричный
Наконец , давайте посмотрим на особые отношения между двоичным и шестнадцатеричным числами.
Есть 16 шестнадцатеричных цифр, и мы уже знаем, что 4 двоичных цифры имеют 16 возможных значений. Ну, именно так они относятся друг к другу:
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф |
Итак, когда люди используют компьютеры (которые предпочитают двоичные числа), гораздо проще использовать одну шестнадцатеричную цифру, а не 4 двоичные цифры.
Например, двоичное число «100110110100» — это «9B4» в шестнадцатеричном формате. Я знаю, что я предпочел бы написать!
Бинарные пальцы!
Бинарные пальцы!Показать рекламу
Скрыть рекламу
О рекламе
Забудьте о счете до 10 на пальцах… вы можете считать до 1000, если хотите!
Правая рука
Правой рукой вы можете сосчитать до 31:
Нет пальцев вверху 0
Большой палец 1
Указательный палец 2
2 и 1
получается 3
Средний палец 4
Добавьте свой большой палец
на 5
4 и
2 делает 6
4 и 2 и 1
получается 7
Безымянный палец 8
.
|
.. и продолжайте узор:На самом деле вы считаете в двоичном формате:
| Число | Сделано | |||||
| 1 | 1 | до | ||||
| 2 | 2 | до | ||||
| 3 | 2+1 | до | до | |||
| 4 | 4 | до | ||||
| 5 | 4+1 | до | до | |||
| 6 | 4+2 | до | до | |||
| 7 | 4+2+1 | до | до | до | ||
| 8 | 8 | до | ||||
| 9 | 8+1 | до | до | |||
| 10 | 8+2 | до | до | |||
| 11 | 8+2+1 | до | до | до | ||
| 12 | 8+4 | до | до | |||
| 13 | 8+4+1 | до | до | до | ||
| 14 | 8+4+2 | до | до | до | ||
| 15 | 8+4+2+1 | до | до | до | до | |
| 16 | 16 | до | ||||
| 17 | 16+1 | до | до | |||
и т. | ||||||