sin2 x — Googlesuche
AlleBilderNewsVideosMapsShoppingBücher
suchoptionen
sin²(x)=??? — Matheboard
www.matheboard.de › архив › резьба
Ich komm mit meinen Vorlesungsunterlagen auch nicht weiter, da ich nicht weiss, wie ich auf eine Umformung von sin²/cos² kommen soll. Der …
Nach x auflösen: sinx = sin2x
Ableitung von sin²(x)
Weitere Ergebnisse von www.matheboard.de
92(х) бестиммен? (Математика, Тригонометрия)Warum ist sin²(x) + cos²(x) = 1?
Weitere Ergebnisse von www.gutefrage.net
Ähnliche Fragen
Was ist sin 2 x?
Был ли это грех²?
Был ли ist cos 2 x?
Был ли синус-квадрат плюс косинус-квадрат?
[PDF] Formelsammlung Mathematik — Falk-Net
www.falk-net.de › fhma › mathematik › docus › ma_formelsammlung
cot x — tan y = cos ( x+y ) / ( sin x · cos г). Доппельтер Auflösung Winkel sin 2x = 2 sin x cos x = 2 tan x / ( 1+ tan² x ) cos 2x = cos² x — sin² x = 1 .
.. 92 x
Теорема дополнений от math.stackexchange.com
Теорема дополнений для синуса и косинуса — Mathepedia
mathepedia.de › Теорема дополнений
Beweis ; sin(2π−x1)= ; cosx1 …
способный sin²(x) — OnlineMathe — das mathe-forum
www.onlinemathe.de › forum ›ableitung-sin2x
Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik . So auch zum Themaableitungsin²(x)92
3.3 Тригонометрическая подстановка. Исчисление Том 2
Цели обучения
- 3.3.1 Решите задачи интегрирования, связанные с извлечением квадратного корня из суммы или разности двух квадратов.
В этом разделе мы исследуем интегралы, содержащие выражения вида a2−x2,a2−x2,a2+x2,a2+x2 и x2−a2,x2−a2, где значения aa положительны. Мы уже встречали и оценивали интегралы, содержащие некоторые выражения этого типа, но многие до сих пор остаются недоступными. Техника тригонометрической подстановки очень удобна при вычислении этих интегралов.
Этот метод использует замену, чтобы переписать эти интегралы как тригонометрические интегралы.
Интегралы с участием a2-x2a2-x2
Перед разработкой общей стратегии для интегралов, содержащих a2−x2,a2−x2, рассмотрим интеграл ∫9−x2dx.∫9−x2dx. Этот интеграл нельзя вычислить ни одним из методов, которые мы обсуждали до сих пор. Однако, если мы сделаем замену x=3sinθ,x=3sinθ, мы получим dx=3cosθdθ.dx=3cosθdθ. После подстановки в интеграл имеем
∫9−x2dx=∫9−(3sinθ)23cosθdθ.∫9−x2dx=∫9−(3sinθ)23cosθdθ.
После упрощения имеем
∫9−x2dx=∫91−sin2θcosθdθ.∫9−x2dx=∫91−sin2θcosθdθ.
Положив 1−sin2θ=cos2θ, 1−sin2θ=cos2θ, мы теперь имеем
∫9−x2dx=∫9cos2θcosθdθ.∫9−x2dx=∫9cos2θcosθdθ.
Предполагая, что cosθ≥0,cosθ≥0, имеем
∫9−x2dx=∫9cos2θdθ.∫9−x2dx=∫9cos2θdθ.
Теперь мы можем вычислить интеграл, используя методы, разработанные для интегрирования степеней и произведений тригонометрических функций.
Прежде чем завершить этот пример, давайте взглянем на общую теорию, стоящую за этой идеей.
Чтобы вычислить интегралы, включающие a2−x2,a2−x2, мы делаем замену x=asinθx=asinθ и dx=acosθ.dx=acosθ. Чтобы увидеть, что это на самом деле имеет смысл, рассмотрим следующий аргумент: областью определения a2−x2a2−x2 является [−a,a].[−a,a]. Таким образом, −a≤x≤a.−a≤x≤a. Следовательно, −1≤xa≤1.−1≤xa≤1. Поскольку диапазон sinxsinx над [−(π/2),π/2][−(π/2),π/2] равен [−1,1],[−1,1], существует единственный угол θθ, удовлетворяющее −(π/2)≤θ≤π/2−(π/2)≤θ≤π/2, так что sinθ=x/a,sinθ=x/a, или, что то же самое, так что x=asinθ.x = asinθ. Если мы подставим x=asinθx=asinθ в a2−x2,a2−x2, получим
a2−x2=a2−(asinθ)2Letx=asinθwhere−π2≤θ≤π2.Упростить.=a2−a2sin2θВычислить из a2.=a2(1−sin2θ)Заменить1−sin2x=cos2x.=a2cos2θИзвлечь квадратный корень.=|acosθ |=acosθ.a2−x2=a2−(asinθ)2Letx=asinθwhere−π2≤θ≤π2.Упростить.=a2−a2sin2θВычислить из a2.=a2(1−sin2θ)Подставить1−sin2x=cos2x.=a2cos2θВозьмите квадратный корень.
=|acosθ|=acosθ.
Поскольку cosθ≥0cosθ≥0 на −π2≤θ≤π2−π2≤θ≤π2 и a>0,a>0, |acosθ|=acosθ.|acosθ|=acosθ. Из этого обсуждения мы можем видеть, что, сделав замену x=asinθ,x=asinθ, мы можем преобразовать интеграл, включающий радикал, в интеграл, включающий тригонометрические функции. После вычисления интеграла мы можем преобразовать решение обратно в выражение, включающее x.x. Чтобы понять, как это сделать, предположим, что 0
Рисунок 3.4 Опорный треугольник может помочь выразить тригонометрические функции, оцениваемые при θθ, через x.x.
Основная часть этого обсуждения резюмируется в следующей стратегии решения проблем.
Стратегия решения проблем
Стратегия решения задач: интегрирование выражений с участием a2−x2a2−x2
- Рекомендуется убедиться, что интеграл нельзя легко вычислить другим способом. Например, хотя этот метод можно применить к интегралам вида ∫1a2−x2dx, ∫1a2−x2dx, ∫xa2−x2dx, ∫xa2−x2dx и ∫xa2−x2dx, ∫xa2−x2dx, каждый из них можно проинтегрировать напрямую либо по формуле, либо по простому и -замещение.
- Сделайте замену x=asinθx=asinθ и dx=acosθdθ.dx=acosθdθ. Примечание : Эта замена дает a2−x2=acosθ.a2−x2=acosθ.
- Упростите выражение.
- Вычислите интеграл, используя приемы из раздела о тригонометрических интегралах.
- Используйте опорный треугольник на рис. 3.4, чтобы переписать результат в x.x. Вам также может понадобиться использовать некоторые тригонометрические тождества и соотношение θ=sin-1(xa).θ=sin-1(xa).
Следующий пример демонстрирует применение этой стратегии решения проблем.
Пример 3.21
Интегрирование выражения, включающего a2-x2a2-x2
Вычисление ∫9-x2dx.∫9-x2dx.
Решение
Начните с замены x=3sinθx=3sinθ и dx=3cosθdθ.dx=3cosθdθ. Поскольку sinθ=x3,sinθ=x3, мы можем построить эталонный треугольник, показанный на следующем рисунке.
Рисунок 3,5 Для примера 3.21 можно построить опорный треугольник.
Thus,
∫9−x2dx=∫9−(3sinθ)23cosθdθSubstitutex=3sinθanddx=3cosθdθ.=∫9(1−sin2θ)3cosθdθSimplify.=∫9cos2θ3cosθdθSubstitutecos2θ=1−sin2θ.=∫3| cosθ|3cosθdθВозьмите квадратный корень.=∫9cos2θdθУпростите. Поскольку −π2≤θ≤π2,cosθ≥0и|cosθ|=cosθ.
Пример 3,22
Интегрирование выражения, включающего a2-x2a2-x2
Вычисление ∫4-x2xdx.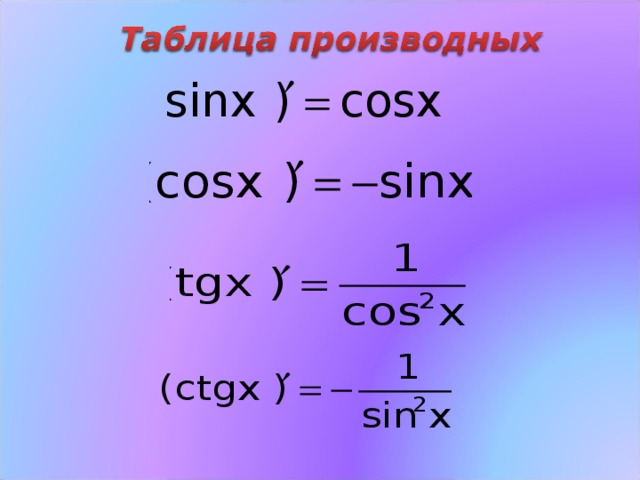
∫4-x2xdx.
Решение
Сначала сделайте замены x=2sinθx=2sinθ и dx=2cosθdθ.dx=2cosθdθ. Поскольку sinθ=x2,sinθ=x2, мы можем построить эталонный треугольник, показанный на следующем рисунке.
Рисунок 3,6 Для примера 3.22 можно построить опорный треугольник.
Таким образом,
∫4 — X2XDX = ∫4- (2SINθ) 22SINθ2COSθdθSubstitUtex = 2sinθAndDX = 2COSθdθ. = ∫2COS2θSinθSUBStitTiteCos2θ = 1-Sin2θ и Soomdify. 2cscθ−2sinθ)dθРазделите числитель, упростите и используйте cscθ=1sinθ.=2ln|cscθ−cotθ|+2cosθ+CEВычислить интеграл.=2ln|2x−4−x2x|+4−x2+C. Перепишите экспрессию в терминах OFXand Simplify.∫4 — x2xdx = ∫4- (2sinθ) 22sinθ2cosθdθsubstitutex = 2sinθanddx = 2cosθdθ. = ∫2cos2θsinθsubStitTitUteCos2θ = 1 -Sin2θ и Simplif (2cscθ−2sinθ)dθРазделить числитель, упростить и использовать cscθ=1sinθ.=2ln|cscθ−cotθ|+2cosθ+CEВычислить интеграл.=2ln|2x−4−x2x|+4−x2+C.Использовать опорный треугольник переписать выражение в терминах xи упростить.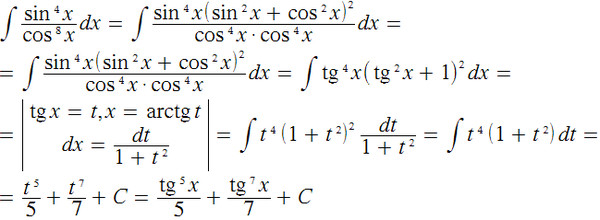
В следующем примере мы видим, что иногда у нас есть выбор методов.
Пример 3,23
Интегрирование выражения, включающего a2−x2a2−x2, двумя способами
Вычисление ∫x31−x2dx∫x31−x2dx двумя способами: сначала с помощью замены u=1−x2u=1−x2, а затем с помощью тригонометрической замены .
Решение
Метод 1
Пусть u=1−x2u=1−x2 и, следовательно, x2=1−u.x2=1−u. Таким образом, du=-2xdx.du=-2xdx. В этом случае интеграл становится равным
∫x31−x2dx=−12∫x21−x2(−2xdx)Сделайте замену.=−12∫(1−u)uduРасширьте выражение.=−12∫(u1/2−u3/2) duВычислить интеграл.=−12(23u3/2−25u5/2)+CПереписать в терминахx.=−13(1−x2)3/2+15(1−x2)5/2+C.∫x31− x2dx=−12∫x21−x2(−2xdx) Сделайте замену.=−12∫(1−u)uduРасширьте выражение.=−12∫(u1/2−u3/2)duВычислите интеграл.=− 12(23u3/2−25u5/2)+CПерепиши через x.=−13(1−x2)3/2+15(1−x2)5/2+C.
Метод 2
Пусть x=sinθ.
x=sinθ. В этом случае dx=cosθdθ.dx=cosθdθ. Используя эту замену, мы имеем
∫x31−x2dx=∫sin3θcos2θdθ=∫(1−cos2θ)cos2θsinθdθLetu=cosθ. −13cos3θ+CИспользуйте треугольник отсчета, чтобы увидеть, что cosθ=1−x2.=15(1−x2)5/2−13(1−x2)3/2+C.∫x31−x2dx=∫sin3θcos2θdθ=∫ (1−cos2θ)cos2θsinθdθLetu=cosθ. Таким образом, du=−sinθdθ.=∫(u4−u2)du=15u5−13u3+CSsubstitutecosθ=u.=15cos5θ−13cos3θ+CИспользуйте треугольник отсчета, чтобы увидеть, что cosθ=1−x2 .=15(1−x2)5/2−13(1−x2)3/2+C.
Контрольно-пропускной пункт 3.14
Перепишите интеграл ∫x325−x2dx∫x325−x2dx, используя соответствующую тригонометрическую замену (интеграл не вычислять).
Интегрирование выражений, включающих a2+x2a2+x2
Для интегралов, содержащих a2+x2,a2+x2, давайте сначала рассмотрим область определения этого выражения. Поскольку a2+x2a2+x2 определено для всех действительных значений x,x, мы ограничиваем наш выбор теми тригонометрическими функциями, которые имеют диапазон всех действительных чисел.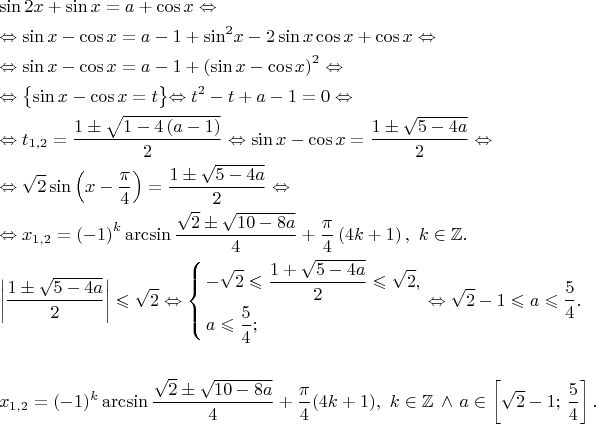
Таким образом, наш выбор ограничен выбором либо x=atanθx=atanθ, либо x=acotθ.x=acotθ. Любая из этих замен на самом деле будет работать, но стандартная замена такова: x=atanθx=atanθ или, что то же самое, tanθ=x/a.tanθ=x/a. С этой заменой мы делаем предположение, что −(π/2)<θ<π/2, −(π/2)<θ<π/2, так что мы также имеем θ=tan−1(x/a) .θ=tan−1(x/a). Процедура использования этой замены описана в следующей стратегии решения проблем.
Стратегия решения проблем
Стратегия решения задач: интегрирование выражений, содержащих a2+x2a2+x2
- Проверьте, можно ли легко вычислить интеграл, используя другой метод. В некоторых случаях удобнее использовать альтернативный метод.
- Замените x=atanθx=atanθ и dx=asec2θdθ.dx=asec2θdθ. Эта замена дает
a2+x2=a2+(atanθ)2=a2(1+tan2θ)=a2sec2θ=|asecθ|=asecθ. |=асекθ. (Поскольку −π2<θ<π2−π2<θ<π2 и secθ>0secθ>0 на этом интервале, |asecθ|=asecθ.)|asecθ|=asecθ.) - Упростите выражение.
- Вычислите интеграл, используя приемы из раздела о тригонометрических интегралах.
- Используйте опорный треугольник на рис. 3.7, чтобы переписать результат в x.x. Вам также может понадобиться использовать некоторые тригонометрические тождества и соотношение θ=tan−1(xa).θ=tan−1(xa). ( Примечание : Эталонный треугольник основан на предположении, что x>0;x>0; однако тригонометрические отношения, полученные из эталонного треугольника, совпадают с отношениями, для которых x≤0.)x≤0.)
Рисунок 3,7 Можно построить эталонный треугольник, чтобы выразить тригонометрические функции, оцениваемые при θθ, через x.x.
Пример 3,24
Интегрирование выражения, содержащего a2+x2a2+x2
Вычислите ∫dx1+x2∫dx1+x2 и проверьте решение дифференцированием.
Решение
Начните с замены x=tanθx=tanθ и dx=sec2θdθ.dx=sec2θdθ. Поскольку tanθ=x,tanθ=x, нарисуйте опорный треугольник на следующем рисунке.
Рисунок 3,8 Контрольный треугольник для примера 3.24.
Таким образом,
∫dx1+x2=∫sec2θsecθdθЗаменитеex=tanθanddx=sec2θdθ. Эта замена дает1+x2=secθ. члены x.=ln|1+x2+x|+C.∫dx1+x2=∫sec2θsecθdθЗаменитеex=tanθanddx=sec2θdθ. Эта замена дает1+x2=secθ.Упростите.=∫secθdθВычислите интеграл.=ln|secθ+tanθ| +CИспользуйте опорный треугольник, чтобы выразить результат через x.=ln|1+x2+x|+C.
Чтобы проверить решение, продифференцируем:
ddx(ln|1+x2+x|)=11+x2+x·(x1+x2+1)=11+x2+x·x+1+x21+x2 =11+x2.ddx(ln|1+x2+x|)=11+x2+x·(x1+x2+1)=11+x2+x·x+1+x21+x2=11+x2.
Поскольку 1+x2+x>01+x2+x>0 для всех значений x,x, мы могли бы переписать ln|1+x2+x|+C=ln(1+x2+x)+C,ln |1+x2+x|+C=ln(1+x2+x)+C, если необходимо.
Пример 3,25
Вычисление ∫dx1+x2∫dx1+x2 с использованием другой замены
Используйте замену x=sinhθx=sinhθ для вычисления ∫dx1+x2.∫dx1+x2.
Решение
Поскольку sinhθsinhθ имеет диапазон всех действительных чисел и 1+sinh3θ=cosh3θ,1+sinh3θ=cosh3θ, мы можем также использовать замену x=sinhθx=sinhθ для вычисления этого интеграла.
В этом случае dx=chθdθ.dx=coshθdθ. Следовательно,
∫dx1+x2 = ∫coshθ1+sinh3θdθsubstitutex = sinhlanddx = coshθdθ.substitute1+sinh3θ = cosh3θ. = ∫coshθcosh3θdθ = | coshθ | = ∫coshθ | coshθcosh3θdθ = | coshθ | = ∫coshl | .=∫1dθВычислить интеграл.=θ+CSincex=sinhθ, мы знаем θ=sinh−1x.=sinh−1x+C.∫dx1+x2=∫coshθ1+sinh3θdθПодставитьex=sinhθanddx=chθdθ.Подставить1+sinh3θ=cosh3θ.= ∫coshθcosh3θdθcosh3θ=|coshθ|=∫coshθ|coshθ|dθ|coshθ|=coshθsincecoshθ>0для всехθ.=∫coshθcoshθdθУпростить.=∫1dθВычислить интеграл.=θ+CSincex=sinhθ, мы знаем θ1x=sinh 1x+С.
Анализ
Этот ответ сильно отличается от ответа, полученного с помощью замены x=tanθ.x=tanθ. Чтобы убедиться, что решения совпадают, установите y=sinh-1x.y=sinh-1x. Таким образом, sinhy=x.sinhy=x. Из этого уравнения получаем:
ey-e-y2=x.ey-e-y2=x.
После умножения обеих частей на 2ey2ey и перезаписи это уравнение принимает вид:
e2y-2xey-1=0.e2y-2xey-1=0.
Используйте квадратное уравнение, чтобы найти ey:ey:
ey=2x±4×2+42.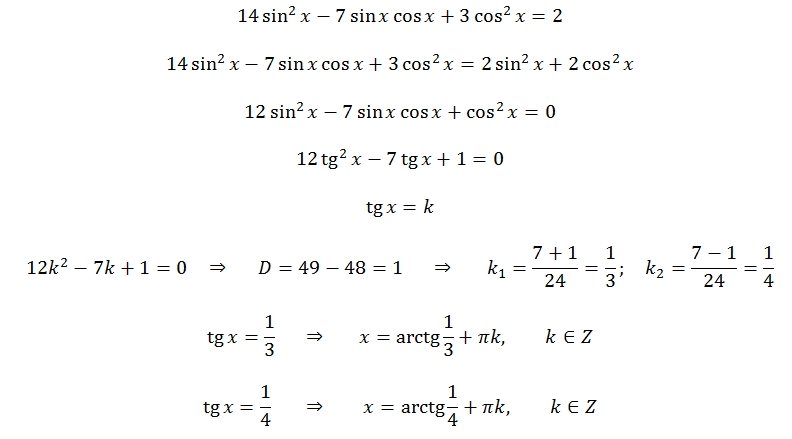
ey=2x±4×2+42.
Упрощая, имеем:
ey=x±x2+1.ey=x±x2+1.
Поскольку x−x2+1<0,x−x2+1<0, должно быть так, что ey=x+x2+1.ey=x+x2+1. Таким образом,
y=ln(x+x2+1).y=ln(x+x2+1).
Наконец, мы получаем
sinh−1x=ln(x+x2+1).sinh−1x=ln(x+x2+1).
После того, как мы сделали последнее наблюдение, что, поскольку x+x2+1>0,x+x2+1>0,
ln(x+x2+1)=ln|1+x2+x|,ln(x +x2+1)=ln|1+x2+x|,
мы видим, что два разных метода дают эквивалентные решения.
Пример 3,26
Определение длины дуги
Найдите длину кривой y=x2y=x2 на интервале [0,12].[0,12].
Решение
Поскольку dydx=2x,dydx=2x, длина дуги определяется как 4x2dx.
Чтобы вычислить этот интеграл, используйте замену x=12tanθx=12tanθ и dx=12sec2θdθ.dx=12sec2θdθ. Нам также необходимо изменить пределы интегрирования. Если x=0,x=0, то θ=0θ=0, а если x=12,x=12, то θ=π4.θ=π4. Таким образом,
∫01/21+4x2dx=∫0π/41+tan2θ12sec2θdθПосле замены 1+4×2=tanθ.
Подставьте1+tan2θ=sec2θи упростите.=12∫0π/4sec3θdθМы получили этот интеграл в предыдущем разделе.=12(12secθnθ|+12ln secθ+tanθ|)|0π/4Вычислить и упростить.=14(2+ln(2+1)).∫01/21+4x2dx=∫0π/41+tan2θ12sec2θdθПосле подстановки,1+4×2=tanθ.Подставить1+tan2θ= sec2θи упростить.=12∫0π/4sec3θdθМы получили этот интеграл в предыдущем разделе.=12(12secθtanθ+12ln|secθ+tanθ|)|0π/4Вычислить и упростить.=14(2+ln(2+1)).
Контрольно-пропускной пункт 3.15
Перепишите ∫x3x2+4dx∫x3x2+4dx, используя замену, включающую tanθ.tanθ.
Интегрирование выражений, включающих x2-a2x2-a2
Областью определения выражения x2−a2x2−a2 является (−∞,−a]∪[a,+∞).(−∞,−a]∪[a,+∞). Таким образом, либо x≤−ax≤−a, либо x≥a.x≥a. Следовательно, xa≤−1xa≤−1 или xa≥1.xa≥1. Поскольку эти интервалы соответствуют диапазону secθsecθ на множестве [0,π2)∪(π2,π],[0,π2)∪(π2,π], имеет смысл использовать замену secθ=xasecθ=xa или, эквивалентно, x=asecθ,x=asecθ, где 0≤θ<π20≤θ<π2 или π2<θ≤π.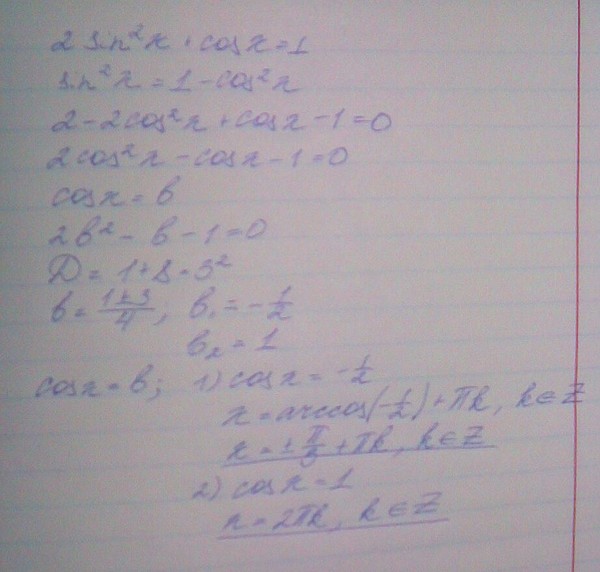
π2<θ≤π. Соответствующая замена для dxdx: dx=asecθtanθdθ.dx=asecθtanθdθ. Процедура для Использование этой замены описано в следующей стратегии решения проблем.0003
Стратегия решения проблем
Стратегия решения задач: интегралы с участием x2-a2x2-a2
- Проверьте, нельзя ли вычислить интеграл другим методом. Если это так, мы, возможно, пожелаем рассмотреть возможность применения альтернативного метода.
- Замените x=asecθx=asecθ и dx=asecθtanθdθ.dx=asecθtanθdθ. Эта замена дает
|.
Для x≥a,x≥a,|atanθ|=atanθ|atanθ|=atanθ и для x≤−a,x≤−a,|atanθ|=−atanθ.|atanθ|=−atanθ. - Упростите выражение.
- Вычислите интеграл, используя приемы из раздела о тригонометрических интегралах.
- Используйте опорные треугольники на рис. 3.9, чтобы переписать результат в x.x. Вам также может понадобиться использовать некоторые тригонометрические тождества и соотношение θ=sec−1(xa).θ=sec−1(xa). ( Примечание : нам нужны оба эталонных треугольника, поскольку значения некоторых тригонометрических отношений различаются в зависимости от того, x≥ax≥a или x≤−a.)x≤−a.) 92). Справа от треугольника находится уравнение sec(theta) = x/a, x
Рисунок 3,9 Используйте соответствующий эталонный треугольник, чтобы выразить тригонометрические функции, вычисленные при θθ, через x.x.
Пример 3,27
Нахождение площади области
Найдите площадь области между графиком f(x)=x2−9f(x)=x2−9 и осью x на интервале [3,5] .[3,5].
Решение
Сначала нарисуйте примерный график области, описанной в задаче, как показано на следующем рисунке.
Рисунок 3.10 Вычисление площади заштрихованной области требует вычисления интеграла с тригонометрической заменой.
Мы видим, что площадь равна A=∫35×2−9dx.A=∫35×2−9dx. Чтобы вычислить этот определенный интеграл, замените x=3secθx=3secθ и dx=3secθtanθdθ.
dx=3secθtanθdθ. Мы также должны изменить пределы интегрирования. Если x=3,x=3, то 3=3secθ3=3secθ и, следовательно, θ=0,θ=0. Если x=5,x=5, то θ=сек-1(53).θ=сек-1(53). После этих замен и упрощения имеемПлощадь=∫35×2−9dx=∫0сек−1(5/3)9tan2θсекθdθUsetan2θ=1−сек2θ.=∫0сек−1(5/3)9(сек2θ−1)секθdθРасшир.=∫0сек−1(5/ 3)9(sec3θ−secθ)dθВычислить интеграл.=(92ln|secθ+tanθ|+92secθtanθ)−9ln|secθ+tanθ||0sec−1(5/3)Упростить.=92secθtanθ−92ln|secθ+tanθ| |0сек−1(5/3)Оценить. Usesec(sec−153)=53andtan(sec−153)=43.=92·53·43−92ln|53+43|−(92·1·0−92ln|1+0|)=10−92ln3.Площадь =∫35×2−9dx=∫0sec−1(5/3)9tan2θsecθdθUsetan2θ=1−sec2θ.=∫0sec−1(5/3)9(sec2θ−1)secθdθExpand.=∫0sec−1(5/3)9 (sec3θ−secθ)dθВычислить интеграл.=(92ln|secθ+tanθ|+92secθtanθ)−9ln|secθ+tanθ||0sec−1(5/3)Упростить.=92secθtanθ−92ln|secθ+tanθ||0sec−1(5/3)Оценить. Usesec(sec-153)=53andtan(sec-153)=43.=92·53·43-92ln|53+43|-(92·1·0-92ln|1+0|)=10-92ln3.
Контрольно-пропускной пункт 3.16
Оценить ∫dxx2−4.∫dxx2−4. Предположим, что x>2.
x>2.Раздел 3.3 Упражнения
Упростите следующие выражения, написав каждое с помощью одной тригонометрической функции.
126.
4−4sin2θ4−4sin2θ
127.
9сек2θ−99сек2θ−9
128.
a2+a2tan2θa2+a2tan2θ
129.
a2+a2sinh3θa2+a2sinh3θ
130.
16кош3θ-1616кош3θ-16
Используйте метод завершения квадрата, чтобы выразить каждый трехчлен как квадрат двучлена или квадрат двучлена плюс константа.
131.
4×2−4x+14×2−4x+1
132.
2×2−8x+32×2−8x+3
133.
−x2−2x+4−x2−2x+4
Интегрировать методом тригонометрической подстановки. Выразите окончательный ответ через переменную.
134.
∫dx4−x2∫dx4−x2
135.
∫dxx2−a2∫dxx2−a2
136.
∫4−x2dx∫4−x2dx
137.
∫dx1+9×2∫dx1+9×2
138.
∫x2dx1−x2∫x2dx1−x2
139.
∫dxx21−x2∫dxx21−x2
140.
∫dx(1+x2)2∫dx(1+x2)2
141.
∫x2+9dx∫x2+9dx
142.
∫x2−25xdx∫x2−25xdx
143.
∫θ3dθ9−θ2∫θ3dθ9−θ2
144.
∫dxx6−x2∫dxx6−x2
145.
∫x6−x8dx∫x6−x8dx
146.
∫dx(1+x2)3/2∫dx(1+x2)3/2
147.
∫dx(x2−9)3/2∫dx(x2−9)3/2
148.
∫1+x2dxx∫1+x2dxx
149.
∫x2dxx2−1∫x2dxx2−1
150.
∫x2dxx2+4∫x2dxx2+4
151.
∫dxx2x2+1∫dxx2x2+1
152.
∫x2dx1+x2∫x2dx1+x2
153.
∫−11(1−x2)3/2dx∫−11(1−x2)3/2dx
В следующих упражнениях используйте замену x=sinhθ,coshθ,x=sinhθ,coshθ или tanhθ.tanhθ. Выразите окончательные ответы через переменную x.
154.
∫dxx2−1∫dxx2−1
155.
∫dxx1−x2∫dxx1−x2
156.
∫x2−1dx∫x2−1dx
157.
∫x2−1x2dx∫x2−1x2dx
158.
∫dx1−x2∫dx1−x2
159.
∫1+x2x2dx∫1+x2x2dx
Используйте метод заполнения квадрата, чтобы вычислить следующие интегралы.
160.
∫1×2−6xdx∫1×2−6xdx
161.
∫1×2+2x+1dx∫1×2+2x+1dx
162.
∫1−x2+2x+8dx∫1−x2+2x+8dx
163.
∫1−x2+10xdx∫1−x2+10xdx
164.
∫1×2+4x−12dx∫1×2+4x−12dx
165.
Вычислите интеграл без исчисления: ∫−339−x2dx.∫−339−x2dx.
166.
Найдите площадь, заключенную в эллипс x24+y29=1.x24+y29=1.
167.
Вычислите интеграл ∫dx1−x2∫dx1−x2, используя две разные подстановки. Во-первых, пусть x=cosθx=cosθ и оцените с помощью тригонометрической замены.
Во-вторых, пусть x=sinθx=sinθ и используется тригонометрическая замена. Совпадают ли ответы?168.
Вычислить интеграл ∫dxxx2−1∫dxxx2−1, используя замену x=secθ.x=secθ. Затем оцените тот же интеграл, используя замену x=cscθ.x=cscθ. Покажите, что результаты эквивалентны.
169.
Вычислите интеграл ∫xx2+1dx∫xx2+1dx, используя форму ∫1udu.∫1udu. Затем оцените тот же интеграл, используя x=tanθ.x=tanθ. Результаты такие же?
170.
Укажите метод интегрирования, который вы использовали бы для вычисления интеграла ∫xx2+1dx.∫xx2+1dx. Почему вы выбрали этот метод?
171.
Укажите метод интегрирования, который вы использовали бы для вычисления интеграла ∫x2x2−1dx.∫x2x2−1dx. Почему вы выбрали этот метод?
172.
Оценка ∫−11xdxx2+1∫−11xdxx2+1
173.
Найти длину дуги кривой на указанном интервале: y=lnx,[1,5].y=lnx,[1,5]. Округлите ответ до трех знаков после запятой.
174.
Найдите площадь поверхности твердого тела, образованного вращением области, ограниченной графиками y=x2, y=0, x=0, и x=2y=x2, y=0, x=0, и x=2 вокруг x — ось. (Округлите ответ до трех знаков после запятой).
175.
Область, ограниченная графиком f(x)=11+x2f(x)=11+x2 и осью x между x=0x=0 и x=1x=1, вращается вокруг x- ось . Найдите объем образовавшегося тела.
Решите задачу начального значения для y как функцию x .
176.
(x2+36)dydx=1,y(6)=0(x2+36)dydx=1,y(6)=0
177.
(64−x2)dydx=1,y(0)=3(64−x2)dydx=1,y(0)=3
178.
( Примечание : нам нужны оба эталонных треугольника, поскольку значения некоторых тригонометрических отношений различаются в зависимости от того, x≥ax≥a или x≤−a.)x≤−a.) 92). Справа от треугольника находится уравнение sec(theta) = x/a, x
dx=3secθtanθdθ. Мы также должны изменить пределы интегрирования. Если x=3,x=3, то 3=3secθ3=3secθ и, следовательно, θ=0,θ=0. Если x=5,x=5, то θ=сек-1(53).θ=сек-1(53). После этих замен и упрощения имеем
x>2.
Во-вторых, пусть x=sinθx=sinθ и используется тригонометрическая замена. Совпадают ли ответы?
