Значение тригонометрических функций углов 30°, 45° и 60°
Найдем значение Sin, Cos, Tg, Ctg трёх примечательных углов 30°, 45° и 60°.
30° и 60°
Начнём с синуса 30°. Для этого построим прямоугольный треугольник с острым углом в 30°. И синус 30° – это будет отношение противолежащего короткого катета к гипотенузе. И для удобства установим длину гипотенузы единица.
И тогда получается что отношение длины катета к гипотенузе равно просто длине катета, и синус 30° будет равен просто а. Кроме того, сумма углов любого треугольника равна 180°, и 2й острый угол равен 180° – 90° – 30° = 60°. И для 2го острого угла отношение короткого катета к гипотенузе – это будет отношение прилежащего катета к гипотенузе то есть косинус. И значит, Cos(60°) тоже будет равен а. А теперь найдем, чему же равно это а. Для этого построим снизу ещё один такой же треугольник, равный исходному — только отраженный зеркально.
И вот что получается: во-первых приглядимся к углу, сложившемуся из двух прямых углов – он развернутый.
Получается, что верхняя и нижняя точки треугольника и вершина прямых углов лежат на одном отрезке. А левый угол складывается из двух углов по 30°, то есть равен он 60°. Следовательно, можно стереть горизонтальный отрезок, и получается треугольник, у которого каждый угол равен 60°.
Равносторонний треугольник, у которого третья сторона равна первым двум сторонам и тоже равна единице. Получилось, что:
а + a = 1
А это означает, что
a = 1/2
И таким образом
Sin(30°) = Cos(60°) = 1/2
Теперь вернемся к исходному треугольнику. Короткий катет теперь известен – это 1/2. А чему же равен длинный катет? Обозначим его буквой b.
Для угла в 30° этот катет b – прилежащий, гипотенуза равна 1. И значит длина этого катета равна отношению длины прилежащего катета к гипотенузе, то есть Cos(30°). А для 60° этот длинный катет – противолежащий. И следовательно длина этого катета равна отношению противолежащего катета к гипотенузе, то есть Sin(60°). И значит
Cos(30°) = Sin(60°) = b
Ну а теперь найдем катет b с помощью теоремы Пифагора.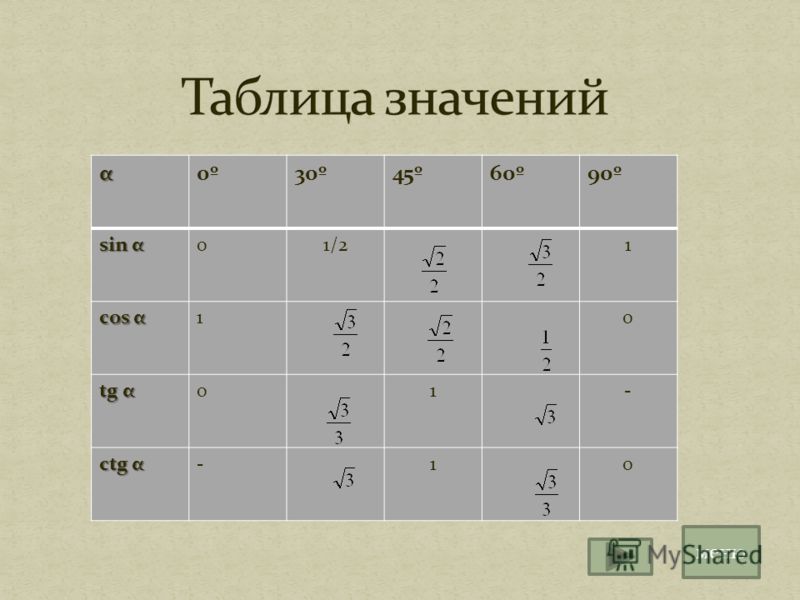
Как известно, сумма квадратов катетов равна квадрату гипотенузы, то есть
(½)² + b² = 1²
¼ + b² = 1
b² = ¾
b = (√3)/2
Таким образом
Cos(30°) = Sin(60°) = (√3)/2
Теперь уже известны оба катета, и можно найти отношение двух катетов. Сначала найдём отношение короткого катета к длинному катету. Для угла в 30° это будет отношение противолежащего катета к прилежащему катету, то есть Tg(30°). А для угла в 60° это будет наоборот – отношение прилежащего катета к противолежащему катету то есть Ctg(60°).
Tg(30°) = Ctg(60°) =
= (1/2) : ((√3)/2) =
= 1 : (√3)
А теперь наоборот длинный катет разделим на короткий катет. Для 30° это будет прилежащий катет разделить на противолежащий, то есть Ctg(30°). А для 60° это будет противолежащий катет разделить на прилежащий, то есть Tg(60°).
Ctg(30°) = Tg(60°) =
= ((√3)/2) : (1/2) =
= (√3) : 1 = √3
45°
Построим прямоугольный треугольник с острым углом 45 градусов.
Гипотенузу опять сделаем единицу и противолежащий катет обозначим буквой e.
Отношение противолежащего катета к гипотенузе и будет равно Sin(45°). Но гипотенуза – единица – поэтому просто длина этого катета равна синусу Sin(45°). Теперь обратим внимание на 2й острый угол. На два острых угла в прямоугольном треугольнике приходится 90°. Значит 2й острый угол равен 90° – 45° = 45°. Выходит что этот прямоугольный треугольник – равнобедренный, и второй катет тоже равен е. И получается что для угла 45° отношение прилежащего катета к гипотенузе такое же, как и противолежащего катета к гипотенузе
Cos(45°) = Sin(45°) = е
Кроме того, даже не зная, чему равно е, можно сказать, какой будет Tg(45°) и Ctg(45°), потому что отношение противолежащего катета к прилежащему или, наоборот, прилежащего катета к противолежащему – будет равно единице.
Tg(45°) = Ctg(45°) = e / e = 1
Ну а теперь можно уже наконец найти, чему равно е. И для этого воспользуемся теоремой Пифагора.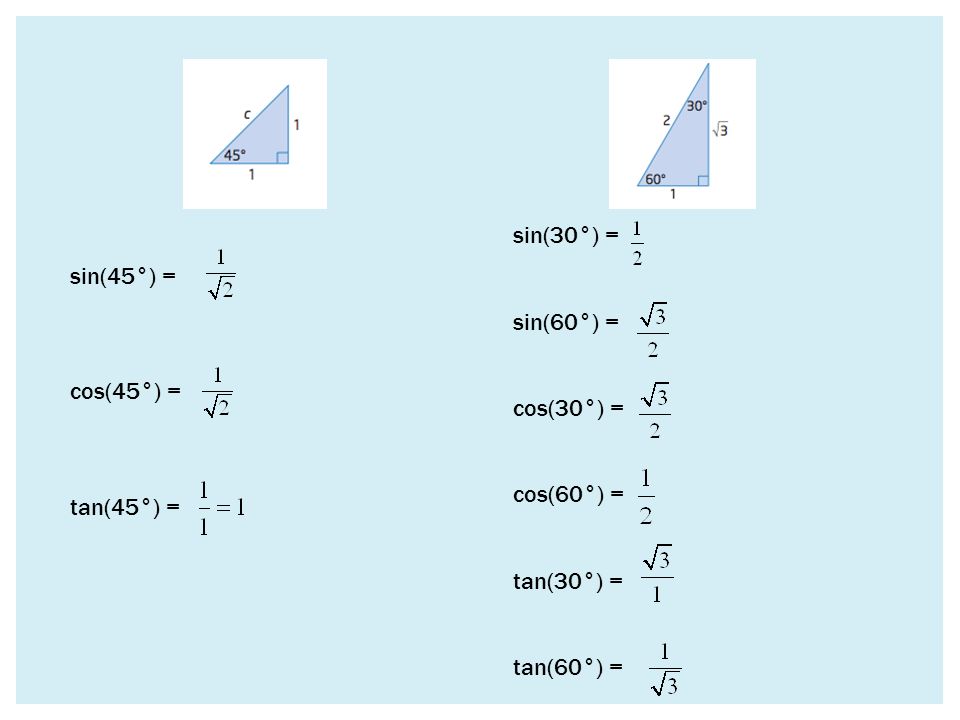
е² + e² = 1²
2 × е² = 1
е² = ½
e = 1/(√2) = (√2)/2
Получается, что:
Cos(45°) = Sin(45°) = (√2)/2
И таким образом найдены значения основных тригонометрических функций углов 30° 45° и 60°.
← Предыдущий урок
Оглавление
Следующий урок →
Таблица синусов
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется калькулятора.
Таблица синусов углов от 1° до 180°
| sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.  292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 | sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.  848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 | sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.  987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 | sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.  669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0. 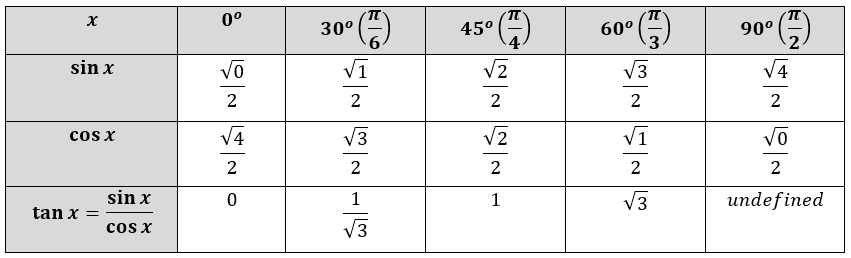 052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(210°) = -0.5 sin(211°) = -0.  515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 | sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.  927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 | sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.  961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 | sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.  601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Статистика
Онлайн всего: 332
Гостей: 332
Жителей: 0
ТАБЛИЦА ТРИГОНОМЕТРИЧЕСКИХ СООТНОШЕНИЙ И ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ КОНКРЕТНЫХ УГЛОВ угол \ тета .
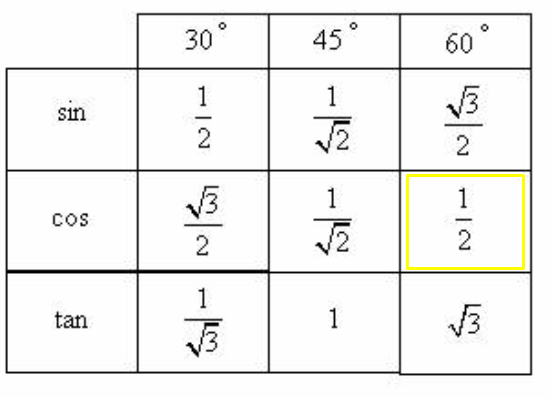Теперь посмотрим, как этот угол \тета связан с тригонометрическими соотношениями и как он образует таблицу тригонометрических соотношений? Угол \theta в тригонометрических соотношениях, связанный с углом \theta прямоугольного треугольника. Имейте это в виду, это поможет вам глубже понять концепцию. Для прямоугольного треугольника угол \ тета находится в пределах от 0 до 9.0005 или до 90 или . [Почему \тета не может превышать 90 o ? Комментарий ниже]
ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ ПОД КОНКРЕТНЫМИ УГЛАМИ
Все тригонометрические отношения имеют некоторое значение для каждого угла. Эту концепцию можно лучше понять на примере.
Пример: Sin 30
oЧто на самом деле означает Sin 30 o . Он имеет 2 компонента.
– 1 st – это Sin , то есть тригонометрическое отношение.
– 2 nd равно 30 o , что является тригонометрическим углом \тета прямоугольного треугольника.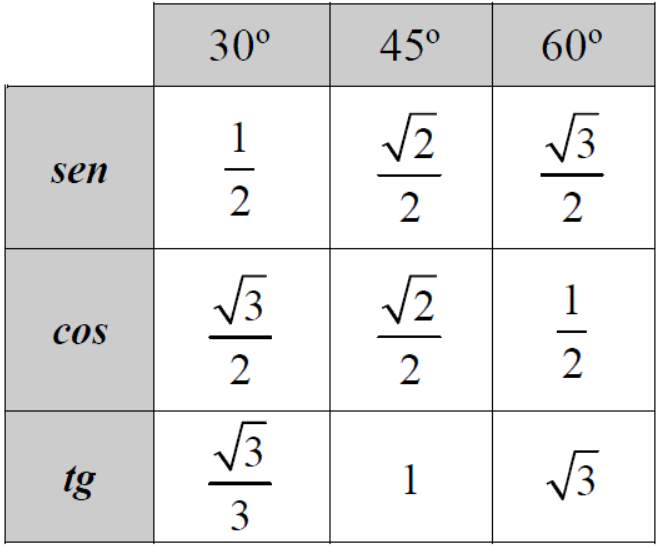
Для большей ясности давайте разберемся с этим в отношении прямоугольного треугольника ABC.
Для этого прямоугольного треугольника ABC мы знаем, что Sin равен AB/AC, то есть отношение перпендикуляра к гипотенузе.
Среднее значение для прямоугольного треугольника ABC с тригонометрическим углом \ тета как 30 o отношение перпендикуляра (AB) и гипотенузы (AC) будет равно Sin 30 или .
Рассчитайте отношение перпендикуляра (AB) и гипотенузы (AC) любого случайного прямоугольного треугольника с углом \theta как 30 o . Он будет равен 0,5, что является фиксированным. Вы можете попробовать это с любым размером треугольника, просто тригонометрический угол должен быть 30 o .
Из приведенной выше анимации мы получили sin 30 o равно 0,5. Аналогичным образом мы можем вычислить значение для всех углов и для всех тригонометрических отношений.
Вы можете использовать калькулятор для перекрестной проверки.
ТРИГОНОМЕТРИЧЕСКАЯ ТАБЛИЦА
До сих пор мы понимали, что каждое тригонометрическое отношение имеет фиксированное значение относительно угла \theta .
Запомнить все значения будет невозможно. Поэтому мы ограничимся только некоторыми конкретными углами, которые показаны ниже в ТРИГОНОМЕТРИЧЕСКОЙ ТАБЛИЦЕ.
Тригонометрическая таблица показывает углы слева направо и тригонометрические отношения сверху вниз.
Не пытайтесь грабить Тригонометрическую таблицу. Попытайтесь понять это. В следующем посте рассматривается техника запоминания тригонометрической таблицы.
Если вы хотите узнать производные каждого угла относительно каждого тригонометрического отношения, нажмите здесь, чтобы получить БЕСПЛАТНУЮ видеолекцию о том же.
Experiment @ Home
Нарисуйте случайные треугольники с тригонометрическим углом \тета как 30 o , 45 o и 60 o . И измерьте тригонометрические отношения с помощью тригонометрических сторон и проверьте правильность таблицы.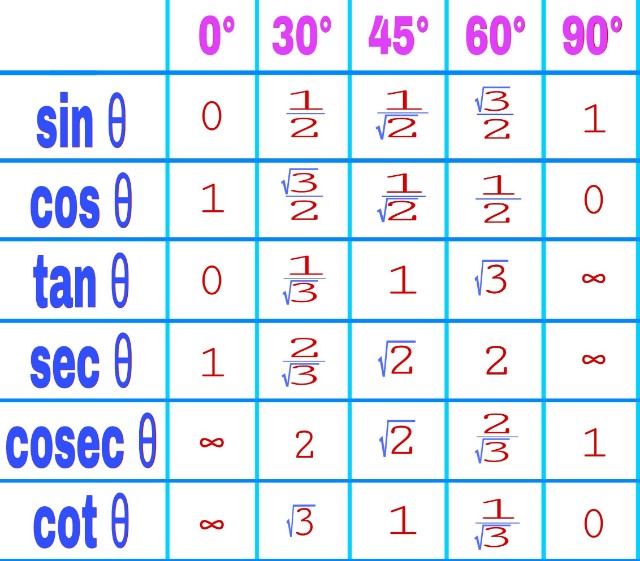
НЕ забудьте прокомментировать результаты.
Вопросы
В) Найдите стороны AB и BC на рисунке?
Во-первых, определите тригонометрические стороны. Нажмите здесь, чтобы узнать, как идентифицировать тригонометрические стороны.
AC= P = Перпендикуляр = 5
AB = B = Основание = ?
до н.э. = H = Гипотенуза = ?
Нам нужно найти основание B и гипотенузу H.
Сначала найдем гипотенузу. Применимое соотношение между перпендикуляром и гипотенузой:
См. тригонометрическую таблицу для значения Sin 30 o .
Мы получили гипотенузу H как 10. т.е. сторона BC равна 10. У нас есть 2 стороны треугольника ABC. Давайте вычислим третью недостающую сторону B.
Мы получили все 3 стороны треугольника ABC.
Альтернативный подход к вопросу:
Как только мы получили гипотенузу H, мы также можем использовать Пифагор, чтобы найти 3-ю недостающую сторону Базы.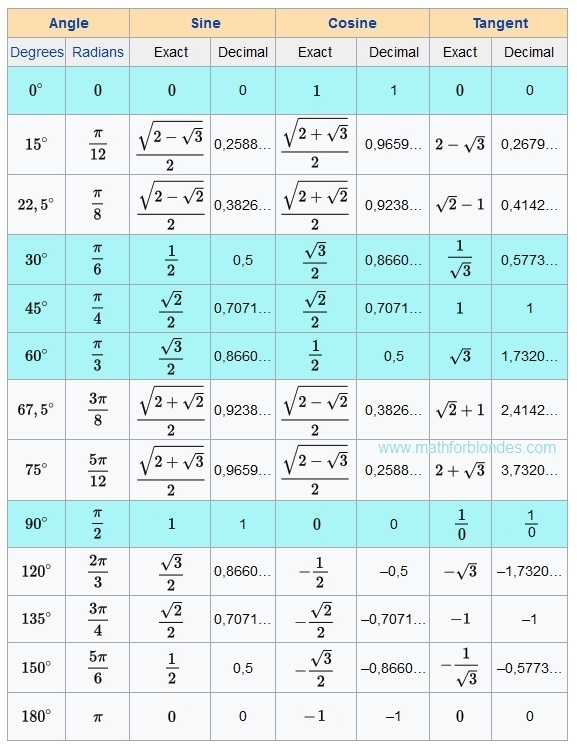
[Комментарий ниже с полным ответом]
Вопрос к вам:
В) Найдите длины всех сторон и всех углов прямоугольного треугольника, приведенного ниже? Площадь треугольника равна 50 \sqrt { 3 }.
[Вставьте свой ответ в раздел комментариев]
[Спросите подсказку в разделе комментариев]
Посмотрите полное видео этой лекции с помощью
Animation Tool.(Визуализируйте концепцию совершенно по-другому)
Это бесплатноУчить больше
Вычислить 2 sin 30° – 3 cos 45° + tan 60°
Тригонометрия – раздел математики, изучающий треугольники и связанные с ними углы. если мы разобьем слово на 2 части, а именно на тригон и геометрию, мы легко поймем, что эта ветвь математики имеет дело с геометрией треугольников. Используя тригонометрию, можно легко понять свойства треугольников и их приложения. Используя тригонометрию, можно найти углы и недостающие стороны любого треугольника с использованием тригонометрических соотношений.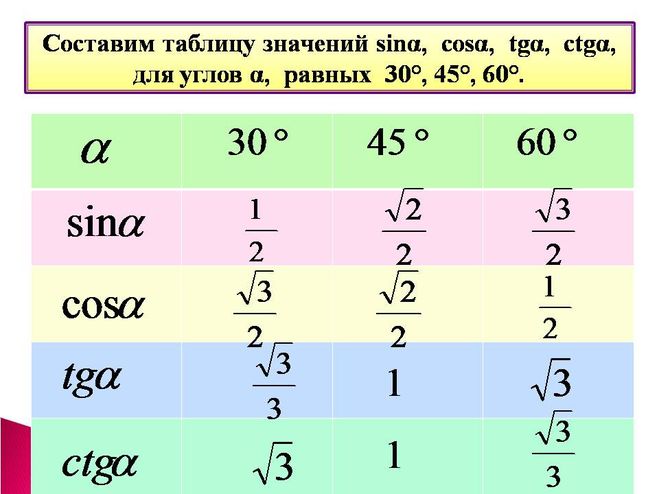
Тригонометрические соотношения
В тригонометрии присутствуют шесть функций или тригонометрических соотношений угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Здесь важно отметить, что тригонометрические формулы работают только с прямоугольным треугольником. Давайте посмотрим на изображение ниже.
В этом прямоугольном треугольнике сторона AC называется гипотенузой. сторона ВС называется основанием треугольника. Сторона АВ называется высотой треугольника. Из приведенного выше треугольника мы можем перечислить формулы, как указано выше,
- sin∅ = AB/AC
- cos∅ = BC/AC
- tan∅ = AB/BC
- cot∅ = BC/AB
- cosec∅ = AC/AB
- BC∅
- sin(90° – x) = cos x
- cos(90° – x) = sin x
- tan(90° – x) = cot x
- cot(90° – x) = tan x
Таблица тригонометрических углов
Ниже приведена таблица, в которой показаны основные значения тригонометрических функций относительно обычных углов относительно 0°, 30°, 45°, 60°, 90°.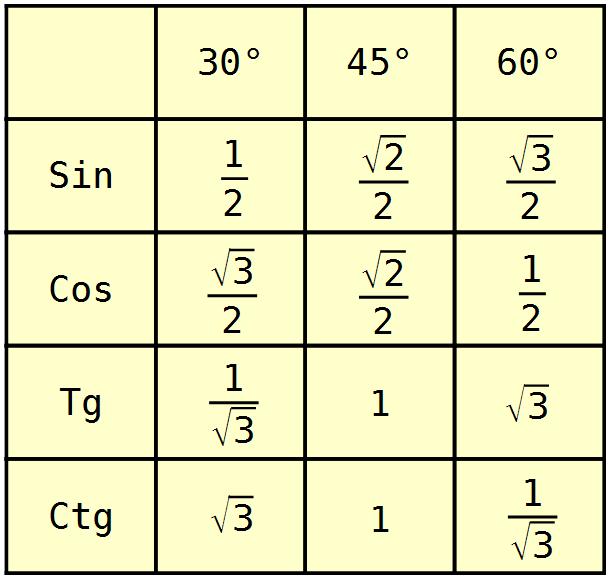
приведенную ниже таблицу необходимо выучить наизусть, чтобы решать задачи, связанные с тригонометрией.
| Ratio\Angle | 0° | 30° | 45° | 60° | 90° |
| sin(θ) | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos(θ) | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan(θ) | 0 | 1/√3 | 1 | √3 | ∞ |
| cosec(θ) | ∞ | 2 | √2 | 2/√ 3 | 1 |
| sec(θ) | 1 | 2/√3 | √2 | 2 | ∞ |
| cot(θ) | ∞ | √3 | 1 | 1/√3 | 0 |
Вычислить 2 sin 30° – 3 cos 45° + tan 60°
Решение :
Из таблицы выше мы знаем, что sin 30° = 1/2, cos45° = 1/2, tan60° = √3
Подставив приведенные выше значения,
2 × 1/2 – 3/√2 + √3
=1 – 2,12 + √3 = 0,612
Аналогичные задачи
2 + cot45°
Решение:
Из таблицы выше мы знаем, что tan45° = cot45° = 1
Заменить вышеуказанные значения,
1 + 1 = 2
Вопрос 2: Оценка √3SEC30 ° — √2COSEC45 °
Решение:
.
